Изучение табличных случаев сложения чисел в пределах 20 — Мегаобучалка

Случаи сложения и вычитания в пределах 20 включают в себя случаи сложения однозначных чисел с переходом через десяток и соответствующие им случаи вычитания. Например: 8+4, 9+5, 12-4, 14-5 и др. Эти случаи называются табличными, в соответствии с требованиями программы они должны быть усвоены детьми наизусть. Названные случаи сложения и вычитания по ныне действующей про­грамме изучаются не вместе. Сначала изучаются все случаи сложения, затем — вычитания.

Сложение начинает изучаться с раскрытия вычислительного приема. Суть этого приема состоит в том, что первое слагаемое дополняется до 10 (в результате чего второе слагаемое представляется в виде суммы удобных слагаемых), затем прибавляется оставшаяся часть второго слагаемого. Например:

8+4=12

/\

8+2+2

Перед изучением этого вычислительного приема, как и при изучении любого другого приема, необходимо провести подготовительную рабо­ту. С детьми следует повторить:

— состав чисел в пределах 10, обратив внимание на состав и числа 10 и на умение дополнить любое однозначное число до 10;

— разрядный состав чисел в пределах 20;

— случаи сложения, основанные на знании разрядного состава чисел в пределах 20.

При раскрытии вычислительного приема целесообразно использовать наборное полотно, содержащее два ряда карманов по 10 в каждом ряду.

При этом с детьми можно провести такой разговор. Учитель. Давайте решим задачу.

Задача. В одной вазе 8 красных яблок, а в другой — 5 зеленых яблок. Сколько всего яблок в двух вазах?

Что нужно сделать, чтобы ответить на вопрос задачи?

Дети. К 8 прибавить 5.

Учитель. Запишем это: 8+5. Значит нам надо решить этот пример. А умеем мы решать такие примеры?

Дети. Нет.

Учитель. Сегодня мы и будем учиться решать такие примеры. Ре­шить этот пример нам поможет вот эта таблица (вывешивает наборное полотно с двумя рядами карманов) и кружочки, их у меня 8 красных и зеленых (показывает детям). Посмотрите на эту таблицу.

Здесь есть кармашки. Давайте посмотрим, сколько их. Считаем все. (Дети хором считают: 10). ‘

Решаем пример: 8 + 5. Я кладу 8 красных кружочков в кармашки верхнего ряда. Теперь нам надо добавить 5 зеленых кружков. Посмотрите, сколько кружков я могу положить еще в верхний ряд?

Дети. 2.

Учитель. Давайте запишем, как мы это делали. К числу 8 мы приба­вили 2, чтобы получить 10 (при этом оформляется запись): 8+5.

Откуда мы взяли 2 зеленых кружочка?

Дети. Из 5 зеленых.

Учитель. Покажем это (ставит стрелочку от 5 к 2). Сколько зеленых кружочков осталось добавить?

Дети. 3.

Учитель. Как вы узнали?

Дети. 5 это 2 и 3.

Учитель. Верно (выкладывает оставшиеся 3 зеленых кружка во вто­рой ряд наборного полотна и заканчивает запись).

Учитель. Молодцы. Давайте повторим, как мы рассуждали (повторяют).

После раскрытия вычислительного приема необходимо провести ра­боту по его усвоению. С детьми решаются ряд примеров на сложение однозначных чисел с переходом через десяток, где дети учатся вести со­ответствующие рассуждения.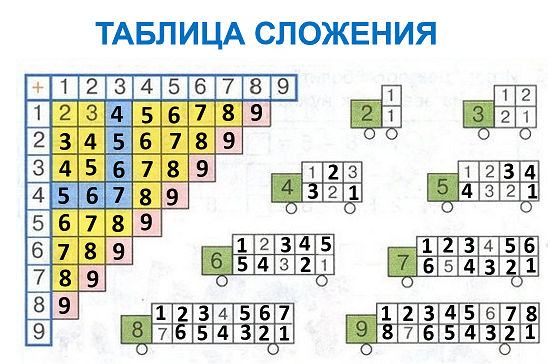

Затем переходим к рассмотрению всех случаев сложения этого вида. Для того, чтобы детям легче было их запомнить, их рекомендуют изу­чать небольшими группами (3-4 случая на одном уроке). При этом предполагается, что на каждом из этих уроков будет продолжаться работа по усвоению детьми вычислительного приема (умение вести рассуждения при вычислении) и даваться установка на запоминание изученных случаев. Здесь начинается работа по рассмотрению и усвоению детьми состава чисел от 11 до 20 из слагаемых. По завершении рассмотрения случаев сложения все они сводятся в таблицу, и продолжается работа по ее заучиванию. При этом учителю необходимо продумывать систему упражнений и виды работы детей на уроке, которые отличались бы разнообразием и способствовали более эффективному усвоению детьми таблицы сложения.

Изучение случаев вычитания, соответствующих табличным

Случаям сложения

Вычитание чисел в пределах 20 начинается с раскрытия вычислительных приемов. Целесообразно показать детям три приема.

1. Прием, когда число вычитается по частям (с использованием наборного полотна с двумя рядами карманов):

12-4

/\

12-2-2

2. Прием, основанный на знании соответствующего случая сложения (т.е. состава числа). Здесь необходимо вспомнить зависимость между компонентами и результатом действия сложения:

12-4

12=4+8

Прием, где все вычисления сводятся к вычислениям в пределах 10

12-4

10-4+2

Названные приемы не обязательно рассматривать все вместе. После усвоения первого из них, следует перейти к изучению случаев вычитания. При их рассмотрении целесообразно придерживаться той последовательности, которая предложена авторами учебников математики для начальных классов. На одном уроке рекомендуется рассмотреть все случаи вычитания из одного числа, начиная с 11. Здесь можно и нужно наряду с применением первого приема показать и другие. В дальнейшем учащимся следует предоставить возможность выбора приема, наиболее легкого для них. При изучении вычитания не следует прекращать работу, направленную на запоминание детьми таблицы сложения. Ее надо продолжить, обучая при этом увязывать случаи сложения с соответствующими случаями вычитания.

Урок по математике. «Таблица сложения и вычитания чисел в пределах 20»

Тема: Таблица сложения и вычитания чисел в пределах 20.

( 2кл. – октябрь 2015г.)

Учитель: Соснина Л.А.

Цель: Обучить пользованию сводной таблицей сложения и

вычитания. Решать задачи изученных видов. Развивать

математическую речь. Воспитывать интерес к строительным профессиям..

Оборудование: Сигнальные блокноты, ватман, части дома, цветные

карточки (разного уровня), TV, мультимедиа,

цифры.

Ход урока:

1. Организационный момент.

Чтобы строить дома,

Чтобы в небо взлететь,

Надо многое знать,

Надо много уметь.

И при этом, ребята,

Заметьте – ка,

Очень важная наука –

Математика!

1. Проверка д/з (по цветным карточкам разного уровня).

Слабые /зел. карточка/ — Умения измерять и чертить отрезки

заданной длины.

Средние /жёлт. карточка/- Знания нахождения разности длин

данных отрезков.

Сильные /розов. карточка/ — Знания нахождения суммы длин

отрезков, и перевода единиц измерения

в дм и см.

Учитель спрашивает по 1 ученику из каждой группы:

средней, слабой и сильной.

3.Устный счёт.

• Ребята, скажите, кто строит дома? / Строители /

• А какие строительные профессии вы знаете? / Каменщик, архитектор, бетонщик, инженер, кровельщик, плотник, маляр, штукатур, монтажник и др. /

• Каждая профессия требует знания математики.

• Сегодня вы тоже будете строителями.

• С чего начинают строить дом? / С фундамента /

1) Решить выражения:

10 + 8 20 — 5

19 – 7 14 + 2

13 + 4 16 – 5

2) — Покажите действие, которым решите задачу.

12 кубиков у Толи,

5 – у маленького брата.

Из них они построят домик.

В нём сколько кубиков, ребята? / 12 + 5 = 17 /

3) Решите задачу.

— Сколько треугольников в этой фигуре? / 4 /

4. Мотивация урока. (Слайд 1,2)

— Сегодня на уроке мы с вами познакомимся с таблицей сложения и вычитания чисел в пределах 20.

5. Чистописание.

а) Прогноз самооценки.

б) Праздник « Покров » / несколько слов /

в) Характеристика числа 14.

г) Запись числа 4 раза (простучать)

1. -Осветим наше строительство солнечным светом! / На ватман помещаем солнце /

5. Актуализация знаний.

• Что будем дальше строить? / Стены /

• Из какого материала строят дома? / Из брёвен, блоков, кирпичей, панелей /

• Наш дом внутри кирпичный. Первые кирпичики уже есть на доске 13 — 7

• Легко ли из 13 – 7? / Нелегко/.

• Чтобы быстро считать нам поможет таблица.

1. Знакомство с таблицей. Новый материал.

а) Объясняет учитель:

• Итак, сейчас мы будем учиться пользоваться таблицей.

• В клетках таблицы заданы суммы чисел, стоящих в соответствующих строках и столбцах 7 + 6 = 13

• Каждому примеру на сложение соответствуют два примера на вычитание: нахождение неизвестных слагаемых.

13 – 6 = 7 и 13 – 7 = 6

б) Объясняет средний ученик. Игра «Учитель — ученик».

– Кто мне подскажет, как из 11 – 7?

в) Объясняет слабый ученик (Учитель помогает.)

— Как из 14 – 5?

2) Первичное закрепление (Слайд 3 )

• Сейчас мы закрепим умения решать выражения, используя таблицу.

• Зачем нам надо уметь пользоваться таблицей? / Чтобы быстро считать. /

• Решите самостоятельно, пользуясь таблицей учебника.

12 – 7 = 14 – 8 =

6. Физкультминутка (подвижная).

— Сейчас мы с вами немного отдохнём!

Все движения изображены на экране TV.

7. Закрепление материала. ( Слайд 4)

1) Решение задачи из учебника. (№2, стр.60)

1. (Разного уровня) задания на карточках. ( Слайды 5-7)

а) Слабым: 15 — 7

(Зелёная карточка) 11 — 6

9 + 4

— Назовите ответы в порядке возрастания. ( Появляется труба в доме)

б) Средним: 20 см = □ дм

(Жёлтая карточка) 1 дм □ см = 17 см

□ дм 3 см = 13 см

Проверка ответов. (На ватмане появляются дверь и ступенька.)

в) Сильным: Решите задачу :

(Розовая карточка) Крокодил Гена выгрузил 12 кирпичей, а

Чебурашка – 5. На сколько кирпичей выгрузил больше Гена, чем Чебурашка?

Проверка решения задачи. (Возле дома появляется дерево)

8. Домашнее задание

Стр. 61 №9, а сильным детям ещё задача №8 стр.59

9. Итог

— У нас получился замечательный дом. Давайте будем жить в нём дружно и сеять добро.

— Всё, как в жизни: дом построили, дерево посадили. И родились у нас хорошие дочки и сыночки.

10. Рефлексия (Слайд 8,9)

— Продолжите фразу:

Я научился ….

Я могу научить друга ….

Я испытывал трудности ….

11. Самооценка в тетради.

— У кого прогноз оправдался?

— Молодцы!

— Всем спасибо за работу !

Типы словесных задач на сложение и вычитание

Словесные задачи часто являются самой большой проблемой для учителей математики. Говорили ли вы что-то вроде «Дети их не понимают». и «Они берут числа и выполняют случайную операцию». Мы пробуем так много разных методов, чтобы попытаться помочь, и они терпят неудачу. Потому что часто мы не концентрируемся на обучении студентов операциям в явном виде. И учить их явно — это то, что нам нужно делать! Стандарты Common Core State излагают различные типы задач на сложение и вычитание, которые должны знать учащиеся. Обучая их явно, мы даем им инструменты, необходимые им для успешного решения проблем. Мы связываем то, как математика, которую они изучают, имеет отношение к их реальной жизни. Мы помогаем им по-настоящему понять математическую операцию и то, как и когда она используется. Сосредоточив внимание на текстовых задачах и их типах, мы сосредоточимся на том, что делает сложение и вычитание тем, чем они являются.

В этом посте подробно рассматриваются все типы задач на сложение и вычитание. Я также даю несколько полезных ссылок внизу, в которых обсуждаются когнитивно-управляемые инструкции или типы задач CGI. Они используют несколько иную лексику, чем CCSS, но имеют тот же набор навыков. Важное замечание: когда я говорю об обучении типов задач на сложение и вычитание в явном виде, я не имею в виду, что они отрабатываются только во время определенного раздела или что мы обучаем определенным ключевым словам для каждого типа задач. Учащиеся должны прочитать задачу и понять контекст. Распознавание типа проблемы может поддержать эту работу, но оно не сосредоточено на ключевых словах. Кроме того, я ежедневно решаю задачи со словами вне нашей основной работы. Я твердо верю в спираль стандартов в текстовых задачах, чтобы учащиеся должны были сосредоточиться на контексте для решения. Для получения дополнительной помощи в решении проблем ознакомьтесь с моей публикацией «Почему ваши ученики борются с задачами в Word и что вы можете с этим поделать».

ЧАСТЬ-ЧАСТЬ-ЦЕЛОЕ

Вероятно, наиболее распространенным типом сложения и вычитания в умах большинства учителей является часть части целого. Мы используем числовые связи и линейчатые модели для моделирования и представления отношений часть/целое. Мы моделируем сложение как объединение двух наборов объектов. Мы вводим вычитание как разделение нашего общего количества объектов на более мелкие части. И это основа для будущей работы с дробями, умножением и делением. Часть-часть-целое — такое важное понятие для понимания математики нашими студентами. Важно, чтобы мы связали эту работу с нашим языком в текстовых задачах. Многие задачи со словами можно рассматривать как сценарии «часть-часть-целое» (даже многие из описанных ниже типов «начало-изменение-конец»).

	ВСЕГО НЕИЗВЕСТНО	ЧАСТЬ НЕИЗВЕСТНО	ОБЕ ЧАСТИ НЕИЗВЕСТНО
	На дереве было 5 синих птиц и 3 кардинала. Сколько птиц всего? 5 + 3 = 8	На дереве 8 птиц. 5 — синие птицы, а остальные — кардиналы. Сколько кардиналов? 8 – 5 = ?	На дереве 8 птиц. Некоторые из них — синие птицы, а некоторые — кардиналы. Сколько может быть птиц каждого вида? ? + ? = 8

Всего неизвестных задачи являются типичными задачами на сложение.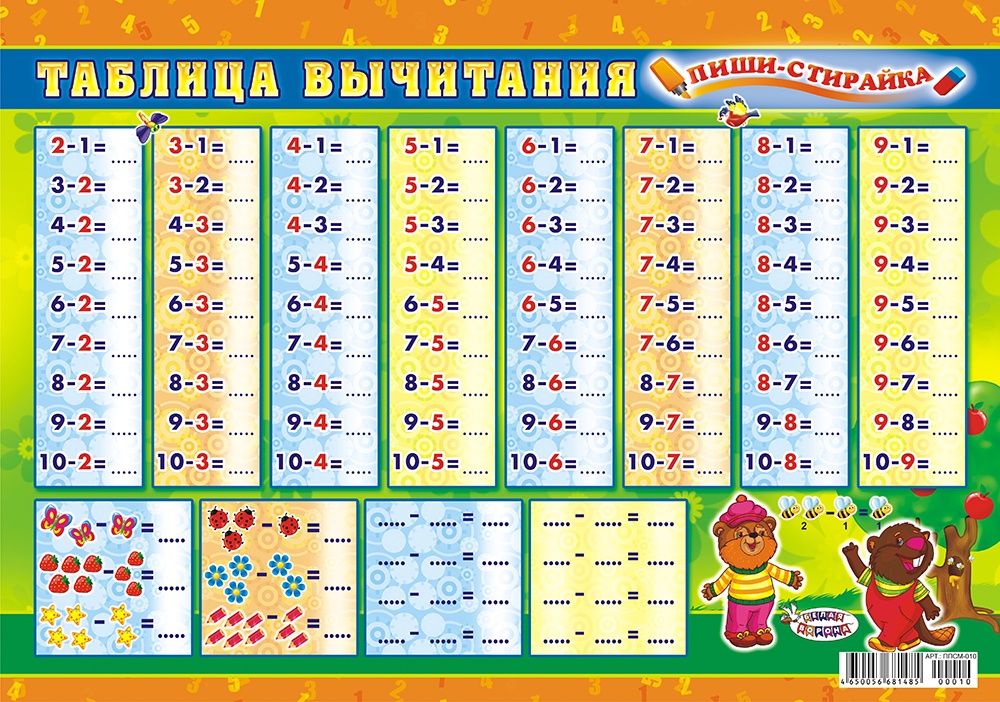 Есть два комплекта, которые идут вместе. Часто это не один и тот же предмет. Например, это могут быть красные яблоки и зеленые яблоки вместе. Или кошек и собак. Когда это один и тот же объект, это часто, но не всегда, сценарий «начало-изменение-конец», потому что изменение заключается в соединении этих двух наборов. Словесная проблема ниже демонстрирует полное неизвестное, имеющее тот же предмет — людей.

Часть неизвестна задачи на вычитание. Мы знаем общее количество предметов, но не знаем их количество в одном из наборов. Работая с частично неизвестными задачами, мы усиливаем обратную связь между сложением и вычитанием. Мы можем написать аналогичное уравнение 5 + ? = 8, чтобы соединить две операции. Важно работать с неизвестными в любом положении, и часть неизвестных задач — это то место, где я предпочитаю работать над обратными операциями и семействами фактов.

Обе части неизвестны Проблемы встречаются реже. Это сценарии с несколькими решениями. Учащиеся знают общее количество предметов и дают возможную схему распределения этих предметов. Обе части неизвестных сценариев — мой любимый способ ввести неизвестные справа от знака равенства 8 = ? + ?. Это помогает учащимся понять, что они не просто решают слева направо и что означает знак равенства.

Для получения дополнительной информации о части, части, целом, у меня есть подробный пост в блоге, в котором показаны практические стратегии, которые я использую для введения и отработки отношений часть/целое.

НАЧАЛО-ИЗМЕНЕНИЕ-КОНЕЦ

Хотя часть-часть-целое является наиболее распространенным типом задачи на сложение и вычитание, по мнению многих учителей, она, вероятно, не самая распространенная в задачах на рассказы. В реальных сценариях сложение и вычитание чаще всего демонстрируются через начало-изменение-результат. В сценариях результатов изменения запуска что-то присоединяется к другим или покидает их. Это типы проблем, когда кто-то что-то получил больше или что-то сломалось. Если мы не преднамеренно решаем задачи со словами, мы склонны по умолчанию решать задачи с неизвестным результатом. Эти типы задач часто имеют такие вопросы, как «сколько осталось?» и «сколько их сейчас?». Действие уже произошло.

Я использую термин «конец» вместо «результат», потому что «конец» противоположен «началу», и я думаю, что у учащихся более четкое понимание, чем с результатом. Это также тот же язык, который я использую для решения проблем с прошедшим временем в 3-м классе, и мне нравится, чтобы мой язык был как можно более последовательным.

В таблице ниже приведены примеры для каждого из 6 типов проблем начала изменения конца. Они довольно просты, поэтому я не буду подробно объяснять каждый из них. Будь то сложение или вычитание, язык указывает местонахождение неизвестного: субъекты в начале, субъекты, которые изменились, или субъекты в конце.

	НАЧАЛО НЕИЗВЕСТНО	ИЗМЕНЕНИЕ НЕИЗВЕСТНО	КОНЕЦ НЕИЗВЕСТНО
Дополнение	Несколько птиц сидели на дереве. На ветку прилетело еще 3 птички и теперь на дереве 8 птичек. Сколько птиц было на дереве в начале? ? + 3 = 8	5 птиц сидели на дереве. На ветку летело несколько птиц и теперь на дереве их 8. Сколько птиц прилетело на ветку? 5 + ? = 8	5 птиц сидели на дереве. На ветку летят 3 птицы. Сколько птиц сейчас на дереве?   5 + 3 = ?
Вычитание	Несколько птиц сидели на дереве. 3 птицы улетели и теперь на дереве 8 птиц. Сколько птиц было на дереве в начале? ? – 3 = 8	11 птиц сидели на дереве. Некоторые птицы улетели и теперь на дереве 8 птиц. Сколько птиц улетело? 11 – ? = 8	11 птиц сидели на дереве. Улетели 3 птицы. Сколько птиц сейчас на дереве? 11 – 3 = ?

Важно, чтобы мы давали студентам возможность попрактиковаться с неизвестными во всех позициях. Студенты видят, что именно через эти типы задач «начало-изменение-конец» их можно попросить определить, сколько чего-то было в начале. Или, что изменение/действие было. С задачами «начало-изменение-конец» учащиеся получают возможность понять, что неизвестные находятся во всех позициях, и развить свою компетентность в отношении сложения и вычитания, являющихся обратными операциями. Через неизвестные в любом месте учащиеся моделируют и решают, используя обратную операцию.

Если начало-изменение-окончание для вас новая концепция, я дам вам инструменты и стратегии в подробном посте об обучении Начать Изменить Завершить.

СРАВНЕНИЯ

Сравнения — самые сложные текстовые задачи для учащихся. Они, естественно, не то, о чем мы думаем, когда думаем об операциях. По этой причине нам нужно учить их и практиковать их. Много!

	РАЗНИЦА НЕИЗВЕСТНО	БОЛЬШЕ НЕИЗВЕСТНО	МЕНЬШЕ НЕИЗВЕСТНО
Сравнить	Сколько еще? У Сары 3 птицы. У Райны 5 птиц. На сколько больше птиц у Райны, чем у Сары? На сколько меньше? У Сары 3 птицы. У Райны 5 птиц. На сколько меньше птиц у Сары, чем у Райны? 5 – 3 = ? 3 + ? = 5	Подробнее У Сары 3 птицы. У Райны на 2 птицы больше, чем у Сары. Сколько птиц у Райны? Меньше У Сары 3 птицы. У нее на 2 птицы меньше, чем у Райны. Сколько птиц у Райны? 3 + 2 = ? ? – 2 = 3	Подробнее У Райны 5 птиц. У нее на 2 птицы больше, чем у Сары. Сколько птиц у Сары? Меньше У Райны 5 птиц. У Сары на 2 птицы меньше, чем у Райны. Сколько птиц у Сары? 5 – 2 = ? 2 + ? = 5

Разница Неизвестно задачи обычно решаются с помощью вычитания. Независимо от вопроса, на сколько больше или на сколько меньше, вопрос хочет знать сумму между ними. Слово «больше» может сбить учащихся с толку, потому что они хотят добавить. Вы можете использовать уравнение сложения, чтобы продемонстрировать его в представленном виде, но, в конечном счете, вычитание — самый простой способ решить его. Мой любимый способ моделирования этих задач — числовая прямая, потому что я могу продемонстрировать оба типа вопросов, считая в прямом или обратном порядке.

В вопросах Большое неизвестное и Меньшее неизвестное все становится немного сложнее. Что касается меня, то, как и в случае с любой проблемой, я прошу студентов начать с сосредоточения внимания на неизвестном в вопросе. С этими проблемами, я думаю, лучше всего работать над ними вместе, потому что их легко запутать.

В моих плакатах типа задачи на сложение и вычитание я комбинирую известную информацию. В обеих описанных выше ситуациях нам говорят, что у кого-то больше, и у них обоих один и тот же вопрос. Сосредоточив внимание на том, что означает «больше», мы показываем учащимся различия в типах вопросов и тонкости между ними. Вы можете скачать мои плакаты с задачами на сложение и вычитание, подписавшись ниже.

Большие Неизвестные задачи в таблице содержат вопрос «Сколько птиц у Райны?». Из-за расположения стола мы понимаем, что у Райны больше птиц, чем у Сары. Но давайте подробнее рассмотрим проблемы.

У Сары 3 птицы. У Райны на 2 птицы больше, чем у Сары. Сколько птиц у Райны?

В этой задаче говорится, что у Райны больше, чем у Сары. Это довольно простая задача на сложение: сложить число Сары и еще одно число — сравнение — чтобы найти общее число Райны.

У Сары 3 птицы. У нее на 2 птицы меньше, чем у Райны. Сколько птиц у Райны?

Эта проблема не так проста. Это говорит нам о том, что у Райны больше, говоря нам, что 3 у Сары на 2 меньше, чем у Райны. Когда учащиеся видят «меньше», они хотят вычесть, но большее число неизвестно. Мы можем смоделировать это уравнение вычитания как неизвестное — 2 дает нам 3 для Сары. Опять же, давайте подробнее рассмотрим проблемы.

У Райны 5 птиц. У нее на 2 птицы больше, чем у Сары. Сколько птиц у Сары?

В этой задаче слово «больше» может заставить учащихся почувствовать, что им нужно добавить. Но вычитание — лучшая операция. Если у Райны на 2 больше, чем у Сары, мы можем вычесть 2 из суммы Сары и суммы Райны. Или, как дополнение, Сара + 2 = Райна 5.

У Райны 5 птиц. У Сары на 2 меньше, чем у Райны. Сколько птиц у Сары?

Эта задача более проста, чем предыдущая. У Сары на 2 меньше, чем у Райны, поэтому ученики, естественно, будут вычитать.

Для этих сценариев я считаю наиболее полезным начать с вопроса. Неизвестный. Если мне нужно знать, сколько птиц у Сары, я держу это в уме, возвращаясь к задаче со словами во второй раз и переформулируя ее. 5 у Райны на 2 больше, чем у Сары. У Сары на 2 меньше, чем у Райны 5. Начав с неизвестного, которое я решаю, я могу лучше понять, что вопрос просит меня сделать, связав его с известным.

Я учу своих учеников внимательно читать каждое слово-задачу. Я связываю это с внимательным чтением, которое мы делаем на уроках ELA. Потому что на самом деле и то, что мы читаем в ELA, и задачи, которые мы решаем, являются сложными текстами. Я использую программу 3 чтения. Первое чтение должно получить общее понимание — суть — контекст. В следующем читается прохождение словесной проблемы с упором на неизвестные и вопрос. Вы можете прочитать больше о моей рутине 3 чтения в этом сообщении в блоге.

Типы задач на сложение и вычитание

У меня есть плакаты для всех типов задач на сложение и вычитание. Вы можете использовать их как часть якорной таблицы, когда вы пишете свои собственные текстовые задачи вместе для каждого типа задач. Вы можете отображать их по мере того, как вводите их. Вы можете распечатать несколько на странице и дать учащимся свои собственные в качестве справочных материалов.

У меня также есть справочный лист по типам задач на сложение и вычитание для вас. Этот одностраничный печатный лист — хороший справочный лист, который вы всегда будете иметь под рукой. Или учащиеся могут сохранить копию в своей папке с математическими справочниками, если она у вас есть. Включенные словесные задачи такие же, как и на этом сайте, а не те, что на плакатах, ссылки на которые приведены выше.

Заполните форму ниже, чтобы подписаться на получение плакатов с задачами на сложение и вычитание.

 

Информационный бюллетень

Подпишитесь, чтобы получать бесплатные плакаты с задачами на сложение и вычитание! После подтверждения электронной почты вы получите файл и будете подписаны на мою еженедельную рассылку.

Загрузка…

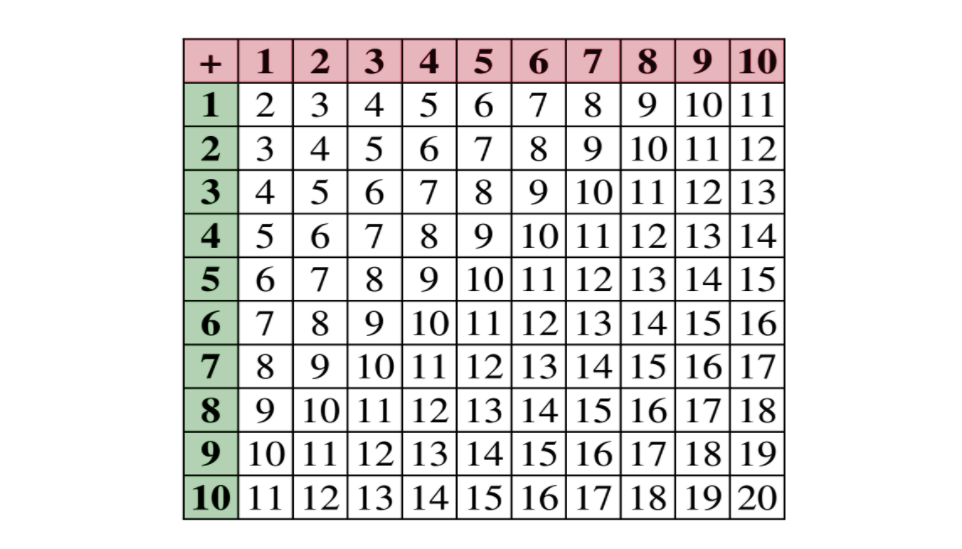
У меня также есть цифровые карточки с задачами на сложение и вычитание. Они организованы по типам текстовых задач и тренируются на сложении и вычитании в пределах 20. В наборах «Часть-Часть-Целое» и «Начало-Изменить-Конец» есть особая практика, позволяющая различать их, когда учащиеся сопоставляют неизвестное и заданное уравнение с заданными сценариями.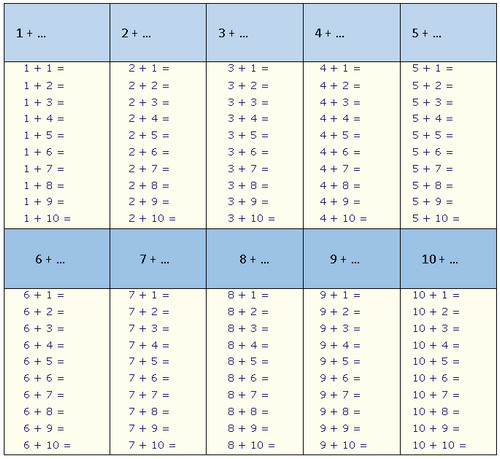

Каждый из наборов дает учащимся специальную практику по каждому типу словесных задач на сложение и вычитание. Учащиеся используют встроенные инструменты для написания уравнений с переменными или символами для неизвестных. После написания уравнения учащиеся используют манипуляторы для моделирования задачи на числовой прямой и десятках кадров. Формат позволяет учащимся практиковать несколько стандартов математической практики, моделируя и решая задачу, а также проверяя свою работу.

В дополнение к типам задач «часть-часть-целое», «начало-изменение-конец» и «сравнение» существует также набор задач «Сложение 3 чисел». Этот набор представлен в сценариях часть/целое или часть-часть-часть-целое. Набор бесплатный, и его можно загрузить из моего магазина TpT, нажав на обложку ниже.

Я надеюсь, что этот пост дал вам идеи и ресурсы для обучения ваших учеников каждому типу задач на сложение и вычитание. Чем больше практики и опыта получают студенты, тем успешнее они будут. Вас также может заинтересовать мой пост «Игры для сложения и вычитания фактов».

Для получения дополнительной информации о типах задач CGI Word, этот пост от Langford Math довольно подробный, и в этой вики есть куча примеров задач Word.

13 Настольные игры на сложение и вычитание для PreK to 3 Class

Этот пост содержит партнерские ссылки.

Ожидается, что дети овладеют навыками сложения в первом классе и навыками вычитания во втором классе. Однако, если вы хотите начать заниматься еще в детском саду, не волнуйтесь.

Я нашел 13 многопользовательских настольных игр, посвященных тренировкам:

• Сложение, например, Ocean Raiders
• Сложение и вычитание, например, Cloud Hoppers

Таблица сравнения настольных игр сложения и вычитания

В этой таблице содержится краткий обзор характеристик каждой настольной игры. Большинство настольных игр идеально подходят для игры дома и в школе.

Игра

Фокус

Возраст

Игроков

For

Price

Rating

Ocean Raiders

Addition

5+

2-4

Families, Teachers

$$

★★★★☆

POP и добавить в 20 игру

Дополнение

4-6

1-2

Учителя

$$$

★★★ ★

СОВЕРСКИ0018 Addition

4-6

1-3

Teachers

$$$

★★★☆☆

Addition Flip and Solve Board

Addition

3-6

1-2

Families, учителя

$$$

★★★ ☆☆

SUM BOLAMP

Дополнение и вычитание

5+

2-4

Family, Teachers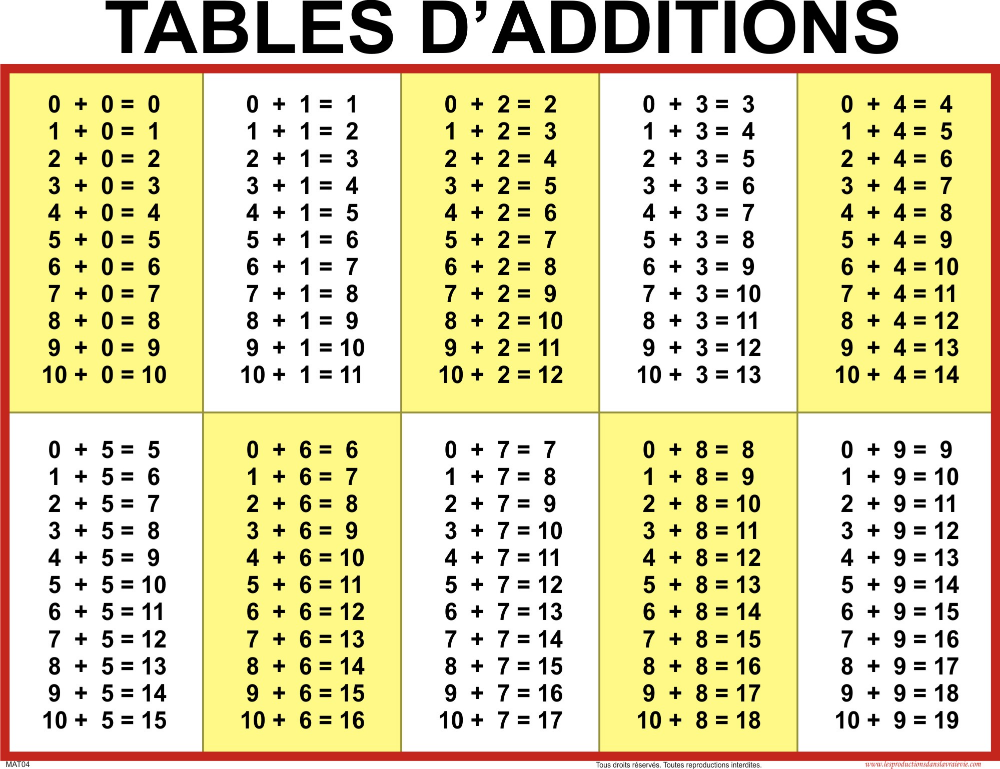

. ★☆

Выиграй! Математическая игра гр. 2

Addition and Subtraction

7

2-4

Teachers

$$$

★★★★☆

Cloud Hoppers

Addition and Subtraction

6+

2-4

Семьи, учителя

$$

★★★★ ☆

Матемагический мир

Дополнение и вычитание

5+

2-4

Семейство, Учителя

$ При

, Учителя

$ При

, Учащивания

$ При

, преподаватели

$ При

. ☆

Bus Stop

Addition and Subtraction

4-7

2-4

Families, Teachers

$$

★★★☆☆

Race to Planet X

Addition and Subtraction

6-8

2-4

Учителя

$$

★★★☆☆

Привет, Хо! Cherry-O

Сложение и вычитание

7–8

2–4

Семьи, учителя

$$

★★★☆☆

Tri-Facta

Addition and Subtraction

6-8

2-4

Teachers

$$$

★★★☆☆

Unicorn Sparkle Суммы

Добавление и вычитание

4-8

1-4

Семейства, учителя

$$

★★★ ☆☆

4 Дополнительные составы для PREK до класса

9030

4 Дополнительные составы для PREK до класса

9030

4 Дополнительные составы для Prek до класса

70

4 Дополнительные составы для Prek до класса 1

9030

4 Дополнительные составы.

(Логические корни)

★★★★☆

Для родителей и учителей | Возраст 5+ | 2-4 игрока

Ocean Raiders — это игра, вдохновленная Snakes and Ladders, но с изюминкой. Числа на доске не в хронологическом порядке, и вы должны добавить число на кубике к вашей текущей позиции на доске, чтобы сделать ход.

Эта настольная игра захватывающая, непредсказуемая и актуальная для детей 5–7 лет потому что они научатся:

• Последовательности чисел
• Счет
• Сложение однозначных и двузначных чисел
• Сложение с 0

Мне нравится:

• Дети научатся складывать большие числа
• В игре есть два режима игры: простой и продвинутый.
• Эту игру можно использовать для обучения вычитанию .

Самое главное, я рекомендую Ocean Raiders, потому что молодых и старых ребенка с разными математическими способностями могут наслаждаться игрой и играть вместе.

Игра Pop and Add to 20 (Lakeshore Learning)

★★★★☆

Для учителей | Возраст 4-6 | 1-2 игрока

Выбери и сложи до 20 Игра учит считать и складывать числа в пределах 20.

В этой игре дети решают задачи на сложение, используя два кубика. Затем они сопоставляют выпавшие числа с жетонами яблок, складывают и записывают сумму на доске.

Положительные черты:

• Игровые компоненты яркие и красочные
• Можно заменить яблоки другими предметами
• Отлично подходит для обучения студентов тактильным навыкам

Несколько напоминаний:

• Маленьким детям может понадобиться помощь, чтобы нажать на кнопки для игры в кости
• Можно использовать только 25 яблок, поэтому практика ограничена
  2 В комплект не входят стираемые маркеры

  . Я рекомендую играть в игру Pop and Add to 20 с детьми из детского сада, потому что она увлекательна и проста в обучении.

  Простое дополнение магнитной активности Tin (Lakeshore Learning)

  ★★★☆☆

  Для учителей| Возраст 4-6 | 1–3 игрока

  В наборе «Простое сложение» дети тренируются в сложении, манипулируя 20 магнитами на 15 разноцветных ковриках для занятий. Он имеет прочный контейнер для хранения, который можно использовать на доске для занятий.

  Эта настольная игра может вместить до 3 игроков, но играть в одиночку гораздо выгоднее.

  Этот набор можно использовать двумя способами:

  • Найдите недостающее слагаемое, чтобы завершить уравнение 9.0382
  • Нахождение суммы для завершения уравнения

  Он не охватывает все факты сложения, но достаточно хорош для введения сложения у детей в возрасте 4-6 лет.

  Дополнительная доска Flip & Solve Board (Lakeshore Learning)

  ★★★☆☆

  Для родителей и учителей | Возраст 3-6 | 1-2 игрока

  В дополнении к доске Flip & Solve Board дети могут практиковаться в сложении чисел в пределах 20.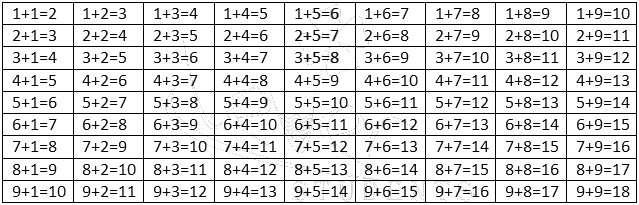

  Играть:

  1. Выберите карточку с уравнением.
  2. Переверните столько плиток бананов, сколько слагаемых в уравнении.
  3. Сосчитай бананы и ответь на уравнение.
  4. Переверните карточку с уравнением, чтобы проверить ответ.

  В этой игре могут участвовать до 2 игроков, но она идеально подходит для одиночной игры . Дети также могут играть самостоятельно, так как на обратной стороне карточек с уравнениями есть ответы.

  Вы можете улучшить эту игру, делая карточки только с суммами, чтобы дети могли практиковаться в разложении чисел в пределах 20.

  9 Настольные игры на сложение и вычитание для детского сада до 3 класса

  Sum Swamp (Учебные материалы)

  ★★★★☆

  Для родителей и учителей | Возраст 5+ | 2-4 игрока

  Игроки мчатся по болоту, решая задачи на сложение и вычитание в Sum Swamp.

  В этой игре игроки бросают числовой кубик и кубик операций (знаки плюс или минус), чтобы решить задачу на сложение или вычитание. Затем они перемещают свое болотное существо в зависимости от ответа.

  Вещи, которые мне нравятся:

  • В игре есть интересных функции таких как ярлыки и бесконечные циклы
  • На доске красивых рисунка и вычитание с большими числами
  • Он учит нечетным и четным числам

  Pop to Win! Математическая игра — гр. 2 (Lakeshore Learning)

  ★★★★☆

  Для родителей и учителей | Возраст: 7 | 2-4 игрока

  Поп, чтобы победить! Математическая игра-гр. 2 игроки путешествуют по игровому полю космической тематики, правильно отвечая на 75 вопросов. Эта игра состоит из игрового поля, четырех жетонов с цветовой кодировкой и 75 карточек со словами с несколькими вариантами ответов.

  Вопросы преподают навыки, такие как:

  • A DSID или вычитание номеров
  • Подсчет денег
  • Рассказывание времени

  The Pros:

  4
  7777777777777777777777777
  777777777
  777777 7. ships 70377

  . SARTS.0073 в виде карточек викторины

• Карточки промаркированы и могут быть отсортированы по сложности и категории
• В комплект входит карточка с ответами для простого подсчета очков и самопроверки

Я рекомендую Win Pop! Математическая игра-гр. 2 , потому что игра предлагает различные подходящие для класса и сложные вопросы, которые помогают познакомить учащихся с математическими понятиями.

Облачные прыгуны (логические корни)

★★★★☆

Для родителей и учителей | Возраст 6+ | 2-4 игрока | Продолжительность игры: 10-15 минут

Cloud Hoppers — настольная игра на сложение и вычитание на тему пришельцев.

Каждый игрок получает два игровых жетона, и им нужно доставить обе части к цветку Цита (20 на игровом поле), чтобы выиграть. Есть два основных правила:

• В облачной зоне вычтите число на кубиках из вашего текущего положения.
• В зоне растений добавьте число, выпавшее на кубике, к вашему текущему положению.

В этой игре потрясающие иллюстрации и прочные игровые элементы. В своде правил также есть интересная история об инопланетянах.

Однако Cloud Hoppers больше фокусируется на вычитании, чем на сложении. Он также начинается с двузначного числа, что может вызвать затруднения у детей младшего возраста. Таким образом, хотя игра поощряет их к умственным вычислениям, может потребоваться, чтобы ваш ребенок использовал ручку и бумагу для решения уравнений.

Матемагический мир (Изобретения разума)

★★★☆☆

Для родителей и учителей | Возраст: 5+| 2-4 игрока | Продолжительность игры: 30 минут

Mathemagical World — настольная игра на вычитание и сложение, в которой участвуют восемь волшебных островов: необитаемый остров, остров динозавров, остров пиратов, остров зомби, остров единорогов, ледяной остров, остров дракона и остров ниндзя. .

Игра предлагает два уровня сложности:

1. Обычный режим – рекомендуется для начинающих (K-Gr. 1 ) для обучения сложению и вычитанию чисел в пределах 12
2. Ускоренный режим 70074 – подходит для первоклассников для тренировки сложение и вычитание чисел в пределах 20

Положительные моменты:

• С его помощью можно познакомить детей дошкольного возраста со счетом
• Это простая в настройке и быстро развивающаяся игра

Я рекомендую Mathemagical World , потому что она также включает сложение и вычитание двойных и половинных понятий , таких как движение вперед на половину четыре, что означает перемещение на два пробела .

Автобусная остановка (садовые игрушки)

★★★☆☆

Для родителей и учителей | Возраст 4-7 | 2-4 игрока

Дети добавляют и вычитают пассажиров по мере того, как они мчатся по игровому полю, чтобы добраться до автобусной остановки. Эта настольная игра содержит 40 карточек пассажиров и четыре автобусные доски.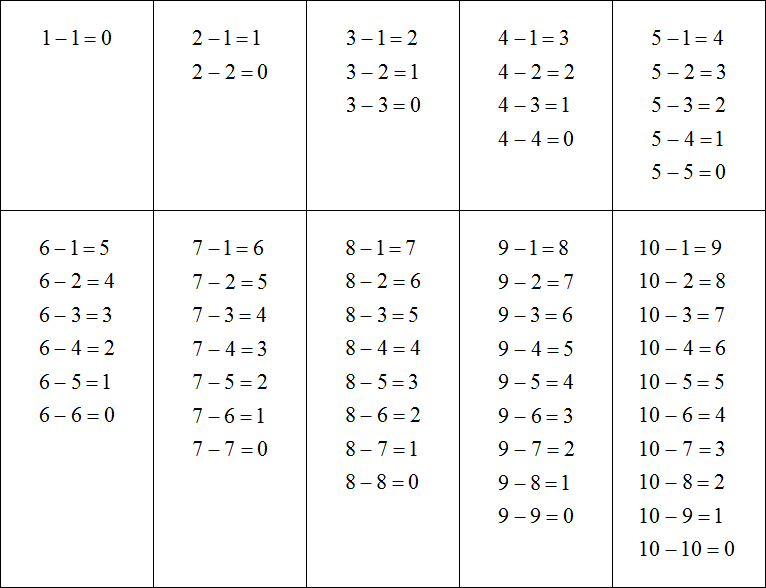

Игроки бросают кости и перемещают автобус на место. Затем прокрутите счетчик, чтобы определить, сколько людей нужно добавить или вычесть из вашего автобуса.

The pros:

• Great for tactile learning students
• Teaches to add and subtract within ten
• Adding and subtracting passengers is a realistic and fun concept

The cons:

• Вычитание значений за вычетом людей в автобусах сбивает детей с толку , как высадка пяти пассажиров, когда их всего 3
• Низкая изменчивость во время игры так как у игроков часто нет пассажиров, потому что на доске больше знаков минус

Гонка на планету X (Little Phone LLC)

★★ ★☆☆

Для учителей | Возраст: 6-8 | 2-4 игрока | Продолжительность игры: 15 минут

Race to Planet X — это настольная гоночная игра на космическую тематику, в которой игроки создают Power Combos, числовые связи, чтобы двигаться вперед.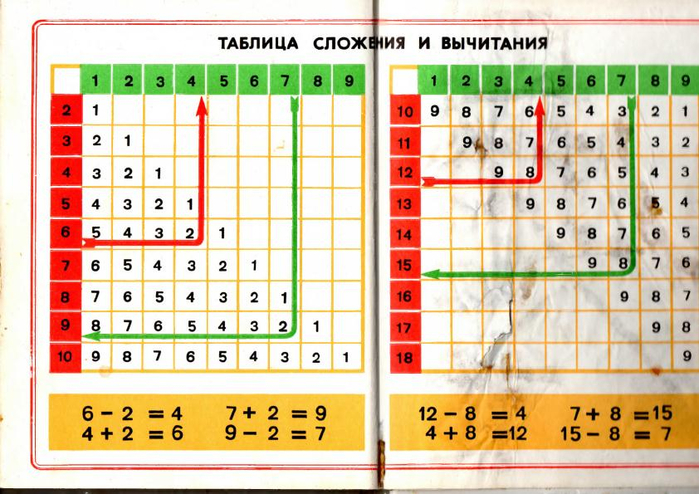 Мощная комбинация — это три карты, которые составляют числовое выражение, например, 7+1=8.

Чтобы научиться играть в эту игру, нужно научиться. Тем не менее, это по-прежнему отличная игра для первоклассников и второклассников , чтобы попрактиковаться в сложении и вычитании чисел в пределах 20. Им также понравятся забавные функции игры:

• Кража карт у противников переместить противников назад

Привет Хо! Cherry-O (Hasbro)         

★★★☆☆

Для учителей и родителей | Возраст: 5-7 лет | 2-4 игрока

Привет, хо! Cherry-O, игроки соревнуются, чтобы наполнить свои корзины десятью фруктами. Каждый игрок может выбрать один из четырех видов фруктов с цветовой кодировкой:

• зеленые для яблок
• синие для черники
• оранжевые для апельсинов
• красные для вишни

Эта игра не обучает непосредственно сложению и вычитанию . Но дети косвенно узнают об этих процессах, когда пытаются сообразить, сколько фруктов им еще нужно, чтобы выиграть. Взрослые также могут укреплять эти навыки во время игры.

Отличительные особенности:

• Компоненты игры привлекательные и красочные
• Легко установить и играть.
• У этой игры есть вариант для совместной игры

Однако эта игра имеет низкую воспроизводимость, особенно для детей с сильными математическими способностями.

Tri-Fact-A (Учебные ресурсы)

★★★☆☆

Для учителей| Возраст: 6-10 | 2-4 игрока

Tri-Facta развивает беглость математических фактов до 20 .

Каждый игрок получает право составить настоящий треугольник фактов – верхнее число должно быть суммой или разностью двух нижних чисел. Первый игрок, избавившийся от всех своих карт, выкрикивает «Три факта» и выигрывает игру.

Я рекомендую эту игру, потому что она сложная . Это также помогает первоклассникам и второклассникам понять взаимосвязь между сложением и вычитанием. Однако карты хлипкие. А детям, у которых проблемы со сложением и вычитанием, это тоже может показаться слишком сложным, и им может потребоваться больше времени, чтобы закончить поворот.

Unicorn Sparkle Sums (Melby Toys)

★★★☆☆

Для родителей и учителей | Возраст 4-8 | 1-4 Players

Unicorn Sparkle Sums — это настольная игра, в которой игроки должны решить задачу на сложение или вычитание, чтобы перемещаться по доске.

Эта настольная игра состоит из игрового поля, четырех жетонов единорогов и трех шестигранных кубиков (2 обычных розовых кубика и один белый кубик со знаками плюс и минус).

Чтобы попрактиковаться в вычитании или сложении двузначных чисел, вы можете добавить больше кубиков или увеличить разрешенный бросок за ход.

Эта игра заслуживает трехзвездочного рейтинга , потому что:

• Доска с изображением единорога визуально привлекательна для детей.
• Игра проста в обучении и игре.