Урок «Состав числа 8. Составление выражений на сложение. Упражнение на нахождение пропущенных чисел, сравнение чисел . Сравнение отрезков за длиною.»
Урок математики
1 класс Скрикеря Л. А.
Тема: «Состав числа 8. Составление выражений на сложение. Упражнение на нахождение пропущенных чисел, сравнение чисел . Сравнение отрезков за длиною.
Цель:
1. Ознакомить с составом числа 8. Упражнять в нахождении пропущенных чисел, сравнении чисел в пределах 8, составлении выражений на сложение.
2. Развивать наблюдательность, логическое мышление.
Развивать умение работать сообща и дружно с одноклассниками;
Развивать психологические процессы: память, мышление, восприятие, внимание, эмоции.
3. Воспитывать положительное отношение к предмету.
Воспитывать усидчивость, уверенность при выполнении заданий, ответственность, любознательность, аккуратность в выполнении работы.
Форма оценивания учебных достижений учащихся: словесное поощрение.
Оборудование: Учебник “Математика” для 1 класса;
набор геометрических фигур , карточки с числами от 1 до 10,
корзина с фруктами и овощами,
таблица «Состав числа 8», презентация,
детали для аппликации веточки рябины.
Ход урока
| Рекомендации |
1.Оргмомент. (1 мин.) -Проверили свою готовность к уроку. — Если я произнесу слово, начинающееся с гласного звука, сядут девочки. С согласного – мальчики. Желаю Удачи! Я действительно желаю вам удачи и хочу, чтоб вам понравился урок. Улыбнулись. Покажите мне свое настроение.
2.Мотивация учебной деятельности. 1 мин.) — За окном — осень! Осень подарила нам много овощей и фруктов. — Какие фрукты вы любите? Замечательно! — Вот и мы на уроке математики тоже попробуем собрать дары осени. — А помогут нам в этом ваши знания и умения. — Вы мне поможете? За каждый правильный ответ Осень будет нас одаривать своими дарами.
3.Контроль, коррекция и закрепление знаний. ( 3 мин.) а) Повторение изученных цифр. Мы отправляемся в сад. Надо вести себя тихо, чтобы услышать звуки сада. (Работа — Стук дятла ( 5 раз) -Чего может быть пять : пять пальцев на руке, у звезды 5 лучей. — Шелест листочка? (7 раз) — Чего может быть 7: сем чудес света, дней недели, 7 цветов радуги — Какой сегодня день недели? — Что вы только что показывали на экранах? (Цифры). — А называли? (Число?) — Значит цифра это знак, запись числа.
б) Задание на нахождение пропущенных чисел. (3 мин.) Подул ветер и рассыпал листочки. Вставь, каких здесь не хватает. 1.2.3….5……..8. (Показать на экранах, один ребенок выставляет число на наборном полотне) -какое число следует за числом 7. (Ответ: назвать следующее число) — какое число предшествует шести. (Ответ: назвать число, которое стоит впереди шести) — сравнение чисел 7 и 6; 5 и 8. -Какие знаки поставим, почему?
4.Изучение нового материала. (5 мин.) а) Состав числа 8. Работа с геометрическим материалом. — С каким числом, цифрой мы познакомились на прошлом уроке? -Из каких геометрических фигур можно это число выложить? (Из 2 кружков) -Что еще можно сложить их двух кружков? (Снеговик, велосипед, очки)
Но вот в наш сад пришел ежик и решил полакомиться нашими яблочками. — Кто хочет побыть ежиком? (У доски ребенок работает, а все дети работают с геометрическим материалом на местах. На доске открываются окошки в домике состава числа 8 ) — Что мы только что делали? («Заселили» домик №8) — Для чего мы должны знать состав чисел? (Для быстрого счета)
Физкульминутка – пальчиковая гимнастика. Мы капусту рубим-рубим. Мы капусту трем-трем Мы капусту солим-солим Мы капусту жмем-жмем.
б) работа в Т. С.16 №2 – заполнение таблицы «Состав числа 8» (3 мин) Чтобы не забыть урок. Закрепить его ты мог. Состав восьми припомним, Таблицу мы заполним.
Работа выполняется коллективно. (Учитель заполняет на доске, а дети в тетрадях)
в) работа по учебнику над выражением с. 33 № 2 (рассчитано на весь урок) — Составление выражения по иллюстрации в учебнике и стихотворению. Цветные и улитки, и ракушки, Подумайте, зачем, друзья – подружки, Их так художник рисовать старался? Чтоб школьник в выражениях упражнялся! ( 3 + 5 = 8.) (2 + 6 = 8.)
5 Развитие и закрепление математических знаний. (3 мин.) а) Игра «Найди пару». (3 мин.) (Игровой материал: карточки с числами от 1 до 8. Дети получают карточки с числами. По сигналу учителя ученики ищут себе пару). — Создайте пару 7 и 8. — Объясните, из каких чисел состоит ваше число? — Почему? Поменялись карточками. 6.Итог урока. Рефлексия. (1-2 мин.) — Урок подошел к концу и в нашей корзинке собраны дары осени. – Закончи предложение: «Сегодня я узнал, что…», « Мне понравилось, что я…», « Я люблю работать в паре с товарищем потому, что…» – Как нам помогут знания, полученные вами сегодня? (Быстро считать) — Калина символ Украины! А еще она умеет нас лечить от простуд и поэтому в каждом саду она растет. Пусть калина оберегает нас и наших гостей. -Давайте создадим аппликационную открытку нашим гостям, разместим ягодки калины на двух кисточках так, чтобы было не равное количество ягод. (Количество ягод 8) — Мне очень понравилось, как вы работали. Спасибо за урок! | Создание условий для возникновения у детей внутренней потребности включения в учебную деятельность, создание ситуации успеха, психологической поддержки.
Если ребенок невнимательный, то удержать внимание может живая, эмоциональная, выразительная речь учителя.
Если ребенок боится отвечать – такой вид работы дает возможность видеть ответы всех детей- самооценка ребенка повышается.
Демонстрация иллюстраций, картинок способствует формированию речи, математических представлений, представлений об окружающем мире
Практическая работа с геометрическим материалом и другими предметами способствует формированию математической речи, математических представлений при составлении выражений.
Если ребенок неусидчивый, то участие в сюжетно-ролевой игре способствует формированию произвольного внимания.
Если работа в тетрадях ведется небрежно, это значит слабо развита моторика пальцев рук. Таким детям надо больше давать задания на работу с аппликацией, мозайкой, лепка и т.д.)
Плохо ориентируется в тетради – значит низкий уровень развития восприятия и ориентации в пространстве. Уроки труда могут помочь в формировании и развитии умения ориентироваться и работать в тетради.
Для формирования познавательных интересов — дидактическая игра.
Упражнения на развитие мелкой моторики – аппликационная работа или графическое задание по обводке сложной для этих детей линии формируют графомоторные навыки, точность и координацию движений как общей, так и мелкой моторики, навык письма, предупреждают утомление. Кроме того развивают волевые процессы, мозг ребёнка, воспитывают трудолюбие.
|
Таблица сложения для начальных классов: что это такое и зачем ее учить
Самое сложное в первом классе на математике — это устный счет. В школе тренировке этого навыка внимание уделяют редко, а результатов требуют, ведь уже во втором классе придется складывать трехзначные числа в столбик. Наш блогер, учитель начальных классов Ольга Катаева, советует выучить с детьми таблицу сложения и дает несколько советов, как сделать это быстро.
Оказывается, кроме таблицы умножения есть еще и таблица сложения — её тоже нужно учить. Про таблицу сложения я узнала, когда сама училась на учителя. Была очень удивлена, что она вообще существует. И чем дольше работала, тем больше понимала: знать её не менее важно, чем таблицу умножения.
Про таблицу сложения я узнала, когда сама училась на учителя. Была очень удивлена, что она вообще существует. И чем дольше работала, тем больше понимала: знать её не менее важно, чем таблицу умножения.
Таблица сложения состоит из двух частей: первая — сложение в пределах 10, вторая — сложение с переходом через десяток в пределах 20. Первая часть таблицы опирается на состав чисел до 10 и на сложение при помощи пальцев. Если записать все равенства, получится довольно большой объём для запоминания. Как его уменьшить? Для нас, взрослых, это все очевидно, но для первоклашек, которые только осваивают сложение, эти советы и правда могут пригодиться.
1. Переместительное свойство сложения
Все помнят правило «от перемены мест слагаемых сумма не меняется». Если ваш первоклассник с ним еще не знаком — срочно это исправьте! С этим правилом объём тех примеров, которые надо выучить, уменьшится вдвое.
2. Сложение с нулём
При сложении с нулём мы получаем то же самое число. Составляя таблицу сложения, исключаем все равенства со слагаемым «ноль» и уменьшаем объём для заучивания ещё на 10 равенств.
Составляя таблицу сложения, исключаем все равенства со слагаемым «ноль» и уменьшаем объём для заучивания ещё на 10 равенств.
3. Сложение с числом 1
Когда к числу прибавляем 1, получаем следующее за ним число в числовом ряду. Если помним это правило и хорошо умеем считать, то уменьшим таблицу сложения ещё на 10 равенств.
Теперь можно составлять таблицу и начинать учить. Сделать это можно несколькими способами: с одинаковым первым слагаемым (2+2, 2+3, 2+4 и т. д.) или с одинаковым вторым слагаемым (2+2, 3+2, 4+2 и т. д.). Легко заучиваются равенства с одинаковыми слагаемыми, например: 2+2=4, 3+3=6 и т. д.
Вторая часть таблицы сложения — в пределах 20. Здесь будет опираться на состав чисел или на приём «добавление до 10». Что такое состав чисел? Например: 11 — это 2 и 9, 3 и 8, 4 и 7, 5 и 6. При составлении второй части таблицы применяем те же правила: переместительное свойство сложения, сложение с 0 и 1. Заучиваются легко равенства с одинаковыми слагаемыми: 5+5=10, 6+6=12. Еще легко складывать с числом 9. Нужно «забрать» от второго числа (которое не 9) единицу. Например: 9+7, от 7 забираю 1 получится 6, значит, 9+7=16. С этим знанием заучивать столбики на сложение с числом 9 уже не надо.
Еще легко складывать с числом 9. Нужно «забрать» от второго числа (которое не 9) единицу. Например: 9+7, от 7 забираю 1 получится 6, значит, 9+7=16. С этим знанием заучивать столбики на сложение с числом 9 уже не надо.
Что такое приём «добавление до 10»? Для примера сложим 6 и 8. Чтобы добавить 6 до 10 нужно взять 4, «забираем» от восьми 4, получаем 10, от восьми осталось 4. Значит, складываем 10 и 4, получается 14. Можно записать так: 6+8=6+4+4=14
После заучивания надо совершенствовать навык устного счёта. Как? Элементарно — постоянно считать. Можно купить тетрадки-тренажеры, их сотни, можно скачать в интернете листочки с примерами. Чтобы было не так скучно, поищите математические раскраски математические раскраски: ответ примера на сложение или вычитание — определённый цвет на картинке. Таких раскрасок в интернете тоже немало.
И про вычитание: можно также составить таблицу и учить по ней, но тем, кто хорошо выучил таблицу сложения, с вычитанием разобраться будет легко. Например, я помню, что 5+6=11. Если нужно посчитать 11-6, то понятно, что это 5 — вторая часть от 11, так как первая — 6.
Например, я помню, что 5+6=11. Если нужно посчитать 11-6, то понятно, что это 5 — вторая часть от 11, так как первая — 6.
С вычитанием хорошо работают логические рассуждения: например, 9-3 — это разница между числами 9 и 3 в числовом ряду, от трёх до девяти 6 шагов, поэтому 9-3=6.
Тем, кому очень сложно складывать и вычитать в пределах 20 и учить таблицу сложения, можно освоить счёт при помощи линейки: сложение — это движение вперёд на увеличение, вычитание — движение назад, к нулю, на уменьшение.
И еще: счёт — это навык, формируется он только благодаря постоянной тренировке. В начальной школе, увы, очень рано дают сложение столбиком. Дорогие учителя и родители, если есть такая возможность — не спешите. Столбиком научиться считать легко, а вот считать в уме — гораздо сложнее. Если хотите, чтобы ваш ребёнок овладел счётом в совершенстве, учите таблицу сложения и оттачивайте навык устного счета.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Иллюстрация: Voranee / Shutterstock / Fotodom
Таблицы экспонент и шаблоны
Горячая математикаВ таблицах степеней целых чисел можно найти много интересных закономерностей.
Полномочия 2 | Полномочия 3 | Полномочия 4 |
| 2 1 «=» 2 | 3 1 «=» 3 | 4 1 «=» 4 |
| 2 2 «=» 4 | 3 2 «=» 9 | 4 2 «=» 16 |
| 2 3 «=» 8 | 3 3 «=» 27 | 4 3 «=» 64 |
| 2 4 «=» 16 | 3 4 «=» 81 | 4 4 «=» 256 |
| 2 5 «=» 32 | 3 5 «=» 243 | 4 5 «=» 1024 |
| 2 6 «=» 64 | 3 6 «=» 729 | 4 6 «=» 4096 |
| 2 7 «=» 128 | 3 7 «=» 2187 | 4 7 «=» 16384 |
| 2 8 «=» 256 | 3 8 «=» 6561 | 4 8 «=» 65536 |
| 2 9 «=» 512 | 3 9 «=» 19683 | 4 9 «=» 262144 |
| 2 10 «=» 1024 | 3 10 «=» 59049 | 4 10 «=» 1048576 |
Одна вещь, которую вы можете заметить, это закономерности в цифрах. В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9,
7
,
1
,
3
,
9
,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит!
В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9,
7
,
1
,
3
,
9
,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит!
В полномочиях 4 таблица, чередуются единичные цифры: 4 , 6 , 4 , 6 . На самом деле, вы можете видеть, что силы 4 совпадают с четными степенями 2 :
4
1
«=»
2
2
4
2
«=»
2
4
4
3
«=»
2
6
и т. д.
д.
Такие же отношения существуют между силы 3 и силы 9 :
Полномочия 3 | Полномочия 9 |
| 3 1 «=» 3 | 91 «=» 9 |
| 3 2 «=» 9 | 9 2 «=» 81 |
| 3 3 «=» 27 | 9 3 «=» 729 |
| 3 4 «=» 81 | 9 4 «=» 6561 |
| 3 5 «=» 243 | 9 5 «=» 59 049 |
| 3 6 «=» 729 | 9 6 «=» 531 441 |
| 3 7 «=» 2187 | 9 7 «=» 4 782 969 |
| 3 8 «=» 6561 | 9 8 «=» 43 046 721 |
| 3 9 «=» 19,683 | 9 9 «=» 387 420 489 |
| 3 10 «=» 59 049 | 9 10 «=» 3 486 784 401 |
силы
10 легко, потому что мы используем
база
10
: для
10
н
просто напишите »
1
» с
н
нули после него. Для
отрицательные силы
10
−
н
, писать »
0.
» с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.
Для
отрицательные силы
10
−
н
, писать »
0.
» с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.
Полномочия 10 | |
| 10 1 «=» 10 | 10 0 «=» 1 |
| 10 2 «=» 100 | 10 − 1 «=» 0,1 |
| 10 3 «=» 1000 | 10 − 2 «=» 0,01 |
| 10 4 «=» 10 000 | 10 − 3 «=» 0,001 |
10 5 «=» 100 000 (сто тысяч) | 10 − 4 «=» 0,0001 (одна десятитысячная) |
10 6 «=» 1 000 000 (один миллион) | 10 − 5 «=» 0,00001 (стотысячный) |
10 7 «=» 10 000 000 (десять миллионов) | 10 − 6 «=» 0,000001 (одна миллионная) |
10 8 «=» 100 000 000 (сто миллионов) | 10 − 7 «=» 0,0000001 (одна десятимиллионная) |
10 9 «=» 1 000 000 000 (один миллиард) | 10 − 8 «=» 0,00000001 (стомиллионный) |
10 10 «=» 10 000 000 000 (десять миллиардов) | 10 − 9 «=» 0,000000001 (одна миллиардная) |
Нажмите
здесь
для большего количества имен для
очень большие и очень маленькие числа
.
Еще одно следствие нашего использования база 10 хороший образец между отрицательными степенями 2 и полномочия 5 .
Полномочия 2 | Полномочия 5 |
| 2 − 5 «=» 1 32 «=» 0,03125 | 5 − 5 «=» 1 3125 «=» 0,00032 |
| 2 − 4 «=» 1 16 «=» 0,0625 | 5 − 4 «=» 1 625 «=» 0,0016 |
| 2 − 3 «=» 1 8 «=» 0,125 | 5 − 3 «=» 1 125 «=» 0,008 |
| 2 − 2 «=» 1 4 «=» 0,25 | 5 − 2 «=» 1 25 «=» 0,04 |
| 2 − 1 «=» 1 2 «=» 0,5 | 5 − 1 «=» 1 5 «=» 0,2 |
| 2 0 «=» 1 | 5 0 «=» 1 |
Что такое составные числа? Объяснение для первичного
Составные числа являются обратными простым числам. Здесь мы объясняем, что именно означает этот раздел теории чисел, рассказываем, как его используют и изучают в начальных школах, и приводим несколько примеров вопросов, связанных с составными числами.
Здесь мы объясняем, что именно означает этот раздел теории чисел, рассказываем, как его используют и изучают в начальных школах, и приводим несколько примеров вопросов, связанных с составными числами.
Учащиеся официально знакомятся с простыми и составными числами в 5-м классе и должны работать в диапазоне от 1 до 100.
Что такое составное число?Простое число может иметь только 2 делителя: 1 и само число. 3 будет простым числом, поскольку его делителями являются только 1 и 3.
Составное число, с другой стороны, может быть любым целым числом, которое имеет более двух делителей. Это может быть четное или нечетное число.
Помните, что составным числом может быть любое данное число, которое является целым положительным числом (или натуральным числом), делители которого являются меньшими целыми положительными числами, при условии, что число имеет минимум 3 делителя.
Обратите внимание, что сложное число имеет большое количество множителей, и объяснение этой концепции ученикам может помочь им вспомнить, что составное число имеет несколько множителей по сравнению с простым числом, которое имеет только два множителя.
Подробнее: Что такое факторы?
Примеры составных чисел включают:
- 4, так как оно имеет три делителя: 1,2 и 4.
- Между 10 есть 5 составных чисел: 4, 6, 8, 9, 10
1 не является ни простым, ни составным числом.
БЕСПЛАТНЫЕ рабочие листы простых и составных чисел
БЕСПЛАТНЫЙ ресурс, включающий 29 вопросов для учащихся 5-х и 6-х классов, которые помогут проверить их способность работать с простыми числами.
Составные числа в начальной школеТермин «составные числа» официально не используется в Великобритании до 5-го класса. использовать словарь простых чисел, простых множителей и составных (не простых) чисел, чтобы установить, является ли число до 100 простым, и вспомнить простые числа до 19».
Учащимся не будет предложено идентифицировать числа как составные вне контекста обсуждения простых чисел.
Составные числа от 1 до 100 Составные числа от 1 до 100… 24 , 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56 , 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88 , 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.
Студенты не должны заучивать этот список наизусть. Использование тестов делимости для нахождения множителей числа очень полезно при определении того, является ли число простым или составным.
Учащиеся должны знать, как находить простые числа до 100, и знать простые числа до 19. Тесты на простоту, такие как решето Эратосфена или просто пробное деление, могут быть методами, которые учащиеся используют, чтобы выяснить, какие числа являются простыми до 19. число n, так как учащиеся будут работать в диапазоне небольших чисел.
Поэтому проще найти простые числа и знать, что числа, не являющиеся простыми, называются составными числами.
Знакомство учащихся 5-х классов с концепцией составных чисел в рамках онлайн-интервенции Third Space Learning. Как это связано с другими областями математики? Помимо идентификации чисел как простых или составных, маловероятно, что учащимся потребуется знать, что числа являются составными. Однако применение составных чисел используется в математике для описания формы, измерения, количественного определения количества объектов и выполнения арифметических операций.
Если вы не работаете в сфере кибербезопасности (где важны простые числа) или не работаете учителем, вы вряд ли столкнетесь с термином «составные числа». Однако применение составных чисел, то есть любого целого числа, не являющегося простым, используется в математике (см. выше).
Пример работы составных чиселВ. Поместите эти числа в таблицу ниже.
2,3,4,5,6,7,8,9,10
| Простой | Составной |
|---|---|
Студенты должны были запомнить простые числа до 19 включительно. Они могли бы использовать это, чтобы записать простые числа в правильную секцию, а затем сделать вывод, что остальные числа составные.
| Prime | Composite |
|---|---|
| 2, 3, 5, 7 | 4, 6, 9, 10 9001 1 |
Учащиеся, которые не знают простых чисел до 19, могут найти множители каждого числа, используя факты умножения.
2 = 2 x 1 (2 фактора)
3 = 3 x 1 (2 фактора)
4 = 4 x 1 = 2 x 2 (3 фактора)
Примеры вопросов с составными числами9 0008 1. Как определяется составное число?
(Ответ: число с более чем двумя делителями)
2. Какие из следующих чисел являются составными? 51, 97, 69, 57, 53, 90
(Ответ: 90, 69, 57, 51)
3. Энди составляет число 17 из простого и составного числа только сложением. Какие могут быть числа?
(Ответы: 2 + 15, 3 + 14, 5 + 12, 7 + 10, 11 + 6, 13 + 4)
4. Чему равно произведение первых 3-х составных чисел?
(ответ: 192)
5. Чен выбирает составное число. Он умножает его на 10, а затем округляет до ближайшей сотни. Его ответ — 300. Напишите все возможные составные числа, которые мог выбрать Чен.
(ответы: 25, 26, 27, 28, 30, 32, 33, 34)
Хотите знать, как объяснить своим детям другие математические слова? Ознакомьтесь с нашим словарем для начинающих по математике или попробуйте эти:
- Что такое овладение математикой?
- Видео: как преподавать простые и составные числа
Вы можете найти множество рабочих листов для учеников начальных классов в Third Space Learning Math Hub.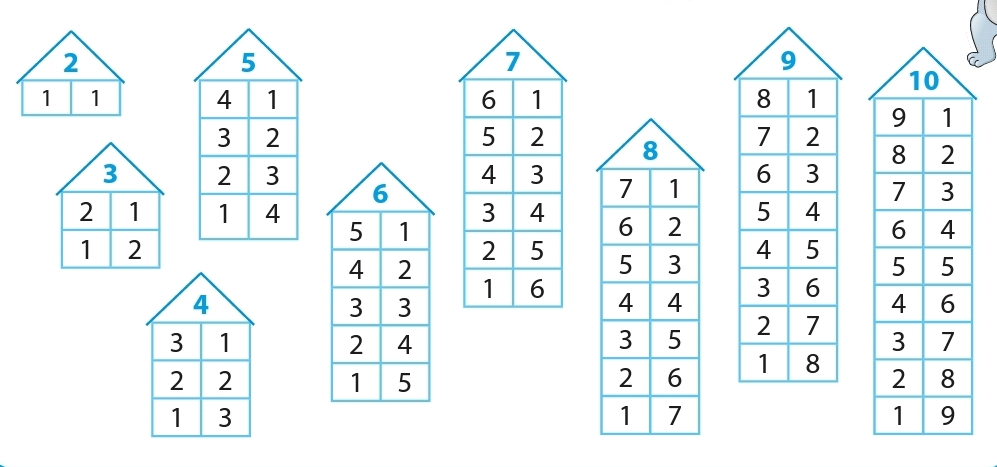

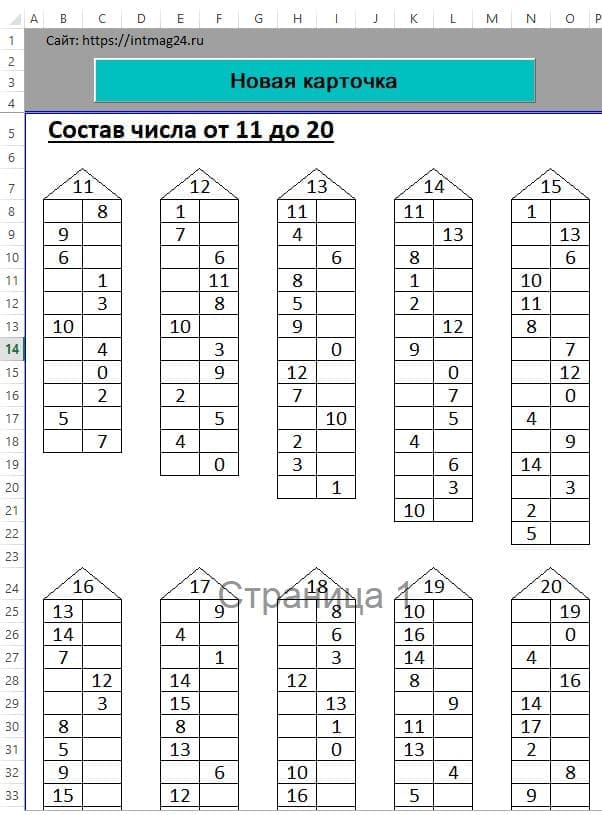
 Он каждый день находил по 8 яблок и прятал их в две норки.
Он каждый день находил по 8 яблок и прятал их в две норки.