Математика — Начальные классы — Сообщество взаимопомощи учителей Педсовет.su
Егорова Елена 5.0
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии «Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у нас пока нет, одни благодарности. Очень простая и понятная инструкция, что немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда коллеги понимают, как можно «упростить» работу учителя.
Наговицина Ольга Витальевна 5.0
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Чапаевка, Новоорский район, Оренбургская область
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология. Очень облегчило аналитическую работу, выявляются узкие места в подготовке к экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 5.0
учитель начальных классов, МБОУ СОШ №1, г.
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво. Мой ученик доволен, свой сертификат он вложил в портфолио. Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 4.0
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!
Арапханова Ашат 5. 0
0
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же составляю табель для работников. Удачи и успехов Вам в дальнейшем!
Дамбаа Айсуу 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и особенно радует, что есть варианты с сочинением, без сочинения, только анализ сочинения! Превосходно!
Тренажер по математике. 1 класс. Сравнение чисел в пределах 20 (2019) сост. Д. В. Овчаров, «Адукацыя і выхаванне»
При покупке на класс, группу предоставляются скидки !!!
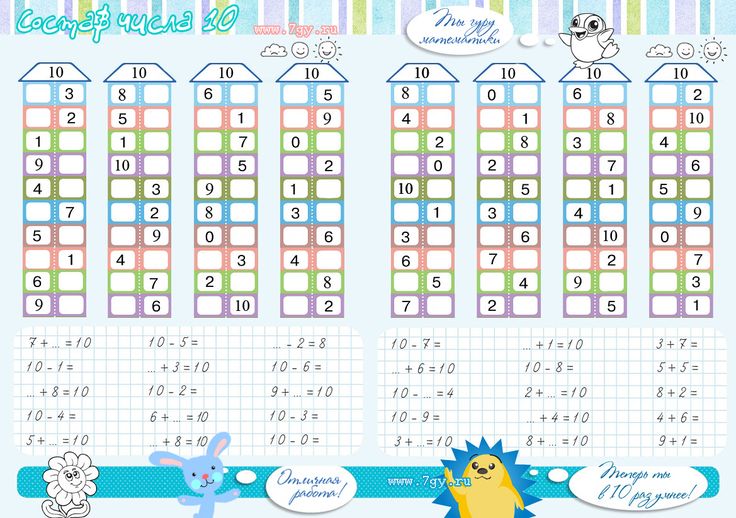
Пособие состоит из двух частей. В первой части сравниваются числа в пределах 10, во второй – в пределах 20. Задания даны блоками. За решение каждого блока положен бонус: капля, желудь и др. Решив четыре блока, ребенок использует полученные бонусы, например поливает цветок или кормит белку желудями.
Задания даны блоками. За решение каждого блока положен бонус: капля, желудь и др. Решив четыре блока, ребенок использует полученные бонусы, например поливает цветок или кормит белку желудями.
Чтобы сформировать и сохранить интерес ребенка к математике, лучше работать с пособием понемногу, но регулярно. За одно занятие с тренажером можно выполнять одну-две страницы заданий.
Пособие адресовано первоклассникам, их родителям, а также учителям начальных классов.
Полистать
Уважаемый покупатель.
Производитель оставляет за собой право изменять характеристики, комплектацию, описание товара. Мы стараемся своевременно вносить изменения на страницах нашего магазина Белка.By.
Характеристики товара получены из открытых источников, в т.ч. из каталогов производителя и официальных сайтов. 100% точность и полнота описаний не гарантированы.
Если Вы нашли неточности в описании и характеристиках, то отправьте нам на e-mail [email protected] наименование товара и пункт, в котором содержится ошибка. Также вы можете указать в отзыве к этому товару о наличии неточностей в описании.
Также вы можете указать в отзыве к этому товару о наличии неточностей в описании.
Данное предложение не является публичной офертой. Выбранный Вами товар может отсутствовать на складе, и/или быть зарезервированным, оплаченным другим покупателем и изменен в цене.
В период повышенного спроса срок сборки заказа может составить 1-10 дней.
| Общие характеристики | |
| Год | 2019 |
| Издательство | Адукацыя і выхаванне |
| Штрихкод | 9789855991527 |
| ISBN | 978-985-599-152-7 |
| 16 | |
| Класс | 1 класс |
| Формат | 14,5×21,5 см |
| Обложка, переплёт | мягкий |
| Производитель | Республиканское унитарное предприятие «Издательство «Адукацыя і выхаванне». Адрес: ул. Будённого, 2-, 220070, г. Минск. |
Ваше имя:
Ваш отзыв:
Примечание: HTML разметка не поддерживается! Используйте обычный текст.
Достоинства:
Недостатки:
Оценка: Плохо Хорошо
Защита от роботовВведите код в поле ниже
Тенденции структура-состав в многокомпонентных боросиликатных стеклах, полученные в результате моделирования молекулярной динамики с улучшенными силовыми полями B-O и P-O
Тенденции структура-состав в многокомпонентных боросиликатных стеклах, полученные в результате моделирования молекулярной динамики с улучшенными силовыми полями B-O и P-O†
Бальцар Стивенссон, а Ян Ю а и Маттиас Эден * и
Принадлежности автора
* Соответствующие авторы
и Кафедра физической химии, кафедра химии материалов и окружающей среды, Стокгольмский университет, SE-106 91 Стокгольм, Швеция
 [email protected]
[email protected]Аннотация
Мы представляем всестороннее молекулярно-динамическое (МД) исследование тенденций состав-структура в наборе из 25 стекол с широким диапазоном составов из следующих четырех систем возрастающей сложности: Na 2 O–B 2 O 3 , Na 2 O–B 2 O 3 –SiO 2 , Na 2 O–CaO–SiO 2 –P 2 O 5 , and Na 2 O–CaO–B 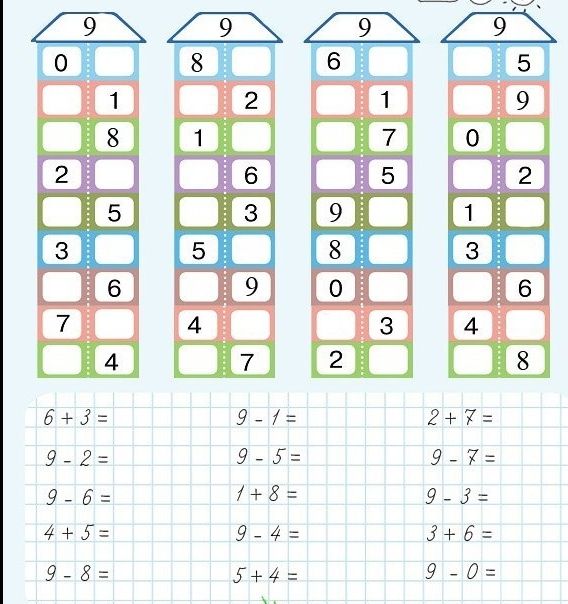 Обсуждается влияние смоделированной скорости охлаждения расплава на составы боратов/фосфатов. Каждый местный {BO 3 , BO 4 , SiO 4 , PO 4 } координационная среда оставалась независимой от точного набора сосуществующих образующих сеть, в то время как все тенденции, наблюдаемые в длинах/углах связей, в основном отражали полимеризацию стеклосетки, т.е. , относительные количества мостикового кислорода (BO) и немостиковые формы кислорода (NBO). Структурные роли катионов Na + /Ca 2+ также были исследованы, нацеливаясь на их локальное координационное окружение и их относительные предпочтения связываться с различными боратными, силикатными и фосфатными остатками. Мы оцениваем и обсуждаем общепринятую классификацию ионов щелочных/щелочноземельных металлов как компенсаторов заряда либо BO 4 тетраэдры или анионы NBO в боросиликатных стеклах, а также менее изученный режим обогащения NBO: катионы Na + /Ca 2+ в основном ассоциируют с BO/NBO разновидностями SiO03 9003 90 4 /BO 3 группы со значительным относительным содержанием Na–BO 4 контакты, наблюдаемые только в богатых бором стеклянных сетях, лишенных частиц NBO, тогда как богатые NBO стеклянные сети также обнаруживают значительное количество NBO- подшипник БО 4 тетраэдры.
Обсуждается влияние смоделированной скорости охлаждения расплава на составы боратов/фосфатов. Каждый местный {BO 3 , BO 4 , SiO 4 , PO 4 } координационная среда оставалась независимой от точного набора сосуществующих образующих сеть, в то время как все тенденции, наблюдаемые в длинах/углах связей, в основном отражали полимеризацию стеклосетки, т.е. , относительные количества мостикового кислорода (BO) и немостиковые формы кислорода (NBO). Структурные роли катионов Na + /Ca 2+ также были исследованы, нацеливаясь на их локальное координационное окружение и их относительные предпочтения связываться с различными боратными, силикатными и фосфатными остатками. Мы оцениваем и обсуждаем общепринятую классификацию ионов щелочных/щелочноземельных металлов как компенсаторов заряда либо BO 4 тетраэдры или анионы NBO в боросиликатных стеклах, а также менее изученный режим обогащения NBO: катионы Na + /Ca 2+ в основном ассоциируют с BO/NBO разновидностями SiO03 9003 90 4 /BO 3 группы со значительным относительным содержанием Na–BO 4 контакты, наблюдаемые только в богатых бором стеклянных сетях, лишенных частиц NBO, тогда как богатые NBO стеклянные сети также обнаруживают значительное количество NBO- подшипник БО 4 тетраэдры.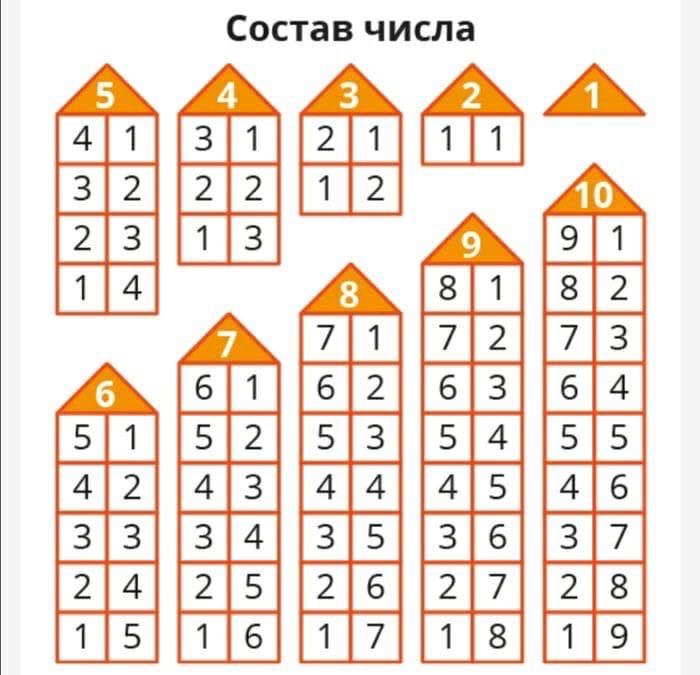
python — Генерация списка случайных чисел, суммируясь с 1
спросил
Изменено 11 месяцев назад
Просмотрено 102 тысячи раз
- Этот вопрос не является дубликатом Получение N случайных чисел, сумма которых равна M, потому что:
- Большинство ответов на посвящены теории, а не конкретному кодовому решению в Python для ответа на этот вопрос
- Принятый ответ здесь на 5 лет старше, чем один ответ в дубликате, который отвечает на этот вопрос.
- Повторяющийся принятый ответ не отвечает на этот вопрос
Как составить список из N (скажем, 100) случайных чисел, чтобы их сумма была равна 1?
Я могу составить список случайных чисел с
r = [random.random() для i в диапазоне (1100)]
Как мне изменить это так, чтобы сумма списка равнялась 1 (это для моделирования вероятности).
- питон
- случайный
15
Самое простое решение — взять N случайных значений и разделить их на сумму.
Более общим решением является использование распределения Дирихле который доступен в numpy.
Путем изменения параметров раздачи можно изменить «случайность» отдельных чисел
>>> импортировать numpy как np, numpy.random
>>> напечатать np.random.dirichlet (np.ones (10), размер = 1)
[[ 0,01779975 0,14165316 0,01029262 0,168136 0,03061161 0,09046587
0,19987289 0,13398581 0,03119906 0,17598322]]
>>> напечатать np.random.dirichlet(np.ones(10)/1000.,size=1)
[[ 2,63435230e-115 4,31961290e-209 1,41369771e-212 1,42417285e-188
0,00000000e+000 5,79841280e-143 0.00000000e+000 9.85329725e-005
9.997e-001 8.37460207e-246]]
>>> напечатать np. random.dirichlet(np.ones(10)*1000.,size=1)
[[ 0,09967689 0,10151585 0,10077575 0,09875282 0,09935606 0,10093678
0,09517132 0,09891358 0,10206595 0,10283501]]
random.dirichlet(np.ones(10)*1000.,size=1)
[[ 0,09967689 0,10151585 0,10077575 0,09875282 0,09935606 0,10093678
0,09517132 0,09891358 0,10206595 0,10283501]]
В зависимости от основного параметра распределение Дирихле будет либо давать векторы, все значения которых близки к 1./N, где N — длина вектора, либо давать векторы, где большинство значений векторов будет ~0, и будет одна 1 или что-то среднее между этими возможностями.
РЕДАКТИРОВАТЬ (через 5 лет после исходного ответа): Еще один полезный факт о распределении Дирихле заключается в том, что вы естественным образом получаете его, если создаете гамма-распределенный набор случайных величин, а затем делите их на их сумму.
17
Лучший способ сделать это — просто составить список из любого количества чисел, а затем разделить их все на сумму. Они совершенно случайны таким образом.
r = [random.random() для i в диапазоне (1100)] с = сумма (г) r = [i/s для i в r]
или, как предложил @TomKealy, сохранить сумму и создание в одном цикле:
rs = []
с = 0
для i в диапазоне (100):
г = случайный. случайный ()
с += г
rs.append(r)
случайный ()
с += г
rs.append(r)
Для максимальной производительности используйте numpy :
import numpy as np а = np.random.random (100) а /= а.сум()
И вы можете дать случайным числам любое распределение, которое вы хотите, для распределения вероятностей:
a = np.random.normal(size=100) а /= а.сум()
—- ГРМ —-
В [52]: %%timeit
...: r = [random.random() для i в диапазоне (1100)]
...: с = сумма (г)
...: r = [i/s для i в r]
....:
1000 циклов, лучшее из 3: 231 мкс на цикл
В [53]: %%timeit
....: rs = []
....: с = 0
....: для i в диапазоне (100):
....: г = рандом.случайный()
....: с += г
....: rs.append(r)
....:
10000 циклов, лучший из 3: 39,9 мкс на цикл
В [54]: %%timeit
....: а = np.random.random (100)
....: а /= а.сумма()
....:
10000 циклов, лучший из 3: 21,8 мкс на цикл
9
Разделение каждого числа на сумму может не дать желаемого распределения.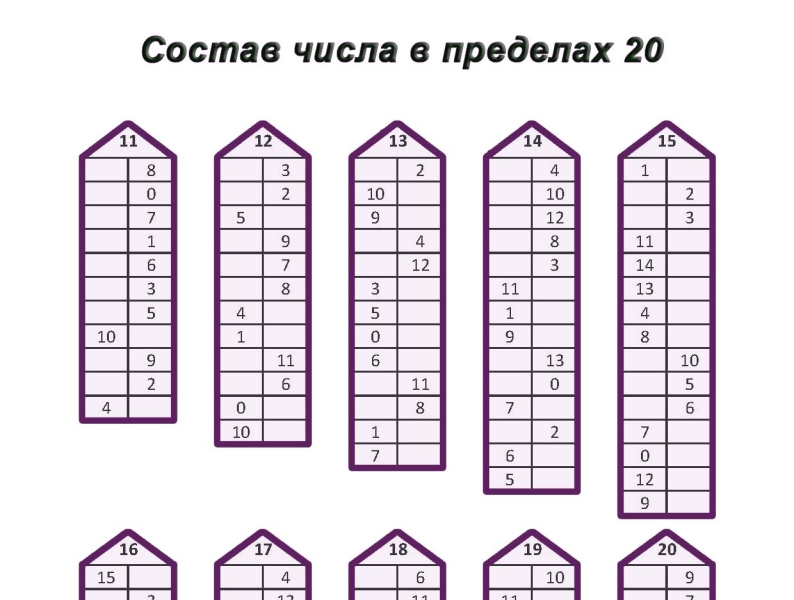 Например, с двумя числами пара x,y = random.random(), random.random() равномерно выбирает точку на квадрате 0<=x<1, 0<=y<1. Деление на сумму «проецирует» эту точку (x, y) на прямую x + y = 1 вдоль линии от (x, y) до начала координат. Точки около (0,5,0,5) будут гораздо более вероятными, чем точки около (0,1,0,9).
Например, с двумя числами пара x,y = random.random(), random.random() равномерно выбирает точку на квадрате 0<=x<1, 0<=y<1. Деление на сумму «проецирует» эту точку (x, y) на прямую x + y = 1 вдоль линии от (x, y) до начала координат. Точки около (0,5,0,5) будут гораздо более вероятными, чем точки около (0,1,0,9).
Тогда для двух переменных x = random.random(), y=1-x дает равномерное распределение вдоль сегмента геометрической прямой.
С 3 переменными вы выбираете случайную точку в кубе и проецируете (радиально, через начало координат), но точки рядом с центром треугольника будут более вероятными, чем точки рядом с вершинами. Полученные точки находятся на треугольнике в плоскости x+y+z. Если вам нужен беспристрастный выбор точек в этом треугольнике, масштабирование бесполезно.
Задача усложняется в n-мерах, но вы можете получить низкую точность (но высокую точность, для всех вас, любителей лабораторных наук!) до N, а затем разделив каждое из них на N.
Недавно я придумал алгоритм для небольших n, N.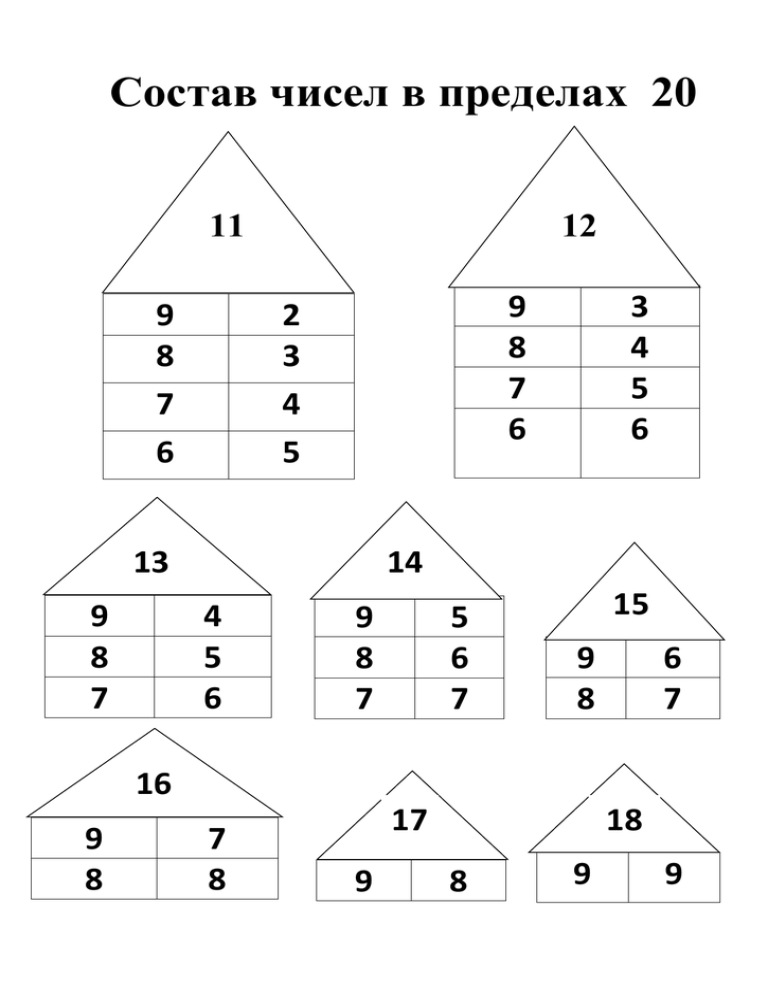 Он должен работать для n = 100 и N = 1 000 000, чтобы давать 6-значные случайные числа. См. мой ответ по адресу:
Он должен работать для n = 100 и N = 1 000 000, чтобы давать 6-значные случайные числа. См. мой ответ по адресу:
Создавать ограниченные случайные числа?
1
Создайте список, состоящий из 0 и 1, затем добавьте 99 случайных чисел. Отсортируйте список. Последовательные различия будут длинами интервалов, которые в сумме дают 1.
Я не очень хорошо владею Python, так что извините меня, если есть более Pythonic способ сделать это. Я надеюсь, что цель ясна:
случайный импорт
значения = [0,0, 1,0]
для я в диапазоне (99):
значения.добавление(случайное.случайное())
значения.sort()
результаты = []
для я в диапазоне (1,101):
results.append (значения [i] - значения [i-1])
распечатать результаты
Вот обновленная реализация в Python 3:
import random
защита сумма_к_одному (n):
значения = [0,0, 1,0] + [random.random() для _ в диапазоне (n - 1)]
значения.sort()
вернуть [значения[i+1] - значения[i] для i в диапазоне (n)]
печать (sum_to_one (100))
В дополнение к решению @pjs мы также можем определить функцию с двумя параметрами.
импортировать numpy как np
по определению сумма_к_х (п, х):
значения = [0,0, x] + список (np.random.uniform (низкий = 0,0, высокий = x, размер = n-1))
значения.sort()
вернуть [значения[i+1] - значения[i] для i в диапазоне (n)]
сумма_к_х(10, 0,6)
Вне:
[0,079058655684546,
0,041686479022,
0,09897491411670578,
0,065152293196646,
0,0005448002664,
0,12329662037166766,
0,09562168167787738,
0,01641359261155284,
0,058273232428072474,
0,020977718663918954]
генерирует 100 случайных чисел независимо от диапазона. суммируйте полученные числа, разделите каждое на общее количество.
Если вы хотите иметь минимальный порог для случайно выбранных чисел (т. е. сгенерированные числа должны быть не менее min_thresh ),
rand_prop = 1 - num_of_values * min_thresh random_numbers = (np.random.dirichlet (np.ones (10), size = 1) [0] * rand_prop) + min_thresh
Просто убедитесь, что у вас есть num_of_values (количество генерируемых значений), чтобы можно было генерировать требуемые числа ( num_values <= 1/min_thesh )
Итак, в основном, мы фиксируем некоторую часть 1 для минимального порога, затем мы создаем случайные числа в другой части. Мы добавляем
Мы добавляем min_thesh ко всем числам, чтобы получить сумму 1.
Например: скажем, вы хотите сгенерировать 3 числа с min_thresh = 0,2. Мы создаем часть для заполнения случайными числами [1 - (0,2x3) = 0,4]. Мы заполним эту часть и добавим 0,2 ко всем значениям, чтобы мы также могли заполнить 0,6.
Стандартное масштабирование и сдвиг, используемые в теории генерации случайных чисел. Кредит принадлежит моему другу Джилу Вайшнаву (я не уверен, есть ли у него профиль SO) и @sega_sai.
Альтернативным решением может быть использование random.choice и деление на сумму:
import random п = 5 rand_num = [random.choice(range(0,100)) for r in range(n)] # создание случайных целых чисел rand_num = [i/sum(rand_num) for i in rand_num] # нормализовать их
3
Вдохновленный ответом @sega_sai с актуальной и рекомендованной реализацией numpy [март 2022]
из numpy.random import default_rng rng = default_rng() rng.dirichlet (np.ones (10), размер = 1) >>> массив([[0.01279836, 0,16891858, 0,01136867, 0,17577222, 0,27944229, 0,06244618, 0,19878224, 0,02481954, 0,01478089, 0,05087103]])
Ссылки:
- Документация по случайной выборке Numpy
- Документация генератора случайных чисел и Документация генератора случайных чисел Дирихле
Вы могли бы легко сделать с:
r.append(1 - sum(r))
1
В духе «разделить каждый элемент в списке на сумму списка» это определение создаст список случайных чисел длины = ЧАСТИ, сумма = ИТОГО, с округлением каждого элемента до МЕСТ (или нет):
случайный импорт
время импорта
ЧАСТИ = 5
ВСЕГО = 10
МЕСТА = 3
def random_sum_split (частей, всего, мест):
а = []
для n в диапазоне (частях):
a.append(случайный.случайный())
б = сумма (а)
c = [x/b для x в a]
д = сумма (с)
е = с
если места != Нет:
e = [округление (x * общее количество мест) для x в c]
f = e[-(части-1):]
г = общее количество - сумма (f)
если места != Нет:
г = раунд (г, места)
f. insert(0, г)
журнал (а)
журнал (б)
журнал (с)
журнал (г)
журнал (е)
журнал (f)
журнал (г)
возврат f
определить тик():
если info.tick == 1:
начало = время.время()
альфа = random_sum_split (ЧАСТИ, ВСЕГО, МЕСТА)
бревно('********************')
log('***** РЕЗУЛЬТАТЫ ******')
лог('альфа: %s' % альфа)
log('всего: %.7f' % сумма(альфа))
log('детали: %s' % ЧАСТЕЙ)
журнал('мест: %s' % PLACES)
конец = время.время()
log('истекшее: %.7f' % (конец-начало))
insert(0, г)
журнал (а)
журнал (б)
журнал (с)
журнал (г)
журнал (е)
журнал (f)
журнал (г)
возврат f
определить тик():
если info.tick == 1:
начало = время.время()
альфа = random_sum_split (ЧАСТИ, ВСЕГО, МЕСТА)
бревно('********************')
log('***** РЕЗУЛЬТАТЫ ******')
лог('альфа: %s' % альфа)
log('всего: %.7f' % сумма(альфа))
log('детали: %s' % ЧАСТЕЙ)
журнал('мест: %s' % PLACES)
конец = время.время()
log('истекшее: %.7f' % (конец-начало))
результат:
Ожидание... Успешно сохранено. [2014-06-13 00:01:00] [0.33561018369775897, 0.4904215932650632, 0.20264927800402832, 0.118862130636748, 0.03107818050878819] [2014-06-13 00:01:00] 1.17862136611 [2014-06-13 00:01:00] [0.28474809073311597, 0.41609766067850096, 0.17193755673414868, 0.10084844382959707, 0.02636824802463724] [2014-06-13 00:01:00] 1.0 [2014-06-13 00:01:00] [2,847, 4,161, 1,719, 1,008, 0,264] [2014-06-13 00:01:00] [2,848, 4,161, 1,719, 1,008, 0,264] [2014-06-13 00:01:00] 2.
 random() для i в диапазоне (1100)]
random() для i в диапазоне (1100)]
 random.dirichlet(np.ones(10)*1000.,size=1)
[[ 0,09967689 0,10151585 0,10077575 0,09875282 0,09935606 0,10093678
0,09517132 0,09891358 0,10206595 0,10283501]]
random.dirichlet(np.ones(10)*1000.,size=1)
[[ 0,09967689 0,10151585 0,10077575 0,09875282 0,09935606 0,10093678
0,09517132 0,09891358 0,10206595 0,10283501]]
 случайный ()
с += г
rs.append(r)
случайный ()
с += г
rs.append(r)
 dirichlet (np.ones (10), размер = 1)
>>> массив([[0.01279836, 0,16891858, 0,01136867, 0,17577222, 0,27944229,
0,06244618, 0,19878224, 0,02481954, 0,01478089, 0,05087103]])
dirichlet (np.ones (10), размер = 1)
>>> массив([[0.01279836, 0,16891858, 0,01136867, 0,17577222, 0,27944229,
0,06244618, 0,19878224, 0,02481954, 0,01478089, 0,05087103]])
 insert(0, г)
журнал (а)
журнал (б)
журнал (с)
журнал (г)
журнал (е)
журнал (f)
журнал (г)
возврат f
определить тик():
если info.tick == 1:
начало = время.время()
альфа = random_sum_split (ЧАСТИ, ВСЕГО, МЕСТА)
бревно('********************')
log('***** РЕЗУЛЬТАТЫ ******')
лог('альфа: %s' % альфа)
log('всего: %.7f' % сумма(альфа))
log('детали: %s' % ЧАСТЕЙ)
журнал('мест: %s' % PLACES)
конец = время.время()
log('истекшее: %.7f' % (конец-начало))
insert(0, г)
журнал (а)
журнал (б)
журнал (с)
журнал (г)
журнал (е)
журнал (f)
журнал (г)
возврат f
определить тик():
если info.tick == 1:
начало = время.время()
альфа = random_sum_split (ЧАСТИ, ВСЕГО, МЕСТА)
бревно('********************')
log('***** РЕЗУЛЬТАТЫ ******')
лог('альфа: %s' % альфа)
log('всего: %.7f' % сумма(альфа))
log('детали: %s' % ЧАСТЕЙ)
журнал('мест: %s' % PLACES)
конец = время.время()
log('истекшее: %.7f' % (конец-начало))