Сочетательные свойства сложения и умножения: Сочетательное свойство умножения – примеры, правила (5 класс, математика)

Содержание

Cочетательное свойство умножения. Cочетательное свойство сложения и умножения.

Альфашкола
Статьи
Сочетательное свойство умножения

Сочетальное свойство умножение помогает при решении примеров, то есть упрощает вычисление.

Запишем это свойство:

$(a*b)*c=a*(b*c)$

То есть данное свойство предоставляет право выбора выполнения действия при умножении, то есть позволяет выбирать более легкий способ решения.

Пример 1. Вычислите

$25*(4*237)$
$125*(8*89)$
$20*(5*543)$

Решение:

$25*(4*237)=(25*4)*237=100*237=23\;700$
$125*(8*89)=(125*8)*89=1000*89=89\:000$
$20*(5*543)$$=(20*5)*543=100*543=54\;300$

Данное свойсвто можно применять разложив один из множителей на множители.

Пример 2. Вычислите

$25*48$
$125*72$
$20*55$

Решение:

$25*48=25*4*12=100*12=1\;200$
$125*72=125*8*9=1\;000*9=9\;000$
$20*55=20*5*11=100*11=1\;100$

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Юлия Игоревна Ярош

Репетитор по математике

Стаж (лет)

Образование:

Брестский государственный университет имени А. С. Пушкина

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Оксана Николаевна Хаустова

Репетитор по математике

Стаж (лет)

Образование:

Саратовский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Светлана Николаевна Комашко

Репетитор по математике

Стаж (лет)

Образование:

Минский государственный лингвистический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

Математика
Репетитор по физике
Репетитор по химии
Репетитор по русскому языку
Репетитор по английскому языку
Репетитор по обществознанию
Репетитор по истории России
Репетитор по биологии
Репетитор по географии
Репетитор по информатике

Специализации

Репетитор по олимпиадной математике
Репетитор по алгебре
Репетитор для подготовки к ОГЭ по физике
Репетитор по грамматике русского языка
Репетитор по грамматике английского языка
ВПР по математике
Репетитор для подготовки к ВПР по английскому языку
ВПР по физике
Репетитор для подготовки к ВПР по обществознанию
Репетитор для подготовки к ОГЭ по обществознанию

§ Свойства умножения и деления

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную
Площадь
Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое
Чётные и нечётные функции

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Нужно уметь извлекать из факта смысл. Максим Горький

на главную

Введите тему

Поддержать сайт

Свойства сложения и вычитания Свойства умножения и деления

Свойства умножения

Переместительное свойство умножения

Запомните!

От перестановки множителей произведение не меняется.

a · b = b · a

Сочетательное свойство умножения

Запомните!

Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

a · (b · c) = (a · b) · c

Переместительное и сочетательное свойства умножения позволяют сформулировать правило преобразования произведений.

Запомните!

При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.

Свойство нуля при умножении

Запомните!

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

a · 0 = 0

0 · a · b · c = 0

Распределительное свойство умножения относительно сложения

Запомните!

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.

(a + b) · c = a · c + b · c

Это свойство справедливо для любого количества слагаемых.

(a + b + с + d) · k = a · k + b · k + c · k + d · k

Распределительное свойство умножения относительно вычитания

Запомните!

Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.

В буквенном виде свойство записывается так:

(a − b) · c = a · c − b · c

Запомните!

Свойства деления

Ни одно число нельзя делить на ноль.
При делении нуля на число получается ноль.
0 : a = 0
При делении любого числа на 1 получается это же число.
b : 1 = b

Запомните!

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

a : b = (a · k) : (b · k)

, где «k» — любое натуральное число.

Обратите внимание, что именно свойство деления выше позволяет нам сокращать дроби.

Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений.

Свойства сложения и вычитания Свойства умножения и деления

Свойства действий с рациональными числами 6 класс онлайн-подготовка на Ростелеком Лицей

Введение

Основные свойства действий с числами:

Первые два свойства – это свойства сложения, следующие два – умножения. Пятое свойство относится к обеим операциям.

Ничего нового в этих свойствах нет. Они были справедливы и для натуральных, и для целых чисел. Они также верны для рациональных чисел и будут верны для чисел, которые мы будем изучать дальше (например, иррациональных).

Перестановочные свойства:

От перестановки слагаемых или множителей результат не меняется.

Сочетательные свойства: , .

Сложение или умножение нескольких чисел можно делать в любом порядке.

Распределительное свойство: .

Свойство связывает обе операции – сложение и умножение. Также если его читать слева направо, то его называют правилом раскрытия скобок, а если в обратную сторону – правилом вынесения общего множителя за скобки.

Следующие два свойства описывают нейтральные элементы для сложения и умножения: прибавление нуля и умножение на единицу не меняют исходного числа.

Еще два свойства, которые описывают симметричные элементы для сложения и умножения, сумма противоположных чисел равна нулю; произведение обратных чисел равно единице.

Следующее свойство: . Если число умножить на ноль, в результате всегда будет ноль.

Последнее свойство, которое мы рассмотрим: .

Умножив число на , получаем противоположное число. У этого свойства есть особенность. Все остальные рассмотренные свойства нельзя было доказать, используя остальные. Это же свойство можно доказать, используя предыдущие.

Умножение на

Докажем, что если умножить число на , то получим противоположное число. Используем для этого распределительное свойство: .

Оно верно для любых чисел. Подставим вместо числа и :

Слева в скобках стоит сумма взаимно противоположных чисел. Их сумма равна нулю (у нас есть такое свойство). Слева теперь . Справа , получаем: .

Теперь слева у нас стоит ноль, а справа – сумма двух чисел. Но если сумма двух чисел равна нулю, то эти числа взаимно противоположны. Но у числа только одно противоположное число: . Значит, – это и есть : .

Свойство доказано.

Такое свойство, которое можно доказать, используя предыдущие свойства, называют теоремой

Почему здесь нет свойств вычитания и деления? Например, можно было бы записать распределительное свойство для вычитания: .

Но так как:

вычитание любого числа можно эквивалентно записать в виде сложения, заменив число на противоположное:

деление можно записать в виде умножения на обратное число:

Значит, свойства сложения и умножения вполне можно применять для вычитания и деления. В итоге список свойства, которые необходимо запомнить, получается короче.

Свойства рациональных чисел

Все рассмотренные нами свойства не являются исключительно свойствами рациональных чисел. Всем этим правилам подчиняются и другие числа, например, иррациональные. Например, сумма и противоположного ему числа равна нулю: .

Решение примеров

Теперь мы перейдем к практической части, решим несколько примеров.

Рациональные числа в жизни

Те свойства предметов, которые мы можем описать количественно, обозначить каким-нибудь числом, называются величинами: длина, вес, температура, количество.

Одну и ту же величину можно обозначить и целым, и дробным числом, положительным или отрицательным.

Например, ваш рост м – дробное число. Но ведь можно сказать, что он равен см – это уже целое число (рис. 1).

Рис. 1. Иллюстрация к примеру

Еще один пример. Отрицательная температура по шкале Цельсия будет положительной по шкале Кельвина (рис. 2).

Рис. 2. Иллюстрация к примеру

При строительстве стены дома один человек может ширину и высоту измерить в метрах. У него получаются дробные величины. Все вычисления дальше он будет проводить с дробными (рациональными) числами. Другой человек может все измерить в количестве кирпичей в ширину и высоту. Получив только целые значения, он и вычисления будет проводить с целыми числами.

Сами величины не бывают ни целыми, ни дробными, ни отрицательными, ни положительными. Но число, которым мы описываем значение величины, уже является вполне конкретным (например, отрицательным и дробным). Это зависит от шкалы измерений. И когда мы от реальных величин переходим к математической модели, то работаем с конкретным типом чисел

Начнем со сложения. Слагаемые можно переставлять так, как нам удобно, и действия выполнять можно в любом порядке. Если слагаемые разных знаков оканчиваются на одну цифру, то удобно сначала выполнять действия с ними. Для этого поменяем слагаемые местами. Например:

Обыкновенные дроби с одинаковыми знаменателями легко складываются.

Противоположные числа в сумме дают ноль. Числа с одинаковыми десятичными «хвостами» легко вычитаются. Используя эти свойства, а также переместительный закон сложения, можно облегчить вычисление значения, например, следующего выражения:

Числа с дополняющими друга десятичными «хвостами» легко складываются. С целыми и дробными частями смешанных чисел удобно работать по отдельности. Используем эти свойства при вычислении значения следующего выражения:

Перейдем к умножению. Есть пары чисел, которые легко перемножить. Используя переместительное свойство, можно переставить множители так, чтобы они оказались рядом. Количество минусов в произведении можно посчитать сразу и сделать вывод о знаке результата.

Рассмотрим такой пример:

Если из сомножителей равен нулю, то произведение равно нулю, например: .

Произведение обратных чисел равно единице, а умножение на единицу не меняет значение произведения. Рассмотрим такой пример:

Рассмотрим пример с использованием распределительного свойства. Если раскрыть скобки, то каждое умножение выполняется легко:

Иногда для упрощения вычислений удобно общий множитель вынести за скобку:

Умножение на ноль дает в результате ноль. Верно и обратное утверждение: если произведение равно нулю, то хотя бы один из сомножителей равен нулю. Иными словами, не бывает так, чтобы перемножили два или несколько чисел, не равных нулю, и в ответе получили ноль. Это свойство позволяет легко решить некоторые уравнения.

Решение некоторых уравнений

Рассмотрим такие уравнения, где одна часть – это произведение нескольких множителей, а другая – ноль.

В этом уравнении левая часть – произведение трех множителей. Произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю. Приравняем каждый множитель к нулю, получим три уравнения.

Ответ: .

При решении таких уравнений нужно быть аккуратным. Кроме того, что один из множителей должен быть равен нулю, все остальные при этом должны иметь смысл.

Рассмотрим такой пример: . Если приравнять первую скобку к нулю, получим корень .Но при второй множитель не определён (деление на ноль не определено). Значит, не имеет смысла и вся левая часть уравнения. Получается, что единственным корнем уравнения будет ноль последней скобки, то есть число .

Ответ: .

Список рекомендованной литературы

Математика 5 класс. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. М.: Мнемозина, 2013.
Математика 5 класс. Ерина Т.М.. Рабочая тетрадь к учебнику Виленкина Н.Я. М.: Экзамен, 2013.
Математика 5 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С., М.: Вентана – Граф, 2013.

Рекомендованные ссылки на ресурсы сети Интернет

School-assistant.ru (Источник).
Cleverstudents.ru (Источник).
Лена24.рф (Источник).

Домашнее задание

1. Упростите выражения:

;

2. Выбрав удобный порядок вычисления, найдите значение выражения:

3. Найдите значение выражения:

Сочетательное и распределительное свойства умножения

Представим себе такую историю…

– 3 умножить на 2 и умножить на 12… так, так, так… Получается 72, – считал Саша.

– Саша, что ты там считаешь? – спросил у друга Паша.

– Папа привёз мне 3 коробки с шоколадными плитками, в каждой коробке по 2 плитки, а в каждой плитке по 12 долек. Мне стало так интересно, это же сколько шоколадных долек я съем. Представляешь, получилось 72 шоколадные дольки, – радовался Саша.

– Здорово! – сказал Паша. – Но я бы посчитал дольки по-другому. Смотри, у тебя есть 3 коробки, а в каждой коробке 2 шоколадные плитки по 12 шоколадных долек каждая… Посчитаем… тоже получается, что у тебя 72 шоколадные дольки.

– Как же это так? – задумался Саша. – Мы с тобой считали совсем по-разному, а количество долек получилось одинаковое. Разве может быть такое?

– Не знаю, – ответил Паша, – но точно знаю, кто может нам помочь!

– Ребята, прежде чем я вам объясню, почему у вас получилось одинаковое количество шоколадных долек, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь вернёмся к вашему вопросу, – продолжил Электроша. – Чтобы посчитать количество шоколадных долек, Саша 3 умножил на 2 и тем самым выяснил сколько шоколадных плиток ему привёз папа. А так как в каждой шоколадной плитке по 12 долек, то Саша полученное произведение умножил на 12. И получил, что всего у него 72 шоколадные дольки.

– Точно, Электроша! Я так и считал, – подтвердил Саша.

– В свою очередь, Паша решил посчитать количество шоколадных долек другим способом. Он 3 умножил на произведение 2 и 12, так как в трёх коробках будет по 2 умножить на 12 шоколадных долек. И тоже получил, что всего 72 шоколадные дольки.

– Да, именно таким способом я считал, – сказал Паша.

– Вы заметили, что способы подсчёта разные, а в результате получается одно и то же число – 72, – продолжил Электроша. – А почему так случилось? Да потому, что оба способа подсчёта верны и показывают нам очередное свойство умножения, которое называется сочетательное свойство умножения.

Запомните! Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.

В буквенном виде это свойство записывают так: .

Сочетательное свойство умножения разрешает в произведении ставить скобки и объединять множители как удобнее.

– Вот, например, давайте найдём значение выражения: , – предложил ребятам Электроша.

– Электроша, это сложный пример, – задумались мальчишки, – в уме нам такой не решить. Сначала нужно умножить 737 на 25, а потом ещё и на 4. Без калькулятора тут нам не обойтись.

– Ребята, пример кажется сложным только на первый взгляд, – подбодрил ребят Электроша. – Давайте применим сочетательное свойство умножения и возьмём в скобки множители 25 и 4. Смотрите, произведение 25 и 4 совсем не сложно найти в уме, оно равно 100. Останется посчитать, чему будет равно произведение 737 и 100.

– Получится 73 700, – сказали мальчишки.

– Молодцы! – похвалил ребят Электроша. – Вы заметили, как быстро мы справились с решением примера?

– Да… мы решили его за 5 секунд, – радовались мальчишки.

– Польза от сочетательного свойства умножения будет ещё больше, если применить его вместе с переместительным свойством. И помните, прежде чем начать вычисления, нужно всегда подумать, как это сделать проще!

– Давайте решим вот такой пример: .

– Сначала воспользуемся переместительным свойством умножения и переставим местами множители 5 и 824, – начал Паша. – А потом применим сочетательное свойство умножения и заключим в скобки множители 5 и 20.

– 5 умноженное на 20 равно 100, – продолжил Саша. – А теперь 824 умножим на 100. Получим 82 400.

– Молодцы! – похвалил ребят Электроша. – А теперь давайте решим вот такую задачку: Саша за 1 минуту может решить 3 примера, а Паша за это же время может решить 4 примера. Сколько примеров решат за 5 минут Саша и Паша вместе?

– Электроша, это же задача про нас! – обрадовались ребята.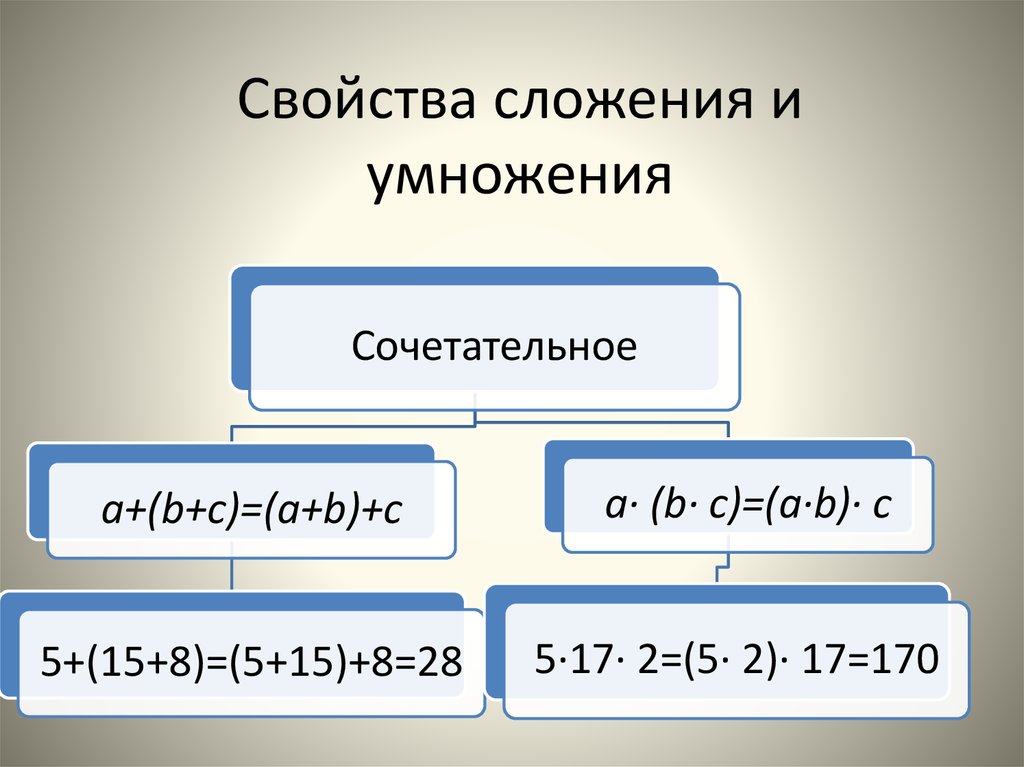

– В задаче сказано, что я могу решить 3 примера за 1 минуту, – начал Саша. – Значит, за 5 минут я могу решить 5 умножить на 3 примеров.

– А я за 1 минуту могу решить 4 примера, – продолжил Паша. – Тогда за 5 минут я смогу решить 5 умножить на 4 примеров.

– Осталось сложить наши решённые примеры, – сказали мальчишки. – И получим, что за 5 минут мы вместе можем решить 35 примеров.

– Молодцы! – похвалил ребят Электроша. – Но эту же задачу можно было решить и другим способом. Смотрите, за 1 минуту вы можете вместе решить 3 + 4 примеров. Тогда за 5 минут вы вместе решите 5 умноженное на сумму 3 и 4. Посчитаем… тоже получаем 35 примеров.

Посмотрите, правые части наших равенств равны, значит, будут равны и левые части. Получаем равенство, которое иллюстрирует распределительное свойство умножения относительно сложения.

Запомните! Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое из слагаемых и полученные произведения сложить.

В буквенном виде это свойство записывают так: .

Из распределительного свойства умножения относительно сложения следует, что это равенство справедливо и справа налево: .

Кстати, распределительное свойство умножения относительно сложения справедливо для трёх и более слагаемых.

– Напомните мне, какую формулу мы применяем для нахождения периметра прямоугольника, – спросил у ребят Электроша.

– , – ответили мальчишки.

– Молодцы! Применяя распределительное свойство умножения относительно сложения, формулу для нахождения периметра прямоугольника можно записать и в таком виде: 𝑃=2𝑎+2𝑏=2(𝑎+𝑏).

– Распределительное свойство умножения действует и относительно вычитания, – продолжил Электроша.

Запомните! Чтобы число умножить на разность двух чисел, можно это число умножить на уменьшаемое и вычитаемое и из первого произведения вычесть второе.

В буквенном виде это свойство записывают так: . Равенства справедливы для всех натуральных чисел при или .

– Давайте решим вот такой пример: , – предложил Электроша.

– Электроша, но тут какие-то сложные вычисления получаются, – расстроился Саша.

– Тут совсем нет ничего сложного, – подбодрил Сашу Электроша. – Применяя распределительное свойство умножения относительно вычитания, мы можем записать это выражение как 4 умножить на 250 минус 4 умножить на 25. Ну а теперь вы можете вычислить?

– Да, – обрадовались мальчишки. – Первое произведение равно 1000, второе – 100. Тогда разность произведений будет равна 900.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним задание.

Задание первое: вычислите наиболее удобным способом:

а) ;

б) ;

в) .

Решение: первое выражение: . Применим переместительное свойство умножения и поменяем местами второй и третий множители. Затем применим сочетательное свойство умножения и заключим в скобки первый и второй множители. Тогда в скобках получим 10. Осталось 10 умножить на 497. В результате получим 4970.

Следующее выражение: . Применим распределительное свойство умножения относительно сложения (справа налево). Получим произведение 209 и суммы чисел 19 и 81. В скобках получаем 100. 209 умножим на 100. В результате получим 20 900.

И последнее выражение: . Применим распределительное свойство умножения относительно вычитания. Получим произведение 28 и разности чисел 160 и 60. В скобках получаем 100. Тогда 28 умножим на 100. В результате получим 2800.

Сочетательное свойство умножения и его применение » Республиканский центр дистанционных олимпиад

Математика 2 класс

Тема урока: Сочетательное свойство умножения и его применение

Цель: учить упрощать выражение, содержащее только действия умножения.

Задачи :

Познакомить с сочетательным свойством умножения.
Формировать представление о возможности использования изученного свойства для рационализации вычислений.
Развивать представления в возможности решения «жизненных» задач средствами предмета «математика».
Развивать интеллектуальные и коммуникативные общеучебные умения.
Развивать организационные общеучебные умения, в том числе умения самостоятельно оценивать результат своих действий, контролировать самого себя, находить и исправлять собственные ошибки.

Тип урока: изучение нового материала.

Оборудование: карточки с заданием, наглядный материал (таблицы), презентация.

ХОД УРОКА

I. Организационный момент

Прозвенел и смолк звонок.
Начинается урок.
Вы зa парты тихо сели
На меня все посмотрели.

II. Устный счёт

– Посчитаем устно:

1) «Весёлые ромашки» (Слайды таблица умножения)

2) Математическая разминка. Игра «Найди лишнее» (Слайд )

485 45 864 947 670 134 (классификация на группы ЛИШНЕЕ 45 – двузначное, 670 – в записи числа нет цифры 4).
9 45 72 90 54 81 27 22 18 (9 – однозначное, 22 не делится на 9)

Строка чистописания. Прописать в тетради числа, чередуя: 45 22 670 9
– Подчеркнуть самую аккуратную запись числа

III. Сообщение темы и задач урока. (Слайд )

– Запишите число, тему урока.
– Прочитайте задачи нашего урока

IV. Подготовка к изучению нового материала

а) №1 – Сравните способы. Какое свойство сложения применили?

б) Верно ли выражение

На доске запись:

(23 + 490 + 17) + (13 + 44 + 7) = 23 + 490 + 17 + 13 + 44 + 7

– Назовите используемое свойство сложения. (Сочетательное)
– Какую возможность даёт сочетательное свойство?

Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок.

43 + 17 + (45 + 65 + 91) = 91 + 65 + 45 + 43 + 17

– Какие свойства сложения мы применяются в данном случае?

Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок. При этом вычисления можно выполнять в любом порядке.

– В таком случае как называется ещё одно свойство сложения? (Переместительное)

V. Изучение нового материала

1) Если мы будем выполнять умножение в том порядке, в каком записаны выражения, то возникнут трудности. Что же поможет нам снять эти трудности?

(2 • 6) • 3 = 2 • 3 • 6

2) Работа по учебнику с. 6, № 2

Сколько рядов? Сколько прямоугольников в каждом ряду? Сколько квадратов в каждом прямоугольнике?

Найдём разными способами количество всех квадратов на рисунке.

а) (3 • 2) • 4 = 6 • 4 = 24 (квадрата).

Объясни запись.

б) 3 • (2 • 4) = 3 • 8 = 24 (квадрата). Объясни запись.

Сравни эти способы. Сделай вывод.

3) Проверь, равны ли значения выражений. Устно.

Запись на доске:

(5 • 2) • 3 и 5 • (2 • 3)
(4 • 7) • 5 и 4 • (7 • 5)

4) Сделай вывод. Правило.

Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
– Расскажите сочетательное свойство умножения.
– Объясните сочетательное свойство умножения на примерах

5) Коллективная работа

На доске: (8 • 3) • 2, (6 • 3) • 3, 2 • (4 • 7)

VI. Физминутка

1) Игра «Зеркало». (Слайд)

Свет мой зеркальце, скажи,
Да всю правду доложи.
Мы ль на свете всех умнее,
Всех забавней и смешнее?
Повторяйте все за мной
Веселые движения физминутки озорной.

2) Физминутка для глаз «Зоркие глазки».

– Закройте глаза на 7 секунд, посмотрите направо, затем налево, вверх, вниз, затем сделайте глазами 6 кругов по часовой стрелке, 6 кругов против часовой стрелки.

VII. Закрепление изученного

1)Работа по учебнику. решение задачи. (№3)

– В тетради решение задачи можно оформить следующим образом: (2 • 4) • 3

2) Работа в парах (по карточкам): (Слайд)

– Поставь знаки, не вычисляя:

(–Какое свойство?)
(15 • 2) •4 15 • ( 2 •4)

(8 • 9) • 6 7 • ( 9 • 6)

(428 • 2) • 0 1 • (2 • 3)

(3 • 4) • 2 3 + 4 + 2

(2 • 3 ) • 4 ( 4 • 2 ) • 3

Проверка: (Слайд)

(15 • 2) •4 =15 • ( 2 •4)

(8 • 9) • 6 >7 • ( 9 • 6)

(428• 2) • 0 <1 • (2 • 3)

(3 • 4) • 2 >3 + 4 + 2

(2 • 3 ) • 4 =( 4 • 2 ) • 3

3) Самостоятельная работа (по учебнику)

(с. 6, № 5 – по вариантам)

Свойства умножения: (Слайд 14).

Переместительное свойство
Сочетательное свойство

– Зачем нужно знать свойства умножения? (Слайд).

Чтобы быстро считать
Выбирать рациональный способ счета
Решать задачи

VIII. Повторение пройденного материала. «Ветряные мельницы». (Слайд)

Числа 485, 583 и 681 увеличить на 38 и записать три числовых выражения (1 вариант)
Числа 583, 545 и 507 уменьшить на 38 и записать три числовых выражения (2 вариант)

485 + 38 523		583 + 38 621		681 + 38 719
583 – 38 545		545 – 38 507		507 – 38 469

Учащиеся выполняют задания по вариантам (двое учащихся решают задания на дополнительных досках).

Взаимопроверка.

IХ. Итог урока

– Чему учились сегодня на уроке?
– В чём же заключается смысл сочетательного свойства умножения?

Х. Рефлексия

– Кто считает, что понял смысл сочетательного свойства умножения? Кто доволен своей работой на уроке? Почему?
– Кто знает, над чем ему еще надо поработать?
– Ребята, если вам урок понравился, если вы довольны своей работой, то поставьте руки на локти и покажите мне ладошки. А если вы были чем-то расстроены, то покажите мне обратную сторону ладошки.

XI. Информация о домашнем задании

– Какое домашнее задание вы бы хотели получить?

№6

По выбору:

1. Выучить правило с. 6
2. Придумать и записать выражение на новую тему с решением

Оценки за урок.

формулы и другие законы произведения, тождества и примеры для 5 класса

Математика

12.11.21

10 мин.

Арифметические операции произведения, сложения, вычитания и деления применяются в различных дисциплинах с физико-математическим уклоном. У каждой из них существуют определенные законы, позволяющие оптимизировать процессы вычисления. Для сложения и произведения следует применять распределительное, переместительное и сочетательное свойства умножения или сложения.

Оглавление:

Общие сведения

Базовые правила

Пример решения

Общие сведения

Для удобства описания арифметических операций следует ввести буквенные обозначения. Пусть первый коэффициент эквивалентен переменной «о», второй — «р», а результат — «r». К базовым арифметическим действиям относятся:

Сложение.
Вычитание.
Умножение.
Деление.

Сложение (+) — операция, увеличивающая исходное число на некоторое значение. Выражение состоит минимум из 3 коэффициентов, т. е. о+р=r. Первый и второй (о и р соответственно) называются слагаемыми, третий — суммой r.

Вычитанием (-) называется арифметическая операция, состоящая из уменьшаемого значения и вычитаемого, результатом которой является разность. Математическая запись имеет такой вид: о-р=r, где о — уменьшаемое, р — вычитаемое, а r — разность.

Третьей операцией является умножение (*), состоящая из коэффициентов, которых может быть более 2: первый и второй — множители, а третий — произведение. Операция записывается таким образом: о*р=r. Кроме того, существует краткая запись, при которой знак «*» не указывается, т. е. ор=r.

Деление (:) — арифметическая операция, позволяющая разделить одно число на другое. Математически она записывается следующим образом: о: р=r («о» — делимое, «р» — делитель и «r» — частное).

Следует отметить, что у каждой операции может быть и другое количество коэффициентов. Например, o*p*s*t=r, где o, p, s, t — множители, а r — результат. Однако при решении задач применяются некоторые законы, существенно оптимизирующие вычисления.

Базовые правила

При вычислении значения выражения математики рекомендуют применять определенные правила. Их можно комбинировать между собой. Эта методика позволяет сократить время на расчеты, а также тренирует мозг, при помощи которого появляется возможность выполнять сложные вычисления в устной форме. Кроме того, законы справедливы для любой арифметической операции.

Методы сложения

Для начала следует рассмотреть основные правила сложения. Они основываются на раскрытии скобок выражения, состоящего из нескольких слагаемых. К ним относятся сочетательный и переместительный. Первый закон можно сформулировать следующим образом: если 2 числа, находящиеся в скобках, связаны операцией сложения, при прибавлении к ним третьего значения можно сложить его с первым, а затем со вторым. Математическая форма записи приобретает такой вид: (о+р)+k=(о+k)+p. Возможна и такая запись: (о+р)+k=(р+k)+о.

Переместительный закон имеет такой вид: от перемены мест слагаемых величина алгебраической суммы не меняется. Математически запись выглядит так: о+р+k=р+k+о=р+о+к=к+о+р=к+р+о. Кроме того, существуют 2 следствия, на основании которых можно существенно сократить объем вычислений:

Если слагаемые эквивалентны между собой, тождество можно записать в виде произведения одного элемента на их количество, т. е. к+к+к+к+к=5к.
Нуль не учитывается при сложении.

Следующей операцией является вычитание. У него также существуют некоторые очень важные свойства.

Свойства вычитания

При выполнении арифметической операции вычитания специалисты рекомендуют придерживаться основных законов. К ним относятся следующие утверждения и формулы:

Если из произвольного «к» вычесть нулевое значение, результат будет эквивалентен этому числу. При вычитании из 0 числа «к» получается отрицательное число, равное величине с противоположным знаком, т. е. 0-к=-к.
Разность двух одинаковых чисел соответствует 0, т. е. к-к=0.
Если вычитаемое представлено суммой двух чисел, можно вычесть из уменьшаемого первое слагаемое, а затем второе, р-(о+к)=р-о-к.
Когда уменьшаемое записано в виде суммы, следует из первого слагаемого вычесть вычитаемое и к результату прибавить второй элемент суммы, т. е. (р+о)-к=р-к+о.

Этих правил будет достаточно для выполнения вычислений любого типа. Кроме операций сложения и вычитания, существуют более сложные арифметические действия.

Умножение и деление

Изучаются законы умножения в 5 классе. Они состоят из следующих формул и утверждений:

Результат умножения любой величины на нулевое значение равен 0.
Если умножить число на 1, получится оно же, т. е. к*1=к.
Переместительный закон произведения: при перемене мест множителей произведение неизменно, т. е. к*р*о=к*о*р=р*о*к=р*к*о=о*к*р=о*р*к.
Сочетательный закон умножения (ассоциативный): если количество множителей в выражении больше 2, можно перемножить 1 и 3, а затем их произведение использовать при расчетах, как второй множитель, т. е. (5*3)*2=(5*2)*3=10*3=30.
Распределительный: при умножении некоторого числа на сумму нужно умножить его на первое слагаемое и на второе, а затем сложить 2 величины, т. е. к (р+о)=кр+ко.

Наиболее сложной операцией является деление. У нее также есть некоторые важные свойства:

На 0 невозможно делить.
Если нуль разделить на произвольное значение, получится 0.
При делении на 1 получается первоначальное значение, т. е. к/1=к.
Переместительный закон: к/р/о=к/о/р.
Сочетательный: (к/р)/о=к/(р/о).

Следует отметить, что при использовании правил, нужно постоянно контролировать выполнение условия неравенства делителя 0. В противном случае тождество будет пустым множеством. Последняя тема изучается в высших учебных заведениях.

Пример решения

Для качественного усвоения материала нужно вычислить значение выражения, используя законы арифметических операций. Тождество имеет такой вид: [5*2*3*6*2+2*3*9*5+2 (о+р)-(р+2о)-(р+2)]/[(2*16*5−7*8)-2 (p-o). Для решения следует руководствоваться алгоритмом:

Расчет 5*2*3*6*2, используя ассоциативный закон: (5*2)*(3*2)*6=10*(6*6)=10*36=360.
Вычисление 2*3*9*5: (2*5)(3*9)=10*27=270.
Раскрытие скобок (распределительный): 2 (о+р)-(р+2о)-(р+2)=2о+2р-р-2о-р-2=-2.
Вычисление величины знаменателя, который не должен быть равен 0: 2*16*5−7*8−2 (р-о)=(2*5)*16−56−2р+2о=160−2р+2о.
Запись результата: [360+270−2]/[160−2р+2о]=628/[160−2р+2о].

Пример наглядно показывает оптимизацию вычислений, которые возможно произвести без помощи калькулятора.

Таким образом, формулы и утверждения для операций умножения, деления, сложения и вычитания используются для ускорения вычислений.

Не успеваете написать работу?

Заполните форму и узнайте стоимость

Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация

Контактные данные — строго конфиденциальны!

Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.

* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

Что такое ассоциативная собственность? Определение, факты и примеры

Что такое ассоциативное свойство в математике?

Ассоциативность определяется тем, что при сложении или умножении более двух чисел результат остается одним и тем же, независимо от того, как они сгруппированы.

Например,

2 × (7 × 6) = (2 × 7) × 6

2 + (7 + 6) = (2 + 7) + 6

Родственные игры

Ассоциативное свойство сложения

Ассоциативное свойство сложения подразумевает, что независимо от того, как сгруппированы числа, окончательная сумма чисел останется неизменной. Это можно выразить так:

( x + y ) + z = x + ( y + z )

Связанные рабочие листы

Ассоциативное свойство умножения

Ассоциативное свойство умножения подразумевает, что независимо от того, как сгруппированы числа, конечный продукт чисел останется одним и тем же. Это можно выразить так:

p × (q × r) = (p × q) × r

Difference between Associative Свойство и свойство коммуникативности

Свойство коммуникативности

Свойство коммуникативности означает, что при умножении или сложении двух чисел результат остается одним и тем же, независимо от их расположения.

Теперь, когда вы знаете об обоих свойствах, вы, должно быть, поняли, что единственная разница заключается в количестве чисел, участвующих в операции.

Два числа участвуют в свойстве коммутативности и более двух чисел участвуют в свойстве ассоциативности.

Применимы ли ассоциативные свойства к делению и вычитанию?

Вам должно быть интересно, почему эти свойства неприменимы к делению и вычитанию. Давайте возьмем пример, чтобы ответить на это «Почему?».

В случае вычитания:

12 – (6 – 2) = 12 – 4 = 8

(12 – 6) – 2 = 6 – 2 = 4

Отсюда следует, 12 – (6 – 2) ≠ (12 – 6) – 2. Значит, свойство ассоциативности для вычитания неприменимо.

В случае деления:

(24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3

24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12

Отсюда следует, (24 ÷ 4) ÷ 2 ≠ 24 ÷ (4 ÷ 2). Итак, свойство ассоциативности для деления неприменимо.

Интересный факт!

Ассоциативное свойство получило свое название от слова «ассоциировать» и относится к группировке чисел.

Решенные примеры

Пример 1: Если (30 × 20) × 15 = 9000, то используйте ассоциативное свойство, чтобы найти (15 × 30) × 20.

Решение: Согласно ассоциативному свойству умножения, (30 × 20) × 15 = (15 × 30) × 20,

Учитывая, что (30 × 20) × 15 = 9000,

(15 × 30) × 20 = 9000,

Пример 2: Проверьте, подразумевается ли ассоциативное свойство сложения в следующих уравнениях.

20 + (60 + 5) = (20 + 60) + 5
30 + (40 + 20) = (30 + 10) + 50

Решение:

По ассоциативному свойству сложения 20 + (60 + 5) = (20 + 60) + 5. Проверим дальше.

LHS : 20 + (60 + 5)

20 +(65)

RHS : (20 + 60) + 5

(80) + 5

LHS. Таким образом, в этом уравнении подразумевается ассоциативное свойство сложения.

По ассоциативному свойству сложения 30 + (40 + 20) = (30 + 10) + 50. Проверим дальше,

Левая сторона: 30 + (40 + 20)

30 + (60)

+ 5 0 Правая сторона: 90

+ 3 9 0005

(40) + 50

Левый ≠ Правый. Таким образом, в этом уравнении не подразумевается ассоциативное свойство сложения.

Пример 3: В соответствии с ассоциативным свойством дополнить недостающее число.

(5 + 10) + 4 = (5 + 4) + __ = 14

Решение: Согласно ассоциативному свойству, при сложении более двух чисел результат остается одним и тем же независимо от того, как они сгруппированы . Следовательно, (5 + 10) + 4 = (5 + 4) + 10 = 14

Практические задачи

Заполните следующее уравнение: 2 × ( _ × 6) = (2 × 5) × _

2, 4

5, 6

4, 6

9,05 9000

Правильный ответ: 5, 6
Согласно свойству ассоциативности, при перемножении более двух чисел результат остается одним и тем же, независимо от того, как они сгруппированы.
Следовательно, $2 × (5 × 6) = (2 × 5) × 6$

Заполните пропуски: 20 + 9 + _ = 9 + 5 + _

5, 20

2, 3

4, 5

7, 4

Правильный ответ: 5, 20 как они сгруппированы.
Следовательно, 20$ + 9 + 5 = 9 + 5 + 20$

Какое из этих уравнений верно?

$(2 + 3) + 6 = 2 × (3 + 6)$

$(5 + 6) + 4 = 5 + (6 + 4)$

$(7 — 10) — 15 = 7 — (10 — 15)$

$(9 ÷ 3) ÷ 3 = 9÷ (3 ÷ 3)$

Правильный ответ: $(5 + 6) + 4 = 5 + (6 + 4)$
Ассоциативность справедлива только для сложения и умножения. Это свойство неприменимо к вычитанию или делению, поэтому остальные уравнения неверны.

Часто задаваемые вопросы

Для скольких чисел можно использовать ассоциативное свойство сложения и умножения?

Ассоциативное свойство сложения и умножения справедливо для 3 и более чисел.

Применяется ли свойство ассоциативности к дробным числам?

Да, ассоциативное свойство сложения и умножения верно для дробных чисел.

Применяется ли свойство ассоциативности к уравнению, в котором есть 0?

Да, свойство ассоциативности верно для уравнения, в котором есть 0.

Ассоциативное свойство сложения и умножения чисел и примеры

Ассоциативное свойство объясняет, что сложение и умножение чисел возможно независимо от того, как они сгруппированы. Под группировкой мы понимаем числа, указанные внутри скобок (). Предположим, вы складываете три числа, скажем, 2, 5, 6. Тогда даже если мы сгруппируем числа в процедурах сложения, таких как 2 + (5 + 6) или (2 + 5) + 6, в обоих случаях результат будет одинаковым. То же правило применяется к умножению, то есть 2 x (5 x 6) = (2 x 5) x 6. Это свойство почти похоже на коммутативное свойство, когда используются только два числа.

Ассоциативное свойство-

Дополнение

2 + (5 + 6) = (2 + 5) + 6

2 + 11 = 7 + 6

13 = 13

Умножение

2 × (5 × 6) = (2 × 5) × 6

2 × 30 = 10 × 6

60 = 60

Математические уравнения имеют свои собственные принципы управления. Эти принципы или свойства помогают нам решать такие уравнения. По сути, есть три свойства, которые определяют основу математики, и эти свойства используются для выполнения различных арифметических операций. Они:

• Ассоциативное свойство
• Коммутативное свойство
• Распределительное свойство

Определение ассоциативного свойства

Ассоциативный, как следует из названия, означает группировку. Происхождение термина «ассоциативный» происходит от слова «ассоциировать». Основные математические операции, которые можно выполнять с помощью ассоциированного свойства, — это сложение и умножение. Обычно это применимо к более чем 2 номерам.

Как и в случае переместительного свойства, порядок группировки не имеет значения в ассоциативном свойстве. Это не изменит результат. Группировка чисел может производиться в скобках независимо от порядка членов. Таким образом, ассоциативный закон выражает, что не имеет значения, какая часть операции выполняется первой; ответ будет тот же.

Примечание: Как ассоциативное, так и коммутативное свойство применимо только для сложения и умножения.

Ассоциативное свойство для добавления

Сложение следует ассоциативному свойству, т. е. независимо от того, как числа заключены в скобки, окончательная сумма чисел будет одинаковой. Ассоциативное свойство сложения утверждает, что:

(x+y)+z = x+(y+z)

Допустим, мы хотим сложить 5+10+4. Видно, что ответ равен 19. Теперь сгруппируем числа; поставить 5 и 10 в скобках. Получаем,

⇒ (5+10)+4 = 15+4 = 19 (помните правило BODMAS)

Теперь давайте перегруппируем такие термины, как 10 и 4 в скобках;

⇒ 5+(10+4) = 5 + 14 = 19

Да, видно, что сумма в обоих случаях одинакова. Это ассоциативное свойство сложения.

Давайте посмотрим еще несколько примеров.

(1) 3+(2+1) = (3+2)+1

3+3 = 5+1

6 = 6

L. H.S = R.H.S

(2) 4+(-6+2) = [4 + (-6)] + 2

4 + (-4) = [4-6] + 2

4-4 = -2+2

0 = 0

L.H.S = R.H.S

Ассоциативное свойство для умножения

Правило ассоциативности умножения:

(xy) z = x (yz)

Решая 5×3×2, мы получаем 30 в виде произведения. Теперь, кроме того, сгруппируем термины:

⇒ (5 × 3) × 2 = 15 × 2 = 30 (правило BODMAS)

После перегруппировки,

⇒ 5 × (3 × 2) = 5 × 6 = 30

Продукты будут одинаковыми.

Таким образом, сложение и умножение ассоциативны по своей природе, а вычитание и деление не ассоциативны.

Например, разделить 100 ÷ 10 ÷ 5

⇒ (100 ÷ 10) ÷ 5 ≠ 100 ÷ (10 ÷ 5)

⇒ (10) ÷ 5 ≠ 100 ÷ (2)

⇒ 2 ≠ 50

Вычесть, 3 — 2 — 1

⇒ (3 − 2) − 1 ≠ 3 − (2 − 1)

⇒ (1) – 1 ≠ 3 – (1)

⇒ 0 ≠ 2

Таким образом, доказано, что свойство ассоциативности неприменимо для методов вычитания и деления.

Ассоциативное свойство рациональных чисел

Рациональные числа следуют ассоциативному свойству сложения и умножения.

Предположим, что a/b, c/d и e/f рациональны, тогда ассоциативность сложения может быть записана как:

(a/b) + [(c/d) + (e/f)] = [(a/b) + (c/d)] + (e/f)

Аналогично, ассоциативность умножения можно записать как:

(a/b) × [(c/d) × (e/f)] = [(a/b) × (c/d)] × (e/f)

Пример: Покажите, что (½) + [(¾) + (⅚)] = [(½) + (¾)] + (⅚) и (½) × [(¾) × (⅚)] = [(½) × (¾)] × (⅚).

Решение: (1/2) + [(3/4) + (5/6)] = (1/2) + [(9 + 10)/12]

= (1/2) + (19/12)

= (6 + 19)/12

= 25/12

[(1/2) + (3/4)] + (5/6) = [(2 + 3)/4] + (5/6)

= (5/4) + (5/6)

= (15 + 10)/12

= 25/12

Следовательно, (½) + [(¾) + (⅚)] = [(½) + (¾)] + (⅚)

Теперь (1/2) × [(3/4) × (5/6)] = (1/2) × (15/24) = 15/48 = 5/16

[(1/2) × (3/4)] × (5/6) = (3/8) × (5/6) = 15/48 = 5/16

Следовательно, (½) × [(¾) × (⅚)] = [(½) × (¾)] × (⅚)

Щелкните здесь, чтобы узнать больше о различных свойствах рациональных чисел.

Часто задаваемые вопросы – Часто задаваемые вопросы

К каким операциям применимо ассоциативное свойство?

Ассоциативное свойство применимо к сложению и умножению.

Что такое ассоциативное свойство?

Ассоциативное свойство гласит, что при сложении (или умножении) трех или более чисел сумма (или произведение) остается одинаковой независимо от группировки слагаемых (или множимых).

Применимо ли ассоциативное свойство к делению и вычитанию?

Ассоциативность не распространяется на вычитание и деление.

Всегда ли умножение ассоциативно?

В математике сложение и умножение действительных чисел ассоциативно.

Какова общая формула ассоциативного свойства?

Ассоциативное свойство сложения
Правило ассоциативного свойства сложения: (x+y)+z = x+(y+z)
Ассоциативное свойство умножения

Правило ассоциативности умножения: (xy) z = x (yz)

Чтобы решить больше задач по теме, загрузите BYJU’S — The Learning App из магазина Google Play и смотрите интерактивные видео. Кроме того, пройдите бесплатные тесты, чтобы потренироваться перед экзаменами.

Ассоциативное свойство сложения — примеры, определение, формула

LearnPracticeDownload

Ассоциативное свойство сложения — это свойство чисел, которое гласит, что способ группировки трех или более чисел не меняет суммы этих чисел. Это означает, что сумма трех или более чисел остается неизменной независимо от того, как они сгруппированы. Давайте узнаем больше об ассоциативном свойстве сложения в этой статье.

1.	Что такое ассоциативное свойство сложения?
2.	Ассоциативное свойство формулы сложения
3.	Ассоциативное свойство сложения и умножения
4.	Часто задаваемые вопросы об ассоциативном свойстве добавления

Что такое ассоциативное свойство сложения?

Ассоциативное свойство сложения — это правило, которое гласит, что при сложении трех и более чисел мы можем сгруппировать их в любую комбинацию, и полученная сумма останется неизменной независимо от того, каким образом они сгруппированы. В этом случае группировка относится к размещению скобок. Например, на приведенном ниже рисунке видно, что сумма чисел не меняется независимо от того, как сгруппированы слагаемые.

Ассоциативное свойство формулы сложения

Формула ассоциативности сложения показывает, что группировка чисел другим способом не влияет на сумму. Скобки, которые группируют числа, помогают упростить процесс сложения. Обратите внимание на следующую формулу для ассоциативного свойства сложения.

Давайте рассмотрим пример, чтобы понять и доказать формулу. Сгруппируем 13 + 7 + 3 тремя способами.

Шаг 1: Мы можем сгруппировать набор чисел как (13 + 7) + 3, 13 + (7 + 3) и (13 + 3) + 7.
Шаг 2: Сложите первый набор чисел, то есть (13 + 7) + 3. Далее это можно решить как 20 + 3 = 23.
Шаг 3: Добавьте второй набор, т. е. 13 + (7 + 3) = 13 + 10 = 23.
Шаг 4: Теперь решите третий набор, то есть (13 + 3) + 7 = 16 + 7 = 23.
Шаг 5: Сумма всех трех выражений равна 23. Это показывает, что как бы мы ни группировали числа с помощью скобок, сумма остается неизменной.

Ассоциативное свойство сложения и умножения

Ассоциативное свойство применимо к сложению и умножению, но не существует к вычитанию и делению. Мы знаем, что ассоциативное свойство сложения говорит о том, что группировка чисел не меняет суммы данного набора чисел. Это означает, что (7 + 4) + 2 = 7 + (4 + 2) = 13. Точно так же ассоциативное свойство умножения говорит о том, что группировка чисел не меняет произведения данного набора чисел. Эта формула выражается как (a × b) × c = a × (b × c). Например, (2 × 3) × 4 = 2 × (3 × 4) = 24,9.0005

Важные примечания:

Ассоциативность применима только к сложению и умножению.
Ассоциативные свойства соответствуют возможности связывать или группировать числа, что невозможно в случае вычитания и деления.
Ассоциативное свойство входит в список математических свойств, полезных при работе с математическими уравнениями и их решениями.

☛ Похожие темы

Свойства дополнения
Коммутативное свойство сложения
Нулевое свойство умножения
Свойство мультипликативной идентичности
Распределительная собственность
Коммутативное свойство
Аддитивная идентичность против мультипликативной идентичности
Распределительная собственность
Ассоциативное свойство дополнительных рабочих листов

Ассоциативное свойство примеров сложения

Пример 1: Следует ли данное уравнение ассоциативному свойству сложения?
(25 + 2) + 8 = 25 + (2 + 8)
Решение: Следующие шаги помогут выяснить, следует ли данное уравнение ассоциативному свойству сложения или нет:
- Шаг 1: Складываем набор чисел, указанный в левой части, то есть (25 + 2) + 8 = 27 + 8 = 35,
- Шаг 2: Теперь сложите набор чисел, указанный в правой части, то есть 25 + (2 + 8) = 25 + 10 = 35.
- Мы видим, что сумма, полученная из левой части уравнения, равна сумме, полученной из правой части. Итак, уравнение следует ассоциативному свойству сложения.
Пример 2: Заполните пропущенное число и напишите сумму:
7 + (10 + 6) = (7 + 10) + ___ = ___
Решение: Согласно ассоциативному свойству формулы сложения, a + (b + c) = (a + b) + c. Если мы подставим значения в эту формулу, мы получим 6 как пропущенное число, то есть 7 + (10 + 6) = (7 + 10) + 6 , а сумма будет 23.
Пример 3: Выберите правильный вариант для отсутствующего номера.
8 + (4 + 2) = (8 + ___) + 2
а) 4
б) 7
в) 6
Решение:
По ассоциативному свойству сложения: а + (b + c) = (a + b) + c. Подставляя значения в формулу: 8 + (4 + 2) = (8 + 4 ) + 2,
Следовательно, пропущенное число равно 4, потому что сумма обоих выражений равна 14,
Следовательно, правильный вариант (а).

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по ассоциативному свойству сложения

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по ассоциативному свойству дополнения

Что такое ассоциативное свойство сложения?

Ассоциативное свойство сложения гласит, что независимо от того, как набор из трех или более чисел сгруппирован вместе, сумма остается неизменной. Группировка чисел осуществляется с помощью скобок. Формула для этого свойства выражается как, a + (b + c) = (a + b) + c = (a + c) + b. Например, если мы сгруппируем числа 3 + 4 + 5 как 3 + (4 + 5) или (3 + 4) + 5, сумма, которую мы получим из обоих наборов, равна 12.

Что является примером ассоциативного свойства сложения?

Ассоциативное свойство сложения гласит, что группировка чисел не меняет их суммы. Например, (75 + 81) + 34 = 156 + 34 = 190; и 75 + (81 + 34) = 75 + 115 = 190. Сумма обеих сторон равна 190.

В чем преимущество использования ассоциативного свойства сложения?

Преимущество ассоциативного свойства сложения заключается в том, что оно помогает формировать более мелкие компоненты, что упрощает вычисление сложения. Группировка чисел с помощью скобок облегчает процесс упрощения выражения.

Как проверить ассоциативность сложения?

Ассоциативность сложения легко проверить, сложив заданный набор чисел. Например, сгруппируем 6 + 7 + 8 двумя способами.

Шаг 1: Мы можем сгруппировать данный набор чисел как (6 + 7) + 8 и 6 + (7 + 8).
Шаг 2: Теперь давайте сложим первый набор чисел, то есть (6 + 7) + 8. В результате получится 13 + 8 = 21.
Шаг 3: Теперь добавим второй набор, то есть 6 + (7 + 8) = 6 + 15 = 21,
Шаг 4: Сумма обоих выражений равна 21. Это доказывает ассоциативное свойство сложения, которое показывает, что независимо от того, как мы группируем числа с помощью скобок, сумма остается неизменной.

Всегда ли ассоциативное свойство сложения включает 3 или более чисел?

Да, ассоциативное свойство сложения всегда включает 3 или более чисел, потому что правило свойства гласит, что изменение группировки слагаемых не меняет суммы, а в случае только двух чисел мы не можем создавать группы.

Какова формула ассоциативного свойства сложения?

Формула ассоциативного свойства сложения утверждает, что сумма трех или более чисел остается неизменной независимо от того, как эти числа сгруппированы. Это выражается как, a + (b + c) = (a + b) + c = (a + c) + b.

В чем разница между коммутативным и ассоциативным свойством сложения?

Следующие пункты показывают разницу между коммутативным и ассоциативным свойством сложения:

Переместительное свойство сложения утверждает, что изменение порядка слагаемых не меняет сумму. Например, 4 + 6 = 6 + 4 = 10. Ассоциативное свойство сложения утверждает, что группировка чисел не меняет сумму. Например, 8 + (2 + 3) = (8 + 2) + 3 = 13.
Переместительное свойство сложения можно применять к двум числам, а ассоциативное свойство применимо к трем и более числам.
В коммутативном свойстве сложения порядок слагаемых не имеет значения, а в ассоциативном свойстве сложения не имеет значения группировка слагаемых.

Как ассоциативное свойство сложения используется в повседневной жизни?

Есть много мест, где можно применить ассоциативное свойство сложения. Например, если мы тратим 3 доллара на кекс, 6 долларов на мороженое и 2 доллара на конфеты, мы можем сложить стоимость предметов в любом порядке как 3 + (6 + 2) или (3 + 6). + 2. Оба выражения дают одну и ту же сумму, то есть 11. Это показывает ассоциативное свойство сложения, которое гласит, что независимо от того, как мы группируем 3 или более чисел, сумма остается неизменной.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Ассоциативное свойство сложения. Рабочий лист

Рабочие листы по математике и
наглядный учебный план

Ассоциативное свойство в сложении и умножении

Сложение и умножение используют ассоциативное свойство, а вычитание и деление — нет. Мы собираемся подробно рассмотреть каждую ситуацию, чтобы получить лучшее представление.

Ассоциативность сложения ♥

Сложение действительно обладает ассоциативным свойством.

Какими бы ни были числа a, b и c, они всегда заканчиваются одним и тем же:

(a + b) + c = a + (b + c) = (a + c) + b

Посмотрите внимательно на следующий пример, который установлен с фактическими числами.

Предположим, что a=3, b= 18 и c=1. Вы уже знаете, что нужно сначала вычислить, что находится между скобками.

(3 + 18) + 1 = 21 + 1 = 22

3 + (18 + 1) = 3 + 19 = 22

(3 + 1) + 18 = 4 + 18 = 22

Так же, как вы видел, независимо от порядка группировки, ответ не меняется.

Теперь я покажу вам более наглядный пример:

Мы собираемся сложить 3 + 2 + 1, связывая числа (группируя фрукты вместе) двумя разными способами.

Во-первых, взглянув на верхний левый квадрат на картинке выше, нам нужно добавить первые два числа, 3 и 2. К любому полученному числу, 5, мы затем добавим 1. Мы в итоге 6. Всего 6 кусочков фруктов.

На картинке справа мы сначала складываем два последних числа, 2 и 1. 2 плюс 1 дает нам 3. После того, как мы прибавляем 3 к 3, получаем 6. Всего 6 кусочков фруктов. ; это тот же ответ.

Кроме того, это ассоциативное свойство: оно позволяет вам изменить порядок, который мы используем для группировки чисел, потому что это не влияет на окончательный ответ.

Ассоциативность в вычитании ×

В отличие от сложения, вычитание не обладает ассоциативностью.

Давайте посмотрим на другой пример. Вычтем 10 – 5 – 3:

(10 – 5) – 3 = 5 – 3 = 2

10 – (5 – 3) = 10 – 2 = 8

Если вычесть первые два числа, 10 минус 5, это дает нам 5. Если мы перейдем к вычитанию 3, это даст нам 2. Однако, если мы вычтем сначала два последних числа, 5 минус 3 будет 2. Если мы вычтем 2 из 10, мы получим 8.

Изменение способа связывания чисел при вычитании меняет ответ. Таким образом, вычитание не обладает свойством ассоциативности.

Ассоциативное свойство в умножении ♥

Сначала попробуйте вычислить (2 x 3) x 4. После этого попробуйте 2 x (3 x 4). Вы получили одинаковый ответ для обоих из них?

Если вы получили тот же ответ, вы молодец, потому что умножение обладает ассоциативным свойством, и ответ не изменится, даже если порядок чисел в задаче изменится. Порядок, в котором связаны числа, не влияет на окончательный ответ.

(a x b) x c = a x (b x c) = (a x c) x b

Если a = 3, b = 5 y c = 10, у нас останется:

(3 x 5) x 10 = 15 x 10 = 150

3 x (5 x 10) = 3 x 50 = 150

(3 x 10) x 5 = 30 x 5 = 150

Теперь давайте посмотрим, как это свойство работает, на более наглядном примере:

Мы собираемся подсчитать количество кубиков, составляющих следующую картинку. Всего 24 кубика.

Помимо подсчета каждого кубика по одному, существует несколько способов подсчета количества кубиков.

Один из способов — сначала подсчитать кубики в одном столбце.

Если внимательно посмотреть на первую колонку, окрашенную в оранжевый цвет, там 3 x 2 = 6, 6 кубиков. Сколько всего столбцов? Есть 4 колонки. Таким образом, 6 умножить на 4 даст нам общее количество кубиков: 24 кубика.

Еще один способ решить задачу — подсчитать количество кубиков в одном ряду

В первом ряду зеленого цвета 4 x 2 = 8 кубиков. Всего имеется 3 ряда, поэтому, чтобы подсчитать общее количество кубиков, нам нужно умножить 8 x 3, что даст 24. Всего 24 кубика.

Вот операции, которые мы использовали:

Независимо от того, как сгруппированы числа, ответ получается одинаковым.

Ассоциативное свойство в Деление ×

Мы собираемся вычислить 8÷2÷2. Сначала попробуйте разделить (8÷2)÷2, что у вас получилось? 8 разделить на 2 — это 4, а 4 на 2 — это 2. Круто.

А теперь попробуйте 8 ÷ (2÷2). Сначала вам нужно поработать над скобками, 2 на 2 — это 1, а 8 на 1 — это 8. Хорошо. Итак, что мы здесь видим?

Мы видим, что получили два совершенно разных ответа.

Давайте посмотрим на другой пример 18 ÷ 6 ÷ 3, снова сгруппировав числа двумя разными способами, и проверим, совпадает ли ответ или нет.

Один способ дает нам 1, а другой дает нам 9. Мы снова видим, что ответы не совпадают.

Итак, мы можем с уверенностью сказать, что деление не обладает свойством ассоциативности.

Прежде чем мы закончим, кое-что еще: если в задаче нет скобок, вы делите слева направо.

Надеюсь, это помогло вам понять это важное свойство. Если вы хотите углубиться, вы можете посетить эти записи, которые мы разместили в нашем блоге:

И если вы хотите продолжать изучать математику, в Smartick мы учим их с помощью джаза. Присоединяйтесь к нам!

Подробнее:

Автор
Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения Smartick (посмотреть все)

9.3.1: Ассоциативные, коммутативные и дистрибутивные свойства

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 64043

Проект NROC

Цели обучения

Определение и использование коммутативных свойств для сложения и умножения.
Определите и используйте ассоциативные свойства для сложения и умножения.
Определите и используйте распространяемое свойство.

Введение

В алгебре много раз нужно упростить выражение. Свойства действительных чисел предоставляют инструменты, которые помогут вам взять сложное выражение и упростить его.

Ассоциативные, коммутативные и дистрибутивные свойства алгебры чаще всего используются для упрощения алгебраических выражений. Вы захотите иметь хорошее представление об этих свойствах, чтобы упростить решение задач по алгебре.

Коммутативные свойства сложения и умножения

Вы можете столкнуться с повседневными делами, в которых порядок задач может быть изменен без изменения результата. Например, подумайте о том, чтобы налить утром чашку кофе. Вы получите ту же вкусную чашку кофе, если вы добавите ингредиенты одним из следующих способов:

Налейте 12 унций кофе в кружку, затем добавьте немного молока.
Добавьте немного молока в кружку, затем добавьте 12 унций кофе.

Порядок добавления ингредиентов не имеет значения. Точно так же не имеет значения, надеваете ли вы сначала левый или правый ботинок, прежде чем отправиться на работу. Если вы выходите из дома в обеих туфлях, вы на правильном пути!

В математике мы говорим, что эти ситуации коммутативны — результат будет одинаковым (кофе приготовлен по вашему вкусу, вы выходите из дома в обеих туфлях) независимо от порядка выполнения задач.

Аналогично, коммутативное свойство сложения гласит, что при сложении двух чисел их порядок можно изменить, не влияя на сумму. Например, $\ 30+25$ имеет ту же сумму, что и $\ 25+30$.

$\ 30+25=55$

$\ 25+30=55$

Аналогично умножение. Коммутативное свойство умножения гласит, что при умножении двух чисел их порядок можно изменить, не влияя на произведение. Например, $\ 7 \cdot 12$ имеет тот же продукт, что и $\ 12 \cdot 7$.

$\ 7 \cdot 12=84$

$\ 12 \cdot 7=84$

Эти свойства применимы ко всем действительным числам. Рассмотрим несколько примеров сложения.

Исходное уравнение	Переписанное уравнение
$\ 1,2+3,8=5$	$\ 3,8+1,2=5$
$\ \frac{1}{2}+\frac{1}{8}=\frac{5}{8}$	$\ \frac{1}{8}+\frac{1}{2}=\frac{5}{8}$
$\ 14+(-10)=4$	$\ (-10)+14=4$
$\ \frac{1}{3}+\left(-1 \frac{2}{3}\right)=-1 \frac{1}{3}$	$\ \left(-1 \frac{2}{3}\right)+\frac{1}{3}=-1 \frac{1}{3}$
$\ (-5,2)+(-3,6)=-8,8$	$\ (-3,6)+(-5,2)=-8,8$

Переместительное свойство сложения

Для любых действительных чисел $\ a$ и $\ b$, $\ a+b=b+a$.

Вычитание не является коммутативным. Например, $\ 4-7$ отличается от $\ 7-4$. Знак $\-$ здесь означает вычитание.

Однако помните, что $\ 4-7$ можно переписать как $\ 4+(-7)$, поскольку вычитание числа равносильно сложению противоположного числа. Применяя здесь свойство коммутативности для сложения, можно сказать, что $\ 4+(-7)$ то же самое, что $\ (-7)+4$. Обратите внимание, как это выражение сильно отличается от $\ 7-4$.

Теперь посмотрите на несколько примеров умножения.

Исходное уравнение	Переписанное уравнение
$\ 4.5 \cdot 2=9$	$\ 2 \cdot 4.5=9$
$\ (-5) \cdot 3=-15$	$\ 3 \cdot(-5)=-15$
$\ \frac{1}{5} \cdot 5=1$	$\ 5 \cdot \frac{1}{5}=1$
$\ \left(-\frac{1}{4}\right) \cdot\left(-\frac{8}{10}\right)=\frac{1}{5}$	$\ \left(-\frac{8}{10}\right) \cdot\left(-\frac{1}{4}\right)=\frac{1}{5}$

Коммутативное свойство умножения

Для любых действительных чисел $\ a$ и $\ b$, $\ a \cdot b=b \cdot a$.

Порядок не имеет значения, пока две величины перемножаются. Это свойство работает для действительных чисел и для переменных, представляющих действительные числа.

Как вычитание не коммутативно, так и деление не коммутативно. $\ 4 \div 2$ не имеет того же частного, что и $\ 2 \div 4$.

Пример

Запишите выражение $\ (-15,5)+35,5$ другим способом, используя свойство коммутативности сложения, и покажите, что оба выражения дают один и тот же ответ.

Раствор

$\ (-15,5)+35,5=20$	Добавление.
$\ 35,5+(-15,5)$	Используя свойство коммутативности, вы можете поменять местами -15,5 и 35,5, чтобы они располагались в другом порядке.
$\ \begin{array}{c} 35,5+(-15,5) \\ 35,5-15,5=20 \end{массив}$	Сложение 35,5 и -15,5 равносильно вычитанию 15,5 из 35,5. Сумма 20.

$\ (-15.5)+35.5=20$ и $\ 35.5+(-15.5)=20$

Упражнение

Перепишем $\ 52 \cdot y$ по-другому , используя свойство коммутативности умножения. Обратите внимание, что $\ y$ представляет собой действительное число.

$\ 5 лет \cdot 2$
$\ 52 года$
$\ 26 \cdot 2 \cdot y$
$\ у \cdot 52$

Ответить

Неверно. Вы не можете переключить одну цифру из 52 и присоединить ее к переменной $\y$. Правильный ответ: $\y\cdot 52$.
Неверно. Это еще один способ переписать $\ 52 \cdot y$, но свойство коммутативности не использовалось. Правильный ответ: $\y\cdot 52$.
Неверно. Вам не нужно множить 52 на $\ 26 \cdot 2$. Правильный ответ: $\y\cdot 52$.
Верно. Порядок факторов обратный.

Ассоциативные свойства сложения и умножения

Ассоциативное свойство сложения утверждает, что числа в выражении сложения можно группировать различными способами без изменения суммы. Вы можете запомнить значение ассоциативного свойства, вспомнив, что когда вы ассоциирует с членами семьи, друзьями и коллегами, в конечном итоге вы формируете с ними группы.

Ниже приведены два способа упрощения одной и той же задачи на сложение. В первом примере 4 сгруппировано с 5 и $\ 4+5=9$.

$\ 4+5+6=9+6=15$

Здесь та же проблема решается сначала группировкой 5 и 6, $\ 5+6=11$.

$\ 4+5+6=4+11=15$

В обоих случаях сумма одинакова. Это показывает, что изменение группировки чисел при сложении дает ту же сумму.

Математики часто используют круглые скобки, чтобы указать, какая операция должна быть выполнена первой в алгебраическом уравнении. Приведенные выше задачи на сложение переписаны здесь, на этот раз с использованием круглых скобок для обозначения ассоциативной группировки.

$\ (4+5)+6=9+6=15$

$\ 4+(5+6)=4+11=15$

Понятно, что скобки не повлиять на сумму; сумма одинакова независимо от того, где расположены скобки.

Ассоциативное свойство сложения

Для любых действительных чисел $\ a$, $\ b$ и $\ c$,

$\ (a+b)+c=a+(b+c)$.

В приведенном ниже примере показано, как свойство ассоциативности можно использовать для упрощения выражений с действительными числами.

Пример

Перепишите $\ 7+2+8,5-3,5$ двумя разными способами, используя ассоциативное свойство сложения. Покажите, что выражения дают один и тот же ответ.

Решение

$\ \begin{массив}{r}
7+2+8.5-3.5 \\
7+2+8.5+(-3.5)
\end{массив}$

Свойство ассоциативности не применяется к выражениям, включающим вычитание. Итак, перепишем выражение как сложение отрицательного числа.

$\ \begin{array}{r}
(7+2)+8,5+(-3,5) \\
9+8,5+(-3,5) \\
17,5+(-3,5) \\
17,5-3,5=14
\конец{массив}$

Группа 7 и 2 и сложите их вместе. Затем прибавьте к этой сумме 8,5. Наконец, добавьте -3,5, что равносильно вычитанию 3,5.

Вычесть 3.5. Сумма 14.

$\ \begin{array}{r}
7+2+(8.5+(-3.5)) \\
7+2+5 \\
9+5
\end{массив}$

Сгруппируйте 8,5 и -3,5 и сложите их вместе, чтобы получить 5. Затем сложите 7 и 2 и прибавьте эту сумму к 5.

Сумма равна 14.

$\ (7+2)+8,5-3,5=14$ и $\ 7+2+(8,5+(-3,5))=14$

Умножение имеет ассоциативное свойство, которое действует точно так же, как и свойство сложения. Ассоциативное свойство умножения гласит, что числа в выражении умножения можно перегруппировать с помощью круглых скобок. Например, приведенное ниже выражение можно переписать двумя разными способами, используя свойство ассоциативности.

Исходное выражение: $\ -\frac{5}{2} \cdot 6 \cdot 4$

Выражение 1: $\ \left(-\frac{5}{2} \cdot 6\right ) \cdot 4=\left(-\frac{30}{2}\right) \cdot 4=-15 \cdot 4=-60$

Выражение 2: $\ -\frac{5}{2} \cdot(6 \cdot 4)=-\frac{5}{2} \cdot 24=-\frac{120}{2}=- 60$

Скобки не влияют на произведение. Произведение одно и то же независимо от того, где стоят скобки.

Ассоциативное свойство умножения

Для любых действительных чисел $\ a$, $\ b$ и $\ c$, $\ (a \cdot b) \cdot c=a \cdot (б \cdot c)$.

Упражнение

Перепишите $\ \frac{1}{2} \cdot\left(\frac{5}{6} \cdot 6\right)$, используя только ассоциативное свойство.

$\ \left(\frac{1}{2} \cdot \frac{5}{6}\right) \cdot 6$
$\ \left(\frac{5}{6} \cdot 6\right) \cdot \frac{1}{2}$
$\ 6 \cdot\left(\frac{5}{6} \cdot \frac{1}{2}\right)$
$\ \frac{1}{2} \cdot 5$

Ответить

Правильно. Здесь числа перегруппированы. Теперь $\ \frac{1}{2}$ и $\ \frac{5}{6}$ сгруппированы в скобках вместо $\ \frac{5}{6}$ и $ \6$.
Неверно. Порядок чисел не меняется, когда вы переписываете выражение, используя ассоциативное свойство умножения. То, как они сгруппированы , должно измениться. Правильный ответ: $\ \left(\frac{1}{2} \cdot \frac{5}{6}\right) \cdot 6$.
Неверно. Порядок чисел не меняется, когда вы переписываете выражение, используя ассоциативное свойство умножения. Только как они сгруппированы должен измениться. Правильный ответ: $\ \left(\frac{1}{2} \cdot \frac{5}{6}\right) \cdot 6$.
Неверно. Умножение в круглых скобках не является применением свойства. Правильный ответ: $\ \left(\frac{1}{2} \cdot \frac{5}{6}\right) \cdot 6$.

Использование ассоциативных и коммутативных свойств

Вы обнаружите, что ассоциативные и коммутативные свойства являются полезными инструментами в алгебре, особенно при вычислении выражений. Используя коммутативные и ассоциативные свойства, вы можете переупорядочивать термины в выражении так, чтобы совместимые числа располагались рядом друг с другом и группировались вместе. Совместимые числа — это числа, которые легко вычислить, например $\ 5+5$, или $\ 3 \cdot 10$, или $\ 12-2$, или $\ 100 \ раздел 20$. (Основным критерием совместимых чисел является то, что они «хорошо работают» вместе.) Два приведенных ниже примера показывают, как это делается.

Пример

Оцените выражение $\ 4 \cdot(x \cdot 27)$, когда $\ x=-\frac{3}{4}$.

Решение

$\ 4 \cdot(x \cdot 27)$	Оригинальное выражение.
$\ 4 \cdot\left(\left(-\frac{3}{4}\right) \cdot 27\right)$	Замените $\ -\frac{3}{4}$ на $\ x$.
$\ \begin{array}{r} \left(4 \cdot\left(-\frac{3}{4}\right)\right) \cdot 27 \\ \left(-\frac{12}{4}\right) \cdot 27 \end{массив}$	Используйте ассоциативное свойство умножения, чтобы перегруппировать множители так, чтобы $\ 4$ и $\ -\frac{3}{4}$ находились рядом друг с другом. Умножение $\ 4$ на $\ -\frac{3}{4}$ делает вычисление выражения немного проще, чем умножение $\ -\frac{3}{4}$ на \ (\ 27\).
$\ -3 \cdot 27=-81$	Умножить. $\ 4$ раз $\ -\frac{3}{4}=-3$, а $\ -3$ раз $\ 27$ равно $\ -81$.

$\ 4 \cdot(x \cdot 27)=-81$ когда $\ x=\left(-\frac{3}{4}\right)$

Пример

Упростить: $\ 4+12+3+4-8$

Решение

$\ 4+12+3+4-8$	Оригинальное выражение.
$\ 12+3+4+4+(-8)$	Определите совместимые номера. $\ 4+4$ равно $\ 8$, и есть $\ -8$. подарок. Вспомните, что вы можете думать о $\ -8$ как о $\ +(-8)$. Используйте свойство коммутативности сложения, чтобы сгруппировать их вместе.
$\ 12+3+(4+4+(-8))$	Используйте ассоциативное свойство для группировки $\ 4+4+(-8)$.
$\ 12+3+0$	Добавить $\ 4+4+(-8)$.
$\ 12+3+0=15$	Добавьте остальные условия.

$\ 4+12+3+4-8=15$

Упражнение

Упростите выражение: $\ -5+25-15+2+8$

Ответить

Неверно. Когда вы используете свойство коммутативности для перестановки слагаемых, убедитесь, что отрицательные слагаемые имеют свои отрицательные знаки. Правильный ответ 15.
Верно. Используйте свойство коммутативности, чтобы изменить выражение так, чтобы совместимые числа располагались рядом друг с другом, а затем используйте свойство ассоциативности, чтобы сгруппировать их.
Неверно. Проверьте свое сложение и вычитание и подумайте о порядке, в котором вы складываете эти числа. Используйте свойство коммутативности, чтобы переставить слагаемые так, чтобы совместимые числа располагались рядом друг с другом. Правильный ответ 15.
Неверно. Похоже, вы проигнорировали отрицательные знаки здесь. Когда вы используете свойство коммутативности для перестановки слагаемых, убедитесь, что отрицательные слагаемые имеют свои отрицательные знаки. Правильный ответ 15.

Распределительное свойство

Распределительное свойство умножения — очень полезное свойство, позволяющее переписывать выражения, в которых вы умножаете число на сумму или разность. Свойство утверждает, что произведение суммы или разности, например $\ 6(5-2)$, равно сумме или разности произведений, в данном случае $\ 6(5)-6( 2)$.

$\ \begin{array}{l}
6(5-2)=6(3)=18 \\
6(5)-6(2)=30-12=18
\end{array}$

Распределительное свойство умножения можно использовать при умножении числа на сумму. Например, предположим, что вы хотите умножить 3 на сумму $\ 10+2$.

$\ 3(10+2)=?$

В соответствии с этим свойством вы можете сначала сложить числа 10 и 2, а затем умножить на 3, как показано здесь: $\ 3(10+2) =3(12)=36$. В качестве альтернативы вы можете сначала умножить каждое слагаемое на 3 (это называется распределением на 3), а затем вы можете сложить продукты. Этот процесс показан здесь.

$\ \begin{array}{l}
3(10+2)=3(12)=36 \\
3(10)+3(2)=30+6=36
\end {массив}$

Продукты одинаковые.

Поскольку умножение является коммутативным, вы можете использовать распределительное свойство независимо от порядка множителей.

Распределительные свойства

Для любых действительных чисел $\ a$, $\ b$ и $\ c$:

Умножение распределяет над сложением:

$\ a(b +в)=а б+а в$

Умножение распределяет по вычитанию:

$\ a(b-c)=a b-a c$

Упражнение

Перепишите выражение $\ 10(9-6)$, используя свойство распределения.

$\ 10(6)-10(9)$
$\ 10(3)$
$\ 10(6-9)$
$\ 10(9)-10(6)$

Ответить

Неверно. Поскольку вычитание не является коммутативным, вы не можете изменить порядок. Правильный ответ: $\ 10(9)-10(6)$.
Неверно. Это правильный способ найти ответ. Но вопрос просил вас переписать задачу, используя свойство дистрибутивности. Правильный ответ: $\ 10(9)-10(6)$
Неверно. Вы изменили порядок чисел 6 и 9. Обратите внимание, что вычитание не является коммутативным, и вы не использовали свойство дистрибутивности. Правильный ответ: $\ 10(9)-10(6)$.
Верно. 10 правильно распределены, так что они используются для умножения 9и 6 отдельно.

Распределение с переменными

Пока переменные представляют действительные числа, свойство распределения может использоваться с переменными. Свойство дистрибутивности важно в алгебре, и вы часто будете встречать такие выражения: $\ 3(x-5)$. Если вас попросят расширить это выражение, вы можете применить распределительное свойство точно так же, как если бы вы работали с целыми числами.

Помните, что когда вы умножаете число и переменную, вы можете просто написать их рядом, чтобы выразить умноженное количество. Таким образом, выражение «тройная переменная $\ x$» может быть записано несколькими способами: $\ 3 x$, $\ 3(x)$ или $\ 3 \cdot Икс$.

Пример

Используйте свойство распределения для расширения выражения $\ 9(4+x)$.

Раствор

$\ 9(4+x)$	Оригинальное выражение.
$\ 9(4)+9(х)$	Распредели 9 и умножь.
$\ 36+9 х$	Умножить.

$\ 9(4+х)=36+9 х$

Пример

Используйте свойство распределения для вычисления выражения $\ 5(2 x-3)$, когда $\ x=2$.

Раствор

$\ 5(2 x-3)$	Оригинальное выражение.
$\ 5(2 х)-5(3)$	Раздать 5.
$\10 х-15$	Умножить.
$\ 10(2)-15$ $\ 20-15=5$	Подставьте 2 вместо $\ x$ и оцените.

Когда $\ х=2,5(2 х-3)=5$.

Как вы думаете, что произойдет в приведенном выше примере, если вы подставите $\ x=2$ перед распределением 5? Получили бы вы такой же ответ 5? В приведенном ниже примере показано, что произойдет.

Пример

Используйте свойство распределения для вычисления выражения $\ 5(2 x-3)$, когда $\ x=2$.

Раствор

$\ 5(2 x-3)$	Оригинальное выражение.
$\ 5(2(2)-3)$	Замените $\ x$ на 2.
$\ \begin{array}{c} 5(4-3) \\ 5(4)-5(3) \end{массив}$	Умножить.
$\ 20-15=5$	Вычтите и оцените.

Когда $\ х=2,5(2 х-3)=5$.

Объединение одинаковых терминов

Распределительное свойство также может помочь вам понять фундаментальную идею алгебры: такие величины, как $\ 3x$ и $\ 12x$, можно складывать и вычитать так же, как числа 3 и 12. Давайте рассмотрим один пример и посмотрим, как это можно сделать.

Пример

Добавить: $\ 3 x+12 x$

Решение

$\ 3(x)+12(x)$	$\ 3 x$ равно 3 раза $\ x$, а $\ 12 x$ равно 12 раз $\ x$
$\ х(3+12)$	Изучая свойство дистрибутивности (а также используя свойство коммутативности), вы знаете, что $\ x(3+12)$ равносильно $\ 3(x)+12(x)$.
$\ \begin{array}{c} x(15) \\ \text { or } \\ 15 x \end{массив}$	Объедините члены в скобках: $\ 3+12=15$.

$\ 3 x+12 x=15 x$

Видите, что произошло? Думая о $\ x$ как о распределенной величине, вы можете увидеть, что $\ 3x+12x=15x$. (Если вы не уверены в этом, попробуйте подставить любое число в это выражение… вы обнаружите, что это верно!)

Группы терминов, состоящие из коэффициента, умноженного на одну и ту же переменную, называются «подобными терминами». В таблице ниже показаны различные группы похожих терминов:

Группы похожих терминов

$\ 3 х, 7 х, -8 х, -0,5 х$

$\ -1,1 г, -4 г, -8 г$

$\ 12 т, 25 т, 100 т, 1 т$

$\ 4 а Ь,-8 а Ь, 2 а Ь$

Всякий раз, когда вы видите одинаковые члены в алгебраическом выражении или уравнении, вы можете складывать или вычитать их точно так же, как если бы вы складывали или вычитали действительные числа. Так, например,

$\ 10 y+12 y=22 y$ и $\ 8 x-3 x-2 x=3 x$.

Будьте осторожны, чтобы не комбинировать термины, которые не имеют одной и той же переменной: $\ 4 x+2 y$ не равно $\ 6 x y$!

Пример

Упрощение: $\ 10 y+5 y+9 x-6 x-x$.

Раствор

$\ 10 у+5 у+9 х-6 х-х$	В этом выражении есть похожие члены, так как все они состоят из коэффициента, умноженного на переменную $\ x$ или $\ y$. Обратите внимание, что $\ -x$ совпадает с $\ (-1) x$.
$\ 15 у+2 х$	Добавить похожие термины. $\ 10 y+5 y=15 y$ и $\ 9 x-6 x-x=2 x$.

$\ 10 y+5 y+9 x-6 x-x=15 y+2 x$

Упражнение

Упростите: $\ 12 x-x+2 x-8 x$.

$\ 23 х$
$\ 5$
$\ 5 х$
$\х$

Ответить

Неверно. Похоже, вы добавили все термины. Обратите внимание, что $\ -x$ и $\ -8 x$ отрицательны. Правильный ответ: $\ 5 х$.
Неверно. Вы правильно объединили целые числа, но не забудьте также включить переменную! Правильный ответ: $\ 5x$.
Верно. Когда вы объединяете эти похожие термины, вы получаете сумму $\ 5x$
Неверно. Похоже, вы вычли все члены из $\ 12x$. Обратите внимание, что $\ -x$ и $\ -8 x$ отрицательны, а $\ 2 x$ положительны. Правильный ответ: $\ 5 х$.

Резюме

Коммутативные, ассоциативные и дистрибутивные свойства помогают преобразовать сложное алгебраическое выражение в более простое. Когда вы переписываете выражение с помощью коммутативного свойства, вы меняете порядок сложения или умножения чисел. Когда вы переписываете выражение, используя ассоциативное свойство, вы группируете другую пару чисел вместе, используя круглые скобки. Вы можете использовать коммутативные и ассоциативные свойства для перегруппировки и изменения порядка любого числа в выражении, если выражение полностью состоит из слагаемых или множителей (а не из их комбинации). Распределительное свойство можно использовать для перезаписи выражений для различных целей. Когда вы умножаете число на сумму, вы можете складывать, а затем умножать. Вы также можете сначала умножить каждое слагаемое, а затем сложить продукты вместе. Тот же принцип применяется, если вы умножаете число на разницу.

Эта страница под названием 9.3.1: Ассоциативные, коммутативные и дистрибутивные свойства распространяется по лицензии CC BY-NC-SA 4.0 и была создана, изменена и/или курирована The NROC Project посредством исходного контента, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Проект NROC
Лицензия
CC BY-NC-SA
Версия лицензии
4,0
Теги
1. source@https://content. nroc.org/DevelopmentalMath.HTML5/Common/toc/toc_en.html

Переписывание выражений с использованием коммутативных и ассоциативных свойств

Результаты обучения

Определение ассоциативных и коммутативных свойств сложения и умножения
Использование ассоциативных и коммутативных свойств сложения и умножения для перезаписи алгебраических выражений

Подумайте о добавлении двух чисел, таких как [латекс]5[/латекс] и [латекс]3[/латекс].

[латекс]\begin{array}{cccc}\hfill 5+3\hfill & & & \hfill 3+5\hfill \\ \hfill 8\hfill & & & \hfill 8\hfill \end{array} [/latex]

Результаты те же. [latex]5+3=3+5[/latex]

Обратите внимание, порядок добавления не имеет значения. То же самое верно и при умножении [латекс]5[/латекс] и [латекс]3[/латекс].

[латекс]\begin{array}{cccc}\hfill 5\cdot 3\hfill & & & \hfill 3\cdot 5\hfill \\ \hfill 15\hfill & & & \hfill 15\hfill \end{ массив}[/латекс]

Опять же, результаты те же! [латекс]5\cdot 3=3\cdot 5[/латекс]. Порядок, в котором мы умножаем, не имеет значения.

Эти примеры иллюстрируют коммутативные свойства сложения и умножения.

Коммутативные свойства

Коммутативное свойство сложения : если [latex]a[/latex] и [latex]b[/latex] — действительные числа, то

[latex]a+b=b+a[/ латекс]

Коммутативное свойство умножения : если [латекс]а[/латекс] и [латекс]b[/латекс] — действительные числа, то

[латекс]а\cdot b=b\cdot а[/латекс]

Коммутативные свойства связаны с порядком. Если изменить порядок чисел при сложении или умножении, результат будет тот же.

пример

Используйте коммутативные свойства, чтобы переписать следующие выражения:
1. [латекс]-1+3=[/латекс]
2. [латекс]4\cdot 9=[/латекс]

Решение:

1.
	[латекс]-1+3=[/латекс]
Используйте свойство коммутативности сложения, чтобы изменить порядок.	[латекс]-1+3=3+\влево(-1\вправо)[/латекс]

2.
	[латекс]4\cdot 9=[/латекс]
Используйте свойство перестановочности умножения, чтобы изменить порядок.	[латекс]4\cdot 9=9\cdot 4[/латекс]

попробуй

Как насчет вычитания? Имеет ли значение порядок, когда мы вычитаем числа? Дает ли [латекс]7 — 3[/латекс] тот же результат, что и [латекс]3 — 7?[/латекс]

[латекс]\begin{array}{ccc}\hfill 7 — 3\hfill & & \hfill 3 — 7\hfill \\ \hfill 4\hfill & & \hfill -4\hfill \\ & \hfill 4 \ne -4\hfill & \end{array}[/latex]
Результаты не совпадают. [latex]7 — 3\ne 3 — 7[/latex]

Поскольку изменение порядка вычитания не дало того же результата, можно сказать, что вычитание не коммутативно.

Давайте посмотрим, что произойдет, если мы разделим два числа. Является ли деление коммутативным?

[латекс]\begin{array}{ccc}\hfill 12\div 4\hfill & & \hfill 4\div 12\hfill \\ \hfill \frac{12}{4}\hfill & & \hfill \ frac{4}{12}\hfill \\ \hfill 3\hfill & & \hfill \frac{1}{3}\hfill \\ & \hfill 3\ne \frac{1}{3}\hfill & \ конец{массив}[/латекс]

Результаты разные. Итак, [latex]12\div 4\ne 4\div 12[/latex]

Поскольку изменение порядка деления не дало того же результата, деление не является коммутативным.

Сложение и умножение коммутативны. Вычитание и деление не коммутативны.

Предположим, вас попросили упростить это выражение.

[латекс]7+8+2[/латекс]

Как бы вы это сделали и каким был бы ваш ответ?

Некоторые люди думают, что [латекс]7+8\текст{ равен }15[/латекс], а затем [латекс]15+2\текст{ равен }17[/латекс]. Другие могут начинаться с [латекс]8+2\текст{ дает }10[/латекс], а затем [латекс]7+10\текст{ дает }17[/латекс].

Оба способа дают одинаковый результат, как показано ниже. (Помните, что круглые скобки — это символы группировки, указывающие, какие операции следует выполнить в первую очередь.)

При добавлении трех чисел изменение группировки чисел не меняет результат. Это известно как ассоциативное свойство сложения.

Тот же принцип справедлив и для умножения. Предположим, мы хотим найти значение следующего выражения:

[латекс]5\cdot \frac{1}{3}\cdot 3[/latex]

Изменение группировки чисел дает тот же результат.

При умножении трех чисел изменение группировки чисел не меняет результат. Это известно как ассоциативное свойство умножения.

Если мы умножим три числа, изменение группировки не повлияет на произведение.

Вы, наверное, знаете это, но терминология может быть для вас новой. Эти примеры иллюстрируют ассоциативные свойства .

Ассоциативные свойства

Ассоциативное свойство сложения : если [латекс]а,б[/латекс] и [латекс]с[/латекс] являются действительными числами, то

[латекс]\влево(а+б\вправо)+ c=a+\left(b+c\right)[/latex]

Ассоциативное свойство умножения : если [latex]a,b[/latex] и [latex]c[/latex] — действительные числа, затем

[latex]\left(a\cdot b\right)\cdot c=a\cdot \left(b\cdot c\right)[/latex]

пример

Используйте ассоциативные свойства для перезаписи следующее:

1. [латекс]\влево(3+0,6\вправо)+0,4=[/латекс]
2. [латекс]\влево(-4\cdot \frac{2}{5}\вправо)\cdot 15 =[/latex]

Показать решение

попробуйте

Помимо использования ассоциативных свойств для упрощения вычислений, мы часто будем использовать их для упрощения выражений с переменными.

Исходное уравнение	Переписанное уравнение
\(\ 1,2+3,8=5\)	\(\ 3,8+1,2=5\)
\(\ \frac{1}{2}+\frac{1}{8}=\frac{5}{8}\)	\(\ \frac{1}{8}+\frac{1}{2}=\frac{5}{8}\)
\(\ 14+(-10)=4\)	\(\ (-10)+14=4\)
\(\ \frac{1}{3}+\left(-1 \frac{2}{3}\right)=-1 \frac{1}{3}\)	\(\ \left(-1 \frac{2}{3}\right)+\frac{1}{3}=-1 \frac{1}{3}\)
\(\ (-5,2)+(-3,6)=-8,8\)	\(\ (-3,6)+(-5,2)=-8,8\)

Исходное уравнение	Переписанное уравнение
\(\ 4.5 \cdot 2=9\)	\(\ 2 \cdot 4.5=9\)
\(\ (-5) \cdot 3=-15\)	\(\ 3 \cdot(-5)=-15\)
\(\ \frac{1}{5} \cdot 5=1\)	\(\ 5 \cdot \frac{1}{5}=1\)
\(\ \left(-\frac{1}{4}\right) \cdot\left(-\frac{8}{10}\right)=\frac{1}{5}\)	\(\ \left(-\frac{8}{10}\right) \cdot\left(-\frac{1}{4}\right)=\frac{1}{5}\)

\(\ 4 \cdot(x \cdot 27)\)	Оригинальное выражение.
\(\ 4 \cdot\left(\left(-\frac{3}{4}\right) \cdot 27\right)\)	Замените \(\ -\frac{3}{4}\) на \(\ x\).
\(\ \begin{array}{r} \left(4 \cdot\left(-\frac{3}{4}\right)\right) \cdot 27 \\ \left(-\frac{12}{4}\right) \cdot 27 \end{массив}\)	Используйте ассоциативное свойство умножения, чтобы перегруппировать множители так, чтобы \(\ 4\) и \(\ -\frac{3}{4}\) находились рядом друг с другом. Умножение \(\ 4\) на \(\ -\frac{3}{4}\) делает вычисление выражения немного проще, чем умножение \(\ -\frac{3}{4}\) на \ (\ 27\).
\(\ -3 \cdot 27=-81\)	Умножить. \(\ 4\) раз \(\ -\frac{3}{4}=-3\), а \(\ -3\) раз \(\ 27\) равно \(\ -81\).

\(\ 4+12+3+4-8\)	Оригинальное выражение.
\(\ 12+3+4+4+(-8)\)	Определите совместимые номера. \(\ 4+4\) равно \(\ 8\), и есть \(\ -8\). подарок. Вспомните, что вы можете думать о \(\ -8\) как о \(\ +(-8)\). Используйте свойство коммутативности сложения, чтобы сгруппировать их вместе.
\(\ 12+3+(4+4+(-8))\)	Используйте ассоциативное свойство для группировки \(\ 4+4+(-8)\).
\(\ 12+3+0\)	Добавить \(\ 4+4+(-8)\).
\(\ 12+3+0=15\)	Добавьте остальные условия.

\(\ 5(2 x-3)\)	Оригинальное выражение.
\(\ 5(2 х)-5(3)\)	Раздать 5.
\(\10 х-15\)	Умножить.
\(\ 10(2)-15\) \(\ 20-15=5\)	Подставьте 2 вместо \(\ x\) и оцените.

\(\ (-15,5)+35,5=20\)	Добавление.
\(\ 35,5+(-15,5)\)	Используя свойство коммутативности, вы можете поменять местами -15,5 и 35,5, чтобы они располагались в другом порядке.
\(\ \begin{array}{c} 35,5+(-15,5) \\ 35,5-15,5=20 \end{массив}\)	Сложение 35,5 и -15,5 равносильно вычитанию 15,5 из 35,5. Сумма 20.

\(\ 9(4+x)\)	Оригинальное выражение.
\(\ 9(4)+9(х)\)	Распредели 9 и умножь.
\(\ 36+9 х\)	Умножить.

\(\ 5(2 x-3)\)	Оригинальное выражение.
\(\ 5(2(2)-3)\)	Замените \(\ x\) на 2.
\(\ \begin{array}{c} 5(4-3) \\ 5(4)-5(3) \end{массив}\)	Умножить.
\(\ 20-15=5\)	Вычтите и оцените.

\(\ 3(x)+12(x)\)	\(\ 3 x\) равно 3 раза \(\ x\), а \(\ 12 x\) равно 12 раз \(\ x\)
\(\ х(3+12)\)	Изучая свойство дистрибутивности (а также используя свойство коммутативности), вы знаете, что \(\ x(3+12)\) равносильно \(\ 3(x)+12(x)\).
\(\ \begin{array}{c} x(15) \\ \text { or } \\ 15 x \end{массив}\)	Объедините члены в скобках: \(\ 3+12=15\).

\(\ 10 у+5 у+9 х-6 х-х\)	В этом выражении есть похожие члены, так как все они состоят из коэффициента, умноженного на переменную \(\ x\) или \(\ y\). Обратите внимание, что \(\ -x\) совпадает с \(\ (-1) x\).
\(\ 15 у+2 х\)	Добавить похожие термины. \(\ 10 y+5 y=15 y\) и \(\ 9 x-6 x-x=2 x\).