Сначала умножение: Порядок выполнения действий в выражениях без скобок и со скобками

Содержание

Порядок выполнения действий в выражениях без скобок и со скобками — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Содержание

Порядок выполнения действий в выражениях без скобок и со скобками — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Сначала сложение или умножение

С самого начала следует напомнить, чтобы потом не путаться: есть цифры – их 10. От 0 до 9. Есть числа, и они состоят их цифр. Чисел бесконечно много. Точно больше, чем звезд на небе.

Математическое выражение − это записанное с помощью математических символов наставление, какие действия нужно произвести с числами, чтобы получить результат. Не «выйти» на искомый результат, как в статистике, а узнать, сколько их точно было. А вот чего и когда было − уже не входит в сферу интересов арифметики. При этом важно не ошибиться в последовательности действий, что сначала — сложение или умножение? Выражение в школе иногда называют «пример».

Сложение и вычитание

Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.

Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.

Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.

Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел.

Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.

Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.

Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.

Умножение

Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M.

Это всего лишь форма записи сложения одинаковых слагаемых.

Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».

Что сначала — умножение или сложение?

Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:

5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все помидоры сдавали учетчику, он укладывал их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
50 + 50 – это кучки малолетних работников;
70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:

500 + 500 +500 +500 +500 + 50 +50 + 70 =?;

Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.

Две кучки по 50 – это тоже можно записать через умножение.

И одна кучка 70 помидоров.

5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?

И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.

2500 + 100 + 70 = 2 670

При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни.

Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.

Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.

Деление

Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов.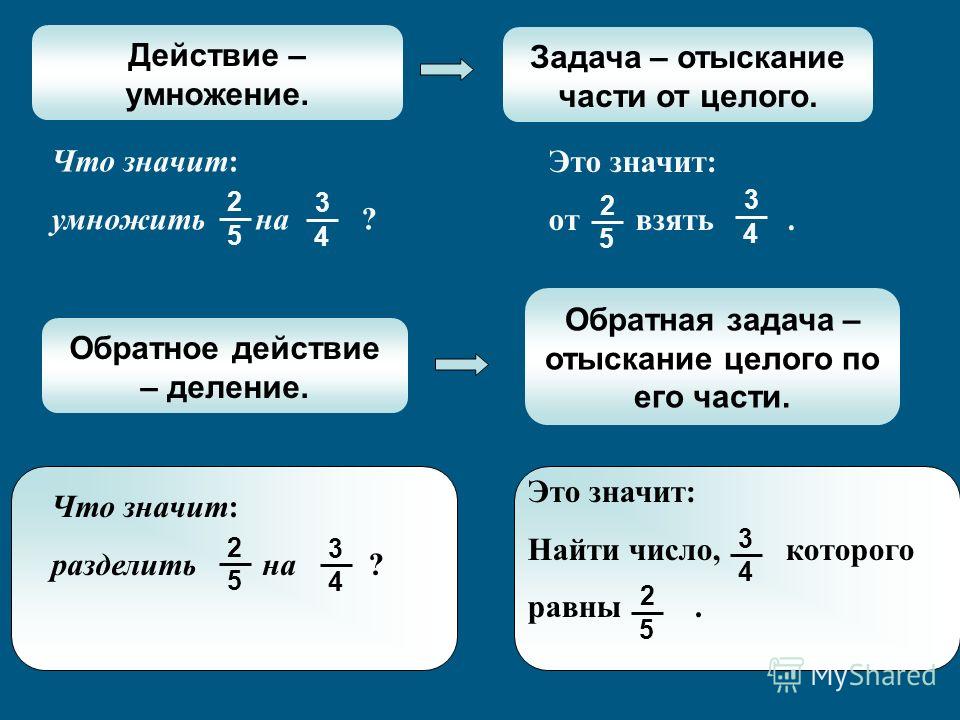 Самый прямой аналог в жизни – это фасовка.

Скобки

Большое значение в решении примеров имеют скобки. Скобки в арифметике – математический знак, используемый для регулирования последовательности вычислений в выражении (примере).

Умножение и деление имеют приоритет выше, чем сложение и вычитание. А скобки имеют приоритет выше, чем умножение и деление.

Все, что записано в скобках, вычисляется в первую очередь. Если скобки вложенные, то сначала вычисляется выражение во внутренних скобках. И это непреложное правило. Как только выражение в скобках вычислено, скобки пропадают, а на их месте возникает число. Варианты раскрытия скобок с неизвестными здесь не рассматриваются. Так делают до тех пор, пока все они не исчезнут из выражения.

Это как коробочки с конфетами в большом мешке. Сначала нужно раскрыть все коробочки и ссыпать в большой мешок: (25 – 5 ) = 20. Пять конфет из коробочки сразу заслали отличнице Люде, которая приболела и в празднике не участвует. Остальные конфеты − в мешок!
Потом связать конфеты в пучки по 5 штук: 20 : 5 = 4.
Потом добавить в мешок еще 2 пучка конфет, чтобы можно было поделить на троих детей без драки. Признаки деления на 3 в данной статье не рассматриваются.

(20 : 5 + 2) : 3 = (4 +2) : 3 = 6 : 3 = 2

Итого: трем детям по два пучка конфет (по пучку в руку), по 5 конфет в пучке.

Если вычислить первые скобки в выражении и переписать все заново, пример станет короче. Метод не быстрый, с большим расходом бумаги, зато удивительно эффективный. Заодно тренирует внимательность при переписывании. Пример приводится к виду, когда остается только один вопрос, сначала умножение или сложение без скобок. То есть к такому виду, когда скобок уже и нет. Но ответ на этот вопрос уже есть, и нет смысла обсуждать, что идет сначала — умножение или сложение.

«Вишенка на торте»

И напоследок. К математическому выражению не применимы правила русского языка – читать и выполнять слева направо:

Это простенький пример может довести до истерики ребенка или испортить вечер его маме. Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку».

«Совсем вишня»

В Сети гуляет пример, вызывающий затруднения у взрослых дяденек и тетенек. Он не совсем по рассматриваемой теме, что сначала — умножение или сложение. Он вроде как про то, что сначала выполняете действие в скобках.

От перестановки слагаемых сумма не изменяется, от перестановки множителей тоже. Нужно просто записывать выражение так, чтобы не было потом мучительно стыдно.

6 : 2 ∙ (1+2) = 6 ∙ ½ ∙ (1+2) = 6 ∙ ½ ∙ 3 = 3 ∙ 3 = 9

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ:

7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.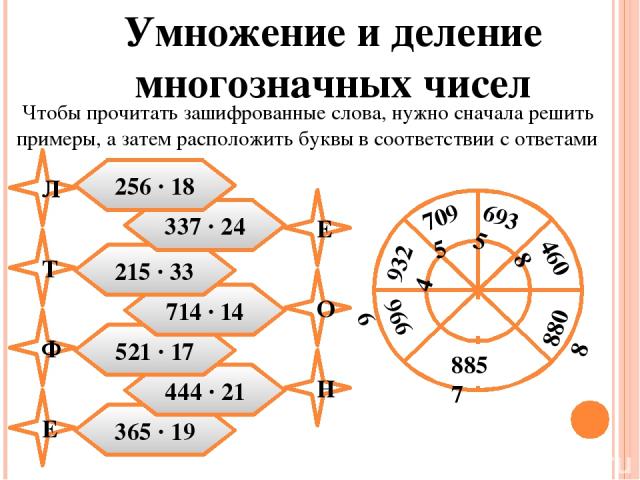

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Сайт для детей и их родителей

Порядок выполнения математических действий

Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.

Итак, вспомним о том, что сначала вычисляются выражения в скобках

1) в скобках: 10 + 6 = 16 ;

2) вычитание: 38 – 16 = 22 .

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

Порядок выполнения действий:

1) слева направо, сначала деление: 10 ÷ 2 = 5 ;

2) умножение: 5 × 4 = 20 ;

10 + 4 – 3 = 11 , т.е.:

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7 ; т. е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54 , т.е.:

1) выражение в скобках: 13 – 9 = 4 ;

2) умножение: 6 × 4 = 24 ;

3) сложение: 30 + 24 = 54 ;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;

2) умножение и деление;

3) сложение и вычитание.

Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.

Математика – 3 классПродолжим изучение предметов, которые изучают наши дети в начальной школе.
Математика – 2 классПродолжим изучение программы математики в начальной школе и на этот.

Понравилась статья — поделитесь с друзьями:

Подпишитесь на новости сайта:

Оставляйте пожалуйста комментарии в форме ниже

«Порядок действий в выражениях без скобок, имеющих действия разных ступеней»

(2 класс, Образовательная система «Перспектива»

Авторы: Дорофеев Г. В., Миракова Т.Н., Бука Т.Б.)

Тема урока: Порядок действий в выражении без скобок, имеющих действия разных ступеней»

Цели урока:

Образовательная: формирование представления о способе выполнения порядка действий в выражениях, имеющих действия разных ступеней. Развивающая: развитие умения наблюдать, сравнивать, анализировать, делать выводы.

Воспитательная: воспитание взаимопомощи, умения слушать своего товарища, принимать точку зрения другого человека отличную от собственной.

I Организационный момент.

— Здравствуйте, ребята! Начинаем урок математики.

— Если вы знаете о чем идет речь, хлопните в ладоши:

переместительное свойство умножения;

таблица умножения и деления на 2, 3, 4;

компоненты умножения;

компоненты деления;

компоненты сложения;

компоненты вычитания

— Как много вы уже знаете! А хотите узнать еще больше? Будьте старательными, активными, внимательными и у вас все получится.

II Актуализация знаний, умений, навыков и способов действий.

– Прочитайте выражения по-разному: (Найти произведение чисел двух и семи; два умножить на семь; первый множитель два, второй множитель — семь, найти произведение; по два взять семь раз и т.д.)

2х7 15:3 17-3 8+9

Учитель:— придумайте свои примеры и прочитайте их разными способами. (Работа в паре)

Дети придумывают свои примеры и читают их разными способами.

Оценка работы. – Что помогло вам успешно справиться с заданием? (знание компонентов сложения, вычитания, умножения и деления, таблица умножения).

Порядок действий в выражении, где только сложение и вычитание.

12-2+3=13

12-2+3=7

— Чем похожи и чем отличаются записанные равенства? (Одинаковые числа, знаки, различный результат)

— Назовите истинное высказывание.

— что нужно сделать, чтобы ложное высказывание стало истинным? (Поставить скобки, в 1 примере скобки можно поставить, можно не ставить, а во 2 ставим обязательно)

Оценка фронтальной работы. – Что помогло вам успешно справиться с заданием? (знание порядка действий, где только сложение и вычитание без скобок и со скобками).

3.Предлагаю вам еще решить примеры.

(На доске записаны примеры.)

Ваня и Аня решали примеры. Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?

19 – 8 + 5 =16

2 * 6 : 3 = 4

2 + 3 * 4 = 20

19 – 8 + 5 = 16

2 * 6 : 3 = 4

2 + 3 * 4 = 14

— Решите первый пример.

— Как выполняли действия? (Сначала выполнили вычитание, а потом сложение.)

— Решите второй пример.

— Как выполняли действия. (Сначала выполнили умножение, а потом деление).

— Как решал третий пример Ваня? (Сначала выполнил сложение, а потом умножение).

— А как решала Аня? (Сначала выполнила умножение, а потом сложение).

— Как вы думаете, кто из ребят верно решил третий пример? Обоснуйте свой ответ. (Мы не можем определить, кто решил верно.)

— Чего мы не знаем? (Мы не знаем, в каком порядке нужно выполнять действия в некоторых примерах.)

— Чему вы должны научиться?

(Решать примеры на порядок действий в выражении без скобок, где есть и сложение, и вычитание, и умножение, и деление)

— Какая тема урока? (Порядок выполнения действий.)

-Какова цель нашего урока? (Научиться устанавливать правильный порядок действий.)

III Открытие нового способа.

— Откройте учебник на с. 97, прочитайте выделенное в рамочку.

— Назовите арифметические действия первой ступени. Расположите их на нужной ступени.

— Назовите арифметические действия второй ступени. Расположите их на нужной ступени.

— Какая ступень выше? (Вторая)

— Сделайте вывод: какое действие надо выполнять первым? (умножение и деление) вторым? (сложение и вычитание)

— Мы получили новое знание. Проверим, правильно ли мы сделали выводы.

Сравним наше новое знание с научным в учебнике. Прочитайте на с.97 выделенное в рамочку.

— Как вы думаете, кто верно решил третий пример: Ваня или Аня? Обоснуйте свой ответ. (Аня, т.к. в этом примере сначала надо выполнить действие умножения, а потом сложения)

IV. Физминутка (из СанПин) зрительная

V. Первичное закрепление с комментированием

1. -Попробуем применить наше новое знание на практике.

(Коллективное выполнение с комментированием.)

3+5 -2 = 2+2+2=

2*3+14= 19- 9 – 10=

4*3:6= 16 – 8 : 2=

— Выберите примеры с действиями только первой ступени.

-Как выполнять действия в первом столбике? (По порядку.)

— Выберите примеры с действиями только второй ступени.

-Как выполнять действия во втором столбике? (По порядку)

— Какие примеры остались? (примеры с действиями обеих ступеней)

— Как будем выполнять действия в третьем столбике? (Сначала выполним действие умножения и деления , а затем сложения и вычитания).

2. — Давайте проверим, «работает» ли открытый нами способ на других примерах?

1. Работа по учебнику.

С. 98, задание№3(1 стр.)

Взаимопроверка. Молодцы! Что помогло вам успешно справиться с решением примеров?

VI. Контроль

Обозначьте порядок действий в выражениях:

а+в ×с-у

у:с-к+а

в-а+р:т

— Сверьте с доской. Самооценка

— Что вам нужно было сделать?

— Удалось ли правильно решить?

— Вы все сделали правильно или были ошибки, недочеты?

— Вы сделали все сами или с чьей-то помощью?

— Оцените свою работу?

Критерии оценивания:

Все задания выполнены самостоятельно, верно – «5»

Все задания выполнены, но было обращение за помощью – «4»

Допущено 1-2 незначительных ошибки – «4»

Выполнено 1 задание из 3, за помощью не обращался – «3»

Не выполнил совсем – «2»

VII Рефлексивная оценка.

— Вы могли в начале урока правильно решить примеры?

— Изменились ли ваши знания? Что нового добавилось к уже имеющимся знаниям?

— Как будете действовать дома при решении примеров, где встречаются разные действия?

VIII Домашнее задание.

Учебник с.98, пр.3 (2 стр.), №4
Придумать два выражения на порядок действий, используя все четыре действия.

Зубодробительная задачка с очень простой математикой

В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:

То, что в скобках, выполняется в первую очередь. Если скобок несколько, они выполняются слева направо.
При отсутствии скобок математические действия выполняются слева направо, сначала умножение и деление, потом — сложение и вычитание.
Между множителем и скобкой (или двумя скобками) может опускаться знак умножения.

Разберём подробнее, что это значит в нашем случае.

1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:

8 / 2(2 + 2) → 8 / 2(4)

2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:

8 / 2(4) → 8 / 2 × 4

3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.

Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.

Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:

8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16

Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.

А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами 🙂

Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:

«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».

Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)

Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!

Та самая цитата.

А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:

«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».

Если апеллировать к Фриде Максовне Шустеф, то выходит, что:

В. Л. Гончаров говорит так: «Ребята, используйте черту и ставьте скобки, чтобы ни у кого не было вопросов про приоритет».
Если у нас всё же битва арифметики и алгебры, то, по П. С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало.

Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.

Полная цитата из Шустеф, которая, оказывается, имеет в виду совсем не то.

Приоритет — Python

Посмотрите внимательно на выражение 2 + 2 * 2 и посчитайте в уме ответ.

Правильный ответ: 6.

Если у вас получилось 8, то этот урок для вас. В школьной математике мы изучали понятие «приоритет операции». Приоритет определяет то, в какой последовательности должны выполняться операции. Например, умножение и деление имеют больший приоритет, чем сложение и вычитание, а приоритет возведения в степень выше всех остальных арифметических операций: 2 ** 3 * 2 вычислится в 16.

Но нередко вычисления должны происходить в порядке, отличном от стандартного приоритета. В сложных ситуациях приоритет можно (и нужно) задавать круглыми скобками, точно так же, как в школе, например: (2 + 2) * 2.

Скобки можно ставить вокруг любой операции. Они могут вкладываться друг в друга сколько угодно раз. Вот пара примеров:

print(3 ** (4 - 2))  # => 9
print(7 * 3 + (4 / 2) - (8 + (2 - 1)))  # => 14
%MINIFYHTML530bef5095a3afe64850403afc3b9cff14%

Главное при этом соблюдать парность, то есть закрывать скобки в правильном порядке. Это, кстати, часто становится причиной ошибок не только у новичков, но и у опытных программистов. Для удобства ставьте сразу открывающую и закрывающую скобку, а потом пишите внутреннюю часть. Редактор на нашем сайте (и большинство других редакторов кода) делают это автоматически: вы пишете (, а редактор сразу добавляет ). Это касается и других парных символов, например, кавычек. О них — в будущих уроках.

Иногда выражение сложно воспринимать визуально. Тогда можно расставить скобки, не повлияв на приоритет. Например, задание из прошлого урока можно сделать немного понятнее, если расставить скобки.

Было:

print(8 / 2 + 5 - -3 / 2)  # => 10.5

Стало:

print(((8 / 2) + 5) - (-3 / 2))  # => 10.5

Запомните: код пишется для людей, потому что код будут читать люди, а машины будут только исполнять его. Для машин код — или корректный, или не корректный, для них нет «более» понятного или «менее» понятного кода.

Задание

Дано вычисление 70 * 3 + 4 / 8 + 2.

Расставьте скобки так, чтобы оба сложения (3 + 4) и (8 + 2) высчитывались в первую очередь. Выведите на экран результат.

Нашли ошибку? Есть что добавить? Пулреквесты приветствуются https://github.com/hexlet-basics

Как использовать PEMDAS и решить с порядком операций (примеры)

Обновлено 21 декабря 2020 г.

Ли Джонсон

Выполнение математической задачи, сочетающей в себе различные операции, такие как умножение, сложение и экспоненты, может вызвать недоумение, если вы не сделаете этого. Не понимаю ПЕМДАС. Простая аббревиатура описывает порядок операций в математике, и вы должны помнить ее, если вам нужно выполнять вычисления на регулярной основе. PEMDAS означает круглые скобки, экспоненты, умножение, деление, сложение и вычитание, сообщая вам порядок, в котором вы беретесь за различные части длинного выражения.Узнайте, как это использовать, и вас никогда не смутят проблемы типа 3 + 4 × 5–10, с которыми вы можете столкнуться.

Совет: PEMDAS описывает порядок операций:

M и D — умножение и деление

A и S — сложение и вычитание.

Решайте любые проблемы с различными типами операций в соответствии с этим правилом, работая сверху (скобки) вниз (сложение и вычитание), отмечая, что операции в одной строке можно выполнять слева направо по мере их появления. в вопросе.

Каков порядок работы?

Порядок операций показывает, какие части длинного выражения нужно вычислить в первую очередь, чтобы получить правильный ответ. Если вы, например, просто подходите к вопросам слева направо, в большинстве случаев вы в конечном итоге рассчитываете что-то совершенно другое. PEMDAS описывает порядок операций следующим образом:

M и D — Умножение и деление

A и S — Сложение и вычитание.

Когда вы решаете длинную математическую задачу с помощью множества операций, сначала вычислите что-нибудь в круглых скобках, а затем переходите к показателям степени (т.е., «степени» чисел) перед умножением и делением (они работают в любом порядке, просто работают слева направо). Наконец, вы можете работать над сложением и вычитанием (опять же, просто работайте слева направо).

Как запомнить PEMDAS

Запоминание аббревиатуры PEMDAS, вероятно, является самой сложной частью его использования, но есть мнемонические средства, которые вы можете использовать, чтобы упростить это. Самым распространенным является «Прошу прощения, моя дорогая тетя Салли», но есть и другие альтернативы: «Люди повсюду принимают решения о суммах» и «Пухлые эльфы могут потребовать перекус». 3-3) × 4

Решения перечислены ниже по порядку, поэтому не прокручивайте вниз, пока не попытаетесь решить проблему.3 — 3) × 4 \\ & = 20 ÷ (8 — 3) × 4 \\ & = 20 ÷ 5 × 4 \\ & = 16 \ end {align}

Правило PEMDAS — Что такое Правило PEMDAS? Определение, примеры

В математике PEMDAS — это аббревиатура, используемая для обозначения порядка операций, которым необходимо следовать при решении выражений, содержащих несколько операций. PEMDAS означает P- круглые скобки, E- экспоненты, M- умножение, D- деление, A- сложение и S- вычитание. В разных странах используются разные аббревиатуры для обозначения порядка операций.Например, в Канаде порядок операций указан как BEDMAS (скобки, экспоненты, деление, умножение, сложение и вычитание). Некоторые люди предпочитают говорить BODMAS (B- скобки, O- порядок или Off), в то время как немногие другие называют это GEMDAS (G- группировка).

В этом уроке вы узнаете о правиле PEMDAS для решения арифметических выражений с последующими решенными примерами и практическими вопросами.

Введение в PEMDAS

PEMDAS или порядок операций — это установленная последовательность для выполнения операций в арифметическом выражении.Существуют разные сценарии, в которых все проходит через различные этапы в фиксированной последовательности. Рассмотрим следующий сценарий. Райан и Рухи посетили фабрику игрушек. Они оба наблюдали за производством игрушек на фабрике. Сначала конструируют игрушки. Далее их собирают и упаковывают в коробки. Наконец, они проверяются на качество перед отправкой в магазины. Все сделано в установленном порядке.

Точно так же арифметические операции выполняются упорядоченным образом.Давайте узнаем порядок операций по математике. Найти ответ на математические операции довольно просто, если задействован только один оператор. Что делать, если задействовано несколько операторов? Это могло быть немного сложнее! Посмотрим как.

Райан и Рухи решили отдельно математическое выражение 5 + 2 × 3. Вот как они это решили.

Метод Рухи

Метод Райана

5 + 2 × 3

= 7 × 3

= 21

5 + 2 × 3

= 5 + 6

= 11

Как видите, Райан и Рухи получили разные ответы.На это выражение в математике может быть только один правильный ответ! Вы можете решить, кто прав?

Не волнуйтесь! PEMDAS поможет вам найти правильный ответ.

Что такое PEMDAS?

PEMDAS — это порядок операций, используемый в математике для упрощения сложных вычислений. В нем говорится, что мы начинаем решать любое арифметическое выражение, решая члены, записанные в скобках или скобках, а затем упрощаем экспоненциальные члены и переходим к операциям умножения и деления, а затем, наконец, мы можем найти ответ, решая операции сложения и вычитания.

PEMDAS: определение

PEMDAS — это набор правил, которым следуют при решении математических выражений. Это правило начинается с скобок , а затем операции выполняются с экспонентами или степенями. Далее выполняем операции умножения или деления слева направо. Наконец, операции сложения или вычитания выполняются слева направо.

п.	[{()}]	Круглые скобки
E	х ²	Экспоненты
м D	× ИЛИ ÷	Умножение ИЛИ Дивизия
А S	+ ИЛИ –	Дополнение ИЛИ Вычитание

Если вы будете придерживаться этого порядка операций в правиле PEMDAS, вы всегда получите правильный ответ. Следующая аббревиатура поможет вам запомнить Правило PEMDAS.

P аренда E xcuse M y D ear A unt S союзник

Давайте разберемся с PEMDAS на примере.

BODMAS против PEMDAS

Правило PEMDAS аналогично правилу BODMAS . Существует различие в сокращении, потому что определенные термины известны под разными именами в разных местах.

Когда использовать PEMDAS?

Когда в математическом выражении содержится более одной операции, мы используем метод PEMDAS. PEMDAS в математике дает вам правильную структуру для получения уникального ответа для каждого математического выражения. При использовании метода PEMDAS необходимо соблюдать последовательность определенных правил. Как только вы освоите эти правила, вы сможете выполнять сразу несколько шагов.

Что следует помнить

Операции, указанные в скобках, должны быть выполнены в первую очередь.
Затем решите степень в выражении.
Двигайтесь слева направо и выполняйте умножение или деление, в зависимости от того, что наступит раньше.
Двигайтесь слева направо и выполняйте сложение или вычитание, в зависимости от того, что наступит раньше.

Распространенные ошибки при использовании правила PEMDAS в математике

Наличие нескольких скобок обычно вызывает путаницу. Если мы не знаем, какую скобку решить в первую очередь, это может привести к неправильному ответу.Теперь мы узнаем, как решить это выражение с несколькими скобками.

4 + 3 [8-2 (6-3)] ÷ 2

Начнем с внутренней стороны скоб. Сначала мы решим самую внутреннюю скобку, а затем двинемся наружу.

Начиная с 6 — 3 = 3, получаем: 4 + 3 [8 — 2 (3)] ÷ 2
Далее, умножая 2 (3) = 6 или 2 × 3 = 6, получаем: 4 + 3 [8 — 6] ÷ 2
Осталась одна скобка, [8 — 6] = 2, получаем: 4 + 3 [2] ÷ 2
Решая 3 [2] или 3 × 2 = 6, получаем: 4 + 6 ÷ 2

Мы видим, что все выражения в скобках решены. Основываясь на PEMDAS, мы знаем, что дальше идет деление, следовательно, 6 ÷ 2 = 3, то есть 4 + 3. И, наконец, сложение 4 + 3 = 7.

Часто задаваемые вопросы о PEMDAS

Как работает правило Пемдаса?

В любом арифметическом выражении, если используется несколько операций, мы должны сначала решить термины, указанные в скобках. Избавившись от скобок, мы решаем операцию умножения и деления, независимо от того, что идет первым в выражении слева направо.Тогда мы получим упрощенное выражение, состоящее только из операций сложения и вычитания. Мы решаем сложение и вычитание слева направо, что бы ни случилось раньше, и получаем окончательный ответ. Так работает PEMDAS.

Что означает PEMDAS?

PEMDAS означает порядок операций для математических выражений, включающих более одной операции. Это означает P- круглые скобки, E- экспоненты, M- умножение, D- деление, A- сложение и S- вычитание.

Как делать Пемдас с дробями?

В выражении с дробными членами нет изменений в использовании правила PEMDAS. Это нужно делать так же, как и любое целочисленное выражение.

Что означает буква P в Пемдасе?

В PEMDAS буква P означает круглые или квадратные скобки. Порядок решения скобок задается как [{()}]. Это означает, что мы всегда сначала решаем самую внутреннюю скобку, а затем переходим к фигурным скобкам и квадратным скобкам.

Вы сначала умножаете или делите в PEMDAS?

В правиле PEMDAS мы решаем операции умножения и деления слева направо.Мы можем выполнить любую операцию, умножение или деление, что бы ни было первым в выражении.

Когда мы применяем правило PEMDAS?

Правило PEMDAS применяется для решения сложного математического выражения, включающего более одной операции, например сложение, вычитание, умножение или деление.

Какое правило для PEMDAS?

Правило PEMDAS дает нам правильную последовательность решения математического выражения. В правиле PEMDAS сначала операции выполняются в скобках.Далее выполняются операции с показателями степени или степенями. Затем следуют операции умножения или деления слева направо, в зависимости от того, что наступит раньше. Наконец, операции сложения или вычитания выполняются слева направо, в зависимости от того, что наступит раньше.

Что такое BODMAS, BIDMAS и PEMDAS?

BODMAS объясняет «Порядок операций» в математике, а BIDMAS и PEMDAS делают то же самое, но используют несколько разные слова. Если для вас все вышесказанное звучит как чепуха, взгляните на наше короткое видео ниже, где Али объясняет, как все это работает.

Что такое аббревиатура?

Аббревиатура — это слово, состоящее из начальных букв слов во фразе. Аббревиатуры можно произносить как отдельные слова.

Подумайте о НАСА и FAQ. Оба они произносятся так, как если бы они были самостоятельным словом. Однако NASA означает N ational A eronautics и S pace A dministration and FAQ означает F обязательно A sked Q uestions.

Подобным образом буквы в BODMAS, BIDMAS и PEMDAS обозначают слова.

Что обозначают буквы в BODMAS, BIDMAS и PEMDAS?

В случае математических сокращений BODMAS, BIDMAS и PEMDAS все они означают одно и то же, и все они служат одной и той же цели. Вот что обозначают буквы:

Кронштейны
Заказы
Дивизия
Умножение
Дополнение
Вычитание

Кронштейны
Индексы
Дивизия
Умножение
Дополнение
Вычитание

Круглая скобка
Показатели
Умножение
Дивизия
Дополнение
Вычитание

Третья серия, приведенная выше, наиболее часто используется в США, в то время как школы Великобритании почти всегда применяют серию 1 или серию 2, указанную выше.Когда ваш ребенок впервые сталкивается с одним из них, вам следует вспомнить, какой именно, потому что в разных школах используются разные. Придерживаясь того же, что и в вашей школе, вы, по крайней мере, избежите одного уровня сложности.

Что такое ордера, индексы и экспоненты?

Заказы, индексы и экспоненты — это маленькие числа в верхнем индексе, обозначающие степени в математике.

Скобки, деление, умножение, сложение и вычитание — это слова, которые нам знакомы, но как насчет второго элемента аббревиатуры — порядков, индексов или экспонентов? Это «числа половинного размера», которые часто встречаются в математических выражениях.В следующем примере 2 — это индекс (единственное число из множественного числа , индексы ):

3 ² = 3 x 3

Что такое математические операции?

Математическая операция может рассматриваться как один из символов , который заставляет что-то случиться в математике. Знак умножения (x) означает, что два числа нужно умножить вместе, а знак сложения (+) означает, что два числа нужно сложить вместе. Это операции .

Каков правильный порядок действий в математике?

Правильный порядок операций в математике: B rackets, O rders, D ivision, M ultiplication, A ddition и S ubtraction.

Если вы используете BIDMAS, замените индикаторы O на индикаторы I .

Вся суть BIDMAS и BODMAS в том, чтобы помочь вам запомнить, какие операции и в каком порядке выполнять.К сожалению, математика подсказывает, что это не порядок слева направо, как вы могли бы ожидать: давайте посмотрим на типичный пример и посмотрим, получите ли вы правильный ответ:

2 + 3 х 4

Вы пришли к выводу, что ответ — 20? Если это так, то вы выполнили расчет слева направо и сказали, что 2 плюс 3 равно 5 , и тогда умножить на 4, чтобы получить 20 . К сожалению, с математической точки зрения это неверно!

Если вы посмотрите на правила BIDMAS / BODMAS, вы увидите, что умножение предшествует сложению (две операции, с которыми мы имеем дело), и поэтому вы должны были иметь дело с умножением ДО , когда вы имели дело с сложением.Следовательно, правильная логика: 3, умноженное на 4, равняется 12 , а затем прибавляется к 2, чтобы получить 14 . 14 — правильный ответ.

Я сбился со счета, сколько раз у меня был по телефону родитель, который говорил: «Вы просто должны ошибаться. Послушайте, я сделал это на своем калькуляторе и нажал 2 + 3 x 4, и он всегда, но всегда, дает мне ответ 20 ».

Из многих тысяч вопросов на сайте образовательных викторин именно этот выпуск Порядка операций чаще всего вызывает запросы у наших учителей — и когда кажется, что у родителей есть калькуляторы, неудивительно, почему!

Используются ли в экзамене 11-Plus BODMAS или BIDMAS?

Вообще-то нет.Это может потребовать некоторой веры, но на экзамене 11-Plus неправильный ответ часто отмечается как правильный, в то время как правильный ответ отмечается вниз! Это связано с тем, что некоторые авторитеты считают, что дети в возрасте до 11 лет не должны знать Порядка операций, как это определено BIDMAS / BODMAS, и поэтому ожидают, что учащиеся будут ошибочно выполнять вычисления слева направо.

Во избежание вероятности того, что кандидат 11-Plus будет оценен за правильный ответ (!), Крайне важно, чтобы вы выяснили в своей школе, следует ли применять правила Порядка операций в математических вопросах.

Каковы правила BODMAS или BIDMAS?

Чтобы увидеть, как правила BIDMAS (или BODMAS) применяются в более сложных сценариях, нам нужно проанализировать математическое выражение, которое содержит все различные элементы. Если вы готовы, то приступим!

2 x 20 ÷ 2 + (3 + 4) x 3 ² — 6 + 15

Шаг 1

Разберитесь с скобами, чтобы получить:

2 x 20 ÷ 2 + 7 x 3 ² — 6 + 15

Шаг 2

Сделайте с индексами (если вы думаете о BIDMAS) или ордерами (если вы думаете о BODMAS), чтобы получить:

2 х 20 ÷ 2 + 7 х 9-6 + 15

Шаг 3

деление и умножение ранжируются одинаково, поэтому обработайте их вместе слева направо, чтобы получить:

20 + 63 — 6 + 15

Шаг 4

Сложение и вычитание имеют одинаковый рейтинг, поэтому обработайте их вместе слева направо, чтобы получить:

Я надеюсь, что эта статья помогла вам разобраться в том, что такое BODMAS, BIDMAS и PEMDAS. Для более подробного ознакомления с порядком операций, а также с некоторыми интересными примерами, вы можете попробовать статью в Wiki по адресу: Порядок операций, но не ожидайте, что у вас не будет головной боли!

Итак, BODMAS, BIDMAS и PEMDAS объяснили — есть ли что-нибудь еще, что вы хотели бы знать? Если у вас есть вопросы об образовании, просмотрите наш банк знаний. У нас есть множество статей, наполненных информацией, советами и советами для родителей. Это ценное оружие в арсенале любого родителя!

Математика 1010 онлайн

Отсутствующий оператор означает умножение

По соглашению, когда оператор опускается, это означает умножение.Например, 3a означает 3 * a , а 3 (4 + 2) равно 18. xy означает x * y .

(На самом деле есть исключение из этого правила в виде смешанные числа которые для нашей цели в основном бесполезны, и их следует избегать.)

Последовательность операций

По соглашению формулы вычисляются в следующей последовательности:

Возведение в степень.
Умножение и деление.
Сложение и вычитание
В случае операций того же уровня приоритета, оценка продолжается слева направо .

Собственно, в приведенном выше списке должен быть пункт 0 перед всеми остальные: стандартные функции, такие как логарифмы, тригонометрические функции и т. д. Однако мы будем не используйте такие функции в Math 1010. (Но вы изучите их в большие детали в Math 1030, 1050 и 1060, а также в Calculus.)

Если бы эти условности были абсолютными, нас бы сильно задушили, Чтобы предотвратить это бедствие, условные обозначения можно изменить, используя круглые скобки:

Сначала вычисляются выражения в скобках.

Проиллюстрируем эти правила на нескольких примерах:

2 + 3 * 4 = 2 + 12 = 14. Обратите внимание, что умножение проводится перед сложением.
(2 + 3) * 4 = 5 * 4 = 20. Вы используете круглые скобки для укажите, что добавление должно быть выполнено в первую очередь.
10 — 4 — 2 = 6 — 2 = 4. Вы выполняете вычитания работают слева направо.
10 — (4-2) = 10-2 = 8. Вы используете круглые скобки выполнить сначала крайнее правое вычитание, которое изменяет отвечать.2r
Скобки могут быть вложенными , т. Е. пары совпадающих круглых скобок могут содержаться в других парах круглые скобки. Например,
12- (6- (4-2)) = 12 — (6-2) = 12-4 = 8.
Чтобы оценить формулы, содержащие вложенные пары круглых скобок, вы начните с самых сокровенных пар и продолжайте работать дальше.
Поддержка правил PEMDAS Страница
Добро пожаловать на страницу правил PEMDAS Math Salamanders.
Здесь вы найдете помощь в использовании PEMDAS с некоторыми простыми инструкциями и множеством рабочих примеров.
Mathway.

PEMDAS обычно вводится примерно в 5-м классе и меняет то, как вы смотрите и читаете вычисления.
Однако это не такое простое правило, как кажется — здесь есть несколько подводных камней, которые рассматриваются ниже!
PEMDAS (иногда называемый PEMDAS, BEDMAS или BODMAS) является математическим сокращение, чтобы помочь вам понять, как работают вычисления.
Аббревиатура относится к порядку, в котором должны выполняться любые вычисления, и обычно вводится примерно в пятом классе.
Аббревиатура означает следующее:
- P = скобки (скобки)
- E = Показатели
- M = умножение
- D = Дивизион
- A = Дополнение
- S = вычитание
Один из популярных способов запомнить правило PEMDAS — это поговорка:
«Прошу прощения, моя дорогая тетя Салли».
PEMDAS выглядит довольно просто из приведенного выше примера.

Это говорит о том, что вам нужно сначала провести вычисления в круглых скобках (скобках), затем в экспонентах и так далее …
Однако правило PEMDAS не так однозначно, как кажется.
Это связано с тем, что некоторые операции имеют одинаковый вес, например умножение и деление или сложение и вычитание.
Вот почему некоторые люди вместо этого называют правило ПЕДМАС.
Правило хорошо видно на диаграмме ниже.
Это ясно показывает, что умножение и деление имеют равный вес. Это также показывает, что сложение и вычитание также имеют одинаковый уровень важности.
PEMDAS за 4 простых шага
Шаг 1) Сделайте круглые скобки (скобки).
Шаг 2) Делаем любые экспоненты.
Шаг 3) Произведите любое умножение ИЛИ деление слева направо
Шаг 4) Выполните любое сложение или вычитание слева направо
Итак, теперь мы знаем, что такое PEMDAS, пора посмотреть, как он работает…

Вот
Пример правила PEMDAS
Пример 1
3 + 4 х 5
Это операции сложения и умножения.
В PEMDAS умножение предшествует сложению.
Итак, 3 + 4 x 5 = 3 + 20 = 23
Пример 2
4 х (2 + 3)
Операции умножения и сложения, также есть круглые скобки (скобки).
При использовании PEMDAS часть в круглых скобках должна стоять первой.
Итак, 4 x (2 + 3) = 4 x 5 = 20
Пример 3
2 ⁴ — (3 х 4)
Есть экспоненты и круглые скобки, а также вычитание и умножение.
При использовании PEMDAS часть в круглых скобках должна стоять первой.
Итак 2 ⁴ — (3 x 4) = 2 ⁴ — 12
При использовании PEMDAS, экспоненты идут дальше.
Итак 2 ⁴ — 12 = 16 — 12 = 4
Пример 4
12 ÷ 3 х 4
Операции деления и умножения имеют одинаковый вес.
Итак, мы просто выполняем операции слева направо.
Итак, 12 ÷ 3 x 4 = 4 x 4 = 16
Пример 5
4–5 + 3
Операции сложения и вычитания имеют одинаковый вес.
Просто выполняйте операции слева направо.
Итак, 4-5 + 3 = -1 + 3 = 2
Пример 6 (сложнее)
4 х (1 + 2) ²
Есть экспоненты и круглые скобки, а также функции сложения и умножения.
При использовании PEMDAS часть в круглых скобках должна стоять первой.
Итак (1 + 2) = 3
Далее идет экспоненциальная часть:
3 ² = 9
И, наконец, умножение:
4 х 9 = 36
Итак, 4 x (1 + 2) ² = 4 x (3) ² = 4 x 9 = 36
Пример 7 (сложнее)
6 x 4 ÷ 3 + 12 — 27 ÷ 3
Здесь есть все четыре операции, поэтому нам нужно сначала выполнить умножение и деление.
6 x 4 ÷ 3 мы можем делать слева направо, так как умножение и деление имеют одинаковый вес.
6 x 4 ÷ 3 = 24 ÷ 3 = 8
Это дает нам 8 + 12 — 27 ÷ 3
Нам нужно сначала сделать деление.
27 ÷ 3 = 9
Остается 8 + 12 — 9.
Мы можем выполнять это вычисление слева направо, так как все операции имеют одинаковый вес.
8 + 12 — 9 = 20 — 9 = 11
Таким образом, 6 x 4 ÷ 3 + 12-27 ÷ 3 = 24 ÷ 3 + 12-9 = 8 + 12-9 = 20-9 = 11
Таблицы в этом разделе включают использование скобок и показателей в простых вычислениях.
Существует также множество рабочих листов, предназначенных для практики и изучения PEMDAS.
Использование этих листов поможет вашему ребенку:
- знать и понимать, как работают круглые скобки;
- понимает, как работают экспоненты в простых вычислениях.
- понимает и использует PEMDAS для решения ряда проблем.
Взгляните на еще несколько наших рабочих листов, похожих на эту тему.
Листы в этой области помогут вашему ребенку понять использование и назначение знака равенства (=) в уравнении.
Это также поможет детям научиться манипулировать и вычислять числовые выражения, чтобы они были эквивалентны.
Это пригодится им, когда они начнут изучать алгебру и манипулировать алгебраическими уравнениями.
Здесь вы найдете ряд распечатанных заданий по умственной математике для 5-го класса, которые понравятся вашему ребенку.
Каждый рабочий лист проверяет детей по ряду математических тем, от числовых фактов до ментальной арифметики. к вопросам геометрии, дроби и меры.

Отличный способ пересмотреть темы или использовать в качестве еженедельной викторины по математике!
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.

Порядок операций
Порядок действий — очень важный навык.Вы используете его каждый день, даже если не подозреваете об этом.
Реальный пример PEMDAS
Скажем, вы идете в супермаркет. Предположим, арахис стоит 3 доллара за фунт, а бутылка воды — 1 доллар. Вы получите 2 фунта арахиса и 1 бутылку воды.
Сколько денег вы платите?
Так как 1 фунт арахиса стоит 3 доллара, а вы купили 2 фунта, арахис стоит 6 долларов. Добавьте это к сумме, которую вы платите за воду (1 доллар), вы заплатили в общей сложности 7 долларов.
Возможно, вы разобрались с этим без каких-либо серьезных проблем. Однако, если я представлю вам следующее уравнение, которое является моделью указанной выше проблемы, у вас может возникнуть тенденция прибавлять 3 к 1 и умножать результат на 2.
2 × 3 + 1
. 8, а оно не равно 7.
Чтобы получить правильный ответ, вы должны сначала выполнить умножение.
При выполнении вычислений всегда соблюдайте порядок операций и всегда выполняйте операции в соответствии со следующим правилом .
Правило :
1. Если используются символы группировки, например круглые скобки, сначала выполните операции внутри символов группировки.
2. Вычислить любые выражения с показателем степени.
3. Умножение и деление слева направо.
4. Сложить и вычесть слева направо.
Правило можно использовать, когда вы видите последовательно умножение, деление или и то, и другое, например, в следующей задаче:
Пример № 1:
4 ² — 6 × 2 ÷ 4 × 3 + 5
Показатель Do:
16-6 × 2 ÷ 4 × 3 + 5
Умножение и деление слева направо
16-12 ÷ 4 × 3 + 5
16-3 × 3 + 5
16-9 + 5
Сложить и вычесть слева направо
16-9 + 5
7 + 5
12
Следующая мнемоника может помочь вам запомнить правило:
PEMDAS (Прошу прощения, моя дорогая тетя Салли)
P означает круглые скобки
E означает экспоненты
M означает умножить
D. означает раздел
. A означает сложение
. S означает вычитание
. Несмотря на то, что M стоит перед D в PEMDAS, две операции имеют одинаковую мощность. Точно так же, даже если A стоит перед S, две операции имеют одинаковую мощность.
Еще примеры порядка работы

Пример № 2:
(2 + 5 ²) + 4 × 3 — 10
Сделать скобку:
(2 + 25) + 4 × 3 — 10
27 + 4 × 3 — 10
Произвести умножение
27 + 12-10
Добавить
39-10
Вычесть
29
Пример № 3:
10-14 ÷ 2 = 10-7 = 3 (Деление предшествует вычитанию )
Помните, что если вы видите умножение и деление одновременно, выполняйте операцию слева направо.
4 + 5 ÷ 5 × 6 = 4 + 1 × 6 = 4 + 6 = 10
Порядок проведения викторины. Посмотрите, как вы понимаете этот урок.
Рабочие листы для операций
Добро пожаловать на страницу рабочих таблиц порядка операций на Math-Drills.com, где мы обязательно выполняем заказы! Эта страница включает рабочие листы Порядок операций с использованием целых, десятичных и дробных чисел.
Учащиеся начальной и средней школы обычно используют аббревиатуры PEMDAS или BEDMAS, чтобы помочь им запомнить порядок, в котором они заполняют многооперационные вопросы. Буквы «P» или «B» в аббревиатуре обозначают круглые или квадратные скобки. Все операции в скобках выполняются первыми. «E» относится к любым показателям; все показатели рассчитываются после скобок. Буквы «M» и «D» взаимозаменяемы, так как умножение и деление завершаются в том порядке, в котором они появляются слева направо. Четвертый и последний шаг — найти сложение и вычитание в том порядке, в котором они появляются слева направо.
В последнее время студентов учат аббревиатуре PEMA для обозначения порядка операций, чтобы избежать путаницы, присущей другим аббревиатурам.Например, в PEMDAS умножение предшествует делению, что, как некоторые ошибочно полагают, означает, что умножение должно выполняться перед делением в вопросе о порядке операций. Фактически, две операции выполняются в том порядке, в котором они выполняются в вопросе слева направо. Это признается в PEMA, который более правильно показывает, что в вопросе о порядке операций необходимо пройти четыре уровня.
Если вы не хотите, чтобы ваши ученики занимались чем-то отличным от остального мира, было бы неплохо научить их понимать эти правила. Здесь не требуется никаких открытий или исследований. Это правила, которые необходимо выучить и применять на практике, и они были приняты в качестве стандартного подхода к решению любой многошаговой математической задачи.
Самые популярные рабочие листы для порядка операций на этой неделе
Порядок операций с листами с целыми числами
Порядок операций с целыми числами на листах различной сложности.
Порядок операций с целыми числами
Ключи ответов для этих рабочих листов порядка операций показывают каждый шаг, поэтому легко определить, где учащиеся могли ошибиться, если они получат другой ответ.Ответы также можно использовать для моделирования того, как следует отвечать на вопросы, и для ознакомления студентов с порядком действий.
Порядок операций с целыми числами
(только сложение и умножение)
Это хорошая отправная точка, когда используются только сложение и умножение (с добавлением нескольких круглых скобок). Эти рабочие листы помогут учащимся понять, что умножение выполняется до сложения, если не используются круглые скобки. Всегда приятно, если вы можете придумать несколько примеров, чтобы проиллюстрировать, что означают некоторые из этих вопросов. Например, 2 + 7 × 3 может относиться к количеству дней в двух днях и трех неделях. (9 + 2) × 15 может означать общую сумму заработка, если кто-то работал 9 часов вчера и 2 часа сегодня за 15 долларов в час.
Порядок операций с целыми числами
(только сложение, вычитание и умножение)
Порядок операций с целыми числами
(без показателей)
Порядок операций с целыми листами
Порядок операций с целыми листами с целыми числами как с отрицательными, так и с положительными целыми числами различной сложности.
Порядок операций с целыми числами
Порядок операций с целыми числами и
без показателей
Порядок действий с таблицами дробей
Порядок операций с
дробями
Как и другие рабочие листы с порядком операций, рабочие листы с порядком дробей требуют некоторых предварительных знаний. Если ваши ученики борются с этими вопросами, вероятно, это больше связано с их способностью работать с дробями, чем с самими вопросами. Внимательно наблюдайте и постарайтесь точно указать, каких необходимых знаний не хватает, а затем потратьте некоторое время на изучение этих концепций / навыков, прежде чем продолжить. В противном случае приведенные ниже рабочие листы должны содержать довольно простые ответы и не должны приводить к чрезмерному выпадению волос.
Порядок операций с десятичными знаками Рабочие листы
Порядок операций с десятичными знаками на листах с положительными и отрицательными десятичными знаками и различной степенью сложности.

Узнаем что сначала — сложение или умножение: правила, порядок выполнения действия и рекомендации

Сложение и вычитание

Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.

Умножение

Что сначала — умножение или сложение?

5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все помидоры сдавали учетчику, он укладывал их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
50 + 50 – это кучки малолетних работников;
70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:

500 + 500 +500 +500 +500 + 50 +50 + 70 =?;

Две кучки по 50 – это тоже можно записать через умножение.

И одна кучка 70 помидоров.

5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?

2500 + 100 + 70 = 2 670

При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.

Деление

Скобки

((25-5) : 5 + 2) : 3 =?

Это как коробочки с конфетами в большом мешке. Сначала нужно раскрыть все коробочки и ссыпать в большой мешок: (25 – 5 ) = 20. Пять конфет из коробочки сразу заслали отличнице Люде, которая приболела и в празднике не участвует. Остальные конфеты − в мешок!
Потом связать конфеты в пучки по 5 штук: 20 : 5 = 4.
Потом добавить в мешок еще 2 пучка конфет, чтобы можно было поделить на троих детей без драки. Признаки деления на 3 в данной статье не рассматриваются.

(20 : 5 + 2) : 3 = (4 +2) : 3 = 6 : 3 = 2

Итого: трем детям по два пучка конфет (по пучку в руку), по 5 конфет в пучке.

«Вишенка на торте»

5 – 8 + 4 = 1;

«Совсем вишня»

6 : 2 ∙ (1+2) = 6 ∙ ½ ∙ (1+2) = 6 ∙ ½ ∙ 3 = 3 ∙ 3 = 9

Теперь точно все!

Умножение | Математика

Умножить одно целое число на другое значит повторить одно число столько раз, сколько в другом содержится единиц. Повторить число значит взять его слагаемым несколько раз и определить сумму.

Определение умножения

Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.

Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.

Умножение есть сложение равных слагаемых.

Данные в умножении называются множимым и множителем, а искомое — произведением.

В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.

Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.

Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.

Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.

Множимое и множитель вместе называются производителями.

При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.

Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.

Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать

7 + 7 + 7

пишут при помощи знака умножения короче:

7 × 3 или 7 · 3

Умножение есть сокращенное сложение равных слагаемых.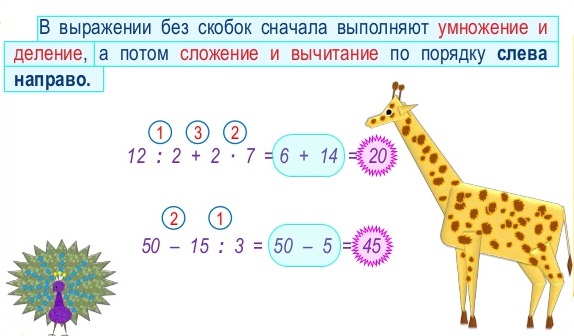

Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).

Связь между данными и искомым числом выражается в умножении

письменно:

7 × 3 = 21 или 7 · 3 = 21

словесно:

семь, умноженное на три, составляет 21.

Чтобы составить произведение 21, нужно 7 повторить три раза

21 = 7 + 7 + 7

Чтобы составить множитель 3, нужно единицу повторить три раза

3 = 1 + 1 + 1

Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.

Основное свойство произведения

Произведение не изменяется от перемены порядка производителей.

Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:

Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.

Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.

Умножение однозначных чисел. Таблица Пифагора

Чтобы умножить два однозначных числа, нужно повторить одно число слагаемым столько раз, сколько в другом содержится единиц, и найти их сумму. Так как умножение целых чисел приводится к умножению однозначных чисел, то составляют таблицу произведений всех однозначных чисел попарно. Такая таблица всех произведений однозначных чисел попарно называется таблицей умножения.

Таблица Пифагора. Изобретение ее приписывают греческому философу Пифагору, по имени которого ее называют таблицей Пифагора. (Пифагор родился около 569 года до н. э.).

Чтобы составить эту таблицу, нужно написать первые 9 чисел в горизонтальный ряд:

1, 2, 3, 4, 5, 6, 7, 8, 9.

Затем под этой строкой надо подписать ряд чисел, выражающих произведение этих чисел на 2. Этот ряд чисел получится, когда в первой строке сложим каждое число само с собою. От второй строки чисел последовательно переходим к 3, 4 и т. д. Каждая последующая строка получается из предыдущей через прибавление к ней чисел первой строки.

Продолжая так поступать до 9 строки, мы получим таблицу Пифагора в следующем виде

Чтобы по этой таблице найти произведение двух однозначных чисел, нужно отыскать одного производителя в первой горизонтальной строке, а другого в первом вертикальном столбце; тогда искомое произведение будет на пересечении соответствующих столбца и строки. Таким образом, произведение 6 × 7 = 42 находится на пересечении 6-й строки и 7-го столбца. Произведение нуля на число и числа на нуль всегда дает нуль.

Так как произведение числа на 1 дает само число и перемена порядка множителей не изменяет произведения, то все различные произведения двух однозначных чисел, на которые следует обратить внимание, заключаются в следующей таблице:

Произведения однозначных чисел, не содержащиеся в этой таблице, получаются по данным, если только изменить в них порядок множителе; таким образом, 9 × 4 = 4 × 9 = 36.

Умножение многозначного числа на однозначное

Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.

Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых

следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.

При этом ход вычислений выражают словесно:

Начинаем умножение с единиц: 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).
Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.
Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.
Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.

Это действие выразится письменно:

Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:

Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.
Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.
Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.
Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.
Умножение продолжается до тех пор, пока не получат полного произведения.

Умножение чисел на 10, 100, 1000 …

Умножить числа на 10 значит простые единицы превратить в десятки, десятки в сотни и т. д., то есть повысить порядок всех цифр на единицу. Этого достигают, прибавляя справа один нуль. Умножить на 100 значит повысить все порядки множимого двумя единицами, то есть превратить единицы в сотни, десятки в тысячи и т. д.

Этого достигают, приписывая к числу два нуля.

Отсюда заключаем:

Для умножения целого числа на 10, 100, 1000 и вообще на 1 с нулями нужно приписать справа столько нулей, сколько их находится во множителе.

Умножение числа 6035 на 1000 выразится письменно:

Когда множитель есть число, оканчивающееся нулями, подписывают под множимым только значащие цифры, а нули множителя приписывают справа.

Умножение на число с нулями в конце

Чтобы умножить 2039 на 300 нужно взять число 2029 слагаемым 300 раз. Взять 300 слагаемых все-равно, что взять три раза по 100 слагаемых или 100 раз по три слагаемых. Для этого умножаем число на 3, а потом на 100, или умножаем сначала на 3, а потом приписываем справа два нуля.

Ход вычисления выразится письменно:

Правило. Чтобы умножить одно число на другое, изображаемое цифрой с нулями, нужно сначала помножить множимое на число, выражаемое значащей цифрой, и затем приписать столько нулей, сколько их находится в множителе.

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

Умножая 3029 на 9, находим:

 3029
×   9 
27261 первое частное произведение

Умножая 3029 на 20, находим:

 3029
×   20 
 60580 второе частное произведение

Умножая 3026 на 400, находим:

 3029
×   400 
1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры.

Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.
Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.
Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.
Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.

Степени

Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:

2 × 2 = 4, 3 × 3 = 9.

Квадраты. Произведение двух равных множителей называется квадратом числа.

В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.

Кубы. Произведение трех равных множителей называется кубом числа.

Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.

Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.

Произведения двух равных множителей или квадраты называются вторыми степенями.

Произведения трех равных множителей или кубы называются третьими степенями, и т. д.

Правила знаков

Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.

Рассмотрим подробней основные правила знаков.

Деление.

Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».

Умножение.

Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».

Вычитание и сложение.

Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.

Правила при умножении (делении) чисел

Множители (делимое и делитель)		Результат
+	+	+
+	—	—
—	+	—
—	—	+

Порядок выполнения действий в выражениях без скобок

Тема: «Порядок выполнения действий в выражениях без скобок»

Тип урока: урок закрепления знаний

Цели урока:

Задачи: -создать условия для усвоения учащимися правила порядка выполнения действий в выражениях без скобок;

— продолжить отработку изученных приёмов устных вычислений( таблица умножения, деления, сложения, вычитания), учить применять на практике правило нахождения значений выражений без скобок;

— развивать наблюдательность, умение сравнивать, анализировать, делать выводы;

— содействовать воспитанию активной личности, воспитывать доброжелательное, уважительное отношение друг к другу.

Планируемые результаты урока:

Личностные — личностная мотивация к познавательной деятельности

Предметные- развитие умений решать учебные и практические задачи, учиться применять правило порядка выполнения действий.

Метапредметные — (регулятивные УУД, познавательные УУД, коммуникативные УУД)- овладение навыками осознанного построения речевых высказываний в соответствии с задачами коммуникации; овладение логическими действиями анализа, синтеза, классификации, причинно-следственных связей, построения рассуждений, отнесения к известным понятиям;

готовность слушать собеседника ,излагать свое мнение и аргументировать свою точку зрения и оценку событий.

Дидактическое обеспечение: : карточки для оценивания, карточки для самостоятельной работы, карточки- помощницы, презентация.

Оборудование :компьютер с мультимедийным проектором.

Добрый день , ребята!

Давайте продолжим учиться считать,
Чтобы скорей математиком стать!

Звонок прозвенел. Он позвал на урок.
Пора! Тишина! К нам наука идёт…

Дети проверяют готовность к уроку

Умение совместно договариваться о правилах поведения и общения в школе и следовать им. (Коммуникативные УУД)

Личностная мотивация к обучению.

Актуализация опорных знаний и способов действий по изученному материалу.

Математика — наука точная. Она требует, чтобы мы точно выполняли ее законы и не нарушали порядка. Как вы понимаете слово порядок с точки зрения математики .

На доске записи .

6×2:3=
35-5+7=
70- 9×5=

Сформулируйте тему нашего урока.

Продолжаем изучать «Порядок выполнения действий в выражениях без скобок». Урок ЗАКРЕПЛЕНИЯ ПРОЙДЕНОГО МАТЕРИАЛА

Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.”

Попробуем сформулировать цель нашего урока

Последовательность , в определённой последовательности, друг за другом.

«Порядок выполнения действий в выражениях без скобок»

Будем учиться расставлять порядок действия в выражения без скобок .

Будем учиться применять правила порядка выполнения действий в выражениях без скобок.

Упражняться в нахождении значений выражений, без скобок

Будем закреплять таблицу умножения .

Будем закреплять таблицу сложения.

Умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя. (Познавательные УУД)

Постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно.

(Регулятивные УУД)

Целеполагание, Познавательные УУД

самостоятельное выделение и формулировка цели.

Прежде чем , работать над арифметическими действиями ,находить значения выражений, мы с вами вспомним «Названия компонентов при +,-, ×,: »

Поработайте 1 минуту парами. Затем вместе обобщим.

Записываем число .Классная работа.

Возвращаемся к записям на доске.

На доске записи :

1) 6×2:3=

2) 35-5+7=

3) 70- 9×5=

Какие действия встречаются в 1 выражении.

Какие действия встречаются во 2 выражении.

Какие действия встречаются в 3 выражении.

Назовите действия по порядку в первом выражении, назовите действия по порядку во втором выражении, назовите действия по порядку в третьем выражении.

Проговаривает действия , дети работают в тетради.

Что закрепляли при выполнении данного вида задания.

Работа в парах, называют по очереди компоненты при умножении, сложении, вычитании, делении.

Дети в тетради записывают число, классная работа.

Считают устно, записывают в тетрадь промежуточный ответ , рядом конечный результат, проверка:

называют ответ, показывают

сигнальную карточку.

Закрепляли названия компонентов при сложении, вычитании, умножении, делении, порядок выполнения действий в выражениях без скобок.

Познавательные УУД

опорное повторение,умение ориентироваться в своей системе знаний.

Формирование умения работать в паре .Коммуникативные УУД

Усвоение новых знаний и способов действий по изученному материалу.

Физминутка

На доске выражения :

1. 42:6×3=

2. 8×2:4=

3. 32:4×5=

Какие математические действия использованы в этих выражениях?

Как принято выполнять действия в выражения такого вида?

Выберите выражение , где 1 действием мы будем выполнять умножение. Под каким номером это выражение. Найдите значение этого выражения. (письменно)

По группам:

1.Найди ошибки, исправь порядок выполнения действий, найди значения выражений.

35:7×3=

27:9×7=

Исправляем ошибки вместе, решаем по вариантам.

2.Догадайся какое число пропущено

6×4: …=8

2×9 : …=6

Итак, каким образом принято выполнять действия в выражения такого вида?

Много ль надо нам, ребята

Много ль надо нам, ребята,

Для умелых наших рук?

Нарисуем два квадрата,

А на них огромный круг,

А потом еще кружочек,

Треугольный колпачок.

Вот и вышел очень, очень

Развеселый чудачек. (Дети рисуют в воздухе геометрические фигуры.)

Посмотрите на схему этого выражения, постройте алгоритм работы над этим выражением .

+ —

Найди значения выражений , соедини с результатом.

Работа в парах по карточкам.

27+13-15= 69

100-20-11= 58

12+28-10+28= 25

Итак,каким образом принято выполнять действия в выражениях такого вида.

Работа с учебником.

№ 8, с.110.

Рассмотрите выражения и скажите какое правило необходимо применять , для нахождения значений данных выражений.

Поработаем с первым столбиком выражений.

Назовите алгоритм выполнения действий в выражениях, используй в своём ответе Сумма, Разность, Произведение, Частное.

В каком выражении 3 действия. Найдём значение данного выражения, напишем решение в тетрадь.

Решение примера!

Выражения, содержащие только умножение и деление.

В выражениях содержащих только умножение и деление, действия принято выполнять по порядку слева направо. (ПАМЯТКА № 1)

В выражениях содержащих только умножение и деление, действия принято выполнять по порядку слева направо.

1.найду сумму двух чисел

2.из суммы буду вычитать число

Это выражение без скобок, содержащее только сложение и вычитание.

Выполняю действия по порядку слева направо.

Работают по карточкам. В паре.

Это выражение без скобок, содержащее только сложение и вычитание.

Выполняю действия по порядку слева направо.

Это выражение без скобок, содержащее все математические действия.

Принято выполнять по порядку слева направо, сначала умножение и деление, затем сложение и вычитание.

Называют устно!

Решение одного примера.

Познавательные УУД

Уметь проговаривать последовательность действий (Регулятивные УУД)

Формирование умения строить речевое высказывание в соответствии с поставленными задачами (Коммуникативные УУД)

Осуществление совместной двигательной

деятельности в группе. (Коммуникативные)

Постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем поискового характера.

( Познавательные УУД)

Формирование коммуникативных УУД

Формирование умения извлекать информацию из схем, иллюстраций, (Познавательные УУД)

Организация контроля и самоконтроля .

Проговаривание порядка выполнения действий в выражениях без скобок.

Памятка № 1

Памятка № 2

Памятка № 3

Умение слушать и понимать других, высказывать своё мнение и аргументировать свой ответ. (Коммуникативные

УУД)

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.” (Д.Пойа)

Мастер изготовил 56 ёлочных игрушек, а его ученик 25 игрушек, 9 игрушек забрали на выставку . Сколько игрушек осталось у мастера и ученика в коллекции?

Попробуйте сформулировать вопросы к условию задачи. Задайте вопросы к условию, которые помогли бы вам выбрать действие к задаче.

«Вопрос ,ответ»

Карточка – помощник!

Краткая запись
План решения
Готовое решение , дополнить пояснение.
* Изменить условие и вопрос задачи , воспользоваться подсказкой. Готовое выражение к задаче.

(56+25) : 9=9

Сравнение двух выражений

56+25-9=72

(56+25):9=9

Предполагаемые вопросы:

Сколько ёлочных игрушек изготовил мастер?

Сколько ёлочных игрушек изготовил его ученик?

Сколько игрушек забрали на выставку?

Что обозначает слово забрали?

1гр.- выполняют решение задачи по краткой записи;

2гр.- выполняют задачу с помощью плана решения задачи;

3гр.- дополняют пояснение к готовому решению.

4гр.* — изменяют условие и вопрос к задаче

Нравственно-этическая ориентация. (Личностные УУД)

Умение определять успешность выполнения своего задания в диалоге с учителем и с детьми.

(Регулятивные УУД)

Осуществление совместной познавательной деятельности в

в группе.

(Коммуникативные УУД)

Тест:

1.Укажи какое действие в выражении будет выполнено первым.

38-4×7=

а) + б) × в) —

2.Укажи какое действие в выражении будет выполнено вторым.

98-7+23=

а) : б) — в) +

3. Укажи какое действие в выражении будет выполнено последним.

56: 7 -1×6+14=

а) + б) : в) — г) ×

Контроль и оценка процесса и результатов деятельности.

( Познавательные, регулятивные УУД )

Рефлексия учебной деятельности

( предметные, метапредметные, личностные результаты)

Чему учились на уроке?

Оцениваю свою деятельность на уроке

Выражения, содержащие только сложение и вычитание

Выражения, содержащие умножение, деление, сложение и вычитание

Зелёный – знаю, умею, могу помочь другим

Жёлтый- знаю, но допускаю ошибки

Красный – нужна помощь учителя, помощь родителей, товарищей.

Какие советы мы можем дать ребятам, которые выбрали жёлтый и красный цвет.

Молодцы, ребята! Спасибо за урок!

Дети оценивают себя, проставляют в таблицу «Светофорики»

Дают рекомендации ребятам , которые выбрали жёлтый и красный цвет.

Уметь оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. (Регулятивные УУД)

Формирование способности к самооценке на основе критерия успешности учебной деятельности (Личностные УУД)

В каком порядке решаются примеры без скобок. Порядок выполнения действий в выражениях без скобок и со скобками

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя .

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления — это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

30 + 6 * (13 — 9)

Вычислим значение выражения.

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

37 + 9 — 6: 2 * 3 =

18: (11 — 5) + 47=

7 * 3 — (16 + 4)=

Рассуждаем так.

37 + 9 — 6: 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

18:(11-5)+47=18:6+47=3+47=50

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
«Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
В. Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.

Festival.1september.ru ().
Sosnovoborsk-soobchestva.ru ().
Openclass.ru ().

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

перемножить в любом порядке.

Методически данное правило имеет целью подготовить ребенка к знакомству со способами умножения в столбик чисел, оканчивающихся нулями, поэтому с ним знакомятся только в четвертом классе. Реально данное свойство умножения позволяет рационализировать устные вычисления как во 2, так и в 3 классе.

Например:

Вычисли: (7 2) 5 = …

В данном случае намного легче вычислить вариант

7 (2 5) = 7 10 — 70.

Вычисли: 12 (5 7) = …

8 данном случае намного легче вычислить вариант (12-5)-7 = 60-7 = 420.

Приемы вычислений

1. Умножение и деление чисел, оканчивающихся нулем: 20 3; 3 20; 60: 3; 80: 20

Вычислительный прием в данном случае сводится к умножению и делению однозначных чисел, выражающих число десятков в заданных числах. Например:

20 3 =… 3 20 =… 60:3 = …

2 дес. 3 = 20 3 = 60 б дес.: 3 = 2 дес.

20 — 3 = 60 3 20 = 60 60: 3 = 20

Для случая 80:20 может быть использовано два способа вычислений: тот, что использовался в предыдущих случаях, и способ подбора частного.

Например: 80: 20 =… 80: 20 =…

8 дес.: 2 дес. = 4 или 20 4 = 80

80: 20 = 4 80: 20 = 4

В первом случае использовался прием представления двузначных десятков в виде разрядных единиц, что сводит рассматриваемый случай к табличному (8:2). Во втором случае цифра частного находится подбором и проверяется умножением. Во втором случае ребенок возможно не сразу подберет верную цифру частного, это означает, что проверка будет выполнена не один раз.

2. Прием умножения двузначного числа на однозначное: 23 4; 4-23

При умножении двузначного числа на однозначное актуализируются следующие знания и умения:

В случае умножения вида 4 23 сначала применяется перестановка множителей, а затем та же схема умножения, что и выше.

3. Прием деления двузначного числа на однозначное: 48:3; 48:2

При делении двузначного числа на однозначное актуализируются следующие знания и умения:

4. Прием деления двузначного числа на двузначное: 68: 17

При делении двузначного числа на двузначное необходимы следующие знания и умения:

Сложность последнего приема состоит в том, что ребенок не может сразу подобрать нужную цифру частного и выполняет несколько проверок подобранных цифр, что требует достаточно сложных вычислений. Многие дети тратят много времени на выполнение вычислений этого вида, поскольку начинают не столько подбирать подходящую цифру частного, сколько перебирают все множители подряд, начиная с двух.

С целью облегчения вычислений могут быть использованы два приема:

1) ориентировка на последнюю цифру делимого;

2) прием округления.

Первый прием предполагает, что при подборе возможной цифры частного ребенок ориентируется на знание таблицы умножения, сразу перемножая подобранную цифру (число) и последнюю цифру делителя.

Например, 3-7 = 21. Последняя цифра числа 68 — это 8, значит нет смысла умножать 17 на 3, последняя цифра делителя все равно не совпадает. Пробуем в частном число 4 — умножаем 7 4 = 28. Последняя цифра совпадает, значит имеет смысл найти произведение 17 4.

Второй прием предполагает округление делителя и подбор цифры частного с ориентиром на округленный делитель.

Например, 68:17 делитель 17 округляется до 20. Примерная цифра частного 3 дает при проверке 20 3 = 60

Эти приемы позволяют сократить затраты сил и времени при выполнении вычислений данного вида, но требуют хорошего знания таблицы умножения и умения округлять числа.

Целые числа, оканчивающиеся цифрами 0,1,2,3,4, округляют до ближайшего целого десятка, отбрасывая эти цифры.

Например, числа 12, 13, 14 следует округлять до 10. Числа 62, 63, 64 округляют до 60.

Целые числа, оканчивающиеся цифрами 5, 6, 7,8,9, округляют до ближайшего целого десятка в большую сторону.

Например, числа 15,16,17,18,19 округляют до 20. Числа 45,47, 49 округляют до 50.

Порядок действий в выражениях, содержащих умножение и деление

Правила порядка выполнения действий задают основные признаки выражений, на которые следует ориентироваться при вычислении их значений.

Первые правила, определяющие порядок действий в арифметических выражениях, задавали порядок действий в выражениях, содержащих действия сложения и вычитания:

1. В выражениях без скобок, содержащих только действия сложения и вычитания, действия выполняются в том порядке, как они записаны: слева направо.

2. Действия в скобках выполняют первыми.

3. Если выражение содержит только действия сложения, то два соседних слагаемых всегда можно заменить их суммой (сочетательное свойство сложения).

В 3 классе изучаются новые правила порядка выполнения действий в выражениях, содержащих умножение и деление:

4. В выражениях без скобок, содержащих только умножение и деление, действия выполняются в том порядке, как они записаны: слева направо.

5. В выражениях без скобок умножение и деление выполняются раньше, чем сложение и вычитание.

При этом установка на выполнение действия в скобках первым сохраняется. Возможные случаи нарушения этой установки были оговорены ранее.

Правила порядка выполнения действий являются общими правилами вычислений значений математических выражений (примеров), которые сохраняются на протяжении всего периода изучения математики в школе. В связи с этим формирование у ребенка четкого понимания алгоритма порядка выполнения действий является важной преемственной задачей обучения математике в начальной школе. Проблема заключается в том, что правила порядка выполнения действий являются достаточно вариативными и не всегда однозначно заданными.

Например, в выражении 48-3 + 7 + 8 следует по общей установке применять правило 1 для выражения без скобок, содержащего действия сложения и вычитания. В то же время, как вариант рациональных вычислений, можно использовать прием замены суммой части 7 + 8, поскольку после вычитания числа 3 из 48 получится 45, к чему удобно прибавить 15.

Однако подобный разбор такого выражения в начальных классах не предусмотрен, поскольку есть опасения, что при неадекватном понимании такого подхода ребенок будет применять его в случаях вида 72 — 9 — 3 + 6. В данном случае замена выражения 3 + 6 суммой невозможна, она приведет к неверному ответу.

Большая вариативность в применении всей группы правил и вариантов правил при определении порядка действий требует значительной гибкости мышления, хорошего понимания смысла математических действий, последовательности мыслительных действий, математического «чутья» и интуиции (математики называют это «чувство числа»). Реально намного проще приучить ребенка жестко соблюдать четко установленный порядок анализа числового выражения с точки зрения тех признаков, на которые ориентировано каждое правило.

Определяя порядок действий, рассуждай так:

1) Если есть скобки, выполняю первым действие, записанное в скобках.

2) Выполняю по порядку умножение и деление.

3) Выполняю по порядку сложение и вычитание.

Данный алгоритм задает порядок действий достаточно однозначно, хотя и с небольшими вариациями.

В этих выражениях порядок действии определен алгоритмом однозначно и является единственно возможным. Приведем другие примеры

После выполнения умножения и деления в данном примере можно было сразу к 54 прибавить 6, а из 18 вычесть 9, пбсле чего результаты сложить. Технически было бы значительно легче, чем путь, обусловленный алгоритмом, возможен изначально другой порядок действий в примере:

Таким образом, вопрос о формировании умения определять порядок действий в выражениях в начальной школе определенным образом противоречит необходимости обучать ребенка способам рациональных вычислений.

Например, в случае порядок действий определен алгоритмом абсолютно однозначно, при этом требует отребенка сложнейших вычислений в уме с переходами через разряд: 42 — 7 и 35 + 8.

Если же после выполнения деления 21:3, выполнить сложение 42 + 8 = 50, а затем вычитание 50 — 7 = 43, что намного легче технически, ответ будет тот же. Этот путь вычислений противоречит установке данного в учебнике

И деление чисел — действиями второй ступени.
Порядок выполнения действий при нахождении значений выражений определяется следующими правилами:

1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом — действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Пример 1. Найдем значение выражения

а) х + 20 = 37;
б) у + 37 = 20;
в) а — 37 = 20;
г) 20 — m = 37;
д) 37 — с = 20;
е) 20 + k = 0.

636. При вычитании каких натуральных чисел может получиться 12? Сколько пар таких чисел? Ответьте на те же вопросы для умножения и для деления.

637. Даны три числа: первое — трехзначное, второе — значение частного от деления шестизначного числа на десять, а третье — 5921. Можно ли указать наибольшее и наименьшее из этих чисел?

638. Упростите выражение:

а) 2а + 612 + 1а + 324;
б) 12у + 29у + 781 + 219;

639. Решите уравнение:

а) 8х — 7х + 10 = 12;
б) 13у + 15у- 24 = 60;
в) Зz — 2z + 15 = 32;
г) 6t + 5t — 33 = 0;
д) (х + 59) : 42 = 86;
е) 528: k — 24 = 64;
ж) р: 38 — 76 = 38;
з) 43m- 215 = 473;
и) 89n + 68 = 9057;
к) 5905 — 21 v = 316;
л) 34s — 68 = 68;
м) 54b — 28 = 26.

640. Животноводческая ферма обеспечивает привес 750 г на одно животное в сутки. Какой привес получает комплекс за 30 дней на 800 животных?

641. В двух больших и пяти маленьких бидонах 130 л молока. Сколько молока входит в маленький бидон, если его вместимость в четыре раза меньше вместимости большего?

642. Собака увидела хозяина, когда была от него на расстоянии 450 м, и побежала к нему со скоростью 15 м/с. Какое расстояние между хозяином и собакой будет через 4 с; через 10 с; через t с?

643. Решите с помощью уравнения задачу:

1) У Михаила в 2 раза больше орехов, чем у Николая, а у Пети в 3 раза больше, чем у Николая. Сколько орехов у каждого, если у всех вместе 72 ореха?

2) Три девочки собрали на берегу моря 35 ракушек. Галя нашла в 4 раза больше, чем Маша, а Лена — в 2 раза больше, чем Маша. Сколько ракушек нашла каждая девочка?

644. Составьте программу вычисления выражения

8217 + 2138 (6906 — 6841) : 5 — 7064.

Запишите эту программу в виде схемы. Найдите значение выражения.

645. Напишите выражение по следующей программе вычисления:

1. Умножить 271 на 49.
2. Разделить 1001 на 13.
3. Результат выполнения команды 2 умножить на 24.
4. Сложить результаты выполнения команд 1 и 3.

Найдите значение этого выражения.

646. Напишите выражение по схеме (рис. 60). Составьте программу его вычисления и найдите его значение.

647. Решите уравнение:

а) Зх + bх + 96 = 1568;
б) 357z — 1492 — 1843 — 11 469;
в) 2у + 7у + 78 = 1581;
г) 256m — 147m — 1871 — 63 747;
д) 88 880: 110 + х = 809;
е) 6871 + р: 121 = 7000;
ж) 3810 + 1206: у = 3877;
з) к + 12 705: 121 = 105.

648. Найдите частное:

а) 1 989 680: 187; в) 9 018 009: 1001;
б) 572 163: 709; г) 533 368 000: 83 600.

649. Теплоход 3 ч шел по озеру со скоростью 23 км/ч, а потом 4 ч по реке. Сколько километров прошел теплоход за эти 7 ч, если по реке он шел на 3 км/ч быстрее, чем по озеру?

650. Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с?

651. Найдите в таблице (рис. 61) все числа по порядку от 2 до 50. Это упражнение полезно выполнить несколько раз; можно соревноваться с товарищем: кто быстрее отыщет все числа?

Н. Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений

Планы конспектов уроков по математике 5 класса скачать , учебники и книги бесплатно, разработки уроков по математике онлайн

Содержание урока

конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации

аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения

рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие

Совершенствование учебников и уроков

исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей

идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

Порядок выполнения действий — Математика 3 класс (Моро)

Краткое описание:

В жизни вы постоянно совершаете различные действия: встаете, умываетесь, делаете зарядку, завтракаете, идете в школу. Как вы думаете, можно ли поменять этот порядок действий? Например, позавтракать, а потом умыться. Наверное, можно. Может быть, будет не очень удобно завтракать неумытому, но ничего страшного из-за этого не случится. А в математике можно ли менять порядок действий по своему усмотрению? Нет, математика – точная наука, поэтому даже малейшие изменения в порядке действий приведут к тому, что ответ числового выражения станет неверным. Во втором классе вы уже познакомились с некоторыми правилами порядка действий. Так, вы, наверное, помните, что руководят порядком в выполнении действий скобки. Они показывают, что действия нужно выполнить первым. Какие существуют другие правила порядка действий? Отличается ли порядок действий в выражениях со скобками и без скобок? На эти вопросы вам предстоит найти ответы в учебнике математики 3 класса при изучении темы «Порядок выполнения действий». Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение!

Составление выражения со скобками

1. Составь из следующих предложений выражения со скобками и реши их.

Из числа 16 вычти сумму чисел 8 и 6.
Из числа 34 вычти сумму чисел 5 и 8.
Сумму чисел 13 и 5 вычесть из числа 39.
Разность чисел 16 и 3 прибавь к числу 36
Разность чисел 48 и 28 прибавь к числу 16.

2. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:

2.1. Папа принёс из леса мешок с орехами. Коля взял из мешка 25 орешков и съел. За тем Маша взяла из мешка 18 орешков. Мама то же взяла из мешка 15 орешков, но положила обратно 7 из них. Сколько осталось в итоге орешков в мешке, если в начале их было 78?

2.2. Мастер ремонтировал детали. В начале рабочего дня их было 38. В первой половине дня он смог отремонтировать 23 из них. После полудня ему принесли еще столько же, сколько было в самом начале дня. Во второй половине он отремонтировал еще 35 деталей. Сколько деталей ему осталось отремонтировать?

3. Реши примеры правильно выполняя последовательность действий:

45: 5 + 12 * 2 -21:3
56 — 72: 9 + 48: 6 * 3
7 + 5 * 4 — 12: 4
18: 3 — 5 + 6 * 8

Решение выражений со скобками

1. Реши примеры правильно раскрывая скобки:

1 + (4 + 8) =	8 — (2 + 4) =	3 + (6 — 5) =	59 + 25 =
82 + 14 =	29 + 52 =	18 + 47 =	39 + 53 =
37 + 53 =	25 + 63 =	87 + 17 =	19 + 52 =

2. Реши примеры правильно выполняя последовательность действий:

2.1. 36: 3 + 12 * (2 — 1) : 3
2.2. 39 — (81: 9 + 48: 6) * 2
2.3. (7 + 5) * 2 — 48: 4
2.4. 18: 3 + (5 * 6) : 2 — 4

3. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:

3.1. На складе было 25 упаковок стирального порошка. В один магазин увезли 12 упаковок. За тем во второй магазин увезли столько же. После этого на склад привезли в 3 раза больше упаковок, чем было раньше. Сколько упаковок порошка стало на складе?

3.2. В гостинице проживало 75 туристов. За первый день из гостиницы уехали 3 группы по 12 человек, а заехали 2 группы по 15 человек. На второй день уехали еще 34 человека. Сколько туристов осталось в гостинице к концу 2 дня?

3.3. В химчистку привезли 2 мешка одежды по 5 вещей в каждом мешке. За тем забрали 8 вещей. После полудня привезли ещё 18 вещей на стирку. А забрали только 5 выстиранных вещей. Сколько вещей в химчистке к концу дня, если в начале дня там было 14 вещей?

ФИ _________________________________

21: 3 * 6 — (18 + 14) : 8 =	63: (81: 9) + (8 * 7 — 2) : 6 =	64:2: 4+ 97-91=
37 *2 + 180: 9 – 36: 12 =	52 * 10 – 60: 15 * 1 =	72: 4 +58:2=
5 *0: 25 + (72: 1 – 0) : 9 =	21: (3 * 7) – (7* 0 + 1)*1 =	6:6+0:8-8:8=
91: 7 + 80: 5 – 5: 5 =	64:4 — 3*5 +80:2=	(19*5 – 5) : 30 =
19 + 17 * 3 – 46 =	(39+29) : 4 + 8*0=	(60-5) : 5 +80: 5=
54 – 26 + 38: 2 =	63: (73) 3=	(160-70) : 18 *1=
200 – 80: 5 + 3 * 4 =	(29+25): (72:8)=	72:25 + 3* 17=
80: 16 + 660: 6 =	3 * 290 – 800=	950:50*1-0=
(48: 3) : 16 * 0 =	90-6*6+29=	5* (48-43) +15:5*7=
54: 9 8 — 14: 7 4 =	63: 74+70:7 5=	24: 67 — 70=
21: 7 * 8 + 32: 8 * 4 =	27: 3* 5 + 26-18 *4=	54: 6*7 — 0:1=
45: 9 * 6 + 7 * 5 – 26 =	28: 7 9 + 6 (54 – 47)=	6*(9: 3) — 40:5 =
21 * 1 — 56: 7 – 8 =	9 * (64: 8) — 18:18	3 *(14: 2) — 63:9=
4 * 8 + 42: 6 *5 =	04+0:5 +8 (48: 8)=	56:7 +76 — 51=
31 * 3 — 17 – 80: 16 * 1 =	57:19 32 — 11 7=	72-96:8 +60:15 *13=
36 + 42: 3 + 23 + 27 *0 =	56:14 *19 — 72:18=	(86-78:13)* 4=
650 – 50 * 4 + 900: 100 =	630: 9 + 120 * 5 + 40=	980 – (160 + 20) : 30=
940 — (1680 – 1600) * 9 =	29* 2+26 – 37:2=	72:3 +280: (14*5)=
300: (5 60) (78: 13) =	63+ 100: 4 – 8*0=	84:7+70:14 – 6:6=
45: 15 – 180: 90 + 84: 7 =	32+51 + 48:6 * 5=	54:6 ?2 – 70:14=
38: 2 – 48: 3 + 0 * 9 =	30:6 * 8 – 6+3*2=	(95:19) *(68:2)=
(300 — 8 * 7) * 10 =	1:1 — 00 + 10 — 1*1=	(80: 4 – 60:30) *5 =
2 * (120: 6 – 80: 20) =	56:4+96:3- 0*7=	20+ 20: 4 — 1*5=
(18 + 14) : 8 – (7 0 + 1) 1 =	(87-2):6 +63: (73)=	(50-5) : 5+21: (3*7)=
19 + 17 * 3 – 60: 15 * 1 =	80: 5 +3*5 +80:2=	54: 9 8-64:4 +160=
72 * 10 — 64: 2: 4 =	84 – 36 + 38:2	91:13+80:5 – 5:5
300 – 80: 5 + 6 * 4 =	950:190 1+14: 74=	(39+29) : 17 + 8*0=
(120 — 30) : 18 * 1- 72: 25 =	210:30*60-0:1=	90-67+3 17=
240: 60 7 – 7 0 =	60:60+0:80-80:80=	720: 40 +580:20=
9 7 – 9 1 + 5 * 0: 25 =	21: 7 * 6 +32: 4 *5=	80:16 +66:6 -63:(81:9)=
(19 * 5 – 5) : 30 + 70: 7 =	15:57 + 63: 7 5=	54: 6 * 7 — (72:1-0):9=
3 290 – 600 – 5 (48 – 43) =	(300-897)10 — 3?2=	(80: 4) +30*2+ 180: 9=
30: 6 * 8 – 6 + 48: 3 + 0 *9 =	(95:19) (68:34) — 60:305=	27: 3*5 — 48:3=
3* 290 – 800 + 950: 50 =	80:16 +660:6*1-0=	90-66+ 15:57=
5(48 — 43) + (48: 3) :160=	280: (145) +630: 90=	300: (506) (78: 6)=

Если в примерах встретится вопросительный знак (?), следует его заменить на знак * — умножение.

1. РЕШИ ВЫРАЖЕНИЯ:

35: 5 + 36: 4 — 3
26 + 6 х 8 – 45: 5 24: 6 + 18 – 2 х 6
9 х 6 – 3 х 6 + 19 – 27:3

2. РЕШИ ВЫРАЖЕНИЯ:

48: 8 + 32 – 54: 6 + 7 х 4
17 + 24: 3 х 4 – 27: 3 х 2 6 х 4: 3 + 54: 6: 3 х 6 + 2 х 9
100 – 6 х 2: 3 х 9 – 39 + 7 х 4

3. РЕШИ ВЫРАЖЕНИЯ:

100 – 27: 3 х 6 + 7 х 4
2 х 4 + 24: 3 + 18: 6 х 9 9 х 3 – 19 + 6 х 7 – 3 х 5
7 х 4 + 35: 7 х 5 – 16: 2: 4 х 3

4. РЕШИ ВЫРАЖЕНИЯ:

32: 8 х 6: 3 + 6 х 8 – 17
5 х 8 – 4 х 7 + 13 — 11 24: 6 + 18: 2 + 20 – 12 + 6 х 7
21: 3 – 35: 7 + 9 х 3 + 9 х 5

5. РЕШИ ВЫРАЖЕНИЯ:

42: 7 х 3 + 2 + 24: 3 – 7 + 9 х 3
6 х 6 + 30: 5: 2 х 7 — 19 90 — 7 х 5 – 24: 3 х 5
6 х 5 – 12: 2 х 3 + 49

6. РЕШИ ВЫРАЖЕНИЯ:

32: 8 х 7 + 54: 6: 3 х 5
50 – 45: 5 х 3 + 16: 2 х 5 8 х 6 + 23 – 24: 4 х 3 + 17
48: 6 х 4 + 6 х 9 – 26 + 13

7. РЕШИ ВЫРАЖЕНИЯ:

42: 6 + (19 + 6) : 5 – 6 х 2
60 – (13 + 22) : 5 – 6 х 4 + 25 (27 – 19) х 4 + 18: 3 + (8 + 27) :5 -17
(82 – 74) : 2 х 7 + 7 х 4 — (63 – 27): 4
8. РЕШИ ВЫРАЖЕНИЯ:

90 – (40 – 24: 3) : 4 х 6 + 3 х 5
3 х 4 + 9 х 6 – (27 + 9) : 4 х 5
(50 – 23) : 3 + 8 х 5 – 6 х 5 + (26 + 16) : 6
(5 х 6 – 3 х 4 + 48: 6) +(82 – 78) х 7 – 13
54: 9 + (8 + 19) : 3 – 32: 4 – 21: 7 + (42 – 14) : 4 – (44 14) : 5

9. РЕШИ ВЫРАЖЕНИЯ:

9 х 6 – 6 х 4: (33 – 25) х 7
3 х (12 – 8) : 2 + 6 х 9 — 33 (5 х 9 — 25) : 4 х 8 – 4 х 7 + 13
9 х (2 х 3) – 48: 8 х 3 + 7 х 6 — 34

10. РЕШИ ВЫРАЖЕНИЯ:

(8 х 6 – 36: 6) : 6 х 3 + 5 х 9
7 х 6 + 9 х 4 – (2 х 7 + 54: 6 х 5) (76 – (27 + 9) + 8) : 6 х 4
(7 х 4 + 33) – 3 х 6:2

11. РЕШИ ВЫРАЖЕНИЯ:

(37 + 7 х 4 – 17) : 6 + 7 х 5 + 33 + 9 х 3 – (85 – 67) : 2 х 5
5 х 7 + (18 + 14) : 4 – (26 – 8) : 3 х 2 – 28: 4 + 27: 3 – (17 + 31) : 6

12. РЕШИ ВЫРАЖЕНИЯ:

(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 х 5 – (60 – 42) : 3 + 9 х 2
(9 х 7 + 56: 7) – (2 х 6 – 4) х 3 + 54: 9

13. РЕШИ ВЫРАЖЕНИЯ:

(8 х 5 + 28: 7) + 12: 2 – 6 х 5 + (13 – 5) х 4 + 5 х 4
(7 х 8 – 14: 7) + (7 х 4 + 12: 6) – 10: 5 + 63: 9

Тест «Порядок арифметических действий» (1 вариант)
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)

110 – (60 +40) :10 х 8

а) 800 б) 8 в) 30

а) 3 4 6 5 2 1 4 5 6 3 2 1

3 4 6 5 1 2

5. В каком из выражений последнее действие умножение?
а) 1001:13 х (318 +466) :22

в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие вычитание?
а) 2025:5 – (524 – 24:6) х45
б) 5870 + (90-50 +30) х8 -90
в) 5400:60 х (3600:90 -90)х5

Выбери верный ответ:
9. 90 – (50- 40:5) х 2+ 30
а) 56 б) 92 в) 36
10. 100- (2х5+6 — 4х4) х2
а) 100 б) 200 в) 60
11. (10000+10000:100 +400) : 100 +100
а) 106 б) 205 в) 0
12. 150: (80 – 60:2) х 3
а) 9 б) 45 в) 1

Тест «Порядок арифметических действий»
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
1. Какое действие в выражении сделаешь первым?
560 – (80+20) :10 х7
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
а) вычитание б) деление в) умножение
3. Выбери правильный вариант ответа данного выражения:
а) 800 б) 490 в) 30
4. Выбери верный вариант расстановки действий:
а) 3 4 6 5 2 1 4 5 6 3 2 1
320: 8 х 7 + 9 х (240 – 60:15) в) 320:8 х 7+9х(240 – 60:15)

3 4 6 5 2 1
б) 320: 8 х 7 + 9 х (240 – 60:15)
5. В каком из выражений последнее действие деление?
а) 1001:13 х (318 +466) :22
б) 391 х37:17 х (2248:8 – 162)
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие сложение?
а) 2025:5 – (524 + 24 х6) х45
б) 5870 + (90-50 +30) х8 -90
в) 5400:60 х (3600:90 -90)х5
7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»
а) по порядку б) х и: , затем + и — в) + и -, затем х и:
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
а) сначала в скобках б)х и:, затем + и — в) по порядку записи
Выбери верный ответ:
9. 120 – (50- 10:2) х 2+ 30
а) 56 б) 0 в) 60
10. 600- (2х5+8 — 4х4) х2
а) 596 б) 1192 в) 60
11. (20+20000:2000 +30) : 20 +200
а) 106 б) 203 в) 0
12. 160: (80 – 80:2) х 3
а) 120 б) 0 в) 1

Какой последовательности действий следует придерживаться при составлении

Какой последовательности действий следует придерживаться при составлении уравнений химической реакции?

1. В левой части уравнения пишут формулы веществ, вступающих в реакцию, а затем ставят стрелку.

2. В правой части пишут формулы веществ, образующихся в результате реакции.

3. Уравнение реакции составляют на основе закона сохранения массы веществ, т. е. в левой и правой частях уравнения должно быть одинаковое число атомов. Это достигается расстановкой коэффициентов перед формулами веществ. Вначале уравнивают число атомов, которых в реагирующих веществах содержится больше. Находят наименьшее общее кратное чисел атомов кислорода в левой и правой частях схемы. При делении наименьшего общего кратного на число соответствующих атомов в левой и правой частях схемы находят соответствующие коэффициенты

4. Уравнивают число атомов остальных химических элементов и заменяют стрелку знаком равенства.

Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий.

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:

действия выполняются по порядку слева направо,
причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Выполните действия 7−3+6 .

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени.

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.

Рассмотрим решения примеров.

Выполните действия в выражении (3+1)·2+6 2 :3−7 .

В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .

Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .

Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Решение

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Решение

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Что такое действия первой и второй ступени

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Порядок вычислений в выражениях со скобками

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

Решение

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

Решение

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

Решение

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

PEMDAS Значение, объясненное примерами — Mashup Math

PEMDAS Значение: почему это важно

Правильное применение порядка операций и использование PEMDAS стало очень популярным в последние годы из-за вирусных математических проблем, которые появляются в социальных сетях. Такие сообщения популярны, потому что люди предполагают, что правильный способ применения порядка операций — выполнять каждую операцию слева направо. Поскольку большинство людей неправильно понимают эти, казалось бы, простые математические задачи, их поощряют комментировать и делиться, что быстро приводит к вирусному распространению сообщения.

Однако, если бы люди могли помнить (A) порядок операций с использованием мнемоники, такой как PEMDAS (или даже более полезной, известной как GEMS), и (B) нюансы для правильного применения порядка операций (а именно отношения между умножением / делением и сложением / вычитанием), то подобные вирусные проблемы можно было бы легко решить без особых споров.

PEMDAS Значение: Заключение

PEMDAS — распространенная, но в некоторой степени полезная мнемоника для запоминания порядка операций в математике.PEMDAS относится к следующему порядку операций: круглые скобки, экспоненты, умножение, деление, сложение и вычитание. Хотя многие люди помнят PEMDAS, используя знаменитую фразу «Пожалуйста, извините мою дорогую тетю Салли», они часто забывают важный нюанс, что умножение не выполняется автоматически перед делением, а сложение не выполняется автоматически перед вычитанием (выполняется умножение / деление и сложение / вычитание. слева направо в зависимости от того, какая операция наступит раньше).Это распространенное заблуждение обесценивает PEMDAS как надежный инструмент памяти и является основной причиной, по-видимому, простых математических задач, которые становятся вирусными в социальных сетях, потому что большой процент взрослых может вспомнить мнемонику спустя десятилетия после начальной школы, но не может получить правильный ответ.

PEMDAS сохранил свою популярность как стратегию запоминания порядка операций больше из-за ностальгии и сопротивления изменениям, чем из-за того, что это самая эффективная стратегия. И хотя использование мнемоники редко бывает хорошей стратегией для понимания математических концепций и развития навыков рассуждения, существуют гораздо лучшие альтернативы PEMDAS, включая GEMS, которые значительно более надежны.

Что является первым сложением или умножением? — AnswersToAll

Что является первым сложением или умножением?

Порядок операций говорит вам сначала выполнить умножение и деление, работая слева направо, прежде чем выполнять сложение и вычитание. Продолжайте выполнять умножение и деление слева направо. Затем сложите и вычтите слева направо. Сначала размножайтесь.

Какой метод сложения дробей?

Чтобы сложить дроби, необходимо выполнить три простых шага: Шаг 1: Убедитесь, что нижние числа (знаменатели) совпадают.Шаг 2: сложите верхние числа (числители), поставьте полученный ответ над знаменателем. Шаг 3. Упростите дробь (при необходимости)

Как вы упорядочиваете операции с дробями?

Сначала выполните операции, заключенные в круглые скобки. Получите общий знаменатель при сложении дробей. Затем оцените показатели. Затем умножьте перед сложением или вычитанием.

Вы используете Пемдас? Если нет скобок?

Правила PEMDAS без скобок подразумевают, что вы должны сначала выполнить деление.С круглыми скобками 3x теперь становится группой.

Применяется ли порядок операций только в круглых скобках?

1. Порядок операций указан в скобках. ученик может не знать, что умножение должно быть выполнено в первую очередь.

Можно ли использовать Bodmas без скобок?

Первоначальный ответ: Применяется ли BODMAS, когда нет скобок? Да. Если скобок нет, следующим шагом будут индексы, затем умножение и / или деление, затем сложение и / или вычитание.

Что означает порядок действий?

Порядок операций — это правило, указывающее правильную последовательность шагов для вычисления математического выражения. Мы можем запомнить порядок, используя PEMDAS: круглые скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо).

Как порядок операций соотносится с реальной жизнью?

В математике порядок операций помогает найти правильное значение для выражения. Порядок действий имеет значение и в повседневной жизни.Например, если вы наденете обувь перед штанами, вам будет сложно одеться.

Как решить положительные и отрицательные целые числа?

Чтобы вычесть целые числа, измените знак целого числа, которое нужно вычесть. Если оба знака положительные, ответ будет положительным. Если оба знака отрицательные, ответ будет отрицательным. Если знаки разные, вычтите меньшее абсолютное значение из большего абсолютного значения.

Что такое BEDMAS?

Существуют акронимы, которые помогают людям запомнить, как выполнять набор процедур в математике.BEDMAS (также известный как PEMDAS) является одним из них. BEDMAS — это аббревиатура, помогающая запомнить порядок операций в основах алгебры. Когда у вас есть математические задачи, требующие использования различных операций (умножение, деление, экспоненты, скобки, вычитание, сложение), порядок необходим, и математики согласовали порядок BEDMAS / PEMDAS. Каждая буква BEDMAS относится к одной части операции, которая будет использоваться. В математике существует согласованный набор процедур для порядка, в котором выполняются ваши операции.Скорее всего, вы получите неправильный ответ, если будете производить расчеты не по порядку. Если вы соблюдаете правильный порядок, ответ будет правильным. Не забывайте работать слева направо, когда вы используете порядок операций BEDMAS. Каждая буква означает:

B — Кронштейны
E — Экспоненты
D — Подразделение
M — Умножение
A — Дополнение
S — вычитание

Вы, наверное, тоже слышали аббревиатуру PEMDAS.При использовании PEMDAS порядок операций такой же, однако P просто означает круглые скобки. В этих ссылках круглые и квадратные скобки означают одно и то же.

При применении порядка операций PEMDAS / BEDMAS следует помнить о нескольких вещах. Скобки / круглые скобки всегда идут первыми, а показатели — вторыми. Когда вы работаете с умножением и делением, вы делаете то, что наступит раньше, слева направо. Если умножение идет первым, сделайте это до деления. То же самое верно и для сложения и вычитания: когда вычитание идет первым, вычитайте, прежде чем добавлять.Возможно, стоит взглянуть на БЕДМЫ так:

Скобки (или круглые скобки)
Экспоненты
Деление или умножение
Сложение или вычитание

Когда вы работаете со скобками и имеется более одного набора скобок, вы будете работать с внутренним набором скобок и переходите к внешним скобкам.

Уловки для запоминания PEMDAS

Чтобы запомнить PEMDAS или BEDMAS, были использованы следующие предложения:
Please Excuse My Dear Aunt Sally.
Большие слоны уничтожают мышей и улиток.
Розовые слоны уничтожают мышей и улиток

Вы можете составить собственное предложение, которое поможет вам запомнить аббревиатуру, и, безусловно, есть другие предложения, которые помогут вам запомнить порядок действий. Если вы креативны, придумайте то, что запомните.

Если вы используете базовый калькулятор для выполнения расчетов, не забудьте ввести вычисления в соответствии с требованиями BEDMAS или PEMDAS. Чем больше вы практикуетесь в использовании BEDMAS, тем легче это становится.

Когда вы освоитесь с пониманием порядка операций, попробуйте использовать электронную таблицу для расчета порядка операций. Таблицы предлагают множество формул и вычислительных возможностей, когда ваш калькулятор неудобен.

В конце концов, важно понимать математику, стоящую за аббревиатурой. Даже если аббревиатура полезна, важнее понять, как, почему и когда она работает.

Произношение: Bedmass или Pemdass
Также известен как: Порядок операций в алгебре.
Альтернативное написание: BEDMAS или PEMDAS (скобки против скобок)
Распространенные орфографические ошибки: Скобки и круглые скобки определяют разницу в аббревиатуре BEDMAS и PEMDAS

Примеры использования BEDMAS для порядка операций

Пример 1

20 — [3 x (2 + 4)] Сначала сделайте внутреннюю скобку (скобки).
= 20 — [3 x 6] Сделайте оставшуюся скобку.
= 20 — 18 Выполните вычитание.
= 2

Пример 2

(6 — 3) ² — 2 x 4 Сделайте скобу (скобки)
= (3) ² — 2 x 4 Вычислить показатель степени.
= 9 — 2 x 4 Теперь умножим
= 9-8 Теперь вычтите = 1

Пример 3

= 2 ² — 3 × (10 — 6) Вычислить в скобках (скобках).
= 2 ² — 3 × 4 Вычислить показатель степени.
= 4 — 3 x 4 Произведите умножение.
= 4 — 12 Выполните вычитание.
= -8

Каков порядок работы? (PEMDAS)

Что такое PEMDAS?

Операции относятся к сложению, вычитанию, умножению и делению в математике.Итак, что такое PEMDAS и как он соотносится с порядком операций?

PEMDAS на самом деле является вспомогательным средством памяти, помогающим запомнить порядок выполнения операций. Вы также можете использовать фразу «Прошу прощения, моя дорогая тетя Салли», чтобы помочь вам вспомнить, как пишется PEMDAS. В некоторых частях мира PEMDAS также известен как BEDMAS. Давайте подробнее рассмотрим различные компоненты PEMDAS.

Каков порядок работы?

один способ запомнить PEMDAS, пожалуйста, извините мою дорогую тетю Салли

Буква P в PEMDAS означает круглые скобки.Он стоит первым в аббревиатуре, напоминая вам, что вы должны сначала взглянуть на все, что находится в круглых скобках (вы можете называть их скобками, и поэтому в некоторых местах вместо этого используется BEDMAS).

Буква «E» в аббревиатуре означает степень. Это включает в себя экспоненты и корни, поэтому ими следует заняться дальше. Затем идут M и D, и это пара. «M» означает «умножить», «D» — «разделить», но вы можете сделать либо — либо сначала. Оба они занимают одинаковое место в рейтинге PEMDAS.Пока вы делаете их перед буквами «A» и «S», что означает «сложение» и «вычитание». Порядок сложения и вычитания также не имеет значения, если все это делается в последнюю очередь. Опять же, их ранг равен.

В общем, когда вы решаете операции с помощью PEMDAS, хорошей привычкой будет движение слева направо. Например, если в вопросе есть сложение и вычитание, а сложение находится левее, сделайте это до того, как вы начнете вычитать.

Если вы рассчитываете операции в неправильном порядке, вы получите неправильный ответ.Очень важно обратить внимание и определить все различные операции, с которыми вы работаете, чтобы вы могли правильно отсортировать их порядок. PEMDAS — это то, что было согласовано математиками давным-давно, чтобы согласовать последовательный метод решения математических задач.

Порядок действий

Вот пример правила PEMDAS, используемого в математике. Давайте попробуем этот вопрос:

пример вопроса PEDMAS

Как нам атаковать это с точки зрения PEMDAS? Мы знаем, что первое, что нам нужно сделать, это скобки.2 \ div 2 = 3 × 10−42 ÷ 2

Затем идет показатель степени. У нас есть показатель степени 2 для числа 4. Мы снова решим эту часть вопроса раньше остальных, получив:

= 3 × 10-16 ÷ 2 = 3 \ умножить на 10-16 \ div 2 = 3 × 10-16 ÷ 2

Деление и умножение — это следующие вещи, которыми мы займемся. Вы можете делать это одно за другим или просто проходить и делать их одновременно. В этом случае мы сделаем 3 × 103 \ × 103 × 10 и 16 ÷ 216 \ div 216 ÷ 2. Сейчас у нас:

= 30-8 = 30-8 = 30-8

В последней части вопроса мы будем заниматься сложением и вычитанием.Никаких добавлений делать не надо, поэтому мы просто минус 8 из 30. Это дает нам окончательный ответ 22.

Краткое описание шагов можно увидеть на этом изображении с цветовой кодировкой, которое позволяет вам сосредоточиться на правилах PEMDAS.

шаги решения вопроса PEDMAS

Попробуйте эту онлайн-игру, в которой вы сможете проверить свое понимание порядка действий. Если вам также нужно место, где можно дважды проверить свои ответы на вопросы PEMDAS, вы можете использовать этот изящный решатель математических уравнений.

Вы сначала складываете или умножаете в математике? — Реабилитационная робототехника.нетто

Вы сначала складываете или умножаете в математике?

Вы сначала складываете или умножаете без скобок?

Если есть несколько операций на одном уровне в порядке операций, двигайтесь слева направо. вы работаете так: сначала обратите внимание, что здесь нет скобок или экспонентов, поэтому мы переходим к умножению и делению.Есть только одно умножение, поэтому мы делаем это сначала и получаем 9-5 + 2.

Что является первым в математических уравнениях?

Со временем математики разработали набор правил, называемых порядком операций, чтобы определить, какую операцию выполнять в первую очередь. Правила следующие: Умножайте и делите слева направо. Сложите и вычтите слева направо.

Что означает Гемдас?

Группирование экспонент, умножение, деление, сложение и вычитание

Каков порядок математических уравнений?

Это означает круглые скобки, экспоненты, умножение / деление, сложение / вычитание.PEMDAS часто расширяется до мнемоники «Прошу прощения, моя дорогая тетя Салли». Канада и Новая Зеландия используют BEDMAS, что означает скобки, экспоненты, деление / умножение, сложение / вычитание.

Какое первое правило алгебры?

Первое правило алгебры — Или: «Нет, Вирджиния — вычитания нет!»

Каков правильный порядок решения алгебраического уравнения?

Порядок операций: скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо). Это можно запомнить двумя способами: «Прошу прощения, дорогая тетя Салли» или PEMDAS.

Какое правило для Пемдаса?

Почему PEMDAS или BODMAS именно в таком порядке?

BODMAS или PEDMAS — это просто соглашение, стандарт, и, как и любой стандарт, он разработан для того, чтобы сделать процессы, в данном случае вычисления, менее беспорядочными и неоднозначными.

Если вы думаете, что 2 + 2 × 2 равно 8, поздравляем! Ты не прав. Правильный ответ — 6. Почему? Поскольку умножение имеет приоритет перед сложением, поэтому сначала умножаются последние две двойки, а затем произведение добавляется к первым двум, так что результат равен 6. Теперь, имея в виду, что 2 × 2-4 ÷ 2 равно? Какая операция тогда имеет приоритет?

Старшая школа научила нас, что, когда мы погрязли в такой проблеме, мы должны искать суверенную БОДМАС, которую часто называют ПЕМДАС. Этот метод показывает нам путь, декларируя кардинальный порядок: Скобки-Порядки-Деление-Умножение-Сложение-Вычитание. Или Скобки-Показатели-Умножение-Деление-Сложение-Вычитание. Согласно порядку, деление имеет приоритет перед умножением, поэтому 2 × 2-4 ÷ 2 равно 2, а не 0. Однако должны ли мы слепо верить этому методу? Почему заказ такой особенный? Почему заказ не BOSAMD или любой из других 240 перестановок?

Если математика — это язык, на котором говорит Вселенная, а эти операции являются ее соединениями, то, конечно, как и следовало ожидать, порядок должен быть основан на логике, а не выбран произвольно, верно? Поразительно, но это не так … но это тоже отчасти.

Почему BODMAS?

BODMAS или PEMDAS — это просто соглашение, стандарт и, как и любой стандарт, он разработан, чтобы сделать процессы, в данном случае вычисления, менее беспорядочными и неоднозначными. В приведенных выше примерах я сознательно воздержался от использования скобок и заметил, насколько неоднозначными, по крайней мере для новичка, становятся вычисления. Именно поэтому мы используем скобки для удобства. Единственная цель пары скобок — сжать то, что обычно записывается как очень длинный и громоздкий расчет.

Сложение и вычитание — это наиболее элементарные операции в том смысле, что на их операцию не влияет направление. Рассмотрим этот расчет:

5 + 5 + 5 + 6 + 7 + 3 + 3 + 3 + 3 + 4 + 1

Мы получаем тот же результат, независимо от того, в каком направлении складываются числа. Фактически, нет необходимости даже добавлять линейный конкретный путь: прибавьте 6 к 1, а результат к 5, то есть можно сложить числа в любом случайном порядке, и результат будет тем же, что и 45.Однако очевидно, что процесс громоздкий.

Мы знаем, что умножение — это просто повторное сложение, а деление — это просто повторное вычитание. Следовательно, мы можем сжать наш расчет до следующего:

(5 × 3) + 6 + 7 + (3 × 4) + 4 + 1

Когда мы собираем блоки или выполняем процесс в обратном порядке, мы осознайте важность скобок. Сейчас кажется некорректным читать сумму как предложение на английском языке, а именно слева направо. Число 3 нельзя складывать с 6, потому что произведение 5 и 3 образует отдельное подвычисление и, следовательно, становится элементарным, — еще одним компонентом, который нужно добавить к остальным компонентам . Чтобы обозначить этот подсчет и его границы, мы используем квадратные скобки. Добавим в наш расчет несколько переменных:

4b + ac + ab + 4d + ad + 4c

Это можно уменьшить до:

(4 + a) (b + c + d)

Можно утверждать, что мы пожертвовали своей свободой выбора порядка, но мы действительно получили больше, чем потеряли. То, что мы достигли, несомненно, проще и легче решить. То, что раньше было суммой шести произведений, теперь является просто произведением двух сумм.В какой-то момент истории математики кто-то понял, что вместо того, чтобы писать длинную строку сложений, вычитаний и, возможно, умножений (E в PEMDAS означает экспоненциальное, что является просто повторным умножением), можно просто сжать их таким образом с помощью помощь скоб. Скобки должны быть открыты в первую очередь, или все, что находится внутри скобок, должно быть сначала вычислено, потому что именно так вычисление логически отменяется. Однако мы доказали обратное.

Далее, причина, по которой умножение и деление должны выполняться перед сложением и вычитанием, заключается в том, что первые два, очевидно, на выше операций. Размышляйте о значении вычислений, а не читайте их как предложение. Если кто-то попросит вас купить 6 яблок и 3 дюжины яиц, будет ли общее количество предметов, которые вы купите, составит 108 или 42? Сумма, которая выглядит как 6+ (3 × 12), равна 42, а не 108. Вот почему BODMAS или PEMDAS могут показаться произвольными и, следовательно, «недоказуемыми», но это определенно логично.

Однако BODMAS — не единственная мнемоника в математике, но она наиболее удобна. Обратная польская нотация — еще одна мнемоника, за исключением того, что она исключительно громоздкая. Большие вычисления на основе RPN были бы практически невозможны. BODMAS, несомненно, лучший мнемоник, который мы когда-либо придумали. (Фото: Wallpoper / Wikimedia Commons)

Фактически, представление о том, что BODMAS или PEMDAS являются строгим «правилом», ухудшило преподавание математики. Правило просто диктует, что сначала должны быть открыты скобки, чтобы развернуть вычисление, после чего должно быть выполнено любое из двух верхних операций перед любое из двух нижних операций .Нет никакого принуждения к делению перед умножением или сложению перед вычитанием; нужно только убедиться, что в первую очередь выполняются более высокие операции. Вот почему, несмотря на то, что головоломка 2 × 2-4 ÷ 2 во введении была решена, в объяснении путем деления на 4 сначала это не является существенным. Умножение и деление равно , ранжируются — можно выполнить первое сначала или, возможно, оба одновременно, но не после вычитания.

Статьи по теме

Точно так же люди часто слепо полагают, что в соответствии с правилом, сложение должно выполняться перед вычитанием. В таком случае не должно ли 8-5 + 3 равняться 0? Правильный ответ, конечно же, 6, который мы получаем, когда записываем сумму как 8 + (- 5) +3. Обратите внимание на то, что, поскольку мы просто складываем числа, на результат не влияет порядок или направление добавления. Помещая -5 в скобки и подразумевая, что вычитание — это просто сложение, но с отрицательным числом, мы получаем правильный ответ. Просто и удобно, но не произвольно.

Умножение всегда на первом месте? — Мворганизация.org

Умножение всегда на первом месте?

Вы умножаете первым, если без скобок?

Просто следуйте правилам BODMAS, чтобы получить правильный ответ. Здесь нет скобок или порядков, поэтому начните с деления и умножения.

Применяется ли Бодмас, если нет скобок?

Почему Бодмас ошибается?

Неверный ответ. Буквы обозначают скобки, порядок (значение степеней), деление, умножение, сложение, вычитание. Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и выполнять сложение с последующим вычитанием: это ошибочно.

Как доказать Бодмас?

а (b + c) = ab + ac. Здесь a = 2, b = 3 и c = 4, поэтому 2 × (3 + 4) = 2 × 3 + 2 × 4. Теперь, BODMAS говорит, что мы должны выполнить умножение перед сложением. 2 × 3 = 6 и 2 × 4 = 8, а 6 + 8 = 14.

Как работает правило Бодмаса?

Правило BODMAS гласит, что мы должны сначала вычислить скобки (2 + 4 = 6), затем приказы (52 = 25), затем любое деление или умножение (3 x 6 (ответ на скобки) = 18) и, наконец, любое сложение или вычитание (18 + 25 = 43).Дети могут получить неправильный ответ из 35, работая слева направо.

Кто изобрел правило Бодмаса?

Ахиллес Ремелельт

Что означает буква O в Bodmas?

порядок надо делать операции

Стоит ли всегда использовать Бодмы?

Абсолютно нет — и по двум причинам. Причина №1: Если мне нужно оценить 2 × (3 + 4), строгое следование BODMAS требует, чтобы вы сначала выполнили сложение, потому что оно заключено в скобки, поэтому вы получите 2 × 7 = 14.Это правильный ответ, но от вас ни в коей мере не требовалось делать это таким образом.

Как долго используется Бодма?

Порядок работы, например, BODMAS, был введен в 1800-х годах.

Является ли Бодмас ложью?

В то время как PEMDAS выполняет действия в порядке скобок, экспонент, умножения / деления, сложения / вычитания. Проблема заключается в том, делите ли вы в первую очередь — или в первую очередь умножаете. Существуют соглашения о порядке действий для решения этой проблемы, иногда называемые BODMAS в школах Великобритании.

Бодмас и Пемдас — одно и то же?

BODMAS означает скобки, порядки, деление, умножение, сложение и вычитание. BIDMAS и PEMDAS делают одно и то же, но используют разные слова. BODMAS объясняет «Порядок операций» математикой, а BIDMAS и PEMDAS делают то же самое, но используют несколько разные слова.

Где используется Бодмас?

Наиболее распространенным в Великобритании, Пакистане, Индии, Бангладеш и Австралии и некоторых других англоязычных странах является BODMAS, означающий Скобки, Порядок, Деление / Умножение, Сложение / Вычитание или Скобки, Из / Деление / Умножение, Сложение / Вычитание.Нигерия и некоторые другие страны Западной Африки также используют BODMAS.

Используют ли калькуляторы Bodmas?

BODMAS или BIDMAS также необходимо использовать при использовании калькулятора. Научные калькуляторы автоматически применяют операции в правильном порядке, однако могут потребоваться дополнительные скобки.

Всегда ли Пемдас правилен?

Просто, правда? Мы используем правило «порядка операций», которое мы запомнили в детстве: «Прошу прощения, моя дорогая тетя Салли», или PEMDAS, что означает «Скобки, экспоненты, умножение, деление, сложение, вычитание».* Эта удобная аббревиатура должна разрешить любые споры — за исключением того, что это не так, потому что это вообще не правило.

Что первично в Пемдасе?

Мы можем запомнить порядок, используя PEMDAS: круглые скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо).

Что означает буква А в Пемдасе?

Краткое содержание урока PEMDAS — это аббревиатура слов скобка, показатель степени, умножение, деление, сложение, вычитание.

Какая скобка решается в первую очередь?

Согласно правилу BODMAS, если выражение содержит скобки ((), {}, []), мы должны сначала решить или упростить скобку, за которой следует «порядок» (что означает степени и корни и т. Д.), Затем деление, умножение , сложение и вычитание слева направо.

Почему мы умножаем перед сложением?

Это многовековое соглашение, которое позволяет нам писать выражения без большого количества скобок. Согласно этому соглашению, умножение имеет более высокий порядок приоритета, чем сложение или вычитание, поэтому вместо того, чтобы заключать в круглые скобки такое выражение, как.

Вы умножаете или складываете, чтобы найти площадь?

Площадь — это измерение поверхности фигуры. Чтобы найти площадь прямоугольника или квадрата, вам нужно умножить длину и ширину прямоугольника или квадрата.

Какой пример задачи умножения слов?

Сколько печенья можно упаковать в 45 картонных коробок? В одну коробку можно упаковать 24х12 печенья.

Порядок выполнения действий в формулах Excel

Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше

В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.

Порядок вычислений

Формулы вычисляют значения в определенном порядке. Формула в Excel всегда начинается со знака равно (=). Excel интерпретирует символы после знака равно как формулу. После знака равно вычисляются элементы (операнды), например константы или ссылки на ячейки. Они разделены операторами вычислений. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.

Приоритет операторов в формулах Excel

Если в одной формуле используется несколько операторов, Microsoft Excel выполняет операции в порядке, указанном в приведенной ниже таблице. Если формула содержит операторы с одинаковым приоритетом ( например, если формула содержит операторы умножения и деления), Excel оценивает операторы слева направо.

Оператор	Описание
: (двоеточие) (один пробел) , (запятая)	Операторы ссылок
–	Знак «минус»
%	Процент
^	Возведение в степень
* и /	Умножение и деление
+ и —	Сложение и вычитание
&	Объединение двух текстовых строк в одну
= < > <= >= <>	Операторы сравнения

org/ListItem»>
Использование скобок в Excel формулах

Чтобы изменить порядок выполнения формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, результатом приведенной ниже формулы будет число 11, поскольку в Microsoft Excel умножение выполняется раньше сложения. В данной формуле число 2 умножается на 3, а затем к результату добавляется число 5.

=5+2*3

Если же с помощью скобок изменить синтаксис, Microsoft Excel сложит 5 и 2, а затем умножит результат на 3; результатом этих действий будет число 21.

=(5+2)*3

В приведенном ниже примере скобки, в которые заключена первая часть формулы, задают следующий порядок вычислений: определяется значение B4+25, после чего полученный результат делится на сумму значений в ячейках D5, E5 и F5.

=(B4+25)/СУММ(D5:F5)

Порядок действий в математике 3 класс: примеры. Что сначала

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

сложение (+)
вычитание (-)
умножение (*)
деление (:)

Операции отношения:

равно (=)
больше (>)
меньше (<)
больше или равно (≥)
меньше или равно (≤)
не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).

2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Сложение и вычитание

Самое простое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно 7. Посчитать можно на счетных палочках, камнях, яблоках– результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.

Деление

Умножение

Что сначала — умножение или сложение?

5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все помидоры сдавали учетчику, он укладывал их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
50 + 50 – это кучки малолетних работников;
70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:

500 + 500 +500 +500 +500 + 50 +50 + 70 =?;

Две кучки по 50 – это тоже можно записать через умножение.

И одна кучка 70 помидоров.

5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?

2500 + 100 + 70 = 2 670

Порядок действий без скобок

Установленный порядок арифметических действий без скобок:

Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):

Первый способ

Каждое действие записывается отдельно со своим номером под примером.
После выполнения последнего действия ответ обязательно записывается в исходный пример.

Запомните! При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

Второй способ называется запись “цепочкой”. Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Запомните! Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Порядок действий со скобками

Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.

В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.

Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.

Секрет безошибочного порядка действий

Всех людей, которые ловко решают примеры на смешанные действия, отличает одно свойство. Точнее даже — навык.

Они умеют «видеть» или воспринимать числа, стоящие по обе стороны от знака умножения или деления не как «отдельно стоящие циферки», а как «единое число» (выраженное в такой странной форме).

Говоря наглядно, в нашем примере:

2 + 6 — 8 : 2

человек «видит» не четыре числа, а только три:

Двойка
Шестерка и
8:2, которые воспринимает как единое число.

Как правило, это неосознанное, невербализованное восприятие. Мозг мгновенно производит эту операцию, и человек не замечает её.

Этот навык вырабатывается долгим «нарешиванием» огромного количества длинных примеров. К старшей школе уже у многих детей есть.

Но можно попробовать ускорить события.

Предложу вам упражнение для отработки такого «видения».

Примеры на порядок действий 3-4 класс для тренировки

Рассмотрим выражения, установим порядок действий и выполним вычисления.

Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

Узнаем, правильно ли определен порядок действий в следующих выражениях.

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Действуем по алгоритму.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Список литературы

М.И. Моро, М. А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
«Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Определи порядок действий в данных выражениях. Найди значение выражений.

***

Определи, в каком выражении такой порядок выполнения действий:

умножение;
деление;.
сложение;
вычитание;
сложение.

Найди значение данного выражения.

***

Составь три выражения, в которых такой порядок выполнения действий:

умножение; 2. сложение; 3. вычитание
сложение; 2. вычитание; 3. сложение
умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.

Если производить действия в порядке их записи.

Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.

Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:

Чтобы не загромождать чрезмерно записи, условились не писать скобок:

в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:

сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Сначала выполняем умножения:

2 · 5 = 10

3 · 3 = 9

затем вычитание:

10 – 9 = 1

Сначала выполняем действия в скобках:

16 – 2 · 7 + 4 = 16 – 14 + 4 = 6

2 + 5 = 7

Теперь выполняем остающиеся действия:

9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43

Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.

Выполняем действия в круглых скобках, имеем:

8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4

действия в квадратных скобках дают:
14 – 3 · 2 = 8

выполняя остающиеся действия скобках находим:

5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29

Порядок действий:

30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150

Расставь порядок действий. Найди значение выражения:

(12 – 0 : 4) : 3 – (7 — 7)*45 + (36 : 6) : (15 : 15)
36 : (12 – 6 : 20 – (0 *5 + 3) – (7 * 8) : 14 : 4
(3 + 27 : 3) * 5 – 60 * 3 : 90 + 8 * (7 – 7) : 4
(630 : 7 + 4 * 9) : (5 + 5 : 5) + (8 – 8) : (35 * 7 + 49)
5 * (48 : 6 + 2 : 2) – 280 : 20 * 3 + (50 – 32) : 9
8040 : 6 + (109004 – 76048) : 7
(64000 : 80 * 3 + 600) : 15 – (3200 * 100) : 2000
240400 – (5796 + 1803200 : 400) * 8
345 * (250 * 125) * (8 * 400)
56432 : 8 * 50 – (223956 + 882630 : 9)
(62456715 + 548185) : 700 – 300 * 80450 : 5000
80 – (17 * 4) : (20 – 380 : 20) + 90 * 40 : 120
(1000 – 999) * 40 – 0 : 24 + 360 : (16 * 5 + 280 : 7)
(600000 – 538704) * 500 : 300
280 : (60 : 15) – (25 + 3 * 8) : 7 + 3 * (720 : 80)
(250 * 840 – 145 * 1008) : 60
(1000 – 832) * 715 : 30 + (104402 – 58842 : 7)

Дополнительные примеры

В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.

Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.

Материалы по теме Адаптация ребенка 3–4 лет к детскому саду

Например,

В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:

Вычисляем:

10 + 15 = 25

25 – 6 = 19

19 – 8 = 11

Полностью пример записываем так:

10 + 15 – 6 – 8 = 25 – 6 – 8 = 19 – 8 = 11

Например,

В числовом выражении 3 арифметических действия: деление, умножение и деление.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:

Вычисляем:

15 : 5 = 3

3 • 4 = 12

12 : 6 = 2

Полностью пример записываем так:

15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2

Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.

15 : 3 = 5

6 • 8 = 48

10 – 5 = 5

5 + 48 = 53

Полностью пример записываем так:

10 – 15 : 3 + 6 • 8 = 10 – 5 + 6 • 8 = 10 – 5 + 48 = 5 + 48 = 53

Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

25 – 10 = 15

15 : 3 = 5

6 • 8 = 48

5 + 48 = 53

Полностью пример записываем так:

(25 – 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53

Например,

В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.

12 : 4 = 3

6 + 3 = 9

18 : 9 = 2

42 + 2 = 44

Полностью пример записываем так:

42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44

Онлайн урок: Порядок выполнения действий по предмету Математика 5 класс

Изучая числовые и буквенные выражения, способы упрощения выражений, свойства арифметических операций, мы рассматривали в основном простые выражения, значение которых найти было несложно.

Сегодня на уроке мы будем рассматривать выражения, в которых содержатся сразу несколько арифметических операций и несколько пар скобок.

Выясним, в какой последовательности необходимо выполнять математические операции при нахождении значения выражения.

Узнаем, какие действия называют действиями первой и второй ступени, зачем нужны скобки.

Разберем множество различных примеров, которые позволят нам лучше усвоить данную тему.

Любой человек каждый день решает множество различных задач: простых и сложных.

Многие из них решаются по определенным правилам- алгоритмам.

У меня есть дополнительная информация к этой части урока!

Закрыть

Например, алгоритмом можно считать инструкцию по эксплуатации какого-либо прибора, рецепт приготовления блюда в кулинарной книге, порядок действий при включении компьютера, порядок выполнения практической работы, расписание уроков, режим дня, правила дорожного движения и многое другое.

5. Если в выражении отсутствуют скобки, и оно содержит действия первой и второй ступени, то сначала выполняются действия второй ступени (умножение и деление) в порядке их следования слева направо, затем выполняются действия первой ступени (сложения и вычитания) так же в порядке их следования слева направо.

2. Если в скобках присутствуют действия первой и второй ступени, то в скобках сохраняется известный нам порядок действий: слева направо выполняются сначала действия деления и вычитания, затем по порядку слева направо сложение и вычитание.

В таком случае выполняются действия последовательно по порядку слева направо: сначала в первой паре скобок, затем во второй паре, далее в третьей и т.д. (пока есть скобки), и только потом выполняются все остальные действия, которые находятся за скобками, согласно правилам, определяющим порядок выполнения математических действий в выражениях.

Так, если выражение в круглых скобках нужно заключить в скобки, то для этого можно использовать квадратные скобки, а если необходимо в скобки заключить выражение, которое содержит круглые и квадратные скобки, то в таком случае можно использовать фигурные скобки

Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.

Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.

Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.

Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.

Маркушевич сказал великие слова: “Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели . ” Добро пожаловать на урок математики!

“Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.” , говорил М.В. Остроградский. Вот и мы сейчас вспомним, что мы только что изучили и применим новые знания на практике.

Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Мы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
Если в примере нет скобок , мы выполняем все действия по порядку, слева направо.
Если в примере есть скобки , то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20. Онлайн тренажер.
2) Примеры со скобками в пределах до 100. Онлайн тренажер.
3) Примеры со скобками. Тренажер №2
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Если в примере нет скобок , сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо.
Если в примере есть скобки , то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
1. Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.
2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»
3. Порядок действий (расставляем порядок и решаем примеры)
Порядок действий в математике 4 класс
Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.
Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:
Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.
Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.
27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).
Научите ребёнка всегда планировать и нумеровать выполняемые действия.
Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.
Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:
Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.
Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.
Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?
Решение примеров со скобками
Разберём конкретный пример:
При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
Начать следует с умножения, далее – сложение.
После того, как выражение в скобках решено, приступаем к действиям вне их.
По правилам порядка действий, следующим шагом будет умножение.
Завершающим этапом станет вычитание.
Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:
Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.
Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.
7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)
Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.
Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.
detskoerazvitie.info
Урок по математике 2 класс Порядок действий в выражениях со скобками.
Успейте воспользоваться скидками до 50% на курсы «Инфоурок»
Цель: 1.
2.
3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и
4. Учить работать в парах с целью развития коммуникативных качеств.
Оборудование * : + — (), геометрический материал.
Раз, два – выше голова.
Три, четыре – руки шире.
Пять, шесть – всем присесть.
Семь, восемь – лень отбросим.
Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:
6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см
Пока мы вспоминали о порядке действий в выражениях, с замком происходили чудеса. Мы были только что у ворот, а теперь попали в коридор. Смотрите, дверь. А на ней замок. Откроем?
1. Из числа 20 вычесть частное чисел 8 и 2.
2. Разность чисел 20 и 8 разделить на 2.
— Чем отличаются результаты?
— Кто сможет назвать тему нашего урока?
(на массажных ковриках)
По дорожке, по дорожке
Скачем мы на правой ножке,
Скачем мы на левой ножке.
По тропинке побежим,
Наше предположение было полностью правильно7
Где выполняются действия сначала, если в выражении есть скобки?
Смотрите перед нами «живые примеры». Давайте «оживим» их.
* : + — ().
m – c * (a + d) + x
k: b + (a – c) * t
6. Работа в парах.
Для их решения вам понадобиться геометрический материал.
Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.
Что нового вы узнали?
8. Домашнее задание.
Тема: Порядок действий в выражениях со скобками.
Цель: 1. Вывести правило порядка действий в выражениях со скобками, содержащих все
4 арифметических действия,
2. Формировать способность к практическому применению правила,
4.Учить работать в парах с целью развития коммуникативных качеств.
Оборудование : учебник, тетради, карточки со знаками действий * : + — (), геометрический материал.
1 .Физминутка.
Девять, десять – тихо сесть.
2. Актуализация опорных знаний.
Сегодня мы с вами отправляемся в очередное путешествие по стране Знаний городу математика. Нам предстоит посетить один дворец. Что-то я забыла его название. Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?
1. Сравните выражения:
2. Расшифруй слово.
3. Постановка проблемы. Открытие нового.
Так как же называется дворец?
А когда в математике мы говорим о порядке?
Что вы уже знаете о порядке выполнения действий в выражениях?
— Интересно, нам предлагают записать и решить выражения (учитель читает выражения, учащиеся записывают их и решают).
20 – 8: 2
(20 – 8) : 2
Молодцы. А что интересного в этих выражениях?
Посмотрите на выражения и их результаты.
— Что общего в записи выражений?
— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?
Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?
Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.
4. Физминутка.
И по этой же дорожке
До горы мы добежим.
Стоп. Немножко отдохнем
И опять пешком пойдем.
5. Первичное закрепление изученного.
Вот мы и пришли.
Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.
6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2
Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.
Как нужно выполнять действия после решения в скобках?
На доске написаны буквенные выражения и лежат карточки со знаками действий * : + — (). Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.
а + (а –в)
а * (в +с) : d – t
m – c * ( a + d ) + x
k : b + ( a – c ) * t
(a – b) : t + d
6. Работа в парах. Автономная некоммерческая организация Бюро судебных экспертиз Судебная экспертиза. Несудебная экспертиза Рецензия на экспертизу. Оценка Автономная некоммерческая организация «Бюро судебных экспертиз» в Москве – центр […]
Особенности бухгалтерского учета субсидий Государство стремится поддержать малое и среднее предпринимательство. Такая поддержка наиболее часто выражается в форме предоставления субсидий – безвозмездных выплат из […]
Жалоба на педиатра Жалоба на педиатра — официальный документ, устанавливающий требования пациента и описывающий суть возникновения таких требований. Согласно статье 4 Федерального закона «О порядке рассмотрения […]
Ходатайство об уменьшении размера исковых требований Один из видов уточнения иска — ходатайство об уменьшении размера исковых требований. Когда истец неправильно определил цену иска. Или ответчик частично исполнил […]
Черный рынок доллара в Киеве Валютный аукцион по покупке доллара в Киеве Внимание: администрация не несёт ответственности за содержание объявлений на валютном аукционе. Правила публикации объявлений на валютном […]

Закрепить знания учащихся о правилах выполнения действий в выражениях без скобок и со скобками; формировать у них умение пользоваться этими правилами при вычислении конкретных выражений; совершенствовать вычислительные навыки; повторить табличные случаи умножения и деления;

Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение(Регулятивные УУД ).

Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД ).

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий.

В таких вычислениях необходимо только знать правила сложения и вычитания и таблицу умножения.
Когда начинаются более сложные упражнения, примеры состоят из двух и более действий, да еще и со скобками, при решении у детей появляются ошибки. И главная из них – неправильный порядок действий.

А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.

Деление простых дробей не так сложно, как кажется на первый взгляд. Достаточно лишь преобразовать задачу – превратить ее в пример с умножением. Сделать это просто – нужно перевернуть дробь так, чтобы знаменатель стал числителем, а числитель – знаменателем.
Пример:

Поскольку такие функции изучаются только в рамках старшей школы, рассматривать их мы не будем, достаточно только сказать, что они, как и в случае со степенями, имеют приоритет при вычислении: сначала находится значение данного выражения, затем порядок вычислений обычный – скобки, умножение с делением, далее по порядку слева направо.

Говоря о главных и неглавных математических действиях, нужно сказать, что четыре основных действия можно свести к двум: сложение и умножение. Если вычитание и деление представляется для школьников сложным, правила сложения и умножения они запоминают быстрее. Действительно, выражение 5 – 2 можно записать иначе:

При решении сложных задач первое действие — то, которое выделено скобками, затем — деление или умножение, потом все остальные действия по порядку.
Когда нужно решить примеры без скобок, вначале выполняется умножение или деление, далее — вычитание либо сложение.

Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста, напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.

Порядок действий – это набор правил, которым необходимо следовать в определенной последовательности при решении выражения. В математике под словом «операции» мы подразумеваем процесс вычисления любого математического выражения, включающий арифметические операции, такие как деление, умножение, сложение и вычитание. Давайте подробно узнаем о правилах порядка действий и о том, насколько хорошо мы можем запомнить правила, используя короткие трюки.

1.	Каков порядок операций?
2.	Порядок действий Правила
3.	PEMDAS против BODMAS
4.	Как использовать порядок операций?
5.	способов запомнить
6.	Реальные приложения
7.	Часто задаваемые вопросы о порядке операций

Порядок Операций — это правило в математике, которое гласит, что сначала мы вычисляем круглые скобки/квадратные скобки, затем степени/порядки, затем деление или умножение (слева направо, в зависимости от того, что наступит раньше), а сложение или вычитание — в конце. последней (слева направо, в зависимости от того, что наступит раньше). В математике при вычислении выражения может быть выполнено несколько операций, и упрощение в конце дает разные результаты. Однако у нас может быть только один правильный ответ для любого вида выражения. Чтобы определить правильный ответ, мы упрощаем любое заданное математическое выражение, используя определенный набор правил. Эти правила вращаются вокруг всех основных операторов, используемых в математике. Такие операторы, как сложение (+), вычитание (-), деление (÷) и умножение (×). Посмотрите на данное изображение, чтобы получить представление о том, как точно выглядит порядок операций.

Как мы обсуждали выше, порядок операций можно определить как набор основных правил старшинства, которые мы используем при решении любого математического выражения, включающего несколько операций. Когда подвыражение появляется между двумя операторами, оператор, который идет первым в соответствии со списком, приведенным ниже, должен применяться первым. Порядок действий, правила выражены здесь:

Порядок работы Правило 1: Обратите внимание на выражение. Первое правило состоит в том, чтобы решить числа, присутствующие в скобках или скобках. Мы решаем операции группировки изнутри наружу. Обратите внимание на шаблон скобок, присутствующих в выражении, существует особый порядок решения скобок, т. Е. [ { ( ) } ]. Сначала решите круглые скобки ( ) → фигурные скобки { } → квадратные скобки [ ]. Внутри скобок соблюдается порядок действий.
Порядок действий Правило 2: После решения чисел в скобках найдите любой термин, представленный в виде показателей степени, и решите его.
Порядок операций Правило 3: Теперь у нас остались четыре основных оператора. Найдите числа с действием умножения или деления, решите их слева направо.
Порядок действий Правило 4: Наконец, найдите условия со сложением или вычитанием и решите их слева направо.

PEMDAS или BODMAS — это две разные аббревиатуры, используемые для изучения правил. Эти два имени указывают порядок, в котором должны выполняться операции в выражении. Вот подробный термин для каждой буквы, используемой в упомянутых аббревиатурах. Во-первых, мы обсудим PEMDAS.

Выражение: 4 × (5 ² )
Решение: 4 × ( 25 ) = 100 (Верно (✔). Это правильный способ решения показателей)
Давайте рассмотрим другой подход для того же выражения.
4 × ( 5 ² ) = 20 ² = 400 ((Неверно (✘). Это неверный способ решения показателей степени)

Мы только что прочитали о двух разных словах PEMDAS и BODMAS. Это лучший способ запомнить порядок операций. PEMDAS можно запомнить по фразе «Пожалуйста, извините мою дорогую тетю Салли». В порядке операций это означает «круглые скобки, показатели степени, умножение и деление, сложение и вычитание». Здесь умножение и деление, сложение и вычитание вместе. Точно так же мы можем запомнить порядок действий со словом BODMAS (скобки, порядок, деление, умножение, сложение и вычитание).

Многие действия в нашей жизни требуют определенного порядка действий, чтобы выполнять их хорошо. Возьмем повседневную проблему. Предположим, вы купили пять пицц с пепперони по 20 долларов каждая и хотите поровну разделить общую стоимость на 5 человек. Чтобы узнать, сколько каждый человек должен заплатить, воспользуемся здесь порядком операций.

Общее количество людей = 5
Общее количество пицц = 5
Стоимость одной пиццы = 20
$ Сформулируем выражение, используя PEMDAS:
Выражение: (20 + 20 + 20 + 20 + 20) ÷ 5 или (5 × 20) ÷ 5
Решение: В соответствии с PEMDAS или BODMAS мы сначала решим скобки.
(100) ÷ 5 = 20
Согласно порядку операций, каждый человек должен заплатить 20 долларов.

Решение: Полученное выражение: 18 ÷ (9 — 2 × 3)
Согласно правилу порядка операций, мы должны сначала решить скобки. Обратите внимание, что здесь в скобках указаны две операции: умножение и вычитание.
Сначала умножьте 2 × 3 = 6
. 18 ÷ (9 — 6)
Теперь из 9 вычтите 6,
. 18 ÷ (3)
Теперь разделите
18 ÷ 3 = 6
Шаг 1: Сначала нам нужно решить числа в скобках. Умножьте 6 на 2 в данном выражении, (6 × 2 — 6 — 1) × 2 ² , получаем, (12 — 6 — 1) × 2 ² .
Шаг 2. Теперь нам нужно вычесть 6 из 12 внутри скобки, так что мы получаем (6 — 1) × 2 ² .
Шаг 3- Снимите скобки после вычитания 6 — 1, мы получим, 5 × 2 ² .
Шаг 4. Решите показатель степени, т. Е. 2 ² = 4.
Шаг 5. Умножьте 5 на 4, чтобы получить окончательный ответ, то есть 5 × 4 = 20.
∴ (6 × 2 — 6 — 1) × 2 ² ^{= 20 .}
Решение: Давайте посмотрим, как мы можем применить правила порядка операций при решении данного выражения.
Шаг 1: Во-первых, нам нужно упростить самую внутреннюю скобку, (1 + 20 — 9 ÷ 3 ² ) ÷ (3 ² + 16 ÷ 2)
Шаг 2: Теперь нам нужно вычислить показатели степени (1 + 20 − 9).÷ 9) ÷ (9 + 16 ÷ 2)
Шаг 3: Теперь нам нужно разделить 9 на 9 и 16 на 2 в скобках, и мы получим (1 + 20 − 1) ÷ (9 + 8)
. Шаг 4: Складываем 1 и 20, получаем 21. Теперь вычитаем 1 из 21, получаем 20. Теперь (20) ÷ (9 + 8)
Шаг 5: Добавьте 9 + 8 и разделите результат на 20. 20 ÷ 17 = 20/17
Шаг 6: ∴ (1 + 20 − 9 ÷ 3 ² ) ÷ ((2 + 1) ² + 16 ÷ 2) = 20/17

Порядок действий в математике представляет собой набор правил, вращающихся вокруг 4 основных операторов. В соответствии с порядком операций существует определенная последовательность, которой мы должны следовать на каждом операторе при решении данного математического выражения.

Чтобы решить порядок операций, сначала обратите внимание на выражение и отметьте, какой схеме оно точно соответствует. Теперь начните использовать PEMDAS или BODMAS для решения данного выражения. В соответствии с правилами порядка операций сначала ищите круглые скобки, затем показатели степени, затем переходите к умножению или делению и сложению или вычитанию слева направо.

Чтобы запомнить порядок операций, мы используем две известные аббревиатуры, а именно PEMDAS и BODMAS. Мы используем любой из двух в соответствии с правилами порядка операций. PEMDAS или BODMAS помогают запомнить процесс решения любого порядка операций для любого n числа выражений.

Согласно PEMDAS, буква E обозначает показатели степени, которые идут вторым шагом в порядке операций. Давайте посмотрим на данный пример, чтобы четко понять, как сделать порядок операций с показателями.
Выражение: 7 × (2 ² )
Решение: 7 × ( 4 ) = 28 (Верно (✔). Это правильный способ решения показателей)
Давайте рассмотрим другой подход для того же выражения.
7 × ( 2 ² ) = 14 ² = 196 ((Неверно (✘). Это неправильный порядок действий с показателями)

Правильный порядок операций можно легко выразить с помощью слова PEMDAS или BODMAS. Эти два слова можно описать как PEMDAS (круглые скобки, показатели степени, умножение или деление и сложение или вычитание). Аналогично, для BODMAS (скобки, порядок , Деление, Умножение, Сложение и Вычитание.)

Идем по правилам порядка операций, если убрать скобки, то останется EMDAS. EMDAS означает (экспоненты, умножение или деление, сложение или вычитание). Если в выражении у нас нет экспоненциального члена, то нам нужно сначала выполнить умножение или деление, а затем перейти к сложению или вычитанию. Ситуация может варьироваться в зависимости от операторов, присутствующих в данном выражении

Многие случаи в нашей жизни проходят через определенный порядок операций, чтобы выполнить ее хорошо. Каждый день мы сталкиваемся с таким сценарием. Например, отправляясь на продуктовый рынок и покупая вещи, мы быстро проделываем в голове порядок действий. Это помогает нам сократить время работы на кассе.

Калькулятор порядка операций — это онлайн-инструмент и самый быстрый метод, с помощью которого мы можем вычислить любое заданное числовое выражение с учетом правил порядка операций. Чтобы использовать калькулятор порядка операций, нам нужно ввести числовое выражение в правильном формате. Попробуйте калькулятор порядка операций Cuemath и быстро решите выражения в течение нескольких секунд.

Целые числа: умножение: первые принципы
что вы узнаете. ..
обзор
На этой странице представлено умножение целых чисел в виде — одно число, множимое, повторяется количество раз, заданное вторым числом, множителем. Суммарный результат повторения подсчитывается или измеряется как произведение умножения. Количество машин 3″ role=»presentation»>33 повторяется 4″ role=»presentation»>44 раза. В результате получается 12″ role=»presentation»>1212. Размер 3″ role=»presentation»>33 повторяется 4″ role=»presentation»>44 раза. Полученная мера равна 12″ role=»presentation»>1212.
То же абстрагируется для умножения в числовом ряду. Определение умножения в первых принципах составляет основу для понимания упрощенной процедуры умножения больших чисел.
повторное добавление
3″ role=»presentation»>33 автомобиля переданы в 4″ role=»presentation»>44 шоу-рума каждый.
.
3″ role=»presentation»>33 машины были отданы в первый шоу-рум, потом во второй, потом в третий, а потом и в четвертый. Так 3″ role=»presentation»>33 было многократно добавлено 4″ role=»presentation»>44 раза, чтобы получить общее количество.
С учетом 3″ role=»presentation»>33 автомобилей отдано 4″ role=»presentation»>44 шоу-румов. Все автомобили показаны на рисунке. Подсчитав количество машин, получается 12″ role=»presentation»>1212.
Есть 4″ role=»presentation»>44 карандаша, каждый из 3″ role=»presentation»>33 сантиметра в длину.
Суммарная длина карандашей составляет 12″ role=»presentation»>1212 сантиметров.
Подразумевается, что задача состоит в повторении повторного сложения .
Длина одного карандаша составляет 3″ role=»presentation»> 33 сантиметра. Чтобы получить общую длину 4″ role=»presentation»>44 таких карандашей, к длине повторно прибавляется 4″ role=»presentation»>44 раза.
Учитывая 4″ role=»presentation»>44 карандаша, каждый по 3 сантиметра в длину. Четыре карандаша расположены рядом, а длина измеряется от 0″ role=»presentation»>00. Мера в конце составляет 12 «роль=»презентация»>1212. Общая длина составляет 12″роль=»презентация»>1212 сантиметров.
Количество или меру количества можно многократно складывать или умножать .
Умножение на приводит к подсчету или измерению комбинированного количества.
Умножение 3×4″ role=»presentation»>3×43×4 в числовой строке указано на рисунке.
Повторяется значение 3″ role=»presentation»>33 4″ role= «презентация»> 44 раза, чтобы попасть в 12 «роль = «презентация»> 1212. Результат умножения равен 12″ role=»presentation»>1212.
Слово «умножение» означает многократное увеличение количества.
множитель, множитель, произведение
Умножение. Первые принципы : Рассматриваются два числа, каждое из которых представляет счет или измерение. Одна из сумм повторяется количество раз, заданное второй суммой, чтобы сформировать результат, представляющий общую сумму из такого повторения.
например: 12×3=36″ role=»презентация»>12×3=3612×3=36
12″ role=»презентация»>1212 — множимое
3″ role=»презентация» >33 — множитель
36″ role=»presentation»>3636 — произведение
Слово «множимое» означает: число или количество, которое многократно прибавляется при умножении.
Слово «множитель» означает: количество повторных сложений количества.
Слово «произведение» означает: результат умножения.
сводка
Умножение — Первые принципы : Рассматриваются два числа, каждое из которых представляет счет или измерение. Одна из сумм повторяется количество раз, заданное второй суммой, чтобы сформировать результат, представляющий общую сумму из такого повторения.
например: 12×3=36″ role=»presentation»>12×3=3612×3=36
12″ role=»presentation»>1212 — множимое
3″ role=» презентация»>33 — это множитель
36″ role=»презентация»>3636 — это произведение
Контур
Схема материала для изучения целых чисел выглядит следующим образом:
Примечание: нажмите здесь для подробного описания целых чисел
• Введение
→ Числа
→ Большие числа
→ Расширенная форма
→ Номиналы и разряды
→ Приближение и оценка
• Сравнение
→ Сравнение двух чисел
→ Числовая строка
→ Предшественник и преемник
→ Самый большой и самый маленький
→ По возрастанию и по убыванию
• Сложение Вычитание
→ Дополнение: Первые принципы
→ Дополнение: упрощенная процедура
→ Вычитание: первые принципы
→ Вычитание: упрощенная процедура
• Деление умножения
→ Умножение: первые принципы
→ Умножение: упрощенная процедура
→ Раздел: Первые принципы
→ Отдел: упрощенная процедура
• Числовое выражение
→ Знакомство с числовыми выражениями
→ Приоритет
→ Последовательность
→ Кронштейны
Порядок, в котором Excel выполняет операции в формулах
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно. .. Меньше
В некоторых случаях порядок, в котором выполняются вычисления, может повлиять на возвращаемое значение формулы, поэтому важно понимать, как определяется порядок и как можно изменить порядок, чтобы получить нужные результаты.
Порядок расчета
Формулы вычисляют значения в определенном порядке. Формула в Excel всегда начинается со знака равенства ( = ). Excel интерпретирует символы, следующие за знаком равенства, как формулу. После знака равенства следуют вычисляемые элементы (операнды), такие как константы или ссылки на ячейки. Они разделены операторами вычисления. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет оператора в формулах Excel
При объединении нескольких операторов в одну формулу Excel выполняет операции в порядке, указанном в следующей таблице. Если формула содержит операторы с одинаковым приоритетом, например, если формула содержит оператор умножения и деления, Excel вычисляет операторы слева направо.
9
Оператор
Описание
: (двоеточие)
(один пробел)
, (запятая)
Эталонные операторы
–
Отрицание (как в –1)
Возведение в степень
* и /
Умножение и деление
+ и –
Сложение и вычитание
и
Соединяет две строки текста (объединение)
=
< >
<=
>=
<>
Сравнение
org/ListItem»>
Использование скобок в формулах Excel
Чтобы изменить порядок вычисления, заключите в круглые скобки ту часть формулы, которая будет вычисляться первой. Например, следующая формула дает 11, потому что Excel выполняет умножение перед сложением. Формула умножает 2 на 3, а затем добавляет к результату 5.
=5+2*3
Напротив, если вы используете круглые скобки для изменения синтаксиса, Excel складывает 5 и 2 вместе, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В следующем примере круглые скобки, заключающие первую часть формулы, заставляют Excel сначала вычислить B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Откройте для себя происхождение деления и умножения
В сегодняшней статье мы объясним происхождение математических символов деления и умножения.
Символ разделения:

Существует множество способов обозначения деления, и мы собираемся объяснить происхождение некоторых наиболее часто используемых и наиболее известных символов.
Горизонтальная черта дробей, введенная арабами, была впервые использована в Европе математиком Фибоначчи в тринадцатом веке, хотя ее использование не получило распространения до шестнадцатого века.
Наклонная черта, вариант горизонтальной, была введена Де Морганом в 1845 году. Это был типографский ресурс в печатных книгах, чтобы можно было писать дробь одной строкой. Символ, который сегодня широко используется для обозначения деления:
. Еще одним из знаков была скобка, хотя в настоящее время она мало используется. Чтобы выразить 21, разделенное на 3, мы напишем 21) 3 и поместим результат деления справа после еще одной скобки: 21) 3 (7, 9).0083
Этот знак встречается в произведении Arithmetica integra (1544) немецкого математика Михаэля Штифеля.
Этот же математик также использовал заглавные буквы M и D для обозначения умножения и деления в своей работе Deutsche Arithmetica (1545). Другие авторы также использовали D, в том числе использование в качестве перевернутой D, например, французы, Ж. Э. Галлимар (1685-1771), и другие авторы, упавшие d, такие как португальцы, Ж. А. да Кухна (1744-1787).
(1659). Этот знак деления очень нагляден, вплоть до того, что черта дроби является общей нормой.
Этот символ не имел большого успеха ни в Швейцарии, ни в Европе. Впрочем, так было и в Великобритании, и в США. В частности, этот символ до сих пор используется в калькуляторах для деления.
Немецкий математик Готфрид В. Лейбниц ввел две точки ( : ), и в настоящее время это наиболее широко используемый символ. Согласно Лейбницу, одно из преимуществ использования этого символа состоит в том, что деление может вестись вдоль той же линии и сохраняет связь деления с умножением, для чего Лейбниц использовал точку.
Что касается гномона или угла, который мы используем для разделения факторов деления (делимое, делитель и частное), информации немного.
Но Бойер в своей History of Mathematics , стр. 282, говорит: «Арабы, а через них позже и европейцы, переняли большую часть своих арифметических ухищрений от индусов, и поэтому весьма вероятно, что метод «длинное деление», известное как «метод галеры» по своему сходству с кораблем с развернутыми парусами, также происходит из Индии». Судя по всему, в «методе галеры» использовался угол, аналогичный используемому в настоящее время.
Символ умножения:
Во времена вавилонян использовали идеограмму: «а-ду». В манускрипте Бахшиили , старейшем манускрипте по индийской математике, они поставили рядом один множитель и ничего больше. Индийский математик Бхаскара Ачария (1114–1185) использовал слово «бхавита» или «бха» сразу после факторов.
Другие математики использовали букву М для умножения и букву D для деления, как мы уже говорили ранее.
В старые времена арифметики многие алгоритмы использовали крест Сан-Андрес для решения продуктов деления и умножения и пропорций. Возможно, по этой причине в 1631 году Утред выбрал этот крест как символ умножения.
Он получил широкое признание, за исключением математиков Готфрида В. Лейбница и Исаака Ньютона, которые не чувствовали себя полностью комфортно с этим символом. Лейбниц в 1698 году в одном из своих писем к математику Иоганну Бернулли пишет: «Мне не нравится символ × как символ умножения, так как его можно принять за х; … Я часто просто связываю две величины точкой, а умножение обозначаю RS · PQ».
По этой причине Лейбниц ввел точку как символ умножения.
Были и другие символы для умножения. Например, швейцарский математик Иоганн Ран (1622-1676) использовал звездочку * в своей работе Teutsche Algebra (1659). А также Лейбниц, который ранее использовал упавшую С открытой стороной вниз в своей Dissertatio комбинаторного искусства (1666).
Я надеюсь, что этот пост о делении и умножении и символах, которые мы используем для их выражения, был интересен.
Если вы хотите узнать больше о делении и умножении, зарегистрируйтесь в Smartick и попробуйте его бесплатно.
Подробнее:
Автор
Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения от Smartick (посмотреть все)
2.4: Значимые цифры в расчетах
Последнее обновление
Сохранить как PDF
Идентификатор страницы
47449
Цели обучения
Правильно использовать значащие цифры в арифметических операциях.
Округление
Прежде чем разбираться с особенностями правил определения значащих цифр в вычисляемом результате, нужно уметь правильно округлять числа. Чтобы округлить число до , сначала решите, сколько значащих цифр должно быть в числе. Как только вы это узнаете, округлите до указанного количества цифр, начиная слева. Если число непосредственно справа от последней значащей цифры меньше 5, оно отбрасывается, а значение последней значащей цифры остается прежним. Если число непосредственно справа от последней значащей цифры больше или равно 5, последняя значащая цифра увеличивается на 1.
Рассмотрим измерение $207,518 \: \text{m}$. Прямо сейчас измерение содержит шесть значащих цифр. Как бы мы последовательно округляли его до все меньшего и меньшего числа значащих цифр? Следуйте процессу, указанному в таблице $\PageIndex{1}$.
Количество значащих цифр Округленное значение Рассуждение
Таблица $\PageIndex{1}$: Примеры округления
6 207,518 Все цифры значащие
5 207,52 8 раундов от 1 до 2
4 207,5 2 выпадает
3 208 5 раундов от 7 до 8
2 210 8 заменяется на 0 и округляет 0 до 1
1 200 1 заменяется на 0
Обратите внимание, что чем больше округление сделано, тем менее надежна цифра. Приблизительного значения может быть достаточно для некоторых целей, но научная работа требует гораздо более высокого уровня детализации.
При математических операциях с числами важно помнить о значащих цифрах. Например, деление 125 на 307 на калькуляторе дает 0,4071661238… с бесконечным числом цифр. Но имеют ли цифры в этом ответе какое-либо практическое значение, особенно когда вы начинаете с чисел, каждое из которых имеет только три значащих цифры? При выполнении математических операций существует два правила ограничения количества значащих цифр в ответе: одно правило для сложения и вычитания, а другое правило для умножения и деления.
В операциях со значащими цифрами ответ сообщается таким образом, чтобы он отражал надежность наименее точной операции. Ответ не более точен, чем наименее точное число, использованное для получения ответа.
Умножение и деление
Для умножения или деления правило состоит в том, чтобы подсчитать количество значащих цифр в каждом умножаемом или делимом числе, а затем ограничить значащие цифры в ответе до наименьшего количества. Например:
Окончательный ответ, ограниченный четырьмя значащими цифрами, равен 4094. Первая отброшенная цифра — 1, поэтому мы не округляем.
Научное обозначение обеспечивает способ передачи значащих цифр без двусмысленности. Вы просто включаете все значащие цифры в начальное число. Например, число 450 имеет две значащие цифры и будет записано в научной записи как 4,5 × 10 ² , тогда как число 450,0 имеет четыре значащих цифры и будет записано как 4,500 × 10 9 .0113 2 . В экспоненциальном представлении все значащие цифры указаны явно.
Пример $\PageIndex{1}$
Напишите ответ для каждого выражения в экспоненциальном представлении с соответствующим количеством значащих цифр.
23,096 × 90,300
125 × 9000
Решение
a
Таблица с двумя столбцами и 1 строкой. Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение. Второй столбец помечен как «Ответ», а под ним в строке находится ответ. 93\)
b
Таблица с двумя столбцами и 1 строкой. Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
Пояснение Ответить
Калькулятор дает ответ 1125, но мы ограничиваем его тремя значащими цифрами. 93\)
Сложение и вычитание
Как обрабатываются значащие числа в вычислениях? Это зависит от того, какой тип расчета выполняется. Если вычисление представляет собой сложение или вычитание, правило следующее: ограничьте сообщаемый ответ крайним правым столбцом, в котором все числа имеют общие значащие цифры. Например, если вы должны сложить 1,2 и 4,71, мы заметим, что первое число останавливает свои значащие цифры в столбце десятых, а второе число останавливает свои значащие цифры в столбце сотых. Поэтому мы ограничиваем наш ответ десятым столбцом.
Мы опускаем последнюю цифру — 1 — потому что она не имеет значения для окончательного ответа.
Отбрасывание позиций в суммах и разностях поднимает тему округления. Несмотря на некоторые соглашения, в этом тексте мы примем следующее правило: окончательный ответ следует округлить в большую сторону, если первая пропущенная цифра 5 или больше, и округлить в меньшую сторону, если первая пропущенная цифра меньше 5.
Пример $\PageIndex{2}$
13,77 + 908.226
1027 + 611 + 363,06
Решение
a
Таблица с двумя столбцами и 1 строкой. Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
Пояснение Ответить
Ответ калькулятора: 92\)
b
Таблица с двумя столбцами и 1 строкой. Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
Пояснение Ответить
Калькулятор дает в качестве ответа 2001,06, но поскольку 611 и 1027 имеют крайнюю правую значащую цифру в разряде единиц, окончательный ответ должен быть ограничен разрядом единиц. 90\)
Помните, что калькуляторы не понимают значащие цифры. Вы тот, кто должен применить правила значащих цифр к результату вашего калькулятора.
Вычисления, связанные с умножением/делением и сложением/вычитанием
На практике химики обычно работают с калькулятором и переносят все цифры в последующих вычислениях. Однако при работе на бумаге мы часто хотим свести к минимуму количество цифр, которые нам приходится записывать. Поскольку последовательное округление может усугубить неточности, промежуточное округление должно выполняться правильно. При работе на бумаге всегда округляйте промежуточный результат, чтобы сохранить хотя бы на одну цифру больше, чем можно оправдать, и переносите это число на следующий шаг в расчетах. Затем окончательный ответ округляется до правильного количества значащих цифр в самом конце.
Видео $\PageIndex{1}$: Значительные цифры в смешанных операциях (https://www.youtube.com/watch?v=yBntMndXQWA). Видео $\PageIndex{2}$: https://www.youtube.com/watch?v=__csP0NtlGI
В рабочих примерах в этом тексте мы часто будем показывать результаты промежуточных шагов расчета. При этом мы покажем результаты только для правильного количества значащих цифр, разрешенных для этого шага, фактически рассматривая каждый шаг как отдельный расчет. Эта процедура предназначена для закрепления правил определения количества значащих цифр, но в некоторых случаях она может давать окончательный ответ, отличающийся последней цифрой от полученного с помощью калькулятора, где все цифры переносятся на последний шаг.
Пример $\PageIndex{3}$
2(1,008 г) + 15,99 г
137,3 с + 2(35,45 с)
$ {118,7 г\более 2} — 35,5 г$
Раствор
а.
Таблица с двумя столбцами и 1 строкой. Первый столбец слева помечен как «Объяснение», а под ним в строке приведено объяснение умножения в первую очередь. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
Пояснение Ответить
2 (1,008 г) + 15,99 г =
Сначала выполнить умножение.
2 (1,008 г 4 знака инжира ) = 2,01 6 г 4 знака инжира
Число с наименьшим количеством значащих цифр равно 1,008 г; число 2 является точным числом и поэтому имеет бесконечное количество значащих цифр .
Затем выполните сложение.
2,01 6 г тысячный разряд + 15,9 9 г сотый разряд (наименее точный) = 18,006 г
91,405 Округлить окончательный ответ
Округлить окончательный ответ до сотых, так как 15.99 имеет крайнюю правую значащую цифру в сотых (наименее точную).
18,01 г (округление)
б.
Таблица с двумя столбцами и одной строкой. Первый столбец слева помечен как «Объяснение», а под ним в строке приведено объяснение умножения в первую очередь. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
Пояснение Ответить
137,3 с + 2(35,45 с) =
Сначала выполнить умножение.
2(35,45 с 4 знака инжир ) = 70,90 с 4 знака инжир
Число с наименьшим количеством значащих цифр равно 35,45; число 2 является точным числом и поэтому имеет бесконечное количество значащих цифр.
Затем выполните сложение.
137,3 с десятый разряд (наименее точный) + 70,90 с сотый разряд = 208,20 с
Округлите окончательный ответ.
Округлите окончательный ответ до десятого места на основе 137,3 с.
208,2 с
в.
Таблица с двумя столбцами и 1 строкой. Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение первого деления. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
Пояснение Ответить
$ {118,7 г \свыше 2} — 35,5 г$ =
Сначала выполнить деление.
$ {118,7 г \более 2} $ 4 знака инжира = 59,35 г 4 знака инжира
Число с наименьшим количеством значащих цифр равно 118,7 г; число 2 является точным числом и поэтому имеет бесконечное количество значащих цифр.
Далее выполнить вычитание.
59,35 г разряд сотых − 35,5 г разряд десятых (наименее точный) = 23,85 г
Округлите окончательный ответ.
Округлите окончательный ответ до десятого места из расчета 35,5 г.
23,9 г (округление)
Упражнение $\PageIndex{3}$
Выполните вычисления и запишите свои ответы, используя правильное количество значащих цифр.
5(1,008 с) — 10,66 с
99,0 см+ 2(5,56 см)
Ответить на
-5,62 с
Ответ б
110,2 см
Сводка
Округление
Если отбрасываемое число больше или равно 5, увеличьте число слева от него на 1 (например, 2,9699, округленное до трех значащих цифр, равно 2,97).
Если отбрасываемое число меньше 5, изменений нет (например, 4,00443, округленное до четырех значащих цифр, равно 4,004).
Правило умножения и деления состоит в том, что в окончательном ответе должно быть столько значащих цифр, сколько в числе с наименьшим количеством значащих цифр.
Правило сложения и вычитания состоит в том, что ответу дается то же количество знаков после запятой, что и члену с наименьшим числом знаков после запятой.
ПОД ЛИЦЕНЗИЕЙ
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или Страница
Лицензия
СК-12
Показать страницу TOC
№ на стр.
Метки
автор @ Генри Агнью
автор@Мариса Альвиар-Агнью
округление
Значащие цифры
источник@https://www.

admin
Навигация по записям
Поваренок разобрать по составу: Страница не найдена
Детские рыбные котлеты рецепт: 👌 Рыбные котлеты для детей, рецепты с фото
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Рубрики
Воспитывать
Дети
Подросток
Правильно
Разное
Рекомендации
Советы
2024 © Все права защищены.

Семейные советы
Как правильно ?
Дети
Воспитание

Оператор	Описание
: (двоеточие) (один пробел) , (запятая)	Эталонные операторы
–	Отрицание (как в –1)
Возведение в степень
* и /	Умножение и деление
+ и –	Сложение и вычитание
и	Соединяет две строки текста (объединение)
= < > <= >= <>	Сравнение

Количество значащих цифр	Округленное значение	Рассуждение
6	207,518	Все цифры значащие
5	207,52	8 раундов от 1 до 2
4	207,5	2 выпадает
3	208	5 раундов от 7 до 8
2	210	8 заменяется на 0 и округляет 0 до 1
1	200	1 заменяется на 0

Порядок выполнения действий в выражениях без скобок и со скобками — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Порядок выполнения действий в выражениях без скобок и со скобками — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Сначала сложение или умножение

Сложение и вычитание

Умножение

Что сначала — умножение или сложение?

Деление

Скобки

«Вишенка на торте»

«Совсем вишня»

Порядок вычисления простых выражений

Что такое действия первой и второй ступени

Порядок вычислений в выражениях со скобками

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Сайт для детей и их родителей

Порядок выполнения математических действий

«Порядок действий в выражениях без скобок, имеющих действия разных ступеней»

Зубодробительная задачка с очень простой математикой

Приоритет — Python

Задание

Как использовать PEMDAS и решить с порядком операций (примеры)

Каков порядок работы?

Как запомнить PEMDAS

Правило PEMDAS — Что такое Правило PEMDAS? Определение, примеры

Введение в PEMDAS

Что такое PEMDAS?

BODMAS против PEMDAS

Когда использовать PEMDAS?

Распространенные ошибки при использовании правила PEMDAS в математике

Часто задаваемые вопросы о PEMDAS

Как работает правило Пемдаса?

Что означает PEMDAS?

Как делать Пемдас с дробями?

Что означает буква P в Пемдасе?

Вы сначала умножаете или делите в PEMDAS?

Когда мы применяем правило PEMDAS?

Какое правило для PEMDAS?

Что такое BODMAS, BIDMAS и PEMDAS?

Что такое аббревиатура?

Что обозначают буквы в BODMAS, BIDMAS и PEMDAS?

Что такое ордера, индексы и экспоненты?

Что такое математические операции?

Каков правильный порядок действий в математике?

Используются ли в экзамене 11-Plus BODMAS или BIDMAS?

Каковы правила BODMAS или BIDMAS?

Математика 1010 онлайн

Последовательность операций

Поддержка правил PEMDAS Страница

Пример правила PEMDAS

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Пример 6 (сложнее)

Пример 7 (сложнее)

Порядок операций

Реальный пример PEMDAS

Еще примеры порядка работы

Порядок проведения викторины. Посмотрите, как вы понимаете этот урок.

Рабочие листы для операций

Самые популярные рабочие листы для порядка операций на этой неделе

Порядок операций с листами с целыми числами

Порядок операций с целыми числами

Порядок операций с целыми числами

Порядок операций с целыми числами

Порядок операций с целыми числами

Порядок операций с целыми листами

Порядок операций с целыми числами

Порядок операций с целыми числами и

Порядок действий с таблицами дробей

Порядок операций с

Порядок операций с десятичными знаками Рабочие листы

Узнаем что сначала — сложение или умножение: правила, порядок выполнения действия и рекомендации

Сложение и вычитание

Умножение

Что сначала — умножение или сложение?

Деление

Скобки

«Вишенка на торте»