Как правильно решить пример без скобок?

Как правильно решить пример без скобок?

Запомните правило:

1. Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. …
2. Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.

Какое первое действие в примере без скобок?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Какие первые действия в математике?

Сначала умножение и деление, затем сложение и вычитание В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Что сначала делается сложение или умножение?

При умножении двух разных единиц измерения получается новая единица измерения, при сложении единицы измерения не меняются. При умножении мы получаем эту самую новую единицу измерения. Если она такая же, как и у первого слагаемого, тогда мы можем выполнить сложение. Это просто правило.

Что это вычитание?

Вычитание — операция обратная сложению. Вычитание возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).

Что такое сложение и вычитание?

Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.

Как решать дроби Сложение и вычитание?

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.

Как называется сложение в математике?

Сложение чисел Результат сложения двух или более чисел называется суммой, а сами числа — слагаемыми. … Складываем числа, аналогично положительным, записываем результат со знаком «минус». Например, (-6)+(-5,3)=-(6+5,3)=-11,3. От перестановки мест слагаемых сумма не изменяется a+b=b+a.

Как называется в математике плюс?

Знаки «плюс» и «минус» (+ и −) — математические символы, используемые для обозначения операций сложения и вычитания, а также положительных и отрицательных величин.

Как называется математическое действие Если стоит знак плюс?

В стране математики живут не только цифры и числа, но и разные математические знаки. Сегодня вы с Лисёнком познакомитесь с ними. … В математике это действие называется сложением и ставится знак плюс.

Как называется действие с минусом?

Вычитание – действие обратное сложению. Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.

Как называется при умножении?

Так же, как и при сложении и вычитании, числа при умножении имеют свое название. Первое число при умножении называется множитель. Второе число при умножении тоже называется множитель. Результат умножения называют произведение.

Что такое результат умножения?

Умноже́ние — одна из основных математических операций над двумя аргументами (множителями или сомножителями). Иногда первый аргумент называют множимым, а второй множителем; результат умножения двух аргументов называется их произведением.

Как умножить два отрицательных числа?

Умножение отрицательных чисел Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство: (-а) * (-b) = a * b.

Как умножить натуральное число на отрицательное?

Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, −b данное равенство считается верным. (−а)⋅(−b)=a⋅b.

Урок для 3 класса по теме: «Порядок выполнения действий в выражениях без скобок и со скобками»

Тема урока: «Порядок выполнения действий в выражениях без скобок и со скобками»

Цель урока: создать условия для изучения правила порядка выполнения действий в составных выражениях без скобок и со скобками.

Задачи:

Образовательные:

— обеспечить усвоение правила порядка выполнения действий в составных выражениях со скобками и без скобок;

— продолжить работу над решением задач.

Развивающие:

— развивать вычислительные навыки, творческое мышление;

— развивать находчивость, сообразительность, логическое мышление, память, речь;

— развивать творческие способности учащихся;

— развивать интерес к математике как к науке.

Воспитательная:

—содействовать формированию культуры межличностных отношений.

Тип урока: комбинированный.

Форма проведения: урок

Оборудование:

— учебник;

— карточки;

— электронная презентация;

— кружки красного и зеленого цвета

— карточки с цифрами.

Ход урока:

1. Орг. момент (звучит песня «Дважды два четыре»). СЛАЙД№2

— Ребята, кто из вас любит математику? Почему вы её любите? Математику любят наши знакомые Миша и Маша, ученики 3 класса. Сегодня они как всегда с нами на уроке. О математике есть много мудрых мыслей. Их на уроке мы услышим неоднократно. Вот одно из них, прочитайте и объясните.

СЛАЙД №3 «Математику уже затем изучать нужно, что она ум в порядок приводит»

Михаил Васильевич Ломоносов, русский учёный, энциклопедист, поэт.

Так давайте приведем свой ум в порядок и продолжим изучать математику.

2. Устная работа.

1. Повторение табличных случаев умножения и деления. Работа в парах с использованием карточек.

— Как вы считаете, какое задание, выполняемое нами на каждом уроке, приводит наш ум в порядок? (повторение таблицы умножения и деления)

— Проверим, чья пара первая справится с этим заданием. (выполняют 3 минуты) Проверка: Называйте ответы по порядку, и вы увидите сюрприз!

Ключ на СЛАЙДЕ № 4. МОЛОДЦЫ, ученики третьего класса!

Поднимите руки те, кто сделал без ошибок? Вы заработали 5 баллов

1-2 ошибки? Вы заработали 4 балла

3-5 ошибок? Вы заработали 3 балла

6 -8 ошибок? Вы заработали 2 балла

9 и более( вы заработали 1 балл

Запишите баллы в оценочный лист.

Прекрасное начало урока! Рада, что вы все справились с заданием!

2. Игра «Да или нет»

— Поиграем в игру «Да или нет». Если вы согласны с моим высказыванием, то показываете «Да» (большой палец вверх), если не согласны – «Нет» (большой палец вниз). Договорились?

— При умножении любого числа на 1 получается 1 (да).

— При делении любого числа на 1, получается 1 (нет).

— Чтобы разделить на 10, достаточно дописать 0 (нет, отбросить).

— Умножать на 0 нельзя (нет, можно).

— Чтобы найти делимое, нужно значение частного умножить на делитель (да).

— Чтобы найти неизвестный множитель, нужно значение произведения умножить на известный множитель (нет, разделить).

— В выражениях без скобок все действия выполняются по порядку слева направо (нет, сначала умножение и деление, потом вычитание и сложение).

В выражениях со скобками, вначале выполняются действия в скобках (да)

— С каждым уроком у вас получается всё лучше! Просто замечательно!

3. Актуализация знаний.

Слайд № 5 Прочитайте и объясните выражение: «Чтобы переварить знания, надо поглощать их с аппетитом.» (А. Франц)

— Вы готовы поглощать их с аппетитом? Тогда внимание! На прошлых уроках мы изучали порядок выполнения действий.

— Посмотрите, пожалуйста, внимательно на слайд№ 6. Выполните задания. Эти задания помогут нам определить тему нашего урока.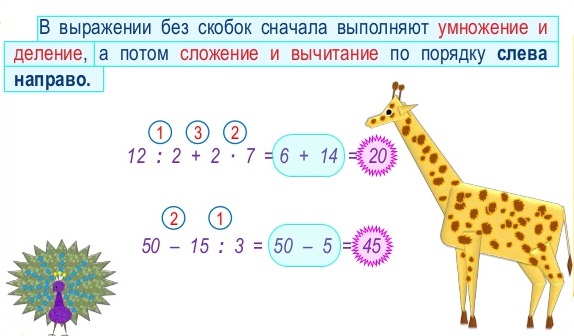 Объясните, почему допущены ошибки?

— Проговорите правило, которое подходит к данным выражениям: Слайд № 7:

• В выражениях без скобок, содержащих только сложение и вычитание – действия I ступени, или умножение и вычитание – действия II ступени, действия выполняются в том порядке, как они записаны : слева направо.

• В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.

• В выражениях со скобками сначала вычисляют значения выражений в скобках. Затем по порядку слева направо выполняется умножение или деление.

— Озвучьте тему нашего урока. (Закрепление правил «Порядок выполнения действий в выражениях со скобками и без скобок») Слайд № 8

— Просто умницы, ловко справились, умело.

VI. Целеполагание.

— Ребята, как вы считаете, достаточно ли хорошо отработана нами тема «Порядок выполнения действий »?

— На что нам сегодня необходимо обратить внимание? Над чем поработать? (Упражняться в нахождении значений выражений, содержащий действия разных ступеней со скобками и без них. Познакомиться с видами выражений, в которых можно допустить ошибки)

V. Постановка и разрешение проблемной ситуации.

— Ребята, послушайте, пожалуйста, что говорил французский математик Д.Пойя: «Лучший способ изучить что-либо — это открыть самому». Слайд № 9

Вы готовы к открытиям?

СЛАЙД № 10

— Даны выражения, посмотрите, как справились с заданием Маша и Миша.

— Кто выполнил задание верно: Маша или Миша? (ответы детей)

— Какие ошибки допущены Машей? Как вы думаете, почему Маша допустила ошибку?

— Я знала, что это задание вам было под силу! Слайд № 11. Великий Песталоцци сказал: «Счет и вычисления — основа порядка в голове.» Давайте, потренируемся, чтобы не допускать ошибок, подобно Маше.

VI. Закрепление:

1. Самостоятельная работа С. 27, № 1

2. Проверка с объяснением. Оценка учителем — 3 учеников, остальные –самооценка. Занесите оценку в оценочный лист по следующему критерию: все выражения решены верно – 3 балла, 2 выражения верно – 2 балла, 1 выражение верно – 1 балл

3. Я горжусь вами, что вам удалось выполнить задание почти без ошибок.

4. А теперь попробуем усложнить задачу: составим выражения по схеме, определим порядок действий и вычислим их значение: с. 27, № 2. Сначала выполним вместе, а потом самостоятельно. (Работа у доски и в тетрадях. Предложить детям, кто понял, как делать, выполнить самостоятельно)

5. Оценивание: Кто работал у доски –оценивает учитель, сам-но, по критерию, как в задании по таблице умножения.

6. — Ребята, у вас получилось лучше, чем я могла бы подумать!

VI. Решение задачи с. 27, № 3

Слайд № 12. « Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.» (Д.Пойа)

1. Составление задач.

2. Самостоятельно запишите решение задач и ответ. Каждому ряду по одной задаче.

3. Проверка и оценивание. За правильное решение и ответ – 2 балла.

Неверно – 0 баллов

4. Я рада, что вы справились.

VII. Итог урока.

— Выполнили ли мы поставленные цели урока? Что планировали? Всё ли у нас получилось? Над чем необходимо поработать?

XIII. Оценивание и рефлексия.

1. Давайте определим, насколько успешно вы работали. Оцениваем критерий: активность.(Учитель объявляет баллы за активность: от 5 до3). Подсчитайте количество баллов: 45 баллов – «5», 34 балла — «4», 22 балла – «3».Поднимите карточки с цифрами.

2. Кто из вас стал увереннее находить значения выражений на порядок действий, поднимите вверх зеленые кружки, кому еще надо потренироваться, чтобы усвоить тему, поднимите вверх красные кружки.

— Вы сегодня просто молодцы, много сделали. Работать с вами просто радость!

XIV. Домашнее задание.

— Что необходимо закрепить дома? (порядок выполнения действий в сложных выражениях) с. 27, под чертой.

Хочу закончить наш урок словами М.И. Калинина

Слайд № 13. «Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.»

Спасибо за урок. А что говорят нам Миша и Маша?

Урок окончен.

Ссылка на источники:

http://festival.1september.ru/articles/633426/

http://www.sch943.edusite.ru/p285aa1.html

Источник шаблона презентации:

Ранько Елена Алексеевна

учитель начальных классов

МАОУ лицей №21

г. Иваново

Сайт: http://elenaranko.ucoz.ru/

5

Урок математики в 3 классе

Что такое правило Бодмаса — порядок операций с примерами

В предметах, ориентированных на логику, таких как математика, порядок операций представляет собой набор стандартных правил, отражающих соглашение о том, какой процесс следует выполнить первым для вычисления заданного числового выражения.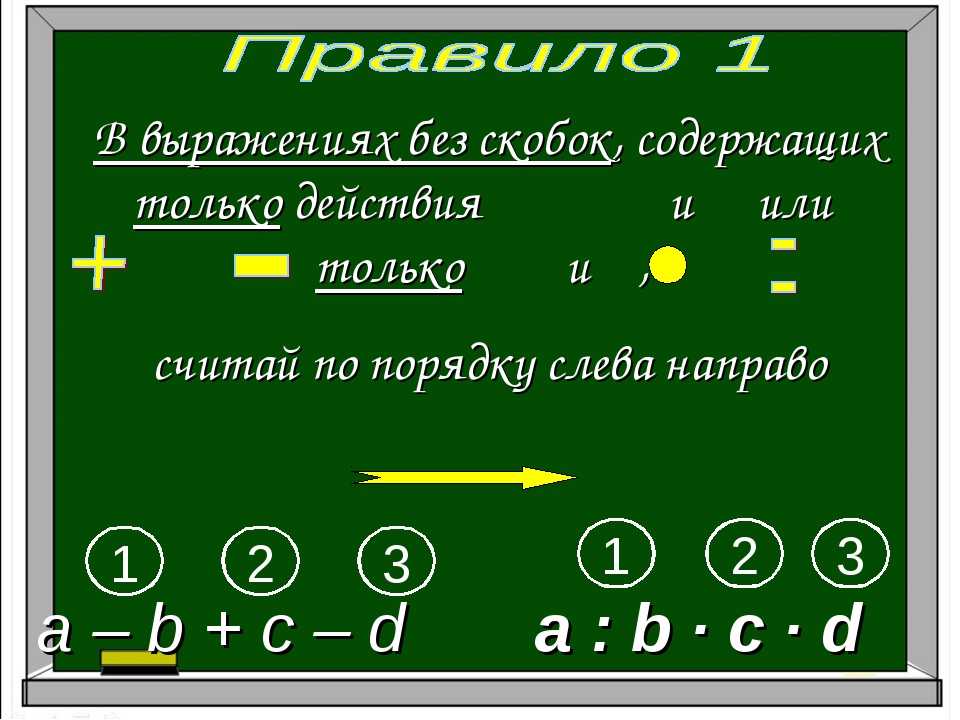 С базовым суммированием, которое состоит только из двух чисел и одной единственной операции или знака, легко вычислить результат. Либо вы выполняете сложение, вычитание, умножение или деление.

 

BODMAS можно определить как набор операций, которые должны быть выполнены в первую очередь, и соглашений, которым необходимо следовать. В противном случае это приведет к неправильному ответу. Поэтому очень важно практиковать и помнить БОДМАС и следовать ему всякий раз, когда это требуется.

Если вы будете считать в неправильном порядке, вы получите неверный ответ. Поэтому изучайте порядок систематически. Сначала идет скобка, потом степени, деление, умножение, сложение, а затем вычитание.

 

Что такое БОДМАС?

БОДМАС — это набор правил или приказ выполнить арифметическое выражение, чтобы упростить вычисление. Математика — это логика, и определенные правила обязательны для соблюдения. BODMAS — один из них, который, если не следовать всему ответу, может пойти не так и привести к ненужной потере оценок.

 

BODMAS можно дополнительно определить как стандартные правила для упрощения выражения, содержащего несколько операторов.

 

Атематические выражения в основном состоят из двух компонентов: чисел и операторов:

• числа

Числа — это значения для выполнения расчетов и представления величин. Есть натуральные числа, целые числа, целые числа, рациональные числа, иррациональные числа, действительные числа, комплексные числа.

• Операторы

Операторы — это комбинация двух символов, образующих выражение или уравнение. Наиболее распространенными являются сложение, умножение. Деление и вычитание. Любое выражение, имеющее только один оператор, решается легко, но когда есть несколько операторов, это становится немного сложнее.

 

Согласно BODMAS, когда нам нужно решить выражение, мы должны сначала решить выражение со скобками, а затем с показателями степени, делением, умножением, сложением и вычитанием. При решении уравнений следует помнить порядок. Если вы просто не будете следовать этому правилу, вы получите неправильный ответ.

Например: 

См. уравнение (3+4)5+6-2

Согласно BODMAS: 

• Первым шагом является добавление числа в скобках, которое равно 3+4=7.

• Следующим шагом является умножение 7 на 5=7×5=35

• Следующим шагом является прибавление 35+6=41 Всякий раз, когда уравнение связано со скобками, необходимо соблюдать сложение и вычитание BODMAS. Эта аббревиатура создана для того, чтобы ее было легче запомнить.

  Основная проблема математики

  Образование

  by Concetta Beretta

  8 месяцев назад

  Каждый день возникают ситуации, в которых математика имеет решающее значение. К сожалению, это не всегда так просто, как сложение и вычитание, особенно при выполнении нескольких математических операций над одним числом в последовательности. Для простой арифметики порядок операций неважен; однако в более сложных задачах часто делаются ошибки из-за неправильного порядка выполнения операций. К счастью, существуют правила, определяющие, какое математическое действие следует выполнять первым в той или иной ситуации. Они известны как правила скобок, порядков, деления/умножения и сложения/вычитания (BODMAS).

  В математике порядок операций следующий: правило БОДМАС (скобки, порядок, деление/умножение, сложение/вычитание). Bodmas используется для решения арифметических задач.

  Согласно правилу, умножение и деление предшествуют сложению и вычитанию.

  Это означает, что вы не можете просто складывать или вычитать вещи, если они уже не были умножены или разделены.
  • Операторы в нижней скобке имеют приоритет над операторами за ее пределами. 5+3*2 — один из примеров. Поскольку 2 * 3 = 6, оно должно вычисляться до 11, что равно пяти плюс три умножить на два, поэтому 3 имеет приоритет над * при выполнении вычислений внутри скобок.
  • Однако, если в скобках есть деление, оно будет выполнено первым, потому что деление имеет приоритет над умножением. 5+3/2 должно равняться 4, потому что 5/2=2,5 и 3/2=1,5.
  • Когда имеется более одного набора скобок, числа внутри них рассчитываются по очереди, поэтому вычисления можно выполнять слева направо, убедившись, что все сделано правильно, прежде чем двигаться дальше.
  • В математике или алгебре, независимо от того, что стоит после знака равенства (=), не нужно следовать BODMAS, потому что = имеет приоритет, а равенства всегда вычисляются первыми.
  • Это верно, даже если за знаком равенства следует символ деления (/). Это просто означает, что все, что находится по одну сторону =, должно быть равно тому, что находится по другую сторону, поэтому 1/2=4 будет 1/(2*4)=1/8.
  • То же самое верно для (+ и -) символов сложения и вычитания. Если a = имеет более одной стороны, оно вычисляется слева направо, как скобки. 24 станет 5-(-1)=6, потому что числа справа вычисляются первыми, а все, что осталось, перемещается к знаку равенства после этого.
  • Скобки — еще одно применение BODMAS в математике и алгебре. Вычисления внутри скобок () можно выполнять в любом порядке, следуя BODMAS, чтобы получить ответ. Например, 3+2*3-1 превращается в (3+2)*3-(1), что равняется девяти, потому что * имеет приоритет над + и -, поэтому 2 умножается на 3 перед прибавлением к единице.
  • Его также можно использовать для таких неравенств, как >, >= и =. Все, что вам нужно помнить с ними, это то, что больше, чем >, имеет приоритет над тем, что имеет приоритет над >=, потому что это тот же символ, но написанный сбоку.