«порядок выполнения действий в выражениях со скобками и без скобок»

«ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ
В ВЫРАЖЕНИЯХ СО СКОБКАМИ И БЕЗ СКОБОК»

(с. 44–45)

Цели: познакомить с правилами о порядке выполнения арифметических действий в выражениях со скобками и без скобок; научить применять эти правила при нахождении значений выражений; закреплять навыки решения задач и уравнений, а также знания о геометрических фигурах.

Ход урока

I. Организационный момент.

II. Устный счёт.

1. Решите «круговые примеры»:

45 – 8 8 + 6 17 – 9

14 + 30 44 + 1 37 – 20

2. Арифметический диктант:

8 ·3 2 · 9 6 · 3

2 · 7 24 : 3 27 : 9

12 : 2 14 : 7 12 : 3

III. Работа над новым материалом.

Ученики рассматривают выражения, данные в учебнике на с. 44 вверху, называют, какие действия они содержат. Затем дети объясняют, почему действия в парах примеров одинаковые, а результаты получились разные.

Учащиеся. Действия в примерах были одинаковые, но выполнялись они в разном порядке. Порядок действий зависел от скобок.

После этого учащиеся читают вводный текст и правило в красной рамочке.

Выполнять действия в следующем порядке:

1) действия, записанные в скобках;

2) умножение и деление;

3) сложение и вычитание.

Далее под руководством учителя дети объясняют порядок действий в выражениях (внизу):

Выражение 100 – 21 : 3 содержит вычитание и деление.

Значит, сначала надо выполнить деление, а затем вычитание.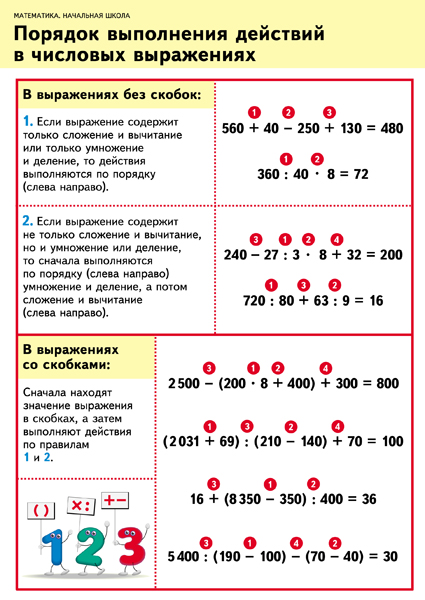

21 : 3 = 7, 100 – 7 = 93.

Выражение 60 + 9 · 3 содержит сложение и умножение.

Значит, сначала выполняем умножение, а потом сложение:

9 · 3 = 27, 27 + 60 = 87.

Выражение 30 + 6 · (13 – 9) содержит действия: сложение, умножение и вычитание. В нем есть скобки, значит, первым действием выполняем действие в скобках, затем умножение, а потом сложение.

13 – 9 = 4, 6 · 4 = 24, 30 + 24 = 54.

Выражение 18 : 2 – 2 · 3 + 12 : 3 содержит деление, вычитание, умножение и сложение. В нем нет скобок, значит, сначала выполняются деление и умножение слева направо, а затем вычитание и сложение по порядку слева направо.

Для закрепления учащимися под руководством учителя выполняется задание № 1 на с. 45. В каждом случае дети называют, какие действия содержит выражение, в каком порядке их надо выполнять, и вычисляют значение выражения. Запись выполняется по образцу учебника.

Ф и з к у л ь т м и н у т к а

Солнце глянуло в кроватку…

Раз, два, три, четыре, пять.

Все мы делаем зарядку,

Надо нам присесть и встать.

Руки вытянуть пошире,

Раз, два, три, четыре, пять.

Наклониться – три, четыре,

И на месте поскакать.

На носок, потом на пятку.

Все мы делаем зарядку.

IV. Работа над пройденным материалом.

1. Решение задач. Задания № 2 и № 4 дети решают самостоятельно с последующей проверкой.

Задание № 3 разобрать с комментированием. После записи условия проводится беседа.

Всего – 48 с.

Прочитала – 3 д. по 9 с.

Осталось – ?

Учитель. Задача простая или составная?

Учащиеся. Составная.

Учитель. Что надо еще найти, прежде чем ответить на главный вопрос задачи?

Учащиеся. Мы должны узнать, сколько страниц прочитала девочка за 3 дня.

Учитель. Как это можно найти?

Учащиеся. Надо 9 · 3.

Учитель. После этого можно узнать, сколько страниц ей осталось прочитать?

Учащиеся. Да. Надо из 48 вычесть полученный результат.

Далее дети оформляют решение и ответ сами.

1) 9 · 3 = 27 (с.) – прочитала

2) 48 – 27 = 21 (с.)

О т в е т: 21 страница осталась.

Аналогично учитель с учащимися разбирает задание № 5.

2. Решение уравнений. Перед выполнением задания № 7 дети должны вспомнить и рассказать правила, как найти неизвестные слагаемое, уменьшаемое, вычитаемое.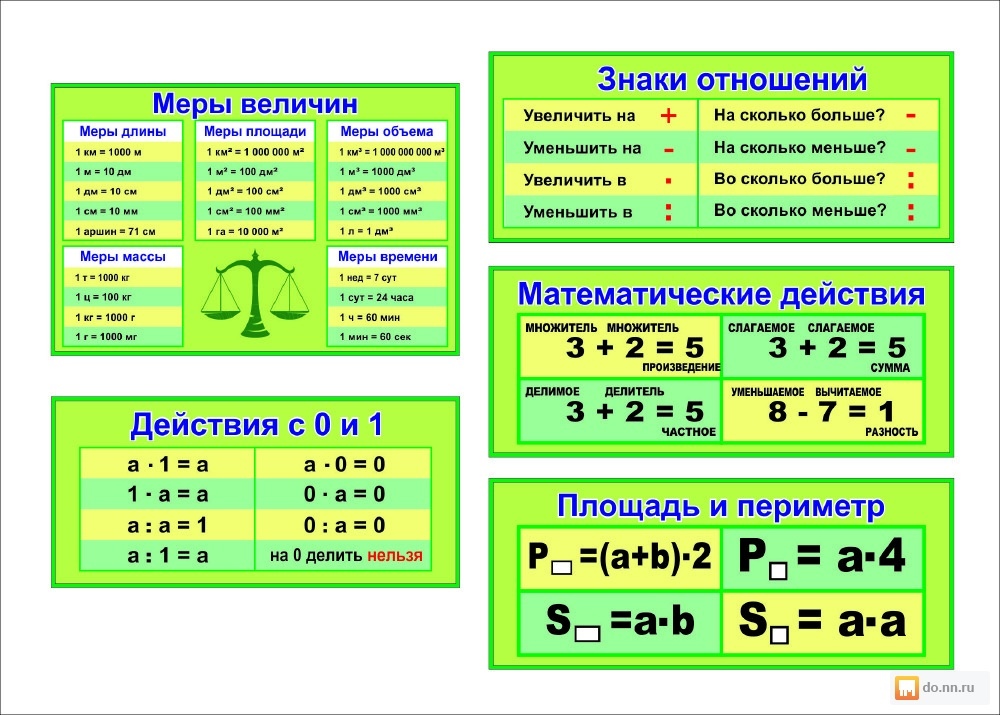

1) Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

2) Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

3) Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

После этого выписывают уравнения по заданию и самостоятельно решают.

3. Работа над геометрическим материалом.

Задание № 6 можно оформить как задачу в тетради. Для этого дети измеряют длину данных отрезков, перечерчивают их в тетрадь, выразив их длину в миллиметрах, вспоминают правило:

Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего вычесть меньшее число.

Выполняя задание № 8, дети должны выписать название треугольников: АВК, ВСД, ВДК, ЕОМ, РЕМ, МОТ.

Названия четырехугольников: АСДК, АВДК, ВСДК, РЕОТ, МЕОТ, РЕОМ.

V. Итоги урока.

Учитель. Ребята, что нового мы сегодня узнали на уроке?

Дети. Мы учились решать выражения со скобками и без скобок.

Учитель. Что повторяли сегодня?

Дети. Мы решали примеры и задачи, уравнения, чертили отрезки и выписывали названия треугольников и четырёхугольников.

Домашнее задание: с. 45, № 6.

Урок для 3 класса по теме: «Порядок выполнения действий в выражениях без скобок и со скобками»

Тема урока: «Порядок выполнения действий в выражениях без скобок и со скобками»

Цель урока: создать условия для изучения правила порядка выполнения действий в составных выражениях без скобок и со скобками.

Задачи:

Образовательные:

— обеспечить усвоение правила порядка выполнения действий в составных выражениях со скобками и без скобок;

— продолжить работу над решением задач.

Развивающие:

— развивать вычислительные навыки, творческое мышление;

— развивать находчивость, сообразительность, логическое мышление, память, речь;

— развивать творческие способности учащихся;

— развивать интерес к математике как к науке.

Воспитательная:

—содействовать формированию культуры межличностных отношений.

Тип урока: комбинированный.

Форма проведения: урок

Оборудование:

— учебник;

— карточки;

— электронная презентация;

— кружки красного и зеленого цвета

— карточки с цифрами.

Ход урока:

1. Орг. момент (звучит песня «Дважды два четыре»). СЛАЙД№2

— Ребята, кто из вас любит математику? Почему вы её любите? Математику любят наши знакомые Миша и Маша, ученики 3 класса. Сегодня они как всегда с нами на уроке. О математике есть много мудрых мыслей. Их на уроке мы услышим неоднократно. Вот одно из них, прочитайте и объясните.

СЛАЙД №3 «Математику уже затем изучать нужно, что она ум в порядок приводит»

Михаил Васильевич Ломоносов, русский учёный, энциклопедист, поэт.

Так давайте приведем свой ум в порядок и продолжим изучать математику.

2. Устная работа.

1. Повторение табличных случаев умножения и деления. Работа в парах с использованием карточек.

— Как вы считаете, какое задание, выполняемое нами на каждом уроке, приводит наш ум в порядок? (повторение таблицы умножения и деления)

— Проверим, чья пара первая справится с этим заданием. (выполняют 3 минуты) Проверка: Называйте ответы по порядку, и вы увидите сюрприз!

Ключ на СЛАЙДЕ № 4. МОЛОДЦЫ, ученики третьего класса!

Поднимите руки те, кто сделал без ошибок? Вы заработали 5 баллов

1-2 ошибки? Вы заработали 4 балла

3-5 ошибок? Вы заработали 3 балла

6 -8 ошибок? Вы заработали 2 балла

9 и более( вы заработали 1 балл

Запишите баллы в оценочный лист.

Прекрасное начало урока! Рада, что вы все справились с заданием!

2. Игра «Да или нет»

— Поиграем в игру «Да или нет». Если вы согласны с моим высказыванием, то показываете «Да» (большой палец вверх), если не согласны – «Нет» (большой палец вниз). Договорились?

— При умножении любого числа на 1 получается 1 (да).

— При делении любого числа на 1, получается 1 (нет).

— Чтобы разделить на 10, достаточно дописать 0 (нет, отбросить).

— Умножать на 0 нельзя (нет, можно).

— Чтобы найти делимое, нужно значение частного умножить на делитель (да).

— Чтобы найти неизвестный множитель, нужно значение произведения умножить на известный множитель (нет, разделить).

— В выражениях без скобок все действия выполняются по порядку слева направо (нет, сначала умножение и деление, потом вычитание и сложение).

В выражениях со скобками, вначале выполняются действия в скобках (да)

— С каждым уроком у вас получается всё лучше! Просто замечательно!

3. Актуализация знаний.

Слайд № 5 Прочитайте и объясните выражение: «Чтобы переварить знания, надо поглощать их с аппетитом.» (А. Франц)

— Вы готовы поглощать их с аппетитом? Тогда внимание! На прошлых уроках мы изучали порядок выполнения действий.

— Посмотрите, пожалуйста, внимательно на слайд№ 6. Выполните задания. Эти задания помогут нам определить тему нашего урока. Объясните, почему допущены ошибки?

— Проговорите правило, которое подходит к данным выражениям: Слайд № 7:

• В выражениях без скобок, содержащих только сложение и вычитание – действия I ступени, или умножение и вычитание – действия II ступени, действия выполняются в том порядке, как они записаны : слева направо.

• В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.

• В выражениях со скобками сначала вычисляют значения выражений в скобках. Затем по порядку слева направо выполняется умножение или деление.

— Озвучьте тему нашего урока. (Закрепление правил «Порядок выполнения действий в выражениях со скобками и без скобок») Слайд № 8

— Просто умницы, ловко справились, умело.

VI. Целеполагание.

— Ребята, как вы считаете, достаточно ли хорошо отработана нами тема «Порядок выполнения действий »?

— На что нам сегодня необходимо обратить внимание? Над чем поработать? (Упражняться в нахождении значений выражений, содержащий действия разных ступеней со скобками и без них. Познакомиться с видами выражений, в которых можно допустить ошибки)

V. Постановка и разрешение проблемной ситуации.

— Ребята, послушайте, пожалуйста, что говорил французский математик Д.Пойя: «Лучший способ изучить что-либо — это открыть самому». Слайд № 9

Вы готовы к открытиям?

СЛАЙД № 10

— Даны выражения, посмотрите, как справились с заданием Маша и Миша.

— Кто выполнил задание верно: Маша или Миша? (ответы детей)

— Какие ошибки допущены Машей? Как вы думаете, почему Маша допустила ошибку?

— Я знала, что это задание вам было под силу! Слайд № 11. Великий Песталоцци сказал: «Счет и вычисления — основа порядка в голове.» Давайте, потренируемся, чтобы не допускать ошибок, подобно Маше.

VI. Закрепление:

1. Самостоятельная работа С. 27, № 1

2. Проверка с объяснением. Оценка учителем — 3 учеников, остальные –самооценка. Занесите оценку в оценочный лист по следующему критерию: все выражения решены верно – 3 балла, 2 выражения верно – 2 балла, 1 выражение верно – 1 балл

3. Я горжусь вами, что вам удалось выполнить задание почти без ошибок.

4. А теперь попробуем усложнить задачу: составим выражения по схеме, определим порядок действий и вычислим их значение: с. 27, № 2. Сначала выполним вместе, а потом самостоятельно. (Работа у доски и в тетрадях. Предложить детям, кто понял, как делать, выполнить самостоятельно)

5. Оценивание: Кто работал у доски –оценивает учитель, сам-но, по критерию, как в задании по таблице умножения.

6. — Ребята, у вас получилось лучше, чем я могла бы подумать!

VI. Решение задачи с. 27, № 3

Слайд № 12. « Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.» (Д.Пойа)

1. Составление задач.

2. Самостоятельно запишите решение задач и ответ. Каждому ряду по одной задаче.

3. Проверка и оценивание. За правильное решение и ответ – 2 балла.

Неверно – 0 баллов

4. Я рада, что вы справились.

VII. Итог урока.

— Выполнили ли мы поставленные цели урока? Что планировали? Всё ли у нас получилось? Над чем необходимо поработать?

XIII. Оценивание и рефлексия.

1. Давайте определим, насколько успешно вы работали. Оцениваем критерий: активность.(Учитель объявляет баллы за активность: от 5 до3). Подсчитайте количество баллов: 45 баллов – «5», 34 балла — «4», 22 балла – «3».Поднимите карточки с цифрами.

2. Кто из вас стал увереннее находить значения выражений на порядок действий, поднимите вверх зеленые кружки, кому еще надо потренироваться, чтобы усвоить тему, поднимите вверх красные кружки.

— Вы сегодня просто молодцы, много сделали. Работать с вами просто радость!

XIV. Домашнее задание.

— Что необходимо закрепить дома? (порядок выполнения действий в сложных выражениях) с. 27, под чертой.

Хочу закончить наш урок словами М.И. Калинина

Слайд № 13. «Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.»

Спасибо за урок. А что говорят нам Миша и Маша?

Урок окончен.

Ссылка на источники:

http://festival.1september.ru/articles/633426/

http://www.sch943.edusite.ru/p285aa1.html

Источник шаблона презентации:

Ранько Елена Алексеевна

учитель начальных классов

МАОУ лицей №21

г. Иваново

Сайт: http://elenaranko.ucoz.ru/

5

Урок математики в 3 классе

Типы чисел Порядок операций

Сложение, вычитание, умножение, деление и возведение в степень — все это операции над действительными числами, т. е. операции, которые вы делаете с действительными числами. Для сложных арифметических выражений важно выполнять операции в правильном порядке. Так что тактика «в каком порядке я хочу» не сработает для вас.

Этот правильный порядок задается волшебной фразой «Пожалуйста, извините, моя дорогая тетя Салли» (PEMDAS). О, бедная, дорогая тетя Салли; иногда она немного запутывается, и ей нужны аббревиатуры, чтобы напомнить ей, как решать ее любимые математические уравнения.

Буквы обозначают P арентезы, E xponents, M умножение и D ivision, A дополнение и S вычитание, в том порядке, в котором мы хотим их делать. Обратите внимание, что «Умножение и деление» и «Сложение и вычитание» сгруппированы вместе. Это потому, что умножение не обязательно должно быть выполнено перед делением — вам просто нужно завершить все ваши умножения и деления, прежде чем вы начнете сложение и вычитание. Не расстраивайтесь, если вы не поняли этого сначала. Тетя Салли 40 лет пытается понять эту концепцию, но она все еще ускользает от нее.

Пример задачи

 

Сначала мы оцениваем значения в скобках. Мм, мы не можем упростить (4) больше, чем это уже есть, так что давайте перейдем к показателям степени.

Затем умножение и деление:

6 – 1

И, наконец, сложение и вычитание:

5

При сложении и вычитании мы работаем слева направо. Проверьте, на подошве какой из ваших туфель написана большая буква «L», если вы не уверены.

Пример задачи

Сколько будет 4–6–2?

У нас нет круглых скобок, показателей степени, умножения, деления или сложения, поэтому мы сразу переходим к вычитанию. Однако, как обычно, мы должны двигаться слева направо.

4 – 6 – 2 =
(4 – 6) – 2 =
-2 – 2 = -4

Обратите внимание, что если бы мы сначала вычли 6 – 2, мы получили бы совершенно другое (и неправильное) ответ:

4 – (6 – 2) =
4 – 4 = 0

Мы также работаем слева направо при оценке умножения и деления.

Пример задачи

Что такое 3 × 4 ÷ 2 ÷ 6?

Здесь у нас есть только умножение и деление, так что давайте прокручиваем слева направо.

3 × 4 ÷ 2 ÷ 6 =
12 ÷ 2 ÷ 6 =
6 ÷ 6 = 1

Если бы мы работали справа налево, мы бы получили другой ответ:

Один из способов отслеживать ваша работа состоит в том, чтобы разбить задачу на части, разделенные знаками сложения или вычитания. Каменный молоток или ступка и пестик должны помочь.

Пример задачи

Теперь вычислите каждую из частей:

=
6 + 2 – 0 – 4

Затем соедините ответы по частям:

6 + 2 – 0 – 4 = 4

4 Пример задачи

 

Ой, какой зверь. Давайте разобьем его на более мелкие части, каждая из которых будет разделена знаком плюс или минус (поскольку сложение и вычитание идут последними).

=
3 + 6 × 16 – 6 × 1

Теперь займемся этим умножением.

3 + 6 × 16 – 6 × 1 =
3 + 96 – 6

И, наконец, качаем сложение и вычитание слева направо.

3 + 96 – 6 = 93

Хорошо, но, пожалуйста, извините, моя дорогая тетя Салли, это очень долгая вещь, которую нужно запомнить. И мы уже потратили последние 10 лет, пытаясь заблокировать ее. Здесь, в Shmoop, мы любим все упрощать («Shmoop» на самом деле является сокращением от «Shmoopalumpagus»).

Мы видели, что вычитание можно заменить добавлением отрицательного числа, а деление можно заменить умножением обратного числа. Так что все мы на самом деле нужно помнить, пожалуйста, извините мою тетю. Сначала сделайте то, что находится внутри скобок, затем возьмите все экспоненты, затем умножьте, затем добавьте. Только помните, что деление = умножение на обратное, а вычитание = прибавление минуса. Да, в любом случае, тебе придется кое-что вспомнить. Это алгебра.

Давайте разработаем последний пример.

Пример задачи

Итак, давайте начнем с того, что заключено в скобки: . Мы хотим превратить его во что-то более управляемое, прежде чем мы его исправим. Нам также, вероятно, следует сменить радиостанцию. Что это, авангард-метал?

Довольно окольный путь, чтобы добраться до номера 1, но мы им воспользуемся.

Теперь, когда мы завершили все операции в скобках, мы ищем показатели степени. Если они сразу не представятся, громко свистнут и потрясут пакетом с угощением — прибегут.

В первой части уравнения у нас есть 1 ² , что, конечно же, равно 1. Затем мы ищем умножение. Поскольку его нет, остается только добавить -13. Вычитание такого несчастливого числа не может быть плохой вещью.

1 + (-13) = -12

Готово! Обозначение

— В чем причина текущего порядка операций? (ПЕМДАС)

спросил 7 лет, 8 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 20 тысяч раз

$\begingroup$

Прочитав несколько других вопросов, я просто задал себе вопрос: Как был определен порядок операций и почему именно этот порядок, а не какой-то другой?

Большинство из нас знает такие вещи, как умножение/деление перед сложением/вычитанием, сначала круглые скобки и т. д., но какова реальная причина этого? Я, вероятно, предубежден, следуя этим правилам с детства, поэтому я не могу придумать другого пути.

2 + 2 х 2 = 6, а не 8

Но если бы порядок был изменен, скажем, на «сложение/вычитание перед умножением/делением», будет ли этот порядок по-прежнему работать, если мы предположим, что математика будет опираться на него? Или есть какая-то странная математическая проблема, если бы мы использовали другой порядок?

Конечно, круглые скобки выполняют функцию группировки, поэтому они всегда должны стоять первыми — в основном я говорю о возведении в степень, умножении/делении, сложении/вычитании (и, возможно, о других операциях).

• обозначение

$\endgroup$

2

$\begingroup$

Как заметил Зак Стоун, порядок операций — это всего лишь соглашение, и если вы решите изменить порядок, все, что произойдет, это то, что вам нужно будет использовать круглые скобки в разных местах.

Все будет хорошо, если вы сделаете правильные настройки. Это, как говорится, есть причина для конвенции. В некотором смысле умножение — это просто многократное сложение. Кроме того, возведение в степень — это просто повторное умножение (пока мы ограничиваемся целыми числами), поэтому имеет смысл сначала превратить все показатели степени в умножение, затем превратить все умножения в сложение, а затем решить задачу сложения. Таким образом, по крайней мере, что касается целых чисел, существует естественный порядок операций, основанный на их определении. Это становится более сложным, когда вы начинаете иметь дело со всеми действительными числами, но порядок наследуется от целочисленной арифметики.

$\endgroup$

10

$\begingroup$

Предположим, что умножение произошло после сложения. Попробуйте написать это без скобок: $$(а\раз б)+с$$ Вам будет очень тяжело.

c$), поэтому показатель степени ставится перед умножением. Умножение распределяется над сложением (т. е. $(a+b)\times c=a\times c+b\times c$), поэтому умножение идет первым. С PEMDAS мы можем избавиться от круглых скобок, используя дистрибутивность. С другим заказом («PEASMD»?) мы не можем.

$\endgroup$

$\begingroup$

В сознании людей и демонов умножение является более важной операцией, чем сложение. Кроме того, люди разработали алгебраическую систему счисления из своего основного языка, который был латинским, когда я родился, но теперь стал английским.

Я до сих пор помню, как Линкольн назвал Геттисбергский адрес. «Четыре и семь лет назад…» Это 4 доллара умножить на 20 + 7 долларов лет. По-немецки он мог бы сказать: «Sieben und achtzig Jahre ſind verfloſſn, šeit unsere Väter auf dieſem Continent einer neue Nation…» Это 7 долларов + 8 умножить на 10 долларов лет. Десятки, десятки, сотни, брутто — вот как вы обращаетесь со многими целыми числами, а затем корректируете их небольшими добавлениями или вычитаниями.

9{2n}}\right).$$

Посмотрите практически любую книгу о языке программирования или даже о языке сценариев, таком как Javascript, и одна из первых вещей, которые вы увидите, неизменно будет таблицей приоритета операций. . Компьютеру, в его славной тупости, нужно указывать, в каком порядке выполнять операции.

$\endgroup$

1

$\begingroup$

Многочлены важны сами по себе, независимо от обозначения. Мы остановились на обозначениях, которые облегчают их запись. Мы могли бы просто использовать круглые скобки между каждой операцией, но это было бы ужасно. Это просто соглашение для упрощения чтения и письма. Изменение соглашения ничего не сломает, нам просто нужно много скобок, чтобы выразить то, что мы хотим.

Одним из мест, где полиномы органично встречаются, являются расширения полей. На самом деле можно было бы немного поработать над теорией Галуа, даже не записывая полином в явном виде. Точно так же полиномы органично встречаются в линейной алгебре (можно использовать тензорные произведения, чтобы абстрагироваться от таких вещей, как характеристические полиномы). Это было бы сложнее, но не менее мощно. Но это помогает объяснить, почему мы заботимся о многочленах и почему мы можем захотеть их записать.

$\endgroup$

9

$\begingroup$

Это действительно лингвистический вопрос, поэтому ответ является типичным лингвистическим ответом: порядок операций такой, какой он есть, потому что это сделало общение более эффективным.

Мы меняем формат нашего обозначения в соответствии с нашими потребностями. В случае порядков операторов обычно было обнаружено, что формулы были более читабельными с порядком операций (вероятно, из-за уменьшения количества группирующих символов). 92)) + (vt) + x_0$ Можно ли так написать? Конечно, но это сложнее.

За прошедшие годы математики сочли текущий порядок операций чрезвычайно удобным и придерживаются его.

Этот нечеткий процесс также является объяснением известной головоломки $6/2(3) = ?$. Некоторые считают, что это должно равняться 9, потому что это то же самое, что $6 / 2 \cdot 3$. Другие считают, что оно должно равняться 1, потому что умножение на круглые скобки связывает «плотнее», чем обычное деление: $\frac{6}{2\cdot3}$. У них есть на что опереться, потому что большинство из нас согласны с тем, что $6/xy == \frac{6}{xy}$, так что неясно, по какому пути идти. Настоящим ответом является то, что это лингвистическая двусмысленность, которая существует потому, что она не была достаточно важной, чтобы большая часть математиков согласилась с ней. Если бы это когда-нибудь действительно стало важным, мы бы так или иначе решили.

$\endgroup$

$\begingroup$

Хотя многие говорят, что (PEMDAS) — это всего лишь условность, мне нравится думать следующее: (Умножение и деление) — это краткие формы представления (сложения и вычитания), поэтому выполнение (MD) перед (AS) помещает все в одном и том же виде операции: т.

е. (AS). Точно так же возведение в степень — это формы представления (умножения и деления), по крайней мере, для целых чисел в степени … и, следовательно, (E) может быть преобразовано в (MD), которое, в свою очередь, может быть преобразовано в (AS). Скобки, с другой стороны, являются способом явного определения приоритета операции, поэтому она должна быть хорошо… расставлена ​​по приоритетам.

$\endgroup$

1

$\begingroup$

PEMDAS устарел, и мы никогда не должны на него полагаться. Всегда используйте () для устранения всей двусмысленности, если вы пишете уравнение или выражение.

Несмотря на то, что для нынешнего соглашения есть достаточно веская причина, больше нет никаких оснований полагаться на то, что читатель запомнит его и правильно интерпретирует уравнение или выражение, использующее его. Единственная причина писать x = y + z * w вместо x = y + (z * w) состоит в том, чтобы сэкономить 2 символа ширины пробела или 2 байта памяти на компьютере.

Когда все было на бумаге, это был разумный способ сэкономить место в текстах и, следовательно, деньги за счет сокращения расходов на бумагу и печать. Позже, когда у компьютеров был крошечный объем памяти, это тоже имело смысл. Я бы сказал, что любые время , сэкономленное при вводе или написании дополнительных символов, было бы более чем компенсировано ошибками и дополнительным временем, затраченным на его расшифровку без (). В настоящее время большинство вещей находятся в Интернете, и у нас достаточно памяти компьютера, поэтому больше нет оправдания вносить какую-либо двусмысленность, опуская ().

Тот факт, что в Интернете есть много страниц, посвященных конвенции PEMDAS, свидетельствует о том, что многие люди считают ее запутанной и часто приводят к ненужным ошибкам. Ошибки, которых можно было бы избежать, просто набрав несколько (), чтобы избежать двусмысленности и путаницы.

По возможности всегда следует избегать двусмысленности, особенно в математике и компьютерном коде.