МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ высшего профессионального образования «Мурманский государственный гуманитарный университет» (ФГБОУ ВПО МГГУ) УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ СД.Ф.13.3. МЕТОДИКИ ПРЕПОДАВАНИЯ РАЗДЕЛ: «МЕТОДИКА ПРЕПОДАВАНИЯ МАТЕМАТИКИ» (спец.) 050715.65 Логопедия Утверждено на заседании кафедрыСПиСП ППИ (протокол № 1 от 09.09.13 г.) Зав. кафедрой СПиСП ______________Ю.А. Афонькина 1.1. Автор программы — к.п.н., доцент кафедры СПиП Голишникова Е.И. 1.2. Рецензенты: Ст.преподаватель кафедры СПиСП Демяшина В.В., к.п.н., доцент филиала НОУВПО СФГА в г. Мурманске Гошева Е.Н. 1. Учебная дисциплина «Методика преподавания математики» введена в процесс обучения для студентов специальности 03.17.00 — Олигофренопедагогика в связи с требованиями государственного стандарта высшего образования. Курс методики начального обучения математики опирается на знание математических понятий, общей и специальной психологии и педагогики. Курс должен дать студентам подготовку, необходимую: для обучения школьников начальных классов математике по введенным в настоящее время программам и внедрения в начальную школу новых вопросов математики; для ориентировки в содержании преподавания математики в средней школе; для дальнейшей самостоятельной работы по углублению и расширению профессиональных знаний. Дисциплина «Методика преподавания математики» имеет основной своей целью повышение профессиональной подготовки будущего учителя-дефектолога. Задачами дисциплины являются:
Требования к уровню освоения содержания дисциплины В процессе изучения дисциплины студенты должны знать:
Студенты должны овладеть практическими умениями:
Программа «Основы математики с методикой преподавания» завершается экзаменом. При составлении программы использовались материалы научно-методических разработок: Перова М.Н. доктор педагогических наук, профессор, МПГУ, г. Москва Горскин Б.Б. кандидат педагогических наук, доцент, МПГУ, г. Москва 1.4. Извлечение из ГОС ВПО
050717.00 Специальная дошкольная педагогика и психология с доп. спец. Логопедия» — 050716.00 Специальная психология с доп. спец. Логопедия – 150715.00Логопедия ДПП.Ф.13 Методика преподавания математики (специальная). Предмет и задачи начального обучения математике в школе для детей с тяжелыми нарушениями речи. Клинико-психологическая характеристика акалькулии и дискалькулии детского возраста. Принципы обучения математике учащихся с речевыми нарушениями. Содержание, методы и средства обучения математике. 1.5. Объем дисциплины и виды учебной работы (для всех специальностей, на которых читается данная дисциплина:
Каталог: umu-umk -> %D0%9F%D0%9F%D0%98 -> 050715.65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F 050715.65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины опд. Ф. 25 (опд. Ф. 13) «Специальная психология» 050715.65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины сд. Ф «Педагогические системы воспитания детей с речевыми нарушениями» 050715.65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины дс 1 (ДС.  Ф. 1)«Теоретические основы семейной коррекционной педагогики» Ф. 1)«Теоретические основы семейной коррекционной педагогики»050715.65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины сд. Ф. 2 Логопедия дс. 1 Логопедия 050715.65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины сд. Ф. 13. 1 «Методика преподавания русского язык» 050715.65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины сд. Ф. 2 Логопедия дс. 1 Логопедия 050715.65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины сд. Ф. «Основы олигофренопедагогики» Скачать 0.72 Mb. Поделитесь с Вашими друзьями: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
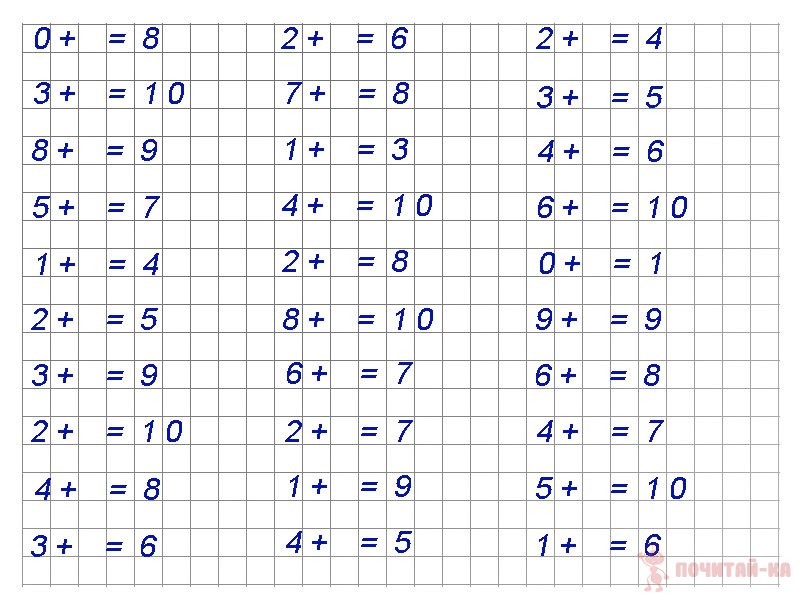
Как заполнить таблицу на сложение. Табличное сложение и вычитание натуральных чисел
Таблица сложения и вычитания натуральных чисел приведена для сложения чисел первого десятка и вычитания чисел от 1 до 18. Таблицей удобно пользоваться при сложении или вычитании по разрядам для натуральных многозначных чисел, устный счет построен на сложении по разрядам, т.е. на сложении по этой таблице.
Таблицей удобно пользоваться при сложении или вычитании по разрядам для натуральных многозначных чисел, устный счет построен на сложении по разрядам, т.е. на сложении по этой таблице.
Работа с таблицей предполагает такой результат: таблицу вы запомните, выучите наизусть в процессе вычислений, что значительно сократит время нахождения результата при сложении и вычитании натуральных чисел.
Правила пользования таблицей
Крайний левый столбец и верхняя строка — числа первого десятка — слагаемые при сложении и разность при вычитании. Чтобы сложить два числа, нужно первое слагаемое взять в крайнем левом столбце, а второе — в верхней строке. На пересечении столбца и строки в поле таблицы считывается результат сложения — сумма.
Чтобы вычесть одно число из другого, в поле таблицы нужно найти уменьшаемое и, двигаясь по этому числу по диагонали поля, выбрать строку, в которой в левом крайнем столбце помещено число вычитаемого. По месту строки и числу уменьшаемого расположен столбец, в верхней строке которого считывается разность (результат вычитания).
Примеры пользования таблицей
Сложение . 3 + 5 = 8
Первое слагаемое (3) взято в левом столбце, второе слагаемое (5) взято в верхней строке. На пересечении столбца и строки — сумма (8).
Вычитание . 8 — 3 = 5.
Уменьшаемое (8) выбираем в ноле таблицы и, двигаясь по диагонали поля с цифрой 8, останавливаемся на строке вычитаемого (3). На пересечении строки с числом 3 и столбца с числом 8 считываем разность (5) в верхней строке.
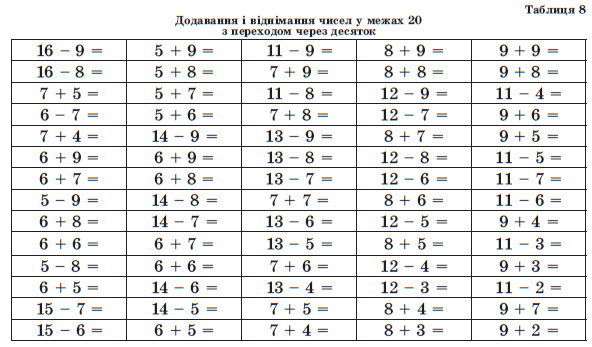
На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
Тема: Знакомство с основными понятиями в математике
Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20
С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток.
Каким способом можно сложить 9 и 7? (рис. 1)
Рис. 1
На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
9 + 1 = 10, значит 7 = 1 + 6. (рис. 2)
Рис. 2
Выполним сложение по частям:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Ответ: 9 + 7 = 16.
Можно сложить эти числа по-другому. (рис. 3)
Рис. 3
Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6.
Рис. 4
Выполним сложение по частям:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.
9 + 5 = 9 + (1 + 4) = 14
Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2.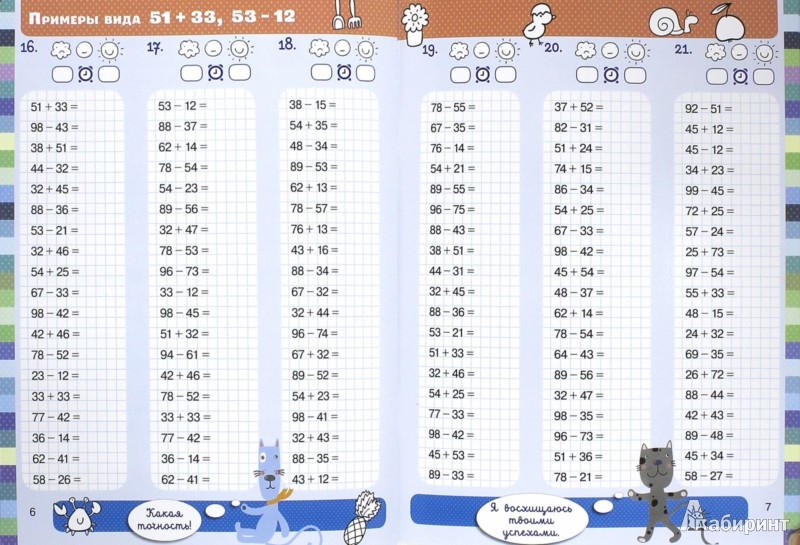 Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.
Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.
6 + 6 = 6 + (4 + 2) = 12
Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
4 + 8 = 4 + (6 + 2) = 12
В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.
15 — 7 = 15 — (5 + 2) = 8
В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
16 — 9 = 16 — (6 + 3) = 7
В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
12 — 4 = 12 — (2 + 2) = 8
Ответ: 12 — 4 = 8.
Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.
На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)
Рис. 7
В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.
9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8)
Рис. 8
В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.
- Социальная сеть работников образования ().

- 5klass.net ().
- Самоучка ().
Домашнее задание
1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.
2. Помогите лягушке решить примеры.
3. Решите примеры и раскрасьте рисунок.
Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу
Таблица сложения до 20 распечатать и скачать
Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.
Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием.
Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием.
Таблица вычитания до 20 распечатать и скачать
В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.
Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах.
Таблица вычитания без ответов распечатать и скачать
На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
Тема: Знакомство с основными понятиями в математике
Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20
С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток.
Каким способом можно сложить 9 и 7? (рис. 1)
Рис. 1
На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как
9 + 1 = 10, значит 7 = 1 + 6. (рис. 2)
Рис. 2
Выполним сложение по частям:
9 + 7 = (9 + 1) + 6 = 10 + 6 = 16
Ответ: 9 + 7 = 16.
Можно сложить эти числа по-другому. (рис. 3)
3)
Рис. 3
Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6.
Рис. 4
Выполним сложение по частям:
7 + 9 = (7 + 3) + 6 = 10 + 6 = 16
Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы.
9 + 5 = 9 + (1 + 4) = 14
Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы.
6 + 6 = 6 + (4 + 2) = 12
Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы.
4 + 8 = 4 + (6 + 2) = 12
В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.
Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы.
15 — 7 = 15 — (5 + 2) = 8
В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
16 — 9 = 16 — (6 + 3) = 7
В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2.
12 — 4 = 12 — (2 + 2) = 8
Ответ: 12 — 4 = 8.
Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть.
На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7)
Рис. 7
В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм.
Найдём значение данных сумм.
9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8)
Рис. 8
В каждой строке записаны суммы с одинаковыми ответами. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.
- Социальная сеть работников образования ().
- 5klass.net ().
- Самоучка ().
Домашнее задание
1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд.
2. Помогите лягушке решить примеры.
3. Решите примеры и раскрасьте рисунок.
Как сделать 10 для вычитания — Учитель с коричневой сумкой
В соответствии со стандартами операций и алгебраического мышления учащиеся 1-го класса должны складывать и вычитать в пределах 20, развивая беглость в пределах 10, используя различные стратегии. (Эталон беглости для детского сада — 5, а для 2-го класса — 20.) «Разнообразие стратегий» включает, но не ограничивается, составление десяти, разложение числа на десятку (т. е. составление 10 для вычитания), соотнесение сложение и вычитание, а также эквивалентные суммы. Как преподаватели, мы предлагаем, подчеркиваем и отмечаем различные стратегии, чтобы у учащихся был «набор инструментов» для выбора при решении проблемы. У учащихся будут индивидуальные предпочтения. Различные ситуации поддаются использованию различных стратегий. Это нормально и ожидаемо.
В 1-м классе число 10 становится контрольным числом, которое поддерживает сложение и вычитание как мыслительный процесс. Сделать 10, чтобы вычесть, является важным навыком для наших начальных учеников. Однако поначалу это может быть трудным навыком. ( Получите ресурсы для своего класса здесь или добавьте/вычтите B здесь.)
Однако поначалу это может быть трудным навыком. ( Получите ресурсы для своего класса здесь или добавьте/вычтите B здесь.)
Поскольку мы помогаем учащимся достичь 10-летнего возраста, это должен быть практический процесс. У учащихся должны быть практические возможности разбивать числа на части, перераспределять их размещение на десяти фреймах и создавать новые уравнения. Студенты должны постоянно строить, перемещать и создавать уравнения со счетчиками и десятью кадрами.
Затем мы переводим учащихся на полубетон, рисуя и иллюстрируя процесс.
Наконец, учащиеся используют числа и числовые связи, чтобы продемонстрировать свое абстрактное мышление.
Если учащиеся испытывают затруднения в рамках этого континуума CSA, мы поддерживаем их. Когда полуконкретное понимание становится борьбой, тогда вернитесь к полуконкретному. Если мы перейдем к полуконкретному и поймем, что это беспорядок, мы вернемся к другому конкретному опыту. Даже когда учащиеся могут «посчитать», важно убедиться, что у них действительно есть концептуальное понимание. Это понимание имеет решающее значение для истинного мастерства в том, как сделать 10, чтобы вычесть.
Даже когда учащиеся могут «посчитать», важно убедиться, что у них действительно есть концептуальное понимание. Это понимание имеет решающее значение для истинного мастерства в том, как сделать 10, чтобы вычесть.
Для многих учащихся (в том числе и для меня) число 10 является не таким естественным ориентиром для вычитания, как сложение. Поэтому может потребоваться больше конкретного опыта и больше игры! В долгосрочной перспективе мы не хотим заставлять студентов использовать эту стратегию, но мы хотим, чтобы они были достаточно опытны, чтобы иметь возможность применять ее, когда того требует проблема или ситуация.
Используя числа, тщательно составленные для поддержки использования функции «Сделай 10, чтобы вычесть», учащиеся решают уравнение. Затем, работая с полубетоном, учащиеся рисуют свое начальное вычитаемое на десятичной системе координат. Затем учащиеся зачеркивают/вычитают второе меньшее вычитаемое. Затем учащиеся записывают уравнения, соответствующие их десяти кадрам. Это идеальная игра для преподавания за учительским столом, а затем для использования в качестве математического центра.
Затем учащиеся записывают уравнения, соответствующие их десяти кадрам. Это идеальная игра для преподавания за учительским столом, а затем для использования в качестве математического центра.
Учащиеся не только имеют возможность построить концептуальное понимание с помощью практического математического опыта, им также нужны строительные леса, чтобы говорить о математике (устно и письменно)!
Математические журналы дают учащимся возможность показать и объяснить свое математическое мышление. Если студентов никогда не просили объяснить их мысли (а не только процесс), это может оказаться непростой задачей. Чем меньше у учащихся опыта написания статей по математике, тем больше учительского моделирования и поддержки им может понадобиться. Моделирование ваших ожиданий в отношении демонстрации работы, математического мышления, использования словарного запаса и удобочитаемости будет жизненно важной частью превращения математических журналов в стоящее предприятие.
После изложения ожиданий и подготовки я часто переношу математические журналы в небольшие группы, где учащиеся имеют больше возможностей устно объяснить свои мысли. Затем, опираясь на устную речь, учащиеся записывают свои мысли.
После моделирования в полной и небольшой группе некоторым учащимся может потребоваться дополнительная поддержка с помощью основ предложений и фреймов. Фреймы — это высший уровень поддержки письма (помимо диктовки), и их следует использовать стратегически. Фрейм убирает значительную часть когнитивного подъема от задачи. В конце концов, цель состоит в том, чтобы эти подсказки стали независимыми действиями. (Леса не должны оставаться на месте вечно.)
Подведение итогов Мы хотим, чтобы наши учащиеся были уверены в своих решениях, когда и следует ли использовать стратегию «Сделать 10, чтобы вычесть». небольшая группа (в группах по математике или RTI), а также возможность практиковаться в играх и центрах.
Итак, когда вы отважитесь на изучение этого стандарта по операциям и алгебраическому мышлению, я буду болеть за вас и ваших учеников. Вы все получили это.
Получите пакет Making 10 to Add & Subtract со скидкой здесь, ресурс Making 10 to Subtract здесь и ресурс Making 10 to Add здесь. Узнайте больше о Making 10 to Add в блоге здесь.
Получите бесплатные учебные материалы!
Присоединяйтесь ко мне, чтобы получать еженедельные обновления и бесплатные ресурсы, которые идеально подходят для вашего урока математики!
Имя
Адрес электронной почты
Мы используем это поле для обнаружения спам-ботов. Если вы заполните это, вы будете отмечены как спамер.
Работает на ConvertKitРазвитие беглости речи в рамках IM K–5 Math™ и между классами, часть 1: сложение и вычитание
Сара Кабан, ведущий писатель 5-го класса, и Дионн Амината, ведущий писатель 2–5-го классов
Когда учащиеся практикуют свои математические факты? Как оценивается беглость по математике?»
— нынешние и будущие преподаватели IM K-5 Math™ во всем мире
Мы ценим эти вопросы по нескольким причинам: 1) Мы уделили большое внимание развитию беглости речи при разработке учебного плана, и мы очень хотим поделиться тем, как мы это сделали, и 2) мы понимаем, что то, как мы включили развитие беглости речи, отличается от большинства учебных программ, и его может быть трудно распознать.
Чтобы показать, как учебная программа IM K–5 Math™ направлена на беглость речи, мы подготовили серию статей в блоге, состоящую из четырех частей. Этот первый пост представляет собой глубокое погружение в наш курс для 1-го класса, чтобы показать, как учащиеся развивают беглость сложения и вычитания в пределах 10. В следующем посте будет освещено развитие процедурной беглости с помощью алгоритмов сложения и вычитания. Последний пост покажет прогресс развития беглости в умножении и делении.
Мы надеемся, что эта серия сообщений в блоге поможет пролить свет на преднамеренный дизайн, который со временем способствует прогрессу учащихся в достижении беглости речи как внутри, так и между классами. Также включены способы, с помощью которых учителя могут отслеживать и оценивать уровень владения математикой учащимися в течение учебного года.
Мы определяем процедурную беглость как « использование процедур гибко, точно, эффективно и надлежащим образом. ”( Складываем: помощь детям в изучении математики от Национального исследовательского совета, 2001 г. ) В учебной программе IM K–5 Math™ используемые представления, стратегии и алгоритмы целенаправленно разработаны для создания последовательного прогресса, при котором концептуальное понимание и беглость процедур развиваются параллельно. Эта прогрессия развивается внутри и между уровнями обучения.
) В учебной программе IM K–5 Math™ используемые представления, стратегии и алгоритмы целенаправленно разработаны для создания последовательного прогресса, при котором концептуальное понимание и беглость процедур развиваются параллельно. Эта прогрессия развивается внутри и между уровнями обучения.
Прогрессирование процедурной беглости сложения и вычитания целых чисел охватывает от детского сада до четвертого класса. Каждый из этих уровней обучения имеет определенные требования к процедурной беглости, которые взаимосвязаны.
Согласованность учебной программы предназначена для учащихся любого класса, чтобы они могли точно и эффективно работать с одним набором чисел в контексте построения концептуального понимания в рамках большего набора чисел. Эта согласованность очевидна в том, как IM K–5 Math предназначен для того, чтобы учащиеся узнавали свои факты на любом заданном уровне обучения.
- Учащиеся изучают значение операций и связи между ними.

- Студенты начинают узнавать факты.
- Учащиеся связывают более сложные факты с более простыми.
- Студенты знают факты.
Чтобы лучше понять замысел учебного плана, мы поделимся своими мыслями о развитии беглости речи в 1 классе. Давайте посмотрим, как учащиеся узнают факты в пределах 10.
1. Учащиеся изучают значение операций и отношения между ними.
Основа для беглого сложения и вычитания в пределах 10 закладывается в детском саду, когда учащиеся впервые узнают о значении сложения и вычитания через задачи на рассказ. Беглость речи в детском саду направлена на то, чтобы научиться точно и эффективно складывать и вычитать в пределах 5, что поддерживает работу 1 класса по составлению и разложению чисел в пределах 10.
В разделе 5 нашего курса для детского сада учащиеся составляют числа до 10 способами имеют для них смысл. Например, на Уроке 13, Упражнении 2 учащимся дается число меньше 10, и они работают с партнером, чтобы определить часть, необходимую для получения 10. Затем они пишут уравнение для каждой 10, которую они составляют, используя рамку 10 = ___ + ___. Учащимся предлагается использовать свои пальцы, счетчики или 10-рамки, чтобы помочь им определить части, необходимые для получения 10.
Затем они пишут уравнение для каждой 10, которую они составляют, используя рамку 10 = ___ + ___. Учащимся предлагается использовать свои пальцы, счетчики или 10-рамки, чтобы помочь им определить части, необходимые для получения 10.
Предлагается, чтобы в ходе обобщения этого задания учителя выделили различные стратегии, используемые на основе заданного числа. Этот важный шаг поддерживает развитие гибкости учащихся. Услышав, как другие учащиеся делятся своими стратегиями, они могут выучить более эффективную стратегию и добавить ее в свой репертуар.
2. Учащиеся начинают узнавать факты.
Имея базовые знания о сложении и вычитании, учащиеся начинают узнавать некоторые факты. Раздел 1 нашего курса для 1 класса начинается с упражнений и центров, посвященных сложению и вычитанию в пределах 10. Работа в этом разделе позволяет учителям оценить понимание учащимися сложения и вычитания, а также их свободное владение фактами в пределах 5, цель детского сада. . Чтобы развить беглость в пределах 10, учащиеся начинают с действий, в которых они прибавляют или вычитают 1 или 2, что не только побуждает учащихся использовать такие стратегии, как счет или обратный счет, но также помогает им связать сложение и вычитание со счетом.
Вот несколько примеров того, как учащиеся продолжают практиковать сложение в пределах 10 во время разминки на протяжении Единиц 1 и 2. Как показано ниже, к Единице 2 учащиеся замечают и используют отношения между фактами, чтобы мысленно находить различия.
Центры в наших материалах играют важную роль в развитии беглости речи. Центры предоставляют учащимся возможность практиковаться, вспоминая факты, вычисляя в уме и записывая истинные уравнения. В следующих примерах учащиеся работают либо с кубиками, либо с карточками с числами, чтобы составить 10 из одной заданной части. Когда учащиеся делятся своими мыслями и пишут уравнения, они начинают узнавать новые факты.
3. Учащиеся связывают более сложные факты с более простыми.
Согласно NCTM, «эффективное преподавание математики строит свободное владение процедурами на основе концептуального понимания, так что учащиеся со временем приобретают навыки гибкого использования процедур при решении контекстуальных и математических задач».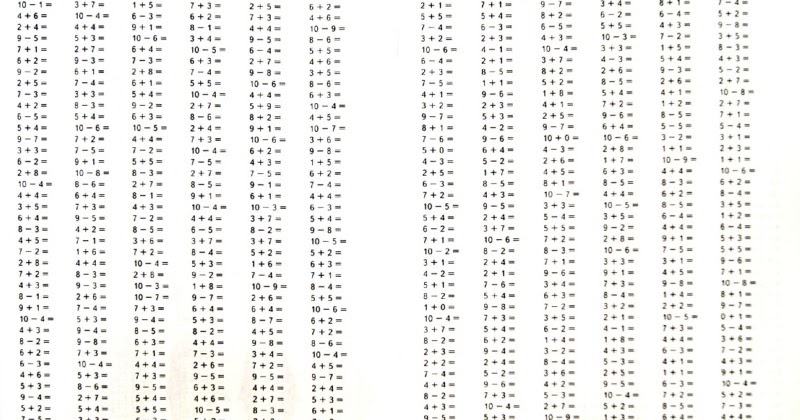 ( Principles to Actions NCTM, 2014) Ни для кого не секрет, что цель IM – помочь учащимся развить концептуальное понимание математики. В IM K–5 Math™ общий дизайн формирует концептуальное понимание, одновременно развивая у учащихся беглость выполнения процедур. Студенты практикуют свои факты таким образом, чтобы они могли показать или объяснить свое мышление. Они анализируют и учатся использовать представления, стратегии и алгоритмы целенаправленным и последовательным образом.
( Principles to Actions NCTM, 2014) Ни для кого не секрет, что цель IM – помочь учащимся развить концептуальное понимание математики. В IM K–5 Math™ общий дизайн формирует концептуальное понимание, одновременно развивая у учащихся беглость выполнения процедур. Студенты практикуют свои факты таким образом, чтобы они могли показать или объяснить свое мышление. Они анализируют и учатся использовать представления, стратегии и алгоритмы целенаправленным и последовательным образом.
Примером параллельного развития процедурной беглости и концептуального понимания в учебной программе является переход учащихся от знания нескольких фактов к связыванию известных им фактов с более сложными фактами. В Разделе 3 нашего курса 1 класса учащиеся начинают с того, что называют суммы в пределах 10, которые они знают. На Уроке 1, Упражнении 2 учащиеся практикуют свои факты, используя карточки с различными выражениями сложения, такими как 2 + 5 и 4 + 4. Они сортируют их на те, которые они могут сделать сразу, и те, над которыми они еще работают.
Во время синтеза деятельности на этом уроке учителя называют годичные ожидания беглости для сложения в пределах 10 и помогают учащимся размышлять над фактами, которые они знают, и над фактами, которые им еще нужно практиковать. Этот процесс помогает учащимся формировать положительную математическую идентичность и побуждает их связывать новые знания с тем, что они уже знают.
По мере изучения модуля учащиеся углубляют свое понимание свойства перестановочности, эквивалентности и взаимосвязи между сложением и вычитанием и применяют это понимание, чтобы использовать более простые факты для поиска более сложных.
4. Учащиеся знают факты.Со временем, после разнообразного опыта, когда они делились своим развивающимся мышлением, узнавали новые факты и практиковались в сопоставлении более сложных фактов с более простыми, учащиеся начинают узнавать больше фактов.
В разделах 4–8 нашего курса для 1-го класса учащиеся продолжают практиковать сложение и вычитание во время центральных и разминочных занятий. У них также есть множество возможностей поразмышлять над тем, какие факты они знают, а какие еще только изучают.
У них также есть множество возможностей поразмышлять над тем, какие факты они знают, а какие еще только изучают.
В приведенном ниже примере показано, как эта практика продолжается до последней части курса. На уроках 1 и 2 модуля 8 учащиеся отмечают суммы и разности, которые они знают по памяти, и создают карточки, чтобы попрактиковаться в фактах, которых они еще не знают.
Оценка беглости речиПоскольку беглость речи развивается с течением времени, а практика в нашей учебной программе происходит по-разному, прогресс учащихся в беглости фактов может показаться трудным для измерения. Чтобы решить эту проблему, IM K–5 Math™ включает контрольные листы для каждого уровня обучения, которые соответствуют целям разделов каждого раздела. В приведенном ниже примере показан прогресс в контрольных листах для 1-го класса в течение года, которые помогают учителям оценивать прогресс учащихся в достижении беглости речи в пределах 10.
Продуманный подход к развитию беглости математических знаний у учащихся учащимся практиковать свои математические факты в занятиях, центрах, практических задачах и разминках.




 спец. Логопедия»
спец. Логопедия» 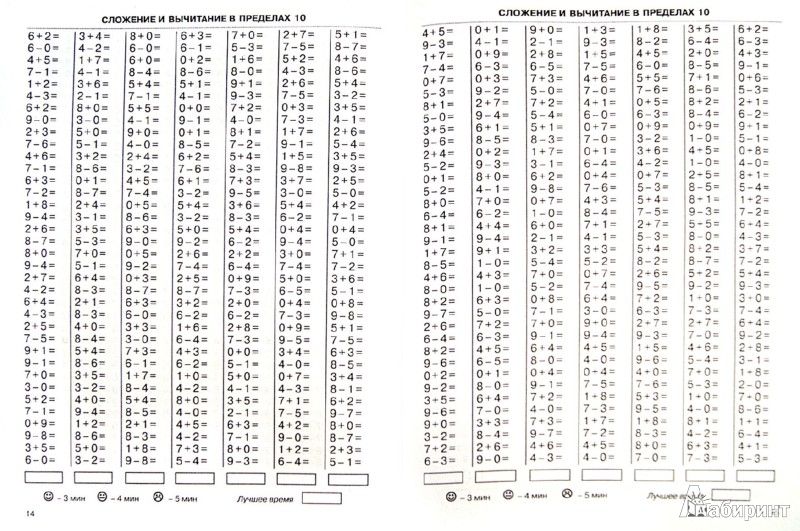 65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины сд. Ф. 13. 4 Методика преподавания: методика развития речи дошкольников (специальная)
65%20%D0%9B%D0%BE%D0%B3%D0%BE%D0%BF%D0%B5%D0%B4%D0%B8%D1%8F -> Учебно-методический комплекс дисциплины сд. Ф. 13. 4 Методика преподавания: методика развития речи дошкольников (специальная)