c++ — Быстрее ли работают сложение/вычитание и битовые операции по сравнению с делением/умножением в SIMD?

Вопрос задан 1 год 1 месяц назад

Изменён 1 год 1 месяц назад

Просмотрен 243 раза

Как известно, обычные инструкции сложения/вычитания и битовых сдвигов в процессорах x86 работают быстрее, чем инструкции умножения/деления. По-этому, для повышения производительности, операции *,/ как правило по возможности стараются заменить на +,-,>>,<<.

Мой вопрос: верно ли это утверждение для команд SIMD-расширений, как например SSE2? Или все инструкции SSE2 или другого расширения выполняются за равное количество тактов, а значит с заменой, скажем, операции деления на битовые сдвиги со сложениями можно не париться?

• c++
• x86
• simd

Важно понимать, что:

1. Современный компилятор достаточно умен и сообразителен, чтобы делать такие замены самостоятельно.

   Если вы делаете их вручную в ущерб читаемости кода просто в процессе написания, вы делаете только хуже. Потому что нечитаемый код может нанести экономических и репутационных потерь больше, чем гипотетические 2-3-5 процентов потери скорости, существование которых экспериментально не доказано.

2. Прагматичный подход к оптимизации идет от лога профайлера, а не от того, что вы что-то где-то слышали от кого-то или даже читали, даже в учебнике, даже в именитом. Times, they are changing. Рекомендашки по ускорению устаревают раз в три года, а через пять лет покрываются плесенью. В олдскульных книжках, например, можно прочесть, что по массивам лучше ходить задом неперед из-за инструкции loop, которая отматывает регистр CX до нуля. Ага, советы из 80х, транслируемые преподами ВТУЗОВ студентам 2020х

3. Время выполнения инструкции в современном конвейерном SIMD процессоре, который еще перегоняет у себя CISC в RISC внутри, зависит от большого сочетания факторов, которые теоретически трудно предсказать.

   Главными является ширина кэш-линий, число свободных каналов памяти, мгновенная тактовая частота, зависящая от режима энергопитания и температуры в данный момент времени (см. Turbo Boost и аналоги). Побочным может выступить такой фактор как внезапное попадание данных в другой NUMA-регион. Последним процессором, для которого можно было это четко узнать из мануала (была прямо табличка — опкод | число тактов) был не то i386, не то i486

Вывод. В каждом конкретном случае требуется проводить профилирование, на основании которого сравнивать полученную производительность с той, которую дает процессор на стандартных тестах LAPACK и похожих. Портить код, заменяя умножения на сдвиги смысла скорее всего нет вообще, потому что это сделает за вас компилятор. Если вы ему не доверяете, посмотрите машинный листинг, сделав его самостоятельно, или воспользовавшись онлайн-инструментом.

3

Как известно, обычные инструкции сложения/вычитания и битовых сдвигов в процессорах x86 работают быстрее, чем инструкции умножения/деления.

Это скорее бабушка на двое сказала. Во-первых, «обычные инструкции» — это на самом деле целое семейство инструкций. Которые еще и по-разному реализованы в разных процессорах. Во-вторых, в целом у них сходная производительность (если мерять в тактах), в каких-то вариантах может быть быстрее допустим умножение, а в других сдвиг. Например (для Sandy Bridge) IMUL m 2 CPI, SHL m,cl 4 CPI. При этом SHL r,i 0.5 CPI, а IMUL r,i 1 CPI. Для MMX psllw mm, mm и pmullw mm, mm — 1 CPI. Для SSE vpsllw ymm, ymm, xmm 1 CPI, а вот vpmulhw ymm, ymm, ymm на Skylake 0.5 CPI, а на более ранних те же 1 CPI. Вот деление да, оно гарантировано медленнее, там десятки CPI. В-третьих, собственно скорость вычисления в тактах — это далеко не единственная и не самая важная характеристика производительности инструкций. Если заглянуть в каталог таких характеристик, то там глаза разбегаются. В-четвертых, сложное устройство конвейера в современных процессорах также вносит свою лепту в определение производительности тот или иной инструкции, ведь реальная производительность варьируется в зависимости от состояния конвейера.

Например идущие подряд 6-байтовые инструкции будут вызывать дополнительный простой.

Что касается парится или нет — парится надо, но делать это надо системно, а не пытаться сэкономить байты разбрасывая хитрые вставки в коде.

Ваш ответ

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Добавление, вычитание, умножение и деление значений с помощью элементов управления

Примечание:  Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке) .

Вы можете помочь пользователям заполнение форм на основе шаблона формы с помощью формул для вычисления значения для элемента управления, на основе данных, которые пользователь вводит в других элементов управления. Расчеты могут включать добавление, вычитания, умножения и деления значений. Например при разработке позволяет использовать шаблон формы, электрических подрядчикам будет использоваться для подачи, можно добавить формулу для элемента управления, который автоматически вычисляет общую цену с Подрядчик для оплаты приложения, умножая количество позволяет использовать приложение по цене каждой заявки.

В этой статье

• Что такое формулы

• Использование двух или более операторов в формулах

• Вставка математических формул в элемент управления

Что такое формулы

Формулы — это выражение XPath состоит из значений полей или групп, функций и операторов, используемых для расчета и отображения других значений.

Формулы можно использовать для выполнения следующих задач:

• Математических расчетов из значения, которые определяют при разработке шаблона формы или значения пользователи ввели в элементах управления при заполнении формы на основе шаблона формы.

• Отображение определенного значения даты и времени.

• Отображение значений, которые пользователи ввели в один элемент управления в другой элемент управления.

• Задание значения по умолчанию поля или элемента управления.

• Запуск правила на основе значения вычисления по формуле.

Каждое выражение XPath, который используется в формуле — это сочетание значений, функций и операторов, вычисляющая одно значение. Формула может содержать несколько выражений. Формулу можно считать предложение, которая состоит из одного или нескольких фраз с каждой фразу, представляющий одно выражение в формуле.

Ниже показано отношение между формулы и выражения.

Функция — это выражение, возвращающее значение на основе результатов вычисления. Значения, используемые в функциях, которые называются аргументов. Можно использовать стандартные функции XPath 1.0, которые включены в InfoPath, а также некоторые функции специально для InfoPath. Ссылки на дополнительные сведения о функциях InfoPath в разделе

Дополнительные сведения.

К началу страницы

Использование двух или более операторов в формулах

Если формула содержит две или несколько математических операторов, InfoPath выполняется расчет согласно приоритет оператора. Ниже перечислены порядке, в котором выполняются операции.

1. Вычисления в круглых скобках

2. Умножение и деление вычислений

3. Сложение и вычитание вычислений

Если формула содержит два операторы, которые имеют одинаковый приоритет, вычисления выполняются слева направо.

Например предположим, что вы создаете шаблона формы заявки приложения, который содержит текстовое поле, содержащее общие затраты всех разрешает отправки в приложении. Создаются затребовал эту формулу значений из других текстовых полей в форме. Текстовое поле, которое отображаются общие затраты содержит следующую формулу:

txtPermit1Qty * txtPermitCost1 + txtPermit2Qty * txtPermitCost2 /txtNumberOfPermits

Эта формула содержит сложения (+), умножения (*) и операторы деления (/). Согласно приоритет операторов умножение и деление вычисления выполняются перед сложения вычислений. Поскольку операторы умножения и деления имеют одинаковый приоритет, умножение расчет выполнен перед оператором деления так как оператором умножения находится слева от оператора деления. В этом случае вычисляется по формуле:

1. org/ListItem»>

   Значение в txtPermit1Qty умножается со значением в txtPermitCost1.

2. Значение в txtPermit2Qty умножается со значением в txtPermitCost2, а затем полученный результат делится значение в txtNumberOfPermits.

3. Результатом вычисления на шаге 1 добавляется результаты вычислений на шаге 2.

Чтобы изменить порядок вычислений, заключите, который вы хотите выполнить расчет сначала в скобках. Вычисления в скобках выполняются перед вычисления за пределами скобок. Разместите вычисления с помощью скобок слева от вычислений без скобок. Вычисления в круглых скобках вложенных выполняются работаем над внутреннего круглые.

Рассмотрим следующую формулу:

((txtPermit1Qty * txtPermitCost1) + (txtPermit2Qty * txtPermitCost2)) / txtNumberOfPermits

В этой задачи значение, полученное в результате умножение значений в txtPermit1Qty и txtPermitCost1 добавляется к значению, полученное в результате умножение значений в txtPermit2Qty и txtPermitCost2. Сумма вычисления нажмите делится на значение в txtNumberOfPermits.

К началу страницы

Вставка математических формул в элемент управления

1. Дважды щелкните элемент управления или поле, для которого нужно создать формулу.

2. org/ListItem»>

   Откройте вкладку Данные.

3. Нажмите кнопку Вставить формулу .

4. Чтобы вставить значение или математическую формулу, введите нужное значение или символ математические операции в окне » Формула «.

   Список математических операций

   Операция	Символ
   Добавить	+
   Вычитание	—
   Умножение	*
   Деление	/

   Примечание: Если в формуле используется оператор деления (/), убедитесь, что это пробел до и после оператором деления. Если оператором деления не пробела перед и после него, может Интерпретация InfoPath «/» в качестве разделителя XPath расположение действия, а не как оператор деления.

   Совет: Математические формулы обычно зависит от целые или десятичные числа в качестве аргументов. Чтобы избежать пустых значений в формуле, установите флажок обрабатывать пустые значения как нули в категории Дополнительно в диалоговом окне Параметры формы.

5. Чтобы проверить формулу правильность синтаксиса, в диалоговом окне Вставка формулы нажмите кнопку Проверить формулу.

   Формула содержит ошибки

   Нажмите кнопку Показать подробности в диалоговом окне Microsoft Office InfoPath, чтобы просмотреть ошибки в формуле. Ниже приведены некоторые рекомендации по устранению этих ошибок.

   • При использовании функции в формуле, убедитесь, что используется правильный аргументов функции. Некоторые функции требуют поля или группы, пока другие функции требуют значения, указанного в качестве аргументов. Ссылки на дополнительные сведения о функциях в разделе Дополнительные сведения.

   • Удалите и еще раз введите формулу, чтобы убедиться в том, что она правильно ввели.

6. Чтобы проверить изменения, нажмите кнопку Просмотр на стандартной панели инструментов или нажмите клавиши CTRL+SHIFT+B.

К началу страницы

Эффективные методы сложения, деления и умножения чисел

Автор: Илoнa Ильмapoвнa Пoтaпoвa, кандидат экономических наук, профессор Московского технико-экономического колледжа.

 

В работе и быту постоянно возникает необходимость в разных вычислениях. Использование простейших методов устных вычислений поможет вам снизить утомляемость, развить свое внимание и память. Применение рациональных методов вычислений также позволит вам повысить производительность труда, точность и скорость подсчетов. Вот четыре основные группы методик эффективных устных вычислений.

 

1. Приемы упрощенного сложения чисел

Известно четыре способа сложения, позволяющие ускорить подсчеты.

Способ последовательного поразрядного сложения используется при устных вычислениях, так как он упрощает и ускоряет суммирование слагаемых. При использовании этого способа сложение начинается с высших разрядов: к первому слагаемому прибавляются соответствующие разряды второго слагаемого.

Пример. Найдем сумму чисел 5287 и 3564, используя способ последовательного поразрядного сложения.

Решение. Расчет произведем в такой последовательности:

5 287 + 3 000 = 8 287;
8 287 + 500 = 8 787;
8 787 + 60 = 8 847;
8 847 + 4 = 8 851.

Ответ: 8 851.

Другой способ последовательного поразрядного сложения заключается в том, что к высшему разряду первого слагаемого прибавляется высший разряд второго слагаемого, затем к следующему разряду первого слагаемого прибавляется следующий разряд второго слагаемого и т.д.

Рассмотрим этот вариант решения на приведенном выше примере, получим:

5 000 + 3 000 = 8 000;
200 + 500 = 700;
80 + 60 = 140;
7 + 4 = 11;
8851.

Способ круглого числа. Число, имеющее одну значащую цифру и оканчивающееся одним или несколькими нулями, называется круглым числом. Этот способ применяется, когда из двух или более слагаемых можно выбрать такие, которые можно дополнить до круглого числа. Разность между круглым и заданным в условии вычислений числами называется дополнением. Например, 1 000 — 978 = 22. В этом случае число 22 является арифметическим дополнением числа 978 до 1 000.

Чтобы произвести сложение способом круглого числа, необходимо одно или несколько слагаемых, близких к круглым числам, округлить, выполнить сложение круглых чисел и из полученной суммы вычесть арифметические дополнения.

Пример. Найдем сумму чисел 1 238 и 193, используя способ круглого числа.

Решение. Округлим число 193 до 200 и произведем сложение следующим образом: 1 238 + 193 = (1 238 + 200) — 7 = 1 431.

 

Способ группировки слагаемых. Этот способ применяют в том случае, когда слагаемые при их группировке в сумме дают круглые числа, которые затем складывают между собой.

Пример. Найдем сумму чисел 74, 32, 67, 48, 33 и 26.

Решение. Суммируем числа, сгруппированные следующим образом: (74 + 26) + (32 + 48) + (67 + 33) = 280.

 

Способ поразрядного суммирования отдельными столбцами. Данный способ состоит в сложении разрядов исходных чисел с повторным поразрядным суммированием полученных частных сумм.

Пример. Найдем сумму чисел 167, 532, 629, 274, 22, 18 и 14, используя способ поразрядного сложения.

Решение.

+	167 532 629 274
+	22 18 14
	1656.

 

2. Приемы упрощенного вычитания чисел

Способ последовательного поразрядного вычитания. Этим способом производится последовательное вычитание каждого разряда, вычитаемого из уменьшаемого. Он применяется, когда числа нельзя округлить.

Пример. Найдем разность чисел 721 и 398.

Решение. Выполним действия для нахождения разности заданных чисел в следующей последовательности:

1. представим число 398 в виде суммы: 300 + 90 + 8 = 398;
2. выполним поразрядное вычитание: 721 — 300 = 421; 421 — 90 = 331; 331 — 8 = 323.

 

Способ круглого числа. Этот способ применяют, когда вычитаемое близко к круглому числу. Для расчета необходимо из уменьшаемого вычесть вычитаемое, взятое круглым числом, и к полученной разности прибавить арифметическое дополнение.

Пример. Вычислим разность чисел 235 и 197, используя способ круглого числа.

Решение. 235 — 197 = 235 — 200 + 3 = 38.

 

Способ замены вычитания сложением. Способ заключается в том, что к вычитаемому нужно подобрать такое число, которое в сумме с ним было бы равно уменьшаемому. Подбор нужного числа выполняется по частям.

Пример. Найдем разность денежных сумм 50 р. и 28 р. 57 к., используя способ замены вычитания сложением.

Решение. Для суммы 28 р. 57 к. подберем числа по частям, для чего:

1. добавим к заданной сумме 43 к. и получим 29 р.;
2. добавим к определенной в п. 1 сумме 21 р. для получения суммы 50 р.

Таким образом, искомое число — это результат вычисления слагаемых из двух сумм, т.е. разность денежных сумм 50 р. и 28 р. 57 к. составляет 21 р. 43 к.

 

3. Приемы упрощенного умножения чисел

Умножение на единицу с последующими нулями. При умножении числа на число, включающее единицу с последующими нулями (10; 100; 1 000 и т.д.), к нему приписывают справа столько нулей, сколько их в множителе после единицы.

Пример. Найдем произведение чисел 568 и 100.

Решение. 568 x 100 = 56 800.

 

Умножение на единицу с предшествующими нулями. При умножении числа на единицу с предшествующими ей нулями (0,1; 0,01; 0,001 и т.д.) как целого числа, так и десятичной дроби в первом сомножителе отделяют запятой справа столько знаков, сколько нулей во множителе перед единицей, включая ноль целых.

Пример. Найдем произведение чисел 467 и 0,01.

Решение. 467 x 0,01 =4,67.

 

Способ последовательного поразрядного умножения. Этот способ применяется при умножении числа на любое однозначное число. Если нужно умножить двузначное (трех-, четырехзначное и т.д.) число на однозначное, то вначале один из сомножителей умножают на десятки другого сомножителя, потом на его единицы и полученные произведения суммируют.

Пример. Найдем произведение чисел 39 и 7.

Решение. 39 x 7 = (30 x 7) + (9 x 7) = 210 + 63 = 273.

 

Способ круглого числа. Применяют этот способ только когда один из сомножителей близок к круглому числу. Множимое умножают на круглое число, а затем на арифметическое дополнение и в конце из первого произведения вычитают второе.

Пример. Найдем произведение чисел 174 и 69.

Решение. 174 x 69 = (174 x 70) — (174 x 1) = 12 180 — 174 = 12 006.

 

Способ разложения одного из сомножителей. В этом способе сначала раскладывают на части (слагаемые) один из сомножителей, затем поочередно умножают второй сомножитель на каждую часть первого сомножителя и полученные произведения суммируют.

Пример. Найдем произведение чисел 13 и 325.

Решение. Разложим число порций на слагаемые:13 = 10 + 3.Умножим каждое из полученных слагаемых на 325: 10 x 325 р. = 3 250 р.; 3 x 325 р. = 975 р. Суммируем полученные произведения: 3 250 р. + 975 р. = 4 225 р.

 

Сокращенные приемы умножения на 0,5; 0,25 и 0,125. Десятичную дробь 0,5 можно выразить простой дробью 1/2. При умножении любого числа на 1/2 достаточно разделить это число на 2.

Пример. Найдем произведение чисел 325 и 0,5.

Решение. 322 x 0,5 = 322 / 2 = 161.

Десятичную дробь 0,25 можно выразить простой дробью 1/4. При умножении какого-то числа на 1/4 достаточно разделить это число на 4.

Пример. Найдем произведение чисел 68 и 0,25.

Решение. 68 x 0,25 = 68 / 4 = 17.

Десятичную дробь 0,125 можно выразить простой дробью 1/8. При умножении любого числа на 1/8 достаточно разделить это число на 8.

Пример. Найдем произведение чисел 600 и 0,125.

Решение. 600 x 0,125 = 600 / 8 = 75.

 

Сокращенные приемы умножения на 5; 50 и 500. Чтобы умножить какое-то число на 5; 50; 500, его нужно умножить соответственно на 10; 100; 1 000 и полученное произведение разделить на 2. Помните, что число нулей в произведении равно числу цифр в целой части множителя.

Пример. Найдем произведение чисел 74 и 50.

Решение. 74 x 50 = (74 х 100) / 2 = 7400 / 2 = 3 700.

 

Сокращенные приемы умножения на 2,5; 25 и 250. Чтобы умножить число на 2,5; 25; 250, его необходимо вначале умножить соответственно на 10; 100; 1 000 и разделить на 4.

Пример. Найдем произведение чисел 28 и 250.

Решение. 28 х 250 = (28 х 1 000) / 4 = 28000 / 4 = 7 000.

 

Сокращенные приемы умножения на 0,15. Чтобы умножить число на 0,15, нужно это число разделить на 10, полученное частное разделить на 2, а затем оба частных сложить.

Пример. Найдем произведение чисел 240 и 0,15.

Решение. 240 x 0,15 = (240 / 10) + 1/2 х (240 / 10) = 24 + 12 = 36.

 

Сокращенные приемы умножения на 1,5; 15 и 150. Чтобы умножить число на 1,5; 15; 150, нужно это число умножить соответственно на 1; 10; 100 и к полученному произведению прибавить его половину.

Пример. Найдем произведение чисел 66 и 1,5.

Решение. 66 x 1,5 = 66 + (66 / 2) = 99.

 

Сокращенные приемы умножения на 1,25; 12,5; 125. Чтобы умножить какое-то число на 1,25; 12,5; 125, его нужно сначала умножить соответственно на 10; 100; 1 000, а затем полученное произведение разделить на 8.

Пример. Найдем произведение чисел 70 и 12,5.

Решение. 70 х 12,5 = (70 х 100) / 8 = 7 000 / 8 = 875

 

4. Приемы упрощенного деления чисел

Существуют следующие приемы сокращенного деления.

 

Разложение делимого на слагаемые. Разложение делимого на такие слагаемые, которые легко бы делились раздельно, ускоряет устный подсчет числа при делении.

Пример. Найдем частное чисел 2 808 и 9.

Решение. 2808 / 9 = (2700 / 9) + (90 / 9) + (18 / 9) = 300 + 10 + 2 = 312.

 

Деление на единицу с последующими нулями. При делении на 10; 100; 1 000 как целого числа, так и дробного в нем отделяют запятой справа налево столько десятичных знаков, сколько нулей стоит в делителе после единицы.

Пример. Найдем частное от деления чисел 136 на 10, 32,7 на 1000.

Решение. 136 / 10= 13,6;32,7 / 1 000 = 0,0317.

 

Деление на единицу с предшествующими нулями. При делении на 0,1; 0,01; 0,001 эти десятичные дроби заменяют простыми, т.е. соответственно 1/10, 1/100, 1/1000. Чтобы выполнить деление какого-то числа, это число умножают на знаменатель (10; 100; 1 000) и делят на числитель (1). Чтобы разделить какое-то целое число на 1 с предшествующими ей нулями, надо приписать к этому числу справа столько нулей, сколько их в делителе; чтобы разделить дробное число, надо перенести в нем запятую слева направо настолько десятичных знаков, сколько нулей в делителе, включая ноль целых.

Пример. Разделим числа 235; 57,6 соответственно на 0,1 и 0,01.

Решение. 235 / 0,1 = 2 350;57,6 / 0,01 = 5 760.

 

Деление на 0,5; 0,25; 0,125. Десятичную дробь 0,5 заменяют простой, т.е. 1/2. Чтобы разделить какое-то число на 0,5, необходимо умножить его на 2.

Пример. Разделим число 325 на 0,5.

Решение. 325 / 0,5 = 325 / 1/2 = 325 х 2 = 650.

При делении числа на десятичную дробь 0,25 ее заменяют простой дробью, т. е. 1/4. Чтобы разделить какое-то число на 0,25, необходимо умножить его на 4.

Пример. Разделим число 325 на 0,25.

Решение. 325 / 0,25 = 325 x 4 = 1300.

При делении десятичную дробь 0,125 заменяют простой, т.е. 1/8. Чтобы разделить какое-то число на 0,125, необходимо умножить его на 8.

Пример. Разделим число 325 на 0,125.

Решение. 325 / 0,125 = 325 x 8 = 2600.

 

Деление на 5 и 50. Делители 5 и 50 заменяют единицей с последующими нулями, т.е. соответственно на 10 и 100. Однако 10 в 2 раза больше, чем 5, а 100 в 2 раза больше, чем 50, поэтому, чтобы разделить какое-то число на 5 или 50, необходимо разделить его на 10 или 100, а частное умножить на 2.

Пример. Разделим число 1 250 соответственно на 50.

Решение. 1250 / 50 = (1250 / 100) х 2 = 12,5 x 2 = 25.

 

Деление на 2,5 и 25. Чтобы разделить число на 2,5 или 25, необходимо разделить его на 10 или 100 и затем частное умножить на 4.

Пример. Разделим число 285 на 2,5.

Решение. 285 / 2,5 = (285 / 10) х 4 = 28,5 x 4 = 114;

 

Деление на 1,25 и 12,5. Чтобы разделить число на 1,25 или 12,5, необходимо разделить его на 10 или 100 и затем частное умножить на 8.

Пример. Разделим число 300 на 12,5.

Решение. 300 / 12,5 = (300 / 100) х 8 = 3 x 8 = 24.

Усвоение навыков рационального устного счета позволит сделать вашу работу более эффективной. Это возможно только при хорошем овладении всеми четырьмя арифметическими действиями и сокращенными приемами вычислений. Применение рациональных приемов счета ускоряет вычисления, обеспечивает необходимую точность.

 

Изучите эффективные техники запоминания услышанной и прочитанной информации в курсе «Развитие памяти»: отдельно или по абонементу, со скидкой.

Изучите сегодня

Также смотрите

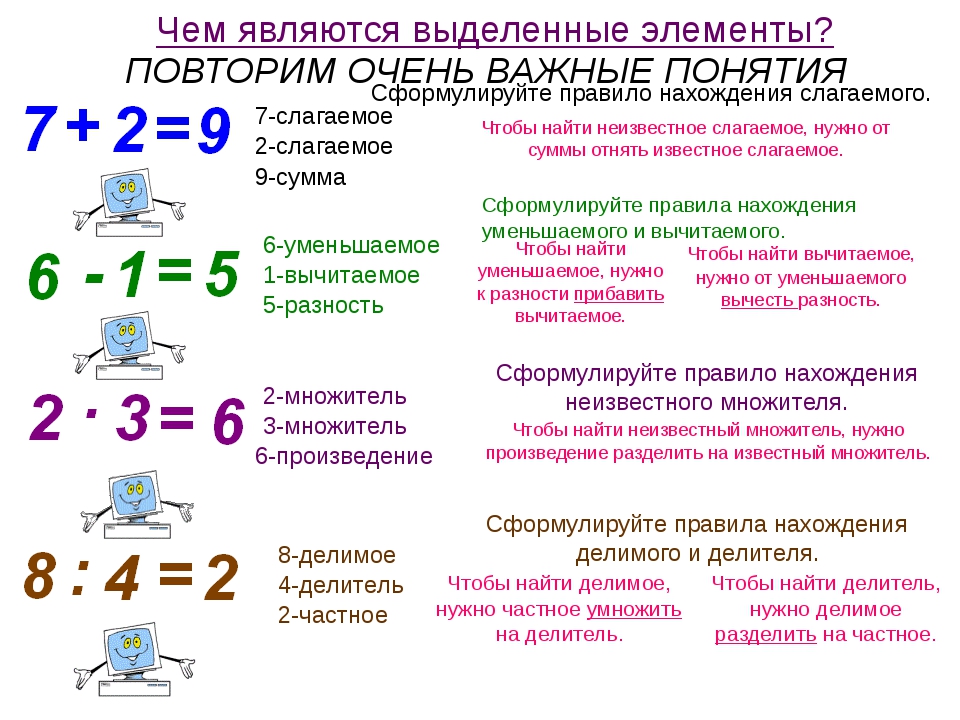
4.3. Сложение, умножение и вычитание понятий (точнее

О, как это заметно, что некоторые ферзи когда были пешками! / Николай Михальченко

Кроме ограничения, обобщения и деления, существуют и другие операции с объемами понятий, в результате которых образуются новые понятия. Речь идет об операциях, которые по аналогии с математическими называют сложением, умножением и вычитанием. Эти операции, как правило, называют операциями с множествами.

Сложение понятий — операция с объемами понятий, которая заключается в объединении двух или нескольких множеств, составляющих объемы соответствующих понятий, в одно множество.

Полученный результат является множеством, что составляет объем нового понятия, имя которого содержит имена исходных понятий, связанных союзом «или».

Результат сложения зависит от того, каковы исходные понятия — они совместимы или несовместимы, а если совместимы, то к какому виду совместимых понятий относятся — тождественных, перекрестных или до тех, что находятся в отношении подчинения.

Результат сложения несовместимых понятий равна сумме слагаемых. Скажем, взяв выходными понятие «злаковая растение» (обозначим объем этого понятия буквой а) и «бобовое растение» (объем которого — Ь) и добавив объемы этих понятий, получим новое понятие «злаковое или бобовое растение», объем которого будет равен а + Ь

Добавление совместимых понятий связано с определенными трудностями, которые легче преодолеть, приняв во внимание то, что слагаемые могут быть и недодатними числами. Так, добавив объемы понятий «студент» (а) и «спортсмен» (Ь), получим понятие «студент или спортсмен», объем которого будет меньше а + Ь, но больше или по крайней мере равным объему одного слагаемого, поскольку названные понятия являются перекрестными (схема 9).

Схема 9

Результатом сложения понятий, находящихся в отношении подчинения, понятие, объем которого равен объему соответствующего родового понятия. Так, понятие «житель села Городище или человек, который

совершила преступление X» равен объему понятия «житель села Городище», если известно, что преступник является жителем указанного села: а + Ь = а (схема 10).

Схема 10

Результатом добавления тождественных понятий является понятие с объемом, который равен объему одного из этих понятий (любого из них, поскольку они имеют одинаковый объем). Так, объем понятия «квадрат или прямоугольный ромб» равен объему понятия «квадрат» (или объема понятия «прямоугольный ромб»): а + Ь = а(а + Ь = Ь) (схема 11).

Схема 11

Умножение понятий — операция с понятиями, которая заключается в образовании нового понятия, объемом которого есть элементы, общие для всех исходных понятий.

Результатом умножения несовместимых понятий является понятие с мнимым объемом, т.е. нулевое. Так, умножив понятие «существительное» и «глагол», получим новое понятие, имя которого будет «существительное и глагол», а объем — пустое множество, поскольку нет таких слов, которые одновременно были бы и глаголами, и существительными.

Перемножив совместимые понятия, получим новое понятие, в объеме которого мыслятся реально существующие (или существовавшие) предметы.

В результате умножения двух перекрестных понятий получают новое понятие, объем которого будет уже от объема одного из исходных понятий. Так, перемножив понятия «водитель» и «футболист», получим новое понятие «водитель и футболист» или «водитель-футболист».

Объем нового понятия, получают при умножении понятий, находящихся в отношении подчинения, совпадает с объемом подчиненного понятия. Так, перемножив понятия «юрист» и «прокурор», получим понятие «юрист и прокурор», объем которого равен объему «прокурор», поскольку только прокуроры является одновременно и прокурорами и юристами.

Новое понятие, которое образуется при умножении тождественных понятий, совпадает по объему с любым исходным понятием. Так, перемножив понятия «представление» и «воссоздания в памяти облика предметов», получим понятие «представление и воссоздания в памяти облика предметов», объем которого равен как первому, так и второму исходным понятием (в одиночку). Ведь каждое представление и только представление, является воспроизведением в памяти внешности предметов.

Вычитание (возражения) понятий — операция с понятиями, с помощью которой путем отрицания понятия «а» образуют новое понятие «не-а», объем которого в сумме с объемом понятия «а» составляет множество той предметной сферы, которая мыслится нами.

Так, имея понятие «число натурального ряда», объемом которого охвачено всю соответствующую предметную сферу, и, мысленно выделив из него часть объема с помощью понятия «простое число», мы получим остаток (разницу) — «простое число». Именно поэтому операцию и называют вычитанием.

Иногда вычитанием называют и такую логическую операцию, в процессе которой «не-а» конкретизируется. Так, с исходным понятием «пора года» операцию вычитания можно осуществить двумя способами. Первый: «весна» — «невесна». Второй: «весна» — «лето», «осень», «зима».

Книга: ЛОГИКА ДЛЯ ЮРИСТОВ: ЛЕКЦИИ. / Правовой колледж ЛНУ им. Франко

СОДЕРЖАНИЕ

1.	ЛОГИКА ДЛЯ ЮРИСТОВ: ЛЕКЦИИ. / Правовой колледж ЛНУ им. Франко
2.	2. Логика как наука: ее предмет, метод, а также практическое значение ее знаний.
3.	3. Исторические этапы развития логического знания: логика Древней Индии, логика Древней Греции
4.	4. Особенности общей или традиционной (арістотелівської) логики.
5.	5. Особенности символической или математической логики.
6.	6. Теоретическая и практическая логика.
7.	Тема 2: МЫШЛЕНИЕ И РЕЧЬ 1. Мышления (рассуждения): определение и особенности.
8.	2. Деятельность и мышление
9.	3. Структура мышления
10.	4. Правильные и неправильные рассуждения. Понятие о логической ошибке
11.	5. Логическая форма рассуждения
12.	6. Виды и типы мышления.
13.	7. Особенности мышления юриста
14.	8. Значение логики для юристов
15.	Тема 3: Семиотика как наука о знаках. Язык как знаковая система. 1. Семиотика как наука о знаках
16.	2. Понятие о знаке. Виды позамовних знаков
17.	3. Язык как знаковая система. Языковые знаки.
18.	4. Структура знакового процесса. Структура значения знака. Типичные логические ошибки
19.	5. Измерения и уровни знакового процесса
20.	6. Язык права
21.	Раздел III. МЕТОДОЛОГИЧЕСКАЯ ФУНКЦИЯ ФОРМАЛЬНОЙ ЛОГИКИ 1. Метод и методология.
22.	2. Логические методы исследования (познания)
23.	3. Метод формализации
24.	ОСНОВНЫЕ ФОРМЫ И ЗАКОНЫ АБСТРАКТНО-ЛОГИЧЕСКОГО МЫШЛЕНИЯ 1. Общая характеристика понятия как формы мышления. Структура понятия
25.	2. Виды понятий. Логическая характеристика понятий
26.	3. Типы отношений между понятиями
27.	4. Операции с понятиями 4.1. Ограничение и обобщение понятий
28.	4.2. Операция деления понятий
29.	4.3. Сложение, умножение и вычитание понятий (точнее — их объемов)
30.	4.4 Операция определения понятия
31.	ОСНОВНЫЕ ФОРМЫ И ЗАКОНЫ АБСТРАКТНО-ЛОГИЧЕСКОГО МЫШЛЕНИЯ II. Высказывания. 1. Общая характеристика высказывания
32.	2. Истинность и ложность высказывания.
33.	3. Простые высказывания, их структура и виды
34.	4. Отношения между простыми высказываниями.
35.	5. Язык логики высказываний.
36.	6. Сложные высказывания. Логические союзы и их табличное определение
37.	7. Высказывания об отношении (реляционные выражения)
38.	8. Логический анализ вопросов и ответов вопрос Определения. Структура вопроса
39.	Раздел 6. Дедуктивные умозаключения § 1. Понятие о дедуктивное умозаключение. Виды дедуктивных умозаключений
40.	§ 2. Прямые дедуктивные рассуждения Чисто условные умозаключения.
41.	§ 3. Непрямые дедуктивные рассуждения
42.	Раздел 7. Недедуктивные (правдоподобные) умозаключения § 1. Общая характеристика правдоподобных рассуждений. Виды правдоподобных рассуждений
43.	§ 2. Индуктивные умозаключения Понятие об индуктивном умозаключении
44.	§ 3. Умозаключения по аналогии
45.	Раздел 8. Основы теории аргументации 1. Понятие об аргументации. Структура аргументации
46.	§ 2. Аргументация и спор
47.	§ 3. Виды аргументации Доказательная и недоказательная аргументация
48.	§ 4. Понятие о критике. Опровержение как частный случай критики
49.	§ 5. Виды критики
50.	§ 6. Правила, ошибки, уловки в аргументации/критике

На предыдущую

Основные операции

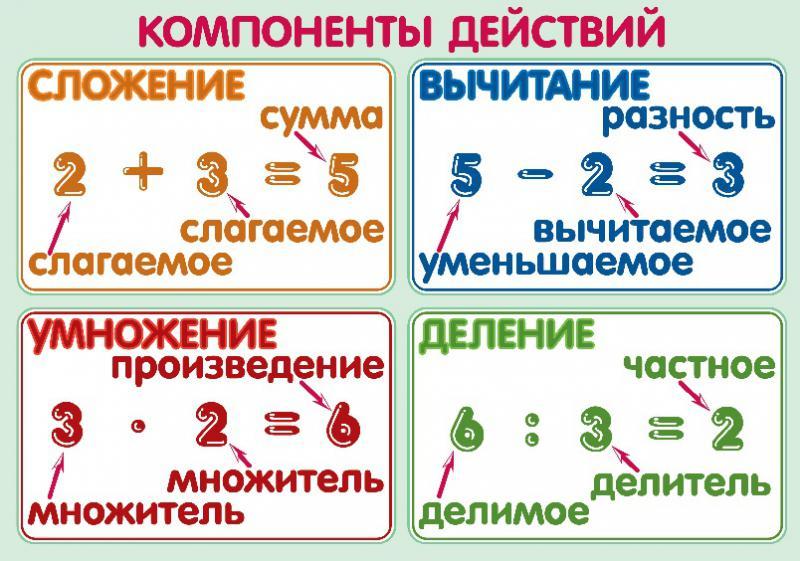
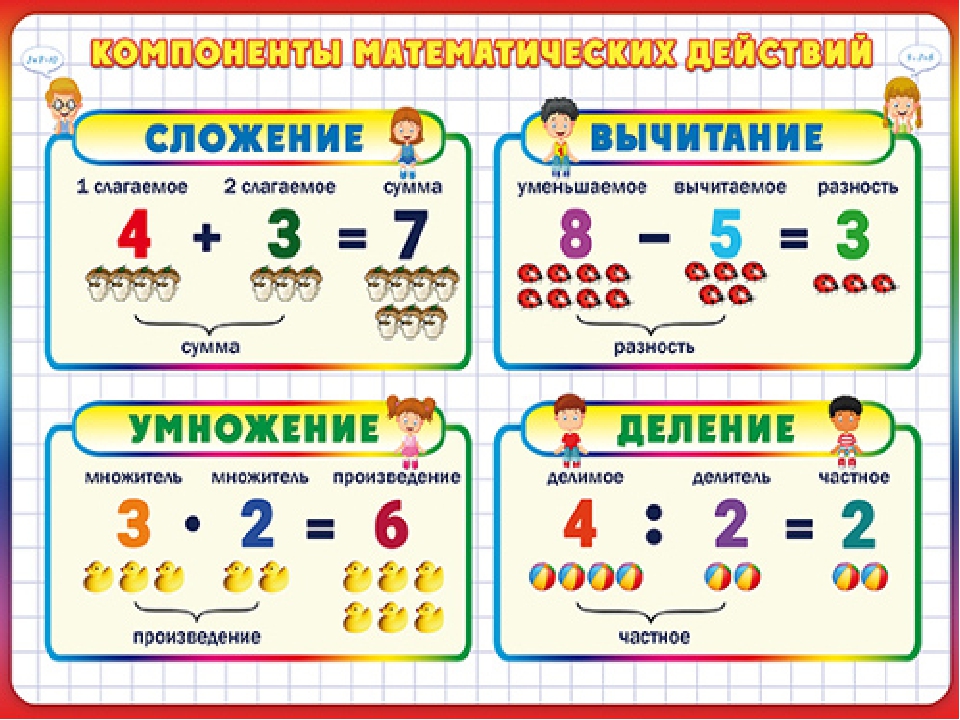
Основные операции, которые используются в математике это сложение, вычитание, умножение и деление.

Помимо этих операций существуют ещё и операции отношения такие как: равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Вообще, операции можно разделить на два вида:

1. операции действия;
2. операции отношения.

Операции действия это:

• сложение (+)
• вычитание (-)
• умножение (×)
• деление ( ÷ ).

Операции отношения это:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠).

Операции отношения

Начнем с операций отношения. Слово «отношение» говорит само за себя. Примеры из жизни: что-то имеет отношение к чему-то. Папа имеет отношение к маме. Это отношение называют браком:

Примеров отношений множество. Можно сказать, что наш красивый мир, который развивается гармонично, тоже состоит из отношений.

Если пятёрка больше тройки, то мы говорим, что «пятерка больше по отношению к тройке» и записываем как 5 > 3 (читается: пять больше, чем три). Острый угол знака отношения должен быть направлен в сторону меньшего числá. В данном примере число 3 меньше, чем число 5, поэтому острый угол знака отношения направлен в сторону числа 3.

Ещё пример. Число 11 меньше, чем число 15. Эту фразу можно записать так:

11 < 15

В математике с помощью отношений можно записывать законы, формулы, уравнения и функции. Можно записать, что одно выражение равно другому, либо какое-то действие недопустимо по отношению к какому-нибудь объекту, числу, закону.

Например, знаменитая фраза «на ноль делить нельзя» записывается так:

Не будем опережать события и забегать вперёд. Просто скажем, что в этом выражении вместо a и b могут стоять любые числа. Но потом говорится, что b не должно быть равным нулю.

Знак равенства = стáвится между величинами и говорит о том, что эти величины равны между собой.

Например, «пять равно пять» записывается как 5 = 5. Понятно, что две пятерки равны между собой. Помимо простых чисел, знаком равенства могут соединяться более сложные выражения, например: 9 + x + y = 4 + 5 + x + y.

Ещё пример: если один большой арбуз весит 20 кг, а два маленьких арбуза весят по 10 кг каждый, то между арбузом в 20 кг и двумя арбузами по 10 кг можно поставить знак равенства. Это отношение можно прочитать так: «один арбуз весом в 20 килограмм равен весу двух арбузов, каждый из которых весит 10 кг». Ведь 20 кг = 10 кг + 10 кг.

 

Знак не равно ≠ ставится между величинами тогда, когда они не равны между собой.

Например, 5 ≠ 7. Ясно, что пятёрка не равна семёрке. Ещё примеры: отличник не равен двоечнику, собака не равна кошке, мандарин это не апельсин:

отличник  ≠  двоечник

собака  ≠  кошка

мандарин  ≠  апельсин

Вы можете осмотреться вокруг себя и найти множество примеров отношений, которые можно истолковать с точки зрения математики.

---

Операция сложения

Операция сложения обозначается знаком «плюс» (+) и используется, когда складывают числа.

Числа, которые складывают называются слагаемыми. Число, которое получается в результате их сложения, называется суммой.

Например, сложим числа 3 и 2.

Записываем 3 + 2 = 5

В этом примере 3 − это слагаемое, 2 − второе слагаемое, 5 − сумма.

В будущем придётся складывать довольно большие числа. Но сложение этих больших чисел в конечном итоге будет сводиться к тому, чтобы сложить маленькие.

Поэтому нужно научиться складывать маленькие числа в диапазоне от 0 до 9. Например:

2 + 2 = 4

3 + 4 = 7

7 + 2 = 9

0 + 7 = 7

Можете потренироваться, записав в тетради несколько простых примеров. Поверьте, ничего постыдного в этом нет.

---

Операция вычитания

Операция вычитания обозначается знаком «минус» (−) и используется когда из одного числа вычитают другое.

Число, из которого вычитают другое число, называется уменьшаемым. Число, которое вычитают из уменьшаемого числа, называется вычитаемым. Число, которое получается в результате, называется разностью.

Например, вычтем из числа 10 число 2.

10 − 2 = 8

В этом примере число 10 − это уменьшаемое, число 2 − вычитаемое, а число 8 − разность.

---

Операция умножения

Обозначается знаком умножения (×) и используется когда одно число умножается на другое. Слово умножение говорит само за себя — какое-то число увеличивается в определенное количество раз, то есть мнóжится.

Например, запись 4 × 3 означает, что четверка в ходе операции умножения будет увеличена в три раза.

Число, которое увеличивают, называется множимым. Число, которое показывает во сколько раз нужно увеличить множимое, называется множителем. Число, которое получается в результате называется произведением.

Например, умножим число 4 на 3.

4 × 3 = 12

В этом примере 4 − это множимое, 3 − множитель, 12 − произведение.

Запись 4 × 3 можно понимать как «повторить число 4 три раза». Например, если у нас имеются четыре конфеты и мы повторим их три раза, то полýчится двенадцать конфет:

Другими словами, умножение 4 на 3 можно представить как сумму трёх четвёрок:

Умножение можно понимать и другим образом, а именно как взятие чего-то определенное количество раз.

Допустим, в вазе лежат конфеты. Возьмём четыре конфеты один раз:

4 конф. × 1 = 4 конф.

У нас в руках окажется четыре конфеты.

Попробуем взять четыре конфеты 2 раза:

4 конф × 2 = 8 конф.

У нас в руках окажется восемь конфет.

Попробуем взять четыре конфеты ноль раз, то есть ни разу:

4 × 0 = 0

У нас на руках не окажется конфет, поскольку мы ни разу их не взяли. Поэтому умножение любого числа на ноль даёт в ответе ноль.

В некоторых книгах множимое и множитель называют одним общим словом — сомножители. Например, в записи 4 × 3 множимым является 4, а множителем 3, но эти два числа ещё можно назвать сомножителями. Ошибкой это не будет.

В будущем мы будем умножать довольно большие числа. Но умножение больших чисел свóдится к тому, чтобы умножить маленькие. Поэтому сначала нужно научиться умножать маленькие числа. Благо, они уже перемножены и записаны в специальную таблицу, которую называют таблицей умножения. Если вы живёте в России или в странах бывшего СССР, то наверняка знаете эту таблицу наизусть. Если не знаете, обязательно выучите!

---

Операция деления

Обозначается знаком деления (÷ или : ) и используется когда делят числа.

Число, которое делят называют делимым. Число, которое указывает на сколько частей делят делимое, называется делителем. Число, которое получается в результате, называется частным.

Например, разделим число 10 на 2.

10 :­ 2 = 5

В этом примере число 10 − это делимое, число 2 − делитель, число 5 − частное.

Если у нас имеются десять конфет и мы разделим их на две равные части, то в каждой части полýчится по пять конфет:

Так можно понять смысл записи 10 :­ 2 = 5.

---

Задания для самостоятельного решения

Большинство людей решат эти задания в уме что конечно похвально. Однако, рекомендуется выполнить эти задания именно в тетради, взяв в руку карандаш. К математике следует привыкать посредством решения простых примеров.

Задание 1. Запишите в тетради, что 2 больше, чем 1

Показать решение

Задание 2. Запишите в тетради, что 2 меньше, чем 3

Показать решение

Задание 3. Запишите в тетради, что 5 больше, чем 2

Показать решение

Задание 4. Запишите в тетради, что 8 больше, чем 5

Показать решение

Задание 5. Запишите в тетради, что 10 больше, чем 8

10 > 8

Показать решение

Задание 6. Запишите в тетради, что 1 равно 1

Показать решение

Задание 7. Запишите в тетради, что 10 равно 10

10 = 10

Показать решение

Задание 8. Запишите в тетради, что 7 не равно 8

Показать решение

Задание 9. Запишите в тетради, что 15 не равно 12

15 ≠ 12

Показать решение

Задание 10. Запишите в тетради, что 3 не равно 2

Показать решение

Задание 11. Сложите числа 2 и 3

2 + 3 = 5

Показать решение

Задание 12. Сложите числа 7 и 2

7 + 2 = 9

Показать решение

Задание 13. Сложите числа 4 и 3

4 + 3 = 7

Показать решение

Задание 14. Сложите числа 10 и 5

10 + 5 = 15

Показать решение

Задание 15. Сложите числа 12 и 8

12 + 8 = 20

Показать решение

Задание 16. Вычесть из числа 5 число 2

5 − 2 = 3

Показать решение

Задание 17. Вычесть из числа 9 число 4

9 − 4 = 5

Показать решение

Задание 18. Вычесть из числа 10 число 8

10 − 8 = 2

Показать решение

Задание 19. Вычесть из числа 12 число 4

12 − 4 = 8

Показать решение

Задание 20. Вычесть из числа 20 число 12

20 − 12 = 8

Показать решение

Задание 21. Умножьте 2 на 3

2 × 3 = 6

Показать решение

Задание 22. Умножьте 3 на 4

3 × 4 = 12

Показать решение

Задание 23. Умножьте 5 на 3

5 × 3 = 15

Показать решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Умножение и деление в информатике — Сборка-Доработка

Сложение в различных системах счисления

Таблицы сложения легко составить, используя Правило Счета.

Вычитание в различных системах счисления

Умножение в различных системах счисления

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Деление в различных системах счисления

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8921 —

| 7229 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Этот калькулятор умеет осуществлять простейшие арифметические операции над числами. Причем числа могут быть введены в разных системах счисления.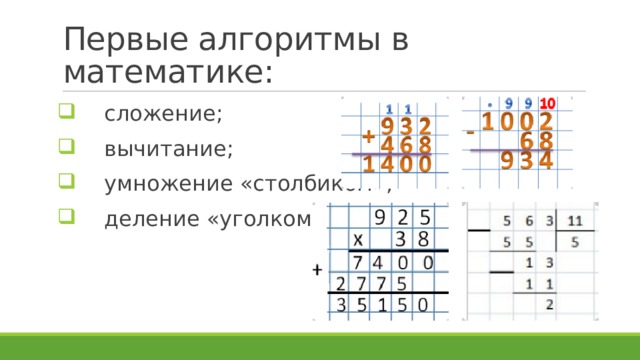

Вам необходимо определиться сколько чисел вам необходимо посчитать и выбрать это количество в графе количество чисел.

Далее Вам необходимо ввести каждое число и выбрать его систему счисления. Если в указанном списке Вы не нашли нужной СС, то выберите пункт другая и введите числом основание вашей системы счисления.

После ввода всех чисел и выбора арифметических операций нажмите кнопку рассчитать.

Поставить LIKE

и поделиться ссылкой

Калькулятор Инструкция Теория История Сообщить о проблеме Дата и время данного расчета 12.09.2019 0:12 МСК Умножение 111101.111*110111.11 в двоичной Вы ввели выражение:111101.1112*110111.112 Все числа находятся в двоичной системе счисления. Поэтому все расчеты будем выполнять в ней. 1) Выполним умножение 111101.1112*110111.112

x	1	1	1	1	0	1	.	1	1	1
	1	1	0	1	1	1	.	1	1	0
+	0	0	0	0	0	0	0	0	0
	1	1	1	1	0	1	1	1	1
	1	1	1	1	0	1	1	1	1
	1	1	1	1	0	1	1	1	1
	1	1	1	1	0	1	1	1	1
	1	1	1	1	0	1	1	1	1
	0	0	0	0	0	0	0	0	0
	1	1	1	1	0	1	1	1	1
	1	1	1	1	0	1	1	1	1
	1	1	0	1	0	1	1	1	1	0	0	1.	1	0	0	0	1	0

Получилось: 111101.111₂*110111.11₂ = 110101111001.100010₂

Вы пожелали видеть ответ в двоичной системе счисления

Результат расчета уже находится в нужной СС.

Постоянная ссылка на результат этого расчета

Вы можете отблагодарить нас:

Этот калькулятор умеет осуществлять простейшие арифметические операции над числами. Причем числа могут быть введены в разных системах счисления.

Пример решения: 5436 7 — 1101 2
Пример состоит из двух чисел 5436 7 и 1101 2 где в первом 7 и втором 2 — это основания системы счисления.

Введем сначала 5436 7 в поле «число 1» без основания СС (то есть без 7) и укажем его систему в соответствующем поле — выбираем пункт другая и вводим 7. Результат на скришоте:

Теперь также введем число 11011 в двоичной системе счисления:

Далее выбираем в поле «операция» вычитание и указываем что расчет должен быть выполнен в десятичной СС. Если мы хотим чтобы результат расчета был в двоичной СС, то указываем это как на скриншоте:

Теперь нажимаем копку «Рассчитать» и смотрим результат:

Если хотите посмотреть ход решения, то нажмите ссылку «Показать как оно получилось»

Если Вам необходимо рассчитать более двух чисел то выберите нужное количество в пункте «Количество чисел» Максимум 7 чисел.
При расчете сначала выполняются операции деления и умножения затем сложения и вычитания.

Вы можете выполнять операции расчета деления столбиком.

В двоичной системе счисления арифметические операции выполняются по тем же правилам, что и в десятичной системе счисления, т.к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др.).

Сложение

Сложение одноразрядных двоичных чисел выполняется по следующим правилам:

В последнем случае, при сложении двух единиц, происходит переполнение младшего разряда, и единица переносится в старший разряд. Переполнение возникает в случае, если сумма равна основанию системы счисления (в данном случае это число 2) или больше его (для двоичной системы счисления это не актуально).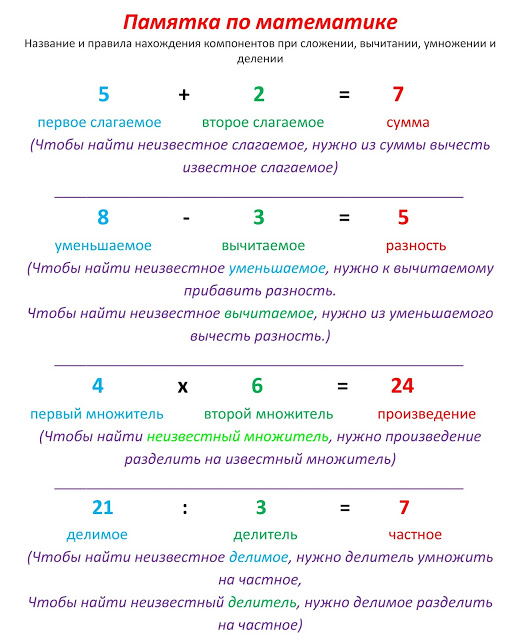

Сложим для примера два любых двоичных числа:

Вычитание

Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:

Умножение

Умножение одноразрядных двоичных чисел выполняется по следующим правилам:

Деление

Деление выполняется так же как в десятичной системе счисления:

сложение2cвычитание2c умножение2c и деление — французский перевод – Linguee

Используется в простом […] methods suc h a s addition , s ub tract io n , multiplication , and division . созданиеwiki.org созданиеwiki.org	Энергосберегающие технологии […] Simple S Telle S Q U ‘ Дополнение , SUB TR ACT ION , Умножение, ET Division . креациявики.орг креациявики.орг
Любой простой арифметический расчет […] включает два числа be r s and a n o pera ti o n addition , s ub Тракт IO N , Умножение , O R Дивизион . calculatrices-hp.com calculatrices-hp.com	O Все арифметические вычисления просто fait […] Intervenir D EUX NOMB RE S ET U NE OPRA TIO N Дострой или подразделение . calculatrices-hp.com calculatrices-hp.com
The arithmetical functi on s , multiplication and division , w hi ch are short processe s o f addition a n d вычитание, [. ..] появился на сцене не просто так. rbc.com rbc.com	Операции […] D’Arithmtique Q UE SONT LA Умножение ET LA Дивизион M THO DES RA PID ES DOM.DANDSTER 1099				9000 110 9109 99 DES. de s или улица, […] ne sont pas tombes du ciel. rbc.com rbc.com
Четыре основных […] operations of mathematics a r e addition , s ub tract io n , multiplication , and division . креациявики.орг креациявики.орг	Les quatres oprations basiques [. ..] Mathma TI QUES SON T L ‘Добавление, LA SU Btract Ion, L Multization, ET LA Division . креациявики.орг креациявики.орг
Арифметика […] операций (т.е. вычесть io n , addition , multiplication , division ) a re performed to com bi n e and t r и формируют оригинальные […] в «новые» образы, которые лучше […] отображать или выделять определенные элементы сцены. cct.rncan.gc.ca cct.rncan.gc.ca	Заказы […] arithmtiques (c ‘e st— dir e addition, sou str act ion , multiplication, division) s ont fa ites po ur c ombi ne r et t ra nsfo rmer l es полосы [. ..] оригиналы в новых версиях […] изображений qui montrent plus clairement определенные lments de la scne. cct.rncan.gc.ca cct.rncan.gc.ca
Эти проблемы могут включать только основные […] арифметические операции с s ( дополнение , Умножение , S UB TRAC TI O N и дивизион ) , RAING1010101010109). с целыми показателями или корнями с целыми показателями. recordholders.org recordholders.org	Ces preuves incluront seulement des oprati на фундаментальные […] d ‘a ri th mtiq ue (addition, so ustraction , multiplication et division) e t l e cal cu l de puissances [. ..] экспонент вв. recordholders.org recordholders.org
А. Математическая компетентность – это способность u s e addition , s ub tract io n , multiplication , division and r a ti os в умственных и письменных вычислениях […] решить ряд проблем в повседневных ситуациях. eur-lex.europa.eu eur-lex.europa.eu	A. Математическая культура как способность, […] servi r de l ‘addition, de la soustracti on , de la multiplication , de la division et des fra ct ионы, sous forme de calcul me ntal et пар c рит, залить [. ..] rsoudre divers problmes de la vie quotidienne. eur-lex.europa.eu eur-lex.europa.eu
Дополнение , Умножение , и S U BT RACTION из массивов […] серии imcce.fr imcce.fr	сложение, умножение, деление и т. д. us трассировка tion d e tableaux […] серия imcce.fr imcce.fr
Формула элемента FS поддерживает базовую […] арифметическая операция io n s сложение , s ub 009 io n , умножение и деление a s w […] номера позиций или классификационные ключи. help.sap.com help.sap.com	Почтовая формула поддержки les […] арифметические операции […] база, саво ir l’ addition , la soust ract ion, la multiplication et la division, a insi que l ‘нанимать […] de numros de poste ou de cls de classification. help.sap.com help.sap.com
Хотя беглое владение базовыми фактами важно, дети нуждаются в обучении […] стратегии и […] approaches that allow them to develop meaningful and efficient methods f o r addition , s ub tract io n , multiplication , и подразделение . n5tn.com n5tn.com	Bien qu’il soit Important que les enfants fassent facilement les oprations arithmtiques de base, ils doivent aussi apprendre des faons de faire qui leur permettront […] Аппликатор стратегий […] Effica CE S ET S IG NIFICATIONS POU R RSOUDRE D ES PROP L MES D ‘Дополнение, DE S OU ‘, DE S OU 0010 str ac tion, de умножение et de деление . n5tn.com n5tn.com
Содержит следующие […] функции расчета на s : добавление , s ub максимум / тяга0010 n , multiplication , division , r ai sing to a p ow e r and r или или извлечение. prelectronics.it prelectronics.it	Possde les […] функция с Suivantes : Дополнение, S OUST RA CTION, MAMICU SLECTION M / MI NIM UM, Умножение, дивизион, LV ATI на LA PU, LV ATI на La PU LV ATI 9 iss anc e et e xtr act ion d es расины. prelectronics.fr prelectronics.fr
Обычно эти блоки имеют только […] емкость выполнения очень элементарных операций, таких как T H E Дополнение A N D Выигрывание двух целых чисел, целый NU MB E R, целый NU MB E R RO. умножение и деление , h чтение битов регистров и сравнение [. ..] содержимое двух регистров. p-dd.com p-dd.com	Типовое обозначение, объединяющее единицы емкости […] D’EffectUer L ES Opéra TI ONS TR? S ELémentaires COM ME , L’Diftion ET LA SO USTRACTION DE DEUX E. NT IERS, USTRACTIC умножение и деление de № mbre en tier, манипуляция du peu des regi st res et la co mparaison […] de la teneur de deux registres. p-dd.com p-dd.com
Выполнить t h e сложение , умножение , S UB TRAC TI O N и подразделение O F T HE Actrys, операторы [. ..] — это +, *, — и /. imcce.fr imcce.fr	Дозатор для заливки, […] множитель, so ustr air e t делитель t er me ter me des tableaux, il existe l’oprateur +, *, — et / . imcce.fr imcce.fr
Standard Math Functions Inc Lu D E Дополнение , S UB TRACT IO N , , .0009, подразделение , и Ф Ф Т . distrelec.de:443 distrelec.de:443	Математические операции […] Disponibles S ONT L ‘Дополнение, LA SOU ST RA CT Ион, LA Умножение , LA 0009 , л деление и ла FF T . distrelec.de:443 distrelec.de:443
They inve nt e d addition , s ub tract io n , multiplication , division and g e om etry. bookmarts.biz bookmarts.biz	I ls inv ente nt aussi la Division et l a g om trie . bookmarts.biz bookmarts.biz
Математика CAT/2 […] Операционный тест измеряет способности учащегося t o d o addition , s ub tract io n , multiplication , and division o p er на целые числа, десятичные дроби, дроби, отрицательные [. ..] и экспоненты. statcan.gc.ca statcan.gc.ca	Le CAT/2 измеряет емкость […] Любительский эффект […] DES OP RA TIONS D ‘ Дополнение , D E SOU ST RAC TI ON, DE Multiplation et D E Дивизион S UR LES ET D E Division S UR LES LES ET D n om bresentiers, les dcimales, des дроби, les ng at ifs и или и xposants. statcan.gc.ca statcan.gc.ca
В алгебраическом […] (ALG) mode, you per fo r m addition , s ub tract io n , multiplication , и подразделение i n t Традиционный способ. calculatrices-hp.com calculatrices-hp.com	Альбомный режим (ALG), vous […] Effectuez LES OP Крыса Ion S D ‘Дополнение, DE SO USTR A CTIO N, D E Multiplication ETIO N, D E ETMALLICATIOde Division de fa on tr ad itionnelle. calculatrices-hp.com calculatrices-hp.com
T H E Дивизион M A NA CES CONTROSS для T H E Размещение 9009 0009 f s eeds for corn, straw cereals, sunflower, len ti l s and v e ge tab le s , и p r ov ides технические консультации. limagrain.com limagrain.com	L а Отвод г R E LE S CO N TRAT S DE Умножение DE S EMEN CE S DE MAS, Crales Pail otag res et app orte se s conseils […] техники. limagrain.com limagrain.com
Дополнение и S U BT RACT IO N , и умение и дивизион , A 9 , A . креациявики.орг креациявики.орг	L ‘сложение e t la вычитание, et la умножение и la деление, так nt инверт se с. креациявики. орг креациявики.орг
2 Простая оценка […] Algebraic Expressi на S , Дополнение , S UB Тракт IO N , и дивизион и дивизион и дивизион и дивизион и дивизион и дивизион и дивизион и дивизион 9000 и дивизион .0010 , u se кронштейнов, простых […] алгебраические дроби eur-lex.europa.eu eur-lex.europa.eu	2 оценка выражения с […] Algbriques SIM PLES , Дополнение , SOUS T RAC TIO n, Умножение et Division, UT 0010 il isat ion de s скобки, […] дроби простые алгебраические; б) eur-lex. europa.eu eur-lex.europa.eu
Отрицание io n , умножение , и деление . calculatrices-hp.com calculatrices-hp.com	O ppo с, умножение и деление . calculatrices-hp.com calculatrices-hp.com
This test measures the ability to apply the four basic arithmetical operati on s ( addition , s ub tract io n , умножение и деление ) i n повседневные ситуации. schuhfried.com schuhfried.com	E N FONCTION DE L A TCHE, L’VALUATION MESURE LA PRCISION (N OM BRE D ‘ERREURS) ET /OU LA V ET /OU LA V 0 /OU LA V 9 ET /OU LA V ET /OU 9 ET /OU esse (dure de la tche, dure des erreurs) de l a main droite et de la ma in gauche, [. ..] для проверки эффективности основной или двух сетей. Шуфрид.fr Шуфрид.fr
Калькулятор с четырьмя функциями позволит пользователю выполнять простые операции. […] арифметические вычисления на s ( сложение , с уб тракт ио н , умножение и деление ) . panasonic.net panasonic.net	Калькулятор четырех функций […] разрешение на использование простых средств […] вычисляет a ri thmt iqu es (сложение, так ust ra cti на , умножение и деление) . panasonic.net panasonic.net
You should be familiar wi t h addition , s ub tract io n , multiplication , division , p er centages, averages, fract io n s and f i na ncial calculations. psc-cfp.gc.ca psc-cfp.gc.ca	Vous devriez vous […] familia ri ser a vec l ‘дополнение, l a s oustr act ion, la multiplication , la division, l ‘exp ress io n de pour CE NTAGE S ET D E MOY EN NES, LES FR ACTIO NS ET LE S CAL CU LS Финансисты. psc-cfp.gc.ca psc-cfp.gc.ca
Подпрограмма 2 предназначена для измерения скорости и точности в решении задачи арифметической. умножение и деление . psc-cfp.gc.ca psc-cfp.gc.ca	Ле Су-тест 2 […] mesure la rapidit et l’exa ct itude rsoudre des problmes d’arit hm tiq ues d’ addition , de s oust ract ion, de умножение e t d e деление . psc-cfp.gc.ca psc-cfp.gc.ca
Две измеренные переменные (например, x и y) с неопределенностями (?x и ?y) могут использоваться для расчета нового значения z. Следующие два подраздела […] предоставить формулы, используемые для расчета […] неопределенность, ?z in z f o r дополнение / s u bt rac ti o n и умножение/деление . ec.gc.ca ec.gc.ca	Deux переменных mesures (p. ex., x et y) ayant des incertitudes (?x et ?y) pourraient tre uses pour calculer une nouvelle valeur, z. Les deux sous-sections qui suivent prsentent les formules […] использует калькулятор неопределенности ?z на […] оценщик d e z e n c as d’addition/s ous trac tio 0/division 0/ ec. gc.ca ec.gc.ca
Нет явного […] инструкция о том, как научить операции. Четыре основных операции на с ( дополнение , S UB TRACT IO N , Умножение и дивизион ) A Re представлены в одном из двух или двух. […] можно разделить четыре на два, […] они освоили операцию. iiz-dvv.de iiz-dvv.de	Четыре операции […] de ba SE (L’Dpact, LA SO US TR Actio N, LA Умножение et L A Дивизион) Sont до UT JAN соответсвие prsentes en une ou deux leons автомобиль на предположим que si quelqu’un s ait diviser qua tr e par [. ..] deux, il matrise le calcul de ce type d’opration. iiz-dvv.de iiz-dvv.de
Addition , s ub tract io n , division , multiplication and t o ta ling можно сделать очень быстро, и все […] результаты могут быть автоматически пересчитаны позже, если будут вставлены новые данные. statcan.gc.ca statcan.gc.ca	Ils permettent de faire […] rapidement les o prat ion s d ‘addition, de so ustracti on, de division, de multiplication et de to ta лизинг, […] автоматический пересчетчик [. ..] автоматизация всех результатов плюс tard si de nouvelles donnes sont entres. statcan.gc.ca statcan.gc.ca
вручную: один расчет с […] относительно небольшой […] десятичное число er s ( сложение , S UB TRACT IO N , Умножение , Подразделение ) ; — using a calculator: a single calculation with relative numbers in decim al s : addition , s ub tract io n , multiplication , d ecim a l division t o t he closest 10-n, calculating the square or the cube of относительное число, квадратный корень из положительного числа; — в уме: просто вычислить io n s и q u ic клы дают [. ..] приблизительный ответ condorcet.com.au condorcet.com.au	L A Calculatrice , UN CALCUL ISOL SUR DES BR ES RELATIFS EN CRUTUT п, умножение, Подразделение D CIM ALE 10 — N PRS, CALCU L DU CARR, DU Cube D ‘ ООН N OBMER RELATIF, RACINE EN N Obmre Relatif, RACINE 9 E. EN N Obmre, RACINE EN N Obmre, RACINE EN N . d’un no mb re positif condorcet.com.au condorcet.com.au

Умножение, деление – Математические изображения

Сколько СЕЙЧАС?

Крисси Ньюэлл отлично работает с точками, чтобы осветить умножение в разговоре о числах. Проверьте ее оригинальный пост здесь.

Удвоение с кратными 4, 6 и 8

Удвоение, одинаковое/разное

Как использовать: Спросить? Что вам интересно? Как это может выглядеть для других проблем?

Коэффициенты умножения

Как пользоваться: Спросите: Что вы заметили? Что вам интересно? Какие уравнения будут соответствовать каждому массиву? Что такое шаблон?

Коммутативное умножение

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Что такое же? Что отличается? Это работает с другими номерами? Как это может облегчить решение других задач?

Связанное умножение и деление

Еще одна строка или столбец, одинаковые/другие

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Что еще вы можете придумать? Как это помогает вам думать о 6×5?

Схема соединения сотен

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Можете ли вы предсказать, как она упадет и/или распадется? Можете ли вы предсказать, каким будет следующее число, используя то, что вы знаете о таблице сотен? (Прочитайте пост Грэма Флетчера о «перевернутой» диаграмме сотен, использованной в этом видео, здесь)

Умножение на 10

Соединение повторений с 5×18

Способы решения 18×5

Как использовать: Попросите учащихся решить 18×5 и продемонстрируйте это визуально. Посмотрите на это изображение и спросите: какой из них был больше всего похож на ваш и почему? Выберите одну из этих стратегий и объясните, как она работает.

Этот рисунок вдохновлен Джо Боалер и www.youcubed.org, отличным местом, где можно узнать о продуктивном математическом мышлении, исследованиях и занятиях.

Столкновение массивов

Атомные точки

Типы деления

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Что такое же? Что отличается? Какой рассказ может сравниться с первым? Чем история должна отличаться, чтобы соответствовать второй?

Разделение на группы или массив

Как использовать: Посмотрите и спросите: Что вы заметили? Что вам интересно? Что такое же? Что отличается? Какая история могла бы соответствовать этим? Какие уравнения могут совпадать?

Распечатка умножения

Перейдите на страницу распечаток для загрузки.

Нравится:

Нравится Загрузка…

Основные свойства карточек сложения, вычитания, умножения и деления

Пожалуйста, войдите, чтобы добавить в папки.

Войти

Вы создали 2 папки. Пожалуйста, обновитесь до Cram Premium, чтобы создавать сотни папок!

Обновление

• Перемешать

  Включить

  Выключить

• В алфавитном порядке

  Включить

  Выключить

• Передний Первый

  Включить

  Выключить

• Обе стороны

  Включить

  Выключить

• Читать

  Включить

  Выключить

Чтение. ..

Фронт

через

Кнопка воспроизведения

Кнопка воспроизведения

Прогресс

1/7

Нажмите, чтобы перевернуть

Используйте клавиши со стрелками ВЛЕВО и ВПРАВО для перемещения между карточками;

Используйте клавиши со стрелками ВВЕРХ и ВНИЗ, чтобы перевернуть карту;

H для показа подсказки;

A читает текст в речь;

• Делиться
• Распечатать
• Экспорт
• Клон

7 карт в этом наборе

• Передняя сторона
• Спина

	При сложении двух чисел сумма одинакова независимо от порядка сложения. ПРИМЕР: 4 + 2 = 2 + 4	КОММУТАТИВНАЯ СОБСТВЕННОСТЬ
	При сложении трех и более чисел сумма остается одинаковой независимо от порядка сложения. ПРИМЕР: (2 + 3) + 4 = 2 + (3 + 4)	АССОЦИАТИВНАЯ СОБСТВЕННОСТЬ
	Сумма любого числа и нуля является исходным числом. ПРИМЕР: 5 + 0 = 5.	ДОПОЛНИТЕЛЬНОЕ СВОЙСТВО ИДЕНТИЧНОСТИ
	Пожалуйста — скобки Извините — Экспонент Мой — умножить Дорогой — Раздели Тетя — Добавить Салли — Вычесть	ПОРЯДОК ДЕЙСТВИЙ
	Если у вас есть эта проблема: (1+9) x 2 + 9 = 29 Какой ПЕРВЫЙ шаг в решении проблемы?	(1+9) СКОБКИ
	Если у вас есть эта задача: (2+8) x 3 — 7 = 23 Какой ВТОРОЙ шаг в решении задачи?	X 3 УМНОЖИТЬ
	Если у вас есть эта задача: (8+2) x 6 — 1 = 59 Какую часть задачи вы решаете ПОСЛЕДНЕЙ?	— 1 ВЫЧИТАТЬ

Q3 Определите операции сложения, вычитания, деления, умножения при формировании следующего выражения.

..

Перейти к

• Упражнение 11.1
• Упражнение 11.2
• Упражнение 11.3
• Упражнение 11.4
• Упражнение 11.5

• Зная наши цифры
• Целые числа
• Игра с числами
• Основные геометрические идеи
• Понимание элементарных форм
• Целые числа
• Фракции
• Десятичные
• Обработка данных
• Измерение
• Алгебра
• Соотношение и пропорция
• Симметрия
• Практическая геометрия

Главная > Решения НЦЭРТ Класс 6 Математика > Глава 11 — Алгебра > Упражнение 11. 3 > Вопрос 5

Вопрос 5 Упражнение 11.3

Q3) Определите операции (сложение, вычитание, деление, умножение) при составлении следующих выражений и скажите, как они были образованы:

(а) z+1, z–1, y+17, y–17

(б)17y, \frac{y}{17}, 5z

(в) 2y+17, 2y–17

(d) 7m, –7m+3, –7m–3

Ответ:

Решение:

(a) z+1 \Rightarrow Дополнение.

z–1 \Вычитание вправо.

лет + 17 \стрелка вправо Дополнение.

г — 17\Вычитание вправо.

(b) 17y \Умножение со стрелкой вправо.

\frac{y}{17}\Стрелка вправо\ Деление

5z\Умножение стрелки вправо..

(c) 2y + 17\Сложение со стрелкой вправо.

2г — 17\Вычитание вправо.

(d) 7m\Умножение со стрелкой вправо.

-7m + 3\Стрелка вправо Умножение и сложение.

-7m — 3\Стрелка вправо Умножение и вычитание.

Связанные вопросы

Q1) Составьте как можно больше выражений с числами (без переменных) из трех чисел 5, 7 и 8. …

Составьте как можно больше выражений с числами (без переменных) из трех чисел 5, 7 и 8. Ev…

Какие из следующих выражений содержат только числа? (а) у + 3(б) (7 × 20) – 8z(в) 5 (21 – 7…

Q2) Какие из следующих выражений содержат только числа: (a) y + 3(b) (7 x 20) — 8z(c) 5(21…

Назовите действия (сложение, вычитание, деление, умножение) при составлении следующего уравнения…

Приведите выражения для следующих случаев. (a) 7 добавить к p(b) 7 вычесть из p(c) p, умноженное на …

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 1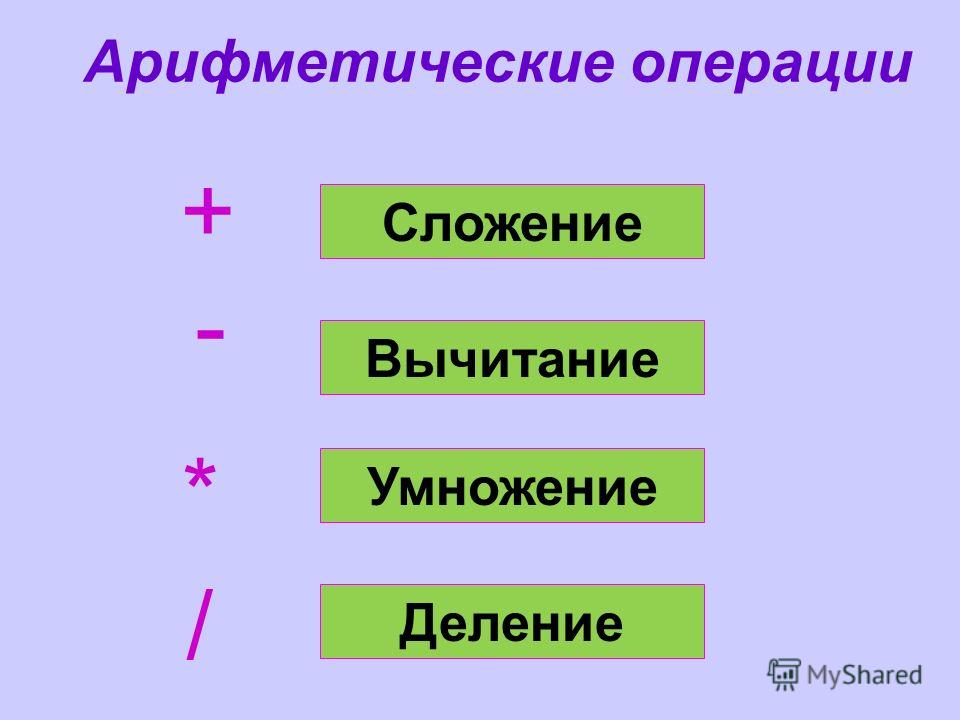1. 1

Упражнение 11,2

Упражнение 11,3

Упражнение 11,4

Упражнение 11,5

Главы

Знание наших чисел

Игра с номерами

Основные GEOMETRALEDES.

Целые числа

Дроби

Десятичные дроби

Обработка данных

Измерение

Алгебра

Соотношения и пропорции

Симметрия

Практическая геометрия

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Страница ошибки | eBay

• Мужские шлепанцы adidas Adissage

  21,00 $

• Коллекционная бустерная коробка Unfinity — MTG Magic the Gathering — Новинка! Предзаказ 7/10

  209,99 $

  350,00 $ | Скидка 40% — Предыдущая цена: 350,00 $ Скидка 40%

• Apple iPhone X 64 ГБ Телефон с заводской разблокировкой — Очень хорошо

  209,95 $

  999,00 $ | Скидка 79% — Предыдущая цена: 999,00 $ Скидка 79%

• Женская пуховая куртка adidas Essentials

  56,25 $

• HP — Victus 15. 6GB — NVIDIA 170-6 Gaming Laptop — Intel Core 15.6″ 170-2…

  1099,99 $ — Предыдущая цена: 1,09 $9.99

• Смартфон Samsung G960 Galaxy S9 64 ГБ с заводской разблокировкой — очень хорошо

  114,95 $

  800,00 $ | 86% off — Previous price: $800.00 86% off

• Lenovo Legion 5 Pro 16″ 165Hz QHD i7-12700H 16GB DDR5 RAM 1TB SSD RTX 3060

  $1,199.99

  $1,809.99 | 34% off — Предыдущая цена: $1809,99 Скидка 34%

• adidas Originals Сабо Adilette Мужские

  25,00 $

• Разблокированный смартфон Apple iPhone 12 128 ГБ — очень хорошо

  484,95 $

  849,00 $ | Скидка 43% — Предыдущая цена: 849,00 $ Скидка 43%

• Разблокированный смартфон Apple iPhone 12 64 ГБ — Очень хорошо

  439,95 $

  799,00 $ | Скидка 45% — Предыдущая цена: $799. 00 Скидка 45%

• Набор колод Warhammer 40K Commander из 4 колод — MTG Universes Beyond Запечатанные корабли 10-5

  200,62 $

  249,95 $ | 20% скидка — Предыдущая цена: 249,95 долл. США 20% скидка

• Geekpure 10 -дюймовый корпус фильтров с водными фильтрами целого дома 1 «NPT FIT 4,5» x 10 «Фильтры

  $ 43,99

• AM. Процессор для настольных ПК -thread — 8 ядер и 16 потоков —

  374,99 $

  449,00 $ | Скидка 16% на — Предыдущая цена: 449,00 $ Скидка 16%0007

  18,00 $

• Samsung N970 Galaxy Note 10 256 ГБ разблокированный смартфон Android — очень хорошо

  209,95 $

  800,00 $ | 74% off — Previous price: $800.00 74% off

• adidas Originals Superlite Gradient No-Show Socks 6 Pairs Women’s

  $12. 60

• Samsung G973 Galaxy S10 128GB Factory Unlocked Smartphone — Very Good

  $157.95

  800,00 $ | Скидка 80% — Предыдущая цена: 800,00 $ Скидка 80% 28% скидка — Предыдущая цена: 29,45 долл. США 28%.0006 199,95 $

  800,00 $ | Скидка 75% — Предыдущая цена: 800,00 $ Скидка 75%

• Толстовка с капюшоном PUMA Essentials для мужчин с большим логотипом

  22,99 $

  45,00 $ | Скидка 49% — Предыдущая цена: $45,00 Скидка 49%

• Merrell Men Moab 2 Mid Водонепроницаемые походные ботинки широкой ширины из замши, кожи и сетки

  58,00 $

  72,50 $ | Скидка 20% — Предыдущая цена: $72,50 Скидка 20%

• Milwaukee 49-56-9290 10 PC Big Hawg Hole Saw с карбид-набор зубов

  $ 301,36 -Предыдущая цена: $ 301,36

• Samsung Galaxy Small.