Серия «Математика». Сложение | Дефектология Проф
Серия «Математика». Сложение | Дефектология ПрофИнститут повышения квалификации и переподготовки
8-800-555-20-50
Добавиться вМенеджер свяжется с Вами сразу в рабочее время с Пн — Пт с 10:00 — 19:00 МСК
Мы позвоним на номер (сменить) в рабочее время.
(с Пн — Пт с 10:00 — 19:00 МСК)
У меня вопрос по
Серия «Математика». Сложение
Серия «Математика». Сложение
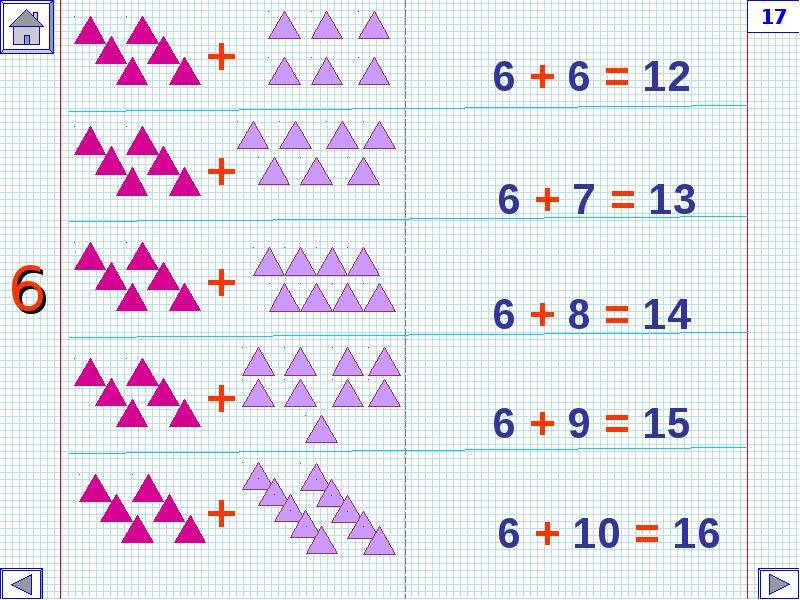
Аннотация:Как вызвать у ребенка — дошкольника интерес к математике? В этом вам помогут книжки нашей математической серии.
Выполняя задания, ребенок сможет освоить действие сложения, научится решать примеры и задачи со знаком «плюс». Если малыш затрудняется, обязательно объясните задание ещё раз, помогите в выполнении. Хорошо, если вы сможете закрепить полученные знания и на дополнительных занятиях и в повседневной жизни.
Доступно бесплатно
Пример содержимого:
Всего листов: 34
Вся информация взята из открытых источников.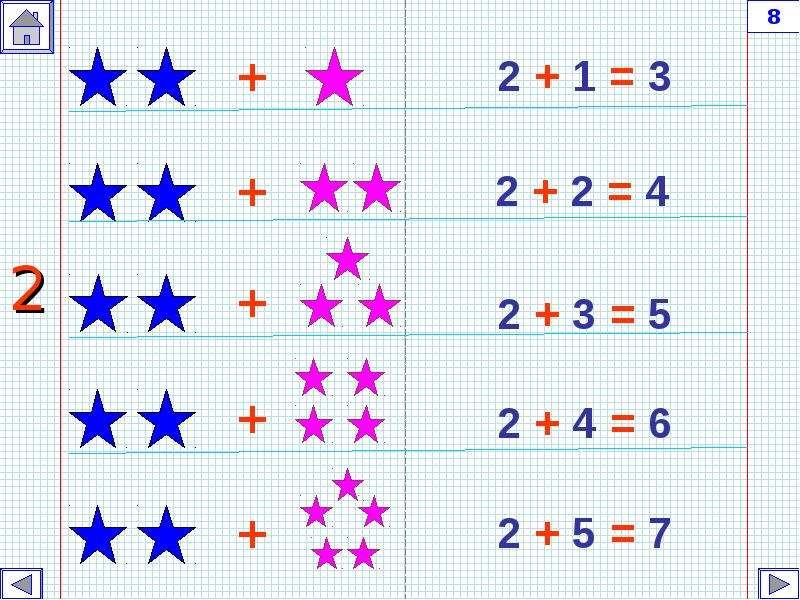
Посмотреть источник: https://vk.com/umnie_knizki?w=wall-44155346_90030
Если вы считаете, что ваши авторские права нарушены, пожалуйста, напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.
Хотите большего? Берите безлимитную карту!
Веб-инструмент для повышения квалификации и личного дохода
Веб-инструмент для повышения квалификации и личного дохода
Веб-инструмент для повышения квалификации и личного дохода
Веб-инструмент для повышения квалификации и личного дохода
Веб-инструмент для повышения квалификации и личного дохода
Веб-инструмент для повышения квалификации и личного доходаВеб-инструмент для повышения квалификации и личного дохода
Веб-инструмент для повышения квалификации и личного дохода
Обучайтесь на профильных и смежных лекциях
Смотрите подборки вебинаров на общие темы
Добавиться в
Добавьтесь в наш
8-800-555-20-50 звонок бесплатный из любой точки России
© 2021 — Полное или частичное копирование материалов сайта возможно только с разрешения администрации и с активной ссылкой на источник.
Бурдина
|
«Сложение»
Страна
— Ничего -AfghanistanAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarcticaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBosnia and HerzegowinaBotswanaBouvet IslandBrazilBritish Indian Ocean TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCanary IslandsCape VerdeCaribbean NetherlandsCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCongo, Democratic RepublicCook IslandsCosta RicaCote D’IvoireCroatiaCubaCyprusCzech RepublicDenmarkDjiboutiDominicaDominican RepublicEast TimorEast TimorEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland Islands (Malvinas)Faroe IslandsFijiFinlandFranceFrench GuianaFrench PolynesiaFrench Southern TerritoriesGabonGambiaGeorgiaGermanyGhanaGibraltarGreeceGreenlandGrenadaGuadeloupeGuamGuatemalaGuineaGuinea-bissauGuyanaHaitiHeard and Mc Donald IslandsHondurasHong KongHungaryIcelandIndiaIndonesiaIran (Islamic Republic of)IraqIrelandIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKorea, Democratic People’s Republic ofKorea, Republic ofKuwaitKyrgyzstanLao People’s Democratic RepublicLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacauMacedonia, The Former Yugoslav Republic ofMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesia, Federated States ofMoldova, Republic ofMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNetherlands AntillesNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorthern Mariana IslandsNorwayOmanPakistanPalauPalestinian Territory, occupiedPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarReunionRomaniaRussian FederationRwandaSaint Kitts and NevisSaint LuciaSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint Maarten (French Antilles)Sint Maarten (Netherlands Antilles)SlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia and the South Sandwich IslandsSouth SudanSpainSri LankaSt. BarthelemySt. EustatiusSt. HelenaSt. Pierre and MiquelonSudanSurinameSvalbard and Jan Mayen IslandsSwazilandSwedenSwitzerlandSyrian Arab RepublicTaiwanTajikistanTanzania, United Republic ofThailandThe Democratic Republic of CongoTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUnited StatesUnited States Minor Outlying IslandsUruguayUzbekistanVanuatuVatican City State (Holy See)VenezuelaViet NamVirgin Islands (British)Virgin Islands (U.S.)Wallis and Futuna IslandsWestern SaharaYemenZambiaZimbabwe
BarthelemySt. EustatiusSt. HelenaSt. Pierre and MiquelonSudanSurinameSvalbard and Jan Mayen IslandsSwazilandSwedenSwitzerlandSyrian Arab RepublicTaiwanTajikistanTanzania, United Republic ofThailandThe Democratic Republic of CongoTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUnited StatesUnited States Minor Outlying IslandsUruguayUzbekistanVanuatuVatican City State (Holy See)VenezuelaViet NamVirgin Islands (British)Virgin Islands (U.S.)Wallis and Futuna IslandsWestern SaharaYemenZambiaZimbabwe
Федоскина. Математика. Сложение и вычитание в пределах 10. 1 класс (Просвещение)
| Переплет | мягкий |
| ISBN | 978-5-09-058397-8 |
| Год издания | 2020 |
| Количество томов | 1 |
| Формат | 70×90/16 (170×215 мм) |
| Количество страниц | 32 |
| Серия | Тренажёр младшего школьника |
| Издательство | Просвещение |
| Автор | Федоскина О. В. В. |
| Возрастная категория | 1 кл. |
| Раздел | Математика |
| Тип издания | Упражнения и тренажеры |
| Язык | русский |
Описание к товару: «Математика.
 1 класс. Сложение и вычитание в пределах 10″
1 класс. Сложение и вычитание в пределах 10″Тетрадь-тренажёр по математике для 1 класса предназначена для закрепления навыков сложения и вычитания в пределах 10. Пособие позволит родителям и педагогам определить степень освоения материала ребёнком, выявить пробелы и организовать дифференцированную работу по их устранению. Пособие предназначено для работы в классе, внеурочной работы, для самостоятельной работы дома и совместных занятий ребенка и взрослого.
Раздел: Математика Издательство: ПРОСВЕЩЕНИЕ
Серия: Тренажёр младшего школьника
Вы можете получить более полную информацию о товаре «Федоскина. Математика. Сложение и вычитание в пределах 10. 1 класс (Просвещение)«, относящуюся к серии: Тренажёр младшего школьника, издательства Просвещение, ISBN: 978-5-09-058397-8, автора/авторов: Федоскина О. В., если напишите нам в форме обратной связи.
ГДЗ по Математике 4 класс Моро часть 1, 2 Учебник
В начальной школе родители уже могут заметить рвение своего чадо к тому или иному предмету, а это значит, что можно задуматься о том, на что конкретно делать упор, будь то гуманитарные науки или же технические. Следующим этапом станет средняя школа, там ученик столкнется с более сложными предметами – алгеброй и геометрией. Математика формирует у ребенка логическое мышление, умение быстро и точно делать подсчеты.
Следующим этапом станет средняя школа, там ученик столкнется с более сложными предметами – алгеброй и геометрией. Математика формирует у ребенка логическое мышление, умение быстро и точно делать подсчеты.
Но не всегда четвероклассник в силах разобраться домашнем задании самостоятельно и если взрослых нет рядом или они просто не могу объяснить тему в силу того, что окончили школу достаточно давно, то на помощь может придти ГДЗ.
Почему решебник по математике для 4 класса (авторы: М. И. Моро, М. А. Бантова, Г. В. Бельтюкова) может стать отличным помощником?
В трудных задачах и пропущенных темах, поможет сборник, который обладает следующими преимуществами:
- упражнения полностью соответствуют стандартам ФГОС;
- доступ к сервису 24/7;
- готовые правильные ответы;
- успешная сдача контрольных и самостоятельных работ;
- уверенность на уроках в школе;
- самостоятельность и ответственность;
Учебник состоит из двух частей и издан компанией «Просвещение» в 2015 году. Решебник содержит в себе все готовые правильные ответы упражнений, которые представлены в бумажном издании.
Решебник содержит в себе все готовые правильные ответы упражнений, которые представлены в бумажном издании.
Родители должны объяснить ребенку, как правильно и в каких целях пользоваться ГДЗ, чтобы избежать бездумного списывания. Такой помощник может повысить успеваемость и в дневнике могут прекратиться систематические «двойки». Конечно можно нанимать дорогостоящих репетиторов или заставлять зубрить материал, но зачем, если можно облегчить задачу всем. Тогда появится больше времени на любые развлечения и хобби, может быть ребенок всегда хотел заниматься пением или танцами, а вынуждать его сидеть за скучной математикой не самое лучшее дело.
Из чего состоит сборник по математике Моро?
При переходе в 5 класс, учащийся уже должен придти с багажом таких тем, как:
- среднее арифметическое;
- числа до 1000;
- числа после 1000;
- сложение и вычитание;
- деление и умножение;
- величины;
- определение скорости, расстояния и т.
 п.
п.
Для преподавателей это отличная возможность дать себе разгрузку после тяжелого дня, ведь домашки в этой куче тетрадей теперь можно проверить и в школе, а дома заняться своими любимыми домашними делами.
Сумма первых n членов серии
Сумма членов последовательности называется ряд .
Если последовательность является арифметика или же геометрический есть формулы для нахождения суммы первых п термины, обозначенные S п , без фактического добавления всех терминов.
(Обратите внимание, что последовательность не может быть ни арифметической, ни геометрической, и в этом случае вам нужно будет добавить с помощью грубой силы или какой-либо другой стратегии.)
Сумма членов арифметической последовательности (арифметической последовательности)
Чтобы найти сумму первых
п
члены арифметической последовательности используют формулу,
S
п
знак равно
п
(
а
1
+
а
2
)
2
,
где
п
это количество терминов,
а
1
это первый член и
а
п
это последний срок.
Пример 1:
Найдите сумму первых 20 члены арифметического ряда, если а 1 знак равно 5 а также а 20 знак равно 62 .
S 20 знак равно 20 ( 5 + 62 ) 2 S 20 знак равно 670
Пример 2:
Найдите сумму первых
40
члены арифметической последовательности
2
,
5
,
8
,
11
,
14
,
⋯
Сначала найдите 40 th срок:
а 40 знак равно а 1 + ( п — 1 ) d знак равно 2 + 39 ( 3 ) знак равно 119
Затем найдите сумму:
S п знак равно п ( а 1 + а п ) 2 S 40 знак равно 40 ( 2 + 119 ) 2 знак равно 2420
Пример 3:
Найдите сумму:
∑ k знак равно 1 50 ( 3 k + 2 )
Первая находка а 1 а также а 50 :
а 1 знак равно 3 ( 1 ) + 2 знак равно 5 а 20 знак равно 3 ( 50 ) + 2 знак равно 152
Затем найдите сумму:
S k знак равно k ( а 1 + а k ) 2 S 50 знак равно 50 ( 5 + 152 ) 2 знак равно 3925
Сумма членов геометрической последовательности (геометрического ряда)
Чтобы найти сумму первых
п
термины геометрической последовательности используют формулу,
S
п
знак равно
а
1
(
1
—
р
п
)
1
—
р
,
р
≠
1
,
где
п
это количество терминов,
а
1
это первый член и
р
это
обычное отношение
.
Пример 4:
Найдите сумму первых 8 члены геометрического ряда, если а 1 знак равно 1 а также р знак равно 2 .
S 8 знак равно 1 ( 1 — 2 8 ) 1 — 2 знак равно 255
Пример 5:
Находить
S
10
геометрического ряда
24
+
12
+
6
+
⋯
.
Сначала найдите р .
р знак равно р 2 р 1 знак равно 12 24 знак равно 1 2
Теперь найдите сумму:
S 10 знак равно 24 ( 1 — ( 1 2 ) 10 ) 1 — 1 2 знак равно 3069 64
Пример 6:
Оценивать.
∑ п знак равно 1 10 3 ( — 2 ) п — 1
(Вы находите S 10 для сериала 3 — 6 + 12 — 24 + ⋯ , обыкновенное отношение которого равно — 2 .)
S п знак равно а 1 ( 1 — р п ) 1 — р S 10 знак равно 3 [ 1 — ( — 2 ) 10 ] 1 — ( — 2 ) знак равно 3 ( 1 — 1024 ) 3 знак равно — 1023
Смотрите также: сигма-обозначение ряда
Арифметическая серия | Purplemath
Purplemath
Арифметический ряд — это сумма членов арифметической последовательности. Геометрический ряд — это сумма членов геометрической последовательности. Существуют и другие типы рядов, но вы вряд ли будете много работать с ними, пока не изучите математический анализ. На данный момент вы, вероятно, в основном будете работать с этими двумя. На этой странице объясняется и показано, как работать с арифметическими рядами.
Геометрический ряд — это сумма членов геометрической последовательности. Существуют и другие типы рядов, но вы вряд ли будете много работать с ними, пока не изучите математический анализ. На данный момент вы, вероятно, в основном будете работать с этими двумя. На этой странице объясняется и показано, как работать с арифметическими рядами.
По причинам, которые будут объяснены в математике, вы можете взять только «частичную» сумму арифметической последовательности. Частичная сумма — это сумма ограниченного (то есть конечного) числа членов, таких как первые десять членов или с пятого по сотый член.
Формула для первых n членов арифметической последовательности, начиная с i = 1, выглядит так:
MathHelp.
 com
comЕсли вы возьмете цифру «2» в правой части знака «равно» из-под числа n и преобразуете ее в умножение на половину в круглых скобках, вы увидите, что формула для суммы имеет следующий вид: , фактически, n раз больше «среднего» первого и последнего членов.
Подобный подход к формуле суммирования может оказаться полезным способом запомнить формулу. (Кстати: формулу суммирования можно доказать с помощью индукции.)
Сумма первых n членов ряда называется « n -я частичная сумма» и часто обозначается как «S n ».
Найдите 35-ю частичную сумму S35 арифметической последовательности с членами
a n = (1/2) n + 1
35-я частичная сумма этой последовательности — это сумма первых тридцати пяти членов. Первые несколько членов последовательности:
Первые несколько членов последовательности:
a 1 = (1/2) (1) + 1 = 3/2
a 2 = (1/2) (2) + 1 = 2
a 3 = (1/2) (3) + 1 = 5/2
Члены имеют общую разницу
d = 1/2, так что это действительно арифметическая последовательность. Последним членом частичной суммы будет:Тогда, подставив формулу, 35-я частичная сумма будет:
(35/2) ( a 1 + a 35)
= (35/2) (3/2 + 37/2)
= (35/2) (40/2)
= 350
Тогда мой ответ:
35-я частичная сумма: S35 = 350
Я мог бы найти общее различие в приведенной выше последовательности, просто взглянув на формулу для членов последовательности. Поскольку это арифметическая последовательность, каждый член на фиксированную величину больше предыдущего. Если бы мы использовали непрерывную переменную, такую как « x », которую мы использовали при построении прямых линий, вместо дискретной переменной n , то «
Поскольку это арифметическая последовательность, каждый член на фиксированную величину больше предыдущего. Если бы мы использовали непрерывную переменную, такую как « x », которую мы использовали при построении прямых линий, вместо дискретной переменной n , то «
Мы можем использовать то, что мы узнали о наклоне прямой и о том, как это соотносится с уравнением для прямой линии, чтобы определить общую разницу в формуле для членов… что может сэкономить время на тестировании.
Найдите значение следующего суммирования:
Из формулы «2 n — 5» для n -го члена я вижу, что каждый член будет на две единицы больше, чем предыдущий член. (Если бы я не был уверен в этом, я всегда мог бы вставить некоторые значения для n для подтверждения.) Так что это действительно арифметическая сумма. Но это суммирование начинается с n = 15, а не с n = 1, и формула суммирования применяется к суммам, начинающимся с n = 1. Итак, как я могу работать с этим суммированием? Используя небольшой трюк:
(Если бы я не был уверен в этом, я всегда мог бы вставить некоторые значения для n для подтверждения.) Так что это действительно арифметическая сумма. Но это суммирование начинается с n = 15, а не с n = 1, и формула суммирования применяется к суммам, начинающимся с n = 1. Итак, как я могу работать с этим суммированием? Используя небольшой трюк:
Самый быстрый способ найти значение этой суммы — найти 14-ю и 47-ю частичные суммы, а затем вычесть 14-ю из 47-й. S14 — это сумма с первого по четырнадцатый слагаемые. Выполняя это вычитание, я вычту с первого по четырнадцатый член из первого по сорок седьмой, так что у меня останется сумма с 15-го по 47-й член.
Первый член:
Другими необходимыми условиями являются четырнадцатый и сорок седьмой:
a 14 = 2 (14) — 5 = 23
a 47 = 2 (47) — 5 = 89
С этими значениями у меня теперь есть все, что мне нужно, чтобы найти две частичные суммы для моего вычитания:
Вычитая, получаем:
Тогда мой ответ:
Кстати, это вычитание можно также выразить как «S 47 — S 14 ». Не удивляйтесь, если вы увидите упражнение, использующее эти обозначения и ожидающее, что вы извлечете из него смысл, прежде чем сможете приступить к вычислениям.
Не удивляйтесь, если вы увидите упражнение, использующее эти обозначения и ожидающее, что вы извлечете из него смысл, прежде чем сможете приступить к вычислениям.
Примечание по форматированию: поскольку это было просто суммирование, можно с уверенностью предположить, что суммируемым выражением является «2 n -5». Однако (и особенно если вы имеете дело с чем-то более сложным) иногда может потребоваться группировка символов, чтобы прояснить смысл. Правильно, автор предыдущего упражнения должен был отформатировать суммирование с помощью группирующих символов следующим образом:
Найдите значение
n , для которого верно следующее уравнение:
Я знаю, что первый член имеет значение:
Я вижу из формулы, что каждый член будет равен 0. На 25 единиц больше, чем в предыдущем члене, поэтому это арифметический ряд с d = 0,25. Тогда формула суммирования арифметических рядов дает мне:
На 25 единиц больше, чем в предыдущем члене, поэтому это арифметический ряд с d = 0,25. Тогда формула суммирования арифметических рядов дает мне:
( n /2 )(2,25 + [0,25 n + 2]) = 21
n (2,25 + 0,25 n + 2) = 42
n (0,25 n + 4,25) = 42
0,25 n 2 + 4.25 n — 42 = 0
n 2 + 17 n — 168 = 0
( n + 24) ( n -7) = 0
Решая это квадратное уравнение, я получаю, что n = –24 (что не имеет смысла в данном контексте) или n = 7. Тогда:
Вы, , могли бы выполнить указанное выше упражнение, добавляя термины, пока не дойдете до требуемой суммы, равной 21. Но ваш инструктор может легко дать вам суммирование, которое потребует, скажем, восьмидесяти шести или тысячи, прежде чем вы подойдете к правильной сумме. Даже если бы вы могли выполнить все шаги , это было бы нелепой тратой времени, особенно на тесте. Поэтому убедитесь, что вы можете выполнять вычисления по формуле.
Но ваш инструктор может легко дать вам суммирование, которое потребует, скажем, восьмидесяти шести или тысячи, прежде чем вы подойдете к правильной сумме. Даже если бы вы могли выполнить все шаги , это было бы нелепой тратой времени, особенно на тесте. Поэтому убедитесь, что вы можете выполнять вычисления по формуле.
Найдите сумму 1 + 5 + 9 + … + 49 + 53
Проверяя термины, я вижу, что это действительно арифметический ряд:
5 — 1 = 4
9–5 = 4
53 — 49 = 4
(И я хочу иметь привычку проверять так, потому что они не всегда говорят мне, особенно на тесте, какие серии они мне дали.)
Мне дали первый и последний термины этой серии, но сколько всего терминов? Я должен разобраться в этом сам.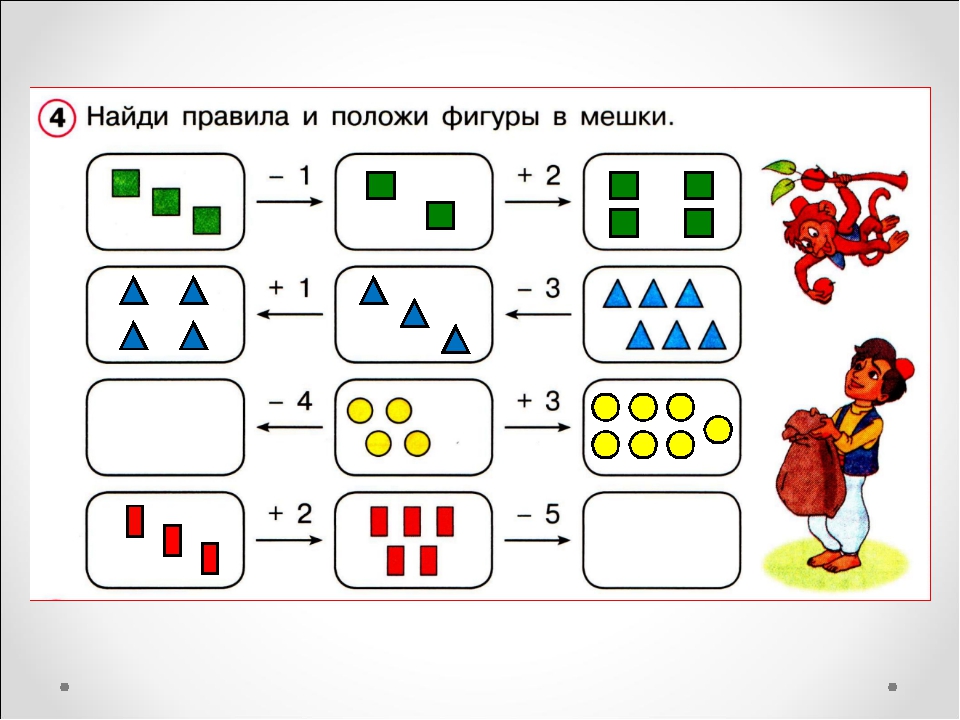
У меня есть формула для n -го члена арифметической последовательности:
Мне дали a 1 = 1, и я выяснил, что d = 4. Подставляя эти значения в формулу, я могу вычислить, сколько там терминов:
a n = a 1 + ( n -1) d
53 = 1 + ( п -1) (4)
53 = 1 + 4 n — 4
53 = 4 n — 3
56 = 4 n
14 = n
Итак, в этой серии 14 терминов.Теперь у меня есть вся необходимая информация, чтобы найти сумму, хотя я не знаю всех суммируемых терминов:
1 + 5 + 9 + … + 49 + 53
= (14/2) (1 + 53)
= (7) (54) = 378
Тогда мой ответ:
Далее мы рассматриваем геометрические ряды.
URL: https://www.purplemath.com/modules/series4.htm
Calculus II — Серия — Основы
Показать мобильное уведомление Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-3: Серии — Основы
В этом разделе мы представим тему, которую будем обсуждать до конца этой главы.\ infty \). Также напомним, что \ (\ Sigma \) используется для представления этого суммирования и называется различными именами. Наиболее распространенные названия: обозначение серии , обозначение суммирования и сигма-обозначение .
Вы должны были видеть эту нотацию, по крайней мере вкратце, когда вы видели определение определенного интеграла в Исчислении I. Если вам нужно быстро освежить в памяти нотацию суммирования, см. Обзор нотации суммирования в примечаниях к Исчислению I.\ infty {{a_i}} = {a_1} + {a_2} + {a_3} + \ cdots + {a_n} + \ cdots \]
Однако мы должны быть осторожны с этим. Это означает, что бесконечный ряд — это просто бесконечная сумма членов, и, как мы увидим в следующем разделе, это не совсем верно для многих рядов.
В следующем разделе мы собираемся более подробно обсудить значение бесконечного ряда, если, конечно, он имеет один, а также идеи сходимости и расхождения.
Этот раздел будет посвящен в основном вопросам нотации, а также тому, чтобы убедиться, что мы можем делать некоторые базовые манипуляции с бесконечными рядами, чтобы мы были готовы к ним, когда нам понадобится иметь возможность иметь дело с ними в следующих разделах.2} + 1}}} \, \, \, \, \, \ и т. Д. \]
Важно еще раз отметить, что индекс будет начинаться с любого значения, с которого начинается последовательность членов ряда, и это может быть буквально что угодно. До сих пор мы использовали \ (n = 0 \) и \ (n = 1 \), но индекс мог начинаться где угодно. Фактически, мы обычно будем использовать \ (\ sum {{a_n}} \) для представления бесконечного ряда, в котором начальная точка индекса не важна. Когда мы опускаем начальное значение индекса, мы также опускаем бесконечность сверху, поэтому не забывайте, что технически она все еще там.
Мы будем опускать начальное значение индекса во многих фактах и теоремах, которые мы будем видеть в этой главе. В этих фактах / теоремах начальная точка ряда не влияет на результат, поэтому для упрощения обозначений и во избежание создания впечатления, что начальная точка важна, мы опустим индекс в обозначениях. Однако не забывайте, что есть отправная точка и что это будет бесконечная серия.
Обратите внимание, однако, что если мы помещаем начальное значение индекса в ряд в факте / теореме, оно присутствует, потому что оно действительно должно быть там.
Теперь, когда некоторые проблемы с обозначениями решены, нам нужно подумать о различных способах манипулирования рядами.
Мы начнем с простой арифметики с бесконечными рядами, так как иногда нам понадобится уметь это делать. У нас есть следующие свойства.
Недвижимость
Если \ (\ sum {{a_n}} \) и \ (\ sum {{b_n}} \) оба сходящиеся ряды, тогда
- \ (\ displaystyle \ sum {c {a_n}} \), где \ (c \) — любое число, также сходится и \ [\ sum {c {a_n}} = c \ sum {{a_n}} \]
- \ (\ displaystyle \ sum \ limits_ {n = k} ^ \ infty {{a_n}} \ pm \ sum \ limits_ {n = k} ^ \ infty {{b_n}} \) также сходится и, \ [\ sum \ limits_ {n = k} ^ \ infty {{a_n}} \ pm \ sum \ limits_ {n = k} ^ \ infty {{b_n}} = \ sum \ limits_ {n = k} ^ \ infty {\ left ({{a_n} \ pm {b_n}} \ right)} \]
Первое свойство просто говорит нам, что мы всегда можем выделить мультипликативную константу из бесконечного ряда и снова вспомнить, что если мы не укажем начальное значение индекса, ряд может начинаться с любого значения. \ infty {\ left ({{a_n} {b_n}} \ right)} \]
\ infty {\ left ({{a_n} {b_n}} \ right)} \]
Чтобы убедиться, что это неправда, рассмотрим следующее произведение двух конечных сумм.3} \]
Ага, это было просто умножение двух многочленов. Каждая из них представляет собой конечную сумму, и поэтому в ней есть смысл. При умножении мы не просто умножали постоянные члены, затем члены \ (x \), и т. Д. . Вместо этого нам пришлось распределить 2 через второй многочлен, затем распределить \ (x \) через второй многочлен и, наконец, объединить похожие члены.
Умножение бесконечного ряда (даже если мы сказали, что нельзя думать о бесконечном ряду как о бесконечной сумме) необходимо производить таким же образом.\ infty {{b_n}}} \ right) = \ left ({{a_0} + {a_1} + {a_2} + {a_3} + \ cdots} \ right) \ left ({{b_0} + {b_1} + {b_2} + {b_3} + \ cdots} \ right) \]
Чтобы выполнить это умножение, нам нужно распределить \ ({a_0} \) через второй член, распределить \ ({a_1} \) через, и т. Д. , а затем объединить похожие члены. Это практически невозможно, поскольку обе серии содержат бесконечный набор терминов, однако для определения произведения двух серий можно использовать следующую формулу.п {{a_i} {b_ {n — i}}} \)
Мы также не можем много сказать о конвергенции продукта. Даже если оба исходных ряда сходятся, продукт может расходиться. Реальность такова, что умножение рядов — довольно сложный процесс, и его по возможности избегают. Мы кратко рассмотрим это в конце главы, когда у нас будет больше работы и мы столкнемся с ситуацией, когда это может быть именно то, что мы действительно хотим сделать.А пока не беспокойтесь об умножении рядов.
Это практически невозможно, поскольку обе серии содержат бесконечный набор терминов, однако для определения произведения двух серий можно использовать следующую формулу.п {{a_i} {b_ {n — i}}} \)
Мы также не можем много сказать о конвергенции продукта. Даже если оба исходных ряда сходятся, продукт может расходиться. Реальность такова, что умножение рядов — довольно сложный процесс, и его по возможности избегают. Мы кратко рассмотрим это в конце главы, когда у нас будет больше работы и мы столкнемся с ситуацией, когда это может быть именно то, что мы действительно хотим сделать.А пока не беспокойтесь об умножении рядов.
Следующая тема, которую нам нужно обсудить в этом разделе, — это смещение индекса . Честно говоря, это не та тема, которую мы часто будем рассматривать в этом курсе. Фактически, мы будем использовать его один раз в следующем разделе и, скорее всего, не будем использовать его снова. Несмотря на то, что мы не будем часто использовать его в этом курсе, это, однако, не означает, что он не часто используется в других классах, где вы можете столкнуться с сериями. Итак, мы кратко рассмотрим это здесь, чтобы вы могли сказать, что видели это.n}}}} \]
Итак, мы кратко рассмотрим это здесь, чтобы вы могли сказать, что видели это.n}}}} \]
Предположим, что по какой-то причине мы хотели начать этот ряд с \ (n = 0 \), но мы не хотели изменять значение ряда. Это означает, что мы не можем просто изменить \ (n = 2 \) на \ (n = 0 \), так как это добавит два новых члена в ряд и, таким образом, изменит его значение.
Выполнение сдвига индекса — довольно простой процесс. Мы начнем с определения нового индекса, скажем \ (i \), следующим образом:
\ [i = n — 2 \]Теперь, когда \ (n = 2 \), мы получим \ (i = 0 \).5}}} + \ cdots \ end {выровнять *} \]
Итак, конечно, две серии имеют точно такие же термины.
На самом деле есть более простой способ выполнить сдвиг индекса. Приведенный выше метод является технически правильным способом выполнения сдвига индекса. Однако обратите внимание, что в приведенном выше примере мы уменьшили начальное значение индекса на 2, и все \ (n \) в членах ряда также увеличились на 2. \ infty {{a_n}} \]
\ infty {{a_n}} \]
В этом примере мы говорим, что вычеркнули первый термин.\ infty {{a_n}} \]
Мы оставим этот раздел с важным предупреждением о терминологии. Не путайте последовательности и серии! Последовательность — это список чисел, записанных в определенном порядке, в то время как бесконечный ряд является пределом последовательности конечных серий и, следовательно, если он существует, будет иметь одно значение.
Итак, еще раз, последовательность — это список чисел, а серия — это одно число, при условии, что имеет смысл даже вычислять ряд. Студенты часто путают их и пытаются использовать факты, относящиеся друг к другу.Однако, поскольку они разные звери, это не сработает. Возникнут проблемы, когда мы будем использовать и последовательности, и серии, поэтому нам всегда нужно помнить, что они разные.
Арифметических последовательностей и серии
Арифметические последовательности
Арифметическая последовательность: последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы d . , Или арифметическая прогрессия, используемая при обращении к арифметической последовательности., представляет собой последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы d .
, Или арифметическая прогрессия, используемая при обращении к арифметической последовательности., представляет собой последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы d .
an = an − 1 + d Арифметическая последовательность
И поскольку an − an − 1 = d, константа d называется общей разностью Константа d , которая получается вычитанием любых двух последовательных членов арифметической последовательности; an − an − 1 = d .. Например, последовательность положительных нечетных целых чисел является арифметической последовательностью,
1,3,5,7,9,…
Здесь a1 = 1, а разница между любыми двумя последовательными членами равна 2.Мы можем построить общий член an = an − 1 + 2, где,
a1 = 1a2 = a1 + 2 = 1 + 2 = 3a3 = a2 + 2 = 3 + 2 = 5a4 = a3 + 2 = 5 + 2 = 7a5 = a4 + 2 = 7 + 2 = 9 ⋮
В общем, учитывая первый член a1 арифметической последовательности и его общую разность d , мы можем написать следующее:
a2 = a1 + da3 = a2 + d = (a1 + d) + d = a1 + 2da4 = a3 + d = (a1 + 2d) + d = a1 + 3da5 = a4 + d = (a1 + 3d) + d = a1 + 4d ⋮
Отсюда мы видим, что любая арифметическая последовательность может быть записана в терминах ее первого элемента, общей разности и индекса следующим образом:
an = a1 + (n − 1) d Арифметическая последовательность
Фактически, любой общий член, линейный в n , определяет арифметическую последовательность.
Пример 1
Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 100 -го члена: 7,10,13,16,19,…
Решение:
Начните с поиска общей разницы,
d = 10-7 = 3
Обратите внимание, что разница между любыми двумя последовательными членами равна 3. Последовательность действительно является арифметической прогрессией, где a1 = 7 и d = 3.
an = a1 + (n − 1) d = 7 + (n − 1) ⋅3 = 7 + 3n − 3 = 3n + 4
Следовательно, мы можем написать общий член an = 3n + 4. Уделите минуту, чтобы убедиться, что это уравнение описывает заданную последовательность. Используйте это уравнение, чтобы найти член 100 th :
а100 = 3 (100) + 4 = 304
Ответ: an = 3n + 4; а100 = 304
Общая разница арифметической последовательности может быть отрицательной.
Пример 2
Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 75 -го члена: 6,4,2,0, −2,…
Решение:
Начните с поиска общей разницы,
d = 4−6 = −2
Затем найдите формулу для общего члена, здесь a1 = 6 и d = −2.
an = a1 + (n − 1) d = 6 + (n − 1) ⋅ (−2) = 6−2n + 2 = 8−2n
Следовательно, an = 8−2n и член 75 th можно рассчитать следующим образом:
a75 = 8−2 (75) = 8−150 = −142
Ответ: an = 8−2n; а100 = −142
Термины между данными членами арифметической последовательности называются средними арифметическими. Термины между данными членами арифметической последовательности.
Пример 3
Найдите все члены арифметической последовательности между a1 = −8 и a7 = 10. Другими словами, найдите все средние арифметические значения между 1 -м и 7 -м членами.
Другими словами, найдите все средние арифметические значения между 1 -м и 7 -м членами.
Решение:
Начните с поиска общей разницы d . В этом случае нам дается первый и седьмой член:
an = a1 + (n − 1) d Используйте n = 7. a7 = a1 + (7−1) da7 = a1 + 6d
Подставляем a1 = −8 и a7 = 10 в приведенное выше уравнение, а затем решаем общую разность d .
10 = −8 + 6d18 = 6d3 = d
Затем используйте первый член a1 = −8 и общую разность d = 3, чтобы найти уравнение для n -го члена последовательности.
an = −8 + (n − 1) ⋅3 = −8 + 3n − 3 = −11 + 3n
При an = 3n − 11, где n — положительное целое число, найдите пропущенные члены.
a1 = 3 (1) −11 = 3−11 = −8a2 = 3 (2) −11 = 6−11 = −5a3 = 3 (3) −11 = 9−11 = −2a4 = 3 (4) — 11 = 12−11 = 1a5 = 3 (5) −11 = 15−11 = 4a6 = 3 (6) −11 = 18−11 = 7} среднее арифметическое a7 = 3 (7) −11 = 21−11 = 10
Ответ: −5, −2, 1, 4, 7
В некоторых случаях первый член арифметической последовательности может не указываться.
Пример 4
Найдите общий член арифметической последовательности, где a3 = −1 и a10 = 48.
Решение:
Чтобы определить формулу для общего члена, нам нужны a1 и d. Линейная система с этими переменными может быть сформирована с использованием данной информации и an = a1 + (n − 1) d:
{a3 = a1 + (3−1) da10 = a1 + (10−1) d⇒ {−1 = a1 + 2d48 = a1 + 9d Используйте a3 = −1. Используйте a10 = 48.
Исключите a1, умножив первое уравнение на -1, и прибавьте результат ко второму уравнению.
{−1 = a1 + 2d48 = a1 + 9d ⇒ × (−1) + {1 = −a1−2d48 = a1 + 9d¯ 49 = 7d7 = d
Подставляем d = 7 в −1 = a1 + 2d, чтобы найти a1.
−1 = a1 + 2 (7) −1 = a1 + 14−15 = a1
Затем используйте первый член a1 = −15 и общую разность d = 7, чтобы найти формулу для общего члена.
an = a1 + (n − 1) d = −15 + (n − 1) ⋅7 = −15 + 7n − 7 = −22 + 7n
Ответ: an = 7n − 22
Попробуй! Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 100 -го члена: 32,2,52,3,72,…
Ответ: an = 12n + 1; а100 = 51
Арифметическая серия
Арифметический ряд Сумма членов арифметической последовательности. представляет собой сумму членов арифметической последовательности. Например, сумма первых 5 членов последовательности, определенной как an = 2n − 1, выглядит следующим образом:
представляет собой сумму членов арифметической последовательности. Например, сумма первых 5 членов последовательности, определенной как an = 2n − 1, выглядит следующим образом:
S5 = Σn = 15 (2n − 1) = [2 (1) −1] + [2 (2) −1] + [2 (3) −1] + [2 (4) −1] + [2 (5) −1] = 1 + 3 + 5 + 7 + 9 = 25
Добавлением 5 положительных нечетных целых чисел, как мы сделали выше, можно управлять. Однако рассмотрите возможность добавления первых 100 положительных нечетных целых чисел. Это было бы очень утомительно. Поэтому затем мы разработаем формулу, которую можно использовать для вычисления суммы первых n членов, обозначенных Sn, любой арифметической последовательности.В целом
Sn = a1 + (a1 + d) + (a1 + 2d) +… + an
Записывая эту серию в обратном порядке, мы имеем,
Sn = an + (an − d) + (an − 2d) +… + a1
И сложив эти два уравнения вместе, члены, включающие d , прибавляют к нулю, и мы получаем n множителей a1 + an:
2Sn = (a1 + an) + (a1 + an) +… + (an + a1) 2Sn = n (a1 + an)
Деление обеих сторон на 2 приводит к формуле для n -й частичной суммы арифметической последовательности Сумма первых n членов арифметической последовательности, заданной формулой: Sn = n (a1 + an) 2. :
:
Sn = n (a1 + an) 2
Используйте эту формулу для вычисления суммы первых 100 членов последовательности, определенной как an = 2n − 1. Здесь a1 = 1 и a100 = 199.
S100 = 100 (a1 + a100) 2 = 100 (1 + 199) 2 = 10 000
Пример 5
Найдите сумму первых 50 членов заданной последовательности: 4, 9, 14, 19, 24,…
Решение:
Определите, есть ли общее различие между данными терминами.
d = 9−4 = 5
Обратите внимание, что разница между любыми двумя последовательными членами равна 5. Последовательность действительно является арифметической прогрессией, и мы можем написать
an = a1 + (n − 1) d = 4 + (n − 1) ⋅5 = 4 + 5n − 5 = 5n − 1
Следовательно, общий член an = 5n − 1. Чтобы вычислить частичную сумму 50 -го этой последовательности, нам понадобятся 1 -е и 50 -е члены:
а1 = 4а50 = 5 (50) -1 = 249
Затем используйте формулу, чтобы определить частичную сумму 50 -й заданной арифметической последовательности.
Sn = n (a1 + an) 2S50 = 50. (A1 + a50) 2 = 50 (4 + 249) 2 = 25 (253) = 6,325
Ответ: S50 = 6,325
Пример 6
Вычислить: Σn = 135 (10−4n).
Решение:
В этом случае нас просят найти сумму первых 35 членов арифметической последовательности с общим членом an = 10−4n. Используйте это, чтобы определить 1 -й и 35 -й член.
a1 = 10−4 (1) = 6a35 = 10−4 (35) = — 130
Затем используйте формулу, чтобы определить частичную сумму 35 -я .
Sn = n (a1 + an) 2S35 = 35⋅ (a1 + a35) 2 = 35 [6 + (- 130)] 2 = 35 (−124) 2 = −2,170
Ответ: −2,170
Пример 7
Первый ряд сидений в амфитеатре под открытым небом содержит 26 сидячих мест, второй ряд — 28 сидений, третий ряд — 30 сидячих мест и так далее. Если рядов 18, какова общая вместимость театра?
Если рядов 18, какова общая вместимость театра?
Рисунок 9.2
Римский театр (Википедия)
Решение:
Начните с поиска формулы, которая дает количество мест в любом ряду.Здесь количество мест в каждом ряду образует последовательность:
26,28,30,…
Обратите внимание, что разница между любыми двумя последовательными членами равна 2. Последовательность представляет собой арифметическую прогрессию, где a1 = 26 и d = 2.
an = a1 + (n − 1) d = 26 + (n − 1) ⋅2 = 26 + 2n − 2 = 2n + 24
Таким образом, количество мест в каждом ряду равно an = 2n + 24. Чтобы рассчитать общую вместимость 18 рядов, нам нужно вычислить частичную сумму 18 -го .Для этого нам понадобятся 1 st и 18 th условия:
а1 = 26а18 = 2 (18) + 24 = 60
Используйте это, чтобы вычислить частичную сумму 18 th следующим образом:
Sn = n (a1 + an) 2S18 = 18⋅ (a1 + a18) 2 = 18 (26 + 60) 2 = 9 (86) = 774
Ответ: Всего 774 места.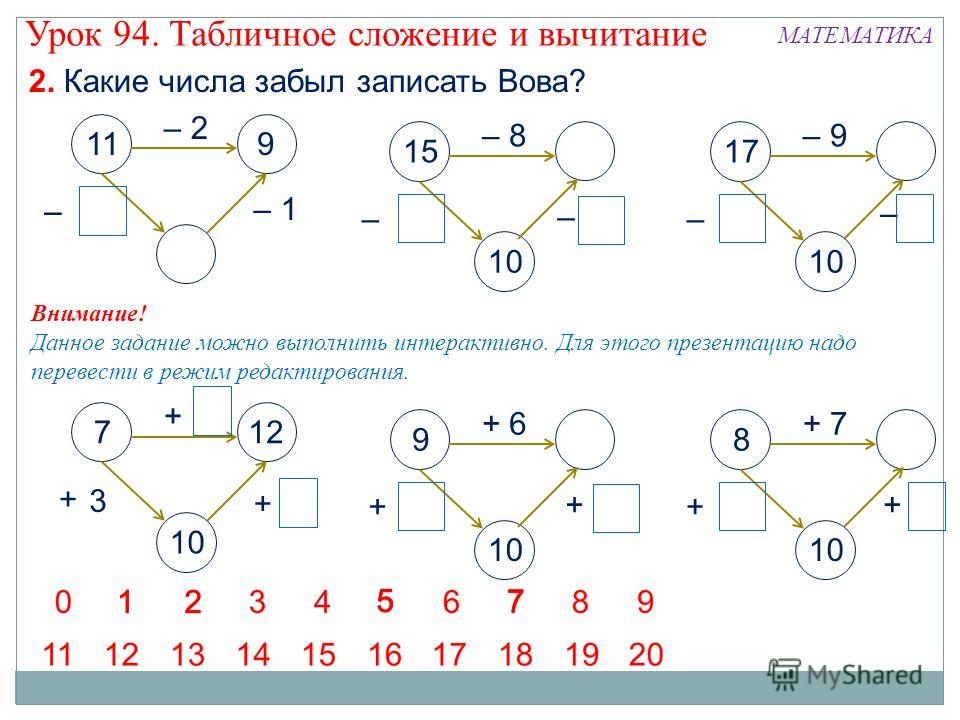
Попробуй! Найдите сумму первых 60 членов заданной последовательности: 5, 0, −5, −10, −15,…
Ответ: S60 = −8,550
Основные выводы
- Арифметическая последовательность — это последовательность, в которой разница d между последовательными членами является постоянной.
- Общий член арифметической последовательности может быть записан в терминах его первого члена a1, общей разности d и индекса n следующим образом: an = a1 + (n − 1) d.
- Арифметический ряд — это сумма членов арифметической последовательности.
- Частичная сумма n арифметической последовательности может быть вычислена с использованием первого и последнего членов следующим образом: Sn = n (a1 + an) 2.
Тематические упражнения
−3, −7, −11, −15, −19,…
−6, −14, −22, −30, −38,…
−5, −10, −15, −20, −25,…
−13, 23, 53, 83, 113,…
13, 0, −13, −23, −1,…
14, −12, −54, −2, −114,…
0.
 8, 2, 3.2, 4.4, 5.6,…
8, 2, 3.2, 4.4, 5.6,…4,4, 7,5, 10,6, 13,7, 16,8,…
Найдите положительное нечетное целое число 50 -е .
Найдите положительное четное число 50 -е .
Найдите 40 -й член в последовательности, которая состоит из всех остальных положительных нечетных целых чисел: 1, 5, 9, 13,…
Найдите 40 -й член в последовательности, состоящей из всех остальных положительных четных целых чисел: 2, 6, 10, 14,…
Какое число представляет собой член 355 в арифметической последовательности −15, −5, 5, 15, 25,…?
Какое число является членом −172 в арифметической последовательности 4, −4, −12, −20, −28,…?
Учитывая арифметическую последовательность, определяемую рекуррентным соотношением an = an − 1 + 5, где a1 = 2 и n> 1, найдите уравнение, которое дает общий член в терминах a1 и общей разности d .

Учитывая арифметическую последовательность, определяемую рекуррентным соотношением an = an − 1−9, где a1 = 4 и n> 1, найдите уравнение, которое дает общий член в терминах a1 и общей разности d .
a4 = −2310 и a21 = −252
Часть A: Арифметические последовательности
Запишите первые 5 членов арифметической последовательности, учитывая их первый член и общую разницу. Найдите формулу для его общего члена.
Найдите формулу для его общего члена.
Учитывая арифметическую последовательность, найдите формулу для общего члена и используйте ее для определения 100 -го члена.
Учитывая члены арифметической последовательности, найдите формулу для общего члена.
Найдите все средние арифметические значения между заданными членами.
∑n = 1160 (3n)
∑n = 1121 (−2n)
∑n = 1250 (4n − 3)
∑n = 1120 (2n + 12)
∑n = 170 (19−8n)
∑n = 1220 (5 − п)
∑n = 160 (52−12n)
∑n = 151 (38n + 14)
∑n = 1120 (1.
 5n − 2,6)
5n − 2,6)∑n = 1175 (-0,2n-1,6)
Найдите сумму первых 200 натуральных чисел.
Найдите сумму первых 400 натуральных чисел.
Сумма первых 50 положительных нечетных целых чисел.

Сумма первых 200 положительных нечетных целых чисел.
Сумма первых 50 положительных четных целых чисел.
Сумма первых 200 положительных четных целых чисел.
Сумма первых k положительных нечетных целых чисел.
Сумма первых k положительных четных чисел.
Первый ряд сидений в малом театре состоит из 8 посадочных мест.
 После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?
После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?Первый ряд сидений в амфитеатре под открытым небом содержит 42 сиденья, второй ряд — 44 сиденья, третий ряд — 46 сидячих мест и так далее.Если рядов 22, какова общая вместимость театра?
Если в треугольной стопке кирпичей 37 кирпичей в нижнем ряду, 34 кирпича во втором ряду и так далее, с одним кирпичом наверху. Сколько кирпичей в стопке?
В каждом последующем ряду треугольной стопки кирпичей на один кирпич меньше, пока наверху не останется только один кирпич.Сколько рядов в стеке, если всего кирпичей 210?
10-летний договор о заработной плате предлагает 65 000 долларов в первый год с повышением на 3200 долларов каждый дополнительный год.
 Определите общую сумму обязательств по заработной плате за 10-летний период.
Определите общую сумму обязательств по заработной плате за 10-летний период.Башня с часами бьет в колокол количество раз, указанное в часах.В час дня он ударяет один раз, в два часа — дважды и так далее. Сколько раз за день башня с часами бьет в колокол?
Часть B: Арифметическая серия
Рассчитайте указанную сумму по формуле для общего члена.
Оценить.
Общий член для последовательности положительных нечетных целых чисел задается как an = 2n − 1, а общий член для последовательности положительных четных целых чисел задается как an = 2n. Найдите следующее.
Является ли последовательность Фибоначчи арифметической последовательностью? Объяснять.
Используйте формулу для n -й частичной суммы арифметической последовательности Sn = n (a1 + an) 2 и формулу для общего члена an = a1 + (n − 1) d, чтобы получить новую формулу для n -я частичная сумма Sn = n2 [2a1 + (n − 1) d].
 При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.
При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.Обсудите методы расчета сумм, в которых индекс не начинается с 1. Например, Σn = 1535 (3n + 4) = 1,659.
Известная история повествует о плохом поведении Карла Фридриха Гаусса в школе.В наказание учитель поручил ему сложить первые 100 целых чисел. Легенда гласит, что молодой Гаусс правильно ответил в считанные секунды. Каков ответ и как, по-вашему, он смог так быстро найти сумму?
Часть C: Обсуждение
ответов
5, 8, 11, 14, 17; ан = 3n + 2
15, 10, 5, 0, −5; ан = 20−5н
12, 32, 52, 72, 92; an = n − 12
1, 12, 0, −12, −1; ан = 32−12н
1.
 8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2
8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2ан = 1.
 2n − 0,4; а100 = 119,6
2n − 0,4; а100 = 119,6
по арифметике и геометрии — IB Math Stuff
Определения
Серия — Ряд образован суммой или сложением членов в последовательности. Например, арифметический ряд формируется путем суммирования членов в арифметической последовательности.
Например, арифметический ряд формируется путем суммирования членов в арифметической последовательности.
Последовательность: | (1) \ begin {формула} 3, 5, 7, 9, … \ end {уравнение} |
Серия: | (2) \ begin {уравнение} 3 + 5 + 7 + 9 + … \ end {уравнение} |
n -е Неполная сумма — определяется как сумма от 1 -го члена до n -го члена в последовательности.Например, частичная сумма 5 th вышеприведенного ряда будет:
(3)\ begin {уравнение} 3 + 5 + 7 + 9 + 11 = 35 \ end {уравнение}
Обозначения для частичных сумм
Имеется два вкуса. Тот, который довольно легко понять и наиболее часто используется в математике SL. Второй — более сложный, пугающий и редко используется в SL.
Первое обозначение: Партиал n -й может быть обозначен как $ S_n $, где n сообщает читателю, сколько членов нужно суммировать. Например, используя арифметический ряд $ 3 + 5 + 7 + 9 + … $, тогда частичная сумма 5 th будет:
Например, используя арифметический ряд $ 3 + 5 + 7 + 9 + … $, тогда частичная сумма 5 th будет:
\ begin {уравнение} S_5 = 3 + 5 + 7 + 9 + 11 = 35 \ end {уравнение}
Стоит отметить, что «частичная сумма n th » обычно относится к фактическому результату сложения, а не к утверждению, показывающему все сложение.
Второе обозначение: Это обозначение часто называется «нотацией суммирования» и включает в себя номер члена, с которого мы начинаем, номер члена, которым мы заканчиваем, и детали того, что мы суммируем.Например:
Это обозначение позволяет нам начать суммирование с любого члена, который мы захотим. В следующем примере суммирование начинается с члена 5 -го и продолжается до члена 7 -го .
«Уравнение» в нотации суммирования работает путем простой подстановки значений n в уравнение, выполняя арифметические вычисления в одном из членов ряда.
Суммирование арифметических рядов
Немного сообразительности и наблюдательности можно создать два уравнения, которые позволяют легко вычислить арифметический ряд:
(5)\ begin {align} S_n = \ frac {n} {2} (u_1 + u_n) \ end {align}
Эта формула требует, чтобы вы знали первый и последний член в ряду.Второе уравнение, показанное ниже, позволяет вычислить сумму, не зная окончательного члена, который вы будете суммировать (умно!). Следующее уравнение позволяет вычислить сумму, если вы знаете первый член и общую разницу.
(6)\ begin {align} S_n = \ frac {n} {2} (2u_1 + (n-1) d) \ end {align}
Это уравнение происходит из предыдущего уравнения, когда выполняется замена $ u_n = u_1 + (n-1) d $ и алгебраическое выражение упрощается.
Примеры
Пример 1 Найдите частичную сумму 12 -го за 4 доллара.5 + 6 + 7,5 + …
долл. СШАСначала найдите общую разницу:
(7)\ begin {уравнение} 6 — 4,5 = 1,5 \ end {уравнение}
Тогда простая замена:
(8) \ begin {align} S_ {12} = \ frac {12} {2} (2 \ cdot 4. 5 + (12-1) 1.5) = 153 \ end {align}
5 + (12-1) 1.5) = 153 \ end {align}
Пример 2 Найдите $ S_ {20} $ за 5 + 2 + -1 + -4 $
Сначала найдите общую разницу:
(9)\ begin {уравнение} 2 — 5 = -3 \ end {уравнение}
Опять же, простая замена:
(10)\ begin {align} S_ {20} = \ frac {20} {2} (2 \ cdot 5 + (20-1) (- 3)) = — 470 \ end {align}
Пример 3 Найдите значение n такое, что $ S_n = 205 $ для $ 7 + 10 + 13 +.2 + 5,5n = 205 \ end {уравнение}
Выберите свой любимый способ решения ..
В любом случае вы должны получить $ n = 10 $. Вот как это решила Wolfram Alpha.
Вы должны заметить, что вы получаете два решения (в конце концов, это квадратичное), в этом случае желателен только положительный ответ, поскольку последовательность / ряд не определен для отрицательных чисел термов. Также второе решение не является целым числом, что обычно указывает на то, что что-то не так.
Суммирование геометрических рядов
Составление уравнения для суммирования геометрического ряда требует большого ума и здоровой дозы того, что кажется волшебством. n)} {1-1.7} \ приблизительно 443 088 \ end {align}
n)} {1-1.7} \ приблизительно 443 088 \ end {align}
Это оставляет нам экспоненциальное уравнение, которое можно решить с помощью логарифма или GDC. И снова вот как это сделал Wolfram Alpha.
Ответ: $ n \ приблизительно 19 $.
Еще несколько определений
Infinite Series — серия, содержащая бесконечное количество членов. Я бы привел пример, но нужно время, чтобы записать…
Divergent Infinite Series — Серия, в которой при сложении всего бесконечного числа членов результатом является положительная или отрицательная бесконечность.Если это похоже на «А, разве это не всегда происходит?» взгляните на следующее определение.
Конвергентная бесконечная серия — Серия, в которой при сложении всего бесконечного числа членов получается конечное (или небесконечное) число. Вы спросите, как такое возможно? Попробуйте сложить на своем калькуляторе ряды, указанные ниже.
(19) \ begin {align} 1+ \ frac {1} {2} + \ frac {1} {4} + \ frac {1} {8} + \ frac {1} {16} + . n $ будет приближаться к нулю.{\ infty} = 0 $ оставим нам уравнение:
n $ будет приближаться к нулю.{\ infty} = 0 $ оставим нам уравнение:
\ begin {align} S_ \ infty = \ frac {u_1} {1-r} \ end {align}
Ницца. А также. Простой.
Пример
Пример 1 Найдите значение бесконечной суммы $ 1 + \ frac {2} {3} + \ frac {4} {9} + … $
Сначала найдите общее отношение:
(23)\ begin {align} \ frac {\ frac {2} {3}} {1} = \ frac {2} {3} \ end {align}
Еще раз небольшая подмена:
(24)\ begin {align} S_ \ infty = \ frac {1} {1- \ frac {2} {3}} = 3 \ end {align}
Хотите добавить или прокомментировать эти заметки? Сделайте это ниже.
методов сложения чисел от 1 до 100 — лучше объяснение
Есть популярная история о том, что у Гаусса, выдающегося математика, был ленивый учитель. Так называемый педагог хотел занять детей, чтобы он мог вздремнуть; он попросил класс сложить числа от 1 до 100.
Гаусс подошел со своим ответом: 5050. Так скоро? Учитель заподозрил чит, но нет. Ручное добавление было для лохов, и Гаусс нашел формулу, чтобы обойти эту проблему:
Так скоро? Учитель заподозрил чит, но нет. Ручное добавление было для лохов, и Гаусс нашел формулу, чтобы обойти эту проблему:
Давайте поделимся несколькими объяснениями этого результата и разберемся с ним интуитивно.В этих примерах мы добавим 1 к 10, а затем посмотрим, как это применимо к 1 к 100 (или 1 к любому числу).
Метод 1: парные числа
Сопряжение номеров — распространенный подход к этой проблеме. Вместо того, чтобы записывать все числа в один столбец, давайте обернем их вокруг, например:
1 2 3 4 5
10 9 8 7 6
Возникает интересная закономерность: сумма каждого столбца равна 11 . По мере увеличения верхней строки нижняя строка уменьшается, поэтому сумма остается неизменной.
Поскольку 1 сочетается с 10 (нашим n), мы можем сказать, что каждый столбец имеет (n + 1). А сколько у нас пар? Ну у нас 2 одинаковых ряда, у нас должно быть n / 2 пар.
, что является формулой выше.
Подождите, а как насчет нечетного количества предметов?
А, я рада, что вы подняли этот вопрос. Что, если мы сложим числа от 1 до 9? У нас нет четного числа элементов для объединения в пары. Многие объяснения просто дадут объяснение выше и оставим все как есть.Я не буду.
Давайте сложим числа от 1 до 9, но вместо того, чтобы начинать с 1, давайте вместо этого будем считать от 0:
0 1 2 3 4
9 8 7 6 5
Считая от 0, мы получаем «дополнительный элемент» (всего 10), поэтому у нас может быть четное количество строк. Однако наша формула будет выглядеть несколько иначе.
Обратите внимание, что в каждом столбце есть сумма n (а не n + 1, как раньше), поскольку 0 и 9 сгруппированы. И вместо того, чтобы иметь ровно n элементов в 2 строках (всего n / 2 пары), у нас есть n + 1 элемент в 2 строках (всего (n + 1) / 2 пары).Если вы подставите эти числа, вы получите:
, это та же формула, что и раньше. Меня всегда беспокоило, что одна и та же формула работает как для нечетных, так и для четных чисел — разве вы не получите дробь? Да, вы получаете ту же формулу, но по разным причинам.
Метод 2: Используйте две строки
Вышеупомянутый метод работает, но вы обрабатываете нечетные и четные числа по-разному. Нет лучшего способа? Да.
Вместо того, чтобы перебирать числа по кругу, давайте запишем их в две строки:
1 2 3 4 5 6 7 8 9 10
10 9 8 7 6 5 4 3 2 1
Обратите внимание, что у нас есть 10 пар, и каждая пара в сумме дает 10 + 1.
Сумма всех вышеперечисленных чисел составляет
.Но нам нужна сумма только одной строки, а не обеих. Таким образом, мы разделим приведенную выше формулу на 2 и получим:
Теперь это круто (насколько крутыми могут быть ряды чисел). Работает как для нечетного, так и для четного количества элементов одинаково!
Техника 3. Создайте прямоугольник
Недавно я наткнулся на другое объяснение, новый подход к старому объяснению спаривания. Разные объяснения лучше подходят для разных людей, и мне больше нравится это.
Вместо того, чтобы записывать числа, представьте, что у нас есть бобы. Мы хотим добавить 1 боб к 2 бобам к 3 бобам… вплоть до 5 бобов.
Мы хотим добавить 1 боб к 2 бобам к 3 бобам… вплоть до 5 бобов.
х
х х
х х х
х х х х
х х х х х
Конечно, мы могли бы перейти к 10 или 100 бобам, но с 5 вы поняли идею. Как мы посчитаем количество бобов в нашей пирамиде?
Ну, ясно, что сумма 1 + 2 + 3 + 4 + 5. Но давайте посмотрим на это с другой стороны. Допустим, мы зеркально отражаем нашу пирамиду (я буду использовать «о» для зеркальных бобов), а затем опрокидываем ее:
x o x o o o o o
х х о о х х о о о о
x x x o o o => x x x o o o
x x x x o o o o x x x x o o
х х х х х о о о о о х х х х х о
Круто, а? Если вам интересно, соответствует ли это «на самом деле», так оно и есть.Взгляните на нижний ряд правильной пирамиды с 5′x (и 1 o). В следующем ряду пирамиды на 1 меньше x (всего 4) и на 1 больше o (всего 2), чтобы заполнить пробел. Как и при спаривании, одна сторона увеличивается, а другая убывает.
А теперь объяснение: сколько всего бобов у нас есть? Ну, это всего лишь площадь прямоугольника.
У нас есть n строк (мы не меняли количество строк в пирамиде), и наша коллекция имеет ширину (n + 1) единиц, так как 1 «o» объединяется со всеми «x».
Обратите внимание, что на этот раз нас не волнует четность или нечетность n — формула общей площади работает отлично. Если n нечетное, в каждой строке будет четное количество элементов (n + 1).
Но, конечно, нам не нужна общая площадь (количество x и o), нам просто нужно количество x. Поскольку мы удвоили x, чтобы получить ноль, x сами по себе составляют лишь половину общей площади:
И мы вернулись к нашей исходной формуле. Опять же, количество x в пирамиде = 1 + 2 + 3 + 4 + 5 или сумма от 1 до n.
Техника 4: Среднее значение
Все мы знаем, что
среднее = сумма / количество позиций
, которое мы можем переписать на
сумма = среднее * количество позиций
Итак, давайте подсчитаем сумму. Если у нас есть 100 чисел (1… 100), то очевидно, что у нас есть 100 элементов. Это было просто.
Это было просто.
Чтобы получить среднее значение, обратите внимание, что все числа распределены равномерно. Для каждого большого числа на другом конце есть небольшое число.Давайте посмотрим на небольшой набор:
1 2 3
Среднее значение 2. 2 уже находится в середине, а 1 и 3 «сокращаются», поэтому их среднее значение составляет 2.
Для четного количества позиций
1 2 3 4
среднее значение от 2 до 3 — это 2,5. Несмотря на то, что у нас есть дробное среднее значение, это нормально — поскольку у нас есть даже элементов, когда мы умножаем среднее значение на количество, уродливая дробь исчезнет.
Обратите внимание, что в обоих случаях 1 находится по одну сторону от среднего, а N одинаково далеко по другую.Итак, мы можем сказать, что среднее значение всего набора на самом деле является просто средним от 1 и n: (1 + n) / 2.
Подставляем это в нашу формулу
И вуаля! У нас есть четвертый способ думать о нашей формуле.
Так почему это полезно?
Три причины:
1) Быстрое сложение чисел может быть полезно для оценки. Обратите внимание, что формула расширяется до этого:
Допустим, вы хотите сложить числа от 1 до 1000: предположим, вы получаете 1 дополнительный посетитель на ваш сайт каждый день — сколько всего посетителей у вас будет через 1000 дней? Поскольку тысяча в квадрате = 1 миллион, мы получаем миллионов / 2 + 1000/2 = 500,500 .
2) Эта концепция добавления чисел от 1 к N встречается и в других местах, например, при вычислении вероятности парадокса дня рождения. Твердое усвоение этой формулы поможет вам разобраться во многих областях.
3) Самое главное, этот пример показывает, что есть много способов понять формулу. Может быть, вам нравится метод спаривания, может быть, вы предпочитаете технику прямоугольника, или, может быть, есть другое объяснение, которое вам подходит. Не сдавайтесь , если вы не понимаете — попробуйте найти другое объяснение, которое работает. Счастливая математика.
Счастливая математика.
Кстати, есть более подробные сведения об истории этой истории и о технике, которую, возможно, использовал Гаусс.
Варианты
Вместо 1 до n, как насчет 5 до n?
Начните с обычной формулы (1 + 2 + 3 +… + n = n * (n + 1) / 2) и вычтите ту часть, которая вам не нужна (1 + 2 + 3 + 4 = 4 * (4 + 1) / 2 = 10).
Сумма для 5 + 6 + 7 + 8 +… n = [n * (n + 1) / 2] - 10
И для любого стартового числа a:
Сумма от a до n = [n * (n + 1) / 2] - [(a - 1) * a / 2]
Мы хотим избавиться от всех чисел от 1 до — 1.
Как насчет четных чисел, например 2 + 4 + 6 + 8 +… + n?
Просто удвойте обычную формулу. Чтобы сложить числа от 2 до 50, найдите 1 + 2 + 3 + 4… + 25 и удвойте:
Сумма 2 + 4 + 6 +… + n = 2 * (1 + 2 + 3 +… + n / 2) = 2 * n / 2 * (n / 2 + 1) / 2 = n / 2 * (п / 2 + 1)
Итак, чтобы получить эвены от 2 до 50, вы должны сделать 25 * (25 + 1) = 650
Как насчет нечетных чисел, например 1 + 3 + 5 + 7 +… + n?
То же, что и четная формула, за исключением того, что каждое число на 1 меньше своего аналога (у нас 1 вместо 2, 3 вместо 4 и т. Д.).Получаем следующее по величине четное число (n + 1) и убираем лишние (n + 1) / 2 «-1 ″ элементов:
Д.).Получаем следующее по величине четное число (n + 1) и убираем лишние (n + 1) / 2 «-1 ″ элементов:
Сумма 1 + 3 + 5 + 7 +… + n = [(n + 1) / 2 * ((n + 1) / 2 + 1)] - [(n + 1) / 2]
Чтобы сложить 1 + 3 + 5 +… 13, получите следующее по величине четное значение (n + 1 = 14) и сделайте
[14/2 * (14/2 + 1)] - 7 = 7 * 8 - 7 = 56 - 7 = 49
Комбинации: выравнивание и офсет
Допустим, вам нужны эвены из 50 + 52 + 54 + 56 +… 100. Найдите все эвены
2 + 4 + 6 +… + 100 = 50 * 51
и вычтите те, которые вам не нужны
2 + 4 + 6 +… 48 = 24 * 25
Итак, сумма от 50 + 52 +… 100 = (50 * 51) — (24 * 25) = 1950
Уф! Надеюсь это поможет.
Рубиновые ботаники: вы можете проверить это с помощью
(50..100) .select {| x | х% 2 == 0} .inject (: +)
1950
фанатов Javascript, сделайте это:
[. .. Array (51) .keys ()]. Map (x => x + 50) .filter (x => x% 2 == 0) .reduce ((x, y) => x + у)
1950
// Примечание: здесь 51 номер от 50 до 100 включительно. Забор!
.. Array (51) .keys ()]. Map (x => x + 50) .filter (x => x% 2 == 0) .reduce ((x, y) => x + у)
1950
// Примечание: здесь 51 номер от 50 до 100 включительно. Забор!
Другие сообщения этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: визуальное руководство
- Quick Insight: интуитивное значение подразделения
- Quick Insight: вычитание отрицательных чисел
- Удивительные узоры в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (как избежать проблемы со столбом)
- Причудливое введение в системы счисления
- Другой взгляд на простые числа
- Интуиция к золотому сечению
- Различные интерпретации числа ноль
Сумма n, n² или n³
Как и в предыдущем разделе, пусть sa, n = ∑k = 1nka.он же
.
 Вычитание
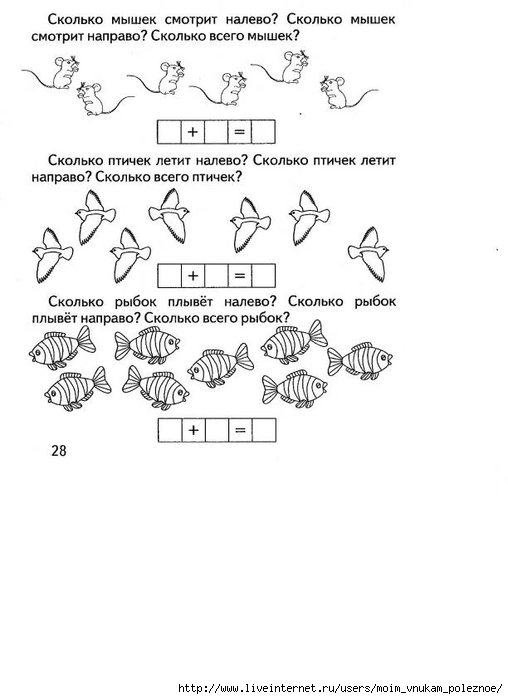
Вычитание Выполняя задания, ребенок освоит порядковый и колличественный счет в пределах десяти, научится соотносить цифру и количество предметов. Если малыш затрудняется, обязательно объясните задание ещё раз, помогите в выполнении. Хорошо, если вы сможете закрепить полученные знания и на дополнительных занятиях и в повседневной жизни.
Выполняя задания, ребенок освоит порядковый и колличественный счет в пределах десяти, научится соотносить цифру и количество предметов. Если малыш затрудняется, обязательно объясните задание ещё раз, помогите в выполнении. Хорошо, если вы сможете закрепить полученные знания и на дополнительных занятиях и в повседневной жизни. Хорошо, если вы сможете закрепить полученные знания и на дополнительных занятиях и в повседневной жизни.
Хорошо, если вы сможете закрепить полученные знания и на дополнительных занятиях и в повседневной жизни. Последовательность событий
Последовательность событий Пусть малыш объяснит выполнение задания.
Пусть малыш объяснит выполнение задания. На каждой страничке две логические задачи. Прочитайте их ребёнку, объясните, если ему
непонятно, задайте наводящие вопросы. Успехов Вам и вашим детям!
На каждой страничке две логические задачи. Прочитайте их ребёнку, объясните, если ему
непонятно, задайте наводящие вопросы. Успехов Вам и вашим детям! п.
п. 8, 2, 3.2, 4.4, 5.6,…
8, 2, 3.2, 4.4, 5.6,…
 5n − 2,6)
5n − 2,6)
 После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?
После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре? Определите общую сумму обязательств по заработной плате за 10-летний период.
Определите общую сумму обязательств по заработной плате за 10-летний период. При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.
При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере. 8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2
8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2 2n − 0,4; а100 = 119,6
2n − 0,4; а100 = 119,6 .. Array (51) .keys ()]. Map (x => x + 50) .filter (x => x% 2 == 0) .reduce ((x, y) => x + у)
1950
// Примечание: здесь 51 номер от 50 до 100 включительно. Забор!
.. Array (51) .keys ()]. Map (x => x + 50) .filter (x => x% 2 == 0) .reduce ((x, y) => x + у)
1950
// Примечание: здесь 51 номер от 50 до 100 включительно. Забор!