Сложение и вычитание обыкновенных и десятичных дробей. смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.
12+
3 месяца назад
Математика от Баканчиковой149 подписчиков
Математика 5 класс. Продолжая тему «Десятичные дроби», сегодня мы расскажем Вам о том, как обращать обыкновенную дробь в десятичную. А начнём мы с объяснения для чего обращают обыкновенную дробь в десятичную. Оказывается это нужно для того, чтобы выполнить сложение или вычитание обыкновенной дроби и десятичной, т.к. не существует правил сложения и вычитания таких дробей. Мы дадим Вам и на конкретных примерах пошагово разберём правило обращения обыкновенной дроби в десятичную дробь. Затем поспорим с авторами современных учебников математики 5 класса о том, что при делении одного натурального числа на другое натуральное число получается обыкновенная дробь. А для обращения обыкновенной дроби в десятичную, числитель необходимо представить сначала в виде десятичной дроби, а затем уже десятичную дробь разделить на знаменатель, потому что при делении десятичной дроби на натуральное число получается десятичная дробь.
 Равные десятичные дроби. Правило нулей. Математика 5 класс. https://rutube.ru/video/73e724f37977aeb256ba64ecb7932f54/
Округление десятичных дробей. Разряды и классы десятичной дроби. Математика 5 класс.
https://rutube.ru/video/27b315e7f6947dcede06cf447ae5e949/
Сложение и вычитание десятичных дробей. Математика 5 класс. https://rutube.ru/video/fde1d5a21516a66460a9744103adeb91/
Решение уравнений на сложение и вычитание десятичных дробей в 5 классе. Примеры решения уравнений. https://rutube.ru/video/14bfaafb1c6047388e14c264284db257/
Умножение десятичных дробей. Математика 5 класс. https://rutube.ru/video/d10e83ffbc0994bff4cc8c131e834c81/
#ДесятичныеДроби #ОбыкновеннуюДробьВДесятичную #СложениеДесятичнойДробиИОбыкновеннойДроби #МатематикаОтБаканчиковой
математика 5 класс, десятичные дроби, как обратить обыкновенную дробь в десятичную, обыкновенную дробь в десятичную, сложение и вычитание обыкновенной и десятичной дроби, сложение и вычитание десятичной и обыкновенной дроби, правило обращения обыкновенной дробь в десятичную
Равные десятичные дроби. Правило нулей. Математика 5 класс. https://rutube.ru/video/73e724f37977aeb256ba64ecb7932f54/
Округление десятичных дробей. Разряды и классы десятичной дроби. Математика 5 класс.
https://rutube.ru/video/27b315e7f6947dcede06cf447ae5e949/
Сложение и вычитание десятичных дробей. Математика 5 класс. https://rutube.ru/video/fde1d5a21516a66460a9744103adeb91/
Решение уравнений на сложение и вычитание десятичных дробей в 5 классе. Примеры решения уравнений. https://rutube.ru/video/14bfaafb1c6047388e14c264284db257/
Умножение десятичных дробей. Математика 5 класс. https://rutube.ru/video/d10e83ffbc0994bff4cc8c131e834c81/
#ДесятичныеДроби #ОбыкновеннуюДробьВДесятичную #СложениеДесятичнойДробиИОбыкновеннойДроби #МатематикаОтБаканчиковой
математика 5 класс, десятичные дроби, как обратить обыкновенную дробь в десятичную, обыкновенную дробь в десятичную, сложение и вычитание обыкновенной и десятичной дроби, сложение и вычитание десятичной и обыкновенной дроби, правило обращения обыкновенной дробь в десятичнуюСложение и вычитание десятичных дробей – методическая разработка для учителей, Камалова Джамиля Джолдасовна
Цели обучения: | 5. | ||||||||||||||||||
Цели урока: | отработать навыки сложения и вычитания десятичных дробей, углубить полученные знания и навыки при решении примеров, уравнений и задач; развить логическое мышление, математическую речь. | ||||||||||||||||||
Критерии успеха: | Научится: самостоятельно складывать и вычитать десятичные дроби; выполнять действия в сотрудничестве с учителем по предложенному плану; самостоятельно выстраивать план действий по решению учебной задачи изученного вида; контролировать и оценивать по эталону свои работы и работы товарищей; получит возможность адекватно воспринимать оценку своей работы учителем, товарищами. | ||||||||||||||||||
Привитие ценностей: | Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни. | ||||||||||||||||||
Языковые цели: | Ученики: — могут объяснить алгоритм операций над десятичными дробями. Учащиеся будут: — комментировать выполнение сравнения дробей и нахождение суммы и разности десятичных дробей; — устно формулировать алгоритм сложения и вычитания десятичных дробей; — устно формулировать вопросы для проверки понимания темы сложения и вычитания десятичных дробей. Предметная лексика и терминология:
— целая часть, дробная часть; — десятичная дробь; — количество знаков, отделяемых запятой; — количество знаков после запятой; — десятая, сотая, тысячная части и т.д. | ||||||||||||||||||
Межпредметные связи: | Алгебра, физика, экономика | ||||||||||||||||||
Навыки использования ИКТ: | На данном уроке используется презентация и ресурсы с сайта BilimLand.kz и Itest.kz | ||||||||||||||||||
Предварительные знания: | Учащиеся могут сравнивать десятичные дроби, умеют правильно читать и записывать десятичные дроби. |
Ход урока
Этапы урока | Запланированная деятельность на уроке | Ресурсы | ||||||||||||||||||
Начало урока 7 мин | Приветствие. Создание коллаборативной среды. Круг радости. Игра «Я люблю свою родину, потому что…». Деление на группы. На доске прикреплены стикеры, на которых написаны примеры на сложение, вычитание, сравнение и изображение на координатном луче. Учащийся выбирает стикер и садится за тот стол, запись с примером которого подходит к названию группы. На столах лежат слова на казахском русском и английском языках. Нужно найти соответствие и закрепить на постере терминологию:
Логическая минутка. По порядку нумерации расшифровать девиз к уроку, слова которого принадлежат нашему Президенту страны Назарбаеву Н.А. Девиз нашего урока: Біздің құатымыз – бірлікте! Проблемный вопрос: Вставьте пропущенные цифры в клеточки, выполняя сложение и вычитание. Учитель: «Как вы думаете, какова тема нашего урока? А какие цели мы ставим перед собой на этот урок? Правильно!» | Презентация Слайд 1-4
Стикеры
Стикеры
Карточки с сайта BilimLand.
Стикеры | ||||||||||||||||||
Критерии успеха | Учащиеся расшифровывают девиз к уроку. Ученики самостоятельно называют тему урока и ставят цели на уроке. |
| ||||||||||||||||||
Середина урока 25 мин | Мотивация изучения материала. Групповые работы. Метод «Джиг-со»: в группе учащиеся делятся на 1, 2, 3, 4 и собираются в новые группы по своей нумерации. 1 за 1 стол. 2 за 2 стол и т.д. Учащимся включают видеоуроки с пунктами:
Для самостоятельного изучения и исследования учащимся предоставляются ноутбуки с подключением к интернету.
Групповые работы. Взаимопроверка по слайду с готовыми ответами. Взаимооценивание по методу «Карусель».
Работа с учебником № 625. | Учебник Видеоролики с сайта BilimLand.kz https://bilimland.kz/ru/courses/math-ru/arifmetika/raczionalnye-chisla/desyatichnye-drobi/lesson/slozhenie-i-vychitanie-desyatichnyx-drobei
Карточки с ресурсами из сайта BilimLand.kz Презентация слайда 5 — 8 Стикеры
| ||||||||||||||||||
Критерии успеха | Умеют осуществлять самооценку на основе критерия успешности учебной деятельности. |
| ||||||||||||||||||
Конец урока 8 мин | Физминутка: «Пальчики»
Самостоятельная работа. Тест. Проверим результаты. Формативное оценивание по критериям: 3 правильных ответа – 100% — высокий уровень 2 правильных ответа – 66% — средний уровень 1 правильный ответ – 33% — низкий уровень Подведение итогов. Подсчет стикеров в группах. Наибольшее количество стикеров у группы победителей. Награждаются победители. Домашнее задание: № 520, 521 Рефлексия «Микрофон». Учащимся предлагается в микрофон ответить на следующие вопросы: Что было понятно? Какую тему мы сегодня прошли? Достиг ли ты цели? Что было легко? Трудно? Что бы хотелось повторить?
Закончить урок хотелось мне следующими строчками: Мой Казахстан! Люблю тебя я За красоту твою, широкие просторы. Мой Казахстан! Велик ты и могуч, Певуч язык твой, величавы горы! Пусть солнце льется на твои просторы В богатстве недр и в золоте зерна. Пусть высится, как снеговые горы, Для добрых дел Отчизна, Родина моя!
Спасибо за урок! До свидания!!! | Видеозарядка Карточки с тестом с сайта Itest.kz
Презентация правильных ответов. Слайд 9
Слайд 10 Слайд 11-12 | ||||||||||||||||||
Критерии успеха | Анализируют работу на уроке через оценку себя |
Дифференциация Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание Как Вы планируете проверить уровень усвоения материала учащимися? Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока. | Здоровье и соблюдение техники безопасности |
Раздаточный материал:
Сложение десятичных дробей и десятичных дробей (определение, метод, шаги и примеры)
Пример 1 : Найдите \(\frac{48}{100} + \frac{4}{10}\).
Решение :
Шаг 1 : Складываемые дроби должны иметь одинаковые знаменатели. Для этого воспользуемся эквивалентными дробями. Здесь мы найдем эквивалентную дробь \(\frac{4}{10}\).
\(\frac{48}{100} + \frac{4}{10} = \frac{48}{100} + \frac{4 \times 10}{10 \times 10} = \frac{48 {100} + \frac{40}{100}\)
Шаг 2 : Добавьте числители.
\(\frac{48 + 40}{100} = \frac{88}{100}\)
Следовательно, \(\frac{48}{100} + \frac{4}{10} = \ frac{88}{100}\)
Пример 2 : Найдите 0,309 + 0,41 + 0,1.
Решение :
Шаг 1 : Запишите десятичные числа в виде дробей.
\(0,309 + 0,41 + 0,1 = \frac{309}{1000} + \frac{41}{100} + \frac{1}{10}\)
Шаг 2 : Добавляемые дроби должны иметь одинаковые знаменатели. Для этого воспользуемся эквивалентными дробями:
\(\frac{309}{1000} + \frac{41}{100} + \frac{1}{10} = \frac{309}{1000} + \frac {41 \times 10}{100 \times 10} + \frac{1 \times 100}{10 \times 100} = \frac{309}{1000} + \frac{410}{1000} + \frac{100 }{1000}\)
Шаг 3 : Добавьте числители.
\(\frac{309 + 410 + 100}{1000} + \frac{819}{1000}\)
Шаг 4 : Запишите сумму в виде десятичного числа.
\(\frac{819}{1000} = 0,819\)
Следовательно, 0,309 + 0,41 + 0,1 = 0,819
-долларовая монета. Найдите общую сумму денег, используя дроби.
Решение :
1 цент равен одной сотой доллара. Никель стоит 5 центов.
Никель стоит 5 центов.
Стоимость 1 никеля \(¢5 = $5 \times \frac{1}{100} = $\frac{5}{100}\)
Стоимость 3 пятицентовых монет \( = $3 \times \frac{5}{100} = $\frac{15}{100}\)
Стоимость десяти центов составляет десять центов или десятую часть доллара.
Стоимость 1 десятицентовой монеты \( = ¢10 = 10 долларов США \times \frac{1}{100} = $\frac{1}{10}\)
Стоимость монеты в полдоллара \( = $\frac{ 1}{2}\)
Общая сумма \( = $\frac{15}{100} + $\frac{1}{10} + $\frac{1}{2}\)
\( = $\frac{15}{100} + $\frac{1 \times 10}{10 \times 10} + $\frac{1 \times 50}{2 \times 50}\)
\( = $\ frac{15}{100} + $\frac{10}{100} + $\frac{50}{100}\)
\( = $(\frac{15 + 10 + 50}{100})\)
\( = $\frac{75}{100}\)
Следовательно, у Эндрю есть \(\frac{75 }{100}\) долларов или 75 центов.
Пример 4:
Тина купила три шоколадки по цене 0,35, 0,25 и 0,2 доллара. Найдите сумму денег, которую она заплатила за эти конфеты.
Решение :
Чтобы найти общую сумму, которую она потратила на шоколад, нам нужно найти 0,35 доллара + 0,25 доллара + 0,2 доллара, выполнив следующие действия.
Шаг 1: Запишите десятичные числа в виде дробей.
\(0,35 + 0,25 + 0,2 = \frac{35}{100} + \frac{25}{100} + \frac{2}{10}\)
Шаг 2: дроби добавленная необходимость иметь одинаковые знаменатели. Для этого воспользуемся эквивалентными дробями:
\(\frac{35}{100} + \frac{25}{100} + \frac{2}{10} = \frac{35}{100} +\frac {25}{100} + \frac{2 \times 10}{10 \times 10} = \frac{35}{100} + \frac{25}{100} + \frac{20}{100}\)
Шаг 3 : Добавьте числители.
\(\frac{35 + 25 + 20}{100 = \frac{80}{100}\)
Шаг 4 : Запишите сумму в виде десятичного числа.
\(\frac{80}{100} = 0,8\)
Пример 5 :
Изучите модель и запишите эквивалентное десятичное число.
Решение :
Выразим картину, используя действительные числа.
\(5 + \frac{3}{10} + \frac{43}{100}\)
Теперь давайте сложим эти дроби, чтобы получить окончательную сумму.
\(5 + \frac{3}{10} + \frac{43}{100} = 5 + \frac{30}{100} + \frac{43}{100}\)
\( = 5 + \frac{30+43}{100}\)
\( = 5 + \frac{73}{100}\)
= 5 + 0,73
= 5,73
Объединение десятичных дробей и дробей. Элементарная математика
Представьте, что вам нужно решить следующую задачу на сложение, в которой объединяет десятичные дроби и дроби:
Не так просто прибавить дробь к десятичной дроби, верно? Гораздо проще складывать дроби к дробям или десятичные дроби к десятичным дробям. Итак, мы можем сделать это двумя способами:
- Изменить десятичную дробь на дробь .
- Измените дробь на десятичную дробь .

Сегодня мы научимся делать первый вариант: превращать десятичные дроби в дроби . Для того, чтобы начать, вам сначала нужно знать, как найти эквивалентные дроби.
В любом случае, в этом посте мы сделаем краткий обзор по нахождению равных дробей:
Нахождение равных дробей
Пример: Вот наша дробь…
И мы хотим сделать ее знаменатель числом 6, или другими словами:
Вы должны спросить себя, на какое число можно умножить 3 (знаменатель), чтобы получить 6… вот и все! Его умножили на 2.
Итак, числитель тоже надо умножить на 2.
Если мы умножим 2 на 2, мы получим 4.
Итак, теперь, когда вы знаете, как найти эквивалент дроби, мы собираемся преобразовать десятичную дробь в дробь.
Замена десятичной дроби
Предположим, у нас есть число…
Как мы можем преобразовать его в дробь? Здесь мы будем следовать этой стратегии, но сначала нам нужно спросить себя, какой знаменатель у числа… какой знаменатель может быть у любого числа, чтобы оно оставалось неизменным?… Вот и все! Число 1.
Теперь мы должны спросить себя, какое число нам нужно подставить в знаменатель эквивалентной дроби? Хитрость заключается в том, чтобы использовать 1 и ставить нули после нее. Итак, первое, что мы сделаем, это попробуем с одним нулем, 10.
Поскольку нам нужно умножить 1 на 10, чтобы получить 10, мы также должны умножить 0,25 (числитель) на 10. .
И у нас осталось….
Мы еще не избавились от всех десятичных знаков, верно? Тогда давайте продолжим добавлять нули!
Если мы умножим на 100, у нас останется:
Хорошо, помните, что дроби можно упростить. Если мы упростим эту дробь, у нас останется
Итак…
И все! Мы преобразовали десятичную дробь в дробь благодаря эквивалентным дробям.
Обзор
Подумайте, сколько нулей нам пришлось добавить после 1, чтобы избавиться от всех десятичных знаков в 0,25? В нем было два десятичных знака, и мы добавили к нему два нуля, или, говоря словами, один ноль для каждого десятичного знака, который у него был. Итак, каждый ноль отменяет один десятичный знак!
Итак, каждый ноль отменяет один десятичный знак!
Подводя итог, когда мы хотим преобразовать десятичную дробь в дробь, мы должны:
- Преобразовать десятичную дробь в дробь больше 1. Таким образом, десятичная дробь будет числителем, а 1 — знаменателем.
- Найдите эквивалентную дробь. Знаменатель этой дроби будет иметь 1, за которой следует столько нулей, сколько десятичных знаков в преобразуемом числе.
- Умножьте десятичную дробь на знаменатель эквивалентной дроби.
- Просто дробь.
Теперь вернемся к проблеме, которую мы видели в начале этого поста!
Затем
Далее
Теперь упростим,
Теперь проблема решена!
Я оставлю вам несколько ресурсов, которые вы можете использовать для ознакомления и практики:
- Обзор того, как складывать дроби
- Практика с некоторыми упражнениями на эквивалентные дроби
- Обзор Как складывать десятичные дроби
В Smartick вы найдете множество других упражнений.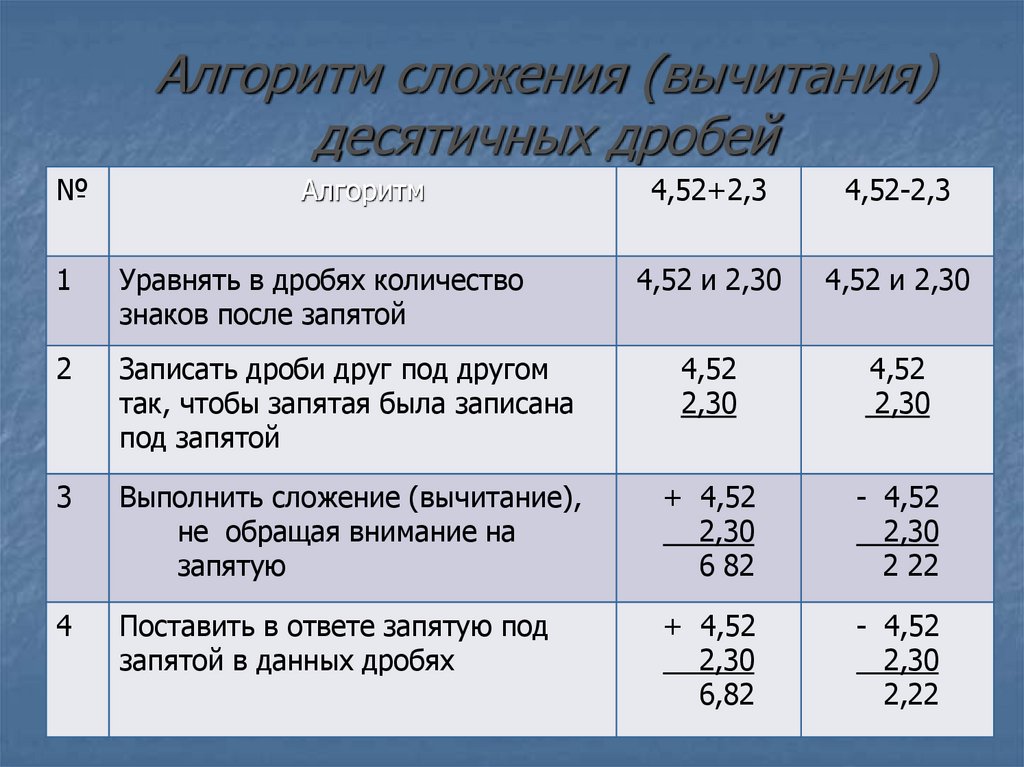
 1.2.27 выполнять сложение и вычитание десятичных дробей.
1.2.27 выполнять сложение и вычитание десятичных дробей.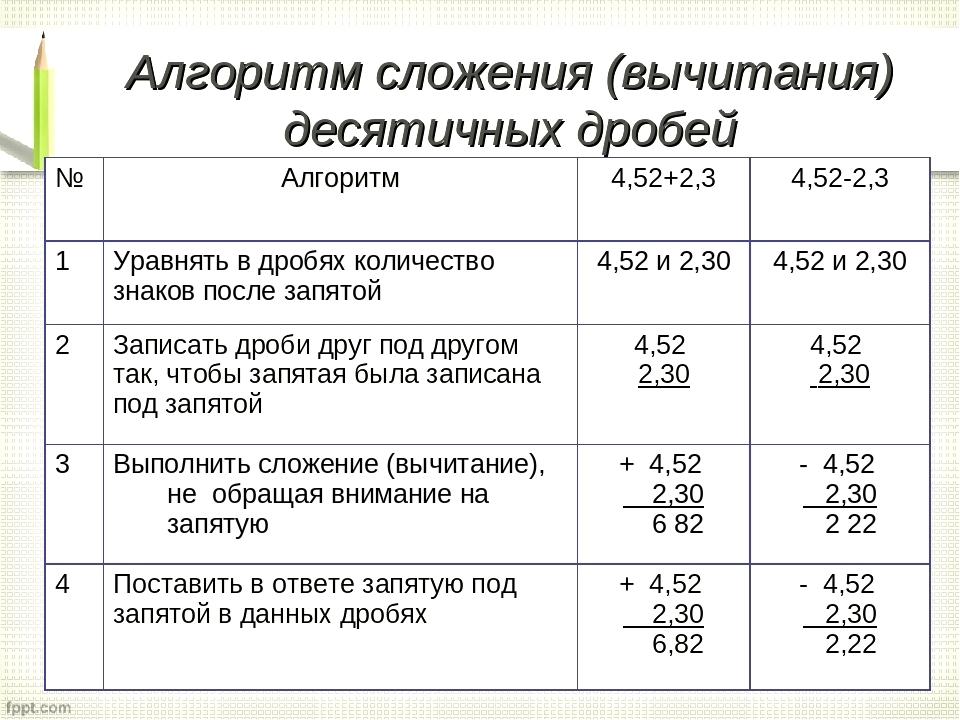

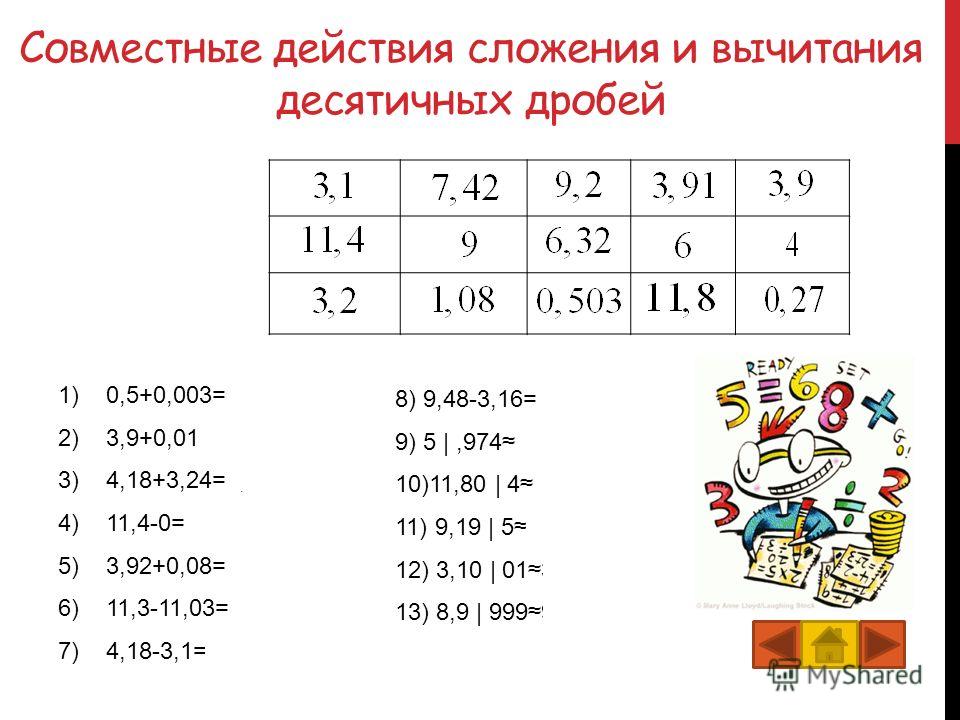

 kz
kz После того, как учащиеся в новых группах понимают и осмысливают данный видеоролик с примерами, все возвращаются в свои «родные» группы и каждый объясняет свою часть новой темы остальным.
После того, как учащиеся в новых группах понимают и осмысливают данный видеоролик с примерами, все возвращаются в свои «родные» группы и каждый объясняет свою часть новой темы остальным.


