Сложение и вычитание дробей с одинаковыми знаменателями / Обыкновенные дроби / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Сложение и вычитание дробей с одинаковыми знаменателями
Ранее мы выполняли сложение и вычитание натуральных чисел. С дробными числами, или дробями, также можно выполнять данные действия.
Рассмотрим брусок:
Разделим его на 6 равных частей — долей:
Закрасим две доли синим цветом и три — зеленым:
То есть получим, что две шестых закрашены синим, три шестых — зеленым, а всего закрашено пять шестых:
То есть мы можем сделать вывод, что:
+ = .
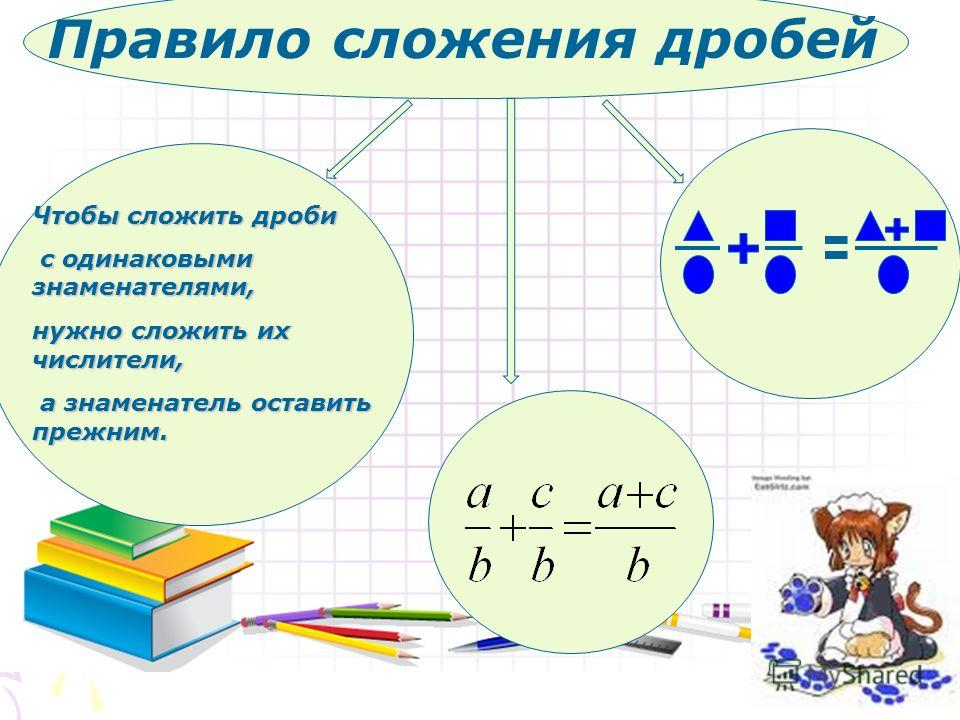
Опираясь на данный пример, можно сформулировать следующее правило:
Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним. |
Мы знаем, что вычитание натуральных чисел определяется на основе сложения: вычесть из одного числа другое — это значит найти такое число, которое при сложении с вычитаемым дает уменьшаемое. Аналогично вычитание дробей дается на основе их сложения.
Например, рассмотрим наш брусок:
Нам известно, что на нем закрашено пять шестых частей, из которых две части синие, а остальные зеленые, нам надо найти какая часть бруска закрашена зеленым цветом:
Чтобы ответить на поставленный вопрос, нам надо найти разность дробей и . Вычесть из дроби дробь , значит найти такое число, которое в сумме с числом дает число . Как было выше сказано + = , поэтому — = . Итак, имеем:
Чтобы найти разность двух дробей с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним. |
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Доли. Обыкновенные дроби
Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1006, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1008, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1041, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1067, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1186, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1240, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1369, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 814, Мерзляк, Полонский, Якир, Учебник
Номер 861, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 290, Мерзляк, Полонский, Якир, Учебник
Номер 296, Мерзляк, Полонский, Якир, Учебник
Номер 509, Мерзляк, Полонский, Якир, Учебник
Номер 956, Мерзляк, Полонский, Якир, Учебник
Номер 962, Мерзляк, Полонский, Якир, Учебник
Задание 635, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 730, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1072, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 582, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 40, Мерзляк, Полонский, Якир, Учебник
Номер 74, Мерзляк, Полонский, Якир, Учебник
Номер 112, Мерзляк, Полонский, Якир, Учебник
Номер 114, Мерзляк, Полонский, Якир, Учебник
Номер 254, Мерзляк, Полонский, Якир, Учебник
Номер 386, Мерзляк, Полонский, Якир, Учебник
Номер 430, Мерзляк, Полонский, Якир, Учебник
Номер 493, Мерзляк, Полонский, Якир, Учебник
Номер 494, Мерзляк, Полонский, Якир, Учебник
Номер 787, Мерзляк, Полонский, Якир, Учебник
Как сложить дроби с одинаковыми знаменателями.
 Вычитание правильной дроби из целого числа
Вычитание правильной дроби из целого числаНайдите числитель и знаменатель. Дробь включает два числа: число, которое расположено над чертой, называется числителем, а число, которое находится под чертой – знаменателем. Знаменатель обозначает общее количество частей, на которые разбито некоторое целое, а числитель – это рассматриваемое количество таких частей.
- Например, в дроби ½ числителем является 1, а знаменателем 2.
Определите знаменатель. Если две и более дроби имеют общий знаменатель, у таких дробей под чертой находится одно и то же число, то есть в этом случае некоторое целое разбито на одинаковое количество частей. Складывать дроби с общим знаменателем очень просто, так как знаменатель суммарной дроби будет таким же, как у складываемых дробей. Например:
- У дробей 3/5 и 2/5 общий знаменатель 5.
- У дробей 3/8, 5/8, 17/8 общий знаменатель 8.
Определите числители. Чтобы сложить дроби с общим знаменателем, сложите их числители, а результат запишите над знаменателем складываемых дробей.
- У дробей 3/5 и 2/5 числители 3 и 2.
- У дробей 3/8, 5/8, 17/8 числители 3, 5, 17.
Сложите числители. В задаче 3/5 + 2/5 сложите числители 3 + 2 = 5. В задаче 3/8 + 5/8 + 17/8 сложите числители 3 + 5 + 17 = 25.
Запишите суммарную дробь. Помните, что при сложении дробей с общим знаменателем он остается без изменений – складываются только числители.
- 3/5 + 2/5 = 5/5
- 3/8 + 5/8 + 17/8 = 25/8
Если нужно, преобразуйте дробь. Иногда дробь можно записать в виде целого числа, а не обыкновенной или десятичной дроби. Например, дробь 5/5 легко преобразуется в 1, так как любая дробь, у которой числитель равен знаменателю, есть 1. Представьте пирог, разрезанный на три части. Если вы съедите все три части, то вы съедите целый (один) пирог.
- Любую обыкновенную дробь можно преобразовать в десятичную; для этого разделите числитель на знаменатель. Например, дробь 5/8 можно записать так: 5 ÷ 8 = 0,625.

Если возможно, упростите дробь. Упрощенная дробь – эта дробь, числитель и знаменатель которой не имеют общих делителей.
- Например, рассмотрим дробь 3/6. Здесь и у числителя, и у знаменателя есть общий делитель, равный 3, то есть числитель и знаменатель нацело делятся на 3. Поэтому дробь 3/6 можно записать так: 3 ÷ 3/6 ÷ 3 = ½.
Если нужно, преобразуйте неправильную дробь в смешанную дробь (смешанное число). У неправильной дроби числитель больше знаменателя, например, 25/8 (у правильной дроби числитель меньше знаменателя). Неправильную дробь можно преобразовать в смешанную дробь, которая состоит из целой части (то есть целого числа) и дробной части (то есть правильной дроби). Чтобы преобразовать неправильную дробь, например, 25/8, в смешанное число, выполните следующие действия:
- Разделите числитель неправильной дроби на ее знаменатель; запишите неполное частное (целый ответ). В нашем примере: 25 ÷ 8 = 3 плюс некоторый остаток.
 В данном случае целый ответ – это целая часть смешанного числа.
В данном случае целый ответ – это целая часть смешанного числа. - Найдите остаток. В нашем примере: 8 х 3 = 24; полученный результат вычтите из исходного числителя: 25 — 24 = 1, то есть остаток равен 1. В данном случае остаток – это числитель дробной части смешанного числа.
- Запишите смешанную дробь. Знаменатель не меняется (то есть равен знаменателю неправильной дроби), поэтому 25/8 = 3 1/8.
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т. к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3.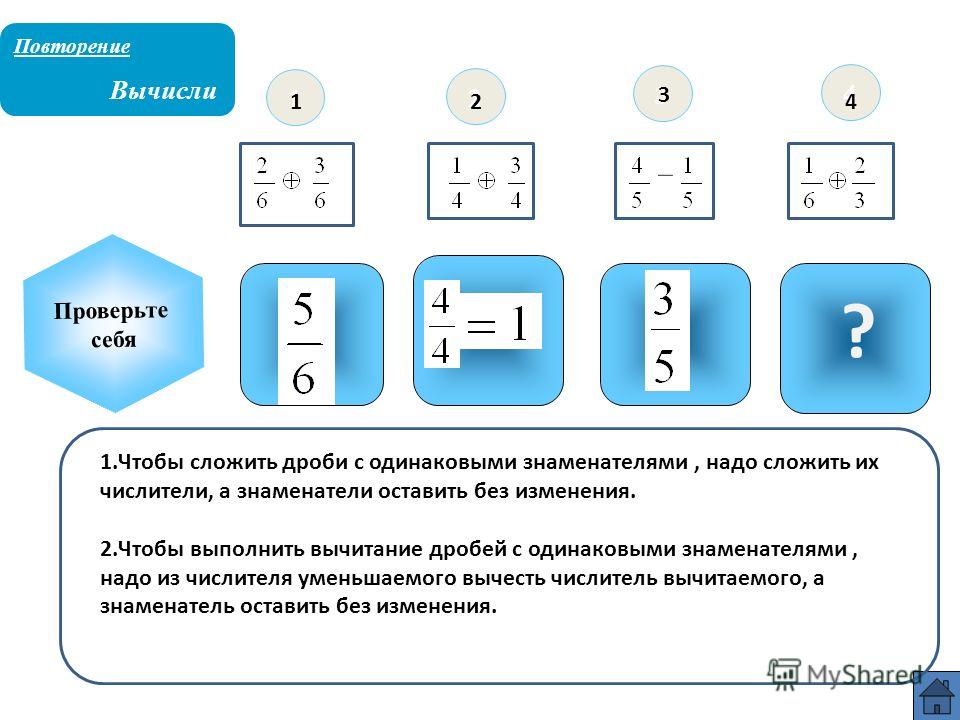 Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числаСейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2 . Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Действия с дробями.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.
Займёмся главным вопросом.
Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.
Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.
Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.
А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.
Сложение и вычитание дробей.
Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:
Числители складываются (вычитаются) и дают числитель результата. Типа:
Короче, в общем виде:
А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:
Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .
Ещё пример:
Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:
Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…
Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.
Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…
Итак, нам надо сложить два дробных выражения:
Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:
Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!
И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)
Вычислить:
Ответы (в беспорядке):
71/20; 3/5; 17/12; -5/4; 11/6
Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Сложение и вычитание дробей с одинаковыми знаменателями
Начнем с рассмотрения самого простого примера — сложения и вычитания дробей с одинаковыми знаменателями. В данном случае необходимо просто произвести действия с числителями — сложить их или вычесть.
В данном случае необходимо просто произвести действия с числителями — сложить их или вычесть.
При сложении и вычитании дробей с одинаковыми знаменателями знаменатель не изменяется!
Главное не производить никакие операции сложения и вычитания в знаменателе, но некоторые школьники забывают об этом. Чтобы лучше понять это правило, прибегнем к принципу визуализации, или говоря простыми словами, рассмотрим жизненный пример:
У Вас есть половина яблока — это ½ от всего яблока. Вам дают еще одну половину, то есть еще ½. Очевидно, что теперь у Вас целое яблоко (не считая, что оно разрезано 🙂). Поэтому ½ + ½ = 1, а не что-то другое, как, например, 2/4. Или же у Вас забирают эту половину: ½ — ½ = 0. В случае вычитания с одинаковыми знаменателями получается вообще особый случай — при вычитании одинаковых знаменателей, мы получим 0, а на 0 делить нельзя, и данная дробь не будет иметь смысла.
Приведем напоследок пример:
Сложение и вычитание дробей с разными знаменателями
Что же делать, если знаменатели разные? Для этого нам необходимо вначале привести дроби к одному знаменателю, а затем действовать как я указал выше.
Приводить дробь к общему знаменателю можно двумя способами. Во всех способах используется одно правило — при умножении числителя и знаменателя на одно и то же число дробь не изменяется .
Существует два способа. Первый — самый простой — так называемый «крест-накрест». Он заключается в том, что первую дробь мы умножаем на знаменатель второй дроби (и числитель и знаменатель), а вторую дробь умножаем на знаменатель первой (аналогично и числитель и знаменатель). После этого действуем как в случае с одинаковыми знаменателями — теперь они действительно одинаковые!
Предыдущий способ универсален, однако в большинстве случаев у дробей знаменателей можно найти наименьшее общее кратное — число, на которое делится и первый знаменатель и второй, причем самое маленькое. В данном методе нужно уметь видеть такие НОКи, потому что специальный поиск их достаточно ёмкий и уступает по скорости методу «крест-накрест». Но в большинстве случаев НОКи довольно хороши видны, если набить глаз и достаточно тренироваться.
Надеюсь, что теперь Вы в совершенстве владеете методами сложения и вычитания дробей!
Как решать дроби с разными знаменателями. Вычитание дробей из целого числа
Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.

Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1
раз. К примеру, если пиццы взять 1
раз, то получится пиццы
К примеру, если пиццы взять 1
раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается , если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ . Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ . Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4 , поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить 7 на знаменатель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7
и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Дробные выражения сложны для понимания ребёнком. У большинства возникают сложности, связанные с . При изучении темы «сложение дробей с целыми числами», ребёнок впадает в ступор, затрудняясь решить задание. Во многих примерах перед тем как выполнить действие нужно произвести ряд вычислений. Например, преобразовать дроби или перевести неправильную дробь в правильную.
Объясним ребёнку наглядно. Возьмём три яблока, два из которых будут целыми, а третье разрежем на 4 части. От разрезанного яблока отделим одну дольку, а остальные три положим рядом с двумя целыми фруктами. Получим ¼ яблока в одной стороне и 2 ¾ — в другой. Если мы их соединим, то получим целых три яблока. Попробуем уменьшить 2 ¾ яблока на ¼, то есть уберём ещё одну дольку, получим 2 2/4 яблока.
Получим ¼ яблока в одной стороне и 2 ¾ — в другой. Если мы их соединим, то получим целых три яблока. Попробуем уменьшить 2 ¾ яблока на ¼, то есть уберём ещё одну дольку, получим 2 2/4 яблока.
Рассмотрим подробнее действия с дробями, в составе которых присутствуют целые числа:
Для начала вспомним правило вычисления для дробных выражений с общим знаменателем:
На первый взгляд всё легко и просто. Но это касается только выражений, не требующих преобразования.
Как найти значение выражения где знаменатели разные
В некоторых заданиях необходимо найти значение выражения, где знаменатели разные. Рассмотрим конкретный случай:
3 2/7+6 1/3
Найдём значение данного выражения, для этого найдём для двух дробей общий знаменатель.
Для чисел 7 и 3 – это 21. Целые части оставляем прежними, а дробные – приводим к 21, для этого первую дробь умножаем на 3, вторую – на 7, получаем:
6/21+7/21, не забываем, что целые части не подлежат преобразованию. В итоге получаем две дроби с одним знаменателям и вычисляем их сумму:
3 6/21+6 7/21=9 15/21
Что если в результате сложения получается неправильная дробь, которая уже имеет целую часть:
2 1/3+3 2/3
В данном случае складываем целые части и дробные, получаем:
5 3/3, как известно, 3/3 – это единица, значит 2 1/3+3 2/3=5 3/3=5+1=6
С нахождением суммы всё понятно, разберём вычитание:
Из всего сказанного вытекает правило действий над смешанными числами, которое звучит так:
- Если же от дробного выражения необходимо вычесть целое число, не нужно представлять второе число в виде дроби, достаточно произвести действие только над целыми частями.

Попробуем самостоятельно вычислить значение выражений:
Разберём подробнее пример под буквой «м»:
4 5/11-2 8/11, числитель первой дроби меньше, чем второй. Для этого занимаем одно целое число у первой дроби, получаем,
3 5/11+11/11=3 целых 16/11, отнимаем от первой дроби вторую:
3 16/11-2 8/11=1 целая 8/11
- Будьте внимательны при выполнении задания, не забывайте преобразовывать неправильные дроби в смешанные, выделяя целую часть. Для этого необходимо значение числителя разделить на значение знаменателя, то что получилось, встаёт на место целой части, остаток – будет числителем, например:
19/4=4 ¾, проверим: 4*4+3=19, в знаменателе 4 остаётся без изменений.
Подведём итог:
Перед тем как приступить к выполнению задания, связанного с дробями, необходимо проанализировать, что это за выражение, какие преобразования нужно совершить над дробью, чтобы решение было правильным. Ищите более рациональные способ решения. Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Чтобы не произошло путаницы при решении дробных выражений, необходимо руководствоваться правилом последовательности. Решайте всё внимательно, не торопясь.
Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
Сложение дробей с одинаковыми знаменателями.
На примере посмотрим, как складывать дроби с общим знаменателем.
Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или \(\frac{1}{5}\) от всего пути. Во второй день они прошли от точки B до D или \(\frac{2}{5}\) от всего пути. Какое расстояние они прошли от начала пути до точки D?
Чтобы найти расстояние от точки A до точки D нужно сложить дроби \(\frac{1}{5} + \frac{2}{5}\).
Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.
\(\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}\)
В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:
\(\bf \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Ответ: туристы прошли \(\frac{3}{5}\) всего пути.
Сложение дробей с разными знаменателями.
Рассмотрим пример:
Нужно сложить две дроби \(\frac{3}{4}\) и \(\frac{2}{7}\).
Чтобы сложить дроби с разными знаменателями нужно сначала найти , а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.
Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь \(\frac{3}{4}\) нужно умножить на 7. Вторую дробь \(\frac{2}{7}\) нужно умножить на 4.
\(\frac{3}{4} + \frac{2}{7} = \frac{3 \times \color{red} {7} + 2 \times \color{red} {4}}{4 \times \color{red} {7}} = \frac{21 + 8}{28} = \frac{29}{28} = 1\frac{1}{28}\)
В буквенном виде получаем такую формулу:
\(\bf \frac{a}{b} + \frac{c}{d} = \frac{a \times d + c \times b}{b \times d}\)
Сложение смешанных чисел или смешанных дробей.

Сложение происходит по закону сложения.
У смешанных дробей складываем целые части с целыми и дробные части с дробными.
Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.
Сложим смешанные числа \(3\frac{6}{11}\) и \(1\frac{3}{11}\).
\(3\frac{6}{11} + 1\frac{3}{11} = (\color{red} {3} + \color{blue} {\frac{6}{11}}) + (\color{red} {1} + \color{blue} {\frac{3}{11}}) = (\color{red} {3} + \color{red} {1}) + (\color{blue} {\frac{6}{11}} + \color{blue} {\frac{3}{11}}) = \color{red}{4} + (\color{blue} {\frac{6 + 3}{11}}) = \color{red}{4} + \color{blue} {\frac{9}{11}} = \color{red}{4} \color{blue} {\frac{9}{11}}\)
Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.
Выполним сложение смешанных чисел \(7\frac{1}{8}\) и \(2\frac{1}{6}\).
Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.
\(7\frac{1}{8} + 2\frac{1}{6} = 7\frac{1 \times \color{red} {3}}{8 \times \color{red} {3}} = 2\frac{1 \times \color{red} {4}}{6 \times \color{red} {4}} =7\frac{3}{24} + 2\frac{4}{24} = 9\frac{7}{24}\)
Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби. В зависимости от типа выражения переходим к алгоритму решения.
Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.
Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.
Пример №1:
Может ли сумма двух в результате получить правильную дробь? Неправильную дробь? Приведите примеры.
\(\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}\)
Дробь \(\frac{5}{7}\) это правильная дробь, она является результатом суммы двух правильных дробей \(\frac{2}{7}\) и \(\frac{3}{7}\).
\(\frac{2}{5} + \frac{8}{9} = \frac{2 \times 9 + 8 \times 5}{5 \times 9} =\frac{18 + 40}{45} = \frac{58}{45}\)
Дробь \(\frac{58}{45}\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac{2}{5}\) и \(\frac{8}{9}\).
Ответ: на оба вопроса ответ да.
Пример №2:
Сложите дроби: а) \(\frac{3}{11} + \frac{5}{11}\) б) \(\frac{1}{3} + \frac{2}{9}\).
а) \(\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}\)
б) \(\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}\)
Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac{9}{47}\) б) \(5\frac{1}{3}\)
а) \(1\frac{9}{47} = 1 + \frac{9}{47}\)
б) \(5\frac{1}{3} = 5 + \frac{1}{3}\)
Пример №4:
Вычислите сумму: а) \(8\frac{5}{7} + 2\frac{1}{7}\) б) \(2\frac{9}{13} + \frac{2}{13}\) в) \(7\frac{2}{5} + 3\frac{4}{15}\)
а) \(8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}\)
б) \(2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} \)
в) \(7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}\)
Задача №1:
За обедам съели \(\frac{8}{11}\) от торта, а вечером за ужином съели \(\frac{3}{11}\). Как вы думаете торт полностью съели или нет?
Как вы думаете торт полностью съели или нет?
Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.
\(\frac{8}{11} + \frac{3}{11} = \frac{11}{11} = 1\)
Ответ: весь торт съели.
Одними из самых сложных для понимания школьника являются разные действия с простыми дробями. Это связано с тем, что детям еще сложно мыслить абстрактно, а дроби, по сути, для них именно так и выглядят. А потому, излагая материал, учителя часто прибегают к аналогиям и объясняют вычитание и сложение дробей буквально на пальцах. Хотя без правил и определений не обходится ни один урок школьной математики.
Базовые понятия
Прежде чем приступить к любым , желательно усвоить несколько базовых определений и правил. Изначально важно понимать, что такое дробь. Под ней подразумевается число, представляющее собой одну или несколько долей единицы. Например, если буханку разрезать на 8 частей и 3 ломтика из них выложить в тарелку, то 3/8 и будет дробью. Причем в таком написании это будет простой дробью, где число над чертой — это числитель, а под ней — знаменатель. А вот если ее записать как 0,375, это уже будет десятичная дробь.
Например, если буханку разрезать на 8 частей и 3 ломтика из них выложить в тарелку, то 3/8 и будет дробью. Причем в таком написании это будет простой дробью, где число над чертой — это числитель, а под ней — знаменатель. А вот если ее записать как 0,375, это уже будет десятичная дробь.
К тому же простые дроби подразделяют на правильные, неправильные и смешанные. К первым относят все те, числитель которых меньше знаменателя. Если наоборот, знаменатель меньше числителя, это уже будет неправильная дробь. В случае если перед правильной стоит целое число, говорят о смешанных числах. Таким образом, дробь 1/2 — правильная, а 7/2 — нет. А если ее записать в таком виде: 3 1 / 2 , то она станет смешанной.
Чтобы легче было разобраться в том, что такое сложение дробей, и с легкостью его выполнять, важно еще запомнить Его суть в следующем. Если числитель и знаменатель умножить на одно и то же число, то дробь не изменится. Именно это свойство позволяет совершать простейшие действия с обыкновенными и другими дробями. По факту это означает, что 1/15 и 3/45, по сути, одно и то же число.
По факту это означает, что 1/15 и 3/45, по сути, одно и то же число.
Сложение дробей с одинаковыми знаменателями
Выполнение этого действия обычно не вызывает больших затруднений. Сложение дробей в этом случае очень сильно напоминает подобное действие с целыми числами. Знаменатель остается без изменений, а числители просто складываются между собой. Например, если нужно сложить дроби 2/7 и 3/7, то решение школьной задачи в тетради будет вот таким:
2/7 + 3/7 = (2+3)/7 = 5/7.
К тому же такое сложение дробей можно объяснить на простом примере. Взять обычное яблоко и разрезать, например, на 8 частей. Выложить отдельно сначала 3 части, а затем добавить к ним еще 2. И в результате в чашке будет лежать 5/8 целого яблока. Саму арифметическую задачу записывают, как показано ниже:
3/8 + 2/8 = (3+2)/8 = 5/8.
Но зачастую встречаются задачи посложнее, где нужно сложить между собой, например, 5/9 и 3/5. Вот здесь и возникают первые сложности в действиях с дробями. Ведь сложение таких чисел потребует дополнительных знаний. Теперь в полной мере потребуется вспомнить об их основном свойстве. Чтобы сложить дроби из примера, для начала их нужно привести к одному общему знаменателю. Для этого необходимо просто перемножить 9 и 5 между собой, числитель «5» умножить на 5, а «3», соответственно, на 9. Таким образом, уже складываются такие дроби: 25/45 и 27/45. Теперь только осталось сложить числители и получить ответ 52/45. На листке бумаги пример будет выглядеть так:
Ведь сложение таких чисел потребует дополнительных знаний. Теперь в полной мере потребуется вспомнить об их основном свойстве. Чтобы сложить дроби из примера, для начала их нужно привести к одному общему знаменателю. Для этого необходимо просто перемножить 9 и 5 между собой, числитель «5» умножить на 5, а «3», соответственно, на 9. Таким образом, уже складываются такие дроби: 25/45 и 27/45. Теперь только осталось сложить числители и получить ответ 52/45. На листке бумаги пример будет выглядеть так:
5/9 + 3/5 = (5 х 5)/(9 х 5) + (3 х 9)/(5 х 9) = 25/45 + 27/45 = (25+27)/45 = 52/45 = 1 7 / 45 .
Но сложение дробей с такими знаменателями не всегда требует простого перемножения чисел под чертой. Сначала ищут наименьший общий знаменатель. К примеру, как для дробей 2/3 и 5/6. Для них это будет число 6. Но не всегда ответ очевиден. В этом случае стоит вспомнить правило поиска наименьшего общего кратного (сокращенно НОК) двух чисел.
Под ним понимают наименьший общий множитель двух целых чисел. Чтобы его найти, раскладывают каждое на простые множители. Теперь выписывают те из них, которые входят хотя бы один раз в каждое число. Перемножают их между собой и получают тот самый знаменатель. На деле все выглядит немного проще.
Чтобы его найти, раскладывают каждое на простые множители. Теперь выписывают те из них, которые входят хотя бы один раз в каждое число. Перемножают их между собой и получают тот самый знаменатель. На деле все выглядит немного проще.
Например, требуется сложить дроби 4/15 и 1/6. Так, 15 получается перемножением простых цифр 3 и 5, а шесть — два и три. Значит, НОК для них будет 5 х 3 х 2 = 30. Теперь, разделив 30 на знаменатель первой дроби, получим множитель для ее числителя — 2. А для второй дроби это будет число 5. Таким образом, остается сложить обыкновенные дроби 8/30 и 5/30 и получить ответ 13/30. Все предельно просто. В тетради же следует эту задачу записать так:
4/15 + 1/6 = (4 х 2)/(15 х 2) + (1 х 5)/(6 х 5) = 8/30 + 5/30 = 13/30.
НОК (15, 6) = 30.
Сложение смешанных чисел
Теперь, зная все основные приемы в сложении простых дробей, можно попробовать свои силы на более сложных примерах. И это будут смешанные числа, под которыми понимают дробь такого вида: 2 2 / 3 . Здесь перед правильной дробью выписана целая часть. И многие путаются при совершении действий с такими числами. В действительности, здесь работают все те же правила.
Здесь перед правильной дробью выписана целая часть. И многие путаются при совершении действий с такими числами. В действительности, здесь работают все те же правила.
Чтобы сложить между собой смешанные числа, отдельно складывают целые части и правильные дроби. А затем уже суммируют эти 2 результата. На практике все намного проще, стоит только немного поупражняться. Например, в задаче требуется сложить такие смешанные числа: 1 1 / 3 и 4 2 / 5 . Чтобы это сделать, сначала складываются 1 и 4 — получится 5. Затем суммируют 1/3 и 2/5, используя приемы приведения к наименьшему общему знаменателю. Решением будет 11/15. А окончательный ответ — это 5 11 / 15 . В школьной тетради это будет выглядеть гораздо короче:
1 1 / 3 + 4 2 / 5 = (1 + 4) + (1/3 + 2/5) = 5 + 5/15 + 6/15 = 5 + 11/15 = 5 11 / 15 .
Сложение десятичных дробей
Помимо обыкновенных дробей, есть и десятичные. Они, кстати, намного чаще встречаются в жизни. Например, цена в магазине выглядит часто таким образом: 20,3 рубля. Это и есть та самая дробь. Конечно, такие складывать намного проще, чем обыкновенные. В принципе, нужно просто сложить 2 обыкновенных числа, главное, в нужном месте поставить запятую. Вот тут и возникают сложности.
Это и есть та самая дробь. Конечно, такие складывать намного проще, чем обыкновенные. В принципе, нужно просто сложить 2 обыкновенных числа, главное, в нужном месте поставить запятую. Вот тут и возникают сложности.
К примеру требуется сложить такие 2,5 и 0,56. Чтобы сделать это правильно, нужно к первой в конце дописать ноль, и все будет в порядке.
2,50 + 0,56 = 3,06.
Важно знать, что любая десятичная дробь может быть преобразована в простую, но не любую простую дробь можно записать как десятичную. Так, из нашего примера 2,5 = 2 1 / 2 и 0,56 = 14/25. А вот такая дробь, как 1/6, будет только приблизительно равна 0,16667. Такая же ситуация будет с другими подобными числами — 2/7, 1/9 и так далее.
Заключение
Многие школьники, не понимая практической стороны действий с дробями, относятся к этой теме спустя рукава. Однако в более эти базовые знания позволят щелкать как орешки сложные примеры с логарифмами и нахождением производных. А потому стоит один раз хорошо разобраться в действиях с дробями, чтобы потом не кусать от досады локти. Ведь вряд ли педагог в старших классах будет возвращаться к этой, уже пройденной, теме. Любой старшеклассник должен уметь выполнять подобные упражнения.
Ведь вряд ли педагог в старших классах будет возвращаться к этой, уже пройденной, теме. Любой старшеклассник должен уметь выполнять подобные упражнения.
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например.
Сложение простых дробей. Действия с дробями
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи.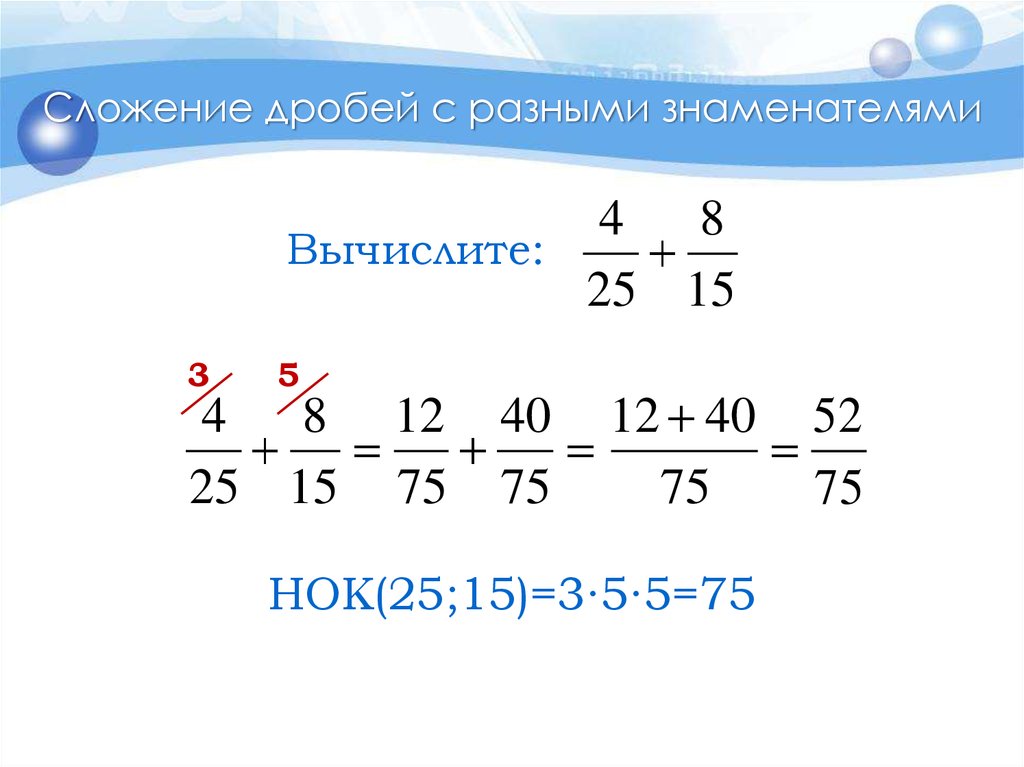 Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например.
- 7 умножаем на знаменатель (2), получается 14,
- к 14 прибавляем верхнюю часть (1), выходит 15,
- и подставляем знаменатель.
- в итоге получается 15/2.
- Дробь правильная, т.е. числитель меньше знаменателя. Тогда полученное после приписывания смешанное число и будет ответом.
- Дробь неправильная, т.е. числитель больше знаменателя. Тогда требуется небольшое преобразование. Неправильную дробь следует превратить в смешанное число, другими словами выделить целую часть. Делается это так:
Чтобы к дроби прибавить целое число, достаточно выполнить ряд действий, а вернее подсчетов.
К примеру у вас 7 — целое число, его нужно прибавить к дроби 1/2.
Действуем следующим образом:
Таким нехитрым способом можно прибавлять целые числа к дробным.
А чтобы выделить целое число из дроби, надо поделить числитель на знаменатель, а остаток — и будет дробь.
Операция прибавления к правильной обыкновенной дроби целого числа не сложна и подчас заключается просто в образовании смешанной дроби, в которой целая часть ставится левее дробной части, например такая дробь будет смешанной:
Однако чаще при добавлении к дроби целого числа получается неправильная дробь, у которой числитель оказывается больше знаменателя. Выполняется эта операция так: целое число представляют в виде неправильной дроби с тем же знаменателем, что и прибавляемая дробь и потом просто складывают числители обеих дробей. На примере это буду выглядеть так:
На примере это буду выглядеть так:
5+1/8 = 5*8/8+1/8 = 40/8+1/8 = 41/8
По-моему это очень просто.
Например, мы имеем дробь 1/4 (это то же самое, что 0,25, то есть четверть от целого числа).
И к этой четверти можно прибавить любое целое число, например 3. Получится три с четвертью :
3,25. Или в дроби это выражается так: 3 1/4
Вот по образцу этого примера можно складывать любые дроби с любыми целыми числами.
Нужно возвести целое число в дробь со знаменателем 10 (6/10). Далее, привести имеющуюся дробь к общему знаменателю 10 (35=610). Ну и выполнить операцию как с обычными дробями 610+610=1210 итого 12.
Можно сделать это двумя способами.
1). Дробь можно перевести в целое число и осуществить сложение. Например, 1/2 это 0,5; 1/4 равняется 0,25; 2/5 это 0,4 и тд.
Берем целое число 5, к которому нужно прибавить дробь 4/5. Преобразуем дробь: 4/5 это 4 разделить на 5 и получаем 0,8. Прибавляет 0,8 к 5 и получаем 5,8 или же 5 4/5.
2). Второй способ: 5 + 4/5 = 29/5 = 5 4/5.
Сложение дробей простое математическое действие, пример, вам нужно сложить целое число 3 и дробь 1/7. Чтобы сложить эти два числа, у вас должно быть один знаменатель, поэтому вы должны три умножить на семь и разделить на эту цифру, тогда вы получаете 21/7+1/7, знаменатель один, складываете 21 и 1, получается ответ 22/7.
Просто взять и прибавить целое число к этой дроби.Допустим надо 6+1/2=6 1/2. Ну и если это десятичная дробь то можно например так 6+1,2=7,2.
Чтобы сложить дробь и целое число, нужно к целому числу прибавить дробное и записать их, в виде комплексного числа, например при сложение обыкновенной дроби с целым числом, получим: 1/2 +3 =3 1/2; при сложении десятичной дроби: 0,5 +3 =3,5.
Дробь сама по себе не является целым числом, по тому что она по своему количеству до него не дотягивает, а потому и нет необходимости переводить целое число в эту дробь. Поэтому целое число остается целым и полноценно демонстрирует полный номинал, а дробь к нему плюсуется, и демонстрирует то, сколько этому целому числу не хватает до прибавления следующего полного балла.
Академический пример.
10 + 7/3 = 10 целых и 7/3.
Если конечно есть целые, то они суммируются с целыми.
12 + 5 7/9 = 17 и 7/9.
Смотря какое целое число и какая дробь.
Если оба слагаемых положительные , следует приписать к целому числу эту дробь. Получится смешанное число. Причем, могут быть 2 случая.
Случай 1.
4/9 + 10 = 10 4/9 (десять целых четыре девятых).
Случай 2.
После этого к целому числу нужно прибавить целую часть неправильной дроби и к полученной сумме приписать ее дробную часть. Таким же образом к смешанному числу прибавляется целое.
1) 11/4 + 5 = 2 3/4 + 5 = 7 3/4 (7 целых три четвертых).
2) 5 1/2 + 6 = 11 1/2 (11 целых одна вторая).
Если одно из слагаемых или оба отрицательные , то сложение производим по правилам сложения чисел с разными или одинаковыми знаками. Целое число представляется в виде отношения этого числа и 1, а затем и числитель, и знаменатель умножается на число, равное знаменателю той дроби, к которой целое число прибавляется.
3) 1/5 + (-2)= 1/5 + -2/1 = 1/5 + -10/5 = -9/5 = -1 4/5 (минус 1 целая четыре пятых).
4) -13/3 + (-4) = -13/3 + -4/1 = -13/3 + -12/3 = -25/3 = -8 1/3 (минус 8 целых одна третья).
Замечание.
После знакомства с отрицательными числами, при изучении действий с ними учащиеся 6 класса должны понимать, что к отрицательной дроби прибавить положительное целое число то же самое, что вычитать из натурального числа дробь. Это действие, как известно, выполняется так:
На самом деле для того чтобы произвести сложение дроби и целого числа нужно просто напросто привести имеющиеся целое число к дробному, а сделать это проще простого. Нужно просто взять знаменатель дроби (имеющейся в примере) и сделать его знаменателем целого числа, умножив его на этот знаменатель и разделив, вот пример:
Нужно просто взять знаменатель дроби (имеющейся в примере) и сделать его знаменателем целого числа, умножив его на этот знаменатель и разделив, вот пример:
2+2/3 = 2*3/3+2/3 = 6/3+2/3 = 8/3
Найдите числитель и знаменатель. Дробь включает два числа: число, которое расположено над чертой, называется числителем, а число, которое находится под чертой – знаменателем. Знаменатель обозначает общее количество частей, на которые разбито некоторое целое, а числитель – это рассматриваемое количество таких частей.
- Например, в дроби ½ числителем является 1, а знаменателем 2.
Определите знаменатель. Если две и более дроби имеют общий знаменатель, у таких дробей под чертой находится одно и то же число, то есть в этом случае некоторое целое разбито на одинаковое количество частей. Складывать дроби с общим знаменателем очень просто, так как знаменатель суммарной дроби будет таким же, как у складываемых дробей. Например:
- У дробей 3/5 и 2/5 общий знаменатель 5.

- У дробей 3/8, 5/8, 17/8 общий знаменатель 8.
Определите числители. Чтобы сложить дроби с общим знаменателем, сложите их числители, а результат запишите над знаменателем складываемых дробей.
- У дробей 3/5 и 2/5 числители 3 и 2.
- У дробей 3/8, 5/8, 17/8 числители 3, 5, 17.
Сложите числители. В задаче 3/5 + 2/5 сложите числители 3 + 2 = 5. В задаче 3/8 + 5/8 + 17/8 сложите числители 3 + 5 + 17 = 25.
Запишите суммарную дробь. Помните, что при сложении дробей с общим знаменателем он остается без изменений – складываются только числители.
- 3/5 + 2/5 = 5/5
- 3/8 + 5/8 + 17/8 = 25/8
Если нужно, преобразуйте дробь. Иногда дробь можно записать в виде целого числа, а не обыкновенной или десятичной дроби. Например, дробь 5/5 легко преобразуется в 1, так как любая дробь, у которой числитель равен знаменателю, есть 1. Представьте пирог, разрезанный на три части. Если вы съедите все три части, то вы съедите целый (один) пирог.
Если вы съедите все три части, то вы съедите целый (один) пирог.
- Любую обыкновенную дробь можно преобразовать в десятичную; для этого разделите числитель на знаменатель. Например, дробь 5/8 можно записать так: 5 ÷ 8 = 0,625.
Если возможно, упростите дробь. Упрощенная дробь – эта дробь, числитель и знаменатель которой не имеют общих делителей.
- Например, рассмотрим дробь 3/6. Здесь и у числителя, и у знаменателя есть общий делитель, равный 3, то есть числитель и знаменатель нацело делятся на 3. Поэтому дробь 3/6 можно записать так: 3 ÷ 3/6 ÷ 3 = ½.
Если нужно, преобразуйте неправильную дробь в смешанную дробь (смешанное число). У неправильной дроби числитель больше знаменателя, например, 25/8 (у правильной дроби числитель меньше знаменателя). Неправильную дробь можно преобразовать в смешанную дробь, которая состоит из целой части (то есть целого числа) и дробной части (то есть правильной дроби). Чтобы преобразовать неправильную дробь, например, 25/8, в смешанное число, выполните следующие действия:
- Разделите числитель неправильной дроби на ее знаменатель; запишите неполное частное (целый ответ).
 В нашем примере: 25 ÷ 8 = 3 плюс некоторый остаток. В данном случае целый ответ – это целая часть смешанного числа.
В нашем примере: 25 ÷ 8 = 3 плюс некоторый остаток. В данном случае целый ответ – это целая часть смешанного числа. - Найдите остаток. В нашем примере: 8 х 3 = 24; полученный результат вычтите из исходного числителя: 25 — 24 = 1, то есть остаток равен 1. В данном случае остаток – это числитель дробной части смешанного числа.
- Запишите смешанную дробь. Знаменатель не меняется (то есть равен знаменателю неправильной дроби), поэтому 25/8 = 3 1/8.
Одними из самых сложных для понимания школьника являются разные действия с простыми дробями. Это связано с тем, что детям еще сложно мыслить абстрактно, а дроби, по сути, для них именно так и выглядят. А потому, излагая материал, учителя часто прибегают к аналогиям и объясняют вычитание и сложение дробей буквально на пальцах. Хотя без правил и определений не обходится ни один урок школьной математики.
Базовые понятия
Прежде чем приступить к любым , желательно усвоить несколько базовых определений и правил. Изначально важно понимать, что такое дробь. Под ней подразумевается число, представляющее собой одну или несколько долей единицы. Например, если буханку разрезать на 8 частей и 3 ломтика из них выложить в тарелку, то 3/8 и будет дробью. Причем в таком написании это будет простой дробью, где число над чертой — это числитель, а под ней — знаменатель. А вот если ее записать как 0,375, это уже будет десятичная дробь.
Изначально важно понимать, что такое дробь. Под ней подразумевается число, представляющее собой одну или несколько долей единицы. Например, если буханку разрезать на 8 частей и 3 ломтика из них выложить в тарелку, то 3/8 и будет дробью. Причем в таком написании это будет простой дробью, где число над чертой — это числитель, а под ней — знаменатель. А вот если ее записать как 0,375, это уже будет десятичная дробь.
К тому же простые дроби подразделяют на правильные, неправильные и смешанные. К первым относят все те, числитель которых меньше знаменателя. Если наоборот, знаменатель меньше числителя, это уже будет неправильная дробь. В случае если перед правильной стоит целое число, говорят о смешанных числах. Таким образом, дробь 1/2 — правильная, а 7/2 — нет. А если ее записать в таком виде: 3 1 / 2 , то она станет смешанной.
Чтобы легче было разобраться в том, что такое сложение дробей, и с легкостью его выполнять, важно еще запомнить Его суть в следующем. Если числитель и знаменатель умножить на одно и то же число, то дробь не изменится. Именно это свойство позволяет совершать простейшие действия с обыкновенными и другими дробями. По факту это означает, что 1/15 и 3/45, по сути, одно и то же число.
Именно это свойство позволяет совершать простейшие действия с обыкновенными и другими дробями. По факту это означает, что 1/15 и 3/45, по сути, одно и то же число.
Сложение дробей с одинаковыми знаменателями
Выполнение этого действия обычно не вызывает больших затруднений. Сложение дробей в этом случае очень сильно напоминает подобное действие с целыми числами. Знаменатель остается без изменений, а числители просто складываются между собой. Например, если нужно сложить дроби 2/7 и 3/7, то решение школьной задачи в тетради будет вот таким:
2/7 + 3/7 = (2+3)/7 = 5/7.
К тому же такое сложение дробей можно объяснить на простом примере. Взять обычное яблоко и разрезать, например, на 8 частей. Выложить отдельно сначала 3 части, а затем добавить к ним еще 2. И в результате в чашке будет лежать 5/8 целого яблока. Саму арифметическую задачу записывают, как показано ниже:
3/8 + 2/8 = (3+2)/8 = 5/8.
Но зачастую встречаются задачи посложнее, где нужно сложить между собой, например, 5/9 и 3/5. Вот здесь и возникают первые сложности в действиях с дробями. Ведь сложение таких чисел потребует дополнительных знаний. Теперь в полной мере потребуется вспомнить об их основном свойстве. Чтобы сложить дроби из примера, для начала их нужно привести к одному общему знаменателю. Для этого необходимо просто перемножить 9 и 5 между собой, числитель «5» умножить на 5, а «3», соответственно, на 9. Таким образом, уже складываются такие дроби: 25/45 и 27/45. Теперь только осталось сложить числители и получить ответ 52/45. На листке бумаги пример будет выглядеть так:
Вот здесь и возникают первые сложности в действиях с дробями. Ведь сложение таких чисел потребует дополнительных знаний. Теперь в полной мере потребуется вспомнить об их основном свойстве. Чтобы сложить дроби из примера, для начала их нужно привести к одному общему знаменателю. Для этого необходимо просто перемножить 9 и 5 между собой, числитель «5» умножить на 5, а «3», соответственно, на 9. Таким образом, уже складываются такие дроби: 25/45 и 27/45. Теперь только осталось сложить числители и получить ответ 52/45. На листке бумаги пример будет выглядеть так:
5/9 + 3/5 = (5 х 5)/(9 х 5) + (3 х 9)/(5 х 9) = 25/45 + 27/45 = (25+27)/45 = 52/45 = 1 7 / 45 .
Но сложение дробей с такими знаменателями не всегда требует простого перемножения чисел под чертой. Сначала ищут наименьший общий знаменатель. К примеру, как для дробей 2/3 и 5/6. Для них это будет число 6. Но не всегда ответ очевиден. В этом случае стоит вспомнить правило поиска наименьшего общего кратного (сокращенно НОК) двух чисел.
Под ним понимают наименьший общий множитель двух целых чисел. Чтобы его найти, раскладывают каждое на простые множители. Теперь выписывают те из них, которые входят хотя бы один раз в каждое число. Перемножают их между собой и получают тот самый знаменатель. На деле все выглядит немного проще.
Например, требуется сложить дроби 4/15 и 1/6. Так, 15 получается перемножением простых цифр 3 и 5, а шесть — два и три. Значит, НОК для них будет 5 х 3 х 2 = 30. Теперь, разделив 30 на знаменатель первой дроби, получим множитель для ее числителя — 2. А для второй дроби это будет число 5. Таким образом, остается сложить обыкновенные дроби 8/30 и 5/30 и получить ответ 13/30. Все предельно просто. В тетради же следует эту задачу записать так:
4/15 + 1/6 = (4 х 2)/(15 х 2) + (1 х 5)/(6 х 5) = 8/30 + 5/30 = 13/30.
НОК (15, 6) = 30.
Сложение смешанных чисел
Теперь, зная все основные приемы в сложении простых дробей, можно попробовать свои силы на более сложных примерах. И это будут смешанные числа, под которыми понимают дробь такого вида: 2 2 / 3 . Здесь перед правильной дробью выписана целая часть. И многие путаются при совершении действий с такими числами. В действительности, здесь работают все те же правила.
И это будут смешанные числа, под которыми понимают дробь такого вида: 2 2 / 3 . Здесь перед правильной дробью выписана целая часть. И многие путаются при совершении действий с такими числами. В действительности, здесь работают все те же правила.
Чтобы сложить между собой смешанные числа, отдельно складывают целые части и правильные дроби. А затем уже суммируют эти 2 результата. На практике все намного проще, стоит только немного поупражняться. Например, в задаче требуется сложить такие смешанные числа: 1 1 / 3 и 4 2 / 5 . Чтобы это сделать, сначала складываются 1 и 4 — получится 5. Затем суммируют 1/3 и 2/5, используя приемы приведения к наименьшему общему знаменателю. Решением будет 11/15. А окончательный ответ — это 5 11 / 15 . В школьной тетради это будет выглядеть гораздо короче:
1 1 / 3 + 4 2 / 5 = (1 + 4) + (1/3 + 2/5) = 5 + 5/15 + 6/15 = 5 + 11/15 = 5 11 / 15 .
Сложение десятичных дробей
Помимо обыкновенных дробей, есть и десятичные. Они, кстати, намного чаще встречаются в жизни. Например, цена в магазине выглядит часто таким образом: 20,3 рубля. Это и есть та самая дробь. Конечно, такие складывать намного проще, чем обыкновенные. В принципе, нужно просто сложить 2 обыкновенных числа, главное, в нужном месте поставить запятую. Вот тут и возникают сложности.
Например, цена в магазине выглядит часто таким образом: 20,3 рубля. Это и есть та самая дробь. Конечно, такие складывать намного проще, чем обыкновенные. В принципе, нужно просто сложить 2 обыкновенных числа, главное, в нужном месте поставить запятую. Вот тут и возникают сложности.
К примеру требуется сложить такие 2,5 и 0,56. Чтобы сделать это правильно, нужно к первой в конце дописать ноль, и все будет в порядке.
2,50 + 0,56 = 3,06.
Важно знать, что любая десятичная дробь может быть преобразована в простую, но не любую простую дробь можно записать как десятичную. Так, из нашего примера 2,5 = 2 1 / 2 и 0,56 = 14/25. А вот такая дробь, как 1/6, будет только приблизительно равна 0,16667. Такая же ситуация будет с другими подобными числами — 2/7, 1/9 и так далее.
Заключение
Многие школьники, не понимая практической стороны действий с дробями, относятся к этой теме спустя рукава. Однако в более эти базовые знания позволят щелкать как орешки сложные примеры с логарифмами и нахождением производных. А потому стоит один раз хорошо разобраться в действиях с дробями, чтобы потом не кусать от досады локти. Ведь вряд ли педагог в старших классах будет возвращаться к этой, уже пройденной, теме. Любой старшеклассник должен уметь выполнять подобные упражнения.
А потому стоит один раз хорошо разобраться в действиях с дробями, чтобы потом не кусать от досады локти. Ведь вряд ли педагог в старших классах будет возвращаться к этой, уже пройденной, теме. Любой старшеклассник должен уметь выполнять подобные упражнения.
Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1
целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается , если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ . Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ . Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4 , поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить 7 на знаменатель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7
и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Сложение и вычитание дробей с разными знаменателями. Сравнение дробей 6 класс онлайн-подготовка на Ростелеком Лицей |
Повторение
Вспомним, что мы уже знаем об обыкновенных дробях.
1. Любая дробь обозначает количество, часть от какого-то числа. Эту часть мы умеем находить. Например, от это : .
2. Одно и то же количество, одну и ту же часть можно выразить разными дробями. Такие дроби называются эквивалентными (Рис. 1).
Рис. 1. Пример эквивалентных дробей
3. При сложении/вычитании дробей с одинаковыми знаменателями складываем/вычитаем числители.
При сложении/вычитании дробей с одинаковыми знаменателями складываем/вычитаем числители.
4. При сравнении двух дробей с одинаковыми знаменателями большей является та, у которой числитель больше (Рис. 2).
Рис. 2. Пример сравнения дробей с одинаковым знаменателем
Сложение дробей с разными знаменателями
Теперь перейдем к вопросу о том, что делать, если у дробей будут разные знаменатели. Например, как нам сложить и (Рис. 3)?
Рис. 3. Иллюстрация к примеру
Если мы заменим одну из дробей на эквивалентную (равную ей), то сумма, очевидно, не изменится.
Для дроби существует бесконечное множество дробей, которые ей эквивалентны. Чтобы их получить, нужно одновременно умножать и числитель, и знаменатель на одно и то же число (, , и т.д.). Тем самым мы получим цепочку эквивалентных дробей:
Аналогично поступим и со второй дробью:
Мы можем заменить исходные дроби эквивалентными. Но выбирать нужно так, чтобы новые дроби имели одинаковые знаменатели, ведь мы уже умеем их складывать. Одинаковый знаменатель у дробей и , заменим исходные дроби на них:
Но выбирать нужно так, чтобы новые дроби имели одинаковые знаменатели, ведь мы уже умеем их складывать. Одинаковый знаменатель у дробей и , заменим исходные дроби на них:
То есть идея оказался очень простой. Если нам нужно сложить две дроби, то смотрим на их знаменатели.
1) Если знаменатели одинаковые, то складываем сразу.
2) Если знаменатели разные, то заменяем исходные дроби эквивалентными, чтобы новые дроби имели одинаковые знаменатели. И складываем эти новые дроби.
Действия над дробями с разными знаменателями. Примеры
Выполните вычисление:
1) 2) 3) 4) 5)
Решение:
1) Несложно заметить, что дробь легко превращается в ей эквивалентную дробь со знаменателем . Для этого нам нужно домножить ее числитель и знаменатель на :
2) Несложно увидеть, что мы вторую дробь можем превратить в дробь со знаменателем , для этого умножим ее числитель и знаменатель на : .
3) Обе дроби мы можем заменить эквивалентными дробями со знаменателем . Числитель и знаменатель первой дроби домножим на , а второй – на :
Таким образом, если знаменатели разные, то нужно заменить исходные дроби равными так, чтобы у новых дробей были одинаковые знаменатели. Такое преобразование называют приведением дробей к одному знаменателю (или к общему знаменателю).
4) Приведем дроби к общему знаменателю. Видно, что первую дробь можно привести к знаменателю . А у второй дроби он уже . Общий знаменатель .
5) Общим знаменателем для этих дробей является число . Числитель и знаменатель первой дроби домножим на , а второй – на : .
Решение более сложных примеров
Ответим теперь сами себе на следующий вопрос: Все ли мы умеем, чтобы сложить две дроби?
Если у них одинаковые знаменатели, то да, несомненно.
Если у них разные знаменатели, то мы начнем заменять дроби равными им, чтобы у новых дробей были одинаковые знаменатели. Иными словами, будем приводить их к общему знаменателю. Всегда ли это легко сделать? Нет, не всегда.
Иными словами, будем приводить их к общему знаменателю. Всегда ли это легко сделать? Нет, не всегда.
Пример . Сложите две дроби: .
Решение. Очевидно, что в знаменателе будет такое число, которое получается и из домножением на что-то, и из 18 домножением на что-то. Но такое число найти нетрудно.
Это .
Числитель и знаменатель первой дроби умножим на . Числитель и знаменатель второй дроби умножим на . Дроби, конечно, стали более громоздкими, но зато теперь у них одинаковый знаменатель: .
Теперь мы можем решить задачу и на сравнение этих дробей: .
Следовательно, первое слагаемое меньше второго: .
Пример . Сравните две дроби и. После этого от большей дроби отнимите меньшую.
Решение. Чтобы сравнить две эти дроби, приведем их к общему знаменателю. Общий знаменатель найдем как произведение .
Чтобы в первой дроби получить знаменатель , умножим ее числитель и знаменатель на : .
Чтобы у второй дроби получить знаменатель , умножим ее числитель и знаменатель на : .
Итак, мы видим, что первая дробь больше: . Значит, .
Вычтем из большей дроби меньшую: .
Заключение
На этом уроке мы научились складывать, вычитать, сравнивать дроби с разными знаменателями. Существуют способы упрощения сложения громоздких дробей. Не всегда общий знаменатель ищут как произведение имеющихся знаменателей. Для этого в шестом классе вы будете изучать такое понятие, как наименьшее общее кратное.
Список рекомендованной литературы
1) Виленкин Н.Я. Математика. 6 класс: учеб. для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с. : ил.
2) Зубарева И.И., Мордкович А.Г. Математика. 6 класс. – М.: Мнемозина.
3) Истомина И.Б. Математика, 6 класс. – М.: Ассоциация ХХI век.
Рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-портал Ru. onlinemschool.com (Источник).
onlinemschool.com (Источник).
2. Интернет-портал Cleverstudents.ru (Источник).
3. Интернет-портал Calc.ru (Источник).
Домашнее задание
1) Виленкин Н.Я. Математика. 6 класс: учеб. для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013., ст. 49-50 чит., ст. 50 № 308, 310.
2) Сложите дроби:
а) б)
3) Укажите разность:
а) б)
4) * Сравните дроби и из большей вычтите меньшую:
а) и б) и в) и
Сравнение дробей
Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше (<).
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Сравнение дробей с одинаковыми знаменателямиДроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Например, сравним дроби и и ответим какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби числитель больше, чем у дроби . Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше ( > )
Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше ( > )
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителями
Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.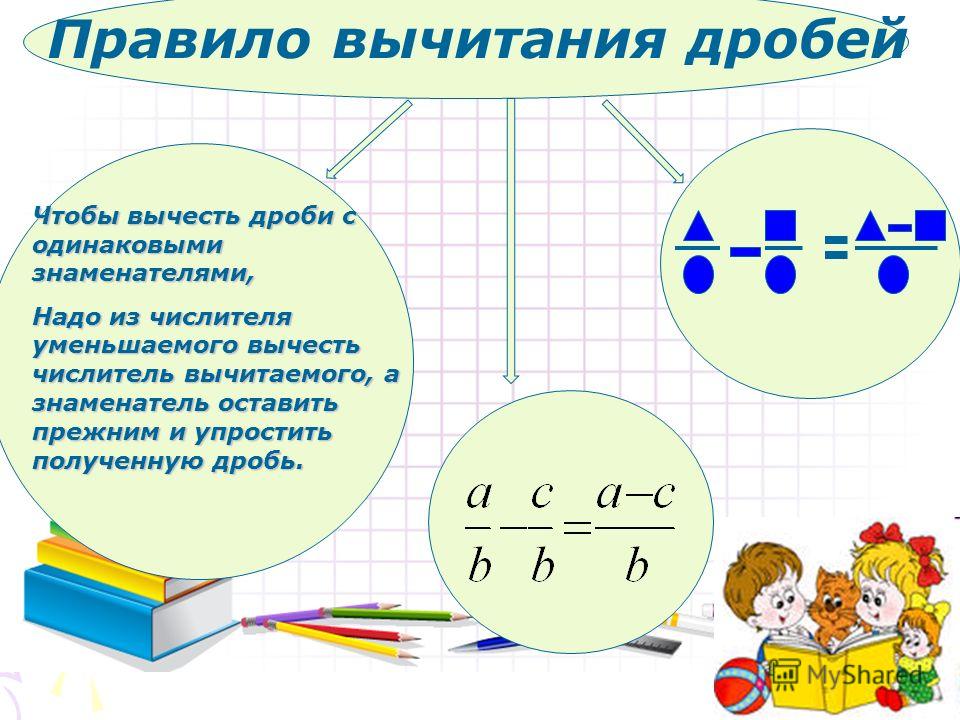
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями. Например, сравнить дроби и .
Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Записываем его над второй дробью:
Умножим дроби на свои дополнительные множители:
Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в неправильной дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби , получим следующее выражение:
Теперь можно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:
2 целые пиццы и пиццы, больше чем пиццы.
Вычитание смешанных чисел. Сложные случаи.
Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Только в этом случае будет получен нормальный ответ.
Например, 10 − 8 = 2
10 — уменьшаемое
8 — вычитаемое
2 — разность
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2
5 — уменьшаемое
7 — вычитаемое
−2 — разность
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример .
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит что уменьшаемое больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:
Теперь сравним дроби и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь
А это значит, что и уменьшаемое меньше, чем вычитаемое
А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.
Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.
Пример 4. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:
Теперь нужно сравнить дроби и . У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое больше, чем вычитаемое
Поэтому мы смело можем продолжить вычисление нашего примера:
Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .
Задания для самостоятельного решения
Задание 1. Сравнить дроби:
Решение:
Показать решение
Задание 2.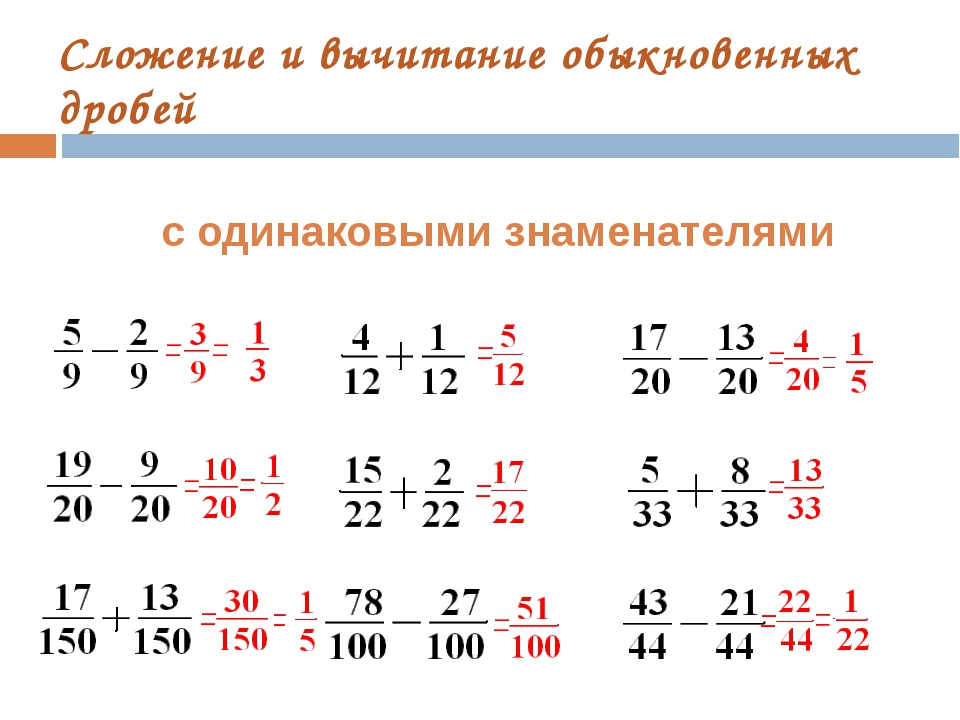 Сравнить дроби:
Сравнить дроби:
Решение:
Показать решение
Задание 3. Сравнить дроби:
Решение:
Показать решение
Задание 4. Сравнить дроби:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями — это продвинутая концепция, которую необходимо изучить после получения глубоких знаний о сложении двух дробей с одинаковым знаменателем. Звучит сложно, но складывать дроби с разными знаменателями несложно. Это одна из тем, изучаемых в начальной школе. Это повышает вычислительные способности учащихся. Эта концепция важна, потому что учащиеся часто путаются между сложением одинаковых и разных дробей. В этой статье мы узнаем, как складывать дроби с разными знаменателями, на множестве примеров.
В этой статье мы узнаем, как складывать дроби с разными знаменателями, на множестве примеров.
Мы должны четко понимать, что такое дроби с разными знаменателями, прежде чем узнаем об их зависимости. Дроби с разными знаменателями называются непохожими дробями. Например, ¾ и ½ не являются дробями. Они не похожи, потому что их знаменатели различны 4 и 2.
Являются ли 3/4 и 3/7 дробями?
Нет! 3/4 и 3/7 не похожи на дроби. Мы видим, что числители у них одинаковые, то есть 3. Но чтобы дроби были одинаковыми, должны быть равны их знаменатели, а не числители. Таким образом, приведенные дроби не похожи на дроби, а не похожи на дроби.
Давайте сначала научимся складывать дроби с одинаковыми знаменателями, чтобы понять принцип сложения разнородных дробей.
Кроме того, когда знаменатели одинаковыЛегче всего складывать подобные дроби. Это точно так же, как сложение двух целых или не дробных чисел. Способ сложения одинаковых дробей приведен ниже:
Шаг 1: Первый шаг — правильно записать дроби со знаком «+» между ними.
Шаг 2: Мы знаем, что знаменатель у этих дробей один и тот же; поэтому дроби, кроме того, дадут один и тот же знаменатель.
Шаг 3: Вы должны сложить числители и записать результат.
Шаг 4: Запишите ответ. Результат сложения p запишите в числителях, поставьте прочерк и запишите q — значение знаменателя. Значение q такое же, как слагаемые.
См. приведенный ниже пример, чтобы понять описанные выше шаги.
Пример: Сложить 2/11 с 3/11
Решение: Внимательно следуя описанным выше шагам, начинаем сложение:
Шаг 1: Записываем числители в правильной форме для сложения, т.е. 2/11 + 3/11
Шаг 2: Поскольку мы складываем одинаковые дроби, знаменатель результата будет равен 11.
Шаг 3: Теперь мы складываем члены числителя, чтобы найти числитель результат. 2 + 3 = 5.
Шаг 4: Наконец, мы запишем полученные дроби как 5/11.
Здесь мы не можем еще больше упростить дроби, так как 5 и 11 не являются общими кратными любого другого числа. Следовательно, ответ 5/11.
Теперь мы хорошо вооружены знаниями о сложении двух дробей с одинаковыми знаменателями. Давайте теперь узнаем, как мы складываем дроби, имеющие разные знаменатели.
Сложение дробей с разными знаменателямиСложение дробей с разными знаменателями намного сложнее, чем сложение, которое мы изучали в предыдущем разделе. Процедура сложения разных дробей включает в себя множество советов и хитростей, которые обязательно должны быть у вас под рукой. Многие ученики часто путаются и делают ошибки при сложении, в отличие от дробей.
Помните, что НОК или наименьшее общее кратное является ключом к решению вопросов, связанных со сложением неодинаковых дробей. При этом, складывая, в отличие от дробей, нужно найти НОК знаменателей. Это делается для того, чтобы привести дроби к общему знаменателю. Мы можем легко сложить дроби с помощью шагов, упомянутых в предыдущем разделе, когда у нас один и тот же знаменатель.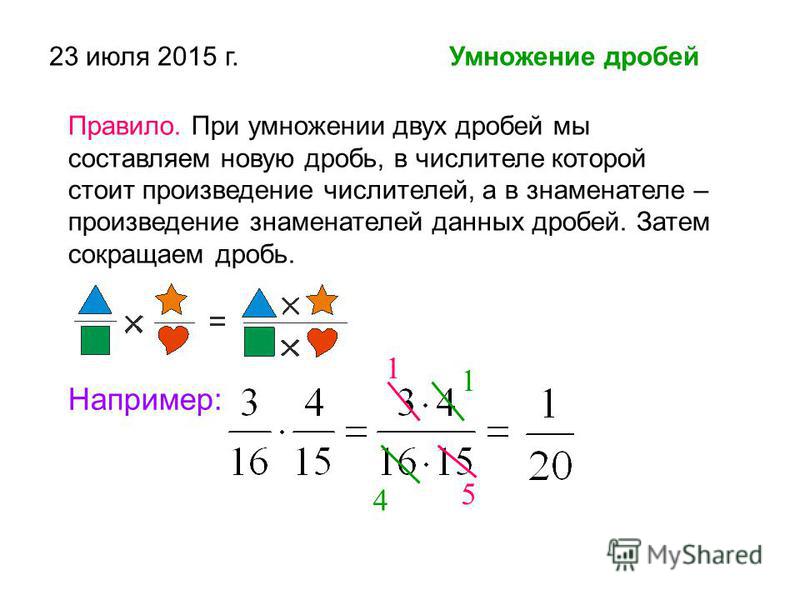 Посмотрите на шаги ниже, чтобы понять этот метод:
Посмотрите на шаги ниже, чтобы понять этот метод:
Шаг 1: Прежде всего, нужно правильно отметить разные дроби знаком «+».
Шаг 2: Попробуйте вывести знаменатель полученной дроби, найдя НОК знаменателей.
Шаг 3: Теперь, соответственно, умножаем числители на значение путем деления НОК на отдельный знаменатель. Сложите соответствующие числа, чтобы получить значение результирующего числителя.
Шаг 4: Последний шаг — зафиксировать результат в дробной форме p/q. Где p — это сумма числителя, а q — знаменатель (НОК).
Пример: Сложите разные дроби 7/3 и 12/9
Решение: Мы решим это, используя пошаговый подход, упомянутый выше:
Шаг 1: Запись неточной формы дробей: 7/3 + 12/9
Шаг 2: Поскольку они не являются дробями, мы должны найти НОК 3 и 9. В этом случае 9 — это НОК, потому что и 3, и 9 кратны.
Шаг 3: Теперь следующим шагом будет соответствующее умножение числителей. Для 7/3, 3 делит 93 раза. Следовательно, мы умножим 7 на 3, что даст 21. Точно так же для 12/9 9 делится на 1 раз; следовательно, 12 умножается на 1, что дает = 12 x 1. Теперь добавим 21, где 12 = 21 + 12 = 33.
Шаг 4: Таким образом, полученная дробь равна 33/9. Его можно еще больше упростить, потому что 33 и 9 кратны 3. Таким образом, полученная дробь равна 11/3.
НОК берется для превращения непохожих дробей в подобные дроби. В остальном процедура остается прежней. Не обязательно находить НОК знаменателей при сложении или вычитании, в отличие от дробей. Любой стандартный кратный будет работать нормально. Таким образом, мы можем получить общее кратное, перемножив два знаменателя. Хотя это дает более крупные числа, его можно свести к простейшей форме. Например, если числа 3 и 9. Их НОК = 9, но мы можем взять любое значение, например 18, 27, 36 и т. д. Поскольку мы имеем дело с наименьшим общим кратным, мы будем рассматривать наименьшее значение.
Поскольку мы имеем дело с наименьшим общим кратным, мы будем рассматривать наименьшее значение.
Складывая дробь с целым числом, мы всегда будем думать о преобразовании целых чисел в их дробную форму. Поскольку мы знаем, что 0 — это наименьшее целое число, следовательно, чтобы сложить любую дробь с 0, мы должны сначала преобразовать 0 в дробную форму. Это можно сделать, поставив «1» на место знаменателя.
Сложение любых дробей с нулем является примером сложения непохожих дробей. Шаги, связанные с добавлением дробей с нулем:
Шаг 1: Запишите целое число ноль как 0/1.
Шаг 2: Поскольку знаменатель в 0/1 равен 1. Знаменатель после сложения будет таким же, как знаменатель другого числа, добавляемого к 0.
Шаг 4: Сложите числители, которые будет (х + 0) = х.
Шаг 5: Запишите дробь в виде x/d. Где «x» — сумма числителей, а «d» — знаменатель числа, отличного от 0.
Из концепции, изученной выше, мы можем видеть, что любая дробь дает саму дробь при сложении с 0. 0 + a /б = а/б.
Можем ли мы сложить число с помощью обратной величины 0?Нет! Обратная величина 0/1 задается как 1/0. Согласно математике, 1/0 не существует. 1/0 не определено. Следовательно, мы можем сказать, что любая дробь, добавленная к обратной величине нуля, не определена.
Примеры
Добавьте следующие дроби. →
1) 10.03 + 11.13
Решение: Мы все знаем об основных шагах из приведенных выше примеров. Итак, приступим непосредственно к расчету.
3/10 + 13/11
НОК знаменателей равен 10 x 11 = 110.
Теперь мы знаем, что 3 нужно умножить на 11, а 13 нужно умножить на 10, чтобы получить желаемый числитель. Следовательно,
3 х 11 = 33, а 13 х 10 = 130. Таким образом, числитель равен 130 + 33 = 163,9.0003
Дробь после сложения 3/10 и 13/11 равна 163/110.
2) 1/2 + 8/3 + 11/10
Решение: В этом случае НОК следует рассматривать с тремя знаменателями. Следовательно, нам нужно найти НОК 2, 3 и 10.
Следовательно, нам нужно найти НОК 2, 3 и 10.
НОК равно 30, потому что это наименьшее число, которое можно разделить на 2 (15 раз), 3 (10 раз) и 10 ( 3 раза). Мы знаем, что ½ будет умножаться на 15, 8/3 будет умножаться на 10, а 11/10 будет умножаться на 3.
Таким образом, числитель будет таким: 1 x 15 + 8 x 10 + 11 x 3 = 15 + 80 + 33 = 128,
Таким образом, результирующая дробь будет 128/30 → 64/15
Подведем итогиИспользуйте следующие процедуры для сложения разнородных дробей:
а) Преобразуйте данные дроби в подобные дроби, включив НОК знаменателя .
b) При сложении числителей оставьте знаменатель одинаковым.
в) Никогда не складывайте числители и знаменатели разнородных дробей отдельно. Это приведет к неправильному результату. Следуйте рекомендациям, изложенным в каждом разделе этой статьи.
Часто задаваемые вопросы
1. Как складывать дроби с необычными знаменателями?
Ответ. Вы можете складывать дроби с необычными знаменателями следующим образом:
Вы можете складывать дроби с необычными знаменателями следующим образом:
Приведение дробей к общему знаменателю.
Сложение числителей каждой дроби, затем вычитание полученного числителя из знаменателя каждой дроби.
2. Как сложить две дроби с разными знаменателями?
Ответ. Легко сложить две дроби с разными знаменателями. Просто перемножьте числители и знаменатели, а затем сложите числа из числителя и числа из знаменателя.
Пример: 5/12 + 4/13 = 5 x 4/13 + 12 = 24/13
3. Добавляете ли вы знаменатель при сложении дробей?
Ответ. Да, при сложении дробей следует включать знаменатель. Это связано с тем, что для выполнения сложения необходимо знать, сколько частей общего количества складывается вместе.
4. Как сделать знаменатели двух или более дробей одинаковыми?
Ответ. Чтобы сделать знаменатели двух или более дробей равными, нужно умножить каждый член на общий множитель.
Например, , допустим, у нас есть 1/2 + 3/4. Чтобы сделать эти знаменатели равными, мы можем умножить оба члена на 2: 2(1/2) = 2 и 2(3/4) = 6. Теперь наши числители равны 1 и 4, поэтому сумма равна 5.
5. Каковы шаги для сложения дробей?
Ответ. 1. Сложите числители каждой дроби
2. Сложите знаменатели каждой дроби
3. При необходимости упростите
Простое руководство по сложению дробей (включая разные знаменатели)
В этом руководстве показано, как складывать дроби с помощью сложения и вычитания. Мы также включили дроби с разными знаменателями, которые требуют немного больше работы.
Во-первых, давайте начнем с видео о том, как складывать и вычитать дроби:
Дроби — это не что иное, как отношение «части» к «целому». Дроби можно складывать, вычитать, умножать и делить, понимая структуру дроби и следуя нескольким простым правилам. Эта статья покажет вам, как это сделать, но сначала давайте рассмотрим основы терминологии дробей.
Дроби можно складывать, вычитать, умножать и делить, понимая структуру дроби и следуя нескольким простым правилам. Эта статья покажет вам, как это сделать, но сначала давайте рассмотрим основы терминологии дробей.
Представьте одну сторону магического куба, как показано ниже. Он разделен на маленькие квадраты разного цвета одинакового размера. Какова доля желтых квадратов?
Чтобы определить эту долю, нам нужно посчитать желтые квадраты и соотнести это значение с общим количеством квадратов. «Часть» в данном случае — это три желтых квадрата, которые известны как числитель дроби. Это значение делится на общее количество квадратов или «целое». Всего квадратов шестнадцать, и это число равно 9.0251 знаменатель дроби.
При написании дроби деление обычно обозначается горизонтальной чертой, при этом числитель пишется вверху, а знаменатель — внизу.
Теперь давайте попробуем написать другую дробь:
Какова доля красных квадратов?
Да, верно! Это \(\frac{4}{16}\). Однако эту дробь можно упростить и записать как: \(\frac{1}{4}\).
Однако эту дробь можно упростить и записать как: \(\frac{1}{4}\).
Пожалуйста, найдите минутку, чтобы просмотреть нашу подробную статью о том, как упростить дроби, чтобы при необходимости просмотреть эту концепцию!
Теперь, если вас спросят, какова доля красных и желтых квадратов вместе взятых, как бы вы ответили? Это так просто, как кажется: просто подсчитайте общее количество красных и желтых квадратов, чтобы получить числитель. Знаменатель остается прежним:
Всего красных и желтых квадратов: 3 + 4 = 7
Доля объединенных красных и желтых квадратов: \(\frac{7}{16}\)
Это означает что если долю желтых квадратов добавить к доле красных квадратов, ответ должен быть \(\frac{7}{16}\).
Прежде чем мы решим другую задачу, вот список полезных вещей, которые следует запомнить:
- При сложении и вычитании дробей знаменатели не меняются. Сложение или вычитание выполняется только с числителями.
- Прежде чем вы сможете складывать или вычитать дроби, знаменатели ваших дробей должны совпадать друг с другом.

- Всегда старайтесь упрощать дроби перед операцией с ними, чтобы числа, с которыми вы работаете, были как можно меньше.
Использование этих квадратов помогает визуализировать концепцию сложения дробей, но помните, что в большинстве случаев визуальные цифры недоступны. Итак, давайте уберем визуальные эффекты и пройдемся по математическим шагам с несколькими примерами:
Предположим, у вас нет доступного квадрата, и вас просто просят добавить \(\frac{3}{16}\) и \(\ гидроразрыва{1}{4}\). Как видите, знаменатели этих дробей не совпадают. Это должно быть исправлено, прежде чем мы сможем двигаться дальше:
Шаг 1Найдите НОК (наименьшее общее кратное) знаменателей обеих дробей. Обратите внимание, что при работе с дробями LCM также называется наименьшим общим знаменателем (LCD), потому что наша цель — сопоставить знаменатели дробей.
У нас есть полезная статья об определении GCF и LCM, которая может быть полезна для обзора, но мы также рассмотрим шаги здесь:
Мини-шаг 1. 1: Перечислите{4}\) = 16
1: Перечислите{4}\) = 16
LCD = 16
Шаг 3(А вот и сложная часть, обратите внимание!)
После того, как мы узнаем LCD каждой дроби внесите корректировку в одну или обе исходные дроби. Давайте посмотрим на одну дробь за раз и ответим на следующий вопрос: соответствует ли знаменатель ЖК?
Первая дробь равна \(\frac{3}{16}\), и ответ на вопрос — да! Знаменатель 16 равен LCD 16. Эту дробь не нужно корректировать.
Вторая дробь равна \(\frac{1}{4}\). Ясно, что 4 не равно LCD, равному 16. Эту дробь необходимо скорректировать, чтобы получить эквивалентную дробь со знаменателем, равным 16. Но как?
Настройка проста: определите число, на которое нужно умножить знаменатель 4, чтобы получить ЖК-дисплей. Для этого просто разделите ЖК на исходный знаменатель. В этом случае \(16\дел 4=4\).
Теперь исходную дробь можно изменить, умножив числитель и знаменатель на этот коэффициент 4, как показано:
\((\frac{4}{4}\times \frac{1}{4})=\frac{4\times 1}{4\times 4}=\frac{4}{16}\)
Помните, что при умножении дробей выполняйте операцию «напрямую», то есть (числитель х числитель) и (знаменатель х знаменатель).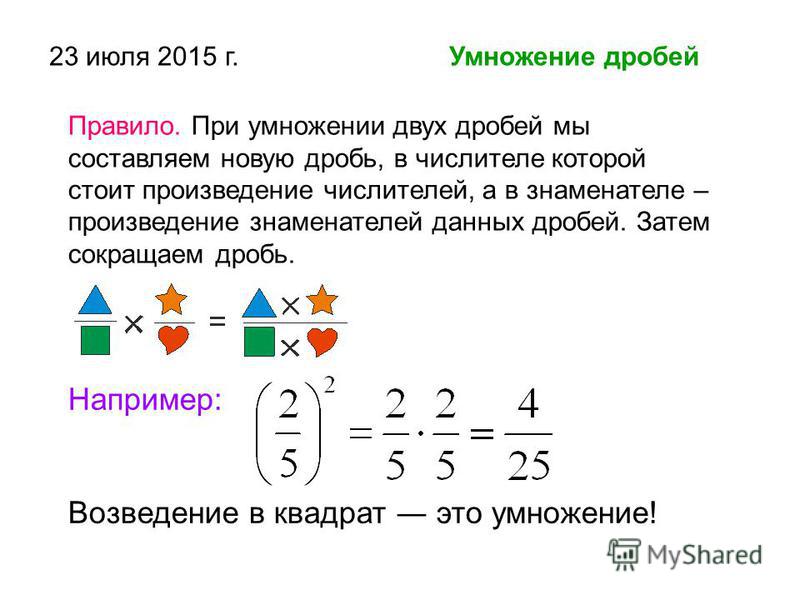
Это умножение на \(\frac{4}{4}\) не меняет значение исходной дроби, поскольку \(\frac{4}{4}\) = 1.
После эквивалентной дроби \ (\frac{4}{16}\) можно сложить дроби:
\(\frac{3}{16}+\frac{4}{16}=\frac{3+4}{ 16}=\frac{7}{16}\)
Как видите, именно это мы и получили, сложив доли желтых и красных квадратов!
Эти рисунки могут быть полезны для тех из вас, кто предпочитает наглядную демонстрацию определения LCD перед сложением или вычитанием дробей:
Давайте рассмотрим еще один пример, где одна дробь является правильной дробью (числитель меньше знаменателя) и вторая — неправильная дробь (числитель больше знаменателя). Способ сложения тот же, и не имеет значения, правильная дробь или неправильная. 9{2} =36\)
LCD = 36
Шаг 3Теперь пришло время выяснить, какие дроби нужно скорректировать, чтобы получить похожие знаменатели. Для каждой дроби спросите: «Соответствует ли знаменатель LCD?»
Первая дробь равна \(\frac{1}{12}\), и мы видим, что 12 не равняется LCD 36, поэтому эту дробь нужно будет скорректировать. Как и прежде, разделите ЖК на исходный знаменатель. В этом случае \(36\div 12=3\).
Как и прежде, разделите ЖК на исходный знаменатель. В этом случае \(36\div 12=3\).
Теперь исходную дробь можно изменить, умножив числитель и знаменатель на 3, как показано:
\((\frac{3}{3}\times \frac{1}{12})=\frac{3\times 1}{3\times 12}=\frac{3}{36}\)
Вторая дробь, \(\frac{19}{18}\), также должна быть скорректирована, так как 18 не соответствует ЖК-дисплею.
Разделите ЖК-дисплей на знаменатель 18: \(36\дел 18=2\).
Умножьте числитель и знаменатель второй дроби на 2, как показано:
\((\frac{2}{2}\times \frac{19}{18})=\frac{2\times 19} {2\times 18}=\frac{38}{36}\)
Теперь, когда каждый знаменатель соответствует ЖК-дисплею, можно сложить эквивалентные дроби:
\(\frac{3}{36}+\frac{38}{36}=\frac{3+38}{36}=\frac{41}{36}\)
Добавление более двух дроби К этому моменту статьи мы надеемся, что вы освоили искусство сложения двух дробей. Если вам нужно добавить более двух фракций, процедура такая же. Давайте сделаем пример, чтобы проиллюстрировать это.
Добавить: \(\frac{4}{5}+\frac{1}{2}+\frac{1}{4}\)
Все эти дроби представлены в простейшей форме, так что давайте начнем процесс найти LCM и настроить каждую дробь так, чтобы знаменатели были одинаковыми. 9{2}\) × 5 = 20
LCD = 20
Шаг 3Теперь пришло время выяснить, какие дроби нужно изменить, чтобы получить похожие знаменатели. Для каждой дроби спросите: «Соответствует ли знаменатель LCD?»
Первая дробь равна \(\frac{4}{5}\), и мы видим, что 5 не равно 20. Как и прежде, разделите LD на исходный знаменатель. В этом случае \(20\дел 5=4\).
Теперь исходную дробь можно изменить, умножив числитель и знаменатель на 4, как показано:
\((\frac{4}{4}\times \frac{4}{5})=\frac{4\times 4}{4\times 5}=\frac{16}{20}\)
Вторая дробь, \(\frac{1}{2}\), также должна быть скорректирована, так как 2 не соответствует ЖК-дисплею.
Разделите LCD на знаменатель, 2: \(20\div 2=10\)
Умножьте числитель и знаменатель второй дроби на 10, как показано:
\((\frac{10}{ 10}\times \frac{1}{2})=\frac{10\times 1}{10\times 2}=\frac{10}{20}\)
Наконец, определите корректировку, которую необходимо преобразован в третью дробь, \(\frac{1}{4}\).
Разделите ЖК-дисплей на знаменатель, 4, чтобы получить коэффициент 5. Отрегулируйте третью дробь, умножив на \(\frac{5}{5}\).
\((\frac{5}{5}\times \frac{1}{4})=\frac{5\times 1}{5\times 4}=\frac{5}{20}\)
Теперь, когда каждый из трех знаменателей соответствует ЖК-дисплею, можно сложить эквивалентные дроби:
\(\frac{16}{20}+\frac{10}{20}+\frac{5}{20} =\frac{16+10+5}{20}=\frac{31}{20}\)
Сложение дробей и целых чиселЕще одна важная концепция, о которой следует помнить при изучении сложения дробей, заключается в том, как добавлять дроби к целым числам. К счастью, любое целое число можно переписать так, чтобы оно «выглядело» как дробь, путем деления его на единицу. Например,
4 = \(\frac{4}{1}\)
30 = \(\frac{30}{1}\)
72 = \(\frac{72}{ 1}\)
После того, как целое число записано в виде доли от единицы, процесс сложения и вычитания аналогичен тому, что мы обсуждали в этой статье.
Вот несколько примеров:
Добавить: 3 + \(\frac{3}{14}\)
Этот вопрос можно переписать так: \(\frac{3}{1}\) + \ (\frac{5}{14}\)
Шаг 1Подумав, выберите ЖК-дисплей. На какое наименьшее число можно разделить без остатка и 14, и 1?
Как насчет 14? Это наименьшее число, на которое можно разделить как 1, так и 14. Используйте его в качестве ЖК-дисплея для настройки первой «дроби», \(\frac{3}{1}\).
Разделите LCD на знаменатель 1: \(14\div 1=14\)
Умножьте первую дробь на \(\frac{14}{14}\).
\((\frac{14}{14}\times \frac{3}{1})=\frac{42}{14}\)
Поскольку знаменатели совпадают, можно складывать дроби:
\(\frac{42}{14}+\frac{3}{14}=\frac{42+3}{14}=\frac{ 45}{14}\)
Заключительные мысли! В этой статье мы узнали, как складывать дроби и как складывать целые числа в дроби. Это довольно полезный навык, который закладывает основу для некоторых сложных математических работ. Хотите сократить путь? Попробуйте наш калькулятор дробей! Посетите остальную часть нашего веб-сайта, чтобы узнать о других интересных и полезных математических понятиях, объясненных простым способом. Нужна дополнительная помощь, видеообзоры или практические вопросы? Кликните сюда!
Хотите сократить путь? Попробуйте наш калькулятор дробей! Посетите остальную часть нашего веб-сайта, чтобы узнать о других интересных и полезных математических понятиях, объясненных простым способом. Нужна дополнительная помощь, видеообзоры или практические вопросы? Кликните сюда!
Сложение и вычитание дробей с разными знаменателями
Результаты обучения
- Сложение и вычитание дробей с разными знаменателями
- Определение и использование дробных операций
Чтобы сложить или вычесть дроби с разными знаменателями, мы сначала должны записать их как эквивалентные дроби с одинаковым знаменателем. Мы будем использовать методы из предыдущего раздела, чтобы найти НОК знаменателей дробей. Напомним, что мы называем это LCD (наименьший общий знаменатель). При нахождении ЖК мы используем только знаменатели дробей, а не числители.
Затем мы можем использовать свойство «Эквивалентные дроби», чтобы алгебраически преобразовать дробь в эквивалентную. Помните, что две дроби эквивалентны, если они имеют одинаковое значение. Шаги для нахождения LCD и свойства Equivalent Fractions повторяются ниже для справки.
Помните, что две дроби эквивалентны, если они имеют одинаковое значение. Шаги для нахождения LCD и свойства Equivalent Fractions повторяются ниже для справки.
Наименьший общий знаменатель
Наименьший общий знаменатель (НОД) двух дробей равен наименьшему общему кратному (НОК) их знаменателей.
Эквивалентные дроби Свойство
Если [latex]a,b,c[/latex] — целые числа, где [latex]b\ne 0,c\ne 0,\text{то}[/latex]
[latex]\Large\frac {a}{b}=\Large\frac{a\cdot c}{b\cdot c}\normalsize\text{ и }\Large\frac{a\cdot c}{b\cdot c}=\Large\ frac{a}{b}[/latex]
После того, как мы преобразовали две дроби в эквивалентные формы с общими знаменателями, мы можем складывать или вычитать их, добавляя или вычитая числители. Попробуйте приведенные ниже примеры и попрактикуйтесь в решении задач, чтобы освежить эти навыки.
Сложение и вычитание дробей с разными знаменателями
- Найдите ЖК-дисплей.
- Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в качестве знаменателя.

- Сложите или вычтите дроби.
- Запишите результат в упрощенной форме.
Пример
Добавить: [latex]\Large\frac{1}{2}+\Large\frac{1}{3}[/latex]
Решение:
| [латекс]\Большой\фракция{1}{2}+\Большой\фракция{1}{3}[/латекс] | |
| Найдите ЖК-дисплей [латекс]2[/латекс], [латекс]3[/латекс]. | |
| Преобразование в эквивалентные дроби с помощью ЖК-дисплея [латекс]6[/латекс]. | [латекс]\Large\frac{1\cdot\color{red}{3}}{2\cdot\color{red}{3}} +\Large\frac{1\cdot\color{red}{2 }}{3\cdot\color{red}{2}}[/latex] |
| Упростите числители и знаменатели. | [латекс]\Большой\фракция{3}{6}+\Большой\фракция{2}{6}[/латекс] |
| Доп. | [латекс]\большой\фрак{5}{6}[/латекс] |
Помните, всегда проверяйте, можно ли упростить ответ. Поскольку [латекс]5[/латекс] и [латекс]6[/латекс] не имеют общих множителей, дробь [латекс]\большой\фрак{5}{6}[/латекс] нельзя сократить.
Поскольку [латекс]5[/латекс] и [латекс]6[/латекс] не имеют общих множителей, дробь [латекс]\большой\фрак{5}{6}[/латекс] нельзя сократить.
Попробуйте
Посмотрите следующее видео, чтобы увидеть больше примеров и пояснений о том, как сложить две дроби с разными знаменателями.
Пример
Вычесть: [латекс]\Большой\фракция{1}{2}-\left(-\Большой\фракция{1}{4}\правый)[/латекс]
Показать решение
Попробуйте
В следующем видео приведены еще два примера вычитания двух дробей с разными знаменателями.
Пример
Добавить: [латекс]\Большой\фрак{7}{12}+\Большой\фрак{5}{18}[/латекс]
Показать решение
Попробуйте
Когда мы используем свойство «Эквивалентные дроби», есть быстрый способ найти число, на которое нужно умножить, чтобы получить ЖК-дисплей. Запишите множители знаменателей и LCD так же, как вы это делали, чтобы найти LCD. «Недостающие» множители каждого знаменателя — это числа, которые вам нужны.
Запишите множители знаменателей и LCD так же, как вы это делали, чтобы найти LCD. «Недостающие» множители каждого знаменателя — это числа, которые вам нужны.
LCD, [латекс]36[/латекс], имеет [латекс]2[/латекс] коэффициенты [латекс]2[/латекс] и [латекс]2[/латекс] коэффициенты [латекс]3[ /латекс].
Twelve имеет два множителя [latex]2[/latex], но только один из [latex]3[/latex] — так что «отсутствует» один [latex]3[/latex]. Мы умножили числитель и знаменатель [latex]\Large\frac{7}{12}[/latex] на [latex]3[/latex], чтобы получить эквивалентную дробь со знаменателем [latex]36[/latex].
В восемнадцати отсутствует один множитель [латекс]2[/латекс] — поэтому вы умножаете числитель и знаменатель [латекс]\большой\фрак{5}{18}[/латекс] на [латекс]2[/латекс] чтобы получить эквивалентную дробь со знаменателем [латекс]36[/латекс]. Мы будем применять этот метод при вычитании дробей в следующем примере.
Пример
Вычесть: [латекс]\Большой\фрак{7}{15}-\Большой\фрак{19}{24}[/латекс]
Показать решение
Попробуйте
Пример
Добавить: [латекс]-\Large\frac{11}{30}+\Large\frac{23}{42}[/latex]
Показать решение
Попробуйте
4.
 8. Сложение и вычитание дробей с разными знаменателями (часть 1)
8. Сложение и вычитание дробей с разными знаменателями (часть 1)- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4995
- ОпенСтакс
- ОпенСтакс
Цели обучения
- Найдите наименьший общий знаменатель (LCD)
- Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея
- Сложение и вычитание дробей с разными знаменателями
- Определение и использование дробных операций
- Используйте порядок операций для упрощения сложных дробей
- Вычислить переменные выражения с дробями
 3.13.
3.13.Найдите наименьший общий знаменатель
В предыдущем разделе мы объяснили, как складывать и вычитать дроби с общим знаменателем. Но как складывать и вычитать дроби с разными знаменателями?
Давайте снова подумаем о монетах. Можете ли вы добавить одну четверть и один цент? Можно сказать, что есть две монеты, но это не очень полезно. Чтобы найти общую стоимость одной четверти плюс один цент, вы заменяете их на одну и ту же единицу — центы. Одна четверть равна \(25\) центам, а один дайм равен \(10\) центам, поэтому сумма равна \(35\) центам. См. рисунок \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Вместе четверть и десятицентовик стоят 35 центов или \(\dfrac{35}{100}\) доллара.
Точно так же, когда мы складываем дроби с разными знаменателями, мы должны преобразовать их в эквивалентные дроби с общим знаменателем. С монетами, когда мы конвертируем в центы, знаменатель равен \(100\). Поскольку в одном долларе содержится \(100\) центов, \(25\) центов равно \(\dfrac{25}{100}\), а \(10\) центов равно \(\dfrac{10}{100} \). Итак, мы добавляем \(\dfrac{25}{100} + \dfrac{10}{100}\), чтобы получить \(\dfrac{35}{100}\), что составляет \(35\) центов.
Итак, мы добавляем \(\dfrac{25}{100} + \dfrac{10}{100}\), чтобы получить \(\dfrac{35}{100}\), что составляет \(35\) центов.
Вы научились складывать и вычитать дроби с общим знаменателем. Теперь посмотрим, что нужно делать с дробями, имеющими разные знаменатели.
Во-первых, мы будем использовать фрагменты дробей для моделирования нахождения общего знаменателя \(\dfrac{1}{2}\) и \(\dfrac{1}{3}\). Мы начнем с одной плитки \(\dfrac{1}{2}\) и плитки \(\dfrac{1}{3}\). Мы хотим найти тайл общей дроби, который мы можем использовать для точного сопоставления и \(\dfrac{1}{2}\) и \(\dfrac{1}{3}\). Если мы попробуем кусочки \(\dfrac{1}{4}\), \(2\) из них в точности совпадают с кусочком \(\dfrac{1}{2}\), но они не точно совпадают с \ (\dfrac{1}{3}\) шт.
Рисунок \(\PageIndex{2}\)
Если мы попробуем части \(\dfrac{1}{5}\), они точно не покроют \(\dfrac{1}{2} \) кусок или \(\dfrac{1}{3}\) кусок.
Рисунок \(\PageIndex{3}\)
Если бы мы попробовали части \(\dfrac{1}{12}\), они бы тоже сработали.
Рисунок \(\PageIndex{4}\)
Даже меньшие фрагменты, такие как \(\dfrac{1}{24}\) и \(\dfrac{1}{48}\), также точно покройте часть \(\dfrac{1}{2}\) и часть \(\dfrac{1}{3}\). Знаменатель наибольшей части, покрывающей обе дроби, равен 9.0013 наименьший общий знаменатель (LCD) двух дробей. Таким образом, наименьший общий знаменатель для \(\dfrac{1}{2}\) и \(\dfrac{1}{3}\) равен \(6\).
Обратите внимание, что все тайлы, покрывающие \(\dfrac{1}{2}\) и \(\dfrac{1}{3}\), имеют нечто общее: их знаменатели являются общими кратными \(2\ ) и \(3\), знаменатели \(\dfrac{1}{2}\) и \(\dfrac{1}{3}\). Наименьшее общее кратное (НОК) знаменателей равно \(6\), поэтому мы говорим, что \(6\) является наименьшим общим знаменателем (НОК) дробей \(\dfrac{1}{2}\) и \(\dfrac{1}{3}\).
Определение: Наименьший общий знаменатель
Наименьший общий знаменатель (НОД) двух дробей – это наименьшее общее кратное (НОК) их знаменателей.
Чтобы найти НОК двух дробей, найдем НОК их знаменателей. Мы следуем процедуре, которую мы использовали ранее, чтобы найти НОК двух чисел. При нахождении ЖК мы используем только знаменатели дробей, а не числители.
Мы следуем процедуре, которую мы использовали ранее, чтобы найти НОК двух чисел. При нахождении ЖК мы используем только знаменатели дробей, а не числители.
Пример \(\PageIndex{1}\): lcd
Найдите ЖК-дисплей для дробей \(\dfrac{7}{12}\) и \(\dfrac{5}{18}\).
Решение
| Разложите каждый знаменатель на его простые числа. | |
| Перечислите простые числа от 12 и простые числа от 18, по возможности выстроив их в столбцы. | |
| Снести колонны. | |
| Умножьте множители. Продукт LCM. | мл = 36 |
| LCM 12 и 18 равен 36, поэтому LCD \(\dfrac{7}{12}\) и \(\dfrac{5}{18}\) равен 36. | LCD для \(\dfrac{7}{12}\) и \(\dfrac{5}{18}\) равно 36. |
Упражнение \(\PageIndex{1}\)
Найдите наименьший общий знаменатель дробей: \(\dfrac{7}{12}\) и \(\dfrac{11}{15}\) .
- Ответить
\(60\)
Упражнение \(\PageIndex{2}\)
Найдите наименьший общий знаменатель дробей: \(\dfrac{13}{15}\) и \(\dfrac{17}{5}\).
- Ответить
\(15\)
Чтобы найти НОК двух дробей, найдите НОК их знаменателей. Обратите внимание, что шаги, показанные ниже, похожи на шаги, которые мы предприняли, чтобы найти LCM.
КАК: НАЙТИ НАИМЕНЬШИЙ ОБЩИЙ ЗНАМЕНАТЕЛЬ (НОД) ДВУХ ДРОБЕЙ
Шаг 1. Разложите каждый знаменатель на его простые числа.
Шаг 2. Перечислите простые числа, по возможности сопоставляя простые числа в столбцах.
Шаг 3. Опустите столбцы.
Шаг 4. Перемножьте коэффициенты. Произведение представляет собой НОК знаменателей.
Шаг 5. НОК знаменателей – это НОК дробей.
Пример \(\PageIndex{2}\):
Найдите наименьший общий знаменатель дробей \(\dfrac{8}{15}\) и \(\dfrac{11}{24}\).
Решение
Чтобы найти ЖК, находим НОК знаменателей. Найдите НОК \(15\) и \(24\).
Найдите НОК \(15\) и \(24\).
НОК для \(15\) и \(24\) равен \(120\). Таким образом, LCD \(\dfrac{8}{15}\) и \(\dfrac{11}{24}\) равен \(120\).
Упражнение \(\PageIndex{3}\)
Найдите наименьший общий знаменатель дробей: \(\dfrac{13}{24}\) и \(\dfrac{17}{32}\).
- Ответить
\(96\)
Упражнение \(\PageIndex{4}\)
Найдите наименьший общий знаменатель дробей: \(\dfrac{9}{28}\) и \(\dfrac{21}{32}\).
- Ответить
\(224\)
Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея
Ранее мы использовали фрагменты фрагментов, чтобы увидеть, что ЖК-дисплеи \(\dfrac{1}{4}\) и \(\dfrac{1}{6}\) равны \(12\). Мы видели, что три \(\dfrac{1}{12}\) отрезка точно покрыты \(\dfrac{1}{4}\) и два \(\dfrac{1}{12}\) отрезка точно покрыты \( \dfrac{1}{6}\), поэтому
\[\dfrac{1}{4} = \dfrac{3}{12} \quad и \quad \dfrac{1}{6} = \dfrac{ 2}{12} \ldotp \nonumber \]
Мы говорим, что \(\dfrac{1}{4}\) и \(\dfrac{3}{12}\) являются эквивалентными дробями, а также что \ (\dfrac{1}{6}\) и \(\dfrac{2}{12}\) — эквивалентные дроби.
Свойство эквивалентных дробей можно использовать для алгебраического преобразования дроби в эквивалентную. Помните, что две дроби эквивалентны, если они имеют одинаковое значение. Свойство Equivalent Fractions повторяется ниже для справки.
Определение: свойство эквивалентных дробей
Если \(a, b, c\) — целые числа, где \(b ≠ 0\), \(c ≠ 0\), то
\[\dfrac{a}{ b} = \dfrac{a \cdot c}{b \cdot c} \quad и \quad \dfrac{a \cdot c}{b \cdot c} = \dfrac{a}{b}\]
Чтобы складывать или вычитать дроби с разными знаменателями, нам сначала нужно преобразовать каждую дробь в эквивалентную дробь с помощью ЖК-дисплея. Давайте посмотрим, как заменить \(\dfrac{1}{4}\) и \(\dfrac{1}{6}\) на эквивалентные дроби со знаменателем \(12\) без использования моделей.
Пример \(\PageIndex{3}\): преобразование
Преобразование \(\dfrac{1}{4}\) и \(\dfrac{1}{6}\) в эквивалентные дроби со знаменателем \(12 \), их ЖК.
Раствор
Найдите ЖК-дисплей. | ЖК-дисплей \(\dfrac{1}{4}\) и \(\dfrac{1}{6}\) равен 12. |
| Найдите число, на которое нужно умножить 4, чтобы получить 12. | \(4 \cdot \textcolor{red}{3} = 12\) |
| Найдите число, на которое нужно умножить 6, чтобы получить 12. | \(6 \cdot \textcolor{red}{2} = 12\) |
| Используйте свойство «Эквивалентные дроби», чтобы преобразовать каждую дробь в эквивалентную дробь с помощью ЖК-дисплея, умножив числитель и знаменатель каждой дроби на одно и то же число. | \(\begin{split} \dfrac{1}{4} \qquad & \dfrac{1}{6} \\ \dfrac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor {red}{3}} \qquad & \dfrac{1 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} \end{split}\) |
| Упростите числители и знаменатели. | \(\dfrac{3}{12} \qquad \dfrac{2}{12}\) |
Полученные дроби не уменьшаем. Если бы мы это сделали, мы бы вернулись к нашим первоначальным дробям и потеряли бы общий знаменатель.
Если бы мы это сделали, мы бы вернулись к нашим первоначальным дробям и потеряли бы общий знаменатель.
Упражнение \(\PageIndex{5}\)
Замените эквивалентные дроби на ЖК-дисплее: \(\dfrac{3}{4}\) и \(\dfrac{5}{6}\), \( LCD = 12\)
- Ответ
\(\dfrac{9}{12}, \dfrac{10}{12}\)
Упражнение \(\PageIndex{6}\)
Замените эквивалентные дроби на ЖК-дисплее: \(- \dfrac{7}{12}\) и \(\dfrac{11}{15}\), \ (ЖК = 60\)
- Ответ
\(-\dfrac{35}{60}, \dfrac{44}{60}\)
КАК: ПРЕОБРАЗОВАТЬ ДВЕ ДРОБИ В ЭКВИВАЛЕНТНЫЕ Дроби, С ИХ ДИСПЛЕЙ В КАЧЕСТВЕ ОБЩЕГО ЗНАМЕНАТЕЛЯ
Шаг 1. Найдите ЖК-дисплей.
Шаг 2. Для каждой дроби определите число, необходимое для умножения знаменателя, чтобы получить ЖКИ.
Шаг 3. Используйте свойство «Эквивалентные дроби», чтобы умножить числитель и знаменатель на число, найденное на шаге 2.
Шаг 4. Упростите числитель и знаменатель.
Пример \(\PageIndex{4}\): преобразование
Преобразование \(\dfrac{8}{15}\) и \(\dfrac{11}{24}\) в эквивалентные дроби со знаменателем \(120\), их LCD.
| Найдите число, на которое нужно умножить 15, чтобы получить 120. | \(15 \cdot \textcolor{red}{8} = 120\) |
| Найдите число, на которое нужно умножить 24, чтобы получить 120. | \(24 \cdot \textcolor{red}{5} = 120\) |
| Используйте свойство «Эквивалентные дроби». | \(\dfrac{8 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} \qquad \dfrac{11 \cdot \textcolor{red}{5}}{24 \cdot\textcolor{красный}{5}}\) |
| Упростите числители и знаменатели. | \(\dfrac{64}{120} \qquad \dfrac{55}{120}\) |
Упражнение \(\PageIndex{7}\)
Замените эквивалентные дроби на ЖК-дисплее: \(\dfrac{13}{24}\) и \(\dfrac{17}{32}\), LCD \(96\)
- Ответ
\(\dfrac{52}{96}, \dfrac{51}{96}\)
Упражнение \(\PageIndex{8}\)
Замена эквивалентных дробей с помощью LCD: \(\dfrac{9}{28}\) и \(\dfrac{27}{32}\), LCD \ (224\)
- Ответить
\(\dfrac{72}{224}, \dfrac{189}{224}\)
Сложение и вычитание дробей с разными знаменателями
После преобразования двух дробей в эквивалентные формы с общими знаменателями мы можем складывать или вычитать их, добавляя или вычитая числители.
КАК: СКЛАДЫВАТЬ ИЛИ ВЫЧИТАТЬ Дроби С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ
Шаг 1. Найдите ЖК-дисплей.
Шаг 2. Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в знаменателе.
Шаг 3. Сложите или вычтите дроби.
Шаг 4. Запишите результат в упрощенной форме.
Пример \(\PageIndex{5}\): добавить
Добавить: \(\dfrac{1}{2} + \dfrac{1}{3}\).
Решение
| Найдите ЖК-дисплей 2, 3. | |
| Преобразование в эквивалентные дроби с помощью ЖК-дисплея 6. | \(\dfrac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \dfrac{1 \cdot \textcolor{red}{2}}{3 \ cdot \textcolor{красный}{2}}\) |
| Упростите числители и знаменатели. | \(\dfrac{3}{6} + \dfrac{2}{6}\) |
| Доп. | \(\dfrac{5}{6}\) |
Помните, всегда проверяйте, можно ли упростить ответ. Поскольку \(5\) и \(6\) не имеют общих множителей, дробь \(\dfrac{5}{6}\) не может быть уменьшена.
Поскольку \(5\) и \(6\) не имеют общих множителей, дробь \(\dfrac{5}{6}\) не может быть уменьшена.
Упражнение \(\PageIndex{9}\)
Добавить: \(\dfrac{1}{4} + \dfrac{1}{3}\).
- Ответить
\(\dfrac{7}{12}\)
Упражнение \(\PageIndex{10}\)
Добавить: \(\dfrac{1}{2} + \dfrac{1}{5}\).
- Ответить
\(\dfrac{7}{10}\)
Пример \(\PageIndex{6}\): вычесть
Вычесть: \(\dfrac{1}{2} — \left(- \dfrac{1}{4}\right)\).
Решение
| Найдите ЖК-дисплей 2 и 4. | |
| Перепишите эквивалентные дроби с помощью ЖК-дисплея 4. | \(\dfrac{1 \cdot \textcolor{red}{2}}{2 \cdot \textcolor{red}{2}} — \left(- \dfrac{1}{4}\right)\) |
| Упростите первую дробь. | \(\dfrac{2}{4} — \left(- \dfrac{1}{4}\right)\) |
Вычесть. | \(\dfrac{2 — (-1)}{4}\) |
| Упрощение. | \(\dfrac{3}{4}\) |
У одной из дробей уже был наименьший общий знаменатель, поэтому нам оставалось только преобразовать другую дробь.
Упражнение \(\PageIndex{11}\)
Вычесть: \(\dfrac{1}{2} — \left(- \dfrac{1}{8}\right)\).
- Ответить
\(\dfrac{5}{8}\)
Упражнение \(\PageIndex{12}\)
Вычесть: \(\dfrac{1}{3} — \left(- \dfrac{1}{6}\right)\).
- Ответить
\(\dfrac{1}{2}\)
Пример \(\PageIndex{7}\): добавить
Добавить: \(\dfrac{7}{12} + \dfrac{5}{18}\).
Раствор
| Найти ЖК-дисплей 12 и 18. | |
| Перепишите как эквивалентные дроби с помощью ЖК-дисплея. | \(\dfrac{7 \cdot \textcolor{red}{3}}{12 \cdot \textcolor{red}{3}} + \dfrac{5 \cdot \textcolor{red}{2}}{18 \ cdot \textcolor{красный}{2}}\) |
Упростите числители и знаменатели. | \(\dfrac{21}{36} + \dfrac{10}{36}\) |
| Добавить. | \(\dfrac{31}{36}\) |
Поскольку \(31\) является простым числом, оно не имеет общих делителей с \(36\). Ответ упрощен.
Упражнение \(\PageIndex{13}\)
Добавить: \(\dfrac{7}{12} + \dfrac{11}{15}\).
- Ответить
\(\dfrac{79}{60}\)
Упражнение \(\PageIndex{14}\)
Добавить: \(\dfrac{13}{15} + \dfrac{17}{20}\).
- Ответ
\(\dfrac{103}{60}\)
Когда мы используем свойство Equivalent Fractions, есть быстрый способ найти число, на которое нужно умножить, чтобы получить LCD. Запишите множители знаменателей и LCD так же, как вы это делали, чтобы найти LCD. «Недостающие» множители каждого знаменателя — это числа, которые вам нужны.
LCD, \(36\), имеет \(2\) коэффициенты \(2\) и \(2\) коэффициенты \(3\). Двенадцать имеет два делителя из \(2\), но только один из \(3\) — так что в нем «не хватает» одного \(3\). Мы умножили числитель и знаменатель \(\dfrac{7}{12}\) на \(3\), чтобы получить эквивалентную дробь со знаменателем \(36\). В восемнадцати отсутствует один множитель \(2\), поэтому вы умножаете числитель и знаменатель \(\dfrac{5}{18}\) на \(2\), чтобы получить эквивалентную дробь со знаменателем \(36\). Мы будем применять этот метод при вычитании дробей в следующем примере.
Двенадцать имеет два делителя из \(2\), но только один из \(3\) — так что в нем «не хватает» одного \(3\). Мы умножили числитель и знаменатель \(\dfrac{7}{12}\) на \(3\), чтобы получить эквивалентную дробь со знаменателем \(36\). В восемнадцати отсутствует один множитель \(2\), поэтому вы умножаете числитель и знаменатель \(\dfrac{5}{18}\) на \(2\), чтобы получить эквивалентную дробь со знаменателем \(36\). Мы будем применять этот метод при вычитании дробей в следующем примере.
Пример \(\PageIndex{8}\): вычесть
Вычесть: \(\dfrac{7}{15} − \dfrac{19}{24}\).
Раствор
Найдите ЖК-дисплей. 15 «отсутствуют» три множителя 2 24 «отсутствует» коэффициент 5 | |
| Перепишите как эквивалентные дроби с помощью ЖК-дисплея. | \(\dfrac{7 \cdot \textcolor{red}{8}}{15 \cdot \textcolor{red}{8}} — \dfrac{19\cdot \textcolor{red}{5}}{24 \cdot \textcolor{red}{5}}\) |
Упростите каждый числитель и знаменатель. | \(\dfrac{56}{120} — \dfrac{95}{120}\) |
| Вычесть. | \(- \dfrac{39}{120}\) |
| Перепишите, указав общий делитель 3. | \(- \dfrac{13 \cdot 3}{40 \cdot 3}\) |
| Удалите общий множитель для упрощения. | \(- \dfrac{13}{40}\) |
Упражнение \(\PageIndex{15}\)
Вычитание: \(\dfrac{13}{24} — \dfrac{17}{32}\).
- Ответить
\(\dfrac{1}{96}\)
Упражнение \(\PageIndex{16}\)
Вычесть: \(\dfrac{21}{32} — \dfrac{9}{28}\).
- Ответить
\(\dfrac{75}{224}\)
Пример \(\PageIndex{9}\): добавить
Добавить: \(- \dfrac{11}{30} + \dfrac{23}{42}\).
Решение
| Найдите ЖК-дисплей. | |
Перепишите как эквивалентные дроби с помощью ЖК-дисплея. | \(- \dfrac{11 \cdot \textcolor{red}{7}}{30 \cdot \textcolor{red}{7}} + \dfrac{23 \cdot \textcolor{red}{5}}{42 \cdot\textcolor{красный}{5}}\) |
| Упростите каждый числитель и знаменатель. | \(- \dfrac{77}{210} + \dfrac{115}{210}\) |
| Доп. | \(\dfrac{38}{210}\) |
| Перепишите, указав общий делитель 2. | \(\dfrac{19 \cdot 2}{105 \cdot 2}\) |
| Удалите общий множитель для упрощения. | \(\dfrac{19}{105}\) |
Упражнение \(\PageIndex{17}\)
Добавить: \(- \dfrac{13}{42} + \dfrac{17}{35}\).
- Ответить
\(\dfrac{37}{210}\)
Упражнение \(\PageIndex{18}\)
Добавить: \(- \dfrac{19}{24} + \dfrac{17}{32}\).
- Ответить
\(-\dfrac{25}{96}\)
В следующем примере одна из дробей содержит переменную в числителе. Выполняем те же действия, что и в случае, когда оба числителя являются числами.
Выполняем те же действия, что и в случае, когда оба числителя являются числами.
Пример \(\PageIndex{10}\): добавить
Добавить: \(\dfrac{3}{5} + \dfrac{x}{8}\).
Решение
Дроби имеют разные знаменатели.
| Найдите ЖК-дисплей. | |
| Перепишите как эквивалентные дроби с помощью ЖК-дисплея. | \(\dfrac{3 \cdot \textcolor{red}{8}}{5 \cdot \textcolor{red}{8}} + \dfrac{x \cdot \textcolor{red}{5}}{8 \ cdot \textcolor{красный}{5}}\) |
| Упростите числители и знаменатели. | \(\dfrac{24}{40} + \dfrac{5x}{40}\) |
| Доп. | \(\dfrac{24 + 5x}{40}\) |
Мы не можем складывать \(24\) и \(5x\), поскольку они не похожи на термы, поэтому мы не можем еще больше упростить выражение.
Упражнение \(\PageIndex{19}\)
Добавить: \(\dfrac{y}{6} + \dfrac{7}{9}\).
- Ответить
\(\dfrac{3y+14}{18}\)
Упражнение \(\PageIndex{20}\)
Добавить: \(\dfrac{x}{6} + \dfrac{7}{15}\).
- Ответить
\(\dfrac{5x+14}{30}\)
Авторы и авторство
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Версия лицензии
- 4,0
- Показать страницу Содержание
- нет
- Теги

Как упростить сложение и вычитание дробей
Страх дробей!Дробь — это новое понятие с совершенно другим обозначением, которое затрудняет понимание учащимися. Одной из причин, по которой студенты находят это утомительным, также является то, что они когда-либо работали только с целыми числами. Поэтому, естественно, дроби кажутся им незнакомыми.
Борьба и вызовы с фракциями реальны.
В Национальной оценке образовательного прогресса, 2005 г. говорится, что «Литература по математическому образованию громогласна в своих выводах о том, что понимание дробей является сложной областью математики для североамериканских учащихся». Именно этот первоначальный страх перед дробями продвигает дальше и делает понимание сложения и вычитания дробей обременительным.
Эта статья поможет учащимся понять, как складывать и вычитать дроби с помощью простых шагов и визуальных моделей. Мы также рассмотрим некоторые приемы, позволяющие упростить сложение и вычитание дробей.
Читайте дальше, чтобы убедиться, что дроби — друзья ваших детей, а не враги!
- Что такое дроби?
- Типы дробей
- Модели для представления дробей
- Как упростить сложение и вычитание дробей
- Шаги по сложению и вычитанию дробей
- Сложение и вычитание дробей – распространенные ошибки
- Обучение дробям с помощью SplashLearn
- Часто задаваемые вопросы
Большинство учебных программ фокусируются на дробях в виде заштрихованных областей или областей, но они выходят за рамки этого. Учащиеся часто рассматривают дроби как процесс деления и закрашивания частей фигур, поэтому они упускают из виду тот факт, что дроби — это числа между целыми числами.
Внимательно посмотрите на изображение линейки ниже. Маркировка между 0 и 1 представляет числа, которые отличаются от целых чисел. Они называются дробями.
Связанное чтение: Блестящие математические цитаты, которыми можно поделиться со студентами, чтобы вдохновить их
Важно подчеркнуть, что дроби — это числа, которые помогают нам быть точными и аккуратными с суммами. У нас не всегда есть один полный килограмм или один полный дюйм при измерении. Поэтому становится критически важным найти способ представления этих «частей», и именно здесь дроби берут на себя ответственность.
Дроби записываются как a/b, где «a» — это число сверху, которое называется числителем. В то время как «b» является числом внизу и называется знаменателем.
Например: Для дроби 1/2; 1 — числитель, 2 — знаменатель.
Студенты часто путают числитель со знаменателем и наоборот. Чтобы запомнить эти запутанные термины, проще всего запомнить их так: D — вниз и D – знаменатель. Так что знаменатель всегда идет вниз!
ТИПЫ Дробей: Наиболее распространенные типы дробей:
Наиболее часто используемые дроби при сложении и вычитании дробей:
Подобные и отличные дроби .
Дроби с одинаковыми знаменателями называются Подобными дробями.
Пример:
Подобные дробиДроби с разными знаменателями называются непохожими дробями .
Пример:
В отличие от дробейЕще один тип дроби, который учащиеся должны знать перед тем, как научиться складывать и вычитать дроби: Эквивалентная дробь
Дроби, имеющие разные числители и знаменатели, но равные одному и тому же значению, называются эквивалентными. Фракции.
Пример:
Все дроби 1/2, 2/4, 3/6 и 4/8 представляют одно и то же значение, равное «ПОЛОВИНЕ». .
Модели для представления фракций:Наиболее распространенные модели для представления фракций:
a) Модель площади:.
Наборы круглых и прямоугольных дробей используются для выработки понимания того, что дроби являются частями целого.
Примеры модели зоны:
модели зоны b) Линейная модель:В линейной модели дроби рассматриваются как длины, а не площади. Числовая линия является важной линейной моделью, позволяющей учащимся воспринимать дроби как числа.
Линейная модель для дроби ¾ будет:
Линейная модель c) Дискретная модель:В дискретной модели под целым понимается набор дискретных объектов. Подмножества этого целого составляют дробные части.
Например, половина класса, 1/3 лотка с яйцами. Счетчики, шарики, кубики или любой другой набор объектов, которые можно посчитать, можно использовать в качестве манипулятора для моделирования дробей.
Как упростить сложение и вычитание дробей ? Работа с дробями > Изучение дробей Первое и главное, что учащиеся должны сделать, изучая сложение и вычитание дробей, — это лучше понимать дроби. Им нужно практиковать дроби, чтобы установить связи с реальным миром, т. е. им нужно складывать листы бумаги, вырезать детали, раскрашивать фигуры и т. д.
Им нужно практиковать дроби, чтобы установить связи с реальным миром, т. е. им нужно складывать листы бумаги, вырезать детали, раскрашивать фигуры и т. д.
Одна из основных проблем с дробями заключается в том, что они не всегда конкретны. Мы начинаем учить дроби с помощью наглядных материалов, но когда дело доходит до операций с дробями, мы переключаемся на правила и процедуры для того же. Механическое заучивание шагов приводит к еще большей путанице.
При сложении дроби мы складываем числители, но не знаменатели. Но при умножении дробей мы умножаем не только числители, но и знаменатели. Это еще больше озадачивает студентов.
Лучше всего использовать визуальные модели, чтобы показать добавление дробей, которые помогут учащимся понять шаги, а не грабить шаги без концептуальной ясности.
Связанное чтение: Наиболее важные математические символы, необходимые учащимся для решения задач
Упражнение:
Чтобы добавить 1/8 и 3/8, возьмите пиццу, разрезанную на 8 ломтиков. из 8 ломтиков,
из 8 ломтиков,
Теперь, если мы сложим или сложим вместе обе дроби/кусочки пиццы, мы получим 3 ломтика из 8 ломтиков пиццы, что означает 3/8.
Конкретный -> Контекстный -> ВычислительныйЧтобы представить новое и сложное понятие, такое как дроби, очень важно предоставить учащимся широкие возможности для его конкретного усвоения. Это означает погружение учащихся в такие занятия, как вырезание бумаги, складывание бумаги, рисование, приготовление пиццы из бумаги, яблоки, шоколадные батончики и т. д. Только используя такой опыт, они смогут увидеть, потрогать и почувствовать концепцию дробей и сделать свои собственные открытия. .
Как только учащиеся получат достаточное количество этого конкретного воздействия, они начнут устанавливать связи между этими объектами и реальным миром.
Много времени должно быть потрачено на создание, изучение, складывание и визуализацию дробей, прежде чем переходить к дробным задачам, связанным с голыми числами.
Например: Прежде чем задать ¼ от 20 =? , мы можем представить реальный сценарий следующим образом:
«У Рона было 20 долларов. Он потратил ¼ из них. Сколько денег у него осталось?»
Это поможет даже учащемуся, плохо разбирающемуся в дробях, начать строить соединения.
Покажите им, «ПОЧЕМУ» правила работаютЕсли представление о дробях как о числах развито хорошо, то легче понять и операции над дробями. Точно так же, как мы складываем и вычитаем числа, можно складывать и вычитать дроби. Важно подчеркнуть концептуальное понимание наряду с процедурным знанием шагов.
Например:
Мы знаем, что 1 яблоко + 1 яблоко = 2 яблока
Точно так же мы можем складывать дроби.
Мы также знаем, что 2 яблока + 3 яблока = 5 яблок
Точно так же мы можем складывать дроби:
Чтобы узнать сумму 2/6 и 3/6; считайте это двумя шестыми и тремя шестыми, которые в сумме дадут пять шестых точно так же, как мы складываем числа.
Теперь давайте рассмотрим пример с вычитанием:
Мы знаем, что 5 яблок – 2 яблока = 3 яблока
Аналогично мы можем вычитать дроби:
В случае «похожих дробей» мы можем просто сложить/вычесть числители и оставить знаменатель прежним. Но мы не можем складывать разные дроби, как складываем одинаковые дроби.
Причина этого очень проста.
Точно так же, как мы не можем сложить 2 яблока и 3 апельсина и сказать, что сумма равна 5 яблок , мы не можем складывать дроби с разными знаменателями. Таким образом, важно сначала определить сложение как комбинацию двух или более одинаковых величин. Точно так же вычитание отнимает подобные единицы количества.
Итак, как складывать/вычитать разные дроби? Давайте посмотрим на это дальше!
Теперь давайте посмотрим на шаги, которые мы можем следовать, чтобы добавить или вычесть фракции:
Шаг 1 : Сделайте знаменатели. То же самое
То же самое
Шаг 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить 2 : Добавить
. или Вычтите числители (сохранив знаменатель)
Шаг 3 : Упростите дробь
Чтобы складывать или вычитать разные дроби, первым делом нужно сделать знаменатели одинаковыми, чтобы числители можно было складывать так же, как мы для подобных дробей.
ШАГ 1: ОДИНАКОВЫЕ ЗНАМЕНАТЕЛИ
Как сделать знаменатели одинаковыми?
В случае одинаковых дробей знаменатели уже будут одинаковыми, поэтому вы можете пропустить шаг 1 и перейти к шагу 2. кратное другому знаменателю
Пример: ½ + ¾
В этом случае – 4 кратно 2. Мы можем умножить 2 на 2, чтобы получить 4, и в результате знаменатели станут одинаковыми. Таким образом, большее число становится общим знаменателем.
Мы можем умножить 2 на 2, чтобы получить 4, и в результате знаменатели станут одинаковыми. Таким образом, большее число становится общим знаменателем.
Применяя:
Таким образом, теперь задача принимает следующий вид:
Если один знаменатель кратен другому, мы можем умножить меньший знаменатель на число (скажем, k) , что даст больший знаменатель. Тогда больший знаменатель становится общим знаменателем.
ii) Если оба знаменателя не имеют общего множителя
Пример: ¼ + ⅗
Связанное чтение: Простые способы сделать математику увлекательной для детей
В этом случае числа 4 и 5 не имеют общих делителей. Мы можем просто перемножить знаменатели, чтобы получить общий знаменатель.
4 х 5 = 20, поэтому 20 является общим знаменателем для обеих дробей.
Если у обоих знаменателей нет общего множителя, то вы умножаете оба знаменателя, чтобы получить общий знаменатель.
Давайте посмотрим, как мы получим 20 в качестве общего знаменателя для обеих дробей:
Если мы умножим знаменатель, мы должны умножить и числитель, чтобы получить эквивалентную дробь.
Итак, теперь задача выглядит следующим образом:
ШАГ 2: СОБЛЮДЕНИЕ/ВЫЧИТАНИЕ ЧИСЛИТОРОВ
Этот шаг довольно прост и прямолинеен. Мы должны сложить/вычесть числители, и результатом их суммы/разности будет новый числитель. Общий знаменатель (как обсуждалось на шаге 1) остается прежним.
Возьмем наши предыдущие примеры и продолжим оттуда:
- ½ + ¾
После того, как знаменатели одинаковы, эта задача выглядит так:
Теперь нам нужно сложить два числителя вместе (2+3=5), чтобы получить новый числитель, в то время как знаменатель (4) остается прежним.
Таким образом, ответ будет 5/4.
- ¼ + ⅗.
После того, как знаменатели одинаковы, эта задача выглядит так:
Теперь нам нужно сложить числители вместе (5 + 12 = 17), чтобы получить новый числитель, в то время как знаменатель (20) остается прежним.
Таким образом, ответ будет 17/20.
ШАГ 3: УПРОЩЕНИЕ Дроби
Ответы, которые мы получили выше, верны, но мы можем упростить дробь до тех пор, пока в числителе и знаменателе не будет общих множителей, кроме 1.
Дробь можно привести к упрощенной форме, удалив общие факторы.
Продолжим наши предыдущие примеры:
И,
В приведенных выше случаях – 5/4 и 17/20 уже упрощенные дроби, так как числитель и знаменатель не имеют общих множителей.
Возьмем несколько примеров дробей, которые можно упростить:
4/12 не упрощается.
4 является общим множителем как в числителе, так и в знаменателе, поэтому его можно привести к упрощенной форме следующим образом:
Обратите внимание: также дроби, записанные в разной (смешанной) форме.
Подытожим эти шаги, взяв по одному примеру сложения и вычитания.
Время попрактиковаться во всех трех шагах вместе!
Задача на сложение: 3/4 + 1/12
Шаг 1: Приведите знаменатели к тому же
Знаменатели равны 4 и 12. 12 кратно 4, поэтому общий знаменатель будет равен 12.
Шаг 3: Упростите дробь
Чтобы упростить 10/12, общий делитель равен 2
Итак, 10/12= 5/6 (в упрощенной форме)
Следовательно, 3/4 + 1/12= 5/6
Теперь давайте рассмотрим задачу на вычитание:
Пример: 2/5 – 1/3
Шаг 1: Совместите знаменатели
Общий знаменатель будет равен 3 x 5 = 15
Шаг 2: Сложите/вычтите числитель 4 9001, сохранив числители одинаковыми. Шаг 3: Упростите дробь 1/15 уже в упрощенной форме, так как 1 и 15 не имеют общих множителей. Очень интересный и полезный метод быстрого сложения/вычитания дробей. В этом методе мы рисуем крылья бабочки, чтобы указать, какие два числа нужно перемножить. Затем мы продолжаем записывать результат в соответствующую антенну. Знаменатели умножаются, а результат записывается внизу живота. В конце мы просто добавляем/вычитаем антенну и пишем ее над брюшком, чтобы получить результат. Учителя должны следить за тем, чтобы учащиеся постепенно переходили от конкретного к контекстуальному и вычислительному уровням. Учащимся нужно дать много примеров, чтобы помочь им преодолеть некоторые распространенные ошибки и неправильные представления: Наиболее распространенная ошибка при сложении дробей — сложение числителей и знаменателей по отдельности, как мы складываем целые числа. Например: при сложении 2/3 и 1/4 распространенной ошибкой является представление каждой дроби, как показано выше, а затем сложение их вместе, чтобы получить 3/7 в качестве ответа. Когда учащиеся складывают, комбинируют или находят сумму, складывая вместе целые числа и обе дробные части, кажется разумным, что они рассматривают каждую дробь независимо друг от друга. Итак, важно подчеркнуть, что дробными частями нельзя манипулировать независимо от их целого. Вот почему важно иметь общий знаменатель. В случае общего знаменателя дроби можно интерпретировать на одной диаграмме и объединять. Давайте посмотрим на этот же пример, но в целом. В этом случае общий знаменатель для 2/3 и 1/4 будет равен 12. Теперь рассмотрим целое, состоящее из 12 частей. Теперь найдем ⅔ и ¼. 2/3 будет 2 из этих 3 равных частей: 2/3 = 8/12 Аналогично, чтобы найти 1/4, мы нужно разделить целое на 4 равные части: 1/4 будет: 1/4 = 3/12
Связанное чтение: Способы умножения чисел всего за секунды
Метод бабочки  Сложение/вычитание числителей и знаменателей
Сложение/вычитание числителей и знаменателей
При сложении/вычитании дробей важно обратить особое внимание на то, как учащиеся представляют их:
, чтобы найти 2/3 первого разделителя целого на 3 равных частей:
2/3 + 1/4 = 8/12+ 3/12 = 11/12
Точно такая же ошибка наблюдается и при вычитании дробей. И числители, и знаменатели вычитаются по отдельности, как вычитаются целые числа.
Например: 5/6 – 1/3 = (5-1)(6-3) = 4/3
Найдем правильный способ решения 5/6 – 1/3 =?
В этом случае общий знаменатель для 5/6 и 1/3 будет равен 6 (общее кратное).
Теперь рассмотрим целое, состоящее из 6 частей:
5/6 будет:
Для 1/3 мы разделим целое на 3 равные части:
1/3 будет одной из этих трех равных частей:
от 5/6 отнимем 1/3, от 5 частей одного и того же целого отнимем 2 части.
5/6 – 1/3 = 5/6 – 2/6 = 3/6
2. Сложение/вычитание числителей без учета знаменателей часто рассматривают их как целые числа.12/13 + 7/8 = 19, потому что 12 + 7 = 19
12/13 – 7/8 = 5, потому что 12 – 7 = 5
Главное здесь – сделать их понимание дробей конкретным , с самого начала.
3. Сложение/вычитание знаменателей без учета числителей Некоторые учащиеся складывают только знаменатели и игнорируют числители. Они смотрят на знаменатели как на два целых числа и складывают/вычитают их.
12/13 + 7/8 = 21, потому что 13 + 8 = 21
13/12 – 7/8 = 5, потому что 13 – 8 = 5
Интересные занятия по сложению и вычитанию дробей дроби. Такие действия, как крестики-нолики, БИНГО или сопоставление, могут быть выполнены, чтобы сделать дроби более увлекательными. Дроби в повседневной жизни
Родители должны поощрять разговоры о дробях с детьми в повседневной жизни. Поощряйте детей применять дроби в повседневных задачах, таких как деление продуктов на равные доли, в измерениях или при приготовлении их любимых новых рецептов. Мы также можем использовать дроби, когда говорим о времени или оценках, которые дети набрали в школе!
Поощряйте детей применять дроби в повседневных задачах, таких как деление продуктов на равные доли, в измерениях или при приготовлении их любимых новых рецептов. Мы также можем использовать дроби, когда говорим о времени или оценках, которые дети набрали в школе!
Рассказывая о дробях, вы избавляетесь от страха перед ними, и детям больше нравится практиковать их.
Игры побуждают учащихся практиковаться в ответах на множество вопросов, которые им обычно не нравятся в других случаях. Ознакомьтесь с этими забавными играми с дробями на SplashLearn
Использование манипулятивных элементов, таких как полоски дробей, модели площадей, кубики лего и числовые линии, делает дроби интересными и увлекательными для детей. Эти манипуляции помогают детям визуализировать дроби и, следовательно, лучше их понимать.
Решение контекстных задач помогает учащимся связать изучение дробей с реальными жизненными ситуациями. Они понимают значение, необходимость и важность дробей и то, как их применять для решения задач. Вы можете проверить эти игры с дробными словами на SplashLearn и сделать дроби намного проще!
Они понимают значение, необходимость и важность дробей и то, как их применять для решения задач. Вы можете проверить эти игры с дробными словами на SplashLearn и сделать дроби намного проще!
- Учащимся важно понимать, что дроби нельзя закрасить и раскрасить.
- Дроби — это числа, которые используются для представления чисел между любыми двумя последовательными целыми числами.
- Помогите учащимся практиковать дроби, вырезая, вставляя и раскрашивая их, чтобы они лучше понимали дроби и весело проводили время с ними.
- Используйте модели дробей, чтобы помочь им визуализировать и понять сложение и вычитание дробей.
- Убедитесь, что они знают, почему шаги сложения/вычитания дробей работают, а не просто слепо применяют шаги.
- Как родитель, используйте дроби в повседневных разговорах, связывайте дроби с контекстом реальной жизни и предоставляйте им примеры из повседневной деятельности, такой как приготовление пищи, выпечка, время и измерения.

Любимое более чем 40 миллионами родителей приложение SplashLearn — это универсальное решение для обучения ваших детей математике и чтению. Вы можете заставить своих маленьких учеников играть в игры на сложение и вычитание дробей или учиться с помощью рабочих листов. Благодаря обучению, согласованному с учебной программой, SplashLearn обеспечивает персонализированный опыт, который адаптируется к потребностям каждого ребенка.
Родители, зарегистрируйтесь бесплатно!
Часто задаваемые вопросы (FAQ)
1. Что такое дроби?
Дроби — это числа между целыми числами (0,1,2,3,4). Они представляют собой часть/часть целого. Дробь состоит из двух частей – числителя и знаменателя.
2. Каковы шаги для сложения и вычитания дробей?
Шаг 1 : Сделать знаменатели одинаковыми
Шаг 2 : Сложить/вычесть числители (сохраняя знаменатель одинаковым)
Шаг 3 : Упростить дробь
3.
 Как складывать и вычитать дроби с разными знаменателями?
Как складывать и вычитать дроби с разными знаменателями?Дроби с разными знаменателями можно складывать путем преобразования их в дроби с одинаковыми знаменателями с помощью эквивалентных дробей.
4. Как складывать и вычитать смешанные числа?
Сначала запишите смешанные числа в виде дробей. Теперь сложите/вычтите так же, как вы делаете это с дробями. В конце не забудьте преобразовать ответ (дробь) в смешанное число!
5. Как складывать и вычитать отрицательные дроби?
Отрицательные дроби можно рассматривать как дроби с отрицательными числителями. Шаги для сложения и вычитания отрицательных дробей остаются такими же, как и для дробей, за исключением того, что теперь детям нужно будет добавлять отрицательные или положительные числители.
Как сложить 3 дроби с разными знаменателями?
Дроби могут быть определены как числа, которые могут быть представлены в виде A/B , где A и B — целые числа, а B не должно быть равно нулю. В дроби верхняя часть называется Числитель , а нижняя часть называется знаменателем .
В дроби верхняя часть называется Числитель , а нижняя часть называется знаменателем .
Примеры: 1/2, 4/5, -2/3 и т. д.
Сложение дробейДля сложения дробей существует правило, которое гласит, что знаменатели складываемых дробей должны быть равны. . Если знаменатели дроби не равны, сделайте их равными, взяв наименьшее общее кратное (НОК) знаменателей.
Как найти LCM?
Чтобы найти НОК чисел (здесь знаменатели), мы будем использовать Метод деления .
Давайте разберемся с этим методом на примере, возьмем два числа 6 и 15 для нахождения НОК методом деления.
Шаг 1: Составьте таблицу, состоящую из левой и правой частей, в правой части укажите числа, НОК которых мы находим.
Шаг 2: Теперь начните с наименьшего числа (не 1) и проверьте, имеет ли любое число из заданных чисел это кратное. В примере 2 — это множитель 6, поэтому используйте его, чтобы разделить 6 в следующей строке.
В примере 2 — это множитель 6, поэтому используйте его, чтобы разделить 6 в следующей строке.
Шаг 3: Теперь во второй строке 3 осталось 15, только множитель 3 равен 3, поэтому разделите его на 3. 3 также является коэффициентом 15, так что разделите 15 также. В результате получается 1, 5.
Шаг 4: Теперь 5 является коэффициентом 5, поэтому делим 5, результат равен 1, 1.
Шаг 5: Процесс завершен, так как мы получаем 1 для всех чисел , теперь умножьте все числа в левой части, которые равны 2, 3, 5, так что кратное из них равно 30.
Сложение 3 дробей с разными знаменателямиШаги для сложения дробей с разными знаменателями:
Шаг 1: Найдите НОК знаменателей.
Шаг 2: Разделите LCM на знаменатель каждого добавляемого числа.
Шаг 3: Умножьте числитель на частное ( найденное на предыдущем шаге).
Шаг 4: Сложите числители, которые мы получаем после умножения с частными, как при простом сложении.
Шаг 5: Знаменатель будет LCM.
Возьмем 3 дроби с разными знаменателями, 1/2, 2/3, 3/4
Шаг 1: Нахождение НОК 2,3,4
Шаг 2: Разделим НОК на знаменатель каждого числа, которое нужно сложить.
LCM = 12, поэтому разделите его на каждое число (знаменатель)
12/2 = 6 частное 1
12/3 = 4 частное 2
12/4 = 3 частное 3
3 Шаг 3:
Умножьте числитель на частное (найденное на предыдущем шаге).Числители равны 1, 2, 3, поэтому умножьте их на соответствующие частные.
1×6 = 6
2×4 = 8
3×3 = 9
Шаг 4: Сложите числители, которые мы получаем после умножения с частными, как простое сложение.
6 + 8 + 9 = 23, что является числителем.
Шаг 5: В знаменателе будет LCM, то есть 12.
Ответ: 23/12
Метод перекрестного умножения , 3/4Шаг 1: Возьмите две дроби за один раз, чтобы взять 1/2 и 2/3
Шаг 2: Сначала мы найдем члены числителя, поэтому мы умножим числитель первого числа на знаменатель первого числа второе число, и аналогичным образом мы умножим числитель второго числа на знаменатель первого числа и сложим оба члена, чтобы получить числитель.
1×3 + 2×2 = 7, что является числителем
Шаг 3: Теперь давайте найдем знаменатель, для этого умножьте знаменатель первого члена на знаменатель второго члена, чтобы получить член знаменателя.
2×3 = 6, что является знаменателем.
Шаг 4: Мы находим новый член, который представляет собой сложение двух дробей, в данном случае новая дробь 7/6.
Шаг 5: Повторите описанную выше процедуру, взяв новую дробь 7/6 и третью дробь 3/4.
Наконец, мы получили ответ, который совпадает с найденным выше.
Примеры вопросов
Вопрос 1: Сложите данные дроби 1/7, 2/7, 3/7.
Ответ:
В данном вопросе знаменатели равны, поэтому просто сложите числители, и знаменатель будет равен 7. 6/7.
Вопрос 2: Найдите LCM 7, 3, 12.
Ответ:
Вопрос 3: Добавить данную фракции, 2/7, 5/12, 10014 . /3.
/3.
Ответ:
Умножьте числитель на частное (найденное на предыдущем шаге).Шаг 1: Нахождение НОК 7,12,3
НОК, которое мы получили, равно 84.
Шаг 2: .
LCM = 84, поэтому разделите его на каждое число (знаменатель)
84/7 = 12 частное 1
84/12 = 7 частное 2
84/4 = 21 частное 3
2 Шаг 3:
Числитель 2, 5, 1, поэтому умножьте их на соответствующие частные.
2×12 = 24
5×7 = 35
1×21 = 21
Шаг 4: Сложите числители, которые мы получим после умножения с частными, как простое сложение.
24 + 35 + 21 = 80, что является числителем. 84
Ответ:
Шаг 1: Нахождение МОК 5,10,3
МОК, которое мы получили, равно 30. быть добавлено.
LCM = 30, поэтому разделите его на каждое число (знаменатель)
30/5 = 6 частное 1
30/10 = 3 частное 2
30/3 = 10 частное 3
2 Шаг 3: Умножьте числитель на частное (найденное на предыдущем шаге).Числители 4, 3, 1, поэтому умножьте их на соответствующие частные.
4×6 = 24
3×3 = 9
1×10 = 10
Шаг 4: Сложите числители, полученные после умножения на частные, как простое сложение.
24 + 9 + 10 = 43, что является числителем.
Шаг 5: Знаменатель будет LCM, поэтому будет 30.
Ответ: 43/30
Вопрос 5: Найдите LCM 7, 3, 12, 13
Ответ:
Вопрос 6: Сложите данные дроби 1/3, 1/4, 1/2 методом перекрестного умножения.
Ответ:
Шаг 1: Возьмем две дроби за раз, так что возьмем 1/3 и 1/4 первое число со знаменателем второго числа, и аналогичным образом мы умножим числитель второго числа на знаменатель первого числа и сложим оба члена, чтобы получить числитель.
1×4 + 1×3 = 7, что является числителем
Шаг 3: Теперь давайте найдем знаменатель, для этого умножьте знаменатель первого члена на знаменатель второго члена, чтобы получить член знаменателя.
3×4 = 12, что является знаменателем.
Шаг 4: Мы находим новый член, который представляет собой сложение двух дробей, в данном случае новая дробь 7/12.
Шаг 5: Снова возьмите 7/12 и третью дробь, которая равна 1/2.
Шаг 6: Нахождение числителя
7×2 + 1×12 = 26, что является числителем
Шаг 7: Нахождение знаменателя
12×2 = 24, что является знаменателем
3
6/4 равно 4 теперь упростив его, мы получим 13/12.
Вопрос 7: Сложите данные дроби 1/5, 2/5, 3/10 методом перекрестного умножения.
Ответ:
Шаг 1: Возьмите две дроби за один раз, поэтому возьмите 1/5 и 2/5
Шаг 2: Сначала мы найдем члены числителя, поэтому мы умножим числитель первого числа на знаменатель второго числа и аналогичным образом умножим числитель второго числа на знаменатель первого числа и сложим оба термина, чтобы получить числитель.


 В данном случае целый ответ – это целая часть смешанного числа.
В данном случае целый ответ – это целая часть смешанного числа.



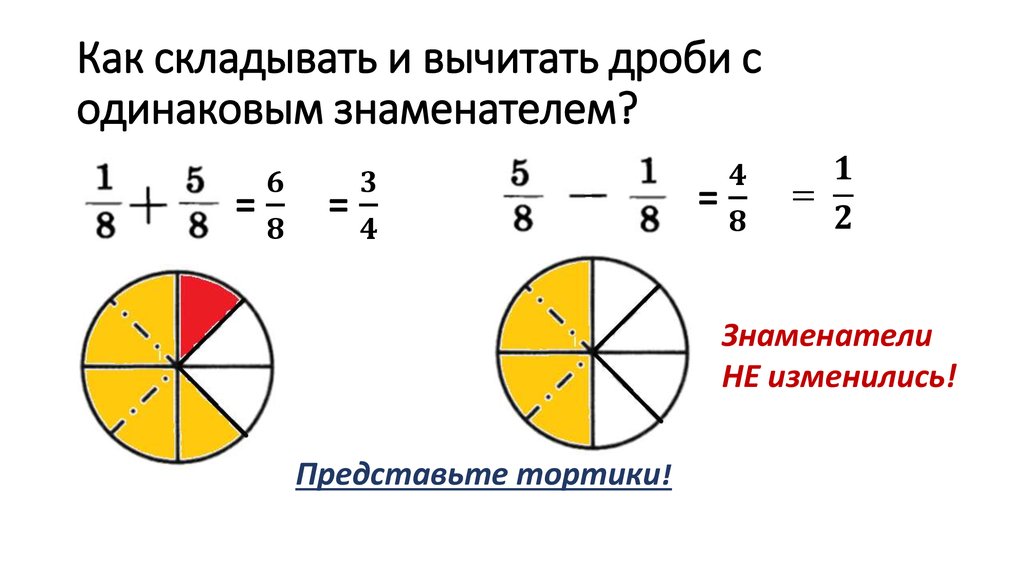

 В нашем примере: 25 ÷ 8 = 3 плюс некоторый остаток. В данном случае целый ответ – это целая часть смешанного числа.
В нашем примере: 25 ÷ 8 = 3 плюс некоторый остаток. В данном случае целый ответ – это целая часть смешанного числа.