деление, умножение, вычитание и сложение обыкновенных дробей.

Как работать с калькулятором обыкновенных дробей?

Калькулятор предназначен для решения простых дробей и дробей с целыми числами (смешанных). В будущем, планируется внедрение функции решения десятичных дробей, но в данный момент она отсутствует.

Для начала работы с дробным калькулятором необходимо понять очень простой принцип ввода данных. Все целые числа вводятся с помощью больших кнопок, расположенных слева. Все числители вводятся с помощью маленьких белых кнопок, расположенных в правом верхнем блоке цифр. Все знаменатели, соответственно, вводятся путем нажатия на кнопки в правом нижнем углу. Данный способ ввода данных является в некотором роде инновационным, поскольку четко разграничивает целое, числитель и знаменатель, что облегчает вычисления, экономит время и делает взаимодействие с приложением более эффективным. », после чего на цифру шесть на основной клавиатуре. В результате, получится готовый пример:

Теперь нажмите на кнопку равно и получите результат калькуляции. В примере выше проиллюстрирован практически весь арсенал возможностей калькулятора дробей. Точно таким же образом, вы можете осуществлять умножение, деление и вычитание дробей, как простых, так и алгебраических, с одинаковыми и разными знаменателями, целыми числами и т.д. Также, калькулятор может вычислить проценты от дробей, что требуется не так часто, но тем не менее очень важно для решения многих актуальных задач.

Если вам требуется сделать положительное число отрицательным, то сначала введите число, а потом нажмите на кнопку «+/-». После этого число или дробь автоматически обернется в скобки с отрицательным значением или наоборот (в зависимости от изначального статуса числа). Если необходимо удалить число, числитель или знаменатель, то воспользуйтесь соответствующей стрелкой Backspace, которая есть в блоке и числителя и знаменателя. Стрелки работают одинаково и по очереди стирают числа или знаки, находящиеся на дисплее калькулятора.

 

Управление калькулятором дробей с клавиатуры.

Использовать калькулятор дробей онлайн можно не только с помощью компьютерной мыши, но и с помощью клавиатуры. Здесь логика очень проста:

1. Все целые числа вводятся как обычно, нажатиями на клавиши чисел.
2. Все числители вводятся с добавлением клавиши CTRL (например, CTRL+1).
3. Все знаменатели вводятся с добавлением клавиши ALT (например, ALT+2).

Действия умножения, деления, сложения и вычитания так же инициируются соответствующими кнопками клавиатуры, если они есть (обычно располагаются в правой части, в так называемой области Numpad). Удаление производится нажатием на клавишу Backspace. Действие очистки (красная кнопка «C») вызывается нажатием на клавишу «C». Квадратный корень – нажатием на соседнюю клавишу «V» . Удаление производится нажатием на клавишу Backspace.

Зачем нужен калькулятор дробей онлайн?

Калькулятор дробей онлайн предназначен для решения обыкновенных и смешанных дробей (с целыми числами). Решение дробей часто требуется школьникам и студентам, а также инженерам и аспирантам. Наш калькулятор предоставляет возможность производить с дробями следующие действия: деление дробей, умножение дробей, сложение дробей и вычитание дробей. Также, калькулятор умеет работать с корнями и степенями, а еще с отрицательными числами, благодаря чему он многократно превосходит аналогичные онлайн приложения.

Калькулятор простых дробей онлайн поможет вам решить примеры с дробями и при этом вам не надо беспокоиться о том, как предварительно сократить дробь. Здесь это сделается автоматически, т.к. приложение само вычисляет общий знаменатель и выдает вам готовый результат на экран.

В чем преимущества такого способа решения дробей?

Калькулятор поддерживает работу со скобками, что позволяет решать дроби даже в сложных математических примерах. В частности, действия со скобками часто требуются при вычислении алгебраических дробей или отрицательных дробей, над которыми постоянно приходится корпеть всем школьникам средних классов. Дополнительно, вы можете использовать этот калькулятор для сокращения дробей или решения дробей с разными знаменателями. Более того, в отличии от многих других бесплатных сервисов, данный калькулятор умеет работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.

Калькулятор обыкновенных дробей полностью бесплатный и не требует регистрации. Вы можете использовать его в любое время дня и ночи. Работать можно с помощью мыши или прямо с клавиатуры (это касается как чисел, так и действий). Мы постарались реализовать максимально удобный интерфейс дробных вычислений, благодаря чему сложные математические калькуляции превратятся для вас в одно удовольствие! 🙂

Please enable JavaScript to view the comments powered by Disqus.

Рациональные числа и действия с ними — что это, определение и ответ

Рациональные числа – это числа, представленные в виде отношения \(\frac{m}{n}\), где m – целое число, а n – натуральное.

Они могут быть как положительными, так и отрицательными.

Целые и дробные числа вместе образуют множество рациональных.

1. Любое целое число является рациональным, потому что его можно записать в виде \(\frac{m}{1}\).

Например:

\(–4 = \frac{- 4}{1}\)

\(2 = \frac{2}{1}\)

\(0 = \frac{0}{1}\)

2. Сумма, разность и произведение двух рациональных чисел – тоже рациональное число. Частное двух рациональных чисел тоже будет рациональным, если знаменатель не равен 0.

3. Любое рациональное число можно записать в виде десятичной или периодической дроби.

Периодическая дробь – это десятичная дробь, в записи которой бесконечное количество раз повторяется цифра или несколько цифр.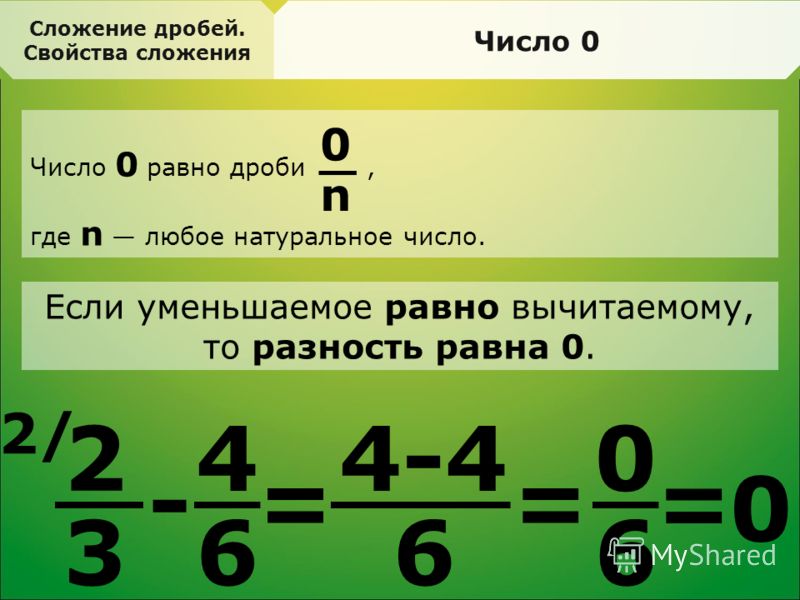

Например:

\(\frac{1}{3} = 0,33333333..\)

Повторяющиеся цифры периодической дроби записывают в скобках, например:

\(\frac{1}{3} = 0,(3)\)

\(\frac{5}{11} = 0,45454545 = 0,(45)\)

СВОЙСТВА РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение:

1. Переместительное свойство:

\(a + b = b + a\)

2. Сочетательное свойство:

\(a + (b + c) = (a + b) + c = (a + c) + b = a + b + c\)

3. Прибавление нуля не меняет рациональное число, а сумма противоположных чисел равна нулю:

\(a + 0 = a\)

\(a + ( — a) = 0\)

Умножение:

1. Переместительное свойство:

\(ab = ba\)

2. Сочетательное свойство:

\(a(bc) = (ab)c = (ac)b = abc\)

3. Умножение на единицу не меняет рациональное число, а произведение обратных чисел равно единице:

\(a \bullet 1 = a\)

\(a \bullet \frac{1}{a} = 1\)

4. Если один из множителей равен нулю, то и всё произведение равно 0:

\(a \bullet 0 = 0\)

\(0 \bullet b = 0\)

\(0 \bullet 0 = 0\)

5. Распределительное свойство:

\((a + b)c = ac + сb\)

ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ

Так как рациональные числа включают в себя блок целых чисел и блок дробных чисел, действия, пройденные в рамках работы с целыми числами, сохраняются и для рациональных чисел. Сравнение, умножение, деление, сложение и вычитание происходит так же, как с целыми числами.

СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Рациональные числа можно представить на координатной прямой, где справа от нуля находятся положительные числа, а слева от нуля – обратные им, отрицательные:

Числа на такой числовой прямой возрастают слева на право, поэтому глядя на прямую можно сказать, какое числе больше.

Например:

1. Сравним числа 1,5 и 4:

Мы знаем, что 4 больше, чем 1,5 и еще раз убедились в этом с помощью числовой прямой.

\(4 > 1,5\)

2. Сравним числа 3,5 и -1:

Если положительные числа справа от нуля, а отрицательные слева, тогда любое положительное числа будет правее отрицательного, а значит будет больше.

\(3,5 > — 1\)

3. Сравним числа -2,5 и -3:

Конечно, 3 больше 2,5, но, когда мы смотрим на отрицательные числа, получается, что -2,5 правее -3, а значит больше.

\(- 2,5 > — 3\)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение рациональных чисел так же можно представить на числовой прямой. Знак «+» означает, что мы двигаемся в положительном направлении (вправо), знак «–» означает, что мы двигаемся в отрицательном направлении (влево).

Например:

1. Найдем сумму положительных чисел 1 + 2,5. Значит от координаты 1 пройдем 2 полных отрезка и ещё половину отрезка в положительном направлении:

Видим, что \(1 + 2,5 = 3,5\).

Сумма положительных чисел – положительное число.

2. Найдем сумму отрицательных чисел -1 + (-2). От координаты -1 пройдем 2 отрезка в отрицательном направлении. При сложении можно опустить знак «+» без изменения знаков слагаемых.

Получилось, что \(- 1 + ( — 2) = — 3.\)

Сумма отрицательных чисел – отрицательное число.

3. Найдем разность положительных чисел 4 – 1,5. Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:

Получилось, что \(4\ –1,5 = 2,5.\)

Сумма положительного и отрицательного числа – положительное число, если из большего вычитают меньшее.

4. Найдем сумму 2 + (-4). От координаты 2пройдем 4 отрезка в отрицательном направлении:

Получим, что \(2–4 = — 2.\)

Сумма положительного и отрицательного числа – отрицательное число, если из меньшего вычитают большее.

5. Найдем разность 1 – (-3). Если нужно пройти в отрицательном направлении дважды, то направление движения станет положительным, то есть 1 – (-3) = 1 + 3:

Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.

6. Найдем сумму двух противоположных чисел 3 + (-3). От координаты 3 пройдем 3 отрезка в отрицательном направлении:

Видим, что \(3 + ( — 3) = 0.\)

Сумма двух противоположных чисел \(\mathbf{= 0.}\)

УМНОЖНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

1. Рациональные числа умножаются и делятся не смотря на знак.

2. Если перемножались или делились числа с одинаковыми знаками, то в результате получается положительное число. Если перемножались числа с разными знаками, то в результате получается отрицательное число.

Например:

\(3 \bullet 4 = 12\)

\(- 6 \bullet ( — \frac{1}{2}) = 3\)

\(7:( — 2) = — 3,5\)

\(- 12:\frac{1}{3} = — 12 \bullet 3 = — 36\)

Вычисления с дробями и целыми числами (8)

Численное и пропорциональное рассуждение‎ > ‎ Вычисления с дробями и целыми числами (8) w3.org/1999/xhtml» cellspacing=»0″> 7.НС.1. Применение и расширение предыдущего понимания сложение и вычитание для сложения и вычитания рациональных чисел; представлять сложение и вычитание по горизонтальному или вертикальному числу линейная схема. 7.НС.2. Применение и расширение предыдущего понимания умножение и деление и дроби умножать и делить рациональное число. Сложение дробей и смешанных чисел 1) При сложении дробей и смешанных чисел должен быть общий знаменатель. Используйте эту таблицу умножения, чтобы найти общий знаменатель! 2) Переименуйте дроби с общим знаменателем (нажмите здесь, если вы забыли, как переименовать дробь). 3) Сложите числители. 4) Оставьте знаменатель прежним. 5) Сложите целые числа вместе. 6) По возможности упростите решение. Если числитель больше знаменателя, превратите его в смешанное число и прибавьте его к целому числу. Если дробь можно сократить на общий множитель, упростите дробь. Вычитание дробей и смешанных чисел 1) При вычитании дробей должен быть общий знаменатель. 2) Переименуйте дроби с общим знаменателем (нажмите здесь, если вы забыли, как переименовать дробь). 3) Посмотрите, сможете ли вы вычесть числители. Если возможно, вычтите числители. Если это невозможно, заимствуйте из целого числа, а затем вычтите. 4) Оставьте знаменатель прежним. 5) По возможности упростите решение. Если дробь можно сократить на общий множитель, упростите дробь. Умножение дробей и смешанных чисел 1) Превратите все смешанные числа в неправильные дроби. (нажмите здесь, если вы забыли, как переименовывать неправильные дроби). 2) Посмотрите, можно ли уменьшить перекрестные произведения. 3) После сокращения перекрестных произведений умножьте два числителя, получив новый числитель. умножьте два знаменателя, получив новый знаменатель. 4) Упростите решение, если это возможно. Если числитель больше знаменателя, преобразовать его в смешанное число. Если дробь можно сократить на общий множитель, упростите дробь. ПРАКТИКА ЗДЕСЬ 1) Превратите все смешанные числа в неправильные дроби. 2) Перепишите задачу следующим образом: Оставив первую дробь как есть. (Сохранить) Замена знака деления на знак умножения. (Изменить) Преобразование второй дроби в обратную. (Перевернуть) 3) Решите задачу, выполнив действия по умножению дробей. ПРАКТИКА ЗДЕСЬ Вернуться к началу Посмотрите следующее видео, в котором повторяются навыки, необходимые для сложения, вычитания, умножения и деления дробей. ПРАКТИКА ЗДЕСЬ (все навыки дроби) (Выберите «случайный оператор» и наибольшее число «20», прежде чем нажать «Перейти») Вернуться к началу

Видео с вопросами: сложение дробей с целыми или линейными алгебраическими выражениями для числителей и различными линейными алгебраическими выражениями для знаменателей

Стенограмма видео

Напишите четыре над 𝑥 плюс один плюс два 𝑥 над двумя 𝑥 плюс три в виде одной дроби в простейшем виде.

Чтобы решить эту задачу, мы видим, что на самом деле у нас есть две алгебраические дроби и мы хотим добавить их. Как и в случае с любым типом дроби, когда вы хотите сложить дроби, вам нужно найти общий знаменатель.

И один метод, который мы действительно можем использовать, — это метод перекрестного умножения, который позволяет нам складывать наши дроби.

Итак, у нас есть две дроби 𝑎 над 𝑏 плюс 𝑐 над 𝑑, тогда мы умножить 𝑎 на 𝑑 — так мы получим 𝑎𝑑 — плюс 𝑐 умножить на 𝑏 — так что 𝑐𝑏. А затем вы умножаете два знаменателя — так что 𝑏 на 𝑑. Таким образом, мы получаем 𝑏𝑑. Хорошо, здорово, так что это на самом деле метод. Это поможет нам решить нашу проблему. Итак, давайте сложим наши алгебраические дроби.

Итак, мы можем сказать, что четыре больше 𝑥 плюс один плюс два 𝑥 больше двух 𝑥 плюс три быть равным четырем умножить на два 𝑥 плюс три плюс два 𝑥 умножить на 𝑥 плюс одна причина опять крестим умножаем на все 𝑥 плюс один умножаем на два 𝑥 плюс три. Хорошо, отлично, мы завершили первый шаг.

Итак, что мы собираемся сделать, так это раскрыть скобки в числителе. Итак, мы получим восемь 𝑥, так как четыре умножили на два 𝑥 плюс 12, потому что мы четыре умножить на три плюс два 𝑥 в квадрате, потому что два 𝑥 умножить на 𝑥 дает нам два 𝑥 в квадрате плюс два 𝑥, а затем все кончено 𝑥 плюс один умножить на два 𝑥 плюс три.

Итак, теперь мы можем упростить наш числитель. Таким образом, мы получаем два 𝑥 в квадрате плюс 10𝑥 плюс 12 сверх 𝑥 плюс один, умноженный на два 𝑥 плюс три. И мы получили это, потому что мы на самом деле объединили похожие термины, которые могли. Итак, у нас было восемь 𝑥 плюс два 𝑥, что дало нам 10𝑥. Хорошо, отлично, теперь мы записали это как одну дробь. Но в простейшей ли форме?

Ну, на самом деле, я думаю, есть еще один шаг, который мы можем сделать, потому что мы действительно можем сделать множитель из нашего числителя. И это дает нам два, умноженные на 𝑥 в квадрате плюс пять 𝑥 плюс шесть, потому что два — это множитель каждого из наших терминов над 𝑥 плюс один, умноженный на два 𝑥 плюс три. Но является ли это окончательным ответом? Ну, на самом деле, если мы посмотрим на это сейчас, мы действительно увидим, что мы попали в числитель квадратный, который мы можем фактически факторизовать. Что ж, давайте быстро посмотрим, как мы собираемся это сделать.