Сложение дробей с разными знаменателями 5 класс. Решено
Как складывать дроби с разными знаменателями?
Правила сложения дробей с разными знаменателями
Правила сложения дробей с разными знаменателями:
1. Найти наименьший общий знаменатель дробей;
2. Привести дроби к наименьшему общему знаменателю;
3. Сложить числители дробей, а знаменатель оставить неизменным.
Пример сложения дробей с разными знаменателями
Сложить две дроби
| 1 | + | 3 |
|---|---|---|
| 4 | 8 |
У этих двух дробей разные знаменатели. Мы можем складывать только дроби с одинаковыми знаменателями. Поэтому нужно привести дроби к общему знаменателю.
1. Найти наименьший общий знаменатель дробей.
Как найти общий знаменатель дробей?
Сначала находим НОК (наименьшее общее кратное) чисел 4 и 8 (это знаменатели наших дробей).
Число 8 делится на 4.
Отсюда сразу делаем вывод, что 8 есть наименьшее общее кратное чисел 8 и 4.
Ответ: нок чисел 4 и 8 равен 8:
НОК(4, 8) = 8
Полученный результат 8 и есть общий знаменатель данных двух дробей.
2. Привести дроби к общему знаменателю.
Как привести дроби к общему знаменателю?
Наш общий знаменатель равен 8.
У второй дроби знаменатель уже равен 8, её оставляем неизменной.
У первой дроби знаменатель равен 4. Её нужно привести к знаменателю 8.
Делим 8 на 4:
8 : 4 = 2
2 есть дополнительный множитель.
Умножаем и числитель, и знаменатель первой дроби на дополнительный множитель:
| 1 * 2 | = | 2 |
|---|---|---|
| 4 * 2 | 8 |
Таким образом мы привели первую дробь к общему знаменателю 8.
Запишем всё вместе:
| 1 | + | 3 | = | 1 * 2 | + | 3 | = | 2 | + | 3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 8 | 4 * 2 | 8 | 8 | 8 |
Теперь мы имеем две дроби с одинаковыми знаменателями.
3. Сложить числители дробей, а знаменатель оставить неизменным.
Складываем только числители полученных дробей с общим знаменателем:
| 2 | + | 3 | = | 5 |
|---|---|---|---|---|
| 8 | 8 | 8 |
Запишем всё вместе:
| 1 | + | 3 | = | 1 * 2 | + | 3 | = | 2 | + | 3 | = | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 8 | 4 * 2 | 8 | 8 | 8 | 8 |
Итак, ответ:
| 1 | + | 3 | = | 5 |
|---|---|---|---|---|
| 4 | 8 | 8 |
Сложение смешанных дробей – примеры (5 класс, математика)
4.6
Средняя оценка: 4.6
Всего получено оценок: 225.
4.6
Средняя оценка: 4.6
Всего получено оценок: 225.
Сложение смешанных дробей представляет собой достаточно сложную тему в рамках математики 5 класса. Проблема в том, что для правильного сложения нужно знать целый набор тем: сложение целых чисел, сложение дробей, смешанные числа. Поэтому, чтобы не допускать досадных ошибок, рассмотрим сложение смешанных дробей.
Что такое смешанная дробь?
Смешанной дробью зовут число, у которого есть целая и дробная части. В примерах целое число, зачастую, преобразуют в неправильную дробь, чтобы не допустить ошибок. Однако умение складывать и вычитать смешанные дроби позволяет куда быстрее решать большие примеры. А скорость вычислений крайне важна при сдаче экзаменов.
Чтобы перевести смешанную дробь в неправильную, нужно умножить целую часть на знаменатель, и прибавить числитель. Так получается числитель неправильной дроби. Знаменатель у неправильной дроби будет тот же, что у дробной части смешанного числа.
Сложение дробей
Перед тем, как говорить о сложении смешанных дробей, поговорим о сложении обыкновенных дробей. Для того, чтобы сложить дроби, требуется привести их к одинаковому знаменателю. Чтобы общий знаменатель дроби, требуется определить НОК двух знаменателей.
Так как НОК может определяться не только для 2, но и для 3, и более чисел, иногда удобнее найти общий знаменатель для всего выражения сразу.
После того, как найден общий знаменатель, числитель и знаменатель каждой дроби домножают так, чтобы у всех слагаемых в знаменателе образовался найденный НОК. Эта процедура называется приведением к общему знаменателю.
После этого числители складываются, при необходимости выделяется целая часть неправильной дроби и сокращается знаменатель.
Сложение смешанных дробей
У смешанных чисел есть две части: целая и дробная. Сложение каждой из частей производится отдельно. Дробную часть временно отделяют от целой и выполняют сложение по всем правилам сложения дробей. После того, как сложение выполнено, части снова соединяют. То есть получившаяся целая часть записывается рядом с результатом сложения дробей.
После того, как сложение выполнено, части снова соединяют. То есть получившаяся целая часть записывается рядом с результатом сложения дробей.
Может возникнуть ситуация, когда результатом сложения дробных частей чисел, станет неправильная дробь. У такой неправильной дроби выделяют целую часть и прибавляют ее к сумме целых частей слагаемых.
Рассмотрим небольшой простой пример:
$$11 {6\over{7}}+ 1 {9\over{11}}$$
Сложим целые части:
11+1=12
Сложим дробные части:
$${6\over{7}}+{9\over{11}}={{6*11}\over{77}}+{{9*7}\over{77}}={{66+63}\over{77}}={129\over{77}}=1 {52\over{77}}$$
Добавим к сумме целых чисел получившуюся 1:
12+1=13
Запишем результат:
$$11 {6\over{7}}+ 1 {9\over{11}}=13 {52\over{77}}$$
Что мы узнали?
Мы поговорили о сложении смешанных дробей. Рассмотрели отдельно сложение дробных частей смешанных чисел. Рассказали о том, как складывать смешанные дроби целиком. Рассмотрели небольшой пример сложения смешанных дробей.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Булат Зинуров
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 225.
А какая ваша оценка?
Сложение смешанных дробей — шаги, правила
Сложение смешанных дробей
| 1. | Сложение смешанных чисел с одинаковыми знаменателями |
| 2. | Сложение смешанных чисел с разными знаменателями |
| 3. | Добавление смешанных дробей и правильных дробей |
4. | Часто задаваемые вопросы о добавлении смешанных фракций |
Сложение смешанных чисел с одинаковыми знаменателями
Сложение смешанных чисел с одинаковыми знаменателями означает сложение тех смешанных дробей, у которых одинаковые знаменатели. Например, \(2\dfrac{2}{3}\), \(1\dfrac{1}{3}\) — смешанные дроби с одинаковыми знаменателями. Эти смешанные фракции можно сложить, используя обычные правила сложения фракций. Однако нам необходимо отметить несколько фактов о смешанных дробях, которые помогут нам легко решить эти вопросы. Вот список нескольких моментов, которые необходимо учитывать при добавлении смешанных дробей лучшим способом:
- Смешанная дробь \(a\dfrac{b}{c}\) также может быть записана как + (b/c)
- Чтобы преобразовать смешанное число в неправильную дробь, нужно умножить целое число на знаменатель правильной дроби и прибавить результат к числителю правильной дроби, сохранив знаменатель. Например, чтобы преобразовать \(1\dfrac{4}{7}\) в неправильную дробь, мы умножаем 1 и 7, т.
 е. 1 × 7 = 7, и результат прибавляем к 4, т. е. 7 + 4 = 11. Таким образом, смешанная дробь превращается в неправильную дробь и записывается как 11/7.
е. 1 × 7 = 7, и результат прибавляем к 4, т. е. 7 + 4 = 11. Таким образом, смешанная дробь превращается в неправильную дробь и записывается как 11/7. - Чтобы преобразовать неправильную дробь в смешанное число, нужно разделить числитель неправильной дроби на ее знаменатель. Частное становится целой частью числа, остаток становится числителем правильной дроби, а знаменатель остается прежним. Например, чтобы преобразовать 13/6 в смешанное число, мы сначала разделим 13 на 6 и получим частное как 2, а остаток как 1. Таким образом, когда 13/6 преобразуется в смешанную дробь, получается \(2\dfrac {1}{6}\)
Давайте рассмотрим пример, чтобы понять, как складывать смешанные дроби с одинаковыми знаменателями.
Пример: Добавьте смешанные дроби \(2\dfrac{2}{3}\) + \(1\dfrac{1}{3}\)
Это можно решить двумя способами.
Метод 1
- Шаг 1: Сначала складываются целые числа обеих дробей, т.
 е. 2 + 1 = 3
е. 2 + 1 = 3 - Шаг 2: Теперь дробные части обоих чисел складываются, т. е. (2/3) + (1/3) = 3/3
- Шаг 3: Результат, полученный на шаге 2, при необходимости следует преобразовать в простейшую форму, т. е. 3/3 = 1
- Шаг 4: Теперь складываем результаты шага 1 и шага 3, т. е. 3 + 1 = 4
Следовательно, результат равен \(2\dfrac{2}{3}\) + \(1\dfrac{1}{3}\) = 4
Метод 2
Теперь давайте решить этот вопрос, используя второй метод, который является основным методом сложения дробей.
Пример: Складываем смешанные дроби \(2\dfrac{2}{3}\) + \(1\dfrac{1}{3}\)
Решение: Преобразуем смешанные дроби в неправильные дроби.
- Шаг 1: Преобразуйте обе смешанные дроби в неправильные дроби. Следовательно, \(2\dfrac{2}{3}\) станет 8/3; и \(1\dfrac{1}{3}\) станет 4/3
- Шаг 2 : Сложите дроби, добавив числители, потому что знаменатели одинаковы.

- Шаг 3: При необходимости уменьшите дробь. Это станет 12/3 = 4. Следовательно, \(2\dfrac{2}{3}\) + \(1\dfrac{1}{3}\) = 4,
Сложение смешанных чисел с разными знаменателями
Смешанные дроби с разными знаменателями – это группа таких смешанных дробей, у которых разные знаменатели. Давайте научимся складывать смешанные дроби с разными знаменателями на примере с помощью следующих шагов.
Пример: Сложите смешанные дроби с разными знаменателями: \(3\dfrac{1}{4}\) + \(6\dfrac{1}{2}\)
Решение:
- Шаг 1: Сначала мы преобразуем данные дроби в неправильные дроби, т. е. \(3\dfrac{1}{4}\) = 13/4 и \(6\dfrac{1}{2}\) = 13/2
- Шаг 2: Теперь дроби можно записать так: (13/4) + (13/2)
- Шаг 3: Знаменатели разные, поэтому нам нужно найти наименьшее общее кратное (НОК) знаменателей, т.
 е. НОК 2 и 4 = 4.
е. НОК 2 и 4 = 4. - Шаг 4: С помощью НОК мы запишем их соответствующие эквивалентные дроби так, чтобы они стали похожи на дроби. Знаменатель первой дроби уже равен 4, поэтому он останется прежним, т.е. д., 13/4. Но вторая дробь изменится на 26/4 .
- Шаг 5: Теперь у нас есть обе дроби с одинаковыми знаменателями, то есть они были преобразованы в одинаковые дроби. Итак, мы можем их сложить, т. е. (13/4) + (26/4) = (13 + 26)/4 = 39./4
- Шаг 6: Эту неправильную дробь (39/4) можно преобразовать в смешанную дробь следующим образом: 39/4 = \(9\dfrac{3}{4}\)
Следовательно, результат \(3\dfrac{1}{4}\) + \(6\dfrac{1}{2}\) = \(9\dfrac{3}{4}\)
Другой способ сложения смешанных дробей с разными знаменателями состоит в том, чтобы сначала сложить целые части данных дробей, а затем сложить правильные дроби. Например, \(3\dfrac{1}{4}\) + \(6\dfrac{1}{2}\) = (3 + 6) + (1/4 + 1/2). Ее можно решить следующим образом.
= 9 + (1/4 + 2/4) (поскольку НОК 2 и 4 равно 4)
= 9 + 3/4
= \(9\dfrac{3}{4}\)
Таким образом, для добавления смешанных фракций можно использовать любой из двух вышеперечисленных методов.
Добавление смешанных дробей и правильных дробей
Добавление смешанных дробей и правильных дробей включает ту же процедуру, за исключением нескольких изменений. Давайте разберемся в этом на следующих примерах.
Случай 1: Смешанная дробь и правильная дробь, имеющие одинаковый знаменатель.
Пример: Добавьте смешанную дробь и правильную дробь \(3\dfrac{2}{5}\) + 1/5
Обратите внимание, что \(3\dfrac{2}{5}\) = 3 + (2/5). Следовательно,
\(3\dfrac{2}{5}\) + (1/5) = 3 + (2/5) + (1/5)
= 3 + (3/5)
= \(3\dfrac{3}{5}\)
Следовательно, \(3\dfrac{2}{5}\) + (1/5) = \(3\dfrac{3}{5}\)
Случай 2: Смешанная дробь и правильная дробь с разными знаменателями.
Пример: Добавьте смешанную дробь и правильную дробь \(5\dfrac{1}{2}\) + 2/3
\(5\dfrac{1}{2}\) + 2/3
= (11 /2) + (2/3) [Мы преобразовали \(5\dfrac{1}{2}\) в неправильную дробь, 11/2]
= [(11 × 3) / (2 × 3) ] + [(2 × 2) / (3 × 2)] [Поскольку НОК 2 и 3 равен 6]
= (33/6) + (4/6)
= 37/6
= \ (6\dfrac{1}{6}\)
Следовательно, \(5\dfrac{1}{2}\) + 2/3 = \(6\dfrac{1}{6}\).
☛ Статьи по теме
- Вычитание смешанных дробей
- Сложение дробей
- Вычитание дробей
- Сложение дробей с разными знаменателями
- Вычитание дробей с разными знаменателями
- Сложение и вычитание дробей
Добавление смешанных чисел Примеры
Пример 1: Добавьте смешанные дроби \(4\dfrac{1}{7}\) и \(5\dfrac{4}{7}\)
Решение: Для данных смешанных дробей \(4\dfrac{1}{7}\) и \(5\dfrac{4}{7}\) мы будем использовать концепцию сложения смешанных дробей с подобными знаменатели.
 Так как знаменатели одинаковые, мы будем складывать целые числа отдельно и дроби отдельно и объединять их результат, чтобы получить окончательный ответ.
Так как знаменатели одинаковые, мы будем складывать целые числа отдельно и дроби отдельно и объединять их результат, чтобы получить окончательный ответ.\(4\dfrac{1}{7}\) + \(5\dfrac{4}{7}\)
= (4 + 5) + (1/7 + 4/7)
= 9 + (5/7)
= \(9\dfrac{5}{7}\)
Таким образом, значение \(4\dfrac{1}{7}\) + \(5\dfrac{ 4}{7}\) = \(9\dfrac{5}{7}\)
Пример 2: Райан хочет сшить рубашку и имеет \(20\dfrac{2}{3}\) м ткани. Он понимает, что ему нужно еще \(7\dfrac{3}{4}\) м ткани, чтобы сшить рубашку. Какова общая длина ткани, которая ему нужна?
Решение: Общая длина ткани, необходимой для сшивания рубашки, равна сумме \(20\dfrac{2}{3}\) и \(7\dfrac{3}{4}\ ). Мы будем использовать концепцию сложения смешанных дробей с разными знаменателями, чтобы найти результат. Поскольку \(20\dfrac{2}{3}\) и \(7\dfrac{3}{4}\) имеют разные знаменатели, поэтому мы сначала преобразуем эти смешанные дроби в неправильные дроби.
 Итак, \(20\dfrac{2}{3}\) = 62/3 и \(7\dfrac{3}{4}\) = 31/4, и теперь нам нужно добавить 62/3 + 31/4. . Поскольку знаменатели не являются общими, найдем НОК их знаменателей и сделаем их похожими на дроби.
Итак, \(20\dfrac{2}{3}\) = 62/3 и \(7\dfrac{3}{4}\) = 31/4, и теперь нам нужно добавить 62/3 + 31/4. . Поскольку знаменатели не являются общими, найдем НОК их знаменателей и сделаем их похожими на дроби.НОК 3 и 4 равно 12
62/3 = (62 × 4) / (3 × 4) = 248/12
31/4 = (31 × 3) / (4 × 3) = 93/ 12
После их сложения получаем,
(248/12) + (93/12)
= 341/12
= \(28\dfrac{5}{12}\)
Следовательно, общая длина ткани, необходимой для сшивания рубашки будет \(28\dfrac{5}{12}\) м.
Пример 3: Укажите верно или неверно в отношении добавления смешанных фракций.
а.) \(2\dfrac{1}{2}\) + 1/2 = 3
б.) \(2\dfrac{1}{2}\) + 1 = \(2\dfrac {1}{2}\)
Решение:
а.) Верно, \(2\dfrac{1}{2}\) + 1/2 = 3, поскольку знаменатели одинаковы, мы можем добавить дроби легко. 2 + 1/2 + 1/2 = 2 + 1 = 3
b.) Неверно, \(2\dfrac{1}{2}\) + 1 = \(3\dfrac{1}{2}\), потому что, когда мы складываем целые числа, мы получаем 2 + 1 = 3 а дробь равна 1/2, поэтому сумма равна \(3\dfrac{1}{2}\), а не \(2\dfrac{1}{2}\)
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Практические вопросы по сложению смешанных дробей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о добавлении смешанных фракций
Как складывать смешанные номера?
Смешанные фракции можно добавлять разными способами. Если смешанные дроби имеют одинаковые знаменатели, то целая и дробная части могут быть сложены отдельно и объединены для получения результата. Для смешанных дробей с разными знаменателями их сначала преобразуют в неправильные дроби. После этого нам нужно сделать знаменатели одинаковыми, поэтому мы находим их НОК, преобразуем их в соответствующие эквивалентные дроби, а затем складываем числители.
Как складывать смешанные дроби с целыми числами?
Чтобы сложить смешанные дроби с целыми числами, мы складываем целую числовую часть смешанной дроби с заданным целым числом и, наконец, объединяем ее с дробной частью, чтобы получить результат.
Например, \(3\dfrac{3}{5}\) + 4
= 3 + (3/5) + 4
= (3 + 4) + (3/5)
= 7 + (3/5)
= \(7\dfrac{3}{5}\)
Это также можно решить, преобразовав смешанное число в неправильную дробь, а затем дроби можно сложить, используя обычный метод сложения дробей.
Каковы этапы сложения дробей и смешанных дробей?
Действия по добавлению фракций и смешанных фракций можно понять с помощью следующего примера. Например, добавим \(5\dfrac{4}{7}\) + (1/7)
- Шаг 1: Преобразуем смешанную дробь в неправильную. Здесь \(5\dfrac{4}{7}\) станет (39/7) .
- Шаг 2: Теперь проверьте, совпадают ли знаменатели. Здесь оба знаменателя одинаковы. (39/7) + (1/7)
- Шаг 3: Если да, сложите числители обеих дробей и запишите результат над общим знаменателем. Итак, (39/7) + (1/7) = 40/7
- Шаг 4: Если знаменатели не совпадают, найдите НОК знаменателей, чтобы сделать их равными, и выполните шаг 3.
 Этот шаг не нужен, поскольку знаменатели одинаковы.
Этот шаг не нужен, поскольку знаменатели одинаковы. - Шаг 5: Предыдущий шаг дает результат в виде неправильной дроби. Превратите его в смешанную дробь. Итак, 40/7 = \(5\dfrac{5}{7}\)
Как сложить смешанные дроби с правильными дробями?
Смешанные фракции могут быть легко добавлены с правильными фракциями. Нам просто нужно преобразовать смешанные дроби в неправильные дроби, а затем сложить их по тем же правилам. Например, добавим \(2\dfrac{2}{5}\) + 3/5, выполнив следующие шаги:
- Преобразуем смешанную дробь в неправильную дробь. Таким образом, \(2\dfrac{2}{5}\) станет (12/5) .
- Теперь проверим, совпадают ли одинаковые знаменатели. Если знаменатели совпадают, их числители можно просто сложить. Если они не совпадают, то находим их НОК, переводим в эквивалентные дроби и затем складываем. В этом случае знаменатели совпадают, поэтому их числители можно сложить. Здесь 12/5 + 3/5 = 15/5. Затем эту сумму можно упростить до наименьшей формы.
 Итак, 15/5 = 3,9.0042
Итак, 15/5 = 3,9.0042
Каковы шаги сложения смешанных дробей с одинаковыми знаменателями?
Сложение смешанных дробей с одинаковым знаменателем может быть легко выполнено путем объединения целых чисел отдельно и дробных частей отдельно. Затем они складываются и объединяются, чтобы получить окончательный ответ.
Например, добавим \(6\dfrac{1}{6}\) + \(2\dfrac{4}{6}\)
= (6 + 2) + (1/6) + (4/6)
= 8 + (5/6)
= \(8\dfrac{5}{6}\)
Как сложить смешанные дроби с разными знаменателями?
Сложение смешанных дробей с разными знаменателями осуществляется путем преобразования смешанных дробей в неправильные дроби. Затем мы находим их НОК, преобразуем их в эквивалентные дроби и добавляем числители. Наконец, сумма преобразуется обратно в смешанную дробь.
Например, добавим \(4\dfrac{5}{8}\) + \(3\dfrac{1}{2}\)
= (37/8) + (7/2)
= (37/8) + (28/8)
= 65/8
= \(8\dfrac{1}{8}\)
Как складывать и вычитать смешанные дроби?
Сложение и вычитание смешанных дробей производится аналогичным образом. Смешанные дроби преобразуются в неправильные дроби, а затем складываются или вычитаются по обычным правилам.
Смешанные дроби преобразуются в неправильные дроби, а затем складываются или вычитаются по обычным правилам.
Скачать БЕСПЛАТНЫЕ учебные материалы
Сложение смешанных дробей Рабочие листы
Сложение смешанных чисел с разными знаменателями
Сложение смешанных чисел
Смешанное число — это тип дроби, который состоит из двух частей: целого числа и правильной дроби. Он также известен как смешанная фракция.
Обычно смешанное число представляет собой число между любыми двумя целыми числами. Мы часто сталкиваемся с примерами смешанных чисел в нашей повседневной жизни.
Рассмотрим дробь $3\frac{5}{8}$. Он состоит из целого числа 3 и дробной части $\frac{5}{8}$. Поскольку дробная часть $\frac{5}{8}$ имеет числитель 5, что меньше знаменателя 8, она представляет собой правильную дробь.
Итак, дробь $3\frac{5}{8}$ представляет собой смешанное число.
Как складывать смешанные числа?
Для сложения смешанных чисел (или сложения смешанных дробей) мы берем целые числа и дроби и складываем их отдельно. Затем мы соединяем их.
Затем мы соединяем их.
Давайте разберемся с этим на примере.
Пример. Найдите сумму $2\frac{1}{8}$ и $3\frac{3}{8}$.
Здесь мы должны сложить два смешанных числа.
Первое число $2\frac{1}{8}$.
Второе число $3\frac{3}{8}$.
Визуально две дроби при сложении будут выглядеть так:
Теперь давайте посмотрим, как мы можем сложить числа $2\frac{1}{8}$ и $3\frac{3}{8}$ без помощи моделей.
Сначала складываем целые части обоих смешанных чисел.
Здесь целыми являются 2 и 3. Давайте сначала сложим их.
2 + 3 = 5
А теперь добавим дробные части.
Дробные части: $\frac{1}{8}$ и $\frac{3}{8}$. Складываем их так, как мы складывали бы две одинаковые дроби, прибавляя числитель к числителю и знаменатель к знаменателю.
$\frac{1}{8} + {3}{8}$
$= \frac{1 + 3}{8}$
$= \frac{4}{8}$
Сейчас что у нас есть отдельные суммы целых и дробей, мы сложим их вместе.
Итак, мы получаем $2\frac{1}{8} +3\frac{3}{8} =5\frac{4}{8}$
Теперь рассмотрим пример сложения двух смешанных чисел. где наша результирующая дробь не является правильной дробью.
где наша результирующая дробь не является правильной дробью.
Например, предположим, что в одной корзине $2\frac{4}{5}$ фунтов яблок, а в другой — $3\frac{3}{5}$ фунтов. Сколько всего яблок в обеих корзинах?
Здесь, чтобы найти количество яблок в обеих корзинах, мы складываем смешанные числа $2\frac{4}{5}$ и $3\frac{3}{5}$. Знаменатели обеих дробных частей одинаковы. Итак, чтобы сложить смешанные числа с одинаковыми знаменателями, мы складываем целые части вместе и дробные части вместе, а затем объединяем сумму двух, как показано ниже:
Складываем целую часть с целой частью и дробную часть с дробной часть.
Если сумма дробных частей является неправильным числом, преобразуйте его в другое смешанное число.
Объединить сумму целых и дробей.
Следовательно, имеется $6\frac{2}{5}$ фунтов яблок.
Математически это сложение будет выглядеть так:
$2\frac{4}{5} +3\frac{3}{5} = 2 + 3 + \frac{4}{5} + \frac{3 {5}$
$= 5 + \frac{7}{5}$
$= 5 + 1\frac{2}{5}$
$= 6\frac{2}{5}$
Сложение смешанных чисел с разными знаменателями
Теперь давайте рассмотрим пример, чтобы понять сложение смешанных чисел с разными знаменателями.
Предположим, что у Сьюзан есть $1\frac{4}{7}$ унций апельсинового сока, а у Кита $2\frac{2}{5}$ унций апельсинового сока. Сколько апельсинового сока у них всего?
Здесь мы найдем ответ, сложив смешанные числа $1\frac{4}{7}$ и $\frac2{2}{5}$. Здесь знаменатели обеих дробных частей разные.
Чтобы сложить смешанные числа с разными знаменателями, лучше всего преобразовать оба смешанных числа в неправильные дроби, а затем сложить их точно так же, как мы складываем две разные дроби.
Шаг 1: Преобразуйте смешанные числа в неправильные дроби.
и
Шаг 2. Сложите неправильные дроби.
Здесь нужно сложить разные дроби $\frac{11}{7}$ и $\frac{12}{5}$
Кратные 7: 14, 21, 28, 35 , 42
Кратно 5: 5, 10, 15, 20, 25, 20, 35 .
Таким образом, НОК равно 35.
Теперь преобразуем дроби в эквивалентные дроби со знаменателем в виде НОК.
$\frac{11}{7} = \frac{11}{7} × \frac{5}{5} = \frac{55}{35}$
$\frac{12}{5} = \frac{12}{5} × \frac{7}{7} = \frac{84}{35}$
Итак,
$\frac{11}{7} + {12}{5} = \frac{55}{35} + 8435 = 55 + 8435 = 13935
Шаг 3: Преобразуйте окончательный результат в неправильную дробь.
$\frac{139}{35}=3\frac{34}{35}$
Решенные примеры
Пример 1. Дэвид съел 3 ½ куска пиццы, а Джай съел 5 ⅔ кусочков пиццы. Сколько кусков пиццы они съели всего?
Решение : Проблема сводится к сложению смешанных чисел. Мы добавим 3 ½ + 5 ⅔.
Пример 2. Рон прошел $3\frac{2}{7}$ мили во время похода в лес, в то время как его друг прошел $2\frac{4}{7}$ мили. Какое расстояние они оба преодолели за время пути?
Решение : Мы найдем ответ, сложив смешанные числа, $3\frac{2}{7}$ и $2\frac{4}{7}$.
Здесь целыми являются 2 и 3. Давайте сначала сложим их.
$2 + 3 = 5$
А теперь добавим дробные части.
Дробные части: $\frac{2}{7}$ и $\frac{4}{7}$.
$\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}$
Итак, мы получаем $3\frac {2}{7} + 2\frac{4}{7}=5\frac{6}{7}$
Итак, Рон и его друг преодолели $5\frac{6}{7}$ миль за поездку. .
.
Практические задачи
1
Найдите сумму двух смешанных дробей $4\frac{2}{6}$ и $5\frac{1}{6}$.
$6\frac{2}{6}$
$9\frac{1}{6}$
$4\frac{2}{6}$
$9\frac{3}{6}$
Правильный ответ: $9\frac{3}{6}$
$4\frac{2}{6} +5\frac{1}{6} = 4 + 5 + \frac{2}{6} + \frac {1}{6}$
$= 9 + \frac{3}{6}$
$= 9\frac{3}{6}$
2
Сэм пробежал трусцой $3\frac{1}{5} $ миль во время марафона, в то время как его друг пробежал $2\frac{1}{5}$ миль. Какое расстояние они преодолели в общей сложности?
$5\frac{2}{5}$
$5\frac{1}{5}$
$2\frac{2}{5}$
$1\frac{1}{25}$
Правильный ответ: $5\frac{2}{5}$
Мы найдем ответ, сложив смешанные числа , $3\frac{1}{5}$ и $2\frac{1}{5}$.
$3\frac{1}{5} +2\frac{1}{5} = 3 + 2 + \frac{1}{5} + \frac{1}{5}$
$= 5 + \frac {2}{5}$
$= 5\frac{2}{5}$
3
Найдите сумму $5\frac{2}{5}$ и $6\frac{4}{5}$ .

 е. 1 × 7 = 7, и результат прибавляем к 4, т. е. 7 + 4 = 11. Таким образом, смешанная дробь превращается в неправильную дробь и записывается как 11/7.
е. 1 × 7 = 7, и результат прибавляем к 4, т. е. 7 + 4 = 11. Таким образом, смешанная дробь превращается в неправильную дробь и записывается как 11/7. е. 2 + 1 = 3
е. 2 + 1 = 3
 е. НОК 2 и 4 = 4.
е. НОК 2 и 4 = 4. Так как знаменатели одинаковые, мы будем складывать целые числа отдельно и дроби отдельно и объединять их результат, чтобы получить окончательный ответ.
Так как знаменатели одинаковые, мы будем складывать целые числа отдельно и дроби отдельно и объединять их результат, чтобы получить окончательный ответ. Итак, \(20\dfrac{2}{3}\) = 62/3 и \(7\dfrac{3}{4}\) = 31/4, и теперь нам нужно добавить 62/3 + 31/4. . Поскольку знаменатели не являются общими, найдем НОК их знаменателей и сделаем их похожими на дроби.
Итак, \(20\dfrac{2}{3}\) = 62/3 и \(7\dfrac{3}{4}\) = 31/4, и теперь нам нужно добавить 62/3 + 31/4. . Поскольку знаменатели не являются общими, найдем НОК их знаменателей и сделаем их похожими на дроби. Этот шаг не нужен, поскольку знаменатели одинаковы.
Этот шаг не нужен, поскольку знаменатели одинаковы.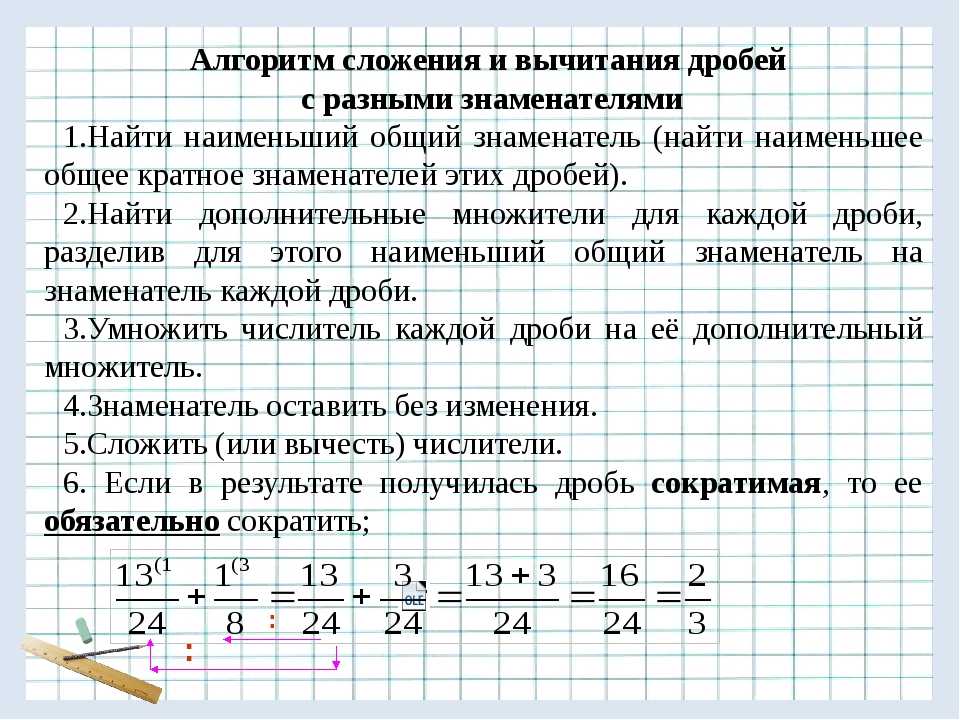 Итак, 15/5 = 3,9.0042
Итак, 15/5 = 3,9.0042