Смешанные числа. Сложение и вычитание
Смешанные числа: определения, примеры
Смешанное число — это число, состоящее из натурального числа и обыкновенной дроби. Пишут в виде .
Где n — целая часть, — дробная часть.
Смешанное число равно сумме своей целой и дробной части. То есть .
Примеры смешанных чисел
Каждое такое смешанное число содержит целую и дробную части.
Чтобы точно определять, какая именно перед вами дробь, запомните:
Дробь виданазывается правильной дробью. В ней числитель всегда меньше знаменателя.
Дробь виданазывается неправильной. В таких дробях числитель больше знаменателя или равен ему.
Дробь виданазывается смешанной дробью/смешанным числом. Такая дробь состоит из целой части (натуральное число) и дробной части.
Смешанные числа можно складывать, вычитать, умножать и делить. Давайте узнаем, как именно это делать.
Давайте узнаем, как именно это делать.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Сложение смешанных чисел
Всего мы рассмотрим три типа сложения со смешанными числами. В каждом подпункте приведено необходимое правило и примеры выполнения решений.
Сложение смешанного числа и натурального числа
Запоминаем
Чтобы сложить смешанное число и натуральное число, прибавьте натурально число к целой части смешанного числа, а дробную часть оставьте нетронутой.
Представим первое правило в виде буквенных выражений.
Выполним сложение смешанного числа и натурального числа d.
Известно, что любое смешанное число равное сумме целой и дробной частей.
Это значит, что .
Тогда .
Рассмотрим примеры сложения смешанных чисел с натуральными числами.
Пример 1. Выполните сложение смешанного числа и натурального числа 18.
Как решаем:
Записываем выражение
Согласно правилу, прибавляем к натуральному числу целую часть смешанного числа и вычисляем: .
Ответ: .
Пример 2. Выполните сложение смешанного числа и натурального числа 10.
Как решаем:
Записываем выражение: .
.
Ответ: .
Пример 3. Выполните сложение смешанного числа и натурального числа 2.
Как решаем:
Записываем выражение:
.
Ответ: .
Сложение смешанного числа со смешанным числом
Запоминаем
Чтобы сложить смешанное число с другим смешанным числом, сложите сначала целые части этих чисел, а затем — дробные части.
Представим правило в виде буквенных выражений.
Выполним сложение смешанного числа и смешанного числа .
Следуя правилу, запишем выражение в виде: .
Рассмотрим примеры сложения смешанных чисел.
Пример 1. Сложите смешанное число и смешанное число .
Как решаем:
Записываем выражение: .
Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:
Решаем: складываем целые части 2 + 7 = 9.
Чтобы выполнить сложение дробных частей, воспользуемся правилом сложения дробей с разными знаменателями: приведем дроби к наименьшему общему знаменателю и выполним сложение.
.
Наименьшее общее кратное — 15.
.
Если в результате сложения получилась сократимая дробь, сокращайте, не задумываясь: сокращаем на .
.
Ответ: .
Пример 2. Сложите смешанное число и смешанное число .
Как решаем:
Записываем выражение: .
Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части: .
Решаем: складываем целые части 13 + 2 = 15.
Складываем дробные части
Наименьшее общее кратное 12 и 20 равно 60.
.
Сокращаем дробь на .
.
Ответ:
Таким же образом можно складывать три, четыре и больше натуральных чисел. Не забывайте сокращать дроби и выделять целые части из неправильных дробей.
Сложение смешанного числа и правильной дроби
Запоминаем
Чтобы выполнить сложение смешанного числа и правильной дроби, прибавьте к дроби дробную часть смешанного числа, а целую часть оставьте без изменений.
Представим правило в виде буквенного выражения.
Если нам нужно сложить смешанное число и правильную дробь , то запишем следующее выражение: .
Рассмотрим примеры сложения смешанных чисел с обыкновенными дробями.
Пример 1. Выполните сложение обыкновенной дроби и смешанного числа
Как решаем:
Записываем выражение:
Согласно правилу, складываем дробь с дробной частью смешанного числа:
.
Складываем дроби .
Наименьшее общее кратное 5 и 20 равно 20.
, сокращаем на 5, получается .
.
Ответ: .
Пример 2. Выполните сложение правильной дроби и смешанного числа .
Как решаем:
Записываем выражение: .
Следуя правилу, складываем дробь с дробной частью смешанного числа:
.
Складываем дроби .
Наименьшее общее кратное 4 и 2 равно 4.
.
.
Ответ: .
Чтобы выполнить сложение смешанного числа и неправильной обыкновенной дроби, выделите целую часть из неправильной дроби и выполните сложение смешанных чисел.
Вычитание смешанных чисел
Рассмотрим три типа вычитания со смешанными числами. В каждом подпункте вы найдете правила и решение примеров с разбором.
Вычитание одного смешанного числа из другого
Запоминаем
Любое смешанное число можно представить в виде суммы целой и дробной части.
Это значит, что .
Исходя из значения дробных частей, вычитание можно выполнять тремя способами.
Если дробная часть уменьшаемого больше дробной части вычитаемого , то выполняем вычитание целой части вычитаемого из целой части уменьшаемого, затем выполняем вычитание дробных частей.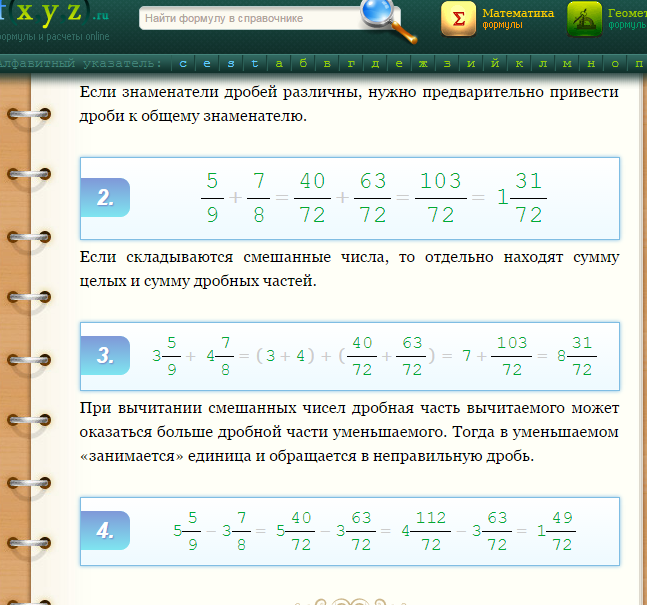
.
Пример. Выполните вычитание .
Как решаем:
Чтобы решить пример, нужно выяснить, какая из дробных частей больше:
или .
Чтобы сравнить две дроби, приведем их к общему знаменателю — 8:
.
По правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, чей числитель больше.
Это значит, что .
.
Следуя правилу, выполняем вычитание .
Вычитаем дробные части .
НОК = 8
.
.
Ответ: .
Запоминаем
Если дробные части смешанных чисел равны, то есть , то разность этих смешанных чисел будет равна разности их целых частей.
при .
Пример. Выполните вычитание:
Как решаем:
Дробные части смешанных чисел равны. Это значит, что .
Следуя правилу, выполним вычитание:
.
Ответ: .
Запоминаем
Если дробная часть уменьшаемого меньше дробной части вычитаемого , то вычитание выполняется вот так .
Пример. Найдите значение разности смешанных чисел и
Как решаем:
Запишем выражение
Сначала выясним, как из дробных частей больше. Для этого приведем их к НОЗ.
НОК 5 и 15 = 15.
Следуя правилу, решаем:
.
Представим число 21 в виде смешанной дроби и выполним вычитание дроби из натурального числа:
Ответ: .
Вычитание смешанного числа из натурального числа
Запоминаем
Чтобы из целого числа вычесть смешанное число, сначала отнимите от натурального числа целую часть смешанного числа, а затем отнимите от этой разности дробную часть смешанного числа.
Представим правило в виде буквенного выражения: .
Пример. Отнимите от натурального числа 15 смешанное число
Как решаем:
Запишем выражение: .
Следуя правилу, выполним вычитание целой части смешанного числа из натурального числа:
Ответ:
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Умножение смешанных чисел
Давайте разберемся как выполнять умножение в примерах, где есть смешанные числа.
Умножение смешанного числа на смешанное число
Запоминаем
Чтобы умножить одно смешанное число на другое, нужно перевести оба смешанных числа в неправильные дроби, а затем выполнить умножение по правилу умножения дробей.
Пример. Выполните умножение смешанного числа и
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанные числа в неправильные дроби.
Выполним умножение: .
Из полученной неправильной дроби выделяем целую часть .
Ответ: .
Умножение смешанного числа на обыкновенную дробь
Запоминаем
Чтобы выполнить умножение смешанного числа и обыкновенной дроби, представьте смешанное число в виде неправильной дроби и выполните умножение дробей.
Пример. Умножьте смешанное число на обыкновенную дробь
Как решаем:
Запишем выражение
Представим смешанное число в виде неправильной дроби.
.
Выполним умножение дробей
Выделим из полученной неправильной дроби целую часть
Ответ: .
Умножение целого числа на дробь
Запоминаем
Чтобы умножить целое число на дробь, просто умножьте это число на числитель дроби.
Пример. Выполните умножение числа 7 на обыкновенную дробь
Как решаем:
Запишем выражение:
Выделим из получившейся неправильной дроби целую часть .
Ответ:
Деление смешанных чисел
Вы уже рассмотрели три типа арифметических действий со смешанными числами. Осталось разобраться, как выполнять деление в примерах, где есть смешанные числа. Давай научимся это делать.
Деление смешанного числа на смешанное число
Запоминаем
Чтобы разделить одно смешанное число на другое, переведите оба числа в неправильные дроби и выполните деление, следуя правилу деления дробей.
Пример. Найдите результат деления смешанного числа на смешанное число
Как решаем:
Запишем выражение:
Следуя правилу, переведем оба смешанных числа в неправильные дроби.
Пользуясь правилом деления дробей, находим частное:
Ответ: .
Деление смешанного числа на целое число
Запоминаем
Чтобы разделить смешанное число на целое число, переведите смешанное число в неправильную дробь и выполните деление.
Пример. Разделите смешанное число на натуральное число 15
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанное число в неправильную дробь
Выполним деление
Ответ: .
Деление целого числа на смешанное число
Запоминаем
Чтобы разделить целое число на смешанное число, переведите смешанное число в неправильную дробь и выполните деление.
Пример. Выполните деление натурального числа 30 на смешанное число
Запишем выражение
Представим смешанное число в виде неправильной дроби .
Выполним деление .
Выделим из полученной неправильной дроби целую часть .
Ответ: .
Деление смешанного числа на обыкновенную дробь
Запоминаем
Чтобы разделить смешанное число на обыкновенную дробь, представьте смешанное число в виде неправильной дроби и выполните деление.
Пример. Разделите смешанное число на обыкновенную дробь
Как решаем:
Запишем выражение .
Представим смешанное число в виде неправильной дроби .
Выполним деление, следуя правилу деления дробей: .
Ответ: .
Смешанные числа
В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дробиВстречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь . Чтобы решить этот пример, нужно число 2 представить в виде дроби . Затем сложить дроби с разными знаменателями:
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: , а конец так: . Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.
Смотрим на его начало и на его конец. Начало у него выглядит так: , а конец так: . Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.
Когда перед нами смешанное число вида , мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения равно
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
Пример 2. Найти значение выражения
Представим число 3 в виде дроби . Затем сложим дроби с разными знаменателями:
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
То есть опустить знак сложения:
Пример 3. Найти значение выражения
Можно записать вместе число 2 и дробь , но этот ответ не будет окончательным, поскольку в дроби можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби . Пять вторых это две целых и одна вторая:
Теперь в главном выражении вместо дроби запишем смешанное число
Получили новое выражение . В этом выражении смешанное число запишем в развёрнутом виде:
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
Теперь свернём полученное смешанное число:
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
Получили . Теперь в главном выражении заменяем дробные части на полученную дробь
Теперь свернем полученное смешанное число:
Таким образом, значение выражения равно . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
Теперь вычислим дробные части:
Получили смешанное число . Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число
Получили выражение . В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:
Сложим целые части. Получаем 9
Сворачиваем готовый ответ:
Таким образом, значение выражения равно .
Полное решение этого примера выглядит следующим образом:
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
Например, сложить 2 и смешанное число . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
Здесь смешанная дробь была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ .
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Пример 2. Найти значение выражения
В этом примере, как и в предыдущем, нужно сложить целые части:
Осталось свернуть целую и дробную части, но дело в том, что дробная часть представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби , и выполнить вычитание дробей с разными знаменателями:
Например, вычесть из числа 1 дробь . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби , и выполнить вычитание дробей с разными знаменателями:
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
Пример 2. Найти значение выражения .
Представим число 2 в виде дроби , и выполним вычитание дробей с разными знаменателями:
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения , не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:
Нужно вычесть из них . Мы помним, что треть выглядит следующим образом:
Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть
Получилось (две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
Пример 3. Найти значение выражения
Представим число 3 в виде дроби . Затем выполним вычитание дробей с разными знаменателями:
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Представим 6 в виде дроби , а смешанное число , в виде неправильной дроби. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
Тогда от той пиццы, от которой отрезали останется пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения:
Например, найдём значение выражения:
Чтобы решить этот пример, нужно смешанные числа и перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
Если от трёх целых пицц вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
Пример 2. Найти значение выражения
Переводим смешанные числа и в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби , а знаменатель оставить без изменения:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Умножим число 3 на числитель дроби
В ответе получилась неправильная дробь , но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
Пример 3. Найти значение выражения
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
Пример 4. Найти значение выражения
Найти значение выражения
Умножим число 3 на числитель дроби
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения
Переведём смешанное число в неправильную дробь. После перевода это число превратится в дробь . Затем можно будет умножить эту дробь на
Допустим, имеются одна целая и половина пиццы:
Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
Поэтому значение выражения было равно 1
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить и . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
Например, перемножить и . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
Теперь разберемся со смешанным множителем . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
Но ещё осталось взять от изначальной целой пиццы и половины, ведь множителем было смешанное число . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь . Здесь число 3 — это делимое, а дробь — делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 3 на дробь
Допустим, имеются три целые пиццы:
Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
Поэтому значение выражения равно 6.
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби . После выделения целой части в этой дроби получим
Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения равно
Пример 3. Найти значение выражения
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 5 на
Дробь это 2 целых и . Проще говоря, две целые и четверть пиццы:
А выражение определяет сколько раз содержится в пяти целых пиццах. Ответом было смешанное число .
То есть пиццы содержится в пяти целых пиццах раза.
Давайте нащупаем в пяти пиццах два раза по
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой от , которые не вместились. Двумя девятыми они являются по той причине, что в пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
Поэтому значение выражения равно
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь на число 2
Чтобы разделить дробь на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
Пусть имеется половина пиццы:
Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно дробь умножить на число, обратное числу 2. Обратное числу 2 это дробь
Пример 3. Найти значение выражения
Умножаем первую дробь на число, обратное числу 3. Обратное числу 3 это дробь
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .
Чтобы решить этот пример, нужно делитель перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель в неправильную дробь, получим . Затем умножим 2 на дробь, обратную дроби . Обратная для дроби это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим делитель в неправильную дробь, получаем . Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь
Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь
Сначала мы получили ответ , затем сократили эту дробь на 5, и получили , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим на 2. Чтобы решить этот пример, нужно делимое перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число в неправильную дробь, получим .
Теперь умножаем на число, обратное числу 2. Обратное числу 2 это дробь
Допустим, имеется одна целая и половина пиццы:
Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:
Для этого сначала разделим на две части целую пиццу:
Затем разделим поровну на две части и половину:
Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переведём делимое в неправильную дробь, получим . Теперь умножаем на число, обратное числу 4. Обратное числу 4 это дробь .
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Как решать дальше мы уже знаем. Первую дробь нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь .
Дорешаем данный пример до конца:
Допустим, имеются две целые и половина пиццы:
Если зададим вопрос «Сколько раз (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
Пример 2. Найти значение выражения
Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь
Сначала мы получили дробь. Эту дробь мы сократили на 9. В результате получили дробь , но такой ответ нас тоже не устроил и мы выделили в дроби целую часть. В результате получили окончательный ответ .
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Показать решение
Задание 2. Найдите значение выражения:
Решение:
Показать решение
Задание 3. Найдите значение выражения:
Решение:
Показать решение
Задание 4. Найдите значение выражения:
Решение:
Показать решение
Задание 5. Найдите значение выражения:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Сложение и вычитание дробей
ГДЗ 1 класс
ГДЗ 10 класс
- Категория: Математика
То, каким образом мы будем складывать или вычитать дроби, напрямую зависит от знаменателей этих дробей. Самое простое: сложение и вычитание дробей с одинаковыми знаменателями. С него и начнем.
Самое простое: сложение и вычитание дробей с одинаковыми знаменателями. С него и начнем.
Cложение и вычитание дробей с одинаковыми знаменателями
Вспоминаем законы сложения дробей из четвертого класса.
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Чтобы вычесть друг из друга дроби с одинаковыми знаменателями, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Убедимся в справедливости этого высказывания на примере. Разделим круг на 5 равных частей. Возьмем из этих пяти 1-у часть и 2 части. Сложим. Вместе они составят 3 части. А поскольку изначально круг был разделен на 5 таких частей, то это 3/5 круга.
1/5 + 2/5 = 3/5
Уберем из целого круга 2 зеленые части (2/5). Останется 3 части (3/5).
5/5 — 2/5 = 3/5
Но если знаменатели разные, то ни сложить, ни вычесть такие дроби сразу нельзя.
Можно складывать и вычитать дроби только с одинаковыми знаменателями.
При сложении смешанных дробей отдельно складываются/вычитаются целые части, отдельно дробные, и опять же только при условии одинаковых знаменателей у дробных частей.
$5\frac27+3\frac17=(5+3)+(\frac27+\frac17)=8+\frac37=8\frac37$
$5\frac27-3\frac17=(5-3)+(\frac27-\frac17)=2+\frac17=2\frac17$
Если при вычитании смешанных дробей складывается такая ситуация, что числитель первой дробной части (уменьшаемое) меньше числителя второй (вычитаемого), то нужно взять единичку от целой части первого числа, представить ее в виде дроби с тем же знаменателем, что и у дробной части, и прибавить эту дробь к дробной части. Целая часть станет на единицу меньше, а дробная будет теперь представлять собой неправильную дробь (числитель больше знаменателя). Зато легко можно будет провести вычитание.
$5\frac17-3\frac27=\mathit4\mathit+\mathit1\mathit+\frac{\mathit1}{\mathit7}\mathit-\mathit3\frac{\mathit2}{\mathit7}\mathit=\mathit4\mathit+\frac{\mathit7}{\mathit7}\mathit+\frac{\mathit1}{\mathit7}\mathit-\mathit3\frac{\mathit2}{\mathit7}=4\frac87-3\frac27=(4-3)+(\frac87-\frac27)=1+\frac67=1\frac67$
Что же делать, если знаменатели разные? Разберемся. 1}{\cancel6_2}=\frac12$
1}{\cancel6_2}=\frac12$
Чтобы привести дроби к одинаковому знаменателю, принято находить наименьший общий знаменатель, а это то же самое, что наименьшее общее кратное (НОК) этих знаменателей. Вспомним, как находить НОК, статья по ссылке >>
$\frac59+\frac16=?$
9 | 3 6 | 2
3 | 3 3 | 3
1 | 1
НОК(6;9) = 3 * 3 * 2 = 18
$\frac59+\frac16=\frac{5\ast2}{9\ast2}+\frac{1\ast3}{6\ast3}=\frac{10}{18}+\frac3{18}=\frac{13}{18}$
Еще примеры:
Если в результате сложения или вычитания получается неправильная дробь, нужно перевести ее в смешанную. Если получается сократимая дробь, результат необходимо сократить.
Вспоминаем: чтобы сократить дробь, нужно разделить ее числитель и знаменатель на одно и то же число — наибольший общий делитель (НОД). Статья о том, как найти НОД по ссылке >>
Для дробей, как и для натуральных чисел, выполняются переместительное и сочетательное свойства сложения:
$\frac ab+\frac cd=\frac cd+\frac ab$
$(\frac ab+\frac cd)+\frac pq=\frac ab+(\frac cd+\frac pq)$
Их нужно применять в заданиях на нахождение наиболее простого способа сложения нескольких дробей.
Пример. Вычислите значение выражения наиболее удобным способом:
Если все равно что-то в теме не поняли, задавайте вопросы в комментариях.
- Назад
- Вперед
умножить наподелить на
- Уроки
- Математика
Вам может пригодиться:
Смешанные числа — сложение, вычитание и умножение дробей с разными знаменателям
Многие ученики, когда подходит время изучать смешанные числа в 6 классе, сомневаются, что подобные вычисления пригодятся им в жизни, в особенности в наше время, когда можно при необходимости воспользоваться калькулятором.
Однако в быту подобными выражениями мы пользуемся чаще, чем может показаться на первый взгляд: при измерении времени, в рецептах блюд, дозировках лекарств и так далее.
Содержание
- Что такое смешанное число
- Как представить смешанное число в виде неправильной дроби
- Как выделить целую часть неправильной дроби
- Как перевести смешанную дробь в десятичную
- Как сократить смешанную дробь
- Сложение смешанных чисел
- Вычитание смешанных чисел
- Как умножать смешанные числа
- Заключение
Что такое смешанное число
Под смешанным числом понимают сумму натурального числа и обычной дроби, записанную без знака «+».
― это смешанное число. Читать данное выражение следует так: «четыре целых пять седьмых».
Где 4 ― это целая, а 5/7 ― дробная часть.
Как представить смешанное число в виде неправильной дроби
Если мы, имея на руках один пирог и ещё половину (то есть 1½), возьмём и дополнительно поделим целый пирог на два равных куска, то у нас в итоге окажется три половинки (или 3/2). Но суть от этого всё равно не изменится: «количество» пирога останется прежним.
Но суть от этого всё равно не изменится: «количество» пирога останется прежним.
Этот пример наглядно показывает, что смешанное число можно превратить в неправильную дробь. Это преобразование можно выполнить за несколько шагов:
Например, 5¾ преобразуется следующим образом:
Данные вычисления можно выразить и в более короткой формуле:
Пример преобразования:
Как выделить целую часть неправильной дроби
Чтобы совершить обратную операцию и превратить неправильную дробь в смешанное число, нужно сначала выделить её целую часть. Она будет равна результату деления числителя на знаменатель.
Если поделилось без остатка, значит больше никаких действий выполнять не нужно.
Если поделить без остатка не получается, то для завершения преобразования в смешанное число, остаток следует вынести в числитель. Знаменатель остаётся тем же.
Знаменатель остаётся тем же.
Как перевести смешанную дробь в десятичную
Так как подобную процедуру часто приходится проделывать не только в школе, выполняя математические задания и решая различные уравнения, но и в повседневности, ― умение проделывать это легко и быстро может оказаться очень полезным.
Для перевода необходимо:
Таким образом, чтобы преобразовать 53/5, нужно:
Как сократить смешанную дробь
При сокращении целая часть не трогается, изменениям подвергается только дробная.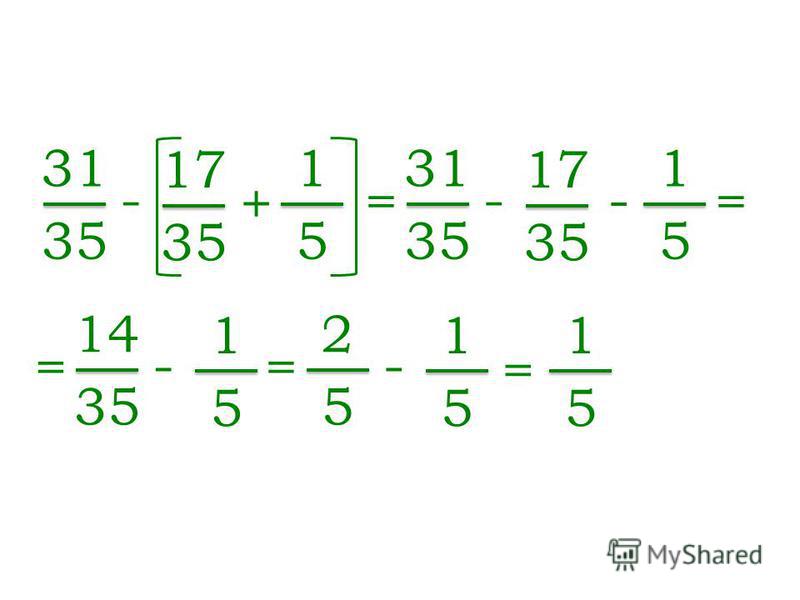 Чтобы сократить её, нужно:
Чтобы сократить её, нужно:
- выявить наибольший общий множитель для числителя и знаменателя;
- поделить их на это число.
Например, чтобы сократить 76/9, необходимо:
Сложение смешанных чисел
Чтобы осуществить сложение, нужно необходимую операцию проделать отдельно для целых и отдельно для дробных частей. А получившиеся результаты сложить.
Например, чтобы решить следующий пример
,
необходимо:

Вычитание смешанных чисел
Для вычитания вычисления аналогичны. Следующую задачу
следует решить так:
Как умножать смешанные числа
Чтобы перемножить смешанные числа, необходимо:
- осуществить их перевод в неправильные дроби;
- полученные выражения перемножить по правилам умножения обыкновенных дробей.
Для примера решим следующее задание:
Заключение
Происхождение чисел сложно точно проследить. Известно только, что человек стал пользоваться ими с самых седых времён. История дробей также берёт своё начало в глубокой древности: подобными понятиями оперировали уже в древнем Египте.
Сегодня просто невозможно представить нашу жизнь без них. Все современные научные достижения, на которых основано наше общество, были бы попросту неосуществимы, не говоря уже о том, что значительно усложнилась бы наша повседневная жизнь. Вот почему так важно знать, что они собой представляют.
Предыдущая
МатематикаКатеты прямоугольного треугольника — свойства, основные формулы и примеры решений
Следующая
МатематикаКоординатная плоскость — определение расположения точек и фигур
Умножение простых и смешанных дробей с разными знаменателями.
Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2.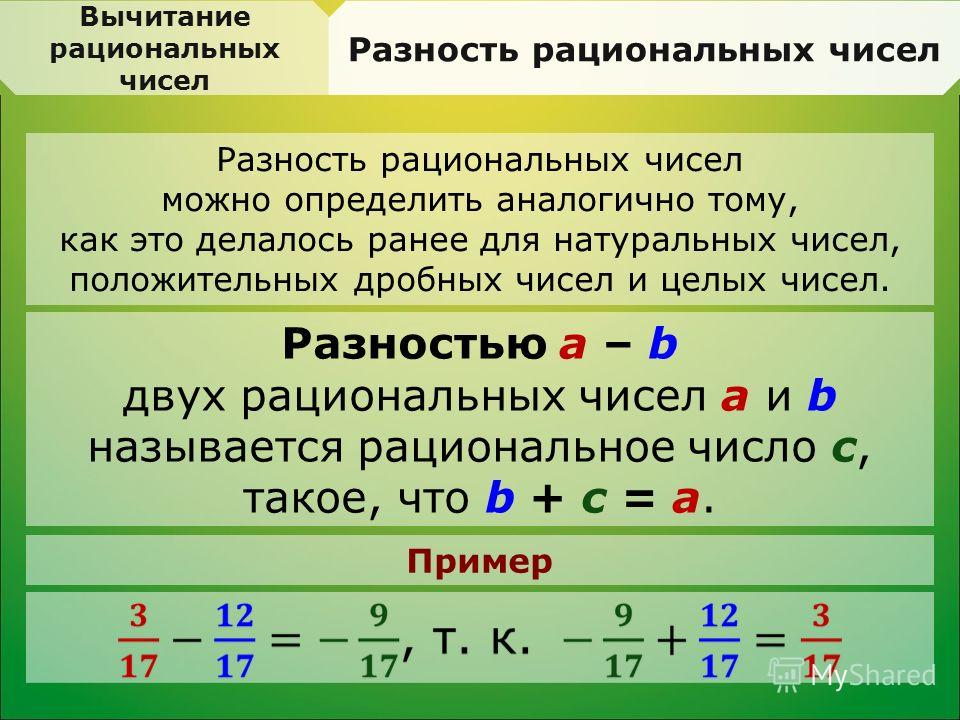 Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается , если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ . Умножить число 4
на числитель дроби, а знаменатель дроби оставить без изменений:
Умножить число 4
на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ . Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4 , поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить 7 на знаменатель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7
и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
С дробями можно выполнять все действия, в том числе и деление. Данная статья показывает деление обыкновенных дробей. Будут даны определения, рассмотрены примеры. Подробно остановимся на делении дробей на натуральные числа и наоборот. Будет рассмотрено деление обыкновенной дроби на смешанное число.
Деление обыкновенных дробей
Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.
Если необходимо произвести деление обыкновенной дроби a b на c d , тогда для определения такого числа нужно произвести умножение на делитель c d , это даст в итоге делимое a b . Получим число и запишем его a b · d c , где d c является обратным c d числу. Равенства можно записать при помощи свойств умножения, а именно: a b · d c · c d = a b · d c · c d = a b · 1 = a b , где выражение a b · d c является частным от деления a b на c d .
Отсюда получим и сформулируем правило деления обыкновенных дробей:
Определение 1
Чтобы разделить обыкновенную дробь a b на c d , необходимо делимое умножить на число, обратное делителю.
Запишем правило в виде выражения: a b: c d = a b · d c
Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.
Перейдем к рассмотрению деления обыкновенных дробей.
Пример 1
Выполнить деление 9 7 на 5 3 . Результат записать в виде дроби.
Решение
Число 5 3 – это обратная дробь 3 5 . Необходимо использовать правило деления обыкновенных дробей. Это выражение запишем так: 9 7: 5 3 = 9 7 · 3 5 = 9 · 3 7 · 5 = 27 35 .
Необходимо использовать правило деления обыкновенных дробей. Это выражение запишем так: 9 7: 5 3 = 9 7 · 3 5 = 9 · 3 7 · 5 = 27 35 .
Ответ: 9 7: 5 3 = 27 35 .
При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.
Пример 2
Разделить 8 15: 24 65 . Ответ записать в виде дроби.
Решение
Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 8 15: 24 65 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Необходимо произвести сокращение, а это выполняется следующим образом: 8 · 65 15 · 24 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Выделяем целую часть и получаем 13 9 = 1 4 9 .
Ответ: 8 15: 24 65 = 1 4 9 .
Деление необыкновенной дроби на натуральное число
Используем правило деления дроби на натуральное число:чтобы разделить a b на натуральное число n , необходимо умножить только знаменатель на n . Отсюда получим выражение: a b: n = a b · n .
Правило деления является следствием правила умножения. Поэтому представление натурального числа в виде дроби даст равенство такого типа: a b: n = a b: n 1 = a b · 1 n = a b · n .
Рассмотрим данное деление дроби на число.
Пример 3
Произвести деление дроби 16 45 на число 12 .
Решение
Применим правило деления дроби на число. Получим выражение вида 16 45: 12 = 16 45 · 12 .
Произведем сокращение дроби. Получим 16 45 · 12 = 2 · 2 · 2 · 2 (3 · 3 · 5) · (2 · 2 · 3) = 2 · 2 3 · 3 · 3 · 5 = 4 135 .
Ответ: 16 45: 12 = 4 135 .
Деление натурального числа на обыкновенную дробь
Правило деления аналогично правилу деления натурального числа на обыкновенную дробь: чтобы разделить натуральное число n на обыкновенную a b , необходимо произвести умножение числа n на обратное дроби a b .
Исходя из правила, имеем n: a b = n · b a , а благодаря правилу умножения натурального числа на обыкновенную дробь, получим наше выражение в виде n: a b = n · b a . Необходимо рассмотреть данное деление на примере.
Необходимо рассмотреть данное деление на примере.
Пример 4
Делить 25 на 15 28 .
Решение
Нам необходимо переходить от деления к умножению. Запишем в виде выражения 25: 15 28 = 25 · 28 15 = 25 · 28 15 . Сократим дробь и получим результат в виде дроби 46 2 3 .
Ответ: 25: 15 28 = 46 2 3 .
Деление обыкновенной дроби на смешанное число
При делении обыкновенной дроби на смешанное числолегко можно свети к делению обыкновенных дробей. Нужно совершить перевод смешанного числа в неправильную дробь.
Пример 5
Разделить дробь 35 16 на 3 1 8 .
Решение
Так как 3 1 8 — смешанное число, представим его в виде неправильной дроби. Тогда получим 3 1 8 = 3 · 8 + 1 8 = 25 8 . Теперь произведем деление дробей. Получим 35 16: 3 1 8 = 35 16: 25 8 = 35 16 · 8 25 = 35 · 8 16 · 25 = 5 · 7 · 2 · 2 · 2 2 · 2 · 2 · 2 · (5 · 5) = 7 10
Ответ: 35 16: 3 1 8 = 7 10 .
Деление смешанного числа производится таким же образом, как и обыкновенных.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
ТЕМА: Деление дробей.
- Изучение правила деления дробей; Формирование элементарных умений выполнять деление дробей;
- развитие основных умений выполнять деление дробей по основному алгоритму; Развитие внимания, логического мышления;
- воспитание интереса к изучению предмета, умений работать в группах.
ПЛАН УРОКА:
1. Организационный момент.
2. Устная работа, приводящая к новому правилу.
3. Введение определения.
4. Работа с карточками на усвоение.
5. Физминутки.
6. Устная работа «найди ошибку».
7. Закрепление: вычисления по цепочке.
8. Подведение итогов урока.
ХОД УРОКА
1) Сегодня на уроке, ребята, нам предстоит
выполнить серьёзную работу. От вас потребуется
усидчивость, стремление, внимание,
последовательность и правильность выполнения
заданий.
Устная работа: назовите число, обратное данному числу:
2) А как проверить правильность выполнения действия умножения? (Действием деления).
Как выполняется деление дробей, мы не знаем. Настало время познакомиться с этим новым действием.
Делить, делиться порой бывает нелегко, поэтому и сама операция деления дробей требует особого внимания.
Вспомним, что такое деление, как математическое действие? (действие, обратное умножению; действие, когда по одному из множителей и произведению находят другой множитель).
Сейчас мы вместе попытаемся увидеть новое для нас правило деления дробей в ходе рассмотрения следующей задачи.
Теперь наши пути решения разойдутся.
Какие у вас есть предложения по решению данного уравнения?
Во-первых, мы умеем решать такие уравнения с использованием понятия взаимно-обратных чисел (достаточно домножить обе части уравнения на число, обратное коэффициенту при переменной Х).
Во-вторых, нам известно стандартное правило
нахождения неизвестного множителя (необходимо
произведение разделить на известный множитель).
Рассмотрим оба этих случая:
Посмотрите внимательно на два получившихся выражения для нахождения значения Х. Это ответы одной и той же задачи, значит ответы должны быть одинаковыми. В одном случае мы умножаем на 7/6, а в другом – делим на 6/7.
Получаем, что при делении на 6/7 должен получиться такой же ответ, если умножить на 7/6. Значит, смысл действия деления дробей сводится к умножению на число, обратное делителю. Это не случайная замеченная нами особенность.
Знакомство с новым правилом на стр. 100 учебника, повторить несколько раз, спросить по памяти нескольких учеников.
3) Используя изученное правило рассмотреть его применение на различных примерах.
Дети получают специальные карточки,
заполнение которых осуществляют вместе с
учителем, с комментариями с места. Следует
рассмотреть деление дроби на дробь, деление
натурального числа на дробь и дроби на
натуральное число, деление смешанных чисел. При
заполнении дети ещё раз проговаривают правило. Особое внимание уделить трём этапам при
выполнении деления: делимое остаётся без
изменений; деление заменяется на умножение;
умножаем на число, обратное делителю.
Особое внимание уделить трём этапам при
выполнении деления: делимое остаётся без
изменений; деление заменяется на умножение;
умножаем на число, обратное делителю.
Деление | Применение | Правило | Преобразование | ||
| 5/7: 3/4 = | 5/7 * 4/3= | (5*4) / (7*3) = | 20/21 | 20/21 | |
| 5: 2/5 = | 5 * | ||||
| 7/8: 2 = | 7/8: 2/1= | 7/8 * | |||
| 4 1/2: 1 1/2= | 9/2: 3/2 = | 9/2 * |
На обратной стороне карточки есть три задания,
которые дети прорешивают после заполнения
карточки на местах, затем проверяют решения и
полученные результаты.
РЕШИ САМ |
| 1. 4/6: 3 = |
| 2. 8: 4/5 = |
| 3 . 1 2/3: 1 1/10 = |
4) Проведение физминутки.
5) Этап усвоения определения.
Проверим, как вы усвоили сегодняшнее правило и выясним, насколько вы внимательны: «НАЙДИ ОШИБКУ»
6) Решение заданий из учебника: № 619 (а,б,г).
7) Работа в группах. Дети по очереди выходят к доске и записывают решение примера.
8) Молодцы. Хорошо поработали. Давайте подведём итоги:
Что нового вы сегодня узнали на уроке?
Как выполняется деление дробей?
Что такое взаимно-обратные числа?
Дома: Правило, № 617.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.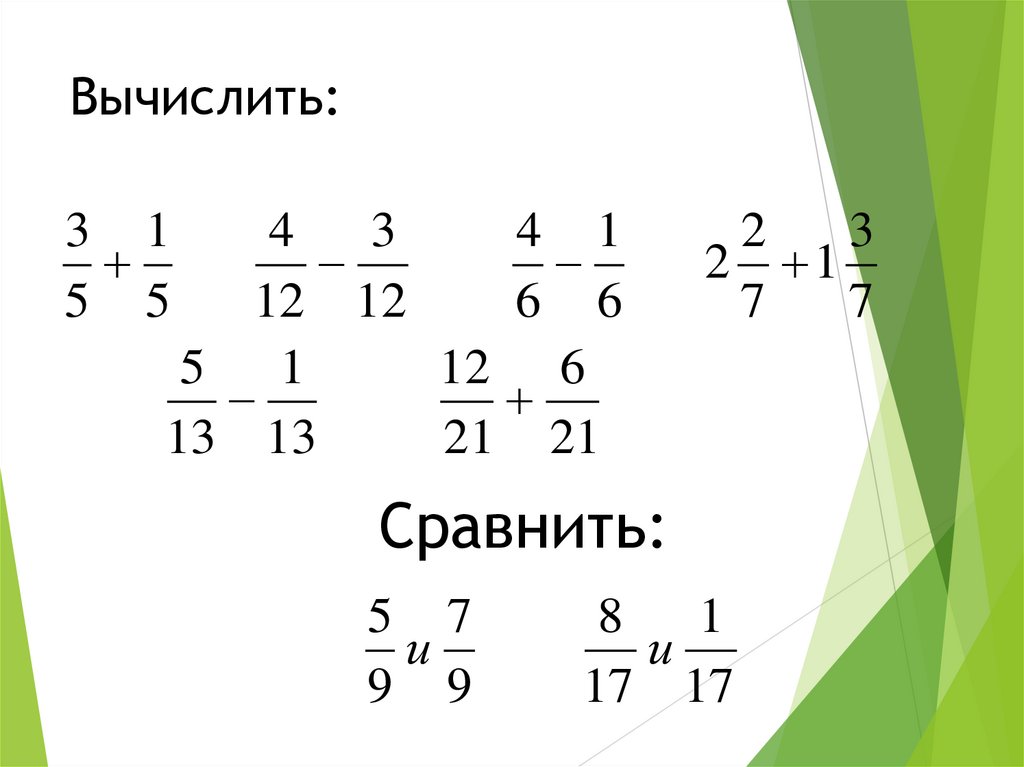
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут.
 В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
В крайнем случае, один минус может выжить — тот, которому не нашлось пары; - Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Вычитание дробей с разными примеры. Вычитание дробей с разными знаменателями. Сложение и вычитание обыкновенных дробей
Дробные выражения сложны для понимания ребёнком. У большинства возникают сложности, связанные с . При изучении темы «сложение дробей с целыми числами», ребёнок впадает в ступор, затрудняясь решить задание. Во многих примерах перед тем как выполнить действие нужно произвести ряд вычислений. Например, преобразовать дроби или перевести неправильную дробь в правильную.
Объясним ребёнку наглядно. Возьмём три яблока, два из которых будут целыми, а третье разрежем на 4 части. От разрезанного яблока отделим одну дольку, а остальные три положим рядом с двумя целыми фруктами. Получим ¼ яблока в одной стороне и 2 ¾ — в другой. Если мы их соединим, то получим целых три яблока. Попробуем уменьшить 2 ¾ яблока на ¼, то есть уберём ещё одну дольку, получим 2 2/4 яблока.
Если мы их соединим, то получим целых три яблока. Попробуем уменьшить 2 ¾ яблока на ¼, то есть уберём ещё одну дольку, получим 2 2/4 яблока.
Рассмотрим подробнее действия с дробями, в составе которых присутствуют целые числа:
Для начала вспомним правило вычисления для дробных выражений с общим знаменателем:
На первый взгляд всё легко и просто. Но это касается только выражений, не требующих преобразования.
Как найти значение выражения где знаменатели разные
В некоторых заданиях необходимо найти значение выражения, где знаменатели разные. Рассмотрим конкретный случай:
3 2/7+6 1/3
Найдём значение данного выражения, для этого найдём для двух дробей общий знаменатель.
Для чисел 7 и 3 – это 21. Целые части оставляем прежними, а дробные – приводим к 21, для этого первую дробь умножаем на 3, вторую – на 7, получаем:
6/21+7/21, не забываем, что целые части не подлежат преобразованию. В итоге получаем две дроби с одним знаменателям и вычисляем их сумму:
3 6/21+6 7/21=9 15/21
Что если в результате сложения получается неправильная дробь, которая уже имеет целую часть:
2 1/3+3 2/3
В данном случае складываем целые части и дробные, получаем:
5 3/3, как известно, 3/3 – это единица, значит 2 1/3+3 2/3=5 3/3=5+1=6
С нахождением суммы всё понятно, разберём вычитание:
Из всего сказанного вытекает правило действий над смешанными числами, которое звучит так:
- Если же от дробного выражения необходимо вычесть целое число, не нужно представлять второе число в виде дроби, достаточно произвести действие только над целыми частями.

Попробуем самостоятельно вычислить значение выражений:
Разберём подробнее пример под буквой «м»:
4 5/11-2 8/11, числитель первой дроби меньше, чем второй. Для этого занимаем одно целое число у первой дроби, получаем,
3 5/11+11/11=3 целых 16/11, отнимаем от первой дроби вторую:
3 16/11-2 8/11=1 целая 8/11
- Будьте внимательны при выполнении задания, не забывайте преобразовывать неправильные дроби в смешанные, выделяя целую часть. Для этого необходимо значение числителя разделить на значение знаменателя, то что получилось, встаёт на место целой части, остаток – будет числителем, например:
19/4=4 ¾, проверим: 4*4+3=19, в знаменателе 4 остаётся без изменений.
Подведём итог:
Перед тем как приступить к выполнению задания, связанного с дробями, необходимо проанализировать, что это за выражение, какие преобразования нужно совершить над дробью, чтобы решение было правильным. Ищите более рациональные способ решения. Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Чтобы не произошло путаницы при решении дробных выражений, необходимо руководствоваться правилом последовательности. Решайте всё внимательно, не торопясь.
Действия с дробями.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.
Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.
Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.
Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.
А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.
Сложение и вычитание дробей.
Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:
Короче, в общем виде:
А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:
Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .
Ещё пример:
Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:
Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…
Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.
Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…
Итак, нам надо сложить два дробных выражения:
Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:
Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные.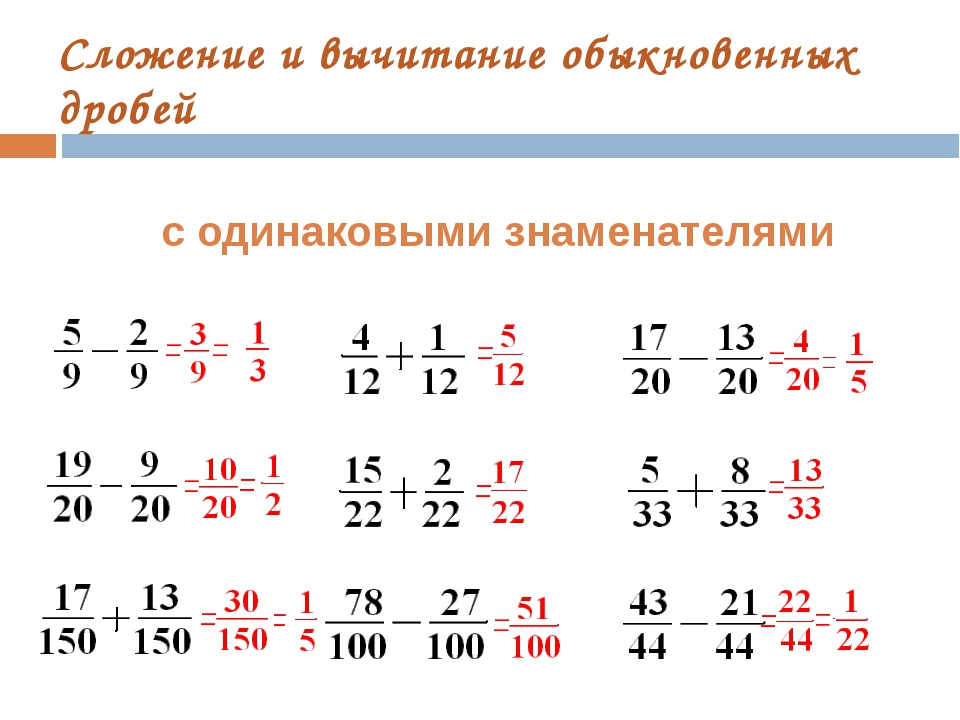 Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!
И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)
Порешаем немного?)
Вычислить:
Ответы (в беспорядке):
71/20; 3/5; 17/12; -5/4; 11/6
Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Ваш ребенок принес домашнее задание из школы, и вы не знаете как его решить? Тогда этот мини урок для вас!
Как складывать десятичные дроби
Десятичные дроби удобнее складывать в столбик. Чтобы выполнить сложение десятичных дробей, надо придерживаться одного простого правила:
- Разряд должен находиться под разрядом, запятая под запятой.
Как вы видите на примере, целые единицы находятся друг под другом, разряд десятых и сотых находится друг под другом.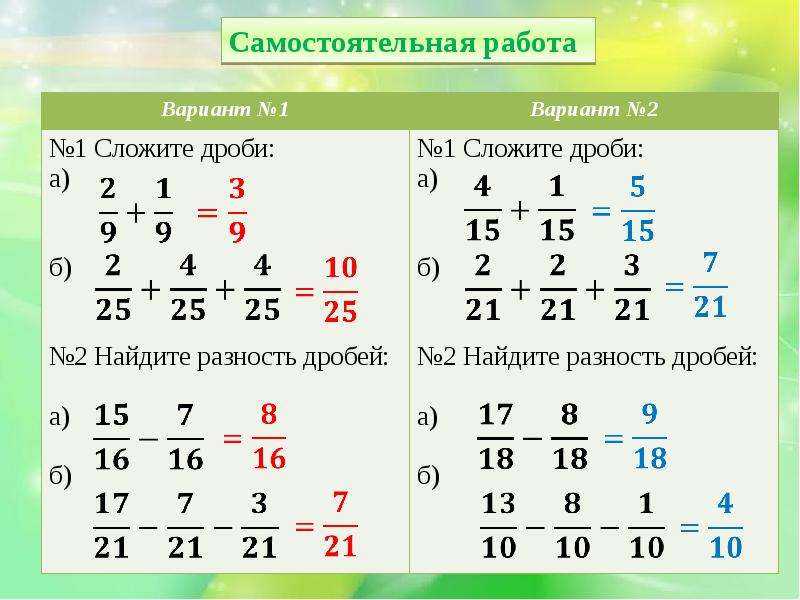 Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.
Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.
Сложение дробей с равными знаменателями
Чтобы выполнить сложение с общим знаменателем, надо сохранить знаменатель без изменения, найти сумму числителей и получим дробь, которая будет являться общей суммой.
Сложение дробей с разными знаменателями методом нахождения общего кратного
Первое, на что надо обратить внимание – это на знаменатели. Знаменатели разные, не делятся ли одно на другое, являются ли простыми числами. Для начала надо привести к одному общему знаменателю, для этого существует несколько способов:
- 1/3 + 3/4 = 13/12, для решения этого примера нам надо найти наименьшее общее кратное число (НОК), которое будет делиться на 2 знаменателя. Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.
- Перемножаем множители и выполняем сложение полученных чисел, получаем 13/12 – неправильную дробь.

- Для того чтобы перевести неправильную дробь в правильную, разделим числитель на знаменатель, получим целое число 1, остаток 1 – числитель и 12 – знаменатель.
Сложение дробей методом умножения крест на крест
Для складывания дробей с разными знаменателями существует еще один способ по формуле “крест на крест”. Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.

- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Сложение дробей с разными знаменателями
Теперь давайте научимся складывать дроби с разными знаменателями. При сложении дробей знаменатели этих дробей должны совпадать. Но они не всегда одинаковы.
Например, дроби
иможно складывать вместе, потому что у них одинаковые знаменатели.
Но дроби
и нельзя сложить сразу, потому что у этих дробей разные знаменатели. В таких случаях дроби необходимо привести к одному (общему) знаменателю.
Существует несколько способов приведения дробей к одному знаменателю. Сегодня мы рассмотрим только один из них, так как остальные могут показаться новичку сложными.
Суть этого метода в том, что сначала ищем наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем LCM делится на знаменатель первой дроби и получается первый дополнительный множитель. Проделайте то же самое со второй дробью — LCM разделите на знаменатель второй дроби и получите второй дополнительный множитель.
Затем LCM делится на знаменатель первой дроби и получается первый дополнительный множитель. Проделайте то же самое со второй дробью — LCM разделите на знаменатель второй дроби и получите второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на их дополнительные множители. В результате дроби с разными знаменателями преобразуются в дроби с одинаковыми знаменателями. И мы уже умеем складывать такие дроби.
Пример 1. Складываем дроби
и
Эти дроби имеют разные знаменатели, поэтому их нужно привести к одному (общему) знаменателю.
Сначала найдите наименьшее общее кратное знаменателей обеих дробей. В знаменателе первой дроби число 3, а в знаменателе второй дроби число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь вернемся к дробям
и . Сначала разделите НОК на знаменатель первой дроби и получите первый дополнительный множитель. НОК равен 6, а знаменатель первой дроби равен 3. Разделив 6 на 3, получим 2.
НОК равен 6, а знаменатель первой дроби равен 3. Разделив 6 на 3, получим 2.
Полученное число 2 является первым дополнительным множителем. Запишите это в первую дробь. Для этого над дробью проведите небольшую диагональную черту и над ней напишите найденный дополнительный множитель:
Проделайте то же самое со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК равно 6, а знаменатель второй дроби равен 2. Разделив 6 на 2, получим 3.
Полученное число 3 является вторым дополнительным множителем. Запишите это во вторую дробь. Снова проведите маленькую диагональную линию над второй дробью и запишите над ней найденный дополнительный множитель:
Теперь все готово для сложения. Осталось умножить числители и знаменатели дробей на их дополнительные множители:
Посмотрите внимательно, к чему мы пришли. Мы пришли к тому, что дроби с разными знаменателями превратились в дроби с одинаковыми знаменателями. И мы уже умеем складывать такие дроби. Решим этот пример до конца:
И мы уже умеем складывать такие дроби. Решим этот пример до конца:
На этом пример закончен. Добавьте к
и вы получите .
Попробуем изобразить наше решение картинкой. Если добавить
пиццы к пицце, то получится одна целая пицца и одна шестая часть пиццы:
Также можно показать приведение дроби к одному (общему) знаменателю. Приведя дроби
ик общему знаменателю, мы получили дроби и . Две фракции будут представлены одними и теми же кусочками пиццы. С той лишь разницей, что на этот раз они будут разделены на одинаковые дроби (приведены к одному знаменателю).
Первая картинка представляет дробь
(четыре штуки по шесть), а вторая картинка представляет дробь (три части по шесть). Складывая эти кусочки, получаем (семь штук по шесть). Эта дробь неправильная, поэтому мы выделили ее целую часть. Получилось (одна целая пицца и еще шестая часть пиццы).
Получилось (одна целая пицца и еще шестая часть пиццы).
Обратите внимание, что мы расписали этот пример слишком подробно. В школах не принято так подробно писать. Нужно уметь быстро находить НОК обоих знаменателей и дополнительных множителей к ним, а также быстро умножать найденные дополнительные множители на их числители и знаменатели. Если бы мы учились в школе, нам пришлось бы записать этот пример следующим образом:
Но есть и обратная сторона медали. Если вы не будете делать подробные заметки на первых этапах изучения математики, вы начнете получать вопросы вроде 9.0079 «откуда взялся этот номер?» , «почему дроби вдруг превращаются в совсем другие дроби?»
Поэтому на первых этапах желательно прописывать каждую мелочь. Похвастаться можно только в будущем, когда освоены азы.
Чтобы было проще складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделите НОК на знаменатель каждой дроби и получите дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на их дополнительные множители;
- Сложите дроби с одинаковыми знаменателями;
- Если ответ представляет собой неправильную дробь, выберите ее целую часть;
Пример 2. Найти значение выражения
Найти значение выражения
.
Воспользуемся приведенными выше инструкциями.
Шаг 1. Найдите НОК знаменателей дробей
Найдите НОК знаменателей обеих дробей. Знаменатели дробей — числа 2, 3 и 4.
Шаг 2: Разделите НОК на знаменатель каждой дроби и получите дополнительный множитель для каждой дроби
Разделите НОК на знаменатель первой фракции. НОК равно 12, а знаменатель первой дроби равен 2. Разделим 12 на 2, получим 6. Получим первый дополнительный множитель 6. Запишем его над первой дробью:
Теперь разделите НОК на знаменатель второй дроби. НОК равно 12, а знаменатель второй дроби равен 3. Делим 12 на 3 и получаем 4. У нас есть второй дополнительный множитель 4. Запишем его над второй дробью:
Теперь разделим НОК на знаменатель третья дробь. НОК равно 12, а знаменатель третьей дроби равен 4. Делим 12 на 4 и получаем 3. У нас есть третий дополнительный множитель 3. Запишем его над третьей дробью:
У нас есть третий дополнительный множитель 3. Запишем его над третьей дробью:
Шаг 3: Умножьте числители и знаменатели фракций на их дополнительные множители
, умножьте числители и знаменатели на их дополнительные множители:
. установили, что дроби с разными знаменателями превращаются в дроби с одинаковыми (общими) знаменателями. Осталось сложить эти дроби. Складываем их:
Добавление не помещалось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это разрешено в математике. Когда выражение не помещается на одной строке, оно переносится на следующую строку, и вы должны поставить знак равенства (=) в конце первой строки и в начале новой строки. Знак равенства во второй строке указывает на то, что это продолжение выражения, которое было в первой строке.
Шаг 5. Если ответом является неправильная дробь, выберите целую часть
Наш ответ — неправильная дробь. Мы должны изолировать целую часть от него. Делаем:
Мы должны изолировать целую часть от него. Делаем:
Получили ответ
Упражнения:
Задание 1. Найти значение выражения:
Решение:
Показать решение
0 Задание 0.00032 выражение:Решение:
Показать решение
Видеоурок
4.5 Сложение и вычитание дробей с разными знаменателями — Преалгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Найдите наименьший общий знаменатель (LCD)
- Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея
- Сложение и вычитание дробей с разными знаменателями
- Определение и использование дробных операций
- Используйте порядок операций для упрощения сложных дробей
- Вычислить переменные выражения с дробями
Приготовься 4.
 12
12Прежде чем приступить к работе, пройдите этот тест на готовность.
Найдите две дроби, равные 56,56.
Если вы пропустили эту проблему, просмотрите пример 4.14.
Приготовься 4.13
Упрощение: 1+5·322+4,1+5·322+4.
Если вы пропустили эту проблему, просмотрите пример 4.48.
Найдите наименьший общий знаменатель
В предыдущем разделе мы объяснили, как складывать и вычитать дроби с общим знаменателем. Но как складывать и вычитать дроби с разными знаменателями?
Давайте снова подумаем о монетах. Можете ли вы добавить одну четверть и один цент? Можно сказать, что есть две монеты, но это не очень полезно. Чтобы найти общую стоимость одной четверти плюс один цент, вы заменяете их на одну и ту же единицу — центы. Одна четверть равна 2525 центам, а один дайм равен 1010 центам, поэтому сумма равна 3535 центам. См. Рисунок 4.7.
Рисунок
4.7
Вместе четверть и дайм стоят 3535 центов, или 3510035100 долларов.
Точно так же, когда мы складываем дроби с разными знаменателями, мы должны преобразовать их в эквивалентные дроби с общим знаменателем. С монетами, когда мы конвертируем в центы, знаменатель равен 100.100. Поскольку в одном долларе 100100 центов, 2525 центов составляют 2510025100, а 1010 центов составляют 10100,10100. Таким образом, мы добавляем 25100+1010025100+10100, чтобы получить 35100,35100, что составляет 3535 центов.
Вы научились складывать и вычитать дроби с общим знаменателем. Теперь посмотрим, что нужно делать с дробями, имеющими разные знаменатели.
Во-первых, мы будем использовать фрагменты дробей для моделирования нахождения общего знаменателя 1212 и 13,13.
Начнем с одной плитки 1212 и плитки 1313. Мы хотим найти плитку общей дроби, которую мы можем использовать для точного соответствия и 1212 и 1313.
Если мы попробуем 1414 штук, 22 из них в точности совпадают с 1212 частями, но они не совсем соответствуют 1313 штукам.
Если мы попробуем 1515 штук, они точно не охватывают 1212 или 1313 штук.
Если мы попробуем 1616 частей, мы увидим, что ровно 33 из них покрывают 1212 частей, и ровно 22 из них покрывают 1313 частей.
Если бы мы попробовали 112112 штук, они бы тоже сработали.
Тайлы даже меньшего размера, такие как 124124 и 148,148, точно покрывают 1212 и 1313 частей.
Знаменатель наибольшей части, покрывающей обе дроби, является наименьшим общим знаменателем (НОД) двух дробей. Итак, наименьший общий знаменатель чисел 1212 и 1313 равен 6,6.
Обратите внимание, что все плитки, покрывающие числа 1212 и 1313, имеют нечто общее: их знаменатели являются кратными числам 22 и 3,3, знаменателям 1212 и 13,13. Наименьшее общее кратное (НОК) знаменателей равно 6,6, поэтому мы говорим, что 66 является наименьшим общим знаменателем (НОК) дробей 1212 и 13,13.
Манипулятивная математика
Выполнение упражнения по манипулятивной математике «Нахождение наименьшего общего знаменателя» поможет вам лучше понять ЖКД.
Наименьший общий знаменатель
Наименьший общий знаменатель (НОД) двух дробей равен наименьшему общему кратному (НОК) их знаменателей.
Чтобы найти НОК двух дробей, найдем НОК их знаменателей. Мы следуем процедуре, которую мы использовали ранее, чтобы найти НОК двух чисел. При нахождении ЖК мы используем только знаменатели дробей, а не числители.
Пример 4,63
Найдите ЖК-дисплей для дробей 712712 и 518,518.
Решение
| Разложите каждый знаменатель на его простые числа. | |
| Перечислите простые числа от 12 и простые числа от 18, по возможности выстроив их в столбцы. | |
| Снести колонны. | |
| Умножьте множители. Продукт LCM. | НОК=36=36 |
LCM 12 и 18 равен 36, поэтому LCD 712712 и 518518 равен 36. | LCD 712712 и 518518 36. |
Попытайся 4.125
Найдите наименьший общий знаменатель дробей: 712712 и 1115,1115.
Попытайся 4.126
Найдите наименьший общий знаменатель дробей: 13151315 и 175,175.
Чтобы найти НОК двух дробей, найдите НОК их знаменателей. Обратите внимание, что шаги, показанные ниже, похожи на шаги, которые мы предприняли, чтобы найти LCM.
Как
Найдите наименьший общий знаменатель (НОД) двух дробей.
- Шаг 1. Разложите каждый знаменатель на его простые числа.
- Шаг 2. Перечислите простые числа, по возможности сопоставляя простые числа в столбцах.
- Шаг 3. Снести колонны.
- Шаг 4. Умножьте факторы. Произведение представляет собой НОК знаменателей.
- Шаг 5. LCM знаменателей — это LCD дробей.
Пример 4,64
Найдите наименьший общий знаменатель дробей 815815 и 1124,1124.
Решение
Чтобы найти ЖК, находим НОК знаменателей.
Найдите LCM 1515 и 24.24.
LCM 1515 и 2424 равен 120,120. Итак, LCD 815815 и 11241124 — 120.120.
Попытайся 4.127
Найдите наименьший общий знаменатель дробей: 13241324 и 1732,1732.
Попытайся 4.128
Найдите наименьший общий знаменатель дробей:
8 и 2132,2132.
Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея
Ранее мы использовали фрагменты дробей, чтобы увидеть, что ЖК-дисплей 1414, когда 1616 равен 12,12. Мы видели, что три 112112 штук точно покрывают 1414, а две 112112 штук точно покрывают 16,16, поэтому
14=312 и 16=212.14=312 и 16=212.
Мы говорим, что 1414 и 312312 — эквивалентные дроби, а также что 1616 и 212212 — эквивалентные дроби.
Мы можем использовать свойство эквивалентных дробей, чтобы алгебраически преобразовать дробь в эквивалентную. Помните, что две дроби эквивалентны, если они имеют одинаковое значение. Свойство Equivalent Fractions повторяется ниже для справки.
Помните, что две дроби эквивалентны, если они имеют одинаковое значение. Свойство Equivalent Fractions повторяется ниже для справки.
Свойство эквивалентных фракций
Если a,b,ca,b,c — целые числа, где b≠0,c≠0,b≠0,c≠0, то
ab=a·cb·canda·cb·c=abab=a ·cb·canda·cb·c=ab
Чтобы складывать или вычитать дроби с разными знаменателями, нам сначала нужно преобразовать каждую дробь в эквивалентную дробь с помощью ЖК-дисплея. Давайте посмотрим, как заменить 1414 и 1616 на эквивалентные дроби со знаменателем 1212 без использования моделей.
Пример 4,65
Перевести 1414 и 1616 в эквивалентные дроби со знаменателем 12,12, их ЖК.
Решение
| Найдите ЖК-дисплей. | ЖК-дисплей моделей 1414 и 1616 равен 12. |
| Найдите число, на которое нужно умножить 4, чтобы получить 12. | |
Найдите число, на которое нужно умножить 6, чтобы получить 12. | |
| Используйте свойство «Эквивалентные дроби», чтобы преобразовать каждую дробь в эквивалентную дробь с помощью ЖК-дисплея, умножив числитель и знаменатель каждой дроби на одно и то же число. | |
| Упростите числители и знаменатели. |
Полученные дроби не уменьшаем. Если бы мы это сделали, мы бы вернулись к нашим первоначальным дробям и потеряли бы общий знаменатель.
Попытайся 4.129
Замена на эквивалентные дроби с помощью ЖКИ:
3434 и 56,56, ЖКИ =12=12
Попытайся 4.130
Замена эквивалентных дробей на ЖК-дисплее:
−712−712 и 1115,1115, LCD =60=60
Как
Преобразуйте две дроби в эквивалентные дроби с их ЖК-дисплеем в качестве общего знаменателя.
- Шаг 1. Найдите ЖК.
- Шаг 2.
Для каждой дроби определите число, необходимое для умножения знаменателя, чтобы получить ЖК.

- Шаг 3. Используйте свойство «Эквивалентные дроби», чтобы умножить числитель и знаменатель на число, которое вы нашли на шаге 2.
- Шаг 4. Упростите числитель и знаменатель.
Пример 4,66
Перевести 815815 и 11241124 в эквивалентные дроби со знаменателем 120,120, их ЖК.
Решение
| ЖК-дисплей 120. Мы начнем с шага 2. | |
| Найдите число, на которое нужно умножить 15, чтобы получить 120. | |
| Найдите число, на которое нужно умножить 24, чтобы получить 120. | |
| Использовать свойство «Эквивалентные дроби». | |
| Упростите числители и знаменатели. |
Попытайся 4.131
Замена на эквивалентные дроби с ЖК-дисплеем:
13241324 и 1732,1732, ЖК-дисплей 9696
Попытайся 4.
 132
132Замена на эквивалентные дроби с ЖК-дисплеем:
8 и 2732,2732, ЖК-дисплей 224224
Сложение и вычитание дробей с разными знаменателями
После преобразования двух дробей в эквивалентные формы с общими знаменателями мы можем складывать или вычитать их, добавляя или вычитая числители.
Как
Сложите или вычтите дроби с разными знаменателями.
- Шаг 1. Найдите ЖК.
- Шаг 2. Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в качестве знаменателя.
- Шаг 3. Сложите или вычтите дроби.
- Шаг 4. Запишите результат в упрощенной форме.
Пример 4,67
Добавить: 12+13.12+13.
Решение
| 12+1312+13 | |
Найдите ЖК-дисплей 2, 3. | |
| Преобразование в эквивалентные дроби с помощью ЖК-дисплея 6. | |
| Упростите числители и знаменатели. | 36+2636+26 |
| Доп. | 5656 |
Помните, всегда проверяйте, можно ли упростить ответ. Поскольку числа 55 и 66 не имеют общих делителей, дробь 5656 сократить нельзя.
Попытайся 4.133
Добавить: 14+13.14+13.
Попытайся 4.134
Добавить: 12+15.12+15.
Пример 4,68
Вычесть: 12-(-14).12-(-14).
Решение
| 12-(-14)12-(-14) | |
| Найдите ЖК-экран 2 и 4. | |
Перепишите эквивалентные дроби с помощью ЖК-дисплея 4. | |
| Упростите первую дробь. | 24-(-14)24-(-14) |
| Вычесть. | 2-(-1)42-(-1)4 |
| Упрощение. | 3434 |
У одной из дробей уже был наименьший общий знаменатель, поэтому нам оставалось только преобразовать другую дробь.
Попытайся 4.135
Упрощение: 12−(−18).12−(−18).
Попытайся 4.136
Упрощение: 13−(−16).13−(−16).
Пример 4,69
Добавить: 712+518.712+518.
Решение
| 712+518712+518 | |
| Найдите ЖК 12 и 18. | |
| Перепишите как эквивалентные дроби с помощью ЖК-дисплея. | |
Упростите числители и знаменатели. | 2136+10362136+1036 |
| Доп. | 31363136 |
Поскольку 3131 — простое число, оно не имеет общих делителей с 36,36. Ответ упрощен.
Попытайся 4.137
Добавить: 712+1115.712+1115.
Попытайся 4.138
Добавить: 1315+1720.1315+1720.
Когда мы используем свойство Equivalent Fractions, есть быстрый способ найти число, на которое нужно умножить, чтобы получить LCD. Запишите множители знаменателей и LCD так же, как вы это делали, чтобы найти LCD. «Недостающие» множители каждого знаменателя — это числа, которые вам нужны.
LCD, 36,36, имеет 22 коэффициента 22 и 22 коэффициента 3,3.
Двенадцать имеет два множителя 2,2, но только один из 33, поэтому ему «не хватает» одного 3,3. Мы умножили числитель и знаменатель 712712 на 33, чтобы получить эквивалентную дробь со знаменателем 36,36.
В восемнадцати отсутствует один делитель 22, поэтому вы умножаете числитель и знаменатель 518518 на 22, чтобы получить эквивалентную дробь со знаменателем 36,36. Мы будем применять этот метод при вычитании дробей в следующем примере.
Мы будем применять этот метод при вычитании дробей в следующем примере.
Пример 4,70
Вычесть: 715−1924,715−1924.
Решение
| 715−1 5−1924 | |
| Найдите ЖК-дисплей. 15 «отсутствует» три множителя из 2 24 «отсутствует» множитель 5 | |
| Перепишите как эквивалентные дроби с помощью ЖК-дисплея. | |
| Упростите каждый числитель и знаменатель. | 56120−9512056120−95120 |
| Вычесть. | −39120−39120 |
| Перепишите, указав общий делитель 3. | −13·340·3−13·340·3 |
| Удалите общий множитель для упрощения. | −1340−1340 |
Попытайся 4.
 139
139Вычесть: 1324−1732,1324−1732.
Попытайся 4.140
Вычесть: 2132−928,2132−928.
Пример 4,71
Добавить: −1130+2342.−1130+2342.
Решение
| −1130+2342−1130+2342 | |
| Найдите ЖК-дисплей. | |
| Перепишите как эквивалентные дроби с помощью ЖК-дисплея. | |
| Упростите каждый числитель и знаменатель. | −77210+115210−77210+115210 |
| Доп. | 3821038210 |
| Перепишите, указав общий делитель 2. | 19·2105·219·2105·2 |
| Удалите общий множитель для упрощения. | 1 |
Попытайся 4.
 141
141Добавить: −1342+1735.−1342+1735.
Попытайся 4.142
Добавить: −1924+1732.−1924+1732.
В следующем примере одна из дробей содержит переменную в числителе. Выполняем те же действия, что и в случае, когда оба числителя являются числами.
Пример 4,72
Добавить: 35+x8.35+x8.
Решение
Дроби имеют разные знаменатели.
| 35+x835+x8 | |
| Найдите ЖК-дисплей. | |
| Перепишите как эквивалентные дроби с помощью ЖК-дисплея. | |
| Упростите числители и знаменатели. | 2440+5×402440+5×40 |
| Доп. | 24+5×4024+5×40 |
Мы не можем добавить 2424 и 5x5x, так как они не похожи на термы, поэтому мы не можем еще больше упростить выражение.
Попытайся 4.143
Добавить: y6+79.y6+79.
Попытайся 4.144
Добавить: x6+715.x6+715.
Определение и использование дробных операций
К этому моменту в этой главе вы научились умножать, делить, складывать и вычитать дроби. В следующей таблице приведены эти четыре дробные операции. Помните: общий знаменатель нужен для сложения или вычитания дробей, но не для умножения или деления дробей
Сводка операций с дробями
Умножение дробей: Умножить числители и умножить знаменатели.
ab·cd=acbdab·cd=acbd
Деление дроби: Умножьте первую дробь на величину, обратную второй.
ab÷cd=ab·dcab÷cd=ab·dc
Сложение дроби: Сложите числители и поместите сумму над общим знаменателем. Если дроби имеют разные знаменатели, сначала преобразуйте их в эквивалентные формы с помощью ЖК-дисплея.
ac+bc=a+bcac+bc=a+bc
Вычитание дробей: Вычтите числители и поместите разницу над общим знаменателем. Если дроби имеют разные знаменатели, сначала преобразуйте их в эквивалентные формы с помощью ЖК-дисплея.
Если дроби имеют разные знаменатели, сначала преобразуйте их в эквивалентные формы с помощью ЖК-дисплея.
ac-bc=a-bcac-bc=a-bc
Пример 4,73
Упрощение:
- ⓐ−14+16−14+16
- ⓑ−14÷16−14÷16
Решение
Сначала мы спрашиваем себя: «Что такое операция?»
ⓐ Операция сложения.
Имеют ли дроби общий знаменатель? №
| −14+16−14+16 | |
| Найдите ЖК-дисплей. | |
| Перепишите каждую дробь как эквивалентную дробь с помощью ЖК-дисплея. | |
| Упростите числители и знаменатели. | −312+212−312+212 |
| Сложите числители и поместите сумму над общим знаменателем. | −112−112 |
Проверьте, можно ли упростить ответ. Оно не может. Оно не может. |
ⓑ Операция деления. Нам не нужен общий знаменатель.
| −14÷16−14÷16 | |
| Чтобы разделить дроби, умножьте первую дробь на величину, обратную второй. | −14·61−14·61 |
| Умножение. | −64−64 |
| Упрощение. | −32−32 |
Попытайся 4.145
Упростите каждое выражение:
- ⓐ −34−16−34−16
- ⓑ −34·16−34·16
Попытайся 4.146
Упростите каждое выражение:
- ⓐ56÷(−14)56÷(−14)
- ⓑ56-(-14)56-(-14)
Пример 4,74
Упрощение:
- ⓐ5×6−3105×6−310
- ⓑ5×6·3105×6·310
Решение
ⓐ Операция вычитания. Дроби не имеют общего знаменателя.
Дроби не имеют общего знаменателя.
| 5×6-3105×6-310 | |
| Перепишите каждую дробь как эквивалентную дробь с помощью ЖК-дисплея, 30. | 5x·56·5−3·310·35x·56·5−3·310·3 |
| 25×30− | |
| Вычтите числители и поместите разницу над общим знаменателем. | 25x− |
ⓑ Операция умножения; нет необходимости в общем знаменателе.
| 5×6·3105×6·310 | |
| Чтобы умножить дроби, умножьте числители и умножьте знаменатели. | 5x·36·105x·36·10 |
| Перепишите, показав общие множители. | 5·x·32·3·2·55·x·32·3·2·5 |
| Удалите общие множители для упрощения. | х4х4 |
Попытайся 4.
 147
147 Упрощение:
- ⓐ(27a−32)36(27a−32)36
- ⓑ2a32a3
Попытайся 4.148
Упрощение:
- ⓐ(24k+25)30(24k+25)30
- ⓑ24k524k5
Использование порядка операций для упрощения сложных дробей
В разделе Умножение и деление смешанных чисел и сложных дробей мы видели, что сложная дробь — это дробь, в которой числитель или знаменатель содержит дробь. Мы упростили сложные дроби, переписав их как задачи на деление. Например,
3458=34÷583458=34÷58
Теперь рассмотрим сложные дроби, в которых можно упростить числитель или знаменатель. Чтобы следовать порядку операций, сначала упростим числитель и знаменатель по отдельности. Затем делим числитель на знаменатель.
Как
Упрощайте сложные дроби.
- Шаг 1. Упростите числитель.
- Шаг 2.
Упростите знаменатель.

- Шаг 3. Разделите числитель на знаменатель.
- Шаг 4. Упростите, если возможно.
Пример 4,75
Упрощение: (12)24+32.(12)24+32.
Решение
| (12)24+32(12)24+32 | |
| Упростите числитель. | 144+32144+32 |
| Упростите член с показателем степени в знаменателе. | 144+9144+9 |
| Сложите члены в знаменателе. | 14131413 |
| Разделите числитель на знаменатель. | 14÷1314÷13 |
| Перепишите как умножение на обратное. | 14·11314·113 |
| Умножение. | 152152 |
Попытайся 4.149
Упрощение: (13)223+2(13)223+2.
Попытайся 4.150
Упрощение: 1+42(14)21+42(14)2.
Пример 4,76
Упрощение: 12+2334−16,12+2334−16.
Решение
| 12+2334−1612+2334−16 | |
| Перепишите числитель с НР равным 6 и знаменатель с НР равным 12. | 36+46912−21236+46912−212 |
| Добавить в числителе. Вычесть в знаменателе. | 7671276712 |
| Разделите числитель на знаменатель. | 76÷71276÷712 |
| Перепишите как умножение на обратное. | 76·12776·127 |
| Перепишите, показав общие множители. | 7·6·26·7·17·6·26·7·1 |
| Упрощение. | 2 |
Попытайся 4.151
Упрощение: 13+1234−1313+1234−13.
Попытайся 4.152
Упрощение: 23−1214+1323−1214+13.
Вычисление переменных выражений с дробями
Раньше мы вычисляли выражения, но теперь мы также можем вычислять выражения с дробями. Помните, чтобы вычислить выражение, мы подставляем значение переменной в выражение, а затем упрощаем.
Помните, чтобы вычислить выражение, мы подставляем значение переменной в выражение, а затем упрощаем.
Пример 4,77
Оценить x+13x+13, когда
- ⓐx=−13x=−13
- ⓑx=-34.x=-34.
Решение
ⓐ Чтобы вычислить x+13x+13, когда x=-13,x=-13, подставьте -13-13 вместо xx в выражении.
| х+13х+13 | |
| Упрощение. | 00 |
ⓑ Чтобы вычислить x+13x+13, когда x=-34,x=-34, мы заменяем xx в выражении на -34-34.
| х+13х+13 | |
| Переписать как эквивалентные дроби с помощью LCD, 12. | −3·34·3+1·43·4−3·34·3+1·43·4 |
Упростите числители и знаменатели. | −912+412−912+412 |
| Доп. | −512−512 |
Попытайся 4.153
Оценка: x+34x+34, когда
- ⓐ x=−74x=−74
- ⓑ х=-54х=-54
Попытайся 4.154
Оценка: y+12y+12, когда
- ⓐ y=23y=23
- ⓑ у=-34у=-34
Пример 4,78
Оценить y-56y-56, когда y=-23.y=-23.
Решение
Подставляем в выражение -23-23 вместо yy.
| г-56г-56 | |
| Переписать эквивалентные дроби с помощью LCD, 6. | −46−56−46−56 |
| Вычесть. | −96−96 |
| Упрощение. | −32−32 |
Попытайся 4.155
Оценка: y-12y-12, когда y=-14. y=-14.
y=-14.
Попытайся 4.156
Вычислить: x−38x−38, когда x=−52.x=−52.
Пример 4,79
Вычислите 2x2y2x2y, когда x=14x=14 и y=-23.y=-23.
Решение
Подставьте значения в выражение. В 2x2y,2x2y показатель степени применяется только к x.x.
| Сначала упростите показатели степени. | |
| Умножение. Произведение будет отрицательным. | |
| Упрощение. | |
| Удалить общие множители. | |
| Упрощение. |
Попытайся 4.157
Оценить. 3ab23ab2, когда a=-23a=-23 и b=-12.b=-12.
Попытайся 4.158
Оценка. 4c3d4c3d, когда c=-12c=-12 и d=-43. d=-43.
d=-43.
Пример 4,80
Оценить p+qrp+qr, когда p=-4,q=-2,p=-4,q=-2 и r=8.r=8.
Решение
Подставляем значения в выражение и упрощаем.
| р+qrp+qr | |
| Сначала добавьте числитель. | −68−68 |
| Упрощение. | −34−34 |
Попытайся 4.159
Оценка: a+bca+bc, когда a=-8,b=-7,a=-8,b=-7 и c=6.c=6.
Попытайся 4.160
Оценка: x+yzx+yz, когда x=9,y=-18,x=9,y=-18 и z=-6.z=-6.
Раздел 4.5 Упражнения
Практика ведет к совершенству
Найдите наименьший общий знаменатель (НОД)
В следующих упражнениях найдите наименьший общий знаменатель (НОД) для каждого набора дробей.
316.
2323 и 3434
317.
3434 и 2525
318.
712712 и 5858
319.
6 и 712712320.
13301330 и 25422542
321.
23302330 и 548548
322.
21352135 и 39563956
323.
18351835 и 33493349
324.
23,16,23,16 и 3434
325.
23,14,23,14 и 3535
Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея
В следующих упражнениях преобразуйте дроби в эквивалентные дроби с помощью ЖК-дисплея.
326.
1313 и 14,14, LCD =12=12
327.
1414 и 15,15, LCD =20=20
328.
512512 и 78,78, LCD =24=24
329.
712712 и 58,58, LCD =24=24
330.
13161316 и -1112,-1112, LCD =48=48
331.
11161116 и -512,-512, LCD =48=48
332.
13,56,13,56 и 34,34, LCD =12=12
333.
13,34,13,34 и 35,35, LCD =60=60
Сложение и вычитание дробей с разными знаменателями
В следующих упражнениях сложите или вычтите. Запишите результат в упрощенной форме.
334.
13+1513+15
335.
14+1514+15
336.
12+1712+17
337.
13+1813+18
338.
13−(−19)13−(−19)
339.
14−(−18)14−(−18)
340.
15-(-110)15-(-110)
341.
12-(-16)12-(-16)
342.
23+3423+34
343.
34+2534+25
344.
712+58712+58
345.
512+38512+38
346.
712−
2−916347.
716−512716−512
348.
1112−381112−38
349.
58−71258−712
350.
23−3823−38
351.
56−3456−34
352.
−1130+2740−1130+2740
353.
−920+1730−920+1730
354.
−1330+2542−1330+2542
355.
−2330+548−2330+548
356.
−3956−2235−3956−2235
357.
−3349−1835−3349−1835
358.
−23−(−34)−23−(−34)
359.
−34−(−45)−34−(−45)
360.
−916−(−45)−916−(−45)
361.
−720−(−58)−720−(−58)
362.
1+781+78
363.
1+561+56
364.
1−591−59
365.
1−3101−310
366.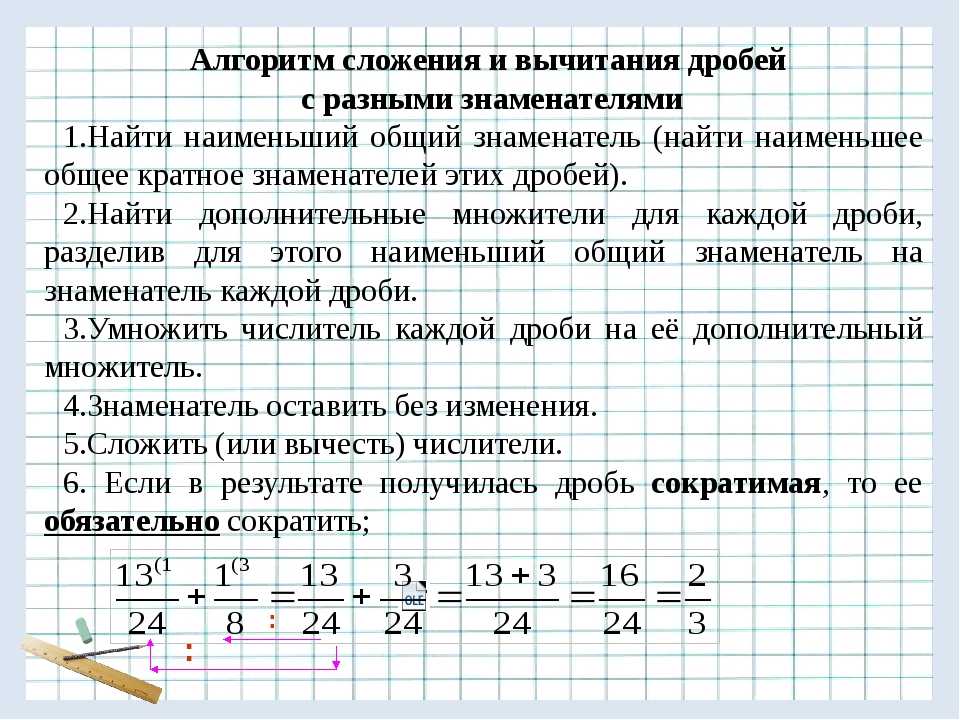
х3+14х3+14
367.
у2+23у2+23
368.
у4-35у4-35
369.
х5-14х5-14
Определение и использование дробных операций
В следующих упражнениях выполните указанные операции. Запишите ответы в упрощенной форме.
370.
- ⓐ34+1634+16
- ⓑ34÷1634÷16
371.
- ⓐ23+1623+16
- ⓑ23÷1623÷16
372.
- ⓐ-25−18-25−18
- ⓑ-25·18-25·18
373.
- ⓐ-45−18-45−18
- ⓑ-45·18-45·18
374.
- ⓐ5n6÷8155n6÷815
- ⓑ5n6−8155n6−815
375.
- ⓐ3a8÷7123a8÷712
- ⓑ3a8−7123a8−712
376.
- ⓐ910·(−11d12)910·(−11d12)
- ⓑ910+(-11d12)910+(-11d12)
377.
- ⓐ415·(−5q9)415·(−5q9)
- ⓑ415+(-5q9)415+(-5q9)
378.
−38÷(−310)−38÷(−310)
379.
−512÷(−59)−512÷(−59)
380.
−38+512−38+512
381.
−18+712−18+712
382.
56−1956−19
383.
59−1659−16
384.
38·(−1021)38·(−1021)
385.
712·(−835)712·(−835)
386.
−715−y4−715−y4
387.
−38−x11−38−x11
388.
1112а·9а161112а·9а16
389.
10y13·815y10y13·815y
Используйте порядок операций для упрощения сложных дробей
В следующих упражнениях упрощайте.
390.
(15)22+32(15)22+32
391.
(13)25+22(13)25+22
392.
23+42(23)223+42(23)2
393.
33−32(34)233−32(34)2
394.
(35)2(37)2(35)2(37)2
395.
(34)2(58)2(34)2(58)2
396.
213+15213+15
397.
514+13514+13
398.
23+1234−2323+1234−23
399.
34+1256−2334+1256−23
400.
78−2312+3878−2312+38
401.
34−3514+2534−3514+25
Смешанная практика
В следующих упражнениях упрощайте.
402.
12+23·51212+23·512
403.
13+25·3413+25·34
404.
1−35÷1101−35÷110
405.
1−56÷1121−56÷112
406.
23+16+3423+16+34
407.
23+14+3523+14+35
408.
38−16+3438−16+34
409.
25+58−3425+58−34
410.
12(920-415)12(920-415)
411.
8(1516−56)8(1516−56)
412.
58+161+161924
413.
16+310143016+3101430
414.
(59+16)÷(23−12)(59+16)÷(23−12)
415.
(34+16)÷(58−13)(34+16)÷(58−13)
В следующих упражнениях оцените заданное выражение. Ответы представьте в упрощенной форме, используя при необходимости неправильные дроби.
416.
x+12x+12 когда
- ⓐx=−18x=−18
- ⓑx=-12x=-12
417.
x+23x+23 когда
- ⓐx=−16x=−16
- ⓑx=-53x=-53
418.
х+(-56)х+(-56) когда
- ⓐx=13x=13
- ⓑx=-16x=-16
419.
х+(-1112)х+(-1112) когда
- ⓐx=1112x=1112
- ⓑх=34х=34
420.
x-25x-25 когда
- ⓐx=35x=35
- ⓑx=-35x=-35
421.
x-13x-13 когда
- ⓐx=23x=23
- ⓑx=-23x=-23
422.
710-w710-w когда
- ⓐw=12w=12
- ⓑw=-12w=-12
423.
512-w512-w когда
- ⓐw=14w=14
- ⓑw=-14w=-14
424.
4p2q4p2q при p=-12p=-12 и q=59q=59
425.
5m2n5m2n при m=−25m=−25 и n=13n=13
426.
2x2y32x2y3, когда x=-23x=-23 и y=-12y=-12
427.
8u2v38u2v3 при u=-34u=-34 и v=-12v=-12
428.
u+vwu+vw при u=-4,v=-8,w=2u=-4,v=-8,w=2
429.
m+npm+np при m=-6,n=-2,p=4m=-6,n=-2,p=4
430.
a+ba-ba+ba-b когда a=-3,b=8a=-3,b=8
431.
r-sr+sr-sr+s при r=10,s=-5r=10,s=-5
Математика на каждый день
432.
Декорирование Ларонда делает чехлы для декоративных подушек на свой диван. На каждую наволочку ей нужно 316316 ярдов набивной ткани и 3838 ярдов однотонной ткани. Какое общее количество ткани нужно Ларонде для каждой наволочки?
433.
Выпечка Ванесса печет печенье с шоколадной крошкой и овсяное печенье. Ей нужно 114114 чашек сахара для шоколадного печенья и 118118 чашек для овсяного печенья. Сколько всего сахара ей нужно?
Письменные упражнения
434.
Объясните, почему для сложения или вычитания дробей необходимо иметь общий знаменатель.
435.
Объясните, как найти ЖК двух дробей.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ После просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующему разделу? Почему или почему нет?
Математика 1010 онлайн — Дроби
Математика 1010 онлайн — ДробиКафедра математики — Колледж науки — Университет Юты
Дробь это выражение
где и находятся
целые числа и . На этой странице мы рассмотрим некоторые основные факты
про дроби. Мы также увидим, почему эти факты верны. Способ
мы будем подходить к вопросам будет типичным для подхода к виду математики
вы узнаете очень глубоко в этом классе.
Мы также увидим, почему эти факты верны. Способ
мы будем подходить к вопросам будет типичным для подхода к виду математики
вы узнаете очень глубоко в этом классе.
Вы знакомы с этими фактами :
- Число над дробью — это .
числитель , а число внизу знаменатель дроби.
Целое число можно рассматривать как дробь со знаменателем, равным до 1.
Умножение числителя и знаменателя дроби на тот же ненулевой множитель не меняет дробь. (в начальной используется термин , эквивалентный дробям, но более зрелый взгляд состоит в том, что эквивалентные дроби обозначают одно и то же действительное число, и, следовательно, не нужно различать, кроме как для ясности и простоты.)
Дроби с одинаковыми знаменателями складываются (или вычитаются) с помощью добавить (или вычесть) числители (с сохранением знаменателя).
Дроби с различными знаменателями сначала переворачиваются
на дроби с одинаковыми знаменателями, умножая числители
и знаменатели с подходящими множителями, а затем сложены по правилу
выше.
Дроби умножаются путем умножения числителей и умножение знаменателей.
обратная дроби получается заменой числители и знаменатели.
Деление дроби на другую эквивалентно умножение на обратную вторую дробь.
Обратите внимание, как мы объясняем сложение дробей с различными знаменатели в виде сложения дробей с одинаковыми знаменатель, а деление дробей по умножение дробей.
Они предоставляют экземпляры принцип, утверждение которого обманчиво простой, но чьи приложения и последствия имеют далеко идущие последствия:
Сведите свою проблему к той, которую вы уже решали раньше.
Что такое дробь?
Фракция, такая как
просто способ обозначить
результат деления 3 на 4. В общем, дробь обозначает результат деления на . (Это верно, даже если
и не являются целыми числами, иллюстрацией
принцип, что мы
давать определения в простых контекстах, а затем обобщать их так, чтобы
все соответствующие правила остаются в силе. Однако, если и не
целое, то выражение
называется отношением или частным.)
Однако, если и не
целое, то выражение
называется отношением или частным.)
Деление определяется как решение умножения проблема. Таким образом, дробь
является решением уравнения В более общем случае дробь является решением уравнение.
Важно понять это основное определение, поскольку все вышеперечисленные правила могут быть выведены из него.
Но нам нужен другой принцип
Если сделать то же самое с обеими частями уравнения, будет создано другое правильное уравнение. :
Умножение числителя и знаменателя на один и тот же множитель
Решение уравнения не изменится, если умножаем слева и справа на один и тот же коэффициент, чтобы получить эквивалентное уравнение . Мы имеем как непосредственное следствие приведенное выше тождество:
Конечно, это уравнение так же легко можно читать и справа налево. слева направо, что является основанием для отмены общие множители или , приводящие к наименьшим условиям.
Сложение дробей с одинаковыми знаменателями.
Предположим, нам даны две дроби
Как мы обсуждали, эти дроби определяются уравнениями
Теперь складываем обе части первого уравнения. Это даст другое правильное уравнение. Однако слева мы не будем использовать число , а вместо выражения . Мы можем сделать это, потому что второе уравнение утверждает, что равно . Отныне мы будем просто скажем, что мы добавляем второе уравнение к первым , но основное рассуждение состоит в том, что мы добавляем одно и то же с обеих сторон первое уравнение, мы просто даем ему разные имена с двух сторон уравнения. Эта операция дает новое уравнение
Его можно переписать как По определению дробей это сводится к утверждению, чтоПонятно, как это рассуждение применимо к обычным дробям с тот же знаменатель, и к вычитание (в отличие от сложение ) дробей.
Сложение дробей с разными знаменателями
При сложении двух дробей типа
а также
мы
сначала преобразовать их в дроби с одинаковым знаменателем, применив
правило номер 3 выше. Таким образом, мы должны найти общий
знаменатель . На практике чем меньше знаменатель, тем
легче манипулировать числами, и поэтому мы любим использовать наименьший общий знаменатель . Однако произведение двух
знаменатели всегда работают, и часто, как в этом случае,
наименьший общий знаменатель.
Итак, в этом примере мы используем
Таким образом, мы должны найти общий
знаменатель . На практике чем меньше знаменатель, тем
легче манипулировать числами, и поэтому мы любим использовать наименьший общий знаменатель . Однако произведение двух
знаменатели всегда работают, и часто, как в этом случае,
наименьший общий знаменатель.
Итак, в этом примере мы используем
Таким образом
Умножение дробей
Предположим, нам даны две дроби
Это означает, что и удовлетворяют уравнениям
Продолжая, как описано выше, и умножая на обе стороны от первого уравнение с , но вызывая его слева, получаем
Это можно переписать как
это другой способ сказать Конечно, мы можем упростить эту дробь, разделив числитель на знаменатель на 3:Разделение дробей
Предположим, мы хотим разделить те же дроби, что и выше. Поэтому мы просим что такое
Деление является обратным процессом умножения, поэтому удовлетворяет уравнение
или же Ответ можно получить, умножив обе части этого уравнение с обратной величиной , т. е. с
. Это становится что упрощает до
е. с
. Это становится что упрощает доНаибольшие общие факторы и наименьшие общие Мультипликаторы
кратное натурального числа равно произведение этого числа на другое натуральное число. За например, 12, 15, и 333333 кратны 3 . Фактор натурального число n — еще одно натуральное число, которое делит n без остатка. Например, (все) множители 12 равны 1, 2, 3, 4, 6, 12 . обыкновенный Множитель двух натуральных чисел m и n есть число, которое является коэффициентом m , а также n . За например, 8 является общим делителем 32 и 48 . Другими общими факторами являются 1, 2, 4, 8, 16 . Наибольший общий делитель — это именно то, что называется предполагает, поэтому наибольший общий делитель 32 и 48 16. Аналогично, обычный кратное двух чисел является кратным обоих, и наименьшее общее кратное наименьшее общее кратное. Например, 24, 120, 180 все распространены.
кратные 4 и 6 и 12 встречаются реже всего.
несколько.
Например, 24, 120, 180 все распространены.
кратные 4 и 6 и 12 встречаются реже всего.
несколько.Актуальность всего этого в том, что общий знаменатель двух дробей является общим кратным двух знаменатели, и наименьший общий знаменатель наименьший общее кратное двух знаменателей.
Наименьшее общее кратное НОК и наибольшая общая коэффициент GCF из двух чисел m и n связаны тем, что
НОК = m*n/GCFНапример, GCF 4 и 6 равен 2 , их наименьшее общее кратное равно 12 и действительно
12 = 4*6/2
Подумай об этом и пришли мне свое объяснение этого факта!
Смешанные номера
Смешанные числа — это дроби, записанные как натуральное число плюс дробь, у которой знаменатель больше числителя. За пример,
Смешанные числа популярны, потому что целая часть дает
указание их размера, но в остальном они мало что могут порекомендовать
их. Они составляют исключение (единственное исключение) из правила, согласно которому
отсутствующий оператор означает умножение, и они делают арифметику
операции выполнять труднее. Мы не будем использовать их в этом классе
и я рекомендую вам игнорировать их существование.
Они составляют исключение (единственное исключение) из правила, согласно которому
отсутствующий оператор означает умножение, и они делают арифметику
операции выполнять труднее. Мы не будем использовать их в этом классе
и я рекомендую вам игнорировать их существование.
Правила делимости
При работе с дробями удобно исключить общие делители в числителе и знаменателе, чтобы сохранить числители и знаменатели как можно меньше.Для больших числителей и знаменателей наиболее практичный способ нахождение общих множителей является евклидовым Алгоритм описан в другом месте, но для многих мелких факторов там доступны простые правила. Они перечислены в следующей таблице. Это хорошее упражнение, чтобы подумать, почему эти правила остаются в силе. если ты не могу понять, напишите мне!
| Factor | Rule | Examples |
| 2 | last digit is 0, 2, 4, 6, or 8 | 2, или 127174 |
| 3 | сумма цифр делится на 3 | 111
(s. o.d. = 1+1+1 = 3.) 111= 3*37, или 212 319 231 (s.o.d. = 24),
212 319 231 = 3*70 773 077. o.d. = 1+1+1 = 3.) 111= 3*37, или 212 319 231 (s.o.d. = 24),
212 319 231 = 3*70 773 077. |
| 4 | последние две цифры образуют номер, который делится на 4. | 1 232 или 12 135 432 196 |
| 5 | последняя цифра 0 или 5 | 58 213 475 |
| 6 | Применить тесты для 2 и 3 | 228 или 5,832 |
| 7 | нет хорошего теста, делим на 7 | 2,443 |
| 8 | последние три цифры образуют число, которое делится на 8. | 25 432 или 2 942 600 |
| 9 | сумма цифр делится на 9 | 111 (s.o.d. = 3+3+3=9.) 333= 9*37. 242 319 231 (s.d. = 27), или 242 319 231 = 9*26 924 359. |
| 10 | последняя цифра 0 | 20 или 123 456 780 |
Существует также хорошо известное правило делимости на 11. Вы образуете один
сумму, добавляя первую, третью, пятую и т. д. цифру, а другую —
прибавляя второе, четвертое, шестое и т.д. Число делится на 11
разница сумм. Например, предположим, что мы хотим
Проверьте
д. цифру, а другую —
прибавляя второе, четвертое, шестое и т.д. Число делится на 11
разница сумм. Например, предположим, что мы хотим
Проверьте
м = 5 123 456 789.
Сумма цифр в нечетных позициях равна 9+7+5+3+1 = 25. Сумма цифр в четных позициях равно 8+6+4+2+5 = 25. Разница 25-25 = 0. 0 делится на 11, поэтому м . Верно,
5 123 456 789 = 11*465 768 799.
Проверьте это!
Как складывать дроби за 3 шага и 5 увлекательных занятий Сложение дробей
Возможно, ваши ученики знают, как обращаться с числителем и знаменателем, но готовы ли они к тому, что будет дальше? Внезапно пора учиться как складывать дроби — и ваш класс запутался.
Чувствуете страх?
Вы не одиноки. Добавление дробей может показаться сложным, но это не обязательно.
Почему учащиеся испытывают трудности с дробями? Дроби — особенно операции с дробями — сложный предмет для большинства учащихся. Проблемы с дробями могут снизить уверенность в математике и привести к математическому беспокойству, если учащиеся не получают достаточной поддержки по предмету.
Проблемы с дробями могут снизить уверенность в математике и привести к математическому беспокойству, если учащиеся не получают достаточной поддержки по предмету.
Фракции — это борьба по нескольким причинам. Исследования показали, что самыми большими проблемами являются:
1. Понимание того, что означают числаПрежде чем дроби, студенты привыкли работать с целыми числами : основные числа, которые представляют целые суммы. Дроби знакомят учащихся с рациональными числами , которые имеют совершенно новый набор правил и шаблонов.
Значение дробей сбивает с толку, если сравнивать их с целыми числами. Целые числа выражаются только одним способом, в то время как дроби могут быть выражены разными способами и по-прежнему представляют одну и ту же сумму.
Например, существует только один способ представления числа три, но ²⁄₄ представляет то же количество, что и ½, 0,5 и 50%. Будучи студентом, это трудно уложить в голове.
Методы сложения, вычитания, умножения и деления целых чисел отличаются от тех же операций с дробями. Правила становятся гораздо более непредсказуемыми и запутанными. Многие учащиеся и учителя имеют ограниченное представление о том, как и почему используются эти методы.
Дроби сложнее представить с помощью визуальных или манипулятивных средств, а правила их добавления труднее понять. Изучение того, как умножать и делить дроби, может еще больше запутать, так как учащиеся должны помнить различия между этими операциями. Это большая корректировка для студентов, которые уже знакомы с арифметикой целых чисел.
Типы дробейСтуденты должны сначала понять разницу между каждым тип фракции , чтобы успешно добавить их.
Начнем с основных компонентов дроби.
Дробь представляет части целого. Числитель (верхнее число) показывает количество деталей, которые у вас есть. Знаменатель (нижнее число) показывает общее количество частей, на которые делится целое.
Знаменатель (нижнее число) показывает общее количество частей, на которые делится целое.
На приведенном выше рисунке наш круг разделен на четыре части. Это означает, что четыре — наш знаменатель. Из этих четырех частей одна выделена. Это означает, что один — наш числитель. Итак, наша дробь равна ¼ или одной четверти.
Существуют три основные категории дробей: Правильные, неправильные и смешанные.
В дополнение к этому уравнения дробей будут разделены на две отдельные категории: с подобными дробям и с непохожими дробями .
Базовые знания об этих типах помогут учащимся понять, что делать, когда они сталкиваются с вопросом о сложении дробей.
Теперь, когда вы знакомы с каждым типом дроби, вы можете приступить к сложению! Научите своих учеников приведенной ниже трехэтапной формуле, чтобы уверенно решать уравнения сложения дробей.
3 простых шага для сложения дробей Сначала это может показаться пугающим, но сложение дробей может быть простым. Все, что вам нужно сделать, это выполнить три простых шага:
Все, что вам нужно сделать, это выполнить три простых шага:
- Шаг 1: Найдите общий знаменатель
- Шаг 2: Сложите числители (и сохраните знаменатель)
- Шаг 3: Упростите дробь
Давайте рассмотрим каждый шаг в немного более подробно.
Шаг 1: Найдите общий знаменательЕсли ваши два знаменателя уже совпадают, вы складываете дроби с как знаменатели . Фантастика! Это означает, что вы можете перейти ко второму шагу.
Если у вас разные знаменатели, вы складываете дроби с в отличие от знаменателей. При сложении разных дробей необходимо найти общий знаменатель , чтобы можно было сложить две дроби вместе.
Посмотрите видео ниже, чтобы понять , почему нам нужен общий знаменатель для сложения дробей.
Вы можете найти общий знаменатель, используя эквивалентных дробей : дроби, имеющие одинаковое значение. Например, ²⁄₄, ³⁄₆ и ⁴⁄₈ являются эквивалентными дробями, потому что все они могут быть уменьшены до ½.
Существует два основных метода нахождения общего знаменателя.
1) Метод общего знаменателяВ этом методе вы умножаете верх и низ каждой дроби на знаменатель другой. Например, рассмотрим следующее уравнение:
⅓ + ⅙
Наши дроби имеют два разных знаменателя: три и шесть. Нам нужно умножить числитель и знаменатель в ⅓ на шесть, а затем умножить числитель и знаменатель в ⅙ на три.
Когда мы это сделаем, наши новые дроби станут ⁶⁄₁₈ и ³⁄₁₈.
Две новые дроби имеют одинаковый знаменатель, так что теперь мы можем их сложить!
2) Метод наименьшего общего знаменателяЭтот метод включает нахождение наименьшего из всех общих знаменателей, а затем умножение исходных дробей для получения этого знаменателя.
Чтобы найти наименьший общий знаменатель, перечислите все числа, кратные числу, и найдите среди них наименьшее число, которое совпадает.
Например, используя то же уравнение, что и раньше, — ⅓ + ⅙ — можно составить таблицу для определения наименьшего общего кратного.
Как видно из нашей таблицы, наименьшее число, кратное одному и тому же, равно шести.
Итак, для ⅓ числитель и знаменатель нужно умножить на два, чтобы получить ²⁄₆. Для ⅙ числа нужно умножить на единицу, чтобы дробь осталась прежней. И снова наши фракции готовы к добавлению!
Шаг 2: Сложите числители (сохраните знаменатель)Этот шаг довольно прост. Сложите числители, чтобы сумма стала новым числителем, а знаменатель остался прежним.
Давайте воспользуемся нашим предыдущим примером:
⅓ + ⅙
Используя наше новое уравнение из метода общего знаменателя — ⁶⁄₁₈ + ³⁄₁₈ — нам нужно сложить шесть и три вместе. В знаменателе по-прежнему будет восемнадцать.
Шесть плюс три равно девять, поэтому наш ответ ⁹⁄₁₈.
Шаг 3: Упростите дробьЕсли ваша дробь содержит большие числа, вам может понадобиться упростить ее.
Упрощение включает в себя нахождение наименьшей возможной эквивалентной дроби. В нашем предыдущем уравнении наш ответ был ⁹⁄₁₈. Это число кажется немного большим, поэтому посмотрим, сможем ли мы упростить его до более простого числа.
В нашем предыдущем уравнении наш ответ был ⁹⁄₁₈. Это число кажется немного большим, поэтому посмотрим, сможем ли мы упростить его до более простого числа.
Чтобы упростить дробь, вам нужен общий делитель : число, которое делится на оба числа поровну. Например, два — это общий делитель четырех и шести, потому что оба числа можно разделить на два.
Два самых простых метода упрощения дроби:
1) Метод проб и ошибокДля этого метода просто продолжайте делить числитель и знаменатель на маленькие числа. Начните с двух, затем трех, четырех и так далее, пока не получите наименьший возможный ответ.
С нашим ответом ⁹⁄₁₈ мы можем продолжать делить на маленькие числа, пока не найдем то, которое работает.
Можно ли разделить девять и восемнадцать на два? Нет. Мы не можем разделить девять на два поровну.
Хорошо, попробуем другой номер.
Можно ли разделить девять и восемнадцать на три? Да! Когда мы делим оба числа на три, наша дробь становится ³⁄₆.
Теперь, когда у нас есть более простой ответ, пришло время посмотреть, сможем ли мы упростить его еще больше. И три, и шесть можно снова разделить на три, поэтому наш окончательный ответ — ½.
2) Найдите наибольший общий делитель (НОД)НОД – это наибольшее число, которое делится на два или более чисел без остатка.
Этот метод похож на нахождение наименьшего общего знаменателя — вы найдете ответ, перечислив все возможные факторы.
Используя наш предыдущий пример с ⁹⁄₁₈, мы найдем и перечислим все делители каждого числа, начиная с единицы. После того, как вы перечислили все множители этого числа, все, что вам нужно сделать, это найти наибольшее число, повторяющееся в обоих списках.
Удобная таблица поможет и в этом.
Воспользуемся нашей таблицей, чтобы найти наибольшее число, общее для обоих чисел. В этом случае наибольший общий делитель для девяти и восемнадцати равен девяти. Теперь мы можем разделить оба числа на девять, чтобы получить уменьшенную дробь: ½.
Если объединить все три шага сложения дробей, получится следующее:
Сложение смешанных дробейВышеприведенные шаги отлично подходят для правильных и неправильных дробей, но как насчет сложения дробей с целыми числами?
Складывать смешанные дроби на самом деле очень просто: просто преобразуйте их в неправильные дроби, и вы готовы начать сложение!
Любую смешанную дробь можно превратить в неправильную. Например, 1 ¾ — это то же самое, что ⁷⁄₄.
Источник изображения: Central Bucks School District
Преобразование смешанных дробей в неправильные осуществляется в три этапа:
1. Умножьте целое число на знаменательВозьмем 1 ¾. Если мы умножим наше целое число (один) на наш знаменатель (четыре), мы получим четыре.
2. Добавьте это число к числителюНаше новое число (четыре) плюс наш числитель (три) равно семи.
3. Напишите новый числитель над исходным знаменателем Наш новый числитель (семь) над исходным знаменателем (четыре) равен ⁷⁄₄. Теперь вы можете сложить дробь!
Теперь вы можете сложить дробь!
Как учитель, вы, вероятно, хорошо знакомы с извечным вопросом, который задают ученики: «Зачем я вообще это делаю?»
В этом контексте это, безусловно, правильный вопрос. Почему сложение дробей так важно для изучения?
Во-первых, у этой арифметики есть множество реальных применений. Во многих случаях вам нужно будет найти общее количество частей целого, когда они объединены.
Вот несколько возможных примеров сложения дробей в реальной жизни:
- Упражнения : Если вы пробежали ¼ мили в понедельник и ¾ мили во вторник, какое расстояние вы пробежали за оба дня?
- Тайм-менеджмент : Если вы работаете 8 ½ часов в понедельник и 6 ¾ часов во вторник, сколько часов вы проработали в оба дня?
- Приготовление пищи/выпечка : Если вы добавите ½ стакана крошки из молочного шоколада и ⅓ чашки стружки из белого шоколада в тесто для печенья, каково общее количество шоколадной стружки в вашем рецепте?
Если этого недостаточно, знание операций с дробями на самом деле очень важно для изучения более сложных математических и естественных наук, что в конечном итоге приводит к успеху во многих академических или карьерных сферах.
Ограниченные знания в операциях с дробями могут привести к более слабым навыкам в более поздних математических и естественных науках. Одно исследование показало, что в Соединенных Штатах и Великобритании знание дробей учащимися начальных классов может предсказать общие математические способности в старшей школе.
Опрос навыков, технологий и методов управления на рабочем месте (STAMP) показал, что 68% работающих людей в возрасте 18 лет и старше использовали дроби в своей повседневной работе. Это означает, что значительному количеству взрослых в Соединенных Штатах требуется твердое базовое знание дробей и их операций. Изучение этих навыков как можно раньше является ключом к успеху на многих рабочих местах.
5 Увлекательные занятия по сложению дробей Теперь, когда вы знаете, чему научить своих учеников складывать дроби, давайте сосредоточимся на том, как. Вдохновитесь этими пятью увлекательными идеями занятий, которые дополнят ваши уроки сложения дробей.
Prodigy – это учебная платформа, ориентированная на учебную программу, с более чем 1 500 навыками, позволяющими детям практиковать математику. Используйте его, чтобы освоить все виды дробей, от базового понимания до более сложных операций, таких как сложение.
Prodigy отправляет игроков в захватывающее приключение, где они отвечают на математические вопросы, чтобы «сразиться» с другими персонажами. Платформа предназначена для того, чтобы вовлечь учащихся в игровой процесс, поэтому они действительно захотят, чтобы продолжала играть и, как результат, больше занималась математикой!
Платформа — отличный инструмент для дополнения уроков, домашних заданий и многого другого. Это также может помочь вам дифференцировать обучение и определить конкретные проблемные места, помогая каждому учащемуся добиться успеха в своем собственном темпе.
«Наш последний тест был на Fractions, и это был первый раз, когда я действительно убедился, что каждый день в Prodigy они отрабатывают эти конкретные навыки, и результаты теста очень отражали дополнительную практику, которую они получили! » — Жюстин Хилл учитель 3-го класса, центральные школы Восточного Сиракуз-Миноа
2) Игра с ударами Стимулируйте здоровую конкуренцию в классе с помощью увлекательной настольной игры, в которой игроки «ударяют» друг друга дроби, чтобы претендовать на место на доске.
Вы можете найти множество игр на разные темы. В этом выпуске с добавлением дробей игроки должны бросать кости, чтобы найти соответствующее уравнение, а затем размещать свои игровые фишки на дроби, которая соответствует ответу.
Игрок, который первым соберет все свои фишки на доске, становится победителем!
4) Словесные задачиСловесные задачи для уравнения дробей представляют собой реальные примеры вопросов, на которые отвечают учащиеся, помогая им понять цель таких вопросов.
Источник изображения: Teachers Pay Teachers
Карточки с задачами Word и рабочие листы — отличный способ задать эти вопросы. Если вы хотите, чтобы ваш класс был более вовлечен, вы можете использовать манипуляторы или даже самих учеников.
Например, «если три человека одеты в зеленое, а двое — в синее, какова доля в классе людей, одетых в зеленое или синее?»
4) Составители уравнений В этом упражнении учащиеся рисуют или строят уравнения, чтобы визуализировать, как выглядит сложение дробей.
Источник изображения: Desert Designed
Попросите учащихся составить уравнения или использовать манипуляции, чтобы лучше понять, что на самом деле означает сложение дробей. Дробные полосы или шкала дробей — отличные варианты, чтобы сделать эту абстрактную концепцию более удобоваримой и конкретной.
Отметьте три типа дробей Примечания
5) Math matesЭта активная игра поднимает учеников со своих мест, сотрудничая с одноклассниками и практикуя математику… все сразу!
У каждого ученика своя фракция. Игроки ходят по комнате, находят партнеров и работают вместе, чтобы сложить свои фракции.
Эта игра отлично подходит для отработки навыков, полученных в классе, и поощрения командной работы.
Заключительные мысли о добавлении дробейПереход от базовых навыков дробей к сложению, безусловно, пугает, но добавление дробей можно упростить, выполнив три простых шага, описанных выше.
Используйте информацию из этого руководства, чтобы победить на следующем уроке математики и упростить сложение дробей для ваших учеников. Далее: вычитание, умножение и деление. О боже!
Далее: вычитание, умножение и деление. О боже!
Создайте или войдите в свою учетную запись учителя на Prodigy — игровой платформе для обучения математике, ориентированной на учебную программу, с полезными инструментами как для преподавателей, так и для учащихся.
Сложение дробей с разными знаменателями Рабочие листы [PDF] Brighterly
- Дом
- >
- Рабочие листы
- >
- Сложение дробей с разными знаменателями. Рабочие листы
Учащиеся сначала знакомятся с дробями в начальной и средней школе. Как правило, эта концепция помогает учащимся узнать о половинках и неравных числах в математике.
Но учителя должны уделить учащимся время и внимание, чтобы понять связь между дробями, десятичными числами и процентами и их приложениями. Любое надежное сложение дробей с листом с разными знаменателями может помочь учащимся быстрее установить эту связь.
Любое надежное сложение дробей с листом с разными знаменателями может помочь учащимся быстрее установить эту связь.
Сложение дробей с разными знаменателями PDF
Посмотреть рабочий лист
Сложение дробей с отличающимися знаменателями Рабочий лист
Сложение дробей с отличающимися знаменателями PDF
Посмотреть рабочий лист
Сложение дробей с разными знаменателями Рабочий лист
Сложение дробей с разными знаменателями PDF
Посмотреть рабочий лист
Рабочий лист сложения непохожих дробей
Сложение дробей с непохожими знаменателями PDF
Посмотреть рабочий лист
Сложение дробей с разными знаменателями. Рабочие листы
Рабочие листы
Преимущества сложения дробей с разными знаменателями. Рабочие листы
Поскольку учащиеся применяют различные методы сложения и вычитания дробей, важно знать, имеют ли дроби одинаковые или разные знаменатели. Этот тип дроби отличается от обычного расчета, такого как ½ + ½ = 1. Таким образом, при решении задач, связанных со сложением и вычитанием дробей, учащимся будет полезно складывать дроби с разными знаменателями, поскольку это упрощает их работу.
Шаги, которые нужно предпринять при работе со сложением дробей с отличающимися знаменателями Рабочий лист
Вы можете получить эти рабочие листы в местном книжном магазине или просто скачать PDF-версии. Когда вы получаете таблицы сложения дробей с разными знаменателями в формате PDF, вы также получаете преимущество в том, что эти материалы можно распечатать.
1:1 Уроки математики
Хотите воспитать гения?
Начните изучать математику с Brighterly
Давайте начнем изучать математику!
Если вы хотите добавить ½ + ⅗; обычные шаги, которые вы можете использовать, чтобы научиться складывать дроби с разными знаменателями с помощью рабочих листов:
Шаг 1: Поскольку знаменатели дробей разные, сначала найдите наименьшее общее кратное (НОК) 2 и 5. НОК из 2 и 5 равно 10.
НОК из 2 и 5 равно 10.
Шаг 2: Затем замените 2 и 5 на 10 и сделайте уравнение 2/10 + 5/10. Итак, теперь у нас есть общий знаменатель.
Шаг 3: Разделите знаменатель на числители: 10/2 и 10/5 = 5 + 6/10 = 11/10
Примеры того, как рабочий лист сложения различных дробей может помочь учащимся
Когда знаменатели равны, сложение дробей с разными знаменателями становится простым. Знаменатели должны быть одинаковыми для работы с неправильными дробями с большими числителями. После этого суммируйте знаменатели.
Сложение дробей с разными знаменателями. Рабочие листы PDF
Сложение дробей с разными знаменателями Рабочий лист
Сложение дробей с разными знаменателями Рабочие листы с ответами
Добавление дробей в отличие от знаменателей Рабочий лист
Добавление дроби с отличающимися знаменателями Рабочий лист
Сложение дробей с разными знаменателями. Рабочий лист PDF
Рабочий лист PDF
Сложение дробей с разными знаменателями. Листы могут помочь учащимся идентифицировать и решать задачи на дроби. Превратите смешанные целые числа в неправильные дроби и сделайте каждый бит равным, если вы объедините их. Любую математическую задачу будет намного проще решить таким образом.
Например, рабочие листы познакомят вас с прямоугольной моделью, где вы можете добавлять дроби ⅓ и ½ соответственно. Разделение модели на три секции и затенение одной области представляют дробь ⅓. Разделив его на два ряда и закрасив одну часть, можно выделить половину целого.
Рабочий лист визуализирует дроби, что далеко от абстрактной математики, которую изучают студенты. Таким образом, дети понимают основные принципы сложения дробей, прежде чем переходить к более сложным модулям. Такой подход помогает им выявлять и интерпретировать схожие деления в реальных жизненных ситуациях, например, при совместном использовании кусочков пиццы.
Книга 1 на 1 урок математикиДетский класс
- Дошкольный
- Детский сад
- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
Электронная почта родителей
Успешно отправлено
Детский класс
- Дошкольный
- Детский сад
- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
Электронная почта родителей
Успешно отправлено
Мы используем файлы cookie, чтобы предоставить вам наилучший сервис. Если вы продолжите использовать веб-сайт, мы поймем, что вы согласны с Условиями. Эти файлы cookie безопасны и надежны. Мы не будем передавать ваши журналы истории третьим лицам.
Показать больше
Если вы продолжите использовать веб-сайт, мы поймем, что вы согласны с Условиями. Эти файлы cookie безопасны и надежны. Мы не будем передавать ваши журналы истории третьим лицам.
Показать больше
Дроби | АСТ Математика | Основы
Популярные учебники
в дробяхКак решить задачу на сравнение двух дробей?
Возникла проблема со словами при сравнении дробей? Нет пота! Посмотрите, как преобразовать текстовую задачу в математическое выражение, упростить ее и сравнить полученные дроби с помощью перекрестных произведений. В этом уроке все описано шаг за шагом!
Как вычитать дроби с разными знаменателями?
Вычитание дробей с разными знаменателями не должно быть кошмаром. Просто найдите общий знаменатель и все успокоится! Посмотрите, как сохранить спокойное вычитание дробей с помощью этого урока.
Как вычитать дроби с одинаковым знаменателем?
Вычитание дробей с одинаковыми знаменателями? Просто вычтите числители и приведите результат к общему знаменателю! Чтобы увидеть этот процесс в действии, ознакомьтесь с этим руководством!
Как превратить смешанную дробь в неправильную дробь?
Работать со смешанными дробями в уравнениях может быть сложно, но все становится проще, если сначала преобразовать их в неправильные дроби.
 Как только вы освоите этот навык, вы обнаружите, что будете использовать его все время, поэтому посмотрите, как преобразовать смешанную дробь в неправильную дробь.
Как только вы освоите этот навык, вы обнаружите, что будете использовать его все время, поэтому посмотрите, как преобразовать смешанную дробь в неправильную дробь.Как найти общий знаменатель и наименьший общий знаменатель?
В этом учебном пособии вы потренируетесь находить общий знаменатель и наименьший общий знаменатель трех дробей. Есть только один наименьший общий знаменатель, но общих знаменателей много. Этот учебник дает вам один. Можете ли вы найти другой?
Как умножать дроби?
Работа с дробями может быть пугающей, но если вы вооружитесь нужными инструментами, вы обнаружите, что работать с дробями не сложнее, чем с простыми числами. В этом уроке вы увидите процесс умножения 3 очень простых дробей. Наслаждаться!
Как складывать дроби с разными знаменателями?
Пытаетесь складывать дроби с разными знаменателями? Сначала вам понадобится общий знаменатель! Следуйте этому руководству и посмотрите, что вам нужно сделать, чтобы сложить эти дроби вместе.

Что такое смешанный номер?
Дроби бывают разных видов, и в этом уроке вы научитесь распознавать смешанные числа.
Что такое неправильная дробь?
Дроби бывают разных видов, и в этом уроке вы научитесь распознавать неправильные дроби.
Как складывать дроби с одинаковым знаменателем?
Хотя складывать дроби может быть сложно, складывать дроби с одинаковым знаменателем так же просто, как складывать числа. Вот почему, когда вы складываете дроби, вы сначала получаете все они с одинаковым знаменателем, а затем складываете их. В этом уроке вы увидите, как легко складывать дроби, если у них одинаковый знаменатель!
Что такое числитель и что такое знаменатель?
Числители и знаменатели являются ключевыми элементами, из которых состоят дроби, поэтому, если вы хотите работать с дробями, вы должны знать, что такое числители и знаменатели.
 К счастью для вас, этот учебник научит вас некоторым отличным приемам, чтобы запомнить, что такое числители и знаменатели.
К счастью для вас, этот учебник научит вас некоторым отличным приемам, чтобы запомнить, что такое числители и знаменатели.Как упростить дробь целого числа?
Сложные дроби, ну, сложные. Но если вы посмотрите этот урок, вы увидите, как сделать эти сложные дроби намного проще!
Что такое сложная дробь?
Вы когда-нибудь задумывались, что делает сложные дроби такими сложными? Посмотрите этот видеоурок и больше не удивляйтесь 🙂
Что такое обратное правило деления?
Когда вы делите дроби, хитрость заключается в том, чтобы переписать деление как умножение. Но правда в том, что вы всегда можете переписать деление как умножение, и в этом уроке вы увидите правило, которое делает это возможным!
Как упростить дробь над дробью?
Сложные дроби могут быть довольно сложными. К счастью, вы можете упростить сложную дробь, чтобы с ней было намного проще работать.
 Посмотрите, как в этом уроке!
Посмотрите, как в этом уроке!Что такое взаимность?
Обратные числа важны, когда дело доходит до деления дробей, нахождения перпендикулярных линий, работы с обратными пропорциями и многого другого! В этом уроке вы можете ознакомиться с основами взаимного обмена.
Как превратить неправильную дробь в смешанную дробь?
В математике часто бывает важно преобразовать дробь одного типа в другой. Это может помочь вам работать с дробью в уравнении или помочь лучше понять ответ. В этом уроке показано, как преобразовать неправильную дробь в смешанную дробь.
Как сократить дробь?
Дробей, содержащих большие числа, может быть немного, но иногда эти дроби можно уменьшить, избавив вас от этих больших чисел. В этом уроке показано, как преобразовать дробь в простейшую форму. Взглянем!
Как сравнивать дроби, находя общий знаменатель?
Упорядочить дроби от наименьшей к наибольшей? У вас нет общих знаменателей? Найдите общий знаменатель, перемножив знаменатели вместе.
 Используйте этот общий знаменатель для создания эквивалентных дробей. Затем сравните числители, чтобы выяснить, что больше! Этот урок покажет вам, как!
Используйте этот общий знаменатель для создания эквивалентных дробей. Затем сравните числители, чтобы выяснить, что больше! Этот урок покажет вам, как!Что такое эквивалентные дроби?
Нахождение эквивалентных дробей является важной частью таких операций, как сложение, вычитание и сравнение дробей. Но что это такое? В этом уроке вы узнаете, что эквивалентные дроби — это просто дроби, которые имеют одинаковое значение, даже если они могут выглядеть очень по-разному! Взгляните на эквивалентные дроби, посмотрев этот урок!
Как вы делите дроби?
Деление дробей? Измените это деление на умножение, умножив делимое на величину, обратную делителю. Узнайте все об этом, посмотрев этот урок!
Как сравнивать дроби путем преобразования в десятичные?
Сравнение дробей с разными знаменателями? Вы можете преобразовать каждую дробь в десятичную и сравнить десятичные дроби в числовой строке.


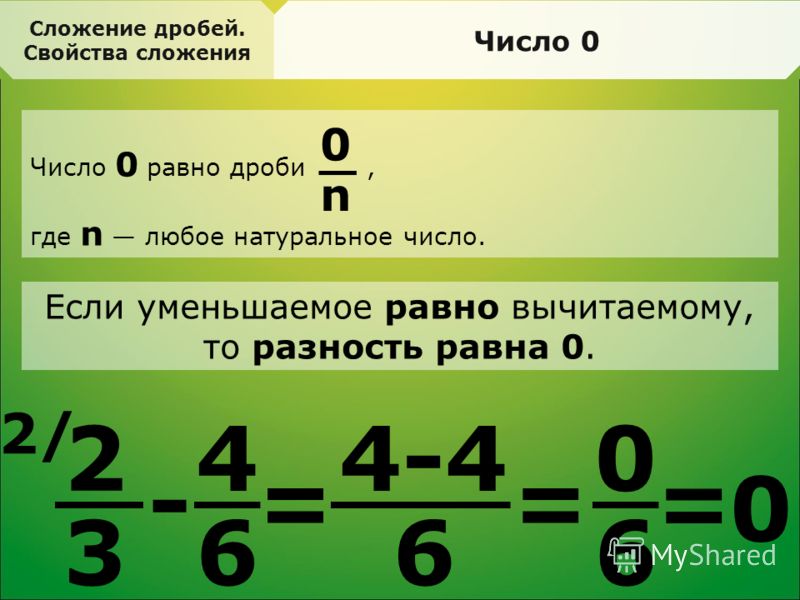

 В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
В крайнем случае, один минус может выжить — тот, которому не нашлось пары;



