Сложение и вычитание дробей – правила (5 класс, математика)

4.1

Средняя оценка: 4.1

Всего получено оценок: 87.

4.1

Средняя оценка: 4.1

Всего получено оценок: 87.

Сложение и вычитание дробей процесс не сложный, но специфический. Поэтому, чтобы в курсе математики 5 класса не возникло проблем с той темой, стоит подробнее разобраться во всех ее аспектах.

Дробь

Что такое дробь? Дробь – это деление, недовведенное до конца. То есть, чтобы получить дробь ${7\over{15}}$ нужно взять число, поделить его на 15 частей и из них оставить только 7 .

Именно дроби лежат в основе многих процессов. Без них невозможно было бы посчитать процент по кредиту, определить, какая часть тепла проходит через окно, даже посчитать, сколько кусочков пиццы причитается каждому из друзей, не получилось бы без дробей.

Но иногда приходится дроби складывать и вычитать согласно сочетательному свойству деления:

а:в+с:в=(а+с):в

В большинстве различных формул стоит знак «+».

Почему? Да потому, что существует определение математического сложения, которое включает в себя как сложение, так и вычитание. Просто вычитание считается сложением положительного и отрицательного числа.

Виды дробей

Перед тем, как преступить к рассмотрению сложения и вычитания дробей, нужно обратить внимание на тот факт, что дроби бывают разные, и в зависимости от вида дробей будет немного меняться и сам процесс сложения.

Виды дробей:

• Правильные и неправильные. Неправильные дроби могут превращаться в смешанные, т.е. дроби, у которых есть целая и дробная часть. Правильными дробями называются дроби, у которых числитель меньше знаменателя.
• Обыкновенные и десятичные. В зависимости от знаменателя выделяют десятичные и обыкновенные дроби. Десятичные дроби имеют знаменатель кратный 10, при этом такая дробь должна быть записана в строку, иначе она считается обыкновенной.

Отдельной строкой идут смешанные числа, то есть неправильные дроби, в которых выделили целую часть.

Эти числа так же условно относятся к дробям.

Сложение и вычитание дробей

Правило сложения и вычитания дробей:

• Сравнение знаменателей. Обратите внимание, что сочетательного свойство, благодаря которому возможны операции над дробями, работает только если у дробей одинаковые числители.
• Если знаменатели различны, то необходимо привести дроби к одинаковому знаменателю. Для этого выписываются оба знаменателя, для них находится наибольшее общее кратное НОК, которое и будет являться знаменателем дроби-результата. Числитель и знаменатель домножаются на одно и то же число так, чтобы дроби приобрели одинаковые знаменатели. Если знаменатели дробей одинаковы, то этот пункт можно пропустить.
• После этого дроби подводят под один знаменатель. Под чертой остается тот самый НОК, который мы нашли, а в числителе записывается сумма или разность, где в качестве первого слагаемого или уменьшаемого выступает числитель первой дроби, а в качестве второго слагаемого или вычитаемого выступает числитель второй дроби.
• Выполняется действие в числителе.
• При необходимости выделяется целая часть дроби.

Десятичные дроби складываются по тому же принципу, что и обычные числа. К числам дописываются разряды так, чтобы получились числа с одинаковым количеством знаков после запятой. Приведем небольшой пример:

3,65-2,6=3,65-2,60=1,05

Что мы узнали?

Мы поговорили о том, что такое дробь. Обговорили порядок действий при сложении и вычитании дробей. Обсудили, как выполнить необходимое условие сложение и привести дроби к одному знаменателю. Выделили виды дробей и поговорили о каждом из них.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.1

Средняя оценка: 4.1

Всего получено оценок: 87.

---

А какая ваша оценка?

Сложение и вычитание простых дробей с разными знаменателями

Рейтинг 5. 00 из 5 на основе опроса 1 пользователя

(1 отзыв клиента)

70,00 ₽

Примеры на сложение и вычитание простых дробей с разными знаменателями в виде логической цепочки. С ответами. Для печати А4.

Артикул: i-1215 Категория: Для учебы Метка: Дроби

• Описание
• Детали
• Отзывы (1)

Описание

Программа формирует примеры на сложение и вычитание простых дробей с разными знаменателями.

Случайным образом генерируется десять примеров. Ответ каждого предыдущего примера является первым числом следующего, что позволяет сформировать цепочку взаимосвязанных примеров. Итоговый ответ, который печатается в правом нижнем углу страницы, позволяет проверить правильность решения всех примеров без проверки каждого из них. Это дает возможность самостоятельно проверить правильность решения без возможности посмотреть ответ в процессе работы.

Правило сложения / вычитания простых дробей с

разными знаменателями:
для того, чтобы сложить / вычесть две простые дроби с разными знаменателем, необходимо
— привести дроби к наименьшему общему знаменателю;
— сложить /вычесть числители дробей, а знаменатель оставить без изменений;
— при необходимости сократить полученную дробь;
— если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную.

Программа написана в Excel с помощью макросов. Примеры генерируются случайным образом, количество генераций не ограниченно.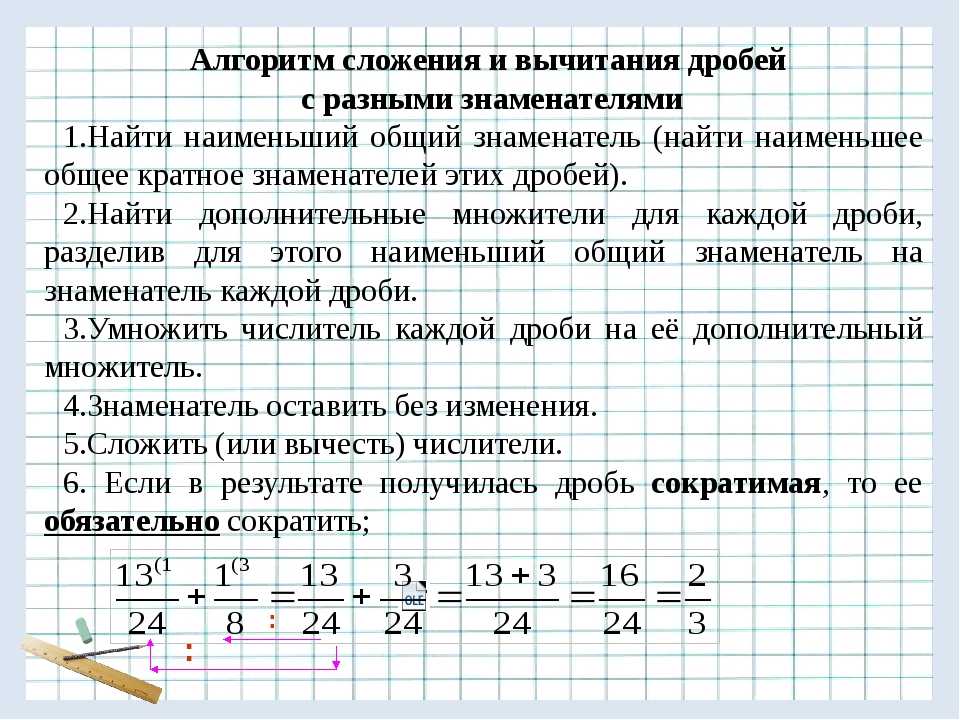
Для ознакомления с программой можно скачать образец примеров, которые получаются при использовании программы.

Для получения новой карточки примеров достаточно скачать, нажать на кнопку и распечатать.

Основные виды дробей, их основное свойство, а также все операции, которые можно выполнять с дробями: сокращение, приведение, сравнение, сложение, вычитание, умножение и деление описаны в статье «Математические дроби – просто о сложном».

Другие программы, которые помогут закрепить навыки счета с дробями:

• Основное свойство дроби
• Сложение и вычитание простых дробей с одинаковыми знаменателями
• Дроби обыкновенные (разные виды операций)
• Десятичные дроби (разные виды операций)
• Дроби смешанные
• Математический диктант 5 класс

На сайте представлен каталог программ, в котором все программы распределены по группам.

С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Вам также будет интересно…

• Продолжить ряд чисел

  125,00 ₽В корзину

• Простые проценты

  Оценка 5.00 из 5

  80,00 ₽В корзину

• Математический диктант 5 класс

  140,00 ₽В корзину

• Дроби смешанные

  100,00 ₽В корзину

• Числовые пирамиды большие (в пределах 50,100 и больше)

  120,00 ₽В корзину

• Головоломка «Спички»

  Оценка 5.00 из 5

  Распродажа! 150,00 ₽ 90,00 ₽ В корзину

• Сложение и вычитание простых дробей с одинаковыми знаменателями

  60,00 ₽В корзину

• Дроби обыкновенные

  80,00 ₽В корзину

• Дроби десятичные

  80,00 ₽В корзину

Правило ключевой дроби – Математика для учителей начальных классов

Дроби

Мы знаем, что это ответ на задачу на деление:

   

представляет собой сумму пирога, которую получает отдельный ребенок, когда пироги делятся поровну между детьми.

Что произойдет, если мы удвоим количество пирогов и удвоим количество детей? Ничего такого! Количество пирога на ребенка осталось прежним:

   

Например, как показано на рисунке, и оба дают по два пирога каждому ребенку.

И утроение числа пирогов и числа детей также не меняет итоговое количество пирогов на одного ребенка, как и учетверение каждого числа или умножение чисел на триллион миллиардов!

   

Это заставляет нас хотеть верить:

Правило ключевой дроби

   

(по крайней мере, для целых положительных чисел ).

 

Мы говорим, что дроби и

эквивалентны .

 

Пример: Дроби, эквивалентные 3/5

Например,

дает тот же результат, что и

   

и

   

 

Подумай / Соедини / Поделись

Запишите множество эквивалентных дробей для , для и для 1.

 

Пример: Возвращение назад0075 отменили

или взяли общий делитель 4 из числителя и знаменателя.

Математики называют этот процесс сокращением дроби до наименьших членов. (Мы уменьшили числитель и знаменатель, насколько это возможно!)

Учителя обычно говорят, что мы упрощаем дробь. (Вы должны признать, что это выглядит проще, чем .)

 

Пример: Как низко вы можете опуститься?

В качестве другого примера можно, безусловно, упростить, заметив, что в числителе и знаменателе есть общий делитель 10:

   

Мы можем пойти дальше, так как 28 и 35 кратны 7:

   

Таким образом, разделение 280 пирогов среди 350 детей дает тот же результат, что и разделение 4 пирогов среди 5 детей!

   

Поскольку 4 и 5 не имеют общих делителей, это все, что мы можем сделать в этом примере (оставаясь целыми числами).

 

Самостоятельно

Смешай и подбери: вверху находятся некоторые дроби, которые не были упрощены. Внизу упрощенные ответы, но в случайном порядке. Какой упрощенный ответ соответствует какой дроби? (Обратите внимание, что ответов меньше, чем вопросов!)

   

   

 

Подумай / Соедини / Поделись

Используйте «Модель пирогов на ребенка», чтобы объяснить , почему действует правило ключевой доли. То есть объясните, почему каждый отдельный ребенок получает одинаковое количество пирога в этих двух ситуациях:

• , если у вас есть пироги и дети, или
.
• , если у вас есть пироги и дети.

Дроби, Определение и правила дробей, Проверка дробей

Оператор: + — * /

 

 

Решение:

Определение дроби

Число, записанное в виде $\frac{a}{b}$ или a/b, где $a$ — целое число, а $b$ — целое число, отличное от нуля, называется дробью .
Число $a$ равно числителю , а $b$ равно знаменателю . Дробь представляет собой либо часть целого, либо любое количество равных частей.
Знаменатель показывает, сколько равных частей составляет целое, а числитель показывает, сколько этих частей мы имеем в виду.

Примеры дробей

Пример 1: Бекки, Мерри и Джон хотят поровну разделить плитку шоколада.
Какую часть бруска займет каждый из них?
В какой части бара Бекки и Мерри будут вместе?

Детям нужно разделить брусок на три части. Таким образом, каждый возьмет $\frac{1}{3}$ плитки шоколада.
Две девушки вместе будут иметь две части, следовательно, математически говоря, они будут иметь $\frac{2}{3}$ бруска.

Пример 2: Какая часть солдат желтая?

Пример 3: Какой части яблок не хватает?

Правила дроби

Сложение: (те же знаменатели)
$\frac{A}{B} +\frac{C}{B} = \frac{A + C}{B}$

Вычитание: (те же знаменатели)
$\frac{A}{B} -\frac{C}{B} = \frac{A — C}{B}$

Сложение: (разные знаменатели)
$\frac{A}{B} +\frac{C}{D} = \frac{A\cdot D}{B\cdot D} +\frac{B\cdot C}{B\cdot D} = \frac{A\cdot D + B\cdot C}{B\cdot D}$

Вычитание: (разные знаменатели)
$\frac{A}{B} -\frac{C}{D} = \frac{A\cdot D}{B\cdot D} -\frac{B\cdot C}{B\cdot D} = \frac{A\cdot D — B\cdot C}{B\cdot D}$

Умножение:
$\frac{A}{B}\times\frac{C}{D} = \frac{A\cdot C}{B\cdot D}$

Деление:
$\frac{A}{B}\div\frac{C}{D} = \frac{A}{B}\times\frac{D}{C}= \frac{A\ cdot D}{B\cdot C}$

Свойства дробей

Свойство I: Все заштрихованные части окружностей представляют собой половину $\frac{1}{2}, \frac{2}{4}$ и $\frac{3}{6}$, следовательно, $\frac{1}{2} = \frac{2}{4} = \frac{3}{6}$

Мы получим $\frac{2}{4}$, если умножим числитель и знаменатель дроби $\frac{1}{2}$ на $2$.

Получим $\frac{3}{6}$, умножив числитель и знаменатель $\frac{1}{2}$ на $3$.

Пусть $a$ — целое число, а $b$ и $c$ — ненулевые целые числа.
Тогда:

$\frac{a}{b}=\frac{a\cdot c}{b\cdot c}$ и $\frac{a}{b}=\frac{a:c}{b:c}$

Свойство II: Если две дроби имеют одинаковые знаменатели, то дробь с большим числителем больше.
Если $a$, $b$ и $c$ являются целыми числами и $c \ne 0$, то:

$\frac{a}{c}>\frac{b}{c}$, если $a>b$

Пример: $\frac{4}{5} > \frac{3}{5} > \frac{2}{5}$

Свойство III: Если у двух дробей числители равны, то больше та дробь, у которой знаменатель меньше.
Если $a$, $b$ и $c$ являются целыми числами, а $b$ и $c$ не равны нулю, то:

$\frac{a}{b}>\frac{a}{c}$, если $b

Пример: $\frac{3}{4} > \frac{3}{5} > \frac{3}{20}$

Тест фракций

1. Теннисист выиграл 6$ из первых 12$ сетов. Затем он выиграл все оставшиеся сеты по $6$. Какую часть сетов выиграл игрок?
$\frac{1}{3}$ $\фракция{2}{3}$ $\фракция{1}{2}$

2. У мальчика было $\$36$. После пары часов покупок у него осталось $\$8$. Какую часть своих денег он потратил?
$\frac{2}{9}$ $\фракция{2}{7}$ $\фракция{7}{9}$

3. В классе с 30$ учениками было $12$ девочек. Затем к классу присоединились $6$ мальчиков. Какую часть класса составляют девочки?
$\frac{1}{2}$ $\фракция{3}{5}$ $\фракция{1}{3}$

4. Если дробь $\frac{n}{40}$ находится между $\frac{1}{5}$ и $\frac{1}{4}$, то н это
$8$ $9$ $10$

5. $\frac{6}{24}$ равно:
$\frac{1}{4}$ $\фракция{3}{4}$ $\фракция{6}{12}$

6. Какая из дробей вдвое больше $\frac{3}{8}$?
$\frac{6}{16}$ $\фракция{3}{16}$ $\frac{3}{4}$     

7. ^* Какая из следующих дробей наибольшая: $\frac{12}{13}, \frac{13}{14}, \frac{14} {15}$ или $\frac{15}{16}$?
$\frac{15}{16}$ $\фракция{12}{13}$ $\frac{14}{15}$     

8. В какой из следующих последовательностей дроби расположены в порядке убывания?
1: $\frac{7}{11}, \frac{5}{8}, \frac{3}{5}, \frac{2}{3}$;

2: $\frac{4}{3}, \frac{7}{11}, \frac{5}{8}, \frac{3}{5}$;

3: $\frac{21}{11}, \frac{2}{3}, \frac{3}{5}, \frac{5}{8}$

$2$ $3$ $1$     

9.