выполните сложение дробей

Вы искали выполните сложение дробей? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и выполнить сложение дробей, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «выполните сложение дробей».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как выполните сложение дробей,выполнить сложение дробей,выполнить сложение и вычитание дробей,вычитание и сложение дробных чисел,дроби с плюсом как решать,дробные числа как складывать,как дроби складывать с целыми числами,как дробь сложить с целым числом,как найти сумму дробей с разными знаменателями,как прибавить дробь на дробь,как решать дроби на сложение с разными знаменателями,как решать дроби с разными знаменателями на сложение,как решать сложение дробей с разными знаменателями,как решить сложение дробей с разными знаменателями,как складывать дроби и целое число,как складывать дроби с разными знаменателями и целыми числами,как складывать дроби с разными знаменателями с целыми числами,как складывать дроби с целым числом,как складывать дроби с целыми числами,как складывать дроби с целыми числами и разными знаменателями,как складывать смешанные дроби с разными знаменателями,как складывать целое число с дробью,как складывать целые числа с дробями,как сложить дроби с разными знаменателями и числителями,как сложить дроби с целым числом,как сложить дробь и целое число,как сложить дробь и число,как сложить дробь с целым числом,как сложить с дробь с целым числом,как сложить смешанные дроби,как сложить целое число и дробь,как сложить целое число с дробью,как сложить число и дробь,как сложить число с дробью,как целое число складывать с дробью,как целое число сложить с дробью,как целые числа складывать с дробями,как число сложить с дробью,правила вычитание и сложение дробей,правила дробей сложение,правила дробей сложение и вычитание,правила сложение дробей,правила сложение и вычитание дробей,правила сложения дробей с разными знаменателями,правила сложения и вычитания дробей,правило сложение дробей,правило сложение и вычитание дробей,правило сложения дробей,правило сложения дробей с разными знаменателями,правило сложения и вычитания дробей,при сложении дробей с разными знаменателями,прибавление дробей,прибавление дробей с разными знаменателями,простые дроби сложения и вычитания решение с целыми числами,с сложение дробей,складывание дробей,складывание дробей с разными знаменателями,складывать дроби,сложение дробей и целых чисел,сложение дробей с,сложение дробей с разными,сложение дробей с разными знаменателями,сложение дробей с разными знаменателями и с целыми,сложение дробей с разными знаменателями и числителями,сложение дробей с разными знаменателями правило,сложение дробей с разными знаменателями примеры для решения,сложение дробей с разными числителями и знаменателями,сложение дробей с целым числом,сложение дробей с целыми числами,сложение дробей с целыми числами и разными знаменателями,сложение дробей с целыми числами с разными знаменателями,сложение дробей с числом,сложение дробей сложных,сложение дроби и целого числа,сложение дроби и числа,сложение дробных чисел,сложение и вычитание дробей правила,сложение и вычитание дробей с разными знаменателями правило,сложение и вычитание дробей с разными знаменателями примеры,сложение неправильных дробей,сложение неправильных дробей с разными знаменателями,сложение простых дробей,сложение простых дробей с разными знаменателями,сложение сложных дробей,сложение смешанных дробей,сложение трех дробей с разными знаменателями,сложение целого числа и дроби,сложение целого числа с дробью,сложение целых чисел и дробей,сложение числа и дроби,сложения дробей с разными знаменателями,сложения дробей с разными знаменателями формула,сложить дроби,смешанные дроби с разными знаменателями как решать,сокращение при сложении дробей,сумма дробей,сумма дробей с разными знаменателями,формула дробей сложения,формула сложения дробей,формула сложения дробей с разными знаменателями,число плюс дробь,чтобы сложить дроби с разными знаменателями нужно.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и выполните сложение дробей. Просто введите задачу в окошко и нажмите «решить» здесь (например, выполнить сложение и вычитание дробей).

Решить задачу выполните сложение дробей вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Сложение и вычитание смешанных чисел 6 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Тема урока: «Сложение и вычитание смешанных чисел».

 

Но дело в том, что это не новые числа. Смешанное число  – это два и еще . Просто сумма двух чисел.

Мы умеем уже складывать целые числа, дробные числа. А сложение смешанных чисел – это то же самое, это сложение целых чисел и сложение обыкновенных дробей. Надо использовать те знания, которые у нас уже есть.

Остается рассмотреть, почему они так пишутся и так называются, и убедиться на примерах, что никаких новых знаний нам не нужно, никаких новых правил учить не понадобится.

 

Пример 1

 

 

Сложить два смешанных числа: , .

 

Напишем у каждого знак «+».

Теперь мы лучше видим все 4 слагаемых. Сложим теперь так, как нам удобнее.

Целые числа 7 и 2 сложить легко.

Обыкновенные дроби мы тоже умеем складывать. Приведем их к общему знаменателю.

Ответ: .

 

Пример 2

 

 

 

Поставим знаки «+»:

Сложим отдельно целые числа и отдельно обыкновенные дроби.

Дробь  уже можно записать как смешанную, убрав знак плюс, но обыкновенную дробь можно записать и проще. Выделим целую часть.

К целой части добавляется еще единица.

Ответ: 
.

 

Пример 3

 

 

 

Поставим знаки «+»:

Можно сложить отдельно целые числа и дроби, но у дроби  можно выделить целую часть, станет проще.

Ответ: .

 

Пример 4

 

 

 

 

Вычитание смешанных дробей

 

 

А как вычитать? Все опять просто.

 

Как можно иначе записать смешанную дробь с минусом впереди?

Минус относится ко всей дроби. Можно поставить скобки и минус перед ними или раскрыть скобки. Минус будет у каждого слагаемого.

 

Пример 5

 

 

 

Здесь полезный навык – это уметь отнять от единицы или другого целого числа правильную дробь.

 

Вычитание правильной дроби из целого числа

 

 

1) 

 

2) 

3) 

Сложение двух отрицательных смешанных дробей не представляет проблемы.

Пример 6

Ответ: .

Необязательно расписывать все подробно.

Если вы чувствуете себя уверенно, то многое можно делать в уме.

 

Задание

 

 

Самостоятельно выполните несколько заданий, а потом проверьте.

 

Проверяем.

 

---

Смешанные числа

Дроби нужны для записи нецелых количеств: треть пути, четверть часа, половина яблока. Это все примеры, когда количество меньше одного. Но нецелое количество может быть и больше одного: полтора литра молока; два с половиной часа; три с половиной километра. Как удобнее всего записывать эти количества?

Если мы делим 7 яблок на троих, то это можно сделать двумя способами:

1) Каждое яблоко делим на три части и раздаем эти части всем участникам. Каждый такой кусочек – это  яблока.

В итоге каждый получит 7 таких кусочков: .

2) Проще каждому раздать по два яблока. А оставшиеся разделить на три части и раздать. Все-таки легче резать одно яблоко, чем семь.

В итоге каждый получит по два целых и еще по одной трети: .

Это разные записи одного и того же количества.

Такие количества, целое плюс дробное, встречаются часто.

Чтобы упростить запись, договорились, что можно не писать знак «+»:

.

В последней записи смешались целое и дробное число. Поэтому такую запись назвали смешанным числом или смешанной дробью.

И неправильная дробь, и смешанная обозначают одно и то же количество.

Какая удобнее? Это зависит от ситуации.

По смешанной легче представить количество.

По левой записи мы понимаем только, что это число больше единицы. А вот по правой – что число почти равно трем, чуть-чуть больше трех, на .

Складывать и вычитать дроби удобнее в виде смешанного числа, а умножать и делить – в виде обыкновенной дроби.

Десятичные дроби очень близки к смешанным числам – это почти одно и то же.

Просто разная запись, но смысл один. Сначала записывается целая часть, потом дробная.

Если у десятичной дроби целая часть равна нулю, то она легко записывается обыкновенной правильной дробью, просто ноль целых в смешанной дроби не пишем.

Итак, между целой и дробной частями смешанной дроби пропущен знак «+». Если это помнить, то не нужно никаких дополнительных правил.

Чтобы превратить смешанную дробь в обыкновенную, нужно сложить целое число и дробь.

Чтобы сложить целое число с дробью, представим 4 как дробь со знаменателем единица, приведем ее к знаменателю 7, домножив числитель и знаменатель на 7.

Или, в другую сторону, вынесем целую часть из неправильной дроби.

Нам давно знаком этот способ. Деление столбиком с остатком – это и есть вынесение целой части.

Вернемся к 7 яблокам, которые мы делим на троих.

Разделим столбиком 7 на 3 с остатком.

Ответ: 2 и 1 в остатке. То есть по два целых яблока уже досталось всем, и одно осталось. Его нужно делить на три части.

Конечно, в таком простом случаем мы обойдемся без деления столбиком.

Число 7 больше трех и не делится на три. Его можно разбить на две части – часть, которая делится на 3 – 6, и остаток, который меньше трех, – 1. 6 яблок делится на 3, это два, и еще одно делим на три. Это .

В более сложных случаях все-таки нужно воспользоваться делением в столбик.

Чтобы вынести целую часть, разделим числитель на знаменатель в столбик.

Получили 27 и 5 в остатке. То есть, мы разбили число 221 на две части: первая, которая делится на 8 и дает в результате 27 (саму эту часть мы не видели, но нетрудно догадаться по остатку, что она равна 216) и остаток, меньший 8, – это 5:

 

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012.

2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия, 2006.

3. Депман И. Я., Виленкин Н.Я. За страницами учебника математики. – Просвещение, 1989. 

4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – ЗШ МИФИ, 2011. 

5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.

6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. – Просвещение, 1989.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «Школьный помощник» (Источник)

2. Интернет-сайт «Гипермаркет знаний» (Источник)

3. Интернет-сайт фестиваля педагогических идей «Открытый урок» (Источник)

 

Домашнее задание

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012. № 376.

2. 

3. 

 

Дроби — как объяснить ребенку действия с дробями

Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.

Как объяснить суть дробей ребенку?

Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.

Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.

Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.

Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.

Что нужно знать о дробях?

1. Дробь — число нецелое, оно обозначает количество долей целого.

2. Дробь меньше целого.

3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.

Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.

Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.

Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.

Что такое смешанные дроби?

В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.

У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.

Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.

Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.

Примеры:

• 14/5 = (5*2+4) / 5 = 2 4/5
• 21/6 = (6*3+ 3) / 6 = 3 3/6

Задание:

Выделите целую часть из неправильных дробей:

• 15/4,
• 22/12,
• 30/7.

Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.

Примеры:

• 3 1/8 = (3*8+1) / 8 = 25/8
• 7 4/9 = (7*9+4) / 9 = 67/9

Задание:

1. Преобразовать в смешанное число неправильную дробь:

• 27/4,
• 18/5,
• 45/7.

2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:

• 3 4/5;
• 12 7/11.

Десятичные дроби

Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.

Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.

Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».

Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления  применяется человечеством с самых древних времен. Она интуитивна понятна и проста.

Задание:

Преобразовать следующие дроби в десятичные:

• 8/10,
• 4/100,
• 7/1000.

Сокращение дробей

Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.

Пример 1. Сократить дробь 8/12

Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:

8/12 = 8:4 / 12:4 = 2/3

Пример 2.

Сократить дробь 10/25

Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:

10/25 = 10:5 / 25:5 = 2/5

Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.

Задание:

Сократите следующие дроби:

• 6/18,
• 20/40;
• 7/21.

Сложение дробей

Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.

Примеры:

• 1/7 + 2/7 = 3/7
• 3/8 + 5/8 = 8/8 = 1

Задание:

Выполни сложение дробей с одинаковыми знаменателями:

Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.

Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:

• 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
• 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.

Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:

• 3*6 / 7*6 = 18/42;
• 2*7 / 6*7 = 14/42.

Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:

• 18/42 + 14/42 = 32/42

Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.

Задание:

Выполни сложение дробей с разными знаменателями:

 

Вычитание дробей

Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.

Пример:

7/9 — 2/9 = (7-2) / 9 = 5/9

Задание:

Выполни вычитание дробей с одинаковыми знаменателями:

Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.

Пример:

6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70

Задание:

Выполни вычитание дробей с разными знаменателями:

Умножение дробей

Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.

Умножение обыкновенных дробей

В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.

Пример:

2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10

Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.

Пример:

24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21

Умножение смешанных дробей

Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.

Пример:

4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24

Задание:

Выполните умножение дробей:

• 5/7 * 6/8;
• 6/11 * 2/3;
• 2 3/7 * 4 5/9;
• 4 6/7 * 7 9/10.

Деление дробей

Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый  знаменатель).

Пример:

4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7

Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.

Пример:

5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18

Задание:

Выполните деление дробей:

• 6/11 : 3;
• 7/15 : 2;
• 9/12 : 4.

Сравнение дробей

Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.

Пример:

1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.

Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.

Пример:

1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.

Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.

Пример:

Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.

Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно.  Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.

Задание:

Определите, какие дроби изображены на рисунке, и сравните их:

Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.

Математика и логика для детей 7-13 лет

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

узнать подробнее

---

Читайте также:

• Таблица умножения для детей
• Как объяснить ребенку состав числа?

---

 

Отображение чисел в качестве дробей

Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше

Используйте формат «Дроб», чтобы отображать или ввести числа как фактические дроби, а не в десятичных числах.

1. Выделите ячейки, которые нужно отформатировать.

2. На вкладке Главная нажмите кнопку вызова диалогового окна рядом с именем группы Число.

3. В списке Категория выберите дроби.

4. В списке Тип выберите нужный тип формата дроби.

Формат дроби	В этом формате 123,456 отображается как
Дробная часть с одной цифрой	123 1/2, округление до ближайшего однозначного значения дроби
Двузначная дробь	123 26/57, округлизация до ближайшего двузначного значения дроби
Трижды значок дроби	123 57/125, округлизация до ближайшего трехзначного значения дроби
Дробный в качестве дробей	123 1/2
Дробный по кварталам	123 2/4
Дробный в качестве частиц	123 4/8
Дробные части в качестве шестнадцатых	123 7/16
Дробный в качестве десятых	123 5/10
Дробные части в качестве сотых	123 46/100

Число в активной ячейке выбранного на этом сайте отображается в поле Образец, чтобы можно было просмотреть выбранные параметры форматирования.

• После применения формата дроби к ячейке дробные числа, а также фактические дроби, которые вы в нее введите, будут отображаться как дроби. Например, если ввести 0,5 или 1/2, то при формате ячейки с типом дроби до одной цифры будет 1/2.

• Если к ячейке не применен формат дроби и вы введите дробную часть, например 1/2,она будет отформатирована как дата. Чтобы отобразить дробную часть, применив формат дроби, а затем впечатаем ее еще раз.

• Если вам не нужно выполнять вычисления с дробями, перед тем как ввести в нее дробную часть, можно отформать ячейку как текст, щелкнув Текст в списке Категория. В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя.

• Чтобы сбросить числовом формате, в диалоговом окне Категория(диалоговое окно Формат ячеек) или Числовом формате(вкладкаГлавная, группа Число) нажмите кнопку Общий. В ячейках с форматом Общий форматирование к числам не применяется.

5 класс. Математика. Обыкновенные дроби — Сложение и вычитание обыкновенных дробей

Комментарии преподавателя

Для на­ча­ла да­вай­те вспом­ним, что такое сме­шан­ные числа. Сме­шан­ное число – число, за­пи­сан­ное в таком виде, что у него есть целая часть и дроб­ная часть. На­при­мер, . Здесь 3 – целая часть,  – дроб­ная.

 Задача 1

Пред­по­ло­жим, нам дали такую за­да­чу. Вася про­бе­жал пер­вый из двух кру­гов ди­стан­ции за 1 ми­ну­ту 40 се­кунд, а вто­рой круг – за 1 ми­ну­ту 20 се­кунд. За какое время Вася про­бе­жал всю ди­стан­цию и на­сколь­ко быст­рее он про­бе­жал вто­рой круг, чем пер­вый?

Ре­ше­ние

Неслож­но ви­деть, что мы можем сло­жить ми­ну­ты с ми­ну­та­ми, се­кун­ды – с се­кун­да­ми. По­лу­чит­ся 2 мин + 60 се­кунд, т. е. 3 мин. Но, с дру­гой сто­ро­ны, 40 се­кунд – это  ми­ну­ты, а 20 се­кунд – . И тогда, по ана­ло­гии, чтобы сло­жить эти сме­шан­ные числа, мы можем не пе­ре­во­дить их в непра­виль­ные дроби, а сразу сло­жить целые ми­ну­ты друг с дру­гом, и от­дель­но – дроб­ные. Это дает 2 ми­ну­ты и , то есть еще одну целую ми­ну­ту. Итого 3 ми­ну­ты.

Можно было все это про­де­лать и так. За­ме­тим, что сме­шан­ное число есть сумма своих целой и дроб­ной ча­стей. А даль­ше вос­поль­зу­ем­ся пе­ре­ме­сти­тель­ным свой­ством:

А что с вы­чи­та­ни­ем? То же самое. Из чисто прак­ти­че­ских со­об­ра­же­ний пер­вый круг по ми­ну­там оди­на­ков со вто­рым, а по се­кун­дам – на 20 доль­ше (или на треть ми­ну­ты). Можно и так:

Думаю, вы уже по­ня­ли ал­го­ритм? Из це­ло­го вы­чи­та­ем (к це­ло­му при­бав­ля­ем) целое, из дроб­но­го – дроб­ное. Рас­смот­рим еще несколь­ко при­ме­ров.

 Примеры на сложение

За­кре­пим эти вы­клад­ки пра­ви­лом. Чтобы сло­жить два сме­шан­ных числа, необ­хо­ди­мо:

• сло­жить их целые части;
• сло­жить их дроб­ные части;
• если нужно, пе­ре­ве­сти сумму дроб­ных ча­стей в сме­шан­ное число;
• сло­жить по­лу­чен­ные числа.

Пе­рей­дем к вы­чи­та­нию. Рас­смот­рим несколь­ко при­ме­ров, после чего сфор­му­ли­ру­ем общий ал­го­ритм.

 

Найти ошиб­ки в при­ме­рах на сло­же­ние

Рас­смот­рим вни­ма­тель­но пер­вый при­мер: сме­шан­ное число  за­ме­ни­ли дро­бью , а число  – , но дан­ные дроби не равны. Если мы решим пе­ре­во­дить дроби в непра­виль­ные, то по­лу­чим сле­ду­ю­щее:

Те­перь пе­рей­дем ко вто­ро­му при­ме­ру, в нем дей­ствия вы­пол­ня­ют­ся со­глас­но рас­смот­рен­но­му нами ал­го­рит­му. Как видим, все дей­ствия вы­пол­не­ны пра­виль­но, од­на­ко при­ня­то за­пи­сы­вать сме­шан­ные числа так, чтобы их дроб­ная часть яв­ля­лась пра­виль­ной дро­бью. По­это­му пред­ста­вим дробь  в виде сме­шан­но­го числа, а потом уже вы­пол­ним сло­же­ние.

 Примеры на вычитание

Если пойти по плану, то надо из  вы­честь . Этого мы сде­лать не можем. Тогда по­сту­пим так, как мы де­ла­ем при вы­чи­та­нии на­ту­раль­ных чисел: зай­мем у стар­ше­го раз­ря­да. Толь­ко роль стар­ше­го раз­ря­да здесь будет иг­рать целая часть. Ведь еди­ни­ца – это , так что можно вме­сто  за­пи­сать . А даль­ше – по плану:

А что де­лать, если при­ш­лось вы­чи­тать из на­ту­раль­но­го числа сме­шан­ное? То же самое:

.

За­кре­пим эти вы­клад­ки пра­ви­лом. Чтобы вы­честь одно сме­шан­ное число из дру­го­го, вы долж­ны:

• срав­нить дроб­ные части умень­ша­е­мо­го и вы­чи­та­е­мо­го;
• если дроб­ная часть умень­ша­е­мо­го боль­ше, то вы­честь из целой части целую часть, из дроб­ной части дроб­ную часть, а ре­зуль­та­ты сло­жить;
• если же боль­ше дроб­ная часть вы­чи­та­е­мо­го, то одну еди­ни­цу от целой части умень­ша­е­мо­го мы пе­ре­во­дим в дробь, чтобы дробь стала непра­виль­ной, а затем вы­чи­та­ем из целой части целую, а из дроб­ной – дроб­ную, и ре­зуль­та­ты скла­ды­ва­ем.

 

Найти ошиб­ки в при­ме­рах на вы­чи­та­ние

Рас­смот­рим пер­вый при­мер. Со­глас­но ал­го­рит­му, мы долж­ны сна­ча­ла 12 пред­ста­вить в виде сме­шан­но­го числа, а затем уже вы­пол­нять вы­чи­та­ние:

Рас­смот­рим вто­рой при­мер. Здесь ошиб­ка при вы­чи­та­нии дроб­ных ча­стей: нам необ­хо­ди­мо из дроб­ной части умень­ша­е­мо­го вы­честь дроб­ную часть вы­чи­та­е­мо­го, а не на­о­бо­рот. Чтобы это вы­пол­нить, нам при­дет­ся за­нять 1 еди­ни­цу и пред­ста­вить ее в виде дроби.

 Заключение

На этом уроке мы по­зна­ко­ми­лись со сме­шан­ны­ми чис­ла­ми, на­учи­лись скла­ды­вать их и вы­чи­тать, сфор­му­ли­ро­ва­ли ал­го­рит­мы для сло­же­ния и вы­чи­та­ния. Узна­ли, что для сло­же­ния и вы­чи­та­ния сме­шан­ных чисел вовсе не обя­за­тель­но пе­ре­во­дить их в непра­виль­ные дроби, а до­ста­точ­но про­сто сло­жить либо вы­честь целые части и сло­жить либо вы­честь дроб­ные части, после чего за­пи­сать окон­ча­тель­ный ответ.

В каж­дом из слу­ча­ев у нас была одна тон­кость. Для сло­же­ния мы по­ни­ма­ли, что ино­гда по­лу­ча­ет­ся сумма дроб­ных ча­стей в виде непра­виль­ной дроби, по­это­му при необ­хо­ди­мо­сти по­лу­чен­ную непра­виль­ную дробь нужно при­во­дить к пра­виль­ной, то есть вы­де­лять целую часть. А при вы­чи­та­нии по­яв­ля­лась такая тон­кость, что не все­гда из дроб­ной части умень­ша­е­мо­го можно вы­честь дроб­ную часть вы­чи­та­е­мо­го, по­это­му нам необ­хо­ди­мо было «за­ни­мать» еди­ни­цу у целой части и пе­ре­во­дить ее в дроб­ную, чтобы по­лу­чить непра­виль­ную дробь, из ко­то­рой уже можно было вы­честь дроб­ную часть.

Источник видео: https://www.youtube.com/watch?v=Q4UViwjnGVQ

Источник конспекта: http://interneturok.ru/ru/school/matematika/5-klass/drobnye-chisla/slozhenie-i-vychitanie-smeshannyh-chisel?seconds=0&chapter_id=842#videoplayer

 Источник теста: Тесты по математике 5 класс к учебнику Зубаревой И. И., Мордкович А.Г. — Рудницкая В.Н. 2013г.

Онлайн урок: Сравнение, сложение и вычитание смешанных чисел по предмету Математика 5 класс

Смешанные числа так же, как и любые другие числа, можно сравнивать, складывать, вычитать, умножать и делить.

На этом уроке рассмотрим правила сравнения, сложения и вычитания смешанных чисел.

Рассмотрим пример решения текстовой задачи на сложение и вычитание смешанных чисел арифметическим и алгебраическим способом.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Смешанное число- это число, состоящее из целой части (натурального числа) и дробной части (дробного числа).

На предыдущем уроке мы узнали, чем правее располагается число на координатном луче, тем оно больше.

Сравнение смешанных чисел сводится к сравнению их целых частей и дробных частей.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

1. Чтобы ответить на вопрос какое смешанное число больше, а какое меньше используют следующее правило:

Большим считается то смешанное число, целая часть которого больше, если же целые части равны, то больше то смешанное число, у которого дробная часть больше.

Соответственно верно и следующее утверждение: смешанные числа считаются равными, если их целая и дробная часть совпадают.

Рассмотрим примеры.

Пример №1.

Сравните два смешанных числа \(\mathbf{22\frac{6}{7}}\) и \(\mathbf{42\frac{5}{7}}\).

Решение:

Целая часть смешанного числа \(\mathbf{22\frac{6}{7}}\) равна 22.

Целая часть смешанного числа \(\mathbf{42\frac{5}{7}}\) равна 42.

Так как 22 < 42, значит и \(\mathbf{\color{orange}{22}\frac{6}{7} < \color{green}{42}\frac{5}{7}}\).

Пример №2.

Сравните два смешанных числа \(\mathbf{26\frac{6}{7}}\) и \(\mathbf{26\frac{5}{7}}\).

Решение:

Целая часть смешанного числа \(\mathbf{26\frac{6}{7}}\) равна 26.

Целая часть смешанного числа \(\mathbf{26\frac{5}{7}}\) равна 26.

Так как целые части смешанных чисел равны: 26 = 26, сравним их дробные части.

Число \(\mathbf{\frac{6}{7}}\)- дробная часть смешанного числа \(\mathbf{26\frac{6}{7}}\).

Число \(\mathbf{\frac{5}{7}}\) дробная часть смешанного числа \(\mathbf{26\frac{5}{7}}\).

Для сравнения обыкновенных дробей с одинаковыми знаменателями, необходимо сравнить их числители в соответствии с правилом: больше та дробь, у которой числитель больше.

Числитель дроби \(\mathbf{\frac{6}{7}}\) больше числителя дроби \(\mathbf{\frac{5}{7}}\), значит \(\mathbf{\color{orange}{\frac{6}{7}} > \color{green}{\frac{5}{7}}}\).

Следовательно \(\mathbf{26\color{orange}{\frac{6}{7}} > 26\color{green}{\frac{5}{7}}}\).

Пример №3.

Сравните два смешанных числа \(\mathbf{175\frac{2}{13}}\) и \(\mathbf{175\frac{2}{13}}\).

Решение:

Так как целая и дробная часть смешанного числа \(\mathbf{175\frac{2}{13}}\) совпадает с целой и дробной частью смешанного числа \(\mathbf{175\frac{2}{13}}\), то эти два числа равны.

\(\mathbf{175\frac{2}{13} = 175\frac{2}{13} }\)

2. Сравнение смешанных чисел с натуральными числами.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Для данного случая действует такое правило:

Если целая часть смешанного числа больше или равна натуральному числу, то смешанное число больше этого натурального числа.

Если целая часть смешанного числа меньше натурального числа, то смешанное число меньше данного натурального числа.

Разберем несколько поясняющих примеров.

Пример №1.

Сравните два числа 85 и \(\mathbf{139\frac{2}{5}}\).

Решение:

Целая часть смешанного числа \(\mathbf{139\frac{2}{5}}\) равна 139.

Число 139 больше 85 (заданного натурального числа), значит смешанное число \(\mathbf{139\frac{2}{5}}\) больше этого натурального числа.

Получаем следующее неравенство:

\(\mathbf{85 < 139\frac{2}{5}}\)

Пример №2.

Сравните два числа 147 и \(\mathbf{147\frac{6}{11}}\).

Решение:

Натуральное число 147 и целая часть смешанного числа \(\mathbf{147\frac{6}{11}}\) равны.

Если целая часть смешанного числа равна натуральному числу, то смешанное число больше этого натурального числа.

Следовательно, смешанное число \(\mathbf{147\frac{6}{11}}\) больше натурального числа 147.

\(\mathbf{147 <147\frac{6}{11}}\)

Пример №3.

Сравните два числа 53 и \(\mathbf{14\frac{6}{18}}\).

Решение:

Целая часть смешанного числа \(\mathbf{14\frac{6}{8}}\), число 14, меньше заданного натурального числа 53, значит, смешанное число \(\mathbf{14\frac{6}{8}}\) меньше натурального числа 53.

\(\mathbf{53 > 14\frac{6}{8}}\)

3. Сравнение смешанных чисел и обыкновенных дробей.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

• Сравнение смешанных чисел и правильных дробей.

Так как смешанное число всегда больше единицы, а правильная дробь всегда меньше единицы, то справедливо правило:

Любое смешанное число всегда больше правильной дроби.

• Сравнение смешанных чисел и неправильных дробей.

Сравнение смешанного числа и неправильной дроби можно осуществлять двумя способами.

Первый способ: сравнение смешанного числа и неправильной дроби можно свести к сравнению двух неправильных дробей.

Для этого смешанное число необходимо перевести в неправильную дробь.

Рассмотрим пример.

Сравните смешанное число \(\mathbf{12\frac{3}{8}}\) и неправильную дробь \(\mathbf{\frac{105}{8}}\).

Решение:

Переведем смешанное число \(\mathbf{12\frac{3}{8}}\) в неправильную дробь.

Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.

\(\mathbf{\color{red}{12}\frac{\color{green}{3}}{\color{blue}{8}} = \frac{\color{red}{12} \cdot \color{blue}{8} + \color{green}{3}}{\color{blue}{8}} = \frac{96 + \color{green}{3}}{\color{blue}{8}} = \frac{99}{\color{blue}{8}}}\)

Вместо \(\mathbf{12\frac{3}{8}}\) подставим соответствующее ему число \(\mathbf{\frac{99}{8}}\).

Сравним неправильные дроби \(\mathbf{\frac{99}{8}}\) и \(\mathbf{\frac{105}{8}}\).

Для сравнения обыкновенных дробей с одинаковыми знаменателями, необходимо сравнить их числители в соответствии с правилом: больше та дробь, у которой числитель больше.

99— числитель дроби \(\mathbf{\frac{99}{8}}\).

105— числитель дроби \(\mathbf{\frac{105}{8}}\).

Так как 99 < 105, то \(\mathbf{\frac{\color{orange}{99}}{8} < \frac{\color{green}{105}}{8}}\).

Известно, что неправильная дробь \(\mathbf{\frac{99}{8}}\) соответствует смешанному числу \(\mathbf{12\frac{3}{8}}\).

В итоге получается следующий результат: \(\mathbf{12\frac{3}{8} < \frac{105}{8}}\).

Второй способ: сравнение смешанного числа и неправильной дроби можно свести к сравнению двух смешанных чисел.

Для этого неправильную дробь необходимо перевести в смешанное число.

Рассмотрим поясняющий пример.

Сравним смешанное число \(\mathbf{12\frac{3}{8}}\) и неправильную дробь \(\mathbf{\frac{105}{8}}\).

Решение:

Переведем неправильную дробь \(\mathbf{\frac{105}{8}}\) в смешанное число.

Разделим числитель дроби на знаменатель, полученное неполное частное будет представлять собой целую часть смешанного числа, остаток от деления- это числитель дробной части смешанного числа, а делитель- знаменатель.

105 ÷ 8 = 13 (ост. 1)

\(\mathbf{\frac{105}{8} = 13\frac{1}{8}}\)

Сравним два смешанных числа \(\mathbf{12\frac{3}{8}}\) и \(\mathbf{13\frac{1}{8}}\).

Целая часть смешанного числа \(\mathbf{12\frac{3}{8}}\) меньше целой части смешанного числа \(\mathbf{13\frac{1}{8}}\).

Так как 12 < 13, то, \(\mathbf{\color{orange}{12}\frac{3}{8} < \color{green}{13}\frac{1}{8}}\).

Смешанное число \(\mathbf{13\frac{1}{8}}\) соответствует неправильной дроби \(\mathbf{\frac{105}{8}}\).

В итоге получается следующий результат: \(\mathbf{12\frac{3}{8} < \frac{105}{8}}\)

При решении одного и того же задания разными способами, получили одинаковые ответы: сравнивая \(\mathbf{12\frac{3}{8}}\) и \(\mathbf{\frac{105}{8}}\) оказалось, что \(\mathbf{\frac{105}{8}}\) больше \(\mathbf{12\frac{3}{8}}\).

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Смешанное число в развернутом виде представляет собой сумму целого и дробного числа.

При сложении смешанных чисел целые части складывают отдельно, дробные- отдельно.

Таким образом получается, что сложение смешанных чисел сводится к уже известным нам правилам сложения натуральных чисел и дробных чисел.

При сложении и вычитании можно использовать свойства, характерные для математических операций сложения и вычитания.

1. Запишем алгоритм сложения смешанных чисел.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

• Сложить целые части смешанных чисел.
• Сложить дробные части смешанных чисел.
• Если при сложении дробных частей получается неправильная дробь, то из нее необходимо выделить целую часть и прибавить ее к уже найденной сумме в п.1.

Соблюдая данную логику, можно складывать любое количество смешанных чисел.

Разберем правило сложения смешанных чисел на примерах.

Пример №1.

Сложите два смешанных числа \(\mathbf{10\frac{2}{5}}\) и \(\mathbf{14\frac{1}{5}}\).

Решение:

Запишем первое и второе смешанное число в виде суммы целой и дробной части и сложим их, получим выражение вида: \(\mathbf{10 + \frac{2}{5} + 14 + \frac{1}{5}}\).

Используя переместительное и сочетательное свойство сложения, сгруппируем отдельно целые части смешанных чисел, отдельно дробные части: \(\mathbf{(10 + 14) + (\frac{2}{5} + \frac{1}{5})}\).

Выполним сложение двух натуральных чисел и сложение двух обыкновенных дробей с одинаковым знаменателем.

\(\mathbf{(10 + 14) + (\frac{2}{5} + \frac{1}{5}) = 24 + \frac{2 + 1}{5} = 24 + \frac{3}{5}}\)

Представим сумму \(\mathbf{24 + \frac{3}{5}}\) в виде смешанного числа:

\(\mathbf{24 + \frac{3}{5} = 24\frac{3}{5}}\)

В таком случае сумма двух смешанных чисел равна:

\(\mathbf{10\frac{2}{5} + 14\frac{1}{5} = 24\frac{3}{5}}\)

Обычно все комментарии и рассуждения выполняются устно, а сложение и вычитание смешанных чисел оформляется в виде непрерывной цепочки действий:

\(\mathbf{10\frac{2}{5} + 14\frac{1}{5} = \color{orange}{10} + \color{green}{\frac{2}{5}} + \color{orange}{14} + \color{green}{\frac{1}{5}} = (\color{orange}{10} + \color{orange}{14}) + (\color{green}{\frac{2}{5}} + \color{green}{\frac{1}{5}}) = 24 + \frac{2 + 1}{5} = 24 + \frac{3}{5} = 24\frac{3}{5}}\)

Пример №2.

Сложите два смешанных числа \(\mathbf{20\frac{3}{5}}\) и \(\mathbf{35\frac{3}{5}}\).

Решение:

Запишем первое и второе смешанное число в виде суммы целой и дробной части и сложим их, получим выражение вида: \(\mathbf{20 + \frac{3}{5} + 35 + \frac{3}{5}}\).

Выполним сложение двух натуральных чисел и сложение двух обыкновенных дробей с одинаковым знаменателем: \(\mathbf{(20 + 35) + (\frac{3}{5} + \frac{3}{5}) = 55 + \frac{6}{5}}\).

При сложении дробных частей получаем неправильную дробь \(\mathbf{\frac{6}{5}}\).

Выделим из нее целую часть.

\(\mathbf{\frac{6}{5} = 6 \div 5 = 1\frac{1}{5}}\)

Заменим неправильную дробь \(\mathbf{\frac{6}{5}}\) на соответствующее ей смешанное число \(\mathbf{1\frac{1}{5}}\).

Сложим целую часть полученного смешанного числа с уже имеющейся.

\(\mathbf{55 + \color{blue}{\frac{6}{5}} = 55 + \color{blue}{1\frac{1}{5}} = 55 + 1 + \frac{1}{5} = (55 + 1) + \frac{1}{5} = 56 + \frac{1}{5} = 56\frac{1}{5}}\)

Запишем решение в общем виде, опуская все комментарии и рассуждения:

\(\mathbf{20\frac{3}{5} + 35\frac{3}{5} = 20 + \frac{3}{5} + 35 + \frac{3}{5} = 55 + \frac{6}{5} = 55 + 1\frac{1}{5} = (55 + 1) + \frac{1}{5} = 56 + \frac{1}{5} = 56\frac{1}{5}}\)

Пример №3.

Сложите два смешанных числа \(\mathbf{15\frac{5}{7}}\) и \(\mathbf{3\frac{2}{7}}\).

Решение:

\(\mathbf{15\frac{5}{7} + 3\frac{2}{7} = \color{orange}{15} + \color{green}{\frac{5}{7}} + \color{orange}{3} + \color{green}{\frac{2}{7}} = (\color{orange}{15} + \color{orange}{3}) + (\color{green}{\frac{5}{7}} + \color{green}{\frac{2}{7}}) = 18 + \frac{7}{7} = 18 + 1 = 19}\)

При сложении двух смешанных чисел получили натуральное число.

2. Сложение смешанного числа и натурального числа.

Натуральное число можно представить в виде смешанного числа, дробная часть которого равна нулю.

В таком случае сумму смешанного числа и натурального числа находят как сумму двух смешанных чисел.

Так как дробная часть натурального числа равна нулю, то при сложении натурального и смешанного числа необходимо найти сумму только их целых частей, дробную же часть смешанного числа нужно оставить без изменений.

Пример.

Сложите два числа \(\mathbf{18\frac{1}{3}}\) и 4.

Решение:

\(\mathbf{18\frac{1}{3} + 4 = \color{orange}{18} + \frac{1}{3} + \color{orange}{4} = (\color{orange}{18} + \color{orange}{4}) + \frac{1}{3} = 22 + \frac{1}{3} = 22\frac{1}{3}}\)

3. Сложение смешанного числа и обыкновенной дроби.

• Сложение смешанного числа и правильной дроби.

Правильную дробь можно представить в виде смешанного числа, целая часть которого равна нулю.

Если целая часть правильной дроби равна нулю, то складывая смешанное число и правильную дробь, находят только сумму дробной части смешанного числа и этой дроби, целую же часть смешанного числа при этом оставляют без изменений.

Пример.

Сложите два числа \(\mathbf{71\frac{3}{10}}\) и \(\mathbf{\frac{1}{10}}\).

Решение:

\(\mathbf{71\frac{3}{10} + \frac{1}{10} = 71 + \color{green}{\frac{3}{10}} + \color{green}{\frac{1}{10}} = 71 + (\color{green}{\frac{3}{10}} + \color{green}{\frac{1}{10}}) = 71 + \frac{4}{10} = 71\frac{4}{10}}\)

• Сложение смешанного числа и неправильной дроби

Возможны два способа сложение смешанного числа с неправильной дробью.

Первый способ: сложение смешанного числа и неправильной дроби можно свести к сумме двух неправильных дробей.

Для этого смешанное число можно представить в виде неправильной дроби и выполнить сложение неправильных дробей.

Второй способ: сложение смешанного числа и неправильной дроби можно свести к сумме двух смешанных чисел.

Для этого из неправильной дроби необходимо выделить целую часть и выполнить сложение двух смешанных чисел.

Рассмотрим несколько примеров.

Пример №1.

Сложите два числа \(\mathbf{3\frac{1}{4}}\) и \(\mathbf{\frac{6}{4}}\).

Решение:

Переведем неправильную дробь \(\mathbf{\frac{6}{4}}\) в смешанное число, разделив с остатком числитель на знаменатель дроби: 6 ÷ 4 = 1 (ост. 2), отсюда \(\mathbf{\frac{6}{4} = 1\frac{2}{4}}\).

Подставим вместо \(\mathbf{\frac{6}{4}}\) соответствующее этой дроби смешанное число \(\mathbf{1\frac{2}{4}}\).

\(\mathbf{3\frac{1}{4} + \color{blue}{\frac{6}{4}} = 3\frac{1}{4} + \color{blue}{1\frac{2}{4}} = 3 + \frac{1}{4} + 1 + \frac{2}{4} = (3 + 1) + (\frac{1}{4}  +\frac{2}{4}) = 4 + \frac{3}{4} = 4\frac{3}{4}}\)

Пример №2.

Сложите два числа \(\mathbf{3\frac{1}{4}}\) и \(\mathbf{\frac{6}{4}}\).

Решение:

Переведем смешанное число \(\mathbf{3\frac{1}{4}}\) в неправильную дробь.

Чтобы перевести смешанное число в неправильную дробь, необходимо умножить целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавить числитель дробной части, затем записать полученный результат суммы в числитель новой дроби, а знаменатель оставить без изменений.

\(\mathbf{3\frac{1}{4} = \frac{3 \cdot 4 + 1}{4} = \frac{13}{4}}\)

Подставим вместо смешанного числа \(\mathbf{3\frac{1}{4}}\) соответствующую ему неправильную дробь \(\mathbf{\frac{13}{4}}\).

\(\mathbf{\color{blue}{3\frac{1}{4}} + \frac{6}{4} = \color{blue}{\frac{13}{4}} + \frac{6}{4} = \frac{13 + 6}{4} = \frac{19}{4}}\)

Ответ запишем в виде смешанного числа, для этого из полученной неправильной дроби \(\mathbf{\frac{19}{4}}\) выделим целую часть: 19 ÷ 4 = 4 (ост. 3), следовательно, \(\mathbf{\frac{19}{4} = 4\frac{3}{4}}\)

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Рассмотрим правила вычитания смешанных чисел.

В зависимости от того, какие значения принимают дробные части смешанных чисел, существуют различные варианты вычисления разности.

1. При вычитании смешанных чисел целые части вычитают отдельно, дробные- отдельно.

Вычитание одного смешанного числа из другого сводится к уже известным нам правилам вычитания натуральных чисел и вычитания дробных чисел.

Чтобы найти разность чисел, необходимо из уменьшаемого вычесть вычитаемое.

Запишем алгоритм вычитания смешанных чисел.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

• Выполнить вычитание целых частей смешанных чисел.
• Выполнить вычитание дробных частей смешанных чисел.
• Сложить полученные результаты.

Сложнее ситуация будет складываться, если дробная часть уменьшаемого меньше дробной части вычитаемого.

В таком случае необходимо:

• Занять одну единицу от целой части уменьшаемого.
• Представить ее в виде дроби, в которой числитель равен знаменателю.
• Прибавить эту дробь к дробной части уменьшаемого.
• Выполнить вычитание целых частей смешанных чисел.
• Выполнить вычитание дробных частей смешанных чисел.
• Сложить полученные результаты.

Рассмотрим на примерах данные правила вычитания смешанных чисел.

Пример №1.

Вычислите разность двух смешанных чисел \(\mathbf{14\frac{2}{5}}\) и \(\mathbf{10\frac{1}{5}}\).

Решение:

Сравним дробные части смешанных чисел.

Для этого необходимо сравнить их числители в соответствии с правилом: больше та дробь, у которой числитель больше.

2— числитель дробной части уменьшаемого смешанного числа \(\mathbf{14\frac{2}{5}}\).

1— числитель дробной части вычитаемого смешанного числа \(\mathbf{10\frac{1}{5}}\).

Так как 2 > 1, значит \(\mathbf{\frac{\color{orange}{2}}{5} > \frac{\color{green}{1}}{5}}\)

Поскольку дробная часть уменьшаемого  больше дробной части вычитаемого , выполним вычитание целых частей смешанных чисел, выполним вычитание дробных частей смешанных чисел, полученные результаты сложим.

\(\mathbf{14\frac{2}{5} — 10\frac{1}{5} = (\color{orange}{14} + \color{green}{\frac{2}{5}}) — (\color{orange}{10} + \color{green}{\frac{1}{5}}) = (\color{orange}{14} — \color{orange}{10}) + (\color{green}{\frac{2}{5}} — \color{green}{\frac{1}{5}}) = 4 + \frac{2 — 1}{5} = 4 + \frac{1}{5} = 4\frac{1}{5}}\)

Пример №2.

Вычислите разность двух смешанных чисел \(\mathbf{31\frac{2}{7}}\) и \(\mathbf{1\frac{4}{7}}\).

Решение:

Сравним дробные части смешанных чисел.

Для этого необходимо сравнить их числители в соответствии с правилом: больше та дробь, у которой числитель больше.

2— числитель дробной части уменьшаемого смешанного числа \(\mathbf{31\frac{2}{7}}\).

4— числитель дробной части вычитаемого смешанного числа \(\mathbf{1\frac{4}{7}}\).

2 < 4, следовательно, \(\mathbf{\frac{\color{orange}{2}}{7} < \frac{\color{green}{4}}{7}}\)

Так как дробная часть уменьшаемого \(\mathbf{\frac{2}{7}}\) меньше дробной части вычитаемого \(\mathbf{\frac{4}{7}}\), займем единицу от целой части уменьшаемого и представим ее в виде дроби со знаменателем 7 (так как знаменатель всех имеющихся дробей в данном примере равен 7), уменьшив при этом целую часть уменьшаемого числа на единицу.

\(\mathbf{31\frac{2}{7} — 1\frac{4}{7} = (31 + \frac{2}{7}) — (1 + \frac{4}{7}) = (\color{red}{31 — 1} + \color{green}{1} + \frac{2}{7}) — (1 + \frac{4}{7}) =}\)

\(\mathbf{= (\color{red}{30} + \color{green}{\frac{7}{7}} + \frac{2}{7}) — (1 + \frac{4}{7}) = (\color{purple}{30} + \color{blue}{\frac{9}{7}}) — (\color{purple}{1} + \color{blue}{\frac{4}{7}}) = (\color{purple}{30} — \color{purple}{1}) + (\color{blue}{\frac{9}{7}} — \color{blue}{\frac{4}{7}}) = 29 + \frac{5}{7} = 29\frac{5}{7}}\)

2. Вычитание смешанного числа из натурального числа.

При вычитании смешанного числа из натурального числа так же приходится занимать единицу от уменьшаемого натурального числа и представлять ее в виде дроби, в которой числитель равен знаменателю.

Рассмотрим поясняющий пример.

Вычислите разность чисел 20 и \(\mathbf{3\frac{4}{5}}\).

Решение:

Уменьшаемое число 20 не содержит дробную часть, займем у него единицу и представим ее в виде дроби со знаменателем 5 (так как знаменатель всех имеющихся дробей в данном примере равен 5), уменьшив при этом уменьшаемое натуральное число на единицу.

\(\mathbf{20 — 3\frac{4}{5} = 20 — (3 + \frac{4}{5}) = (\color{red}{20 — 1} + \color{green}{1}) — (3 + \frac{4}{5}) = (\color{red}{19} + \color{green}{\frac{5}{5}}) — (3 + \frac{4}{5}) =}\)

\(\mathbf{= (19 — 3) + (\frac{5}{5} — \frac{4}{5}) = 16 + \frac{1}{5} = 16\frac{1}{5}}\)

3. Вычитание натурального числа из смешанного числа.

При вычитании из смешанного числа натурального числа необходимо вычесть из целой части смешанного числа натуральное число, оставив при этом дробную часть без изменений.

Пример.

Вычтем из смешанного числа \(\mathbf{15\frac{1}{5}}\) натуральное число 12.

\(\mathbf{15\frac{1}{5} — 12 = (15 + \frac{1}{5}) — 12 = (\color{orange}{15} + \frac{1}{5}) — \color{orange}{12} = (\color{orange}{15} — \color{orange}{12}) + \frac{1}{5} = 3\frac{1}{5}}\)

4. Вычитание из смешанного числа обыкновенной дроби.

• Вычитание из смешанного числа правильной дроби.

При вычитании правильной дроби из смешанного числа необходимо вычесть дробь из дробной части этого смешанного числа, а целую часть его оставить неизменной.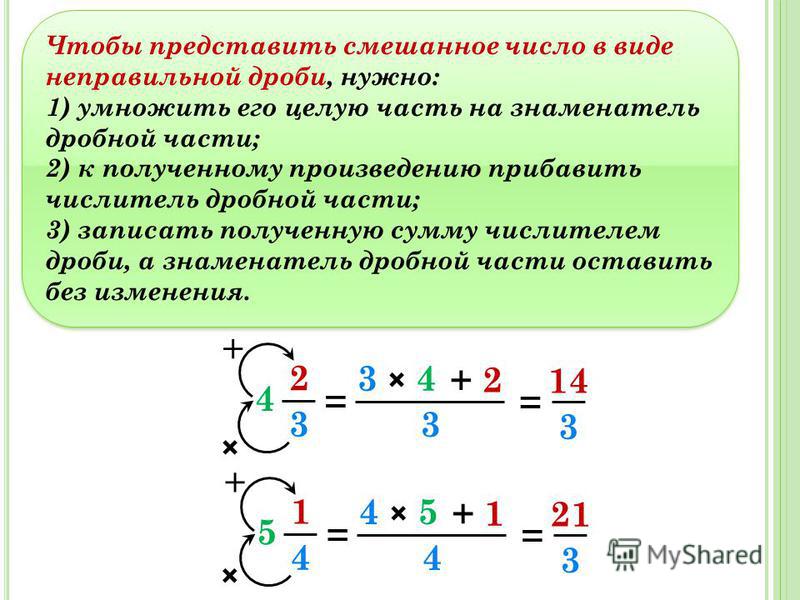

Однако, если вычитаемая дробь больше чем дробная часть смешанного числа, то из его целой части придется занять единицу, представив ее в виде дроби, знаменатель которой равен числителю, целую часть смешанного числа при этом необходимо уменьшить на единицу.

Пример№ 1.

Найдите разность чисел \(\mathbf{19\frac{7}{12}}\) и \(\mathbf{\frac{4}{12}}\).

Решение:

Сравним числитель дробной части смешанного числа и вычитаемой дроби.

Числитель дроби \(\mathbf{\frac{7}{12}}\) равен 7.

Числитель дроби \(\mathbf{\frac{4}{12}}\) равен 4.

7 > 4, следовательно, \(\mathbf{\frac{\color{orange}{7}}{12} > \frac{\color{green}{4}}{12}}\).

В таком случае действия просты, необходимо вычесть дробь из дробной части смешанного числа, а целую часть его оставить неизменной.

\(\mathbf{19\frac{7}{12} — \frac{4}{12} = (19 + \color{green}{\frac{7}{12}}) — \color{green}{\frac{4}{12}} = 19 + (\color{green}{\frac{7}{12}} — \color{green}{\frac{4}{12}}) = 19 + \frac{3}{12} = 19\frac{3}{12}}\)

Пример №2.

Найдите значение выражения \(\mathbf{8\frac{7}{11} — \frac{8}{11}}\).

Решение:

Вычтем из смешанного числа \(\mathbf{8\frac{7}{11}}\) обыкновенную дробь \(\mathbf{\frac{8}{11}}\).

Сравним числители дробной части смешанного числа и вычитаемой дроби.

Числитель дроби \(\mathbf{\frac{7}{11}}\) равен 7.

Числитель дроби \(\mathbf{\frac{8}{11}}\) равен 8.

7 < 8, значит \(\mathbf{\frac{\color{orange}{7}}{11} < \frac{\color{green}{8}}{11}}\).

Так как дробная часть уменьшаемого смешанного числа меньше вычитаемой дроби, займем единицу из целой части смешанного числа и представим ее в виде дроби со знаменателем 11 (так как знаменатель всех имеющихся дробей в данном примере равен 11), уменьшив при этом целую часть смешанного числа на единицу.

\(\mathbf{8\frac{7}{11} — \frac{8}{11} = (8 + \frac{7}{11}) — \frac{8}{11} = (\color{red}{8 — 1} + \color{green}{1} + \frac{7}{11}) — \frac{8}{11} = (\color{red}{7} + \color{green}{\frac{11}{11}} + \frac{7}{11}) — \frac{8}{11} = }\)

\(\mathbf{= (7 + \frac{18}{11}) — \frac{8}{11} = 7 + (\frac{18}{11} — \frac{8}{11}) = 7 + \frac{10}{11} = 7\frac{10}{11}}\)

5. Вычитание из неправильной дроби смешанного числа.

Первый способ: вычитание смешанного числа из неправильной дроби и неправильной дроби из смешанного числа можно свести к разности двух неправильных дробей.

Для этого смешанное число можно представить в виде неправильной дроби и выполнить вычитание неправильных дробей.

Второй способ: вычитание смешанного числа из неправильной дроби и неправильной дроби из смешанного числа можно свести к разности двух смешанных чисел.

Для этого из неправильной дроби необходимо выделить целую часть и выполнить вычитание двух смешанных чисел.

Рассмотрим несколько примеров.

Пример №1.

Найдите значение выражения \(\mathbf{\frac{122}{3} — 4\frac{2}{3}}\).

Решение:

Переведем неправильную дробь \(\mathbf{\frac{122}{3}}\) в смешанное число, разделив с остатком числитель на знаменатель дроби: 122 ÷ 3 = 40 (ост. 2), значит \(\mathbf{\frac{122}{3} = 40\frac{2}{3}}\).

Подставим в исходное выражение вместо неправильной дроби \(\mathbf{\frac{122}{3}}\) соответствующее ему смешанное число \(\mathbf{40\frac{2}{3}}\).

Найдем разность двух смешанных чисел.

\(\mathbf{\color{blue}{\frac{122}{3}} — 4\frac{2}{3} = \color{blue}{40\frac{2}{3}} — 4\frac{2}{3} = (40 — 4) + (\frac{2}{3} — \frac{2}{3}) = 36 + 0 = 36}\)

Дробные части уменьшаемого и вычитаемого оказались равными, в итоге дробная часть оказалась равна нулю.

Пример №2.

Найдите значение выражения \(\mathbf{\frac{21}{3} — 6\frac{2}{3}}\).

Решение:

Переведем \(\mathbf{6\frac{2}{3}}\) в неправильную дробь: \(\mathbf{6\frac{2}{3} = \frac{6 \cdot 3 + 2}{3} = \frac{20}{3}}\).

Подставим в исходное выражение вместо смешанного числа \(\mathbf{6\frac{2}{3}}\) соответствующую ему неправильную дробь \(\mathbf{\frac{20}{3}}\).

Найдем разность двух неправильных дробей.

\(\mathbf{\frac{21}{3} — \color{blue}{6\frac{2}{3}} = \frac{21}{3} — \color{blue}{\frac{20}{3}} = \frac{21 — 20}{3} = \frac{1}{3}}\)

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Арифметические операции сложения и вычитания часто используют при решении различных задач.

При решении задач арифметическим или алгебраическим способом используют основные свойства математических операций, применяют известные правила упрощения и преобразования выражений.

Часто одну и ту же текстовую задачу можно решить разными способами, отличающимися друг от друга логикой рассуждения.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Попробуем решить составную текстовую задачу на сложение и вычитание смешанных чисел.

Задача.

За три дня собрали \(\mathbf{17\frac{2}{3}}\) кг ягод.

В первый день собрали \(\mathbf{5\frac{1}{3}}\).

Во второй день собрали на \(\mathbf{\frac{8}{3}}\) кг больше, чем в первый день.

Сколько килограммов ягод собрали в третий день?

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

1. Решим данную задачу арифметическим способом (составлением выражения).

Запишем кратко условие задачи.

Собрали в первый день: \(\mathbf{5\frac{1}{3}}\) кг.

Собрали во второй день: \(\mathbf{5\frac{1}{3} + \frac{8}{3}}\) кг.

Всего ягод собрали за три дня: \(\mathbf{17\frac{2}{3}}\) кг.

Собрали ягод на третий день- неизвестно.

Чтобы найти сколько ягод собрали на третий день необходимо из общего количества ягод, собранных за три дня, вычесть ягоды, собранные в первый и во второй день.

Составим выражение.

\(\mathbf{17\frac{2}{3} — 5\frac{1}{3} — (5\frac{1}{3} + \frac{8}{3})}\)

Найдем значение полученного выражения.

Данное выражение содержатся сразу несколько арифметических операций и скобки.

Определим порядок действий в данном выражении, используя правила, которые определяют порядок выполнения действий в математических выражениях.

1) Это выражение содержит скобки, поэтому выполним сначала действия в них.

Для этого найдем сумму смешанного числа и неправильной дроби.

Сложение смешанного числа и неправильной дроби можно свести к сумме двух смешанных чисел (из неправильной дроби необходимо выделить целую часть и выполнить сложение двух смешанных чисел).

Переведем неправильную дробь \(\mathbf{\frac{8}{3}}\) в смешанное число, разделив с остатком числитель на знаменатель дроби: 8 ÷ 3 = 2 (ост. 2), получаем \(\mathbf{\frac{8}{3} = 2\frac{2}{3}}\).

\(\mathbf{5\frac{1}{3} + \color{blue}{\frac{8}{3}} = 5\frac{1}{3} + \color{blue}{2\frac{2}{3}} = \color{purple}{5} + \color{blue}{\frac{1}{3}} + \color{purple}{2} + \color{blue}{\frac{2}{3}} = (5 + 2) + (\frac{1}{3} + \frac{2}{3}) = 7 + \frac{3}{3} = 7 + 1 = 8}\)

Так как оставшиеся за скобками действия- это действия первой ступени, то они выполняются по порядку слева направо.

2) Найдем разность смешанных чисел \(\mathbf{17\frac{2}{3} — 5\frac{1}{3}}\).

Чтобы найти разность двух смешанных чисел, необходимо выполнить вычитание целых частей смешанных чисел, затем выполнить вычитание дробных частей этих чисел и сложить полученные результаты.

\(\mathbf{17\frac{2}{3} — 5\frac{1}{3} = (\color{orange}{17} + \color{green}{\frac{2}{3}}) — (\color{orange}{5} + \color{green}{\frac{1}{3}}) = (\color{orange}{17} — \color{orange}{5}) + (\color{green}{\frac{2}{3}} — \color{green}{\frac{1}{3}}) = 12 + \frac{1}{3} = 12\frac{1}{3}}\)

3) Найдем разность значений, полученных во втором и первом действии, т.е. из смешанного числа \(\mathbf{12\frac{1}{3}}\) вычтем натуральное число 8.

Чтобы вычесть из смешанного числа натуральное число, необходимо вычесть из целой части смешанного числа натуральное число, оставив при этом дробную часть без изменений.

\(\mathbf{12\frac{1}{3} — 8 = \color{orange}{12} + \frac{1}{3} — \color{orange}{8} = (\color{orange}{12} — \color{orange}{8}) + \frac{1}{3} = 4 + \frac{1}{3} = 4\frac{1}{3}}\) (кг) ягод собрали на третий день.

Ответ: \(\mathbf{4\frac{1}{3}}\) (кг).

Эту же задачу можно решить арифметическим способом, но по действиям.

Запишем кратко условие задачи.

Собрали в первый день: \(\mathbf{5\frac{1}{3}}\) кг.

Собрали во второй день: \(\mathbf{5\frac{1}{3} + \frac{8}{3}}\) кг.

Всего ягод собрали за три дня: \(\mathbf{17\frac{2}{3}}\) кг.

Собрали ягод в третий день- неизвестно.

В таком случае решение данной задачи будет состоять из следующих этапов:

• первым делом найдем сколько ягод, собрали во второй день.
• далее, сложив полученный результат с ягодами, которые были собраны в первый день, найдем какое количество ягод собрали за первый и второй день.
• затем полученную сумму вычтем из общего количества ягод, собранных за три дня, в итоге получим сколько килограммов ягод, собрали за третий день.

1) \(\mathbf{5\frac{1}{3} + \color{blue}{\frac{8}{3}} = 5\frac{1}{3} + \color{blue}{2\frac{2}{3}} = \color{purple}{5} + \color{blue}{\frac{1}{3}} + \color{purple}{2} + \color{blue}{\frac{2}{3}} = (5 + 2) + (\frac{1}{3} + \frac{2}{3}) = 7 + \frac{3}{3} = 7 + 1 = 8}\) (кг) ягод собрали во второй день.

2) \(\mathbf{5\frac{1}{3} + 8 = 5 + \frac{1}{3} + 8 = (\color{blue}{5} + \color{blue}{8}) + \frac{1}{3} = 13 + \frac{1}{3} = 13\frac{1}{3}}\) (кг) ягод собрали за первый и второй день.

3) \(\mathbf{17\frac{2}{3} — 13\frac{1}{3} = (\color{orange}{17} + \color{green}{\frac{2}{3}}) — (\color{orange}{13} + \color{green}{\frac{1}{3}}) = (\color{orange}{17} — \color{orange}{13}) + (\color{green}{\frac{2}{3}} — \color{green}{\frac{1}{3}}) = 4\frac{1}{3}}\) (кг) ягод собрали на третий день.

Ответ: \(\mathbf{4\frac{1}{3}}\) (кг).

2. Решим задачу алгебраическим способом.

Кратко запишем условие задачи.

Собрали в первый день: \(\mathbf{5\frac{1}{3}}\) кг ягод.

Собрали во второй день: \(\mathbf{5\frac{1}{3} + \frac{8}{3}}\) кг ягод.

Пусть х (кг) ягод собрали на третий день.

Зная, что всего собрали за три дня \(\mathbf{17\frac{2}{3}}\) кг ягод.

Составим уравнение.

\(\mathbf{5\frac{1}{3} + (5\frac{1}{3} + \frac{8}{3}) + x = 17\frac{2}{3}}\)

Упростим данное уравнение.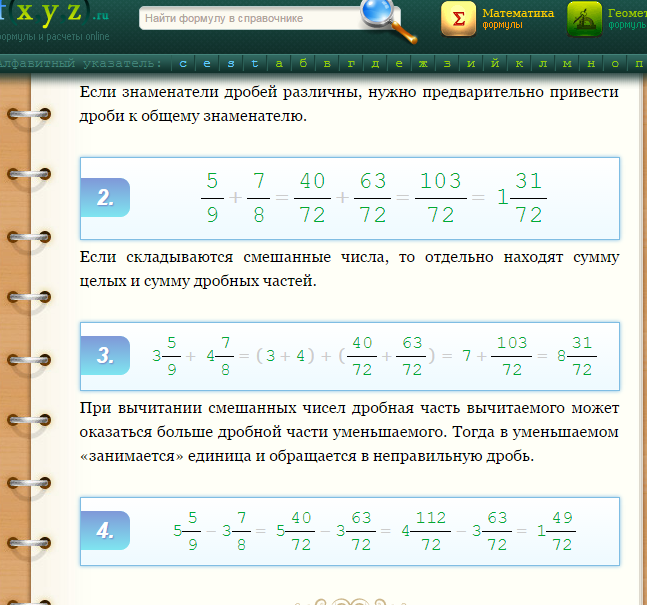

Выполним действие в скобках, т.е. найдем сумму смешанного числа \(\mathbf{5\frac{1}{3}}\) и неправильной дроби \(\mathbf{\frac{8}{3}}\), полученный результат сложим с первым слагаемым \(\mathbf{5\frac{1}{3}}\) (эти действия мы уже выполняли, решая задачу арифметическим способом).

\(\mathbf{5\frac{1}{3} + \frac{8}{3} = 5\frac{1}{3} + 2\frac{2}{3} = (5 + 2) + (\frac{1}{3} + \frac{2}{3}) = 7 + \frac{3}{3} = 7 + 1 = 8}\)

\(\mathbf{5\frac{1}{3} + 8 = 5 + \frac{1}{3} + 8 = (5 + 8) + \frac{1}{3} = 13 + \frac{1}{3} = 13\frac{1}{3}}\)

Получается, что выражение \(\mathbf{5\frac{1}{3} + (5\frac{1}{3} + \frac{8}{3})}\) тождественноравно выражению \(\mathbf{13\frac{1}{3}}\).

Подставим в исходное уравнение вместо суммы \(\mathbf{5\frac{1}{3} + (5\frac{1}{3} + \frac{8}{3})}\) смешанное число \(\mathbf{13\frac{1}{3}}\).

Получим простое уравнение с неизвестным слагаемым:

\(\mathbf{13\frac{1}{3} + x = 17\frac{2}{3}}\)

Чтобы найти неизвестное слагаемое, необходимо вычесть из суммы известное слагаемое.

\(\mathbf{13\frac{1}{3} + x = 17\frac{2}{3}}\)

\(\mathbf{x = 17\frac{2}{3} — 13\frac{1}{3}}\)

\(\mathbf{x = (17 + \frac{2}{3}) — (13 + \frac{1}{3})}\)

\(\mathbf{x = (17 — 13) + (\frac{2}{3} — \frac{1}{3})}\)

\(\mathbf{x = 4 + \frac{1}{3}}\)

\(\mathbf{x = 4\frac{1}{3}}\) (кг) ягод собрали на третий день.

Ответ: \(\mathbf{4\frac{1}{3}}\) (кг).

Все три варианта решения задачи равноправны, дают одинаковый результат.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна зарегистрированным пользователям

Как сложить целое число с дробью

Обновлено 31 октября 2020 г.

Автор: Лиза Мэлони

Вы уже знаете, что такое целые числа, даже если не знали, что означает их название: это числа, которые вы используется, когда вы впервые начали считать, начиная с 0, а затем считая 1, 2, 3, 4 и так далее. Дроби представляют часть целого числа. Есть два способа складывать дроби и целые числа, но при этом необходимо соблюдать несколько основных правил.

Использование торта в качестве примера 

Это поможет, если вы подумаете о дробях и целых числах в терминах пиццы, пирогов или любой другой вкусной круглой вещи, которую можно разрезать на кусочки и съесть. Подумайте о тортах: каждое знакомое целое число представляет собой целый торт. У вас может быть 1 торт, 2 торта, 3 торта и так далее. Если вы разрезаете торт на кусочки, вы создаете дробь, где нижнее число дроби говорит вам, на сколько частей вы разрезаете каждый торт, а верхнее число говорит вам, сколько частей осталось.

Сложение целых чисел и дробей

Если представить целые числа и дроби с точки зрения кусочков торта, то легко представить себе, как складываются целые числа и дроби. Допустим, у вас на столе осталось 2 целых торта, плюс один торт, который был разрезан на 6 равных частей, но кто-то съел кусок, так что теперь на тарелке осталось только 5 кусочков. Вы можете выразить этот нарезанный торт в виде дроби с количеством кусочков, оставшихся сверху, и количеством кусочков, изначально разрезанных снизу:

\frac{5}{6}

Вы можете выразить общее количество торта – 2 торта плюс 5/6 торта – в виде смешанного числа, которое записывается как

2 \frac{5}{6 }

Если у вас есть целое число и дробь, вы можете просто сложить их вместе, в результате чего получится так называемое смешанное число. Например, смешанное число

8 \frac{3}{4}

понимается как означающее то же самое, что и

8 + \frac{3}{4}

, поскольку все согласны с тем, что они означают одно и то же. , вам не нужно записывать символ сложения, когда вы пишете смешанное число.

Торты как неправильные дроби

Иногда вас попросят сложить целые числа с дробями и оставить их в форме неправильной дроби вместо того, чтобы записывать их как смешанные числа. Неправильная дробь — это просто дробь, в которой верхнее число (количество оставшихся ломтиков) больше нижнего числа (количество ломтиков, на которые был разрезан каждый торт). Хороший пример из реальной жизни: вы разрезаете два торта на 6 частей каждый, а затем кто-то съедает 5 кусочков из одного торта. Это означает, что у вас остался один целый торт и 1/6 от другого торта, который был съеден. Чтобы дать свой ответ полностью в форме дроби, вы должны понять, как записать весь торт в виде дроби.

Целые числа можно записать в виде дробей

Вот как представить целые числа в виде дробей: Если вы разрежете торт на 8 равных частей и оставите их все на тарелке, у вас останется 8/8 кусков торта. плита. Другими словами, торт был порезан на кусочки, но целое осталось на месте. Вот что представляет собой целое число в форме дроби. Таким образом, дробь, в которой верхнее число (количество оставшихся кусочков) совпадает с нижним числом (количество кусочков, которые вы разрезали в первую очередь), равна 1 целому торту, пирогу или чему-то еще, что вы считаете. .

Это означает, что

\frac{8}{8} = 1 \\ \,\\ \frac{25}{25} = 1 \\ \,\\ \frac{649}{649} = 1

и так далее. Неважно, какое число находится вверху, а какое внизу, главное, чтобы они были одинаковыми. Вы также можете выразить другие целые числа в виде дробей; просто умножьте целое число на дробь, у которой такое же число сверху и такое же число снизу. Точно так же, как по волшебству, это превращает целое число в форму дроби без изменения его значения, потому что все, что вы сделали, это умножили его на 1.

Итак, чтобы записать целое число в виде дроби, умножьте целое число на дробь, в которой число в числителе и знаменателе совпадает. Например, если вы хотите записать целое число 5 в виде дроби с 8 в знаменателе, вы должны умножить

5 × \frac{8}{8} = \frac{40}{8}

Сложение Преобразование целых чисел в неправильные дроби

Теперь, когда вы знаете, как записывать целые числа в виде дробей, легко добавлять целые числа к существующей дроби и оставлять их в форме неправильной дроби. Все, что вам нужно сделать, это убедиться, что знаменатели — числа в нижней части дробей — совпадают. (Если бы вы попытались рассказать о тортах, нарезанных на кусочки разного размера, это не имело бы особого смысла, не так ли? То же самое и с дробями.)

Итак, если вы пытаетесь сложить 3 и 5/9, вы должны сначала преобразовать 3 в дробную форму:

3 × \frac{9}{9} = \frac{27}{9}

Затем вы можете сложить дроби 5/9 и 27/9 вместе. Когда две дроби имеют одинаковый знаменатель, вы просто складываете числители и записываете их над одним и тем же знаменателем. Таким образом, у вас будет

5 + 27 = 33

в числителе и 9 в знаменателе, или 33/9 в качестве окончательного ответа.

Как сложить смешанные дроби с целыми числами?

Прежде чем узнать, как мы можем складывать смешанные дроби с целыми числами, мы должны знать, что такое дроби и целые числа. Система счисления является основной концепцией целых чисел и смешанных дробей. Если у нас есть ясность относительно системы счисления, мы можем легко решить концепцию сложения смешанных дробей с целыми числами. В системе счисления есть такие понятия, как целые числа, натуральные числа, целые числа и действительные числа.

Система счисления представляет собой комбинацию натуральных чисел, целых чисел, целых и действительных чисел.

Натуральные числа: Натуральные числа — это числа, которые могут считать числа. Мы также можем сказать, что числа начинаются от 1 до бесконечности без включения 0. Примеры:

Натуральные числа = {1,2,3,4,5,6,7,8,9,10,11,12,13….}

Целые числа: Целые числа числа в союзе натуральных чисел и нуля (0). Целое число — это один из типов системы счисления, в котором ноль входит в число натуральных чисел. Примеры,

Целые числа = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,15,16,17,18….}

Целые числа: Целочисленная система — это система счисления, в которой отрицательные числа и положительные натуральные числа включаются с нулем (0). Целые числа — это числа, представляющие собой объединение отрицательных целых чисел и целых чисел. Примеры:

Целые числа={…-2,-1,0,1,2…..}

Рациональные числа: Рациональные числа — это числа, представленные только в форме r/a, где а не должен равняться нулю. Рациональные числа также называют конечными числами.

Примеры,

Рациональные числа: 0/1, 1/1, 2/1, 3/1,1.9999 и т. д.

Иррациональные числа: Иррациональные числа — это форма r/b, где b не должно равняться нулю, а также они называются неконечными числами.

Примеры,

Иррациональные числа: √2,√3, 0,12356… 

Вещественные числа: Вещественные числа являются частью системы счисления, состоящей из рациональных и иррациональных чисел.

Дроби: Дроби основаны на числителе и знаменателе. Дроби подобны рациональным числам, представленным как часть целых чисел. Предположим, что прямоугольник разделен на четыре части, так что каждая часть делится на 1/3 и представляет собой 1:3, где 1/3 или 1:3 — дробная часть прямоугольника.

Примеры дробей: 

7/8, где 7 — числитель, а 2 — знаменатель.

1/4, где 1 — числитель, а 4 — знаменатель.

9/3, где 9 — числитель, а 3 — знаменатель.

Дроби бывают трех типов. Вот они,

1. Правильная дробь: Правильная дробь — один из видов дроби. Правильная дробь объясняется тем, что числитель должен быть меньше знаменателя.
   Примеры правильных дробей: 1/2, 3/5, 6/8….
2. Неправильная дробь: Неправильная дробь — один из видов дроби. Он определяется как числитель, который должен быть больше знаменателя.
   Примеры неправильных дробей: 8/6, 9/7, 3/2 и т. д.
3. Смешанная дробь: Смешанная дробь представляет собой объединение дробной части (содержит как правильные, так и неправильные) и натуральных чисел.
   Ниже приведены примеры смешанных дробей:
    здесь 1 – целое число, 2 – числитель, 3 – знаменатель.

Как преобразовать смешанные дроби в форму p/q?

Шаг 1: Сначала умножьте целое число на знаменатель.

Шаг 2: Сложите числитель и результат умножения целого числа на знаменатель.

Шаг 3: Результат шага 2 должен быть помещен в часть числителя, где знаменатель такой же, как в смешанной дроби. Следовательно, мы получили смешанную дробь в правильной форме p/q.

Как преобразовать неправильные дроби в смешанные дроби?

Возьмем 8/6 как неправильную дробь

Шаг 1: Сначала разделите числитель со знаменателем 8//6 = 1 на частное, а остаток на 2.

Шаг 2: Остаток 2 , который делится на 6. знаменатель. Если есть отмена, которая происходит, отмените с соответствующим коэффициентом.

Шаг 4: Когда мы рационализируем 2/6, мы получаем 1/3. Объединяя ответ шага 1 и шага 4, получаем

Как сложить целое число со смешанной дробью?

1. Сначала мы должны преобразовать смешанную дробь в форму p/q.
2. Затем преобразуйте эту форму p/q в десятичную форму.
3. Затем сложение целого числа с десятичной формой p/q.

Примеры задач

Задача 1. Решите приведенный ниже вопрос, который имеет форму сложения целых чисел и смешанной дроби?

                                                                    10 + 

Решение:

Чтобы решить эту задачу, мы должны сначала решить смешанные дроби.

Решение смешанной дроби: преобразуется в форму p/q следующим образом.

Шаг 1 : Умножьте целое число 10 на знаменатель 3, как показано на диаграмме = 10×3=30.

Шаг 2 : Добавление числителя 2 с результатом в Шаге 1 = 2+30=32.

Шаг 3 : В виде p/q числитель p=32 и знаменатель q=3. Следовательно, 32/3=10,7 является правильной формой p/q.

После преобразования части смешанной дроби в правильную форму p/q. Сложите целое число со смешанной дробью.

Прибавляем 10 к 32/3=10,7 получаем 20,7 в результате сложения.

Следовательно, решив вышеуказанную задачу, мы получим результат 20,7, который также представлен в виде p/q=207/10.

Задача 2: Решите вопрос ниже, который находится в форме сложения целых чисел и смешанной дроби?

                                                 20 +

Решение:

Чтобы решить эту задачу, мы должны сначала решить смешанные дроби.

Решение смешанной дроби: преобразуется в форму p/q следующим образом.

Шаг 1 : Умножьте целое число 1 на знаменатель 3, как показано на диаграмме = 1×3=3.

Шаг 2 : Добавление числителя 2 с результатом в Шаге 1 = 2+3=5.

Шаг 3 : В P/q сформируйте числитель p=5 и знаменатель q=3. Следовательно, 5/3=1,7 является правильной формой p/q.

После преобразования части смешанной дроби в правильную форму p/q. Сложите целое число со смешанной дробью.

Прибавим 20 к 5/3=1,7 и получим в результате сложения 21,7.

Следовательно, решив вышеуказанную задачу, мы получим результат 21.7, который также обозначается как p/q form 217/10.

Задача 3: Решите вопрос ниже, который находится в форме сложения целых чисел и смешанной дроби?

                                               13 +                                                                                  

Решение:

.

Решение смешанной дроби: преобразуется в форму p/q следующим образом.

Шаг 1 : Умножьте целое число 2 на знаменатель 3, как показано на диаграмме = 2×3=6.

Шаг 2 : Добавление числителя 1 с результатом в Шаге 1 = 1+6=7.

Шаг 3 : В виде p/q числитель p=7 и знаменатель q=3. Следовательно, 7/3=2,33 является правильной формой p/q.

После преобразования части смешанной дроби в правильную форму p/q. Сложите целое число со смешанной дробью.

Прибавив 13 к 7/3=2,33, мы получим 15,33 в результате сложения.

Следовательно, решив вышеуказанную задачу, мы получим результат 15,33, который также обозначается как p/q form 153,3/10.

Задача 4: Решите вопрос ниже, который находится в форме сложения целых чисел и смешанной дроби?

16 +

Решение:

Для решения этой проблемы мы должны сначала решить смешанные фракции.

Решение смешанной дроби: преобразуется в форму p/q следующим образом.

Шаг 1 : Умножьте целое число 3 на знаменатель 3, как показано на диаграмме = 3×3=9.

Шаг 2: Добавление числителя 1 с результатом в Шаге 1 = 1+9=10.

Шаг 3 : В p/q сформируйте числитель p=10 и знаменатель q=3. Следовательно, 10/3=3,33 является правильной формой p/q.

После преобразования части смешанной дроби в правильную форму p/q. Сложите целое число со смешанной дробью.

Прибавляем 16, где 10/3=3,33, в результате сложения получаем 19,33.

Следовательно, решив вышеуказанную задачу, мы получим результат 19,33, который также обозначается как p/q form 193,3/10.

Деление целых чисел на дроби

Что мы делаем, когда делим целые числа на дроби? Разделив целое число на дробь, мы найдем количество групп дроби, которое мы можем поместить в целое. Самый распространенный способ деления целого числа на дробь — это умножение заданного целого числа на обратную дробь. Следующая статья поможет вам понять, как разделить целое число на дробь. Изучите различные способы деления целых чисел на дроби.

Умножение обратной дроби

Первый метод является наиболее распространенным методом, в котором мы умножаем целое число на обратную дробь. Следующий пример поможет вам полностью понять этапы деления целого числа на дробь.

Шаг 1: Начните с преобразования целого числа в дробь. Мы можем сделать это, поместив целое число в числитель дроби. На место знаменателя поставим 1.

Например , если нам нужно вычислить 3 ÷ 2/5

Мы заменим 3 на 31

Шаг 2: Далее мы найдем обратную дробь, заданную как делитель. Обратная величина любого числа является его обратной величиной. Так, в случае дроби данный числитель станет знаменателем, а знаменатель будет новым числителем.

Например, обратная величина 2/5 будет равна 5/2

Шаг 3: Теперь, когда у нас есть две дроби, мы их умножим. Для умножения мы сначала умножаем числители, а затем знаменатели.

Например, 3/1 * 5/2 = 15/2

Шаг 4: Наконец, мы упростим дробь, если это необходимо. Итак, мы сведем его к самым низким условиям. Если у нас есть неправильная дробь, т. е. числитель дроби больше знаменателя, мы изменим его на смешанное число.

Например, 15/2 = 7*1/2

Умножение нижнего числа дроби

Существует более простой способ деления целых чисел на дроби для тех, кто хочет иметь меньше шагов вычислений.

Шаг 1. Умножим знаменатель дроби (т.е. нижнее число) на целое число.

Шаг 2 . Получив произведение, упростим дробь. Если ответом является неправильная дробь, мы преобразуем ее в смешанную форму.

Например, 32   ÷ 7

Сначала мы умножим нижнее число, то есть 2, на целое число.

Таким образом,   3/2 * 7 = 3/1 * 4

Поскольку эту дробь нельзя упростить, это и есть ответ.

Деление целого числа на десятичное

Теперь давайте изучим процесс деления целых чисел на десятичные числа. Одним из самых популярных способов деления целого числа на десятичное является преобразование десятичного числа в дробь.

Итак, мы сначала преобразуем десятичную дробь в дробь, удалив десятичную точку и добавив 10 ^x в знаменатель, где x представляет количество цифр после запятой.

Например, 2 ÷ 0,05

Мы можем преобразовать 0,05 в дробь следующим образом:

 2 ÷ 005/100

Далее мы выполним те же действия, что и при делении целых чисел на дроби.

2 * 100/5

200/5 = 40

Ответ равен 40.

Упражнение: Это упражнение поможет вам изучить деление дробей на целое число. Возьмите две полоски бумаги. Убедитесь, что обе полоски имеют одинаковую длину. Разрежьте одну из полос на 3 равные части. Теперь у вас останется 1/3 часть полоски. Затем вам нужно разрезать эту треть на 4 равные части. Наконец, у вас останется определенная порция. Сравните эту часть с другой полосой. Подсказка: 1/3 ÷ 4

Как разделить дробь на целое число?

Теперь, когда мы знаем, как делить целые числа на дроби, давайте проверим обратное. Вот как разделить дробь на целое число.

Шаги деления дроби на целое число остаются прежними. Итак, мы сначала преобразуем целое число в дробь. Следующие шаги помогут вам понять способ деления дроби на целое число.

Например, разделить 2/5 ÷ 4

Шаг 1: Сначала мы напишем задачу, а затем преобразуем целое число в дробь. Мы добавляем 1 в качестве знаменателя целого числа. Таким образом, целое число становится числителем.

Например,   2/5 ÷ 4/1

Шаг 2: Далее мы умножим две дроби, и для этого запишем обратную величину целого числа. Итак, числитель, который является нашим целым числом, станет знаменателем, а знаменатель станет числителем.

Например, 2/ 5 * 1/ 4

Шаг 3: Перемножим две дроби. Сначала найдем произведение двух числителей, а затем двух знаменателей, как указано ниже:

2/ 20

Шаг 4: Теперь мы можем упростить полученное произведение и свести его к минимуму .

Итак, 2/ 20 может быть уменьшить до 1/ 10

Таким образом, ответ будет 1/10.

Применение деления целых чисел на дроби в реальной жизни

Деление целых чисел на дроби или деление дробей на целые числа имеет несколько применений в нашей повседневной жизни. Вот наиболее распространенные примеры применения деления целых чисел на дроби и наоборот.

• При раздаче кусочков пиццы членам семьи или друзьям
• Когда мы делим буханку хлеба на кусочки.
• Деление бумаги на полоски при выполнении поделок
• В играх и занятиях

Решаемые примеры на деление целых чисел на дроби

Пример 1. Разделите следующие целые числа на дроби:

2 2156 2

3
1. 40 ÷ 1/2
2. 44 ÷ 6/3

Решение: а) 22 ÷ 2/3

Сначала мы преобразуем целое число в дробь, добавив 1 в качестве знаменателя.

22/1 ÷ 2/3

Теперь напишем обратную дробь.

22/1 * 3/2

Перемножим две дроби, чтобы получить произведение.

22/1 ÷ 2/3 = 44/3

Так как произведение является неправильной дробью, мы преобразуем его в смешанную дробь.

Ответ: 14÷2/3.

б. )   40 ÷ 1/2

Сначала мы преобразуем целое число в дробь, добавив 1 в качестве знаменателя.

40/1 ÷ 1/2

Теперь напишем обратную дробь.

22/1 ÷ 2/1

Перемножим две дроби, чтобы получить произведение.

22/1 ÷ 2/1 = 44/1

Ответ: 44.

c.) 44 ÷ 6/3

Сначала мы преобразуем целое число в дробь, добавив 1 в качестве знаменатель.

44/1 ÷ 6/3

Теперь напишем обратную дробь.

22/1 * 3/6

Перемножим две дроби, чтобы получить произведение.

22/1 * 3/6 = 66/6

Поскольку произведение представляет собой неправильную дробь, мы обычно преобразуем ее в смешанную дробь, но здесь мы можем упростить ее.

Ответ: 11.

Пример 2: Хейзел устраивает вечер спагетти у себя дома. У нее есть ½ чашки начинки, чтобы равномерно посыпать 3 тарелки. Сколько начинки (в пересчете на чашки) она кладет в каждую тарелку?

Решение: У Хейзел ½ стакана начинки

Количество мисок = 3 

Дано: В каждой тарелке одинаковое количество начинки

Количество начинки, которую Хейзел кладет в каждую тарелку = 1/2 ÷ 3

Итак, мы сначала преобразуем целое число в дробь, добавив 1 в качестве знаменателя. Затем мы напишем значение, обратное делителю, и перемножим две дроби, чтобы получить произведение.

1/2 ÷ 3/1 

= 1/2 * 1/3 = 1/6

 Ответ: Хейзел кладет ⅙ начинки в каждую тарелку.

Практические задачиВопрос 1: Разделите следующее: a. 5 ÷ 4/6 б. 6 ÷ 1/2 в. 3 ÷ 2/4 д. 11 ÷ 2/5 эл. 8 ÷ 11/2 ф. 67 ÷ 1/2 г. 45 ÷ 2/3 час. 9 ÷ 8/12 I. 4 ÷ 1/8 л. 5 ÷ 8/9 Вопрос 2: Дэвид купил пачку конфет. Он весит 1/6 фунта. Он наполняет 3 тарелки этими конфетами. Вычислите вес каждой миски, если он наполняет миски поровну. Вопрос 3: У Сиры было 1/2 фунта печенья. Она распределила печенье поровну между двумя своими дочерьми. Какова доля каждой дочери?

Часто задаваемые вопросы

1. Что такое деление дробей на целые числа?

Ответ. Когда вы делите дробь на целое число, вы просто берете верхнее число и делите его на нижнее число. Например, если у вас есть 1/3 и вы хотите разделить ее на 2, то вы должны умножить 1 на 2 и получить 2. Затем вы должны умножить 3 на 2 и получить 6. Таким образом, ваш окончательный ответ будет 1/ 3 разделить на 2, что равно 1/6.

2. Какое правило деления дробей на целые числа?

Ответ. Правило деления дробей с целыми числами простое:

Разделить числитель на знаменатель.

Вот оно! Давайте посмотрим на пример. Предположим, вы хотите разделить 1/2 на 8. Первый шаг — разделить числитель вашей дроби (1) на знаменатель вашей дроби (8). Это дает вам 1, деленное на 8 = 0,125, или 0 1/8, что произносится как «одна восьмая».

3. Как вы делите дроби на целые числа?

Ответ. Есть несколько разных способов разделить дроби с целыми числами, но самый простой способ — убедиться, что обе части вашего уравнения находятся в одном знаменателе. Допустим, у вас есть 1/4 и 5/8. Чтобы разделить их, нам нужно превратить их в дроби со знаменателем 2. Мы можем сделать это, умножив верхнее число на 2, а затем разделив его на нижнее число. Таким образом, для нашего примера мы получим: 2 (1/4) / 8 = ½ 9.0003

4. Как решить деление дроби на целые числа?

Ответ. 1. Разделить числитель на знаменатель.

2. Запишите ответ и при необходимости упростите.

3. Если в вашем ответе есть десятичная точка, округлите ее в большую или меньшую сторону до ближайшего целого числа.

5. Как разделить целое число на дробь?

Ответ. Чтобы разделить целое число на дробь, вам просто нужно сделать то же самое, что и при делении любого другого числа на другое число. Допустим, мы хотим разделить 45 на 5. Поэтому запишем это так: 45/5. Теперь давайте умножим обе части этого уравнения на 10: 4500/50=4500/5. Теперь мы можем вычесть другую часть из обеих сторон и продолжать, пока не избавимся от всех этих лишних нулей: 4500-4500=0/5=0.

1.2 Сложение целых чисел — Предварительная алгебра 2e

Цели обучения

К концу этого раздела вы сможете:

• Использовать сложение
• Модель сложения целых чисел
• Добавление целых чисел без моделей
• Перевод словосочетаний в математическую запись
• Добавление целых чисел в приложения

Приготовься 1.

1

Прежде чем приступить к работе, пройдите этот тест на готовность.

Какое число моделируется блоками base-10base-10?

Если вы пропустили эту проблему, просмотрите [ссылка].

Приготовься 1,2

Напишите цифрами число триста сорок две тысячи шесть?
Если вы пропустили эту проблему, просмотрите [ссылка].

Использовать дополнительную нотацию

Студент колледжа работает неполный рабочий день. На прошлой неделе он работал 33 часа в понедельник и 44 часа в пятницу. Чтобы найти общее количество часов, которые он отработал на прошлой неделе, он добавил 33 и 4,4.

Операция сложения объединяет числа для получения суммы. Обозначение, которое мы используем, чтобы найти сумму 33 и 44:

3+43+4

Мы читаем это как три плюс четыре и результат есть сумма трех и четырех. Числа 33 и 44 называются слагаемыми. Математическое выражение, включающее числа и операции, называется выражением.

Дополнительные обозначения

Для описания сложения мы можем использовать символы и слова.

Операция	Обозначение	Выражение	Читать как	Результат
Дополнение	++	3+43+4	три плюс четыре	сумма 33 и 44

Пример 1.11

Перевод из математической записи в слова:

1. ⓐ 7+17+1
2. ⓑ 12+1412+14

Решение

• ⓐ Выражение состоит из символа плюс, соединяющего слагаемые 7 и 1. Мы читаем это как семь плюс один . Результат сумма семи и одного .
• ⓑ Выражение состоит из символа плюс, соединяющего слагаемые 12 и 14. Мы читаем это как двенадцать плюс четырнадцать . Результатом является сумма двенадцати и четырнадцати .

Попытайся 1,21

Перевод из математической записи в слова:

1. ⓐ 8+48+4
2. ⓑ 18+1118+11

Попытайся 1,22

Перевод из математической записи в слова:

1. ⓐ 21+1621+16
2. ⓑ 100+200100+200

Модель Сложение целых чисел

Сложение на самом деле просто подсчет. Мы будем моделировать сложение с помощью блоков base-10base-10. Помните, блок представляет 11, а стержень представляет 10,10. Начнем с моделирования выражения сложения, которое мы только что рассмотрели, 3+4,3+4.

Каждое слагаемое меньше 10,10, поэтому мы можем использовать блоки единиц.

Начнем с моделирования первого числа с 3 блоками.
Затем мы моделируем второй номер с 4 блоками.
Подсчитайте общее количество блоков.

Всего 77 блоков. Мы используем знак равенства (=)(=), чтобы показать сумму. Математическое предложение, которое показывает, что два выражения равны, называется уравнением. Мы это показали. 3+4=7,3+4=7.

Манипулятивная математика

Работа с рабочими листами по манипулятивной математике Упражнение «Образец сложения целых чисел» поможет вам лучше понять, как складывать целые числа.

Пример 1.12

Модель сложение 2+6.2+6.

Решение

2+62+6 означает сумму 22 и 66

Каждое слагаемое меньше 10, поэтому мы можем использовать единицы.

Смоделируйте первое число из 2 блоков.
Смоделируйте второе число из 6 блоков.
Подсчитайте общее количество блоков	Всего 88 блоков, поэтому 2+6=8,2+6=8.

Попытайся 1,23

Модель: 3+6,3+6.

Попытайся 1,24

Модель: 5+1,5+1.

Когда в результате получится 1010 или более блоков единиц, мы обменяем 1010 блоков на один стержень.

Пример 1.13

Модель сложение 5+8.5+8.

Решение

5+85+8 означает сумму 55 и 8,8.

Каждое слагаемое меньше 10, поэтому мы можем использовать единицы.
Смоделируйте первое число из 5 блоков.
Смоделируйте второе число из 8 блоков.
Подсчитайте результат. Блоков больше 10, поэтому мы обмениваем 10 блоков единиц на 1 стержень десятков.
Теперь у нас есть 1 десяток и 3 единицы, то есть 13.	5 + 8 = 13

Обратите внимание, что мы можем описать модели как единицы блоков и десятки стержней, или мы можем просто сказать единицы и десятки . С этого момента мы будем использовать более короткую версию, но имейте в виду, что они означают одно и то же.

Попытайся 1,25

Модель сложение: 5+7.5+7.

Попытайся 1,26

Модель сложение: 6+8.6+8.

Далее мы будем моделировать сложение двузначных чисел.

Пример 1.14

Модель сложение: 17+26.17+26.

Решение

17+2617+26 означает сумму 17 и 26.

Модель 17.	1 десяток и 7 единиц
Модель 26.	2 десятка и 6 единиц
Комбайн.	3 десятка и 13 единиц
Обмен 10 единиц на 1 десяток.	4 десятка и 3 единицы 40+3=4340+3=43
Мы показали, что 17+26=4317+26=43

Попытайся 1,27

Модель каждого сложения: 15+27,15+27.

Попытайся 1,28

Модель каждого сложения: 16+29,16+29.

Сложение целых чисел без моделей

Теперь, когда мы использовали модели для сложения чисел, мы можем перейти к сложению без моделей. Прежде чем мы это сделаем, убедитесь, что вы знаете все факты сложения одной цифры. Вам нужно будет использовать эти числовые факты при добавлении больших чисел.

Представьте, что вы заполняете таблицу 1. 1, добавляя каждый номер строки слева к каждому номеру столбца вверху. Убедитесь, что вы получили каждую показанную сумму. Если у вас есть проблемы, смоделируйте это. Важно, чтобы вы запомнили любые факты о числах, которые вы еще не знаете, чтобы вы могли быстро и надежно использовать факты о числах при сложении больших чисел.

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

Стол 1. 1

Вы заметили, что происходит, когда вы добавляете ноль к числу? Сумма любого числа и нуля и есть само число. Мы называем это свойством идентичности сложения. Нуль называется аддитивной идентичностью.

Идентификационное свойство добавления

Сумма любого числа aa и 00 является числом.

а+0=а0+а=аа+0=а0+а=а

Пример 1,15

Найдите каждую сумму:

1. ⓐ 0+110+11
2. ⓑ 42+042+0

Решение

ⓐ Первое слагаемое равно нулю. Сумма любого числа и нуля есть число.	0+11=110+11=11
ⓑ Второе слагаемое равно нулю. Сумма любого числа и нуля есть число.	42+0=4242+0=42

Попытайся 1,29

Найдите каждую сумму:

1. ⓐ 0+190+19
2. ⓑ 39+039+0

Попытайся 1.

30

Найдите каждую сумму:

1. ⓐ 0+240+24
2. ⓑ 57+057+0

Посмотрите на пары сумм.

2+3=52+3=5	3+2=53+2=5
4+7=114+7=11	7+4=117+4=11
8+9=178+9=17	9+8=179+8=17

Обратите внимание, что при изменении порядка слагаемых сумма не меняется. Это свойство называется коммутативным свойством сложения, которое гласит, что изменение порядка слагаемых не меняет их суммы.

Коммутативное свойство сложения

Изменение порядка слагаемых aa и bb не меняет их суммы.

а+б=б+аа+б=б+а

Пример 1,16

Добавить:

1. ⓐ 8+78+7
2. ⓑ 7+87+8

Решение

• ⓐ
  Доп.	8+78+7
  	1515

• ⓑ
  Доп.	7+87+8
  	1515

Вы заметили, что изменение порядка слагаемых не изменило их суммы? Мы могли бы сразу узнать сумму из части ⓑ, просто зная, что слагаемые такие же, как в части ⓐ, но в обратном порядке. В результате обе суммы равны.

Попытайся 1,31

Добавить: 9+79+7 и 7+9,7+9.

Попытайся 1,32

Добавить: 8+68+6 и 6+8,6+8.

Пример 1.17

Добавить: 28+61.28+61.

Решение

Чтобы сложить числа, состоящие из более чем одной цифры, часто бывает проще написать числа вертикально в столбцах.

Напишите числа так, чтобы единицы и десятки располагались вертикально.	28+61____28+61____
Затем добавьте цифры в каждом разряде. Складываем единицы: 8+1=98+1=9 Складываем десятки: 2+6=82+6=8	28+61____8928+61____89

Попытайся 1,33

Добавить: 32+54.32+54.

Попытайся 1,34

Добавить: 25+74.25+74.

В предыдущем примере сумма единиц и сумма десятков меньше 10,10. Но что произойдет, если сумма будет 1010 или больше? Давайте используем нашу модель base-10base-10, чтобы выяснить это. На рис. 1.10 снова показано добавление 1717 и 2626.

Рисунок 1.10

Если сложить единицы, 7+6,7+6, то получится 1313 единиц. Поскольку у нас более 1010 единиц, мы можем обменять 1010 единиц на 11 десятков. Теперь у нас 44 десятка и 33 единицы. Не используя модель, мы показываем это как маленькую красную цифру 11 над цифрами в разряде десятков.

Когда сумма в столбце разряда больше 9,9, мы переносимся в следующий столбец слева. Перенос — это то же самое, что перегруппировка путем обмена. Например, 1010 единиц за 11 десятков или 1010 десятков за 11 сотен.

Как

Добавьте целые числа.

1. Шаг 1. Напишите числа так, чтобы каждое значение разряда располагалось вертикально.
2. Шаг 2. Добавьте цифры в каждое значение разряда. Работайте справа налево, начиная с места единиц. Если сумма разряда больше 9,9, перенести на следующее разрядное значение.
3. Шаг 3. Продолжайте добавлять каждое разрядное значение справа налево, добавляя каждое разрядное значение и перенося при необходимости.

Пример 1,18

Добавить: 43+69.43+69.

Решение

Напишите числа так, чтобы они располагались вертикально.	43+69____43+69____
Добавьте цифры в каждом месте. Добавьте единицы: 3+9=123+9=12
Запишите 22 в разряде единиц в сумме. Добавьте 11 десятков к разряду десятков.	413+69____2413+69____2
Теперь сложите десятки: 1+4+6=111+4+6=11 Впишите 11 в сумму.	413+69____112413+69____112

Попытайся 1,35

Добавить: 35+98.35+98.

Попытайся 1,36

Добавить: 72+89,72+89.

Пример 1.19

Добавить: 324+586.324+586.

Решение

Напишите числа так, чтобы цифры располагались вертикально.
Добавьте цифры в каждом разряде. Сложите единицы: 4+6=104+6=10 Запишите 00 в разряде единиц в сумме и перенесите 11 десятков в разряд десятков.
Сложите десятки: 1+2+8=111+2+8=11 Запишите 11 в разряде десятков в сумме и перенесите 11 сотен в сотни
Сложите сотни: 1+3+5=91+3+5=9 Запишите 99 в разряде сотен.

Попытайся 1,37

Добавить: 456+376.456+376.

Попытайся 1,38

Добавить: 269+578.269+578.

Пример 1,20

Добавить: 1 683+479,1 683+479.

Решение

Напишите числа так, чтобы они располагались вертикально.	1 683+479______1 683+479______
Добавьте цифры в каждом разряде.
Добавьте единицы: 3+9=12,3+9=12. Запишите 22 в разряд единиц суммы и перенесите 11 десятков в разряд десятков.	1,6813+479______21,6813+479______2
Сложите десятки: 1+7+8=161+7+8=16 Запишите 66 в разряде десятков и перенесите 11 сотен в разряд сотен.	1,61813+479______621,61813+479______62
Сложите сотни: 1+6+4=111+6+4=11 Запишите 11 в разряде сотен и перенесите 11 тысяч в разряд тысяч.	1,61813+479______1621,61813+479______162
Добавьте тысячи 1+1=21+1=2. Запишите 22 в тысячном разряде суммы.	1,161813+479______2,1621,161813+479______2,162

Если слагаемые имеют разное количество цифр, будьте внимательны, чтобы выровнять соответствующие разрядные значения, начиная с единиц и двигаясь влево.

Попытайся 1,39

Добавить: 4 597+685,4 597+685.

Попытайся 1,40

Добавить: 5 837+695,5 837+695.

Пример 1,21

Добавить: 21 357+861+8 596,21 357+861+8 596.

Решение

Напишите числа так, чтобы разрядные значения располагались вертикально.	21,357861+8,596_______21,357861+8,596_______
Добавьте цифры в каждом разряде.
Сложите единицы: 7+1+6=147+1+6=14 Запишите 44 в разряд единиц суммы и перенесите 11 в разряд десятков.	21,3517861+8,596_______421,3517861+8,596_______4
Сложите десятки: 1+5+6+9=211+5+6+9=21 Запишите 11 в разряде десятков и перенесите 22 в разряд сотен.	21,32517861+8,596_______1421,32517861+8,596_______14
Складываем сотни: 2+3+8+5=182+3+8+5=18 Запишите 88 в разряде сотен и перенесите 11 в разряд тысяч.	21,132517861+8,596_______81421,132517861+8,596_______814
Добавьте тысячи 1+1+8=101+1+8=10. Напишите 00 в разряде тысяч и перенесите 11 в разряд десятков тысяч.	211,132517861+8,596_______0814211,132517861+8,596_______0814
Добавьте десять тысяч 1+2=31+2=3. Запишите 33 в десятитысячном разряде суммы.	211,132517861+8,596_______30,814211,132517861+8,596_______30,814

В этом примере было три слагаемых. Мы можем добавить любое количество слагаемых, используя один и тот же процесс, если мы тщательно выстроим значения мест.

Попытайся 1,41

Добавить: 46 195+397+6 281,46 195+397+6 281.

Попытайся 1,42

Добавить: 53 762+196+7 458,53 762+196+7 458.

Перевод словосочетаний в математическую запись

Ранее в этом разделе мы переводили математические обозначения в слова. Теперь обратим процесс. Мы переведем словосочетания в математическую запись. Некоторые словосочетания, обозначающие добавление, перечислены в таблице 1.2.

Эксплуатация	слов	Пример	Выражение
Дополнение	плюс сумма увеличилась на более всего прибавлено к	11 плюс 22 сумма 33 и 44 55 увеличена на 66 88 больше 77 сумма 99 и 55 66 добавлена ​​к 44	1+21+2 3+43+4 5+65+6 7+87+8 9+59+5 4+64+6

Стол 1. 2

Пример 1,22

Переведите и упростите: сумма 1919 и 23,23.

Решение

Слово в сумме говорит нам сложить. Слова из 1919 и 2323 говорят нам о слагаемых.

	Сумма 1919 и 2323
Перевести.	19+2319+23
Доп.	4242
	Сумма 1919 и 2323 равна 42,42.

Попытайся 1,43

Переведите и упростите: сумма 1717 и 26,26.

Попытайся 1,44

Переведите и упростите: сумма 2828 и 14,14.

Пример 1,23

Переведите и упростите: 2828 увеличилось на 31,31.

Решение

Слова , увеличенные на , говорят нам о сложении. Приведенные числа являются слагаемыми.

	2828 увеличилось на 31,31.
Перевести.	28+3128+31
Доп.	5959
	Итак, 2828, умноженное на 3131, равно 59.. 59.

Попытайся 1,45

Переведите и упростите: 2929 увеличилось на 76,76.

Попытайся 1,46

Переведите и упростите: 3737 увеличилось на 69,69.

Добавление целых чисел в приложения

Теперь, когда мы попрактиковались в сложении целых чисел, давайте применим полученные знания для решения реальных задач. Начнем с составления плана. Во-первых, нам нужно прочитать задачу, чтобы определить, что мы ищем. Затем мы пишем словосочетание, которое дает информацию, чтобы найти его. Затем мы переводим словосочетание в математическую запись, а затем упрощаем. Наконец, мы пишем предложение, чтобы ответить на вопрос.

Пример 1,24

Хао получил оценки 87, 93, 68, 95 и 8987, 93, 68, 95 и 89 на пяти тестах семестра. Какое общее количество баллов он заработал на пяти тестах?

Решение

Нас просят найти общее количество баллов по тестам.

Напишите фразу.	сумма баллов по тестам
Перевод в математическую запись.	87+93+68+95+8987+93+68+95+89
Тогда мы упрощаем, добавляя.
Так как цифр несколько, будем писать их вертикально.	837936895+89____432837936895+89____432
Напишите предложение, чтобы ответить на вопрос.	Хао заработал в общей сложности 432 очка.

Обратите внимание, что мы добавили точки , поэтому сумма равна 432432 точки . Важно включать соответствующие единицы во все ответы на прикладные задачи.

Попытайся 1,47

Марк готовится к велогонке. На прошлой неделе он проехал 1818 миль в понедельник, 1515 миль в среду, 2626 миль в пятницу, 4949 миль в субботу и 3232 мили в воскресенье. Какое общее количество миль он проехал на прошлой неделе?

Попытайся 1,48

Средняя школа Линкольна имеет три класса. Количество учеников в каждом классе составляет 230 165 и 325, 230 165 и 325 человек. Каково общее количество студентов?

Некоторые проблемы с приложениями связаны с формами. Например, человеку может понадобиться знать расстояние вокруг сада, чтобы поставить забор, или вокруг картины, чтобы поставить ее в рамку. Периметр – это расстояние вокруг геометрической фигуры. Периметр фигуры — это сумма длин ее сторон.

Пример 1,25

Найдите периметр показанного патио.

Решение

Нас просят найти периметр.
Напишите фразу.	сумма сторон
Перевод в математическую запись.	4+6+2+3+2+94+6+2+3+2+9
Упростите, добавив.	2626
Напишите предложение, чтобы ответить на вопрос.
Мы добавили футы, так что сумма составляет 2626 футов.	Периметр внутреннего дворика составляет 2626 футов.

Попытайся 1,49

Найдите периметр каждой фигуры. Все длины указаны в дюймах.

Попытайся 1,50

Найдите периметр каждой фигуры. Все длины указаны в дюймах.

Раздел 1.2 Упражнения

Практика ведет к совершенству

Используйте дополнительное обозначение

В следующих упражнениях переведите следующие математические выражения в слова.

59.

5+25+2

60.

6+36+3

61.

13+1813+18

62.

15+1615+16

63.

214+642214+642

64.

438+113438+113

Модель сложения целых чисел

В следующих упражнениях смоделируйте сложение.

65.

2+42+4

66.

5+35+3

67.

8+48+4

68.

5+95+9

69.

14+7514+75

70.

15+6315+63

71.

16+2516+25

72.

14+2714+27

Добавление целых чисел

В следующих упражнениях заполните пропущенные значения в каждой диаграмме.

73.

74.

75.

76.

77.

78.

В следующих упражнениях доп.

79.

1. ⓐ 0+130+13
2. ⓑ 13+013+0

80.

1. ⓐ 0+5,2800+5,280
2. ⓑ 5 280+05 280+0

81.

1. ⓐ 8+38+3
2. ⓑ 3+83+8

82.

1. ⓐ 7+57+5
2. ⓑ 5+75+7

83.

45+3345+33

84.

37+2237+22

85.

71+2871+28

86.

43+5343+53

87.

26+5926+59

88.

38+1738+17

89.

64+7864+78

90.

92+3992+39

91.

168+325168+325

92.

247+149247+149

93.

584+277584+277

94.

175+648175+648

95.

832+199832+199

96.

775+369775+369

97.

6 358+4926 358+492

98.

9 184+5789 184+578

99.

3 740+18 5933 740+18 593

100.

6 118+15 9906 118+15 990

101.

485 012+619 848 485 012+619,848

102.

368 911+857 289368 911+857 289

103.

24 731+592+3 86824 731+592+3 868

104.

28 925+817+4 59328 925+817+4 593

105.

8 015+76 946+16 5708 015+76 946+16 570

106.

6 291+54 107+28 6356 291+54 107+28 635

Перевод словосочетаний в математическую запись

В следующих упражнениях переведите каждую фразу в математическую запись, а затем упростите.

107.

сумма 1313 и 1818

108.

сумма 1212 и 1919

109.

сумма 9090 и 6565

110.

сумма 7070 и 3838

111.

3333 увеличилось на 4949

112.

6868 увеличилось на 2525

113.

250250 более 599599

114.

115115 более 286286

115.

сумма 628628 и 7777

116.

сумма 593593 и 7979

117.

1 4821 482 добавлено к5

118.

2 7192 719 добавлено к 682682

Добавление целых чисел в приложения

В следующих упражнениях решите задачу.

119.

Ремонт дома София переделала свою кухню и купила новую плиту, микроволновую печь и посудомоечную машину. Плита стоила 1100–1100 долларов, микроволновая печь — 250–250 долларов, а посудомоечная машина — 525–525 долларов. Какова общая стоимость этих трех приборов?

120.

Спортивный инвентарь Эйден купил бейсбольную биту, шлем и перчатку. Бита стоила 299–299 долларов, шлем — 35–35 долларов, а перчатка — 68–68 долларов. Какова общая стоимость спортивного инвентаря Эйдена?

121.

Езда на велосипеде Итан проехал на велосипеде 1414 миль в понедельник, 1919 миль во вторник, 1212 миль в среду, 2525 миль в пятницу и 6868 миль в субботу. Сколько всего миль проехал Итан?

122.

Бизнес У Хлои есть цветочный магазин. На прошлой неделе она сделала 1919 цветочных композиций в понедельник, 1212 во вторник, 2323 в среду, 2929 в четверг и 4444 в пятницу. Сколько всего цветочных композиций сделала Хлоя?

123.

Площадь квартиры Джексон живет в 77-комнатной квартире. Количество квадратных футов в каждой комнате составляет 238 120 156 196 100 132 238 120 156 196 100 132 и 225 225. Какова общая площадь всех 77 комнат?

124.

Вес Семь человек арендовали рыбацкую лодку. Вес мужчин составлял 175 192 148 169 205 181 175 192 148 169 205 181 и 225 225 фунтов. Каков был общий вес семи человек?

125.

Зарплата В прошлом году зарплата Натали составила 82 572 доллара. 82 572 доллара. Два года назад ее зарплата составляла 79 316 долларов, 79 316 долларов, а три года назад — 75 298, 75 298 долларов. Какова общая сумма зарплаты Натали за последние три года?

126.

Продажа домов Эмма — риелтор. В прошлом месяце она продала три дома. Продажные цены на дома составляли 292 540 долларов, 505 875 долларов, 292 540 долларов, 505 875 долларов и 423 699 долларов. 423 699 долларов. Какова была сумма трех продажных цен?

В следующих упражнениях найдите периметр каждой фигуры.

127.

128.

129.

130.

131.

132.

133.

134.

Математика на каждый день

135.

Калории На обед Полетт съела салат из жареной курицы, заправку «Ранч» и напиток на 16 унций. В таблице питания ресторана она увидела, что каждое блюдо имеет следующее количество калорий:

Салат с жареной курицей – 320320 калорий
Заправка «Ранч» – 170170 калорий
16 унций напитка на 16 унций – 150150 калорий калории обеда Полетт?

136.

Калории Фред съел бутерброд с жареной курицей, небольшой заказ картофеля фри и шоколадный коктейль на 12 унций12 унций на ужин. В таблице питания ресторана указана следующая калорийность каждого блюда:

Сэндвич с курицей на гриле — 420420 калорий
Картофель фри — 230230 калорий
Шоколадный коктейль на 12 унций — 580580 калорий

Какова общая калорийность ужина Фреда?

137.

Результаты тестов Студенту необходимо набрать в общей сложности 400400 баллов по пяти тестам, чтобы пройти курс. Студент набрал 82,9 балла1,75,88 и 70,82,91,75,88 и 70. Ученик прошел курс?

138.

Лифты Максимальная грузоподъемность лифта составляет 11501150 фунтов. В лифте шесть человек. Их вес составляет 210 145 183 230 159 и 164 210 145 183 230 159 и 164 фунта. Общий вес ниже максимальной грузоподъемности лифта?

Письменные упражнения

139.

Насколько вы уверены в своем знании дополнительных фактов? Если вы не уверены в себе полностью, что вы будете делать, чтобы улучшить свои навыки?

140.

Как вы использовали модели, чтобы помочь вам изучить факты сложения?

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.

ⓑ Изучив этот контрольный список, что вы сделаете, чтобы стать уверенным в выполнении всех задач?

Объединение смешанных номеров и порядок операций

Добавление смешанных номеров

В предыдущем разделе мы научились добавлять и вычесть две дроби.

Если нам нужно сложить два смешанных числа, мы можем просто сложить целые части числа, а затем добавить дробные части.

Пример

Добавить

            2 1      
3 + 2
7 5   

Решение

Сначала складываем дробные части:

          2 1             2 х 5         1 х 7
+ знак равно + LCM из 7 а 5                           
7 5 35 35

17     
знак равно 2 х 5 + 1 х 7 = 10 + 7 = 17
35

Теперь сложите целые части числа

        3 + 2  =  5

Окончательный ответ:

        
            2 1             17
3 + 2        = 5
7 5             35

Пример

Добавить

            3 5      
4 + 5
4           6   

Сначала складываем дробные части:

          3 5             3 х 3         5 х 2    90 160 + знак равно +
4 6 12 12     LCM из 4 а 6 равно 12

. 19
знак равно 3 х 3 + 5 х 2 = 9 + 10 = 19
12

7     
= 1 3 х 3 + 5 х 2 = 9 + 10 = 19
12

Целые части числа — это числа из исходных смешанных дробей и тот, что от 17/12. Эта дополнительная «1» аналогична идее переноса в дополнение к целые числа. У нас есть

        4 + 5 + 1  = 10  

Окончательный ответ:

        
            3 5 7
4 + 5 =  10
4           6 12

Упражнения

Добавить

1. 3 2      
   5 + 8
   10           15   
   Наведите указатель мыши на желтый прямоугольник для решение
   

2. 5 11      
   3 +  2
   912   
   Наведите указатель мыши на желтый прямоугольник для решение

Вычитание смешанных чисел

Вычитание смешанных чисел аналогично сложению в том, что мы рассматриваем целые числа отдельно от дробной части.

Пример

Вычесть

            3 1      
8 — 3
5          6   

Решение

Сначала вычитаем дробные части:

          3 1             3 х 6         1 х 5
— знак равно — LCM из 5 и 6 равно 30                     
5 6 30 30

13     
знак равно 3 х 6 — 1 х 5 = 18 — 5 = 13
30

Теперь вычтите часть целого числа

        8 + 3  =  5

Окончательный ответ:

        
            3 1             13
8 — 3        = 5
5           6 30

Иногда нам нужно позаимствовать 1 из целого числа, чтобы вычесть дроби.

Пример

Вычесть

            3 7      
6 — 3
4           8   

Решение

Если мы попытаемся вычесть дробные части, мы вскоре увидим, что мы не могу этого сделать.

          3 7 6         7
— знак равно —
4         8 8         8

Начиная с 

          6 7
<
8          8

мы должны заимствовать из целого числа.

            3 3 1 х 4 + 3 7
6 =  5 + 1       =  5 + знак равно 5
4 4 4 4

Теперь мы можем вычесть дробные части:

          7 7             7 х 2         7
— знак равно —           LCM 4 и 8 равно 8                          
4 8 35           8

7     
знак равно 7 х 2 — 7 = 14 — 7 = 7
8

Теперь вычтите часть целого числа

        5 — 3  =  2

Окончательный ответ:

        
            3 7             7
6 — 3        = 2
4 8             8

Упражнения

Вычитание

1. 5 4      
   9 — 4
   9 21   
   Наведите указатель мыши на желтый прямоугольник для решение
   

2. 3 3      
   7 — 3
   10 4   
   Наведите указатель мыши на желтый прямоугольник для решение

Дроби и порядок операций

Те же правила порядка операции применяются к выражениям с дробями. В частности, заказ:

1. Скобки
   

2. Экспоненты
   

3. Умножение и деление
   

4. Сложение и вычитание

Слева направо при наличии галстук.

Легочный,  «Пожалуйста, Извините, моя дорогая тетя Салли»  поможет нам запомнить этот приказ. 
      

Пример

          1 4         7
+ Икс
3           7 30        Умножение стоит перед дополнением

1 2 ² 4 ¹ 7
знак равно + х                             
3 15 ¹ 7 ¹⁵ 30

1 х 5 2 7        
знак равно + знак равно
15 15 15       

Пример

2 16     
знак равно Экспоненты сначала                     
3           25        

¹ 2 25 25 1
знак равно Икс знак равно или   1
3           ⁸ 16 24 24

Упражнения

Оценка с использованием правильного порядка операций

1.        6 1 11  
   —
   7 3         21   
   Наведите указатель мыши на желтый прямоугольник для решение
   

2. 
   Наведите указатель мыши на желтый прямоугольник для решение

Дроби и десятичные дроби: Дроби: сложение

Числа и счет|Арифметика| Дроби и десятичные дроби |Предварительная алгебра|Карта сайта

Нам нужно с чего-то начинать, так что давайте начнем с добавления дробей. Самое важное в добавлении дробей — это то, что они должны быть похожи на дроби. Это означает, что вам нужно убедиться, что оба сложения (числа добавляются) имеют общий знаменатель . 5/6 + 6/7 могут показаться сложными, но когда они имеют общий знаменатель 42, это простая задача на сложение. Давайте начнем.

Начнем с легких. На уроке вам будут даны слагаемые с одинаковым знаменателем. Все, что вам нужно сделать, это сложить числителей (числа сверху), а затем упростить свой ответ. Давайте попробуем.

1/13 + 6/13 = ?
• Создайте общие знаменатели. Они уже одинаковые в 13, так что ничего не делаем.
• Сложите числители из двух слагаемых. 1 + 6 = 7
• Запишите сумму числителей над общим знаменателем. 7/13.
•Упростите дробь. 7/13 нельзя упростить. Вы сделали.
Ответ: 1/13 + 6/13 = 7/13

5/9 + 1/9 = ?
• Создайте общие знаменатели: знаменатели одинаковы. Ничего не делать.
• Сложите числители: 5 + 1 = 6
• Запишите сумму числителей над общим знаменателем: 6/9.
• Упростите: 6 и 9 имеют общий делитель 3. При делении числителя и знаменателя на 3 получается 2/3.
Ответ: 5/9 + 1/9 = 6/9 = 2/3

Давайте более продвинуты. Как насчет сложения разных дробей? У вас нет общих знаменателей. Мы рассматривали создание эквивалентных дробей на предыдущих страницах. Вы будете использовать этот процесс здесь.

1/7 + 1/3 = ?
•Составьте общие знаменатели: у нас есть 7 и 3. У них нет общих делителей, поэтому давайте просто умножим, чтобы получить две новые эквивалентные дроби. Помните, как мы умножали на эквиваленты 1? Это было так…
1/7 = 1/7 * 1 = 1/7 * 3/3 = (1*3)/(7*3) = 3/21
1/3 = 1/3 * 1 = 1/3 * 7 /7 = (1*7)/(3*7) = 7/21
Теперь у вас есть общий знаменатель 21. Теперь вы можете переписать задачу как 3/21 + 7/21 = ?
• Сложите числители: 3 + 7 = 10
• Запишите сумму числителей над общим знаменателем: 10/21
• Упростите: 10/21 нельзя упростить. Вы сделали.
Ответ: 1/7 + 1/3 = 10/21

У вас теперь под контролем общие знаменатели и разные дроби. Давайте рассмотрим пример со смешанными числами, прежде чем идти дальше. В нашем первом примере мы рассмотрим смешанные числа, имеющие общие знаменатели.

2 2/9 + 4 3/9 = ?
• Проверьте общие знаменатели: они похожи на дроби со знаменателем 9. Ничего не делайте.
• Сложите числители каждой дроби: 2 + 3 = 5
• Запишите сумму числителей над общим знаменателем: 5/9
• Сложите целые числа: 2 + 4 = 6
• Запишите смешанное число: 6 5/9
• Упростить: 5/9 нельзя упростить. Вы сделали.
Ответ: 2 2/9 + 4 3/9 = 6 5/9

Что произойдет, если в ответе окажется неправильная дробь? Вам нужно упростить эту неправильную дробь, а затем добавить целые числа. Мы будем использовать пример, подобный последнему. Мы только что сделали первое дополнение немного больше.

2 7/9 + 4 3/9 = ?
• Проверьте общие знаменатели: они похожи на дроби со знаменателем 9. Ничего не делайте.
• Сложите числители каждой дроби: 7 + 3 = 10
• Запишите сумму числителей над общим знаменателем: 10/9
• Сложите целые числа: 2 + 4 = 6
• Запишите новое смешанное число : 6 10/9
• Упростить: в этом примере есть неправильная дробь, которую нужно упростить. Вам нужно использовать деление, чтобы создать новую фракцию. 10 ÷ 9= 1р1. Новое смешанное число будет 1 1/9. Вам нужно будет добавить это новое целое число к исходным 6. Весь процесс выглядит следующим образом…
6 10/9 = 6 + 10/9 = 6 + 1 1/9 = 6 + 1 + 1/9 = 7 1/9
Ответ: 2 7/9 + 4 3/9 = 7 1/9

Давайте соберем все вместе на примере, в котором есть разные дроби. Вам нужно будет найти общий знаменатель с этим и упростить неправильную дробь.

2 5/8 + 5 3/4 = ?
Общие знаменатели: Начните с дробей. У нас есть 4 и 8. У них есть общий делитель четыре, поэтому нам нужно исправить только дробь 3/4.
3/4 = 3/4 * 1 = 3/4 * 2/2 = (3*2)/(4*2) = 6/8
Добавьте числители: 5 + 6 = 11
Перепишите дробь : Сумма числителей над общим знаменателем: 11/8
Сложите целые числа: 2 + 5 = 7
Новое смешанное число 7 11/8
Упростим: Получилась неправильная дробь. Начать деление… 11 ÷ 8 = 1r3. Ваше новое смешанное число — 1 3/8. Добавьте новое смешанное число к исходному 7.
7 11/8 = 7 + 11/8 = 7 + 1 3/8 = 7 + 1 + 3/8 = 8 3/8
Ответ: 2 5/8 + 5 3/4 = 8 3/8

Теперь дело за вами. Если вы хотите продолжить, продолжайте вычитать дроби. Это очень близко к дополнению, так что у вас все получится.

► СЛЕДУЮЩАЯ СТРАНИЦА ПО ДРОБЯМ И ДЕСЯТИЧНЫМ ЗНАКАМ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ

► Или выполните поиск на сайтах…

---

• Обзор
• Типы номеров
• Факторы
• Дроби
• Структура
• Редуктор
• Больше или меньше
• Смешанные номера
• Смешанные номера 2
• Дополнение
• Вычитание 1
• Вычитание 2
• Умножение
• Подразделение
• Проблемы со словами
• Реальный мир
• Десятичные числа
• Проценты
• Оценка
• Передаточные числа
• Деньги
• Виды деятельности
• Дополнительные темы по математике

---

---

Википедия:
https://en.