Сложение целого числа и дроби: Сложение и вычитание смешанных чисел (разные знаменатели) — урок. Математика, 5 класс.

Содержание

Сложение и вычитание смешанных чисел (Слупко М.В.) | Математика | 5 класс

На этом уроке мы научимся складывать и вычитать смешанные числа и рассмотрим все возможные сложные случаи, которые связаны с данной темой.

Введение

Сумму целого числа и обыкновенной правильной дроби для краткости часто записывают без знака плюс и называют смешанным числом, имея в виду, что в этой записи есть и целая и дробная части: .

Если дробь неправильная (числитель больше и равен знаменателю), то сначала выделяют целую часть, а потом записывают в виде смешанного числа: .

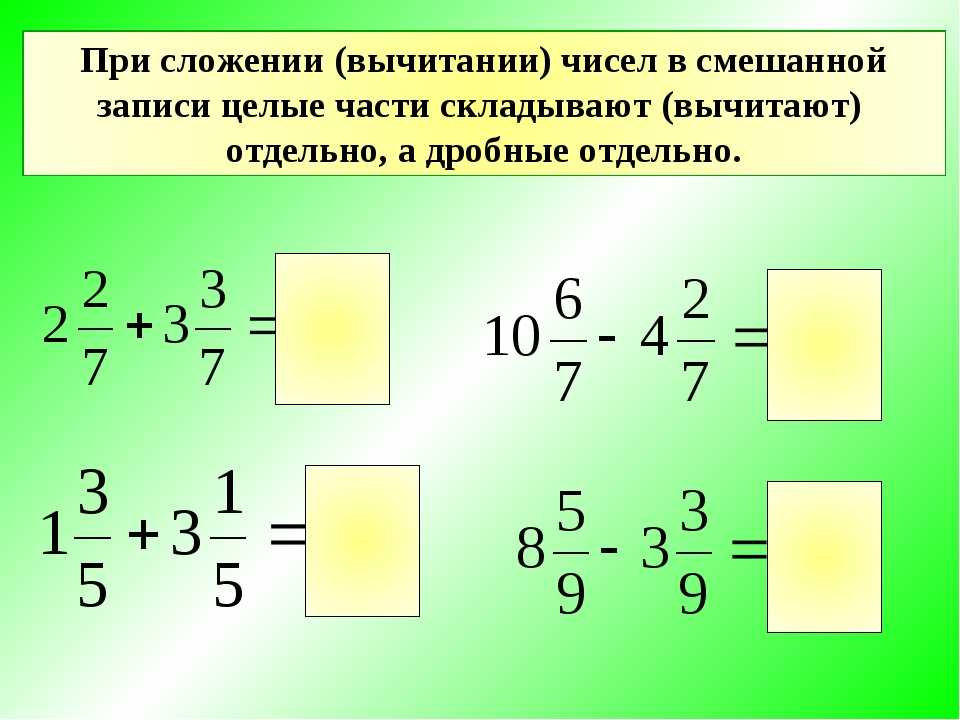
Сложение и вычитание смешанных чисел

Тогда вопрос сложения или вычитания смешанных чисел сводится к сложению или вычитанию целых чисел и обыкновенных дробей:

Но все это мы уже умеем делать. Поэтому никаких новых правил нам изучать не нужно.

Примеры со сложением

1) Сумма целого числа и дроби: .

Здесь мы просто пользуемся определением смешанного числа. Сумму записываем кратко, без знака плюс: .

2) Сумма целого и смешанного чисел: .

Распишем подробнее смешанное число. Сложим целые слагаемые, снова запишем сумму кратко в виде смешанного числа: .

Для краткости записи можно не расписывать смешанное число как сумму, а сразу складывать целые числа: .

3) Сумма смешанного числа и дроби: .

Распишем смешанное число как сумму. Сложим дроби, запишем сумму кратко как смешанное число: .

Необязательно расписывать смешанное число. Сразу сложим дроби: .

4) Сумма двух смешанных чисел.

Распишем каждое смешанное число. Сложим отдельно целые числа и отдельно дроби. Запишем сумму в виде смешанной дроби: .

В этой сумме распишем каждое смешанное число. Сложим целые числа и дроби. Полученная дробь оказалась неправильной. Вынесем целую часть. Сложим целое и смешанное числа:

Запись будет короче, если не расписывать смешанные числа: .

Итак, чтобы складывать целые, дробные и смешанные числа, удобнее всего складывать целые с целыми, а дробные с дробными числами.

Примеры с вычитанием

1) Разность целого и дробного чисел.

Представим единицу в виде дроби . Вычтем из одной дроби другую: .

Мы уже умеем вычитать из единицы правильную дробь. Распишем 5 как и . Вычитаем из единицы дробь, записываем ответ в виде смешанного числа: .

Постараемся выполнить вычитание, не расписывая целое число: .

2) Разность целого и смешанного чисел.

Распишем смешанное число. Так как минус перед ним относится ко всем числу (и к целой и дробной части), то .

Попробуем выполнить действия, не расписывая смешанное число. Вычтем сначала целую часть. Осталось вычесть дробь: .

3) Разность смешанных чисел.

Вычтем отдельно целые части, отдельно дробные: .

Сначала вычтем целые части. Мы не можем вычесть сразу из первой дробной части вторую, так как вторая больше первой. Вычтем тогда, то, что можем, . Осталось вычесть из целого числа дробное. Мы это уже делали:

Случаи при вычитании смешанных чисел

Итак, при вычитании из одного смешанного числа другого смешанного числа могут встретиться два случая.

Первая дробная часть больше или равна второй. Тогда из целой части вычитаем целую, из дробной – дробную: .

Первая дробная часть меньше второй. Тогда из целой части вычитаем целую. Из дробной части вычитаем столько, сколько сможем (то есть первую дробную часть). И в конце вычитаем из целого числа остаток дробной части: .

Алгоритм

Если нужно сложить или вычесть целые числа, дроби и смешанные числа, то удобнее всего поступить так.

Выполнить действие с целыми числами.
Выполнить действия с дробными частями.

Если сразу не удается вычесть из первой дробной части вторую, то делаем это в два этапа.

Примеры. Обобщение

Заключение

Чтобы закрепить навыки, обязательно выполните примеры в тренажерах к этому уроку. Чтобы научиться ездить на велосипеде, не так важно смотреть, как ездят другие, а необходимо пробовать это делать самостоятельно.

Список рекомендованной литературы

Математика 5 класс. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И., 31-е изд., стер. М: Мнемозина, 2013.
Математика 5 класс. Ерина Т.М.. Рабочая тетрадь к учебнику Виленкина Н.Я., М.: Экзамен, 2013.
Математика 5 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С. М.: Вентана – Граф, 2013.

Рекомендованные ссылки на ресурсы сети Интернет

Yaklass.ru (Источник).
School-assistant.ru (Источник).
Libraryedu.ru (Источник).

Домашнее задание

Вычислите: ; ; .
Вычислите: ; ; .
Вычислите: .

Смешанные дроби и действия с ними — что это, определение и ответ

Смешанные дроби – это дроби, в записи которых есть целые числа. Любую смешанную дробь можно представить неправильной дробью.

Неправильная дробь – это дробь, числитель которой больше знаменателя. В таком случае у дроби выделяется целая часть и её можно записать в виде смешанной.

Например,

\(\frac{7}{4} = \frac{4}{4} + \frac{3}{4} = 1 + \frac{3}{4} = 1\frac{3}{4}\)

1 – целая часть, а \(\frac{3}{4}\) – дробная часть смешанного числа \(1\frac{3}{4}\).

АЛГОРИТМ ПЕРЕВОДА НЕПРАВИЛЬНОЙ ДРОБИ В СМЕШАННУЮ:

Разделить числитель на знаменатель в столбик с остатком.
Неполное частное будет целой частью.
Остаток (если он есть) станет числителем дробной части смешанной дроби, а делитель — знаменателем.

Например,

Переведем неправильную дробь \(\frac{48}{9}\) в смешанную:

Неполное частное \(= 5\), остаток \(= 3,\) делитель \(= 9\), тогда эту неправильную дробь можно записать как: \(5\frac{3}{9}\).

АЛГОРИТМ ПЕРЕВОДА СМЕШАННОЙ ДРОБИ В НЕПРАВИЛЬНУЮ:

Перемножить целую часть со знаменателем дробной части.
К полученному произведению прибавить числитель дробной части.
Записать полученную сумму в числитель неправильной дроби, а знаменатель оставить без изменений.

Например,

Переведем смешанную дробь \(4\frac{5}{7}\) в неправильную:

Числитель неправильной дроби будет равен

\((4 \bullet 7) + 5 = 28 + 5 = 33\).

Знаменатель останется прежний и будет равен 7.

Получим: \(4\frac{5}{7} = \frac{33}{7}\)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ СМЕШАННЫХ ДРОБЕЙ:

При сложении и вычитании смешанных чисел отдельно складывают целые части, отдельно дробные по правилам сложения обыкновенных дробей.

Если суммой дробных частей является неправильная дробь, то из нее выделяют целую часть и прибавляют к сумме целых частей.

Например:

\(5\frac{3}{8} + 2\frac{6}{8} = (5 + 2) + (\frac{3}{8} + \frac{6}{8}) = 7 + \frac{9}{8} = 7 + 1\frac{1}{8} = 8\frac{1}{8}\)

Если при вычитании дробная часть уменьшаемого меньше дробной части вычитаемого, то поступают так:

\(7\frac{3}{5}\ –\ 2\frac{4}{5} = (7 + \frac{3}{5})\ –\ 2\frac{4}{5} = (6 + 1 + \frac{3}{5})\ –\ 2\frac{4}{5} = (6 + 1\frac{3}{5})\ –\ 2\frac{4}{5} = (6 + \frac{8}{5})\ –\ 2\frac{4}{5} = 6\frac{8}{5} + 2\frac{4}{5}\)

Таким образом мы выделили из целой части единицу и прибавили её к дробной. Теперь можно считать разность:

\(7\frac{3}{5}\ –\ 2\frac{4}{5} = 6\frac{8}{5} + 2\frac{4}{5} = (6\ –\ 2) + (\frac{8}{5}\ –\ \frac{4}{5}) = 4 + \frac{4}{5} = 4\frac{4}{5}\)

Так же поступают при вычитании смешанной дроби из целого числа.

Например:

\(3\ –\ 1\frac{2}{6} = (2 + \frac{6}{6})\ –\ 1\frac{2}{6} = (2\ –\ 1) + (\frac{6}{6}\ –\ \frac{2}{6}) = 1\frac{4}{6}\)

Как сложить смешанные дроби с целыми числами?

Прежде чем узнать, как мы можем складывать смешанные дроби с целыми числами, мы должны знать, что такое дроби и целые числа. Система счисления является основной концепцией целых чисел и смешанных дробей. Если у нас есть ясность относительно системы счисления, мы можем легко решить концепцию сложения смешанных дробей с целыми числами. В системе счисления есть такие понятия, как целые числа, натуральные числа, целые числа и действительные числа.

Система счисления представляет собой комбинацию натуральных чисел, целых чисел, целых и действительных чисел.

Натуральные числа: Натуральные числа — это числа, которые могут считать числа. Мы также можем сказать, что числа начинаются от 1 до бесконечности без включения 0. Примеры:

Натуральные числа = {1,2,3,4,5,6,7,8,9,10,11,12,13….}

Целые числа: Целые числа числа в союзе натуральных чисел и нуля (0). Целое число — это один из типов системы счисления, в котором ноль входит в число натуральных чисел. Примеры,

Целые числа = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,15,16,17,18….}

Целые числа: Целочисленная система — это система счисления, в которой отрицательные числа и положительные натуральные числа включают ноль (0). Целые числа — это числа, представляющие собой объединение отрицательных целых чисел и целых чисел. Примеры:

Целые числа={…-2,-1,0,1,2…..}

Рациональные числа: Рациональные числа — это числа, представленные только в форме r/a, где а не должен равняться нулю. Рациональные числа также называют конечными числами.

Примеры,

Рациональные числа: 0/1, 1/1, 2/1, 3/1,1,9999 и т. д.

Иррациональные числа: форма r/b, где b не должно равняться нулю, а также они называются неконечными числами.

Примеры,

Иррациональные числа: √2,√3, 0,12356…

Вещественные числа: Вещественные числа являются частью системы счисления, состоящей из рациональных и иррациональных чисел.

Дроби: Дроби основаны на числителе и знаменателе. Дроби подобны рациональным числам, представленным как часть целых чисел. Предположим, что прямоугольник разделен на четыре части, так что каждая часть делится на 1/3 и представляет собой 1:3, где 1/3 или 1:3 — дробная часть прямоугольника.

Примеры дробей:

7/8, где 7 — числитель, а 2 — знаменатель.
1/4, где 1 — числитель, а 4 — знаменатель.
9/3, где 9 — числитель, а 3 — знаменатель.

Дроби бывают трех типов. Вот они,

Правильная дробь: Правильная дробь — один из видов дроби. Правильная дробь объясняется тем, что числитель должен быть меньше знаменателя.
Примеры правильных дробей: 1/2, 3/5, 6/8….
Неправильная дробь: Неправильная дробь — один из видов дроби. Он определяется как числитель, который должен быть больше знаменателя.
Примеры неправильных дробей: 8/6, 9/7, 3/2 и так далее.
Смешанная дробь: Смешанная дробь представляет собой объединение дробной части (содержит как правильные, так и неправильные) и натуральных чисел.
Примеры смешанных дробей показаны ниже:
здесь 1 – целое число, 2 – числитель, а 3 – знаменатель.

Как преобразовать смешанные дроби в форму p/q?

Шаг 1: Сначала умножьте целое число на знаменатель.
Шаг 2: Сложите числитель и результат умножения целого числа на знаменатель.
Шаг 3: Результат шага 2 должен быть помещен в часть числителя, где знаменатель такой же, как в смешанной дроби. Следовательно, мы получили смешанную дробь в правильной форме p/q.

Как преобразовать неправильные дроби в смешанные дроби?

Возьмем 8/6 как неправильную дробь
Шаг 1: Сначала разделите числитель со знаменателем 8//6 = 1 на частное, а остаток на 2.
Шаг 2: Остаток 2 , который делится на 6. знаменатель. Если есть отмена, которая происходит, отмените с соответствующим коэффициентом.
Шаг 4: Когда мы рационализируем 2/6, мы получаем 1/3. Объединяя ответ шага 1 и шага 4, получаем

Как сложить целое число со смешанной дробью?

Сначала мы должны преобразовать смешанную дробь в форму p/q.
Затем преобразуйте эту форму p/q в десятичную форму.
Затем сложение целого числа с десятичной формой p/q.

Примеры задач

Задача 1: Решите приведенный ниже вопрос, который имеет форму сложения целых чисел и смешанной дроби?

10 +

Решение:

Чтобы решить эту задачу, мы должны сначала решить смешанные дроби.
Решение смешанной дроби: преобразуется в форму p/q следующим образом.
Шаг 1 : Умножьте целое число 10 на знаменатель 3, как показано на диаграмме = 10×3=30.
Шаг 2 : Добавление числителя 2 с результатом в Шаге 1 = 2+30=32.
Шаг 3 : В виде p/q числитель p=32 и знаменатель q=3. Следовательно, 32/3=10,7 является правильной формой p/q.
После преобразования части смешанной дроби в правильную форму p/q. Сложите целое число со смешанной дробью.
Прибавляем 10 к 32/3=10,7 получаем 20,7 в результате сложения.
Следовательно, решив вышеуказанную задачу, мы получим результат 20,7, который также представлен в виде p/q=207/10.

Задача 2: Решите вопрос ниже, который находится в форме сложения целых чисел и смешанной дроби?

20 +

Решение:

Чтобы решить эту задачу, мы должны сначала решить смешанные дроби.
Решение смешанной дроби: преобразуется в форму p/q следующим образом.
Шаг 1 : Умножьте целое число 1 на знаменатель 3, как показано на диаграмме = 1×3=3.
Шаг 2 : Добавление числителя 2 с результатом в Шаге 1 = 2+3=5.
Шаг 3 : В P/q сформируйте числитель p=5 и знаменатель q=3. Следовательно, 5/3=1,7 является правильной формой p/q.
После преобразования части смешанной дроби в правильную форму p/q. Сложите целое число со смешанной дробью.
Прибавим 20 к 5/3=1,7 и получим в результате сложения 21,7.
Следовательно, решив вышеуказанную задачу, мы получим результат 21.7, который также обозначается как p/q form 217/10.

Задача 3: Решите вопрос ниже, который находится в форме сложения целых чисел и смешанной дроби?

13 +

Решение.

Решение смешанной дроби: преобразуется в форму p/q следующим образом.

Шаг 1 : Умножьте целое число 2 на знаменатель 3, как показано на диаграмме = 2×3=6.

Шаг 2 : Добавление числителя 1 с результатом в Шаге 1 = 1+6=7.

Шаг 3 : В виде p/q числитель p=7 и знаменатель q=3. Следовательно, 7/3=2,33 является правильной формой p/q.

После преобразования части смешанной дроби в правильную форму p/q. Сложите целое число со смешанной дробью.

Прибавив 13 к 7/3=2,33, мы получим 15,33 в результате сложения.

Следовательно, решив вышеуказанную задачу, мы получим результат 15,33, который также обозначается как p/q form 153,3/10.

Задача 4: Решите вопрос ниже, который находится в форме сложения целых чисел и смешанной дроби?

16 +

Решение этой задачи: 0

8
3 сначала решить смешанные дроби.
Решение смешанной дроби: преобразуется в форму p/q следующим образом.
Шаг 1 : Умножьте целое число 3 на знаменатель 3, как показано на диаграмме = 3×3=9.
Шаг 2: Добавление числителя 1 с результатом в Шаге 1 = 1+9=10.
Шаг 3 : В виде p/q числитель p=10 и знаменатель q=3. Следовательно, 10/3=3,33 является правильной формой p/q.
После преобразования части смешанной дроби в правильную форму p/q. Сложите целое число со смешанной дробью.
Прибавляем 16, где 10/3=3,33, в результате сложения получаем 19,33.
Следовательно, решив вышеуказанную задачу, мы получим результат 19,33, который также обозначается как p/q form 193,3/10.

Видео с вопросами: сложение двух смешанных чисел
Стенограмма видео
Вычислите три и четыре девятых плюс четыре и шесть седьмых.
Здесь мы складываем два смешанных числа. Смешанное число – это комбинация целого числа и дроби. Итак, в нашем примере три и четыре — это целые числа, а четыре девятых и шесть седьмых — наши дроби.
Чтобы решить эту задачу на сложение, мы должны сложить наши целые числа и дроби. Наши целые числа снова три и четыре; поэтому сложите их вместе, чтобы получить семь. И наши дроби, которые мы складываем, — это четыре девятых и шесть седьмых. Для того, чтобы сложить эти дроби, нам нужен общий знаменатель. Мы хотим, чтобы девять и семь были одним и тем же знаменателем. Итак, нам нужно найти число, в которое входят и девять, и семь. И на самом деле это должно быть наименьшее число, в которое они оба входят. Это число будет шестьдесят три. Итак, если шестьдесят три будут нашим общим знаменателем, как мы перешли от знаменателя девяти к знаменателю, равному шестидесяти трем? Нам нужно умножить девять на семь. Однако, если вы собираетесь умножить знаменатель на семь, вам также нужно будет умножить числитель на семь. Теперь, взглянув на шесть седьмых, вместо семи в знаменателе у нас будет шестьдесят три в качестве знаменателя. Чтобы получить от семи до шестидесяти трех, мы должны умножить это число на девять. Поэтому, если мы умножим наш знаменатель на девять, мы умножим наш числитель на девять.

Давайте упростим. Не забудьте сбить свою семерку. А теперь нам нужно умножить четыре девятых на семь седьмых. Итак, мы умножаем числители вместе, четыре раза по семь, что равно двадцати восьми, и наши знаменатели вместе, девять раз по семь, что равно шестидесяти трем. Теперь мы возьмем шесть раз девять, умножив наши числители, а затем возьмем семь раз девять внизу, наши знаменатели. Шесть раз девять дает нам пятьдесят четыре, а семь раз девять дает нам шестьдесят три.

Теперь, когда наши дроби похожи, то есть у них один и тот же знаменатель, мы можем сложить их вместе, добавив числители и сохранив общий знаменатель. Итак, двадцать восемь плюс пятьдесят четыре равно восьмидесяти двум. Итак, у нас есть семь плюс восемьдесят два шестьдесят третьих. Это не будет смешанным числом, потому что смешанное число — это комбинация целого числа, равного семи — и это здорово, — и дроби. Ну восемьдесят два шестьдесят третьих, да это дробь. Но это неправильная дробь. Неправильная дробь – это дробь, которая больше или равна единице.