Деление столбиком. Онлайн калькулятор.

Введите делимое

Введите делитель

Деление десятичных дробей столбиком

Если при делении столбиком делимое или делитель десятичная дробь, то для упрощения расчётов необходимо делитель и делимое преобразовать в целые числа.

Разберём пример

Разделим 0.125 на 0.05 для этого умножим оба числа на 1000.
0.125×1000=125
0.05×1000=50.
В итоге наш пример сведётся к делению 125 на 50.

—	1	2	5	5	0
	1	0	0	2	.	5	50 × 2 = 100
	—	2	5	0			125 — 100 = 25
		2	5	0			50 × 5 = 250
				0			250 — 250 = 0

Деление дробей в столбик

Разделим 5220 на 36

—	5	2	2	0	3	6
	3	6			1	4	5	36 × 1 = 36
—	1	6	2					52 — 36 = 16
	1	4	4					36 × 4 = 144
	—	1	8	0				162 — 144 = 18
		1	8	0				36 × 5 = 180
				0				180 — 180 = 0

Выделим первое полное делимое 52
Делим 52 на 36.
Получится 1 с остатком
Под чертой в ответе пишем цифру 1.
Проверяем умножением 36х1=36.
Вычитаем и сравниваем, разница должна быть меньше делителя.
52-36=16, 16

Сносим 2
Делим 162 на 36
Получится 4 с остатком
Под чертой в ответе пишем цифру 4.
Проверяем умножением 36х4=144.
Вычитаем и сравниваем, разница должна быть меньше делителя.
162-144=18, 18

Сносим 0
Делим 180 на 36
Получится 5 без остатка
Под чертой в ответе пишем цифру 5.
Проверяем умножением 36х5=180.
Вычитаем и сравниваем
180-180=0
Сносить больше нечего
Расчёт окончен.

Алгоритм деления в столбик

• Если делимое или делитель являются десятичными дробями преобразуем их в целые числа.
• Если делитель и делимое целые числа и на концах есть нули, необходимо их сократить для упрощения.
• Записываем пример в столбик.
• Ищем первое неполное делимое.
• Делим неполное делимое.
• Проверяем умножением.
• Записываем в ответ первую цифру.
• Ищем остаток, он должен быть меньше делителя.
• Сносим следующую цифру и повторяем всё заново.

Что может калькулятор

Делить десятичные дроби столбиком

Делить в столбик натуральные числа

Разделить уголком десятичную дробь на натуральное число

Разделить столбиком натуральное число на десятичную дробь

Разделить 408 на 17 столбиком
Разделить 920 на 10 столбиком
Разделить 966 на 23 столбиком
Разделить 476 на 4 столбиком
Разделить 56 на 2 столбиком
Разделить 952 на 2 столбиком

Похожие калькуляторы

Вычитание чисел столбиком

Сложение чисел столбиком

Умножение в столбик онлайн

Деление многочленов столбиком онлайн

Примеры решенийРанг матрицыМетод КрамераУмножение матриц Определитель матрицы Метод обратной матрицы Обратная матрица Метод Гаусса онлайн LU разложение матрицы Производная онлайн

Для любых многочленов f(x) и g(x), g(x) ≠ 0, существуют единственные полиномы q(x) и r(x), такие что f(x)/g(x)=q(x)+r(x)/g(x).

Алгоритм деления в столбик применяется в частности при нахождении интегралов.

• Решение онлайн
• Видеоинструкция

Инструкция. Для получения решения в онлайн режиме необходимо ввести числитель и знаменатель.

При оформлении в качестве переменной использовать xtzupλ

Пример деления в столбик. Найти частное деления и остаток многочлена:

№1.

x3 -12x2-42	x -3
x3 -3x2	x2
-9x2-42

№2.

x3 -12x2-42	x -3
x3 -3x2	x2 -9x
-9x2-42
-9x2 + 27x
-27x -42

№3.

x3 -12x2-42	x -3
x3 -3x2	x2 -9x -27
-9x2-42
-9x2 + 27x
-27x -42
-27x + 81
-123

Целая часть: x² -9x ^{-27
Остаток: -123}

Таким образом, ответ можно записать как:
см. также и другие примеры решение столбиком.

Пример №1. Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x⁵+3x³-x²+4x+1, Q(x)=2x²-x+1

Пример №2. Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x⁴+6x³-2x²+x-2, Q(x)=x-6
Решение.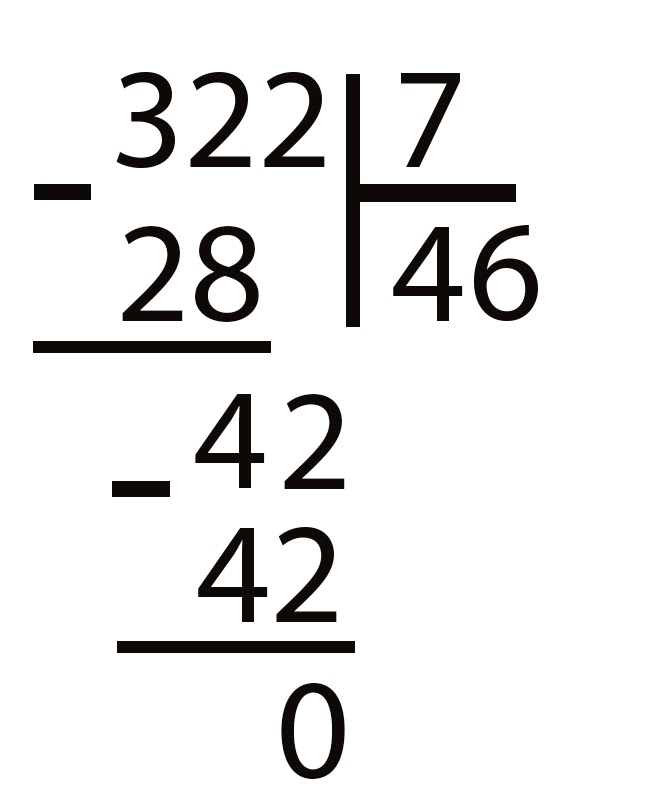 Выделим общий множитель (x-6).

-x³(x-6)-2x(x-6)-12x+x-2 = -x³(x-6)-2x(x-6)-11(x-6)-66-2 = -x³(x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Калькулятор длинного деления с десятичными дробями

Базовый калькулятор

Поделись этим калькулятором и страницей

Калькулятор Используйте

Делайте деление в длинное с десятичными числами и смотрите пошаговые вычисления. Введите положительные или отрицательные десятичные числа для делителя и делимого и рассчитайте частное.

Как выполнить деление в длинное число с десятичными дробями

1. Если число, на которое вы делите, содержит десятичную дробь, переместите запятую полностью вправо, считая количество позиций, на которые вы ее переместили.
   Затем переместите запятую в числе, которое вы делите на такое же количество знаков, вправо.
2. Вставьте десятичную точку в частное (ответ) точно над десятичной точкой в ​​числе под чертой деления.
3. Делите до тех пор, пока остаток не станет равным нулю или пока в вашем ответе не будет достаточно знаков после запятой. Вы также можете остановиться, если остаток повторяется, потому что это указывает на то, что ваш ответ является повторяющимся десятичным числом.

Вычислить десятичные разряды для частного ответа

Как далеко вы хотите вычислить десятичные разряды для ответа? Вот несколько примеров:

• 31 разделить на 16 = 1,937500 с точностью до 6 знаков после запятой
• 31 разделить на 16 = 1,937 с точностью до 3 знаков после запятой
• 22 разделить на 15 = 1,466666666 с учетом 9 знаков после запятой
• 22 разделить на 15 = 1,466666 с учетом 6 знаков после запятой
• 22 разделить на 15 = 1,466 с точностью до 3 знаков после запятой

Обратите внимание, что это не то же самое, что округляет до определенного числа знаков после запятой.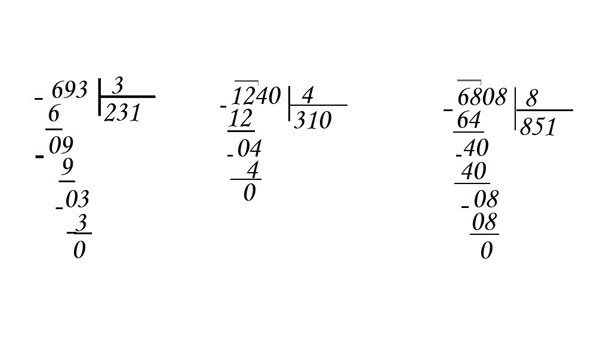 Например, 22 разделить на 15 = 1,466, если рассчитывается как с 3 знаками после запятой, потому что вы останавливаетесь, как только достигаете третьего знака после запятой. С другой стороны, 22 разделить на 15 = 1,467, когда округляется до с 3 знаками после запятой. Для округления до третьего знака после запятой необходимо

рассчитайте до по крайней мере до четвертого знака после запятой, чтобы вы знали, как округлить третий знак после запятой. Смотрите наши Калькулятор округления чисел для получения дополнительной информации.

Смотрите также наши Длинное деление с остатками, чтобы увидеть работу для длинного деления с остатками.

Части деления

Для задачи деления 471 разделить на 32:

• 471 — делимое
• 32 это делитель
• 14,718 — частное, рассчитанное до 3 знаков после запятой

Как выполнить длинное деление с десятичными дробями: пример

В этой задаче мы делим 4,71 на 3,2 до 3 знаков после запятой в ответе на частное.

3.

2

4.

7

1

Решите задачу с длинной разделительной скобой. Поместите делимое внутрь скобки, а делитель снаружи слева.

3

2

4

7.

1

Если делитель представляет собой десятичное число, переместите десятичную дробь до упора вправо. Подсчитайте количество разрядов и переместите запятую в делимом на такое же количество разрядов. При необходимости добавьте нули.

Поскольку 3.2 не является целым числом, переместите десятичную точку на один разряд вправо. 32 — целое число. Проделайте то же самое с делимым и переместите запятую на один разряд вправо.

Так как мы вычисляем до 3 знаков после запятой, добавляем к делимому два нуля в конце.

Вставьте десятичную точку над разделительной чертой, непосредственно над новым десятичным разрядом в делимом.

3

2

4

7.

1

Разделите самое левое число делимого на делитель, в данном случае разделите 4 на 32.

Поскольку 4 разделить на 32 не является целым числом, первая цифра частного равна 0.

Умножьте делитель 32 на частное 0, чтобы получить произведение 0. Вычтите 0 из 4, чтобы получить остаток 4.

3

2

4

7.

1

Далее, снесите 7 из дивиденда, поэтому вы получите 47.

3

2

4

7.

10003

888 Сколько будет 47 разделить на 32? Или, другими словами, сколько раз 32 входит в число 47? Только один раз, с остатком.

Вставьте 1 в частное. Чтобы найти остаток, умножьте делитель на 1 и из второго делимого 47 вычтите произведение 32. Остаток равен 15.

3

2

4

7.

1

Снова сократите следующую цифру делимого, 1, и поместите ее в конец остатка.

3

2

4

7.

1

 

−

1

2

8

 

 

Повторите шаги. Чему равно 151 разделить на 32? Или сколько раз 32 входит в 151?

32 входит в число 151 четыре раза. Поставьте 4 на следующем месте в частном и умножьте 32 на 4, чтобы получить 128.

Вычтите это произведение из 151, чтобы найти остаток от 23.

3

2

4

7.

1

—

1

2

8

Уволить 0 из дивиденда и вставьте его после 23, чтобы получить 230.

1.

4

1.

4

3

2

4

7.

1

—

1

2

8

0002 2

2

4

 

Сколько 230 разделить на 32? 32 входит в число 230 семь раз. Поставьте 7 на следующем месте в частном.

32 умножить на 7 будет 224.

230 минус 224 дает в остатке 6.

1.

4

7

3

2

4

7.

1

—

1

2

8

—

2

2

4

Теперь. .

1.

4

7

1

3

2

4

7.

1

—

1

0002 2

8

—

2

2

4

32 Заходит в 60 только один раз. Поставьте 1 на следующем месте в частном.

32 умножить на 1 будет 32.

Если из 60 вычесть 32, получится остаток 28.

Википедия: длинное деление

 

Подписаться на калькуляторSoup:

Visual Long Division Calculator

Поделиться в PinterestPinterestПоделиться в FacebookFacebookПоделиться в PocketPocketПоделиться в TwitterTwitterПоделиться в EmailEmailПоделиться в FlipboardFlipboard

Worksheets

Printables

PuzzlesT-shirts

Math Worksheets

3 90 Ad Free!

Рабочие листы по основной математике

Рабочие листы с дробями

Словесные задачи

Алгебра

Прочие рабочие листы

Measurement & Conversions

Patterns and Puzzles

Color by Number

Holiday & Seasonal

Early Learning

Printables

Calculators

Math Worksheets by Grade

Worksheet News

Предыдущий

Больше онлайн-калькуляторов!

Следующий

Использование калькулятора деления на длинное деление

Использовать калькулятор деления на длинное деление очень просто! Введите в поля делитель и делимое, и калькулятор покажет всю работу, необходимую для решения задачи на деление в длину.

Если вам нужен калькулятор деления, который не только вычислит частное, но и покажет работу, необходимую для правильного деления, то вы его нашли. Когда вы вводите частное и делимое, сама задача мгновенно становится частью работы калькулятора деления в длину, показывающего ответ, и вы можете выделить части шагов деления, чтобы увидеть, как они соотносятся друг с другом.

Как выполнить длинное деление

Шаги длинного деления применяются многократно для решения задачи на длинное деление.

1. Разделить

   Посмотреть, сколько раз делитель входит в наименьшую возможную часть делимого. Это даст вам цифру для использования в качестве части частного.

2. Умножение

   Возьмите цифру частного из первого шага и умножьте ее на делитель, написав ее под частичным делимым, чтобы настроить операцию вычитания.

3. Вычесть

   Вычесть произведение предыдущего шага из частичного дивиденда, чтобы получить оставшуюся сумму. Эта сумма всегда должна быть меньше частного.

4. Уменьшить

   Уменьшить числа из делимого, увеличивая остаток от предыдущего шага, пока эта сумма не станет больше делителя, затем повторить.

5. Повторять

   Повторять до тех пор, пока не будут введены все цифры. Любой результат, который нельзя разделить дальше, является остатком задачи деления в длину.

Если после того, как вы записали все цифры, оставшееся число меньше делителя, это значение является остатком. Калькулятор длинного деления показывает остаток со стрелкой, возвращающей его к частному.

Это те же шаги, которые использует калькулятор деления в длину, чтобы показать работу для задачи деления в длину, когда генерируется остаток. Первая цифра ответа в частном отображается в длинном делении.

Самая сложная часть выполнения длинных шагов деления вручную — это начальный шаг деления. Определить, сколько раз частичное делимое делится на делитель, может быть непросто, особенно при работе с многозначными делителями.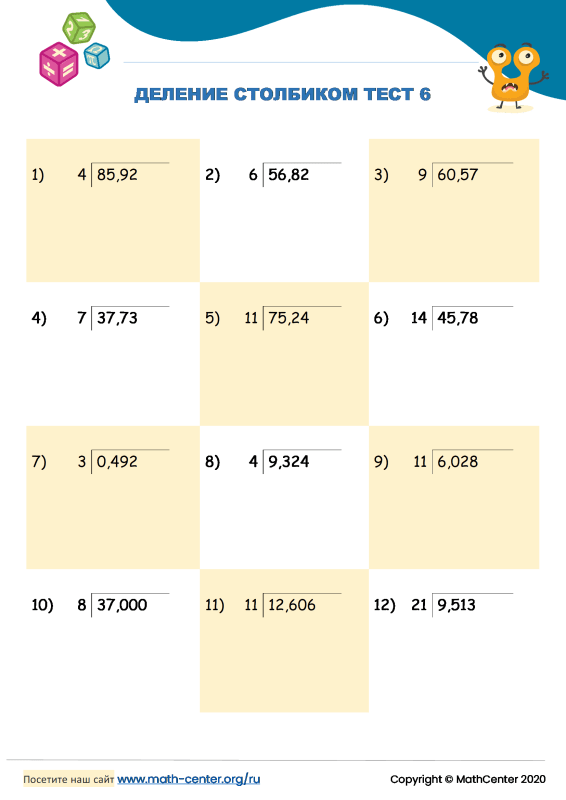 В качестве проверки, если произведение шага умножения больше делителя, вы знаете, что частичное частное на первом шаге можно увеличить. Вы можете наблюдать это в работе, показанной в калькуляторе деления на длинные. Обратите внимание, что произведение шага умножения всегда меньше остатка.

Пример деления в длинное с остатками

Самый простой способ понять деление в длинное — посмотреть пример. Этот калькулятор длинного деления позволяет сделать это для любой задачи! Вы можете ввести задачу и изучить отдельные шаги, наведя курсор на части работы, показанные в калькуляторе, но даже с этой дополнительной помощью деление в полные числа может быть трудным для понимания. В приведенном ниже примере рассматривается проблема с использованием того же вывода «покажи свою работу», который калькулятор деления в длинную генерирует для типичной задачи. Это должно помочь вам поместить вывод калькулятора в контекст и помочь вам понять, как решать задачи на деление в длину самостоятельно!

Мы будем работать с этим примером задачи деления 12322 на 3, которая иллюстрирует деление в длинное с остатками. Это хорошая задача, потому что она показывает некоторые из более сложных шагов для решения деления в длину, а делимое и делитель дают остаток.

Первый шаг в длинном делении, шаг «разделения», заключается в попытке найти наименьшую часть делимого, которая может быть разделена на делитель. Глядя на первую цифру делимого, мы видим, что 1 нельзя разделить на 3, поэтому нужно продолжить и посмотреть еще и на вторую цифру. 12 можно разделить на 3, поэтому начнем с 4 в качестве первой цифры в частном.

Следующий шаг, шаг «умножения», требует, чтобы мы взяли только что вычисленную цифру ответа и умножили ее на делитель. Это дает нам продукт, который мы будем использовать на следующем шаге. На самом деле это довольно просто, потому что мы только что вычислили 12, деленное на 3 на предыдущем шаге, поэтому мы сразу знаем, какое произведение нужно записать. Это становится сложнее с многозначным делением в длину, поэтому не стоит недооценивать этот шаг…

Следующая задача после наших шагов в длинном делении — вычесть это произведение из частичного делимого. Поскольку частичное частное, которое мы рассчитали до сих пор, может быть недостаточно большим, может быть некоторая остаточная разница, которую нам нужно отслеживать. В этом случае 12 разделить на 3 равно 4 без остатка, поэтому результат этой операции вычитания равен нулю. Но подождите, потому что через минуту мы увидим, что это не всегда так!

Теперь пора начать выводить цифры из делимого, чтобы у нас было больше делимых. Этот калькулятор деления на длинные показывает это маленькой серой стрелкой, и вы можете видеть, что эти опущенные цифры добавляются к разнице, которую мы рассчитали на предыдущем шаге. В этом случае мы опускаем число 3, которое, очевидно, очень аккуратно делится на наш делитель, так что на этом шаге мы закончили опускание цифр.

Теперь пора снова делить! И, конечно же, 3 разделить на 3 равно единице, поэтому мы добавляем эту цифру к нашему частичному частному, и мы готовы перейти к следующему шагу. А это значит, что время умножения снова! Этот математический факт 3, деленный на 3, который мы только что использовали, снова появляется здесь, и произведение 3, умноженное на 1, записывается для настройки шага вычитания.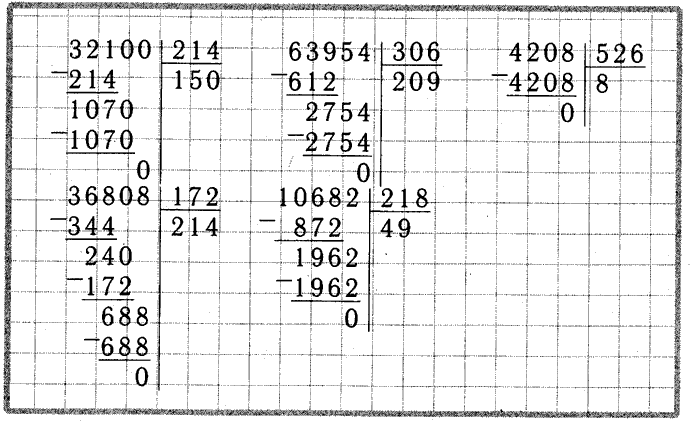

На этом шаге вычитания мы тривиально вычитаем 3 из 3 и на этот раз получаем ноль в качестве остатка. Однако не дайте себя обмануть! Это не значит, что мы закончили! У нас еще остались цифры в делимом, которые мы не использовали, так что продолжим.

Следующая цифра, которую мы не использовали в частном, — это 2, и калькулятор деления в длинную очередь ставит эту цифру рядом с нулем. Мы не можем разделить 3 на 2 и получить целое число, поэтому мы не можем перейти к шагу деления. Но мы использовали цифру из дивиденда, и нам нужно следить за этим. Итак, мы пока добавим этот ноль к частному, но что нам делать дальше?

Снизьте еще одну цифру! Это дает нам 22, деленное на 3, что мы определенно можем сделать. Теперь 22, деленное на 3, — это число больше семи, но меньше 8, поэтому мы знаем, что они останутся чем-то лишним, но это нормально. Вы будете

Время еще раз, чтобы умножить эту цифру из частного и настроить для вычитания. Вспомните, что 22, разделенное на 3, не было абсолютно четным делением, поэтому мы знаем, что на этом шаге умножения мы получим что-то немного другое, и, конечно же, 3 умножить на 7 равно 21, и это то, что нам нужно записать.

Теперь пришло время еще раз вычесть. 22 минус 21 дает нам разницу в 1.

Если бы наше делимое было длиннее, мы бы начали процесс сначала и начали выводить цифры, но мы исчерпали количество цифр в делимом, поэтому мы подошли к конец наших длинных шагов деления. Разница, которую мы вычислили на последнем шаге вычитания, становится остатком в частном, и все готово!

Дополнительные ресурсы для изучения деления в длинное число

Я надеюсь, что этот калькулятор деления в длинное число поможет вам определить этапы деления в длинное число и узнать, откуда берутся остатки. Но в Интернете есть много отличных руководств по длинным делениям.

Конечно же, в Википедии есть длинная дискуссия о делении в длинных числах, которая может быть немного многословной, но примерно посередине есть хорошее анимированное изображение, описывающее многозначные делители, которые вдохновили некоторые из того, что этот калькулятор показывает в результатах работы.

Если вы ищете несколько иной способ деления в длину, попробуйте посмотреть это видео о частичном делении на частные.