Как складывать дроби с числом
Сложение дробей
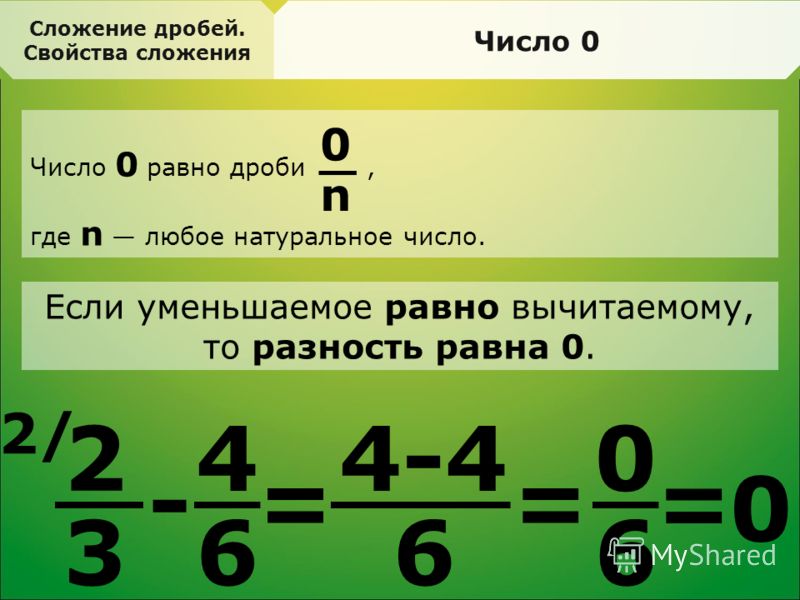
Определение: Суммой дробей с одинаковыми знаменателями называют дробь,числитель которой равен сумме числителей исходных дробей,и со знаменателем равным знаменателю обеих дробей.
Формула
Сложим две дроби с одинаковым с одинаковыми знаменателями
По формуле складываем числители, а знаменатель оставляем исходный
Важно: Если есть возможность сократить дробь, то в конечный ответ мы записываем сокращенную дробь.
Пример: При сокращении дроби у нас получится число 1/2
Сложение дробей с разными знаменателями:
Определение: Для того, чтобы найти сумму дробей с разными знаменателями сначала нужно дроби привести к общему знаменателю, а затем сложить их как дроби с одинаковыми знаменателями.
Задача:
Ход решения:
1) Приводим дроби к общему знаменателю.
Для этого ищем НОК — наименьшее общее кратное, для знаменателей 7 и 6 это число 42.
Делим число 42 на знаменатели дробей 3/7 и 2/6
Так мы нашли дополнительные множители.
Дальше домножаем дроби на дополнительные множители и получаем выражение:
2) Складываем дроби.
В нашем случае дробь можно сократить на 2 , и в конечный ответ записываем число 16/21
Сложение дроби и целого числа:
Определение: Для того, чтобы сложить дробь с целым числом, нужно сначала представить целое число как дробь со знаменателем равным 1.
Алгоритм расчета:
1) Приводим дроби к общему знаменателю.
2) Складываем дроби
3) Если есть возможность, то сокращаем полученную дробь.
4) Если же получилась неправильная дробь, то вычисляем из нее целую часть.
Пример:
Решение:
Вычисляем целую часть, и получаем ответ
Сложение смешанных дробей:
Определение: Для того, чтобы сложить смешанные дроби нужно отдельно сложить целые части, и отдельно сложить дробные части.
Формула
Пример:
Подставляем цифры в формулу:
Получаем:
Из дроби вычисляем целую часть т.к она неправильная,и получаем выражение 7+2=9.
Сложение дробей: теория и практика
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 − 0,2)/15.
Алгебраические — состоят из переменных, например, (x + y)/(x − y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной называют такую дробь, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1/4.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
- От перестановки мест слагаемых сумма не меняется: a + b = b + a.
- Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
- Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
- При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.

Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить сумму двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
1. Найдем наименьшее общее кратное знаменателей (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в произведении дают значения знаменателей складываемых дробей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 × 2 × 3 × 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
- 90 : 15 = 6,
- 90 : 18 = 5.

Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, тренируйтесь решать примеры на сложение дробей как можно чаще.
Смешанные числа
В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дробиВстречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь . Чтобы решить этот пример, нужно число 2 представить в виде дроби . Затем сложить дроби с разными знаменателями:
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: , а конец так: . Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.
Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.
Когда перед нами смешанное число вида , мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения равно
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
Пример 2. Найти значение выражения
Представим число 3 в виде дроби . Затем сложим дроби с разными знаменателями:
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
Пример 3. Найти значение выражения
Можно записать вместе число 2 и дробь alt=»пять вторых» width=»12″ height=»43″ />, но этот ответ не будет окончательным, поскольку в дроби alt=»пять вторых» width=»12″ height=»43″ />можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби . Пять вторых это две целых и одна вторая:
Теперь в главном выражении вместо дроби запишем смешанное число
Получили новое выражение . В этом выражении смешанное число запишем в развёрнутом виде:
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
Теперь свернём полученное смешанное число:
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
Сложение смешанных чиселВстречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
Получили . Теперь в главном выражении заменяем дробные части на полученную дробь
Теперь свернем полученное смешанное число:
Таким образом, значение выражения равно . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 5 + 3 = 8 . В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
Теперь вычислим дробные части:
Получили смешанное число . Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число
Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число
Получили выражение . В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:
Сложим целые части. Получаем 9
Сворачиваем готовый ответ:
Таким образом, значение выражения равно .
Полное решение этого примера выглядит следующим образом:
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
Сложение целого и смешанного числаВстречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
Здесь смешанная дробь была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ .
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Пример 2. Найти значение выражения
Найти значение выражения
В этом примере, как и в предыдущем, нужно сложить целые части:
Осталось свернуть целую и дробную части, но дело в том, что дробная часть представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
Вычитание дроби из целого числаВстречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби , и выполнить вычитание дробей с разными знаменателями:
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
Пример 2. Найти значение выражения .
Представим число 2 в виде дроби , и выполним вычитание дробей с разными знаменателями:
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения , не приводя на бумаге никаких вычислений.
Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения , не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:
Нужно вычесть из них . Мы помним, что треть выглядит следующим образом:
Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть
Получилось (две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
Пример 3. Найти значение выражения
Представим число 3 в виде дроби . Затем выполним вычитание дробей с разными знаменателями:
Вычитание смешанного числа из целого числаТеперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Представим 6 в виде дроби , а смешанное число , в виде неправильной дроби. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
Тогда от той пиццы, от которой отрезали останется пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чиселВстречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения:
Чтобы решить этот пример, нужно смешанные числа и перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
Если от трёх целых пицц вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
Пример 2. Найти значение выражения
Переводим смешанные числа и в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробьЧтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь alt=»одна вторая» width=»12″ height=»43″ />. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби alt=»одна вторая» width=»12″ height=»43″ />, а знаменатель оставить без изменения:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Умножим число 3 на числитель дроби
В ответе получилась неправильная дробь , но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
Пример 3. Найти значение выражения
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
Пример 4. Найти значение выражения
Умножим число 3 на числитель дроби
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения
Переведём смешанное число в неправильную дробь. После перевода это число превратится в дробь . Затем можно будет умножить эту дробь на
Допустим, имеются одна целая и половина пиццы:
Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
Поэтому значение выражения было равно 1
Умножение смешанных чиселВстречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить и . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
Теперь разберемся со смешанным множителем . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
Но ещё осталось взять от изначальной целой пиццы и половины, ведь множителем было смешанное число . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
Деление целого числа на дробьЧтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь alt=»одна вторая» width=»12″ height=»43″ />. Здесь число 3 — это делимое, а дробь alt=»одна вторая» width=»12″ height=»43″ />— делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 3 на дробь
Допустим, имеются три целые пиццы:
Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз» .
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
Поэтому значение выражения равно 6.
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби alt=»три вторых» width=»12″ height=»43″ />. А обратная дробь для дроби alt=»три вторых» width=»12″ height=»43″ />это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби . После выделения целой части в этой дроби получим
После выделения целой части в этой дроби получим
Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения равно
Пример 3. Найти значение выражения
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 5 на
Дробь это 2 целых и . Проще говоря, две целые и четверть пиццы:
А выражение определяет сколько раз содержится в пяти целых пиццах. Ответом было смешанное число .
Ответом было смешанное число .
То есть пиццы содержится в пяти целых пиццах раза.
Давайте нащупаем в пяти пиццах два раза по
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой от , которые не вместились. Двумя девятыми они являются по той причине, что в пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
Поэтому значение выражения равно
Деление дроби на целое числоЧтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь на число 2
Чтобы разделить дробь alt=»одна вторая» width=»12″ height=»43″ />на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь alt=»одна вторая» width=»12″ height=»43″ />
Пусть имеется половина пиццы:
Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
Тогда каждая получившаяся часть будет одной четвертой пиццы:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно дробь умножить на число, обратное числу 2. Обратное числу 2 это дробь
Пример 3. Найти значение выражения
Умножаем первую дробь на число, обратное числу 3. Обратное числу 3 это дробь
Деление целого числа на смешанное числоВстречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .
Чтобы решить этот пример, нужно делитель перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель в неправильную дробь, получим . Затем умножим 2 на дробь, обратную дроби . Обратная для дроби это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз (одна целая и половина пиццы) содержится в двух целых пиццах?» . Похожий пример мы решали ранее, когда учились делить целое число на дробь.
Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим делитель в неправильную дробь, получаем . Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь
Сначала мы получили ответ , затем сократили эту дробь на 5, и получили , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
Деление смешанного числа на целое числоЧтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим /> на 2. Чтобы решить этот пример, нужно делимое /> перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число в неправильную дробь, получим .
Теперь умножаем на число, обратное числу 2. Обратное числу 2 это дробь
Допустим, имеется одна целая и половина пиццы:
Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:
Затем разделим поровну на две части и половину:
Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переведём делимое в неправильную дробь, получим . Теперь умножаем на число, обратное числу 4. Обратное числу 4 это дробь .
Деление смешанных чиселЧтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Как решать дальше мы уже знаем. Первую дробь нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь .
Дорешаем данный пример до конца:
Допустим, имеются две целые и половина пиццы:
Если зададим вопрос «Сколько раз (одна целая и четверть пиццы) содержится в двух целых и половине пиццы» , то ответом будет «два раза»:
Пример 2. Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь
Сначала мы получили дробь. Эту дробь мы сократили на 9. В результате получили дробь , но такой ответ нас тоже не устроил и мы выделили в дроби целую часть. В результате получили окончательный ответ .
В результате получили окончательный ответ .
Сложение дробей. — tutomath.ru репетитор по математике
Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
Сложение дробей с одинаковыми знаменателями.
На примере посмотрим, как складывать дроби с общим знаменателем.
Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или \(\frac{1}{5}\) от всего пути. Во второй день они прошли от точки B до D или \(\frac{2}{5}\) от всего пути. Какое расстояние они прошли от начала пути до точки D?
Решение:
Чтобы найти расстояние от точки A до точки D нужно сложить дроби \(\frac{1}{5} + \frac{2}{5}\).
Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.
\(\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}\)
В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:
\(\bf \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Ответ: туристы прошли \(\frac{3}{5}\) всего пути.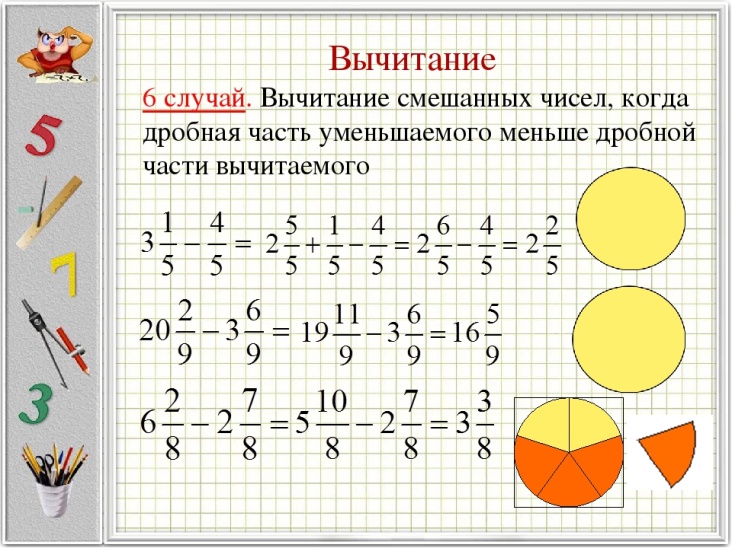
Сложение дробей с разными знаменателями.
Рассмотрим пример:
Нужно сложить две дроби \(\frac{3}{4}\) и \(\frac{2}{7}\).
Чтобы сложить дроби с разными знаменателями нужно сначала найти общий знаменатель, а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.
Как найти общий знаменатель можно посмотреть здесь, нажав на ссылку>>
Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь \(\frac{3}{4}\) нужно умножить на 7. Вторую дробь \(\frac{2}{7}\) нужно умножить на 4.
\(\frac{3}{4} + \frac{2}{7} = \frac{3 \times \color{red} {7} + 2 \times \color{red} {4}}{4 \times \color{red} {7}} = \frac{21 + 8}{28} = \frac{29}{28} = 1\frac{1}{28}\)
В буквенном виде получаем такую формулу:
\(\bf \frac{a}{b} + \frac{c}{d} = \frac{a \times d + c \times b}{b \times d}\)
Сложение смешанных чисел или смешанных дробей.
Сложение смешанных дробей происходит по закону сложения.
У смешанных дробей складываем целые части с целыми и дробные части с дробными.
Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.
Сложим смешанные числа \(3\frac{6}{11}\) и \(1\frac{3}{11}\).
\(3\frac{6}{11} + 1\frac{3}{11} = (\color{red} {3} + \color{blue} {\frac{6}{11}}) + (\color{red} {1} + \color{blue} {\frac{3}{11}}) = (\color{red} {3} + \color{red} {1}) + (\color{blue} {\frac{6}{11}} + \color{blue} {\frac{3}{11}}) = \color{red}{4} + (\color{blue} {\frac{6 + 3}{11}}) = \color{red}{4} + \color{blue} {\frac{9}{11}} = \color{red}{4} \color{blue} {\frac{9}{11}}\)
Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.
Выполним сложение смешанных чисел \(7\frac{1}{8}\) и \(2\frac{1}{6}\).
Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.
\(7\frac{1}{8} + 2\frac{1}{6} = 7\frac{1 \times \color{red} {3}}{8 \times \color{red} {3}} = 2\frac{1 \times \color{red} {4}}{6 \times \color{red} {4}} =7\frac{3}{24} + 2\frac{4}{24} = 9\frac{7}{24}\)
Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби. В зависимости от типа выражения переходим к алгоритму решения.
Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.
Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.
Пример №1:
Может ли сумма двух правильных дробей в результате получить правильную дробь? Неправильную дробь? Приведите примеры.
Решение:
\(\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}\)
Дробь \(\frac{5}{7}\) это правильная дробь, она является результатом суммы двух правильных дробей \(\frac{2}{7}\) и \(\frac{3}{7}\).
\(\frac{2}{5} + \frac{8}{9} = \frac{2 \times 9 + 8 \times 5}{5 \times 9} =\frac{18 + 40}{45} = \frac{58}{45}\)
Дробь \(\frac{58}{45}\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac{2}{5}\) и \(\frac{8}{9}\).
Ответ: на оба вопроса ответ да.
Пример №2:
Сложите дроби: а) \(\frac{3}{11} + \frac{5}{11}\) б) \(\frac{1}{3} + \frac{2}{9}\).
а) \(\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}\)
б) \(\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}\)
Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac{9}{47}\) б) \(5\frac{1}{3}\)
а) \(1\frac{9}{47} = 1 + \frac{9}{47}\)
б) \(5\frac{1}{3} = 5 + \frac{1}{3}\)
Пример №4:
Вычислите сумму: а) \(8\frac{5}{7} + 2\frac{1}{7}\) б) \(2\frac{9}{13} + \frac{2}{13}\) в) \(7\frac{2}{5} + 3\frac{4}{15}\)
Решение:
а) \(8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}\)
б) \(2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} \)
в) \(7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}\)
Задача №1:
За обедам съели \(\frac{8}{11}\) от торта, а вечером за ужином съели \(\frac{3}{11}\). Как вы думаете торт полностью съели или нет?
Как вы думаете торт полностью съели или нет?
Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.
\(\frac{8}{11} + \frac{3}{11} = \frac{11}{11} = 1\)
Ответ: весь торт съели.
«Сложение дробей с одинаковыми знаменателями». 4-й класс
Образовательная программа: «Школа 2000…»
Класс: 4.
Тип урока: ОНЗ.
Цели:
- сформировать умение складывать дроби с одинаковыми знаменателями;
- повторить понятие дроби, закрепить умение читать и сравнивать дроби;
- тренировать вычислительные навыки, умение решать задачи на нахождение части;
- формировать УУД.

Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, аналогия, обобщение.
Ход урока
1. Мотивация к учебной деятельности— Сегодня у нас урок ОНЗ – урок открытия новых знаний. По какому плану вы открываете новые знания?
План:
- Исследуем и наблюдаем.
- Открываем новое знание.
- Применяем знания.
- Контролируем.
- Оцениваем.
— Всё правильно. А сначала повторим то, что нам понадобится для изучения нового.
2. Актуализация знаний и фиксация затруднения в пробном действииНа доске записаны числа:
— На какие две группы можно разбить эти числа? (Натуральные и дроби)
— Что вы уже знаете о натуральных числах и что умеете делать с ними? (Знаем, что такое натуральные числа; умеем их записывать; отмечать на числовом луче; сравнивать; складывать; вычитать; умножать; делить. )
)
— Что вы уже знаете о дробях и что умеете делать с дробями? (Знаем, что такое дробь; умеем записывать дроби; изображать графические модели дробей, отмечать на числовом луче; сравнивать дроби; находить части числа и число по его части; части, которую одно число составляет от другого.)
— Проверим, насколько хорошо вы умеете это делать.
Проводится опрос-тест с помощью программы Plickers:
- Вычисли 5/8 от 16.
- Вычисли 3/11 от 33.
- Вычисли 7% от 600.
- Найди число, 2/9 которого равны 8.
- Найди число, 5% которого равны 35.
— Для чего служат натуральные числа, а для чего – дроби? (Натуральные числа служат для счёта предметов, а дроби – для выражения их частей.)
— Интересно, Что ещё математики древности высоко ценили умение оперировать дробями. Вот одна старинная задача. У Пифагора спросили однажды, сколько у него учеников. Он ответил: «Половина моих учеников изучают прекрасную математику, четверть исследуют тайны природы, седьмая часть упражняет силу духа. Добавьте ещё к ним трёх юношей, их которых Теон самый способный».
Добавьте ещё к ним трёх юношей, их которых Теон самый способный».
— Чтобы ответить на вопрос этой задачи, надо сложить несколько чисел. Трудность в том, что эти числа – дроби!
— Сможете ли вы решить эту задачу? (Нет.)
— Что вы ещё не умеете делать? (Складывать дроби.)
— Сформулируйте цель нашего урока. (Научиться складывать дроби.)
— Но дроби бывают разные: с одинаковыми знаменателями и разными. Сегодня вы научитесь складывать дроби с одинаковыми знаменателями.
— Найдите среди чисел на доске дроби с одинаковыми знаменателями. ()
— Что показывает каждое число в записи дроби? (Под чертой – знаменатель, он показывает, на сколько равных частей разделили целое. Над чертой – числитель, он показывает, сколько равных долей взято.)
— Что, значит, сложить числа? (Объединить в одно целое.)
— Попробуйте сложить эти дроби.
Что у вас получилось? ()
— Кто не смог получить ответ? Почему? (Мы не можем сложить дроби .
— Кто из получивших ответ сможет доказать, что ответ верный? (Не можем доказать)
3. Выявление места и причины затруднения— Какое задание вы выполняли? (Складывали дроби .)
— Что особенного в записи этих дробей? (Одинаковые знаменатели.)
— Как пробовали выполнить сложение дробей? (Учащиеся объясняют свои действия.)
— Почему возникли затруднения? (Не знаем единого способа сложения дробей.)
4. Построение проекта выхода из затруднения— Какова же цель урока? (Научиться складывать дроби и построить алгоритм сложения дробей с одинаковыми знаменателями.)
— Уточним тему урока. (Сложение дробей с одинаковыми знаменателями.)
— Что вам может помочь? (Графические модели. Числовой луч.)
На доске составляется план выхода из затруднения.
План:
1) Выполнить сложение с помощью графических моделей.
2) Проанализировать результат.
3) Сформулировать вывод. Записать его в общем виде.
4) Оформить алгоритм.
— Сейчас вы будете работать в группах по составленному плану. Вспомните правила работы в группе.
У каждой группы в конвертах лежат необходимые материалы для работы: графическая модель, блоки для составления алгоритма, карточки для составления опорного конспекта.
— Выполнить сложение с помощью графической модели. На реализацию плана отводится 5 минут.
— Итак, сравним опорные конспекты, которые вы дополнили. Конспекты вывешиваются на доске. Что можете сказать? (Получились одинаковые конспекты.)
— Чтобы проверить правильность выполнения задания посмотрите видео-урок (отрывок) Ю.К.Грачёвой на портале «Знайка».
— Правильно ли вы составили опорные конспекты?
— А теперь посмотрим, какие алгоритмы получились в группах.
Представитель одной группы зачитывает алгоритм. Остальные группы соглашаются или не соглашаются с ним. В ходе обсуждения на доске появляется правильный алгоритм.
Остальные группы соглашаются или не соглашаются с ним. В ходе обсуждения на доске появляется правильный алгоритм.
— Можно ли данный способ (алгоритм) применить для выполнения пробного действия? (Да.)
— Правило сложения дробей есть в учебнике. С ним вы можете сравнить свои выводы. Откройте учебник и прочитайте правило на стр.7. Сравните с вашим результатом. (Похожи.)
6. Первичное закрепление во внешней речи— Чем вы пользовались, чтобы сложить дроби? (графической моделью)
— Расскажите, как складывали дроби с помощью числового луча.
(Объяснения детей.)
— Откройте в учебнике № 2, 3 на стр. 7. Выполните задания, работая в парах с проговариванием.
Проверка результатов.
— Где возможна ошибка при решении таких примеров? (При сложении чисел в числителях и на применение алгоритма.)
— Каким правилом пользовались для сложения дробей?
7. Самостоятельная работа с самопроверкой по эталону
Самостоятельная работа с самопроверкой по эталону— Проверим, как вы научились ли вы складывать дроби с одинаковыми знаменателями? Для этого проведём самостоятельную работу. № 4 на стр.7.
Проверка по эталону.
— Кто допустил ошибки? В каком месте, и по каким причинам?
— Что нужно сделать, чтобы не допускать ошибки? (Тренироваться.)
— Какое задание в учебнике можно использовать для тренировки? (№ 7, стр. 8)
— Кто выполнил верно?
8. Включение в систему знаний и повторение— Где вы можете применить новый способ? (При решении уравнений, задач.)
Задача на слайде:
«Помидорами занято 4/11 поля, а помидорами — 2/11 поля. Какая часть поля занята огурцами и помидорами?»
— Прочитайте текст задачи. Выполните анализ. Решите задачу.
Проверка по эталону на слайде.
— Кто допустил ошибки? В каком месте, и по каким причинам?
— Кто выполнил верно?
— Каким правилом пользовались для сложения дробей?
На слайде иллюстрация сложения дробей.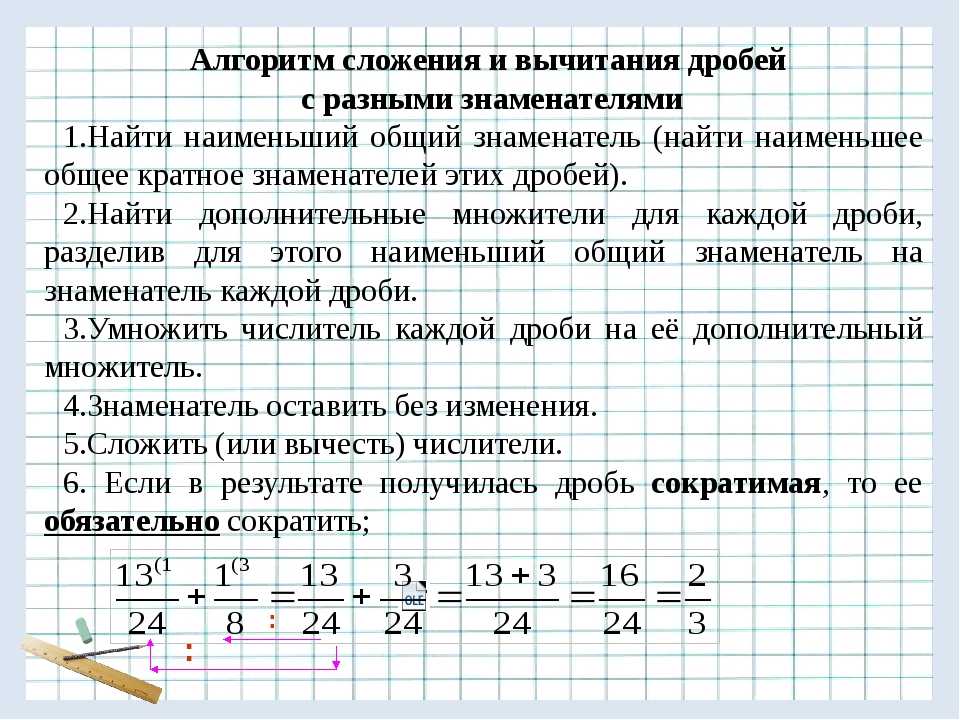
— Какая часть рисунка закрашена?
— Как посчитали?
9. Рефлексия учебной деятельности на уроке— Какова была цель сегодняшнего урока? (Научиться складывать дроби с одинаковым знаменателем. Построить алгоритм сложения дробей с одинаковыми знаменателями.)
— Достигли ли вы этой цели? (Да.)
— Сможете ли вы теперь решить задачу Пифагора? Почему?
— Да, вам ещё многому надо научиться!
Слайд.
Домашнее задание: стр. 8, № 7, 8.
Вычитание и сложение дробей: правила
Предположим, вы выполнили часть домашнего задания вчера и еще одну сегодня. Должен же быть способ подсчитать, сколько домашней работы осталось и сколько всего вы сделали, верно? Вы можете выполнять операции сложения, вычитания, умножения и деления дробей точно так же, как и с целыми числами! В этой статье мы собираемся изучить, как именно выполнять вычитание и сложение дробей.
Правила и шаги: Сложение и вычитание дробей
Дробь — это число, выраженное в виде частного. Многие числа представлены таким образом, и это означает, что они не являются целыми числами. Частное состоит из старшего числа, числителя , и меньшего числа, знаменателя .
Как мы видим ниже, числитель расположен над горизонтальной линией, а знаменатель под ней. В математике эта горизонтальная линия эквивалентна символу деления. Таким образом, дробь представляет собой деление верхнего числа (числителя) на нижнее число (знаменатель).
Пример дроби с обозначением числителя и знаменателя — StudySmarter Originals
Дроби с одинаковым знаменателем
При сложении и вычитании дробей следует помнить одно важное правило: Если дроби нужно складывать или вычитать имеют одинаковые знаменатели, их числители можно складывать или вычитать, сохраняя знаменатель постоянным. Это правило является основой для всех операций сложения и вычитания дробей.
Проиллюстрируем этот процесс более подробно. Предположим, мы хотим вычислить . Поскольку знаменатели идентичны, мы можем просто выполнить вычитание числителей, сохраняя знаменатель постоянным (т. Е. Знаменатель = 9). Другими словами, мы выполняем 5 — 4 = 1 на числителях. Окончательный ответ: Шаги можно записать так:
Дроби с разными знаменателями
Прежде чем складывать или вычитать дроби с разными знаменателями, мы должны манипулировать дробями так, чтобы у них были одинаковые знаменатели. Для этого нам сначала нужно найти наименьший общий знаменатель (LCD).
Наименьший общий знаменатель (LCD) двух дробей — это наименьший возможный знаменатель, который может быть общим для каждой дроби, сохраняя при этом числовое значение каждой дроби одинаковым.
Чтобы найти наименьший общий знаменатель двух дробей, важно сначала убедиться, что каждая дробь представлена в самой упрощенной форме. Это означает, что все общие множители в числителе и знаменателе исключены. Следующим шагом является рассмотрение или перечисление всех множителей каждого знаменателя. Затем мы можем выбрать наименьшее кратное, общее для обоих списков. Это наименьший общий знаменатель! Рассмотрим подробнее этот процесс на следующем примере.
Следующим шагом является рассмотрение или перечисление всех множителей каждого знаменателя. Затем мы можем выбрать наименьшее кратное, общее для обоих списков. Это наименьший общий знаменатель! Рассмотрим подробнее этот процесс на следующем примере.
Найдите наименьший общий знаменатель дробей и
1. Убедитесь, что каждая дробь представлена в самой упрощенной форме.
Первая дробь, которую мы видим, не в самой упрощенной форме. Мы можем упростить эту дробь, убрав коэффициент 32 сверху и снизу.
Вторая дробь уже в самом упрощенном виде, так как нет множителей, которые можно вынести как из верха, так и из низа. Это оставляет нас с дробями и
2. Перечислите кратные каждого знаменателя.
Кратные 2: 2, 4, 6, 8, 10, 12, 14…
Кратные 10: 10, 20, 30, 40, 50, 60, 70…
Из каждого из этих списков видно, что 10 — это наименьшее кратное, общее для обоих знаменателей. Следовательно, это наименьший общий знаменатель .
Следовательно, это наименьший общий знаменатель .
После нахождения ЖК-дисплея можно использовать следующую процедуру для сложения или вычитания дробей с разными знаменателями:
Шаг 1: Установите знаменатель каждого члена с наименьшим общим знаменателем (LCD).
Шаг 2: Установите числитель каждого члена равным.
Шаг 3: Теперь, когда все знаменатели одинаковы, вы можете складывать или вычитать члены в числителе, чтобы получить ответ.
Сложите дроби и
Из нашего предыдущего примера мы знаем, что наименьшее общее кратное и равно 10.
1. Установите знаменатель каждого члена с наименьшим общим знаменателем (LCD).
и
2. Установить числитель каждого члена равным
Поскольку исходный знаменатель второй дроби уже равен 10, ее числитель не нужно преобразовывать.
У нас остались дроби и
3. Теперь, когда все знаменатели одинаковы, вы можете сложить члены в числителе, чтобы получить ответ.
Теперь, когда все знаменатели одинаковы, вы можете сложить члены в числителе, чтобы получить ответ.
В этом примере использовался более длинный способ вычисления; однако, как только вы поймете основы, вам будет намного проще выполнять следующие вычисления:
Примеры сложения и вычитания дробей
(1) Вычислить
Решение:
знаменатели одинаковы, мы можем напрямую вычесть числители.
(2) Оценка
Решение:
LCM знаменателей (18 и 12) составляет 36. С. (20, 12, 30 и 3) равно 60.
Чтобы сложить или вычесть смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.
Сложение и вычитание смешанных дробей
Смешанная дробь — это число, представленное как целое число и частное, например
Сложение и вычитание смешанных дробей требует преобразования их в неправильные дроби.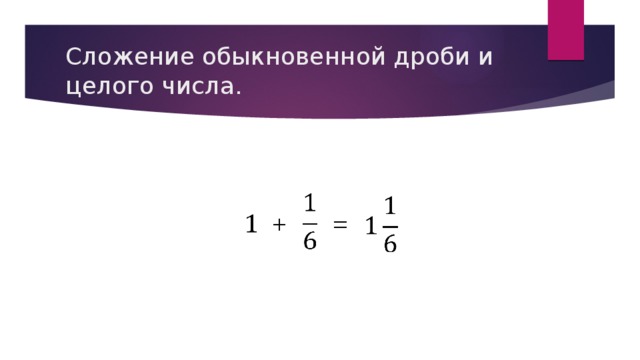 Затем мы можем выполнить стандартный процесс сложения и вычитания дробей, как мы это делали раньше. Неправильная дробь – это дробь, числитель которой больше или равен знаменателю.
Затем мы можем выполнить стандартный процесс сложения и вычитания дробей, как мы это делали раньше. Неправильная дробь – это дробь, числитель которой больше или равен знаменателю.
Чтобы преобразовать смешанную дробь в неправильную дробь, мы должны преобразовать целую числовую часть смешанной дроби в дробь с тем же знаменателем, что и в частном. Затем мы просто добавляем их. Давайте посмотрим на пример.
Преобразуйте следующую смешанную дробь в неправильную дробь.
Решение:
1. Преобразовать целую числовую часть неправильной дроби в дробь с тем же знаменателем, что и у частного.
2. Добавьте эту новую дробь к частному исходной смешанной дроби, чтобы получить неправильную дробь.
И так получаем результат:
Оценка
Решение:
Преобразование смешанных фракций в ненадлежащие фракции, которые мы получаем:
положительных и отрицательных дробей
Как и любое другое число, которое вы встретите, дроби могут быть положительными или отрицательными. К счастью, правила сложения и вычитания положительных и отрицательных дробей такие же, как и для любого другого числа! Давайте посмотрим на несколько примеров, чтобы увидеть, как это работает.
К счастью, правила сложения и вычитания положительных и отрицательных дробей такие же, как и для любого другого числа! Давайте посмотрим на несколько примеров, чтобы увидеть, как это работает.
(1) Вычислить
Решение:
Вычитание отрицательного числа аналогично сложению. Таким образом, наша сумма становится:
(2) Оценка
Решение:
Поскольку добавление отрицательного отрицательного, что и вычитание, наша сумма становится:
(3) Оценка
Решение:
При вычитании отрицательного числа из отрицательного мы складываем числа, но сохраняем знак минус. Итак,
Сложение и вычитание десятичных дробей
Десятичные дроби – это дроби, знаменатель которых несколько кратен десяти, например .
Десятичные дроби складываются и вычитаются почти так же, как и любые другие дроби, рассмотренные ранее. Во-первых, они должны быть преобразованы в форму с наименьшим общим знаменателем, а затем числители могут быть добавлены или вычтены по мере необходимости. Удобная вещь в сложении и вычитании десятичных дробей заключается в том, что наименьший общий знаменатель всегда является наибольшим знаменателем в сумме! Давайте рассмотрим еще несколько примеров.
Во-первых, они должны быть преобразованы в форму с наименьшим общим знаменателем, а затем числители могут быть добавлены или вычтены по мере необходимости. Удобная вещь в сложении и вычитании десятичных дробей заключается в том, что наименьший общий знаменатель всегда является наибольшим знаменателем в сумме! Давайте рассмотрим еще несколько примеров.
(1) Оценить
Решение:
Сначала мы приводим каждое к наименьшему общему знаменателю, который, как мы видим, равен 100.
И затем выполняем сложение.
(1) Оценка
Решение:
Сначала мы преобразуем каждый в самый низкий общий знаменатель, который мы видим, — 1000.
, а затем мы выпускаем субтракцию.
Вычитание и сложение дробей — основные выводы
- Если дроби, которые нужно складывать или вычитать, имеют одинаковые знаменатели, их числители можно просто складывать или вычитать, сохраняя знаменатель постоянным.

- Если нам нужно складывать или вычитать дроби с разными знаменателями, мы сначала манипулируем дробями так, чтобы они имели одинаковые знаменатели.
- Чтобы сложить или вычесть смешанные дроби, сначала преобразуйте их в неправильные дроби.
- Сложение и вычитание положительных и отрицательных дробей работает так же, как и любое другое число.
Как складывать дроби с отрицательными числами?
Дробь — это числовое значение, определяющее часть целого. Оно происходит от слова «fractio» — ломать. Он используется для решения повседневных жизненных задач, таких как разделение продуктов питания, припасов, валюты и т. д. Число в форме a/b можно назвать дробью. Где а, b — любые числа. Например, 2/3, 12/4 и т. д. Рациональные, иррациональные числа, имеющие форму a/b, можно рассматривать как дроби.
Часть дроби
Дробь состоит из двух частей:
- Знаменатель: Наименьшая часть дроби называется знаменателем.
 Он показывает, на сколько частей будет делиться данное целое число. Например, 2/3, здесь 3 называется знаменателем.
Он показывает, на сколько частей будет делиться данное целое число. Например, 2/3, здесь 3 называется знаменателем. - Числитель: Верхняя часть дроби называется числителем. Он представляет, в каком количестве разделов дроби. Например, 2/3, здесь 3 называется числителем 9.0301
Тип дроби
Ниже приведены типы дробей:
- Правильная дробь: Правильные дроби — это дроби, в которых числитель всегда меньше знаменателя. Например, 5/16, 1/4 и т. д.
- Неправильная дробь: Неправильные дроби — это те дроби, в которых числитель всегда больше или равен знаменателю. Например, 5/2, 11/4 и т. д.
- Дробная единица: Дробная единица — это дробь, в числителе которой стоит только 1. Например, 1/2, 1/14 и т. д.
- Смешанная фракция: Смешанные фракции – это те фракции, которые содержат смесь цельных и правильных фракций. Например, и т.
 д.
д. - Эквивалентная дробь: Эквивалентные дроби — это дроби, содержащие одинаковые значения. Например, 2/9 х 2/2 = 4/18.
- Подобная дробь: Подобные дроби — это те дроби, которые содержат одинаковые знаменатели. Например, 2/8, 4/8 и т. д.
- Отличие от дроби: Отличие от дроби — это те дроби, которые содержат разные знаменатели. Например, 2/9, 8/13 и т. д.
Сложение дробей с отрицательными числами
Как мы знаем, сложение — это основная операция математики. Он используется для нахождения суммы двух положительных или отрицательных чисел. Мы также можем складывать дроби с одинаковыми или разными знаменателями. Нам разрешено также добавлять дроби с отрицательными числами. Некоторые правила, которые нам нужно помнить, когда мы выполняем сложение или вычитание между любыми положительными или отрицательными числами. Они указаны ниже:
Правило 1: При умножении двух положительных чисел мы получаем положительный результат.
(+) x (+) = +
Пример: 5×2=10
Правило 2: результат умножения отрицательный.
(-) x (-) = +
Пример: (-7)×(-2)= 14
Здесь два отрицательных символа сокращаются друг с другом.
Правило 3: При перемножении положительных и отрицательных целых чисел результирующее число будет отрицательным.
(-) x (+) = –
Пример: (-7) x 2 = -14 числа.
Шаги для сложения дробей с отрицательными числами:
У нас есть дробь a/b и отрицательное число -c. Теперь мы добавляем их, используя следующие шаги:
Шаг 1: Преобразуйте их символы в соответствии с приведенным выше правилом. Здесь a/b + (-c) = a/b – c
Шаг 2: a/b – c также можно записать как a/b -c/1
Шаг 3: Теперь возьмите LCM на b и 1
Шаг 4: Теперь окончательное уравнение (a – c)/b и решить это уравнение, чтобы получить окончательный результат.
Примеры вопросов
Вопрос 1: (1/2) + (-1) = ?
Решение:
Здесь у нас операция + перед отрицательным числом. По правилу-3 при умножении + на – получается отрицательный символ.
(1/2) + (-1) будет преобразовано в (1/2) – 1
Этот (1/2) – 1 можно переписать в (1/2) – (1/1)
НОК двух знаменателей 2,1 равно 2.
(1/2) – (1/1) = (1 – 2)/2
= -1/2
= -0,5
Вопрос 2: -(1/2) + (-1) = ?
Решение:
Здесь у нас операция + перед отрицательным числом. По правилу-3 при умножении + на – получается отрицательный символ.
-(1/2) + (-1) будет преобразовано в -(1/2) – 1
Это -(1/2) – 1 можно переписать в (-1/2) – (1/ 1)
НОК 2 знаменателя 2,1 равно 2.
(-1/2) – (1/1) = (-1 – 2)/2
= -3/2
= -1,5
Вопрос 3: -(1/3) + (3/6) = ?
Решение:
НОК двух знаменателей 3, 6 равно 6.
(-1/3) + (3/6) = (-2 + 3)/6
910002 = 6Вопрос 4: -(1/3) + (3/8) = ?
Решение:
НОК 2 знаменателя 3,8 равно 24.
(-1/3) + (3/8) = ((-1 x 8) + (3 x 3) )/24
=(-8 + 9) /24
= 1/24
Вопрос 5: -(1/3) + (-2) = ?
Решение:
Здесь у нас операция + перед отрицательным числом. По правилу-3 при умножении + на – получается отрицательный символ.
(-1/3) + (-2) будет преобразовано в (-1/3)-(2)
Это -(1/3) – 2 можно переписать в (-1/3) – (2/1)
НОК из 2 знаменателей 3, 1 равно 3.
(-1/3) – (2 /1) = (-1 – 2)/3
= -3/3
= -1
просто, при сложении или вычитании
дробей требуется больше шагов.Дробь состоит из числа — числитель — деленное на другое число — называется знаменателем .
Обычно оба этих числа являются положительными целыми числами (целыми числами).
Например, в \(\frac{4}{15}\) числитель равен 4, а знаменатель равен 15.
Общая формулаОсновная формула для сложения дробей:
\(\frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd}\)
На словах это означает, что вы умножаете каждый числитель на напротив демониматора и сложите эти результаты, чтобы получить новый числитель. Новый знаменатель является произведением исходных знаменателей.
Вычитание использует тот же расчет, за исключением того, что вместо плюса используется минус:
\(\frac{a}{b} – \frac{c}{d} = \frac{ad – bc}{bd}\)
На этой странице я буду использовать примеры, использующие только вычисления сложения.
Например:
Объяснение формулы\(\frac{2}{5} + \frac{3}{8} = \frac{2 \times 8 + 3 \times 5}{5 \times 8} = \frac{31}{40}\ )
Вы можете использовать эту формулу без понимания ее , но она поможет вам запомнить ее и проявить творческий подход, если вы ее понимаете.
Представьте, что у вас есть две пиццы одинакового размера:
- Пицца 1 нарезана на \(b\) одинаковых кусочков, из которых вы съедите \(a\) из них.
- Пицца 2 нарезана на \(d\) одинаковых кусочков, из которых вы будете есть \(c\) из них.
Всего вы съедите \(\frac{a}{b} + \frac{c}{d}\) пиццы. Сколько это стоит?
Представьте, что вы аккуратно разрезаете каждый кусок первой пиццы на \(d\) кусочков. Ломтики теперь намного меньше — пицца разделена на \(bd\) кусочки — и вы будете есть \(ad\) из них.
Затем каждый кусок второй пиццы разрежьте на \(b\) кусочков. Эта пицца и теперь разделена на \(bd\) ломтики — и вы будете есть \(bc\) из них.
Всего вы съели \(ad + bc\) кусочков, каждый из которых был \(\frac{1}{bd}\) целой пиццы.
Упрощенные дробиДробь упрощенная , если нет простых чисел, которые делят на как числитель, так и знаменатель . Например, \(\frac{40}{60}\) — это , а не упрощенно, потому что \(2\) делится на \(40\) и \(60\).
На самом деле, то же самое относится и к \(5\), и даже к некоторым большим непростым числам, таким как \(20\). Если вы разделите верх и низ дроби на \(20\), дробь станет \(\frac{2}{3}\), что является упрощенной формой.
На этой странице я предполагаю, что вам нужно складывать или вычитать дроби, которые уже упрощены, что обычно для соревнований по ментальной арифметике. В конце есть примечание, описывающее, что вам следует делать, если они не упрощены.
Смешанные дробиДробь считается неправильной , если числитель больше знаменателя. Например, \(\frac{14}{3}\) — неправильная дробь. Неправильные дроби можно записать как смешанных дробей — с целой частью и правильной дробной частью. Например, \(\frac{14}{3} = 4 \frac{2}{3}\)
В соревнованиях по устному счету вы должны давать все ответы в смешанной форме. Неправильные дроби отмечены как неправильные!
Чтобы преобразовать неправильную дробь в смешанную, сначала разделите числитель на знаменатель и получите остаток:
\(14 \дел 3 = 4\) остат.
\(2\)
Целая часть — это результат деления — \(4\) — а остаток — \(2\) — это числитель смешанной дроби.
\(\frac{14}{3} = 4 \frac{2}{3}\)
Полный пример:
Случаи, требующие упрощения\(\frac{2}{3} + \frac{4}{5} = \frac{22}{15} = 1 \frac{7}{15}\)
Если два числа — \(b\) и \(d\) — не имеют общих множителей, они называются со-премьер . Это то же самое, что сказать, что \(\frac{b}{d}\) будет упрощенной дробью.
Если два знаменателя — \(b\) и \(d\) — взаимно просты, то гарантируется, что полученная дробь не будет нуждаться в упрощении. Но в противном случае вам также нужно будет попытаться упростить конечную дробь.
В соревнованиях по устному счету вы должны давать все ответы в упрощенной форме. Неупрощенные дроби отмечены неправильно!
\(8\) и \(24\) — это , а не взаимно просты, так как оба четны, поэтому мы должны упростить в конце:
\(\frac{3}{8} + \frac{7}{24} = \frac{3 \times 24 + 7 \times 8}{8 \times 24} = \frac{128}{192} = \фракция{2}{3}\)
В этом вычислении использовались довольно большие числа, и было бы хуже, если бы у исходных дробей были большие знаменатели! К счастью, есть короткий путь:
- Найдите любое число, на которое делятся оба знаменателя — чем меньше, тем лучше.
В приведенном выше примере вы могли бы использовать \(48\), но лучше всего использовать \(24\).
- Выразите обе дроби, используя этот новый знаменатель: \(\frac{9}{24} + \frac{7}{24}\). В этом случае вторую дробь менять не нужно, но в первой делиноматор был умножен на \(3\), чтобы получить от \(8\) до \(24\). Значит, нужно было умножить его числитель так же: \(3 \times 3 = 9\).
- Просто добавьте числители и поместите их над новым знаменателем.
\(\frac{3}{8} + \frac{7}{24} = \frac{9}{24} + \frac{7}{24} = \frac{16}{24} = \frac {2}{3}\)
Обратите внимание, что иногда — как здесь — нам нужно сделать шаг упрощения в конце, даже если мы уже упростили на более раннем этапе.
Доказательство того, что сложение простых дробей с взаимно простыми знаменателями никогда не требует упрощенияВы можете пропустить этот абзац, если в настоящее время вас не интересует математика, стоящая за методом.

Требуется ли упрощение результата формулы \(\frac{ad + bc}{bd}\)?
Предположим, что \(b\) и \(d\) не имеют общих простых делителей, т. е. взаимно просты. Делится ли любой множитель \(b\) на числитель \(ad + bc\)?
Конечно будет делить на \(bc\). Но оно не делится на \(ad\), потому что \(b\) не имеет общих простых множителей ни с \(d\), ни с \(a\) (поскольку \(\frac{a}{ б}\) уже было упрощено). Поскольку делит на \(bc\), а , а не на \(ad\), оно не может делиться на их сумму.
По тому же аргументу числитель также не имеет общих простых множителей с \(d\).
Следовательно, нет простых чисел — и, следовательно, целых чисел любого типа, — на которые мы можем разделить, чтобы упростить \(\frac{ad + bc}{bd}\).
Окончательный итог для вычислений в умеПри сложении или вычитании дробей с помощью вычислений в уме:
- Проверьте или предположите, что дроби нельзя упростить.
- Проверить, имеют ли знаменатели общие множители.
903:00 Если у них нет общих множителей, используйте общую формулу и оставьте свой ответ в виде смешанной дроби.- Если у них есть общие множители, вы можете либо использовать общий метод (более простой), либо просто изменить дроби вручную, чтобы они имели одинаковый знаменатель (более простая арифметика). Затем упростите окончательный ответ, если это необходимо.
- Помните, что не следует записывать какие-либо промежуточные этапы подготовки к соревнованиям!
В качестве последнего примера:
- Используя общую формулу:
\(3 \frac{1}{4} – \frac{5}{6} = 3 \frac{6 – 20}{24} = 3 – \frac{14}{24} = 2 \frac{10 }{24}= 2 \фракция{5}{12}\)
- В качестве альтернативы, путем изменения дробей вручную:
\(3 \frac{1}{4} – \frac{5}{6} = 3 \frac{3}{12} – \frac{10}{12}= 3 – \frac{7}{12 } = 2 \frac{5}{12}\)
Здесь мы должны проверить, можно ли упростить \(2 \frac{5}{12}\), но нельзя.




 Он показывает, на сколько частей будет делиться данное целое число. Например, 2/3, здесь 3 называется знаменателем.
Он показывает, на сколько частей будет делиться данное целое число. Например, 2/3, здесь 3 называется знаменателем. д.
д.


 Обычно оба этих числа являются положительными целыми числами (целыми числами).
Обычно оба этих числа являются положительными целыми числами (целыми числами).
 На самом деле, то же самое относится и к \(5\), и даже к некоторым большим непростым числам, таким как \(20\). Если вы разделите верх и низ дроби на \(20\), дробь станет \(\frac{2}{3}\), что является упрощенной формой.
На самом деле, то же самое относится и к \(5\), и даже к некоторым большим непростым числам, таким как \(20\). Если вы разделите верх и низ дроби на \(20\), дробь станет \(\frac{2}{3}\), что является упрощенной формой.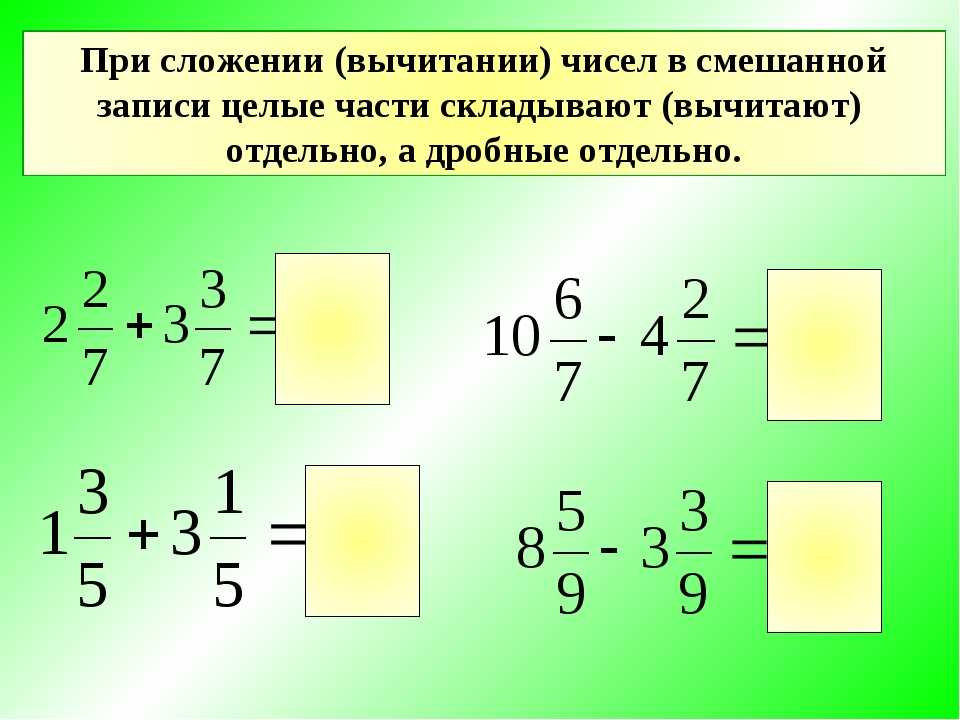 \(2\)
\(2\) В приведенном выше примере вы могли бы использовать \(48\), но лучше всего использовать \(24\).
В приведенном выше примере вы могли бы использовать \(48\), но лучше всего использовать \(24\).