Деление в столбик — подробное описание алгоритма, примеры

Повторяем термины

Если вы уже немного знакомы с арифметическими действиями, то, наверное, знаете, как называются числа, с которыми придется иметь дело:

• делимое

  — это то, что вам нужно разделить;

• делитель

  — на него всегда делят;

• частное

  — то, что получается в итоге.

В Интернете есть немало сайтов, где это действие можно выполнить с помощью онлайн-калькулятора.

Важно! Если вы хотите объяснить принцип деления ребенку, не забудьте проверить, помнит ли он правила умножения.

Без умения перемножать числа в этом случае никак не обойтись, ведь результат всегда нужно проверить, а сделать это можно только обратным действием, то есть умножением. Конечно, навыки сложения и вычитания при освоении деления тоже не повредят.

Как записать?

Даже ученик начальных классов знает, как записываются примеры. Между делимым и делителем ставится двоеточие, после примера — знак равенства, а в конце пишется результат. Но простенькие задания с однозначными числами занимают всего одну строчку, а как быть в случае со столбиком, ведь придется делить двузначные, трехзначные и даже еще более крупные числа? Да точно так же, двоеточие вполне годится. Но есть и второй способ — вот такой значок

I_

Такой способ записи называется “уголком”. Слева от вертикальной линии пишется число, которое мы будем делить, над горизонтальной черточкой — делитель, а под ней — частное. Обычный тетрадный лист подходит для такой записи больше, но при желании все возможно и в ворде

Иметь дело мы будем с целыми числами, а вот в результате может получиться и десятичная дробь, в зависимости от того, допустимо ли в задании частное с остатком. Для начала попробуем разделить трехзначное число на однозначное.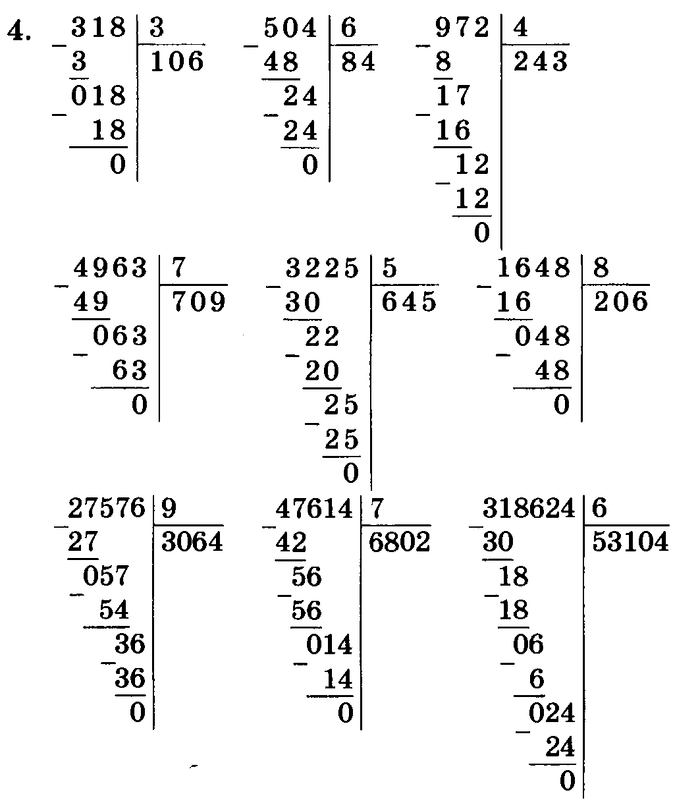

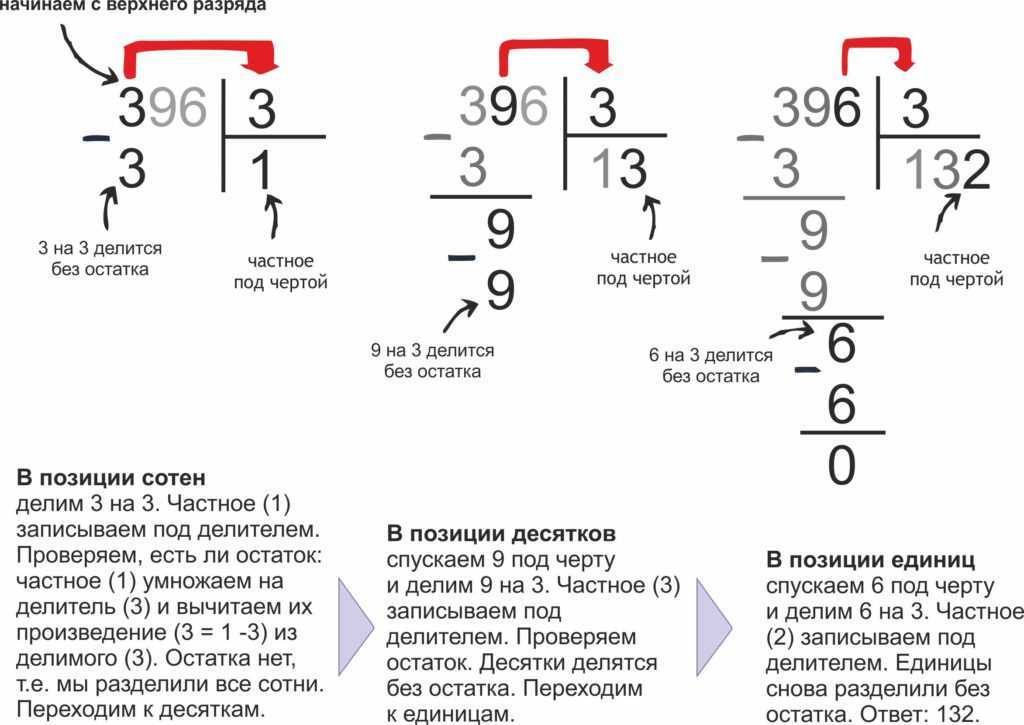
Пример 1

Возьмем 216 разделить 3. Попробуем записать пример:

Посмотрим, какая из первых цифр делится нацело на 3. Двойка? Нет. Значит, берем две цифры — 21. Получится 7, а промежуточное действие будет выглядеть так:

Теперь остается разделить на 3 последнюю цифру — 6, потому после первого шага остаток не образовался. Шестерку в столбике надо написать строго под той, что стоит в примере — в этом главный фокус, иначе можно очень легко сбиться. Что ж, давайте запишем аккуратно. Например, вот так:

Пример 2

Но может быть и другая ситуация. Например, когда первые две цифры на однозначное число нацело не делятся. Ничего страшного. Записываем:

Первым делом придется делить 76, никуда не денешься. Ближайшее число, кратное 8 (то есть то, которое делится без остатка), — 72. Его и будем отнимать. Получим 9, которое сразу запишем в частное, и 4 в остатке — его нужно поместить под чертой:

Следующий шаг — дописать к этой четверке последнюю цифру. Получится 48, его мы на 8 и разделим, от этого действия получится вторая цифра в результате — 6. Наш пример будет выглядеть теперь вот так:

Двузначный делитель

Что будет, если попробовать выполнить другую операцию — разделить то же самое число 768 не на 8, а, скажем, на 16? Да то же самое. Возьмем первые две цифры, посмотрим, какое ближайшее число кратно 16 — это 64. Отнимаем его от 72, получаем 8. К восьмерке приписываем цифру делимого, которую мы еще не задействовали, то есть 8. Пример принимает следующий вид:

Да, но 88 на 16 тоже не делится! Во всяком случае, без остатка. Что ж, тогда поступаем так:

Можно, конечно, больше ничего не делать и записать ответ как 45 (остаток 8). Но есть и другие варианты решения. Если бы число было четырехзначным — все оказалось бы куда проще! А почему бы и не превратить его в четырехзначное? Представим, что делимое у нас записано иначе — 768,0. Тогда мы можем после пятерки тоже поставить запятую и превратить целое число в десятичную дробь. В данном случае она конечна, но бывают примеры и с бесконечными дробями. Вот что получается:

Деление меньшего числа на большее

А можно ли в столбик разделить меньшее число на большее? Ничто не помешает это сделать. Вообще-то арифметика — это веселая и увлекательная игра со своими правилами. Главное — учимся соблюдать порядок. Итак, пробуем быстро разделить 36 на 540. Записываем выражение так:

Поскольку первое число меньше второго, то и результат будет меньше единицы, то придется иметь дело с нулями. Объяснение простое: частное показывает, сколько раз делитель укладывается в делимое. Если нисколько — значит, результат начинается с нуля:

А дальше действуем, как в предыдущих примерах:

Числа в столбике начинают повторяться, то есть получается бесконечная десятичная дробь.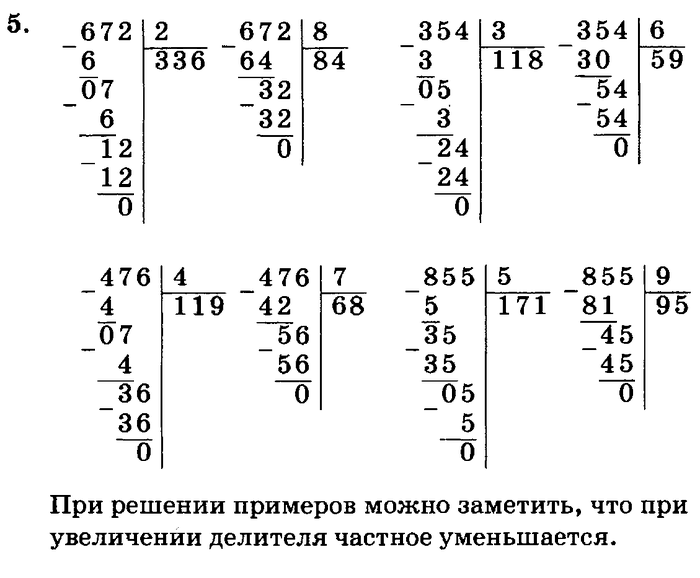

Как проверить результат деления?

Результат, как и всегда, проверяется умножением. Если остатка не было, просто перемножаем частное и делитель любым удобным способом — кстати, умножать в столбик тоже удобно. Если делить нацело не получилось, опять же, перемножаем частное и делитель, а затем прибавляем остаток.

Важно! Если результатом получилась бесконечная десятичная дробь, проверка может быть лишь приблизительной — в результате умножения у вас должно получиться число, очень близкое к делимому.

Эти навыки очень помогут потом, когда придется считать не числа, обозначенные цифрами, а действовать в мире одночленов и многочленов. Ведь полиномы — это тоже числа, только выраженные иначе. Еще больше наглядных примеров деления в столбик смотрите в предложенном ниже видео.

Синтетический отдел

• НАЗАД
• СЛЕДУЮЩИЙ

Мы начинаем терять терпение. Мы хотим начать восхождение на Полиномиальную гору, но мы не сможем добраться до вершины без синтетического деления , более причудливого типа полиномиального деления. Может, он синтетический, потому что сделан из какого-то полимера космической эры?

Пример задачи

Разделить x ² + 8 x + 15 на x + 3.

Для начала мы удалим все наши переменные из нашего многочлена и поместим числа в открытый ящик, например:

Эй, подождите секунду. Это -3 не из полинома и не из коробки. Что дает?

В синтетическом делении мы всегда делим многочлен на x – a . Вот откуда взялось -3; это . Мы делим на x + 3, что равно 9.0018 х

– (-3). Теперь мы можем осуществить разделение.

Шаг первый — опускаем первый коэффициент (из 1 x ² ) под чертой. Затем мы умножим эту 1 на a , -3 и поместим во второй столбец.

Получаем еще -3. Нам лучше поторопиться, пока они не начали бесконтрольно размножаться. Мы добавим его к 8 уже в этом столбце и поместим результат ниже.

Теперь мы просто продолжаем, как и раньше: умножаем число внизу на -3, а затем добавляем результат в следующий столбец. Мы будем делать это, пока не закончатся номера.

Уже все пропало? Ну что ж. В любом случае, самое правое число под чертой — это остаток от нашего деления. Это 0, поэтому у нас нет остатка. Это означает, что х + 3 является коэффициентом х ² + 8 х + 15, так как делится поровну.

Наши оставшиеся числа под полем дают нам ответ на задачу о делении. Справа они начинаются с остатка, затем константы, в данном случае 5, и увеличиваются в степени по мере движения влево. Это означает, что у нас есть x + 5 как наше частное.

Наш окончательный ответ таков: x ² + 8 x + 15 = ( x + 3)( x + 5).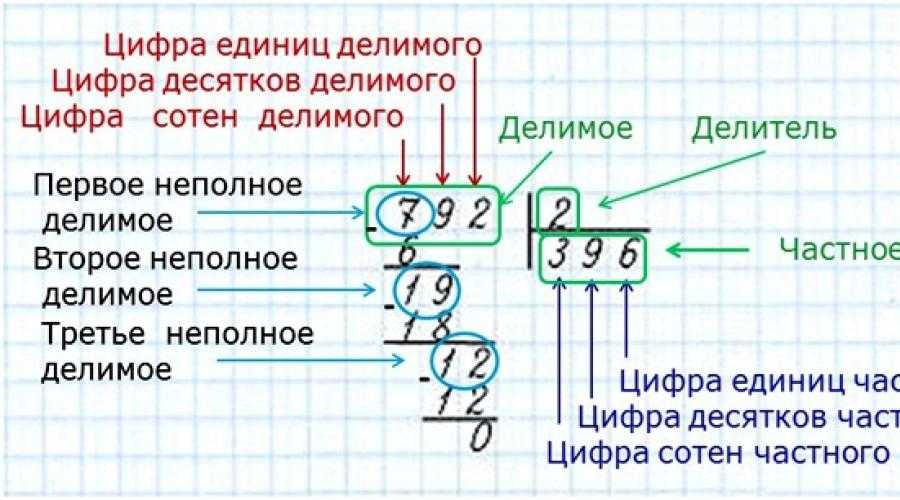 Нет, подождите, наш окончательный ответ: (D) банка майонеза. Мы победили, Регис? Мы? Станем ли мы миллионерами?

Ой. Нет. Раньше мы были правы.

Одно небольшое замечание, прежде чем мы закончим. Если наш многочлен пропускает какие-либо степени x , нам нужно использовать 0 в качестве заполнителя в нашем синтетическом делении. Например, если бы мы делили x ³ + 2 x + 50 на x + 4, верхняя строка нашего синтетического блока деления будет 1, 0, 2, 50. Это потому, что наш многочлен пропустил

x ² на самом деле мы делим x ³ + 0 x ² + 2 x + 50. Понятно?

Это было последнее, что нам нужно было сделать перед запуском Polynomial Mountain. Мы надеемся, что это пройдет легче, чем восхождение на Эверест.

• НАЗАД
• СЛЕДУЮЩИЙ

Процитировать эту страницу

Питон | Pandas dataframe.div() — GeeksforGeeks

Улучшить статью

Сохранить статью

• Уровень сложности: Эксперт
• Последнее обновление: 25 авг, 2021

Читать

Обсудить

Улучшить статью

Сохранить статью

Python — отличный язык для анализа данных, прежде всего благодаря фантастической экосистеме пакетов Python, ориентированных на данные. Pandas

— один из таких пакетов, который значительно упрощает импорт и анализ данных.
Pandas dataframe.div() используется для поиска плавающего деления фрейма данных и других элементов. Эта функция похожа на dataframe/other, но с дополнительной поддержкой для обработки отсутствующего значения в одном из входных данных.
 

Синтаксис: DataFrame.div(other, axis=’columns’, level=None, fill_value=None)
Параметры: 
другое : Серия, DataFrame или константа
ось : Для ввода серии ось должна соответствовать индексу серии
fill_value : Заполнить отсутствующие (NaN) значения этим значением. Если оба местоположения DataFrame отсутствуют, результат будет отсутствовать 
level : Широковещательная рассылка по уровню, совпадающая со значениями индекса на переданном уровне MultiIndex
Возвраты:

result : DataFrame 
 

Пример №1: Использование div () для поиска плавающего разделения элементов фрейма данных с постоянным значением. Также обработайте значение NaN, присутствующее в кадре данных.
 

Python3

import pandas as pd   df = pd.DataFrame({ "A" :[ 5 , 3 , None , 4 ],                     "B" :[ None , 2 , 4 , 3 ],                     "C" :[ 4 , 3 , 8 , 5 ] , "D" : [ 5 , 4 , 2 , 2 , 2 , 200 df

Now find the division of each dataframe element with 2
 

Python3

df. div( 2 , fill_value = 50 )

Вывод:

Вывод представляет собой кадр данных с ячейками, содержащими результат деления каждой ячейки значением NaN 5 на 2. дивизион.
  
Пример №2: Используйте функцию div(), чтобы найти плавающее разделение фрейма данных с объектом серии по оси индекса.
 

Python3

import pandas as pd   df = pd.DataFrame({ "A" :[ 5 , 3 , 6 , 4 ],                     "B" :[ 11 , 2 , 4 , 3 ],                     "C" : [ 4 , 3 , 8 , 5 ],                     "D" :[ 5 , 4 , 2 , 8 ]}) . Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт