Mathway | Популярные задачи

1	Найти объем	сфера (5)	
2	Найти площадь	окружность (5)	
3	Найти площадь поверхности	сфера (5)	
4	Найти площадь	окружность (7)	
5	Найти площадь	окружность (2)	
6	Найти площадь	окружность (4)	
7	Найти площадь	окружность (6)	
8	Найти объем	сфера (4)	
9	Найти площадь	окружность (3)	
10	Вычислить	(5/4(424333-10220^2))^(1/2)
11	Разложить на простые множители	741
12	Найти объем	сфера (3)	
13	Вычислить	3 квадратный корень из 8*3 квадратный корень из 10
14	Найти площадь	окружность (10)	
15	Найти площадь	окружность (8)	
16	Найти площадь поверхности	сфера (6)	
17	Разложить на простые множители	1162
18	Найти площадь	окружность (1)	
19	Найти длину окружности	окружность (5)	
20	Найти объем	сфера (2)	
21	Найти объем	сфера (6)	
22	Найти площадь поверхности	сфера (4)	
23	Найти объем	сфера (7)	
24	Вычислить	квадратный корень из -121
25	Разложить на простые множители	513
26	Вычислить	квадратный корень из 3/16* квадратный корень из 3/9
27	Найти объем	прямоугольный параллелепипед (2)(2)(2)	
28	Найти длину окружности	окружность (6)	
29	Найти длину окружности	окружность (3)	
30	Найти площадь поверхности	сфера (2)	
31	Вычислить	2 1/2÷22000000
32	Найти объем	прямоугольный параллелепипед (5)(5)(5)	
33	Найти объем	прямоугольный параллелепипед (10)(10)(10)	
34	Найти длину окружности	окружность (4)	
35	Перевести в процентное соотношение	1. 2-4*-1+2
45	Разложить на простые множители	228
46	Вычислить	0+0
47	Найти площадь	окружность (9)	
48	Найти длину окружности	окружность (8)	
49	Найти длину окружности	окружность (7)	
50	Найти объем	сфера (10)	
51	Найти площадь поверхности	сфера (10)	
52	Найти площадь поверхности	сфера (7)	
53	Определить, простое число или составное	5
54	Перевести в процентное соотношение	3/9
55	Найти возможные множители	8
56	Вычислить	(-2)^3*(-2)^9
57	Вычислить	35÷0. 2
60	Преобразовать в упрощенную дробь	2 1/4
61	Найти площадь поверхности	сфера (12)	
62	Найти объем	сфера (1)	
63	Найти длину окружности	окружность (2)	
64	Найти объем	прямоугольный параллелепипед (12)(12)(12)	
65	Сложение	2+2=
66	Найти площадь поверхности	прямоугольный параллелепипед (3)(3)(3)	
67	Вычислить	корень пятой степени из 6* корень шестой степени из 7
68	Вычислить	7/40+17/50
69	Разложить на простые множители	1617
70	Вычислить	27-( квадратный корень из 89)/32
71	Вычислить	9÷4
72	Вычислить	2+ квадратный корень из 21
73	Вычислить	-2^2-9^2
74	Вычислить	1-(1-15/16)
75	Преобразовать в упрощенную дробь	8
76	Оценка	656-521
77	Вычислить	3 1/2
78	Вычислить	-5^-2
79	Вычислить	4-(6)/-5
80	Вычислить	3-3*6+2
81	Найти площадь поверхности	прямоугольный параллелепипед (5)(5)(5)	
82	Найти площадь поверхности	сфера (8)	
83	Найти площадь	окружность (14)	
84	Преобразовать в десятичную форму	11/5
85	Вычислить	3 квадратный корень из 12*3 квадратный корень из 6
86	Вычислить	(11/-7)^4
87	Вычислить	(4/3)^-2
88	Вычислить	1/2*3*9
89	Вычислить	12/4-17/-4
90	Вычислить	2/11+17/19
91	Вычислить	3/5+3/10
92	Вычислить	4/5*3/8
93	Вычислить	6/(2(2+1))
94	Упростить	квадратный корень из 144
95	Преобразовать в упрощенную дробь	725%
96	Преобразовать в упрощенную дробь	6 1/4
97	Вычислить	7/10-2/5
98	Вычислить	6÷3
99	Вычислить	5+4
100	Вычислить	квадратный корень из 12- квадратный корень из 192

Страница 108 — ГДЗ Математика 3 класс.

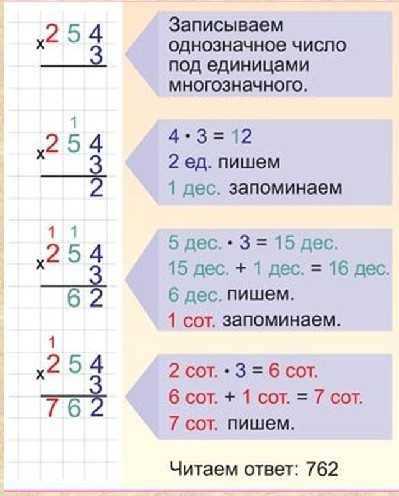Моро, Бантова. Учебник часть 1

1. Главная
2. ГДЗ
3. 3 класс
4. Математика
5. Моро, Бантова. Учебник
6. Что узнали. Чему научились
7. Страница 108. Часть 1

Вернуться к содержанию учебника

Что узнали.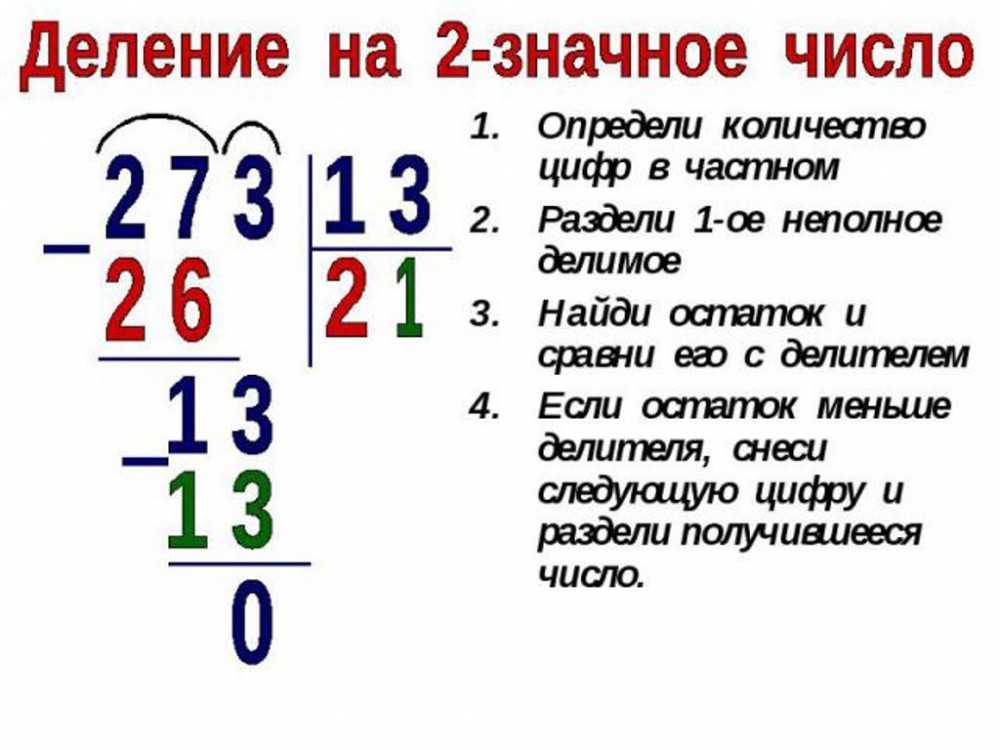 Чему научились

Вопрос

32. В мастерской было 3 куска тюля — всего 92 м. Длина первого куска 23 м, а второго — 39 м. Сколько метров тюля в третьем куске?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

33. В марте Нина прочитала 8 сказок, а в апре­ле — на 2 сказки меньше. Сколько всего сказок она прочитала за эти месяцы?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

34. Маме 28 лет, а её дочке в 7 раз меньше. На сколько лет мама старше дочки?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

35. Составь по кратким записям задачи и реши их.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

36. Вычисли и выполни проверку.

75 — 27

39 + 28

96 — 49

17 + 36

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

37. Реши уравнения

36 — х = 14	х + 20 = 48	х — 44 = 18
х • 26 = 26	х — 0 = 19	х : 1 = 24

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

38. Найди значения выражений b + с и b — с при b=30 и с = 14, b = 27 и с = 19.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

39. Найди длину ломаной и начерти отрезок такой же длины.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

40.  Проверь себя. Заметь время по часам и выясни, сможешь ли ты правильно выполнить за 2 мин вычисления, записывая только ответы

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

---

Матрицы

Матрица представляет собой массив чисел:

Матрица
(у нее 2 строки и 3 столбца)

Мы говорим об одной матрице или нескольких матрицах .

Есть много вещей, которые мы можем с ними сделать…

Добавление

Чтобы сложить две матрицы: сложите числа в совпадающих позициях:

Вот расчеты:

3+4=7	8+0=8
4+1=5	6−9=−3

Две матрицы должны быть одинакового размера, т. е. строки должны совпадать по размеру, а столбцы должны совпадать по размеру.

Пример: матрица с 3 строки и 5 столбцов может быть добавлена ​​к другой матрице 3 строки и 5 столбцов .

Но его нельзя было добавить в матрицу с 3 строки и 4 столбца (столбцы не совпадают по размеру)

Отрицательное

Отрицательное значение матрицы также простое:

Вот расчеты:

−(2)=−2	−(−4)=+4
−(7)=−7	−(10)=−10

Вычитание

Чтобы вычесть две матрицы: вычтите числа в совпадающих позициях:

Вот расчеты:

3−4=−1	8−0=8
4−1=3	6−(−9)=15

Примечание: вычитание фактически определяется как сложение отрицательной матрицы: A + (−B)

Умножение на константу

Мы можем умножить матрицу на константу (значение 2 в этом случае) :

Вот расчеты:

2×4=8	2×0=0
2×1=2	2×−9=−18

Мы называем константу скаляром , поэтому официально это называется «скалярным умножением».

Умножение на другую матрицу

В число умножить две матрицы вместе немного сложнее… прочитайте Умножение матриц, чтобы узнать, как это сделать.

Деление

А деление? Ну, мы не на самом деле делим матрицы, мы делаем это так:

A/B = A × (1/B) = A × B ^-1

, где B ^-1 означает «обратное» значение B.

Таким образом, мы не делим, вместо этого мы умножить на обратное .

И есть специальные способы найти инверсию, узнайте больше в инверсии матрицы.

Транспонирование

Чтобы «транспонировать» матрицу, поменяйте местами строки и столбцы.

Мы ставим букву «Т» в верхнем правом углу, что означает транспонирование:

Обозначение

Матрица обычно обозначается заглавной буквой (например, A или B)

Каждая запись (или «элемент») обозначается строчной буквой с «нижним индексом» из строк, столбцов :

Строки и столбцы Итак, где строка, а где столбец? Ряды идут влево-вправо Столбцы идут вверх-вниз Чтобы помнить, что строки идут перед столбцами, используйте слово «дуга» : а р,с

Пример:

В =

Вот несколько примеров записей:

b _1,1 = 6 (запись в строке 1, столбец 1 равна 6)

b _1,3 = 24 (запись в строке 1 , столбец 3 равен 24)

b _2,3 = 8 (запись в строке 2, столбце 3 равна 8)

 

 

Операции со строками матрицы

Над строками используются 3 основные операции.

матрица когда вы используете матрицу для решить систему линейных уравнений . Обычно цель состоит в том, чтобы левая часть матрицы выглядела как единичная матрица .

Три операции:

• Переключение строк
• Умножение строки на число
• Добавление строк

Переключение строк

Вы можете поменять местами строки матрицы, чтобы получить новую матрицу.

[ 2 3 − 2 6 0 0 3 − 6 1 0 2 − 3 ] → [ 1 0 2 − 3 2 3 − 2 6 0 0 3 − 6 ]

В примере, показанном выше, мы перемещаем строку 1 грести 2 , Ряд 2 грести 3 , и Строка 3 грести 1 . (Причина для этого состоит в том, чтобы получить 1 в левом верхнем углу.)

Умножение строки на число

Вы можете умножить любую строку на число. (Это означает умножение каждой записи в строке на одно и то же число.)

[ 1 0 2 − 3 2 3 − 2 6 0 0 3 − 6 ] → р 3 : 1 3 р 3 [ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ]

В этом примере мы умножили строку 3 матрицы на 1 3 . (Это дает нам 1 нам нужно в строке 3 , Столбец 3 .)

Добавление строк

Вы также можете добавить две строки вместе и заменить строку результатом.

Например, в матрицу, полученную в последнем примере, мы можем добавить строки 2 и 3 вместе, запись за записью:

[ 2 3 − 2 6 ] + [ 0 0 1 − 2 ] _ [ 2 3 − 1 4 ]

Затем мы заменяем строку 2 с результатом.

[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ] → р 2 : р 2 + р 3 [ 1 0 2 − 3 2 3 − 1 4 0 0 1 − 2 ]

Добавление нескольких строк

Мы сказали, что было всего три операции, и они есть. Но, используя последние две операции в сочетании, мы можем добавлять целые кратные строки к другим строкам, чтобы ускорить работу.

Шаг назад, поэтому у нас есть матрица:

[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ]

Теперь вместо того, чтобы просто добавить строку 2 + Строка 3 , Добавить ряд 2 + ( 2 × Ряд 3 ) :

[ 2 3 − 2 6 ] + [ 0 0 2 − 4 ] _ [ 2 3 0 2 ]

Затем замените строку 2 с результатом.

[ 1 0 2 − 3 2 3 − 2 6 0 0 1 − 2 ] → р 2 : р 2 + 2 р 3 [ 1 0 2 − 3 2 3 0 2 0 0 1 − 2 ]

Таким образом, мы получаем 0 в строке 2 , Столбец 3 .

Мы можем сделать это снова, чтобы получить 0 в строке 2 , Столбец 1 . Здесь мы умножаем ряд 1 от − 2 , добавьте строку 2 и замените строку 2 с результатом.

[ 1 0 2 − 3 2 3 0 2 0 0 1 − 2 ] → р 2 : − 2 р 1 + р 2 [ 1 0 2 − 3 0 3 − 4 8 0 0 1 − 2 ]

Мы покажем еще несколько шагов, чтобы получить 3 × 3 единичная матрица слева (и, таким образом, решить систему).

Следующим шагом является добавление Ряд 2 + ( 4 × Ряд 3 ) чтобы получить 0 в строке 2 , Столбец 3 .

[ 1 0 2 − 3 0 3 − 4 8 0 0 1 − 2 ] → р 2 : р 2 + 4 р 3 [ 1 0 2 − 3 0 3 0 0 0 0 1 − 2 ]

Далее нам нужен ноль в строке 1 , Столбец 3 .

[ 1 0 2 − 3 0 3 0 0 0 0 1 − 2 ] → р 1 : р 1 − 2 р 3 [ 1 0 0 1 0 3 0 0 0 0 1 − 2 ]

Последний шаг — это просто применение второй операции, умножение строки на число.

[ 1 0 0 1 0 3 0 0 0 0 1 − 2 ] → 1 3 р 3 [ 1 0 0 1 0 1 0 0 0 0 1 − 2 ]

Теперь у нас есть решение в виде заказанной тройки ( 1 , 0 , − 2 ) .

Важная заметка: Если уравнения, представленные вашей исходной матрицей, представляют собой одинаковые или параллельные линии, вы не сможете получить единичную матрицу, используя эти операции со строками.