Умножение в столбик десятичных чисел. Умножение десятичных дробей: правила, примеры, решения

§ 1 Применение правило умножения десятичных дробей

В этом уроке Вы познакомитесь и научитесь применять правило умножения десятичных дробей и правило умножения десятичной дроби на разрядную единицу, такую как 0,1, 0,01 и т.д. Кроме того, мы рассмотрим свойства умножения при нахождении значений выражений, содержащих десятичные дроби.

Решим задачу:

Скорость движения автомобиля составляет 59,8 км/ч.

Какой путь преодолеет автомобиль за 1,3 часа?

Как известно, чтобы найти путь, необходимо скорость умножить на время, т.е. 59,8 умножить на 1,3.

Давайте запишем числа в столбик и начнем их перемножать, не замечая запятых: 8 умножить на 3, будет 24, 4 пишем 2 в уме, 3 умножить на 9 это 27, да еще плюс 2, получаем 29, 9 пишем, 2 в уме. Теперь 3 умножаем на 5, будет 15 и еще прибавляем 2, получаем 17.

Переходим ко второй строке: 1 умножить на 8, будет 8, 1 умножить на 9, получаем 9, 1 умножить на 5, получаем 5, складываем эти две строчки, получаем 4, 9+8 равно 17, 7 пишем 1 в уме, 7+9 это 16 да еще 1, будет 17, 7 пишем 1 в уме, 1+5 да еще 1 получаем 7.

А теперь посмотрим, сколько знаков после запятых стоит в обеих десятичных дробях! В первой дроби одна цифра после запятой и во второй дроби одна цифра после запятой, всего два знака. Значит, справа в полученном результате нужно отсчитать две цифры и поставить запятую, т.е. будет 77,74. Итак, при умножении 59,8 на 1,3 получили 77,74. Значит ответ в задаче 77,74 км.

Таким образом, чтобы перемножить две десятичные дроби надо:

Первое: выполнить умножение, не обращая внимания на запятые

Второе: в полученном произведении отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.

Если же цифр в полученном произведении меньше, чем надо отделить запятой, то тогда впереди необходимо приписать один или несколько нулей.

Например: 0,145 умножить на 0,03 у нас в произведении получается 435, а запятой необходимо отделить 5 цифр справа, поэтому мы приписываем перед цифрой 4 еще 2 нуля, ставим запятую и приписываем еще один нуль. Получаем ответ 0,00435.

§ 2 Свойства умножения десятичных дробей

При умножении десятичных дробей сохраняются все те же свойства умножения, что действуют для натуральных чисел. Давайте выполним несколько заданий.

Задание №1:

Решим данный пример, применив распределительное свойство умноженияотносительно сложения.

5,7 (общий множитель) вынесем за скобку, в скобках останется 3,4 плюс 0,6. Значение этой суммы равно 4, и теперь 4 надо умножить на 5,7, получаем 22,8.

Задание № 2:

Применим переместительное свойство умножения.

2,5 сначала умножим на 4, получим 10 целых, а теперь нужно 10 умножить на 32,9 и получаем 329.

Кроме этого, при умножении десятичных дробей можно заметить следующее:

При умножении числа на неправильную десятичную дробь, т.е. большую или равную 1, оно увеличивается или не изменяется, например:

При умножении числа на правильную десятичную дробь, т.е. меньшую 1, оно уменьшается, например:

Давайте решим пример:

23,45 умножить на 0,1.

Мы должны 2 345 умножить на 1 и отделить три знака запятой справа, получим 2,345.

Теперь давайте решим другой пример: 23,45 разделить на 10, мы должны перенести запятую влево на один знак, потому что 1 ноль в разрядной единице, получим 2,345.

Из этих двух примеров можно сделать вывод, что умножить десятичную дробь на 0,1, 0,01, 0,001 и т. д. это значит разделить число на 10, 100, 1000 и т.д., т.е. надо в десятичной дроби перенести запятую влево на столько знаков, сколько нулей стоит перед 1 во множителе.

Используя полученное правило, найдем значения произведений:

13,45 умножить на 0,01

перед цифрой 1 стоит 2 нуля, поэтому перенесем запятую влево на 2 знака, получим 0,1345.

0,02 умножить на 0,001

перед цифрой 1 стоит 3 нуля, значит переносим запятую на три знака влево, получаем 0,00002.

Таким образом, в этом уроке Вы научились перемножать десятичные дроби. Для этого нужно всего лишь выполнить умножение, не обращая внимания на запятые, и в полученном произведении отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе. Кроме того, познакомились с правилом умножения десятичной дроби на 0,1, 0,01 и т.д., а также рассмотрели свойства умножения десятичных дробей.

Список использованной литературы:

1. Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
2. Дидактические материалы по математике 5 класс. Автор — Попов М.А. — 2013 год
3. Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. — 2014 год
4. Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. — 2010 год
5. Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012 год
6. Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009

В этом уроке мы рассмотрим каждую из этих операций по отдельности.

Содержание урока

Сложение десятичных дробей

Как мы знаем, десятичная дробь имеет целую и дробную часть. При сложении десятичных дробей, целые и дробные части складываются по отдельности.

Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.

Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой»

.

Запишем дроби в столбик так, чтобы запятая оказалась под запятой:

Начинаем складывать дробные части: 2 + 3= 5. Записываем пятёрку в дробной части нашего ответа:

Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:

Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :

Получили ответ 8,5. Значит выражения 3,2 + 5,3 равно 8,5

На самом деле, не всё так просто, как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.

Разряды в десятичных дробях

У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.

Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.

Разряды в десятичных дробях хранят в себе некоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.

Например, рассмотрим десятичную дробь 0,345

Позиция, где находится тройка, называется разрядом десятых

Позиция, где находится четвёрка, называется разрядом сотых

Позиция, где находится пятёрка, называется разрядом тысячных

Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .

Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345

Видно, что сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345.

При сложении десятичных дробей соблюдаются те же принципы и правила, что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.

Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой» . Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.

Пример 1. Найти значение выражения 1,5 + 3,4

В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:

Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:

Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:

Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9

Пример 2. Найти значение выражения: 3,51 + 1,22

Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»

В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:

Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:

Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:

Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:

Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73

3,51 + 1,22 = 4,73

Как и в обычных числах, при сложении десятичных дробей может произойти . В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.

Пример 3. Найти значение выражения 2,65 + 3,27

Записываем в столбик данное выражение:

Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:

Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:

Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:

Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92

2,65 + 3,27 = 5,92

Пример 4. Найти значение выражения 9,5 + 2,8

Записываем в столбик данное выражение

Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:

Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3

9,5 + 2,8 = 12,3

При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.

Пример 5 . Найти значение выражения: 12,725 + 1,7

Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:

Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:

Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:

Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:

Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425

12,725+ 1,700 = 14,425

Вычитание десятичных дробей

При вычитании десятичных дробей нужно соблюдать те же правила, что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».

Пример 1. Найти значение выражения 2,5 − 2,2

Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:

Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:

Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3

2,5 − 2,2 = 0,3

Пример 2. Найти значение выражения 7,353 — 3,1

В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.

Теперь можно записать в столбик данное выражение и вычислить его:

Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253

7,353 — 3,1 = 4,253

Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.

Пример 3. Найти значение выражения 3,46 − 2,39

Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:

Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:

Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07

3,46−2,39=1,07

Пример 4 . Найти значение выражения 3−1,2

В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,23 оказалась под числом 3

Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:

Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:

Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:

Отделяем запятой целую часть от дробной:

Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8

Умножение десятичных дробей

Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.

Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.

Пример 1. Найти значение выражения 2,5 × 1,5

Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:

Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.

Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75

2,5 × 1,5 = 3,75

Пример 2. Найти значение выражения 12,85 × 2,7

Перемножим эти десятичные дроби, не обращая внимания на запятые:

Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.

Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:

Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695

12,85 × 2,7 = 34,695

Умножение десятичной дроби на обычное число

Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.

Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.

Например, умножим 2,54 на 2

Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:

Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.

Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08

2,54 × 2 = 5,08

Умножение десятичных дробей на 10, 100, 1000

Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.

Например, умножим 2,88 на 10

Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:

Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.

Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8

2,88 × 10 = 28,8

Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.

Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.

2,88 × 10 = 28,8

Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288

2,88 × 100 = 288

Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.

2,88 × 1000 = 2880

Умножение десятичных дробей на 0,1 0,01 и 0,001

Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.

Например, умножим 3,25 на 0,1

Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:

Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.

Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:

Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325

3,25 × 0,1 = 0,325

Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.

Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325

3,25 × 0,1 = 0,325

Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325

3,25 × 0,01 = 0,0325

Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325

3,25 × 0,001 = 0,00325

Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.

При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.

А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.

Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.

Деление меньшего числа на большее. Продвинутый уровень.

В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.

Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»

Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.

Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.

При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.

Итак, разделим 1 на 2. Решим этот пример уголком:

Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:

Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:

Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:

Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:

Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10

Получили ответ 0,5. Значит дробь равна 0,5

Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:

Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см

Пример 2. Найти значение выражения 4: 5

Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:

Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:

Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.

Завершаем пример, умножив 8 на 5, и получив 40:

Получили ответ 0,8. Значит значение выражения 4: 5 равно 0,8

Пример 3. Найти значение выражения 5: 125

Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:

Умножаем 0 на 5, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0

Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:

Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0

Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50

Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:

Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:

Завершаем пример, умножив 4 на 125, и получив 500

Получили ответ 0,04. Значит значение выражения 5: 125 равно 0,04

Деление чисел без остатка

Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:

Допишем ноль к остатку 4

Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:

40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:

9: 5 = 1,8

Пример 2 . Разделить 84 на 5 без остатка

Сначала разделим 84 на 5 как обычно с остатком:

Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0

Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:

и завершаем пример, проверив есть ли еще остаток:

Деление десятичной дроби на обычное число

Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:

• разделить целую часть десятичной дроби на это число;
• после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.

Например, разделим 4,8 на 2

Запишем этот пример уголком:

Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:

Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:

4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2

8: 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:

Получили ответ 2,4. Значение выражения 4,8: 2 равно 2,4

Пример 2. Найти значение выражения 8,43: 3

Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:

Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:

Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:

24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:

Получили ответ 2,81. Значит значение выражения 8,43: 3 равно 2,81

Деление десятичной дроби на десятичную дробь

Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.

Например, разделим 5,95 на 1,7

Запишем уголком данное выражение

Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:

После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:

Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?

Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9: 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.

Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:

(9 × 2 ) : (3 × 2 ) = 18: 6 = 3

Как видно из примера, частное не поменялось.

Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.

На самом деле внутри этого процесса происходило умножение на 10. Вот как это выглядело:

5,91 × 10 = 59,1

Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.

Деление десятичной дроби на 10, 100, 1000

Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и . Например, разделим 2,1 на 10. Решим этот пример уголком:

Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.

Решим предыдущий пример этим способом. 2,1: 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21

Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:

2,1: 100 = 0,021

Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:

2,1: 1000 = 0,0021

Деление десятичной дроби на 0,1, 0,01 и 0,001

Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и . В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.

Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.

После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:

Значит значение выражения 6,3: 0,1 равно 63

Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.

Решим предыдущий пример этим способом. 6,3: 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63

Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630

Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:

6,3: 0,001 = 6300

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

В этой статье мы рассмотрим такое действие, как умножение десятичных дробей. Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100 , 10 и др.)

В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.

Yandex.RTB R-A-339285-1

Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.

Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.

Посмотрим, как решаются такие задачи.

Пример 1

Вычислите произведение 1 , 5 и 0 , 75 .

Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0 , 75 – это 75 / 100 , а 1 , 5 – это 15 10 . Мы можем сократить дробь и произвести выделение целой части. Полученный результат 125 1000 мы запишем как 1 , 125 .

Ответ: 1 , 125 .

Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.

Пример 2

Умножьте одну периодическую дробь 0 , (3) на другую 2 , (36) .

Для начала приведем исходные дроби к обыкновенным. У нас получится:

0 , (3) = 0 , 3 + 0 , 03 + 0 , 003 + 0 , 003 + . . . = 0 , 3 1 — 0 , 1 = 0 , 3 9 = 3 9 = 1 3 2 , (36) = 2 + 0 , 36 + 0 , 0036 + . . . = 2 + 0 , 36 1 — 0 , 01 = 2 + 36 99 = 2 + 4 11 = 2 4 11 = 26 11

Следовательно, 0 , (3) · 2 , (36) = 1 3 · 26 11 = 26 33 .

Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:

Ответ: 0 , (3) · 2 , (36) = 0 , (78) .

Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.

Пример 3

Вычислите произведение 5 , 382 … и 0 , 2 .

Решение

У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5 , 382 … ≈ 5 , 38 . Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5 , 38 · 0 , 2 = 538 100 · 2 10 = 1 076 1000 = 1 , 076 .

Ответ: 5 , 382 … · 0 , 2 ≈ 1 , 076 .

Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:

Определение 1

Умножение десятичных дробей столбиком выполняется в 2 шага:

1. Выполняем умножение столбиком, не обращая внимание на запятые.

2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.

Разберем примеры таких расчетов на практике.

Пример 4

Умножьте десятичные дроби 63 , 37 и 0 , 12 столбиком.

Решение

Первым делом выполним умножение чисел, игнорируя десятичные запятые.

Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4 . Дописывать нули не придется, т.к. знаков достаточно:

Ответ: 3 , 37 · 0 , 12 = 7 , 6044 .

Пример 5

Подсчитайте, сколько будет 3 , 2601 умножить на 0 , 0254 .

Решение

Считаем без учета запятых. Получаем следующее число:

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:

Ответ: 3 , 2601 · 0 , 0254 = 0 , 08280654 .

Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д

Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:

Определение 2

Если мы умножим десятичную дробь на 0 , 1 , 0 , 01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.

Так, для умножения 45 , 34 на 0 , 1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4 , 534 .

Пример 6

Умножьте 9 , 4 на 0 , 0001 .

Решение

Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9 , 4 · 0 , 0001 = 0 , 00094 .

Ответ: 0 , 00094 .

Для бесконечных десятичных дробей мы пользуемся тем же правилом. Так, к примеру, 0 , (18) · 0 , 01 = 0 , 00 (18) или 94 , 938 … · 0 , 1 = 9 , 4938 … . и др.

Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.

Пример 7

Подсчитайте, сколько будет 15 · 2 , 27 .

Решение

Умножим столбиком исходные числа и отделим два знака запятой.

Ответ: 15 · 2 , 27 = 34 , 05 .

Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.

Пример 8

Вычислите произведение 0 , (42) и 22 .

Приведем периодическую дробь к виду обыкновенной.

0 , (42) = 0 , 42 + 0 , 0042 + 0 , 000042 + . . . = 0 , 42 1 — 0 , 01 = 0 , 42 0 , 99 = 42 99 = 14 33

0 , 42 · 22 = 14 33 · 22 = 14 · 22 3 = 28 3 = 9 1 3

Итоговый результат можем записать в виде периодической десятичной дроби как 9 , (3) .

Ответ: 0 , (42) · 22 = 9 , (3) .

Бесконечные дроби перед подсчетами надо предварительно округлить.

Пример 9

Вычислите, сколько будет 4 · 2 , 145 … .

Решение

Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:

4 · 2 , 145 … ≈ 4 · 2 , 15 = 8 , 60 .

Ответ: 4 · 2 , 145 … ≈ 8 , 60 .

Как умножить десятичную дробь на 1000, 100, 10 и др

Умножение десятичной дроби на 10 , 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:

Определение 3

Чтобы умножить десятичную дробь на 1000 , 100 , 10 и др., нужно перенести ее запятую на 3 , 2 , 1 цифры в зависимости от множителя и отбросить слева лишние нули. Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.

Покажем на примере, как именно это делать.

Пример 10

Выполните умножение 100 и 0 , 0783 .

Решение

Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007 , 83 ​​​​​Нули, стоящие слева, можно отбросить и записать результат как 7 , 38 .

Ответ: 0 , 0783 · 100 = 7 , 83 .

Пример 11

Умножьте 0 , 02 на 10 тысяч.

Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0 . В итоге получилось 0 , 02000 ,перенесем запятую и получим 00200 , 0 . Игнорируя нули слева, можем записать ответ как 200 .

Ответ: 0 , 02 · 10 000 = 200 .

Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.

Пример 12

Вычислите произведение 5 , 32 (672) на 1 000 .

Решение: первым делом мы запишем периодическую дробь как 5 , 32672672672 … , так вероятность ошибиться будет меньше. После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326 , 726726 … Заключим период в скобки и запишем ответ как 5 326 , (726) .

Ответ: 5 , 32 (672) · 1 000 = 5 326 , (726) .

Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.

Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.

Пример 13

Умножьте 0 , 4 на 3 5 6

Решение

​Cначала переведем десятичную дробь в обыкновенную. Имеем: 0 , 4 = 4 10 = 2 5 .

Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1 , 5 (3) .

Ответ: 1 , 5 (3) .

Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.

Пример 14

Вычислите произведение 3 , 5678 . . . · 2 3

Решение

Второй множитель мы можем представить как 2 3 = 0 , 6666 …. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3 , 568 и 0 , 667 . Посчитаем столбиком и получим ответ:

Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2 , 379856 ≈ 2 , 380 .

Ответ: 3 , 5678 . . . · 2 3 ≈ 2 , 380

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Как обычные числа.

2. Считаем число знаков после запятой у 1-ой десятичной дроби и у 2-ой. Их число складываем.

3. В итоговом результате отсчитываем справа налево такое число цифр, сколько получилось их в пункте выше, и ставим запятую.

Правила умножения десятичных дробей.

1. Умножить, не обращая внимания на запятую.

2. В произведении отделяем после запятой такое количество цифр, сколько их после запятых в обоих множителях вместе.

Умножая десятичную дробь на натуральное число, необходимо:

1. Умножить числа, не обращая внимания на запятую;

2. В результате ставим запятую так, чтобы справа от нее было столько цифр, сколько в десятичной дроби.

Умножение десятичных дробей столбиком.

Рассмотрим на примере:

Записываем десятичные дроби в столбик и умножаем их как натуральные числа , не обращая внимания на запятые. Т.е. 3,11 мы рассматриваем как 311, а 0,01 как 1.

Результатом является 311. Далее считаем число знаков (цифр) после запятой у обеих дробей. В 1-ой десятичной дроби 2 знака и во 2-рой — 2. Общее число цифр после запятых:

2 + 2 = 4

Отсчитываем справа налево четыре знака у результата. В итоговом результате цифр меньше, чем нужно отделить запятой. В этом случае необходимо слева дописать не хватающее количество нулей.

В нашем случае не достает 1-ой цифры, поэтому дописываем слева 1 ноль.

Обратите внимание:

Умножая любую десятичную дробь на 10, 100, 1000 и так далее, запятая в десятичной дроби переносится вправо на столько знаков, сколько нулей после единицы.

Например :

70,1 . 10 = 701

0,023 . 100 = 2,3

5,6 . 1 000 = 5 600

Обратите внимание:

Для умножения десятичной дроби на 0,1; 0,01; 0,001; и так далее, нужно в этой дроби перенести запятую влево на столько знаков, сколько нулей перед единицей.

Считаем и ноль целых!

Например:

12 . 0,1 = 1,2

0,05 . 0,1 = 0,005

1,256 . 0,01 = 0,012 56

Переходим к изучению следующего действия с десятичными дробями , сейчас мы всесторонне рассмотрим умножение десятичных дробей . Сначала обговорим общие принципы умножения десятичных дробей. После этого перейдем к умножению десятичной дроби на десятичную дробь, покажем, как выполняется умножение десятичных дробей столбиком, рассмотрим решения примеров. Дальше разберем умножение десятичных дробей на натуральные числа, в частности на 10, 100 и т.д. В заключение поговорим об умножении десятичных дробей на обыкновенные дроби и смешанные числа.

Сразу скажем, что в этой статье мы будем говорить лишь об умножении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях умножение рациональных чисел и умножение действительных чисел .

Навигация по странице.

Общие принципы умножения десятичных дробей

Обсудим общие принципы, которых следует придерживаться при проведении умножения с десятичными дробями.

Так как конечные десятичные дроби и бесконечные периодические дроби являются десятичной формой записи обыкновенных дробей, то умножение таких десятичных дробей по сути является умножением обыкновенных дробей . Иными словами, умножение конечных десятичных дробей , умножение конечной и периодической десятичных дробей , а также умножение периодических десятичных дробей сводится к умножению обыкновенных дробей после перевода десятичных дробей в обыкновенные .

Рассмотрим примеры применения озвученного принципа умножения десятичных дробей.

Пример.

Выполните умножение десятичных дробей 1,5 и 0,75 .

Решение.

Заменим умножаемые десятичные дроби соответствующими обыкновенными дробями. Так как 1,5=15/10 и 0,75=75/100 , то . Можно провести сокращение дроби , после чего выделить целую часть из неправильной дроби , а удобнее полученную обыкновенную дробь 1 125/1 000 записать в виде десятичной дроби 1,125 .

Ответ:

1,5·0,75=1,125 .

Следует отметить, что конечные десятичные дроби удобно умножать столбиком, об этом способе умножения десятичных дробей мы поговорим в .

Рассмотрим пример умножения периодических десятичных дробей.

Пример.

Вычислите произведение периодических десятичных дробей 0,(3) и 2,(36) .

Решение.

Выполним перевод периодических десятичных дробей в обыкновенные дроби:

Тогда . Можно полученную обыкновенную дробь перевести в десятичную дробь :

Ответ:

0,(3)·2,(36)=0,(78) .

Если среди умножаемых десятичных дробей присутствуют бесконечные непериодические, то все умножаемые дроби, в том числе конечные и периодические, следует округлить до некоторого разряда (смотрите округление чисел ), после чего выполнять умножение полученных после округления конечных десятичных дробей.

Пример.

Выполните умножение десятичных дробей 5,382… и 0,2 .

Решение.

Сначала округлим бесконечную непериодическую десятичную дробь, округление можно провести до сотых, имеем 5,382…≈5,38 . Конечную десятичную дробь 0,2 округлять до сотых нет необходимости. Таким образом, 5,382…·0,2≈5,38·0,2 . Осталось вычислить произведение конечных десятичных дробей: 5,38·0,2=538/100·2/10= 1 076/1 000=1,076 .

Ответ:

5,382…·0,2≈1,076 .

Умножение десятичных дробей столбиком

Умножение конечных десятичных дробей можно выполнять столбиком, аналогично умножению столбиком натуральных чисел .

Сформулируем правило умножения десятичных дробей столбиком . Чтобы умножить десятичные дроби столбиком, надо:

• не обращая внимания на запятые, выполнить умножение по всем правилам умножения столбиком натуральных чисел;
• в полученном числе отделить десятичной запятой столько цифр справа, сколько десятичных знаков в обоих множителях вместе, при этом если в произведении не хватает цифр, то слева нужно дописать нужное количество нулей.

Рассмотрим примеры умножения десятичных дробей столбиком.

Пример.

Выполните умножение десятичных дробей 63,37 и 0,12 .

Решение.

Проведем умножение десятичных дробей столбиком. Сначала умножаем числа, не обращая внимания на запятые:

Осталось в полученном произведении поставить запятую. Ей нужно отделить 4 цифры справа, так как в множителях в сумме четыре десятичных знака (два в дроби 3,37 и два в дроби 0,12 ). Цифр там хватает, поэтому нулей слева дописывать не придется. Закончим запись:

В итоге имеем 3,37·0,12=7,6044 .

Ответ:

3,37·0,12=7,6044 .

Пример.

Вычислите произведение десятичных дробей 3,2601 и 0,0254 .

Решение.

Выполнив умножение столбиком без учета запятых, получаем следующую картину:

Теперь в произведении нужно отделить запятой 8 цифр справа, так как общее количество десятичных знаков умножаемых дробей равно восьми. Но в произведении только 7 цифр, поэтому, нужно слева приписать столько нулей, чтобы можно было отделить запятой 8 цифр. В нашем случае нужно приписать два нуля:

На этом умножение десятичных дробей столбиком закончено.

Ответ:

3,2601·0,0254=0,08280654 .

Умножение десятичных дробей на 0,1, 0,01, и т.д.

Довольно часто приходится умножать десятичные дроби на 0,1 , 0,01 и так далее. Поэтому целесообразно сформулировать правило умножения десятичной дроби на эти числа, которое следует из рассмотренных выше принципов умножения десятичных дробей.

Итак, умножение данной десятичной дроби на 0,1 , 0,01 , 0,001 и так далее дает дробь, которая получается из исходной, если в ее записи перенести запятую влево на 1 , 2 , 3 и так далее цифр соответственно, при этом если не хватает цифр для переноса запятой, то нужно слева дописать необходимое количество нулей.

Например, чтобы умножить десятичную дробь 54,34 на 0,1 , надо в дроби 54,34 перенести запятую влево на 1 цифру, при этом получится дробь 5,434 , то есть, 54,34·0,1=5,434 . Приведем еще один пример. Умножим десятичную дробь 9,3 на 0,0001 . Для этого нам нужно в умножаемой десятичной дроби 9,3 перенести запятую на 4 цифры влево, но запись дроби 9,3 не содержит такого количества знаков. Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, имеем 9,3·0,0001=0,00093 .

Заметим, что озвученное правило умножения десятичной дроби на 0,1, 0,01, … справедливо и для бесконечных десятичных дробей. К примеру, 0,(18)·0,01=0,00(18) или 93,938…·0,1=9,3938… .

Умножение десятичной дроби на натуральное число

По своей сути умножение десятичных дробей на натуральные числа ничем не отличается от умножения десятичной дроби на десятичную дробь.

Конечную десятичную дробь умножать на натуральное число удобнее всего столбиком, при этом следует придерживаться правил умножения столбиком десятичных дробей, рассмотренных в одном из предыдущих пунктов.

Пример.

Вычислите произведение 15·2,27 .

Решение.

Проведем умножение натурального числа на десятичную дробь столбиком:

Ответ:

15·2,27=34,05 .

При умножении периодической десятичной дроби на натуральное число, периодическую дробь следует заменить обыкновенной дробью.

Пример.

Умножьте десятичную дробь 0,(42) на натуральное число 22 .

Решение.

Сначала переведем периодическую десятичную дробь в обыкновенную дробь:

Теперь выполним умножение: . Этот результат в виде десятичной дроби имеет вид 9,(3) .

Ответ:

0,(42)·22=9,(3) .

А при умножении бесконечной непериодической десятичной дроби на натуральное число нужно предварительно провести округление.

Пример.

Выполните умножение 4·2,145… .

Решение.

Округлив до сотых исходную бесконечную десятичную дробь, мы придем к умножению натурального числа и конечной десятичной дроби. Имеем 4·2,145…≈4·2,15=8,60 .

Ответ:

4·2,145…≈8,60 .

Умножение десятичной дроби на 10, 100, …

Довольно часто приходится умножать десятичные дроби на 10, 100, … Поэтому целесообразно подробно остановиться на этих случаях.

Озвучим правило умножения десятичной дроби на 10, 100, 1 000 и т.д. При умножении десятичной дроби на 10, 100, … в ее записи нужно перенести запятую вправо на 1, 2, 3, … цифры соответственно и отбросить лишние нули слева; если в записи умножаемой дроби не хватает цифр для переноса запятой, то нужно дописать необходимое количество нулей справа.

Пример.

Умножьте десятичную дробь 0,0783 на 100 .

Решение.

Перенесем в записи дроби 0,0783 на две цифры вправо, при этом получим 007,83 . Отбросив два нуля слева, получаем десятичную дробь 7,38 . Таким образом, 0,0783·100=7,83 .

Ответ:

0,0783·100=7,83 .

Пример.

Выполните умножение десятичной дроби 0,02 на 10 000 .

Решение.

Чтобы умножить 0,02 на 10 000 , нам нужно перенести запятую на 4 цифры вправо. Очевидно, в записи дроби 0,02 не хватает цифр для переноса запятой на 4 цифры, поэтому допишем несколько нулей справа, чтобы можно было осуществить перенос запятой. В нашем примере достаточно дописать три нуля, имеем 0,02000 . После переноса запятой получим запись 00200,0 . Отбросив нули слева, имеем число 200,0 , которое равно натуральному числу 200 , оно и является результатом умножения десятичной дроби 0,02 на 10 000 .

Умножение и деление в столбик: примеры

Математика сродни головоломкам. Особенно это касается деления и умножения в столбик. В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Советы тем, кто хочет хорошо знать математику

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

1. До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
2. Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
3. То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Алгоритм умножения в столбик десятичных дробей

Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.

Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.

Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:

• Записать эти дроби нужно так, чтобы число 33 было под 25.
• Теперь правую тройку нужно умножить на 25. Получится 75. Записать его полагается так, чтобы пятерка оказалась под тройкой, на которую выполнялось умножение.
• Потом умножать 25 на первую 3. Опять будет 75, но написано оно будет так, чтобы 5 оказалось под 7 предыдущего числа.
• После сложения этих двух чисел получается 825. В десятичных дробях запятыми отделены 4 цифры. Поэтому в ответе нужно отделить запятой тоже 4 цифры. Но их всего три. Для этого перед 8 придется написать 0, поставить запятую, перед ней еще один 0.
• Ответом в примере окажется число 0,0825.

С чего начать обучение делению?

До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.

После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?

После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.

Алгоритм деления чисел в столбик

Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:

• До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
• Записать делимое. Справа от него — делитель.
• Прочертить слева и снизу около последнего уголок.
• Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
• Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
• Записать результат от умножения этого числа на делитель.
• Написать его под неполным делимом. Выполнить вычитание.
• Снести к остатку первую цифру после той части, которая уже разделена.
• Снова подобрать число для ответа.
• Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере — 12082 : 863.

• Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
• После вычитания получается остаток 345.
• К нему нужно снести цифру 2.
• В числе 3452 четыре раза умещается 863.
• Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
• Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как быть, если делимое заканчивается на ноль?

Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.

Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения — 224, остаток — 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Если в примере разные дроби…

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

Умножение: по-японски, по-итальянски и методом майя

• Аналия Йоренте
• BBC Mundo

13 января 2018

Автор фото, Getty Images

Подпись к фото,

Не заболела бы голова…

«Математика такая трудная…» Вы наверняка не раз слышали эту фразу, а, может быть, даже сами ее произносили вслух.

Для многих математические вычисления — дело непростое, но вот вам три несложных способа, которые помогут выполнить хотя бы одно арифметическое действие — умножение. Без калькулятора.

Вполне вероятно, что в школе вы познакомились с наиболее традиционным способом умножения: сначала вы выучили на память таблицу умножения, а уж затем стали в столбик перемножать каждую из цифр, которыми записываются многозначные числа.

Если вам надо перемножить многозначные числа, то, чтобы найти ответ, потребуется большой лист бумаги.

Но если от этого длинного набора идущих одна под другой строчек с цифрами у вас голова идет кругом, то есть и другие, более наглядные методы, которые могут вам помочь в этом деле.

Но тут пригодятся некоторые художественные навыки.

Давайте порисуем!

Как минимум три способа умножения связаны с рисованием пересекающихся линий.

1. Способ индейцев майя, или японский метод

Относительно происхождения этого способа существует несколько версий.

Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер

Подпись к видео,

Трудно умножать в уме? Попробуйте метод майя и японцев

Некоторые говорят, что его придумали индейцы цивилизации майя, населявшие районы Центральной Америки до прибытия туда конкистадоров в XVI веке. Он также известен как японский метод умножения, поскольку учителя в Японии используют именно этот визуальный способ, когда учат младших школьников умножению.

Суть в том, что параллельные и перпендикулярные линии представляют цифры тех чисел, которые нужно перемножить.

Давайте умножим 23 на 41.

Для этого нам надо нарисовать две параллельные линии, представляющие 2, и, немного отступя, еще три линии, представляющие 3.

Затем, перпендикулярно к этим линиям мы нарисуем четыре параллельные линии, представляющие 4 и, чуть отступя, еще одну линию для 1.

Теперь нам надо пересчитать все точки пересечения этих линий. Именно так мы и получаем наш результат — 943, как если бы мы умножали в столбик.

Ну как, неужели трудно?

2. Индийский способ, или итальянское умножение «решеткой» — «джелозия»

Происхождение этого способа умножения тоже не ясно, однако он хорошо известен по всей Азии.

«Алгоритм «джелозия» передавался из Индии в Китай, затем в Аравию, а оттуда в Италию в XIV-XV веках, где он получил название «джелозия», поскольку внешне был похож на венецианские решетчатые ставни», — пишет Марио Роберто Каналес Виллануэва в своей книге, посвященной различным способам умножения.

Автор фото, Getty Images

Подпись к фото,

Индийская или итальянская система умножения похожа на венецианские жалюзи

Давайте снова возьмем пример с умножением 23 на 41.

Теперь нам потребуется начертить таблицу из четырех клеток — по клетке на цифру. Подпишем сверху у каждой клетки соответствующую цифру — 2,3,4,1.

Затем надо разделить каждую клетку надвое по диагонали, чтобы получились треугольники.

Теперь мы сначала умножим первые цифры каждого числа, то есть 2 на 4, и запишем в первом треугольнике 0, а во втором 8.

Потом перемножим 3×4 и запишем 1 в первом треугольнике, а 2 во втором.

Проделаем то же самое и с другими двумя цифрами.

Когда все клетки нашей таблицы будут заполнены, мы складываем цифры в такой последовательности, как показано на видео, и записываем получившийся результат.

Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер

Подпись к видео,

Трудно умножать в уме? Попробуйте индийский метод

Первая цифра у нас будет 0, вторая 9, третья 4, четвертая 3. Таким образом, результат получился: 943.

Как вам показалось, проще этот способ или нет?

Давайте попробуем еще один метод умножения с помощью рисунка.

3. «Массив», или метод таблицы

Как и в предыдущем случае, для этого потребуется нарисовать таблицу.

Возьмем тот же пример: 23 x 41.

Тут нам надо разделить наши числа на десятки и единицы, поэтому 23 мы запишем как 20 в одной колонке, и 3 в другой.

По вертикали мы запишем наверху 40, а внизу 1 .

Затем мы перемножим числа по горизонтали и вертикали.

Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер

Подпись к видео,

Трудно умножать в уме? Нарисуйте таблицу.

Но вместо того чтобы умножать 20 на 40, мы отбросим нули и просто перемножим 2 x 4, получив 8.

То же самое сделаем, умножая 3 на 40. Мы удерживаем в скобках 0 и умножаем 3 на 4 и получаем 12.

Проделаем то же самое с нижним рядом.

Теперь добавим нули: в левой верхней клетке у нас получилось 8, но мы отбросили два нуля — теперь мы их допишем и получится 800.

В правой верхней клетке, когда мы умножали 3 на 4(0), у нас получилось 12; теперь мы допишем ноль и получим 120.

Сделаем так же со всеми прочими удержанными нулями.

И наконец, мы складываем все четыре числа, полученных умножением в таблице.

Результат? 943. Ну как, помогло?

Важно разнообразие

Автор фото, Getty Images

Подпись к фото,

Все способы хороши, главное — чтобы ответ сошелся

Что точно можно утверждать, — так это то, что все эти разные способы дали нам один и тот же результат!

Нам все-таки пришлось кое-что перемножить в процессе, но каждый шаг был проще, чем при умножении традиционным способом, и гораздо более наглядный.

Так почему же мало где в мире в обычных школах учат этим методам вычисления?

Одной из причин может быть упор на обучение «вычислениям в уме» — чтобы развивать умственные способности.

Однако Дэвид Уиз, учитель математики из Канады, работающий в государственных школах в Нью-Йорке, объясняет это иначе.

«Недавно я прочитал, что причина, по которой используется традиционный метод умножения, — это экономия бумаги и чернил. Этот метод не был придуман как самый простой для использования, но как самый экономный с точки зрения ресурсов, поскольку чернила и бумага были в дефиците», — объясняет Уиз.

Автор фото, Getty Images

Подпись к фото,

Для некоторых методов вычисления только головы недостаточно, нужны еще и фломастеры

Невзирая на это, он полагает, что альтернативные методы умножения очень полезны.

«Я не думаю, что это полезно — сразу учить школьников умножению, заставляя их выучивать таблицу умножения, но не объясняя им при этом, откуда она взялась. Поскольку если они забудут одно число, то как они смогут продвинуться в решении задачи? Метод майя или японский метод необходим, потому что с его помощью вы можете понять общую структуру умножения, а это хорошее начало», — полагает Уиз.

Существует и ряд других способов умножения, например, русский или египетский, они не требуют дополнительных навыков рисования.

Как говорят специалисты, с которыми мы беседовали, все эти методы помогают лучше понять процесс умножения.

«Понятно, что все идет на пользу. Математика в сегодняшнем мире открыта как внутри, так и снаружи классной комнаты», — резюмирует Андреа Васкес, учительница математики из Аргентины.

Конспект урока по математике «Умножение двузначного числа на однозначное в столбик» 3 класс

Какой следующий шаг урока?

-№2 с 36 решение у доски с проговариванием вслух

1)учитель 56х7

По аналогии с комментированием примеров на сложение, решение

примеров на умножение в столбик можно прокомментировать так:

Умножаю единицы: 6х7=42 (ед.). 2 единиц пишу под единицами, а 4

десятка запоминаю.

Умножаю десятки: 5х7=35 (дес.), добавляю 4десятка: 35+4=39.

Пишу 9 в разряде десятков, а 3 – в разряде сотен.

Ответ: 392

2) ученик у доски

3,4) в парах

-Запишите ответы, комментируя решение в парах: один пример

объясняет ученик первого варианта, ответ записывают оба в тетрадь

на печатной основе. Затем дети меняются ролями).

-Проверим, проговаривая (Образец) Чья пара справилась?

-Готовы работать самостоятельно? Следующий шаг. Ещё раз

проговорим алгоритм умножения двузначного числа на однозначное .

-Рабочая тетрадь – урок 13 №3 (3 примера)

-Выберите любые 3 примера и запишите решение столбиком в

тетрадях. Вы можете пользоваться опорной схемой и алгоритмом.(на

партах)Даю 2 минуты.

-Проверим ответы по образцу.

-Поднимите руку, у кого были ошибки в работе? Какие?

-О чём говорят ваши ошибки?

-Оценим свои результаты при помощи сигнальных карточек. (Если у

вас остались недоработки, поставьте знак «?», а если ошибок не было

– «+»).

-Мы использовали запись умножения двузначного числа на

однозначное столбиком при решении примеров. А в каких еще

случаях можно применить эту форму записи?

-Решим задачу №9(а)

-Прочитаем условие задачи.

-Что известно?

«Тренировка в решении примеров на умножение

двузначного числа на однозначное в «столбик»»

Решают уравнения

«Самостоятельная работа»

Решают самостоятельно, проверяют по образцу

на доске.

Возникли трудности в записи столбиком,

Вычислительные ошибки.

Необходимо повторить таблицу умножения;

учитывать разрядные единицы, которые

запоминали при умножении; быть

внимательным при сложении и т.д.)

Оценивают результат при помощи сигнальных

карточек.

При решении уравнений и задач.

Известно, что 15 кг винограда разложили в 3

ящика.

Калькулятор онлайн примеры в столбик по действиям. Как научиться делить столбиком: примеры и решения

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:

В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.

К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:

Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:

1340: 23 = 58 (остаток 6)

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:

3: 10 = 0 (остаток 3)

Калькулятор деления столбиком

Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения.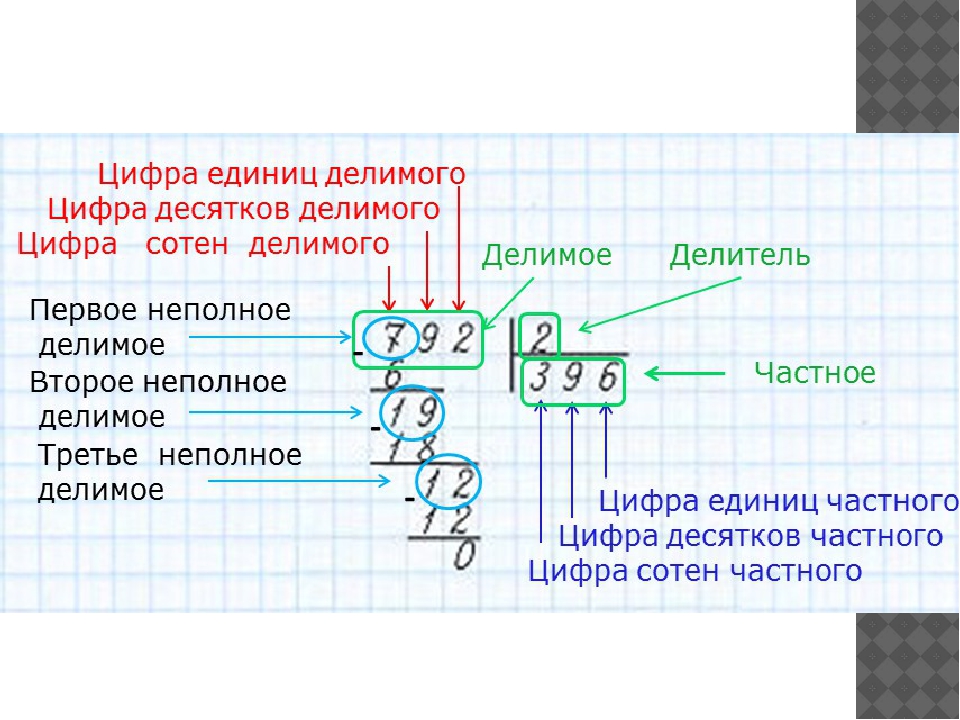 Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

1. До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
2. Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
3. То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Алгоритм умножения в столбик десятичных дробей

Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.

Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.

Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:

С чего начать обучение делению?

До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.

После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?

После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.

Алгоритм деления чисел в столбик

Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:

• До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
• Записать делимое. Справа от него — делитель.
• Прочертить слева и снизу около последнего уголок.
• Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
• Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
• Записать результат от умножения этого числа на делитель.
• Написать его под неполным делимом. Выполнить вычитание.
• Снести к остатку первую цифру после той части, которая уже разделена.
• Снова подобрать число для ответа.
• Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере — 12082: 863.

• Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
• После вычитания получается остаток 345.
• К нему нужно снести цифру 2.
• В числе 3452 четыре раза умещается 863.
• Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
• Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как быть, если делимое заканчивается на ноль?

Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.

Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения — 224, остаток — 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Если в примере разные дроби…

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.

Особенности

Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .

Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:

1. Цифры.
2. Знаки арифметических действий.
3. Удаление раннее введенных символов.

Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.

Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:

• умножение;
• деление;
• сложение;
• вычитание.

Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.

Достоинства и недостатки

1. Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
2. Очень простой, интуитивно понятный интерфейс для каждого пользователя.
3. Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
4. Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.

Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.

Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.

Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.

Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).

Из этой статьи вы узнаете

Принцип деления для малышей

Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.

Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.

Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.

Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.

Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.

Как обучить малыша делению в столбик

Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.

Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.

Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.

При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.

Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.

Умножаем и делим с помощью таблицы

При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.

И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.

Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.

Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.

Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.

В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.

Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.

Делим с помощью столбика

Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.

Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.

В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.

Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.

Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.

Чтобы было проще обучить малыша процессу деления необходимо:

• в 2-3 года понимание отношения целое-часть.
• в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.

Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.

Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.

Математический калькулятор. Подробный онлайн калькулятор всех математических операции.

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

С ← ( ) ±

7 8 9 ÷ %

4 5 6 х √

1 2 3 — x²

0 . = + ¹/_x

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1/x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Пример:

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Пример:

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Пример:

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Пример:

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Пример:

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Пример:

Возведение в квадрат целого числа { (3) ² = 9 }

Возведение в квадрат десятичных дробей { (2,2) ² = 4,84 }

Перевод в десятичные дроби.

Пример:

{ 1/3 = 0,33 }

{ ½ = 0,5 }

Вычисление процентов от числа

Пример:

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Умножение по-китайски

Что приходит в голову многим из вас при выражении «зазубрить»? Наверняка большинство вспомнит таблицу умножения. Мы запоминаем её как стихотворение и каждый раз произносим про себя левую часть выражения, чтобы вспомнить правую. Но даже прекрасное знание этой таблицы не облегчает трудную для многих операцию умножения. А вот, например, в Японии и Китае ученики первого класса могут перемножать двухзначные и даже трёхзначные числа, не зная таблицу умножения.

Эта статья была опубликована в журнале OYLA №9. Оформить подписку на печатную и онлайн-версию можно здесь.

Как же они это делают? Возможно, это связано с тем, что японцы и китайцы используют иероглифы.

Один иероглиф может нести в себе смысл, который на нашем языке мог быть записан целым абзацем. И может быть поэтому восточным народам легче воспринимать мир через призму «картинок»-иероглифов, то есть визуально.

Приведём пример. Вы, читая эти строки, сначала видите отдельные буквы, далее складываете их в слова, а уж потом слова соединяете в предложения. Затем, читая предложения одно за другим, вы начинаете понимать смысл рассказа. У загадочных японцев и китайцев все совсем иначе. Иероглифы у них обозначают сразу какое-то слово, а порой и целую фразу. То есть, можно сказать, что они не читают рассказ, а видят его. Так же самое верно и для чисел.Попробуйте умножить, например, 54 на 96, используя японские иероглифы. Страшно представить, что у вас из этого получится. Ведь наверняка единственным способом, которым вы умете умножать, будет «в столбик».

Однако в Японии и Китае принято умножать иначе. Для оригинальных китайцев и японцев наш метод умножения в столбик очень неудобен и непривычен, как и наше чтение по буквам. Им опять нужна визуализация, проще говоря — картинка. Таким образом, японский и китайский способ умножения чисел также необычен, как и чтение. Давайте рассмотрим его.

Умножение — объяснения и примеры

Что такое умножение?

Умножение — это математическая операция по нахождению результата двух или более чисел путем повторного сложения чисел.

Умножение обычно обозначается крестиком (x). Однако также используются другие символы, такие как звездочка (*), точка (.) И фраза «время».

Части умножения

Предложение умножения состоит из двух частей: математического выражения и произведения.Математическое выражение состоит из множителей и оператора или символа умножения.

Например, , в математическом выражении: 5 x 2 = 10, часть «2 x 5» представляет собой математическое выражение, состоящее из 2 и 5 как факторов и операторов. В данном случае произведение равно 10.

Мы можем далее разбить множители на множимое и множимое:

• Множаемое — это число, умноженное на другое число.
• Множитель — это число, на которое нужно умножить.
• Произведение является результатом умножения.

Свойства умножения

Изучение свойств умножения помогает упростить и решить математические задачи, связанные с умножением.

В умножении свойство коммутативности подразумевает, что умножение двух или более чисел не влияет на окончательный ответ. В общем, для предложения умножения: m x n = n x m. Например, 4 x 5 — это то же самое, что 5 x 4. Это свойство также применяется при умножении большой группы чисел.Например, 4 x 3 x 2 = 2 x 3 x 4.

При умножении ассоциативное свойство утверждает, что группировка чисел не влияет на окончательный ответ при умножении ряда чисел вместе. Обычно группировки в любом математическом выражении обозначаются круглыми или квадратными скобками. Мы можем суммировать это свойство как: m x (n x p) = (m x n) x p. Например, (2 x 4) x 6 = 2 x (4 x 6).

Это свойство указывает, что умножение любого числа на единицу не меняет его значения.Другими словами, это свойство можно записать как 1 x a = a. Например, 1 x 8 = 8.

Свойство распределения для умножения утверждает, что выражение, состоящее из сложения или вычитания значений, умноженных на число, эквивалентно сумме или разности чисел выражений.

В общем случае m x (n + p) = m x n + m x p, а m x (n — p) = m x n — m x p. Например, 2 x (3 + 4) = 2 x 3 + 2 x 4.

Таблица умножения

Массив — это сетка / диаграмма умножения, состоящая из чисел в строках и столбцах.Умножение с использованием таблицы умножения проще, потому что произведение двух чисел находится путем подсчета количества строк и умножения на соответствующее количество столбцов.

Например, , в захвате, состоящем из 9 в столбце и 6 в строке, продукт в сетке равен 54.

9 0062 7

x	1	2	3	4	5	6	7	8	9	10	0 12
1	1	2	3	4	5	6	7	8	9	10	11	12
2	2	4	6	8	10	12	14	16	18	20	22	24
3	3	6	9	12	15	18	21	24	27	30	33	36
4	4	8	12	16	20	24	28	32	36	40	44	48
5	5	10	15	20	25	30	35	40	45	50	55	60
6	6	12	18	24	30	36	42	48	54	60	66	72
7	14	21	28	35	42	49	56	63	70	77	84
8	8	16	24	32	40	48	56	64	72	80	88	96
9	9	18	27	36	45	54	63	72	81	90	99	108
10	10	20	30	40	50	60	70	80	90	100	110	120
11	11	22	33	44 9 0065	55	66	77	88	99	110	121	132
12	12	24	36	48	60	72	84	96	108	120	132	144

Как создавать предложения умножения?

Умение составлять предложения умножения — важный навык для учащихся, поскольку он подготавливает их к практическому использованию математики.Учащийся, который знает, как составлять свои собственные предложения умножения, может взглянуть на сетку чисел четыре на четыре и обязательно скажет, что сетка состоит из 16 элементов.

Как составить предложение из слова Задача

Создание предложений умножения, кажется, сбивает студентов с толку. Однако после прочтения и понимания этой статьи ученикам будет легче решать задачи со словами.

Например, предположим, что Мэри собрала корзину апельсинов, если у нее достаточно апельсинов, чтобы разместить 15 апельсинов в 3 ряда.Сколько апельсинов она собрала? В этом примере предложение умножения можно записать как 15 x 3 = 45. Таким образом, Мэри собрала 45 апельсинов.

Практические вопросы

1. Файл состоит из 4 папок, каждая из которых содержит 56 листов бумаги. Подсчитать общее количество листов в файле?
2. В коробке с печеньем 24 пакета, а в каждой пачке 12 печенья? Посчитать общее количество печенья, которое можно упаковать в 45 картонных коробок?
3. Стоимость учебника 67 долларов.Посчитать стоимость таких 102 учебников?
4. Мужчина получает 2625 долларов в месяц. Сколько он зарабатывает в год?
5. Стоимость стула и стола составляет 452 и 1750 долларов соответственно. Посчитать общую стоимость 15 стульев и 30 столов?

Ответы

1. 1. 1344 листа.
   2. 12 960 печенья.
   3. $ 6834
   4. $ 31 500
   5. $ 59280

Предыдущий урок | Главная страница | Следующий урок

Умножение × | Основы арифметики

На этой странице описаны основы умножения (×) .

См. Другие наши арифметические страницы для обсуждения и примеров: Сложение (+), Вычитание (-) и Деление ( ÷ ).

Умножение

При записи общий знак умножения — « × ». В электронных таблицах и некоторых других компьютерных приложениях символ « * » (или звездочка) используется для обозначения операции умножения.

Чтобы выполнять вычисления умножения без калькулятора или электронной таблицы, вам необходимо знать, как складывать числа.См. Нашу страницу добавления, чтобы узнать, как добавить.

Когда вы «умножаете» или «умножаете» число, вы добавляете его к самому себе несколько раз, например, умножение 4 на 3 — это то же самое, что сказать 4 + 4 + 4 = 12. Следовательно, умножение — это более быстрый способ сложения одно и то же число много раз, например 3 × 4 = 12. Этот расчет аналогичен выражению, если у меня есть 3 пакета по 4 яблока, сколько всего яблок у меня есть?

Основные правила умножения:

---

• Любое число, умноженное на 0, равно 0.200 × 0 = 0
• Любое число, умноженное на 1, остается неизменным. 200 × 1 = 200.
• Когда число умножается на два, мы удваиваем число. 200 × 2 = 400.
• Когда целое число умножается на 10, мы можем просто написать 0 в конце (один ноль из 10, потому что это 1 × 10). 200 × 10 = 2000.
• При умножении на 100 мы записываем два нуля в конце, на тысячу записываем три нуля в конце и так далее. Например, 4 × 2000 — это 4 × 2 = 8 с 3 нулями: 8000.

Для простого и быстрого умножения полезно запомнить умножение или «таблицу умножения », как показано ниже. Эта таблица дает ответы на все умножения до 10 × 10. Чтобы получить ответ на 4 × 6, например, найдите 4 в верхней (заштрихованной красным) строке и найдите 6 в левом (заштрихованном красным) столбце — столбец точка пересечения двух линий и есть ответ: 24 .

Неважно, с какой стороны искать числа; если вы найдете 4 в первом столбце и 6 в первой строке, вы получите тот же ответ, 24.

Таблица умножения

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Приведенная выше таблица может помочь нам быстро вычислить ответ на следующую проблему.Меган ведет трех братьев в кинотеатр, ей нужно купить всего 4 билета, каждый из которых стоит 8 фунтов стерлингов. Во сколько обойдется поездка? Нам нужно вычислить 4 лота по 8 фунтов стерлингов, что написано 4 × 8.

Найдите 4 в вертикальном красном столбце и 8 в горизонтальном красном столбце, ответ находится в ячейке, где пересекаются две линии: 32 . Стоимость похода в кинотеатр составит 32 фунтов стерлингов.

Часто необходимо умножать числа больше 10.В этом случае приведенная выше таблица умножения не может дать немедленного ответа. Однако мы все еще можем использовать его, чтобы упростить расчет.

Лиза занимается ресторанным бизнесом. Она должна доставить бутерброды 23 предприятиям, в каждом из которых работает 14 сотрудников. Если предположить, что каждый сотрудник съедает один бутерброд, сколько бутербродов нужно приготовить Лизе?

23 предприятиям нужно 14 бутербродов, что составляет 23 лота по 14 или, другими словами, 23, умноженные на 14. Как мы уже обнаружили, мы можем записать расчет наоборот.14 × 23. Ответ будет таким же.

Нам нужно найти ответ на расчет 23 × 14.

Сначала запишите свои числа в столбцы, представляющие сотни, десятки и единицы (за помощью см. Нашу страницу чисел ).

Сот	Десятки	Квартир
	2	3
	1	4

Шаг 1: Начиная с правого столбца (единицы), умножьте 4 на 3.При необходимости вы можете обратиться к приведенной выше таблице умножения. Напишите ответ (12) под своим вычислением, стараясь поставить 1 в столбце десятков и 2 в столбце единиц.

Синие числа — это те, над которыми мы сейчас работаем, а розовые числа — это первая часть нашего ответа.

Сот	Десятки	Квартир
	2	3
	1	4
	1	2

Шаг 2: Затем мы умножаем 4 на следующее число, равное 2 (или 20, потому что оно находится в столбце десятков).Напишите свой ответ внизу в столбце десятков: мы пишем 8 в столбце десятков (4 раза по 2 десятка) и ноль в столбце единиц (4 раза по 2 десятка это то же самое, что 4 × 20 = 80).

Сот	Десятки	Квартир
	2	3
	1	4
	1	2
	8	0

Шаг 3: В приведенных выше шагах мы умножили единицы нижнего числа (4) на верхнее число (23).Затем нам нужно умножить десятки в нижнем числе (1) на верхнее число (23). Теперь мы работаем с цифрой в столбце десятков нижнего числа и повторяем шаги, описанные выше. Оглядываясь на наши основные правила умножения, приведенные выше, мы знаем, что, умножая число на 10, мы пишем ноль в конце. На этом этапе, поскольку мы переместились по столбцу и работаем с десятками, мы должны не забыть записать нули в первый столбец (единицы).

Выполните 1 × 3. Как и выше, мы записываем наш ответ (3) в столбец десятков и (0) в столбец единиц.

Сот	Десятки	Квартир
	2	3
	1	4
	1	2
	8	0
	3	0

Шаг 4: Последнее умножение, которое нам нужно выполнить, — 1 × 2.Оба числа находятся в столбце десятков, поэтому мы умножаем один лот из 10 на два лота по 10. Используя правила, которые мы узнали на предыдущих шагах, нам нужно записать ноль в столбец единиц и ноль в столбец десятков. Наш ответ (1 × 2 = 2) записан в столбце сотен, потому что мы фактически вычислили 10 × 20 = 200.

Сот	Десятки	Квартир
	2	3
	1	4
	1	2
	8	0
	3	0
2	0	0

Этап 5: На этом этапе мы закончили умножение; остается только сложить все наши ответы (розовые числа), чтобы найти общее количество необходимых бутербродов.См. Нашу страницу Дополнение , если вам нужна помощь с суммированием чисел.

	Сот	Десятки	Квартир
		2	3
		1	4
		1	2
		8	0
		3	0
	2	0	0
Всего:	3	2	2

12 + 80 + 30 + 200 = 322. Мы подсчитали, что Лизе нужно сделать в общей сложности 322 бутербродов.

В приведенном выше примере показано, как выполнить умножение, разделенное на все возможные части, но по мере повышения уверенности можно пропустить шаги.

Мы могли бы, например, умножить 4 на 23, разбив сумму на две части:

4 × 20 = 80
4 × 3 = 12
80 + 12 = 92

Сот	Десятки	Квартир
	2	3
	1	4
	9	2

То же для второго столбца:

10 × 23 = 230

Сот	Десятки	Квартир
	2	3
	1	4
	9	2
2	3	0

Наконец, мы складываем два наших ответа:

	Сот	Десятки	Квартир
		2	3
		1	4
		9	2
	2	3	0
Всего:	3	2	2

92 + 230 = 322.

---

Умножение более двух чисел

Если вам нужно перемножить более двух элементов, обычно проще перемножить первые два элемента, получить результат, а затем умножить следующее число на первое число. Например, если Джо хотел вычислить, сколько часов он проработал за четырехнедельный период, то расчет выглядел бы так:

Джо работает 7 часов в день 5 дней в неделю в течение четырех недель.

Шаг первый:

7 × 5 = 35 (количество часов, которые Джо работает в неделю).

Шаг второй:

Чтобы узнать, сколько часов Джо работает за четыре недели, мы можем затем умножить этот ответ (35) на 4. 35 × 4 = 140.

Если мы знаем, что Джо платят 12 фунтов в час, мы можем затем подсчитать, сколько денег он заработал за четырехнедельный период: 12 × 140.

Быстрый способ решить это — вычислить:
10 × 140 = 1400 (помните, что если мы умножаем на 10, мы просто добавляем ноль в конец числа, на которое умножаем).
2 × 140 = 280 то же, что 2 × 14 (с нулем на конце) или 140 + 140.

Мы складываем наши ответы вместе: 1400 + 280 = 1680.
Таким образом, Джо заработал 1 680 фунтов стерлингов за четыре недели.

Умножение отрицательных чисел

---

Умножение отрицательного числа на положительное всегда дает отрицательный ответ:

15 × (−4) = −60

Умножение отрицательного числа на другое отрицательное число всегда дает положительный ответ:

(−15) × (−4) = 60

---

Как научить этому шаг за шагом

Метод длинного умножения может быть очень трудным в обучении в 5 и 6 классах, что знает любой, кто раньше преподавал верхний KS2.

Несмотря на самые лучшие намерения, всегда найдутся ученики, которые либо не уверены в более простом подходе 4 на 1 цифру, либо не уверены в своих таблицах умножения.

Если этот учебный год будет вашим первым в шестом классе, у вас есть все, чего стоит ожидать, но не отчаивайтесь — это происходит каждый год.

Что такое длинное умножение?

Длинное умножение — это процесс умножения двух- или трехзначных чисел на другое число , состоящее из двух или более цифр, с использованием письменного метода.Это часто называют умножением по столбцам

В 5-м и 6-м классе начальной школы длинное умножение означает умножение числа, состоящего как минимум из трех цифр, на одно, состоящее из двух или более цифр.

Прежде чем приступить к длинному умножению на KS2, дети в идеале должны быть уверены в своей таблице умножения и понимать ключевые термины, такие как множимое и множитель.

• Множитель — это число, с которого вы начинаете умножение.
• Множитель — это то, сколько групп из них вам нужно; сколько раз вы собираетесь умножить множимое на.

Долгое умножение в национальной учебной программе

В Национальной учебной программе по математике для Англии формальный метод длинного умножения упоминается как для 5-го, так и для 6-го года обучения

• В целях умножения и деления 5-го года указано, что «учеников следует научить умножать числа до 4-х цифр на одно- или двузначные числа, используя формальный письменный метод, включая долгое умножение двузначных чисел».

• В этом году 6 целей по умножению и деление говорит, что учеников должны умножать многозначные числа до 4 цифр на двузначное целое число, используя формальный письменный метод длинного умножения.’

Приложение к групповым целям на конец года дает нам представление о том, как это выглядит:

Это красиво излагает модель прогресса для учителей после того, как класс будет комфортно умножать 3- или 4-значные числа на однозначное число.

Длинные вопросы на умножение в SAT

Быстрый просмотр арифметической работы SAT 2019 показывает, что есть 4 оценки, которые можно взять за правильные ответы на длинные вопросы умножения, а также множество примеров учеников, которым необходимо выбрать этот метод в двух листах рассуждения поскольку это был бы наиболее эффективный по времени метод выбора, чтобы пройти через бумагу.

Поэтому очень важно, чтобы ученики свободно владели этим методом. Когда я говорю «беглый», я имею в виду:

«Беглость — это процесс извлечения информации из долговременной памяти без каких-либо усилий в нашей рабочей памяти, освобождение ценного места в нашей рабочей памяти, чтобы уделять внимание другим вещам. . ‘

Подробнее: Свободное владение, рассуждение и решение проблем

Что такое метод длинного умножения?

Формальный метод длинного умножения — это пошаговый метод, помогающий детям понять концептуально и практически, как умножить одно трех- или четырехзначное число на другое двухзначное или большее число.

Метод длинного умножения, шаг за шагом

Вот метод длинного умножения, разбитый шаг за шагом с использованием второго примера из Приложения к национальной учебной программе

Как сделать длинное умножение шаг за шагом

Пример: 124 x 26

1. Задайте вопрос формальным методом
2. Не забудьте начать процесс умножения с единиц
3. Умножьте 6 на 4
4. Запишите ответ правильно — включая любые несущие
5. Умножьте 6 на 2
6. Добавьте все, что у вас есть перенесено из предыдущего умножения.
7. Умножить 6 на 2
8. Запишите ответ правильно
9. Отбросьте ноль, так как мы теперь умножаем на 10
10. Умножаем 2 на 4
11. Запишите ответ правильно
12. Умножьте 2 на 2
13. Запишите ответ
14. Умножьте 2 на 1
15. Напишите ответ правильно
16. Сложите два ответа правильно

Это в общей сложности 16 шагов, которые детям необходимо освоить, изучая этот новый процесс, чтобы прийти к окончательному ответу.Принимая во внимание ограничения нашей рабочей памяти, это требует больших усилий, и они могут довольно легко перегрузить ее и предотвратить кодирование этой информации.

Итак, ответ на вопрос: как сделать длинное умножение? просто следуйте инструкциям!

Но здесь упускается важный этап обучения — переход от процедурного к концептуальному пониманию происходящего.

Остальная часть этой статьи объясняет, как научить долгому умножению иметь наибольшее влияние на ваш класс.Он включает ссылки на длинные таблицы умножения, чтобы дать вам много практики.

Как когнитивная наука повлияла на мое учение о длинном умножении

Два урока когнитивной науки сильно изменили мой подход к обучению методу длинного умножения.

1.

Долговременная и краткосрочная память

Первым было понимание того, что у нас есть долговременная память, которая почти безгранична в информации, которую она может хранить; и рабочая память, где мы делаем наши сознательные мысли.

Важно отметить, что пространство в нашей рабочей памяти ограничено, многие исследователи полагают, что оно составляет от 4 до 7 элементов. Оливер Кавилиоли любезно нарисовал замечательный плакат, демонстрирующий этот процесс.

Из https://www.olicav.com/#/diagrams/

Из модели мы видим, что человек использует свое внимание, чтобы переносить вещи из окружающей среды в рабочую память. Затем мы пытаемся закодировать эту информацию в нашей долговременной памяти, но некоторая информация может быть забыта по множеству причин.

Когда эта информация находится в нашей долговременной памяти, мы можем вернуть ее на передний план нашей рабочей памяти, чтобы использовать ее. Однако, если эти воспоминания остаются бездействующими слишком долго (то есть мы не вспоминаем эти воспоминания в течение длительного периода времени), они тоже могут быть забыты.

Подробнее: Обучение и память в классе

2. Теория когнитивной нагрузки

Еще один урок когнитивной науки, который повлиял на мое обучение, касался теории когнитивной нагрузки.Теория когнитивной нагрузки пытается объяснить, почему мы не можем закодировать новую информацию из нашей рабочей памяти в нашу долговременную память.

Это могло быть вызвано многими причинами, такими как: слишком сложная работа; покрывается слишком быстро; слишком много отвлекающих факторов в окружении; не имея предварительных знаний по теме (мы вернемся к этому позже) и т. д.

Как это помогает нам обучать методу длинного умножения? Что ж, давайте сначала проясним кое-что.

Мой результат на первом или втором уроке — дать моим ученикам уверенность в том, что они изучат метод.Только после этого мы перейдем к остальным

Как обучить методу длинного умножения

Основные знания об умножении предшественников

Перед тем, как мы начнем работать над долгим умножением, я всегда проверю, какие члены моего класса уже боролись с умножением на третьем году обучения. или 4.

Если ребенок не уверен в своих фактах умножения, вам необходимо организовать вмешательство, чтобы ускорить его — вопреки мнению, изучение фактов умножения важно, и хотя вы можете научить таблицу умножения на мгновение Вспомните, в более раннем возрасте, верхним KS2 очень сложно найти время.

Вам также могут понравиться: 35-кратные настольные игры, подходящие для дома и в школе — выбирайте одну или две в неделю для домашнего обучения, если вашим ученикам все еще нужно формировать последовательность.

Как упростить длинное умножение

Я определенно убедился в том, что ученики, которые знают свое слово, свободно владеют умножением с 3 или 4 на 1 цифру, и им легче работать с этими большими числами.

Это имеет смысл, поскольку, если они свободно владеют этими областями, они эффективно сокращают объем работы своей рабочей памяти.Предполагая, что они свободно владеют этими двумя вещами, то, что им нужно выучить, сокращается с 16 до 4-6 вещей.

Ребенок, который не уверен в умножении, вероятно, будет использовать так много своей рабочей памяти для решения части вопроса, связанной с умножением, что все остальные шаги, как мы видели в модели ранее, будут забыты.

Это важный момент, который учителя должны осознать: дело не в том, что один ребенок имеет врожденную способность выполнять долгое умножение, а один — нет. Дело в том, что один ребенок просто сохранил важные знания, необходимые для достижения успеха, и поэтому может установить связь с предыдущими знаниями, чтобы резко сократить то, что ему нужно для активной работы.

Как сказал Осубель: «Самый важный фактор, влияющий на обучение, — это то, что ученик уже знает. Убедитесь в этом и обучите их соответствующим образом »

KS2 Рабочие листы для длинного умножения

Дайте вашим ученикам фору в практике их навыков длительного умножения с помощью этого бесплатного пакета рабочих листов для умножения.

Метод длинного умножения: Урок 1

Независимо от того, с чего ученики исходят, в классе есть вещи, которые мы можем сделать, чтобы помочь им освоить процедуру длинного умножения.Как я уже упоминал ранее, моя цель на первых уроках — укрепить уверенность в методе.

Для этого я гарантирую, что наш первый множитель равен 11. Сделав второй множитель равным 11, все, что здесь требуется, — это умножить на единицу. Мне еще предстоит встретить ребенка, который может бороться с умножением и не знает таблицу умножения на 1.

Это значительно снижает когнитивную нагрузку и помогает высвободить всю рабочую память для изучения процедуры длительного умножения.Конечно, этим ученикам все равно придется усвоить факты умножения, но это просто помогает сломать эти барьеры и помогает им добиться успеха.

Внезапно процедура выглядит так:

Пошаговый процесс решения проблемы такой же, как в примере выше, но мы значительно снизили нагрузку на рабочую память.

Это увеличивает вероятность того, что процедуру запомнят, поскольку ученики могут сосредоточить все свое внимание на понимании процедуры, а не на умножении.Опять же, я хотел бы подчеркнуть, что цель этого состоит в том, чтобы ученики могли освоить процедуру, чтобы ее можно было усвоить.

Шаг 1 — Установление предварительных знаний об умножении

Чтобы начать урок, у меня на доске было несколько вопросов 4 на 1 цифру, чтобы класс мог пройти их самостоятельно, убедившись, что я дойду до всех учеников, которые Я считаю, что можно бороться с этим и выяснить, с чем они борются — это умножение или процедура? Если бы это было первое, я бы помог им с их таблицами умножения, а если бы второе, я бы провел с ними пример.

Пример серии вопросов умножения 4 × 1 из онлайн-класса Third Space Learning.

По прошествии достаточного времени я просматривал вопросы на доске, чтобы проверить понимание процедуры и их знание «умножения»:

• Что такое множимое и множитель? (т.е. «верхнее число» и «нижнее число»)
• Как мне записать это в метод столбца?
• Каков результат умножения ___ на ____?
• Что произойдет, если произведение больше одной цифры?
• С какого разряда мне начать умножение?

Ответы учеников на эти вопросы помогут спланировать будущие мероприятия.По моему опыту, я не встречал многих учеников, чьи предварительные достижения означают, что они не могут правильно изложить метод умножения по столбцам.

Если вам действительно нужно проследить путь назад, чтобы создать более прочную основу для умножения, тогда есть учебный лагерь для 5-го и 6-го классов умножения или более подробное руководство по обучению умножению для каждой годовой группы на протяжении KS2. Если родители хотят поддержать своих детей умножением, тогда в этой статье дается простое резюме: Что такое долгое умножение?

Шаг 2 — Знакомство с новой идеей длинного умножения

В этой следующей части урока я бы показал пример типа вопроса, на который они должны будут ответить к концу урока — в данном случае это будет умножение 4 на 2 цифры на любую цифру с использованием метода длинного умножения.

Я бы очень быстро попросил их потратить 30 секунд на обсуждение друг с другом, чтобы увидеть, чем отличается этот вопрос от того, который они задали в начале урока.

Как только они поймут, что в качестве множителя используется двузначное число, я решал это молча в нормальном темпе — причина этого в том, чтобы показать, насколько легко это может быть, и вселить в них уверенность в том, что с ними не нужно бороться.

Затем я бы показал им другой пример, на этот раз с множителем 11 — это будет на том же слайде, что и предыдущий пример.

Тогда я бы спросил: «Большой палец вверх — за да, большой палец вниз — за нет. Изменился ли способ, которым я представил расчет в методе столбцов, когда множитель состоит из двух цифр? »

Тогда я бы надеялся увидеть все «пальцы вниз». Если ребенок поднял палец вверх, я бы участвовал в диалоге со всем классом, чтобы понять, почему это так, и сослаться на пример на доске.

Шаг 3 — Определение метода длинного умножения

Мой следующий шаг — записать вычисление в метод столбца для длинного умножения.

Моя следующая инструкция для класса: «Для начала мы рассмотрели примеры, в которых множитель представлял собой однозначное число. Это число будет в значении «единицы». Таким образом, с числом, которое находится в «единицах» в этом двузначном числе, мы поступаем точно так же ».

Чтобы убедиться, что все участвуют, я бы попросил их показать мне пальцами или мини-доской ответ на умножение. вопросы — не потому, что я думаю, что они этого не знают, а для того, чтобы твердо держать рабочую память на математике под рукой.

На доске у меня теперь:

Теперь мы переходим к новой части информации, которую мы хотим, чтобы ученики усвоили, поэтому я бы замедлился и объяснил, что здесь происходит, снова используя этот момент, чтобы усилить значение места.

«Пока все, что было раньше, для нас не ново. Теперь у нас новый шаг. Чтобы понять, что происходит, нам нужно активизировать наши знания о числовой стоимости. Первая цифра множителя — единицы, и она равна единице.

Вторая цифра находится в разряде десятков, поэтому она равна 10.Это означает, что мы умножаем 10 на 3. Чтобы показать, что мы умножаем на 10, мы можем поставить ноль вместо единиц, чтобы он действовал как заполнитель. ”

Тогда я бы написал ноль в правильном месте.

«Затем мы можем умножить числа в множимом, как если бы мы умножали их на 1.»

Затем я бы призвал всех учеников решить умножение, снова показывая мне на пальцах, чтобы гарантировать участие.

Наконец, я бы попросил учеников взглянуть на другой проработанный пример на доске и рассказать своему партнеру, каким будет последний шаг — добавление двух продуктов.Класс делал это со мной, показывая ответы пальцами / мини-доской.

В результате мы получим готовый продукт:

Шаг 4 — Повторяющиеся примеры метода длинного умножения

Повторите описанный выше процесс с еще двумя примерами.

По мере прохождения каждого примера попросите учеников больше объяснять, особенно когда дело доходит до отбрасывания нуля и напоминания друг другу о необходимости сложить два произведения.Если вы обнаружите, что дети борются с трудностями, остановитесь и порепетируйте это, чтобы убедиться, что используется правильный язык.

Настаивайте на правильных ответах в полных предложениях и на правильном языке. Когда ученики не могут это сделать, я прошу выбранного мной добровольца, который может это сделать, , чтобы дать типовой ответ, а затем предлагаю исходным ученикам, которые сначала не смогли ответить, повторить сказанное.

Шаг 5 — очередь учеников с методом длинного умножения

Затем я бы предложил два длинных вопроса умножения, которые я попросил бы учеников ответить самостоятельно.В течение этого времени я буду наблюдать и поддерживать по мере необходимости.

В предыдущих блогах я упоминал, что нужно осознавать важность обучения и выполнения, и это ничем не отличается. Несмотря на то, что ученики слышат действительно четко сформулированные ответы на шаге 2 или правильно отвечают на оба вопроса на шаге 3, я все же очень хорошо осознаю, что, хотя эти ученики хорошо успевают, в их долговременной памяти ничего не изменилось, поскольку они просто повторяют то, что было показал им.

В зависимости от результата шага 3 мне нужно будет либо: просмотреть больше примеров и изменить свои пояснения, либо перейти к шагу 4.

Шаг 6 — Повторяющаяся практика учеников длинного умножения

Счастлив, что ученики могут копировать процесс и понимать его, теперь я предоставлю им для заполнения длинный рабочий лист умножения.

Нет необходимости различать рабочий лист; каждый ребенок будет иметь равный доступ к работе.

Дифференциация рабочего листа приведет только к увеличению разрыва в достижениях. Дифференциация будет происходить из дополнительных инструкций, которые я могу дать в это время.

Рабочий лист, который я бы дал, не будет содержать 20 вопросов на одну и ту же тему. Здесь я бы использовал чередование. 10 вопросов из того, чему я учил, будут на листе в случайном порядке, остальные 10 вопросов будут составлены из ранее преподаваемого содержания.

Подробнее: 8 стратегий дифференциации для вашего класса, которые можно использовать для преодоления разрыва в успеваемости

Опять же, они будут распределяться в случайном порядке, так что ученики должны переключаться между тем, чему учили в данный момент, и усилением извлечения ранее изученный контент.Это непрерывное переключение помогает процессу кодирования.

По возможности сделайте содержание относящимся к тому, чему учили; например, поскольку я учил умножению, у меня были бы некоторые вопросы о делении из целей предыдущего года, чтобы укрепить то, что деление — это обратное умножению.

Чередование связанного содержимого, например разделение может быть отличным способом встраивания обучения.

При пересмотре SAT вы можете захотеть перемежать задачи длинного умножения с проблемами длинного деления, чтобы еще больше укрепить взаимосвязь между ними.

Последний вопрос умножения также будет иметь множитель, отличный от 11, чтобы увидеть, могут ли ученики применить процесс, когда потребность в рабочей памяти больше.

По мере того, как это происходит, я бы разошелся по аудитории, чтобы оценить, как идут дела у учеников — не только по вопросам из этого урока, но и по предыдущему содержанию. Ученики могут пропускать вопросы, в которых они не уверены.

Шаг 7 — Общая оценка

На этом этапе учеников попросят дать ответы, и весь класс сможет ставить отметки, когда они слышат ответ.Если некоторые из них не согласны с ответом, мы можем обсудить его в классе, пока не будет найден правильный ответ.

Шаг 8 — Диагностический вопрос s

Диагностические вопросы и диагностическая оценка в целом — невероятно эффективный способ оценить понимание учениками концепции. Они работают, задавая вопрос и давая 4 возможных ответа.

Хотя один ответ правильный, три других отвлекающих фактора будут тщательно спланированы, чтобы показать конкретное заблуждение.

Ниже приведен пример того, что я использовал в этом уроке.

Пример диагностического вопроса с длинным умножением

Какой вопрос с длинным умножением показывает правильный ответ?

В этом примере каждый неправильный ответ показывает заблуждение в игре.

• A правильный , но вы можете видеть, как ответ друг друга может быть ошибкой, которую может сделать ребенок:
• В B они потеряли ноль при умножении на единицы.
• В языке C они забыли отбросить ноль при умножении на столбец десятков.
• В D они забыли добавить тот, который был перенесен при добавлении 8 к 6.

Именно выбор неправильных ответов делает диагностические вопросы настолько мощными; они четко определяют, о чем думает ученик, и могут незамедлительно дать вам обратную связь об успеваемости, которую вы можете исправить на основе полученного ответа.

Делая это на уроках, я присваиваю каждой букве номер, таким образом, A = 1, B = 2 и т. Д., Что соответствует количеству пальцев, которые я хочу, чтобы они держали. Затем я даю команду «подумай». Ученики подумают, какой будет правильный ответ.

Затем я скажу «спрячься», и они накроют пальцы, которые они хотят показать на одной руке, другой. Наконец, я говорю «покажите», и ученики показывают мне соответствующий палец, и я могу быстро осмотреть класс, чтобы увидеть ответы, которые они дали.

Другое преимущество диагностических вопросов заключается в том, чтобы обсудить неправильные ответы и понять, почему они ошибочны. Они создают фантастические темы для обсуждения и действительно заставляют класс задуматься и попытаться найти ошибки.

Если вас интересуют другие диагностические вопросы, вы можете загрузить бесплатный набор диагностических тестов по математике для 5-го и 6-го классов или посетить Третий центр космической математики, чтобы получить большой набор диагностических тестов по каждой теме учебной программы KS2. .

Завершение вашего первого длительного урока умножения!

Будем надеяться, что постепенная прогрессивная структура урока — или может быть два или три, в зависимости от вашего класса — показывает, как можно уверенно преподавать метод длинного умножения и усвоить его большинством учеников 5 и 6 классов.

Стоит повторить еще раз, что основная цель первого урока — вызвать у учеников уверенность и начать изучать этот метод умножения.

По мере роста их уверенности и дальнейшего внедрения процесса множитель может быть изменен, а вопросы для обоснования и решения проблем могут быть введены и даны ответы с большей независимостью.

Примеры длинного умножения

Если вам нужны более длинные примеры умножения, слайды и рабочие листы урока «Белая роза» от Third Space Learning для 6-го класса. Четыре операции дают вам больше возможностей для проработки этапов шаг за шагом.

Вот два примера длинного умножения.

Пример 1: 6321 x 15 = 94,815

Пример 2: 6321 x 25 = 158,025

Вопросы на длинное умножение

Вот несколько длинных вопросов на умножение и ответы для начала:

1. 1543 x 11 = 16,973
2. 2374 x 13 = 30,862
3. 4,537 x 27 = 122,499
4. 8,983 x 37 = 332,371
5. 9,452 x 48 = 453,696
Если вы

Если вам нужны дополнительные вопросы и длинные листы умножения, зарегистрируйтесь, чтобы получить здесь дополнительные ресурсы по первичной математике.

Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Каждую неделю репетиторы-специалисты по математике Third Space Learning поддерживают тысячи учеников в сотнях школ, проводя еженедельные индивидуальные онлайн-уроки и занятия по математике, призванные восполнить пробелы и ускорить успеваемость.

С 2013 года мы помогли более чем 70 000 учеников начальной школы стать более уверенными и способными математиками. Узнайте больше или запросите индивидуальное предложение для вашей школы, чтобы рассказать нам о потребностях вашей школы и о том, как мы можем помочь.

Умножение

Умножение означает умножение (или повторное сложение). Символ используется для умножения ». Например, 4 6 = 24. Это читается как четыре раза шесть равно двадцать четыре или просто четыре умножить на шесть будет двадцать четыре. Примечание: Знание умножения очень важно. Итак, если ты слаб в умножении вы должны попытаться достичь мастерства в следующих «таблица умножения». Ваша уверенность и способность изучать математику будут во многом зависеть от ваше знание умножения. Итак, вы должны стремиться освоить вышеперечисленное «таблица умножения». Пример 8 Найдите произведение 8 9. Решение: 8 9 = 72 Примечание: Произведение — результат умножения двух (или более) чисел. Чтобы вычислить 8 9, вспомним «таблицу восьмикратного умножения». Умножение больших чисел Чтобы умножить большое число на другое, мы можем использовать короткое умножение или длинное умножение. Краткое умножение Чтобы умножить большое число на однозначное число, напишите числа вертикально, причем большее число умножается на меньшее номер. Затем мы используем «таблицу умножения», чтобы найти произведение чисел как проиллюстрировано в следующем примере. Пример 9 Рассчитать 89 7. Решение: Чтобы вычислить 89 7, разложите его вертикально с меньшим числом помещается под большим числом, как показано ниже. Затем вычислите 7 9. Теперь вычислите 7 8 и прибавьте 6, чтобы получить 62. Это записывается, как показано ниже. Расстановка Мы часто предлагаем следующее решение: Примечание: 7 9 = 63.Так что поместите 3 в столбец единиц и перенесите 6 (т.е. шесть десятков). Затем вычислите 7 8 и прибавьте 6, чтобы получить 62 (т. Е. 62 десятка). Пример 10 Рассчитать 38 60. Решение: Примечание: Умножение 38 на 60 быстрее, чем умножение 60 на 38 как 60 содержит ноль. В столбце единиц помещается ноль. Затем мы вычисляем 6 38 как показано выше. Пример 11 Рассчитать 385 500. Решение: Примечание: Умножение 385 на 500 быстрее, чем умножение 500 на 385 как 500 содержит два нуля. Ноль помещается в столбец единиц, а также в столбец десятков. Затем мы вычисляем 5 385, как показано выше. Длинное умножение Чтобы умножить два больших числа, напишите числа вертикально с большее число умножается на меньшее число, которое называется множитель. Мы используем «таблицу умножения», чтобы найти произведение большего числа на каждую цифру множителя, складывая результаты. Не забудьте добавить ноль для каждого разряда после умножения цифра. Например, если умножающая цифра исчисляется сотнями В столбце добавьте два нуля для столбца десятков и столбца единиц. Пример 12 Рассчитать 269 78. Решение: Примечание: Чтобы умножить 269 на 78, поместите 78 под 269. Затем мы вычисляем 8 269 и 70 269, как показано выше. Коммутативный закон умножения Всего: Если a и b — два числа, то: a b = b a Это известно как закон перестановки для умножения . Ассоциативный закон умножения Всего: Если a , b и c — три числа, то: ( a b ) c = a ( b в ) Это известно как ассоциативный закон для умножения . Пример 13 Рассчитать 3 2 5. Решение: Пример 14 Рассчитать 7 5 4. Решение: Ключевые термины умножение, раз, раз стол, продукт, короткий умножение, длинное умножение, коммутативный закон умножения, Ассоциативный закон умножения

Умножение матриц

— Бесплатная справка по математике

Вы, наверное, уже знаете, что такое матрица, если вас интересует умножение матриц.Однако быстрый пример не повредит. Матрица — это просто двумерная группа чисел. Вместо списка, называемого вектором, матрица представляет собой прямоугольник, как показано ниже:

Вы можете установить переменную как матрицу так же, как вы можете установить переменную как число. В этом случае x — это матрица, содержащая эти четыре числа (в определенном порядке). Теперь предположим, что у вас есть две матрицы, которые нужно умножить. Умножение чисел довольно просто, но как это сделать для матрицы?

Вот ключевой момент: Вы не можете просто умножить каждое число на соответствующее число в другой матрице .Умножение матриц не похоже на сложение или вычитание. Это сложнее, но общий процесс освоить несложно. Сначала приведу пример, а потом я объясню, что я сделал :

Пример

Решение:

Вы, наверное, задаетесь вопросом, как вообще я получил этот ответ. Что ж, вы вправе так думать. Умножение матриц — непростая задача для изучения, и вам нужно быть внимательными, чтобы избежать одной или двух ошибок по неосторожности.Вот процесс:

• Шаг 1. Переместитесь через верхнюю строку первой матрицы и вниз по первому столбцу второй матрицы:

• Шаг 2: Умножьте каждое число из верхней строки первой матрицы на число в первом столбце второй матрицы. В данном случае это означает умножение 1 * 2 и 6 * 9. Затем возьмите сумму этих значений (2 + 54):

• Шаг 3. Вставьте полученное значение в матрицу ответов.Поскольку мы умножаем 1-ю строку и 1-й столбец, наш ответ помещается в этот слот в матрице ответов:

• Шаг 4: Повторите для других строк и столбцов. Это означает, что вам нужно пройти по первой строке первой матрицы и на этот раз по второму столбцу второй матрицы. Затем вторая строка первой матрицы и первый столбец второй, и, наконец, нижняя часть первой матрицы и правый столбец второй матрицы:

• Шаг 5: Вставьте все эти значения в матрицу ответов.Я только что показал вам, как делать верхний левый и нижний правый. Если вы работаете с двумя другими числами, вы получите 1 * 2 + 6 * 7 = 44 и 3 * 2 + 8 * 9 = 78. Вставьте их в матрицу ответов в соответствующие позиции, и вы получите:

Теперь я знаю, о чем вы думаете. Это было действительно сложно !!! Ну, так будет казаться, пока вы не привыкнете к процессу. Это может помочь вам записать всю свою работу и даже нарисовать стрелки, чтобы запомнить, в каком направлении вы двигаетесь по строкам и столбцам. Просто не забудьте умножить каждую строку первой матрицы на каждый столбец второй матрицы .

Что делать, если матрицы не квадраты? Затем вам нужно добавить еще один шаг. Для умножения двух матриц матрица слева должна иметь столько столбцов, сколько строк в матрице справа. Таким образом, вы можете сопоставить каждую пару во время умножения. Размер окончательной матрицы определяется строками в левой матрице и столбцами в правой. Вот что я делаю:

Записываю размеры матриц. Левая матрица имеет 2 строки и 3 столбца, поэтому мы ее и пишем.Строки, столбцы в указанном порядке. Другая матрица представляет собой матрицу 3×1, потому что у нее 3 строки и только 1 столбец. Если числа в середине совпадают, вы можете умножать. Внешние числа дают вам размер ответа. Даже если вы все испортите, в конце концов вы все поймете, потому что вы не сможете размножаться.

Важное напоминание: умножение матриц не коммутативно. Это означает, что вы не можете изменить порядок и ожидать того же результата ! Обычное умножение говорит нам, что 4 * 3 = 3 * 4, но это не умножение в обычном смысле.

Наконец, вот пример с неравномерными размерами матрицы, чтобы подвести итог:

Пример:

Если вам нужна дополнительная помощь в умножении матриц, посетите нашу доску справочных сообщений по математике, прочтите еще один урок по умножению матриц или поищите в Google больше уроков по умножению матриц.

эффективных стратегий обучения многозначному умножению

Многозначное умножение — сложная концепция для обучения.Давно прошли те времена, когда мы учили одному методу, например, долгому умножению, и просто * надеялись *, что все наши ученики поймут и смогут эффективно использовать этот метод. Сегодня мы осознаем важность стратегического обучения умножению чисел с несколькими числами. Это гарантирует, что каждый ученик в вашем классе сможет в некотором роде добиться успеха. Это также гарантирует, что знания студентов будут основаны на стратегии, и что они действительно ПОНИМАЮТ процесс многозначного умножения.

Теперь, прежде чем я начну говорить о некоторых методах многозначного умножения, я хочу сообщить вам, что у меня есть бесплатный мини-курс по этой теме — Обучение многозначному умножению и делению для НАСТОЯЩЕГО понимания .Если вы готовы, наконец, разработать план успеха учеников, обязательно приходите! РЕГИСТРАЦИЯ ЗДЕСЬ.

В качестве альтернативы, если вы ищете ресурс, где вся работа сделана за вас, вас может заинтересовать Станция многозначного умножения, где учащиеся работают над различными стратегиями в своем собственном темпе, осваивая каждую из них по мере необходимости. идти. Стратегии интегрированы стратегическим образом, что позволяет учащимся постепенно расширять свое понимание.См. Станцию ​​многозначного умножения ЗДЕСЬ.

Итак, с чего начать обучение многозначному умножению?

Важно начинать со стратегий, которые помогут студентам мысленно решать многозначные уравнения. Вместо того, чтобы сразу переходить к длинному умножению или эффективной альтернативе, начните со следующего:

1. Коммутативные и ассоциативные свойства .Прежде всего, ученикам важно помнить об этих свойствах. Коммутативное свойство гласит, что порядок факторов не меняет продукт. Например, 4 × 3 и 3 × 4 равны 12. Ассоциативное свойство утверждает, что факторы могут быть сгруппированы по-разному. Например, (7 × 2) x5 дает то же произведение, что и (2 × 5) x7. Эти свойства помогают учащимся понять, что они могут манипулировать уравнениями, чтобы их было легче решать.

2. Использование факторов. Это отличный способ научить студентов манипулировать числами, чтобы облегчить решение уравнения.Когда мы учим многозначное умножение, наша цель не всегда — как можно быстрее получить правильный ответ. Иногда наша цель — уметь творчески мыслить, когда дело касается чисел. Это один из таких случаев. Мы могли бы взять уравнение 4 × 15 и разбить 15 на его множители, 3 и 5. Теперь у нас есть это уравнение: 4x3x5. Теперь мы можем решить это так: (4 × 3) x5 -> 12 × 5 -> 60. Это просто, чтобы показать, что существует не только один правильный способ решить это уравнение.

3. Умножение на 10, 100 и 1000, а также на числа, кратные 10, 100 и 1000. Хотя я сгруппировал эти две концепции вместе для целей этого сообщения в блоге, этому следует учить медленно и осторожно, по частям. Когда вы преподаете эту концепцию, важно сосредоточиться на правилах определения места, прежде чем обучать трюкам, таким как трюк с добавлением нулей. Например, когда учащиеся сталкиваются с уравнением 45 × 100, они должны понимать, что значения разряда увеличиваются на 2 разряда, чтобы получить произведение 4500. Аналогичным образом, при умножении такого уравнения, как 3 × 1000, значения разряда увеличиваются на 3 места сделать 3000.После того, как учащиеся усвоят эту концепцию, мы можем научить их, что, когда в множителях есть 2 нуля, мы добавляем 2 нуля к произведению. Имейте в виду, что этим трюкам следует обучать только ПОСЛЕ того, как учащиеся овладеют отличным пониманием математики, лежащей в основе концепции.

4. Разделение номеров. Это одна из самых полезных стратегий ментальной математики. Это включает в себя разбиение одного из факторов, умножение на группы, а затем сложение этих групп вместе. Вот пример: в этом примере мы разбиваем 12 на 10 и 2, а затем умножаем их на части.Таким образом, 12 × 30 становится (10 × 30) + (2 × 30). Решить это намного проще!

Мы также можем использовать эту стратегию для умножения больших чисел, например 103 × 9. Мы можем разбить 103 на 100 и 3, а затем умножить на части, например: (100 × 9) + (3 × 9).

5. Метод окна / окна. Мне нравится метод «окно / окно», потому что он использует расширенную форму каждого фактора, что делает его отличной стратегией для усиления концепций определения числа. Чтобы использовать эту стратегию, мы рисуем прямоугольник (количество столбцов и строк зависит от количества цифр в множителях), а затем записываем развернутые формы множителей сверху и сбоку.Затем мы умножаем каждую часть и складываем части, когда закончим. Если вы хотите получить более подробное руководство по этой стратегии, см. ЭТО сообщение в блоге, которое также включает видеоурок.

6. Частичные продукты. Это одна из самых важных стратегий, которую следует преподавать как альтернатива долгому умножению. В частичных произведениях уравнение строится так же, как и при традиционном долгом умножении, но способ умножения отличается. Например, для уравнения 35 × 3 мы сначала умножаем 3 × 5, чтобы получить 15.Затем мы умножаем 3 × 30, чтобы получить 90. Обратите внимание, что мы умножили на ТРИДЦАТЬ, а не на три. Это потому, что 3 представляет 30. Это дает нам 90. Теперь мы складываем 15 и 90 вместе, чтобы получилось 105. Если вам нужно более подробное руководство по этой стратегии, см. ЭТО сообщение в блоге, которое также включает видеоурок. .

Стратегии, которые я описал выше, являются САМЫМИ важными для обучения многозначному умножению. Все эти стратегии делают упор на понимание чисел и гарантируют, что учащиеся действительно понимают, что означают числа в каждом уравнении.Но как насчет таких стратегий, как традиционное длинное умножение?

Это спорная тема. Некоторые учителя считают, что наше обучение должно быть сосредоточено ТОЛЬКО на чувстве чисел, чтобы мы не учили стратегии, не фокусирующиеся на понимании числа. Эти учителя склонны использовать такие стратегии, как частичные произведения в течение всего года, как очень эффективную альтернативу традиционному долгому умножению. Другие учителя считают, что мы должны учить так, как умножение преподавалось много лет назад.Тогда это работало, так почему бы не работать сейчас ?! Эти учителя, как правило, больше сосредотачиваются на таких стратегиях, как традиционное длинное умножение, и меньше на более современных методах, таких как коробка / окно или частичные произведения.

Я здесь не для того, чтобы указывать вам, какой путь лучше 🙂 Это зависит от вас и ваших учеников. Однако я скажу вам свое личное мнение. Лично я не склонен впадать в крайности. Я очень верю в стратегии, способствующие пониманию чисел. Однако я также считаю, что для НЕКОТОРЫХ ваших учеников есть место традиционным методам.Здесь тебе придется быть судьей. Если у вас есть ученики, которые борются с многозначным умножением, вы, вероятно, предпочтете позволить им сосредоточиться на частичных продуктах и ​​коробке / окне и оставить все как есть. Зачем вносить еще больше путаницы? Они могут быть очень успешными с этими стратегиями. ОДНАКО, у вас могут быть ученики, которые прекрасно понимают, чему вас учили, и готовы к новым испытаниям! Эти ученики могут преуспеть с другими методами, менее ориентированными на числа, поскольку они уже хорошо разбираются в математических концепциях.Для этих студентов я собираюсь рассказать о паре других стратегий.

Эти следующие стратегии менее ориентированы на числа, но они могут быть интересным способом умножения для тех учащихся, которые готовы принять вызов.

1. Решеточное умножение. Это действительно забавный метод, который включает рисование сетки и использование этой сетки для организации чисел. Некоторые учителя считают, что ученикам, использующим этот метод, легче носить, потому что числа расположены диагональными рядами, поэтому легче увидеть, где их нужно добавить.Для объяснения этой стратегии требуется время, поэтому, пожалуйста, просмотрите ЭТО сообщение в блоге, которое также включает видеоурок по стратегии.

1. Деление пополам и удвоение. Это действительно изящная стратегия умножения на числа вроде 5, 10, 25, 50 и т. Д. Все, что вам нужно сделать, — это разделить один множитель пополам, а второй — удвоить, чтобы изменить уравнение и облегчить его решение. Например, если у нас есть уравнение типа 25 × 14, мы могли бы удвоить 25, чтобы получить 50, и разделить 14 пополам, чтобы получить 7.Теперь у нас есть 50 × 7, который НАМНОГО проще решить! Мы можем очень быстро вычислить это мысленно и получить результат 350. Для этой стратегии ученики должны понимать, что она хорошо работает только с определенными числами, и им потребуется много практики, чтобы знать, с какими уравнениями она хорошо работает.
2. Традиционное долгое умножение. Это подводит нас к традиционному длинному умножению. Я не собираюсь объяснять, как это сделать, потому что я думаю, что большинство из нас уже это знает, но этому можно научить студентов, которые готовы к дополнительным испытаниям.

Если вам нужна дополнительная поддержка по этим стратегиям, я рекомендую записаться на мини-курс «Стратегии многозначного умножения и деления». Это займет всего около часа, и вы уйдете с планом действий по решению проблемы многозначного умножения и деления в классе.

Удачного дня,

Шелли

Умножение матриц — примеры

М.Борн

На этой странице вы можете увидеть множество примеров умножения матриц.

Вы можете повторно загружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел и матриц. Вы также можете выбрать матрицы разного размера (внизу страницы).

(Если вам сначала нужна справочная информация о матрицах, вернитесь к разделу «Введение в матрицы» и «Умножение матриц»).

Пример

Умножение матриц A и B .

А = 6 4 7 -2 3 5 8 0 9

, B = 1 6 -4 -2 2 3 5 -3 -1

Ответ

Для экономии работы мы сначала проверяем, можно ли их умножить.

У нас есть (3 × 3) × (3 × 3), и поскольку количество столбцов в A совпадает с количеством строк в B (в данном случае средние два числа равны 3), мы можем перемножить эти матрицы. Нашим результатом будет матрица (3 × 3).

Первый шаг — записать две матрицы рядом, как показано ниже:

AB = 6 4 7 -2 3 5 8 0 9

1 6 -4 -2 2 3 5 -3 -1

Мы умножаем отдельные элементы в первой строке матрицы A на соответствующие элементы в первом столбце матрицы B и складываем результаты.Это дает нам число, которое нам нужно поместить в первую строку, первую позицию столбца в матрице ответов.

1 6 -4 -2 2 3 5 -3 -1

6 × 1 + 4 × -2 + 7 × 5 = 33

После этого мы умножаем элементы в первой строке матрицы A на соответствующие элементы во втором столбце матрицы B , затем складываем результаты.Это дает нам ответ, который нам нужно будет поместить в первую строку, второй столбец матрицы ответов.

1 6 -4 -2 2 3 5 -3 -1

6 × 6 + 4 × 2 + 7 × -3 = 23

Продолжаем по строкам и столбцам следующим образом:

1 6 -4 -2 2 3 5 -3 -1

=		6 × 1 + 4 × -2 + 7 × 5	6 × 6 + 4 × 2 + 7 × -3	6 × -4 + 4 × 3 + 7 × -1
		-2 × 1 + 3 × -2 + 5 × 5	-2 × 6 + 3 × 2 + 5 × -3	-2 × -4 + 3 × 3 + 5 × -1
		8 × 1 + 0 × -2 + 9 × 5	8 × 6 + 0 × 2 + 9 × -3	8 × -4 + 0 × 3 + 9 × -1

=		33	23	-19
		17	-21	12
		53	21	-41

Посмотреть другой пример?

Вы можете обновить эту страницу, чтобы увидеть другой пример с матрицами другого размера и другими числами; ИЛИ

Выберите нужные вам размеры матрицы и нажмите кнопку.