Решение примеров 1 класс: Тренажер по математике — 1 класс — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Содержание

Конспект урока по математике «Решение примеров +3,

Конспект по математике

в 1 классе

Разработан

Власовой Дарьей Дмитриевной

Тема: «Решение примеров + 3, — 3»

Урок-закрепление полученных знаний и умений.

Задачи:

1) Познавательные

— продолжить формировать умение выполнять сложение и вычитание вида +3, -3 на основе прибавления и вычитания по частям;

— продолжить формировать умение решать примеры и задачи в пределах десяти на основе состава числа;

2) Развивающие:

Развитие УУД

Регулятивных:

— развитие регулятивного УУД целеполагания в процессе анализа учебной проблемы и постановки учебной задачи урока;

— развитие регулятивного УУД самоконтроля при анализе собственных ошибок;

— развитие регулятивного УУД контроля при анализе ошибок ребят;

— развитие рефлексивно-оценочных действий на этапе итога урока при осознании результатов учебной деятельности;

Познавательных:

— развитие УУД : анализа, при выделении порядка действий в примерах, при рассматривании иллюстрации

Коммуникативных:

— формирование умения обосновывать свою точку зрения по поводу сущности проблемы , при выполнении заданий;

— формирование оценочных суждений о степени успешности деятельности на этапе итога урока;

3) Воспитательные

— воспитание аккуратности, прилежности;

1. Организационный момент: Здравствуйте ребята! Сегодня чудесный день. Я надеюсь , что настроение у вас тоже чудесное. Улыбнитесь друг другу и пожелайте успехов. Я тоже желаю вам успехов. Будьте внимательны и активны, и тогда у вас все получится.

Проверим готовность к уроку. Я буду называть предметы, если они нужны нам на уроке и они есть у вас на парте хлопайте в ладоши, если этот предмет на уроке не нужен не хлопайте.

Учебник, корзинка, тарелка, тетрадь в клетку, чайник, рабочая тетрадь на печатной основе, пенал.

Молодцы ребята, я рада, что вы все готовы к уроку, и мы не будем отвлекаться на уроке.

2. Повторение:

Устный счет: У: Посчитайте хором от 1 до 10.

Д: 1 2 3 4 5 6 7 8 9 10

У: Посчитайте хором от 10 до 1.

Д: 10 9 8 7 6 5 4 3 2 1

У: Молодцы. Сейчас я дам вам мяч, вам надо будет выполнить мое задание и передать мяч следующему человеку, которого я назову. Посчитать от 6 до 15, Матвей.

Д: 6 7 8 9 10 11 12 13 14 15

У: Посчитать от 14 до 2, Лиза.

Матвей передавай мяч Лизу и Лиза выполняет задание.

Д: 14 13 12 1110 9 8 7 6 5 4 3 2

У: Посчитать от 1 до 10, через 1, Женя. Лиза передаем эстафету Жене.

Д: 1 3 5 7 9.

У: Сейчас я шепотом, скажу Арсению на ушко задание. Он даст только ответ, а вы должны будете сказать, какое задание я задала Арсению.

(Говорю на ушко: назови соседей числа 8)

Д: 7 и 9.

У: Итак ребята, как вы думаете, какое задание я дала Арсению.

Д: Назвать соседей числа 8.

У: Правильно. Следующее задание. Ксюша.

( Назови последующее число для числа 3)

Д: 4

У: Какое задание я дала Ксюше?

Д: Назвать следующее число за числом 3.

У: Молодцы. Сейчас выполним «узелки на память». Решаем про себя. Говорим только последний, окончательный ответ всей цепочки.

1+3=>4-2=>2+2=>4+1= >5

Проговариваю: сумма 1 и 3, из получившейся суммы вычесть 2, к полученной разности прибавить 2, к получившемуся числу прибавить 1.

Д: ответ 5.

У: 1+3 = ?

Д: 4

У: 4-2= ?

Д: 2

У: 2+2= ?

Д: 4

У: 4+1= ?

Д: 5

Вывод этапа:

У: Правильно, молодцы. Ребята, что мы с вами сейчас повторяли?

Д: порядок натурального ряда чисел, решали пример.

У: Верно эти знания нам пригодятся сегодня уроке, когда мы будем решать примеры и задачи.

3.Актуализация имеющихся знаний.

У: Сейчас немного поиграем. Вы разделитесь на три команды, то есть три ряда: 1, 2, и 3. На доске вы видите примеры. Я вам раздала карточки! Первый столбик примеров решает первый ряд, и все ребята первого ряда показывают мне ответ первого примера, подняв карточку вверх. Итак, выполняете все мои задание, затем второй ряд, и третий. Пока задание выполняет одна команда, другие должны следить правильно ли отвечает первая команда ,на все вопросы ли отвечает. Затем мы посмотрим, какой ряд самый внимательный!

Итак на доске примеры для первого ряда: (2+1= ,5+1=, 4 -1 =,6-1 = )

Д: 3, 6, 3,5 (примеры решаются по очереди и учащиеся по очереди поднимают карточки)

У: Хорошо, с примерами вы справились. Ответьте на мой дополнительный вопрос: Что значит прибавить к числу 1?

Д: Это назвать последующее число.

У: Что значит из числа вычесть 1?

Д: Назвать предыдущее число.

У: Вы справились с заданиями. Работали дружно. Посмотрим, справится ли с заданиями второй ряд. Решаем второй столбик примеров.

На доске примеры: ( 2+2 = ,4+2= , 6-2 = , 7- 2 = )

Д: 4,6,4,5 ( по очереди показывают карточки)

У: Какие вы молодцы! Теперь и вам дополнительный вопрос, что значит к числу прибавить два?

Д: Это прибавить 1 и еще 1.

У: Что значит из числа вычесть два?

Д: Это вычесть сначала 1, потом еще 1.

У: Отлично. Задание третьего ряда. Решаем примеры .

На доске: (2+ 3= , 4+3 =, 6- 3=, 5-3=)

Д: 5, 7. 3, 2(по очереди показывают карточки)

У: И вам дополнительный вопрос: Что значит из числа вычесть 3?

Д: это вычесть 1, 1, 1. Или вычесть 2 и 1.

У: Что значит к числу прибавить 3?

Д: Это прибавить 1,1,1 или прибавить 2 и 1.

Вывод этапа: У: Вы все справились с заданиями. Вы помогали друг другу. Старались быстро решать примеры. Как вы думаете для чего мы с вами повторяли , как решать примеры вида +1,-1,+2,-2,+3,-3 ?

Д: Чтобы лучше решать примеры, быстро решать задачи и примеры, и.т.д.

У: Вы совершенно правы, эти знания нам сегодня с вами пригодятся!

4.Постановка целей и задач урока:

На доске записаны примеры: 5+3 7+3 6+3 3+3

6-3 7- 3 10 – 3

У: Что вы заметили общего у этих примеров?

( Если затруднение, то прошу обратить внимание на второе слагаемое, и вычитаемое)

Д: Выполняется сложение и вычитание числа 3.

У: Вы уже учились решать примеры вида +3, — 3. Сегодня мы продолжим эту работу. Как вы думаете, для чего мы продолжаем работу?

Д: Чтобы закрепить знания. Чтобы лучше решать примеры и задачи.

У: Кто может сказать, какая задача сегодня стоит перед нами?

Д: Научиться решать примеры и задачи, решать примеры вида + 3 ,- 3

У: Верно. Я заметила, когда вы выполняли мои задания, некоторым из вас было тяжело сразу дать ответ, приходилось долго считать. Мы с вами должны постараться решать примеры уже не по частям, а целиком. Мы должны запомнить эти примеры, чтобы легко и быстро выполнять задания. Тема нашего урока: « Решение примеров + 3, — 3»

5.Первичное закрепление:

1)Типовые упражнения ( в знакомой ситуации)

У: Ребята, кто из вас может сказать, что значит к числу прибавить 3?

Д: Это прибавить 1, еще 1, и еще 1. Прибавить 2 и 1.

У: Что значит из числа вычесть 1?

Д: Это вычесть 1, 1 и 1. Это вычесть 2 и 1.

У: Молодцы. Перейдем к работе с учебником. Откройте учебники на странице 1-0-8. Выполним номер 1. Карина, прочитай, что нам нужно сделать.

Д: Заполнить пропуски , выполнив вычисления.

У: Выполним это задание по цепочке. Поставьте пальчик , чтобы следить. Арсений , реши первый пример.

Д: 0+3 = 3

У: Правильно, когда мы прибавляем к нулю какое-либо число, получится это же число.

Ева реши следующий пример.

Д: 1+3=4

( по цепочке решаем примеры)

Высвечиваю слайд с ответами : Посмотрите на первый столбик, на первые слагаемые. Что вы заметили? Они увеличиваются или уменьшаются на 1?

Д: Увеличиваются на один.

У: Хорошо, посмотрите, менялась ли второе слагаемое?

Д: Нет.

У: Что происходило с суммой? Она увеличивалась или уменьшалась?

Д: Увеличивалась.

У: На сколько?

Д: на 1.

У: Теперь перейдем к примерам , связанные с вычитанием числа 3

( по цепочке решаем примеры в разнобой)

Посмотрите на слайд: Что происходило с уменьшаемым ? Оно увеличивалось или уменьшалось?

Д: уменьшалось.

У: Изменялось ли вычитаемое во втором столбике?

Д: нет.

У: Что происходило с разностью? Она увеличивалась или уменьшалась?

Д: Уменьшалась.

Ребята, мы с вами выполнили это задание. Постарайтесь запомнить эти примеры, они помогут вам быстро решать примеры и задачи.

2) Конструктивные упражнения (в измененной ситуации)

У: Выполним задание №2 из учебника. Соня прочитай, что нужно сделать в этом задании.

Д: составить примеры по рисункам и решить их.

У: Ребята, мы с вами будем решать примеры на основе состава числа. Рассмотрите первый рисунок. Что на нем изображено?

Д: Грибы.

У: Сколько белых грибов?

Д: 4

У: Сколько красных грибов?

Д: 3

У: Сколько всего грибов на рисунке?

Д: 7

У: Рассмотрите два примера под иллюстрацией. Что у них общего?

Д: ответ одинаковый, одни и те же числа используются.

У: Верно ребята. Решим следующий пример. Опираясь на примеры , предложенные выше, скажите чему будет равна разность 7 и 4.

Д: 3

У: Чему будет равна разность 7 и з?

Д: 4.

У: Я с вами согласна. Посмотрите на следующую иллюстрацию. Кто на ней изображен?

Д: Птички. Воробьи и синички.

У: Посмотрите на первый пример, предложенный внизу иллюстрации. Кто может составить задачу к этому примеру.

Д: Было два воробья, прилетело три синички. Сколько всего стало птичек?

У: Сколько всего стало птиц?

Д: 5

У: Кто может сказать, чему будет равна сумма чисел 3 и 2 в следующем примере?

Д: 5.

У: Правильно. Ребята, кто уже догадался, какое число нужно вставить в пропущенный квадратик, чтобы при вычитании из этого числа 2, разность будет равна 3?

Д: Нужно вставить число 5.

У: Молодцы. Кто может составить задачу по этому примеру?

Д: Сидело 5 птиц, 2 воробья улетели. Сколько осталось птиц?

У: Я с вами согласна. Какое число нужно вставить в окошко в последнем примере?

Д: 5.

У: Вы все сделали правильно. Самостоятельно запишите последний столбик примеров в тетрадях в клетку, отступив две клетки от предыдущего задания.(проверяю)

Ребята, что изображено на последней иллюстрации.

Д: круги зеленые и красные.

У: Хорошо. Рома, какой пример ты записал первым?

Д: 5+3 = 8

У: Молодец, ты справился с этим примером. Кто может сказать , какой будет следующий пример?

Д: 3+5 = 8

У: Какие числа вы вставили в пропущенные окошки в третьем примере?

Д: 8 – 5 = 3

У: Умнички. И какой последний пример вы записали?

Д: 8 – 3 = 5

Вывод этапа: У: Ребята, какие умения мы с вами отрабатывали в этом задании?

Д: решать примеры, составлять примеры и задачи.

У: Мы выполнили с вами все задания?

Д: да.

У: Отлично, с этим заданием вы справились. Перейдем к работе в рабочей тетради на печатной основе. Откройте тетради на странице 9 – 4.

Выполним первое задание. Кто может сказать, что нам нужно сделать?

Д: решить примеры.

У: Решите первый столбик примеров самостоятельно. ( выполняют)

Проверим, правильно ли вы решили эти примеры с помощью карточек, которые я вам раздала. Поднимите карточку с ответом на первый пример.(итак по очереди)

Д: 8, 5, 6

У: Ребята, все согласны?

Д: Да/нет

У: Перейдем к решению примеров во втором столбике. Чем они отличаются от примеров первого столбика?

Д: Здесь даны примеры в два действия.

У: Верно. Посмотрите на первый пример. Какое действие будет первым в этом примере?

Д: 5 – 1

У: Чему равна разность 5 и 1?

Д: 4.

У: Напишите карандашом 4 над примером 5-1. Теперь прибавляем к числу 4 число 2. Какой ответ получится?

Д: Число 6.

У: Ксюша реши следующий пример, комментируя его. Остальные внимательно слушают и помогают.

Д: Из 6 вычесть 3 равно 3. Пишу карандашом 3 над примером 6 – 3. К 3 прибавляю 1, получаю 4. Записываю ответ.

У: Умничка. Арсений реши последний пример с комментированием, используя слова «сумма» и «разность».

Д: Сумма чисел 4 и 2 равна 6. Пишу карандашом 6 над примером. Разность чисел 6 и 1 равна 5. Записываю ответ в пустой квадрат.

У: Молодец. Последний столбик решите самостоятельно. Потом проверим получившиеся результаты.

Какой ответ в первом примере, покажите карточкой?

Д: 7

У: Какой число вы записали в ответ во втором примере?

Д: 3

У: Ответ в третьем примере это число –

Д: 2.

Вывод: У: Ребята, какие умения мы отрабатывали с вами в этом задании?

Д: решать примеры, решать примеры в два действия, работать самостоятельно.

6. Решение текстовых задач.

У: Вы все сделали правильно. Перейдем к следующему заданию. Номер 2. Ярослав прочитай вслух, громко и четко задание 2 номера.

Д: Придумать задачу по рисунку. Записать решение задачи и ответ.

У: Спасибо. Ребята, посмотрите на задание 2 из учебника, которое мы с вами выполняли. Нам дана была одна картинка, но зато мы к ней смогли придумать много примеров и задач. Эта задачу мы с вами будем решать тоже разными способами. Первый ряд, решает эту задачу с помощью вычитания. Второй ряд с помощью вычитания, и третий ряд с помощью сложения. Решаем самостоятельно, затем мы с вами осуществим проверку.

Итак, Первому ряду нужно было решить задачу с помощью сложения. Ксюша идет работать к доске. Остальные проверяют: правильно ли Ксюша решила задачу. Сначала расскажи, какую задачу по рисунку ты придумала.

Д: На поляне росло 7 цветов. 5 фиолетовых цветов срезали. Сколько цветов осталось на поляне?

У: Верно. Запиши решение этой задачи.

Д: 7 – 5 = 2.

У: Ребята, все согласны?

Д: да.

У: Второму ряду тоже нужно было решить задачу с помощью вычитания. Ребята все решили также, как Ксюша или есть тот, кто решал по -другому?

Д: На поляне росло 7 цветов, 2 из них срезали. Сколько цветов росло на поляне?

7-2 =5.

У: Молодцы. И третьему ряду задачу нужно было решить с помощью сложения. Диана иди к доске.

Д: На поляне росло 5 цветов фиолетовых и 2 синих. Сколько всего цветов росло на поляне?

У: Хорошо. Запиши решение.

Д: 5+2 = 7.

У: Выполним задание 3. Прочитаем, что нужно сделать в этом задании.

Д: Дополнить схему и решить задачу.

У: Прочитайте саму задачу. Вика, прочитай.

Д: читает.

У: Посмотрите на схему после задачи. Если нам сказано, что Саша съел 2 конфеты, нам нужно дорисовать две конфеты или зачеркнуть две?

Д: Зачеркнуть две конфеты.

У: Правильно. Запишите самостоятельно решение это задачи. Затем сверьтесь с решением, записанным на доске.

На доске с ошибкой: 6+2 =8.

Ребята, у вас такое же решение? Я правильно решила задачу или у меня ошибка?

Д: У вас ошибка.

У: Лиза выйди к доске и исправь меня.

Д: 6 – 2 =4

У: Почему это задачу мы решали вычитанием?

Д: Потому что мы не добавляли конфеты, а убирали.

Вывод: У: Какие умения нам помогло отработать это задание?

Д: дополнять схему, решать задачу, контролировать свою работу, и.т.д

У: Вы очень внимательны. Молодцы!

7.Обобщение и систематизация знаний:

У: Ребята, Решим примеры, чтобы закрепить и систематизировать знания, полученные на уроке.

7+3 = 6+3 – 3 = 4+2 – 3 =

8 – 3 = 5- 3+3 = 3+3 – 1 =

Вывод: У: Для чего мы с вами должны запомнить примеры вида +3, — 3?

Д: чтобы быстро решать задачи, примеры.

В резерв: задание №5 рабочая тетрадь, страница 95.

8.Рефлексия урока:

У: Ребята, вы справились со всеми заданиями, которые я вам приготовила. Подведем итог урока.

Какая задача сегодня стояла перед нами на уроке?

Д: Решать примеры с числом 3, решать примеры и задачи.

У: Выполнили ли мы эту задачу?

Д: Да.

У: Что вам понравилось делать на уроке?

Д: ответы.

У: Какие трудности у вас возникли?

Д: ответы.

У: Как вы думаете, почему они возникли?

Д: ответы.

У: Спасибо вам за урок. Мне было приятно с вами работать. Вы были очень активны и внимательны. Хочу похвалить……

конспект урока математики для 1 класса по теме «Решение примеров и задач в пределах 5» | План-конспект урока по математике (1 класс):

ГБОУ «Алексеевская общеобразовательная школа-интернат

План-конспект открытого урока

по математике

в 1 классе

Подготовила и провела

учитель начальных классов

Выходцева Людмила Ивановна

Тема урока. «Решение примеров и задач в пределах 5».

Цель: обучение учащихся сложению и вычитанию чисел в пределах 5. Задачи:

Предметные: совершенствовать вычислительные навыки в пределах 5, формировать умение решать простые задачи.

Личностные: формировать учебно-познавательный интерес к новому материалу, формировать положительное отношение к учению, самооценка своих возможностей.
Регулятивные: планировать свои действия в соответствии с поставленной задачей с помощью учителя, производить контроль своих действий, планировать свою деятельность.

Коммуникативные: создать условия для учебного сотрудничества учитель-обучающийся, уметь слушать и вступать в диалог.

Познавательные: строить сообщения в устной форме, развивать активный речевой словарь.

Оборудование: учебник «Математика» 1 класс счётный материал, индивидуальный раздаточный материал, геометрический материал, ноутбук, проектор, презентация.

Ход урока.

I. Организационный момент.

Психологический настрой.

Поудобнее садитесь,

Не шумите, не вертитесь.

Всё внимательно считайте,

А спрошу вас – отвечайте.

Математика нас ждет,

Начинаем устный счет.

II. Устный счет.

Мне сегодня хочется пригласить вас в необычное сказочное путешествие. Так как у нас урок математики, то и сказка у нас будет математическая.

В сказку за наукой сегодня пойдем

Смекалку, фантазию с собою возьмем,

Дорогой с пути никуда не свернем.

А что бы узнать, в какой сказке мы побываем в гостях, вам нужно отгадать загадку.

В этом доме – вот так да!

Поместились без труда

Муха, мышка, да лягушка,

Зайка серый с петушком.

Мишка втиснулся, как мог,

Но развалился … (теремок).

А чтобы попасть в теремок, мы должны из полосок составить дорожку.

Работа с полосками.

Выложите дорожку в такой последовательности, как показано на рисунке.

1 – коричневая, 2 – зеленая, 3 – синяя, 4 – желтая , 5 – красная.
— Давайте пройдем от тропинки к теремку, посчитайте полоски (прямой счет), а теперь вернемся обратно на тропинку (обратный счет).

— Какая по счету красная полоска? Желтая? Синяя? Коричневая? Зеленая?
— За какой полоской лежит зеленая полоска, желтая, красная?

— Перед какой полоской лежит синяя полоска, красная, зеленая?

— Назовите соседей у желтой полоски, у зеленой, у синей.

III. Сообщение темы и целей урока.

Стоит в поле теремок, теремок.

Он не низок, не высок.

— Посмотрите внимательно на рисунок и скажите, какой номер у теремка? (номер 5)

— Правильно. Сегодня на уроке мы с вами будем считать, сравнивать числа, решать примеры и задачу в пределах 5.

IV. Работа над темой урока.

1) Пальчиковая гимнастика.

Пальчики, пора вставать!

Раз, два, три, четыре, пять,

Будем мы скакать в присядку,

Будем прыгать и плясать.

Раз, два, три, четыре, пять!

2) Минутка каллиграфии.

По полю муха-горюха летела. Увидела она теремок и решила в нем поселиться, но чтобы мухе-горюхе в теремок попасть, надо ей научиться цифру 5 писать. Ей в одиночку не справиться, мы должны ей помочь.

— Обведем за карандашом газами.

— Пропишем ручкой в воздухе.

— Напишем цифру 5 в тетрадях.

3) Математический диктант.

Мышка-норушка по полю бежала. Увидела теремок и тоже решила в нем поселится, но чтобы стала мышка жить в теремке, ей нужно написать математический диктант, состоящий из математических знаков и цифр.

а) устно назовите математические знаки, которые вы знаете (+, -, =, >.

б) письмо цифр и знаков под диктовку

3 5 1 2 4

= > +

4) Сравнение чисел.

По полю лягушка-квакушка прыгала. Увидела теремок и ей захотелось жить вместе с мухой-горюхой и мышкой-норушкой. Чтобы лягушке в теремке поселиться, ей нужно сравнить числа. Она не умеет это делать. Надо ребята, лягушке-квакушке помочь.

(Дети по одному выходят к доске и сравнивают числа.)

ФИЗМИНУТКА

5) Решение примеров.

Зайка по полю бежал, ему тоже понравился теремок. Чтобы зайка стал жить в теремочке, ему надо научиться примеры решить. Будем примеры решать и зайчику помогать.

а) дети самостоятельно решают примеры.

б) проверка самостоятельной работы.

6) Решение задачи.

Идет по полю петушок. Увидел теремок и тоже захотел поселиться в нем. Чтобы петушок стал жить в теремочке, ему нужно решить задачу.

На листике сидели 5 мух. Подул ветер и улетели 3 мухи. Сколько мух осталось на ветке?

а) Разбор и решение задачи устно.

Сколько мух сидело на листике? (5) Что произошло потом? (улетели 3 мухи) – это условие задачи. Что нужно узнать? О чем спрашивается в задаче? (сколько мух осталось на листике?) – это вопрос задачи. Что значит решить задачу? (Ответить на её вопрос.) Какой же вопрос в задаче? Как узнать, сколько мух осталось на листике? Нужно прибавлять, или отнимать? Подумайте, мух стало больше или меньше? Так что же надо сделать? (5 – 3 = 2) – это решение задачи. Ответили мы на вопрос задачи? Значит, мы решили задачу. Кто скажет ответ? (на листике осталось 2 мухи.)

б) Письменное выполнение задачи.

(1 ученик решает у доски, остальные в тетрадях).

— Ребята, сколько зверюшек в теремке живет? (5)

7) Геометрический материал.

Шел по полю медведь. Увидел теремок и тоже захотел в нем поселиться. Полез он в дом и развалил все кругом. Заплакали зверята: «Где же жить нам, косолапый?»

— Давайте поможем зверятам построить новый теремок.

— Посмотрите на рисунок. Какие геометрические фигурки нам помогут построить теремок?

(дети из геометрических фигурок строят теремок)

V. Итог урока.

Все задания мы выполнили. Сказка прощается с нами.

Вы сегодня все считали,

Прибавляли, вычитали,

И задачу дружно решали.

Всем героя сказки помогли!

Всё сумели, всё смогли!

Сегодня, ребята, вы МОЛОДЦЫ!

Примеры на сложение и вычитание в пределах 20тренажёр по математике (1 класс) на тему — Справочник

Примеры по математике 1 класс в пределах 20

В карточке желательно указывать количество ошибок и время, потраченное на решение. Это нужно, чтобы отслеживать в динамике успехи ребенка.

По теме: методические разработки, презентации и конспекты

Урок математики 1 класс по теме «Закрепление изученного.

Решение текстовых задач, примеров на сложение и вычитание в пределах 10, сравнение чисел в пределах 10»

Учащиеся учатся решать задачи изученных видов; решать примеры на сложение и вычитание чисел 1,2,3; принимать и сохранять цели и задачи учебной деятельности; находить средства и способы её осуществлени.

По теме методические разработки, презентации и конспекты.

Nsportal. ru

09.06.2019 18:35:53

2019-06-09 18:35:53

Источники:

Https://nsportal. ru/nachalnaya-shkola/matematika/2018/03/12/primery-na-slozhenie-i-vychitanie-v-predelah-20

Примеры в пределах 20, 1 класс | Тренажёр по математике (1 класс): | Образовательная социальная сеть » /> » /> .keyword { color: red; }

Примеры по математике 1 класс в пределах 20

По теме: методические разработки, презентации и конспекты

Урок по математике в 1 классе» Решение задач и примеров в пределах 10″

Урок по математике в 1 классе коррекционной школы I — II вида. Тема: «Решение задач и примеров в пределах 10»Цель: 1) закрепить знание чисел в пределах 10.

Урок математики в 1 классе «Решение задач и примеров в пределах 10»

Тема урока: « Решение задач и примеров в пределах 10».Заключительный урок по теме «Числа от 1 до 10 и число 0. Сложение и вычитание» Цель урока: отработка знаний, полученных при изучении те.

Презентация к уроку математики в 1 классе «Решение задач и примеров в пределах 10»

Урок математики во 2 классе (1-4) Тема: «Решение задач и примеров в пределах 100. Закрепление».

Закрепить знания и умения решать и составлять задачи на нахождение числа, которое на несколько единиц больше или меньше данного, составлять и решать примеры;-.

Урок математики во 2 классе. Решение примеров в пределах 20 без перехода через десяток

Конспект урока математики для учащихся коррекционной школы.

Открытый урок по математике в 4 классе «Решение примеров в пределах 100»

Урок — экскурсия в город Простоквашино, встреча с его героями, которые задают ребятам различные математические задания.

1.3000 примеров по математике. 1 класс. Устный счёт. Счёт в пределах 20. Узорова О. В.

В этом пособии представлен материал, направленный на формирование навыков устного счёта по теме «Счёт в пределах 20» для 1 класса. Устный счёт развивает сообразительность и внимание учащих.

Урок по математике в 1 классе» Решение задач и примеров в пределах 10″

Урок математики в 1 классе «Решение задач и примеров в пределах 10»

Презентация к уроку математики в 1 классе «Решение задач и примеров в пределах 10»

Урок математики во 2 классе (1-4) Тема: «Решение задач и примеров в пределах 100. Закрепление».

Урок математики во 2 классе. Решение примеров в пределах 20 без перехода через десяток

Конспект урока математики для учащихся коррекционной школы.

Открытый урок по математике в 4 классе «Решение примеров в пределах 100»

1.3000 примеров по математике. 1 класс.

Устный счёт. Счёт в пределах 20. Узорова О. В.

В этом пособии представлен материал, направленный на формирование навыков устного счёта по теме Счёт в пределах 20 для 1 класса.

Nsportal. ru

23.12.2020 16:30:18

2020-12-23 16:30:18

Источники:

Https://nsportal. ru/nachalnaya-shkola/matematika/2021/01/12/primery-v-predelah-20-1-klass

Примеры по математике для 1 класса (скачать и распечатать) » /> » /> .keyword { color: red; }

Примеры по математике 1 класс в пределах 20

Обучение математике проходит намного легче, если тренировать навыки каждый день. Генератор примеров предлагает задания Для учеников 1 класса: тренажер позволяет усовершенствовать навыки сложения и вычитания до 20. Арифметические действия с целыми числами должен освоить каждый ученик. Именно эти знания являются базовыми для дальнейшего изучения математики.

Первоклассникам не желательно много времени проводить за компьютером, поэтому все задания можно скачать и распечатать. Очень удобно, что Генератор показывает разные примеры при каждом запуске страницы. Так родители получают доступ к неограниченному количеству заданий. Дополнительно можно распечатать лист с ответами, чтобы тратить меньше времени на проверку.

После освоения простых арифметических действий можно переходить к более сложным. Преподаватели рекомендуют на следующем этапе осваивать умножение и деление. Тренажер разработан таким образом, что ученики 1 класса могут справиться самостоятельно со всеми примерами. Не стоит слишком сильно нагружать ребенка, максимальное количество – 1 лист в день.

Генератор примеров предлагает задания для учеников 1 класса тренажер позволяет усовершенствовать навыки сложения и вычитания до 20.

O-krohe. ru

20.10.2017 3:27:31

2017-10-20 03:27:31

Источники:

Https://o-krohe. ru/math/1-klass/

Математические примеры для 1. Решение примеров в несколько действий. Игра «Быстрый счет»

Каждый родитель должен понимать, что высокое качество полученных знаний в первом классе — это возможность в дальнейшем усваивать весь программный материал в школе.

Начиная обучение в школе, нужно научить ребенка решать примеры для первого класса по математике правильно и быстро.

Какие особенности мышления нужно учитывать?

Любые задачи и примеры для первого класса по математике должны быть рассчитаны на работу с наглядным пособием. У ребенка 5-7 лет не развито абстрактное мышление, поэтому работать со сложением и вычитанием в уме ему сложно.

Чтобы помочь малышу понять смысл этих действий, нужно пользоваться счетным материалом. Это могут быть обычные палочки, спички, карандаши. Лучше и интересней ребенку будет решать примеры для первого класса по математике, если условие составить на основе любимых мультипликационных героев.

Такие действия должны и могут делать все родители. Достаточно взять картинки, карточки с любимыми сказочными героями, выстроить машинки, куклы в ряд и составлять примеры на сложение и вычитание. В игре решается любой пример или задача быстро и легко. Постепенно такие действия будут доведены до автоматизма, и ребенок запомнит вычитание и сложение в пределах десятка.

Важно знать! Огромной ошибкой родителей является счет на пальцах. Учить ребенка такому счету нельзя. К середине 1 класса примеры по математике будут иметь несколько действий, в том числе и переход через десяток. Если дома ученик сможет видеть пальцы рук и ног, решать примеры, то в школе такие действия не будут доступны.

Математика (первый класс): примеры

Какие варианты примеров нужно давать детям? В чем секрет быстрого счета?

Во-первых, ученик должен уметь не только складывать или вычитать числа, но и четко понимать понятия «всего», «сумма», «разность». Каждое из этих понятий в последующем будет играть важную роль в решении задач.

Во-вторых, важно заучить наизусть таблицу состава числа. Она в последующем поможет быстро решать примеры первого десятка и складывать или вычитать с переходом через десяток.

Предложите своему ребенку примеры по типу:

2+2; 4+3; 7+3; 8+2; 10-3; 5-2.

Помогают запомнить состав числа примеры такого типа:

… +3=10; 5+… =8; 10-… =7; 8-…=6; … -2=4; 4+…=7.

Дайте ребенку возможность в игре получить знания, запоминать состав числа и складывать, вычитать, развлекаясь.

Первый класс. Математика. Примеры и задачи

Чтобы ученик быстро решал задачи, нужно с ним разобрать все общие понятия, которые в условии будут ключевыми вопросами. Он должен понимать значение фраз «сколько всего», «вместе», «добавить». Они будут требовать сложения имеющихся числовых значений в задаче. В случае наличия фраз «разница», «на сколько больше», «на сколько меньше» — это действие вычитания.

Предложите решение задач в форме игры. Например:

В магазине Дед Мороз купил 5 машин. 1 из них он подарил Саше, вторую — Мише, а все остальные принес вашему малышу. Сколько машин получил ваш ребенок?
Мама принесла домой 2 килограмма конфет, а папа — 3. Сколько всего конфет будет дома?
Лунтик получил от кузнечика Кузи 10 конфет. 5 он отдал Миле, 3 — бабушке Капе. Сколько конфет осталось у Лунтика?

Задачи и примеры для первого класса по математике — это фундамент, который поможет в последующем получать знания и осмысленно их применять в учебе.

На этом уроке мы научимся решать примеры в несколько действий на сложение и вычитание. Также мы поймем, для чего в примерах ставятся скобки, и в каком порядке решать такие примеры. Полученные знания помогут нам в дальнейшем решать более сложные задачи.

Тема: Знакомство с основными понятиями в математике

Урок: Решение примеров в несколько действий

Необходимо представить следующие действия с помощью математического выражения и решить пример.

На рисунке изображены 4 геометрические фигуры:

После этого добавим еще 2:

Эти действия можно записать следующим математическим выражением:

В результате получили пример в 2 действия: первое действие — сложение, второе действие — тоже сложение.

Примеры в несколько действий решаются по порядку — слева направо, как и выполнялось прибавление фигур.

1-е действие: ;

2-е действие: : .

Ответ: 9

Пример 2:

На рисунке даны 4 геометрические фигуры:

Добавим к этим фигурам еще 3 геометрические фигуры:

Затем уберем 2 фигуры:

Данные действия можно представить с помощью следующего математического выражения:

В результате получили выражение с двумя действиями: первое действие — сложение, второе — вычитание.

1-е действие: ;

2-е действие: : .

Ответ: 5.

Пример 3:

Необходимо решить следующее математическое выражение:

В условии этого примера есть скобки. В математике скобки указывают, что, если они присутствуют в примере, значит, нужно это действие выполнить первым.

Значит, первым действием выполним сложение в скобках , а затем полученный результат вычтем из 7.

1-е действие: ;

2-е действие: .

Ответ: 3.

Если в примере несколько действий, то действия выполняются по порядку — слева направо.

При решении примеров в несколько действий действие в скобках необходимо выполнять в первую очередь, а затем все остальные действия по порядку.

Итак, на этом уроке мы научились решать примеры в несколько действий на сложение и вычитание. Необходимо помнить порядок выполнения действий в примерах без скобочек и с ними.

Список литературы

Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.

Социальная сеть работников образования ().
Учительский портал ().
Myshared.ru ().

Домашнее задание

1. Необходимо представить следующие действия с помощью математического выражения и решить пример.

Тренажеры могут быть использованы для дополнительной работы с первоклассниками учителями и родителями в классе и дома как для индивидуальной, так и коллективной подготовки. Они способствуют автоматизации вычислительных навыков у ребенка, отработке умений складывать, вычитать, сравнивать и решать простые задачи.

Основа математики 1 класса — состав числа. Зная состав числа, а начать следует с домиков, ребенок гораздо быстрее сможет решить абсолютно любой пример на сложение или вычитание. Поэтому составу числа мы отводим целую страницу, кликните по картинке, чтобы

Освоили домики? Теперь можно браться за настоящие примеры на сложение и вычитание сначала в пределах десятка, а затем и в пределах 20.

Если есть необходимость повторить всю программу первого класса, начиная с азов, посмотрите тренажеры, размещенные ниже.

Чтобы посмотреть и скачать полную версию тренажера, кликните на картинку.

Примеры по математике за 1 класс

Пособие соответствует ФГОС второго поколения для начальной школы. Каждая работа в пособии рассчитана на недельную нагрузку. Систематическое выполнение заданий закрепит учебные навыки и умения по изучаемым темам курса математики, доведет до автоматизма умение решать задачи, числовые выражения, равенства и неравенства. 12 листов на 12 недель.

Тренажер по математике для 1 класс. Обучение решению задач. А.В.Белошистая

Пособие составлено в соответствии с базовой программой по математике для начальных классов и содержит задания для обучения решению задач в 1 классе. Такие задачи могут использоваться как учителем в школе, так и родителями для обучения и закрепления материала дома.

Математический лабиринт

Необходимо провести дорожку по тем ячейкам, сумма чисел в которых равна 10. Задание развивает не только математические способности, но и внимание, и умение удерживать внимание.

Конспект урока по математике в 1 классе на тему «Решение примеров на сложение и вычитание»

Тема: решение примеров на сложение и вычитание.

Цель: формирование и закрепление навыка решения примеров на сложение и вычитание в пределах 4.

Задачи:

1.Образовательные:

– формировать навыки счёта в пределах 4;

– формировать умения самостоятельно применять свои знания на практике.

2.Коррекционно-развивающие:

-способствовать развитию и коррекции устной речи, зрительного, слухового восприятия, мыслительных процессов, пространственной ориентировки.

3.Воспитательные:

-воспитывать интерес, эмоционально-положительное отношение к учёбе, культуру поведения на уроке, аккуратность в оформлении письменных работ.

Оборудование: дерево, яблоки, карточки с цифрами по количеству обучающихся, компьютер, проектор, экран.

Ход урока.

Организационный момент.

-Ребята, посмотрите, всё ли у вас готово к уроку?

– Какой сейчас урок?

– Какой по счёту урок?

– Кто отсутствует?

Актуализация знаний. Сообщение темы урока.

– Вот так чудо из чудес,

Мы попали с вами в лес.

У зверей идёт урок.

Медведь-учитель очень строг.

– Ребята, куда это мы попали? (это Лесная школа).

– Кто учится в этой школе? (Лесные звери…).

-Какой урок у них проходит?

-Что мы делаем на уроках математики?

-С какой цифрой познакомились на прошлых уроках?

(На доске – дерево, на дереве карточки с примерами).

-Сегодня нам предстоит вспомнить и назвать цифры, которые вы уже знаете, мы будем выполнять действия сложения и вычитания при решении примеров.

Слайд 3

– Посмотрите внимательно и скажите, какие деревья окружают школу? (Ёлочки).

– Покажите карточкой сколько деревьев слева от школы? (1).

– Сколько деревьев справа от школы? (2).

– Сколько деревьев перед школой? (2).

– Сколько больших деревьев? (2).

– Сколько маленьких деревьев? (1).

– Что можно сказать об их количестве? (больших деревьев больше, чем маленьких).

Слайд 4

-Догадайтесь, какая ёлочка должна продолжить ряд?

Минутка чистописания

-Откройте тетрадки, положите правильно перед собой, сядьте ровно, нарисуйте елочки в тетрадках.

-Покажите цифру, которая обозначает число елочек на рисунке (3)

-Вспомним написание цифры 3. Через клеточку запишите 3 цифры 3.

Повторение изученного материала.

1. Построение числового ряда.

Составьте числовой ряд на парте: 0 1 2 3 4

2. Работа с числовым рядом.

· Сейчас возьмите, пожалуйста, карточки с числами и показывайте нужный ответ:

1. за каким числом следует число 4? (3)

2. какое число предшествует числу 3? (2)

3. какое число стоит между числами 2 и 4? (3)

4. между какими числами стоит число 2? (1 и 3)

3. Игра «Хлопай—топай…».

· А теперь немного поиграем. Я буду показывать вам цифру и давать определённую команду, а вы будете выполнять её столько раз, сколько я вам показываю.

· ты похлопай столько раз, сколько покажу сейчас (4)

· ты потопай столько раз, сколько покажу сейчас. (3)

* покивай столько раз, сколько покажу сейчас. (2)

· И с этим заданием вы хорошо справились.

Изучение новых знаний

-Первое задание. Нарисуйте два синих квадрата, дорисуйте один красный. Сколько всего квадратов? (3)

-Какой пример составим? (2+1=3). Запишите

-Поменяйте квадраты местами. Какого цвета квадрат надо сначала нарисовать? (красного)

-Какие квадраты добавим? (синего цвета)

-Какой пример запишем? (1+2=3)

-Каким правилом мы пользовались? ( при сложении числа можно менять местами)

-Чтобы выполнить следующее задание мы дадим отдохнуть нашим глазкам

3-1=2

Физ. минутка для глаз

Вот стоит большая елка,
Вот такой высоты.
У нее большие ветки.
Вот такой ширины.
Есть на елке даже шишки,
А внизу – берлога мишки.

Выполняют движения глазами.
Посмотреть снизу вверх.
Посмотреть слева направо.
Посмотреть вверх.
Посмотреть вниз.
Зажмурить глаза, потом поморгать 10 раз

Закрепление. Работа по карточкам

– Составьте по рисунку пример на сложение, используя карточки на партах ( 3+1=4). Запишите.

Поменяйте в примере цифры местами и запишите (1+3=4).

-Проверьте (запись на доске). Кто составил такие же примеры нарисуйте зеленый кружок, кто допустил 1 ошибку –желтый кружок, поднимите руку, кому было тяжело справиться с заданием

Итог урока. Рефлексия.Тема: решение примеров на сложение и вычитание.

Цель: формирование и закрепление навыка решения примеров на сложение и вычитание в пределах 4.

Задачи:

1. Образовательные:

– формировать навыки счёта в пределах 4;

– формировать умения самостоятельно применять свои знания на практике.

2.Коррекционно-развивающие:

3.Воспитательные:

Оборудование: дерево, яблоки, карточки с цифрами по количеству обучающихся, компьютер, проектор, экран.

Ход урока.

Организационный момент.

-Ребята, посмотрите, всё ли у вас готово к уроку?

– Какой сейчас урок?

– Какой по счёту урок?

– Кто отсутствует?

Актуализация знаний. Сообщение темы урока.

– Вот так чудо из чудес,

Мы попали с вами в лес.

У зверей идёт урок.

Медведь-учитель очень строг.

– Ребята, куда это мы попали? (это Лесная школа).

– Кто учится в этой школе? (Лесные звери…).

-Какой урок у них проходит?

-Что мы делаем на уроках математики?

-С какой цифрой познакомились на прошлых уроках?

(На доске – дерево, на дереве карточки с примерами).

Слайд 3

– Посмотрите внимательно и скажите, какие деревья окружают школу? (Ёлочки).

– Покажите карточкой сколько деревьев слева от школы? (1).

– Сколько деревьев справа от школы? (2).

– Сколько деревьев перед школой? (2).

– Сколько больших деревьев? (2).

– Сколько маленьких деревьев? (1).

– Что можно сказать об их количестве? (больших деревьев больше, чем маленьких).

Слайд 4

-Догадайтесь, какая ёлочка должна продолжить ряд?

Минутка чистописания

-Откройте тетрадки, положите правильно перед собой, сядьте ровно, нарисуйте елочки в тетрадках.

-Покажите цифру, которая обозначает число елочек на рисунке (3)

-Вспомним написание цифры 3. Через клеточку запишите 3 цифры 3.

Повторение изученного материала.

1. Построение числового ряда.

Составьте числовой ряд на парте: 0 1 2 3 4

2. Работа с числовым рядом.

· Сейчас возьмите, пожалуйста, карточки с числами и показывайте нужный ответ:

1. за каким числом следует число 4? (3)

2. какое число предшествует числу 3? (2)

3. какое число стоит между числами 2 и 4? (3)

4. между какими числами стоит число 2? (1 и 3)

3. Игра «Хлопай—топай…».

· ты похлопай столько раз, сколько покажу сейчас (4)

· ты потопай столько раз, сколько покажу сейчас. (3)

* покивай столько раз, сколько покажу сейчас. (2)

· И с этим заданием вы хорошо справились.

Изучение новых знаний

-Первое задание. Нарисуйте два синих квадрата, дорисуйте один красный. Сколько всего квадратов? (3)

-Какой пример составим? (2+1=3). Запишите

-Поменяйте квадраты местами. Какого цвета квадрат надо сначала нарисовать? (красного)

-Какие квадраты добавим? (синего цвета)

-Какой пример запишем? (1+2=3)

-Каким правилом мы пользовались? ( при сложении числа можно менять местами)

-Чтобы выполнить следующее задание мы дадим отдохнуть нашим глазкам

3-1=2

Физ. минутка для глаз

Закрепление. Работа по карточкам

– Составьте по рисунку пример на сложение, используя карточки на партах ( 3+1=4). Запишите.

Поменяйте в примере цифры местами и запишите (1+3=4).

Итог урока. Рефлексия.

Тема: решение примеров на сложение и вычитание.

Цель: формирование и закрепление навыка решения примеров на сложение и вычитание в пределах 4.

Задачи:

1.Образовательные:

— формировать навыки счёта в пределах 4;

— формировать умения самостоятельно применять свои знания на практике.

2.Коррекционно-развивающие:

3.Воспитательные:

Оборудование: дерево, яблоки, карточки с цифрами по количеству обучающихся, компьютер, проектор, экран.

Ход урока.

Организационный момент.

-Ребята, посмотрите, всё ли у вас готово к уроку?

— Какой сейчас урок?

— Какой по счёту урок?

— Кто отсутствует?

Актуализация знаний. Сообщение темы урока.

— Вот так чудо из чудес,

Мы попали с вами в лес.

У зверей идёт урок.

Медведь-учитель очень строг.

— Ребята, куда это мы попали? (это Лесная школа).

— Кто учится в этой школе? (Лесные звери…).

-Какой урок у них проходит?

-Что мы делаем на уроках математики?

-С какой цифрой познакомились на прошлых уроках?

(На доске – дерево, на дереве карточки с примерами).

Слайд 3

– Посмотрите внимательно и скажите, какие деревья окружают школу? (Ёлочки).

– Покажите карточкой сколько деревьев слева от школы? (1).

– Сколько деревьев справа от школы? (2).

– Сколько деревьев перед школой? (2).

– Сколько больших деревьев? (2).

– Сколько маленьких деревьев? (1).

– Что можно сказать об их количестве? (больших деревьев больше, чем маленьких).

Слайд 4

-Догадайтесь, какая ёлочка должна продолжить ряд?

Минутка чистописания

-Откройте тетрадки, положите правильно перед собой, сядьте ровно, нарисуйте елочки в тетрадках.

-Покажите цифру, которая обозначает число елочек на рисунке (3)

-Вспомним написание цифры 3. Через клеточку запишите 3 цифры 3.

Повторение изученного материала.

1. Построение числового ряда.

Составьте числовой ряд на парте: 0 1 2 3 4

2. Работа с числовым рядом.

Сейчас возьмите, пожалуйста, карточки с числами и показывайте нужный ответ:

за каким числом следует число 4? (3)
какое число предшествует числу 3? (2)
какое число стоит между числами 2 и 4? (3)
между какими числами стоит число 2? (1 и 3)

3. Игра «Хлопай—топай…».

А теперь немного поиграем. Я буду показывать вам цифру и давать определённую команду, а вы будете выполнять её столько раз, сколько я вам показываю.
ты похлопай столько раз, сколько покажу сейчас (4)
ты потопай столько раз, сколько покажу сейчас. (3)

* покивай столько раз, сколько покажу сейчас. (2)

И с этим заданием вы хорошо справились.

Изучение новых знаний

-Первое задание. Нарисуйте два синих квадрата, дорисуйте один красный. Сколько всего квадратов? (3)

-Какой пример составим? (2+1=3). Запишите

-Поменяйте квадраты местами. Какого цвета квадрат надо сначала нарисовать? (красного)

-Какие квадраты добавим? (синего цвета)

-Какой пример запишем? (1+2=3)

-Каким правилом мы пользовались? ( при сложении числа можно менять местами)

-Чтобы выполнить следующее задание мы дадим отдохнуть нашим глазкам

3-1=2

Физ. минутка для глаз

Выполняют движения глазами.
Посмотреть снизу вверх.
Посмотреть слева направо.
Посмотреть вверх.
Посмотреть вниз.
Зажмурить глаза, потом поморгать 10 раз

Закрепление. Работа по карточкам

— Составьте по рисунку пример на сложение, используя карточки на партах ( 3+1=4). Запишите.

Поменяйте в примере цифры местами и запишите (1+3=4).

Итог урока. Рефлексия.

Как решать примеры 1 1. Решение примеров в несколько действий. Работа над пройденным материалом

Чтобы посмотреть и скачать полную версию тренажера, кликните на картинку.

Примеры по математике за 1 класс

Тренажер по математике для 1 класс. Обучение решению задач. А.В.Белошистая

Математический лабиринт

Какие особенности мышления нужно учитывать?

Математика (первый класс): примеры

Какие варианты примеров нужно давать детям? В чем секрет быстрого счета?

Предложите своему ребенку примеры по типу:

2+2; 4+3; 7+3; 8+2; 10-3; 5-2.

Помогают запомнить состав числа примеры такого типа:

… +3=10; 5+… =8; 10-… =7; 8-…=6; … -2=4; 4+…=7.

Первый класс. Математика. Примеры и задачи

Предложите решение задач в форме игры. Например:

В магазине Дед Мороз купил 5 машин. 1 из них он подарил Саше, вторую — Мише, а все остальные принес вашему малышу. Сколько машин получил ваш ребенок?
Мама принесла домой 2 килограмма конфет, а папа — 3. Сколько всего конфет будет дома?
Лунтик получил от кузнечика Кузи 10 конфет. 5 он отдал Миле, 3 — бабушке Капе. Сколько конфет осталось у Лунтика?

Тема: Знакомство с основными понятиями в математике

Урок: Решение примеров в несколько действий

Необходимо представить следующие действия с помощью математического выражения и решить пример.

На рисунке изображены 4 геометрические фигуры:

После этого добавим еще 2:

Эти действия можно записать следующим математическим выражением:

В результате получили пример в 2 действия: первое действие — сложение, второе действие — тоже сложение.

Примеры в несколько действий решаются по порядку — слева направо, как и выполнялось прибавление фигур.

1-е действие: ;

2-е действие: : .

Ответ: 9

Пример 2:

На рисунке даны 4 геометрические фигуры:

Добавим к этим фигурам еще 3 геометрические фигуры:

Затем уберем 2 фигуры:

Данные действия можно представить с помощью следующего математического выражения:

В результате получили выражение с двумя действиями: первое действие — сложение, второе — вычитание.

1-е действие: ;

2-е действие: : .

Ответ: 5.

Пример 3:

Необходимо решить следующее математическое выражение:

Значит, первым действием выполним сложение в скобках , а затем полученный результат вычтем из 7.

1-е действие: ;

2-е действие: .

Ответ: 3.

Если в примере несколько действий, то действия выполняются по порядку — слева направо.

Список литературы

Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.

Социальная сеть работников образования ().
Учительский портал ().
Myshared.ru ().

Домашнее задание

1. Необходимо представить следующие действия с помощью математического выражения и решить пример.

Развитие навыков решения проблем у детей | Стратегии и советы

Мы сделали обучение детей навыкам решения задач намного проще! Продолжайте читать и комментируйте ниже любые другие советы, которые у вас есть для вашего класса!

Навыки решения проблем для детей: настоящее дело

Представьте себе: Вы тщательно подготовили задание для своего класса. Пошаговые инструкции кристально ясны. Во время занятий вы проходите по всем направлениям, и реакция потрясающая. Ваши ученики готовы! Наконец-то пришло время для них начать работать индивидуально, а затем… 8 рук поднимаются с вопросами. Вы слышите, как один из студентов бормочет вдалеке: «Подождите, я этого не понимаю», а затем пугает: «Что мы должны делать снова?»

Когда я был новым учителем информатики, у меня была именно такая ситуация. В результате я в конечном итоге изо всех сил пытался помочь каждому ученику с его проблемами, пока половина урока не была съедена. Я предположил, что для того, чтобы мои ученики лучше учились, мне нужно было быть рядом, чтобы помочь сразу ответить на вопросы, чтобы они могли двигаться вперед и выполнять задание.

Вот что я хотел бы знать, когда начал преподавать программирование ученикам начальной школы — процесс изучения содержания задания может быть важнее, чем завершение его продукта. Тем не менее, не каждый ученик знает, как бороться или бороться, чтобы добраться до «ага!» момент и решить проблему самостоятельно. Хорошая новость заключается в том, что способность творчески решать проблемы не является фиксированным навыком. Его могут изучать ученики, взращивать учителя и практиковать каждый!

Ваши ученики абсолютно способны ориентироваться в задачах и решать их самостоятельно. Вот несколько стратегий, советов и ресурсов, которые могут помочь:

Навыки решения проблем для детей:

Когда увидишь		Подумай
добавить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более		+
минус, меньше, разность, меньше, меньше, меньше		—
умножить, раз, произведение, коэффициент		×
разделить, частное, на, из, отношение, отношение, процент, показатель		÷
увеличить или уменьшить		геометрия формулы
Скорость, скорость		расстояние формулы
Как долго, дни, часы, минуты, секунды		время

Стратегии для учащихся
Это стратегии, которые ваши учащиеся могут использовать во время самостоятельной работы, чтобы научиться творчески решать проблемы.
1. Шаг за шагом выполняйте последовательность решения проблем
Разместите опорные диаграммы и ссылки для решения проблем на стене своего класса или прикрепите их к своему Google Классу — сделайте все, чтобы сделать их доступными для учащихся. Когда они просят о помощи, предложите им сначала обратиться к диаграммам.
Последовательность решения задач, созданная Kodable
2. Пересмотрите прошлые проблемы
Если учащийся застрял, он должен спросить себя: «Сталкивался ли я когда-нибудь с такой задачей раньше? Если да, то как я ее решил?» Скорее всего, ваши ученики уже решали что-то подобное и могут использовать те же стратегии, которые они использовали раньше, чтобы решить проблему на этот раз.
3. Задокументируйте, что
не работает работает
Иногда поиск ответа на проблему требует процесса исключения. Пусть ваши ученики попытаются решить проблему как минимум двумя разными способами, прежде чем обращаться к вам за помощью. Еще лучше, попросите их записать свои «не-ответы», чтобы вы могли видеть их мыслительный процесс, когда вы все же вмешаетесь, чтобы поддержать. Круто, скорее всего, вам это не понадобится! Пытаясь решить проблему несколькими способами, учащиеся часто находят ответ самостоятельно.
4. «3 Before Me»
Допустим, ваши ученики прошли процесс решения проблем, пересмотрели прошлые проблемы и задокументировали, что не работает. Теперь они знают, что пришло время попросить кого-нибудь о помощи. Большой! Но прежде чем прыгнуть в спасение дня, потренируйтесь в «3 Before Me». Это означает, что учащиеся должны задать свой вопрос трем другим одноклассникам, прежде чем задавать их учителю. Делая это, учащиеся отрабатывают полезные навыки 21-го века, такие как сотрудничество и общение, и обычно могут найти нужную информацию по пути.
Навыки решения проблем для детей:
Советы учителям
Эти советы вы, учитель, можете использовать, чтобы помочь учащимся развить творческие навыки решения проблем у детей.
1. Задавайте открытые вопросы
Когда учащийся просит о помощи, может возникнуть соблазн дать ему ответ, который он ищет, чтобы вы оба могли двигаться дальше. Но на самом деле это мешает учащемуся развить навыки, необходимые для самостоятельного решения проблемы. Вместо того, чтобы давать ответы, попробуйте использовать открытые вопросы и подсказки. Вот несколько примеров:
Открытые вопросы от Lemon Lime Adventures
2. Поощряйте борьбу
Борьба – это все, что может сделать учащийся, столкнувшись с проблемой, не имеющей четкого решения. Как объясняется в этой статье от Edutopia, это не , а означает настойчивость! Борьба — это нечто большее: она включает в себя критическое мышление, задавание вопросов, наблюдение за фактами, задавание большего количества вопросов, формирование гипотез и построение глубокого понимания проблемы.
The Engineer Design Process by Kids Steam Lab
Существует множество способов предоставить возможности для борьбы. Все, что включает в себя процесс инженерного проектирования, является хорошим! Примеры включают:
Инженерные или художественные проекты
Задачи дизайнерского мышления
Проекты по информатике
Научные эксперименты
3.
Делайте акцент на процессе, а не на продукте
помогает им развивать мышление роста. Получение ответа «неправильно» не должно быть чем-то плохим! Самое важное — это шаги, которые они предприняли, чтобы добиться этого, и то, как они могут изменить свой подход в следующий раз. Как учитель, вы можете поддержать учащихся в изучении этого процесса рефлексии.
Сила «пока» от Working Moms World
4. Смоделируйте стратегии самостоятельно!
По мере того, как дети осваивают навыки творческого решения проблем, вероятно, будут моменты, когда они будут разочарованы или неуверенны. Вот несколько простых способов смоделировать, как выглядит и звучит творческое решение проблем.
Задавайте уточняющие вопросы, если вы что-то не понимаете
Признавайте, если не знаете правильный ответ
Обсуждайте несколько возможных исходов для разных ситуаций
Вербализируйте, что вы чувствуете, когда обнаруживаете проблему
Практика этих стратегий со своими учениками поможет создать учебную среду, в которой приветствуется борьба, неудачи и рост!
Навыки решения проблем для детей
Мы пропустили что-нибудь из ваших любимых? Комментируйте и делитесь ими ниже!
Хотите добавить в свой класс творческое решение задач?
Создайте бесплатную учетную запись учителя и научите своих учеников программировать.
Развитие навыков решения проблем у детей | Стратегии и советы Джон Маттингли
Решение словесных вопросов
МНОГО примеров!
В алгебре у нас часто возникают словесные вопросы, например:
Пример: Сэм и Алекс играют в теннис.
В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.
Сколько игр сыграл Алекс?
Как их решить?
Хитрость заключается в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем используйте алгебру для решения.
Превращение английского языка в алгебру
Превратить английский язык в алгебру поможет:
Сначала прочитайте все
Сделайте набросок если возможно
Назначить буквы для значений
Найти или вычислить формулы
Вы также должны записать то, что на самом деле запрашивается , чтобы вы знали, куда вы идете и когда вы прибыли!
Также ищите ключевые слова:
Когда увидишь Подумай
добавить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более
+
минус, меньше, разность, меньше, меньше, меньше
—
умножить, раз, произведение, коэффициент
×
разделить, частное, на, из, отношение, отношение, процент, показатель
÷
увеличить или уменьшить геометрия
формулы
Скорость, скорость расстояние
формулы
Как долго, дни, часы, минуты, секунды время
Мыслить ясно
Некоторые формулировки могут быть сложными, из-за чего трудно думать «правильно», например:
$
Пример: У Сэма на 2 доллара меньше, чем у Алекса.
Как мы запишем это в виде уравнения?
Пусть S = доллары У Сэма есть
Пусть A = долларов У Алекса есть
Теперь … это: S − 2 = A
или должно быть: S = A − 2
или должно быть: S = 2 − A

Правильный ответ S = A − 2
( S − 2 = A – распространенная ошибка, так как вопрос написан «Сэм… на 2 меньше… Алекс»)
Пример: на нашей улице собак вдвое больше, чем кошек. Как мы запишем это в виде уравнения?
Пусть D = количество собак
Пусть C = количество кошек
Теперь… это: 2D = C
или должно быть: D = 2C
Теперь хорошенько подумайте!
Правильный ответ D = 2C
( 2D = C — распространенная ошибка, так как вопрос пишется «дважды… собаки… кошки»)
Примеры
Давайте начнем с действительно простого примера , чтобы мы увидели, как это делается:
Пример: прямоугольный сад размером 12 м на 5 м, какова его площадь?

Превратите английский в алгебру:
Эскиз:
Буквы:
Используйте w для ширины прямоугольника: w = 12 м
Используйте h для высоты прямоугольника: h = 5 м
Формула для площади прямоугольника: A = w × h
Нас спрашивают о площади.

Решите:
A = w × h = 12 × 5 = 60 м ²
Площадь 60 квадратных метров .
Теперь давайте попробуем пример из верхней части страницы:
Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алексей?

Превратите английский в алгебру:
Буквы:
Используйте S для того, сколько игр сыграл Сэм
Используйте A для того, сколько игр сыграл Алекс
Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4
И мы знаем, что вместе они сыграли 12 игр: S + A = 12
Нас спрашивают, сколько игр, в которые играл Алекс: A

Решите:
Начните с: S + A = 12
S = A + 4 , поэтому мы можем
заменить «A + 4» на S: (A + 4) + A = 12
Упростить: 2A + 4 = 12
Вычесть 4 из обеих частей: 2A = 12 − 4
Упростить: 2A = 8
Разделить обе части на 2: A = 4
Это означает, что Алекс сыграл 4 игры в теннис.

Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр. Вместе они сыграли 8 + 4 = 12 игр. Да!
Чуть более сложный пример:
Пример: Алекс и Сэм тоже строят столы.

Вместе они делают 10 столов за 12 дней.
Алекс, работая в одиночку, может сделать 10 штук за 30 дней.
Сколько времени потребуется Сэму, работающему одному, чтобы сделать 10 столов?

Превратите английский в алгебру:
Буквы:
Используйте a для скорости работы Алекса
Используйте s для скорости работы Сэма
12 дней Алекса и Сэма — это 10 столов, поэтому: 12a + 12s = 10
30 дней одного Алекса — это тоже 10 столов: 30a = 10
Нас спрашивают, сколько времени займет Сэм сделать 10 столов.
Решите:
30a = 10 , значит, курс Алекса (столов в день): a = 10/30 = 1/3
Начнем с: 12a + 12s = 10
5 /3″ для a: 12(1/3) + 12s = 10
Упрощение: 4 + 12S = 10
Вычитание 4 с обеих сторон: 12S = 6
Разделите обе стороны на 12: S = 6/12
, что упрощает: S = 1/2
, что означает с = 1/2
, что означает с = 1/2
, что означает с = 1/2
. что скорость Сэма составляет полстола в день (быстрее, чем у Алекса!)
Таким образом, 10 столов займут у Сэма всего 20 дней.
Интересно, Сэму нужно платить больше?
И еще пример «подстановки»:
Пример: Дженна усердно тренируется, чтобы пройти отбор на Национальные игры.
У нее регулярный еженедельный распорядок: в некоторые дни она тренируется по пять часов в день, а в другие дни — по 3 часа.
Всего она тренируется 27 часов в неделю. Сколько дней она тренируется по пять часов?
Буквы:
Количество «5-часовых» дней: d
Количество «3-х часовых» дней: e
Мы знаем, что в неделе семь дней, поэтому: d + e = 7
И она тренируется 27 часов в неделю, из них d 5 часов в день и e 3 часа в день: 5d + 3e = 27
Нас спрашивают, сколько дней она тренируется по 5 часов: d

= 7
Итак: e = 7 − d
Подставим это в 5d + 3e = 27 5d + 3(7−d) = 27
2
Упростим: 5901
Вычесть 21 с обеих сторон: 5d − 3d = 6
Упростить: 2d = 6
Разделите обе части на 2: d = 3
Число «5-часовых» дней равно 3
Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому тренироваться по 3 часа в день в остальные 4 дня недели.
3 × 5 часов = 15 часов плюс 4 × 3 часа = 12 часов дает в сумме 27 часов
Несколько примеров из геометрии:
Пример: площадь круга 12 мм
² , каков его радиус?
Буквы:
Используйте A для области: A = 12 мм ²
Используйте r для радиуса
А формула площади такова: A = π r ²
Нас спрашивают о радиусе.
Решите:
Нам нужно изменить формулу, чтобы найти площадь
Начните с: A = π r ²
Поменяйте местами стороны: π r ²3 = A 90003
Разделение обеих сторон на π : R ² = A / π
Квадратный корень с обеих сторон: R = √ (A / π) 3
9000 3
9000 3
9000 3
9000 3
9000 3
9000 3
9000 3
9 3
9000 3
9 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 39 формула: r = √(12/ π)
И получаем: r = 1,954 (на 3 знака)
Пример: куб имеет объем 125 мм
³ , какова площадь его поверхности?
Сделать быстрый набросок:
Буквы:
Использовать V для тома
Используйте A для Зоны
Используйте s для длины стороны куба
Формулы:
Объем куба: V = s ³
Площадь поверхности куба: A = 6s ²
Нас спрашивают о площади поверхности.
Решите:
Сначала вычислите s по формуле объема:
Начните с: V = S ³
СОЗДАНИЕ СОЗДАНИЕ: S ³ = V
Корень куба с обеих сторон: S = ∛ (V )
и we Get: We )
и мы Get Get: We )
и мы Get Get: ) (125 ) = 5
Теперь мы можем рассчитать площадь поверхности:
СТАРЬ С: A = 6S ²
и мы получаем: A = 6 (5) ²99135 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000
А = 6 × 25 = 150 мм ²
Пример про Деньги:
Пример: Джоэл работает в местной пиццерии. Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки.
Одну неделю Джоэл работал 40 часов по обычной ставке, а также работал сверхурочно 12 часов. Если Джоэл в общей сложности заработал 660 долларов за эту неделю, какова его нормальная ставка?

Письма:
Обычная ставка Джоэла: $N в час
Формулы:
Джоэл работает 40 часов за N долларов в час = 40N долларов
Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1,25 N долларов в час
Джоэл работает 12 часов за 1,25 н. долл. США в час = (12 × 1¼ Н) = 15 н. долл. США
И вместе он заработал 660 долларов, так что:
$40N + $(12 × 1¼N) = $660
Нас спрашивают об обычной ставке Джоэла в $N.

Решите:
Начните с 40N $ + (12 × 1¼N) = 660 $
Упростите: 40N $ + 15N = 660 $
Упростить больше: $ 55N = 660 долл. США
Разделите обе стороны на 55: $ n = 12 долларов
, так что нормальная ставка Джоэла — 12 долларов США в час
. составляет 12 долларов в час, поэтому его ставка сверхурочных составляет 1¼ × 12 долларов в час = 15 долларов в час. Таким образом, его обычная заработная плата 40 × 12 = 480 долларов плюс оплата сверхурочных 12 × 15 = 180 долларов дает нам в сумме 660
долларов.
Подробнее о деньгах, с этими двумя примерами, связанными со сложными процентами
Пример: Алекс кладет в банк 2000 долларов под сложные проценты в размере 11% годовых. Сколько он будет стоить через 3 года?
Это формула сложных процентов:
Поэтому мы будем использовать эти буквы:
Приведенная стоимость PV = 2000 долларов США
Процентная ставка (в виде десятичной дроби): r = 0,11
Количество периодов: n = 3
Будущая стоимость (значение, которое мы хотим): FV
Нас спрашивают о будущем значении: FV

Решите:
Начните с: FV = PV × (1+r) ⁿ
FV9 = что мы знаем: 4 $2000 × (1+0,11) ³
Вычислить: FV = $2000 × 1,367631
Вычислить: FV = $2735,26 (с точностью до 3 центов) 900
Пример: Роджер положил 1000 долларов на сберегательный счет.
Начисленные проценты начислялись ежегодно по той же ставке. Через девять лет депозит Роджера вырос до 1551,33 доллара 9.0025
Какова была годовая процентная ставка по сберегательному счету?
Формула сложных процентов:
С:
Текущая стоимость PV = $1,000
Процентная ставка (значение, которое мы хотим): r
Количество периодов: n = 9
Будущая стоимость: FV = $1551,33
Нас спрашивают о процентной ставке: r

Решите:
Начните с: FV = PV × (1+r) ⁿ
Поместите то, что мы знаем: $ 1,551,33 = 1000 × (1+R) ⁹
Swap Sides: $ 1000 × (1+R) ⁹ = $ 1,551,333 3333.3335.3333.3335.33339513 9035.333.333.333.9513 9035.10013 9035.10013 9035.10013 9035.10013 9035.10013 9035 9.333.3339513 9013. : (1+r) = 1 551,33 долл. США / 1000 долл. США
Упрощение: (1+R) ⁹ = 1,55133
9th Root: 1+1,555135
.
Рассчитать: 1+r = 1,05
Рассчитать: r = 0,05 = 5%
Таким образом, годовая процентная ставка составляет 5%
Чек : 1000 долл. США × (1,05) ⁹ = 1000 долл. США × 1,55133 = 1551,33 долл. США
И пример вопроса о соотношении:
Пример: В начале года соотношение мальчиков и девочек в классе было 2 : 1
Но сейчас, спустя полгода, из класса ушли четыре мальчика и две новые девочки. Соотношение мальчиков и девочек теперь 4 : 3
Сколько сейчас всего учеников?
Письма:
Количество мальчиков сейчас: б
Количество девушек сейчас: г
Коэффициент тока составляет 4: 3
B G = 4 3
, который может быть перестановлен до 3B = 4G
В начале года. 4) мальчиков и (г — 2) девочек, а соотношение было 2 : 1
б + 4 г — 2 = 2 1
Которое можно преобразовать в b + 4 = 2(g − 2)
Нас спрашивают, сколько всего учеников сейчас: b + g
Решите :
Начало с: B + 4 = 2 (g — 2)
Упрощение: B + 4 = 2G — 4
Подряд 4 с обеих сторон: B =
. 8
Умножаем обе части на 3 (получаем 3b): 3B = 6G — 24
Помните 3B = 4G : 4G = 6G — 24
6G От оба С. С. С. С. С. С. С. С. С. СИДЫ 40002 6G от оба С. С. С. СИДЕР : — 40003
. Разделите обе части на −2: г = 12
Есть 12 девочек !
И 3b = 4g , поэтому b = 4g/3 = 4 × 12 / 3 = 16 , значит, 16 мальчиков
Итак, теперь в классе 12 девочек и 16 мальчиков, что составляет всего 28 учащихся .
Чек
Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек 16 : 12 = 4 : 3
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20 : 10 = 2 : 1
А теперь немного квадратных уравнений:
Пример: Произведение двух последовательных четных целых чисел равно 168. Что это за целые числа?
Последовательный означает один за другим. А их даже , так что они могут быть 2 и 4, или 4 и 6, и т. д.
Мы назовем меньшее целое число n , поэтому большее целое число должно быть n+2
И нам говорят, что произведение ( то, что мы получаем после умножения) равно 168, поэтому мы знаем:
n(n + 2) = 168
Нас просят ввести целые числа
Решить:
Начать с: n(n + 2) = 168
Развернуть: n ² + 2n = 168
Вычесть 168 с обеих сторон: n ² + 2n − 168 = 0
Это квадратное уравнение, и есть много способов его решения. Используя Решатель квадратных уравнений, мы получаем -14 и 12.
Проверка -14: -14(-14 + 2) = (-14)×(-12) = 168 ДА
Проверка 12: 12( 12 + 2) = 12×14 = 168 ДА
Итак, есть два решения: −14 и −12 — одно, 12 и 14 — другое.

Примечание: мы могли бы также попробовать «угадать и проверить»:
Мы могли бы попробовать, скажем, n=10: 10(12) = 120 НЕТ (слишком маленький)
Далее мы можем попробовать n=12: 12(14) = 168 ДА
Но если мы не будем помнить, что умножение двух отрицательных чисел дает положительное, мы можем упустить из виду другое решение (−14)×(−12).
А:
Пример: Вы архитектор. Ваш клиент хочет, чтобы комната была в два раза длиннее, чем ее ширина. Они также хотят веранду шириной 3 метра вдоль длинной стороны.
У вашего клиента есть 56 квадратных метров красивой мраморной плитки, чтобы покрыть всю площадь.
Какой длины должна быть комната?
Давайте сначала сделаем эскиз, чтобы все получилось правильно!:
Буквы:
длина комнаты: L
ширина комнаты: Ш
Общая площадь включая веранду: А
Мы знаем:
ширина комнаты равна половине ее длины: Ш = ½Д
общая площадь равна (ширине комнаты + 3), умноженной на длину: А = (Ш+3) × Д = 56
Нас спрашивают о длине комнаты: Д
Решите:
Начните с: (Ш + 3) × Д = 56
Замените Ш = ½Д : (½Д1 + 3) × l = 56
Упрощайте: ½l ² + 3L = 56
Умножение все термины на 2: L ² + 6L = 112
^{23 + 6L = 112
2 23 + 6L = 112
23 + 6L = 112
23 + 6L = 112 9000 3 ^{23 + 6L = 112 9000 3}}3 + 61 2 9000 9000 2 23 + 6 л. л ² + 6 л — 112 = 0
Это квадратное уравнение , есть много способов решить его, на этот раз давайте воспользуемся факторингом:
Начнем с: L ² + 6L − 112 = 0
Два числа, которые умножаются, чтобы дать ас=-112,
и сложите, чтобы получить b = 6, 14 и -8: L ² + 14L — 8L — 112 = 0
Группа: L(L +14) — 8(L + 14) = 0
Группа : (L − 8)(L + 14) = 0
Итак, L = 8 или −14
Есть два решения квадратного уравнения, но возможно только одно из них, так как длина комнаты не может быть отрицательной!
Итак, длина комнаты 8 м
Чек
L = 8, поэтому W = ½L = 4
Итак, площадь прямоугольника = (W+3) × L = 7 × 8 = 56
Вот и мы…
… Я надеюсь, что эти примеры помогут вам понять, как обращаться со словесными вопросами. Теперь как насчет практики?

Обучение навыкам решения проблем | Центр педагогического мастерства
Многие преподаватели инженерного дела, математики и естественных наук заставляют студентов решать «задачи».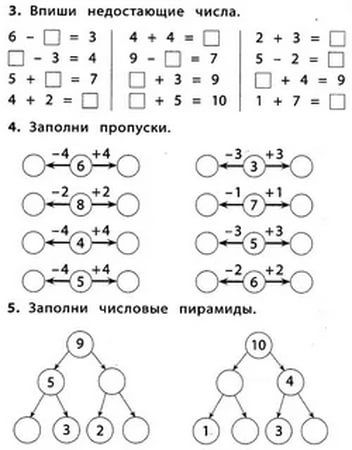 Но решают ли их ученики настоящие задачи или просто упражнения? Первый подчеркивает навыки критического мышления и принятия решений, тогда как последний требует только применения ранее изученных процедур. Истинное решение проблемы — это процесс применения неизвестного заранее метода к проблеме, которая подчиняется определенному набору условий и которую человек, решающий проблему, раньше не видел, чтобы получить удовлетворительное решение.
Ниже вы найдете несколько основных принципов обучения решению задач и одну модель, которую можно использовать в обучении в классе.
Принципы обучения решению задач
Моделирование полезного метода решения задач . Решение проблем может быть трудным, а иногда и утомительным. Покажите студентам на своем примере, как быть терпеливыми и настойчивыми и как следовать структурированному методу, такому как описанная здесь модель Вудса. Сформулируйте свой метод по мере его использования, чтобы учащиеся увидели связи.
Обучение в конкретном контексте . Обучайте навыкам решения задач в том контексте, в котором они будут использоваться (например, расчет мольных долей в курсе химии). Используйте реальные проблемы в объяснениях, примерах и экзаменах. Не учите решению проблем как самостоятельному, абстрактному навыку.
Помогите учащимся понять задачу . Для решения задач учащиеся должны определить конечную цель. Этот шаг имеет решающее значение для успешного обучения навыкам решения проблем. Если вам удастся помочь учащимся ответить на вопросы «что?» и «почему?», найти ответ на «как?» будет легче.
Потратьте достаточно времени . Планируя лекцию/руководство, выделите достаточно времени для: понимания проблемы и определения цели как индивидуально, так и в классе; работа с вопросами от вас и ваших студентов; совершать, находить и исправлять ошибки; и решать целые проблемы за один сеанс.
Задавайте вопросы и вносите предложения . Попросите учащихся предсказать, «что произойдет, если…» или объяснить, почему что-то произошло. Это поможет им развить навыки аналитического и дедуктивного мышления. Кроме того, задавайте вопросы и вносите предложения о стратегиях, чтобы побудить учащихся задуматься о стратегиях решения проблем, которые они используют.
Связать ошибки с заблуждениями . Используйте ошибки как доказательство ошибочных представлений, а не небрежности или случайных предположений. Постарайтесь выделить неправильное представление и исправить его, а затем научите студентов делать это самостоятельно. Мы все можем учиться на ошибках.
Модель решения задач Вудса
Определите проблему
Система . Предложите учащимся определить изучаемую систему (например, металлический мост, на который действуют определенные силы), интерпретируя информацию, представленную в постановке задачи. Нарисовать диаграмму — отличный способ сделать это.
Известные и концепции . Перечислите все, что известно о проблеме, и определите знания, необходимые для ее понимания (и, в конечном счете), ее решения.
Неизвестный(ые) . Когда у вас есть список известных, идентификация неизвестных становится проще. Одно неизвестное обычно является ответом на проблему, но могут быть и другие неизвестные. Убедитесь, что учащиеся понимают, что они должны найти.
Единицы и символы . Одним из ключевых аспектов решения проблем является обучение студентов тому, как выбирать, интерпретировать и использовать единицы и символы. Подчеркните использование единиц, когда это применимо. Выработайте привычку всегда использовать соответствующие единицы измерения и символы.
Ограничения . Все проблемы имеют некоторые установленные или подразумеваемые ограничения. Научите учащихся искать только слова «должен», «пренебрегать» или «предполагать», чтобы помочь определить ограничения.
Критерии успеха . Помогите учащимся с самого начала обдумать, каким должен быть логический тип ответа. Какими характеристиками он будет обладать? Например, количественная задача потребует ответа в той или иной форме числовых единиц (например, $/кг продукта, квадратный сантиметр и т. д.), в то время как задача оптимизации требует ответа в виде числового максимума или минимума.
Подумай об этом

«Пусть закипит». Используйте эту сцену, чтобы обдумать проблему. В идеале, на этом этапе учащиеся должны создать мысленный образ проблемы.
Идентифицировать определенные знания . Студенты должны сами определить необходимые базовые знания из иллюстраций, примеров и проблем, рассмотренных в курсе.
Сбор информации . Предложите учащимся собрать соответствующую информацию, такую как коэффициенты преобразования, константы и таблицы, необходимые для решения задачи.
План решения
Рассмотреть возможные стратегии . Часто тип решения будет определяться типом проблемы. Вот некоторые распространенные стратегии решения проблем: вычисление; упрощать; использовать уравнение; сделать модель, диаграмму, таблицу или диаграмму; или работать в обратном порядке.
Выберите лучшую стратегию . Помогите учащимся выбрать наилучшую стратегию, еще раз напомнив им, что им нужно найти или вычислить.
Выполнить план
Будьте терпеливы . Большинство проблем не решаются быстро или с первой попытки. В других случаях выполнение решения может быть самым простым шагом.
Будьте настойчивы . Если план не работает сразу, не позволяйте учащимся отчаиваться. Поощряйте их попробовать другую стратегию и продолжать попытки.
Оглянись назад
Поощряйте учащихся к размышлению. Когда решение найдено, учащиеся должны задать себе следующие вопросы:
Ответ имеет смысл?
Соответствует ли он критериям, установленным на шаге 1?
Ответил ли я на вопросы?
Чему я научился, делая это?
Можно ли было решить задачу по-другому?
Ресурсы
Фошай, Р., Киркли, Дж. (1998). Принципы обучения решению проблем. http://www.plato.com/pdf/04_principles.pdf
Хейс, младший (1989). Полное решение проблем. 2-е издание. Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates.
Вудс, Д.Р., Райт, Дж.Д., Хоффман, Т.В., Свартман, Р.К., Дойг, И.Д. (1975). Обучение навыкам решения проблем.
Инженерное образование. Том 1, № 1. с. 238. Вашингтон, округ Колумбия: Американское общество инженерного образования.
Эта лицензия Creative Commons позволяет другим микшировать, настраивать и использовать нашу работу в некоммерческих целях при условии, что они ссылаются на нас и указывают, были ли внесены изменения. Используйте следующий формат цитирования: Обучение навыкам решения проблем. Центр педагогического мастерства Университета Ватерлоо .
Стратегии решения текстовых задач
Простое добавление этих слов увеличивает сложность (а иногда и математическую тревогу) примерно в 100 раз!
Как вы можете помочь своим ученикам научиться уверенно решать текстовые задачи? Обучая своих учеников решать текстовые задачи поэтапно и организованно, вы дадите им инструменты, необходимые для решения текстовых задач гораздо более эффективным способом.

Вот семь стратегий, которые я использую, чтобы помочь учащимся решать текстовые задачи.
1. Прочтите задачу целиком
Прежде чем учащиеся будут искать ключевые слова и пытаться понять, что делать, им нужно немного замедлиться и прочитать задачу целиком один раз (а еще лучше, дважды). Это помогает детям получить более широкую картину, чтобы понять ее немного лучше.

2.
Подумайте о текстовой задаче
Учащиеся должны задавать себе три вопроса каждый раз, когда они сталкиваются с текстовой задачей. Эти вопросы помогут им составить план решения проблемы.
Вот вопросы:
A. В чем именно вопрос?
В чем проблема? Часто составители учебных программ включают в задачу дополнительную информацию, казалось бы, без веской причины, разве что для того, чтобы научить детей игнорировать эту постороннюю информацию (грррр!). Студенты должны быть в состоянии оставаться сосредоточенными, игнорировать эти лишние детали и выяснять, в чем заключается настоящий вопрос в конкретной задаче.

B. Что мне нужно, чтобы найти ответ?
Учащиеся должны еще больше сузить круг, чтобы понять, что нужно для решения задачи, будь то сложение, вычитание, умножение, деление или их комбинация. Им потребуется общее представление о том, какая информация будет использоваться (или не использоваться) и что они будут делать.
Здесь очень помогают ключевые слова. Когда учащиеся учатся распознавать, что одни слова означают сложение (например, всего, вместе взятые ), а другие означают вычитание, умножение или деление, это помогает им решить, как поступить немного лучше
Вот таблица ключевых слов, которую я люблю использовать для обучения словесным задачам. Раздаточный материал можно было бы скопировать в меньшем размере и вклеить в интерактивные математические тетради. Его можно поместить в папки по математике или в папки под математическим разделом, если ваши учащиеся используют папки.
Однажды я сделал огромные математические знаки (символы сложения, вычитания, умножения и деления) и написал вокруг них ключевые слова. Они служили постоянным напоминанием о ключевых словах для текстовых задач в классе.

Если вы хотите загрузить этот БЕСПЛАТНЫЙ раздаточный материал по ключевым словам, нажмите здесь:
C. Какая информация у меня уже есть?
Здесь учащиеся сосредоточатся на числах, которые будут использоваться для решения задачи.

3. Напишите в Word Задача
Этот шаг закрепляет размышления, сделанные на шаге номер два. Учащиеся используют карандаш или цветные карандаши, чтобы записывать информацию на рабочих листах (конечно, не в книгах, если только они не расходные материалы). Есть много способов сделать это, но вот что я люблю делать:
Обведите любые цифры, которые вы будете использовать.

Слегка зачеркните ненужную информацию.

Подчеркните фразу или предложение, в котором точно указано, что вам нужно найти.

4. Нарисуйте простое изображение и подпишите его
Рисование изображений с использованием простых форм, таких как квадраты, круги и прямоугольники, помогает учащимся визуализировать проблемы. Добавление номеров или имен в качестве меток также помогает.
Например, если в словесной задаче сказано, что было пять коробок, и в каждой коробке было 4 яблока, дети могут нарисовать пять квадратов с числом четыре в каждом квадрате.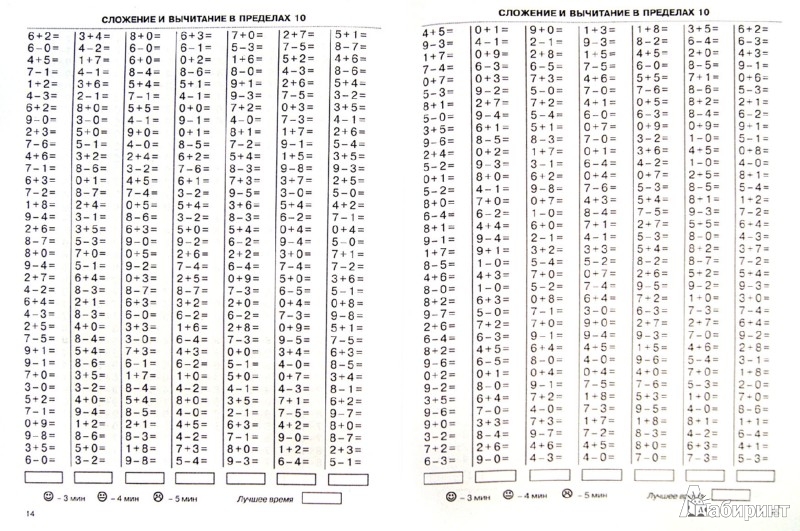 Мгновенно дети могут увидеть ответ намного проще!

5. Оцените ответ перед решением
Имея общее представление о примерном ответе на задачу, учащиеся узнают, является ли их фактический ответ разумным или нет. Эта быстрая приблизительная оценка — хорошая математическая привычка. Это помогает учащимся по-настоящему задуматься о точности своего ответа, когда проблема будет окончательно решена.

6. Проверка выполненной работы
Эта стратегия дополняет пятую стратегию. Одна из фраз, которые я постоянно использую во время занятий по математике, звучит так: Ваш ответ разумен ? Я хочу, чтобы учащиеся делали больше, чем просто считали, но действительно думали о том, что означают эти цифры.
Кроме того, когда учащиеся привыкают проверять работу, они более склонны выявлять ошибки по невнимательности, которые часто являются причиной неправильных ответов.

7.
Часто тренируйтесь решать словесные задачи
Точно так же, как требуется практика, чтобы научиться играть на кларнете, вести мяч в футболе и реалистично рисовать, нужна практика, чтобы стать мастером решения словесных задач.
Когда учащиеся решают текстовые задачи, часто происходит несколько вещей. Словесные задачи становятся менее страшными (нет, правда).
Они начинают замечать сходство в типах проблем и способны быстрее понять, как их решать. Они приобретут уверенность даже при работе с новыми типами текстовых задач, зная, что они успешно решали многие текстовые задачи в прошлом.

Если вам нужны карточки с текстовыми задачами, у меня их довольно много для учащихся 3-5 классов.
В этом наборе карточек с заданиями по математике для 3-го класса есть задачи со словами почти в каждом из 30 наборов карточек с заданиями.
Существуют также специальные наборы, предназначенные для решения текстовых задач и двухэтапных текстовых задач.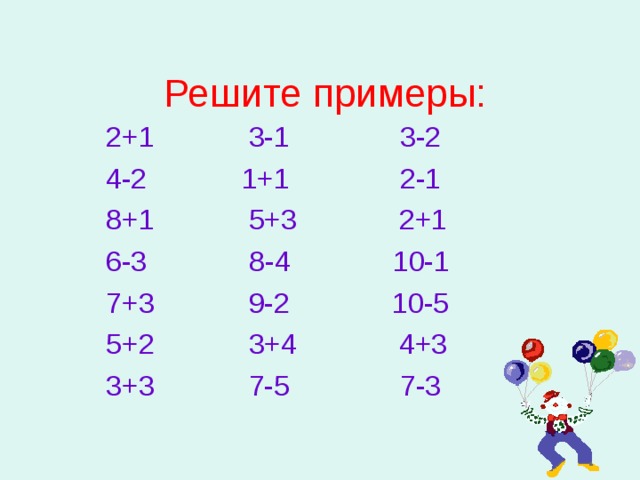 Я люблю их, потому что для каждого стандарта есть набор карточек с заданиями.
НАЖМИТЕ ЗДЕСЬ, чтобы посмотреть на 3-й класс:
В этом наборе карточек с задачами по математике для 4-го класса также есть множество текстовых задач почти в каждом из 30 наборов карточек с задачами. Эти карты идеально подходят для центров, всего класса и один на один.
НАЖМИТЕ ЗДЕСЬ, чтобы увидеть 4-й класс:
Этот комплект карточек с задачами по математике для 5-го класса также содержит текстовые задачи, чтобы ваши ученики могли сосредоточиться на практике.
НАЖМИТЕ ЗДЕСЬ, чтобы взглянуть на 5-й класс:
Хотите попробовать БЕСПЛАТНЫЙ набор карточек с математическими задачами, чтобы узнать, что вы думаете?
Карточки с заданиями для 3-го класса: округление целых чисел
Карточки с заданиями для 4-го класса: Преобразование дробей и десятичных знаков
Дробная деятельность, которую любят студенты
Дроби могут быть жесткими! Хотя для того, чтобы учащиеся действительно поняли дроби, требуется время и повторное знакомство с дробями, их очень много
Подробнее »
Математические игры с использованием игральных костей
На мой взгляд, игры являются важной частью занятий по математике. Дети могут не только практиковать навыки, которым мы уделяем особое внимание
Подробнее »
Математические игры с использованием домино
Математические игры всегда были частью нашей математики. Мне нравится тот факт, что каждый раз, когда я представляю математическую игру, я знаю, что
Подробнее »
Линейные уравнения — определение, формула, график, примеры
Линейное уравнение — это уравнение, в котором наивысшая степень переменной всегда равна 1. Оно также известно как уравнение одной степени. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Здесь x — переменная, A — коэффициент, B — постоянная. Стандартная форма линейного уравнения с двумя переменными имеет вид Ax + By = C. Здесь x и y — переменные, A и B — коэффициенты, а C — константа.
1. Что такое линейное уравнение?
2. Формула линейного уравнения
3. График линейных уравнений
4. Часто задаваемые вопросы о линейных уравнениях
Что такое линейное уравнение?
Уравнение, имеющее наивысшую степень 1, называется линейным уравнением. Это означает, что ни одна переменная в линейном уравнении не имеет показатель степени больше 1. График линейного уравнения всегда образует прямую линию.
Линейное уравнение Определение: Линейное уравнение — это алгебраическое уравнение, где каждый член имеет показатель степени 1, и когда это уравнение изображается на графике, оно всегда приводит к прямой линии. Вот почему оно называется «линейным уравнением».
Существуют линейные уравнения с одной переменной и линейные уравнения с двумя переменными. Давайте научимся определять линейные уравнения и нелинейные уравнения с помощью следующих примеров.
Уравнения Линейный или нелинейный
у = 8х — 9 Линейный
у = х ² — 7 Нелинейный, степень переменной x равна 2
√у + х = 6 Нелинейный, степень переменной y равна 1/2
у + 3х — 1 = 0 Линейный
у ² — х = 9 Нелинейный, степень переменной y равна 2
Формула линейного уравнения
Формула линейного уравнения — это способ выражения линейного уравнения. Это можно сделать разными способами. Например, линейное уравнение может быть выражено в стандартной форме, в форме точки пересечения или в форме точка-наклон. Теперь, если мы возьмем стандартную форму линейного уравнения, давайте узнаем, как оно выражается. Мы видим, что оно варьируется от случая к случаю в зависимости от количества переменных, и следует помнить, что наивысшая (и единственная) степень всех переменных в уравнении должна быть 1.
Линейные уравнения в стандартной форме
Стандартная форма или общая форма линейных уравнений с одной переменной записывается как Ax + B = 0; , где A и B — действительные числа, а x — единственная переменная. Стандартная форма линейных уравнений с двумя переменными выражается как Ax + By = C; , где A, B и C — любые действительные числа, а x и y — переменные.
График линейных уравнений
График линейного уравнения с одной переменной x образует вертикальную линию, параллельную оси y, и наоборот, тогда как график линейного уравнения с двумя переменными x и y образует прямую линию. Построим график линейного уравнения с двумя переменными с помощью следующего примера.
Пример: Постройте график для линейного уравнения с двумя переменными, x — 2y = 2.
Построим график линейного уравнения, используя следующие шаги.
Шаг 1: Данное линейное уравнение имеет вид x — 2y = 2.
Шаг 2: Преобразуйте уравнение в форму y = mx + b. Это даст: y = x/2 — 1.
Шаг 3: Теперь мы можем заменить значение x на другие числа и получить результирующее значение y для создания координат.
Шаг 4: Когда мы подставляем x = 0 в уравнение, мы получаем y = 0/2 — 1, то есть y = -1. Точно так же, если мы подставим значение x вместо 2 в уравнение y = x/2 — 1, мы получим y = 0,
.
Шаг 5: Если мы заменим значение x на 4, мы получим y = 1. Значение x = -2 дает значение y = -2. Теперь эти пары значений (x, y) удовлетворяют заданному линейному уравнению y = x/2 — 1. Поэтому мы перечисляем координаты, как показано в следующей таблице.
х 0 2 4 -2
у -1 0 1 -2
Шаг 6: Наконец, мы наносим эти точки (4,1), (2,0), (0,-1) и (-2,-2) на график и соединяем точки в получить прямую линию. Так линейное уравнение изображается на графике.
Линейные уравнения с одной переменной
Линейное уравнение с одной переменной — это уравнение, в котором присутствует только одна переменная. Оно имеет форму Ax + B = 0, где A и B — любые два действительных числа, а x — неизвестная переменная, имеющая только одно решение. Это самый простой способ представить математическое утверждение. Это уравнение имеет степень, которая всегда равна 1. Линейное уравнение с одной переменной решается очень просто. Переменные разделяются и подводятся к одной стороне уравнения, а константы объединяются и подводятся к другой стороне уравнения, чтобы получить значение неизвестной переменной.
Пример: Решить линейное уравнение с одной переменной: 3x + 6 = 18.
Чтобы решить данное уравнение, подносим числа в правой части уравнения и сохраняем переменную в левая сторона. Это означает, что 3x = 18 — 6. Затем, когда мы решим для x, мы получим 3x = 12. Наконец, значение x = 12/3 = 4.
Линейные уравнения с двумя переменными
Линейное уравнение в Две переменные имеют вид Ax + By + C = 0, где A, B, C — действительные числа, а x и y — две переменные, каждая из которых имеет степень 1. Если мы рассмотрим два таких линейных уравнения, они называются одновременными линейными уравнениями. Например, 6х + 2у + 9= 0 — линейное уравнение с двумя переменными. Существуют различные способы решения линейных уравнений с двумя переменными, такие как графический метод, метод подстановки, метод перекрестного умножения, метод исключения и метод определителя.
Как решать линейные уравнения?
Уравнение похоже на весы с одинаковыми весами с обеих сторон.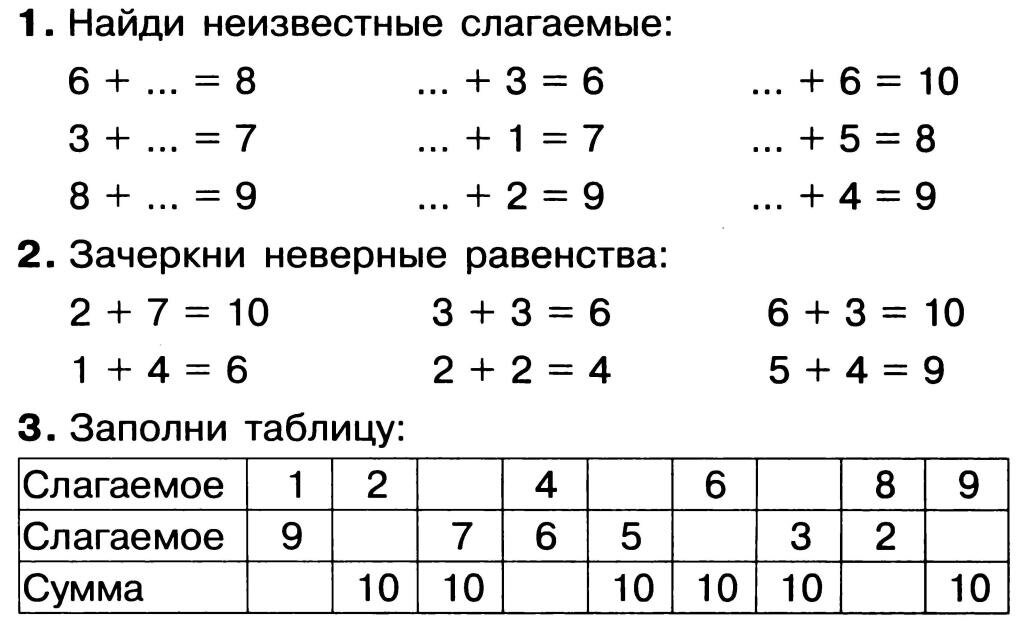 Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно останется верным. Точно так же, если мы умножаем или делим одно и то же число в обеих частях уравнения, это правильно. Мы подносим переменные к одной стороне уравнения, а константу к другой стороне, а затем находим значение неизвестной переменной. Это способ решения линейного уравнения с одной переменной. Давайте разберемся в этом с помощью примера.
Пример: Решите уравнение, 3x — 2 = 4.
Выполняем математические операции с левой (левой) и правой (правой) частями так, чтобы равновесие не нарушалось. Итак, давайте добавим 2 с обеих сторон, чтобы уменьшить LHS до 3x. Это не нарушит баланс. Новая левая сторона равна 3x — 2 + 2 = 3x, а новая правая сторона равна 4 + 2 = 6. Теперь давайте разделим обе части на 3, чтобы уменьшить левую часть до x. Таким образом, мы имеем х = 2 . Это один из способов решения линейных уравнений с одной переменной.
Советы по линейным уравнениям:
Значение переменной, которая делает линейное уравнение верным, называется решением или корнем линейного уравнения.
На решение линейного уравнения не влияет сложение, вычитание, умножение или деление одного и того же числа на обе части уравнения.
График линейного уравнения с одной или двумя переменными всегда образует прямую линию.
☛ Статьи по теме:
Решения линейного уравнения
Введение в графику
Линейный полином
Калькулятор решения линейных уравнений

Примеры линейных уравнений
Пример 1: Сумма двух чисел равна 44. Если одно число на 10 больше другого, найдите числа, составив линейное уравнение.
Решение:
Пусть число равно x, значит, другое число равно x + 10. Мы знаем, что сумма обоих чисел равна 44. Следовательно, линейное уравнение можно представить в виде x + x + 10. = 44. В результате получается 2x + 10 = 44. Теперь давайте решим уравнение, изолируя переменную с одной стороны и вводя константы с другой стороны. Это означает, что 2x = 44 — 10. Упрощая RHS, мы получаем 2x = 34, поэтому значение x равно 17. Это означает, что одно число равно 17, а другое число равно 17 + 10 = 27,
Ответ: Следовательно, эти два числа — 17 и 27.
Пример 2: Число, умноженное на шесть, равно 48. Составьте линейное уравнение и найдите неизвестное число.
Решение: Пусть неизвестное число равно x. Шесть раз это число равно 48, что означает 6x = 48. Итак, это линейное уравнение можно решить, чтобы найти значение x, которое является неизвестным числом. 6x = 48 означает, что x = 48/6 = 8.
Ответ: Следовательно, неизвестное число равно 8.
Пример 3: Решите заданное линейное уравнение: 5x — 95 = 75.
Решение: Данное уравнение составляет 5x — 95 = 75.
⇒ 5x = 75 + 95
= 170
⇒ x = 34
Ответ: Следовательно, значение x равно 34.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими экспертами Cuemath
Запишитесь на бесплатный пробный урок
Практические вопросы по линейным уравнениям

перейти к слайдуперейти к слайду
Часто задаваемые вопросы о линейном уравнении
Что такое линейное уравнение? Объясните на примере.
Линейное уравнение — это уравнение, в котором наивысшая степень переменной всегда равна 1. Оно также известно как уравнение одной степени. Когда это уравнение изображается на графике, оно всегда приводит к прямой линии. По этой причине его называют «линейным уравнением». Существуют линейные уравнения с одной переменной, с двумя переменными, с тремя переменными и так далее. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Уравнение вида Ax + By = C называется линейным уравнением с двумя переменными. Вот несколько примеров линейных уравнений: 5x + 6 = 1, 42x + 32y = 60, 7x = 84 и т. д.
Какая формула линейного уравнения?
Формула линейного уравнения — это способ выражения линейного уравнения. Это может быть выражено в стандартной форме, в форме пересечения наклона или в форме точка-наклон. Стандартная форма линейного уравнения с одной переменной имеет вид Ax + B = 0. Здесь x — переменная, A — коэффициент при x, а B — константа. Стандартная форма линейного уравнения с двумя переменными имеет вид Ax + By = C. Здесь x и y — переменные, а A, B и C — любые действительные числа.
Почему линейное уравнение называют линейным?
Линейное уравнение называется линейным, потому что когда мы пытаемся построить график данной линейной функции, получается прямая линия.
Как вы решаете линейные уравнения?
Мы можем решить линейное уравнение с одной переменной, переместив переменные в одну часть уравнения, а числовую часть — в другую. Например, x — 1 = 5 — 2x можно решить, переместив числовые части в правую часть уравнения, оставив переменные в левой части. Следовательно, мы получаем x + 2x = 5 + 1. Таким образом, 3x = 6. Это дает x = 2,
Могут ли линейные уравнения содержать дроби?
Да, линейные уравнения могут иметь дроби только до тех пор, пока знаменатель в дробной части является постоянной величиной. Переменные не могут быть частью знаменателя любой дроби в линейном уравнении.
Что такое линейные уравнения с одной переменной?
Линейное уравнение с одной переменной — это уравнение, в котором присутствует только одна переменная. Оно имеет форму Ax + B = 0, где A и B — любые два действительных числа, а x — неизвестная переменная, имеющая только одно решение. Например, 9x + 78 = 18 — линейное уравнение с одной переменной.
Что такое линейные уравнения с двумя переменными?
Линейное уравнение с двумя переменными имеет форму Ax + By + C = 0, где A и B — коэффициенты, C — постоянный член, а x и y — две переменные, каждая со степенью 1 Например, 7x + 9y + 4 = 0 — это линейное уравнение с двумя переменными. Если мы рассмотрим два таких линейных уравнения, они называются одновременными линейными уравнениями.
Чем квадратные уравнения отличаются от линейных уравнений?
Линейные уравнения не имеют степени, отличной от 1, в любом члене. Общая форма линейного уравнения выражается как Ax + By + C = 0, где A, B и C — любые действительные числа, а x и y — переменные. Принимая во внимание, что квадратные уравнения имеют по крайней мере один член, содержащий переменную, которая возведена во вторую степень. Общая форма квадратного уравнения выражается как ax ² + bx + c = 0. Другое различие между двумя типами уравнений заключается в том, что линейное уравнение образует прямую линию, тогда как квадратное уравнение образует на графике параболу.
Как строить графики линейных уравнений?
Когда мы рисуем линейные уравнения, они образуют прямую линию. Чтобы построить график уравнения формы Ax + By = C, мы получаем два решения, которые соответствуют точкам пересечения x и y. Преобразуем уравнение к форме y = mx + b. Затем мы заменяем значение x другими числами и получаем значение y, которое создает набор координат (x, y). Эти координаты можно нанести на график, а затем соединить линией.
Как решать линейные уравнения с дробями?
Линейные уравнения с дробями решаются так же, как мы решаем обычные уравнения. Нам нужно ввести переменную с одной стороны и константы с другой стороны и найти переменную. Например, давайте решим уравнение (2a/3) — 10 = 12.
Шаг 1: Здесь мы приведем константы в правой части, то есть (2a/3) = 12 + 10.
Шаг 2: Теперь у нас есть (2a/3) = 22. Далее это можно записать как 2a = 22 × 3,
Шаг 3: Следовательно, значение a = 66/2 = 33.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист линейных уравнений
Функция «один к одному» — график, примеры, определение
Термин «отношение один к одному» на самом деле относится к отношениям между любыми двумя элементами, в которых один элемент может принадлежать только одному другому элементу. . В математическом смысле эти отношения можно назвать функциями один к одному, в которых имеется равное количество элементов, или один элемент может быть соединен только с одним другим элементом. Имя человека и номер зарезервированного места этого человека в поезде — это простой повседневный пример функции «один к одному».
Если вам интересно, что делает функции one-to-one особенными, то эта статья поможет вам узнать об их свойствах и оценить эти функции. Используя решенные примеры, давайте рассмотрим, как идентифицировать эти функции на основе выражений и графиков.
1. Что такое функция «один к одному»?
2. Проверка горизонтальной линии
3. Свойства функции One to One
4. Как определить, является ли функция один к одному?
5. График функции «один к одному»
6. Обратная функция один к одному
7. шага, чтобы найти функцию, обратную единице
8. Часто задаваемые вопросы о функции One to One
Что такое функция «один к одному»?
Обычная функция может фактически иметь два разных входных значения, которые могут дать один и тот же ответ, тогда как функция «один к одному» этого не делает. Давайте продолжим и начнем с определения и свойств функций one-to-one.
Определение функции «один к одному»
Функция «один к одному» — это специальная функция, которая сопоставляет каждый элемент диапазона ровно с одним элементом своей области, т. е. выходные данные никогда не повторяются. Например, функция g(x) = x — 4 является функцией один к одному, поскольку она дает разные ответы для каждого входа. Кроме того, функция g(x) = x ² НЕ является функцией один к одному, поскольку она выдает 4 в качестве ответа, когда входные данные равны 2 и -2. Функция, которая не является взаимно однозначной, называется функцией многие к одному.
Алгебраически мы можем определить функцию один к одному следующим образом:
функция g: D -> F называется взаимно однозначной, если ) ⇒ х ₁ = х ₂
для всех элементов x ₁ и x ₂ ∈ D. Функция один к одному также считается инъекцией, т. е. функция инъективна, только если она является взаимно однозначной. Противоположностью этому определению является функция g: D -> F взаимно однозначна, если x ₁ ≠ х ₂ ⇒ г (х ₁ ) ≠ г (х ₂ ). Давайте визуализируем это, сопоставив две пары значений для сравнения функций, которые являются и не являются один к одному.
На рис. (а) (один к одному) x — это домен, а f (x) — кодовый домен, аналогично на рис. (b) (который не один к одному) x — домен и g(x) является доменом кода.
На рис. (a) для каждого значения x существует только одно уникальное значение f(x), и, таким образом, f(x) является функцией один к одному.
На рис. (b) разные значения x, 2 и -2 сопоставляются с общим значением g(x) 4 и (также разные значения x -4 и 4 сопоставляются с общим значением 16). Таким образом, g(x) — это функция, которая не является взаимно однозначной функцией.
Проверка горизонтальной линии
Тест горизонтальной линии используется для определения того, является ли функция однозначной, когда задан ее график. Мы уже видели условие (g(x ₁) = g(x ₂) ⇒ x ₁ = x ₂ ), чтобы определить, является ли функция g(x) однозначной алгебраически. С другой стороны, чтобы проверить, является ли функция один-один на ее графике,
просто возьмите горизонтальную линию (рассмотрите горизонтальную палочку) и проведите ее через график.
Если горизонтальная линия НЕ проходит более чем через одну точку графика в любой момент времени, то функция один-один.
Если горизонтальная линия в какой-то момент проходит более чем через одну точку графика, то функция НЕ является однозначной.
Пример: Рассмотрим график ниже.
На приведенном выше графике
f(x) = x ² (квадратичная функция) НЕ является единицей, так как она не прошла тест горизонтальной линии (поскольку горизонтальная линия проходит через более чем одну точка графика)
f(x) = x ³ (которое является кубической функцией) равно единице, так как оно прошло тест горизонтальной линии (поскольку горизонтальная линия каждый раз проходит только через одну точку графика)
Свойства функции «один к одному»
Взаимно-однозначная функция, т. е. инъективная функция, которая отображает отдельные элементы своей области определения в различные элементы своей сообласти. Вот некоторые свойства, которые помогают нам понять различные характеристики функций один к одному:
Если две функции f(x) и k(x) равны один к одному, то составная функция f ◦ тоже одна функция. (f ◦ k) (x ₁ ) = (f ◦ k) (x ₂ ) ⇒ f(k(x ₁ )) = f(k(x ₂ )) ⇒ k(x ₁ ) = k(x ₂ ) ⇒ x _{1
5 = x} 2
Область определения функции g равна области значений g ^-1, а область значений g равна области значений g ^-1
Если рассматривать функцию как один к одному, то ее график будет либо всегда возрастать, либо всегда убывать.
g ^-1 (g(x)) = x для каждого x в области определения g и g(g ^-1 (x)) = x для каждого x в домене g ^-1 .
Если f ◦ k является взаимно однозначной функцией, то k(x) также гарантированно является взаимно однозначной функцией
График функции и график обратной функции симметричны друг другу относительно прямой y = x.
Как определить, является ли функция один к одному?
Проверка вертикальной линии используется для определения того, является ли данное отношение функцией или нет. Кроме того, мы можем определить, является ли функция взаимно однозначной, используя два метода:
Проверка функции один к одному графически: если график g(x) каждый раз проходит через уникальное значение y, то говорят, что функция является функцией один к одному (проверка горизонтальной линией).
Алгебраическая проверка функции один к одному: говорят, что функция g является взаимно однозначной, если a = b для каждого g(a) = g(b)
Проверка функции один к одному с использованием производных: говорят, что функция g(x) является взаимно однозначной тогда и только тогда, когда либо g'(x) > 0, либо g'(x) < 0 во всей области. т. е. если функция либо возрастает, либо убывает повсюду, то она однозначна. Например, экспоненциальная функция f(x) = e ^x является полностью возрастающей функцией во всей своей области определения (-∞, ∞) и, следовательно, однозначно. Нарисуй один раз и проверь.
График функции «один к одному»
Любую функцию можно представить в виде графика. Эта функция представлена путем рисования линии/кривой на плоскости в соответствии с декартовой системой. Домен отмечен горизонтально относительно оси x, а диапазон отмечен вертикально в направлении оси y. Если функция g взаимно однозначна, то никакие две точки (x ₁ , y ₁ ) и (x ₂ , y ₂ ) имеют одинаковое значение y. Следовательно, никакая горизонтальная линия не пересекает график уравнения y = g(x) более одного раза. На следующем рисунке (график прямой линии y = x + 1) показана функция один-один. Обратите внимание, что никакие две точки на нем не имеют одинаковую координату y (или) он проходит тест горизонтальной линии.
Обратная функция один к одному
Для того, чтобы понимать концепцию обратных функций и решать определенные типы уравнений, необходимо понимать концепцию взаимно однозначных функций. Во-первых, у функции g есть обратная функция, g ^-1 тогда и только тогда, когда g один к одному. На приведенном ниже изображении функция, обратная однозначной функции g, обозначена как g ^-1 , где упорядоченные пары g ^-1 получаются путем замены координат в каждой упорядоченной паре g. Здесь домен g становится диапазоном g ^-1 , а диапазон g становится доменом g ^-1 .
Свойства функции, обратной функции «один к одному»
Функция, обратная функции «один к одному», отменяет то, что исходная функция сделала со значением в своей области, чтобы вернуться к исходному значению y. Вот свойства обратной функции один к одному:
Функция f имеет обратную функцию тогда и только тогда, когда f является взаимно однозначной функцией, т. е. только взаимно однозначные функции могут иметь обратную.
Если функции g и f обратны друг другу, то обе эти функции можно рассматривать как взаимно однозначные.
Если f и g обратны друг другу тогда и только тогда, когда (f ◦ g) (x) = x, x в области определения g и (g ◦ f) (x) = x, x в области определения f. Здесь f ◦ g — функция композиции, состоящая из ‘f’ из ‘g’.
Если f и g обратны друг другу, то область определения f равна области значений g, а область значений g равна области определения f.
Если f и g обратны друг другу, то их графики будут отражать друг друга на прямой y = x.
Если точка (c, d) находится на графике f, то точка (d, c) находится на графике f ^-1 .
шага, чтобы найти обратную функцию один к одному
Пошаговая процедура получения обратной функции g ^-1 (x) для взаимно однозначной функции g(x) выглядит следующим образом:
Установить g(x) равным y
Поменяйте местами x с y, так как каждый (x, y) имеет (y, x) партнера
Найти у
В только что найденном уравнении переименуйте y как g ^-1 (x).
Пример: Найти обратную функцию g ^-1 (x) функции g(x) = 2 x + 5,
Теперь давайте выполним 4 шага:
Установите g(x) = y у = 2х + 5
Переключатель x с y х = 2у + 5
Найдите у у = (х — 5)/2
Переименовать y как g ^-1 (x). Это обратное. г ^-1 (х) = (х — 5)/2
Важные примечания по функции One to One:
Вот несколько моментов, которые следует помнить при изучении функции «один к одному»:
В математическом смысле функции «один к одному» — это функции, в которых имеется равное количество элементов в домене и в диапазон, или один может быть соединен только с другим элементом.
Для того, чтобы понимать концепцию обратных функций и решать определенные типы уравнений, важно понимать концепцию функций один к одному.
Можно легко определить, является ли функция взаимно однозначной как геометрически, так и алгебраически.
☛ Связанные темы:
Графические функции
Линейные функции
Калькулятор обратной функции
Часто задаваемые вопросы о функции One to One
Что такое определение функции «один к одному»?
Функции «один к одному» — это специальные функции, которые сопоставляют каждый элемент диапазона с единичным элементом домена. Это означает, что функция y = f(x) является однозначной только тогда, когда ни для каких двух значений x и y мы имеем f(x), равный f(y). Обычная функция может фактически иметь два разных входных значения, которые могут дать один и тот же ответ, тогда как функция «один к одному» этого не делает.
В чем разница между тестом вертикальной линии и тестом горизонтальной линии?
Вот различия между тестом вертикальной линии и тестом горизонтальной линии.
Проверка вертикальной линии Проверка горизонтальной линии
Проверка вертикальной линии используется для определения того, является ли отношение функцией. Тест горизонтальной линии используется для определения того, является ли функция один-один.
Чтобы использовать этот тест, проведите вертикальную линию через график, и если вертикальная линия НЕ совпадает с графиком более чем в одной точке в любом случае, то график является функцией. Чтобы использовать этот тест, проведите через график горизонтальную линию, и если горизонтальная линия НЕ пересекается с графиком более чем в одной точке в любом случае, то график представляет собой функцию один к одному.
Как проверить, является ли функция взаимно однозначной?
Можно проверить, является ли функция один к одному, используя любой из этих двух методов:
Геометрическое тестирование функции один к одному: если график функции проходит тест горизонтальной линии, то функцию можно рассматривать как единицу. к одной функции.
Алгебраическая проверка функции один к одному: Говорят, что функция g является однозначной, если для каждого g(x) = g(y), x = y.
Какие типы функций относятся к функциям One-to-One?
Функция «один к одному» либо строго убывающая, либо строго возрастающая.
Если f(x) возрастает, то f'(x) > 0 для каждого x в его области определения
Если f(x) убывает, то f ‘(x) < 0 для каждого x в его области определения
В функции «один к одному» одинаковые значения не назначаются двум разным элементам домена.
Что это значит, если функция не является функцией один к одному?
В функции, если горизонтальная линия проходит через график функции более одного раза, то функция не считается однозначной функцией. Функция, которая не является один к одному, считается как много к одному.
Каковы этапы решения обратной однозначной функции?
Вот шаги решения обратной однозначной функции g(x):
Переименовать g(x) в y
Поменять местами переменные x и y.
Решите уравнение для y. Если есть только одно решение, то может существовать и обратное; иначе нельзя.
В только что найденном уравнении переименуйте y как g ^-1 (x).
Что является примером функции «один к одному»?
Функция f(x) = x + 5 является функцией один к одному, поскольку она дает разные выходные данные для разных входных данных x. И чтобы функция была один к одному, она должна возвращать уникальный диапазон для каждого элемента в своей области. Здесь f(x) возвращает 6, если x равно 1, 7, если x равно 2, и так далее. Человек и его тень — реальный пример функции один к одному.
Что не является функцией один к одному?
Функция f(x) = x ² не является функцией один к одному, поскольку она дает 9 в качестве ответа, когда входные данные равны 3 и -3. И чтобы функция была один к одному, она должна возвращать уникальный диапазон для каждого элемента в своей области. Здесь f(x) возвращает 9в качестве ответа для двух разных входных значений 3 и -3.

1.	Что такое линейное уравнение?
2.	Формула линейного уравнения
3.	График линейных уравнений
4.	Часто задаваемые вопросы о линейных уравнениях

Уравнения	Линейный или нелинейный
у = 8х — 9	Линейный
у = х ² — 7	Нелинейный, степень переменной x равна 2
√у + х = 6	Нелинейный, степень переменной y равна 1/2
у + 3х — 1 = 0	Линейный
у ² — х = 9	Нелинейный, степень переменной y равна 2

1.	Что такое функция «один к одному»?
2.	Проверка горизонтальной линии
3.	Свойства функции One to One
4.	Как определить, является ли функция один к одному?
5.	График функции «один к одному»
6.	Обратная функция один к одному
7.	шага, чтобы найти функцию, обратную единице
8.	Часто задаваемые вопросы о функции One to One

Установите g(x) = y	у = 2х + 5
Переключатель x с y	х = 2у + 5
Найдите у	у = (х — 5)/2
Переименовать y как g ^-1 (x). Это обратное.	г ^-1 (х) = (х — 5)/2