Задачи по математике для 2 класса, 3500 занимательных заданий с ответами и решением — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Математические диктанты 2 класс, часть 2
Сложение и вычитание с переходом через разряд
Выполни вычисления столбиком.
Вариант 1
а) 30 – 18; г) 94 – 49; ж) 39 + 39;
б) 61 – 38; д) 38 + 18; з) 96 – 7;
в) 17 + 17; е) 91 – 24; и) 54 + 46.
Какую закономерность в ответах ты видишь?
Вариант 2
а) 46 + 45; г) 18 + 46; ж) 29 + 8;
б) 91 – 9; д) 93 – 38; з) 63 – 35;
в) 36 + 37; е) 18 + 28; и) 52 – 33.
Какую закономерность в ответах ты видишь?
Запиши решение столбиком и вычисли.
45 увеличь на 38.

Найди разность чисел 74 и 36.
На сколько 47 меньше 55?
Найди сумму чисел 46 и 18.
Уменьши 61 на 46.
Уменьшаемое 54, вычитаемое 28. Найди разность.
Из 83 вычти 48.
К 36 прибавь 37.
Первое слагаемое 38, второе – 49. Чему равна сумма?
Сколько получится, если из 60 вычесть 16?
Проверь решение примеров, записывая их в столбик. Найди ошибки.
а) 26 + 35 = 61; е) 35 + 49 = 84;
б) 43 – 15 = 28; ж) 6 + 29 = 89;
в) 18 = 42 = 50; з) 51 – 29 = 22;
г) 38 + 13 = 51; и) 54 + 18 = 72;
д) 74 – 48 = 26; к) 37 + 39 = 76.
Найди ошибки в решении примеров.
 Реши примеры верно.
Реши примеры верно.
1 10
а) _36 б) _92 в) _37 г) _71 д) _35
18 7 5 15 19 54 95 87 64 16
Выполни вычисления, записывая решения столбиком.
_54 _60 _48 _37 _76 _73 _70 _18
37 15 24 4 24 19 26 54
_97 _92 _42 _33 _40 _84 _54 _35
18 29 18 48 29 57 28 48
_14 _60 _37 _52 _44 _62 _17 _34
27 29 44 38 49
Вычисли, записывая решение каждого действия столбиком. Стрелка покажет, какое действие нужно выполнить с полученным результатом.

а) 15 + 37 + 18 – 36 – 17 + 28 – 19 + 74 …
б) 49 + 25 – 18 + 24 – 63 +36 – 28 – 9 …
в) 54 – 18 – 29 + 56 – 48 +37 + 18 – 61 …
г) 95 – 37 – 29 + 57 – 48 +54 – 14 – 58 …
д) 14 + 39 + 38 – 74 + 48 – 26 + 51 – 62 …
е) 90 – 37 – 26 + 45 – 54 +28 + 46 – 78 …
ж) 34 + 16 – 27 + 69 – 73 + 15 + 37 – 35 …
з) 23 + 8 + 29 – 33 + 56 – 45 + 27 – 46 …
и) 96 – 27 – 58 + 39 + 27 – 56 + 75 – 57 …
к) 15 + 37 – 38 + 67 – 33 – 19 + 57 – 38 …
7. Реши круговые примеры. Ответ каждого предыдущего является началом следующего. Начни с примера, обозначенного *.
Вариант 1
_94 _91
* _ 35 67 24 _ 13
59 48
94
_53 _32
38 19
_27
26 _74
_61 39
24
_67 _37
35 37
Вариант 2
* _97
28 _ 42
69 13
_ 69 _27
27 63
_29 _ 85
56 36
_73
_74
47 _49
24
_ 90 _ 18
7 56
Уравнение.
2-й класс
Тип урока: урок введения новых знаний.
Цель: дать учащимся новое математическое понятие «уравнение».
Задачи:
- Образовательная: сформировать представление об уравнении, решение уравнений;
- Развивающая: развивать умение сравнивать, анализировать; совершенствовать вычислительные навыки;
- Воспитательная: формировать культуру общения в классом коллективе.
Оборудование урока:
- Учебник Математика 2 класс 1 часть М.И. Моро и др.
- Мультимедийный проектор, компьютер, презентация.
Ход урока
I.
Самоопределение к деятельности.
Психологический настрой: Покажите вашу прямую спинку, покажите правую руку, умные глазки. Подарите мне и друг другу добрые улыбки.
Подарите мне и друг другу добрые улыбки.
С новой темой познакомится класс.
Сегодня узнаем мы без сомнения
«Имя» этого выражения: х+4=12.
II.
Актуализация знаний и фиксация затруднений в деятельности.
– А сейчас нас ждет интересная работа – устный счет.
Назовите действия и компоненты. (Слайд 2)
- 30 + 7 = 37
- 47 – 5 = 42
Найдите значения выражений. (Слайд 3)
- 32 + 2 =
- 13 + 20 =
- 40 – 7 =
- 53 – 20 =
- х + 3 = 33
– Со всеми выражениями справились? (Нет)
– Чем отличается последнее выражение?
III.
Постановка учебной задачи.
– Такое выражение называется – уравнением. Умеем ли мы решать уравнение? (Нет) (Слайд 4)
– Чему будем учиться на уроке? (Решать уравнения, составить алгоритм решения уравнений)
IV.

Построение проекта выхода из проблемной ситуации, затруднения.
– Давайте разберемся, что же такое уравнение. Прочтите выражения. (Слайд 5)
- … — 4 = 6
- 2 + … = 8
- … + 3 = 7
- 9 — … = 5
– Что объединяет эти выражения? (Это примеры с неизвестным)
– Что нужно знать, чтобы решить их? (Необходимо знать состав чисел, название действий, название компонентов, нахождение неизвестных компонентов)
– Чтобы открыть новое, нам необходимо хорошо повторить то, что мы уже знаем.
| 1С + 2С = СУММА | У – В = Р | |
| 1С = СУММА – 2С | У = Р + В | |
| 2С = СУММА – 1С | В = У — Р |
Вывод: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. (Слайд 6)
(Слайд 6)
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое. (Слайд 7)
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
– В математике принято вместо отсутствующего компонента писать буквы латинского алфавита:
х (икс), а (а), b (бе) c (це) и другие. (Слайд 8)
– Попробуем сделать вывод из всего сказанного.
Вывод: уравнение – это … (х + 3 = 33) равенство, содержащее … (х + 3 = 33) неизвестное число, которое надо найти. (Слайд 9)
– Что надо сделать с неизвестным числом? ( Его надо найти)
– Как обозначается неизвестное число? (Латинскими буквами)
– Молодцы, ваша работа достойна похвалы. А сейчас проверьте себя, прочтите в учебнике на странице 68.
– Давайте составим алгоритм решения уравнения. (Слайд 10)
Алгоритм решения уравнений:
- Прочитай уравнение.

- Назови действие, компоненты.
- Вспомни, как найти неизвестный компонент.
- Запиши и вычисли.
- Проверь.
V.
Первичное закрепление учебного материала.
– А теперь давайте решать уравнения. Что нам поможет сделать это? (Алгоритм) (Слайд 11)
VI. Самостоятельная работа.
– Пользуясь алгоритмом, решите самостоятельно уравнения на стр. 68 №1.
Вариант 1. Верхнюю строку.
Вариант 2. Нижнюю строку.
– Взаимопроверка работы. (Слайды 12, 13)
VII.
Включение новых знаний в систему и повторение.
– Из данных выражений найдите уравнения и запишите их номера: (Слайды 14, 15)
- 8 – 4 = 4
- 6 – х = 4
- 12 + х = 20
- а – 6
- а – 6 = 18
- 13 – 1 = 12
- 10 + у
- 10 + у = 23
VIII.

Рефлексия деятельности.
– Назовите тему урока, над которой работали сегодня.
– Какую цель ставили перед собой?
– Выполнили?
– Так что такое уравнение?
7 способов помочь младшему школьнику с математикой
Предположим, что математика уже в начальной школе ребёнка идёт туго, со скрипом. Трудно и скучно складывать и вычитать, не говоря уже о чём-то более сложном. Новые темы никак не хотят укладываться в голове. Писательница и мама троих детей Ксения Букша рассказывает, основываясь на собственном опыте, как помочь ребёнку освоить математику.
Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу
Раскладываем трудности по полочкам
На уровне 1–5-го классов неспособных к математике детей не бывает. Но бывают дети с конкретными трудностями, которые можно и нужно преодолеть. Подумаем, почему ребёнку трудно с математикой.
Вот возможные варианты или их комбинации.
- Плохо считает, нет навыка счёта.
 Не очень хорошо знаком с числами.
Не очень хорошо знаком с числами. - Не может вникнуть в суть поставленной задачи, с трудом понимает, что надо делать. Пробует все варианты («Так неправильно? Тогда попробую разделить», «В три раза больше — здесь нужен плюс или минус?»).
- Усваивает шаблонное решение, но не может его доработать. Столкнувшись с малейшим изменением условий, впадает в ступор.
- Не умеет читать сложные тексты. В результате не понимает ни описания правил, ни текста задачи. Если на пальцах объяснить, что надо делать, сразу решает нормально.
- В голове не укладываются концепции. С трудом их понимает и быстро забывает. Такой ребёнок может сто раз услышать объяснение, что такое икс (неизвестное), но так и не понять.
- Не развит навык наглядного представления. Не может представить себе, нарисовать схематичную картинку, «увидеть в уме».
- Короткое внимание: всё понимает, но делает кучу ошибок, особенно в длинных сложных примерах.
Как видим, математика раскладывается на множество разных навыков. Когда мы выяснили, в чём проблема, мы можем её решать. Заранее прошу прощения у учителей и методистов: я всего лишь родитель, а мои мысли по этому поводу — всего лишь частное мнение, хотя я стараюсь его обосновывать.
Когда мы выяснили, в чём проблема, мы можем её решать. Заранее прошу прощения у учителей и методистов: я всего лишь родитель, а мои мысли по этому поводу — всего лишь частное мнение, хотя я стараюсь его обосновывать.
Ждём, пока созреет способность абстрактно мыслить
Мозг нейротипичного ребёнка дозревает до абстрагирования и обобщения далеко не сразу. У некоторых это происходит раньше, у других позже. Например, не все дети могут соотнести число и количество. Для очень многих и во 2–3-м классе есть только «15 яблок», а просто «15» нет.
При этом они как-то привыкают оперировать числами, и пробел в базовом понимании не очень заметен, пока речь не заходит о чуть более сложных вещах. Например, именно им трудновато понять, почему не может быть «полтора» в ответе на вопрос «сколько землекопов?». А уж когда начинаются проценты или задачи на скорость и расстояние, становится совсем сложно.
Стоит вернуться назад к конкретике. Возможно, для понимания дробей пока нужно проговаривать «в числителе арбузы, в знаменателе мальчики; 21 арбуз достался 42 мальчикам — каждому по половинке арбуза». Даже в пятом классе почти все концепции ещё можно заземлить до конкретики.
Даже в пятом классе почти все концепции ещё можно заземлить до конкретики.
Развиваем навыки счёта
Просто учиться считать — это скучно. Нам помогут всевозможные игры с числами. Для начала — усложнённые ходилки с 2–3 кубиками (когда за один ход максимум — 18 очков, а не 6), потом — разнообразные игры в кости, где нужно считать очки.
Самая простая игра известна мне под названием «единичка»: игроки по очереди бросают один кубик (или два, или три), пытаясь добраться до сотни очков. Серия прерывается, когда у игрока выпадает хотя бы одна единичка: в этом случае очки за эту серию сгорают, и нужно уметь остановиться вовремя.
Очень рекомендую покер на костях. В этой игре есть ряд комбинаций, каждую из которых надо выбросить за три попытки. Эти попытки можно копить. Игроки делают ходы по очереди, выигрывает тот, кто первым выполнит все комбинации. Помимо простого навыка складывания очков, покер постепенно развивает тонкое понимание случайности и вероятности, просчитываемого риска и шансов. В такой покер может научиться играть даже шести- или семилетка.
В такой покер может научиться играть даже шести- или семилетка.
Для отработки деления и умножения мы с дочкой говорили о числах как о «родственниках». Например, у числа 72 очень большая «семья»: у него есть «детки» 24 и 36, есть «внуки» — 2, 3, 4, 6, 12, 18. А вот число 37 не завело себе никакой «семьи», оно простое. Зато если «поженить» его с другим «одиночкой» — 41, у них получится вместе 78, теперь можно «заводить детей и внуков». Это хорошо помогает ориентироваться в таблице умножения.
Учим видеть и наглядно обобщать задачу
Чтобы хорошо схематизировать, надо уметь выделять именно то, что важно для условия задачи, и схематично изображать это на картинке. Сначала мы учимся выделению главного. Это знаменитые игры «что лишнее?», в которых может быть и несколько ответов. Арбуз, аист, абрикос, виноград — что лишнее? Смотря по какому признаку.
В учебнике Петерсон есть чудесные задачи, загромождённые кучей ненужных данных или лишённые необходимых условий. В задании автор просит найти и выделить только те условия, которые нужны для решения, а если их нет — указать, чего не хватает. Научившись видеть задачу, можно перейти к схематизации.
Научившись видеть задачу, можно перейти к схематизации.
Многие дети вообще не понимают, зачем рисовать схемы к задачам и почему это проще. Всё потому, что схемы эти даны готовыми. Но по какому принципу они строятся? Почему, например, неважно, какой длины сам поезд, если он едет из А в Б? Как нарисовать «3 часа»? А «все груши, посаженные мальчиками»?
Можно вместе рисовать схемы разных задач, а потом предлагать ребёнку придумывать похожие. Такие задания есть и в учебниках, но там их мало. Для некоторых эта трудность вообще определяет все отношения с математикой, да и вообще с упорядочиванием данных, абстрагированием, обобщением, поиском решения.
Оттачиваем логику
Логика — один из инструментов, которые нужны всем. Нет людей, которые были бы не склонны к логике, есть те, у кого она «не поставлена». Это как умение орудовать шуруповёртом: научиться может каждый, у кого есть руки. Вы можете сами оценить, насколько железная у вас логика. Я очень люблю вот этот чудесный тест.
Человека с логикой не способна заморочить никакая пропаганда или реклама, его не запутает недобросовестный банк, он гораздо лучше ориентируется в окружающем мире.
С детьми можно начать с простых силлогизмов, которые иногда звучат смешно, но приводят к пониманию очень важных штук. Например, услышав от кого-нибудь сентенцию «мальчики не плачут», ребёнок может уточнить: «некоторые или все?»
Если дети не проходят понятие множества, стоит хоть немножко вместе с ним порисовать «кружочки» (не обязательно сразу вводить все понятия) и порешать соответствующие задачи: вот мальчики, вот коты, а вот те, кого зовут Вася. Где мальчики, которых зовут не Вася? А где тут девочки? А где кот Барсик?
Развиваем воображение
Воображение необходимо для всего, что связано с математикой и логикой. (Я даже не пишу «как ни странно», потому что это совершенно не странно.) Особенно умение мыслить образами.
Я очень люблю игру, в которой родитель и ребёнок по очереди задают друг другу «графические загадки», не имеющие точного ответа. Каждый рисует серию непонятных геометрических фигур или их комбинаций (точка в треугольнике, молния и круг, несколько кругов, касательные…), а другой дорисовывает их так, чтобы получилась картинка. Чем остроумнее решение, тем больше удовольствия получают оба игрока.
Каждый рисует серию непонятных геометрических фигур или их комбинаций (точка в треугольнике, молния и круг, несколько кругов, касательные…), а другой дорисовывает их так, чтобы получилась картинка. Чем остроумнее решение, тем больше удовольствия получают оба игрока.
Существует много древних и новых игр, в которых нужно складывать узоры из деталей и фрагментов яйца (колумбово яйцо), квадрата, по-разному раскрашенных граней кубика («Сложи узор»). Есть и трёхмерные наборы, например «Пентамино». Речь не о том, чтобы выполнять задания, хотя все эти наборы можно использовать и так, но именно о творчестве из имеющихся деталей и об умении увидеть образ.
А можно ещё вырезать снежинки, дорисовывать симметричных бабочек и человечков, придумывать шифры, рисовать лабиринты и карты. Всё это и есть развитие математического воображения.
Учим ребёнка вычленять, чего конкретно он не понимает (метакогниция)
Я уже не раз писала про неё — и в связи с математикой, и в связи с сочинениями. Вкратце метакогниция — это умение «понимать, как я думаю», «знать, чего именно я не знаю», осознание своего мыслительного процесса. Именно этому почти никогда не учат в школе, а иногда даже портят уже развитую способность. Предполагается ведь, что есть простые и сложные способы решения той или иной задачи. Часто это так и есть, но порой гораздо ценнее умение идти самому и по шагам проверять себя: «Так нужно делать? Я прав?»
Вкратце метакогниция — это умение «понимать, как я думаю», «знать, чего именно я не знаю», осознание своего мыслительного процесса. Именно этому почти никогда не учат в школе, а иногда даже портят уже развитую способность. Предполагается ведь, что есть простые и сложные способы решения той или иной задачи. Часто это так и есть, но порой гораздо ценнее умение идти самому и по шагам проверять себя: «Так нужно делать? Я прав?»
Совместные рассуждения (и я не про математику) ценны и тем, что сближают ребёнка и родителя, и тем, что мы показываем, как проходит процесс думания. Он не должен быть гладким и автоматическим. В нём есть тупики, неожиданные повороты. «Наше первоначальное предположение неверно, а это значит, что нужно идти не по дороге 1, а по дороге 2». Кстати, это пригодится и в школьной математике, когда нужно будет понимать доказательства теорем. Ведь хорошо запоминается только то, что прошёл сам своим умом, когда смог повторить чужие рассуждения и знаешь в них каждый поворот.
Распечатанные рабочие листы для задач по математике для второго класса
Проблемы со словами могут быть сложной задачей для учащихся, особенно для второклассников, которые, возможно, еще учатся читать. Но вы можете использовать базовые стратегии, которые будут работать практически с любым учеником, даже с теми, кто только начинает изучать письменные навыки.
Инструкции и стратегии
Чтобы помочь второклассникам научиться решать задачи со словами, научите их выполнять следующие действия:
- Изучите математическую задачу: Прочтите слово «задача», чтобы понять ее общий характер.Поговорите со своими учениками о проблеме и обсудите, какие части являются наиболее важными.
- Прочтите математическую задачу: Прочтите вопрос еще раз. На этот раз сосредоточьтесь на конкретных деталях проблемы. Какие части проблемы связаны друг с другом?
- Задайте вопросы о задействованных операциях: Поразмышляйте еще раз.
 Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения. - Спросите себя о предпринятых шагах: Просмотрите каждый сделанный шаг.Определите, кажется ли ваш ответ разумным. Если возможно, сверьте свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.
- Завершите: Просмотрите текст словесных задач, которые вы будете решать, чтобы определить любые слова, которые вы не узнаете. Перечислите их и определите их значение, прежде чем решать проблемы. Напишите краткие определения терминов для справки при решении проблемы.
Решение проблем
Изучив эти стратегии, используйте следующие бесплатные распечатки задач со словами, чтобы студенты могли практиковать то, что они узнали.Есть только три рабочих листа, потому что вы не хотите перегружать своих второклассников, когда они только учатся решать задачи со словами.
Начните медленно, при необходимости повторите шаги и дайте своим ученикам возможность усвоить информацию и освоить словесные методы решения проблем в расслабленном темпе.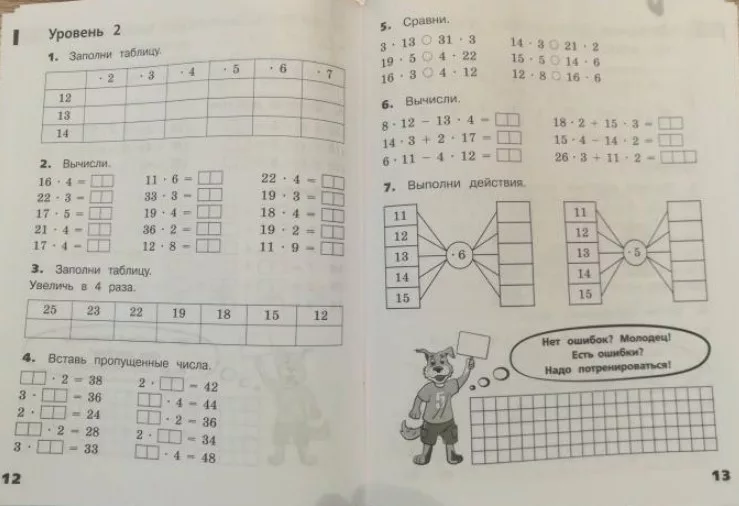 В печатных материалах содержатся термины, которые будут знакомы молодым студентам, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
В печатных материалах содержатся термины, которые будут знакомы молодым студентам, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
Д. Рассел
В эту распечатку включены восемь математических задач, которые покажутся второклассникам многословными, но на самом деле они довольно просты.Задачи на этом листе включают задачи со словами, сформулированные в виде вопросов, например: «В среду вы видели 12 малиновок на одном дереве и 7 на другом дереве. Сколько всего малиновок вы видели?» и «У всех ваших 8 друзей есть двухколесные велосипеды, сколько всего это колес?»
Если студенты озадачены, прочитайте задачи вслух вместе с ними. Объясните: как только вы вычеркнете слова, это будут простые задачи сложения и умножения, где ответ на первый будет следующим: 12 робинов + 7 робинов = 19 малиновок; а ответ на второй будет: 8 друзей x 2 колеса (для каждого велосипеда) = 16 колес.
Д. Рассел
Рассел
Эта последняя печатная форма в наборе содержит немного более сложные задачи, такие как эта, связанная с деньгами: «У вас есть 3 квартала, и ваша выписка обошлась вам в 54 цента. Сколько денег у вас осталось?»
Чтобы ответить на этот вопрос, предложите учащимся изучить проблему, а затем прочитать ее всем классом. Задайте такие вопросы, как: «Что может помочь нам решить эту проблему?» Если учащиеся не уверены, возьмите три четверти и объясните, что они равны 75 центам. Тогда задача превращается в простую задачу вычитания, поэтому завершите ее, указав числовую операцию на доске следующим образом: 75 центов — 54 цента = 21 цент.
Задачи по обучению словарю во 2-м классе
Если вы ищете лучший способ научить словесным задачам и, что более важно, хотите, чтобы ваши ученики были более успешными в решении словесных задач, я здесь, чтобы помочь. Учить словесные задачи во 2-м классе не должно быть проблемой.
Почему во 2-м классе так сложно учить словесные задачи?
Когда я только начал преподавать, я учил своих учеников использовать ключевые слова, подчеркивать и обводить, выделять и вставлять рамку… и все же это не помогло.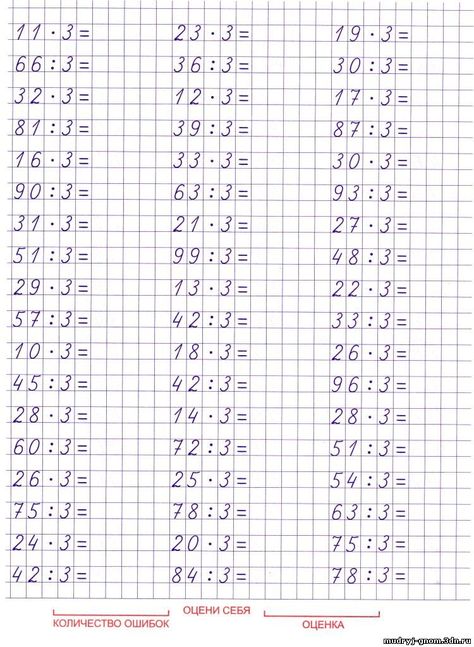 Они все еще не знали, когда складывать, а когда убирать.
Они все еще не знали, когда складывать, а когда убирать.
И мои ученики не понимали и не успевали лучше.
Не помогало то, что я постоянно не учил и не позволял своим ученикам практиковаться в решении словесных задач.
Задачи со словом всегда были источником разногласий для моих учеников, независимо от того, в каком классе я преподавал (1-й, 2-й и 4-й), и всегда были тем, что я преподавал наугад в рамках принятой математической программы.
Большинство учебных программ по математике предлагают следующее:
- Задачи на 1 или 2 слова в конце каждого урока, но на самом деле не предлагают способ научить учеников решать задачи со словами
- 1 глава о «решении задач»
И серьезно, ни то, ни другое полезно.
Я хотел, чтобы мои ученики ежедневно практиковались в стратегических задачах.
И знаете что? Когда я начал последовательно и стратегически преподавать задачи со словами во 2-м классе, мои ученики были менее разочарованы и гораздо более искусно решали задачи со словами.
Итак, какое решение?
Сейчас я следую 4-дневному плану обучения и оцениваю его на 5-й день.
Я больше не учу ключевые слова или подчеркивание, обводку, выделение и / или бокс… вместо этого я учу своих учеников искать закономерности в том, как структурированы проблемы со словами… ситуации со словами.
Кроме того, я посвящаю 5-10 минут каждый день обучению и практике словесных задач.
Как я узнаю, чему учить?
Начну со стандарта.
Честно говоря, что бы я ни преподаю, именно здесь я начинаю. Мне нужно точно знать, чего я ожидаю, чтобы потом я мог помочь своим ученикам справиться с этим.
Стандарт Common Core для 2-го класса гласит:
CCSS.MATH.CONTENT.2.OA.A.1
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e. g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.

Хотя многие штаты больше не используют термин «Common Core», многие принятые ими стандарты совпадают или, по крайней мере, схожи.
MAFS.2.OA.1.1 (стандарты Флориды)
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e.g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Итак, второклассники должны уметь решать:
- Сложение / вычитание в пределах 100
- Одно- и двухступенчатое
- Добавить к
- Взять из
- Соединить
- Разобрать
- Сравнить
Когда вы посмотрите на то, что должны делать второклассники, неудивительно, что учить словесные задачи так сложно, не говоря уже о том, что студенты действительно их осваивают.
Как я учу задачи по словам во 2-м классе:
В начале года ученики знакомятся с нашей рутинной задачей со словом после первых двух недель в школе.
Я объясняю, что задачи со словами похожи на истории, которые мы должны читать и понимать, что происходит в рассказе. Мы называем эти слова «проблемными ситуациями».
Затем я учу студентов, что есть 4 вещи, которые они всегда должны делать, решая задачу со словами:
- Напишите числовое предложение
- Используйте стратегию для решения
- Я объясняю студентам, что я не могу залезть в их мозг, чтобы увидеть, что они думают, и если я не знаю, о чем они думают, я не может помочь им лучше решать проблемы со словами.
- Учащиеся могут рисовать картинки, использовать семейство фактов, базовые 10 блоков и / или стандартный алгоритм.
- Вычисление
- Я смотрю, чтобы убедиться, что ученик дал правильный ответ.
- Ответ в предложении
- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки». Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.

- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки». Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.
Запуск рутинной задачи со словом — это все о моделировании и рутине. Студентам не нужно много времени, чтобы научиться этому.
Я проделал за вас тяжелую работу — у меня на весь год есть задачи по словам во 2-м классе, готовые для вас!
Что такое рутинная задача для 2-х классов?
По понедельникам я использую слово «проблемная ситуация». Я считаю полезным, чтобы студенты «разыгрывали» ситуацию. Используйте пример на ситуационном плакате / диаграмме привязки, чтобы показать учащимся образец.(Я учу студентов, что подчеркнутые части числового предложения — это известные нам части, а квадрат представляет неизвестное.)
Смоделируйте и решите практическую задачу со словами и поделитесь своими отзывами со студентами.
В течение следующих 3 дней мы моделируем и решаем задачу со словом, которая имеет ту же ситуацию, что и понедельник. Так что мы не скучаем. Это очень систематично.
Наконец, по пятницам ученики самостоятельно решают 2 задачи со словами, следуя той же ситуации, которую мы использовали всю неделю.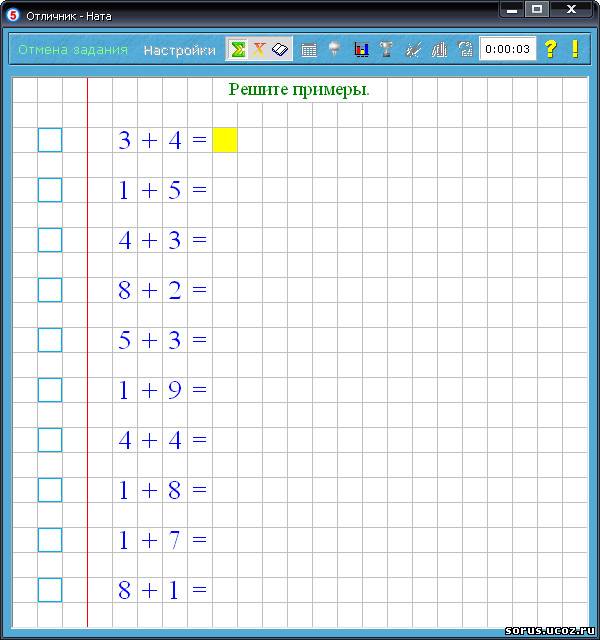
Для дифференциации или расширения учащиеся могут написать задачу на обратной стороне своего экзамена, которая соответствует той же ситуации, которую они изучали на этой неделе. Это отличный способ узнать, действительно ли студенты понимают ситуацию, которую мы узнали на той неделе.
Возможно вам понравится:
Давайте подключимся!
Instagram // Pinterest // Facebook // Учителя платят учителям
многоступенчатых уравнений | 2-й класс по математике
Научитесь решать многоступенчатые уравнения
😎 Итак, вы научились складывать и вычитать числа.
Что произойдет, если вам нужно будет сложить и вычесть в одном уравнении? 🤔
👉 Давайте посмотрим на пример:
У вас в ланч-боксе 5 печений . Ваш друг дает вам еще 3 файлов cookie.Вы съели 2 печенья. Сколько файлов cookie у вас осталось?
Мы начинаем с , записывая уравнение для задачи.
5 + 3 — 2 =?
Как вы решите это многошаговое уравнение ? 🤔
Решите многоэтапных уравнений с помощью , упрощая одну операцию за раз.
😃 Операция — это слово для сложения или вычитания.
👉 Идем с слева направо . Итак, сначала мы начнем с сложения.
5 + 3 = 8
Теперь мы можем переписать наше исходное уравнение и поместить 8 вместо 5 + 3 .
А теперь вычитаем!
8 — 2 = 6
Отличная работа! 👏 Наш ответ: 6.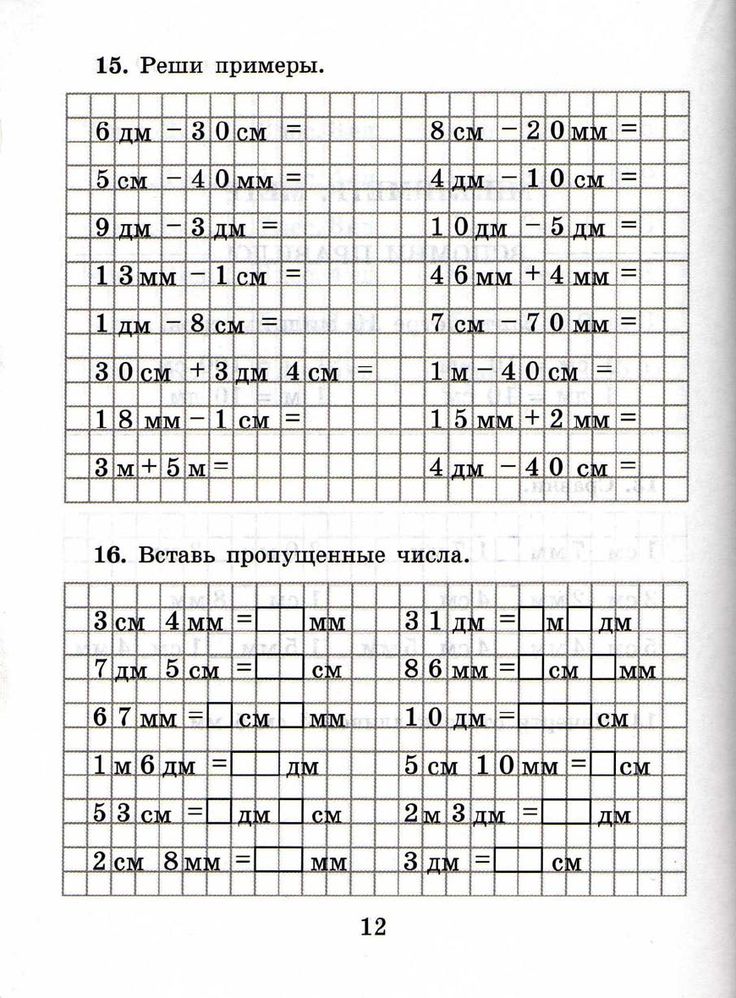
Другой пример
👉 Давайте попробуем это уравнение.
20-11 + 5 =?
✅ На этот раз вычитание — первая операция, которую мы упростили, .
20-11 = 9
Теперь мы можем поставить 9 вместо первого уравнения.
Все, что нам осталось сделать, это добавить!
9 + 5 = 14
Отличная работа! 👍
Теперь вы можете переходить к практике.
примеров общих основных математических задач для 2-го класса — математический класс [2021]
Примеры операций и алгебраического мышления
Эти стандарты просят студентов работать со сложением и вычитанием различными способами, включая простые вычисления и более сложные решения проблем.
- В классе мисс Винки 24 ученика. Однажды к ним пришли еще трое детей, но четверо из обычных учениц мисс Винки отсутствуют. Сколько детей в классе в этот день? Покажите свое решение как минимум двумя способами.
- Автобус номер три обычно занимает 14 минут, чтобы добраться от автобусной остановки Сьюзи до ее школы. Сегодня автобус застревает в пробке еще на 5 минут. Сколько времени нужно, чтобы добраться от автобусной остановки Сьюзи до школы?
- Карлос и его семья любят гулять.В минувшие выходные собрали 28 желудей! Карлос уронил 6 из них по дороге домой и отдал 2 своему младшему брату. Сколько желудей у него осталось?
- Что на семь больше четырех? Что на четыре меньше семи?
- Джозеф покупает пачки жевательной резинки для своих друзей и семьи. Если в каждой пачке есть пять палочек жевательной резинки, а Джозеф покупает три пачки, сколько палочек жевательной резинки покупает Джозеф?
Числа и операции в десятичных примерах
Эти стандарты основываются на чувстве числа учащихся, предлагая им понять, что представляет каждая цифра в трехзначном числе и как разные числа соотносятся друг с другом.
- Что означает цифра «7» в числе 374? Как можно представить эту «7» цифрами? Используете блоки по основанию десять?
- Если вы пропускаете счет от 10 до 200, сколько раз вам придется считать?
- Что на десять больше, чем 67? Как вы можете ответить на этот вопрос, не производя вычислений?
- Как решить задачу 34 — 17? Покажите свою работу, используя как минимум две разные стратегии.
Примеры измерений и данных
Стандарты в этой области просят ваших учеников измерять длину предметов и работать с длиной в контексте решения проблем.Они также просят ваших второклассников поработать над задачами, требующими времени, денег и базового представления данных.
- Измерьте длину трех разных предметов в классе. Объясните, как вы решили, какой измерительный инструмент использовать для каждого объекта, и запишите их измерения, используя наиболее подходящую единицу измерения.
- Если в прошлом году рост Сисси составлял 48 дюймов, а в этом году она выросла на три дюйма, то какого она роста сейчас?
- Школа начинается в 8:50 каждое утро.
 Обед — через три часа десять минут после начала учебного дня. Когда будет ланч?
Обед — через три часа десять минут после начала учебного дня. Когда будет ланч? - Если у Лоуренса две четверти и пятак, сколько у него денег?
- Джоди хочет, чтобы ее мама купила ей куклу и кукольное платье. Кукла стоит 36 долларов, а платье — 11 долларов. Сколько денег Джоди просит маму вообще потратить?
- Вместе со своим классом создайте гистограмму, показывающую, сколько букв содержится в именах учащихся в вашем классе. Вместе обсудите график и объясните, что он показывает и что заставляет вас думать.
Примеры геометрии
Эти стандарты требуют, чтобы учащиеся могли рисовать и распознавать формы и разбивать их в соответствии с контрольными дробями.
- Как вы называете двухмерную форму с пятью сторонами?
- Нарисуйте прямоугольник. Разделите прямоугольник на три ряда и три столбца квадратов одинакового размера. Сколько всего квадратов в прямоугольнике?
- Нарисуйте круг. Разделите круг на три равные части. Как вы называете эти акции?
Контрольный список навыков для 2-го класса: математика
Контрольные листы подготовки ко второму классу
Математика
Номера, операции и решение проблем
- Считает по 1, 2, 5 и 10 с
- Определяет, упорядочивает и записывает цифры от 0 до 100
- Знает факты сложения и вычитания до 50
- Складывает и вычитает двузначные числа до 99 без перегруппировки
- Показывает начальное понимание разряда
- Делает разумные оценки количеств
- Обозначает целые, половину, трети и четверти
- Называет и использует порядковые номера, такие как первый, второй, третий и т.
 Д.
Д. - Отображает и определяет положительные целые числа в числовой строке
Геометрия и измерения
- Обозначает и рисует основные формы
- Исследует и решает простые пространственные и измерительные задачи, используя манипуляторы (практические объекты, которые можно подсчитать или сортировать) и чертежи.
- Признает и использует стандартные измерительные инструменты, такие как линейки, весы и термометры.
- Понимает основные концепции пространственных отношений, симметрии и отражений.
Математика в действии: определение времени, счет денег, реальная математика
- Распознает и добавляет деньги к 1 доллару.00
- Показывает время с точностью до часа
- Использует рисунки и слова для описания математического мышления
- Собирает и записывает данные с помощью таблиц, списков, диаграмм и графиков
- Считывает график или диаграмму и делает выводы
- Классифицирует, сортирует и сравнивает физические объекты по множеству схем классификации и шаблонов (сходство, различие, звук, цвет, текстура, размер, вес, температура, продолжительность и т.
 Д.).
Д.). - Создает, копирует и расширяет шаблоны с действиями, объектами и словами
Советы для родителей, которые помогут детям чувствовать себя уверенно при решении числовых и числовых задач:
- Создайте банку для монет, в которую вы бросаете мелочь и даете своему ребенку регулярную работу по сортировке и подсчету этих монет (с вашей помощью) на регулярной основе.
- Ведите общий семейный календарь и пусть ваш ребенок отмечает дни, считает дни до предстоящих событий и отслеживает дни рождения.
- Поощряйте ребенка помогать рассортировать банки и коробки в кладовой по размеру или весу.
- Включите ребенка в простые кулинарные упражнения и моделируйте его из мерных чашек или ложек; опишите, что вы делаете, когда используете эти измерительные инструменты.
- Играйте в игры на счет, когда находитесь в машине или на прогулке; выберите «магическое число» и предложите ребенку определить это количество собак, затем магическое количество больших деревьев или красных машин и т.
 д.
д.
навыков математики для 2-го класса, чему научится ваш ребенок
Во втором классе по математике дети начинают работать с большими числами и лучше понимают их значение. Студенты также изучают повседневные навыки, такие как определение времени, работа с деньгами и измерение.
Мы, родители, можем помочь нашим детям преуспеть во втором классе по математике, узнав больше о том, что они собираются изучать.В течение года ваш ребенок научится:
1. Считать в пределах 1000
Второклассники учатся читать и записывать числа до 1000. Они учатся пропускать счет на 5, 10 и 100, поскольку замечают закономерности среди чисел.
Дома: Создайте возможности для чтения и записи трехзначных чисел. Например, попросите ребенка прочитать числа на этикетках с питанием.
Вы также можете попросить ребенка устно пропустить счет на 10 или 100 секунд. Начните с 10 или 100, а затем предложите второкласснику не учитывать другие числа, например 60 или 204.
2. Понимание разряда в трехзначных числах
По мере того, как дети учатся считать с точностью до 1000, они будут более внимательно смотреть на трехзначные числа. Глядя на закономерности в числах, дети начинают понимать числовую ценность.
Дома: помогите своему ребенку, спросив, сколько единиц, десятков и сотен в трехзначных числах.
3. Сравните трехзначные числа
Узнав о разрядах и счетах в пределах 1000, второклассники смогут сравнивать трехзначные числа.Они смогут использовать свои знания о числовой стоимости, чтобы посмотреть на два числа и сказать, какое из них больше или меньше другого. Дети узнают, как использовать символы и = для сравнения трехзначных чисел.
Дома. Помогите ребенку отработать навыки сравнения, задав такие вопросы, как «Что больше: 943 или 783?» Развивайте мышление ребенка, спрашивая, почему одно число больше другого.
4. Складывать и вычитать в пределах 1 000
Во втором классе дети привыкают складывать и вычитать числа в пределах 100.Они решают одно- и двухэтапные задачи со словами, например: «У Тимми было 39 игрушечных машинок. Он получил еще 12, затем отдал 18. Сколько машин осталось у Тимми? »
После работы над сложением и вычитанием в пределах 100 дети будут использовать свои знания трехзначных чисел, чтобы практиковать сложение и вычитание в пределах 1000.
Дома: составьте несколько словесных задач, подобных приведенной выше, используя любимые игрушки или еду вашего ребенка.
5. Измерение
Второклассники развивают свое понимание измерения, оценивая длины и измеряя их с использованием различных единиц. Они сравнивают длины, аналогично тому, как они проводят сравнение с числами, и используют сложение и вычитание, чтобы узнать, насколько длиннее или короче объекты.
Дома: дайте ребенку линейку и попросите его измерить три разных предмета в доме. Затем попросите ребенка расположить предметы в порядке от самого короткого до самого длинного и объяснить, насколько каждый предмет длиннее или короче других.
Затем попросите ребенка расположить предметы в порядке от самого короткого до самого длинного и объяснить, насколько каждый предмет длиннее или короче других.
6. Определение времени с точностью до ближайших пяти минут
В первом классе учащихся познакомили с функцией определения времени.Теперь второклассники могут расширить свое понимание времени до ближайших пяти минут. Дети также смогут отличить AM от PM.
Попросите вашего ребенка научиться определять время с точностью до пяти минут — напомните ему использовать AM и PM!
7. Задачи со словами, связанные с деньгами
Второклассники решат множество задач со словами, связанных с сложением и вычитанием, в том числе с деньгами.
Дома: дайте ребенку стопку монет и задание посчитать общую сумму.Или поиграйте в «магазин» и попросите ребенка попрактиковаться в покупке предметов на разные суммы денег, а затем вычислить, сколько центов осталось.
8. Картинка и гистограммы
Картинка и гистограммы
Во втором классе ваш ребенок научится пользоваться картинками и гистограммами до четырех категорий.
Предложите ребенку пройти опросы дома и представить собранные данные в виде графика.
Приятно провести время, погрузившись в математику для второго класса!
Нашли это полезным? Ознакомьтесь с нашими руководствами по математике от детского сада до 5 класса
Написано Лили Джонс, Лили Джонс любит учиться всему.Она была воспитателем детского сада и первого класса, инструктором по обучению, разработчиком учебной программы и наставником учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
О Komodo — Komodo — это увлекательный и эффективный способ улучшить математические навыки K-5. Komodo, разработанный для детей от 5 до 11 лет для использования в домашних условиях, использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в напряженный семейный распорядок. Komodo помогает пользователям развить беглость и уверенность в математических вычислениях — , не задерживая их долгое время за экраном .
Komodo помогает пользователям развить беглость и уверенность в математических вычислениях — , не задерживая их долгое время за экраном .
Узнайте больше о Komodo и о том, как он помогает тысячам детей каждый год лучше учиться по математике — вы даже можете попробовать Komodo бесплатно.
Задачи по математике для 2-го класса — миссис Латс и мисс Уилл
2 класс
GO Math
2016-2017
Цели и учебные цели
Глава 1: Числовые концепции
числа до 20 как четные или нечетные.
· Напишите уравнения с равными слагаемыми для представления четных чисел.
· Используйте разряд для описания значений цифр в двузначных числах.
· Напишите 2-значные числа в развернутой форме.
· Записывайте двузначные числа в форме слова, развернутой и стандартной форме.
· Применяйте концепции разряда, чтобы найти эквивалентные представления чисел.
· Решайте проблемы, находя различные комбинации десятков и единиц для представления двухзначных чисел, используя стратегию «найти образец».
· Расширить последовательности подсчета в пределах 100 на 1, 5 и 10
· Расширить последовательности подсчета в пределах 1000 на 1, 5, 10 и 100 секунд.
Глава 2: Числа до 1 000
· Записывайте трехзначные числа в развернутой и стандартной форме.
· Применяйте концепции разряда, чтобы найти эквивалентные представления чисел.
· Определите на 10 больше, на 10 меньше, на 100 больше или на 100 меньше, чем любое заданное число
· Расширьте числовые шаблоны, считая на 10 или 100.
· Решайте проблемы, связанные со сравнением чисел, используя стратегию «создать модель».
· Сравните 3-значные числа, используя символы .
Глава 3: Основные факты и взаимосвязи
· Используйте двойные факты как стратегию для нахождения сумм для почти двойных фактов.
· Вспомните суммы основных фактов, используя свойства и стратегии.
· Вызов сумм для сложения фактов, используя стратегию «сделать десять».
· Найдите суммы трех слагаемых, применяя коммутативные и ассоциативные свойства сложения.
· Используйте обратную зависимость сложения и вычитания, чтобы вспомнить основные факты.
· Вспомните различия основных фактов, используя умственные стратегии.
· Найдите различия на числовой прямой, чтобы разработать мысленную стратегию разложения для упрощения фактов.
· Используйте линейчатые модели для представления различных ситуаций сложения и вычитания.
· Решайте проблемы с участием равных групп, используя стратегию «разыграй все».
· Напишите уравнения, используя повторное сложение, чтобы найти общее количество объектов в массивах.
Глава 4: 2-значное дополнение
· Найдите сумму, разделив однозначное сложение, чтобы двузначное сложение стало кратным 10.
· Используйте компенсацию для развития гибкое мышление для сложения двух цифр.
· Применяйте концепцию разряда при использовании стратегии разделения для двухзначного сложения.
· Модель 2-значного сложения с перегруппировкой.
· Нарисуйте быстрые картинки и запишите сложение двух цифр, используя стандартный алгоритм.
· Запишите сложение двух цифр, используя стандартный алгоритм.
· Практикуйте сложение двух цифр с перегруппировкой и без нее.
· Перепишите задачи горизонтального сложения по вертикали в стандартном формате алгоритма.
· Решайте задачи, связанные со сложением двух цифр, используя стратегию «нарисовать диаграмму».
· Представляйте ситуации сложения числовыми предложениями, используя символ для неизвестного числа.
· Найдите суммы трех двузначных чисел.
· Найдите суммы четырех двузначных чисел.
Глава 5: Вычитание двух цифр
· Разделите однозначное вычитание на части, чтобы вычесть его из двузначного числа.
· Разделите 2-значное вычитаемое, чтобы вычесть его из 2-значного числа.
· Модель вычитания двух цифр с перегруппировкой.
· Нарисуйте быстрые картинки и запишите двузначное вычитание, используя стандартный алгоритм.
· Запишите двузначное вычитание, используя стандартный алгоритм.
· Практикуйте вычитание двух цифр с перегруппировкой и без нее.
· Перепишите задачи горизонтального вычитания по вертикали в стандартном формате алгоритма.
· Используйте сложение, чтобы найти различия.
· Решайте задачи вычитанием двух цифр, используя стратегию «нарисовать диаграмму».
· Представляйте ситуации вычитания числовыми предложениями, используя символ неизвестного числа.
· Анализируйте текстовые задачи, чтобы определить, какие операции использовать для решения многоступенчатых задач.
Глава 6: Сложение и вычитание 3-х цифр
- Нарисуйте быстрые картинки для представления 3-значного сложения.
- Примените концепцию разряда при использовании стратегии разделения для 3-значного сложения.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки единиц.

- Запишите 3-значное сложение с использованием стандартного алгоритма с возможной перегруппировкой десятков.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки единиц и десятков.
- Решайте задачи, связанные с вычитанием трех цифр, используя стратегию «создать модель».
- Запишите сложение трех цифр с использованием стандартного алгоритма с возможной перегруппировкой сотен.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки сотен и десятков.
- Запись вычитания с использованием стандартного алгоритма, когда в уменьшаемом значении есть нули.
Глава 7: Деньги и время
- Найдите общую стоимость коллекций в десять центов, пятак и центов.
- Закажите монеты в коллекции по стоимости, а затем найдите общую стоимость.
- Обозначает денежные суммы меньше доллара с использованием двух различных комбинаций монет.

- Покажите один доллар разными способами.
- Найдите и запишите общую ценность денежных сумм, превышающих доллар.
- Решайте словесные задачи, связанные с деньгами, используя стратегию «разыграй это».
- Сообщите и запишите время с точностью до часа и получаса.
- Сообщите и запишите время с точностью до 5 минут.
- Сообщите и запишите время, используя A.M. и П.
Глава 8: Длина в обычных единицах
- Используйте конкретные модели для измерения длины объектов в дюймах.
- Сделайте дюймовую линейку и используйте ее для измерения длины предметов.
- Оцените длину предметов, мысленно разделив их на дюймы.
- Измерьте длину объектов с точностью до дюйма с помощью дюймовой линейки.
- Решайте задачи сложения и вычитания, связанные с длинами объектов, используя стратегию «рисовать диаграмму».
- Измерьте длину объектов в дюймах и футах, чтобы изучить обратную зависимость между размером и количеством единиц.

- Оцените длину предметов в футах.
- Выберите подходящие инструменты для измерения различной длины.
- Измерьте длину объектов и используйте линейный график для отображения данных измерений.
Глава 9: Длина в метрических единицах
- Используйте конкретную модель для измерения длины объектов в сантиметрах.
- Оцените длину объектов в сантиметрах, сравнив их с известной длиной.
- Измерьте длину предметов с точностью до сантиметра с помощью сантиметровой линейки.
- Измерьте длину объектов в сантиметрах и метрах, чтобы изучить обратную зависимость между размером и количеством единиц.
- Оцените длину объектов в метрах.
- Измерьте, а затем найдите разницу в длине двух объектов.
Глава 10: Данные
· Соберите данные в опросе и запишите эти данные в итоговую таблицу.
· Интерпретируйте данные в графических изображениях и используйте эту информацию для решения проблем.
· Сделайте графические изображения для представления данных.
· Интерпретируйте данные в виде гистограмм и используйте эту информацию для решения проблем.
· Создавайте гистограммы для представления данных.
· Решайте проблемы, связанные с данными, используя стратегию построения графика.
Глава 11: Понятия геометрии и дроби
· Определите трехмерные формы.
· Определите трехмерные формы по количеству граней, ребер и вершин.
· Создавайте трехмерные формы, используя кубы и другие объекты.
· Назовите 3-4-5-6-сторонние формы в соответствии с количеством сторон и вершин,
· Определите углы в двухмерных формах.
· Сортировка двухмерных фигур по их атрибутам.
· Разделите прямоугольники на квадраты одинакового размера и найдите общее количество этих квадратов.
· Определите и назовите равные части кругов и прямоугольников половинками, третями или четвертями.
· Формы разделов для отображения половин, третей или четвертей.
· Определите и опишите одну равную часть как половину трети или четверть целого.
Задания по математике для 2 класса — задачи по математике для детей 2 класса
Четыре причины изучать математику во 2 классе
Развитие логического мышления
Математика учит анализировать данные, устанавливать взаимосвязи и находить оптимальное решение. Эти навыки помогут справиться не с одной жизненной задачей.
Достижение успеха в любой профессии
Умение оперировать цифрами нужно не только экономистам. Математика необходима даже в таких творческих профессиях, как архитектор и фотограф.
Повышение авторитета в своем окружении
В школе разбирающийся в математике ребенок будет пользоваться уважением сверстников, а вне учебы не позволит обмануть себя, например, на кассе в магазине.
Развитие коммуникативных навыков
Неочевидно, но факт: те, у кого все хорошо с математикой, более стройно, логично и последовательно излагают свои мысли. А значит, с ними приятнее общаться.
Какой должна быть математика для учеников 2 класса?
Интересные задачи вместо
длинных примеров
Задачи даются в игровой форме. Школьник просто следит за ходом интересной истории, как в мультфильме, и помогает продвигаться сюжету, решая несложные и увлекательные математические задачи на логику.
Развитие логики вместо
оперирования числами
Математика учит не только быстро считать, но и думать, рассуждать, анализировать и искать решения, опираясь на логику. Лучше всего развивать нужные навыки с детства — они пригодятся как в школе, так и в жизни.
Лучше всего развивать нужные навыки с детства — они пригодятся как в школе, так и в жизни.
Занятия всего от нескольких
минут в день
Каждый урок курса математики длится 30-40 минут и посвящен отдельной теме. Ребенок может делить занятия, как удобно, занимаясь хоть по 5-10 минут в день, и возвращаться к задачам в любое время.
Какие задачи по математике для 2 класса предлагает Умназия?
Задачи на классификацию
Поиск закономерностей
Математические задачи на логику
Задачи на истину и ложь
Волшебные квадраты
Математические ребусы
Задачи на переливание
Задачи на взвешивание
Задачи, решаемые с конца
Задачи на скорость
Задачи, решаемые методом перебора
Геометрические задачи
Начать заниматься
Примеры заданий по математике для 2 класса
Задача 1
Иван-Царевич заметил, что перед избушкой Бабы-яги спят несколько трёхголовых Горынычей и стадо гусей.
Сколько гусей в стаде?
Решить задачу
Задача 2
Лягушки на пруду соревновались в ловле мух. Соревнования длились 20 минут. Известно, что Квакша поймала на 7 мух меньше, чем Тревор, Тревор и Аква вместе поймали 100 мух, а Квакша ловила по 2 мухи в минуту.
Кто занял первое место, а кто — последнее?
Решить задачу
Задача 3
На новогоднем утреннике веселилось 20 малышей. Каждый из них был одет в костюм либо зайчика, либо снежинки, либо пирата. Второклассник Петя заметил, что зайчиков на празднике было в 6 раз больше, чем снежинок, а пиратов оказалось меньше, чем зайчиков.
Решить задачу
Решать задачи по математике для 2 класса
Познакомьтесь с форматом курса «Математическое мышление». Пройдите сюжетную игру и решите три математические задачи!
Пройдите сюжетную игру и решите три математические задачи!
Решать задачи
В Умназии дети развивают логическое мышление, решая увлекательные сюжетные задачи по математике
Продуманная программа
Курсы математического мышления разработаны на базе множества источников, экспертизы методистов и педагогов, разделены на 10 тем с теорией и игровыми заданиями с объяснением
Увлекательные задания
Ребенок решает сюжетные игровые задачи по математике для изучения новых тем и закрепления пройденного по каждому курсу. Никакой скуки! Ни одно задание не повторяется!
Никакой скуки! Ни одно задание не повторяется!
Дипломы и награды
В конце каждого курса ребенок решает тест или проходит игру, получая сертификат в случае успешного выполнения. Вы будете уверены в его знаниях!
Решение задач по математике во 2 классе
Во втором классе дети начинают учить таблицу умножения и получают первые оценки по итогам уроков и выполнения домашних заданий. Ученикам впервые приходится запоминать определенный объем информации.
Но зубрежка без логики не имеет смысла: заученные наизусть цифры и параграфы быстро забываются. Интерактивные сюжетные задания по математике помогут развить логическое мышление, научат ребенка анализировать и структурировать материал.
Купите курс математики для детей со скидкой 40 % уже сейчас
Математика 2 класс – какие темы нужно выучить ребенку?
После того, как ребенок отправился в школу, у родителей появляется множество новых переживаний: хорошо ли он был подготовлен к обучению, сможет ли найти общий язык с учителями и одноклассниками, будет ли преуспевать в учебе? В частности, маме и папе очень хочется, чтобы малыш хорошо учился и к концу года смог освоить всю школьную программу. Если первый класс – это по сути закрепление навыков подготовительного класса, то второй год школы – новые темы и предметы, поэтому и усилий нужно прилагать больше как по письму, чтению, так и по математике.
Если первый класс – это по сути закрепление навыков подготовительного класса, то второй год школы – новые темы и предметы, поэтому и усилий нужно прилагать больше как по письму, чтению, так и по математике.
Главная задача второклашки – к концу года освоить таблицу умножения или же быть полностью подготовленным к ее изучению. Для этого ученик должен освоить сложение и вычитание, уметь считать с переходом через десяток в пределах ста. Ведь прежде, чем перейти на новый уровень – умножение, необходимо выучить переместительный, сочетательный и распределительный законы математики. Многие школы дают возможность детям постепенно и самостоятельно изучить их во время летних каникул, когда происходит переход из второго класса в третий.
Математика второй класс – основные темы
Какие же темы проходят по математике во втором классе? В основном ребята изучают геометрические фигуры и их свойства, решают простейшие задачи, изучают единицы измерения, знакомятся с основными законами математики, учатся складывать и вычитать единицы и десятки, стараются применять в жизни приемы устного счета.
Конечно, завершающим этапом второго класса является таблица умножения. Чтобы быть готовым к ее изучению, ребенку необходимо хорошо закрепить уже пройденный материал. Если таблица умножения была задана на лето, то есть возможность еще раз пройти все темы на каникулах в свободном режиме.
Хорошо подготовленные ученики, которые успешно закончили первый класс, легче переносят нагрузку второго класса, ведь у них уже есть определенная база. Поэтому не стоит пренебрегать подготовкой сына или дочки к школе еще до того, как он пошел учиться.
Умножение и деление
Хорошо выученная таблица умножения – это очень важный навык, который необходим для того, чтобы успешно осваивать математику, а в дальнейшем алгебру и геометрию. Ведь программа средних и старших классов строится, в том числе и на умении умножать и делить. Если не усвоить умножение во втором классе, то отставание как снежный ком будет только нарастать. Очень важно объяснить ребенку, что залог понимания математики в том, чтобы последовательно и качественно усвоить все темы, которые перетекают одна в другую.
Родителям стоит помочь малышу выучить таблицу умножения и довести процесс табличного умножения и деления до автоматизма. Полезным будет узнать о некоторых хитростях этого процесса. Есть четыре стадии, каждую из которых необходимо пройти успешно для закрепления этого навыка:
- Ребенок должен понимать принцип и последовательность действий. Происходит запоминание терминов и понятий.
- Ученик запоминает алгоритм действий, чтобы пробовать самостоятельно выполнять вычисления.
- Нарабатывается опыт применения навыка. Это важная стадия, во время которой не стоит торопиться.
- Заключительная стадия, во время которой таблица умножения постепенно доводится до автоматизма с наращиванием скорости.
Тренажер по математике 2 класс – обучение в игре
Несмотря на то, что второклассник уже не маленький ребенок, а школьник, его все также привлекают интересные занятия в виде игр. Важно сделать обучение, в том числе и заучивание таблицы умножения, увлекательным и необычным. Академия развития интеллекта AMAKids предлагает ученикам воспользоваться удобной платформой Амаматика, где их ждет 12 игр на табличное умножение и деление, а также 10 полезных игр на внетабличное. Благодаря этим занятиям ребята смогут с легкостью освоить эту тему. Со временем навык табличного умножения будет доведен до автоматизма, причем ребенок будет точно понимать свои действия во время вычислений. Также скорость счета будет очень высокой.
Академия развития интеллекта AMAKids предлагает ученикам воспользоваться удобной платформой Амаматика, где их ждет 12 игр на табличное умножение и деление, а также 10 полезных игр на внетабличное. Благодаря этим занятиям ребята смогут с легкостью освоить эту тему. Со временем навык табличного умножения будет доведен до автоматизма, причем ребенок будет точно понимать свои действия во время вычислений. Также скорость счета будет очень высокой.
Тренажер по математике за второй класс поможет не только выучить и закрепить навык табличного умножения, но и позволит развить внимание, усидчивость, логику и другие важные способности учеников. Кроме того, платформа предлагает и другие математические направления.
Выбор программы по математике для 2 класса
После окончания второго класса, очень важно закрепить полученные навыки. Отличным помощником в этом станет математический тренажер. Амаматика позволит повторить пройденный материал, а также повысить уровень знаний.
Платформа предлагает отдельную программу по таблице умножения, где ученики смогут довести до автоматизма умножение и деление. Отрабатывать можно отдельно каждую тему, используя междисциплинарные связи. После закрепления таблицы умножения, следует перейти к решению задач и примеров с применением уже отработанного навыка. Обучение на курсе Амаматика позволит детям обучаться с удовольствием и интересом.
Отрабатывать можно отдельно каждую тему, используя междисциплинарные связи. После закрепления таблицы умножения, следует перейти к решению задач и примеров с применением уже отработанного навыка. Обучение на курсе Амаматика позволит детям обучаться с удовольствием и интересом.
ГДЗ по математике 2 класс учебник Моро, Волкова 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бельтюкова Г. В.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Решебник — страница 87Готовое домашнее задание
Номер 3.
Ответ:
Номер 4.
Выполни действия и объясни, как получено в каждом столбике второе равенство из первого.
Ответ:
Вычитание можно проверять как сложением, так и вычитанием.
38 – 8 = 30 27 – 20 = 7 38 – 30 = 8 27 – 7 = 20
56 – 30 = 26 56 – 20 = 36 56 – 26 = 30 56 – 36 = 20
В первом примере мы находим разность путем вычитания из уменьшаемого вычитаемого. А вторым примером проверяем правильность выполнения вычитания. В данном случае мы проверяем вычитание вычитанием. Таким образом, из первого примера, мы можем найти вычитаемое путем вычитания от уменьшаемого разности.
Номер 5.
Выполни вычитание и проверку.
Ответ:
49 – 9 = 40 14 – 6 = 8
40 + 9 = 49 6 + 8 = 14
74 – 30 = 44 82 – 40 = 42
30 + 44 = 74 42 + 40 = 82
80 – 20 = 60 100 – 30 = 70
60 + 20 = 80 30 + 70 = 100
Номер 6.
После того как из вазы взяли 6 груш, в вазе осталось еще 5 груш. Сколько груш было в вазе сначала? Составь и реши две задачи, обратные данной.
Ответ:
Было – ? гр.
Взяли – 6 гр.
Осталось – 5 гр.
6 + 5 = 11 (гр.) – было в вазе.
Ответ: 11 груш.
Обратная задача 1:
В вазе было 11 груш, из неё взяли 5 груш. Сколько груш осталось в вазе?
Было — 11 гр.
Взяли — 5 гр.
Осталось — ? гр.
11 – 5 = 6 (гр.) – осталось в вазе.
Ответ: 6 груш.
Обратная задача 2:
В вазе было 11 груш. Когда из неё взяли несколько груш, то в ней осталось 6 груш. Сколько груш взяли из вазы?
Было — 11 гр.
Взяли — ? гр.
Осталось — 6 гр.
11 – 6 = 5 (гр.) – взяли из вазы.
Ответ: 5 груш.
Задание внизу страницы
Вычисли разности и выполни проверку двумя способами.
Ответ:
14 − 9 = 5 59 − 40 = 19 80 − 20 = 60 14 − 5 = 9 59 − 19 = 40 80 − 60 = 20 9 + 5 = 14 40 + 19 = 59 60 + 20 = 80
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
ГДЗ по Математике 2 класс
Часть 1
Страница 4
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 5
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Поля |
Страница 6
| 1 | 2 | 3 | 4 | Поля |
Страница 7
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 8
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 9
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 10
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 11
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 12
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Страница 13
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 14
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 15
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 16
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 17
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 18.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 | 5 |
Страница 20. Что узнали. Чему научились
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
Страница 22.
 Проверим себя — Вариант 1
Проверим себя — Вариант 1| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Страница 23.
 Проверим себя — Вариант 2
Проверим себя — Вариант 2| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Страница 24.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 |
Страница 26
| 1 | 2 | 3 | 4 | 5 |
Страница 27
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 28
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 29
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 30
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Страница 31
| 1 | 2 | 3 | 4 | 5 |
Страница 32
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 34
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Поля |
Страница 36.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 | 5 |
Страница 38
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 40
| 1 | 2 | 3 | 4 | 5 |
Страница 41
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 42
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 44
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Страница 46
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 47
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 50.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 |
Страница 52. Что узнали. Чему научились
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
Страница 57
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 58
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 59
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 60
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 61
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 62
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 63
| 1 | 2 | 3 | 4 | 5 | 6 |
Страница 64
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 65
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 66
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 67
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 68
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 69
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 70.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 | 5 |
Страница 72. Что узнали. Чему научились
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
Страница 76
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 78
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 79
| 1 | 2 | 3 | 4 | Поля |
Страница 80
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 82
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Страница 83
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 84
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 86
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 88
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 89
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 90.
 Что узнали. Чему научились
Что узнали. Чему научились| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Страница 94.
 Задания базового уровня
Задания базового уровня| 1 | 2 | 3 | 4 | 5 |
Страница 96. Задания повышенного уровня
| 1 | 2 | 3 | 4 | 5 |
Часть 2
Страница 4
| 1 | 2 | 3 | Поля |
Страница 5
| 1 | 2 | 3 | 4 | Поля |
Страница 6
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 7
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Страница 9
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Страница 10
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Поля |
Страница 12
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 13
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 14
| 1 | 2 | 3 | 4 | 5 | 6 |
Страница 15
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Страница 16
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 17
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 18
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 19
| 1 | 2 | 3 | 4 | Поля |
Страница 20.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 | 5 |
Страница 22. Что узнали. Чему научились
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |
Страница 28.
 Странички для любознательных
Странички для любознательныхСтраница 29
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 30
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Поля |
Страница 31
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Страница 32
| 1 | 2 | 3 | 4 |
Страница 33
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 34
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 35
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 38.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 | 5 |
Страница 40. Что узнали. Чему научились
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
Страница 46.
 Странички для любознательных
Странички для любознательныхСтраница 48
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 49
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 50
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Поля |
Страница 51
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Страница 52
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Поля |
Страница 53
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 54
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 55
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Страница 56
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 57
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 58
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 59
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 60
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 61
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 62
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Страница 63.
 Что узнали. Чему научились
Что узнали. Чему научились| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Страница 64.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 | 5 | 6 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 |
Страница 71.
 Верно? Неверно?
Верно? Неверно?Страница 72
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 73
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 74
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 75
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 76
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 77
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Поля |
Страница 78.
 Проверим себя — Вариант 1
Проверим себя — Вариант 1| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 79. Проверим себя — Вариант 2
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 80
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 81
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Поля |
Страница 82
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 83
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 84
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Поля |
Страница 85
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Поля |
Страница 86.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 88. Что узнали. Чему научились
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
Страница 90
| 1 | 2 | 3 | 4 | 5 | 6 | Поля |
Страница 91
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 92
| 1 | 2 | 3 | 4 | 5 | Поля |
Страница 93
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Поля |
Страница 94
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Страница 95.
 Странички для любознательных
Странички для любознательных| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 96. Что узнали. Чему научились
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
Страница 100.
 Проверим себя — Вариант 1
Проверим себя — Вариант 1| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Страница 101.
 Проверим себя — Вариант 2
Проверим себя — Вариант 2| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Страница 102.
 Нумерация
Нумерация| 1 | 2 | 3 | 4 | 5 | 6 |
Страница 103, Числовые и буквенные выражения
Страница 103, Равенство, Неравенство, Уравнение
| 1 | 2 | 3 | 4 |
Страница 104.
 Сложение и вычитание
Сложение и вычитаниеСтраница 105. Свойства сложения
Страница 105. Таблица сложения
| 5 | 6 | 7 | 8 |
Страница 106. Решение задач
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Страница 109.
 Геометрические фигуры
Геометрические фигурыСтраница 110. Задания базового уровня
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Страница 111. Задания повышенного уровня
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
ГДЗ по математике для 2 класса Моро – это сборник готовых домашних заданий по задачам и примерам из учебника по арифметике, составленного известными российскими авторами – М. И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Он используется в большинстве общеобразовательных школ России.
И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. Он используется в большинстве общеобразовательных школ России.
Структура ГДЗ по учебнику математики второго класса от Моро
Во втором классе школьники знакомятся с базовыми понятиями арифметики, которые помогут им постигнуть алгебру и геометрию в старших классах, сформировать общее представление о предмете и науке. Они изучают числовой ряд от 1 до 100, порядок действий в сложных примерах, уравнения первого порядка с одной переменной. Они учатся рассчитывать периметр прямоугольника и проводить устные вычисления.
ГДЗ по математике 2 класса Моро, составленные на основе учебника 2015 года в его 6-м издании, включают в себя примеры и задачи на такие темы:
- числа от 1 до 100;
- проведение измерений, миллиметры и метры;
- денежная система исчислений: рубли и копейки;
- сложение и вычитание, скобки и порядок действий;
- измерение времени: часы и минуты;
- периметр многоугольника и длина ломаной линии;
- решение уравнений с одной переменной;
- угол и виды углов;
- прямоугольник и квадрат, их площадь и периметр;
- умножение, деление и их свойства.

Глубокое понимание представленных выше тем – гарантия успешного изучения алгебры и геометрии в старших классах. Ученики должны не просто списать примеры и задачки из решебника, но вникнуть в алгоритм решения.
Готовое домашнее задание для 2 класса на сайте ГДЗ Путина – замена репетиторов, помощь родителям, основа высокой успеваемости младших школьников.
Правильные решения от ГДЗ Путина по математике 2 класса к Моро
В интернете немало сайтов с готовыми домашними заданиями. В чем же преимущества портала ГДЗ от Путина для учеников младших классов и их родителей?
- наличие нескольких вариантов решения одной и той же задачи;
- ответы по самым свежим изданиям учебников российских школ;
- оформление готовых домашних заданий в соответствии с требованиями Министерства образования РФ;
- бесплатный доступ с любого устройства – смартфона, планшета, компьютера.
Эти критерии делают ГДЗ по математике 2 класса к учебнику Моро незаменимым помощником родителей. Теперь им не придется вникать в решения своего чада – подробные алгоритмы представлены на сайте, а также пользоваться дорогостоящими услугами репетиторов.
Теперь им не придется вникать в решения своего чада – подробные алгоритмы представлены на сайте, а также пользоваться дорогостоящими услугами репетиторов.
Ответы на задачки, примеры и уравнения в нескольких вариантах упростят постижение арифметики второклассниками – откроют им путь к постижению новых горизонтов в математике.
Урок математики во 2-м классе на тему: «Вычитание вида: 30—4»
Цели урока
Деятельностные:
- формировать способность к выделению существенного свойства предметов в группе;
- тренировать способность к исследованию ситуации;
- тренировать способности к фиксированию затруднения в учебной деятельности;
- тренировать способность к проектировочной деятельности на основе интуиции;
- тренировать способность к определению новых понятий.
Воспитательные:
- формировать систему ценностей, направленную на
максимальный личный вклад в совместную
деятельность.

Учебные:
- учить правильно использовать термины компонентов сложения и вычитания;
- познакомить с новым приёмом вычитания для случаев вида 30-4;
- повторить разрядные единицы.
Развивающие:
- формировать способности к классификации по определённым признакам, анализу и синтезу при решении задач.
Этап положительного самоопределения к учебной деятельности.
Математика – королева наук,
Без неё не летят корабли,
Без неё не поделишь ни акра земли.
Даже хлеба не купишь, рубля не сочтёшь,
Что почём, не узнаешь,
А, узнав, не поймёшь. (Запись на доске.)
Учитель:
“Ну-ка проверь, дружок,
Ты готов начать урок?
Всё ль на месте?
Всё ль в порядке?
Ручка, книжки и тетрадки?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать только лишь оценку “5”!
Сегодня на уроке к нам за помощью обратилась
падчерица из сказки “12 месяцев”. Мачеха велела
принести ей полную корзину подснежников.
Мачеха велела
принести ей полную корзину подснежников.
Поможем падчерице? (За выполнение каждого задания в корзину кладём цветок — подснежник).
2. Групповая деятельность учащихся на основе имеющихся способностей.
У каждой группы на столе лежат карточки с примерами.
Реши примеры и найди лишний.
Дети решают примеры, при проверке каждый читает по 1 примеру, а капитаны групп выходят с лишними примерами к доске. (За правильно решённые примеры группы получают по подснежнику.)
Проблема.
Мы не умеем решать такие примеры. А кто попробует сформулировать тему нашего урока?
Сегодня мы будем решать примеры.
Когда надо из круглого числа вычесть однозначное число (тема урока).
На доске запись темы урока: Н. 30-6.
“А я умею”, — говорит Воробьёва Надя. (Она
получает карточку).
(Она
получает карточку).
30-5 20-6
40-6 80-7
50-8 70-4
80-9 60-1
(Надя правильно решает все примеры и получает подснежник).
3. Организация, выявление и согласование причин затруднения в учебной деятельности.
Учитель.
А давайте попробуем решить эти примеры (дети работают в группах).
4. Проективная деятельность в группах.
(Группы формируют свои версии, которые затем поручают изложить своему представителю).
Весь класс выслушивает гипотезы: Как можно решить эти примеры?
(Группа нашла ответ “32” только на кружочках.)
Выбирают самый удобный способ решения этих примеров и на доске выводят алгоритм решения таких примеров.
Алгоритм решения:
- У круглого числа занимаем один десяток.

- Десятков остаётся на один меньше.
- Из десяти вычитаем единицы.
- Оставшиеся десятки и единицы складываем и записываем ответ.
5. Закрепление нового материала.
Откройте учебник на с.51 № 2, № 3. С объяснением по алгоритму реши примеры:
50-6 80-4
70-4 60-8
90-3 100-4
100-9 43-2
70-5 43-20
(За каждый правильно решённый пример в корзину кладём по одному подснежнику.)
6. Самостоятельная работа.
(Дети получают карточки с примерами, которые решают в парах. Те, кто решили и получили ответ “5” получают подснежник).
1 вариант: 13-5+6-4+50-5-40=5
2 вариант: 7+9+20-6-7+2-20=5
3 вариант: 12-6+60+4-5-60=5
4 вариант: 18-9+6+70-40-40=5
7. Работа над пройденным материалом.
На доске Мороз Иванович. Он дунул и все числа
разлетелись. Дети должны вставить нужные числа,
чтобы данное решение соответствовало условию
задачи и её краткой записи.
Дети должны вставить нужные числа,
чтобы данное решение соответствовало условию
задачи и её краткой записи.
Задача. В первой коробке было … ёлочных шаров. Во второй — на … шаров меньше, чем в первой. А в третьей на … больше, чем во второй. Сколько ёлочных шаров в третьей коробке?
Найди нужные числа и вставь в пропуски:
15 5 4 2 7 3 1 10 6 9 8 12
(Вся работа проводится на магнитной доске).
1 способ
1. — …ш.
2. — …ш., на … меньше
3. — …ш., на … больше
2 способ
1. — …ш.
2. — …ш., на … больше
3. — …ш., на … меньше
Решение задачи.
(12+8)-4=16(ш).
Ответ: 16 шаров в третьей коробочке.
Решений может быть много. Главное, чтобы всё было доказано.
8. Подведение итогов.
Давайте посчитаем все подснежники в корзине. Все цветы как в сказке превращаются в золотые монеты. Если правильно расставить эти монеты, то мы получаем слова:
М О Л О Д Ц Ы ! У М Н И Ц Ы !
9. Рефлексия урока.
Рефлексия урока.
Дети отвечают на вопросы.
Что нового узнали на уроке?
Для чего это нужно?
Какие знания нам пригодились, чтобы решать примеры и задачи?
Как я работал на уроке?
10. Домашнее задание.
Реши 10 примеров на эту тему.
Как преподавать математические задачи во 2-м классе
Автор: Мэри Кейт Болиндер
- Поделиться
- Твит
Ваши ученики усвоили математические факты. Они понимают основные операции. Теперь пришло время решить некоторые словесные задачи! Читайте дальше, чтобы узнать о стратегиях и ресурсах, которые помогут обучать словесным задачам учащихся 2-го класса.
Почему важно обучать словесным задачам?
Почему важно обучать словесным задачам? Ответ: не только потому, что это стандарт для класса! Словесные задачи позволяют учащимся продемонстрировать полное понимание математических навыков и операций, которые они изучили. Словесные задачи также позволяют учащимся использовать логику, критическое мышление, применять пошаговый подход и находить необходимую информацию. Все перечисленные навыки являются не только важными математическими навыками, но и важными жизненными навыками!
Словесные задачи также позволяют учащимся использовать логику, критическое мышление, применять пошаговый подход и находить необходимую информацию. Все перечисленные навыки являются не только важными математическими навыками, но и важными жизненными навыками!
5 Стратегии решения текстовых задач для 2-го класса
Существует множество различных стратегий обучения учащихся решению математических задач для 2-го класса. Попробуйте одну, некоторые или все перечисленные стратегии, чтобы охватить учащихся всех уровней и способностей.
1. Определите ключевые слова для каждой операции
В каждой задаче по математике для 2-го класса есть важное ключевое слово. Это ключевое слово разблокирует ответ, сообщив вам, какую операцию необходимо использовать для правильного решения проблемы. Чтобы учащиеся могли определить правильную операцию, им необходимо распознать и понять ключевые слова задачи на сложение и вычитание.
Общие ключевые слова для задач на сложение слов:
- всего
- Всего
- Сумма
- Всего
- увеличилось на
- плюс
- Комбинированные
- Добавлено к
Обычные ключевые слова для слов выявления:
- Меньше.

- меньше
- осталось больше/осталось
- осталось
- минус
- сколько еще
Потренируйтесь вместе читать текстовые задачи вслух. Могут ли ваши ученики найти ключевое слово в каждой задаче?
2. Математическая стратегия CUBES для решения текстовых задач
Стратегия CUBES является полезным способом решения текстовых задач для 2-го класса. Используйте эту аббревиатуру, чтобы запомнить шаги, необходимые для решения задач со словами:
C : Обведите числа
U : Подчеркните вопрос дополнительная информация
S : Решите и проверьте задачу
Используя стратегию КУБИКИ, учащийся может разбить текстовую задачу на небольшие, управляемые части. Этот пост в блоге о стратегии CUBES объясняет все, что вам нужно знать об использовании этой стратегии с учащимися 2-го класса. Вы можете БЕСПЛАТНО скачать математическую стратегическую диаграмму CUBES здесь.
3.
 Нарисуйте картинку для решения математических задач
Нарисуйте картинку для решения математических задачЗадача — это математический рассказ. Визуальным учащимся может быть полезно нарисовать картинку, чтобы решить математическую задачу. Не нужно быть художником! Учащиеся могут рисовать простые фигуры для представления элементов словесной задачи.
Словесная задача на сложение Пример: В саду 21 фиолетовая бабочка и 8 розовых бабочек. Сколько всего бабочек?
Чтобы решить эту задачу, учащийся должен нарисовать 21 фиолетовую бабочку (или точки/символы, обозначающие бабочку) и 8 розовых бабочек. Затем посчитайте всех бабочек, чтобы получить ответ.
Словесная задача на вычитание Пример: В саду живет 21 бабочка. 8 улетают. Сколько бабочек осталось?
Чтобы решить эту задачу со словами, учащиеся должны снова нарисовать 21 бабочку. Чтобы показать вычитание, поставьте крестик над 8 бабочками. Сколько осталось?
В этом видео показано, как использовать картинки для решения математической задачи:
youtube.com/embed/jnMKPsYK4LI?feature=oembed» allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>4. Используйте предметы для решения математической задачи
Используйте математические манипуляции для решения математической задачи! Учащимся 2-го класса будет полезно это наглядное практическое учебное пособие! Некоторые математические манипуляции, которые можно использовать для решения текстовых задач, включают в себя кубики unifix, десятичные блоки, счетчики, ластики, танграммы, палочки от эскимо — подойдет все тактильное, что поможет учащимся визуализировать задачу! Кроме того, вот список некоторых из наших любимых математических манипуляций. Из Lucky Little Toolkit можно распечатать множество манипуляций.
Скачать Math Manipulatives здесь
5. Напишите числовое предложение
Вы нашли числа. Вы знаете, какую операцию использовать. Теперь пришло время показать эту работу, написав числовое предложение! Решите, чтобы найти свой ответ. Нужно больше практики с текстовыми задачами? Ознакомьтесь с бесплатным обзором Spiral Math Review, чтобы получить уровневый обзор!
Нужно больше практики с текстовыми задачами? Ознакомьтесь с бесплатным обзором Spiral Math Review, чтобы получить уровневый обзор!
Скачать Spiral Math ЗДЕСЬ
- Поделиться
- Твит
Преподавание словесных задач во 2 классе
Если вы ищете лучший способ преподавания текстовых задач и, что более важно, хотите, чтобы ваши ученики более успешно решали текстовые задачи, я здесь, чтобы помочь. Преподавание текстовых задач во 2-м классе не должно быть проблемой.
Почему так сложно учить задачи со словами во 2-м классе?
Когда я впервые начал преподавать, я учил своих учеников использовать ключевые слова, подчеркивать и обводить, выделять и выделять прямоугольниками… и все же это не помогло. Они по-прежнему не знали, когда прибавить, а когда вычесть.
И мои ученики не поняли и не стали лучше.
Не помогало и то, что я постоянно не преподавал и не позволял своим ученикам практиковаться в решении текстовых задач.
Словесные задачи всегда были источником разногласий для моих учеников, независимо от того, в каком классе я преподавал (1-й, 2-й и 4-й), и всегда были чем-то, что я преподавал наугад в рамках принятой учебной программы по математике.
Большинство учебных программ по математике предлагают следующее:
- 1 или 2 задачи в конце каждого урока, но на самом деле не предлагают способ научить учеников решать текстовые задачи
- 1 главу о «решении задач»
А если серьезно, ни одна из них не поможет.
Я хотел, чтобы мои ученики ежедневно практиковались в решении стратегических задач.
И знаете что? Когда я начал преподавать текстовые задачи во 2-м классе последовательно и стратегически, мои ученики были менее разочарованы и гораздо более умело решали текстовые задачи.
Итак, какое решение?
Теперь я следую 4-дневному учебному плану и оцениваю на 5-й день.
Я больше не учу ключевым словам или подчеркиванию, обведению, выделению и/или заключению в рамку… вместо этого я учу своих учеников искать закономерности в структуре словесных задач… ситуации со словесными задачками.
Кроме того, каждый день я посвящаю 5-10 минут обучению и отработке текстовых задач.
Откуда мне знать, чему учить?
Начну со стандарта.
Честно говоря, независимо от того, чему я учу, с этого я и начну. Мне нужно точно знать, каковы ожидания, чтобы затем я мог помочь своим ученикам справиться с этим.
Стандарт Common Core для 2-го класса гласит:
CCSS.MATH.CONTENT.2.OA.A.1
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухшаговых задач со словами, включающих ситуации сложения , взятие, соединение, разъединение и сравнение с неизвестными во всех положениях, например, с помощью рисунков и уравнений с символом неизвестного числа для представления проблемы.
Хотя многие штаты больше не используют термин «Common Core», многие из принятых ими стандартов одинаковы или, по крайней мере, похожи.
MAFS.2.OA.1.1 (стандарты Флориды)
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухшаговых задач со словами, включающих ситуации сложения, отнимания, сложения, разъединения и сравнения, с неизвестными во всех позициях, например, с помощью рисунков и уравнений с символом неизвестного числа для представления проблемы.

Итак, вот что должны уметь решать второклассники:
- Сложение/вычитание в пределах 100
- Одношаговый и двухэтапный
- Добавить к
- Взять из
- Собрать вместе
- Разобрать
- Сравнить
Если посмотреть на то, что должны делать второклассники, то это неудивительно. так сложно, не говоря уже о том, что студенты действительно осваивают их.
Как я преподаю словесные задачи во 2-м классе:
В начале года учащиеся знакомятся с нашей программой словесных задач после первых двух недель в школе.
Я объясняю, что задачи со словами похожи на рассказы, которые мы должны читать и понимать, что происходит в рассказе. Мы называем эти слова проблемными ситуациями.
Затем я учу студентов, что есть 4 вещи, которые они всегда должны делать при решении задачи со словами:
- Написать числовое предложение
- Использовать стратегию для решения
- Я объясняю студентам, что я не могу прыгать внутрь их мозги, чтобы видеть, о чем они думают, и если я не знаю, о чем они думают, я не могу помочь им лучше решать словесные задачи.

- Учащиеся могут нарисовать картинку, использовать семейство фактов, блоки с основанием 10 и/или стандартный алгоритм.
- Я объясняю студентам, что я не могу прыгать внутрь их мозги, чтобы видеть, о чем они думают, и если я не знаю, о чем они думают, я не могу помочь им лучше решать словесные задачи.
- Вычисление
- Я смотрю, правильно ли ответил учащийся.
- Ответ в предложении
- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки». Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.
Запуск рутинной задачи Word полностью посвящен моделированию и рутине. Студентам не нужно много времени, чтобы освоиться.
Я проделал для вас тяжелую работу — у меня есть задачки для 2-го класса на весь год, готовые для вас!
Что такое задача со словами во 2-м классе?
По понедельникам я ввожу слово «проблемная ситуация». Я считаю полезным, чтобы учащиеся «разыгрывали» ситуацию. Используйте пример на плакате/привязке ситуации, чтобы показать учащимся закономерность. (Я учу студентов, что подчеркнутые части числового предложения — это части, которые мы знаем, а квадрат представляет неизвестное.)
(Я учу студентов, что подчеркнутые части числового предложения — это части, которые мы знаем, а квадрат представляет неизвестное.)
Смоделируйте и решите задачу с практическими словами и дайте обратную связь учащимся.
В течение следующих 3 дней мы моделируем и решаем задачу со словами, которая имеет ту же ситуацию, что и понедельник. Так что не промахиваемся. Это очень систематично.
Наконец, по пятницам учащиеся самостоятельно решают задачи на 2 слова, следуя той же ситуации, которую мы использовали всю неделю.
Для дифференциации или расширения учащиеся могут написать задачку на обороте своей оценки, которая соответствует той же ситуации, которую они изучили на этой неделе. Это отличный способ проверить, действительно ли ученики понимают ситуацию, которую мы узнали на этой неделе.
ПРИМЕР ЗАДАЧИ СЛОВА
Зарегистрируйтесь со своей домашней электронной почтой, чтобы получить бесплатную
УРА! Ваша БЕСПЛАТНОСТЬ уже в пути!
Вам также может понравиться:
- Книги, которые научат вас слушать
- Позитивное управление классом
- Как представить работы учащихся
- Первый день в школе
Instagram // Pinterest // Facebook // Учителя платят учителям
Важные математические навыки для второго класса
Хотите помочь своему второкласснику освоить основы математики во втором классе? Вот некоторые из навыков, которые ваш ребенок будет осваивать в классе.
Цифры
Счет до одной тысячи
Счет вперед в пределах 1000. Счет до 5 с. Сосчитайте и прибавьте по 10 и 100. Для любого заданного числа от 100 до 900, мысленно прибавить 10 или 100 или вычесть 10 или 100.
Нечетные и четные числа
Понимать нечетные и четные числа. Определите, нечетное или четное количество предметов в группе (до 20 предметов), разделив их на пары и/или сосчитав на два.
Чтение и запись больших чисел
Чтение и запись чисел до 1000, используя числа (352, 621, 1000) и названия чисел ( «триста пятьдесят два», «шестьсот двадцать один», «один тысяча» ).
Связь между большими числами
Понимать связь между единицами, десятками и сотнями: десять единицы равные единице десять; десять десятки равны сотне, десять сотни равны одной тысяче. Поймите, что в трехзначном числе первая цифра представляет количество сотен, вторая цифра представляет количество десятков, а третья цифра представляет количество единиц, например, 843 равно 8 сотням (800), 4 десяткам. (40) и 3 единицы (3).
(40) и 3 единицы (3).
Сравнение больших чисел
Сравните трехзначные числа, используя символы > (больше или больше), = (равно) и < (меньше или меньше), и объясните, используя сотни, десятки и единицы .
Сложение, вычитание, умножение и деление
Большие числа
Быстро и точно складывать числа, которые в сумме не превышают 20, и вычитать из чисел до 20.
Одно- и двухшаговые задачи
Решите одноэтапные и двухэтапные задачи со словами путем сложения или вычитания чисел до 100.
Сложение больших цифр
Поймите, что при сложении двух трехзначных чисел вы складываете сотни и сотни, десятки и десятки, единицы и единицы, и вам может понадобиться составить новую десятку или новую сотню. Используйте модели или рисунки и объясните свой письменный метод.
Сложение в пределах 1000
Научитесь складывать в пределах 1000.
Вычитание больших цифр
Поймите, что при вычитании одного трехзначного числа из другого трехзначного числа вы вычитаете сотни из сотен, десятки из десятков и единицы из единиц, и вам может понадобиться получить больше десятков и единиц по порядку вычесть.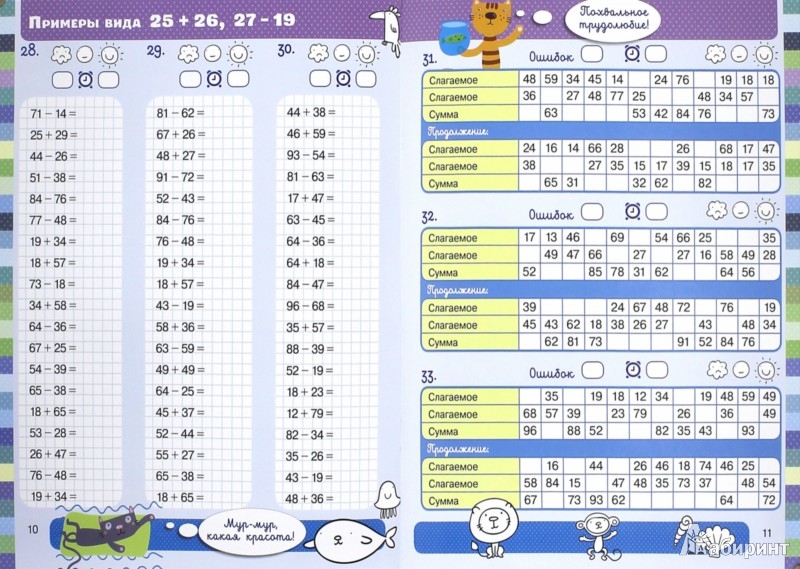 Используйте модели или рисунки и объясните свой письменный метод.
Используйте модели или рисунки и объясните свой письменный метод.
Вычитание в пределах 1000
Научитесь вычитать в пределах 1000.
Измерения и данные
Считывание цифровых и аналоговых часов
Считайте часы с круглым циферблатом и цифровые часы, чтобы узнать время с точностью до ближайших пяти минут. Поймите понятие утра и вечера. в 24-часовой день. Уметь называть время вслух и писать время разными способами, используя слова «утра» и «после полудня».
Измерение и оценка длины
Измерение и оценка длины линий или объектов в стандартных единицах измерения, таких как дюймы, футы, сантиметры и метры. Запишите и прочитайте размеры в дюймах (дюймах) или сантиметрах (см). Сравните размеры (на сколько больше, на сколько меньше).
Решение задач со словами
Решение задач со словами на сложение и вычитание с длинами в одних и тех же единицах (в пределах 100).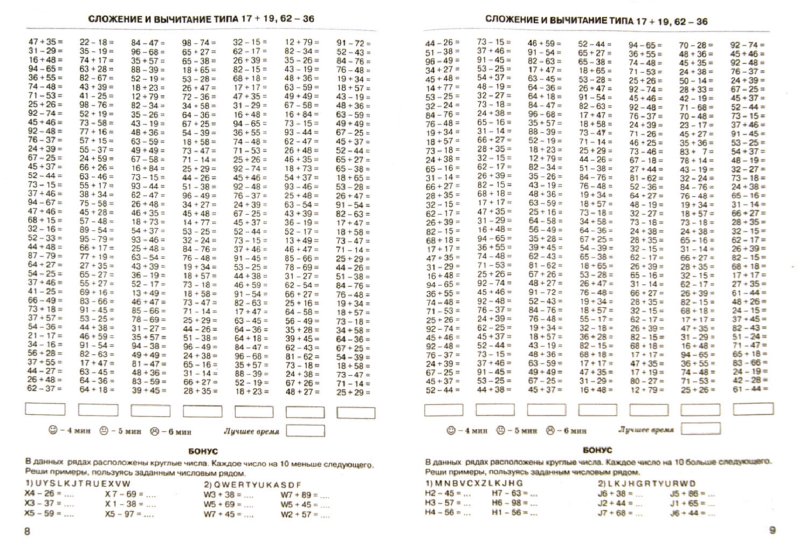
Пример:
Новый рулон ленты содержит 72 дюйма ленты. Саре нужно 26 дюймов ленты, чтобы обернуть подарок на день рождения. Если она отрежет 26 дюймов от начала нового рулона, сколько дюймов ленты останется?
Решение задач на деньги
Решение задач на сложение и вычитание на деньги – монеты (пенни, никель, десять центов, четвертак) и долларовые купюры.
Пример:
У Антония есть четвертак, две десятицентовика и пять пенни. Он хочет купить свисток, который стоит один доллар. Сколько еще денег ему нужно? Какая комбинация монет даст ему нужные деньги?
Изображения и гистограммы
Чтение и создание графических изображений и гистограмм для отображения измерений, количеств или других данных в четырех категориях. Решайте задачи на сложение, вычитание и сравнение слов, используя информацию, представленную в виде гистограммы.
Фигуры
Определение общих фигур
Определение треугольников (трехсторонние фигуры), четырехугольников (четырехсторонние фигуры), пятиугольников (пятиугольники) и шестиугольников (шестиугольники). Анализировать фигуры по количеству сторон и углов (углов).
Анализировать фигуры по количеству сторон и углов (углов).
Разделение фигур
Разделите прямоугольник на несколько рядов квадратов одинакового размера и посчитайте, чтобы найти количество квадратов. Разделите круги и прямоугольники на половинки, трети или четверти.
Чтобы получить советы, которые помогут вашему второкласснику на уроке математики, посетите нашу страницу с советами по математике для второклассников.
Ресурсы TODAY’s Parenting Guides были разработаны NBC News Learn с помощью профильных экспертов и приведены в соответствие с Common Core State Standards.
Математика 2 класса — K-5 Интеграция технологий
Сложение и вычитание Сложение 2-х и 1-х цифр — Решите задачи на сложение. Marble Drop — Соберите шарики, количество которых в сумме равно указанному целевому числу. Математическое Бинго. Выберите сложение или вычитание и играйте в Бинго, решая математические задачи. Математические ряды. Очистите шарики, составляя пары, сумма которых равна выбранному вами числу. Take the Cake — Соревнуйтесь со своими покупателями до того, как мышка возьмет торт, тренируясь в сложении и вычитании. Сравнение чисел Графики, таблицы и метки Измерение Определение длины с помощью линейки — Используя сантиметры или дюймы, используйте линейку для облегчения измерения. Измерьте это — тренируйтесь измерять в сантиметрах или дюймах. Деньги Прилавок для выставления счетов. Потренируйтесь добавлять деньги, когда покупаете предметы в магазине. Изготовитель сдачи — определите, сколько сдачи вы получите обратно после покупки чего-либо. Нечетное или четное Разрядное значение и блоки с основанием 10 Фигуры, танграммы и блоки узоров Пропустить счет Adventure Man and the Counting Quest — выберите число, чтобы пропустить счет и потренироваться во время игры. Счет по 2 — Сосчитай по 2 и узнай, какое число идет после заданного числа. Счет до 5 — Счет до 5 позволяет определить число, которое идет после заданного числа. Счет до 10 — Тренируйтесь считать вперед и назад до 10. Время Аналогово-цифровое — сравнение и определение времени с помощью аналоговых и цифровых часов. Время тик-так — установите стрелки часов на заданное время. Словесные задачки |
Математические задачки для второклассников
Головоломки / Математические головоломки
Команда LogicLike создала эти текстовые задачи для 2-го класса. Мы поместили основные математические понятия в контекст для второклассников и сделали решение задач увлекательным.
Добавление словесных задач
В зоопарке 32 азиатских слона и 29 африканских слонов.
Сколько всего слонов?
Показать ответ
32+29=61
На дереве сидело 46 воробьев. К дереву подлетели еще 24 воробья.
Сколько всего воробьев было на дереве?
Показать ответ
46+24=70
У Джона 15 книг. У Люка 29 книг. Сколько книг у них вместе?
Показать ответ
15+29=44
В обезьяннике живут 19 шимпанзе и 26 мартышек.
Сколько всего обезьян?
Показать ответ
19+26=45
Стул стоит 72 доллара, кресло — 119 долларов,
а диван стоит столько же, сколько стул и кресло вместе взятые.
Сколько стоит диван?
Показать ответ
72+119=191
Совершенствуйте свои математические навыки с помощью забавных математических головоломок и становитесь умнее!
Проблемы со словами на вычитание
В автобусе ехали 16 детей.
На остановке в автобус сели еще несколько детей.
Тогда всего в автобусе было 24 ребенка.
Сколько детей сели в автобус на остановке?
Показать ответ
24-16=8
Сегодня день рождения папы. Ему 38 лет. Сколько лет было папе 15 лет назад?
Показать ответ
38-15=23
У продавца фруктов было 83 яблока. Он продал 57 яблок s.
Сколько яблок у него осталось?
Показать ответ
83-57=26
На дереве сидело 14 попугаев. Еще несколько подлетают к дереву.
Тогда на дереве было 56 попугаев. Сколько еще подлетело к дереву?
Показать ответ
56-14=42
У мамы в корзине с фруктами было 32 персика.
Она пошла в сад и собрала персики, чтобы запастись ими.
Сейчас есть 89 персиков. Сколько она выбрала?
Показать ответ
89–32=57
Вы готовы к более сложным задачам? Посмотрите на математические загадки.
Смешанные задачи на сложение и вычитание
В ящике для игрушек Тома 24 машины, 17 грузовиков и 9 мотоциклов.
На сколько больше грузовиков и автомобилей вместе взятых, чем мотоциклов?
Показать ответ
24+17-9=32
Мама заказала 14 пицц с сыром и 18 пицц с пеперони на день рождения.
Гости съели 26 пицц. Сколько пицц осталось?
Показать ответ
14+18-26=6
В пятницу 37 пациентов записались на прием к доктору Грейс, а 9 пациентов не явились. Также 3 пациента поступили без предварительной записи.
Сколько пациентов было у доктора Грейс в пятницу?
Показать ответ
37-9+3=31
Ящик с яблоками весит 37 кг.
Ящик с бананами весит 25 кг.
Коробка салата весит 13 кг.
Насколько тяжелее фрукты, чем салат?
Показать ответ
37+25-13=49
У Мартина 26 карт в мешке и 55 карт в коробке.
Уильям достает из коробки 14 карт.
Сколько карточек осталось у Мартина?
Показать ответ
26+55-14=67
Присоединяйтесь к другим пользователям LogicLikers онлайн!
Станьте частью нашего удивительного сообщества детей и взрослых, семей и друзей, и решайте головоломки отовсюду!
Хорошо! Пойдем!
Реальное решение задач по математике во втором классе
Edgewood Magnet School в Нью-Хейвене, штат Коннектикут, является специализированной школой искусств, включающей искусство в учебную программу. Студентам в этой среде рекомендуется использовать стратегии наблюдения, интерпретации и анализа, чтобы улучшить свои мыслительные навыки по каждому предмету. С этой миссией и учителя, и ученики используют уникальные и захватывающие подходы к «основам» и работают вместе, чтобы обеспечить участие всех учащихся.
Студентам в этой среде рекомендуется использовать стратегии наблюдения, интерпретации и анализа, чтобы улучшить свои мыслительные навыки по каждому предмету. С этой миссией и учителя, и ученики используют уникальные и захватывающие подходы к «основам» и работают вместе, чтобы обеспечить участие всех учащихся.
Для большинства второклассников начало года – это время освежения знаний и навыков, полученных в первом классе. Лето вдали от прямого обучения и возможностей для практики и руководства иногда означает потерю твердого понимания изученных концепций математики. Этот трех-четырехнедельный блок предназначен для повторения и формирования нового понимания одноэтапного решения словесных задач с использованием сложения и вычитания, поскольку учащиеся развивают навыки и стратегии, которые они будут использовать в течение всего года. Учащиеся, выполняя ряд математических сценариев, будут использовать типы задач, указанные в таблице 1 Общего глоссария по основной математике, которая охватывает сложение и вычитание. 1
1
Common Core концентрируется на четком наборе математических навыков и понятий. Учащиеся изучают концепции организованно в течение учебного года, а также в разных классах. Стандарты побуждают учащихся решать реальные проблемы. 2
Common Core требует большего внимания к математике. Вместо того, чтобы мчаться, чтобы охватить множество тем в учебной программе шириной в милю и глубиной в дюйм, стандарты просят учителей математики значительно сузить и углубить то, как время и энергия тратятся в классе. Это означает резкое сосредоточение внимания на основной работе каждого класса, которая для классов от детского сада до второго класса включает понятия, навыки и решение задач, связанных со сложением и вычитанием.
Округ государственных школ Нью-Хейвена использует сингапурский подход Math in Focus, — учебную программу на основе Common Core для учащихся от детского сада до пятого класса. Студенческие книги и рабочие тетради следуют учебному пути, который включает изучение понятий и навыков с помощью наглядных уроков и инструкций учителя для понимания того, как и почему; закрепление концепций и навыков с помощью практики, занятий и математических журналов для глубокого понимания математики, практической работы в парах и небольших группах; и, , применяя концепции и навыки посредством обширной практики решения проблем и задач для создания реальных решений проблем. 3
3
Этот подход включает решение задач на протяжении каждого урока и поощряет частую практику как в вычислениях, так и в решении задач. Словесные задачи появляются в каждой главе и прогрессируют от 1 шага до 2 шагов и многошаговых. Каждая глава завершается сложной задачей или набором задач, которые требуют от учащихся решения некоторых нестандартных вопросов. Чтобы решить эти проблемы, учащиеся должны опираться на свои глубокие предварительные знания, а также недавно приобретенные концепции и навыки, сочетая стратегии решения проблем с навыками критического мышления, включая классификацию, сравнение, упорядочивание, определение частей и целого, выявление закономерностей и отношений, индукция и дедукция и пространственная визуализация.
Текст второго класса начинается с чисел до 1000. Учащиеся начинают с выражения чисел в стандартной форме (231), расширенной форме (200 + 30 + 1) и словесной форме (двести тридцать один). Это сопровождается конкретными представлениями с помощью десятичных блоков, а для двузначных чисел и нескольких трехзначных чисел — представлением последовательностей стержней длиной 1, 10 и 100. Эта начальная глава также включает порядковые числа и сравнение с использованием больше, чем и меньше, чем терминология, а затем сразу перейти к сложению и вычитанию дву- и трехзначных чисел. Здесь вывод должен быть таким: если у вас больше сотен, то десятки и единицы не имеют большого значения; а если у вас такое же количество сотен, но больше десятков, то единицы не имеют никакого значения. Большинство моих учеников (если не все) борются с самого начала! У них, похоже, нет прочного фундамента для понимания чисел до 100 или концепции разрядности в целом. Этот модуль предназначен для того, чтобы опередить разочарование, которое учащиеся испытывают, когда их толкают слишком быстро, прежде чем они получат четкое представление о принципах позиционной стоимости и свойствах операций.
Эта начальная глава также включает порядковые числа и сравнение с использованием больше, чем и меньше, чем терминология, а затем сразу перейти к сложению и вычитанию дву- и трехзначных чисел. Здесь вывод должен быть таким: если у вас больше сотен, то десятки и единицы не имеют большого значения; а если у вас такое же количество сотен, но больше десятков, то единицы не имеют никакого значения. Большинство моих учеников (если не все) борются с самого начала! У них, похоже, нет прочного фундамента для понимания чисел до 100 или концепции разрядности в целом. Этот модуль предназначен для того, чтобы опередить разочарование, которое учащиеся испытывают, когда их толкают слишком быстро, прежде чем они получат четкое представление о принципах позиционной стоимости и свойствах операций.
Этот модуль открывает учебный год одношаговыми задачами на сложение и вычитание всех типов с использованием чисел до 10. Цель состоит в том, чтобы потратить время на отработку основных вычислений с числами, с которыми учащийся может работать, прежде чем сразу перейти к школьной программе округа. Как только будет достигнут уровень понимания этих наборов задач (от чисел до 10), учащиеся перейдут к решению одноэтапных задач с использованием чисел для подростков, а затем к числам до 100. Большинство задач в учебной программе в начале года требуют дополнения. и вычитание трехзначных чисел. Некоторые учащиеся быстро справятся с наборами задач с числами до 100 и будут готовы работать с обычной учебной программой.
Как только будет достигнут уровень понимания этих наборов задач (от чисел до 10), учащиеся перейдут к решению одноэтапных задач с использованием чисел для подростков, а затем к числам до 100. Большинство задач в учебной программе в начале года требуют дополнения. и вычитание трехзначных чисел. Некоторые учащиеся быстро справятся с наборами задач с числами до 100 и будут готовы работать с обычной учебной программой.
В течение всего модуля основное внимание будет постоянно уделяться решению, а затем созданию набора текстовых задач, которые обеспечивают надежную и сбалансированную практику. Наборы задач будут основаны на сценарии, который обеспечит суть истории. Каждый сценарий позволит нам выделить несколько проблем, изменив числа и убедившись, что каждый набор чисел создает разумную проблему. Эта идея выглядит следующим образом: У Джона в коробке 8 мелков. Он делит 3 с Сэмом. Сколько мелков осталось в коробке у Джона? У Джона в коробке есть карандаши. Он делит 3 с Сэмом. У Джона в коробке осталось 5 мелков. Сколько мелков было у Джона? У Джона 5 мелков. У Сэма на 2 меньше, чем у Джона. Сколько карандашей у Сэма? Джон и Сэм делятся мелками. У Джона 5, а у Сэма 3. Сколько карандашей у друзей? Два ученика участвуют в нескольких историях с обменом мелками, в которых используется один и тот же набор чисел, но в несколько разных ситуациях. Некоторые ситуации более очевидны и прямолинейны, в то время как другие требуют больше размышлений. Важно предоставить учащимся возможность работать и решать различные типы задач, которые могут быть созданы из одного набора чисел. 4
Сколько мелков было у Джона? У Джона 5 мелков. У Сэма на 2 меньше, чем у Джона. Сколько карандашей у Сэма? Джон и Сэм делятся мелками. У Джона 5, а у Сэма 3. Сколько карандашей у друзей? Два ученика участвуют в нескольких историях с обменом мелками, в которых используется один и тот же набор чисел, но в несколько разных ситуациях. Некоторые ситуации более очевидны и прямолинейны, в то время как другие требуют больше размышлений. Важно предоставить учащимся возможность работать и решать различные типы задач, которые могут быть созданы из одного набора чисел. 4
Таксономия типов задач на сложение и вычитание, определенная в Common Core State Standards of Mathematics Glossary, представляет собой структуру, которая сортирует одношаговые задачи на три широких класса: изменение , сравнение и часть-часть-целое . Затем каждый из трех классов далее разделяется на 14 типов задач, отсортированных следующим образом: изменение , в котором некоторая величина либо прибавляется, либо отнимается от другой величины с течением времени; сравнение , в котором одно количество описывается как большее или меньшее, чем другое количество; и часть-часть-целое , в котором сумма состоит из двух частей. 5
5
В группе задач на изменение есть две подгруппы: изменение-увеличение , в которой количество прибавляется к исходной сумме и изменение-уменьшение , в котором количество берется из исходного количества. Мы могли бы узнать эти подгруппы более привычно как «добавить к» или «отнять». Кроме того, в каждой из этих подгрупп есть три возможных неизвестных величины. Один сценарий для показа изменение-увеличение : 2 котенка играли с пряжей. К ним присоединяются еще 3 котенка. Сейчас с пряжей играют 5 котят. При использовании этих величин неизвестным может быть результат (2 + 3 = ?), неизвестное количество изменения (2 + ? = 5) или неизвестная начальная сумма (? + 3 = 5). В подгруппе изменение-уменьшение снова есть три возможных неизвестных. Сценарий для этого примера: 5 птиц сидят на ветке. 2 улетают. Теперь на ветке сидят 3 птицы. Здесь снова учащиеся могут определить окончательную сумму (5 – 2 = ?), сумму сдачи (5 – ? = 3) или начальную сумму (? – 2 = 3). Это дает все шесть типов проблем с изменениями.
Это дает все шесть типов проблем с изменениями.
Точно так же задачи сравнения также можно разделить на две подгруппы: сравнения-больше , в которых одна величина описывается как больше или больше другой, и сравнение-меньше, в которой одна величина описывается как меньше или меньше чем другой. Здесь снова каждая из этих двух подгрупп имеет три возможных неизвестных, всего 6 типов. У Сэма 6 шариков. У Джеймса 8 шариков. У Джеймса на 2 шарика больше, чем у Сэма. Неизвестная величина может быть меньшей суммой (? + 2 = 8), неизвестной большей величиной
(6 + 2 = ?), или неизвестная разность (8 – 6 = ?) одной величины больше и другой меньше. Используя тот же сценарий для набора из задачи без сравнения , формулировка должна измениться с «больше чем» на «меньше чем». Вот как можно представить этот набор с языковой настройкой: у Сэма 6 шариков. У Джеймса 8 шариков. У Сэма на 2 шарика меньше, чем у Джеймса.
Часть-часть-целое задачи представляют собой набор из двух величин, частей, которые при соединении составляют целое количество.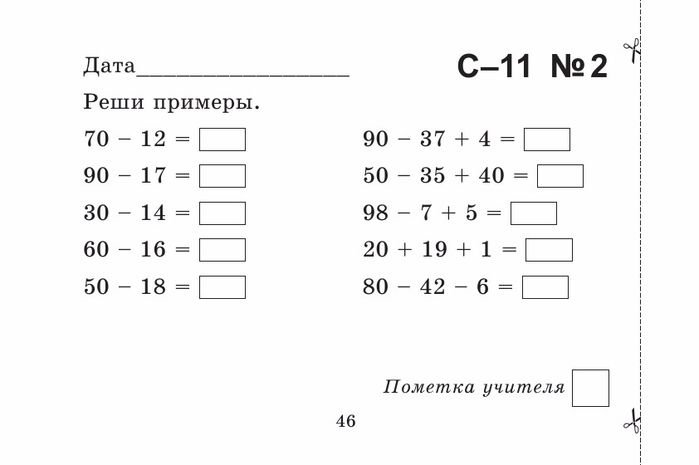 Этот тип проблемы очень похож на изменить категорию , но в этом типе проблемы нет изменений с течением времени. Две части играют эквивалентные роли, что допускает только две возможные категории неизвестного: либо часть неизвестна, либо целое является неизвестным. Есть 4 большие собаки и 3 маленькие собаки. Всего 7 собак. Одна из частей может быть неизвестной (4 + ? = 7 или ? + 3 = 7) или неизвестным может быть размер целого (4 + 3 = ?). Поскольку детали взаимозаменяемы, в этом классе задач всего 2 типа.
Этот тип проблемы очень похож на изменить категорию , но в этом типе проблемы нет изменений с течением времени. Две части играют эквивалентные роли, что допускает только две возможные категории неизвестного: либо часть неизвестна, либо целое является неизвестным. Есть 4 большие собаки и 3 маленькие собаки. Всего 7 собак. Одна из частей может быть неизвестной (4 + ? = 7 или ? + 3 = 7) или неизвестным может быть размер целого (4 + 3 = ?). Поскольку детали взаимозаменяемы, в этом классе задач всего 2 типа.
Следующая диаграмма упорядочивает эти классы и категории в структуре. В Приложении А этого модуля находится набор примеров задач, иллюстрирующих каждый из этих 14 типов.
Тип проблемы | Неизвестная сумма | ||||
Изменить | Увеличение Дополнение к | Начальный | Изменить | Финал | |
Уменьшение Вычесть из | Начальный | Изменить | Финал | ||
Сравнение | Больше / Подробнее | Меньший | Больше | Разница | |
Меньше / Меньше | Меньший | Больше | Разница | ||
Часть-Часть-Целое | Деталь | Целиком | |||
Сценарии проблем
Для второклассников школьная жизнь — большая часть их мира. Большинство моих учеников приехали в Эджвуд на год в детском саду и остались там до первого класса, сделав год во втором классе, по сути, третьим годом в той же школе. Они чувствуют себя комфортно в здании и знают многих других студентов. Они станут активными участниками математических историй, которые я и мы вместе сочиним. Действия, которые происходят в классе, в столовой, на игровой площадке и в автобусе, кажутся узнаваемыми ситуациями, которые помогут с базовым пониманием контекста.
Большинство моих учеников приехали в Эджвуд на год в детском саду и остались там до первого класса, сделав год во втором классе, по сути, третьим годом в той же школе. Они чувствуют себя комфортно в здании и знают многих других студентов. Они станут активными участниками математических историй, которые я и мы вместе сочиним. Действия, которые происходят в классе, в столовой, на игровой площадке и в автобусе, кажутся узнаваемыми ситуациями, которые помогут с базовым пониманием контекста.
Кроме того, у учащихся есть возможность включить темы и обучение, которые встречаются в других предметах, таких как естественные науки, социальные науки, грамотность, искусство, музыка и, в нашей школе, танцы и драма. Одним из примеров может быть создание набора сюжетных задач, посвященных жизненному циклу бабочки, что является единицей изучения каждый год во втором классе. С общими знаниями, которые получат учащиеся, этот контент может стать сценарием для текстовых задач. Примером может быть: Семь гусениц взобрались на ветку и образовали свои куколки. Позже в тот же день еще три гусеницы забрались на ветку и сформировали свои куколки. Сколько куколок висит на ветке? Аналогичным образом, использование персонажей книги, прочитанной вместе, в качестве класса может дать персонажей в новом наборе задач. У Любопытного Джорджа была связка бананов. Он съел 4 из них. Теперь у него 3. Со сколькими бананами начал Любопытный Джордж? Использование общего или тематического содержания не только свяжет все размышления и практики, но и обеспечит осязаемые и реальные ситуации. По установленному сценарию учащиеся будут работать с набором чисел, определяя неизвестное в рамках каждого из типов задач.
Позже в тот же день еще три гусеницы забрались на ветку и сформировали свои куколки. Сколько куколок висит на ветке? Аналогичным образом, использование персонажей книги, прочитанной вместе, в качестве класса может дать персонажей в новом наборе задач. У Любопытного Джорджа была связка бананов. Он съел 4 из них. Теперь у него 3. Со сколькими бананами начал Любопытный Джордж? Использование общего или тематического содержания не только свяжет все размышления и практики, но и обеспечит осязаемые и реальные ситуации. По установленному сценарию учащиеся будут работать с набором чисел, определяя неизвестное в рамках каждого из типов задач.
Создание проблем
Вопрос, на который часто отвечают с догадками: «Что мы должны сделать, чтобы ответить на вопрос, чтобы решить задачу со словами?» Фундаментальное понимание того, о чем спрашивают, не очевидно для студентов, что делает решение недоступным. Большинство первоклассников, поступающих во второй класс, имеют базовое понимание, когда история (задача) классифицируется как окончательный неизвестный или полностью неизвестный , но большинство других компонентов таксономии им незнакомы или слишком сложны для расшифровки. Чтобы начать помогать им в их мышлении, они будут использовать конкретные модели, такие как они сами (2 ребенка сидят за столом для чтения, еще 4 присоединяются к ним), разыгрывая сценарии. Многие основные материалы в классе — карандаши, тетради, папки, мелки — можно использовать для создания и разработки сценариев с представлением каждого типа проблемы.
Чтобы начать помогать им в их мышлении, они будут использовать конкретные модели, такие как они сами (2 ребенка сидят за столом для чтения, еще 4 присоединяются к ним), разыгрывая сценарии. Многие основные материалы в классе — карандаши, тетради, папки, мелки — можно использовать для создания и разработки сценариев с представлением каждого типа проблемы.
Решение проблем
Следуя общему плану сингапурской математической программы, учащиеся будут решать задачи, используя конкретный, изобразительный и абстрактный подходы. Поскольку это стандартный подход к обучению математике в нашем школьном округе в течение всего года, учащиеся начнут с этого набора стратегий для решения наборов задач.
Задачи Word написаны в виде рассказов и сценариев, что позволяет учитывать язык при создании задач для начинающих второклассников. Словесные задачи так же связаны с языком и чтением, как и с математикой. Если история непонятна, как учащиеся могут начать понимать, что делать с цифрами, которые им дали, и с вопросом, который им задали? Таким образом, слова и словарный запас должны быть подходящими и полезными для различных уровней чтения поступающих учащихся. Структура текстовых задач должна быть понятной и ясной, доступной как в языке, так и в цифрах. Кроме того, следует обсудить язык, особенно слова, которые выражают взаимосвязь между вовлеченными величинами, чтобы убедиться, что он знаком всем учащимся.
Структура текстовых задач должна быть понятной и ясной, доступной как в языке, так и в цифрах. Кроме того, следует обсудить язык, особенно слова, которые выражают взаимосвязь между вовлеченными величинами, чтобы убедиться, что он знаком всем учащимся.
Это четкая интеграция словесности и математики, а также метод, с помощью которого учащиеся могут связать математику с реальным миром, в данном случае, посредством занятий, которыми они занимаются в школе. Навыки чтения и вычислительные навыки помогают решать даже самые простые текстовые задачи.
Структура сборника задач
Введение в содержание на протяжении всего этого раздела включает в себя определенную последовательность и структуру, чтобы помочь учащимся решить 14 типов задач. В начале модуля учащиеся будут работать только с числами до 10. Это важная отправная точка для обеспечения понимания. Большинство моих второклассников умеют складывать и вычитать до 10, но им не так комфортно со словесными задачками. Итак, во-первых, учащиеся будут испытывать больше проблем с языком, чем с арифметикой. Студенты будут практиковаться в выяснении того, что именно задают проблемы, с проблемами, с которыми они знакомы, прежде чем перейти к новому шагу. Практика всех типов задач улучшит и повысит стратегии и уверенность!
Итак, во-первых, учащиеся будут испытывать больше проблем с языком, чем с арифметикой. Студенты будут практиковаться в выяснении того, что именно задают проблемы, с проблемами, с которыми они знакомы, прежде чем перейти к новому шагу. Практика всех типов задач улучшит и повысит стратегии и уверенность!
После освоения сложения и вычитания в пределах 10 следующая фаза модуля переходит к числам до 20. Ключевым моментом является продолжение сценариев, которые очевидны и повторяются по мере введения новых чисел. Примером такого перехода могут быть следующие параллельные задачи:
6 студентов сели в автобус на первой остановке. На второй остановке в автобус сели 3 студента. После второй остановки сколько учеников в автобусе? ( изменение-увеличение, окончательная неизвестна)
Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 3 студента. Сейчас их 9студенты в автобусе. Сколько студентов вошло на первой остановке? ( изменение-увеличение, начальное неизвестно)
Теперь они становятся:
11 учеников сели в автобус на первой остановке. 7 студентов сели в автобус на второй остановке. После второй остановки сколько учеников в автобусе? ( изменение-увеличение, окончательная неизвестна)
7 студентов сели в автобус на второй остановке. После второй остановки сколько учеников в автобусе? ( изменение-увеличение, окончательная неизвестна)
Некоторые студенты сели в автобус на первой остановке. 7 студентов сели в автобус на второй остановке. Сейчас в автобусе 18 студентов. Сколько студентов вошли на первой остановке? ( изменение-увеличение, исходное неизвестно)
При работе с числами до 20 важно, чтобы учащиеся понимали, что «подростковые» числа (11-19) на самом деле равны 10 и некоторым единицам. Учащиеся должны работать с числами в пределах 20, создавая уравнения, используя свои знания и умение сначала составлять десять. В случае 7+6 составление новой десятки выглядит так:
7 + 6 = 7 + 3 + 3 = 10 + 3 = 13
Поскольку 7 требуется 3, чтобы получить десять, а 6 состоит из 3 + 3, это уравнение показывает последовательность получения 10 и некоторых других. Практика этого метода с использованием двух десятков кадров наглядно демонстрирует процесс. В приведенном выше примере учащиеся используют десять кадров, чтобы показать 7 и 6 по отдельности. Чтобы сделать новые 10, учащиеся передвигают 3 из 6, что теперь показывает 10 и еще 3 или 13.
В приведенном выше примере учащиеся используют десять кадров, чтобы показать 7 и 6 по отдельности. Чтобы сделать новые 10, учащиеся передвигают 3 из 6, что теперь показывает 10 и еще 3 или 13.
Как было сказано ранее, очевидно, что наиболее доступными типами задач для учащихся, поступающих во второй класс, являются изменение-увеличение или изменение-уменьшение, результат неизвестен и часть-часть-целое, целое неизвестно. Общая стратегия решения задач со словами, кажется, состоит в том, чтобы просто взять два числа, которые вы видите, и сложить их вместе, или, может быть, вычесть, но часто ученики просто не уверены. Похоже, что это наиболее распространенные типы задач, из-за чего учащиеся не имеют сбалансированного опыта со всеми 14 типами и, в конечном счете, без некоторых стратегий, которые можно использовать при решении задач. Студенты должны увидеть широкий круг задач, чтобы получить четкое представление о том, как используются сложение и вычитание и как они связаны друг с другом. Понятие достаточности примеров означает, что учащиеся должны быть ознакомлены с широким спектром примеров, чтобы обеспечить всестороннюю практику с концепцией. 6
Понятие достаточности примеров означает, что учащиеся должны быть ознакомлены с широким спектром примеров, чтобы обеспечить всестороннюю практику с концепцией. 6
Подходы к этому разделу учебной программы различаются в зависимости от стилей обучения всех учащихся.
Общий формат основан на модели мастерской. Концепции и навыки преподаются с помощью серии мини-уроков, посвященных цели, с использованием следующих методов:
.Экспериментальное обучение: большинству молодых студентов необходимо начинать с практического обучения. Использование конкретных моделей для разработки математических историй позволяет учащимся увидеть проблему и манипулировать частями по мере развития истории. Этот тип обучения является важным первым шагом.
Дифференцированное обучение: Уроки и занятия будут направлены на максимальное обучение. Студенты будут использовать различные подходы, работая иногда индивидуально, а иногда в небольших группах, что определяется сложностью работы. Некоторые учащиеся будут двигаться быстрее по мере овладения навыками, а некоторым потребуется больше возможностей для практики.
Некоторые учащиеся будут двигаться быстрее по мере овладения навыками, а некоторым потребуется больше возможностей для практики.
Совместное обучение: учащимся будет предоставлена возможность работать в совместных группах над созданием математических историй для представления классу. Эта стратегия позволит учащимся работать совместно, взяв на себя различные роли, необходимые для завершения работы, с акцентом на успех для всех.
Упражнение 1: Последовательность типов задач — задачи до 10
Вводная (и обзорная) часть модуля охватывает все типы задач, но в последовательном порядке. Цель состоит в том, чтобы учащиеся прочитали и интерпретировали словесную задачу с помощью инструкции, сопровождаемой самостоятельной практикой. Из-за множества типов задач эта часть займет несколько дней повторения и практики, прежде чем учащиеся смогут начать писать свои собственные наборы задач. Основываясь на потребностях учащихся и темпе их понимания, я ожидаю, что этот раздел будет состоять из четырех-шести дней занятий, а при необходимости и больше.
Последовательность следующая: часть-часть-целое ; изменение-увеличение и изменение-уменьшение ; и, наконец, сравнение-больше и сравнение-меньше . Следующие вводные занятия предназначены для всей группы, когда учащиеся либо сидят за партами, либо собираются на коврике рядом с доской или мольбертом. Вся групповая порция должна длиться не более 20 минут. В конце каждого занятия я даю студентам решить от 5 до 10 похожих задач. Более способные учащиеся могут начать генерировать собственные задачи во время самостоятельной работы.
Начало с основ дает хорошую возможность познакомиться с навыками учащихся, что полезно при подготовке дифференцированной работы и создании групп,
На этом уроке учащиеся будут интерпретировать проблемы реального мира и с помощью манипулятивных упражнений и картинок решать истории «часть-часть-целое», используя сложение и вычитание.
6 девушек играют
С ними играют 3 мальчика.
Сколько всего детей играет?
Начните историю со всего неизвестного, как в этом примере. Этот тип истории идеально подходит для учащихся, чтобы разыграть их прямо в классе. Напишите историю на доске или листе бумаги и попросите студентов стать актерами. Когда учащиеся решат задачу, напишите математическое предложение, чтобы показать, что получилось: 6 + 3 = 9.ученики. Объясните, что две части (мальчики и девочки) составили одно целое (дети). Пока учащиеся все еще находятся в действующей позиции, представьте новый подход к этому сценарию:
.Играют 9 учеников.
6 из них девочки.
Сколько мальчиков играет?
На этом наглядном примере учащиеся должны сразу увидеть, сколько. Важная концепция, которую необходимо продемонстрировать, заключается в том, что части могут быть определены, когда известны целое и одна часть, в этом случае 9 известно как целое, а 6 как одна часть. Снова напишите математическое предложение, чтобы показать этот расчет: 6 + ? = 9и включите стратегию начала с целого, чтобы определить недостающую часть как предложение вычитания 9 — 6 = 3. Практика обоих подходов к решению поможет учащимся связать сложение и вычитание и понять, как они используются вместе.
Практика обоих подходов к решению поможет учащимся связать сложение и вычитание и понять, как они используются вместе.
Поскольку этот урок требует, чтобы учащиеся читали задачи, я буду объединять бегло читающих с теми, кто менее бегло читает, давать счетчики тем, кто хочет их, и позволять партнерам работать вместе над решением проблем и делиться стратегиями, которые они использовали.
Для демонстрации я использую еще два примера, подобных приведенным ниже, не забывая писать на доске слово «проблема» и математическое предложение. Я также переформулирую задачи так, чтобы часть была неизвестной.
У Ханны 5 красных маркеров.
У нее 3 синих маркера
Сколько маркеров всего у Ханны?
7 учеников рисуют мелками.
2 ученика рисуют цветными карандашами.
Сколько учеников рисуют?
Продолжая ту же идею, следующий набор типов задач включает изменение-увеличение и изменение-уменьшение . Хотя часть-часть-целое — это язык, который учащиеся могут принять и использовать при обсуждении своей работы, язык изменение-увеличение и изменение уменьшение немного сложнее. Использование слова изменить больше подходит учащимся, чтобы продемонстрировать, что некоторая сумма была либо добавлена, либо вычтена из первоначальной суммы.
Использование слова изменить больше подходит учащимся, чтобы продемонстрировать, что некоторая сумма была либо добавлена, либо вычтена из первоначальной суммы.
Введите ниже слово «проблема», которое является примером неизвестного результата в категории «изменение-увеличение».
В начале дня у Джейсона было 8 наклеек «поймал на хорошем счету».
За учебный день он заработал еще 2 стикера.
Сколько наклеек у Джейсона на графике в конце дня?
Учащийся может решить задачу, как написано, и, используя тот же сценарий, предложить им создать изменение-неизвестно и начальная неизвестная история . Одним из примеров может быть:
У Джейсона было несколько наклеек с надписью «поймал, что он хороший» на его графике на
.начало дня.
За учебный день он заработал еще 2 стикера.
В конце дня у него 10 наклеек.
Сколько наклеек было у Джейсона в начале дня?
Это устное задание, когда я пишу скорректированную версию через доску, помещая математическое предложение под ним. Важно позволить учащимся работать над составлением проблемы, чтобы они могли начать видеть взаимосвязь между проблемами и тем, что они задают.
Важно позволить учащимся работать над составлением проблемы, чтобы они могли начать видеть взаимосвязь между проблемами и тем, что они задают.
Результат Неизвестно Версия 8 + 2 = ? | Изменить Неизвестно Версия 8 + ? = 10 | Начальный Неизвестно Версия ? + 2 = 10 |
Цель состоит в том, чтобы учащиеся поняли, а не просто решили. Я могу неформально оценить во время обсуждения переписывания текста проблемы слова, с более формальной оценкой позже в блоке.
Следующей категорией, которую необходимо ввести, являются типы задач изменения-уменьшения . Следуя тому же формату, что и раньше, я ввожу неизвестный результат , изменяю неизвестный , а затем исходный неизвестный.
Кристалл собрала 7 листьев для своего проекта.
2 листа унесло ветром.
Сколько листьев осталось у Кристал для своего проекта?
Результат Неизвестно 7 — 2 = ? | Изменить Неизвестно 7 — ? = 5 | Начальный Неизвестно ? — 2 = 5 |
Опять же, цель состоит в том, чтобы учащиеся поняли, а не просто решили.
Третий широкий класс, сравните, сложнее для моих учеников 2 и классов. Это требует, чтобы текст словесных задач был очень прямолинейным. Студенты не должны запутаться, когда они учатся извлекать данные из задачи. Помните, что использование точной терминологии — это не цель, а скорее понимание сути проблемы. Вот три способа, которыми я представлю сценарий, показывающий типы проблем 9.0021 сравнение-больше и три способа показать сравнение-меньше. Ученики должны быть ознакомлены и иметь возможность практиковать все типы. Конечно, не все эти примеры следует использовать одновременно. Когда я записываю задачи на листе бумаги и вывешиваю их в классе, учащиеся могут начать видеть и делать свои собственные сравнения и противопоставления, когда один и тот же сценарий объясняется по-разному. Использование слов «больше» и «меньше» должно быть выделено и объяснено по мере того, как набор проблем вводится и работает над ним. Моя роль здесь состоит в том, чтобы позволить учащимся начать замечать тонкие различия в формулировках и то, как они меняют мышление. Лучше начать с простого!
Лучше начать с простого!
У Оливии на 4 ластика больше, чем у Джона. У Джона есть 2 ластика. Сколько ластиков у Оливии? (сравнение больше, большее неизвестно) 2 + 4 = ? | У Джона на 4 ластика меньше, чем у Оливии. У Джона есть 2 ластика. Сколько ластиков у Оливии? (без сравнения, большее неизвестное) 4 + 2 = ? |
У Оливии на 4 ластика больше, чем у Джона. У Оливии 6 ластиков. Сколько ластиков у Джона? (сравнение-больше, меньше неизвестно) 6 – 4 = ? | У Джона на 4 ластика меньше, чем у Оливии. У Оливии 6 ластиков. Сколько ластиков у Джона? (без сравнения, меньше неизвестно) 6 – 4 = ? |
У Оливии 6 ластиков. У Джона есть 2 ластика. На сколько больше ластиков у Оливии, чем у Джона (сравнение-больше, разница неизвестна 6 – 2 = ? 2 + ? = 6 | У Джона есть 2 ластика. У Оливии 6 ластиков. На сколько меньше ластиков у Джона, чем у Оливии? (без сравнения, разница неизвестна) 6 – 2 = ? |
На этих вводных занятиях мы с учащимися проводим мозговой штурм сценариев, которые в конечном итоге можно использовать в собственных текстовых задачах. Идеи должны рождаться из школьных занятий и материалов, побуждая учащихся думать о том, что ученики могут на самом деле использовать для манипулирования или, как в первом сценарии, быть в состоянии действовать, чтобы решить. Сохраняя список идей на диаграмме в качестве справочного материала, учащиеся не будут бороться со словарным запасом или подходящими сценариями; они будут заниматься решением своих проблем. Этот список подготовит студентов ко второй части модуля.
Занятие 2: Сценарии в классе/школе
Как указывалось ранее, слова и словарный запас должны быть доступны для учащихся, а не должны быть проблемой или препятствием. Цель состоит в том, чтобы обдумать истории и использовать информацию, собранную во время мозгового штурма. Чтобы начать эту часть, просмотрите диаграммы и добавьте новые, если у учащихся появятся новые идеи. Для целей составления текстовых задач может быть полезно иметь информацию в категориях, таких как эти:
Цель состоит в том, чтобы обдумать истории и использовать информацию, собранную во время мозгового штурма. Чтобы начать эту часть, просмотрите диаграммы и добавьте новые, если у учащихся появятся новые идеи. Для целей составления текстовых задач может быть полезно иметь информацию в категориях, таких как эти:
Материалы, которые мы используем
Классы, которые мы посещаем
Занятия в школе
Имена одноклассников
Я создам группы из двух или трех учеников, чтобы они написали свои собственные задачи, чтобы поделиться ими с классом. Поскольку этот урок требует, чтобы учащиеся читали и писали сюжетные задачи, опять же, беглые читатели и писатели с теми, кто менее беглый, предоставляют счетчики для тех, кто хочет их, и позволяют партнерам работать вместе для решения проблем и обмена стратегиями, которые они использовали. .
Цель в течение этого периода времени состоит в том, чтобы предложить учащимся написать ту же задачу, но попробовать ее по-другому, выбрать другой тип, когда они рассказывают историю. Группы студентов будут работать вместе во время прибытия в качестве утренней работы и во время математического семинара во время обучения математике. Это позволит учащимся работать до 30 минут в день со своими партнерами над созданием математических историй.
Группы студентов будут работать вместе во время прибытия в качестве утренней работы и во время математического семинара во время обучения математике. Это позволит учащимся работать до 30 минут в день со своими партнерами над созданием математических историй.
Я подчеркну, что важно сохранить их коллекцию вместе, так как большая часть их работы станет частью рабочей тетради, которую они создадут в конце этого раздела. Папки и математические журналы могут быть полезны, или мой ежедневный сбор незавершенной работы — еще один вариант.
Занятие 3: Научные сценарии
Первый блок в 2 -й -й степени науки — исследование и исследование жизненного цикла бабочки. Студенты получают гусениц в начале семестра, наблюдают и записывают изменения в жизни гусеницы. Работа, которую учащиеся выполняют на уроках естествознания, может стать информацией и сценариями, которые они могут использовать для решения текстовых задач.
Используя все разные типы задач, мы напишем несколько вместе как класс. Это дополнительная возможность очень конкретно интегрировать математику в наши научные исследования и работу. Учащимся важно признать, что, хотя их обучение было разделено на предметные области, практически невозможно разделить все это на категории. Таким образом, эта часть модуля использует математику, естественные науки и чтение, чтобы помочь учащимся узнать о жизненном цикле бабочки (а также других животных).
Это дополнительная возможность очень конкретно интегрировать математику в наши научные исследования и работу. Учащимся важно признать, что, хотя их обучение было разделено на предметные области, практически невозможно разделить все это на категории. Таким образом, эта часть модуля использует математику, естественные науки и чтение, чтобы помочь учащимся узнать о жизненном цикле бабочки (а также других животных).
Учащиеся создадут наборы задач, используя свой ежедневный опыт отслеживания своих гусениц. У каждого ученика есть 2-3 гусеницы, за которыми нужно наблюдать и записывать информацию, что может стать началом словесных задач. Примеры для начала: Если в Таблице 3 есть 8 гусениц и 2 гусеницы присоединяются к этой группе, сколько гусениц наблюдается в Таблице 3? В классе 28 учеников. Каждому ученику нужна одна чашка еды для гусениц. Есть 30 чашек корма для гусениц. На сколько чашек с едой больше, чем студентов?
Часто встречаются студенты, проявляющие большой интерес к другим областям науки. Это область, которую следует поощрять, если учащиеся рады делиться своими знаниями. Некоторые учащиеся будут более склонны использовать единицу изучения, происходящую в классе, но в течение дня, посвященного обучению грамоте, учащиеся сталкиваются с большим количеством научно-популярных или информационных текстов, которые, безусловно, могли бы обогатить наши проблемы со словами. .
Это область, которую следует поощрять, если учащиеся рады делиться своими знаниями. Некоторые учащиеся будут более склонны использовать единицу изучения, происходящую в классе, но в течение дня, посвященного обучению грамоте, учащиеся сталкиваются с большим количеством научно-популярных или информационных текстов, которые, безусловно, могли бы обогатить наши проблемы со словами. .
На протяжении всего научного блока учащиеся будут продолжать писать текстовые задачи различных типов, чтобы в конечном итоге включить их в наш окончательный проект — рабочую тетрадь. Эти задачи можно писать во время утренней работы, во время математического семинара и в конце урока естествознания. К концу раздела у каждого учащегося должно быть две задачи для добавления в главу «Наука» рабочей тетради.
Мероприятие 4: Создание рабочей тетради / Празднование публикации
Целью этой части модуля является сортировка текстовых задач по «главам» и создание рабочей тетради для демонстрации на Празднике публикации. Главы будут названы по предмету или категории, в зависимости от выбора учащегося и предложения учителя. Идеи включают в себя «Начало рассказов», «Занятия в классе», «Развлечение на игровой площадке», «Науку и математику» и «Связи по общественным наукам». Пусть учащиеся творчески подходят к названиям!
Главы будут названы по предмету или категории, в зависимости от выбора учащегося и предложения учителя. Идеи включают в себя «Начало рассказов», «Занятия в классе», «Развлечение на игровой площадке», «Науку и математику» и «Связи по общественным наукам». Пусть учащиеся творчески подходят к названиям!
Учащиеся отправят свою работу, которая будет включать как минимум одну текстовую задачу для каждой главы. Они также должны представить решения своих проблем, чтобы их можно было включить в ключ ответа. В каждой главе будет не менее 25 задач с примерами всех типов и разного уровня сложности. Словесные задачи можно либо напечатать, либо написать от руки для итоговой рабочей тетради, в зависимости от того, что учащиеся решат в классе. По одной рабочей тетради на каждого учащегося необходимо будет скопировать и каким-либо образом переплести для празднования.
За две недели до Праздника Публикации учащиеся создадут приглашение для своей семьи и друзей, пригласив их на «Праздник решения проблем».
 Реши примеры верно.
Реши примеры верно.
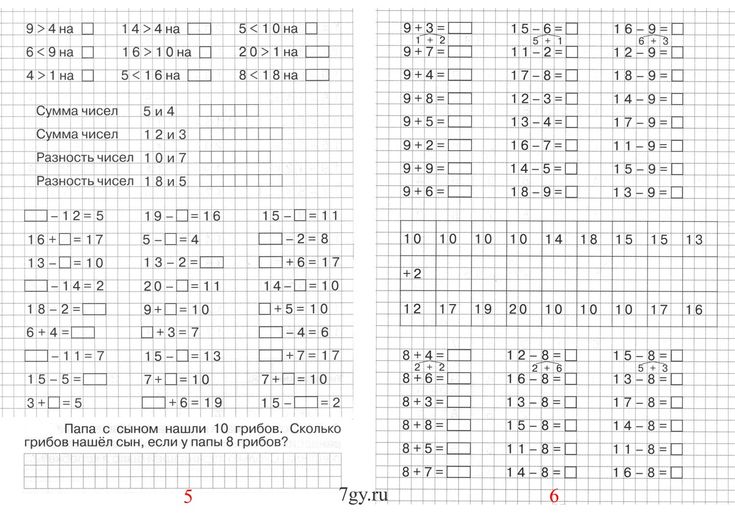
 Не очень хорошо знаком с числами.
Не очень хорошо знаком с числами. Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.

 Вы съели 2 печенья. Сколько файлов cookie у вас осталось?
Вы съели 2 печенья. Сколько файлов cookie у вас осталось? Обед — через три часа десять минут после начала учебного дня. Когда будет ланч?
Обед — через три часа десять минут после начала учебного дня. Когда будет ланч? Д.
Д. Д.).
Д.). д.
д.