Морфологический разбор слова «созреть»
Часть речи: Инфинитив
СОЗРЕТЬ — слово может быть как одушевленное так и неодушевленное, смотрите по предложению в котором оно используется.
Начальная форма слова: «СОЗРЕТЬ»
| Слово | Морфологические признаки |
|---|---|
| СОЗРЕТЬ |
|
Все формы слова СОЗРЕТЬ
СОЗРЕТЬ, СОЗРЕЛ, СОЗРЕЛА, СОЗРЕЛО, СОЗРЕЛИ, СОЗРЕЮ, СОЗРЕЕМ, СОЗРЕЕШЬ, СОЗРЕЕТЕ, СОЗРЕЕТ, СОЗРЕЮТ, СОЗРЕВ, СОЗРЕВШИ, СОЗРЕЕМТЕ, СОЗРЕЙ, СОЗРЕЙТЕ, СОЗРЕВШИЙ, СОЗРЕВШЕГО, СОЗРЕВШЕМУ, СОЗРЕВШИМ, СОЗРЕВШЕМ, СОЗРЕВШАЯ, СОЗРЕВШЕЙ, СОЗРЕВШУЮ, СОЗРЕВШЕЮ, СОЗРЕВШЕЕ, СОЗРЕВШИЕ, СОЗРЕВШИХ, СОЗРЕВШИМИ
Разбор слова по составу созреть
созре
ть
| Основа слова | созре |
|---|---|
| Приставка | со |
| Корень | зре |
| Глагольное окончание | ть |
Разобрать другие слова
Разбор слова в тексте или предложении
Если вы хотите разобрать слово «СОЗРЕТЬ» в конкретном предложении или тексте, то лучше использовать
морфологический разбор текста.
Примеры предложений со словом «созреть»
1
Как же тут не созреть, какие пойти в семена при одной мысли о монументе!
2
Зимою дождь не оживляет семян, лето не дает тепла, чтобы созреть плодам.
Статьи о революции, Максимилиан Волошин, 1920г.
3
Но, к тому времени, в голове должно созреть новое и очень смелое предложение.
Стоимость. Процесс труда как процесс создания стоимости, Виктор Васильевич Дрожжин
4
Если уже созрел этот плод «прогресса» у одного христианского народа, то почему бы не созреть ему и во всем человечестве?
Собрание сочинений в 20 т.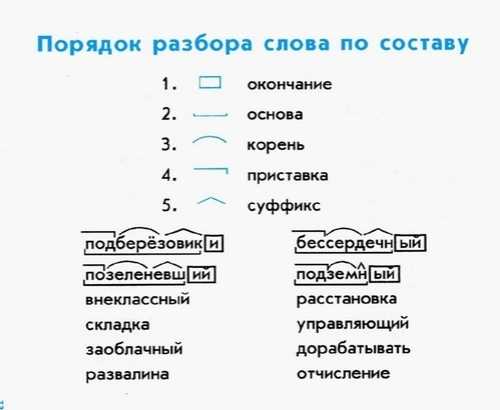 Том 14. Тайна трёх, Д. С. Мережковский, 1925г.
Том 14. Тайна трёх, Д. С. Мережковский, 1925г.
5
Даррелл никуда не торопится, он дает себе волю отвлечься, а новым замыслам – отлежаться и созреть.
Александрийский квартет: Жюстин. Бальтазар, Лоренс Даррелл, 1957, 1958г.
Найти еще примеры предложений со словом СОЗРЕТЬ
|
|
Зрелый взгляд на монады
В предыдущих сообщениях о Haskell я много говорил о монадах.
Я пытался объяснить монадическую концепцию и буду продолжать это делать. На данный момент я добился значительного прогресса в этом вопросе, но хочу сделать больше. Предыдущие посты, этот и некоторые будущие посты прольют больше света на монады.
Я являюсь участником Quora, сайта, где люди задают вопросы, а другие отвечают на них. (На странице «Обо мне» этого блога вы можете найти ссылку с моими ответами в Quora.) В Quora кто-то (я не знаю кто) спросил:
Какова важность теории категорий в компьютере наука?
Отличный вопрос. Мой ответ есть в Quora, но я повторю его здесь для потомков:
Информатика получает концепции из теории категорий, чтобы позволить разработчикам создавать высококачественное программное обеспечение.
В функциональном программировании мы можем математически комбинировать более мелкие программы для создания сложных, и мы можем математически рассуждать о надежности и правильности программы. Но это только если программа чисто функциональная.
Программа является чисто функциональной, если она не содержит побочных эффектов. IO, состояние и все, что отличается от функций, которые принимают только аргументы в качестве входных данных и возвращают результат, — все это примеры побочных эффектов, то есть вычислений, которые не являются чисто функциональными.
Монады помогают инкапсулировать побочные эффекты и контролировать их таким образом, чтобы программы не теряли своих чистых функциональных преимуществ (мы по-прежнему можем математически комбинировать более мелкие программы и математически рассуждать о программах).
Но инкапсуляция и контроль побочных эффектов — не единственная причина, по которой монады полезны. Позволь мне объяснить.
Позволь мне объяснить.
Всякий раз, когда разработчик создает новый тип, он должен «объяснить» языку, как новый тип будет вести себя, когда он будет вовлечен в композицию функций. Новый тип, вооруженный этой информацией (которую предоставляет разработчик), — это монада.
Таким образом, грубо говоря, монада — это новый тип, который язык умеет обрабатывать при составлении функций.
Этот новый тип может инкапсулировать побочные эффекты или просто выполнять вычисления. Во всех случаях целостность программы сохраняется, а также легче комбинировать более мелкие программы для создания более крупных. Это потому, что новый тип/монада способен упаковать много мощности без ущерба для математической корректности программы.
Например, можно спроектировать монаду, которая является синтаксическим анализатором. Хорошо, парсер можно создать на любом языке. Но монадический синтаксический анализатор может хранить не только результат синтаксического анализа, но и любые ошибки синтаксического анализа, номера строк и много другой информации. Вся эта полезная и дополнительная информация может быть побочными эффектами или побочными вычислениями, но на самом деле все это чисто функциональное поведение.
Вся эта полезная и дополнительная информация может быть побочными эффектами или побочными вычислениями, но на самом деле все это чисто функциональное поведение.
Итак, монады обладают большой силой. Они могут инкапсулировать побочные эффекты или просто чисто функциональные вычисления и в то же время выполнять все это, делая композицию функций возможной, математически точной и простой.
Программа, написанная с монадами, может быть намного меньше и менее запутанной, чем программа, написанная без них. Вы должны увидеть это, чтобы поверить в это.
Есть и другие понятия из теории категорий, которые определяют вычисления и помогают компьютерным наукам. В дополнение к монадам у нас есть функторы и стрелки. На самом деле, все эти трое связаны между собой. От наиболее частного к наиболее общему эти концепции идут следующим образом:
Типы -> Новые (повышенные) типы -> Функторы -> Аппликативные функторы -> Монады -> Стрелки.
Как правило, теория категорий помогает информатике, обнаруживая «вычислительные закономерности». Теория категорий открывает их и изучает, чтобы найти их математические свойства. Затем компьютерные науки могут использовать эти знания, чтобы дать разработчикам возможность создавать программное обеспечение более лаконичным и правильным способом.
Вы можете спросить, почему описанная здесь парадигма лучше парадигмы объектно-ориентированного программирования. ООП включает инкапсуляцию (правда, в совершенно другом контексте) и очень интуитивно понятен. Проблема с ООП заключается в том, что объекты имеют состояние, что сильно отличает парадигму ООП от чисто функциональной парадигмы. Таким образом, мы не можем *математически* рассуждать о правильности или масштабируемости ООП-программы. И это очень жаль.
Вы также можете спросить, есть ли «подвох» в описанной здесь парадигме. Описанная здесь парадигма основана на вычислительных шаблонах, которые теория категорий обнаруживает, математически описывает и изучает, а затем передает их компьютерным наукам, чтобы их распознали и использовали для того, чтобы сделать программы более краткими и правильными.
Ну, на мой взгляд, в этом подходе есть «зацепка», существенная. Вы должны быть очень хорошо осведомлены, чтобы иметь возможность программировать, используя эту парадигму. В то время как ООП интуитивно понятен, концепции, вытекающие из теории категорий, трудны для понимания. Вы должны мыслить в терминах абстракций, чтобы понять концепции теории категорий, которые используются в компьютерных науках. Вы должны иметь абстрактное мышление и много учиться, чтобы иметь возможность программировать, используя эту парадигму.
Вам нужно потратить много времени, мыслей и энергии, чтобы иметь возможность использовать концепции теории категорий в компьютерных науках. Я считаю, что время, мысли и энергия потрачены не зря. Но вы должны решить для себя.
Итак, это был мой ответ на вопрос, заданный в Quora. Я постарался сделать свой ответ максимально исчерпывающим. Вообще-то, я не сразу написал ответ целиком. Вместо этого я написал первые несколько абзацев и разместил их. Потом я понял, что хочу сказать больше. Поэтому я добавил к своему ответу. И так далее. В общем, я немного поработал над этим ответом. Я думаю, что мы должны обратить особое внимание на то, что я написал в Quora, потому что мы можем обнаружить некоторые интересные факты.
Потом я понял, что хочу сказать больше. Поэтому я добавил к своему ответу. И так далее. В общем, я немного поработал над этим ответом. Я думаю, что мы должны обратить особое внимание на то, что я написал в Quora, потому что мы можем обнаружить некоторые интересные факты.
Если новичок в Haskell спросит, что такое монады, я найду отличный ответ, что это метод, с помощью которого мы можем вводить побочные эффекты в чисто функциональные вычисления, позволяя вычислениям сохранять свою особенность. Этот ответ правильный, и именно поэтому монады были введены в Haskell. Но по мере того, как новичок продвигается в Haskell и его знания начинают накапливаться, этот ответ, хотя поначалу и дает возможность, начинает становиться помехой.
Видите ли, новичок начнет искать побочные эффекты всякий раз, когда и где бы он ни встретил монады. И правда в том, что нам не нужны побочные эффекты, чтобы иметь монады. У нас могут быть чисто функциональные вычисления, которые могут помочь нам рассматривать как побочные эффекты, как побочные вычисления, или у нас могут вообще не быть побочных вычислений.
В дальнейшем считайте a и b встроенными типами Haskell, такими как, например, Int и String.
Монада — это конструктор типа, оснащенный функциями возврата и связывания. Конструктор типа (назовем его М) создает новый тип. Сигнатура возвращаемой функции: a -> M a. Таким образом, для типа a создается тип M a. Сигнатура функции связывания: M a -> (a -> M b) -> M b. Таким образом, он позволяет составить две функции вида x -> M a и a -> M b. Это замечательно, так как выход M a первой функции не того же типа, что и вход a второй функции.
Таким образом, монада «поднимает» типы в «область» M и предоставляет нам способ составить две функции a -> M b и b -> M c. Конечно, мы напишем код для функций возврата и привязки. Но когда мы закончим писать этот код, у нас будет функциональность Монады.
Итак, вот что такое монада: конструктор типа M, который мы создали (чтобы он мог «поднять» тип a до типа M a) и который мы также сделали способным составлять функции вида a -> М б.
Таким образом, монада M — это конструктор типа M, умеющий составлять функции типа a -> M b. Таким образом, всякий раз, когда мы создаем конструктор типа, мы можем также «обновить» его до монады, если нам нужна функциональность компоновки.
Когда мы создаем конструктор типа M, мы можем «обновить» его до функтора, сделав его способным «поднимать» не только типы, но и функции. И мы достигаем этого, предоставляя определение (a -> b) -> M a -> M b. Таким образом, мы инструктируем M, как перейти от функции a -> b к функции M a -> M b.
Мы также можем «обновить» наш функтор до аппликативного, предоставив определение M (a -> b) -> M a -> M b. Таким образом, мы инструктируем M, как перейти от функции M (a -> b) к функции M a -> M b.
Наконец, мы можем обновить нашу аппликативную функцию до монады, предоставив определение для M a -> (a -> M b) -> M b, которое является определением того, как составить две функции типов x -> М а и а -> М b.
До сих пор Haskell не нуждался в том, чтобы конструктор типа был аппликативным, чтобы мы могли «обновить» его до монады. Мы могли бы «обновить» конструктор типа до Functor и Applicative независимо от «обновления» его до монады. Будущие реализации Haskell будут настаивать на том, чтобы сначала «обновить» конструктор типа до Functor и Applicative, прежде чем сделать его монадой. Это будет сделано для того, чтобы Haskell был более корректным и более согласованным с определениями этих понятий из теории категорий. Действительно, в теории категорий монада — это прежде всего функтор.
Мы могли бы «обновить» конструктор типа до Functor и Applicative независимо от «обновления» его до монады. Будущие реализации Haskell будут настаивать на том, чтобы сначала «обновить» конструктор типа до Functor и Applicative, прежде чем сделать его монадой. Это будет сделано для того, чтобы Haskell был более корректным и более согласованным с определениями этих понятий из теории категорий. Действительно, в теории категорий монада — это прежде всего функтор.
То, как мы определяем и реализуем наш конструктор типов, определяет его функциональность и то, производит ли он побочные эффекты или нет. Мы можем создать очень полезный конструктор типа, такой как конструктор списка, без каких-либо побочных вычислений или побочных эффектов. Мы также можем создать очень полезный конструктор типа, такой как Maybe, который не дает побочных эффектов чистой функциональности, но который мы можем вообразить в своем воображении, что он несет побочные вычисления или «побочные результаты». Действительно, «Может быть» может означать наличие либо результата, либо его отсутствия. И в нашем сознании отсутствие результата можно рассматривать как «побочный результат». Но это ничего не нарушает чистой функциональности вычислений. Это просто умный и удобный способ упаковать больше в одну вещь и уменьшить объем кода, который нам нужно написать. Например, с помощью Maybe мы можем избежать написания большого количества каскадных операторов if.
И в нашем сознании отсутствие результата можно рассматривать как «побочный результат». Но это ничего не нарушает чистой функциональности вычислений. Это просто умный и удобный способ упаковать больше в одну вещь и уменьшить объем кода, который нам нужно написать. Например, с помощью Maybe мы можем избежать написания большого количества каскадных операторов if.
С другой стороны, есть монады, которые имеют побочные эффекты, такие как монада IO. Они тем более полезны, поскольку вводят побочные эффекты таким образом, чтобы не нарушать чистую функциональность приложения. И они достигают этого, позволяя нам составлять функции вида a -> M b.
Итак, да, монады позволяют нам добавлять управляемые побочные эффекты к чистой функциональности, но это не обязательно. Монады — это просто конструкторы типов, которые знают, как выполнять композицию типов. Всякий раз, когда кто-то хочет создать конструктор типа, он также может «обновить» его до монады. Создатель конструктора типов должен определить его назначение и функциональные возможности.
Одним из конструкторов типов, преобразованных в монаду, является хорошо изученный Maybe. Как конструктор типа, Maybe имеет определение
. данные Возможно a = Ничего | Просто
Здесь нет побочных эффектов. Может быть, инкапсулирует результат или его отсутствие. Это очень удобно. Как конструктор типов, Maybe предоставляет функциональность, для которой он был разработан. Когда Maybe превращается в монаду (предоставляя функцию возврата и функцию связывания), она знает, как составлять функции типа a -> Maybe b и b -> Maybe c. Итак, как монада, Maybe является конструктором типа, который знает, как составить две такие функции и, таким образом, обеспечивает эту функциональность композиции.
Настоящая мощь монады исходит из определения конструктора базового типа. Когда конструктор типа «обновляется» до монады, он получает функциональность композиции функций. Вот и все, что нужно сделать.
В своем блоге под названием «Разочаровывающая монада состояния» я изучил монаду состояния. Его определение:
Его определение:
новый тип State s a = State {runState::s -> (a, s)}
(Ключевое слово «newtype» делает то же, что и «данные». Оно вводит новый тип. Между «новым типом» и «данными» есть тонкая разница, но она выходит за рамки этой записи в блоге.)
Я охарактеризовал State Monad как разочаровывающую, потому что ее определение не имеет побочных эффектов. State s — это просто переносимое и передаваемое значение, но программа никогда не теряет ни малейшей части чистой функциональности. Мы можем думать о состоянии как о «состоянии», но на самом деле это просто значение.
С другой стороны, монада IO действительно предоставляет монаду, включающую побочные эффекты. IO Moand действительно выполняет IO, что является побочным эффектом чистой функциональности.
Я хотел бы привести последний пример конструктора типа, который был «обновлен» до монады. Это конструктор типа Parser:
синтаксический анализатор нового типа a = синтаксический анализатор (строка -> [(a, строка)])
Целью конструктора типа Parser является предоставление платформы для анализа входных данных, таких как текстовые строки.
Если вы хотите узнать больше о Parser, я рекомендую статью под названием «Монадический анализ в Haskell», написанную Грэмом Хаттоном и Эриком Мейером. Найдите его в Интернете. Это легко найти.
В статье, которую я только что упомянул, описано, как Parser можно «обновить» до монады. Опять же, обновляя парсер до монады, все, чего мы достигаем, — это указание ему, как составлять функции типов a -> парсер b и b -> парсер c. Настоящая сила Parser исходит из его определения. Он рассказывает о строке и предоставляет список кортежей. Каждый кортеж имеет объект типа a (обычно дерево) и строку. Это позволяет нам анализировать начальную часть входной строки и предоставлять результат анализа в виде объекта типа a (первый элемент кортежа), а остальную часть строки — в виде строки (второй элемент кортежа). Нам нужен список кортежей, потому что нам может понадобиться предоставить более одного ответа, как в случае с неоднозначными грамматиками. Пустой список означает неудачу. Таким образом, как конструктор типов/монада, Parser может быть очень ценным и очень мощным. Тем не менее, в его определении нет никаких побочных эффектов. Вывод синтаксического анализатора — [(a, String)], и там есть результат и оставшаяся строка. Мы можем решить рассматривать любую часть вывода, которую хотим, как побочное вычисление или побочный эффект, но это не обязательно. На самом деле вывод является чисто функциональным, и нам не нужно рассматривать его по-другому.
Тем не менее, в его определении нет никаких побочных эффектов. Вывод синтаксического анализатора — [(a, String)], и там есть результат и оставшаяся строка. Мы можем решить рассматривать любую часть вывода, которую хотим, как побочное вычисление или побочный эффект, но это не обязательно. На самом деле вывод является чисто функциональным, и нам не нужно рассматривать его по-другому.
Таким образом, монада — это конструктор типа, который научился вести себя при составлении его функций. Конструктор типа может вносить побочные эффекты в чистую функциональность, но это, конечно, не обязательно. А монадическая концепция направляет нас только в части функциональности композиции функций. Нужно ли нам «обновлять» все наши конструкторы типов до монад? Ну, мы делаем, если мы собираемся использовать с ними композицию функций. В противном случае мы можем оставить их как есть.
Так:
Нравится Загрузка…
Проект MUSE — T-единица как мера синтаксической сложности в стихах Эмили Дикинсон
Вместо аннотации приведу краткую выдержку из содержания:
The Emily Dickinson Journal 11. 1 (2002) 91-103
1 (2002) 91-103
[Доступ к статье в формате PDF]
Т-единица как мера синтаксической сложности в стихах Эмили Дикинсон 90 163
Синтия Л. Халлен и Дженнифер Шекспир
Эмили Дикинсон создавала стихи с большим синтаксическим разнообразием и структурной сложностью. Сила ее языка на уровне фразы, предложения и дискурса свидетельствует о ее поэтическом гении. Как сказал один ритор из Новой Англии девятнадцатого века: «В лучших стихах всех наций мы находим почти бесконечное разнообразие статей, фраз и абзацев» (Hunt, Principles 304). Тем не менее лаконичный синтаксис и нестандартная пунктуация Дикинсона могут вызвать трудности, когда читатели пытаются определить, где в стихотворении заканчивается одно предложение и начинается другое.
Некоторые люди определяют предложение как завершенную идею, заканчивающуюся точкой. Однако Дикинсон часто выражает свои мысли в неполных эллиптических структурах, опуская подлежащие или сказуемые составляющие, и она не всегда заканчивает предложения точками или другими маркерами окончания. Поэтому многие ее стихи бывает трудно разобрать и прочитать. Одним из ответов на такие проблемы может быть «минимальная конечная единица» или «Т-единица», предложенная Келлогом У. Хантом, исследователем композиции двадцатого века. T-единица состоит из основного предложения и всех его модификаторов, включая любые встроенные или присоединенные предложения, так что «разделение отрывка на T-единицы будет резать его на самые короткие части, которые грамматически допустимо расставлять в виде предложений». (Хант, «Синтаксис» 4).
Поэтому многие ее стихи бывает трудно разобрать и прочитать. Одним из ответов на такие проблемы может быть «минимальная конечная единица» или «Т-единица», предложенная Келлогом У. Хантом, исследователем композиции двадцатого века. T-единица состоит из основного предложения и всех его модификаторов, включая любые встроенные или присоединенные предложения, так что «разделение отрывка на T-единицы будет резать его на самые короткие части, которые грамматически допустимо расставлять в виде предложений». (Хант, «Синтаксис» 4).
Сложность прочтения полупунктурного эллиптического синтаксиса Дикинсона заключается в том, чтобы отличить главные предложения от зависимых предложений и фрагментов. Т-единица Ханта — полезный инструмент для идентификации предложений в поэзии Дикинсона, потому что она определяет предложения по их грамматической структуре, а не по пунктуации. Идентификация Т-единиц в стихотворении Дикинсона может помочь читателям, переводчикам и ученым установить правдоподобные интерпретации текста. [End Page 91]
[End Page 91]
Кроме того, длина Т-блока может служить мерой синтаксической сложности и когнитивной зрелости писателя или автора. Менее опытные писатели, как правило, соединяют более короткие предложения в паратактическом стиле, в то время как опытные писатели склонны объединять предложения в более длинные главные предложения с подчиненными зависимыми предложениями в гипотактическом стиле:
Paratactic: Эмили поступила в Академию Амхерст [5], а затем в Колледж Маунт-Холиок [7].
Гипотактический: После того, как Эмили поступила в Академию Амхерст, она поступила в Колледж Маунт-Холиок (12).
Паратаксическое предложение состоит из двух коротких T-элементов, с пятью словами в одном главном предложении и семью словами в другом, в среднем шесть слов на T-элемент. Гипотактическое предложение состоит из одной T-единицы средней длины с двенадцатью словами в главном предложении и модифицирующем предложении. Короткие Т-единицы состоят из одного-восьми слов в предложении; Т-единицы средней длины содержат от девяти до двадцати слов в предложении; в то время как длинные Т-единицы содержат двадцать одно или более слов в предложении (Хант, «Грамматический» 30). Молодые писатели и менее образованные писатели, как правило, используют более короткие T-единицы, чем продвинутые писатели. Продвинутые писатели также используют некоторые короткие Т-образные единицы, но у них больше средних и длинных предложений, потому что они добавляют больше фразовых модификаторов и встраивают или присоединяют больше зависимых предложений.
Молодые писатели и менее образованные писатели, как правило, используют более короткие T-единицы, чем продвинутые писатели. Продвинутые писатели также используют некоторые короткие Т-образные единицы, но у них больше средних и длинных предложений, потому что они добавляют больше фразовых модификаторов и встраивают или присоединяют больше зависимых предложений.
Хант проанализировал среднюю длину T-блока в образцах прозы из тысячи слов, написанных детьми и взрослыми с разным уровнем образования и происхождения. Он обнаружил корреляцию между средним количеством слов в Т-единице и синтаксической зрелостью:
На протяжении школьных лет, от детского сада до выпускного, дети учатся использовать в своем письме все большее и большее количество трансформаций, объединяющих предложения, на одно главное предложение. Опытные взрослые развивают ту же тенденцию еще дальше. . . Это объясняет непосредственно наблюдаемое увеличение числа . . . слов на пункт. («Синтаксический» 9)
Он обнаружил, что взрослые, как правило, пишут более длинные Т-единицы, чем дети, потому что они создают более сложные предложения:
Писатели старшего возраста имеют более широкий репертуар синтаксических средств, которые они могут использовать, когда сталкиваются с проблемами построения предложений.
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав