Слова «ответ» морфологический и фонетический разбор
Объяснение правил деление (разбивки) слова «ответ» на слоги для переноса.
Онлайн словарь Soosle.ru поможет: фонетический и морфологический разобрать слово «ответ» по составу, правильно делить на слоги по провилам русского языка, выделить части слова, поставить ударение, укажет значение, синонимы, антонимы и сочетаемость к слову «ответ».
Содержимое:
- 1 Слоги в слове «ответ» деление на слоги
- 2 Как перенести слово «ответ»
- 3 Морфологический разбор слова «ответ»
- 4 Разбор слова «ответ» по составу
- 5 Сходные по морфемному строению слова «ответ»
- 6 Синонимы слова «ответ»
- 7 Антонимы слова «ответ»
- 8 Ударение в слове «ответ»
- 9 Фонетическая транскрипция слова «ответ»
- 10 Фонетический разбор слова «ответ» на буквы и звуки (Звуко-буквенный)
- 11 Предложения со словом «ответ»
- 12 Сочетаемость слова «ответ»
- 13 Значение слова «ответ»
- 14 Склонение слова «ответ» по подежам
- 15 Как правильно пишется слово «ответ»
- 16 Ассоциации к слову «ответ»
Слоги в слове «ответ» деление на слоги
Количество слогов: 2
По слогам: о-твет
По правилам школьной программы слово «ответ» можно поделить на слоги разными способами. Допускается вариативность, то есть все варианты правильные. Например, такой:
Допускается вариативность, то есть все варианты правильные. Например, такой:
от-вет
По программе института слоги выделяются на основе восходящей звучности:
о-твет
Ниже перечислены виды слогов и объяснено деление с учётом программы института и школ с углублённым изучением русского языка.
т примыкает к этому слогу, а не к предыдущему, так как не является сонорной (непарной звонкой согласной)
Как перенести слово «ответ»
от—вет
Морфологический разбор слова «ответ»
Часть речи:
Имя существительное
Грамматика:
часть речи: имя существительное;
одушевлённость: неодушевлённое;
род: мужской;
число: единственное;
падеж: именительный, винительный;
отвечает на вопрос: (есть) Что?, (вижу/виню) Что?
Начальная форма:
ответ
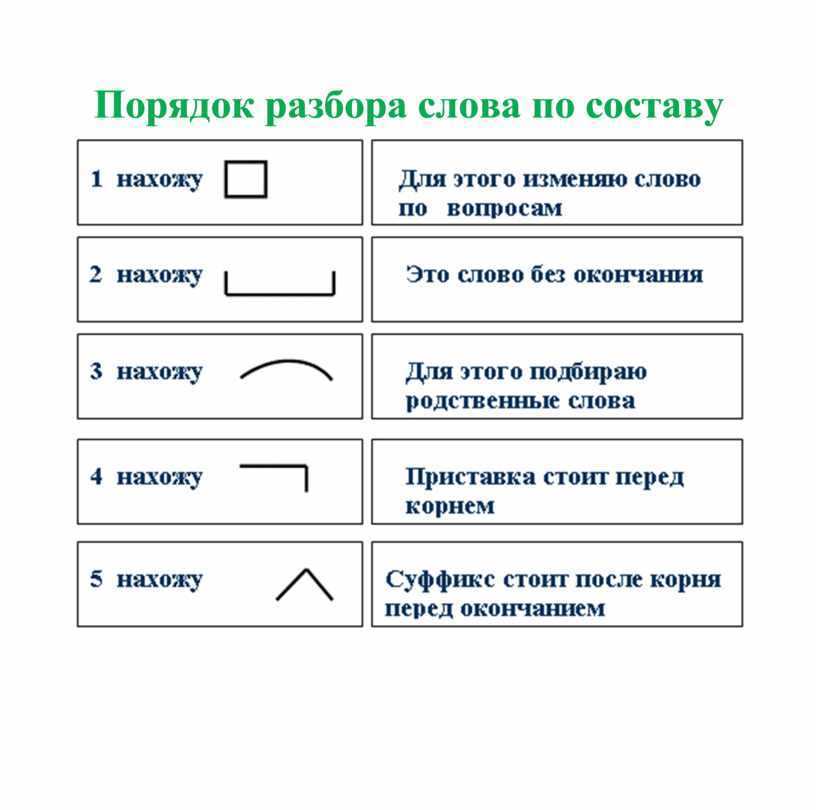
Разбор слова «ответ» по составу
| ответ | корень |
| ø | нулевое окончание |
ответ
Сходные по морфемному строению слова «ответ»
Сходные по морфемному строению слова
Синонимы слова «ответ»
1. отклик
отклик
2. отчет
3. реакция
4. рецензия
5. автоответ
6. эхо
7. рескрипт
8. реплика
9. отзыв
10. контрответ
11. отголосок
12. отзвук
13. результат
14. ответственность
15. отгадка
16. отписка
17. отповедь
18. показание
19. решение
20. согласие
21. антидот
Антонимы слова «ответ»
1. вопрос
Ударение в слове «ответ»
отве́т — ударение падает на 2-й слог
Фонетическая транскрипция слова «ответ»
[атв’`эт]
Фонетический разбор слова «ответ» на буквы и звуки (Звуко-буквенный)
| Буква | Звук | Характеристики звука | Цвет |
|---|---|---|---|
| о | [а] | гласный, безударный | о |
| т | [т] | согласный, глухой парный, твёрдый, шумный | т |
| в | [в’] | согласный, звонкий парный, мягкий | в |
| е | [`э] | гласный, ударный | е |
| т | [т] | согласный, глухой парный, твёрдый, шумный | т |
Число букв и звуков:
На основе сделанного разбора делаем вывод, что в слове 5 букв и 5 звуков.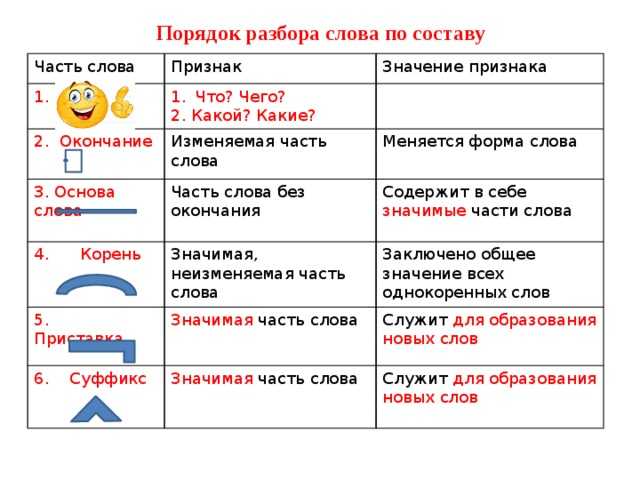
Буквы: 2 гласных буквы, 3 согласных букв.
Звуки: 2 гласных звука, 3 согласных звука.
Предложения со словом «ответ»
В конце концов я получу кое-какие ответы на вопросы.
Источник: Райчел Мид, Принцесса по крови.
Я угрюмо ждал ответа.
Источник: А. С. Шмат, Бейссел, 2011.
Не дожидаясь ответа, он прикоснулся губами к её щеке, а затем поцеловал прямо в губы.
Источник: Ксения Василькевич, Путешествие в неизвестность.
Сочетаемость слова «ответ»
1. правильный ответ
2. отрицательный ответ
3. утвердительный ответ
4. в ответ на приветствие
5. в ответ на улыбку
6. в ответ на замечание
7. в поисках ответа
8. в ожидании ответа
в ожидании ответа
9. вопрос ответа
10. ответ пришёл
11. ответ гласил
12. ответ напрашивается
13. получить ответ
14. не дожидаться ответа
15. улыбнуться в ответ
16. (полная таблица сочетаемости)
Значение слова «ответ»
ОТВЕ́Т , -а, м. 1. Вызванные вопросом или обращением слова (слово), заключающие в себе подтверждение или отрицание чего-л., сообщение о чем-л. и т. п. Положительный ответ. Дать ответ. (Малый академический словарь, МАС)
Склонение слова «ответ» по подежам
| Падеж | Вопрос | Единственное числоЕд.ч. | Множественное числоМн.ч. |
|---|---|---|---|
| ИменительныйИм. | что? | ответ | ответы |
| чего? | ответа | ответов | |
| ДательныйДат. | чему? | ответу | ответам |
ВинительныйВин. | что? | ответ | ответы |
| ТворительныйТв. | чем? | ответом | ответами |
| ПредложныйПред. | о чём? | ответе | ответах |
Как правильно пишется слово «ответ»
Правописание слова «ответ»
Орфография слова «ответ»
Правильно слово пишется: отве́т
Нумерация букв в слове
Номера букв в слове «ответ» в прямом и обратном порядке:
- 5
о
1 - 4
т
2 - 3
в
3 - 2
е
4 - 1
т
5
Ассоциации к слову «ответ»
Запрос
Вопрос
Приветствие
Ворчание
Тирада
Реплика
Расспрос
Пожатие
Кивок
Загадка
Ультиматум
Бормотание
Призыв
Молчание
Дан
Анкета
Оракул
Хохот
Замечание
Однозначный
Исчерпывающий
Отрицательный
Удовлетворительный
Риторический
Вопросительный
Адекватный
Невысказанный
Заданный
Положительный
Правдивый
Нечленораздельный
Немедленный
Невнятный
Очевидный
Категоричный
Остроумный
Прямой
Неразборчивый
Правильный
Пространный
Гробовой
Одобрительный
Окончательный
Дружный
Двусмысленный
Красноречивый
Логичный
Вежливый
Недвусмысленный
Ехидный
Неправильный
Неубедительный
Неразрешимый
Дожидаться
Уклониться
Промычать
Напрашиваться
Дождаться
Уклоняться
Последовать
Удовлетвориться
Задавать
Медлить
Прозвучать
Проорать
Помедлить
Помахать
Удовлетворить
Прокричать
Задать
Сформулировать
Замешкаться
Обдумывать
Отсалютовать
Подыскивать
Вопрошать
Получить
Заготовить
Улыбнуться
Кивать
Призвать
Потребовать
Задаваться
Расслышать
Прошелестеть
Услышать
Ожидать
Выслушивать
Снизойти
Пробурчать
Утруждать
Воздержаться
Обескуражить
Постучаться
Буркнуть
Незамедлительно
Невнятно
Утвердительно
Заранее
Морфологический разбор слова «ответ»
Часть речи: Существительное
Начальная форма слова: «ОТВЕТ»
| Слово | Морфологические признаки |
|---|---|
| ОТВЕТ |
|
| ОТВЕТ |
|
Все формы слова ОТВЕТ
ОТВЕТ, ОТВЕТА, ОТВЕТУ, ОТВЕТОМ, ОТВЕТЕ, ОТВЕТЫ, ОТВЕТОВ, ОТВЕТАМ, ОТВЕТАМИ, ОТВЕТАХ
Разбор слова по составу ответ
| Основа слова | ответ |
|---|---|
| Корень | ответ |
| Нулевое окончание |
Разобрать другие слова
Разбор слова в тексте или предложении
Если вы хотите разобрать слово «ОТВЕТ» в конкретном предложении или тексте, то лучше использовать
морфологический разбор текста.
Найти синонимы к слову «ответ»
Примеры предложений со словом «ответ»
1
Твой Хозяин ищет ответ на этот вопрос, но он не сможет найти ответ на него, потому что он не может знать ответ на него.
Учение По, Виталий Александрович Кириллов, 2017г.
2
Заметьте, как это выходит: «Что у вас?» Ответ слышал один Гарвей, и ответ был: «Бегущая по волнам».
Бегущая по волнам, Александр Грин, 1926г.
3
Кровь же народная, за нее ответ надо дать – да какой же ты ответ дашь, если ты не чист?
Сашка Жегулев, Леонид Андреев, 1911г.
4
И далее пошел разговор, вопрос – ответ, вопрос – ответ.
Записки нетрезвого человека, Александр Володин, 1967, 1999г.
5
Фрэнк пробурчал что-то в ответ, и тренер Боб сказал: – Но нельзя же схватить девчонку за титьку и думать, что не получишь в ответ по яйцам, правда?
Отель «Нью-Гэмпшир», Джон Ирвинг, 1981г.
Найти еще примеры предложений со словом ОТВЕТ
Композиция функций — определение, предметная область, составная функция
Композиция функций — это процесс объединения двух или более функций в одну функцию. Функция представляет некоторую работу. Возьмем приготовление хлеба. Пусть x — мука, кухонный комбайн выполняет функцию приготовления теста с использованием муки (и пусть эта функция равна g(x)) и пусть печь выполняет функцию приготовления хлеба (и пусть эта функция равна f (Икс)). Для приготовления хлеба выход g(x) нужно поместить в функцию f(x) (т. е. приготовленное тесто нужно поставить в печь). Результат обозначается f(g(x)) и представляет собой композицию функций f(x) и g(x).
Для приготовления хлеба выход g(x) нужно поместить в функцию f(x) (т. е. приготовленное тесто нужно поставить в печь). Результат обозначается f(g(x)) и представляет собой композицию функций f(x) и g(x).
Давайте посмотрим, что такое композиция функций в математике вместе с ее вычислением. Давайте также посмотрим, как найти его домен и диапазон.
| 1. | Что такое композиция функций? |
| 2. | Символ композиции функций |
| 3. | Как решать составные функции? |
| 4. | Нахождение составной функции на графике |
| 5. | Поиск составной функции из таблицы |
| 6. | Домен составных функций |
| 7. | Диапазон составных функций |
| 8. | Часто задаваемые вопросы о составе функций |
Что такое композиция функций?
Состав функций f(x) и g(x), где g(x) действует первым, представляется как f(g(x)) или (f ∘ g)(x). Он объединяет две или более функций, чтобы получить другую функцию. В составе функций выход одной функции, находящейся внутри скобок, становится входом внешней функции. т. е.
Он объединяет две или более функций, чтобы получить другую функцию. В составе функций выход одной функции, находящейся внутри скобок, становится входом внешней функции. т. е.
- В f(g(x)), g(x) является входом f(x).
- В g(f(x)), f(x) является входом g(x).
Мы можем понять это, используя следующую цифру:
т. е. чтобы найти f(g(x)) (которое читается как «f от g от x»), мы должны сначала найти g(x), а затем подставить результат в f(x).
Символ композиции функций
Символ композиции функций ∘. Его также можно показать без использования этого символа, но с помощью скобок. т. е.
- (f ∘ g)(x) = f(g(x)) и читается как «f of g of x». Здесь g — внутренняя функция, а f — внешняя функция.
- (g ∘ f)(x) = g(f(x)) и читается как «g of f of x». Здесь f — внутренняя функция, а g — внешняя функция.
Как решать составные функции?
Используя BODMAS, мы всегда сначала упрощаем то, что находится в скобках. Таким образом, чтобы найти f (g (x)), сначала необходимо вычислить g (x) и подставить его в f (x). Точно так же, чтобы найти g (f (x)), сначала нужно вычислить f (x) и подставить его в g (x). т. е. при нахождении составных функций порядок имеет значение. Это означает, что f(g(x)) НЕ может быть равно g(f(x)). Для любых двух функций f(x) и g(x) составную функцию f(g(a)) находим, используя следующие шаги:
Таким образом, чтобы найти f (g (x)), сначала необходимо вычислить g (x) и подставить его в f (x). Точно так же, чтобы найти g (f (x)), сначала нужно вычислить f (x) и подставить его в g (x). т. е. при нахождении составных функций порядок имеет значение. Это означает, что f(g(x)) НЕ может быть равно g(f(x)). Для любых двух функций f(x) и g(x) составную функцию f(g(a)) находим, используя следующие шаги:
- Найдите g(a), подставив x = a в g(x).
- Найдите f(g(a)) подставив x = g(a) в f(x).
Мы можем понять эти шаги, используя пример ниже. Здесь мы находим f(g(-1)) при f(x) = x 2 — 2x и g(x) = x — 5.
Мы можем обобщить этот процесс с помощью простых математических вычислений, как показано ниже. :
f(g(-1)) = f(-1-5)
= f(-6)
= (-6) 2 — 2 (-6)
= 36 + 12
= 48
Поиск составной функции по графику
Чтобы найти составную функцию двух функций (которые не определены алгебраически), показанную графически, мы должны вспомнить, что если (x, y) — точка на функции f(x), то f(x) = y. Используя это, найти f(g(a)) (т.е. f(g(x)) при x = a):
Используя это, найти f(g(a)) (т.е. f(g(x)) при x = a):
- Сначала найти g(a) (т.е. координату y на графике g (x), что соответствует x = a)
- Найти f(g(a)) (т.е. координату y на графике f(x), которая соответствует g(a))
Пример: Найдите f(g(5)) на следующем графике.
Решение:
f(g(5)) = f(3) (Поскольку g(5) = 3, поскольку (5, 3) находится на g(x))
= 2 (Поскольку f(3) = 2, так как (3, 2) принадлежит f(x))
Следовательно, f(g(5)) = 2.
Поиск составной функции из таблицы
Мы уже видели, как найти составную функцию, если задан график функций. Иногда точки на графике функций изображают таблицами. Таким образом, мы применяем ту же процедуру, что описана в предыдущем разделе.
Пример: Найдите g(f(-3)) с помощью следующих таблиц.
| х | ф(х) |
|---|---|
| -1 | -4 |
| -2 | -3 |
| -3 | -2 |
| -4 | -1 |
| x | г(х) |
|---|---|
| -4 | 1 |
| -3 | 0 |
| -2 | -1 |
| -1 | -2 |
Решение:
Из таблицы f(x), f(-3) = -2.
Итак, g(f(-3))=g(-2).
Из таблицы g(x), g(-2) = -1.
Таким образом, g(f(-3)) = -1.
Домен составных функций
В общем случае, если g : X → Y и f : Y → Z, то f ∘ g : X → Z, т. е. областью определения f ∘ g является X, а область значений — Z. Но когда функции определены алгебраически, вот шаги, чтобы найти область определения составной функции f (g (x)).
- Найти область определения внутренней функции g(x) (пусть это будет A)
- Найдите область определения функции, полученной путем нахождения f(g(x)) (пусть это будет B)
- Найдите пересечение A и B и A ∩ B дает область определения f(g(x))
Пример: Найдите область определения f(g(x)) при f(x) = 1/(x+2) и g(x) = 1/(x+3).
Решение:
В f(g(x)) внутренней функцией является g(x), а ее областью определения является A = {x | х ≠ -3}.
Теперь вычислим f(g(x)).
\(\begin{выровнено}
f(g(x)) &=f\left(\frac{1}{x+3}\right) \\
&=\frac{1}{\frac{1}{x+3}+2} \\
&=\frac{1}{\frac{1+2 x+6}{x+3}} \\
&=\фракция{х+3}{2х+7}
\end{aligned}\)
Его домен B = {x : x ≠ -7/2}
Таким образом, домен f(g(x)) равен A ∩ B = {x : x ≠ — 3 и х ≠ -7/2}.
В интервальной записи это (-∞, -7/2) U (-7/2, -3) U (-3, ∞).
Диапазон составных функций
Диапазон составной функции рассчитывается так же, как диапазон любой другой функции. Это не зависит от внутренних или внешних функций. Вычислим диапазон f(g(x)), показанный в последнем примере. Мы получили f(g(x)) = \(\frac{x+3}{2 x+7}\). Предположим, что y = \(\frac{x+3}{2 x+7}\). Это рациональная функция. Следовательно, мы решаем это для x и устанавливаем знаменатель не равным нулю, чтобы найти диапазон.
(2x + 7) y = x + 3
2xy + 7y = x + 3
2xy — x = 3 — 7y
x (2y — 1) = 3 — 7y
x = (3 — 7y) ) / (2y — 1)
Для диапазона 2y — 1 ≠ 0, что дает y ≠ 1/2.
Следовательно, диапазон = {y : y ≠ 1/2}.
☛ Связанные темы:
- Производные сложных функций
- Алгебра функций
- Алгебраическая функция
Часто задаваемые вопросы о составе функций
Что такое определение составной функции?
Составная функция из двух функций объединяет данные две функции в заданном порядке. т. е. для любых заданных двух функций f(x) и g(x) может быть 4 составные функции:
т. е. для любых заданных двух функций f(x) и g(x) может быть 4 составные функции:
- f(g(x)) которая заменяет g(x) в f(x)
- g(f(x)) который заменяет f(x) на g(x)
- f(f(x)), которая заменяет f(x) на себя
- g(g(x)), который подставляет g(x) в себя
Как найти состав функций?
Чтобы вычислить составную функцию f(g(x)) при некотором x = a, сначала вычислите g(a), подставив x = a в функцию g(x). Затем подставьте g(a) в функцию f(x), подставив x = g(a). Точно так же мы можем вычислить и g(f(a)).
Важен ли порядок в составных функциях?
Да, в составных функциях порядок действительно важен. т. е. f (g (x)) ≠ g (f (x)) (т. е. они могут не быть равными все время). Но иногда они могут быть равны.
Как найти область определения составной функции?
Чтобы найти область определения составной функции, найдите область определения внутренней функции и область определения результирующей функции. Возьмите пересечение обоих доменов.
Как найти диапазон составной функции?
Диапазон составной функции не зависит от внутренних или внешних функций. Его диапазон вычисляется так же, как мы вычисляем диапазон любой другой функции.
Как найти состав функций из графиков?
Если даны графики двух функций f(x) и g(x), то для нахождения g(f(a)):
- Найти f(a) (по точке (a, f(a)) на f(x))
- Найти g(f(a)) (используя точку (f(a), g(f(a)) ) на графике g(x))
Как разбить состав функций?
Мы можем разбить составную функцию на две функции с помощью некоторого наблюдения. Не забудьте перепроверить свой ответ после взлома. Если f(g(x)) = sin(x + 1), то можно сказать, что g(x) = x + 1 и f(x) = sin x. Давайте перепроверим ответ.
f(g(x)) = f (x + 1) = sin (x + 1) и, следовательно, наш ответ правильный.
Ключевые слова | Текущие студенты UNSW
Что такое слова-подсказки?
На экзаменах, включающих сочинение или вопросы с кратким ответом, большинство вопросов содержат слово-подсказку.
Ключевые слова — это слова, которые лектор использует, чтобы указать угол, под которым вы отвечаете на вопрос. Ключевые слова говорят вам, что именно нужно делать в сочинении, поэтому они чрезвычайно важны на экзаменах по сочинению.
Поиск ключевых слов в экзаменационных вопросах
Экзамен подобен умственной игре, в которой лекторы говорят вам, чего они хотят. Чтобы успешно играть в игру, вам нужно знать точную формулировку вопросов и точное значение слов-подсказок. Как только вы нашли слова-подсказки и поняли, что они означают, вы сможете правильно ответить на вопрос.
Экзаменационный вопрос: Сравните цели либерального и социалистического феминизма
Ключевое слово: Ключевое слово в этом вопросе — сравните .
Если бы вам задавали вопрос «Оценить цели…», то требовался бы совершенно другой ответ.
Ниже приведен список наиболее распространенных слов-подсказок и их значений в экзаменационных вопросах, которые помогут вам подготовиться к экзаменам сочинения. Поскольку список длинный, рекомендуется прочитать прошлые экзаменационные работы, чтобы ознакомиться с наиболее часто используемыми ключевыми словами в вашей дисциплине. Во многих школах в библиотеке есть прошлые экзаменационные работы.
Поскольку список длинный, рекомендуется прочитать прошлые экзаменационные работы, чтобы ознакомиться с наиболее часто используемыми ключевыми словами в вашей дисциплине. Во многих школах в библиотеке есть прошлые экзаменационные работы.
Таблица слов-подсказок к экзаменам
| Ключевое слово | Значение |
| Анализ | Чтобы найти основные идеи, как они связаны и почему они важны. |
| Комментарий к | Обсуждать, критиковать или объяснять его значение настолько полно, насколько это возможно. |
| Сравнить | Чтобы показать как различия, так и сходства. |
| Контраст | Сравнить, показав различия. |
| Критиковать | Чтобы дать свое суждение или обоснованное мнение о чем-либо, показывая его хорошие и плохие стороны. Однако атаковать не обязательно. Однако атаковать не обязательно. |
| Определить | Придать формальное значение, отделив его от родственных терминов. Часто это вопрос запоминания определения. |
| Описать | Написать подробный рассказ или словесную картину в логической последовательности или в форме рассказа. |
| Схема | Чтобы сделать график, диаграмму или рисунок. Обязательно пометьте его и при необходимости добавьте краткое пояснение. |
| Обсудить | Чтобы представить аргументы за и против точки зрения и прийти к выводу. Аргументы должны быть подкреплены соответствующими доказательствами. |
| Перечислить | В список — назовите и перечислите основные идеи одну за другой. |
| Оценка | Дать мнение, подкрепленное некоторыми экспертными мнениями, об истинности или важности концепции. Покажите преимущества и недостатки. Покажите преимущества и недостатки. |
| Проиллюстрировать | Объяснить или прояснить на конкретных примерах, сравнениях или аналогиях. |
| Переводчик | Объяснить смысл, используя примеры и личные комментарии, чтобы прояснить что-то. |
| Обоснование | Объяснить, почему вы так думаете. Обоснуйте свое утверждение или вывод. |
| Список | Для создания списка слов, предложений или комментариев; то же значение, что и перечислить. |
| Внешний вид | Подвести итоги. Он должен содержать ряд основных идей, подкрепленных второстепенными фактами. Покажите организацию идеи. |
| Доказать | Чтобы показать с помощью аргументов или логики, что что-то верно. |