занятия по английскому языку: способы запоминания новых слов и фраз

Память – вещь непредсказуемая. Человек может на всю жизнь запомнить дату Куликовской битвы, но в обед забыть, что ел на завтрак. Трудно приходиться, когда вы учитесь чему-то новому. Например, изучаете английский онлайн. Много новой информации, которую необходимо разложить по полочкам: слова, грамматика, произношение и так далее. Вроде бы материал, по которому вы занимались на онлайн — занятии по английскому языку, вы усвоили, но не можете вспомнить на следующий день. Необходимо заглядывать в тексты, словарь и список правил неоднократно. Сразу после повторения вы легко можете воспроизвести изученный материал. Через 5-7 минут это уже не так просто. Через 1-2 часа вспомнить информацию будет еще сложнее. А через месяц? А что останется в памяти через год?

 

Трудно запомнить то, чем вы не пользуетесь в повседневной жизни. Поэтому лучший способ выучить иностранный язык – это полностью погрузиться не только в процесс обучения, но и найти применение полученным знаниям. Изучение английского онлайн с носителем языка дает возможность не только практиковать разговорный навык и восприятие речь на слух, но и навсегда запомнить выученный материал. Но если вы только начинаете изучать английский, то вот несколько эффективных способов тренировать память.

1. Использование стикеров и карточек. Вас повсюду окружают предметы, поэтому постарайтесь запомнить их значение на английском. Таким образом вы пополните свой лексический запас бытовыми терминами. Если этот способ вам кажется примитивным, то используйте приложение QUIZLET на смартфоне. Составляйте собственные карточки со словами, которые встречались вам на онлайн — занятии по английскому языку. В QUIZLET есть множество упражнений, которые подойдут именно вам.
    
2. Составление простых фраз с новыми словами. Новое слово на иностранном языке, даже если вы его хорошо запомнили, само по себе бесполезно.
   Его нужно использовать как инструмент коммуникации. Попробуйте объяснить его значение хотя бы на родном языке, а потом запишите несколько простых предложений на английском. Постепенно усложняйте себе задачу: составляйте больше предложений, делайте их длиннее.
    
3. Обучение с помощью картинок и ассоциаций. Лучше один раз увидеть, чем сто раз услышать. Наш мозг лучше воспринимает новую информацию визуально, поэтому на онлайн — занятии по английскому языку часто применяют методику запоминания новых слов по картинкам.
    
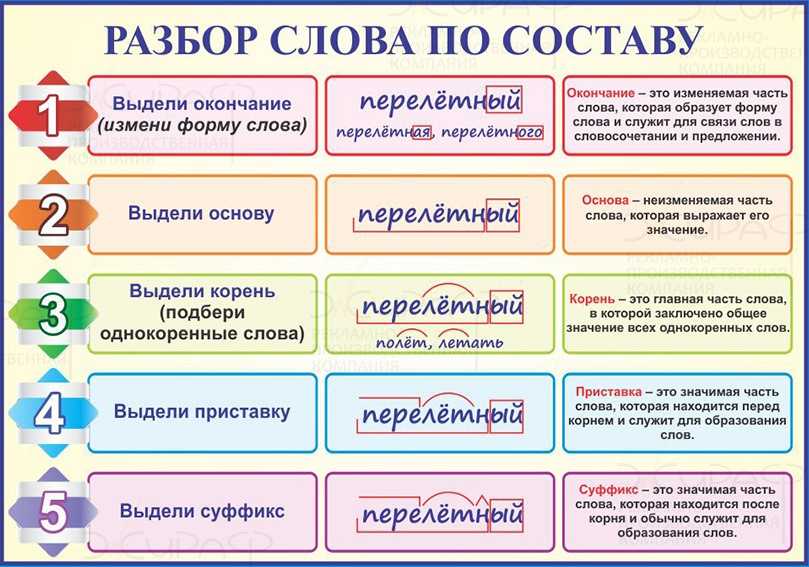
4. Разбор слов по составу. В английском языке часто одно слово состоит из нескольких. Например, вы навсегда запомните слово «waterfall» (водопад), если разобьете его на слова «water» (вода) и «fall» (падать). Также старайтесь запомнить распространенные суффиксы (-able, -ly, -ent, -tion, -ive) и приставки (un-, dis-, con-, micro-). Благодаря этому вы сможете догадаться о значении новых для вас слов.

Чтобы любое дело было успешно доведено до конца, необходимо, чтобы под рукой были все средства. Преподаватели на онлайн — занятиях по английскому языку помогают каждому ученику изучать любую тему с уверенностью и интересом. Уроки разработаны по современной коммуникативной методике, которая позволяет облегчить запоминание материала. Изучение английского онлайн с носителем языка происходит поэтапно, начинается с простых тем. Это помогает мотивировать учеников продолжать работу, поверить в то, что выучить иностранный язык им по силам. Постепенно изучение английского онлайн с носителем языка усложняется. Преподаватель дает не только материал, но и хорошие инструменты в изучении нового языка. К тому же, часто изучение английского онлайн с носителем языка проходит в игровом формате с дополнительными практическими упражнениями, которые помогают воспринимать речь на слух и избавиться от акцента.

Поділися з друзями

Написание интерпретатора с нуля

Некоторые говорят, что «все сводится к единицам и нулям» — но действительно ли мы понимаем, как наши программы преобразуются в эти биты?

И компиляторы, и интерпретаторы берут необработанную строку, представляющую программу, анализируют ее и анализируют. Хотя интерпретаторы являются более простыми из двух, написание даже очень простого интерпретатора (который выполняет только сложение и умножение) будет поучительным. Мы сосредоточимся на том, что общего у компиляторов и интерпретаторов: лексическом анализе и разборе входных данных.

Что нужно и что нельзя делать при написании собственного интерпретатора

Читатели могут задаться вопросом Что не так с регулярным выражением? Регулярные выражения — это мощное средство, но грамматика исходного кода недостаточно проста для их анализа. Ни один из них не является доменно-ориентированным языком (DSL), и клиенту может потребоваться собственный DSL, например, для выражений авторизации. Но даже не применяя этот навык напрямую, написание интерпретатора значительно упрощает оценку усилий, стоящих за многими языками программирования, форматами файлов и DSL.

Правильное написание синтаксических анализаторов вручную может быть сложной задачей со всеми задействованными пограничными случаями. Вот почему существуют популярные инструменты, такие как ANTLR, которые могут генерировать синтаксические анализаторы для многих популярных языков программирования. Существуют также библиотеки, называемые комбинаторами синтаксических анализаторов , которые позволяют разработчикам писать синтаксические анализаторы непосредственно на предпочитаемых ими языках программирования. Примеры включают FastParse для Scala и Parsec для Python.

Мы рекомендуем читателям в профессиональном контексте использовать такие инструменты и библиотеки, чтобы не изобретать велосипед. Тем не менее, понимание проблем и возможностей написания интерпретатора с нуля поможет разработчикам более эффективно использовать такие решения.

Обзор компонентов интерпретатора

Интерпретатор — это сложная программа, поэтому она состоит из нескольких этапов:

1. лексер — это часть интерпретатора, которая преобразует последовательность символов (обычный текст) в последовательность символов. жетоны.
2. Анализатор , в свою очередь, берет последовательность токенов и создает абстрактное синтаксическое дерево (AST) языка. Правила, по которым работает синтаксический анализатор, обычно определяются формальной грамматикой.
3. Интерпретатор — это программа, которая интерпретирует AST исходного кода программы на лету (без предварительной компиляции).

Здесь мы не будем создавать специальный интегрированный интерпретатор. Вместо этого мы рассмотрим каждую из этих частей и их общие проблемы на отдельных примерах. В итоге код пользователя будет выглядеть так:

 val input="2*7+5"
токены val = Lexer(input).lex()
val ast = Parser(токены).parse()
val res = Интерпретатор(ast).interpret()
println(s"Результат: $res")
 

После трех этапов мы ожидаем, что этот код вычислит окончательное значение и напечатает Результат: 19 . В этом руководстве используется Scala, потому что он:

• Очень лаконичный, умещает большой объем кода на одном экране.
• Ориентирован на выражения, без необходимости использования неинициализированных/нулевых переменных.
• Надежный тип, с мощной библиотекой коллекций, перечислениями и классами case.

В частности, код здесь написан в синтаксисе необязательных фигурных скобок Scala3 (подобный Python синтаксис на основе отступов). Но

ни один из подходов не является специфичным для Scala , а Scala похожа на многие другие языки: читатели найдут простым преобразование этих примеров кода на другие языки. За исключением этого, примеры можно запускать онлайн с помощью Scastie.

Наконец, секции Lexer, Parser и Interpreter содержат различных примера грамматик . Как показано в соответствующем репозитории GitHub, зависимости в более поздних примерах немного меняются для реализации этих грамматик, но общие концепции остаются прежними.

Компонент интерпретатора 1: Написание лексера

Допустим, мы хотим лексировать эту строку: "123 + 45 true * false1" . Он содержит различные типы токенов:

• Целочисленные литералы
• А + оператор
• А * оператор
• A истинный буквальный
• Идентификатор,
  false1

В этом примере пробелы между токенами будут пропущены.

На данном этапе выражения не обязательно должны иметь смысл; лексер просто преобразует входную строку в список токенов. (Работа по «осмыслению токенов» возложена на синтаксический анализатор.)

Мы будем использовать этот код для представления токена:

 case class Token(
  tpe: Token.Type,
  текст: строка,
  startPos: Int
)
Токен объекта:
  Тип перечисления:
    случай Число
    чехол Плюс
    чехол раз
    Идентификатор случая
    случай Истинно
    случай Ложь
    случай EOF
 

Каждый токен имеет тип, текстовое представление и позицию в исходном вводе. Позиция может помочь конечным пользователям лексера с отладкой.

Маркер EOF — это специальный маркер, который отмечает конец ввода. Его нет в исходном тексте; мы используем его только для упрощения этапа парсера.

Это будет вывод нашего лексера:

 Ввод лексинга:
123 + 45 правда * ложь1
Токены:
Список(
  Токен (tpe = число, текст = "123", tokenStartPos = 0),
  Токен (tpe = Плюс, текст = "+", tokenStartPos = 4),
  Токен (tpe = число, текст = "45", tokenStartPos = 6),
  Token(tpe = True, text = "true", tokenStartPos = 9),
  Токен (tpe = раз, текст = "*", tokenStartPos = 14),
  Токен (tpe = идентификатор, текст = "false1", tokenStartPos = 16),
  Token(tpe = EOF, text = "", tokenStartPos = 22)
)
 

Давайте рассмотрим реализацию:

 class Lexer(input: String):
  def lex(): Список[Токен] =
    val tokens = mutable.ArrayBuffer.empty[Token]
    переменная текущая позиция = 0
    в то время как currentPos < input.length делать
      val tokenStartPos = currentPos
      val lookahead = input (currentPos)
      если lookahead.isWhitespace то
        currentPos += 1 // игнорировать пробелы
      иначе, если смотреть вперед == '+' тогда
        текущийПос += 1
        tokens += Token(Type.  Plus, lookahead.toString, tokenStartPos)
      иначе, если смотреть вперед == '*' тогда
        текущийПос += 1
        tokens += Token(Type.Times, lookahead.toString, tokenStartPos)
      иначе если lookahead.isDigit тогда
        переменный текст = ""
        в то время как currentPos < input.length && input(currentPos).isDigit do
          текст += ввод (currentPos)
          текущийПос += 1
        tokens += Token(Type.Num, text, tokenStartPos)
      else if lookahead.isLetter then // сначала должна быть буква
        переменный текст = ""
        в то время как currentPos < input.length && input(currentPos).isLetterOrDigit do
          текст += ввод (currentPos)
          текущийПос += 1
        val tpe = совпадение текста
          case "true" => Type.True // специальные регистровые литералы
          case "false" =>
  Type.False
          case _ => Type.Identifier
        tokens += Token(tpe, text, tokenStartPos)
      еще
        error(s"Неизвестный символ $lookahead в позиции $currentPos")
    tokens += Token(Type. EOF, "", currentPos) // специальный маркер конца
    tokens.toList
 

Мы начинаем с пустого списка токенов, затем просматриваем строку и добавляем токены по мере их поступления.

Мы используем упреждающий символ, чтобы определить тип следующего токена . Обратите внимание, что опережающий символ не всегда является самым дальним исследуемым символом. Основываясь на предварительном просмотре, мы знаем, как выглядит токен, и используем currentPos для сканирования всех ожидаемых символов в текущем токене, а затем добавляем токен в список:

Если опережение содержит пробелы, мы пропускаем его. Однобуквенные токены тривиальны; мы добавляем их и увеличиваем индекс. Для целых чисел нам нужно позаботиться только об индексе.

Теперь мы подошли к кое-чему немного сложному: идентификаторы против литералов. Правило состоит в том, что мы берем максимально длинное совпадение и проверяем, является ли оно литералом; если нет, то это идентификатор.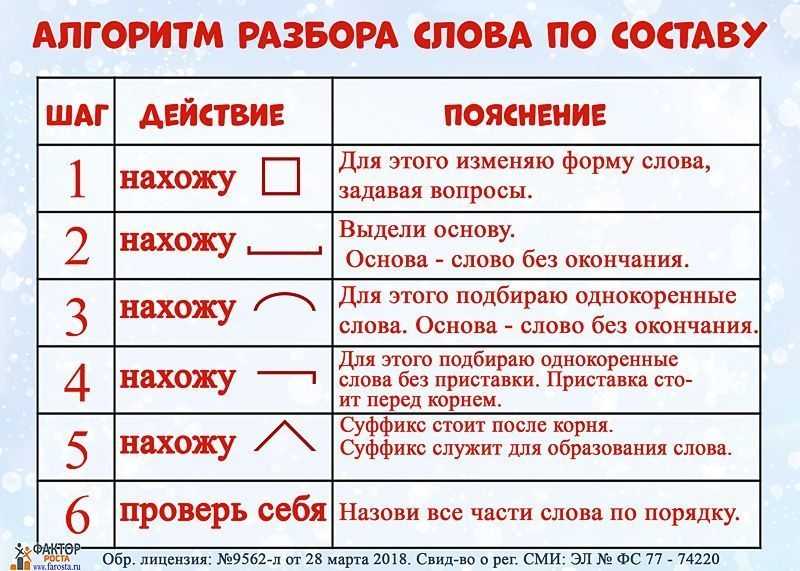

Будьте осторожны при работе с такими операторами, как < и <= . Там вы должны посмотреть вперед еще один символ и посмотреть, если это = , прежде чем сделать вывод, что это оператор <= . В противном случае это просто < .

После этого наш лексер создал список токенов.

Компонент интерпретатора 2: Написание синтаксического анализатора

Мы должны дать некоторую структуру нашим токенам — мы мало что можем сделать со списком. Например, нам нужно знать:

Какие выражения являются вложенными? Какие операторы применяются в каком порядке? Какие правила области применения применяются, если таковые имеются?

Древовидная структура поддерживает вложенность и порядок. Но сначала мы должны определить некоторые правила построения деревьев. Мы хотели бы, чтобы наш синтаксический анализатор был однозначным — всегда возвращал одну и ту же структуру для данного ввода.

Обратите внимание, что следующий синтаксический анализатор не использует предыдущий пример лексера . Это для добавления чисел, поэтому его грамматика имеет только две лексемы, '+' и NUM :

 expr -> expr '+' expr
выражение -> ЧИСЛО
 

Эквивалент с использованием вертикальной черты ( | ) как символ «или», как и в регулярных выражениях:

 expr -> expr '+' expr | ЧИСЛО
 

В любом случае у нас есть два правила: одно говорит, что мы можем суммировать два expr s, а другое говорит, что expr может быть токеном NUM , что здесь будет означать неотрицательное целое число.

Правила обычно задаются формальной грамматикой . Формальная грамматика состоит из: Сами правила, как показано выше Начальное правило (первое указанное правило согласно соглашению) Два типа символов для определения правил: Терминалы: «буквы» (и другие символы) нашего языка — несократимые символы, из которых состоят токены.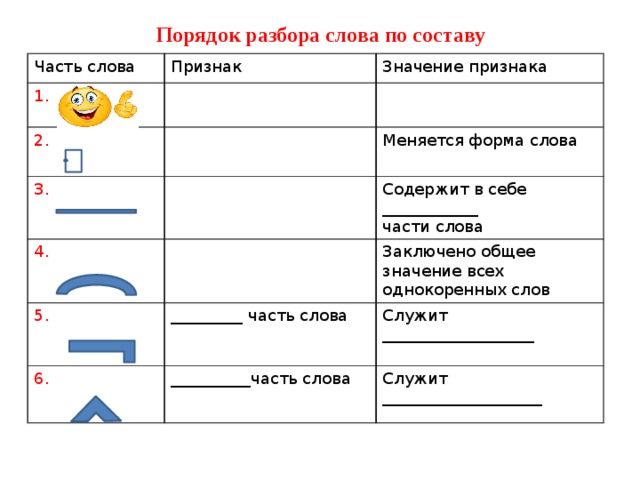 Нетерминалы: промежуточные конструкции, используемые для синтаксического анализа (т. е. символы, которые можно заменить)

Слева от правила может находиться только нетерминал; правая часть может иметь как терминалы, так и нетерминалы. В приведенном выше примере терминалами являются '+' и NUM , а единственным нетерминалом является expr . Для более широкого примера, в языке Java у нас есть терминалы, такие как 'true' , '+' , Identifier и '[' , и нетерминалы, такие как BlockStatements , ClassBody 4, и

2 MethodOrFieldDecl .

Есть много способов реализовать этот синтаксический анализатор. Здесь мы будем использовать метод разбора «рекурсивный спуск». Это самый распространенный тип, потому что его проще всего понять и реализовать.

Анализатор рекурсивного спуска использует одну функцию для каждого нетерминала в грамматике.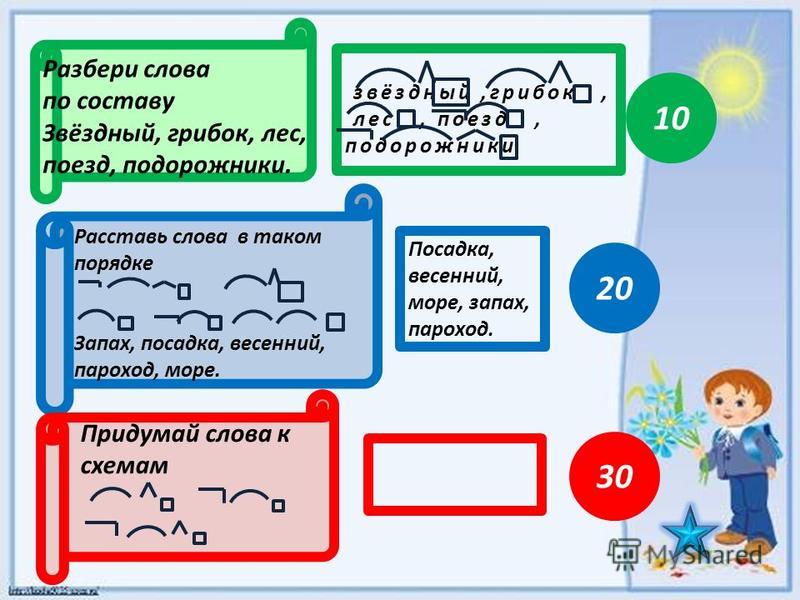 Он начинается с начального правила и спускается оттуда (отсюда «спуск»), выясняя, какое правило применить в каждой функции. «Рекурсивная» часть жизненно важна, потому что мы можем рекурсивно вкладывать нетерминалы! Регулярные выражения не могут этого сделать: они даже не могут обрабатывать сбалансированные скобки. Поэтому нам нужен более мощный инструмент.

Парсер для первого правила будет выглядеть примерно так (полный код):

 def expr() =
  выражение()
  есть('+')
  выражение()
 

Функция eat() проверяет, соответствует ли предпросмотр ожидаемому токену, а затем перемещает упреждающий индекс. К сожалению, это пока не сработает, потому что нам нужно исправить некоторые проблемы с нашей грамматикой.

Неоднозначность грамматики

Первая проблема — неоднозначность нашей грамматики, которая может быть незаметна на первый взгляд:

 выражение -> выражение '+' выражение | ЧИСЛО
 

Учитывая ввод 1 + 2 + 3 , наш синтаксический анализатор может сначала вычислить либо левое выражение , либо правое выражение в результирующем AST:

Левосторонние и правосторонние AST.

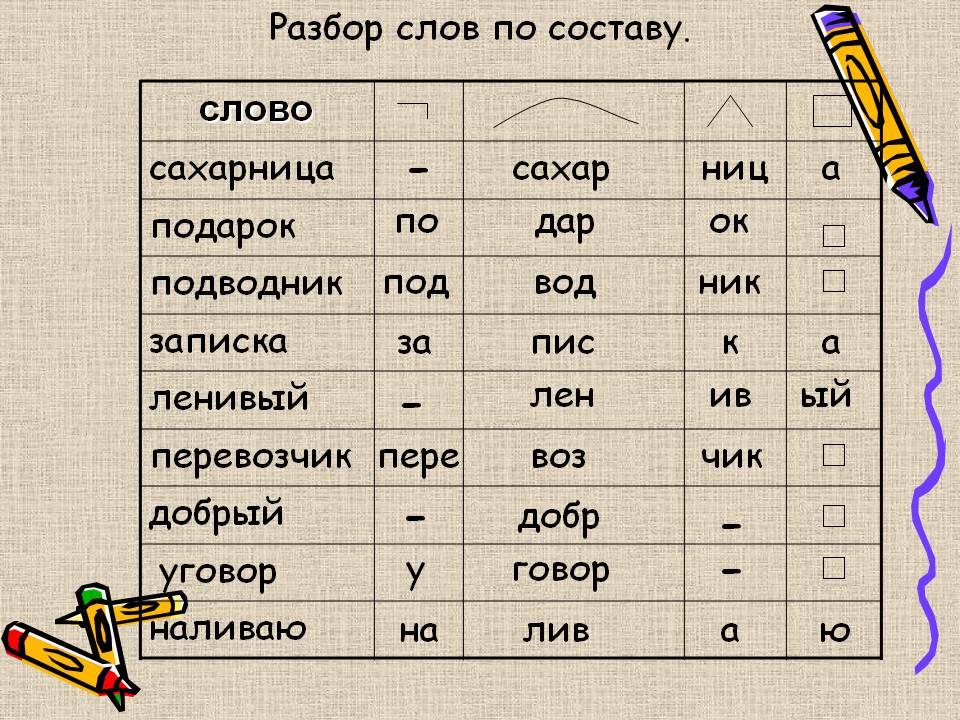
Вот почему нам нужно ввести некоторую асимметрию :

 expr -> expr '+' NUM | ЧИСЛО
 

Набор выражений, которые мы можем представить с помощью этой грамматики, не изменился со времени ее первой версии. Только сейчас однозначно : Анализатор всегда идет влево. Как раз то, что нам было нужно!

Это делает нашу операцию + левой ассоциативной , но это станет очевидным, когда мы перейдем к разделу Интерпретатор.

Лево-рекурсивные правила

К сожалению, приведенное выше исправление не решает другую нашу проблему, левую рекурсию:

 def expr() =
  выражение()
  есть('+')
  есть(ЧИСЛО)
 

У нас есть бесконечная рекурсия здесь. Если бы мы вошли в эту функцию, то в конечном итоге получили бы ошибку переполнения стека. Но теория разбора может помочь!

Предположим, у нас есть такая грамматика, где альфа может быть любой последовательностью терминалов и нетерминалов:

 A -> A альфа | Б
 

Мы можем переписать эту грамматику как:

 A -> B A'
А' -> альфа А' | эпсилон
 

Здесь эпсилон — пустая строка — ничего, нет токена.

Возьмем текущую версию нашей грамматики:

 expr -> expr '+' NUM | ЧИСЛО
 

Следуя описанному выше методу перезаписи правил синтаксического анализа с alpha является нашим '+' токеном NUM , наша грамматика становится:

 expr -> NUM exprOpt
exprOpt -> '+' ЧИСЛО exprOpt | эпсилон
 

Теперь с грамматикой все в порядке, и мы можем разобрать ее с помощью анализатора рекурсивного спуска. Давайте посмотрим, как такой синтаксический анализатор будет искать эту последнюю итерацию нашей грамматики:

 class Parser(allTokens: List[Token]):
  импортировать Token.Type
  
  частные токены var = allTokens
  частный var lookahead = tokens.head
  
  деф синтаксический анализ(): Единица измерения =
    выражение()
    если lookahead.tpe != Type.EOF, то
      error(s"Неизвестный токен '${lookahead.text}' в позиции ${lookahead.tokenStartPos}")
  частное выражение выражения(): Unit =
    есть(Тип.Число)
    exprOpt()
  
  частная защита exprOpt(): Unit =
    если lookahead. tpe == Type.Plus, то
      есть(Тип.Плюс)
      есть(Тип.Число)
      exprOpt()
    // иначе: конец рекурсии, эпсилон
  
  частное определение (tpe: Type): Unit =
    если lookahead.tpe != tpe, то
      error(s"Ожидается: $tpe, получено: ${lookahead.tpe} в позиции ${lookahead.startPos}")
    жетоны = жетоны.хвост
    просмотр вперед = tokens.head
 

Здесь мы используем токен EOF , чтобы упростить наш синтаксический анализатор. Мы всегда уверены, что в нашем списке есть хотя бы один токен, поэтому нам не нужно обрабатывать частный случай пустого списка.

Кроме того, если мы переключимся на потоковый лексер, у нас будет не список в памяти, а итератор, поэтому нам нужен маркер, чтобы знать, когда мы подошли к концу ввода. Когда мы подойдем к концу, токен EOF должен быть последним оставшимся токеном.

Просматривая код, мы видим, что выражение может быть просто числом. Если ничего не осталось, следующий жетон не будет Плюс , чтобы мы прекратили парсинг. Последним токеном будет EOF , и мы закончим.

Если во входной строке больше токенов, то они должны выглядеть как + 123 . Вот где рекурсия по exprOpt() срабатывает!

Генерация AST

Теперь, когда мы успешно проанализировали наше выражение, трудно что-либо сделать с ним как есть. Мы могли бы поместить несколько обратных вызовов в наш парсер, но это было бы очень громоздко и нечитаемо. Вместо этого мы вернем AST, дерево, представляющее входное выражение:

 класс случая Expr(num: Int, exprOpt: ExprOpt)
перечисление Expropt:
  case Opt(num: Int, exprOpt: ExprOpt)
  чехол Эпсилон
 

Это похоже на наши правила, использующие простые классы данных.

Теперь наш синтаксический анализатор возвращает полезную структуру данных:

 class Parser(allTokens: List[Token]):
  импортировать Token.Type
  
  частные токены var = allTokens
  частный var lookahead = tokens.head
  
  деф разбор(): Выражение =
    val res = expr()
    если lookahead. tpe != Type.EOF, то
      error(s"Неизвестный токен '${lookahead.text}' в позиции ${lookahead.tokenStartPos}")
    еще
      разрешение
  частное выражение выражения(): выражение =
    val num = есть(Тип.Число)
    Expr(num.text.toInt, exprOpt())
  
  частная защита exprOpt(): ExprOpt =
    если lookahead.tpe == Type.Plus, то
      есть(Тип.Плюс)
      val num = есть(Тип.Число)
      ExprOpt.Opt(num.text.toInt, exprOpt())
    еще
      Экспроопт.Эпсилон
 

Информацию о eat() , error() и других деталях реализации см. в соответствующем репозитории GitHub.

Упрощение правил

Наш нетерминал ExpOpt можно улучшить:

 '+' NUM expOpt | эпсилон
 

Трудно распознать шаблон, который он представляет в нашей грамматике, просто взглянув на него. Оказывается, эту рекурсию можно заменить более простой конструкцией:

 ('+' NUM)*
 

Эта конструкция просто означает '+' NUM встречается ноль или более раз.

Теперь наша полная грамматика выглядит так:

 expr -> NUM exprOpt*
exprOpt -> '+' ЧИСЛО
 

И наш AST выглядит лучше:

 case class Expr(num: Int, exprOpts: Seq[ExprOpt])
класс case ExprOpt (число: Int)
 

Полученный синтаксический анализатор такой же длины, но более простой для понимания и использования. Мы исключили Epsilon , что теперь подразумевается, если начать с пустой структуры.

Нам даже 9 не понадобилось0041 ExprOpt класс здесь. Мы могли бы просто указать case class Expr(num: Int, exprOpts: Seq[Int]) или в формате грамматики NUM ('+' NUM)* . Так почему же мы этого не сделали?

Учтите, что если бы у нас было несколько возможных операторов, таких как - или * , то у нас была бы такая грамматика:

 expr -> NUM exprOpt*
exprOpt -> [+-*] ЧИСЛО
 

В этом случае AST требуется ExpOpt для размещения типа оператора:

 case class Expr(num: Int, exprOpts: Seq[ExprOpt])
класс case ExprOpt (op: String, num: Int)
 

Обратите внимание, что синтаксис [+-*] в грамматике означает то же самое, что и в регулярных выражениях: «один из этих трех символов». Мы скоро увидим это в действии.

Компонент интерпретатора 3: Написание интерпретатора

Наш интерпретатор будет использовать наш лексер и синтаксический анализатор, чтобы получить AST нашего входного выражения, а затем оценить это AST любым удобным для нас способом. В данном случае мы имеем дело с числами и хотим вычислить их сумму.

В реализации нашего примера интерпретатора мы будем использовать эту простую грамматику:

 expr -> NUM exprOpt*
exprOpt -> [+-] ЧИСЛО
 

И этот AST:

 case class Expr(num: Int, exprOpts: Seq[ExprOpt])
класс case ExprOpt (op: Token.Type, num: Int)
 

(Мы рассмотрели, как реализовать лексер и парсер для похожих грамматик, но любой читатель, который застрял, может просмотреть реализации лексера и парсера для этой грамматики в репозитории.)

Теперь посмотрим, как написать интерпретатор для приведенной выше грамматики:

 class Interpreter(ast: Expr):
  деф интерпретировать (): Int = eval (аст)
  частная оценка (выражение: выражение): Int =
    var tmp = expr. num
    expr.exprOpts.foreach { exprOpt =>
      если exprOpt.op == Token.Type.Plus
      затем tmp += exprOpt.num
      иначе tmp -= exprOpt.num
    }
    температура
 

Если мы разобрали наши входные данные в AST без ошибок, мы уверены, что у нас всегда будет хотя бы одна ЧИСЛО . Затем мы берем необязательные числа и добавляем их к нашему результату (или вычитаем из него).

Замечание с самого начала о левой ассоциативности + теперь ясно: мы начинаем с крайнего левого числа и добавляем другие, слева направо. Это может показаться неважным для сложения, но рассмотрим вычитание: выражение 5 - 2 - 1 оценивается как (5 - 2) - 1 = 3 - 1 = 2 , а не как 5 - (2 - 1) = 5 - 1 = 4 !

Но если мы хотим выйти за рамки интерпретации операторов плюс и минус, нужно определить еще одно правило.

Приоритет

Мы знаем, как анализировать простое выражение, такое как 1 + 2 + 3 , но когда дело доходит до 2 + 3 * 4 + 5 , у нас возникает небольшая проблема.

Большинство людей согласны с тем, что умножение имеет более высокий приоритет, чем сложение. Но парсер этого не знает. Мы не можем просто вычислить его как ((2 + 3) * 4) + 5 . Вместо этого нам нужно (2 + (3 * 4)) + 5 .

Это означает, что нам нужно сначала оценить умножение . Умножение должно быть на дальше от корня AST , чтобы принудительно оценить его перед добавлением. Для этого нам нужно ввести еще один уровень косвенности.

Исправление наивной грамматики от начала до конца

Это наша исходная леворекурсивная грамматика, не имеющая правил приоритета:

 expr -> expr '+' expr | выражение '*' выражение | ЧИСЛО
 

Во-первых, мы даем ему правила приоритета и удаляем его неоднозначность :

 выражение -> выражение '+' термин | срок
термин -> термин '*' ЧИСЛО | ЧИСЛО
 

Затем он получает нелеворекурсивных правила :

 expr -> term exprOpt*
exprOpt -> '+' термин
срок -> ЧИСЛО срокОпт*
termOpt -> '*' ЧИСЛО
 

Результатом является красиво выразительный AST:

 case class Expr(term: Term, exprOpts: Seq[ExprOpt])
класс случая ExprOpt(term: Term)
класс case Term (число: Int, termOpts: Seq[TermOpt])
класс case TermOpt (число: Int)
 

Это дает нам краткую реализацию интерпретатора:

 class Interpreter(ast: Expr):
  деф интерпретировать (): Int = eval (аст)
  частная оценка (выражение: выражение): Int =
    var tmp = eval(expr. term)
    expr.exprOpts.foreach { exprOpt =>
      tmp += eval(exprOpt.term)
    }
    температура
  частная оценка (срок: срок): Int =
    var tmp = термин.номер
    term.termOpts.foreach {termOpt =>
      tmp *= termOpt.num
    }
    температура
 

Как и прежде, идеи в отношении необходимого лексера и грамматики были рассмотрены ранее, но при необходимости читатели могут найти их в репозитории.

Следующие шаги в написании интерпретаторов

Мы не рассматривали это, но обработка ошибок и отчеты являются важными функциями любого синтаксического анализатора. Как разработчики, мы знаем, как неприятно, когда компилятор выдает запутанные или вводящие в заблуждение ошибки. Это область, в которой нужно решить много интересных проблем, таких как предоставление правильных и точных сообщений об ошибках, не отпугивание пользователя большим количеством сообщений, чем необходимо, и изящное восстановление после ошибок. Разработчики должны написать интерпретатор или компилятор, чтобы обеспечить их будущим пользователям лучший опыт.

В наших примерах лексеров, синтаксических анализаторов и интерпретаторов мы только поверхностно коснулись теорий, лежащих в основе компиляторов и интерпретаторов, которые охватывают такие темы, как:

• Области действия и таблицы символов
• Статические типы
• Оптимизация времени компиляции
• Статические анализаторы программ и линтеры
• Форматирование кода и красивая печать
• Доменные языки

Для дальнейшего чтения я рекомендую следующие ресурсы:

• Шаблоны языковой реализации Теренса Парра
• Бесплатная онлайн-книга, Crafting Interpreters , Боба Нистрома
• Введение в грамматику и синтаксический анализ Пола Клинта
• Написание хороших сообщений об ошибках компилятора Калеб Мередит
• Заметки из курса Университета Восточной Каролины «Перевод и компиляция программ»

Понимание основ

• Как создать интерпретатор?

  Чтобы сначала создать интерпретатор, вам нужно создать лексер для получения токенов вашей программы ввода. Затем вы создаете синтаксический анализатор, который берет эти токены и, следуя правилам формальной грамматики, возвращает AST вашей входной программы. Наконец, интерпретатор берет этот AST и каким-то образом интерпретирует его.

• В чем разница между компилятором и интерпретатором?

  Компилятор берет программу на языке более высокого уровня и преобразует ее в программу на языке более низкого уровня. Интерпретатор берет программу и запускает ее на лету. Он не создает никаких файлов.

• На каком языке написан переводчик?

  Интерпретаторы могут быть написаны на любом языке программирования. Популярным выбором являются функциональные языки, потому что они имеют отличные абстракции для преобразования данных.

• Как работает переводчик?

  Интерпретаторы в основном выполняют по одному оператору за раз. Они берут AST, возвращенный синтаксическим анализатором, и выполняют его. В этом процессе они обычно используют некоторые вспомогательные конструкции, такие как таблицы символов, генераторы и оптимизаторы.

• Как работает лексер?

  Лексер принимает строку символов и возвращает список токенов, которые в основном представляют собой сгруппированные символы. Токены обычно определяются с помощью регулярных выражений.

• Как работают синтаксические анализаторы программирования?

  Парсер программирования определяется формальной грамматикой, описывающей правила языка, который он анализирует. Наиболее распространенным видом является анализатор рекурсивного спуска, и он напоминает данную грамматику, имея одну функцию для каждого нетерминала. Он принимает последовательность токенов в качестве входных данных и возвращает AST в качестве выходных данных.

• Что подразумевается под абстрактным синтаксическим деревом?

  Абстрактное синтаксическое дерево (AST) представляет собой представление структуры исходного кода программы. Он содержит только те данные, которые важны для интерпретатора или компилятора. Он не содержит пробелов, фигурных скобок, точек с запятой и подобных частей входной программы.

• Для чего используется абстрактное синтаксическое дерево?

  Абстрактное синтаксическое дерево используется как промежуточное представление входной программы. Затем интерпретатор/компилятор может делать с ним все, что ему нужно: оптимизировать, упрощать, выполнять или что-то еще.

Правильно + Эффективно + Красиво

Вы могли бы написать свой собственный лексер и синтаксический анализатор с нуля. Но многие языки включают инструменты для автоматического создания лексеров и парсеров из формальных описаний синтаксиса языка. Предки многие из этих инструментов — lex и yacc, которые генерируют лексеры и парсеры соответственно; lex и yacc были разработаны в 1970-е годы для C.

В составе стандартного дистрибутива OCaml предоставляет лексер и синтаксический анализатор. генераторы с именами ocamllex и ocamlyacc. есть еще современный генератор парсеров по имени менгир, доступный через opam; менгир – это «90% совместим» с ocamlyacc и обеспечивает значительно улучшена поддержка отладки сгенерированных парсеров.

9.2.1. лексерс

Генераторы Lexer, такие как lex и ocamllex, построены на теории детерминированные конечные автоматы, которые обычно рассматриваются в дискретной математике или курс теории вычислений. Такие автоматы принимают обычных языков , которые можно описать с помощью регулярных выражений . Итак, вход в генератор лексеров представляет собой набор регулярных выражений, описывающих токены языка. На выходе — автомат, реализованный на языке высокого уровня, таком как C (для lex) или OCaml (для ocamllex).

Этот автомат сам принимает на вход файлы (или строки), и каждый символ файл становится входом для автомата. В конце концов автомат либо распознает последовательность символов, которую он получил как действительный токен в язык, и в этом случае автомат производит вывод этого токена и сбрасывает себя на распознавание следующего маркера, или отклоняет последовательность символов как недопустимый токен.

9.

2.2. Парсеры Генераторы парсеров

, такие как yacc и menhir, аналогичным образом построены на теории автоматы. Но они используют автоматы с выталкиванием вниз , похожие на конечные автоматы, которые также поддерживать стек, в который они могут помещать и извлекать символы. Стек позволяет им принять более широкий класс языков, известных как контекстно-свободных языков (CFL). Одно из больших улучшений КЛЛ по сравнению с обычные языки, заключается в том, что CFL могут выражать идею о том, что разделители должны быть сбалансированный — например, что каждая открывающая скобка должна быть уравновешена закрывающая скобка.

Точно так же, как обычные языки могут быть выражены специальной записью (обычные выражения), то же самое можно сказать и о КЛЛ. Контекстно-свободные грамматики используются для описания CFL. А контекстно-свободная грамматика — это набор продукционных правил , которые описывают, как один символ могут быть заменены другими символами. Например, язык сбалансированного круглые скобки, которые включают такие строки, как (()) и ()() и (()()) , но не такие строки, как ) или (() , генерируется по этим правилам:

• \(S \стрелка вправо (S)\)

• \(S \стрелка вправо\)

• \(S \стрелка вправо \эпсилон\)

В этих правилах встречаются символы \(S\), \((\) и \()\). \(\эпсилон\) обозначает пустую строку. Каждый символ является либо нетерминалом , либо терминал в зависимости от того, является ли он токеном описываемого языка. \(S\) является нетерминалом в приведенном выше примере, а ( и ) являются терминалами.

В следующем разделе мы изучим Бэкуса-Наура Форма (BNF), который является стандартным обозначения для контекстно-свободных грамматик. Входные данные для генератора синтаксического анализатора обычно BNF-описание синтаксиса языка. Вывод генератора парсера это программа, которая распознает язык грамматики. В качестве входных данных эта программа ожидает вывод лексера. На выходе программа выдает значение Тип AST, представляющий принятую строку. Программы, выводимые таким образом, генератор синтаксического анализатора и генератор лексера зависят от другого и по типу АСТ.

9.2.3. Форма Бэкуса-Наура

Стандартный способ описания синтаксиса языка — математический обозначение под названием Бэкуса-Наура, форма (BNF), названное в честь его изобретателя Джона Бэкуса. и Питер Наур. Существует множество вариантов БНФ. Здесь мы не будем слишком придирчивы о приверженности тому или иному варианту. Наша цель состоит в том, чтобы иметь разумную хорошая нотация для описания синтаксиса языка.

BNF использует набор правил вывода для описания синтаксиса языка. Давайте начни с примера. Вот описание BNF крошечного языка выражения, которые включают только целые числа и сложение:

 е ::= я | е + е
я ::= <целые числа>
 

Эти правила говорят, что выражение e является либо целым числом i , либо двумя выражения, между которыми стоит символ + . Синтаксис «целых чисел» не определяется этими правилами.

Каждое правило имеет вид

 метапеременных ::= символов | ... | символы
 

Метапеременная — это переменная, используемая в правилах BNF, а не переменная в описываемого языка. ::= и | , фигурирующие в правилах, метасинтаксис : синтаксис BNF, используемый для описания синтаксиса языка. Символы есть последовательности, которые могут включать метапеременные (например, i и e ), а также токены языка (например, + ). Пробелы в этих правилах неуместны.

Иногда мы можем захотеть легко сослаться на отдельные вхождения метапеременные. Мы делаем это, добавляя некоторый отличительный знак к метапеременная (ы). Например, мы могли бы переписать первое правило выше как

 е ::= я | е1 + е2
 

или как

 е ::= я | е + е'
 

Теперь мы можем говорить о e2 или e' вместо того, чтобы говорить « e на правая часть + ».

Если сам язык содержит один из токенов ::= или | — и OCaml действительно содержит последнее — тогда написание BNF может стать немного затруднительным. сбивает с толку. Некоторые нотации BNF пытаются справиться с этим, используя дополнительные разделители, чтобы отличить синтаксис от метасинтаксиса. Мы будем более расслабленными и предположим, что читатель может их различить.

9.2.4. Пример: SimPL

В качестве рабочего примера мы будем использовать очень простой язык программирования, который мы называем СимПЛ. Вот его синтаксис в BNF:

 е ::= х | я | б | e1 боп e2
    | если е1 то е2 иначе е3
    | пусть x = e1 в e2
боп ::= + | * | <=
х ::= <идентификаторы>
я ::= <целые числа>
б ::= истина | ЛОЖЬ
 

Очевидно, в этом языке многого не хватает, особенно функций. Но этого достаточно для изучения важных понятий интерпретаторов не слишком отвлекаясь на множество языковых функций. Позже мы рассмотрим более крупный фрагмент OCaml.

Мы собираемся разработать полноценный интерпретатор SimPL. Вы можете скачать готовый интерпретатор здесь: simpl.zip. Или просто следуйте за тем, как мы строим каждую его часть.

9.2.4.1. АСТ

Поскольку AST является самой важной структурой данных в интерпретаторе, давайте спроектируйте его в первую очередь. Мы поместим этот код в файл с именем ast.ml :

.

 тип боп =
  | Добавлять
  | Мульт
  | Лек
введите выражение =
  | Var строки
  | Целое число
  | Бул из бул
  | Binop of bop * expr * expr
  | Пусть строки * expr * expr
  | Если expr * expr * expr
 

Для каждой из синтаксических форм выражений в БНФ. Для базовых примитивных синтаксических классов идентификаторов, целых чисел, и логические, мы используем собственные типы OCaml string , int и bool .

Вместо определения типа bop и одного конструктора Binop мы могли бы определили три отдельных конструктора для трех бинарных операторов:

 введите выражение =
  ...
  | Добавление expr * expr
  | Множественное выражение * выражение
  | Leq expr * expr
  ...
 

Но, исключив тип bop , мы сможем избежать большого количества кода. дублирование позже в нашей реализации.

9.2.4.2. Парсер Менгира

Давайте начнем с парсинга, а потом вернемся к лексике. Мы поставим все Менгиры код, который мы пишем ниже в файле с именем parser. mly . Расширение .mly указывает что этот файл предназначен для входа в Menhir. («y» намекает на yacc.) Это файл содержит определение грамматики для языка, который мы хотим разобрать. синтаксис определений грамматики описан на примере ниже. Будьте предупреждены, что это может быть немного странным, но это потому, что он основан на инструментах (таких как yacc), которые были разработаны довольно давно. Menhir обработает этот файл и создаст файл с именем parser.ml в качестве вывода; он содержит программу OCaml, которая анализирует язык. (Здесь нет ничего особенного в названии парсера ; это просто описательный.)

Определение грамматики состоит из четырех частей: заголовка, объявлений, правил и трейлер.

Заголовок. Заголовок появляется между %{ и %} . Это код, который будет скопировано буквально в сгенерированный parser.ml . Здесь мы используем его только для открытия Модуль Ast , чтобы позже в определении грамматики мы могли написать такие выражения, как Int i вместо Ast. Int i . Если бы мы хотели, мы могли бы также определить некоторые функции OCaml в заголовке.

 %{
открыть Аст
%}
 

Декларации. Раздел объявлений начинается с того, что лексический токенов языка есть. Вот объявления токенов для SimPL:

 %токен  INT
%token <строка> ID
%токен ИСТИНА
%токен ЛОЖЬ
%токен LEQ
%токен РАЗ
%токен ПЛЮС
%токен LPAREN
%токен RPAREN
%токен ПОЗВОЛЬТЕ
%токен РАВНО
%токен ВХОДИТ
%токен ЕСЛИ
%токен ТОГДА
%токен ИНАЧЕ
%токен EOF
 

Каждое из них — просто описательное имя токена. Ничто пока не говорит об этом LPAREN действительно соответствует ( , например. Мы позаботимся об этом, когда будем определить лексер.

Токен EOF — это специальный токен конца файла , который лексер вернет, когда он подходит к концу потока символов. В этот момент мы знаем полную программа прочитана.

Токены, в которых есть аннотация , заявляют, что они будут нести некоторые дополнительные данные вместе с ними.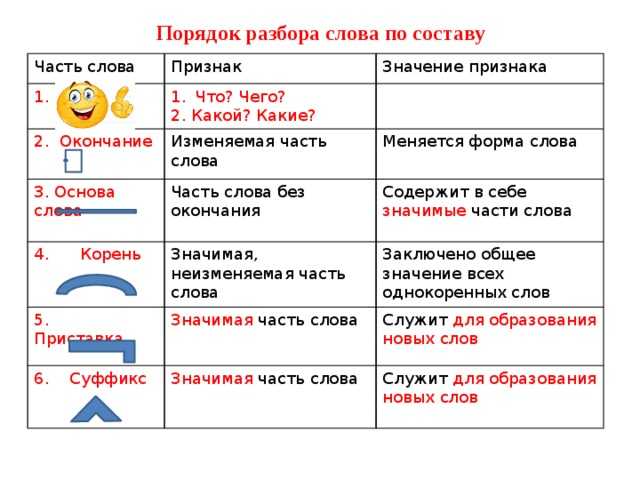 В случае INT , это OCaml int . В случае ID это строка OCaml .

После объявления токенов мы должны предоставить некоторую дополнительную информацию о старшинство и ассоциативность . Следующие объявления говорят, что PLUS является левоассоциативный, IN не ассоциативен, а PLUS имеет более высокий приоритет, чем В (поскольку ПЛЮС появляется в строке после В ).

 %nonassoc IN
%nonassoc ИНАЧЕ
% левый LEQ
% осталось ПЛЮС
% осталось РАЗ
 

Поскольку PLUS является левой ассоциативностью, 1 + 2 + 3 будет проанализировано как (1 + 2) + 3 и не как 1 + (2 + 3) . Поскольку PLUS имеет более высокий приоритет, чем IN , выражение пусть x = 1 в x + 2 будет анализироваться как пусть x = 1 в (x + 2) , а не как (пусть х = 1 в х) + 2 . Другие объявления имеют аналогичный эффект.

Правильное определение приоритета и ассоциативности является одним из более сложные части разработки определения грамматики. Он помогает развивать определение грамматики постепенно, добавляя всего пару токенов (и их связанные правила, обсуждаемые ниже) одновременно с языком. Менгир позволит вы знаете, когда вы добавили токен (и правило), для которого он запутался что вы предполагаете, что приоритет и ассоциативность должны быть. Затем вы можете добавить декларации и проверить, чтобы убедиться, что вы поняли их правильно.

После объявления ассоциативности и приоритета нам нужно объявить, что отправной точкой является разбор языка. Следующее объявление говорит начните с правила (определенного ниже) с именем prog . В декларации также говорится, что анализ программы вернет значение OCaml типа Ast.expr .

 %start  прог
 

Наконец, %% завершает раздел объявлений.

Правила. раздел rules содержит продукционные правила, напоминающие BNF, хотя там, где в BNF мы бы написали «::=», эти правила просто пишут «:». формат правила

 имя:
  | производство1 { действие1 }
  | производство2 { действие2 }
  | ...
  ;
 

Произведение — это последовательность из символов , которым соответствует правило. Символ либо токен, либо имя другого правила. Действие — это значение OCaml для вернуть, если соответствует . Каждое производство может bind значение, переносимое символ и использовать это значение в своем действии. Это, пожалуй, лучше всего понимают например, так что давайте углубимся.

Первое правило с именем prog имеет только одну продукцию. В нем говорится, что prog - это expr , за которым следует EOF . Первая часть производства, e=expr , говорит, что нужно сопоставить expr и связать полученное значение с e . действие просто говорит вернуть это значение и .

 прог:
  | е = выражение; EOF {е}
  ;
 

Второе и последнее правило, названное expr , содержит продукцию для всех выражений. в СимПЛ.

 выражение:
  | я = INT {целое я}
  | х = ID {Вар х}
  | ИСТИНА { логическая истина }
  | FALSE { Логическое значение false }
  | e1 = выражение; ЛЭК; e2 = выражение {Binop (Leq, e1, e2)}
  | e1 = выражение; РАЗ; e2 = expr {Binop (Mult, e1, e2)}
  | e1 = выражение; ПЛЮС; e2 = expr {Binop (Добавить, e1, e2)}
  | ПОЗВОЛЯТЬ; х = идентификатор; РАВНО; e1 = выражение; В; e2 = expr { Пусть (x, e1, e2) }
  | ЕСЛИ; e1 = выражение; ЗАТЕМ; e2 = выражение; ЕЩЕ; e3 = выражение {Если (e1, e2, e3)}
  | ЛПАРЕН; е=выражение; РАРЕН {е}
  ;
 

• Первая продукция, i = INT , говорит, что для сопоставления токена INT необходимо привязать результирующее значение OCaml int в i и вернуть узел AST Int i .

• Вторая продукция, x = ID , говорит, что для сопоставления токена ID необходимо привязать результирующее значение строки OCaml в x и возврат узла AST Var x .

• Третье и четвертое произведения соответствуют TRUE или FALSE маркер и возврат соответствующий узел AST.

• Пятая, шестая и седьмая продукции обрабатывают бинарные операторы. Для например, e1 = выражение; ПЛЮС; e2 = expr говорит, что соответствует expr , за которым следует Токен PLUS , за которым следует еще один expr . Первый expr привязан к e1 и второй до e2 . Возвращаемый узел AST — Binop (Add, e1, e2) .

• Восьмое производство, ЛЕТ; х = идентификатор; РАВНО; e1 = выражение; В; e2 = expr , говорит чтобы соответствовать токену LET , за которым следует токен ID , за которым следует токен EQUALS за которым следует выражение expr , за которым следует токен IN , за которым следует еще одно выражение expr . Строка, содержащаяся в идентификаторе ID , привязана к x , и два выражения привязан к e1 и e2 . Возвращенный узел AST равен 9.0041 Пусть (x, e1, e2) .

• Последнее производство, LPAREN; е = выражение; RPAREN говорит, что соответствует LPAREN токен, за которым следует выражение expr , за которым следует RPAREN . Выражение связано на e и вернулся.

Окончательная продукция может удивить, потому что она не была включена в БНФ. мы писали для SimPL. Эта БНФ была предназначена для описания абстрактного синтаксиса языка, поэтому он не включал конкретных деталей того, как выражения могут быть сгруппированы скобками. Но определение грамматики, которое мы писали, нужно описать конкретный синтаксис , включая такие детали, как круглые скобки.

Также может быть раздел трейлер после правил, который, как и заголовок, Код OCaml, который копируется непосредственно в выходной файл parser. ml .

9.2.4.3. Ocamllex Lexer

Теперь давайте посмотрим, как используется генератор лексеров. Многое покажется знакомым из нашего обсуждения генератора парсеров. Мы поместим весь код ocamllex, который мы пропишите ниже в файл с именем lexer.mll . Расширение .mll указывает, что этот файл предназначен для ввода в ocamllex. (буква «l» намекает на лексику.) Это файл содержит определение лексера для языка, который мы хотим лексировать. Менгир обработает этот файл и создаст на выходе файл с именем lexer.ml ; это содержит программу OCaml, которая лексизирует язык. (ничего особенного про имя лексер здесь; это просто описание.)

Определение лексера состоит из четырех частей: заголовка, идентификаторов, правил и трейлер.

Заголовок. Заголовок появляется между { и } . Это код, который будет просто скопируйте буквально в сгенерированный lexer. ml .

 {
открыть парсер
}
 

Здесь мы открыли модуль Parser , который представляет собой код в parser.ml , который был произведен Menhir из parser.mly . Причина, по которой мы открываем его, заключается в том, что мы может использовать объявленные в нем имена токенов, например, TRUE , LET и INT , внутри наше определение лексера. В противном случае нам пришлось бы писать Parser.TRUE и т. д.

Идентификаторы. Следующий раздел определения лексера содержит идентификаторов , которые называются регулярными выражениями. Они будут использоваться в раздел правил, далее.

Вот идентификаторы, которые мы будем использовать с SimPL:

 пусть белый = [' ' '\t']+
пусть цифра = ['0'-'9']
пусть int = '-'? цифра+
пусть буква = ['a'-'z' 'A'-'Z']
пусть id = буква+
 

Приведенные выше регулярные выражения предназначены для пробелов (пробелов и табуляции), цифр (0 до 9), целые числа (непустые последовательности цифр, которым может предшествовать знак минус), буквы (от a до z и от A до Z) и имена переменных SimPL. (непустые последовательности букв), также известные как идентификаторы или «идентификаторы», хотя сейчас мы употребляя это слово в двух разных смыслах.

FYI, это не совсем то же самое, что и определения целых чисел в OCaml и идентификаторы.

Раздел идентификаторов фактически не требуется; вместо того, чтобы писать белый в правила, мы могли бы просто написать регулярное выражение для него. Но идентификаторы помогают сделать определение лексера более самодокументируемым.

Правила. Раздел правил определения лексера записан в нотации, которая также напоминает BNF. Правило имеет вид

 имя правила =
  разобрать
  | регулярное выражение1 { действие1 }
  | регулярное выражение2 { действие2 }
  | ...
 

Здесь правило и разбор являются ключевыми словами. Сгенерированный лексер попытается для сопоставления с регулярными выражениями в порядке их перечисления. Когда соответствует регулярному выражению, лексер создает токен, указанный его действие .

Вот (единственное) правило для лексера SimPL:

 правило чтения =
  разобрать
  | белый { читать lexbuf }
  | "правда правда }
  | "ложь" {ЛОЖЬ}
  | "<=" {LEQ}
  | "*" {РАЗ}
  | "+" {ПЛЮС}
  | "(" {ЛПАРЕН}
  | ")" {RPAREN}
  | "Пусть" {ПУСТЬ}
  | "=" {РАВНО}
  | "в" {В}
  | "если если }
  | "потом" {ТО}
  | "иначе" { ИНАЧЕ }
  | id { ID (Lexing.lexeme lexbuf) }
  | int { INT (int_of_string (Lexing.lexeme lexbuf)) }
  | конец {конец}
 

Большинство регулярных выражений и действий говорят сами за себя, но пара нет:

• Первый, white { read lexbuf } , означает, что если пробел соответствует, вместо того, чтобы возвращать токен, лексер должен просто снова вызвать правило read и вернуть любые результаты токена. Другими словами, пробелы будут пропущены.

• Два идентификатора и целое число используют выражение Lexing.lexeme lexbuf . Это вызывает функция лексема , определенная в модуле Lexing , и возвращает строку которое соответствует регулярному выражению. Например, в правиле id будет вернуть последовательность прописных и строчных букв, которые образуют переменную имя.

• Регулярное выражение eof — это специальное выражение, которое соответствует концу файла (или строка) лексируется.

Обратите внимание, важно, чтобы регулярное выражение id встречалось почти последним в список. В противном случае ключевые слова типа true и , если будет использоваться как переменная имена, а не токены TRUE и IF .

9.2.4.4. Генерация парсера и лексера

Теперь, когда мы завершили определения парсера и лексера в parser.mly и lexer.mll , мы можем запустить Menhir и ocamllex для создания парсера и лексера от них. Давайте организуем наш код следующим образом:

 - <какая-то корневая папка>
  - дюна-проект
  - источник
    - аст.мл
    - дюна
    - лексер.млл
    - парсер. mly
 

В src/dune напишите следующее:

 (библиотека
 (вставка имени))
(менгир
 (парсер модулей))
(окамлекс лексер)
 

Это организует всю папку src в библиотеку с именем Interp . parser и lexer будут модулями Interp.Parser и Interp.Lexer в этом библиотека.

Запустите dune build , чтобы скомпилировать код, тем самым сгенерировав синтаксический анализатор и лексер. Если вы хотите увидеть сгенерированный код, посмотрите в _build/default/src/ для parser.ml и lexer.ml .

9.2.4.5. Водитель

Наконец, мы можем объединить лексер и синтаксический анализатор, чтобы преобразовать строку в АСТ. Поместите этот код в файл с именем src/main.ml :

.

 открытый Аст
let parse (s : string) : expr =
  пусть lexbuf = Lexing.from_string s в
  let ast = Parser.prog Lexer.read lexbuf в
  аст
 

Эта функция принимает строку s и использует стандартную библиотеку Модуль Lexing создать из него лексерный буфер . Думайте об этом буфере как о потоке маркеров. Затем функция лексизирует и анализирует строку в AST, используя Lexer.read и Parser.prog . Функция Lexer.read соответствует правилу с именем читать в нашем определении лексера, а функция Parser.prog в правиле с именем прог в нашем определении парсера.

Обратите внимание, как этот код запускает лексический анализ строки; есть соответствующая функция from_channel для чтения из файла.

Теперь мы можем использовать parse в интерактивном режиме для разбора некоторых строк. Начать сверху и загрузите библиотеку, объявленную в src , с помощью этой команды:

 $ дюн utop src
 

Теперь Interp.Main.parse доступен для использования:

 # Interp.Main.parse "пусть x = 3110 в x + x";;
- : Interp.Ast.expr =
Interp.Ast.Let("x", Interp.Ast.Int 3110,
 Interp.Ast.Binop (Interp.