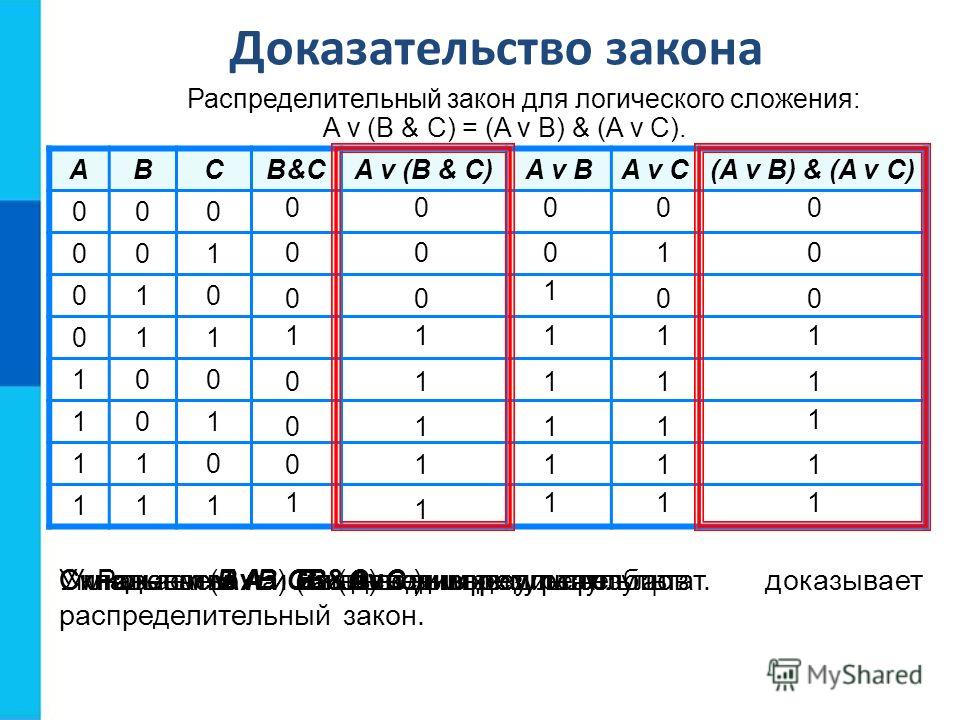
Законы математики
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае — к тому что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
5 + 2 = 7
2 + 5 = 7
Если на одну чашу весов положить пакет, в котором 10 килограмм яблок, и на другую чашу так же положить пакет, в котором 10 килограмм яблок, то весы выровнятся, и не важно что яблоки в пакетах лежат вразброс.
Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
5 + 2 = 2 + 5
7 = 7
Полагаем что вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
a + b = b + a
Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
5 × 2 = 10
2 × 5 = 10
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
10 = 10
Запишем переместительный закон умножения с помощью переменных:
a × b = b × a
Для записи законов в качестве переменных необязательно использовать именно буквы a и b. Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
x × y = y × x
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
(3 + 5) × 2
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
(3 + 5) = 8
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
Или ещё короче:
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7
Задания для самостоятельного решения
Задание 1. Найдите значение выражения, используя распределительный закон умножения:
3 × (7 + 8)
Решение:
3 × (7 + 8) = 3 × 7 + 3 × 8 = 21 + 24 = 45
Показать решение
Задание 2. Найдите значение выражения, используя распределительный закон умножения:
Найдите значение выражения, используя распределительный закон умножения:
5 × (6 + 8)
Решение:
5 × (6 + 8) = 5 × 6 + 5 × 8 = 30 + 40 = 70
Показать решение
Задание 3. Найдите значение выражения, используя порядок выполнения действий:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
Показать решение
Задание 4. Найдите значение выражения, используя распределительный закон умножения:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
4 × (5 + 4) + 9 × (3 + 2) = 4 × 5 + 4 × 4 + 9 × 3 + 9 × 2 = 20 + 16 + 27 + 18 = 81
Показать решение
Задание 5. Найдите значение выражения, используя распределительный закон умножения:
16 × (2 + 7) + 5 × (4 + 1)
Решение:
16 × (2 + 7) + 5 × (4 + 1) = 16 × 2 + 16 × 7 + 5 × 4 + 5 × 1 = 32 + 112 + 20 + 5 = 169
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Основные законы сложения и умножения
Основные законы сложения и умножения — МАТВОКСПерейти к содержанию
ПОИСК
Страница Вконтакте открывается в новом окне
Вы здесь:
Основные законы сложения и умножения
- Переместительный закон сложения.

- Сочетательный закон сложения.
- Переместительный закон умножения.
- Сочетательный закон умножения.
- Распределительный закон умножения по отношению к сложению.
1. Переместительный закон сложения.
От перестановки мест слагаемых сумма не меняется:
Пример:
Действительно:
2 Сочетательный закон сложения.
Результат сложения нескольких слагаемых не зависит от порядка действий.
Или можно сочетательный закон сложения сформулировать иначе.
Сумма нескольких слагаемых не изменится, если какую-нибудь группу рядом стоящих слагаемых заменить их суммой.
Этот закон позволяет группировать слагаемые для удобства их вычислений.
ПримерДействительно,
Этот
пример отчетливо показывает важность сочетательного закона сложения.Пусть нужно найти значение выражения:
Если не пользоваться сочетательным законом, то, будем складывать числа последовательно:
1 действие
2 действие
Тогда:
А теперь
воспользуемся сочетательным законом сложения.
Если внимательно посмотреть на выражение, то, очевидно, проще сначала сложить 5 и 95, а затем прибавить 37.
1 действие
2 действие
Тогда:
Очевидно, второй способ вычисления выражения удобнее использовать.
3. Переместительный закон умножения
От перемены порядка сомножителей произведение не изменится.
Пример:
Действительно:
4. Сочетательный закон умножения
Результат произведения нескольких множителей не зависит от порядка действий.
Или можно сочетательный закон умножения сформулировать иначе.
Произведение нескольких сомножителей не изменится, если какую-нибудь группу рядом стоящих сомножителей заменить их произведением.
Этот закон позволяет группировать множители для удобства их вычислений.
ПримерДействительно,
Этот пример отчетливо показывает
важность сочетательного закона умножения.
Пусть нужно найти значение выражения:
Если не пользоваться сочетательным законом, то, будем перемножать числа последовательно:
1 действие
2 действие
Тогда:
А теперь
воспользуемся сочетательным законом умножения.Если внимательно посмотреть на выражение, то, очевидно, проще сначала перемножить 0,5 и 10, а затем результат умножить на 13.
1 действие
2 действие
Тогда:
Очевидно, второй способ вычисления выражения удобнее использовать.
5. Распределительный закон умножения по отношению к сложению
Распределительный закон умножения позволяет вместо умножения суммы на число, умножить каждое слагаемое по отдельности на число, после чего результат сложить.
Чтобы умножить сумму двух (или нескольких) чисел на какое-либо число, можно каждое слагаемое умножить на это число и полученный результат сложить.
или:
Распределительное свойство справедливо и в том случае, когда число умножается на сумму трех и более слагаемых, например,
Пример 1Пример 2
Число 2 является общим множителем.
или:
Иногда бывает выгоднее поступить наоборот. Вместо того, чтобы умножать каждое слагаемое на одно и то же число, сначала находят сумму этих слагаемых и умножают ее на данное число. Это действие называют «внесение множителя в скобки»:
Пример 1Пример 2
Если при умножении суммы на число
множитель вносят в скобки, умножая каждое слагаемое на этот множитель (скобки затем опускают):то при
вынесении множителя за скобки, каждое слагаемое делят на этот множитель:Из переместительного и сочетательного свойств сложения следует
следующее свойство:В любой
сумме можно как угодно переставлять слагаемые и произвольным образом объединять их в группы.ПримерНайти значение выражения:
Решение
Очевидно, что проще сложить 1,18 и 4,32, а также 12,1 и 1,4. Так как от перестановки мест слагаемых и от порядка действий сумма не меняется, то можем записать:
Так как от перестановки мест слагаемых и от порядка действий сумма не меняется, то можем записать:
Из свойств произведения следует
следующее свойство:
В любом
произведении можно как угодно переставлять множители и произвольным образом объединять их в группы.ПримерВычислить:
Очевидно, что проще перемножить 0,5 и 28, а также 0,25 и 4. Так как от перестановки мест множителей и от порядка действий произведение не меняется, то можем записать:
9E09BEAE0A118E93DED3D74128EA2C147A65428915829EB11235F7758F7B38C3
MATHVOX
Вверх
Этот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Privacy & Cookies Policy
Don`t copy text!
Переместительный закон сложения — правило и примеры решения задач » Kupuk.
 net
netВ математике для решения задач применяются сочетательный и переместительные законы сложения. У многих учеников они могут вызвать некоторые сложности, поскольку не все понимают школьную программу 5 класса. Для этих целей специалисты разработали универсальный алгоритм обучения, который позволит не только хорошо усвоить материал, но и претендовать на высокие оценки.
Общие сведения
Сложение — математическая операция, при помощи которой происходит увеличение исходного числа на определенное значение. Ее элементами являются минимум два слагаемых и результат. Последний называется суммой. Всего существуют два закона сложения. К ним относятся следующие:
Первый еще называется переместительным, а второй — сочетательным. Многие школьники путают правила сложения и умножения. Следует отметить, что для последнего предусмотрены три закона, т. е. распределительный, сочетательный и переместительный. У деления и умножения правила похожи, а вот для вычитания, как и для сложения, предусмотрено также два свойства.
У деления и умножения правила похожи, а вот для вычитания, как и для сложения, предусмотрено также два свойства.
Чтобы не путать термины, необходимо рассмотреть каждое арифметическое действие по группам.
Сложение и вычитание
Сложение и вычитание являются взаимосвязанными математическими операциями. Для примера необходимо разобрать числовое выражение «10+20+30+40=100». Оно состоит из пяти элементов: четырех слагаемых и одного результата. Это математическое выражение можно записать в обратном виде 100−40−30−20=10. Данное тождество называется вычитанием.
Иными словами, вычитание — математическая операция уменьшения заданного числа (уменьшаемого) на определенное число (вычитаемое), результатом которой является разность. Для сложения и вычитания применимо всего два закона: переместительный и сочетательный. Они используются для оптимизации вычислений.
Следует отметить, что методика ускорения расчетов используется также в программировании и информатике.
Кроме того, эти правила применяются и в высшей математике. Например, для сложения или вычитания векторов, а также для работы с числовыми множествами.
Переместительное правило
Переместительный закон сложения гласит: от перемены мест слагаемых значение суммы не изменится. Для доказательства этого утверждения можно воспользоваться числовым выражением 12+32+16+40=100. Если поменять местами элементы (слагаемые) в левой части, то должна также получиться сотня, т. е. 32+12+40+16=100. Утверждение доказано. Математическая запись или формула закона выглядит таким образом: R+T+S=T+S+R=S+T+R=M.
Специалисты рекомендуют самостоятельно придумать числовое выражение и доказать истину формулировки переместительного свойства. Для вычитания также существует переместительный закон, который может быть сформулирован следующим образом: если поменять местами вычитаемое, то разность останется прежней.
Для доказательства правила можно использовать такой же видоизмененный пример, что и для суммы «100−40−16−32=12». В нем вычитаемое эквивалентно группе элементов 40, 16 и 32. Если эти числа поменять местами, то результат не изменится, т. е. 100−32−40−16=12. Правило доказано. Для вычитания переместительный закон записывается в таком виде: М-R-T=S, М-R-S=T и М-T-S=R. Далее необходимо рассмотреть сочетательные правила.
Сочетательный закон
Сочетательное правило сложения и вычитания похожи. Их суть заключается в перегруппировке элементов. Следует отметить, что последняя не влияет на результат. Она необходима для упрощения вычислений. Сочетательный закон сложения формулируется таким образом: значение суммы не зависит от группировок слагаемых.
Например, 4+11+6+9=30. Для удобства можно записать пример в таком виде: (4+6)+(11+9)=30. Результат не изменился. Кроме того, производить вычисления стало проще. В виде формулы закон можно записать в таком виде: М+R+T=М+(R+T)=(М+T)+R=S.
Для вычитания формулировка правила звучит следующим образом: разность не изменится, если перегруппировать вычитаемые компоненты, т. е. 30−6−11−4=30-(6+4)-4=9. Формула закона имеет вид: М-R-T-P= М-R-(T+P)= N. Следует отметить, что числа можно группировать в произвольном порядке. Главное — придерживаться принципа вынесения знака за скобку (касается только вычитания).
Некоторые ученики часто приписывают к арифметическим операциям сложения и вычитания распределительное свойство. Это большая ошибка, поскольку для суммы и разности его не существует вообще. Далее необходимо рассмотреть операции, в которых оно применяется.
Произведение и деление
Для умножения и деления применимы те же правила, что и для сложения и вычитания, но к ним добавляется еще и третье — распределительное свойство. В итоге список законов имеет такой вид:
Следует отметить, что формулировки для переместительного закона сложения и умножения практически идентичны. Для последней математической операции он звучит таким образом: произведение не изменится, когда будет выполнено перемещения одного сомножителя на место другого. Например, 2*3*4=2*4*3=24.
В математической форме правило записывается в виде соотношения «RST=SRT=TRS=O». Для деления также используется возможность перемещения делителей, т. е. O: S: T=R или O: Т: S=R. На примере реализация правила выглядит таким образом: 60:2:15=2 или 60:15:2=2.
Для умножения сочетательный закон формулируется в таком виде: значение произведения не изменится при группировке в любом порядке сомножителей, т. е. S*T*R=S*R*T=R*T*S=N. Для деления у него немного другой вид: делители могут группироваться в любом порядке, и это не повлияет на частное. Математическая форма записи выглядит следующим образом: N: T: R: M=N:T:(R:M)=O.
Распределительное свойство для умножения и деления формулируется практически одинаково: произведение (деление) суммы или разности двух элементов на число эквивалентно умножению (делению) каждого элемента суммы или разности на искомый элемент. Законы имеют такие формы записи:
Законы имеют такие формы записи:
Если обратить внимание на формулы, то для сложения запись невозможна, поскольку это уже будет сочетательный закон. Например, в первом пункте необходимо заменить знак «*» на сложение. Соотношение будет иметь следующий вид: (S+T)+M — сочетательное свойство операции сложения. Далее необходимо разобрать пример на применение всех законов.
Пример задачи
Для закрепления теоретического материала специалисты рекомендуют разобрать пример, в котором можно будет применить все законы арифметических операций. Числовое выражение задачи имеет такой вид: 5+6+5+4+20+(25+100)/5+(11+4)*4. Необходимо вычислить результат оптимальным методом. Решать задание нужно по такому алгоритму:

Следует отметить, что к числовому выражению свойства арифметических операций можно применять многократно. Специалисты рекомендуют использовать алгоритм такого вида для оптимизации вычислений.
Таким образом, законы математических операций применяются для оптимизации вычислений для нахождения результатов.
переместительный и сочетательный. Сумма нескольких слагаемых — «Семья и Школа»
Содержание
переместительный и сочетательный. Сумма нескольких слагаемых
Переместительный закон сложения
Если слагаемые поменять местами, то сумма не изменится. Это можно легко проверить, посчитав количество звёздочек, представленных на рисунке:
Можно сначала посчитать зелёные звёздочки, потом жёлтые и сложить полученные результаты, получится 9 звёздочек. Или можно сначала посчитать жёлтые звёздочки, а потом зелёные, в результате сложения жёлтых и зелёных звёздочек сумма будет опять равна 9.
Или можно сначала посчитать жёлтые звёздочки, а потом зелёные, в результате сложения жёлтых и зелёных звёздочек сумма будет опять равна 9.
Таким образом, для любых натуральных чисел a и b верно равенство:
a + b = b + a,
выражающее переместительный закон сложения:
От перестановки слагаемых сумма не меняется.
Сумма нескольких слагаемых
При сложении нескольких слагаемых действия можно выполнять в любом порядке.
Пример. Найти сумму трёх слагаемых: 5, 3 и 2.
Решение: Сумму трёх слагаемых можно найти тремя способами:
1-й способ:
5 + 3 = 8,
8 + 2 = 10.
2-й способ:
5 + 2 = 7,
7 + 3 = 10.
3-й способ:
3 + 2 = 5,
5 + 5 = 10.
Сочетательный закон сложения
Если при сложении чисел 5, 2 и 3 заменить какие-нибудь два числа их суммой, то результат сложения не измениться. Это можно легко проверить посчитав звёздочки на картинке:
Можно посчитать зелёные, синие и жёлтые звёздочки отдельно, а потом сложить полученные результаты, получим 10 звёздочек. Или можно посчитать зелёные звёздочки отдельно, а синие и жёлтые вместе и после к зелёным звёздочкам прибавить сумму синих с жёлтыми, в результате получим опять 10 звёздочек.
Или можно посчитать зелёные звёздочки отдельно, а синие и жёлтые вместе и после к зелёным звёздочкам прибавить сумму синих с жёлтыми, в результате получим опять 10 звёздочек.
Из примера следует, что результат сложения не зависит от объединения слагаемых в сумму. Таким образом, для любых натуральных чисел a, b и c верно равенство:
a + b + c = a + (b + c) = b + (a + c)
выражающее сочетательный закон сложения:
Сумма трёх и более слагаемых не изменится, если какие-нибудь из них заменить их суммой.
Математические Законы
Переместительный закон сложения
Начнем изучать основные законы математики со сложения натуральных чисел.
Переместительный закон сложения От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так: m + n = n + m |
Переместительный закон сложения работает для любых чисел.
Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.
Приведем пример с весами, которые используют продавцы в магазинах.
Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.
При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.
Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:
Формула переместительного закона для обыкновенных дробей:
Чтобы сложить две дроби нужно сложить числители, а знаменатель оставить прежним. Вот так:
Вот так:
Сочетательный закон сложения
Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.
Сочетательный закон сложения: два способа
|
Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.
Рассмотрим сумму из трех слагаемых:
Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:
- 1 + 3 + 4 = (1 + 3) + 4 = 5 + 4 = 8
Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:
- 1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8
В обоих случаях получается один и тот же результат — что и требовалось доказать.
Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:
- (1 + 3) + 4 = 1 + (3 + 4)
- 8 = 8
Отразим сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Формула сочетательного закона для обыкновенных дробей:
Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.
Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.
Значит, сочетательный закон справедлив и для обыкновенных дробей.
Переместительный закон умножения
С каждым новым правилом решать задачки по математике все интереснее.
Переместительный закон умножения От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится. |
Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:
В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.
Переместительный закон умножения с помощью переменных выглядит так:
a * b = b * a
Сочетательный закон умножения
Рассмотрим еще один полезный закон в математике.
Сочетательный закон умножения Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий. Другими словами, умножайте числа в любом порядке — как вам больше нравится. |
Рассмотрим пример:
Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:
- 2 * 3 = 6
- 6 * 4 = 24
- 2 * 3 * 4 = 24
А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:
- 3 * 4 = 12
- 2 * 12 = 24
- 2 * 3 * 4 = 24
Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.
- (2 * 3) * 4 = 2 * (3 * 4)
- 6 * 4 = 2 * 12
- 24 = 24
Для любых натуральных чисел a, b и c верно равенство:
a * b * с = (a * b) * с = a * (b * с)
Пример
Вычислить: 5 * 6 * 7 * 8.
Как решаем:
Это выражение можно вычислять в любом порядке. Вычислим слева направо:
5 * 6 = 30
30 * 7 = 210
210 * 8 = 1680
5 * 6 * 7 * 8 = 1680
Ответ: 1680
Распределительный закон умножения
Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:
Распределительный закон умножения
|
То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:
Проверим на примере:
Сначала выполним действие в скобках:
В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:
- (3 + 5) * 2 = 3 * 2 + 5 * 2
- 3 * 2 = 6
- 5 * 2 = 10
- 6 + 10 = 16
Отразим распределительный закон умножения с помощью переменных:
(a + b) * c = a * c + b * c
Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.
Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b)
. Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:
Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:c * (a + b) = c * a + c * b
Пример 1
Решить: 5 * (3 + 2).
Как решаем:
Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:
5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25
Ответ: 25
Пример 2
Найти значение выражения 2 * (5 + 2).
Как решаем:
Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:
2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14
Ответ: 4.
Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.
Пример 3
Решить: 4 * (6 − 2).
Как решаем:
Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:
4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16
Ответ: 16
Распределительный закон умножения для суммы обыкновенных дробей:
Распределительный закон умножения для разности обыкновенных дробей:
Проверим справедливость этого закона:
Посчитаем, чему равна левая часть равенства.
Теперь посчитаем, чему равна правая часть равенства.
Так мы доказали справедливость распределительного закона.
Задания для самопроверки
Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂
Задание 1. Найти значение выражения: 8 * (1 + 6).
Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).
Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).
Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).
Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)
Задание 6. Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?
Задание 7. В смартфоне 32 гб памяти. Какое количество приложений можно установить, если одно занимает 1,2 гб?
Задание 8. Верно ли равенство: 8 * 5 = 49?
Верно ли равенство: 8 * 5 = 49?
Ответы
- 56;
- 28;
- 100;
- 81;
- 173;
- Деление;
- 26;
- Неверно.
|
1. |
Равенство по рисунку (домино)
|
3 |
|
2. |
Равенство по схеме
|
4 |
|
3. |
Пропущенное число (справа)
|
1 |
|
4. 
|
Пропущенное число (справа)
|
1 |
|
5. |
Значения двух сумм
|
2 |
|
6. |
Применение переместительного закона
|
3 |
|
7. |
Текстовая задача. Населённые пункты
|
4 |
|
8. |
Текстовая задача. Количество детей
|
4 |
|
9. 
|
Текстовая задача. Количество цветов
|
4 |
Переместительный закон сложения — правило и примеры решения задач
Общие сведения
Сложение — математическая операция, при помощи которой происходит увеличение исходного числа на определенное значение. Ее элементами являются минимум два слагаемых и результат. Последний называется суммой. Всего существуют два закона сложения. К ним относятся следующие:
- Коммутативный.
- Ассоциативный.
Первый еще называется переместительным, а второй — сочетательным. Многие школьники путают правила сложения и умножения. Следует отметить, что для последнего предусмотрены три закона, т. е. распределительный, сочетательный и переместительный. У деления и умножения правила похожи, а вот для вычитания, как и для сложения, предусмотрено также два свойства.
Чтобы не путать термины, необходимо рассмотреть каждое арифметическое действие по группам.
Сложение и вычитание
Сложение и вычитание являются взаимосвязанными математическими операциями. Для примера необходимо разобрать числовое выражение «10+20+30+40=100». Оно состоит из пяти элементов: четырех слагаемых и одного результата. Это математическое выражение можно записать в обратном виде 100−40−30−20=10. Данное тождество называется вычитанием.
Иными словами, вычитание — математическая операция уменьшения заданного числа (уменьшаемого) на определенное число (вычитаемое), результатом которой является разность. Для сложения и вычитания применимо всего два закона: переместительный и сочетательный. Они используются для оптимизации вычислений.
Следует отметить, что методика ускорения расчетов используется также в программировании и информатике.Кроме того, эти правила применяются и в высшей математике. Например, для сложения или вычитания векторов, а также для работы с числовыми множествами.
Переместительное правило
Переместительный закон сложения гласит: от перемены мест слагаемых значение суммы не изменится. Для доказательства этого утверждения можно воспользоваться числовым выражением 12+32+16+40=100. Если поменять местами элементы (слагаемые) в левой части, то должна также получиться сотня, т. е. 32+12+40+16=100. Утверждение доказано. Математическая запись или формула закона выглядит таким образом: R+T+S=T+S+R=S+T+R=M.
Специалисты рекомендуют самостоятельно придумать числовое выражение и доказать истину формулировки переместительного свойства. Для вычитания также существует переместительный закон, который может быть сформулирован следующим образом: если поменять местами вычитаемое, то разность останется прежней.
Для доказательства правила можно использовать такой же видоизмененный пример, что и для суммы «100−40−16−32=12». В нем вычитаемое эквивалентно группе элементов 40, 16 и 32. Если эти числа поменять местами, то результат не изменится, т. е. 100−32−40−16=12. Правило доказано. Для вычитания переместительный закон записывается в таком виде: М-R-T=S, М-R-S=T и М-T-S=R. Далее необходимо рассмотреть сочетательные правила.
В нем вычитаемое эквивалентно группе элементов 40, 16 и 32. Если эти числа поменять местами, то результат не изменится, т. е. 100−32−40−16=12. Правило доказано. Для вычитания переместительный закон записывается в таком виде: М-R-T=S, М-R-S=T и М-T-S=R. Далее необходимо рассмотреть сочетательные правила.
Сочетательный закон
Сочетательное правило сложения и вычитания похожи. Их суть заключается в перегруппировке элементов. Следует отметить, что последняя не влияет на результат. Она необходима для упрощения вычислений. Сочетательный закон сложения формулируется таким образом: значение суммы не зависит от группировок слагаемых.
Например, 4+11+6+9=30. Для удобства можно записать пример в таком виде: (4+6)+(11+9)=30. Результат не изменился. Кроме того, производить вычисления стало проще. В виде формулы закон можно записать в таком виде: М+R+T=М+(R+T)=(М+T)+R=S.
Для вычитания формулировка правила звучит следующим образом: разность не изменится, если перегруппировать вычитаемые компоненты, т. е. 30−6−11−4=30-(6+4)-4=9. Формула закона имеет вид: М-R-T-P= М-R-(T+P)= N. Следует отметить, что числа можно группировать в произвольном порядке. Главное — придерживаться принципа вынесения знака за скобку (касается только вычитания).
е. 30−6−11−4=30-(6+4)-4=9. Формула закона имеет вид: М-R-T-P= М-R-(T+P)= N. Следует отметить, что числа можно группировать в произвольном порядке. Главное — придерживаться принципа вынесения знака за скобку (касается только вычитания).
Некоторые ученики часто приписывают к арифметическим операциям сложения и вычитания распределительное свойство. Это большая ошибка, поскольку для суммы и разности его не существует вообще. Далее необходимо рассмотреть операции, в которых оно применяется.
Произведение и деление
Для умножения и деления применимы те же правила, что и для сложения и вычитания, но к ним добавляется еще и третье — распределительное свойство. В итоге список законов имеет такой вид:
- Переместительный.
- Сочетательный.
- Распределительный.
Следует отметить, что формулировки для переместительного закона сложения и умножения практически идентичны. Для последней математической операции он звучит таким образом: произведение не изменится, когда будет выполнено перемещения одного сомножителя на место другого. Например, 2*3*4=2*4*3=24.
Для последней математической операции он звучит таким образом: произведение не изменится, когда будет выполнено перемещения одного сомножителя на место другого. Например, 2*3*4=2*4*3=24.
В математической форме правило записывается в виде соотношения «RST=SRT=TRS=O». Для деления также используется возможность перемещения делителей, т. е. O: S: T=R или O: Т: S=R. На примере реализация правила выглядит таким образом: 60:2:15=2 или 60:15:2=2.
Для умножения сочетательный закон формулируется в таком виде: значение произведения не изменится при группировке в любом порядке сомножителей, т. е. S*T*R=S*R*T=R*T*S=N. Для деления у него немного другой вид: делители могут группироваться в любом порядке, и это не повлияет на частное. Математическая форма записи выглядит следующим образом: N: T: R: M=N:T:(R:M)=O.
Распределительное свойство для умножения и деления формулируется практически одинаково: произведение (деление) суммы или разности двух элементов на число эквивалентно умножению (делению) каждого элемента суммы или разности на искомый элемент. Законы имеют такие формы записи:
Законы имеют такие формы записи:
- Умножение: (S+T)*M=SM+TM или (S-T)*M=SM-TM.
- Деления: (S+T)/M=S/M+T/M или (S-T)/M=S/M-T/M.
Если обратить внимание на формулы, то для сложения запись невозможна, поскольку это уже будет сочетательный закон. Например, в первом пункте необходимо заменить знак «*» на сложение. Соотношение будет иметь следующий вид: (S+T)+M — сочетательное свойство операции сложения. Далее необходимо разобрать пример на применение всех законов.
Пример задачи
Для закрепления теоретического материала специалисты рекомендуют разобрать пример, в котором можно будет применить все законы арифметических операций. Числовое выражение задачи имеет такой вид: 5+6+5+4+20+(25+100)/5+(11+4)*4. Необходимо вычислить результат оптимальным методом. Решать задание нужно по такому алгоритму:
- Переместительный: 5+5+4+6+20+(25+100)/5+(11+4)*4.

- Сочетательный: (5+5+20)+(4+6)+(25+100)/5+(11+4)*4.
- Распределительный: (5+5+20)+(4+6)+25/5+100/5+11*4+4*4.
- Математические преобразования: 40+5+20+44+16
- Переместительный: 40+20+44+16+5.
- Сочетательный: (40+20)+(44+16)+5.
- Вычисление и результат: 125.
Следует отметить, что к числовому выражению свойства арифметических операций можно применять многократно. Специалисты рекомендуют использовать алгоритм такого вида для оптимизации вычислений.
Таким образом, законы математических операций применяются для оптимизации вычислений для нахождения результатов.
Навигация по справочнику TehTab.
| ||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected]ab.ru | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||
Законы сложения целых чисел. — tutomath репетитор по математике
Законы сложения целых чисел нужны для того, чтобы упростить сложения чисел. Ведь, прибавить все подряд числа не всегда легко, иногда лучше их сгруппировать. Для этого и нужны законы сложения целых чисел.
Переместительный закон сложения.
Правило и формула переместительного закона сложения.
Сложение двух целых чисел не зависит от их порядка.
a+b=b+a
Пример:
Если мы сложим 3+5=8 или 5+3=8 результат сложения не измениться.
Если мы сложим (-3)+7=4 или 7+(-3)=4 результат сложения не измениться.
Сочетательный закон сложения.
Правило и формула сочетательного закона сложения.
К сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего, и результат не измениться.
(a+b)+c=a+(b+c)
Рассмотрим пример:
(3+5)+9=8+9=17
3+(5+9)=3+14=17
От сочетания слагаемых сумма не поменялась.
Делаем вывод на основе переместительного и сочетательного законов:
- Можно слагаемые менять местами.
- Записывать пример со слагаемыми без скобок. Скобки в сложении нужны для удобства восприятия примера.
- Записывать пример со слагаемыми со скобками, для более простого вычисления суммы.

Доказательство:
a+b+c+d=(a+b+c)+d=d+(a+b+c)= d+((a+b)+c)= d+(c+(a+b))=(d+c)+(a+b)=(c+d)+(a+b)
a+b+c+d=(c+d)+(a+b)
6+8+(-6)+(-8)=(6+(-6))+(8+(-8))=0+0=0
Вопросы по теме:
Какие законы сложения вы знаете?
Ответ: переместительный и сочетательный закон.
Можно ли менять местами слагаемые?
Ответ: да по переместительному закону.
Обязательно ли при сложении числа заключать в скобки?
Ответ: нет.
Пример №1:
Вычислите, применяя законы сложения: а) 12+479+88 б) 3+154+16
Решение:
а) 12+479+88=(12+88)+479=100+479=579
б) 3+154+16=3+(154+16)=3+170=173
Пример №2:
Примените переместительный закон сложения: а) 4+5 б) 1298+34
Решение:
а) 4+5=5+4=9
б) 1298+34=34+1298=1332
Пример №3:
Примените сочетательный закон сложения: а) 2+(-4+5) б) (-1+3)+(-8)
Решение:
а) 2+(-4+5)=(2+(-4))+5=(-2)+5=3
б) (-1+3)+(-8)=-1+(3+(-8))=-1+(-5)=-6
Пример №4:
Вычислите, применяя законы сложения: а) 23+((-23)+50) б) -2+(-4)+(-8)+8+4+2
Решение:
а) 23+((-23)+50)=(23+(-23))+50=0+50=50
б) -2+(-4)+(-8)+8+4+2=(-2+2)+(-4+4)+(-8+8)=0
Сложение.
 Свойства переместительного и сочетательного законов.
Свойства переместительного и сочетательного законов.Сложение натуральных чисел.
Прибавить одно число к другому довольно просто. Рассмотрим пример, 4+3=7. Это выражение означает, что к четырем единицам добавили три единицы и в итоге получили семь единиц.
Числа 3 и 4, которые мы сложили называется слагаемыми. А результат сложение число 7 называется суммой.
Сумма — это сложение чисел. Знак плюс “+”.
В буквенном виде этот пример будет выглядеть так:
a+b=c
Компоненты сложения:
a — слагаемое, b — слагаемые, c – сумма.
Если мы к 3 единицам добавим 4 единицы, то в результате сложения получим тот же результат он будет равен 7.
Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые ответ остается неизменным:
4+3=3+4
Называется такое свойство слагаемых переместительным законом сложения.
Переместительный закон сложения.
От перемены мест слагаемых сумма не меняется.
В буквенной записи переместительный закон выглядит так:
a+b=b+a
Если мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 4. И выполним сложение в таком порядке, сначала прибавим 1+2, а потом выполним сложение к получившейся сумме 4, то получим выражение:
(1+2)+4=7
Можем сделать наоборот, сначала сложить 2+4, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так:
1+(2+4)=7
Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод:
(1+2)+4=1+(2+4)
Это свойство сложения называется сочетательным законом сложения.
Переместительный и сочетательный закон сложения работает для всех неотрицательных чисел.
Сочетательный закон сложения.

Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.
(a+b)+c=a+(b+c)
Сочетательный закон работает для любого количества слагаемых. Этот закон мы используем, когда нам нужно сложить числа в удобном нам порядке. Например, сложим три числа 12, 6, 8 и 4. Удобнее будет сначала сложить 12 и 8, а потом прибавить к полученной сумме сумму двух чисел 6 и 4.
(12+8)+(6+4)=30
Свойство сложения с нулем.
При сложении числа с нулем, в результате сумма будет тем же самым числом.
3+0=3
0+3=3
3+0=0+3
В буквенном выражение сложение с нулем будет выглядеть так:
a+0=a
0+a=a
Вопросы по теме сложение натуральных чисел:
Таблица сложения, составьте и посмотрите как работает свойство переместительного закона?
Таблица сложения от 1 до 10 может выглядеть так:
Второй вариант таблицы сложения.
Если посмотрим на таблицы сложения, видно как работает переместительный закон.
В выражении a+b=c суммой, что будет являться?
Ответ: сумма — это результат сложения слагаемых. a+b и с.
В выражении a+b=c слагаемыми, что будет являться?
Ответ: a и b. Слагаемые – это числа, которые мы складываем.
Что произойдет с числом если к нему прибавить 0?
Ответ: ничего, число не поменяется. При сложении с нулем, число остается прежнем, потому что нуль это отсутствие единиц.
Сколько слагаемых должно быть в примере, чтобы было можно применить сочетательный закон сложения?
Ответ: от трех слагаемых и больше.
Запишите переместительный закон в буквенном выражении?
Ответ: a+b=b+a
Примеры на задачи.
Пример №1:
Запишите ответ у представленных выражений: а) 15+7 б) 7+15
Ответ: а) 22 б) 22
Пример №2:
Примените сочетательный закон к слагаемым: 1+3+5+2+9
1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20
Ответ: 20.
Пример №3:
Решите выражение:
а) 5921+0 б) 0+5921
Решение:
а) 5921+0 =5921
б) 0+5921=5921
Калькулятор закона Вина
С помощью этого калькулятора закона Вина можно легко оценить температуру объекта , основываясь на максимальной длине волны или частоте его спектра теплового излучения. Прочтите о законе смещения Вина, изучите формулу закона Вина и самостоятельно оцените температуру поверхности Солнца, лавы или любого горячего тела!
Закон смещения Вина
Закон смещения Вина описывает одно из соотношений между спектром излучения черного тела и его температурой .В нем говорится, что чем выше температура, тем меньше длина волны λ max , для которой кривая излучения достигает своего максимума.
Сдвиг в сторону более коротких волн соответствует фотонам более высоких энергий. Другими словами, λ max (максимальная длина волны) обратно пропорциональна температуре .
Закон Стефана-Больцмана учитывает полную мощность, излучаемую телом при любой температуре, и вместе с законом Вина они происходят из распределения Планка .
Формула закона Вена
Уравнение, описывающее закон Вина, очень простое:
λ макс = б / т ,
где:
-
λ max— вышеупомянутая пиковая длина волны света -
T— абсолютная температура черного тела -
b = 2,8977719 мм * K— постоянная смещения Вина
Хотя соотношение между длиной волны и частотой электромагнитных волн довольно простое ( λ * f = c ), мы не можем вычислить пиковую частоту f max по этой аналогии.Причина в том, что спектральная яркость является своего рода функцией плотности энергии, поэтому ее форма и максимум зависят от аргумента (в нашем случае от длины волны или частоты). Зная, что формула для пиковой частоты:
f макс = k * T ,
, где k = 5,8789232 * 10¹⁰ Гц / K — числовая константа.
Формула закона Вина не может быть получена из классической физики. Среди экспериментов есть многочисленные наблюдения, подтверждающие этот закон (например,ж., фотоэлектрический эффект), которые способствуют созданию квантовой механики.
Как оценить температуру поверхности Солнца? — пример использования
Вы знаете, как ученые могут определить температуру далеких объектов? Обычно они проводят спектроскопическое наблюдение, подгоняют функцию Планка к измерению и получают параметр, которым является температура.
Однако мы также можем получить хорошую оценку, применив к результатам закон смещения Вина.Попробуем вычислить температуру поверхности Солнца:
- Найдите максимальную длину волны солнечного спектра. Это примерно
λ max = 501,7 нм(или5,017 * 10⁻⁷ мв научном представлении). - Преобразуйте формулу закона Вина, чтобы получить температуру:
T = b / λ max = 2,8977719 мм * K / 501,7 нм = 5776 K.
Хотя черное тело — это всего лишь идеализированная модель, закон Вина универсален и может быть очень точным приближением для реальных объектов.Вы также можете определить температуру любого тела, например горячего металла или лавы, в зависимости от цвета излучаемого света — воспользуйтесь калькулятором закона Вина и выясните, удивит вас результат или нет!
| Закон смещения Вина | λmaxT = 2,898 × 10−3м⋅KλmaxT = 2,898 × 10−3m⋅K |
| Закон Стефана | P (T) = σAT4P (T) = σAT4 |
| Постоянная Планка | ч = 6.626 × 10–34Дж⋅с = 4,136 × 10–15 эВ⋅ш = 6,626 × 10–34Джс = 4,136 × 10–15 эВ⋅с |
| Квант энергии излучения | ΔE = hfΔE = hf |
| Закон излучения черного тела Планка | I (λ, T) = 2πhc2λ51ehc / λkBT − 1I (λ, T) = 2πhc2λ51ehc / λkBT − 1 |
| Максимальная кинетическая энергия фотоэлектрона | Kmax = eΔVsKmax = eΔVs |
| Энергия фотона | Ef = hfEf = hf |
| Энергетический баланс фотоэлектрона | Kmax = hf − ϕKmax = hf − ϕ |
| Частота среза | fc = ϕhfc = ϕh |
| Релятивистский инвариант уравнение энергии | E2 = p2c2 + m02c4E2 = p2c2 + m02c4 |
| Зависимость энергии от импульса для фотона | pf = Efcpf = Efc |
| Энергия фотона | Ef = hf = hcλEf = hf = hcλ |
| Величина импульса фотона | pf = hλpf = hλ |
| Линейный вектор импульса фотона | p → f = ℏk → p → f = ℏk → |
| Комптоновская длина волны электрона | λc = hm0c = 0. 00243нм λc = hm0c = 0,00243нм 00243нм λc = hm0c = 0,00243нм |
| Комптоновский сдвиг | Δλ = λc (1 − cosθ) Δλ = λc (1 − cosθ) |
| Формула Бальмера | 1λ = RH (122−1n2) 1λ = RH (122−1n2) |
| Формула Ридберга | 1λ = RH (1nf2−1ni2), ni = nf + 1, nf + 2,… 1λ = RH (1nf2−1ni2), ni = nf + 1, nf + 2,… |
| Первое условие квантования Бора | Ln = nℏ, n = 1,2,… Ln = nℏ, n = 1,2,… |
| Второе условие квантования Бора | hf = | En-Em | hf = | En-Em | |
| Радиус водорода Бора | a0 = 4πε0ℏ2mee2 = 0. 529Åa0 = 4πε0ℏ2mee2 = 0,529Å 529Åa0 = 4πε0ℏ2mee2 = 0,529Å |
| Радиус Бора n -й орбиты | rn = a0n2rn = a0n2 |
| Значение энергии в основном состоянии, предел ионизации | E0 = 18ε02mee4h4 = 13.6eVE0 = 18ε02mee4h4 = 13.6eV |
| Энергия электрона на n -й орбите | En = -E01n2En = -E01n2 |
| Энергия основного состояния водорода | E1 = −E0 = −13,6 эВE1 = −E0 = −13,6 эВ |
| n -я орбита водородоподобного иона | rn = a0Zn2rn = a0Zn2 |
| n энергия водородоподобного иона | En = −Z2E01n2En = −Z2E01n2 |
| Энергия материальной волны | E = hfE = hf |
| Длина волны де Бройля | λ = hpλ = hp |
| Соотношение частота-длина волны для волн материи | λf = cβλf = cβ |
| Принцип неопределенности Гейзенберга | ΔxΔp≥12ℏΔxΔp≥12ℏ |
Сложение векторов
С векторами и над векторами можно выполнять множество математических операций. Одна из таких операций — сложение векторов. Два вектора можно сложить вместе, чтобы определить результат (или результат). Этот процесс добавления двух или более векторов уже обсуждался в предыдущем разделе. Вспомните в нашем обсуждении законов движения Ньютона, что результирующая сила , испытываемая объектом, была определена путем вычисления векторной суммы всех индивидуальных сил, действующих на этот объект. То есть чистая сила была результатом (или результатом) сложения всех векторов силы.Во время этого блока правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Одна из таких операций — сложение векторов. Два вектора можно сложить вместе, чтобы определить результат (или результат). Этот процесс добавления двух или более векторов уже обсуждался в предыдущем разделе. Вспомните в нашем обсуждении законов движения Ньютона, что результирующая сила , испытываемая объектом, была определена путем вычисления векторной суммы всех индивидуальных сил, действующих на этот объект. То есть чистая сила была результатом (или результатом) сложения всех векторов силы.Во время этого блока правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Эти правила суммирования векторов были применены к диаграммам свободного тела, чтобы определить результирующую силу (т. Е. Векторную сумму всех отдельных сил). Примеры приложений показаны на схеме ниже.
В этом модуле задача суммирования векторов будет расширена на более сложные случаи, в которых векторы направлены в направлениях, отличных от чисто вертикального и горизонтального направлений. Например, вектор, направленный вверх и вправо, будет добавлен к вектору, направленному вверх и влево. Векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Например, вектор, направленный вверх и вправо, будет добавлен к вектору, направленному вверх и влево. Векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Существует множество методов для определения величины и направления результата сложения двух или более векторов. В этом уроке будут обсуждаться два метода, которые будут использоваться на протяжении всего модуля:
Теорема Пифагора
Теорема Пифагора — полезный метод для определения результата сложения двух (и только двух) векторов , образующих прямой угол друг к другу.Этот метод неприменим для добавления более двух векторов или для сложения векторов , а не под углом 90 градусов друг к другу. Теорема Пифагора — это математическое уравнение, которое связывает длину сторон прямоугольного треугольника с длиной гипотенузы прямоугольного треугольника.
Чтобы увидеть, как работает метод, рассмотрим следующую задачу:
Эрик покидает базовый лагерь и отправляется в поход на 11 км на север, а затем на 11 км на восток.
Определите результирующее смещение Эрика.
В этой задаче требуется определить результат сложения двух векторов смещения, расположенных под прямым углом друг к другу. Результат (или результат) ходьбы на 11 км на север и 11 км на восток — это вектор, направленный на северо-восток, как показано на диаграмме справа. Поскольку смещение на север и смещение на восток расположены под прямым углом друг к другу, теорема Пифагора может использоваться для определения результирующей (то есть гипотенузы прямоугольного треугольника).
Результат сложения 11 км, север плюс 11 км, восток — вектор с величиной 15,6 км. Позже будет обсуждаться метод определения направления вектора.
Давайте проверим ваше понимание с помощью следующих двух практических задач. В каждом случае используйте теорему Пифагора, чтобы определить величину векторной суммы . По завершении нажмите кнопку, чтобы просмотреть ответ.
Использование тригонометрии для определения направления вектора
Направление результирующего вектора часто можно определить с помощью тригонометрических функций. Большинство студентов вспоминают значение полезной мнемоники SOH CAH TOA из своего курса тригонометрии. SOH CAH TOA — мнемоника, которая помогает запомнить значение трех общих тригонометрических функций — синуса, косинуса и тангенса. Эти три функции связывают острый угол в прямоугольном треугольнике с отношением длин двух сторон прямоугольного треугольника. Функция синуса связывает меру острого угла с отношением длины стороны, противоположной углу, к длине гипотенузы.Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Функция касательной связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, примыкающей к углу. Три уравнения ниже суммируют эти три функции в форме уравнения.
Большинство студентов вспоминают значение полезной мнемоники SOH CAH TOA из своего курса тригонометрии. SOH CAH TOA — мнемоника, которая помогает запомнить значение трех общих тригонометрических функций — синуса, косинуса и тангенса. Эти три функции связывают острый угол в прямоугольном треугольнике с отношением длин двух сторон прямоугольного треугольника. Функция синуса связывает меру острого угла с отношением длины стороны, противоположной углу, к длине гипотенузы.Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Функция касательной связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, примыкающей к углу. Три уравнения ниже суммируют эти три функции в форме уравнения.
Эти три тригонометрические функции могут быть применены к задаче туриста, чтобы определить направление общего перемещения туриста.Процесс начинается с выбора одного из двух углов (кроме прямого) треугольника. После выбора угла любую из трех функций можно использовать для определения меры угла. Напишите функцию и выполните соответствующие алгебраические шаги, чтобы найти меру угла. Работа представлена ниже.
После выбора угла любую из трех функций можно использовать для определения меры угла. Напишите функцию и выполните соответствующие алгебраические шаги, чтобы найти меру угла. Работа представлена ниже.
После определения меры угла можно определить направление вектора. В этом случае вектор составляет угол 45 градусов относительно востока.Таким образом, направление этого вектора записывается как 45 градусов. (Вспомните, как говорилось ранее в этом уроке, что направление вектора — это угол поворота против часовой стрелки, который вектор совершает относительно востока.)
Расчетный угол не всегда соответствует направлению
Мера угла, определяемая с помощью SOH CAH TOA, составляет , а не всегда в направлении вектора. Следующая векторная диаграмма сложения является примером такой ситуации.Обратите внимание, что угол внутри треугольника определен как 26,6 градуса с использованием SOH CAH TOA. Этот угол представляет собой угол поворота на юг, который вектор R делает по отношению к Западу. Тем не менее, направление вектора, выраженное условным обозначением CCW (против часовой стрелки с востока), составляет 206,6 градуса.
Тем не менее, направление вектора, выраженное условным обозначением CCW (против часовой стрелки с востока), составляет 206,6 градуса.
Проверьте свое понимание использования SOH CAH TOA для определения направления вектора, попробовав следующие две практические задачи.В каждом случае используйте SOH CAH TOA для определения направления результирующего. По завершении нажмите кнопку, чтобы просмотреть ответ.
В приведенных выше задачах величина и направление суммы двух векторов определяется с помощью теоремы Пифагора и тригонометрических методов (SOH CAH TOA). Процедура ограничивается сложением двух векторов, образующих прямые углы друг к другу.Когда два вектора, которые должны быть добавлены, не находятся под прямым углом друг к другу, или когда необходимо сложить более двух векторов, мы будем использовать метод, известный как метод сложения векторов голова к хвосту. Этот метод описан ниже.
Использование масштабированных векторных диаграмм для определения результата
Величину и направление суммы двух или более векторов можно также определить с помощью точно нарисованной масштабированной векторной диаграммы. Используя масштабированную диаграмму, метод «голова к хвосту» используется для определения векторной суммы или результата. Обычная физическая лаборатория включает векторных прогулок . Либо используя смещения сантиметрового размера на карте, либо смещения метрового размера на большой открытой местности, ученик выполняет несколько последовательных смещений, начиная с назначенной начальной позиции. Предположим, вам дали карту вашего района и 18 направлений, по которым вам нужно следовать. Начиная с домашней базы , эти 18 векторов смещения могут быть суммированы вместе последовательно, чтобы определить результат сложения набора из 18 направлений.Возможно, первый вектор измеряется 5 см, восток. Когда это измерение закончится, начнется следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда одно измерение заканчивалось, начиналось следующее измерение. По сути, вы использовали бы метод сложения векторов «голова к хвосту».
Используя масштабированную диаграмму, метод «голова к хвосту» используется для определения векторной суммы или результата. Обычная физическая лаборатория включает векторных прогулок . Либо используя смещения сантиметрового размера на карте, либо смещения метрового размера на большой открытой местности, ученик выполняет несколько последовательных смещений, начиная с назначенной начальной позиции. Предположим, вам дали карту вашего района и 18 направлений, по которым вам нужно следовать. Начиная с домашней базы , эти 18 векторов смещения могут быть суммированы вместе последовательно, чтобы определить результат сложения набора из 18 направлений.Возможно, первый вектор измеряется 5 см, восток. Когда это измерение закончится, начнется следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда одно измерение заканчивалось, начиналось следующее измерение. По сути, вы использовали бы метод сложения векторов «голова к хвосту».
Метод «голова к хвосту» включает рисование вектора для масштабирования на листе бумаги, начиная с заданной начальной позиции.Там, где заканчивается голова этого первого вектора, начинается хвост второго вектора (таким образом, метод «голова к хвосту» ). Процесс повторяется для всех добавляемых векторов. После того, как все векторы были добавлены по направлению «голова к хвосту», результирующий результат протягивается от хвоста первого вектора к началу последнего вектора; т.е. от начала до конца. Как только результат нарисован, его длину можно измерить и преобразовать в реальных единиц, используя заданный масштаб. Направление полученного результата можно определить, используя транспортир и измерив его угол поворота против часовой стрелки с востока.
Пошаговый метод применения метода «голова к хвосту» для определения суммы двух или более векторов приведен ниже.
- Выберите масштаб и укажите его на листе бумаги. Наилучший выбор масштаба — такой, при котором диаграмма будет как можно больше, но при этом умещается на листе бумаги.

- Укажите начальную точку и нарисуйте первый вектор в масштабе в указанном направлении. Обозначьте величину и направление шкалы на диаграмме (например,г., МАСШТАБ: 1 см = 20 м).
- Начиная с того места, где заканчивается голова первого вектора, нарисуйте второй вектор в масштабе в указанном направлении. Обозначьте величину и направление этого вектора на диаграмме.
- Повторите шаги 2 и 3 для всех добавляемых векторов
- Нарисуйте результат от хвоста первого вектора к голове последнего вектора. Обозначьте этот вектор как Resultant или просто R .
- Используя линейку, измерьте длину полученного результата и определите его величину путем преобразования в действительные единицы с помощью шкалы (4.4 см х 20 м / 1 см = 88 м).
- Измерьте направление результирующей, используя условные обозначения против часовой стрелки, о которых говорилось ранее в этом уроке.
Пример использования метода «голова к хвосту» проиллюстрирован ниже.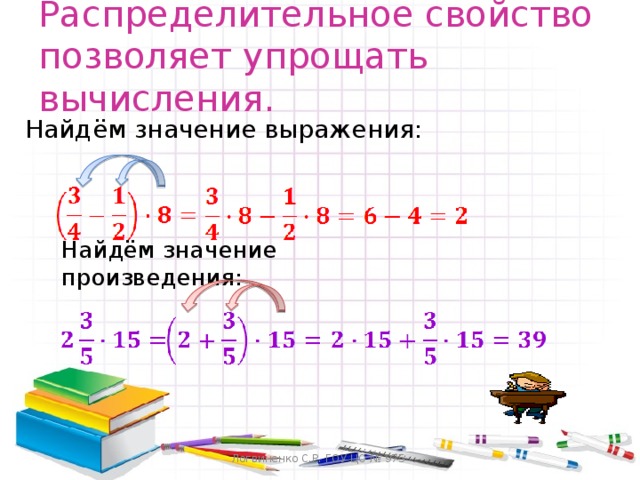 Задача заключается в сложении трех векторов:
Задача заключается в сложении трех векторов:
20 м, 45 град. + 25 м, 300 град. + 15 м, 210 град.
МАСШТАБ: 1 см = 5 м
Метод «голова к хвосту» используется, как описано выше, и определяется результат (выделен красным).Его величина и направление обозначены на схеме.
МАСШТАБ: 1 см = 5 м
Интересно, что порядок, в котором добавляются три вектора, не влияет ни на величину, ни на направление результирующего. Результирующий по-прежнему будет иметь ту же величину и направление. Например, рассмотрим сложение тех же трех векторов в другом порядке.
15 м, 210 град.+ 25 м, 300 град. + 20 м, 45 град.
МАСШТАБ: 1 см = 5 м
При сложении в этом другом порядке эти же три вектора по-прежнему дают результат с той же величиной и направлением, что и раньше (20. м, 312 градусов). Порядок, в котором векторы добавляются с использованием метода «голова к хвосту», не имеет значения.
МАСШТАБ: 1 см = 5 м
Дополнительные примеры сложения векторов методом «голова к хвосту» приведены на отдельной веб-странице.
Мы хотели бы предложить …
Иногда просто прочитать об этом недостаточно. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов». Все три интерактивных элемента можно найти в разделе «Интерактивная физика» на нашем веб-сайте и обеспечить интерактивный опыт с навыком добавления векторов.
Закон Вены о перемещении | Постановление и уравнение
Закон смещения Вина (названный в честь немецкого физика) описывает смещение этого пика с точки зрения температуры.
Закон смещения Вина и тот факт, что частота обратно пропорциональна длине волны, также указывает на то, что пиковая частота f max ( цвет объекта ) пропорциональна абсолютной температуре T черного тела.
Согласно закону смещения Вина , спектральная яркость излучения черного тела на единицу длины волны достигает пика на длине волны λ max , определяемой по формуле:
, где T — абсолютная температура в Кельвинах, b — a константа пропорциональности, известная как константа смещения Вина , равна 2,8978 × 10 −3 км .
Как видно из рисунка, кривая излучения абсолютно черного тела для различных температур имеет максимум на длине волны, обратно пропорциональной температуре. Закон Вена (названный в честь немецкого физика) описывает смещение этого пика с точки зрения температуры. Закон смещения Вина и тот факт, что частота обратно пропорциональна длине волны, также указывает на то, что пиковая частота f max ( цвет объекта ) пропорциональна абсолютной температуре T черного тела. Таким образом, при повышении температуры цвет свечения меняется с красного на желтый, с белого на синий.
Согласно закону смещения Вина , спектральная яркость излучения черного тела на единицу длины волны достигает пика на длине волны λ max определяется по формуле:
, где T — абсолютная температура в Кельвинах, b — a Константа пропорциональности, известная как Константа смещения Вина , равна 2.8978 × 10 −3 км . Следует отметить, что даже при раскаленной добела температуре 2000 К около 99% лучистой энергии все еще излучается в инфракрасном (невидимом) спектре.
Хотя смещение этого пика является прямым следствием закона Планка , он был открыт Вильгельмом Вином за несколько лет до того, как Макс Планк разработал это более общее уравнение.
Излучение черного тела
Известно, что количество энергии излучения, испускаемого поверхностью на данной длине волны, зависит от материала тела и состояния его поверхности , а также температуры поверхности . Следовательно, различные материалы излучают разное количество лучистой энергии, даже если они имеют одинаковую температуру. Тело , которое излучает максимальное количество тепла для своей абсолютной температуры, называется черным телом .
Следовательно, различные материалы излучают разное количество лучистой энергии, даже если они имеют одинаковую температуру. Тело , которое излучает максимальное количество тепла для своей абсолютной температуры, называется черным телом .
Черное тело — это идеализированное физическое тело, обладающее определенными свойствами. По определению, черное тело в тепловом равновесии имеет коэффициент излучения , равный ε = 1,0 . Реальные объекты не излучают столько тепла, как идеальное черное тело.Они излучают меньше тепла, чем черное тело, и поэтому называются серыми телами.
Поверхность черного тела излучает тепловое излучение примерно 448 Вт на квадратный метр при комнатной температуре (25 ° C, 298,15 K). Реальные объекты с коэффициентом излучения менее 1,0 (например, медная проволока) излучают с соответственно более низкой интенсивностью (например, 448 x 0,03 = 13,4 Вт / м 2 ). Коэффициент излучения играет важную роль в решении проблем теплопередачи. Например, солнечные коллекторы тепла включают отдельные поверхности с очень низким коэффициентом излучения.Эти коллекторы тратят очень мало солнечной энергии из-за теплового излучения.
Коэффициент излучения играет важную роль в решении проблем теплопередачи. Например, солнечные коллекторы тепла включают отдельные поверхности с очень низким коэффициентом излучения.Эти коллекторы тратят очень мало солнечной энергии из-за теплового излучения.
Поскольку коэффициент поглощения и коэффициент излучения связаны между собой Законом Кирхгофа теплового излучения, черное тело также является идеальным поглотителем электромагнитного излучения.
Закон теплового излучения Кирхгофа :
Для произвольного тела, излучающего и поглощающего тепловое излучение в термодинамическом равновесии, коэффициент излучения равен коэффициенту поглощения.
коэффициент излучения ε = поглощающая способность α
Черное тело поглощает все падающее электромагнитное излучение, независимо от частоты или угла падения. Его поглощающая способность , таким образом, равна единице, что также является максимально возможным значением. Таким образом, черное тело является идеальным поглотителем (и идеальным излучателем ).
Его поглощающая способность , таким образом, равна единице, что также является максимально возможным значением. Таким образом, черное тело является идеальным поглотителем (и идеальным излучателем ).
Обратите внимание, что видимое излучение занимает очень узкую полосу спектра от 0.4–0,76 нм, мы не можем судить о черноте поверхности на основе визуальных наблюдений. Например, рассмотрим белую бумагу, которая отражает видимый свет и поэтому кажется белой. С другой стороны, он практически черный для инфракрасного излучения (коэффициент поглощения α = 0,94 ), поскольку они сильно поглощают длинноволновое излучение.
Ссылки:
Теплопередача:
- Основы тепломассообмена, 7-е издание. Теодор Л. Бергман, Эдриенн С.Лавин, Фрэнк П. Инкропера. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
- Тепло- и массообмен. Юнус А. Ценгель. McGraw-Hill Education, 2011.
 ISBN: 9780071077866.
ISBN: 9780071077866. - Министерство энергетики США, термодинамики, теплопередачи и потока жидкости. Справочник Министерства энергетики США, том 2 от 3 мая 2016 г.
Ядерная и реакторная физика:
- Дж. Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Аддисон-Уэсли, Ридинг, Массачусетс (1983).
- Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную инженерию, 3-е изд., Прентис-Холл, 2001, ISBN: 0-201-82498-1.
- У. М. Стейси, Физика ядерных реакторов, John Wiley & Sons, 2001, ISBN: 0-471-39127-1.
- Гласстон, Сесонске. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4-е издание, 1994 г., ISBN: 978-0412985317
- W.S.C. Уильямс. Ядерная физика и физика элементарных частиц. Clarendon Press; 1 издание, 1991 г., ISBN: 978-0198520467
- G.Р.Кипин. Физика ядерной кинетики. Аддисон-Уэсли Паб. Co; 1-е издание, 1965 г.
- Роберт Рид Берн, Введение в работу ядерных реакторов, 1988 г.

- Министерство энергетики, ядерной физики и теории реакторов США. Справочник по основам DOE, том 1 и 2. Январь 1993 г.
- Пол Ройсс, Нейтронная физика. EDP Sciences, 2008. ISBN: 978-2759800414.
Advanced Reactor Physics:
- K. O. Ott, W. A. Bezella, Введение в статику ядерных реакторов, Американское ядерное общество, пересмотренное издание (1989), 1989, ISBN: 0-894-48033-2.
- К. О. Отт, Р. Дж. Нойхольд, Введение в динамику ядерных реакторов, Американское ядерное общество, 1985, ISBN: 0-894-48029-4.
- Д. Л. Хетрик, Динамика ядерных реакторов, Американское ядерное общество, 1993, ISBN: 0-894-48453-2.
- Э. Льюис, В. Ф. Миллер, Вычислительные методы переноса нейтронов, Американское ядерное общество, 1993, ISBN: 0-894-48452-4.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
 Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Сложение и вычитание векторов: графические методы
Используйте графическую технику для добавления векторов, чтобы найти полное смещение человека, который идет следующими тремя путями (смещениями) на плоском поле.Сначала она проходит 25,0 м в направлении 49,0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0 ° к югу от востока.
Стратегия
Изобразите каждый вектор смещения графически стрелкой, обозначив первый A , второй B и третий C , сделав длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад.Описанный выше метод «голова к хвосту» дает возможность определить величину и направление результирующего смещения, обозначенное R .
Решение
(1) Нарисуйте три вектора смещения.
(2) Поместите векторы голова к хвосту, сохраняя их начальную величину и направление.
(3) Нарисуйте результирующий вектор, R .
(4) Используйте линейку, чтобы измерить звездную величину R , и транспортир, чтобы измерить направление R .Хотя направление вектора можно указать разными способами, самый простой способ — измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх дном и измеряем угол между осью, направленной на восток, и вектором.
Рисунок 11
В этом случае видно, что полное смещение R имеет величину 50,0 м и лежит в направлении 7.0º к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0 ° к югу от востока.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результат не зависит от порядка добавления векторов. Следовательно, мы можем складывать векторы в любом порядке, как показано на рисунке 12, и мы все равно получим то же самое решение.
Также важно отметить, что результат не зависит от порядка добавления векторов. Следовательно, мы можем складывать векторы в любом порядке, как показано на рисунке 12, и мы все равно получим то же самое решение.
Здесь мы видим, что когда одни и те же векторы добавляются в другом порядке, результат тот же. Эта характеристика верна во всех случаях и является важной характеристикой векторов. Сложение вектора — , коммутативное . Векторы можно добавлять в любом порядке.
A + B = B + A.
(Это верно и для сложения обычных чисел — например, вы получите тот же результат, прибавляете ли вы 2 + 3 или 3 + 2 ).
Получение закона смещения Вина из закона Планка
Закон смещения Вина утверждает, что кривая излучения черного тела для различных температур достигает пика на длине волны, обратно пропорциональной температуре. {\ frac {h \ nu} {k_B T}} — 1 \ right)} \ label {Planck2} \]
Нам нужно вычислить производную уравнения \ ref {Planck2} по отношению к \ (\ nu \) и установить ее равной нулю, чтобы найти максимальную длину волны. {10} Гц / К) \, T \ end {align} \]
{10} Гц / К) \, T \ end {align} \]
В результате форма функции излучения абсолютно черного тела будет пропорционально изменяться по частоте с температурой. Когда Макс Планк позже сформулировал правильную функцию излучения черного тела, она не включала в явном виде постоянную Вина. Скорее, постоянная Планка h была создана и введена в его новую формулу. Из постоянной Планка h и постоянной Больцмана k можно получить постоянную Вина (уравнение \ ref {eq20}).
Авторы и авторство
.
Урок по теме «Распределительный закон умножения»
Методическая информация.
1. Тип урока по основной дидактической цели - урок закрепления и систематизации знаний; выработки умений по применению распределительного закона умножения.
2. Цели урока:
1) образовательные: систематизировать,
расширить и углубить знания, формировать умение
применять распределительный закон умножения при
решении задач, продолжить выявление пробелов в
знаниях и ликвидировать их.
2) развивающие: способствовать развитию наблюдательности, умения находить наиболее рациональные пути решения задач, развивать вычислительные навыки, продолжить формирование у учащихся умения самостоятельно работать.
3) воспитательные: воспитание чувства ответственности за результат, воспитывать культуру умственного труда, развивать коммуникативные качества личности, развивать способность самооценки.
3. Задачи урока:
Активизировать знания учащихся о распределительном законе, расширить и углубить знания по теме. Создать условия для того, чтобы учащиеся могли применять их на практике при решении примеров, уравнений и текстовых задач. Развивать устойчивый познавательный интерес к изучению математики. Вырабатывать умение самокритично оценивать свои знания и выбирать задания соответственно своему уровню знаний.
4. Знании, умения, навыки и качества, которые
закрепят ученики в ходе урока:
Знании, умения, навыки и качества, которые
закрепят ученики в ходе урока:
продолжить выработку умений применять распределительный закон умножения при упрощении выражений, путем вынесения общего множителя за скобки, для более рационального счета, решать уравнения и составлять их при решении текстовых задач.
5. Оборудование:
Слайдовая презентация урока “Распределительный закон умножения”, классная доска, ноутбук, экран, медиа-проектор, учебник “Математика, 5” автор Н.Я. Виленкин, В.И. Жохов, индивидуальные оценочны листы, карточки с заданиями к “Математической эстафете”, карточки с задачами, карточки с тестами, листы с заданиями для самостоятельной работы трех уровней.
Ход урока
1 этап. Организационный момент урока – 2 мин.
Учитель приветствует учащихся, сообщает тему
урока (Приложение 1. Слайд №1), эпиграф (Приложение
1. Слайд №2), ставит перед классом цели урока (Приложение
1. Слайд №3), план урока (Приложение 1.Слайд
№4), правила заполнения индивидуальных
оценочных листов.
Слайд №1), эпиграф (Приложение
1. Слайд №2), ставит перед классом цели урока (Приложение
1. Слайд №3), план урока (Приложение 1.Слайд
№4), правила заполнения индивидуальных
оценочных листов.
Здравствуйте, ребята! Сегодня на уроке нам предстоит повторить распределительный закон умножения и подготовиться к контрольной работе. Будьте внимательны! Наш урок
будет состоять из нескольких этапов, вы их видите на слайде (Приложение 1. Слайд №3), оценку за урок мы будем накапливать (Приложение 1. Слайд №5) и в конце урока подведем итоги. Ваша работа будет считаться успешной и получаете оценку “5”, если вы наберете от 37 до 41 баллов, если вы набираете от 29 до 36 баллов, то вы получаете оценку “4”, если от 20 до 28 – оценку “3”, менее 20 баллов — оценку “2”.
2 этап. Проверка домашнего задания – 5 мин.

Цель этапа: подчеркнуть важность выполнения домашнего задания, искать рациональные пути решения для упрощения вычислительной работы, выявление пробелов в знаниях.
Знания: вынесение за скобки общего множителя числового или буквенного.
Умения: составление уравнений и их решение, нахождение неизвестной компоненты.
Форма работы: фронтальная, самопроверка.
Используемые цифровые ресурсы или их компоненты – (Приложение 1. Слайд №6).
Домашнее задание:
1. Упростите выражение.
2. Вычислите наиболее простым способом.
3. Решите уравнение.
4. Решите задачу.
В семье 4 человека: мама, папа, сын и дочь. Вместе им 110 лет. Мама старше дочери в 5 раз, и младше отца на 6 лет, а дочь младше сына в 2 раза. Сколько лет каждому из членов семьи?
| № задания | Ответ: |
№1. а) а) |
97а |
| б) | 9m+48 |
| в) | 0 |
| г) | 100 |
| №2. а) | 246900 |
| б) | 25(26-24)+23(24-22)+21(22-20)+19(20-18)+17(18-16)+15(16-14)= = 2(25+15+23+17+21+19) = 2(40+40+40) = 240 |
| №3. а) | x = 2 |
| б) | x = 5 |
| в) | x = 3 |
| №4. | Уравнение: x+2x+5x+5x+6=110; х = 8; 8 лет, 16 лет, 40 лет, 46 лет |
Деятельность учителя – учитель зачитывает
верные ответы к заданиям домашней работы.
Деятельность ученика – сверяет свои ответы с готовыми на экране.
Задания домашней работы проецируются на экран с готовыми ответами. Учащимся предлагается сравнить их со своими ответами и оценить каждое верно выполненное задание 1 баллом. Максимальное число баллов на данном этапе – 10. Полученные баллы учащиеся заносят в индивидуальный оценочный лист.
— Ребята, а каким способом вы решали задание №2?
Часть учащихся решали по действиям, другие с помощью распределительного закона. Сравниваем и делаем вывод, что второй способ не требует больших вычислений и он более рациональный. При разборе задачи №4 выясняем, что учащиеся принимали за х, какое уравнение составили и какой ответ получили.
3 этап. “Разминка” — тест с взаимопроверкой (в парах) – 7мин.
Цель этапа: актуализировать знания по теме,
осуществлять самостоятельную деятельность на
уроке, развивать коммуникативные качества.
Умения: применять распределительный закон умножения, находить ошибки в решении товарища, составить уравнение по тексту задачи и решить его.
Форма работы: индивидуальная, а во время проверки — в парах.
Используемые цифровые ресурсы — (Приложение 1. Слайды №7, №8, №9).
Деятельность учителя – консультирует детей, дает рекомендации по выполнению заданий теста, контролирует самостоятельность решения.
Деятельность ученика: самостоятельно выполняет задания, затем после обмена работами осуществляет проверку работы товарища, сравнивая с готовыми ответами на экране, оценивает баллами его работу. Заносит баллы в индивидуальный оценочный лист. Готовые ответы проецируются на экран. Задания №1 и №2 оцениваются в 1 балл,
№3 – 2 балла. Максимальное число баллов – 9.
Во время проверки теста учитель предлагает
учащимся прочитать законы умножения.
Спрашивает ребят: “Кто не ошибся и набрал максимальное количество баллов?”
Большинство ребят сделали верно, настроение улучшается, повышается мотивация, ребята стремятся к дальнейшим победам.
1. Соедините линиями соответствующие законы умножения:
Оценка: 3 балла ( по баллу за каждое верное соединение).
1. Отметить знаком “+” верно выполненные выражения.
Оценка – 4 балла за каждое верно выбранное или верно не выбранное выражение.
2. Составьте уравнение к задаче:
Ученик задумал число, умножил его на 8, затем это же число отдельно умножил на 15 и результаты сложил. В сумме получилось 276. Какое число задумал ученик?
Оценка – 2 балла.
4 этап. “Математическая эстафета” — 8 мин.
Цель этапа: выявление пробелов в знаниях,
развитие коммуникативных качеств учащихся.
Умения: вынесение общего множителя за скобки, находить неизвестную компоненту в уравнениях.
Форма работы: групповая — в парах и группа 8-9 человек.
Используемые цифровые ресурсы — (Приложение 1. Слайд №10, №11).
Деятельность учителя – консультирует по правилам игры. Организует проверку результатов.
На последней парте каждого ряда находятся по листу с 9 заданиями (по два задания каждой парте). Эти же задания высвечены на экране (Приложение 1. Слайд №10).
Ученики последней парты, решив два первых
задания, передают впереди сидящим учащимся,
после чего решают последующие задания
высвеченные на экране. Если удаётся решить все
задания верно и быстрее своей команды, то ученик
получает оценку “5”. На общем листе два задания
ученики решают парами. Одно из заданий: решить
уравнение, второе – упростить выражение. Эстафет
считается оконченной, когда все три листа лежат
на первой парте.
Эстафет
считается оконченной, когда все три листа лежат
на первой парте.
Задания 1), 3), 5), 7), 9) — Решить уравнение;
Задания 2), 4), 6), 8) — Упростить выражение.
| 1 ряд | 2 ряд | 3 ряд | |||
| 1 | 25x + 87x = 336 | 1 | 66y – 29y = 74 | 1 | 54x + 41x = 190 |
| 2 | 41y — 21y + y | 2 | 92x + x – 33x | 2 | 63a + a – 51a |
| 3 | 16a – 9a + 5 = 75 | 3 | 25k – 16k + 5 = 86 | 3 | 39x – 27x + 15 = 63 |
| 4 | 45b + 24b – 69b | 4 | 74c + 47c – 121c | 4 | 45y + 31y – 76y |
| 5 | 18x + 62x — 15 = 145 | 5 | 16a + 73a – 26 = 152 | 5 | 58x + 96x – 54 = 100 |
| 6 | 99k – 19k + k — 81 | 6 | 46d – 24d + d — 23 | 6 | 61k – 57k + k — 5 |
| 7 | 44x — 22x = 880 | 7 | 77y – 55y = 660 | 7 | 99d — 11d = 176 |
| 8 | n + 2n – 3n + 2008 | 8 | 9t – 5t – 4t + 2009 | 8 | x + 5x – 6x + 2010 |
| 9 | 55x – 13x – 17x = 625 | 9 | 47y + 53y – 80y = 180 | 9 | 42 y + 98y – 40y = 600 |
Ответы к “Математической эстафете”:
| 1 ряд | 2 ряд | 3 ряд | |||
| 1 | x = 3 | 1 | y = 2 | 1 | x = 2 |
| 2 | 21y | 2 | 60x | 2 | 13a |
| 3 | a = 10 | 3 | k = 9 | 3 | x = 4 |
| 4 | 0 | 4 | 0 | 4 | 0 |
| 5 | x = 2 | 5 | a = 2 | 5 | x = 1 |
| 6 | 81k — 81 | 6 | 23d — 23 | 6 | 5k — 5 |
| 7 | x = 40 | 7 | y = 30 | 7 | d = 2 |
| 8 | 2008 | 8 | 2009 | 8 | 2010 |
| 9 | x = 25 | 9 | y = 9 | 9 | y = 6 |
Деятельность ученика – решают задания,
записывают решение в общий лист, который
передают вперед, следующей паре учащихся. Затем
команды обмениваются листами с решениями и
осуществляют проверку, соотнося с готовыми
ответами на экране (Приложение 1. Слайд №11),
выставляют баллы — по 1 за каждое верно решенное
задание. Максимум — 9 баллов. Первой, сдавшей
решение команде, добавляется 2 балла, второй –
1 балл. Учащиеся заносят командные баллы в
оценочный лист.
Затем
команды обмениваются листами с решениями и
осуществляют проверку, соотнося с готовыми
ответами на экране (Приложение 1. Слайд №11),
выставляют баллы — по 1 за каждое верно решенное
задание. Максимум — 9 баллов. Первой, сдавшей
решение команде, добавляется 2 балла, второй –
1 балл. Учащиеся заносят командные баллы в
оценочный лист.
5. “Решение задач с помощью уравнений”. – 7 мин.
Цель этапа: развитие логико – смыслового мышления.
Умения: введя переменную х и переведя текст задачи на математический язык, составить математическую модель — в виде уравнения, решить его, ответить на вопрос задачи.
Форма работы: групповая — 3 ряда — 3 команды.
Используемые цифровые ресурсы — (Приложение 1. Слайд №12, №13)
Деятельность учителя – выбирает любого из
учеников для решения у доски, контролирует
правильность решения, оценивает объяснение
решения у доски, грамотно заданные вопросы с
места. Уравнения и ответы высвечиваются на
экране.
Уравнения и ответы высвечиваются на
экране.
Деятельность ученика – решают задачу своей команды на местах, поправляют ответ участников своей команды, решающих у доски ( в случае ошибок отвечающего), задают вопросы соперникам, изображая непонимание. Рефлексия: осознание учеником деятельности: того как, каким способом получен результат, какие при этом встречались затруднения, как они были устранены, и что чувствовал ученик при этом.
Верно решившие задачу, заносят в оценочный лист — 3 балла.
Задача 1 ряда.
Маша, Оля и Таня пошли в лес за грибами. Маша собрала в 3 раза больше грибов, чем Таня, а Оля в 2 раза больше, чем Таня. Сколько грибов собрала каждая девочка, если всего они собрали 84 гриба?
_________________________________________________________________________________
Задача 2 ряда.
В лесу жили хамелеоны. Синих хамелеонов было в 7
раз больше, чем красных, а красных в 5 раз больше,
чем зеленых. Сколько хамелеонов каждого цвета
жило в лесу, если всего их было насчитано 123
хамелеона?
Синих хамелеонов было в 7
раз больше, чем красных, а красных в 5 раз больше,
чем зеленых. Сколько хамелеонов каждого цвета
жило в лесу, если всего их было насчитано 123
хамелеона?
_________________________________________________________________________________
Задача 3 ряда.
В зоопарке жили хищные животные. Тигров было в 2 раза больше, чем ягуаров и в 4 раза меньше, чем пантер. Сколько хищников каждого вида жило в зоопарке, если всего насчитывалось 55 животных?
6 этап. Самостоятельная разно — уровневая работа с самопроверкой — 10 мин.
Вначале этапа учащимся демонстрируются 3 уровня работы и предлагается выбрать самим, оценив реально свои возможности, для получения наибольшего балла
(Приложение 1. Слайды №14, №15, №16).
Цель этапа: проверка знаний по теме, с учетом уровня приобретённых знаний.
Умения: применять распределительный закон
умножения для рационального счета, при
решении уравнений, составлять
математическую модель к текстовой задаче.
Форма работы: индивидуальная работа.
Используемые цифровые ресурсы или их компоненты — (Приложение 1. Слайды №14 – 19)
Деятельность учителя – организация контроля за самостоятельностью решения и процедуры проверки, сбор карточек с решениями.
Деятельность ученика – учащиеся, которые
выбрали задание 1 уровня – заполняют пропуски
в решении заданий, 2 уровня – решают типичные
задания, 3 уровня – олимпиадные задания. Проводят
проверку, сверяя с готовыми ответами на экране,
выставляют баллы в индивидуальные оценочные
листы. Задания 1 и 2 уровня сложности
оцениваются — 1 баллом, их всего шесть, итого
максимум – 6 баллов, задания 3 уровня сложности,
требующие больше времени на их выполнение – 2
баллами, их четыре, итого – 8 баллов. Рефлексия:
осознание учеником деятельности: того как, каким
способом получен результат, какие при этом
встречались затруднения , как они были устранены,
и что чувствовал ученик при этом.
Методы: самоконтроль полученных знаний.
Если позволит время, то можно разобрать на доске задания третьего уровня : №1(б), №2, составить уравнение к заданию №3.
Задания к самостоятельной работе:
Уровень 1.
№1. Упростите выражение. Заполните пропуски.
а) 15x + 20x + x = (_ + _ + _)• x = ?•x,
б) 24a – 12a – 78 = (_ — _) • а — 78 = _•а — _,
в) y + 55y – 56y + 45 = (_ + _ — _) • y + _ = _y + _ = _,
№2. Решите уравнение.
| а) 78x + 92x = 340 | б) 49y – 27y + 34 = 100 |
| (_ + _) • x = 340 | (_ — _)•y + 34 = 100 |
| _ • x = 340 | _ y = 100 _ 34 |
| x = 340: _ | _ y = _ |
| x = _ | y = _:_ |
| Ответ: | y = _. Ответ: Ответ: |
№3. По данной к задаче таблице составь уравнение:
| Собрали яблок | |
| Петя | 4х яблок |
| Галя | х яблок |
| Коля | 7х яблок |
Вместе дети собрали — 72 яблока.
Уровень 2.
Задания к самостоятельной работе. Оценка – максимум 6 баллов.
№1. Упростите выражение.
а) 46х + 87х – 38х;
б) 84y — 37y + 41y – 124;
в) 65а + 36а – а – 100;
№2. Решите уравнение:
а) 43х + 2• 3х = 98; б) 59а – 38а – 95 = 10.
№3. Решите задачу.
| Выразить через “х” сколько животных | ||
| кенгуру | В 5 раз больше, чем пони | |
| пони | В 2 раза больше, чем бегемотов | |
| бегемоты |
Всего в зоопарке было 26 животных.
Уровень 3. Задания к высокому уровню.
Оценка — по 2 балла за каждое верно решенное задание.
№1. Вычислить как можно более простым способом:
а) 5•2 + 5•22 + 5• 222 + 5 •2222;
б) 33•25 — 25•23 + 10•15 — 40•5.
№2. Решите уравнение.
(((7х – 2•2х)+6х) – 7х) + 2•4х = 1000.
№3. Решите задачу.
| Выразить через “х” | ||
| сорок | в 2 раза больше, чем синиц и в 3 раза меньше, чем снегирей |
|
| синиц | ||
| снегирей |
Всего на дереве сидело — 18 птиц.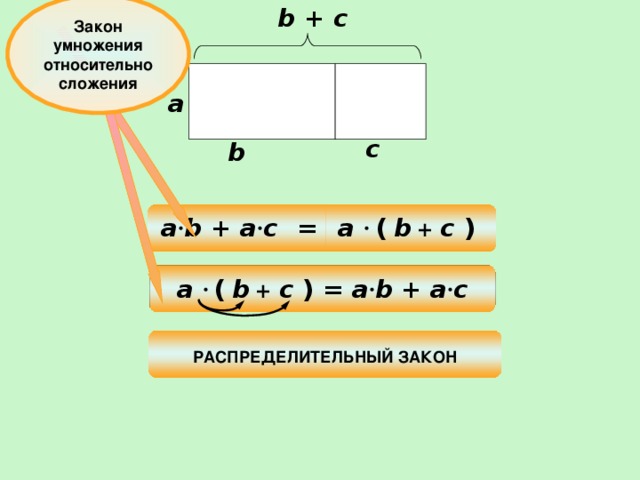
7 этап. Подведение итогов урока — 5 мин.
Цель этапа: подведение итогов урока, достижения целей урока.
Используемые цифровые ресурсы или их компоненты — (Приложение 1. Слайд №20)
Деятельность учителя- отмечает в какой мере достигнуты цели урока, на что требуется обратить внимание. Комментирует результаты работы учащихся. Выставляет оценки, созданная во время урока “ситуация успеха” принесла удовлетворенность результатами, радость преодоленной трудности.
Деятельность ученика- подсчитывают баллы в индивидуальных оценочных листах, выставляют оценки, в соответствии с заданными критериями.
8. Дифференцированное творческое домашнее задание — 1 мин.
Цель этапа: развитие творческого мышления учащихся
Деятельность учителя- ориентирует на
домашнее задание, которое предусматривает
уровневую дифференциацию, ориентировано на
достигнутый уровень знаний.
Деятельность ученика — записывает домашнее задание.
Спасибо за урок, дети! (Приложение 1. Слайд №21).
Приложение 1 (Презентация)
Распределительный закон умножения относительно сложения :: SYL.ru
Улыбнулась в ответ: женщины склонны заражаться чужими чувствами сильнее мужчин
Коротко, но со вкусом: 10 модных многослойных стрижек длиной до подбородка
Морковь и черника: продукты, которые помогут коже в осенние месяцы
Брондирование возвращается: тенденции модного осеннего окрашивания волос
Фолаяж как хит осени 2022: тенденции и особенности окрашивания
Хлеб из минимума продуктов: готовим вкусное блюдо к завтраку
Наносим праймер на Т-зону: техники макияжа для проблемной кожи
Облепиха — самая полезная ягода сентября: как заварить чай и заморозить на зиму
Лучшие модели удобной домашней одежды
Никаких ярких цветов и гулек: прически, которые выйдут из моды осенью 2022 года
Автор Елизавета Фоменко
Математики — ленивые люди, поэтому они всё время создавали какие-то формулы, законы, обозначения. Их старания не прошли зря, теперь современный человек может легко решать уравнения и задачи. С лёгкостью доказывать теоремы по геометрии, и всё это благодаря формулам, обозначениям, свойствам!
Их старания не прошли зря, теперь современный человек может легко решать уравнения и задачи. С лёгкостью доказывать теоремы по геометрии, и всё это благодаря формулам, обозначениям, свойствам!
Законы умножения и сложения
Их для умножения и сложения чисел всего три. Они очень полезны, благодаря им можно с лёгкостью решать большие уравнения. Каждый из них имеет свою формулу и название.
Первый закон умножения и сложения — сочетательный. Числа в таком случае группируют, зная, что сумма и произведение все равно не изменятся.
Второй закон умножения и сложения — переместительный. В этом случае числа перемещают так, как будет удобно, зная, что сумма и произведение также останутся теми же.
Третий, наиболее часто используемый, — распределительный закон. Его смысл в том, чтобы выполнять действия не отдельно для каждого числа, а умножать сразу на сумму. И наоборот, вносить множитель в скобки, умножая на каждое слагаемое. Это действительно удобно, и стоит научиться использовать этот закон!
Эти законы нельзя использовать для деления и вычитания, так как они могут изменить конечный результат.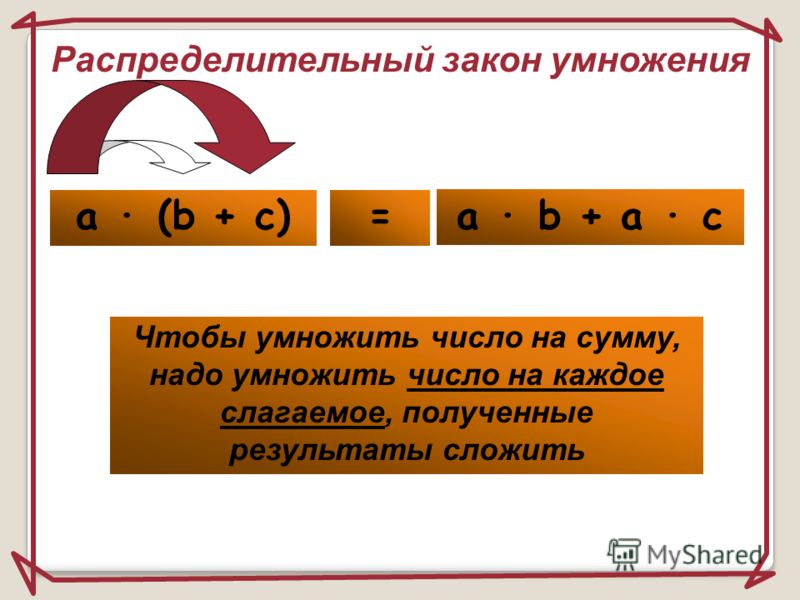
Распределительный закон
Он очень удобен, ведь с его помощью можно умножать число на сумму без каких-либо трудностей! А всё потому, что распределять намного удобнее, чем просто умножать на каждый множитель.
Для наглядности можно рассмотреть пример, где он применяется при умножении и сложении.
Дано выражение: 3 х 2 + 3 х 5.
Так выглядит обычное выражение. Если мы будем использовать распределительный закон, оно будет выглядеть так: 3 х (2 + 3) = 3 х 5 = 15.
Как видим, пользуясь этим удобным «средством», можно намного быстрее решать различные уравнения!
Всё на свете имеет своё название и формулировку, распределительный закон — не исключение! Стоит заучить его формулировку, чтобы с лёгкостью пользоваться им в любых условиях и при любых обстоятельствах. Стоит понять его действие!
Пример, где применяется распределительный закон умножения относительно сложения
Рассмотрим ещё один пример, где применим этот закон: 2 х 5 + 2 х 3 = 16.
Такое выражение было первоначально, а потом оно стало таким: 2 х (5 + 3) = 2 х 8 = 16.
Как видим, ответ не изменился, а выполнять действия стало намного легче! Это же прекрасно! Мы смогли облегчить себе жизнь!
Распределительный закон умножения относительно сложения очень полезен, поэтому им нужно пользоваться! Не стоит бояться пробовать что-то новое! Все свойства, теоремы и формулы есть в математике неспроста!
Похожие статьи
- Правила, по которым происходит сложение векторов
- Правило «Законы не имеют обратной силы»: описание, примеры и особенности
- Правило Парето 20/80
- Логическое выражение: построение и упрощение
- Логистика — что это такое? Транспортная и складская логистика. Задачи логистики
- Суть закона Мура
- Ст.
 130 УК РФ. Оскорбление личности
130 УК РФ. Оскорбление личности
Также читайте
Коммутативные, ассоциативные и дистрибутивные законы
Вау! Какой набор слов! Но идеи простые.
h2zsWdHC_V8
Коммутативные законы
«Законы коммутации» говорят, что мы можем поменять местами числа и все равно получить тот же ответ…
… когда мы добавляем :
а + б = б + а
Пример:
… или когда мы умножить :
а × б = б × а
Пример:
Проценты тоже!
Поскольку a × b = b × a, также верно, что:
а% от б = б% от
Пример: чему равно 8% от 50?
8% от 50 = 50% от 8
= 4
Почему «коммутативный » . .. ?
.. ?
Потому что числа могут двигаться вперед и назад, как пригородный .
4591, 4599, 4615, 4639, 4647, 4592, 4600, 4616
КБфнкУГЭМВИ
Ассоциативные законы
«Ассоциативные законы» говорят, что не имеет значения, как мы группируем числа (т.е. какие мы вычисляем первыми)…
… когда мы добавляем :
(а + б) + в = а + (б + в)
… или когда мы умножаем :
(а × б) × в = а × (б × в)
Примеры:
| Это: | (2 + 4) + 5 = 6 + 5 = 11 |
| Имеет тот же ответ, что и этот: | 2 + (4 + 5) = 2 + 9 = 11 |
| Это: | (3 × 4) × 5 = 12 × 5 = 60 |
| Имеет тот же ответ, что и этот: | 3 × (4 × 5) = 3 × 20 = 60 |
Использование:
Иногда проще складывать или умножать в другом порядке:
Сколько будет 19+36+4?
19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59
Или немного переставить:
Что такое 2 × 16 × 5?
2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160
4603, 4610, 4627, 4631, 4643, 4654, 4606, 4612
0v-G6OwcKmU
Распределительный закон
«Распределительный закон» — САМЫЙ ЛУЧШИЙ из всех, но требует особого внимания.
Вот что он позволяет нам делать:
3 партии (2+4) то же, что и 3 партии 2 плюс 3 партии по 4 шт.
Итак, 3× можно «распределить» по 2+4 , на 3×2 и 3×4
И пишем так:
a × (b + c) = a × b + a × c
Попробуйте посчитать сами:
- 3 × ( 2 + 4 ) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
В любом случае ответ один.
По-английски мы можем сказать:
Мы получим тот же ответ, если:
- умножим число на группу чисел, сложенных вместе или
- сделать каждый умножить отдельно, затем добавить их
Использование:
Иногда бывает проще разбить сложное умножение:
Пример: Что такое 6 × 204?
6 × 204 = 6 × 200 + 6 × 4
= 1200 + 24
= 1224
Или комбинировать:
Пример: Сколько будет 16 × 6 + 16 × 4?
16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160
Мы можем использовать его и при вычитании:
Пример: 26×3 – 24×3
26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6
Мы могли бы использовать его и для длинного списка дополнений:
Пример: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6 ×7 + 2 ×7 + 3 ×7 + 5 ×7 + 4 ×7
= (6+2+3+5+4) × 7
= 140
5656, 5657, 5658, 5659, 5660, 5661, 3172
Таковы Законы.
 . .
. .. . . но не заходите слишком далеко!
Коммутативный закон выполняет , а не работу для вычитания или деления:
Пример:
- 12/3 = 4 , но
- 3 / 12 = =
Ассоциативный закон заставляет , а не работать для вычитания или деления:
Пример:
- (9 – 4) – 3 = 5 – 3 = 2 , но
- 9 – (4 – 3) = 9 – 1 = 8
Распределительный закон делает , а не работой для деления:
Пример:
- 24 / (4 + 8) = 24 / 12 = 2 , но
- 24/4 + 24/8 = 6 + 3 = 9
Резюме
| Коммутативные законы: | a + b = b + a a × b = b × a |
| Ассоциативные законы: | (a + b) + c = a + (b + c) (a × b) × c = a × (b × c) |
| Распределительное право: | a × (b + c) = a × b + a × c |
Деятельность: Коммутативная, Ассоциативная и Распределительная
Что такое распределительная собственность? Определение, пример формулы, факты
Распределение собственности Определение
«Раздать» означает разделить что-либо или передать долю или часть чего-либо.
Так что же означает распределительная собственность в математике?
Распределительный закон умножения по отношению к основным арифметическим действиям, таким как сложение и вычитание, известен как распределительное свойство.
Что такое распределительная собственность?
В соответствии с этим свойством умножение суммы двух или более слагаемых на число даст тот же результат, что и умножение каждого слагаемого по отдельности на число с последующим сложением произведений.
Другими словами, согласно дистрибутивному свойству, выражение вида A (B $+$ C) может быть решено как A (B $+$ C) $=$ AB $+$ AC.
Это свойство применимо и к вычитанию.
A (B $–$ C) $=$ AB $–$ AC
Указывает, что операнд А является общим для двух других операндов.
Давайте посмотрим на формулу распределительной собственности:
Где A, B и C — любые действительные числа.
Вот пример того, как результат не меняется при обычном решении и при решении с использованием распределительного свойства:
Это свойство помогает упростить сложные задачи. Вы можете использовать это свойство умножения, чтобы переписать выражение, распределив или разбив множитель на сумму или разность двух чисел.
Вы можете использовать это свойство умножения, чтобы переписать выражение, распределив или разбив множитель на сумму или разность двух чисел.
Распределительное свойство умножения над сложением
Когда нам нужно умножить число на сумму двух чисел, мы используем это свойство умножения над сложением. Давайте поймем, как лучше использовать распределительное свойство на примере:
Пример: Решите выражение: $6$ $(20 + 5)$, используя распределительное свойство умножения над сложением.
Воспользуемся этим свойством для вычисления выражения $6$ $(20 + 5)$, число 6 распределено между двумя слагаемыми. Проще говоря, мы умножаем каждое слагаемое на 6, после чего можно складывать произведения.
$6 20 + 6 5 = 120 + 30 = 150 $
Возьмем другой пример:
Пример: Решите выражение $2$ $(2 + 4)$, используя распределительный закон умножения над сложением.
Решение: $2 (2 + 4) = 2 2 + 2 4 = 4 + 8 = 12$
Если мы попытаемся решить это выражение с помощью правила PEMDAS, нам придется сложить числа в скобках и затем умножьте сумму на число за скобками. Отсюда следует:
Отсюда следует:
$2 (2 + 4)$ $= 2 \times 6 =$ $12$
Таким образом, мы получаем один и тот же результат независимо от используемого метода.
Распределительное свойство умножения над вычитанием
Распределительное свойство умножения над вычитанием эквивалентно распределительному свойству умножения над сложением, за исключением операций сложения и вычитания.
A(B − C) и AB − AC эквивалентны выражениям.
Рассмотрим приведенные ниже примеры распределительной собственности.
Пример: Решите выражение $6 (20 – 5)$, используя распределительное свойство умножения над вычитанием.
Решение : Использование распределительного свойства умножения над вычитанием
Пример : Решите выражение 2 (4 – 3), используя распределительный закон умножения на вычитание.
Решение : $2 (4 – 3) = 2 4 – 2 3 = 8 – 6 = 2$
Опять же, если мы попытаемся решить выражение с порядком операций или PEMDAS, нам придется вычесть числа в скобках , затем умножьте разницу на число за скобками, что означает:
$2 (4 – 3) = 2 1 = 2$
Распределительное свойство вычитания доказано, поскольку оба метода дают одинаковый результат.
Забавные факты
Несмотря на то, что деление является обратным умножению, закон распределения верен только в случае деления, когда делимое распределяется или разбивается на частичные дивиденды, которые полностью делятся на делитель.
Например, используя распределительный закон для 1326
132, можно разбить его на 60 + 60 + 12 долларов, что упрощает деление.
Мы не можем разбить 132 6 как $(50 + 50 + 32) 6$.
Кроме того, мы не можем разорвать делитель: $132(4+2)$ даст неверный результат.
Заключение
Мы поняли, как свойство дистрибутивности можно использовать для упрощения сложных уравнений и задач. Откройте для себя новый способ изучения математики с помощью SplashLearn,
предлагает интерактивную платформу для детей, где каждая концепция превращается в игровую сессию. С интересными таблицами, увлекательными викторинами и простыми для понимания темами измените то, как ваш ребенок понимает математику!
Примеры решения
Пример 1. Решите $(5 + 7 + 3) 4 $ .
Решите $(5 + 7 + 3) 4 $ .
Решение : Использование распределительного свойства умножения над сложением
A (B $+$ C) = AB $+$ AC
$(5 + 7 + 3) 4 = 5 4 + 7 4 + 3 4 = 20 + 28 + 12 = 60$
Или,
$(5 + 7 + 3) 4 = 15 4 = 60$
Пример 2: Решите следующее уравнение распределения $−2 (−x − 7)$ .
Решение : Используя свойство распределения,
A (B $–$ C) $=$ AB $–$ AC
$−2 (−$x$ − 7) = (−2)(− $x$) − (−2)(7) = 2$x$ − (−14) = 2$x$ + 14$
Пример 3. Какое свойство делает уравнение $3 (4 − 9) = 3 4 − 3 9$ показать?
Решение : Приведенное выше уравнение показывает распределительное свойство умножения над вычитанием.
Практические задачи
x $+ 42$
$7$x $+ 13$
$7$x $+ 42$
$7$x $+ 6$
Правильный ответ: $7$x $+ 42 $
Используя распределительное свойство умножения над сложением,
A (B $+$ C) $=$ AB $+$ AC
$7 ($x $+ 6) = 7($x$) + 7(6) = 7$x $+ 42$
$13$x
$7$x$ – 24$
$21$x$ – 24$
$21$x$ – 8$
Правильный ответ: $21$x$ – 24$
Используя распределительное свойство умножения над вычитанием,
A (B $–$ C) $=$ AB $–$ AC
$3 (7$x $– 8) = 3 (7$x$) – 3 (8) = 21$x$ — 24$
$3$mn $– 9$n
$3$mn $– 9$
$3$mn $– 9$m
$3$mn$+9$m
Правильный ответ: $3$mn $– 9$ m
Используя распределительное свойство умножения над вычитанием,
A (B $–$ C) $=$ AB $–$ AC
m $(3$n $– 9)$ $=$ m $(3$n$ ) –$ m $(9) = 3 млн $– 9 млн $
4260
3550
2130
426
Правильный ответ: 4260
Общее количество собранных бананов определяется выражением $355 x 12$.
Дюжина или 12 могут быть распределены как 10 и 2.
Общее количество собранных бананов $= 355 \times (10 + 2)$
Используя распределительное свойство умножения на сложение,
A (B $+$ C) $=$ AB $+$ AC
$= 355 \times 10 + 355 \times 2$
$= 3550 + 710 = 4260$
Всего на ферме было собрано 4260 бананов.
Часто задаваемые вопросы
Применяется ли раздел имущества также и к разделу?
Распределительное свойство применяется к делению так же, как и к умножению. Однако понятие «разбивка» или «распределение» может быть применено к делению только путем деления числителя на более мелкие суммы, которые точно делятся на делитель.
Например, чтобы решить $\frac{125}{5}$, мы можем разделить числитель (125) как: (50 + 50 + 25), поэтому: $\frac{125}{5}$ = $\ frac{50}{5}$ + $\frac{50}{5}$ + $\frac{25}{5}$ = 10 + 10 + 5 = 25,
Каково правило распределительной собственности?
Согласно распределительному свойству, умножение суммы двух или более слагаемых на число дает тот же результат, что и при умножении каждого слагаемого на число по отдельности и сложении произведений.
Как распределительная собственность может помочь в решении сложных вопросов?
Распределяющее свойство распределяет сложные выражения в более простые термины и, таким образом, облегчает решение задач, особенно с несколькими факторами.
Можно ли убрать скобки после распространения?
Да, при применении распределительного свойства внешний множитель умножается на каждое слагаемое в скобках. Это позволяет избавиться от скобок.
Ассоциативное свойство сложения, коммутативное свойство умножения
Распределительное свойство — определение, формула, примеры
Распределительное свойство — это хорошо известное свойство, связанное с числами и алгеброй в математике. Как следует из названия, это свойство фокусируется на распределении или делении количества через соответствующие условия. Распределительное свойство или распределительный закон действует только в умножении чисел и алгебре. Поэтому его также называют дистрибутивным законом умножения.
Примечание: Распределительное свойство никогда не может применяться при сложении или вычитании чисел. Даже если вы подадите заявку, результат будет недействительным или приведет к ошибкам в решении.
Прежде чем мы углубимся в распределительное свойство умножения, давайте кратко рассмотрим другие важные математические свойства. Они перечислены ниже:
- Коммутативное свойство: Это свойство указывает, что числа или термины могут коммутировать или перемещать свои места в выражении без изменения результата. Это верно для сложения и умножения. Например, (1 + 4) = (4 + 1) и (2 * 4) = (4 * 2). Вычитание не следует этому свойству, например, (1 – 4) = -3 не равно (4 – 1) = 3,
- Ассоциативное свойство: Это свойство указывает, что количество терминов в выражении может ассоциироваться друг с другом или группироваться друг с другом без изменения результата. Это верно для сложения и умножения. Например, (1 + 4) + 3 = 1 + (4 + 3).
Давайте теперь обсудим, что означает распределительная собственность, и некоторые примеры распределительной собственности.
Давайте сначала разберемся с простой концепцией. Если вам нужно что-то раздать, скажем, шоколад, с друзьями, вы делите плитку шоколада на кусочки, чтобы облегчить раздачу, верно! Математика следует тем же концепциям. Когда нам нужно упростить сложную задачу, распределительное свойство помогает разбить выражение на сумму или разность двух чисел.
Математически свойство дистрибутивности утверждает, что любое выражение, представленное в форме K × (L + M), может быть легко разрешено как K × (L + M) = KL + KM. Кроме того, это известно как распределительный закон применения умножения. Точно так же распределительный закон верен и для выражений, содержащих вычитание. Это выражается как K × (L – M) = KL – KM.
Как вы все можете видеть, К распределяется как на сложение, так и на вычитание. Здесь K известен как операнд, а термины внутри выражения известны как слагаемые.
Давайте изучим некоторые важные термины, которые мы уже изучили:
- Операнд: Распределяемый термин известен как операнд.

- Добавления: Термины в скобках, которые добавляются или вычитаются, называются добавлениями.
- Распределительное свойство сложения: K × (L + M) = KL + KM
- Распределительное свойство вычитания: K × (L – M) = KL – KM
Теперь мы можем визуализировать, что распределительное свойство утверждает, что когда операнд умножается на сумму или разность слагаемых, он равен сумме или разности отдельных произведений операнда и слагаемых.
Формула распределительного свойстваФормула для распределительного свойства данного значения может быть сформулирована как
c * ( a + b ) = ca + cb
На этом завершаются все теоретические аспекты распределительного свойства умножения. Далее давайте подробно рассмотрим распределительный закон умножения над сложением и вычитанием с соответствующими примерами.
Распределительное свойство сложения При умножении числа (операнда) на сумму двух целых чисел (сложение) мы используем распределительное свойство сложения. Хорошим примером является умножение трех на сумму 10 + 8. 3 x (10 + 8) является математическим выражением для этого.
Хорошим примером является умножение трех на сумму 10 + 8. 3 x (10 + 8) является математическим выражением для этого.
Пример: Распределительный принцип сложения может решить формулу 3 x (10 + 8).
Решение: Используя распределительное свойство, мы умножаем каждое слагаемое на три, используя распределительное свойство, прежде чем решать формулу 3 x (10 + 8). После этого мы можем сложить продукты, разделив число 3 между двумя слагаемыми. Это означает, что сложение произойдет до умножения 3 (18), а 3 х (10) + 3 х (8) = 30 + 24 = 54 является результатом свойства распределения сложения.
Распределительное свойство вычитания Аналогично, при умножении числа (операнда) на разность двух целых чисел (сложение) мы используем распределительное свойство вычитания. Умножение трех на разницу от 10 до 8 — хороший пример распределительного свойства вычитания. Математическое выражение для этого уравнения: 3 x (10 – 8).
Пример: Для решения формулы 3 x (10 – 8) можно использовать распределительный принцип вычитания.
Решение: Используя распределительное свойство, мы умножаем каждое слагаемое на три перед решением формулы 3 x (10 – 8). После этого мы можем вычесть произведения, разделив число 3 между двумя слагаемыми. Это означает, что вычитание произойдет раньше, чем умножение 3 х (18) и 3 х (10) – 3 х (8) = 30 – 24 = 6 является результатом распределительного свойства вычитания.
Мы так много говорили о свойстве распределения, но как оно проявляется в математике? Есть ли способ проверить это свойство? Действительно есть проверка. Продолжайте читать статью, чтобы узнать, почему.
Проверка свойства распределения Давайте посмотрим, как свойство распределения работает для различных операций. Мы будем использовать распределительный закон, чтобы применять две основные операции сложения и вычитания по отдельности.
- Распределительное свойство сложения : Мы уже знаем, что распределительное свойство сложения выражается как k × (l + m) = kl + lm. Теперь пришло время проверить это свойство на примере.
Пример: Возьмем выражение, скажем, 10 х (3 + 6).
Решение: Обычно мы решаем это выражение, используя стандартные правила БОДМАС.
На первом шаге мы всегда будем решать выражения внутри скобок. В этом случае (3 + 6 ) = 9. На втором шаге мы умножим 10 на полученное число, то есть на 9. Это даст нам результат 10 x 9 = 90.
Теперь решите это, используя распределительное свойство дополнения:
10 x ( 3 + 6 ) = (10 x 3) + (10 x 6)
= 30 + 60
= 90
Как мы видим, оба метода дают одинаковый результат.
- Распределительное свойство вычитания : Теперь давайте проверим то же самое для распределительного свойства вычитания. Все мы уже знаем, что распределительное свойство сложения выражается как k × (l – m) = kl – lm.
 Теперь пришло время проверить это свойство на примере.
Теперь пришло время проверить это свойство на примере.
Пример: Возьмем выражение, скажем, 10 x (6 – 3).
Решение: Обычно мы решаем это выражение, используя стандартные правила БОДМАС.
На первом шаге мы всегда будем решать выражения внутри скобок. В этом случае ( 6 – 3 ) = 3. На втором шаге мы умножим 10 на полученное число, т.е. на 3. Это даст нам результат 10 x 3 = 30.
Теперь решите это, используя распределительное свойство сложения:
10 х ( 6 – 3 ) = (10 х 6) – (10 х 3)
= 60 – 30
= 30
Как мы видим, оба метода снова дают один и тот же результат.
Таким образом, мы проверили, что свойство распределения сложения и вычитания верно.
Распределительное свойство деления Распределительное свойство деления такое же, как распределительный закон умножения, только знак умножения меняется на деление вместе с операцией. Больший член делится на меньшие множители (сложение), а делитель выступает в роли операнда. Вы лучше поймете это на примере, приведенном ниже.
Вы лучше поймете это на примере, приведенном ниже.
Пример: Используя распределительное свойство деления, решите 36 ÷ 12.
Решение: 36 можно записать как 24 + 12
Следовательно, мы можем записать 36 ÷ 12 = (24 + 12) ÷ 15 9000
Теперь давайте распределим 12 внутри скобки
⇒ (24 ÷ 12) + (12 ÷ 12)
⇒ 2 + 1
Это дает нам ответ как 3.
Пример 1: Решите выражение 2 (11 + 7), используя распределительное свойство.Решение:
Используя формулу распределительного свойства,
k × (l + m) = (k × l) + (k × m)
= (2 × 11) + (2 × 7)
= 22 + 14
= 36
Следовательно, значение 2 (11 + 7) = 36
Пример 2: Докажите, что 5 x (3 – 12) имеет отрицательный результат, используя распределительное свойство умножения .
Решение:
Используя формулу распределительного свойства,
k × (l – m) = (k × l) – (k × m)
= (5 × 3) – (5 × 12)
= 15 – 60
= -45
Следовательно, значение 5 x (3 – 12) = – 45, что является отрицательным целым числом.
Теперь вы должны быть на 100 процентов уверены в том, что означает распределительное свойство и как решать проблемы, связанные с этим свойством. Если вы не совсем уверены и пропустили какое-либо из понятий в статье, вы можете снова посетить эту страницу для получения теории и решений. Более того, начните готовиться к предстоящему экзамену прямо сейчас и затмите других, обучаясь и практикуясь.
Часто задаваемые вопросы?1.
Что такое примеры распределительной собственности?Распределяющее свойство — это правило, утверждающее, что вы можете распространять члены выражения. Он используется, когда у вас есть один термин, который умножается на другой термин, но вы хотите распределить термин, умноженный на другое число.
Например:
5(x+y) = 5x + 5y
В этом случае x и y умножаются на 5, что означает, что мы можем распределить 5 по ним. Поэтому мы перепишем это как 50x + 50y.
Давайте рассмотрим другой пример:
(6x+2)(x-1) = 6×2 – 2x – 1
2.
 Какое имущество является распределительным?
Какое имущество является распределительным? Распределительное свойство — это свойство, позволяющее разделить целое на его части. Обычно используется в математике и алгебре. Например, если у вас есть сумма двух чисел и вы хотите найти сумму их частей, вы должны использовать распределительное свойство.
3.
Какое распределительное свойство числа 3?Распределяющее свойство числа 3 — это математическое правило, позволяющее распределить одно число на каждый член суммы.
Например, если вы хотите сложить 2+3+4, вы не можете просто сказать «добавьте 6», потому что 2+3=5 и 4+3=7. Вам нужно найти способ разделить 6 между этими двумя терминами.
Распределяющее свойство числа 3 говорит нам, как это сделать: мы умножим каждое слагаемое на 3, прежде чем складывать их вместе. Итак, наш ответ 9+12=21.
4.
Как вы делаете распределительный метод? 92) + (4(-2)) + (8) + (-8) = 16 – 0 + 0 = 165.
Почему мы используем распределительное свойство? Распределительное свойство превращает задачу на умножение в задачу на сложение. Например, если у вас есть x * y, где x и y — положительные числа, а x больше 1, то вы можете переписать это как (x — 1) * y + x * y.
Например, если у вас есть x * y, где x и y — положительные числа, а x больше 1, то вы можете переписать это как (x — 1) * y + x * y.
Распределительное свойство также полезно при решении уравнений с показателями. Например, если у вас 5(x+1) = 10(x), то вы можете переписать это как 5x + 5 = 10x.
Коммутативные, ассоциативные и дистрибутивные законы
Горячая математика Коммутативные законы (или коммутативные свойства)коммутативные законы заявить, что порядок, в котором вы складываете или умножаете два вещественные числа не влияет на результат.
Коммутативный закон сложения:
а + б знак равно б + а
Пример:
3 + 5 знак равно 5 + 3 знак равно 8 20 + ( − 3 ) знак равно ( − 3 ) + 20 знак равно 17
Коммутативный закон умножения:
а б знак равно б а
Пример:
4 ⋅ 5 знак равно 5 ⋅ 4 знак равно 20 ( − 2 ) ( 8 ) знак равно ( 8 ) ( − 2 ) знак равно − 16
Ассоциативные законы (или ассоциативные свойства)
ассоциативные законы
Укажите, что при сложении или умножении любых трех действительных чисел группировка (или ассоциация) чисел не влияет на результат.
Ассоциативный закон сложения:
( а + б ) + с знак равно а + ( б + с )
Пример:
( 2 + 3 ) + 5 знак равно 5 + 5 знак равно 10 2 + ( 3 + 5 ) знак равно 2 + 8 знак равно 10
Ассоциативный закон умножения:
( а б ) с знак равно а ( б с )
Пример:
( 5 ⋅ 7 ) ⋅ 6 знак равно 35 ⋅ 6 знак равно 210 5 ⋅ ( 7 ⋅ 6 ) знак равно 5 ⋅ 42 знак равно 210
Распределительный закон
Посмотрим, что произойдет, если мы сделаем 4 ( 7 + 3 ) :
4 ( 7 + 3 ) знак равно 4 ( 10 ) знак равно 40
Это следует
ПЕМДАС (англ. Порядок операций
).
Порядок операций
).
Но . . . 4 ( 7 ) + 4 ( 3 ) знак равно 28 + 12 знак равно 40 тоже, как видно на этой картинке:
| Это либо 4 × 10 прямоугольник из точек или 4 × 3 прямоугольник рядом с 4 × 7 . |
Давайте напишем это как
4
(
7
+
3
)
знак равно
4
(
7
)
+
4
(
3
)
.
Мы говорим, что «распространяем» 4 к условия внутри.
Это переводится как общее кейс:
а ( б + с ) знак равно а б + а с а также ( б + с ) а знак равно б а + с а
Это известно как
Распределительное право
или
Распределительное свойство
. Нажмите
здесь
для получения дополнительных примеров его использования.
Коммутативное, ассоциативное и дистрибутивное свойство? (Видео и практика)
Как вы, возможно, уже поняли за годы уроков математики и домашних заданий, математика по своей природе является последовательной, а это означает, что каждое понятие основано на предыдущей работе. Арифметические навыки необходимы для овладения алгебраическими понятиями, которые затем развиваются для дальнейшего использования в вычислениях и так далее. По мере того как вы со временем выстраиваете эти концепции, математический процесс может стать автоматическим, но причина или оправдание работы могут быть давно забыты.
В этом видео мы вернемся к основам, чтобы рассмотреть коммутативные, ассоциативные и дистрибутивные свойства действительных чисел, которые учитывают математическую механику алгебры и не только.
Коммутативное свойство
Имена свойств, которые мы собираемся рассмотреть, помогают расшифровать их значения. Рассмотрим слово , коммутативное . О чем вы думаете, когда видите это слово? Когда я смотрю на это слово, я вижу слово «коммутировать». Это слово напоминает мне о «перемещении», которое свойство коммутативности позволяет вам делать при сложении или умножении алгебраических членов. Коммутативность математически выглядит следующим образом: 9{2}\) и так далее. Чтобы доказать, что перемещение или перестановка термов допустимы, давайте рассмотрим несколько примеров использования свойства коммутативности в задачах на сложение.
О чем вы думаете, когда видите это слово? Когда я смотрю на это слово, я вижу слово «коммутировать». Это слово напоминает мне о «перемещении», которое свойство коммутативности позволяет вам делать при сложении или умножении алгебраических членов. Коммутативность математически выглядит следующим образом: 9{2}\) и так далее. Чтобы доказать, что перемещение или перестановка термов допустимы, давайте рассмотрим несколько примеров использования свойства коммутативности в задачах на сложение.
Пример 1
Если мы сложим \(5+3\), то получим \(8\). Но если мы поменяем наши условия и сделаем это \(3 + 5\), мы все равно получим \(8\). Итак, \(5+3=3+5\).
Пример 2
Давайте немного изменим один из наших терминов для следующего примера. \(5+(-3)=2\) и \((-3)+5=2\). Итак, \(5+(-3)=(-3)+5\). Обратите внимание, что существует очень важное различие между сложением отрицательного целого числа и операцией вычитания. Важно отметить это различие, потому что свойство коммутативности не применяется к операции вычитания. {2}\)
{2}\)
\(3+10+3=10+3+3\)
\(16=16\)
После сложения каждой стороны у нас останется 16 с обеих сторон, что верно. . \(16=16\).
Следующее свойство, которое мы рассмотрим, — это ассоциативное свойство.
Ассоциативное свойство
Опять же, название дает полезный намек на его значение. Что приходит на ум, когда вы слышите слово , ассоциативное с ? Для меня выделяется слово ассоциированное , которое могло бы также навести на мысль слово группа . Соответственно, свойство ассоциативности позволяет нам группировать термины, которые соединяются сложением или умножением различными способами. Скобки используются для группировки терминов и устанавливают порядок операций. Работа внутри скобок всегда выполняется в первую очередь. Математически это свойство выглядит так:
Ассоциативность сложения : \((a+b)+c=a+(b+c)\)
Ассоциативность умножения : \(( а\cdot b)\cdot c=a\cdot (b\cdot c)\)
Давайте рассмотрим пример использования этого свойства в задаче на сложение.
Пример 1
Этот пример покажет, что добавление сначала двух последних терминов или добавление первых двух терминов просто не имеет значения. Давайте посмотрим на \(3+(4+5)=(3+4)+5\). Итак, сначала делаем то, что в скобках. \(4+5=9\) и \(9+3=7\). Так \(12=12\), потому что это обе стороны уравнения. Точно так же не имеет значения и порядок, в котором мы выполняем умножение.
Пример 2
Допустим, у нас есть \((3\cdot 4)\cdot 5=3\cdot (4\cdot 5)\).
\(12\cdot 5=3\cdot 20\)
\(60=60\)
Перестановочное свойство умножения показывает, что при умножении допустимо переставлять члены. Напротив, ассоциативное свойство умножения перемещает скобки в порядке умножения.
Распределительное свойство
Наконец, последнее свойство, которое мы рассмотрим, — это свойство распределения, которое выглядит следующим образом: \(a\cdot (b+c)=a\cdot b+a\cdot c\)
Обозначение, опять же, диктует, что это свойство применимо только к операциям умножения и сложения. В частности, если термин умножается на выражение в круглых скобках, то умножение выполняется для каждого из терминов. Вот пример, доказывающий, что этот алгебраический ход оправдан. \(2(3+7)=2\cdot 3+2\cdot 7\)
В частности, если термин умножается на выражение в круглых скобках, то умножение выполняется для каждого из терминов. Вот пример, доказывающий, что этот алгебраический ход оправдан. \(2(3+7)=2\cdot 3+2\cdot 7\)
Скобки слева говорят нам сначала добавить 3+7.
\(2(10)=6+14\)
\(20=20\)
Сумма произведений в правой части уравнения дает тот же результат, что и умножение в левой.
Обзор
Хорошо, теперь, когда мы рассмотрели три свойства, давайте проверим вашу память. Для каждой проблемы укажите свойство (коммутативное, ассоциативное или дистрибутивное), которое оправдывает утверждение. Идите вперед и приостановите видео, если вам нужно больше времени.
Задача 1:
9{2}\)\(5\cdot (2\cdot x)=(5\cdot 2)\cdot x\)
Думаю, вы поняли? Посмотрим! Ответ для числа 1 является ассоциативным свойством, потому что скобки перемещаются в порядке умножения. Ответом на вопрос номер два является распределительное свойство, потому что 3 умножается на оба члена в скобках. Это оставляет нас с ответом на вопрос номер три, являющимся коммутативным свойством, потому что мы просто переставили члены.
Ответом на вопрос номер два является распределительное свойство, потому что 3 умножается на оба члена в скобках. Это оставляет нас с ответом на вопрос номер три, являющимся коммутативным свойством, потому что мы просто переставили члены.
Как видно из нашей работы в этом видео, вы использовали коммутативные, ассоциативные и дистрибутивные свойства в течение довольно долгого времени, даже не задумываясь над тем, «почему». Вас попросят снова подумать об этих концепциях на курсах математики более высокого уровня, когда некоторые из этих свойств просто не выдерживают критики! До тех пор продолжайте уверенно использовать эти правила, чтобы управлять своей работой и мыслительными процессами.
Надеюсь, этот отзыв был вам полезен. Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Что такое свойство коммутативности в математике?
A
Свойство коммутативности применимо к сложению и умножению. В свойстве указано, что термины могут «перемещаться» или перемещаться, и на результат это не повлияет. Это выражается как \(a+b=b+a\) для сложения и \(a×b=b×a\) для умножения. Коммутативное свойство не применяется к вычитанию или делению.
Это выражается как \(a+b=b+a\) для сложения и \(a×b=b×a\) для умножения. Коммутативное свойство не применяется к вычитанию или делению.
Q
Какие 2 примера коммутативного свойства?
A
Свойство коммутативности применимо к сложению и умножению. Например, если у вас есть 4 монеты в левом кармане и 5 монет в правом кармане, всего у вас будет 9 монет, независимо от того, в каком кармане вы считаете первым.
\(a+b=b+a\)
\(4+5=5+4\)
То же самое относится и к умножению. Например, в лотке для кубиков льда с 2 рядами по 10 кубиков всего будет 20 кубиков, независимо от того, как вы их считаете. Подсчет 2 строк по 10 или подсчет 10 строк по 2 дадут одинаковый результат.
\(a×b=b×a\)
\(2×10=10×2\)
Q
Как проверить свойство коммутативности?
A
Свойство коммутативности можно проверить с помощью сложения или умножения. Это связано с тем, что порядок членов не влияет на результат при сложении или умножении.
Например, при умножении 5 и 7 порядок не имеет значения. \((5)\times(7)=35\) и \((7)\times(5)=35\). Умножение 5 стульев в ряду на 7 рядов даст вам всего 35 стульев, а умножение 7 стульев в ряду на 5 рядов также даст вам 35 стульев.
Точно так же порядок терминов не имеет значения при добавлении. Например, \((5)+(7)=12\) и \((7)+(5)=12\). Если я добавлю 7 синих шариков жвачки к 5 красным шарикам жвачки, у меня будет всего 12 шариков жевательной резинки. И если я добавлю 5 синих жевательных резинок к 7 красным, у меня все равно будет 12 круглых жевательных резинок.
Q
Является ли деление коммутативным свойством?
A
Свойство коммутативности не распространяется на деление. Например, \(500\div2=250\), но \(2\div500=0,004\). Когда термины «ездят на работу» или меняют местоположение, ответ меняется. При делении порядок членов имеет значение.
Q
Что такое пример ассоциативного свойства?
A
Ассоциативное свойство указывает, что при добавлении или умножении трех или более чисел и использовании символов группировки результат не изменится независимо от того, где расположены символы группировки. Например, если у вас есть 5 зеленых, 9 желтых и 4 синих шарика, всего у вас будет 18 шариков, независимо от того, какие два цвета вы объедините первыми.
Например, если у вас есть 5 зеленых, 9 желтых и 4 синих шарика, всего у вас будет 18 шариков, независимо от того, какие два цвета вы объедините первыми.
\((а+б)+с=а+(б+с)\)
\((5+9)+4=5+(9+4)\)
\((14)+4=5+(13)\)
\(18=18\)
Аналогично, группировка символы также несколько произвольны при умножении. Например, при вычислении объема прямоугольной призмы длиной 5 дюймов, шириной 4 дюйма и высотой 3 дюйма порядок умножения не влияет на результат. Умножение длины и ширины, а затем высоты даст тот же результат, что и умножение ширины и высоты, а затем длины.
\((a×b)×c=a\times(b×c)\)
\((5×4)×3=5×(4×3)\)
\((20)×3= 5×(12)\)
\(60=60\)
Q
Что такое формула ассоциативного свойства?
A
Ассоциативное свойство указывает, что при сложении или умножении символы группировки можно перемещать, не влияя на результат. Формула для состояний сложения \((a+b)+c=a+(b+c)\) и формула для состояний умножения \((a×b)×c=a×(b×c)\).
Q
В чем разница между ассоциативным свойством и распределительным свойством?
A
Ассоциативное свойство гласит, что при сложении или умножении символы группировки можно переставлять, и это не повлияет на результат. Это указывается как \((a+b)+c=a+(b+c)\). Распределительное свойство — это метод умножения, который включает умножение числа на все отдельные слагаемые другого числа. Это указывается как \(a(b+c)=ab+ac\).
Q
Что такое распределительное свойство в математике?
A
Распределительное свойство — это метод умножения, при котором каждое слагаемое умножается отдельно. Например, вместо умножения \(5\times46\) мы можем разбить 46 на отдельные слагаемые \((40+6)\) и умножить 5 на каждую часть отдельно. \(5\times46\) становится \(5\times40\) плюс \(5\times6\). По сути, 5 «распределяется» по каждому дополнению. Распределительное свойство часто используется в алгебре при упрощении выражений или уравнений. 2+10x\).
2+10x\).
Q
Что такое формула коммутативного свойства?
A
Формула коммутативного свойства применима к сложению и умножению. Формула сложения утверждает, что \(a+b=b+a\), а формула умножения утверждает, что \(a×b=b×a\). Эти формулы используются для описания концепции, согласно которой при сложении или умножении термины могут «коммутировать» или перемещаться, а результат не изменится.
Q
Что такое распределительное свойство в математике 3-го класса?
A
Распределительное свойство является полезным методом умножения многозначных чисел. Например, \(3\times4{,}562\) на первый взгляд может показаться сложной задачей. Однако, если разбить 4562 на \(4{,}000+500+60+2\), с ними будет гораздо легче справиться. Теперь мы можем умножить 3 на каждую из этих «кусочков». Распределительное свойство часто делает многозначное умножение более управляемым.
«Распределить» 3 на все слагаемые (умножить).
\(3\times4{,}000=12{,}000\)
\(3\times500=1{,}500\)
\(3\times60=180\)
\(3\times2=6\)
Теперь сложите части. Всего 13 686.
Всего 13 686.
Практические вопросы
Вопрос № 1:
Какое из следующих определений ассоциативного свойства является правильным?
Если термин умножается на выражение в скобках, то умножение производится над каждым из членов
При сложении или умножении чисел не имеет значения, как сгруппированы числа
Любое число, умноженное на 1, само является
При сложении или умножении чисел вы можете свободно перемещать термины
Показать Ответ
Ответ:
не имеет значения, как сгруппированы числа, то есть не имеет значения, где вы ставите скобки.
Скрыть ответ
Вопрос № 2:
Что из следующего является правильным примером ассоциативного свойства?
\((8-11)-2=8-(11-2)\)
\((17+2)-3=17+(2-3)\)
\((4+3 )+(7+11)=4+(3+7)+11\)
\((21+3)-11=(3+21)-11\)
Показать ответ
Ответ:
Правильный ответ: \((4+3)+(7+11)=4+(3+7)+11\). Ассоциативное свойство говорит о том, что не имеет значения, как сгруппированы добавленные термины. Поскольку все эти термины добавляются друг к другу, скобки можно ставить в любом месте.
Ассоциативное свойство говорит о том, что не имеет значения, как сгруппированы добавленные термины. Поскольку все эти термины добавляются друг к другу, скобки можно ставить в любом месте.
Скрыть ответ
Вопрос №3:
К какой из следующих операций применимо свойство ассоциативности?
Сложение и умножение
Сложение и вычитание
Умножение и деление
Вычитание и деление
Показать Ответ
Ответ:
Правильный ответ — сложение и умножение. Ассоциативность относится к сложению и умножению, но не к вычитанию и делению. Вычитание и деление — это операции, которые требуют выполнения в очень определенном порядке, в отличие от умножения и деления.
Скрыть ответ
Вопрос № 4:
Какой из следующих способов не является правильным переписыванием выражения \(4×11×21÷3÷7\)?
\((4×11×21)÷3÷7\)
\((4×11)×21÷3÷7\)
\(4×(11×21)÷3÷7\) )
\(4×11×21÷(3÷7)\)
Показать ответ
Ответ:
Правильный ответ: \(4×11×21÷(3÷7)\). Ассоциативное свойство применяется к умножению, но не к делению, поэтому разделенные термины нельзя перегруппировать.
Ассоциативное свойство применяется к умножению, но не к делению, поэтому разделенные термины нельзя перегруппировать.
Скрыть ответ
Вопрос № 5:
Что из следующего является правильным примером ассоциативного свойства?
\(4÷(3÷7)=(4÷3)÷7\)
\(4×3×7=7×3×4\)
\(4×(3×7)= (4×3)×7\)
\(4÷3÷7=7÷3÷4\)
Показать ответ
Ответ:
Правильный ответ: \(4×(3×7) )=(4×3)×7\). Ассоциативное свойство говорит, что вы можете перегруппировать умноженные термины любым способом. Перестановка умноженных членов является примером коммутативного свойства. Ни одно из этих свойств не применимо к делению.
Скрыть ответ
Вопрос № 6:
Какое утверждение лучше всего иллюстрирует свойство коммутативности?
\(4×3=12\)
\(6+5=5+6\)
\(34-2=2-34\)
\(6×6=5×5\)
Показать ответ
Ответ:
Правильный ответ: \(6+5=5+6\). Коммутативное свойство утверждает, что значения можно перемещать или менять местами при сложении или умножении, и результат не изменится. По сути, порядок не имеет значения при сложении или умножении.
Коммутативное свойство утверждает, что значения можно перемещать или менять местами при сложении или умножении, и результат не изменится. По сути, порядок не имеет значения при сложении или умножении.
Скрыть ответ
Вопрос № 7:
Используйте свойство перестановочности, чтобы найти пропущенное значение:
\(45+44+43=43+44+\)_____
4 0 90 4 0 0 4 0 4 0 0 0 4 9 0
45
Показать ответ
Ответ:
Правильный ответ: 45. Коммутативное свойство позволяет складывать или умножать числа в любом порядке.
Скрыть ответ
Вопрос №8:
Используйте свойство коммутативности, чтобы найти пропущенные значения:
\(4+6+\) ____\(=6+\)____ \(+8\)
\(4+6+\mathbf6=6+\mathbf4 +8\)
\(4+6+\mathbf4=6+\mathbf4+8\)
\(4+6+\mathbf8=6+\mathbf4+8\)
\(4+6+ \mathbf4=6+\mathbf5+8\)
Показать ответ
Ответ:
Правильный ответ: \(4+6+\mathbf8=6+\mathbf4+8\). Помните, что с коммутативным свойством порядок чисел не имеет значения при сложении и умножении.
Помните, что с коммутативным свойством порядок чисел не имеет значения при сложении и умножении.
Скрыть ответ
Вопрос № 9:
Если \(x=2\), \(y=5\) и \(z=1\), что из следующего верно в отношении этого уравнения :
\(2x+4y+9z=9z+4y+2x\)
Обе стороны равны 44.
Обе стороны равны 33.
Левая часть равна 33, а правая часть равна 44.
Левая часть равна 44, а правая сторона равна 33.
Показать ответ
Ответ:
Правильный ответ: Обе стороны равны 33.. Несмотря на то, что термины перечислены в другом порядке, левая и правая часть уравнения равны 33,
Скрыть ответ
Вопрос №10:
Перепишите выражение \(45+6+19\), используя свойство коммутативности.
\(6-19-45\)
\(45+19-6\)
\(6+45+19\)
\(45-19+6\)
Показать ответ
Ответ:
Правильный ответ: \(6+45+19\). Выражение \(45+6+19\) эквивалентно \(6+45+19\), потому что изменение порядка добавления не влияет на результат.
Скрыть ответ
Распределительное свойство – определение и примеры
Среди всех свойств в математике довольно часто используется распределительное свойство . Это связано с тем, что любой метод умножения числа на другое число использует распределительное свойство. Это свойство было введено в начале 18 века, когда математики начали анализировать абстракции и свойства чисел.
Слово дистрибутивное взято от слова « распределять », что означает, что вы делите что-то на части. Это свойство распределяет или разбивает выражения на сложение или вычитание двух чисел.
Что такое распределительная собственность?
Распределительное свойство — это свойство умножения, используемое при сложении и вычитании. Это свойство утверждает, что два или более условия сложения или вычитания с числом равны сложению или вычитанию произведения каждого из слагаемых с этим числом.
Распределительное свойство умножения
В соответствии с распределительным свойством умножения произведение числа на сложение равно сумме произведений этого числа на каждое слагаемое. Распределительное свойство умножения также верно для вычитания, где вы можете либо сначала вычесть числа и умножить их, либо сначала умножить числа, а затем вычесть.
Рассмотрим три числа A , B и C , сумма A и B , умноженная на C , равна сумме каждой добавления, умноженная на C , I.E.E.E.
(
(
(
(
(
(
(
(Multiplyed на C , I.E.E. 9000
( A + B ) × C = AC + BC
Аналогично, вы можете написать свойство распределения для умножения для выявления,
( A — B 6). 1026 = ac – bc
1026 = ac – bc
Распределительное свойство с переменными
Как было сказано ранее, распределительное свойство довольно часто используется в математике. Следовательно, это действительно полезно и для упрощения алгебраических уравнений.
Чтобы найти неизвестное значение в уравнении, мы можем выполнить следующие шаги:
- Найдите произведение числа с другими числами в скобках.
- Расположите члены так, чтобы постоянные члены и переменные члены находились на противоположных сторонах уравнения.
- Решите уравнение.
Пример приведен в последнем разделе.
Распределительное свойство с показателямиРаспределительное свойство также полезно в уравнениях с показателями. Показатель степени означает, сколько раз число умножается само на себя. Если вместо числа имеется уравнение, свойство также выполняется.
Вам необходимо выполнить следующие шаги, чтобы решить задачу экспоненты с помощью распределительного свойства:
- Разверните данное уравнение.

- Найти все продукты.
- Добавьте или вычтите одинаковые термины.
- Решите или упростите уравнение.
Пример приведен в последнем разделе.
Распределительное свойство с дробямиПрименение распределительного свойства к уравнениям с дробями немного сложнее, чем применение этого свойства к любой другой форме уравнения.
Используйте следующие шаги для решения уравнений с дробями с использованием распределительного свойства:
- Определите дроби.
- Преобразуйте дробь в целые числа, используя распределительное свойство. Для этого умножьте обе части уравнений на НОК.
- Найти продукты.
- Изолируйте термины с переменными и термины с константами.
- Решите или упростите уравнение.
Пример приведен в последнем разделе.
Примеры Чтобы решить задачи на дистрибутивные слова, всегда нужно вычислять числовое выражение, а не искать ответы. Прежде чем приступать к словесным задачам, мы рассмотрим некоторые основные задачи.
Прежде чем приступать к словесным задачам, мы рассмотрим некоторые основные задачи.
Пример 1
Решите следующее уравнение, используя свойство распределения.
9 ( x – 5) = 81
Решение
- Шаг 1: Найдите произведение числа с другими числами в скобках.
9 ( x ) – 9 (5) = 81
9x – 45 = 81
- против уравнения.
9 x – 45 + 45 = 81 + 45
9 x = 126
- Шаг 3: Решите уравнение.
9 x = 126
x = 126/9
x = 14
Пример 2
Solve Solve Solve Solve Sealte. Следующая уравнение.
(7 x + 4) 2
Решение
- Шаг 1: Расширьте уравнение.
(7 x + 4) 2 = (7 x + 4) (7 x + 4)
- Шаг 2.
 Найдите все продукты.
Найдите все продукты.
(7 x + 4) (7 x + 4) = 49 x 2 + 28 x + 28 x + 16
- 9024 x + 16 9023
- . условия.
49 x 2 + 56 x + 16
Пример 3
Решите следующее уравнение, используя свойство распределения.
x – 5 = x /5 + 1/10
Решение
- Шаг 1: Найдите дроби.
В правой части две дроби.
- Шаг 2: Найдите НОК 5, 10, что равно 10.
Умножьте на НОК с обеих сторон.
10 ( х – 5) = 10 ( х /5 + 1/10)
- Шаг 3: Упростить,
10 x – 50 = 2 x + 1
- Шаг 4: Изолировать термины и термины с переменными.
10 x — 2 x = 1 + 50
- Шаг 5:
8 x = 51
9000 2 9025 x = = = = = = = = = = = = = .
У вас есть два друга, Майк и Сэм, родившиеся в один день. Вам нужно подарить им на день рождения такой же комплект из рубашек и брюк. Если рубашка стоит 12 долларов, а брюки — 20 долларов, каковы общие затраты на покупку подарков?
Решение
Есть два способа решить эту проблему.
Метод 1:
- Шаг 1: Найдите общую стоимость каждого комплекта.
12 долларов + 20 долларов = 32 доллара
- Шаг 2: Поскольку друзей двое, умножьте общую стоимость на 2.
$32 × 2
- Шаг 3: Найдите общую стоимость.
32 долл. США × 2 = 64 долл. США
Метод 2:
- =Шаг 1: Поскольку друзей двое, удвойте стоимость рубашки.
12 $ × 2 = 24 $
- Шаг 2: Так как друзей двое, удвойте стоимость брюк.
20 $ × 2 = 40 $
- Шаг 3: Найдите общую стоимость.
24 доллара + 40 долларов = 64 доллара
Пример 5
У трех друзей по две десятицентовика, три пятака и десять пенни у каждого. Сколько денег у них всего?
Сколько денег у них всего?
Решение
Опять же, есть два способа решить эту проблему.
Метод 1:
- Шаг 1: Найдите общую стоимость монет каждого типа.
DIMES:
2 × 10 ¢ = 20 ¢
Никель:
3 × 5 ¢ = 15 ¢
Pennies:
10 × 1 ¢ = 10 ¢
- . три друга, поэтому умножьте каждый тип монет на 3 .
Десятицентовики:
3 × 20 центов = 60 центов
Никели:
3 × 15 центов = 45 центов
Пенни:
3 × 10 центов = 30 центов
- Шаг 3: Найдите общую сумму денег.
60 центов + 45 центов + 30 центов = 135 центов
Шаг 4: Конвертируйте в доллары.
135/100 = 1,35 доллара США
Метод 2:
- Шаг 1: У каждого человека есть две десятицентовика, три пятака и десять пенни.
2 × 10 ¢ + 3 × 5 ¢ + 1 × 10 ¢
- Шаг 2: Сумма денег у каждого человека.

2 × 10 центов + 3 × 5 центов + 1 × 10 центов = 45 центов
- Шаг 3: Всего денег у трех человек.
45 центов + 45 центов + 45 центов = 135 центов
- Шаг 4: Конвертируйте в доллары. Пример 6 Найдите длину и ширину прямоугольника, если его площадь равна 18 кв.
Решение
- Шаг 1: Определите длину и ширину прямоугольника.
Длина представлена как x .
Следовательно, ширина = x + 3
- Шаг 2: Площадь прямоугольника составляет 18 квадратных единиц.
Площадь = длина × ширина
x ( x + 3) = 18
- Шаг 3: Используйте свойство распределения.
x 2 + 3 x = 18
- Шаг 4: Перепишите в виде квадратного уравнения.
x 2 + 3 x – 18 = 0
- Шаг 5: Факторизация и решение.


 Кроме того, эти правила применяются и в высшей математике. Например, для сложения или вычитания векторов, а также для работы с числовыми множествами.
Кроме того, эти правила применяются и в высшей математике. Например, для сложения или вычитания векторов, а также для работы с числовыми множествами.
 Кроме того, эти правила применяются и в высшей математике. Например, для сложения или вычитания векторов, а также для работы с числовыми множествами.
Кроме того, эти правила применяются и в высшей математике. Например, для сложения или вычитания векторов, а также для работы с числовыми множествами.

 ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Детский сад — 7 класс. / / Законы сложения и умножения. Переместительный, сочетательный и распределительный законы. Они же: коммутативный, ассоциативный и дистрибутивный законы. Примерно 5 класс (10-11 лет)
ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Детский сад — 7 класс. / / Законы сложения и умножения. Переместительный, сочетательный и распределительный законы. Они же: коммутативный, ассоциативный и дистрибутивный законы. Примерно 5 класс (10-11 лет)


 Определите результирующее смещение Эрика.
Определите результирующее смещение Эрика.
 ISBN: 9780071077866.
ISBN: 9780071077866.
 Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором. 130 УК РФ. Оскорбление личности
130 УК РФ. Оскорбление личности
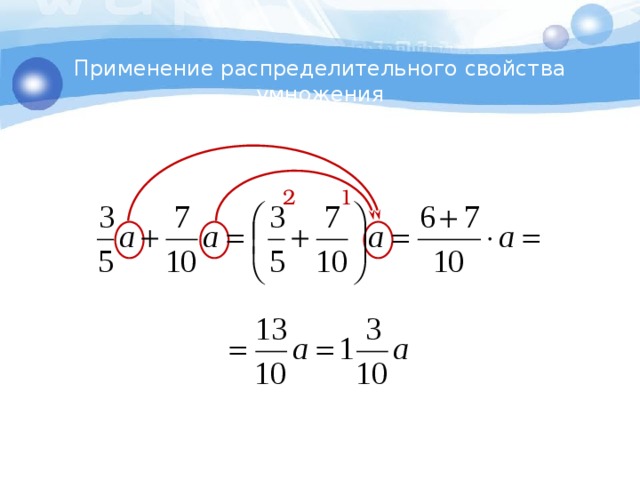 Теперь пришло время проверить это свойство на примере.
Теперь пришло время проверить это свойство на примере.
 Найдите все продукты.
Найдите все продукты. 
