I Организационный момент Ребята, вчера, в одном журнале я прочитала статью о великом русском учёном Михаиле Васильевиче Ломоносове, которому в этом году 19 ноября исполнилось 300 лет со Дня рождения. И вы знаете, какие ёмкие слова он сказал о математике. Я даже решила вынести их на слайд. Слайд 1.«Математику уже за то любить следует, что она ум в порядок приводит». | ||||
Деятельность учителя | Деятельность ученика | |||
— Объясните смысл высказывания. — выделите ключевые слова. Слайд 2, 3. Прочтите, в какие науки внёс вклад М.В.Ломоносов. | Объяснение смысла записи | |||
Слайд 4, 5. Устный счёт проводится с целью развития и формирования прочных вычислительных навыков и умений, повышения у детей познавательного интереса к урокам математики. | ||||
Давайте приводить наш ум в порядок. Посмотрите на слайд и решите логические задачи: — Масса индейки – 8 кг и ещё половина её собственной массы. Сколько весит индейка? — Когда сутки короче: зимой или летом? -1,2,3,4,5,6,7,8,9,0.Что больше сумма этих чисел или их произведение? А теперь продолжим приводить ум в порядок с помощью примеров: 2500 + 60 + 8 12 х 4 100: 25 7 + 100 + 1000 100 х 5 72 : 3 9600 + 400 6 х 40 720 : 30 3 000 + 9 000 11 х 9 91 : 7 1 000 : 100 84 : 42 910 : 70 — С какой целью мы выполняли устный счёт? | 12 одинаковые Сумма, так как при умножении на 0 получается 0. | |||
II Активизация знаний (который заканчивается постановкой детьми учебной задачи) | ||||
— Посмотрите на равенства. Слайд 6. — Распределите выражения в два столбика, по какому признаку мы это сделаем? Сформулируйте переместительное свойство сложения, умножения; Сочетательное свойство относительно сложения, умножения. — Зачем нужно знать свойства в математике? — Давайте выберем соответствующие таблички с переменными соединим их с названием свойств. — Почему последнее выражение не вошло ни в один столбик? — Как нашли результат? — Давайте выпишем его отдельно. Как по другому можно решить это выражение? Выполните у доски. — Может вы вспомните как это свойство называется в математике? | (248 + 7309) + 96 = 248 + (7 309 + 96) – сочетательное свойство сложения 269 + 1050 = 1050 +269 – переместительное свойство сложения (105 х 2) х 3 =105 х (2 х 3) – сочетательное свойство относительно умножения 13 х 25 = 25 х 13 – переместительное свойство умножения. (90 + 25)х 4 = 460 (потому, что у него есть результат; потому, что записано только умножение сумы на число … ) Чтобы облегчить решение. Сначала выполнили действие в скобках, затем умножение Чтобы сумму двух чисел умножить на какое – нибудь число, можно каждое из них умножить на это число, а результаты сложить. Распределительное свойство умножения относительно сложения. | |||
III. Первичное закрепление. | ||||
-Используя распределительное свойство умножения относительно сложения, запишите выражения, равные данным. Взаимопроверка (Раздаётся карточка помощница слабым детям (85 +6) х5 = 85 х5 + 6 х 5 Цель: вспомнить правило умножения суммы на число. — Так как умножить сумму на число? | (№379 с.89) (112 + 44) х3; (7 +4) х 132 (16 + 18) х 25; (36+ 24) х 9 Учащиеся обмениваются тетрадями и проверяют по образцу. Чтобы умножить сумму двух чисел на какое – нибудь число, можно каждое слагаемое умножить на это число и сложить полученные результаты. | |||
IV. «Открытие детьми нового знания» | ||||
— Найдите значение выражения двумя способами. Слайд 7. — В каком случае пользоваться при вычислении распределительным свойством неудобно? В каком случае распределительным свойством пользоваться неудобно? Откройте учебник на с.90, з.381 Прочитайте выражения, с которым работают в лесной школе. — Как выполнял сложение Слон? -Как Мышь умножала разность чисел 90 и 25 на число 4? Сравните вычисления. Чей способ лучше и почему? Сформулируйте правило свойства умножения относительно вычитания. С переменными мы уже работать умеем, заменим в этом выражении цифровую запись на буквенную. Кто желает выполнить это у доски? — Что мы можем сказать о значении переменных, которые они могут принимать? Давайте коллективно обсудим. | (№ 380 с.90) (50 +19) х 2 = 69х2=138 (50 +19) х 2 = 50х2 + 19х2=100 + 38 =138 (72 + 28) х 7 = 100х7=700 (72 + 28) х 7 = 72х7 + 28х7= 504 + 196 = 700 (72 + 28) х 7 = 72х7 + 28х7 (90 — 25) х 4=260 Слон 90 65 -25 х 4 65 260 Мышь (90 – 25) х 4 = 90 х 4 – 25 х4= 360 – 100 = 260 Способ лучше у Мышки, потому, что она использует устные вычисления, а Слон письменные. Чтобы разность умножить на какое – нибудь число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе. (а + в) х с = ас + вс (а – в) х с (а + в) х с Равенство, выражающее распределительное свойство умножения относительно сложения, верно при любых значениях переменных а, в и с; Если же умножается разность на число, то в запись свойства вводятся ограничения: исключаются случаи, когда в разности а – в число а меньше числа в. | |||
V. Физкультминутка | «Качания головой» упражнение стимулирует мыслительные процессы: дышите глубоко, расслабьте плечи и уроните голову вперёд Позвольте голове медленно качаться из стороны в сторону, при помощи дыхания уходит напряжение. (15 раз) «Ленивые восьмёрки» упражнение активизирует структуру мозга, улучшает память, повышает внимание: нарисуйте в воздухе в горизонтальной плоскости «восьмёрки» по три раза каждой рукой, а затем обеими руками. «Шапка для размышлений» упражнение для улучшения внимания, восприятия, речи: «наденьте шапку», то есть мягко заверните уши от верхней точки до мочки три раза. «Моргания» (полезно при всех видах нарушения зрения): моргайте на каждый вдох и выдох) «Отдых для глаз» упражнение укрепляют мышцы век, способствуют кровообращению: плотно закрыть и широко открыть глаза. | |||
VI . | ||||
— Работаем с учебником с.91 №383 (по вариантам) — Выполним вычисления так, как это делала Мышка. — Давайте ещё раз проверим, выполняется ли у нас ограничение в разности а и в, а меньше? Слайд 8 (Задания для сильных учащихся) | Объяснение инструкции к заданию. Запись выражения равного данному. (42 – 15) х 2= 42 х2 -15х2= 84-30=54 (31 – 8) х 5=31х5 – 8х5 = 155 – 40 =115 Да, выполняется. 42 больше 15 и 31 больше 8. (135 – 84) х 3 =135 х 3 – 84 х 3 1в. – 1 столбик, 2в. – 2 столбик Проверка по образцу. | |||
VII. Резерв. Самостоятельная работа. Решение задачи по заданному выбору представления решения. | ||||
— Прочитайте задачу. — Какие величины известны в задаче? 1ряд решает выражением; 2 ряд – по вопросам; 3 ряд – по действиям. Проверим по образцу | №395 с.92 Группа туристов проплыла 2ч на плоту, проплывая каждый час 4 км, а затем прошла пешком 3ч, проходя каждый час 6 км. Найдите дину всего маршрута туристов. 4 х 2+6 х 3 1)Чему равен путь туристов на плоту?4х2=8 (км) 2)Чему равен путь туристов пешком? 6 х 3=18(км) 3)Чему равен весь путь? | |||
VIII. Закрепление. — Чему научились новому на уроке? — Еще раз сформулируем правила распределительного свойства относительно сложения и вычитания. | ||||
— Проверим, как вы научились с помощью теста пользоваться распределительным свойством умножения относительно сложения и вычитания. Ключ к проверке теста Проверяем взаимопроверкой: 1 вариант 1) б 2) б 3) а 4) а | 2 вариант 1) в 2) а 3) б 4) б | Тест 1. Какие из равенств являются распределительным свойством умножения? 1 вариант | 2 вариант | |
а) а х(в х с)=(а х в)хс; б) (а + в)хс = ас + вс; в) (а + в)х с = а — с + в; | а)а х в = в х а; б)а — (в+с) = а-в -с; в)(а + в) х с= ас + вс; | 80 х 5 – 2 х 5 | ||
равно | ||||
а) 30; б) 300; в)103 | а) 390; б) 400; в)102; | 60 х 2 + 19 х 2 | ||
равно | ||||
а) 720; б) 106; в) 60 | а)150; б) 158; в)108; | |||
а) (60 + 1) х 4; б) (17 – 13) х 5; | а) (67 – 17) х 4; б) (30 – 2) х 5; | |||
Этап | Деятельность учителя | Деятельность обучающихся | Универсальные действия | Самоопределение к деятельности Организационный момент. | Формирую группы. На перемене к стулу прикрепляю карточки с таблицей умножения. К доске выходят ребята первого варианта и выбирают таблицу, которую хотят сегодня повторить, таким образом, образовывается пара на время устного счёта. 1)Повторение в паре таблицы умножения и деления. 2)Решение и объяснение примеров на деление. Приветствие. Напоминание о правилах работы в группах. (Слайд№2) -Желаю, чтобы глаз у вас был острым, ум гибким, а знания, которые вы приобретёте на уроке – крепкими. — Запишите число, «Классная работа». 1 вариант 2 вариант (Слайд№3)
928:4 640:4 632:8 532:4 Оценка работы группы смайлик Поменялись быстро местами и заняли каждый своё место. | Рассматривают карточки и садятся на тот стул, который выбрали и в паре повторяют таблицу. | Личностные : самоопределение; регулятивные : целеполагание; коммуникативные: планирование учебного сотрудничества с учителем и сверстниками | Актуализация знаний и фиксация затруднений в деятельности Постановка учебной задачи Построение проекта выхода из затруднения Первичное закрепление Самостоятельная работа с самопроверкой по эталону Отработка и закрепление Применение Обратная связь: Рефлексия деятельности (итог урока) | 1. Решение задач на нахождение неизвестного по двум разностям
-С какими трудностями встретились при выполнении домашнего задания? — Как записали условие задачи? — Кто научился решать задачи данного вида? 2. Игра молчанка, математический диктант. 1) Устный счёт (Слайд№5), (Слайд№6) 2500 + 60 + 8 100: 25 1 000 : 100 7 + 100 + 1000 100 • 5 72 : 3 9600 + 400 6 • 40 720 : 30 3 000 + 9 000 11 • 9 91 : 7 84 : 42 910 : 70 2) Арифметический диктант (Слайд№7) проверка — 736 увеличить на 20. 2)- Повторение переместительного и сочетательного законов умножения и сложения (Слайд №8) — Посмотрите на равенства. Прежде чем мы с ними начнём работать, обратите внимание на математические действия. Какие действия встречаются в этих выражениях? 3)- Распределите выражения в два столбика. По какому признаку мы это сделаем? (Слайд№9) (248 + 7309) + 96 = 248 + (7 309 + 96) 269 + 1050 = 1050 +269 (105 х 2) х 3 =105 х (2 х 3) 13 х 25 = 25 х 13 Сочетательное свойство Переместительное свойство — Сформулируйте переместительное свойство сложения, умножения; Сочетательное свойство сложения, умножения. — Зачем нужно знать свойства в математике? Почему последнее выражение не вошло ни в один столбик? — Как нашли результат? (Сначала выполнили действие в скобках, затем умножение). — Давайте выпишем его отдельно. Как по-другому можно решить это выражение? Выполните у доски. — Может, вы вспомните, как это свойство называется в математике? Тема урока (Слайд №10) — Чему будем учиться на уроке? — Давайте посмотрим, как ученики лесной школы выполнили умножение суммы на число. Откройте учебники на стр. 89, прочитайте ещё раз распределительное свойство умножения относительно сложения (№379 с.89) — Используя распределительное свойство умножения относительно сложения, запишите выражения, равные данным (по вариантам) 1 в. 2в. (112 + 44) х3; (7 +4) х 132 (16 + 18) х 25; (36+ 24) х 9 — Так как умножить сумму на число? Чтобы умножить сумму двух чисел на какое-нибудь число, можно каждое слагаемое умножить на это число и сложить полученные результаты. (№ 380 с.90) — Найдите значение выражения двумя способами. (Слайд №11) (50 +19) х 2 = 69х2=138 (50 +19) х 2 = 50х2 + 19х2=100 + 38 =138 (72 + 28) х 7 = 100х7=700 (72 + 28) х 7 = 72х7 + 28х7= 504 + 196 = 700 — В каком случае пользоваться при вычислении распределительным свойством неудобно? (72 + 28) х 7 = 72х7 + 28х7 3 . Физкультминутка (слайд №12) А)Вычислите удобным способом. Поработайте в группах. (13 + 17) х 5 (14 + 16) х 9 (12 + 18) х 7
В) Решение задач (слайд №13) — Двое рабочих изготавливают одинаковые детали. Один рабочий делает за час 27 деталей, а другой – 32 детали. Сколько всего деталей они изготовят за 8 часов? — Два поезда одновременно выехали навстречу друг другу из двух пунктов. Скорость первого поезда 85 км/ч, а второго – 65 км/ч. Проверка (Слайд№14) Итог урока (Слайд№15)
9. Самооценка (слайд№16) — Какая была проблема? — Какой способ умножения многозначного числа на однозначное мы использовали сегодня? — Какое свойство произведения нам помогло? — О каких способах поговорим на следующем уроке?
Заполните отметочники до конца. Д/з С. 91 № 386, 387. Литература:
| ИНДИВИДУАЛЬНАЯ РАБОТА (у доски 3 человека) Самооценка Записывают только значение выражений. Самопроверка, самооценка в отметочниках. 1 ученик у доски записывает ответы, проверка, самооценка ФРОНТАЛЬНАЯ РАБОТА Находят и читают свойства Чтобы облегчить решение Фронтальная работа у доски ЦЕЛЬ для ученика: самоопределение, постановка личных и познавательных задач Формулировка целей урока 1. Научиться применять это свойство 2. Увидеть важное практическое значение этого свойства — Осознание смыслов, самостоятельные «открытия» нового знания — Взаимопроверка. Учащиеся обмениваются тетрадями и проверяют по образцу. Фронтальная работа (3 человека у доски) Парная работа Выполняют задания, один отчитывается по плану 1. 2.Не умеем умножать ОТМЕТОЧНИК
ИНДИВИДУАЛЬНАЯ РАБОТА — Способ разложения на сумму разрядных слагаемых. -Распределительное. — Кому необходимо доучить таблицу умножения? — Кто считает, что ему надо повторить свойства умножения | Развитие у школьников монологической и диалогической речи Смайлик Коммуникативные : планирование учебного сотрудничества с учителем и сверстниками; познавательные: логические – анализ объектов с целью выделения признаков |
Распределительное свойство умножения – применение (6 класс, математика)
4.2
Средняя оценка: 4.2
Всего получено оценок: 190.
4.2
Средняя оценка: 4.2
Всего получено оценок: 190.
Свойства умножения – это, прежде всего, возможность быстро произвести вычисление. Знание распределительного свойства поможет вам без проблем посчитать сложный пример или решить уравнение. Рассмотрим в в подробностях применение распределительного свойства умножения.
Рассмотрим в в подробностях применение распределительного свойства умножения.
Умножение
Умножение – это сокращенный процесс сложения. Что это значит? Первый множитель это число, которое складывается само с собой число раз, равное второму множителю.
3*6=3+3+3+3+3+3=18 – вот как это выглядит на практике. Умножение было изобретено во время, когда потребовались большие вычисления, которые неудобно записывать в виде сложения.
Можно 3 раза сложить число 6, а можно 6 раз сложить число 3. Результат от этого не поменяется, в этом заключается смысл переместительного свойства умножения.
Умножение позволило решить достаточно много проблем, но вместе с ним в математику пришло и деление, как противоположная операция.
Свойства умножения
Всего у умножения 3 свойства:
- Переместительное: от перемены мест множителя произведение не меняется. Для произведения в 2 множителя это не критично, но для примеров с 3 и более множителями, это свойство может сэкономить время.

- Сочетательное свойство. Это свойство так же используется для примеров от 3 и более множителей. Суть свойства в том, что можно перемножить первые два множителя, а потом результат умножить на третий. Причем порядок перемножения может быть любым.
- Распределительное свойство. Это свойство применяется для умножения числа на сумму или разность. Это свойство сокращает время решения при правильном подходе. Суть свойства в том, что при умножении числа на сумму или разность, то можно каждое слагаемое умножить на число, а потом выполнить сложение.
Распределительное свойство
Распределительно свойство можно использовать для быстрого расчета. Рассмотрим большой пример для 6 класса с применением этого свойства умножения:
$$({3\over{4}}-{2\over{8}})*(18-16)+{1\over{15}}*((13+30)-(16-3))+{16\over{17}}*(-34+17)$$
$$-({20\over{21}}-{38\over{42}})*({7\over{3}}+{56\over{3}})$$
Обратите внимание, что пример представляет собой сумму слагаемых, каждый из которых представлен произведением. Рассмотрим каждое произведение в отдельности, а потом сложим результаты.
Рассмотрим каждое произведение в отдельности, а потом сложим результаты.
- $$({3\over{4}}-{2\over{8}})*(18-16)$$ – Найдем значение дроби в первой скобке, а затем умножим его на уменьшаемое и делитель во второй скобке по распределительному свойству.
$${3\over{4}}-{2\over{8}}={6\over{8}}-{2\over{8}}={4\over{8}}={1\over{2}}$$
$${1\over{2}}*18-{1\over{2}}*16=9-8=1$$ – такие ответы иногда бывают в сложных на вид примерах.
- $${1\over{15}}*((13+30)-(16-3))$$ – здесь слишком много слагаемых, чтобы использовать распределительное свойство, поэтому просто выполним действия во второй скобке и произведем умножение:
$$(13+30)-(16-3)=43-13=30$$
$${1\over{15}}*30=2$$
- $${16\over{17}}*(-34+17)$$ – обратите внимание, в знаменателе дроби стоит число 17, которое является делителем для чисел в скобках. Это признак того, что можно и нужно воспользоваться распределительным свойством умножения.
$${16\over{17}}*(-34+17)= {16\over{17}}*(-34)+ {16\over{17}}*17=-32+16=16$$
- $$({20\over{21}}-{38\over{42}})*({7\over{3}}+{56\over{3}})$$ – если посмотреть на вторую скобку, то видно, что в ней можно выполнить сложение дробей без приведения к общему знаменателю.

$$({7\over{3}}+{56\over{3}})={63\over{3}}=21$$ – теперь воспользуемся распределительным свойством и умножим число 21 на каждое из чисел в скобках:
$$({20\over{21}}-{38\over{42}})*21=20-{38\over{2}}=20-19=1$$
- Сведем все получившиеся значения в один пример и вычислим результат:
1+2+16-1=18 – вот такой маленький ответ получился в большом примере.
При решении этого примера, важно понять, что не всегда нужно использовать распределительное свойство умножения. Важно понимать, когда лучше им воспользоваться, а когда решить другим путем.
Что мы узнали?
Мы узнали, что такое умножение. Поговорили о свойствах умножения и особенно выделили распределительное свойство умножения. Решили большой пример на тему применения этого свойства.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Александр Плотников
10/10
Roman Tazhinov
8/10
Вет Громов
7/10
Оценка статьи
4. 2
2
Средняя оценка: 4.2
Всего получено оценок: 190.
А какая ваша оценка?
Распределительное свойство умножения — определение, формула, примеры
Согласно распределительному свойству умножения, когда мы умножаем число на сумму двух или более слагаемых, мы получаем результат, равный результату, который получается, когда мы умножьте каждое слагаемое в отдельности на число. Распределительное свойство умножения распространяется на сумму и разность еще двух чисел.
| 1. | Что такое распределительное свойство умножения? |
| 2. | Распределительное свойство формулы умножения |
| 3. | Распределительное свойство умножения на сложение |
| 4. | Распределительное свойство умножения над вычитанием |
| 5. | Часто задаваемые вопросы о распределительном свойстве умножения |
Что такое распределительное свойство умножения?
Распределительное свойство умножения, справедливое для сложения и вычитания, помогает распределить заданное число на операцию, чтобы легко решить данное уравнение. Простыми словами, когда число умножается на сумму двух чисел, то произведение такое же, как произведение, которое мы получаем, когда число распределяется на два числа внутри скобок и умножается на каждое из них в отдельности. Давайте разберемся в этом на примере. Когда мы получаем выражение вроде 6(3 + 5), мы используем порядок операций, сначала раскрывая скобки, а затем умножая результат на другое число следующим образом: 6(3 + 5) = 6 (8) = 6 × 8 = 48,
Простыми словами, когда число умножается на сумму двух чисел, то произведение такое же, как произведение, которое мы получаем, когда число распределяется на два числа внутри скобок и умножается на каждое из них в отдельности. Давайте разберемся в этом на примере. Когда мы получаем выражение вроде 6(3 + 5), мы используем порядок операций, сначала раскрывая скобки, а затем умножая результат на другое число следующим образом: 6(3 + 5) = 6 (8) = 6 × 8 = 48,
Однако, когда мы применяем распределительное свойство умножения к тому же выражению 6(3 + 5), мы распределяем число 6 на 3, а затем на 5 следующим образом: (6 × 3) + (6 × 5) = 48. Мы получаем одинаковый результат обоими методами. Теперь вопрос в том, почему мы используем свойство дистрибутивности, если мы получаем один и тот же результат обоими методами. Ответ заключается в том, что распределительное свойство используется для решения выражений, в которых вместо чисел используются переменные. Поскольку разные переменные нельзя складывать или вычитать, в этом случае помогает распределительное свойство.
Распределительное свойство формулы умножения
Формула распределительного свойства умножения: a(b + c) = ab + ac. Эта формула объясняет, что мы получаем один и тот же продукт в обеих частях уравнения, даже если мы умножаем «а» на сумму «b» и «с» в левой части или когда мы распределяем «а» на «b», а затем «c» справа. Обратите внимание на следующую формулу распределительного свойства умножения. Следует отметить, что это свойство применимо к сложению и вычитанию.
Распределительное свойство умножения на сложение
Распределительное свойство умножения над сложением гласит, что умножение суммы двух или более слагаемых на число дает тот же результат, что и умножение каждого слагаемого по отдельности на число и последующее сложение произведений вместе. Это свойство умножения над сложением используется, когда нам нужно умножить число на сумму. Например, решим выражение 7(9+ 3). Если решить его в обычном порядке действий, то мы сначала решим скобки, а затем умножим число на полученный результат. 7(9 + 3) = 7(12) = 84
7(9 + 3) = 7(12) = 84
Однако, в соответствии с распределительным свойством умножения над сложением, мы умножаем 7 на каждое слагаемое. Это называется распределить число 7 на 9 и 3, а затем мы добавляем каждый продукт. Итак, найдем произведение распределенного числа: 7 × 9 и 7 × 3. Это дает нам: 7(9) + 7(3) = 63 + 21 = 84. Это показывает, что мы получаем одно и то же произведение.
Обратите внимание на следующее уравнение, которое показывает обычный метод в левой части и распределительное свойство умножения над сложением в правой части. Применяя распределительное свойство, мы распределяем число 7 на 9 и 3, затем умножаем соответствующие числа на 7 и складываем результаты. В каждом случае результат одинаков.
7(9 + 3) = 7(9) + 7(3)
7(12) = 63 + 21
84 = 84
Распределительное свойство умножения на вычитание
Распределительное свойство умножения над вычитанием гласит, что умножение числа на разность двух других чисел равно разности произведений распределенного числа. Формула распределительного свойства умножения над вычитанием: a(b — c) = ab — ac. Например, решим: 9(20 — 10).
Формула распределительного свойства умножения над вычитанием: a(b — c) = ab — ac. Например, решим: 9(20 — 10).
Используя обычный порядок действий, находим разность чисел, указанных в скобках, а затем умножаем результат на 9.
9(20 -10) = 9(10) = 90
Теперь давайте воспользуемся распределительным свойством умножения над вычитанием, чтобы решить 9(20 — 10). Мы умножаем 9 на каждое значение внутри скобки, а затем находим разницу произведений.
Итак, перемножим: 9 × 20 и 9 × 10. Получим: 9(20) — 9(10) = 180 — 90 = 90. Результат такой же, как и выше.
Обратите внимание на следующее уравнение, в котором обычный метод показан в левой части, а распределительное свойство умножения применяется в правой части. Применяя распределительное свойство умножения над вычитанием, мы распределяем число 9до 20 и 10, затем умножаем соответствующие числа на 9 и вычитаем произведения. В обоих случаях мы получаем один и тот же ответ.
9(20 — 10) = 9(20) — 9(10)
9(10) = 180 — 90
90 = 90
Связанные статьи умножение.

- Формула распределительной собственности
- Ассоциативное свойство умножения
- Умножение
Часто задаваемые вопросы о распределительном свойстве умножения
Что такое распределительное свойство умножения в математике?
Согласно распределительному свойству умножения, когда мы умножаем число на сумму двух или более слагаемых, мы получаем результат, равный результату, который получается при умножении каждого слагаемого в отдельности на число. Распределительное свойство умножения распространяется на сумму и разность еще двух чисел. Он используется для простого решения выражений путем распределения числа на числа, указанные в скобках. Например, если мы применим свойство дистрибутивности для решения выражения: 3(2 + 4), мы решим его следующим образом: 3(2 + 4) = (3 × 2) + (3 × 4) = 6 + 12 = 18,
Что такое распределительное свойство формулы умножения?
Распределительное свойство формулы умножения применяется к сложению и вычитанию и выражается как:
- a(b+c) = ab + bc
- а(б-в) = аб-бк
Как решить распределительное свойство умножения на сложение?
Распределительное свойство умножения над сложением используется, когда мы умножаем значение на сумму двух или более чисел. Например, решим выражение: 5(5 + 9). Это выражение можно решить, умножив 5 на оба слагаемых. Итак, 5(5) + 5(9) = 25 + 45 = 70.
Например, решим выражение: 5(5 + 9). Это выражение можно решить, умножив 5 на оба слагаемых. Итак, 5(5) + 5(9) = 25 + 45 = 70.
Как решить распределительное свойство умножения над вычитанием?
Распределительное свойство умножения по сравнению с вычитанием применяется, когда мы умножаем значение на разность двух чисел. Например, решим выражение: 3(9 — 5). Выражение можно решить, умножив 3 на каждый член, а затем найти различия произведений. Итак, 3(9) — 3(5) = 27 — 15 = 12,9.0003
Как выглядит распределительное свойство умножения?
Распределительное свойство умножения можно увидеть с помощью его формулы, которая применима к сложению и вычитанию следующим образом:
- Распределительное свойство умножения над сложением: a(b+c) = ab + bc.
- Распределительное свойство умножения над вычитанием: a(b-c) = ab — bc
Приведите пример распределительного свойства умножения.
Распределительное свойство умножения можно понять на различных примерах. Например, решим выражение 4(7 + 3). Распределим число 4 на 7 и 3. Получится 4(7) + 4(3) = 28 + 12 = 40.
Например, решим выражение 4(7 + 3). Распределим число 4 на 7 и 3. Получится 4(7) + 4(3) = 28 + 12 = 40.
Свойства умножения | Математика 4-го класса
Умножение — это сложение одного и того же числа снова и снова.
Если хотите пофантазировать, то можете сказать, что умножение — это повторяющееся сложение.
Давайте узнаем о пять свойств умножения.
Совет: Свойства — это правила, упрощающие умножение чисел.
1. Свойство идентичности Свойство идентичности умножения говорит вам, что умножение числа на 1 дает то же самое число.
Взгляните:
1 × 56 = 569017 8 1
147
× 971 = 9713,829 × 1 = 3,829
Nothing changes when you multiply a number by 1.
2. Zero Свойство
Свойство нуля умножения говорит нам, что любое число, умноженное на 0, равно нулю.
65 × 0 = 0
872 × 0 = 0
0 × 34 561 = 0
Независимо от того, какое число вы умножаете на ноль, ответ всегда будет равен нулю.
3. Переместительное свойство
Переместительное свойство умножения говорит вам, что изменение порядка делителей не меняет ответ.
Взгляните
4 × 3 = 12 = 3 × 4
The property is true even if we have three numbers we multiply together:
2 × 3 × 4 =
4 × 3 × 2
обе стороны выше равной 24.
4. Association.0148 говорит нам, что если мы умножаем три или более множителя, то изменение порядка, в котором мы умножаем сначала
, не меняет произведение или ответ.Рассмотрим пример:
2 × 5 × 4 = ?
Попробуем сначала перемножить первые два множителя.
(2 × 5) × 4 = 10 × 4 = 40
Теперь давайте сначала попробуем умножить два последних множителя.
2 × (5 × 4) = 2 × 20 = 40
Ответ тот же.
Таким образом, изменение того, какой из множителей мы умножили первым, не изменило ответ! Это ассоциативное свойство умножения. 😀
5. Распределительное свойство
Распределительное свойство умножения помогает нам решать уравнения следующим образом:
8 × (5 + 7) = ?
Свойство распределения говорит, что мы можем распространять, или раздавать 8 x каждому из дополнений.
After we distribute, we end up with:
(8 × 5 ) + (8 × 7 ) =
40 + 56 =
96 ✅
Проверим, получим ли мы тот же ответ без распределения:
8 × (5 + 7) =
8 × 12 =
96
. × (5 + 7) = (8 × 5) + (8 × 7) ✅
× (5 + 7) = (8 × 5) + (8 × 7) ✅
Вот еще один пример распределительного свойства:
Отличная работа по изучению свойств умножения.
Вы помните все пять? Завершите практику, чтобы узнать.
Распределительное свойство умножения | Упражнение
Онлайн-упражнение
Играть Задайте это упражнение
Помогите четвероклассникам закрепить свои знания об умножении, научив их свойству распределения и тому, как оно может помочь им в решении задач.
См. в пошаговом уроке
Оценка
4 класс
Предмет
MathMultiplicationProperties of MultiplicationDistributive Property of Multiplication
Посмотреть согласованные стандарты Общие базовые стандарты штата Техасские основные знания и навыки (TEKS) Стандарты обучения штата Вирджиния (SOL) Стандарты успеваемости Британской Колумбии Программа обучения Альберты Австралийская учебная программа (ACARA) Учебная программа штата Виктория (F-10) Не можете найти свой стандарт?
4. НБТ.Б.5
НБТ.Б.5
Математика 3-й степени 3.4.Г 3.4.Е 3.4.F 4 класс 4.4.Г
Математика
3-й степени
CE. 3.4.а
CE.3.4.b
CE.3.4.с
4 класс
CE.4.4.d
3.4.а
CE.3.4.b
CE.3.4.с
4 класс
CE.4.4.d
Математика 3-й степени е
Нет стандартов, связанных с этим контентом.
Математика
5 год
ACMNA100.


 Прежде чем мы с ними начнём работать повторим название компонентов при сложении и умножении.
Прежде чем мы с ними начнём работать повторим название компонентов при сложении и умножении.

 Для этого придадим переменным значения а=7, в=9, с=6
Для этого придадим переменным значения а=7, в=9, с=6
 Закрепление.
Закрепление.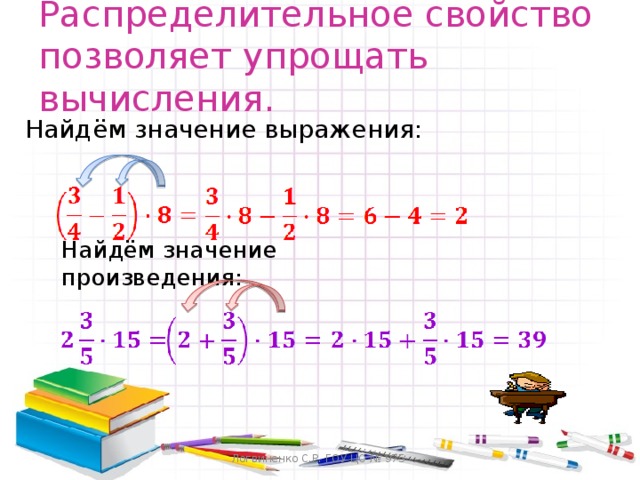

 В.Н. Рудницкая, Т.В. Юдачева. Математика: 4 класс: Методика обучения. – М.: Вентана – Граф, 2007. – 192с. – (Начальная школа 21 века)
В.Н. Рудницкая, Т.В. Юдачева. Математика: 4 класс: Методика обучения. – М.: Вентана – Граф, 2007. – 192с. – (Начальная школа 21 века)
 Проверка домашнего задания (Слайд№4)
Проверка домашнего задания (Слайд№4)


 Через 4 часа они встретились. Каково расстояние между пунктами, из которых выехали поезда?
Через 4 часа они встретились. Каково расстояние между пунктами, из которых выехали поезда?
 Задание до конца не выполнили.
Задание до конца не выполнили.
