Таблица вычитания чисел по математике: тренажер, распечатать
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
Используйте эту таблицу вычитания чисел для 1-2 класса для быстрых вычислений, а также, пустой бланк для проверки своих знаний. Обе версии можно распечатать.
| — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | +/- 1 | +/- 2 | +/- 3 | +/- 4 | +/- 5 | +/- 6 | +/- 7 | +/- 8 | +/- 9 |
| 2 | +/- 1 | 0 | +/- 1 | +/- 2 | +/- 3 | +/- 4 | +/- 5 | +/- 6 | +/- 7 | +/- 8 |
| +/- 2 | +/- 1 | 0 | +/- 1 | +/- 2 | +/- 3 | +/- 4 | +/- 5 | +/- 6 | +/- 7 | |
| 4 | +/- 2 | +/- 1 | 0 | +/- 1 | +/- 2 | +/- 3 | +/- 4 | +/- 5 | +/- 6 | |
| 5 | +/- 4 | +/- 3 | +/- 2 | +/- 1 | 0 | +/- 1 | +/- 2 | +/- 3 | +/- 4 | +/- 5 |
| 6 | +/- 5 | +/- 4 | +/- 3 | +/- 2 | +/- 1 | 0 | +/- 1 | +/- 2 | +/- 3 | +/- 4 |
| 7 | +/- 6 | +/- 5 | +/- 4 | +/- 3 | +/- 2 | +/- 1 | 0 | +/- 1 | +/- 2 | +/- 3 |
| 8 | +/- 7 | +/- 6 | +/- 5 | +/- 4 | +/- 3 | +/- 2 | +/- 1 | 0 | +/- 1 | +/- 2 |
| 9 | +/- 8 | +/- 7 | +/- 6 | +/- 5 | +/- 4 | +/- 3 | +/- 2 | +/- 1 | 0 | +/- 1 |
| 10 | +/- 9 | +/- 8 | +/- 7 | +/- 6 | +/- 5 | +/- 4 | +/- 3 | +/- 2 | +/- 1 | 0 |
microexcel.
ru
Смотрите также: “Как вычитать числа в Экселе”
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Таблица сложения и вычитания в пределах 10
Вы можете ознакомиться и скачать презентацию на
тему Таблица сложения и вычитания в пределах 10.
Доклад-сообщение содержит 13 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Слайд 1
Описание слайда:
Слайд 2
Описание слайда:
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
Слайд 5
Описание слайда:
Слайд 6
Описание слайда:
Слайд 7
Описание слайда:
Слайд 8
Описание слайда:
Слайд 9
Описание слайда:
Слайд 10
Описание слайда:
Слайд 11
Описание слайда:
Слайд 12
Описание слайда:
Слайд 13
Описание слайда:
Заучивание наизусть — Начальная школа на весь день
Запоминание:
«Процесс запоминания чего-либо или заучивания чего-либо наизусть».
— Оксфордский словарь.
Запоминание математических фактов — это то, над чем работают все учащиеся во время учебы в начальной и начальной школе. Дети выполняют повторяющиеся упражнения, чтобы выучить 5 + 5 = 10 и 8 – 5 = 3. Дети начальной школы Монтессори работают над запоминанием тех же основных уравнений. Однако в подходе Монтессори мы сначала знакомим детей с общей концепцией четырех операций, чтобы они поняли, что на самом деле означает 5+5. Дети используют практические материалы, чтобы узнать, что сложение — это «9».0015 объединение небольших количеств в большое количество ». Они играют в игры, чтобы определить, что умножение — это «, сложив одно и то же число несколько раз, чтобы получить большее количество ». Только после большого опыта работы с этими общими понятиями мы вводим запоминание основных математических фактов. Затем дети обнаруживают, что заучивание этих уравнений наизусть помогает им выполнять четыре операции с большей точностью.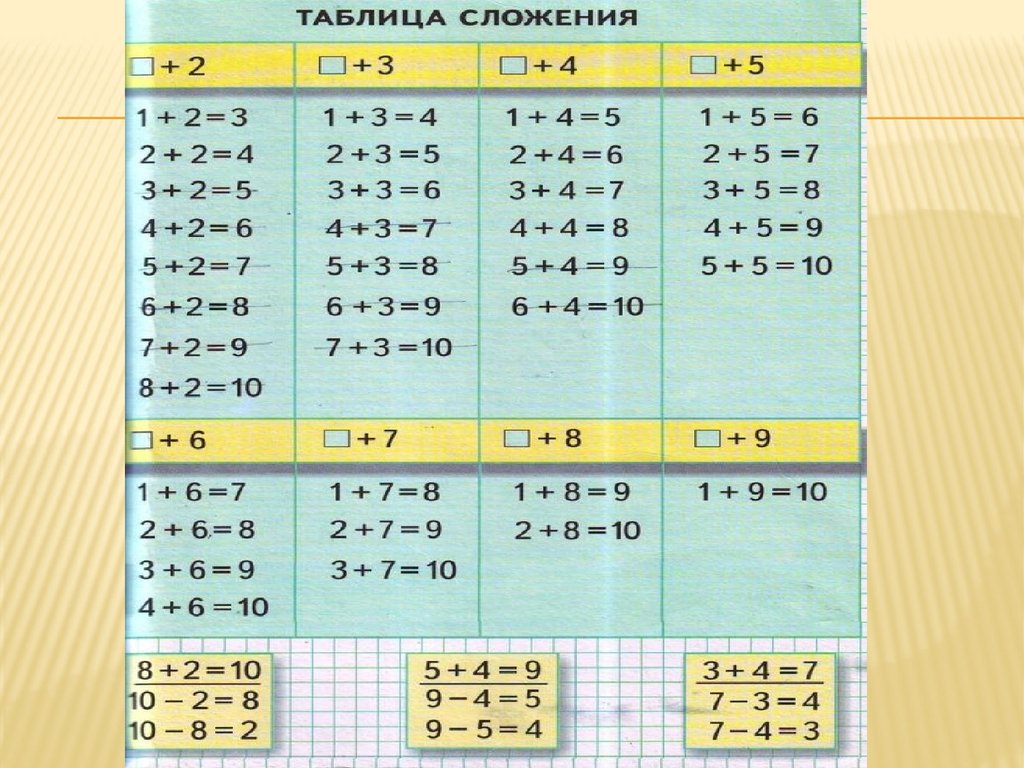
В классе Монтессори мы знакомим детей с практическими материалами, которые помогают им выводить математические факты. Приведенные ниже действия представляют собой возможности для повторения с запоминанием после того, как эти практические уроки были отработаны.
Дополнительная полоска для детей от 5 до 5,5 лет и старше
Указания: Распечатайте дополнительную полоску и полоски на картоне. Вырежьте красную и синюю дополнительные полоски. Распечатайте таблицы дополнений. Для начала расположите синие полоски по порядку над левой стороной диаграммы. Расположите красные полоски по порядку над правой стороной диаграммы. Прочитайте первое уравнение, указанное в таблице дополнений. Используйте одну синюю и одну красную полоски, чтобы найти ответ на уравнение. Запишите ответ в таблицу. Продолжайте, пока не изучите все таблицы 1-9.. Используйте контрольную таблицу, чтобы проверить свои ответы. Когда вы закончите, скрепите листы уравнений вместе, чтобы получился дополнительный буклет.
Со временем перейдите ко второму набору таблиц сложения, в которых уравнения смешаны.
* Дополнительную доску лучше всего использовать после официальной презентации преподавателя.
дополнительная полосовая доска.pdf
106 КБ
Скачать
Контрольная схема добавления 1.pdf
101 КБ
Скачать
Контрольная схема добавления 2.pdf
244 КБ
Скачать
Набор дополнительных таблиц 1.pdf
196 КБ
Скачать
Набор дополнительных таблиц 2.pdf
197 КБ
Скачать
Буклеты с дополнительными комбинациями для дома.pdf
56 КБ
Скачать
Упражнения на сложение для детей от 5 до 5,5 лет и старше
Указания: Распечатайте тренировочную таблицу сложения.
Распечатайте и вырежьте уравнения сложения. Прочитайте каждое уравнение существенного сложения. Попробуйте определить ответ, не используя пальцы и не считая в уме. Если ответ сразу приходит вам в голову, значит, вы знаете это уравнение наизусть. В противном случае используйте тренировочную таблицу для решения уравнения сложения. Запишите все неизвестные уравнения на математическом листе ниже и повторите полное уравнение с ответом (8 + 8 = 16), чтобы лучше запомнить. Продолжайте, пока не изучите все 72 уравнения. Используйте контрольную таблицу, чтобы проверить свои ответы и убедиться, что вы запомнили правильное уравнение. Когда вы закончите, скрепите листы уравнений вместе, чтобы получился дополнительный буклет. Со временем вам вообще не придется пользоваться диаграммой!
Дополнительная таблица 1.pdf
40 КБ
Скачать
Дополнительная таблица 2.pdf
38 КБ
Скачать
Дополнительная таблица 3.
pdf
43 КБ
Скачать
Уравнения сложения.pdf
38 КБ
Скачать
Контрольная схема добавления 1.pdf
101 КБ
Скачать
Контрольная схема добавления 2.pdf
244 КБ
Скачать
Math Booklet Covers.pdf
25 КБ
Скачать
Буклет с математическими уравнениями.pdf
20 КБ
Скачать
Дополнительная пустая таблица для детей от 5 до 5,5 лет и старше
Указания: Распечатайте дополнительную пустую диаграмму и плитки с дополнительными ответами. Вырежьте плитки и расположите их над пустой диаграммой, сгруппировав их как числа.
Распечатайте и вырежьте уравнения сложения. Прочитайте каждое уравнение существенного сложения и определите ответ. Найдите плитку с ответом. Пальцами найдите место на пустой таблице, где должна быть размещена плитка с ответами (аналогично тому, как вы использовали таблицу для практики сложения 1). Продолжайте до тех пор, пока не будет заполнена вся таблица и не будут размещены все плитки с ответами.
Дополнение Пустая таблица.pdf
49 КБ
Скачать
Уравнения сложения.pdf
38 КБ
Скачать
Доска для вычитания полосок для детей от 5 до 5,5 лет и старше
Примечания: Доска для вычитания немного сложнее, чем доска для сложения, и ее лучше всего использовать после официальной презентации учителя. Подробные инструкции по использованию этого материала см. в руководстве для вашего ребенка.
доска для вычитания.
pdf
424 КБ
Скачать
Таблица контроля вычитания.pdf
94 КБ
Скачать
Набор таблиц для вычитания 1.pdf
361 КБ
Скачать
Набор таблиц для вычитания 2.pdf
361 КБ
Скачать
Учебная таблица вычитания для детей от 5,5 лет и старше
Указания: Распечатайте таблицу упражнений на вычитание. Распечатайте и вырежьте уравнения вычитания. Прочитайте каждое основное уравнение вычитания. Попробуйте определить ответ, не используя пальцы и не считая в уме. Если ответ сразу приходит вам в голову, значит, вы знаете это уравнение наизусть. В противном случае используйте тренировочную таблицу для решения уравнения вычитания. Запишите уравнение на математическом листе ниже и повторите полное уравнение с ответом (18 — 9= 9), чтобы помочь с сохранением.
Продолжайте, пока не изучите все уравнения. Используйте контрольную таблицу, чтобы проверить свои ответы и убедиться, что вы запомнили правильное уравнение. Когда вы закончите, скрепите свои листы уравнений вместе с титульным листом, чтобы сделать буклет вычитания. Со временем вам вообще не придется пользоваться диаграммой!
Таблица практики вычитания.pdf
31 КБ
Скачать
Уравнения вычитания.pdf
40 КБ
Скачать
Таблица контроля вычитания.pdf
94 КБ
Скачать
Math Booklet Covers.pdf
25 КБ
Скачать
Буклет с математическими уравнениями.pdf
20 КБ
Скачать
Пустая таблица вычитания для детей от 5,5 лет
Указания: Распечатайте пустую таблицу вычитания и плитки с ответами на вычитание.
Вырежьте плитки и расположите их над пустой диаграммой, сгруппировав их как числа. Распечатайте и вырежьте уравнения вычитания. Прочитайте каждое основное уравнение вычитания и определите ответ. Найдите плитку с ответом. Пальцами найдите место, где должна быть размещена плитка с ответами на пустой диаграмме (аналогично тому, как вы использовали тренировочную диаграмму вычитания). Продолжайте до тех пор, пока не будет заполнена вся таблица и не будут размещены все плитки с ответами.
Пустая таблица вычитания.pdf
40 КБ
Скачать
Уравнения вычитания.pdf
40 КБ
Скачать
Числа для детей от 6 лет и старше
Направления: Используйте математические факты сложения и вычитания, чтобы решить головоломку с числами.
Головоломки с числами.pdf
44 КБ
Скачать
Головоломки с числами 2.
pdf
35 КБ
Скачать
Доска для умножения для детей от 5,5 лет
Примечания. Доска для умножения требует больше усилий, чем многие другие материалы для запоминания, и ее лучше всего использовать после формальной презентации учителя. Подробные инструкции по использованию этого материала см. в руководстве для вашего ребенка.
Плата умножения.pdf
86 КБ
Скачать
Набор таблиц умножения 1.pdf
208 КБ
Скачать
Набор таблиц умножения 2.pdf
210 КБ
Скачать
Контрольная таблица умножения-1.pdf
120 КБ
Скачать
Контрольная таблица умножения-2.
pdf
117 КБ
Скачать
Умножение на десять Возраст от 5 ½ и старше
Примечания: После работы с бисеринками умножения дети узнают закономерность, которая возникает, когда число взято десять раз. Это позволяет им быстро решать задачи с любым числом, умноженным на 10.
Направления: Распечатайте рабочий лист и решите задачи на умножение. При необходимости используйте запятые при записи ответа. Прочитайте ответ вслух как составное число (13 254 = тринадцать тысяч двести пятьдесят четыре).
Умножение X 10.pdf
41 КБ
Скачать
Учебные таблицы по умножению для детей от 5,5 лет и старше
Указания: Распечатайте тренировочную таблицу умножения. Распечатайте и вырежьте уравнения умножения. Прочитайте каждое основное уравнение умножения. Попробуйте определить ответ, не используя пальцы и не считая в уме.
Если ответ сразу приходит вам в голову, значит, вы знаете это уравнение наизусть. В противном случае используйте тренировочную таблицу для решения уравнения умножения. Запишите все неизвестные уравнения на математическом листе ниже и повторите полное уравнение с ответом (8 x 8 = 64), чтобы облегчить запоминание. Продолжайте, пока не изучите все уравнения. Используйте контрольную таблицу, чтобы проверить свои ответы и убедиться, что вы запомнили правильное уравнение. Когда вы закончите, скрепите листы с уравнениями вместе, чтобы получился буклет по умножению. Со временем вам вообще не придется пользоваться диаграммой!
Практическая таблица умножения 1.pdf
40 КБ
Скачать
Практическая таблица умножения 2.pdf
39 КБ
Скачать
Контрольная таблица умножения-2.pdf
117 КБ
Скачать
Уравнения умножения.
pdf
42 КБ
Скачать
Math Booklet Covers.pdf
25 КБ
Скачать
Буклет с математическими уравнениями.pdf
20 КБ
Скачать
Пустая таблица умножения для детей от 6 лет
Указания: Распечатайте пустую таблицу умножения и плитки с ответами на умножение. Вырежьте плитки и расположите их над пустой диаграммой, сгруппировав их как числа. Распечатайте и вырежьте уравнения умножения. Прочитайте каждое основное уравнение и определите ответ. Найдите плитку с ответом. Пальцами найдите место на пустой таблице, где должна быть размещена плитка с ответами (аналогично тому, как вы использовали таблицу для практики умножения 1). Продолжайте до тех пор, пока не будет заполнена вся таблица и не будут размещены все плитки с ответами.
Пустая таблица умножения.
pdf
47 КБ
Скачать
Уравнения умножения.pdf
42 КБ
Скачать
Доска подразделений для детей от 6 лет и старше
Примечания. Доска деления единиц используется, чтобы помочь детям вывести основные уравнения деления. Этот урок немного сложнее, чем многие другие материалы для запоминания, и его лучше всего использовать после формальной презентации учителя. Подробные инструкции по использованию этого материала см. в руководстве для вашего ребенка.
Unit Division Board.pdf
75 КБ
Скачать
Таблицы разделов.pdf
145 КБ
Скачать
Таблица тренировок дивизиона для детей от 6 лет и старше
Указания: Распечатайте тренировочную таблицу дивизии.
Распечатайте и вырежьте уравнения деления. Прочитайте каждое основное уравнение деления. Попробуйте определить ответ, не используя пальцы и не считая в уме. Если ответ сразу приходит вам в голову, значит, вы знаете это уравнение наизусть. В противном случае используйте тренировочную таблицу для решения уравнения деления. Запишите все неизвестные уравнения на математическом листе ниже и повторите полное уравнение с ответом (64 / 8 = 8), чтобы лучше запомнить. Продолжайте, пока не изучите все уравнения. Используйте контрольную таблицу, чтобы проверить свои ответы и убедиться, что вы запомнили правильное уравнение. Когда вы закончите, скрепите листы с уравнениями вместе, чтобы получился буклет по умножению. Со временем вам вообще не придется пользоваться диаграммой!
Таблица практики дивизиона.pdf
43 КБ
Скачать
Уравнения деления.pdf
44 КБ
Скачать
Карта управления дивизией.
pdf
44 КБ
Скачать
Math Booklet Covers.pdf
25 КБ
Скачать
Буклет с математическими уравнениями.pdf
20 КБ
Скачать
Часть Часть Целое со Сложением и Вычитанием
Изучение отношений часть-часть-целое имеет решающее значение при обучении сложению и вычитанию. Чтобы учащиеся хорошо понимали сложение и вычитание, им необходимо понимать, что представляет каждый из них. Хотя это полезно при работе с уравнениями с неизвестными во всех областях, крайне важно, чтобы учащиеся хорошо понимали сложение и вычитание, чтобы они могли применять оба навыка в реальных сценариях. Понимание части-части-целого — гораздо более эффективная стратегия обучения решению проблем, чем ключевые слова, хотя они все же имеют свое место. Вот посмотрите, как вы можете применить часть части к целому в своем блоке сложения и вычитания.
НЕИЗВЕСТНОЕ
Одной из первых частей обучения части части целому является неизвестное; вопрос. Учащиеся должны часто знакомиться с неизвестными различных типов — переменными, вопросительными знаками, пустыми строками, прямоугольниками и т. д., чтобы понять, что все они представляют одно и то же. Крайне важно, чтобы неизвестное находилось в разных положениях, особенно слева от знака равенства ( x = 6 + 2), чтобы учащиеся усвоили его значение. Неизвестное следует определить как ЦЕЛОЕ или ЧАСТЬ на раннем этапе, чтобы они могли позже перенести свое обучение на текстовые задачи.
Здесь учащиеся используют ключевые слова. Студенты могут использовать ключевые слова для идентификации чего-либо как «части» или «неизвестного». Однако всегда следует возвращаться к «части» или «целому», поскольку это помогает построить фундаментальное понимание операций. Ключевые слова не должны преподаваться как основа понимания проблемы и не должны представлять собой ряд категорически заученных терминов.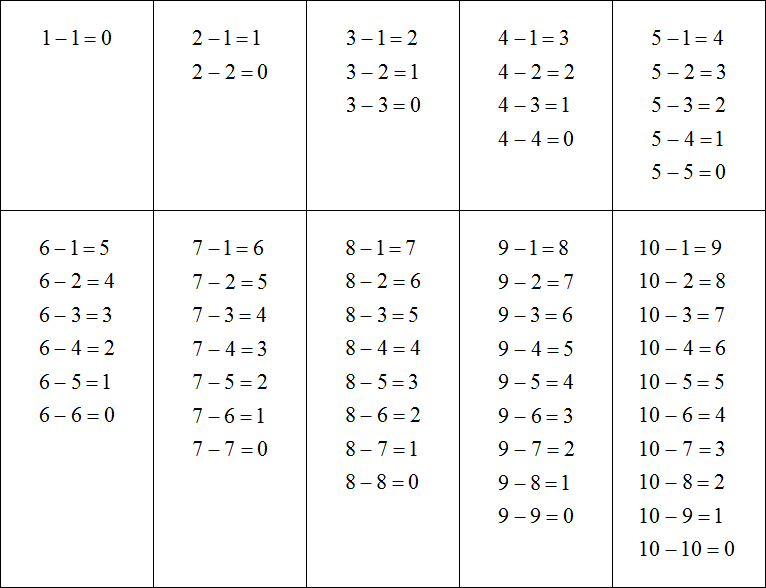
Тем не менее, они относятся к части и целому и могут помочь учащимся понять представляемый контекст. Подробнее читайте в моем посте «Почему студенты борются со словесными задачами».
Вы можете скачать весь постер выше в формате pdf, зарегистрировавшись в форме ниже.
СЛОЖЕНИЕ ЦЕЛОЕ НЕИЗВЕСТНО
Сложение — это объединение частей для нахождения общего или целого. Дети строят это понимание, считая группы объектов вместе, чтобы найти их общее количество. Учащиеся изучают суммы, используя манипуляции, и строят свое понимание сложения, а также своих фактов посредством практических исследований.
Один из моих любимых инструментов для сложения моделей для учащихся — это большая магнитная десятичная рамка от Learning Resources. Поскольку магниты бывают двух цветов, вы можете представить обе части уравнения. Я использую их в качестве моделей во время уроков, но мои ученики также любят использовать их, когда они работают в центрах или играют во время Fun Friday.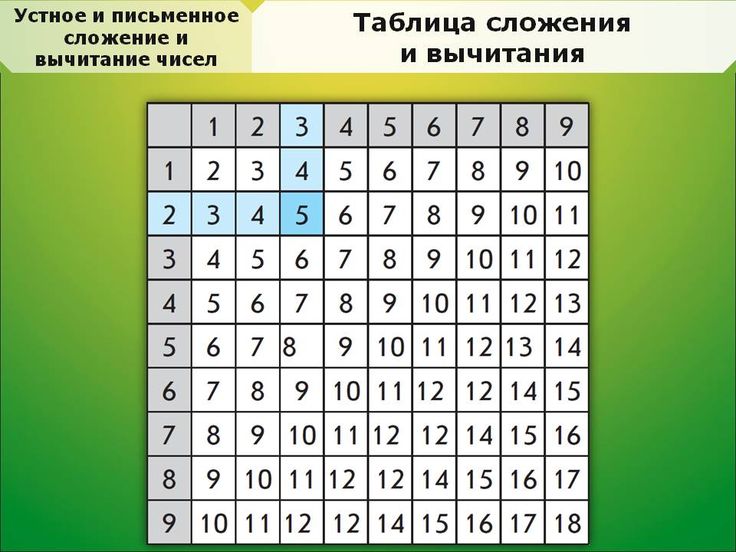
Десять кадров — это идеальные визуальные модели для «часть-часть-целое», потому что учащиеся могут легко увидеть, что каждый цвет представляет собой отдельную часть сценария.
Вы можете купить магнитные рамки Tens на Amazon или во многих магазинах товаров для учителей. Это из учебных ресурсов.
Я также создал уменьшенные версии десятичных рамок для учащихся, используя скотч Scotch Expressions, формочки для печенья, магниты и цветные точки. Я разделил каждый лист печенья на четыре десятка рамок из-за размера, но одну или две можно было бы легко использовать на них. Каждая сторона магнита представляет собой цветную точку (стороны разные), и я помещаю их в небольшие контейнеры наборами по 10 штук. Они доступны для использования учащимися во время самостоятельной работы, чтобы помочь им моделировать и решать уравнения, и они могут занять больше времени. чем один контейнер, если они нужны для большего числа. Я получил все от Dollar Tree, поэтому, хотя это и заняло некоторое время, это был совсем не дорогой проект.
Посмотреть этот пост в Instagram
Провел пятничную ночь, делая десятки кадров для центров. Листы для печенья Dollar Tree, магнитные пуговицы от Wal Mart, цветные этикетки от Dollar Tree и 2 рулона скотча Scotch Expressions. Они оказались совершенно несовершенными и готовыми к работе на этой неделе. Дешевый и удобный центр! @scotchproducts #scotchexpressions #dollartree #walmart
Сообщение, опубликованное Tessa-Tales Outside Classroom (@talestessa)
У меня также есть ресурс цифровых десятков кадров. Он работает через 10 со сложением и вычитанием. Всего 16 видов деятельности. Прибавление к 10, вычитание из 10, пропущенные сложения в пределах 10 и вычитание в пределах 10 действий представлены в 4 разных темах.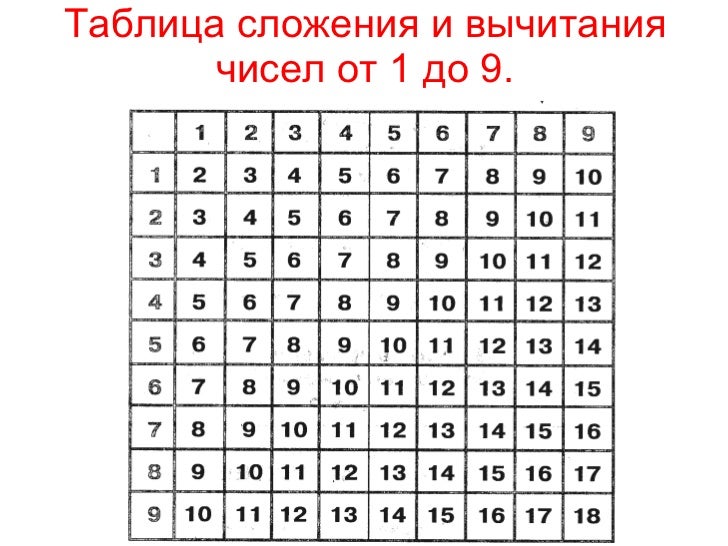
Вы можете более подробно ознакомиться с моим цифровым сложением и вычитанием из 10 десятков кадров ниже. Вас также может заинтересовать мой пост в блоге с 44 Free Tens Frames Activity.
Учащиеся также могут использовать блоки с основанием 10, чтобы найти способы сложения. Блокирующие кубы также можно легко использовать для отработки того же навыка. Студенты исследуют связанные числа, которые являются «частями», составляющими «целое». У вас может быть заранее определенное количество кубиков, уже разделенных, или пусть учащиеся возьмут несколько кубиков и исследуют числа, которые можно соединить, чтобы получить это число.
ВЫЧИТАНИЕ — ЧАСТЬ НЕИЗВЕСТНА
Вычитание — это взятие целого и разбиение на части. Это понимание строится так же, как и дополнение — через исследование с группами предметов.
Предоставление учащимся группы объектов для разделения на более мелкие части помогает сформировать это понимание. Работа с базовыми десятью кубами или связывающими кубами выше помогает учащимся увидеть, что одно и то же количество объектов может быть разделено на части разных размеров, а также что размеры двух частей обратно пропорциональны.
Задачи сравнения — это вычитание, так как две части — это известное число и число, которое нужно сложить, чтобы получить другое число (сумму). Они находят разницу между числами. «Насколько больше» и «насколько меньше» представляют собой задачи сравнения. Десять рамок также являются отличными моделями для построения задач на сравнение, поскольку учащиеся видят, сколько еще нужно, чтобы получить общее количество.
Мне нравится использовать разделенные пластины для работы в режиме «часть-часть-целое». Для вычитания я помещаю все манипуляции (M&M’s и Skittles немного хитовые!) в большую часть тарелки, а затем перемещаю установленное количество в одну из меньших частей, чтобы соответствовать уравнению.
Вы также можете писать на пластиковых тарелках сухостираемыми маркерами и маркировать «части» и «целое». Тарелки и любые виды счетчиков, которые у вас уже есть под рукой, являются идеальным ресурсом для студентов, поскольку они работают со сложением и вычитанием независимо друг от друга во время центров.
Посмотреть эту публикацию в Instagram
Мне нравится использовать эти разделенные пластины для работы с частью-частью-целым. Плюс M&M’s за победу!
Сообщение, опубликованное Tessa-Tales Outside Classroom (@talestessa)
ФАКТОВЫЕ СЕМЬИ ПРЕДСТАВЛЯЮТ ЧАСТЬ ЧАСТЬ ЦЕЛОЕ
Учебные фактические семьи также должны быть укоренены в части части целого. Семейные треугольники фактов помогают учащимся визуально увидеть частичные и целые отношения.
При обучении семьям фактов я использую изображение дома, изображенное ниже. Я всегда помещаю уравнения сложения и вычитания, связанные с частью и целым в треугольнике для крыши, чтобы помочь учащимся сосредоточиться на отношениях между ними и помочь им понять факт семейных треугольников.
Вы можете получить изображение выше в виде постера в формате pdf для показа, зарегистрировавшись в форме ниже.
Когда мы работаем с семействами фактов, мы также используем наши руки, чтобы построить треугольник и помочь добавить кинестетические движения в наше обучение. Мы соединяем руки вместе над головой для целого и вытягиваем руки в каждую сторону для каждой части (как треугольник выше). Кинестетические движения помогают учащимся сохранить знания и дают им простой инструмент, который можно использовать позже, когда это необходимо.
ПЕЧАТИ ЧАСТЬ-ЧАСТЬ-ЦЕЛОЕ
Существует множество различных моделей отношений часть-часть-целое. Двумя наиболее распространенными являются стержневые модели и числовые связи.
Я считаю, что столбчатые модели наиболее полезны при работе с текстовыми задачами, поскольку учащиеся могут визуально видеть части, относящиеся к целому, и какая часть является неизвестной. Связи чисел, на мой взгляд, более уместны при рассмотрении фактов как суммы и построении понимания числовых отношений и семейств фактов. Десять рамок также являются отличными инструментами, помогающими учащимся визуализировать частичные и целые отношения, особенно когда учащиеся работают с числами до 10 и числами до 20.
Я собрал 12 страниц печатных форм, которые вы можете использовать для работы с моделями «часть-часть-целое» со счетчиками, десятью частями, блокирующими кубиками или чем-то еще, что есть у вас в классе.
Есть страницы для числовых связей, десяти рамок и семейств фактов. Страницы включают в себя практику как для сложения, так и для вычитания. Знак равенства стоит слева от уравнения на некоторых страницах. Две половинчатые страницы также включены для работы в центрах. Все страницы черно-белые, поэтому вы можете распечатать их на цветной бумаге и заламинировать или сразу распечатать и использовать.
Вы можете получить все плакаты и печатные материалы, представленные здесь, заполнив форму ниже. Как только вы подтвердите свой адрес электронной почты, они будут отправлены прямо вам!
ОТПРАВИТЬ НА МОЙ ВХОДЯЩИЙ ЯЩИК!
После отправки этой формы плакаты и печатные формы будут отправлены прямо на ваш почтовый ящик. Вы также получите по электронной почте некоторые специальные ресурсы для 1-го класса!
Загрузка…
ЗАДАЧИ СЛОВА
Понимание учащимися операций сложения, вычитания и части-части-целого проявляется в их понимании словесных задач. С помощью сюжетных задач учащиеся демонстрируют, что они могут использовать контекст для определения используемой операции и могут применять ее независимо. Чтобы специально отработать сценарии «часть-часть-целое», у меня есть эти цифровые словесные задачи «часть-часть-целое» для 1-го класса. Они практикуют сложение и вычитание в пределах 20 в реальном контексте.
Учащиеся читают задачу, строят уравнение и решают, используя встроенные числовые линии и десятки кадров, чтобы смоделировать сценарий.
Вы можете более подробно ознакомиться с моими задачами на часть, часть, целое слово для 1-го класса. Включены 4 разных типа задач: набор для идентификации неизвестного как части или целого; набор для всего неизвестного; набор на неизвестную деталь; и набор для обеих частей неизвестен. Они созданы для использования как в Google Slides, так и в SeeSaw.
У меня также есть бесплатная версия для добавления 3 номеров. Каждый из этих сценариев представлен в отношениях часть-целое. Набор задач «Добавление 3 чисел» дает вам представление о том, как настроен набор «Часть-Часть-Целое».
В дополнение к отработке определенных типов задач, когда это является предметом нашего обучения, важно дать студентам возможность попрактиковаться вне этого. Я решаю задачу дня вне моей учебной программы по математике, чтобы убедиться, что учащиеся сталкиваются с различными типами задач и постепенно отрабатывают навыки в течение года, а не работают с одним навыком за раз.
Это помогает учащимся не просто полагаться на «содержание недели» при решении; они действительно должны использовать контекст для решения.
Моя задача дня для 1-го класса состоит из двух задач на странице. Существует два разных формата: последовательные страницы рядом и одна и та же страница дублируется рядом. У моих учеников есть задача с рассказом в ежедневном переплете, поэтому я предпочитаю, чтобы они были у них последовательно. Если вы хотите продублировать их для учащихся, вам может подойти альтернативный формат. В ходе ежедневной работы со словесными задачами учащиеся заполняют таблицы «часть-часть-целое», таблицы «начало-изменение-конец», пишут уравнения, моделируют задачи и записывают свои ответы полными предложениями. Учащиеся строят свое глубокое понимание математических центров 1-го класса посредством ежедневной практики и спирали. Учащиеся работают с различными типами задач и хорошо понимают, что такое часть-часть-целое, а также сложение и вычитание. Вы можете увидеть весь годовой пакет в моем магазине TpT Word Word Problem of the Day для 1-го класса или щелкнув изображение ниже.
Пакет разбит на месячные наборы и может быть приобретен отдельно.
Для более подробного ознакомления со всеми форматами задач на сложение и вычитание, в дополнение к задаче «часть-часть-целое», ознакомьтесь с моей записью в блоге «Сценарии задач на сложение и вычитание».
НАЧАТЬ-ИЗМЕНИТЬ-КОНЕЦ СО СЛОЖЕНИЕМ И ВЫЧИТАНИЕМ
В дополнение к обучению своих учеников части-части-целому я также учу начало-изменение-конец сложения и вычитания. В реальных сценариях сложение и вычитание — это либо (а иногда и то, и другое) начало-изменение-конец или часть-часть-целое. Я учу и тому, и другому в явном виде со своими 1-м и 2-м классом, и мы говорим о наших текстовых задачах в связи с обоими. Вы можете прочитать о типах проблем start-change-end в этом посте.
УМНОЖЕНИЕ И ДЕЛЕНИЕ С ЧАСТЬЮ-ЧАСТЬЮ-ЦЕЛОЕ
Будучи учителем третьего класса, когда я знакомлю учащихся с умножением и делением, я связываю их обратно с частью-частью-целым. Мы меняем «часть» на «количество групп» и «количество в каждой группе».
Если учащиеся имеют четкое представление о частях и целом, они намного легче понимают отношения умножения и деления, когда они вводятся и связаны обратно с частью и целым. При работе со словесными задачами на умножение и деление основное внимание уделяется тому, неизвестно ли целое, чтобы определить, какая операция используется. Четыре операции могут быть идентифицированы в текстовых задачах, когда учащиеся идентифицируют неизвестную и данную информацию, поскольку они относятся к части-части-целому и группам.
СКЛАДЫВАНИЕ И ВЫЧИТАНИЕ БЕЗОПАСНОСТЬ
После того, как учащиеся получат четкое представление о сценариях «часть-часть-целое» и «начало-изменение-конец», мы продолжаем развивать их мастерство сложения и вычитания и беглость фактов посредством постоянной игры и практики. Я люблю использовать игры и центры, чтобы развить беглость сложения и вычитания моих учеников, потому что ученики не испытывают стресса, который они испытывают в сценариях с временными интервалами.