Приоритеты операторов | Microsoft Learn
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
Когда в выражении содержится несколько операций, каждая часть вычисляется и разрешается в предопределенном порядке, который называется приоритетом операторов.
)
=)-)< >)*, /)<)\)>)Mod)< =)+, -)> =)&)Когда умножение и деление выполняются в одном выражении, каждая операция вычисляется слева направо в порядке следования операций.
Когда сложение и вычитание выполняются в одном выражении, каждая операция вычисляется слева направо в порядке следования операций.
Скобки можно использовать для переопределения порядка применения и для принудительного вычисления некоторых частей раньше других. Операторы в скобках всегда выполняются перед операторами вне скобок. Однако внутри скобок действие приоритета операторов сохраняется.
Оператор & объединения строк не является арифметическим оператором, но по приоритету он следует всем арифметическим операторам и предшествует всем операторам сравнения.
С точки зрения приоритета оператор Like соответствует всем операторам сравнения, хотя и является оператором сравнения с помощью шаблонов сопоставления.
Оператор Is — это оператор сравнения ссылок на объекты. Он не сравнивает объекты или их значения, он только проверяет, относятся ли две ссылки на объект к одному и тому же объекту.
- Сводка операторов
Поддержка и обратная связь
Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см.
в статье Поддержка Office VBA и обратная связь.
Приоритет операторов — JavaScript | MDN
Приоритет операторов определяет порядок, в котором операторы выполняются. Операторы с более высоким приоритетом выполняются первыми.
Ассоциативность определяет порядок, в котором обрабатываются операторы с одинаковым приоритетом. Например, рассмотрим выражение:
a OP b OP c
Левая ассоциативность (слева направо) означает, что оно обрабатывается как (a OP b) OP c, в то время как правая ассоциативность (справа налево) означает, что они интерпретируются как a OP (b OP c). Операторы присваивания являются право-ассоциативными, так что вы можете написать:
a = b = 5;
с ожидаемым результатом, что a и b будут равны 5. Это происходит, потому что оператор присваивания возвращает тот результат, который присваивает. Сначала b становится равным 5, затем a принимает значение b.
3 > 2 && 2 > 1 // вернёт true 3 > 2 > 1 // вернёт false, потому что 3 > 2 возвращает true, в свою очередь true > 1 вернёт false // Добавление скобок значительно повышает читаемость выражения: (3 > 2) > 1
Операторы упорядочены с самого высокого (19) до самого низкого (1) приоритета.
Обратите внимание, что spread-оператор (...) намеренно не включен в таблицу, потому что он вообще не является оператором и правильно говорить spread-синтаксис. Подробнее можно почитать в ответе на Stack Overflow (en).
| Приоритет | Тип оператора | Ассоциативность | Конкретные операторы |
|---|---|---|---|
| 19 | Группировка | не определено | ( … ) |
| 18 | Доступ к свойствам | слева направо | … . … |
Доступ к свойствам с возможностью вычисления | … [ … ] | ||
new (со списком аргументов) | не определено | new … ( … ) | |
| Вызов функции | слева направо | … ( … ) | |
Оператор опциональной последовательности (?. ) | ?. | ||
| 17 | new (без списка аргументов) | справа налево | new … |
| 16 | Постфиксный инкремент (en-US) | не определено | … ++ |
Постфиксный декремент (en-US) | … -- | ||
| 15 | Логическое отрицание (!) (en-US) | справа налево | ! … |
| Побитовое отрицание (~) (en-US) | | ||
| Унарный плюс (en-US) | + … | ||
| Унарный минус (en-US) | - … | ||
| Префиксный инкремент (en-US) | ++ … | ||
| Префиксный декремент (en-US) | -- … | ||
| typeof | typeof … | ||
| void | void … | ||
| delete | delete … | ||
| await | await … | ||
| 14 | Возведение в степень (**) (en-US) | справа налево | … ** … |
| 13 | Умножение (*) (en-US) | слева направо | … * … |
| Деление (/) (en-US) | … / … | ||
| Остаток от деления (%) (en-US) | … % … | ||
| 12 | Сложение (+) (en-US) | слева направо | … + … |
| Вычитание (-) (en-US) | … - … | ||
| 11 | Побитовый сдвиг влево (<<) | слева направо | … << … |
| Побитовый сдвиг вправо (>>) (en-US) | … >> … | ||
| Сдвиг вправо с заполнением нулей (>>>) (en-US) | … >>> … | ||
| 10 | Меньше (<) | слева направо | … < … |
| Меньше или равно (<=) (en-US) | … <= … | ||
| Больше (>) (en-US) | … > … | ||
| Больше или равно (>=) (en-US) | … >= … | ||
| in | … in … | ||
| instanceof | … instanceof … | ||
| 9 | Равенство (==) (en-US) | слева направо | … == … |
| Неравенство (!=) (en-US) | … != … | ||
| Строгое равенство (===) (en-US) | … === … | ||
| Строгое неравенство (!==) (en-US) | … !== … | ||
| 8 | Побитовое «И» (&) (en-US) | слева направо | … & … |
| 7 | Побитовое исключающее «ИЛИ» (^) (en-US) | слева направо | … ^ … |
| 6 | Побитовое «ИЛИ» (|) (en-US) | слева направо | … | … |
| 5 | Логическое «И» (&&) (en-US) | слева направо | … && … |
| 4 | Логическое «ИЛИ» (||) (en-US) | слева направо | … || … |
| Оператор нулевого слияния (??) | … ?? … | ||
| 3 | Условный (тернарный) оператор | справа налево | … ? … : … |
| 2 | Присваивание (en-US) | справа налево | … = … |
… += … | |||
… -= … | |||
… **= … | |||
… *= … | |||
… /= … | |||
… %= … | |||
… <<= … | |||
… >>= … | |||
… >>>= … | |||
… &= … | |||
… ^= … | |||
… |= … | |||
… &&= … | |||
… ||= … | |||
… ??= … | |||
| yield | справа налево | yield … | |
| yield* | yield* … | ||
| 1 | Запятая / Последовательность | слева направо | … , … |
Found a content problem with this page?
- Edit the page on GitHub.
- Report the content issue.
- View the source on GitHub.
Want to get more involved?
Learn how to contribute.
This page was last modified on by MDN contributors.
Обозначение— Что такое $48\div2(9+3)$?
$\begingroup$
На этот вопрос уже есть ответы здесь :
Имеют ли значения, присоединенные к целым числам, неявные круглые скобки? (11 ответов)
Закрыта 9 лет назад.
В Интернете ведутся ожесточенные споры о значении $48\div2(9+3)$.
Я считаю, что ответ $2$, поскольку я считаю, что это часть операции со скобками в BEDMAS. Mathway дает тот же ответ. Я также считаю, что если бы запросили $48\div2\times(9+3)$, это было бы $288$, с чем Mathway также согласен.
Тем не менее, WolframAlpha говорит, что это $288$ в любом случае.
Мой друг (который лучше разбирается в математике) сказал мне, что не существует такой вещи, как «неявное умножение», есть только сокращенное, так что оно фактически выполняется после деления (слева направо, не обязательно потому, что деление происходит до умножение, но причину явно не назвал)
Какой ответ и почему?
- обозначения
- арифметика
$\endgroup$
29
$\begingroup$
Нет Верховного суда по математическим обозначениям; на Синае не было ниспослано никаких заповедей относительно оперативного старшинства; все, что есть, это условность, и разные люди могут свободно придерживаться разных условностей. Мудрые люди вставят достаточно скобок, чтобы никто не мог ошибиться в значении. Если они имеют в виду, $(48\div2)(9+3)$, так и напишут; если они имеют в виду $48\div\bigl(2(9+3)\bigr)$, они так и напишут.
$\endgroup$
9
$\begingroup$
Это неоднозначно, в этом случае нет ни одного правильного ответа, кроме, возможно, того, что он не определен. Ты можешь иметь
$$\frac{48}{2(9+3)} = 2$$
или
$$\frac{48}{2}(9+3) = 288$$
Следовательно, нет смысла обсуждая это.
Обратите внимание, что причина, по которой вы получаете разные ответы от mathway и google калькулятора, заключается в том, что алгоритмы, которые они используют для анализа ввода, различны. Эти алгоритмы, по-видимому (и понятно), в данном случае оставляют на усмотрение пользователя вводить данные, которые можно интерпретировать только одним способом. Это не так, и поэтому их ответы различаются.
$\endgroup$
2
$\begingroup$
Я бы сказал, что это даже не точно определено.
В теории групп вы обычно проходите мимо утверждения, в котором говорится: «ассоциативность означает, что $(1 + 2) + 3$ равно $1 + (2+3)$, поэтому мы можем написать $1 + 2 + 3$». без двусмысленности». $\div$ не обладает однозначностью.
Это одно из преимуществ использования $\frac{48}{2}(9+3)$ или $\frac{48}{2(9+3)}$ — это не совсем ассоциативно, но не двусмысленно. Я не видел $\div$ с начальной школы, наверное, именно по этой причине.
$\endgroup$
3
$\begingroup$
Нет разницы в порядке между неявным и явным умножением. Purplemath предполагает, что подразумеваемое умножение вне круглых скобок также имеет приоритет порядка скобок над всеми другими умножениями (делениями). Таким образом, они интерпретируют подразумеваемое умножение в скобках как $48\div(2\times(9+3)) = 2$.
В качестве альтернативы, все калькуляторы с неявными возможностями, которые я пробовал, дают те же результаты, что и Wolfram Alpha, который интерпретирует импликацию как $(48\div2)\cdot(9+3) = 288$
Некоторую путаницу также может вызвать сам символ деления $\div$, поскольку $48/2(9+3)$ визуально поддерживает взаимное подразумеваемое умножение в скобках Wolfram Alpha: $\frac{48}{ 2}\cdot(9+3) = 288$
Короткий ответ заключается в том, что формулу в том виде, в каком она написана, слишком легко неправильно истолковать, и автор должен уточнить ее, чтобы обеспечить ее правильный расчет.
PS: чтобы еще больше нахмурить брови — использование скобок в качестве переменной дает разные результаты. Итак, $48\div2c$, где $c=9+3$ дает $2$, но это объединяет различие между скобками и синтаксисом переменной-коэффициента. $48\div2\cdot c$, где $c=9+3$ дает $288$.
$\endgroup$
4
Очень активный вопрос . Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа.
Приоритет оператора — OeisWiki
Правила приоритета оператора помогают математикам писать выражения (например, уравнения и неравенства) чисто и однозначно. Например, подразумевается, что такое выражение, как 4x−7y{\displaystyle 4x-7y}, отличается либо от 4(x−7y){\displaystyle 4(x-7y)}, либо от (4x−7)y{\displaystyle (4х-7)у}. [1]
Для стандартной арифметики приоритет операций следующий:
«1.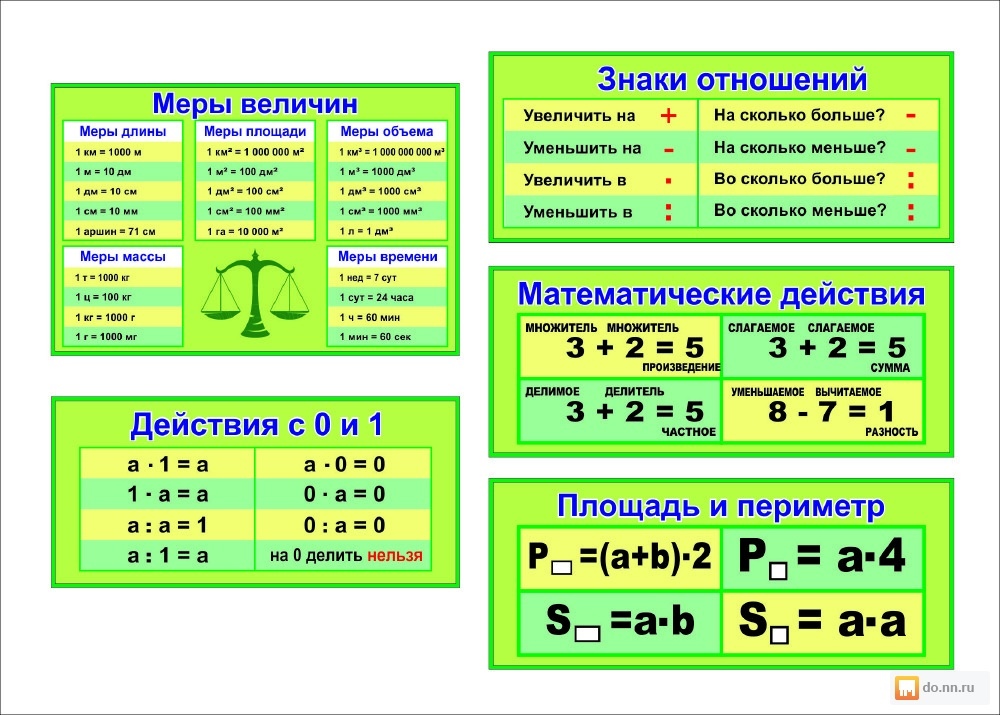
Скобки,
Однако некоторые преподаватели могут отказаться от факториалов. Mnemonic, иногда используемый студентами, — « P Lease E XCUSE M Y D EAR A UNT S ALLY» ( P Arentheeses, E Xponents и ROOT , d ivision, a дополнение, s вычитание). [3]
Содержание
- 1 Скобки
- 2 Приоритет одного уровня
- 3 Выражения с операторами итерации
- 4 Приоритет оператора в компьютерном программировании
- 5 Каталожные номера
Подразумеваемые круглые скобки
Когда выражения не ограничиваются одной строкой, круглые скобки часто подразумеваются. Например, в ab+c{\displaystyle {\frac {a}{b+c}}} подразумевается, что добавление b{\displaystyle b} к c{\displaystyle c} должно быть выполнено перед делением {\displaystyle a} на это количество.
9{2}-4ас))/2а}.
Приоритет одного уровня
В некоторых случаях выражение содержит операции, находящиеся на одном уровне. Например, 4÷7×3{\displaystyle 4\div 7\times 3}. Умножение и деление находятся на одном уровне приоритета. По необходимости одна из двух операций должна быть указана первой, и это не следует понимать так, будто умножение имеет несколько более высокий уровень приоритета.
Как правило, такие выражения должны оцениваться слева направо. Таким образом, в примере первое, что нужно сделать, это разделить 4 на 7, а затем умножить промежуточный результат на 3.
Если сначала нужно выполнить умножение 7 на 3, следует добавить круглые скобки, чтобы переопределить вычисление слева направо: 4÷(7×3){\displaystyle 4\div (7\times 3) }. Поскольку круглые скобки находятся на самом высоком уровне приоритета, это больше не является выражением приоритета того же уровня.
Когда выражения не ограничены одной строкой, приоритет операторов обычно более четкий, например, 47 × 3 ≠ 47 × 3.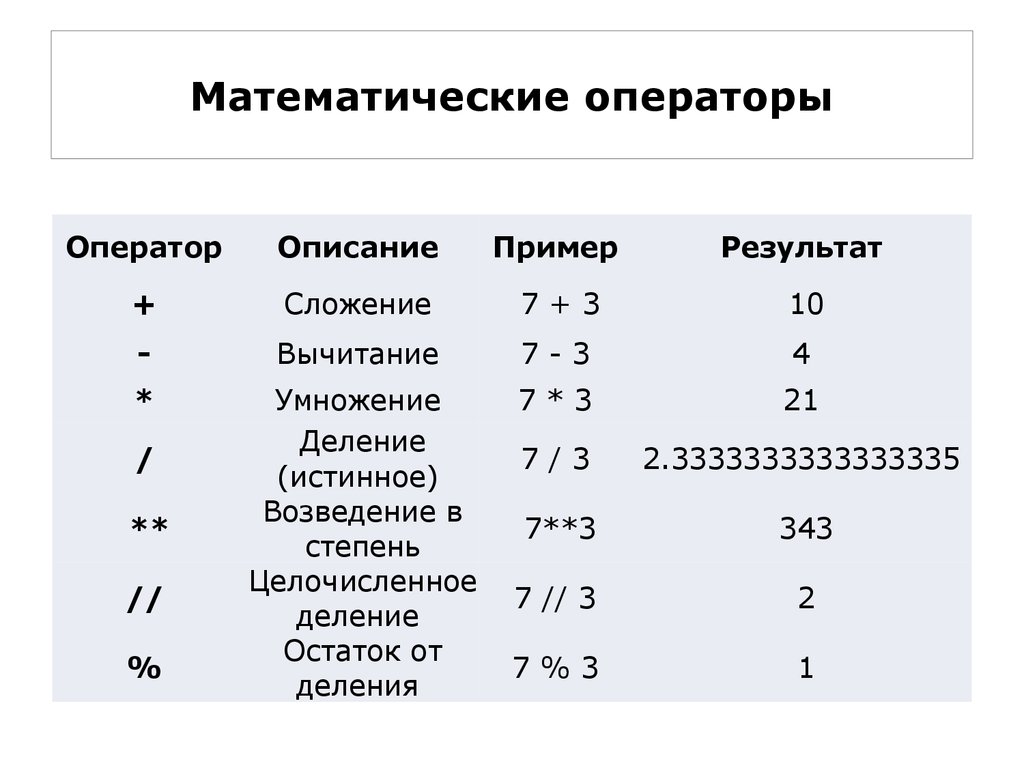
{\ displaystyle {\ frac {4} {7}} \ times 3 \ neq {\ frac { 4}{7\times 3}}.}
В некоторых старых текстах круглые скобки иногда подразумеваются для того, что кажется выражениями приоритета того же уровня. Участникам OEIS рекомендуется делать явные скобки, которые подразумевались забытыми обычаями, чтобы соответствовать современной практике. 9(2н)) , чтобы правильно передать смысл.
Приоритет операторов в компьютерном программировании
Компьютеры, как правило, хуже умеют справляться с неоднозначностью, чем люди, поэтому необходимо, чтобы все операторы были определены для приоритета и ассоциативности, включая операторы сравнения, такие как =, <, >. В приведенном выше первом примере выражения даже передовой CAS, такой как Mathematica, необходимо указать выражение (ai+1){\displaystyle \left(a_{i}+1\right)}, а не ai+1{\displaystyle a_{ i}+1}, чтобы получить желаемый результат.
Форд и Теори пишут, что «Неправильное понимание правил приоритета операторов часто может привести к выражениям, которые неправильно оценивают данные».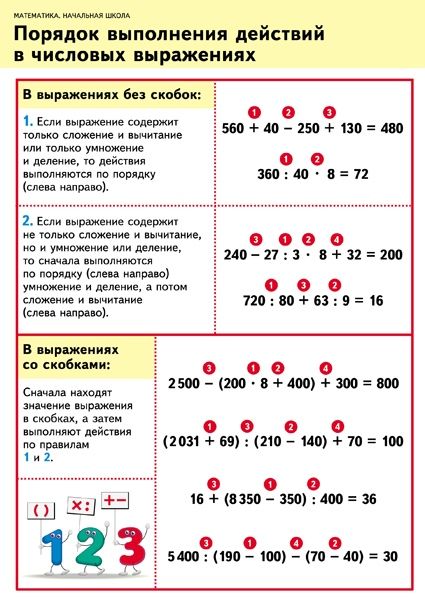
n), {n, 100}] дает желаемую последовательность всех нулей (A000004).
Ссылки
- ↑ Возможность того, что могут быть значения любой переменной, которые заставляют выражения вычислять одно и то же, не должна отвлекать от нецелесообразности обращения с ними как с эквивалентными. В первых двух примерах y=0{\displaystyle y=0} сокращает оба выражения до 4x{\displaystyle 4x}.
- ↑ Пегг, Эд младший. «Приоритет». Из MathWorld — веб-ресурса Wolfram, созданного Эриком В. Вайсштейном. http://mathworld.wolfram.com/Precedence.html
- ↑ Ронда Хюттенмюллер, 9 лет0206 Демистификация алгебры: руководство для самообучения McGraw-Hill New York (2003): 164
- ↑ ϕ{\displaystyle \phi} здесь, конечно же, золотое сечение, A001622. С. Р. Финч, Математические константы , Кембридж, 2003 г., раздел 1.2.5. «Факториалы Фибоначчи» с. 10
- ↑ Глава 2, «Распространенные синтаксические и семантические ошибки» от Энн Р. Форд и Тоби Дж. Теори
