Принципы ментальной арифметики

Развиваем оба полушария для максимально эффективной работы мозга

Ментальная арифметика — это методика, которая обучает быстрому счету в уме, когда два наших полушария мозга начинают работать одновременно, что позволяет развиваться творческому и логическому мышлению.

Эта методика гармоничного развития интеллекта пришла к нам из Древнего Китая, она использует азиатскую технологию вычислений при помощи разновидности счетов — абакуса (китайское название) или соробана (японское название).

Какие принципы лежат в основе ментальной арифметики?

Принцип индивидуального подхода — сначала ребенок начинает работать на реальном абакусе (соробане), освоив его, под руководством педагога ребенок начинает работать уже с воображаемыми счетами. Здесь очень важна эмпатия со стороны педагога, он должен тонко чувствовать, когда ребенок готов выйти на новый уровень.

Для большей эффективности и вовлеченности ребенка в процесс ментального счета, преподаватель может дополнять каждый урок захватывающими фактами по тем темам, которые интересны конкретно этому ученику (например, из астрономии или японской анимации).

Уроки ментальной арифметики могут включать в себя интересные задания на логику или другие интерактивные, чаще всего творческие упражнения.

Принцип счета — занимаясь ментальной арифметикой, ребенок изучает новый способ складывать, вычитать, умножать и делить сложные числа в уме. Он начинает работать с новым объектом — счетами абакус (соробан), что позволяет ему буквально чувствовать цифры на кончиках пальцев.

Это никак не противоречит тому, что ребенок будет проходить или уже проходит в школе. Таблица умножения, подсчет в столбик и калькулятор никуда не денутся из его жизни =)

Ментальная арифметика даёт новый инструмент счета, который привлекает ребенка своей магией. По крайней мере, так выглядит со стороны сам процесс работы с цифрами =)

Также занятия ментальной арифметикой показывают ребенку, что мир без гаджетов и современных технологий довольно интересен. И он, ребенок, может почувствовать себя супергероем, который легко и быстро справляется со сложными вычислениями.

Принцип всестороннего развития — занятия ментальной арифметикой соединяют в себе логику и креатив, рациональное и творческое, что способствует развитию у ребенка способности нестандартно мыслить. Навык решения задач и проблем креативным (нестандартным) способом уже сейчас является наиболее востребованным при приеме на работу в любой сфере профессиональной деятельности человека.

Как показывают исследования ученых-футурологов, в будущем будут востребованы именно те навыки, которые можно объединить словом креативность. Почему? Потому что это одно из важнейших преимуществ человеческого мозга перед компьютером.

А пока ваш ребенок растет и занимается ментальной арифметикой, магия происходящего служит его вдохновением, а демонстрация своих умений среди друзей и родственников способствует повышению самооценки.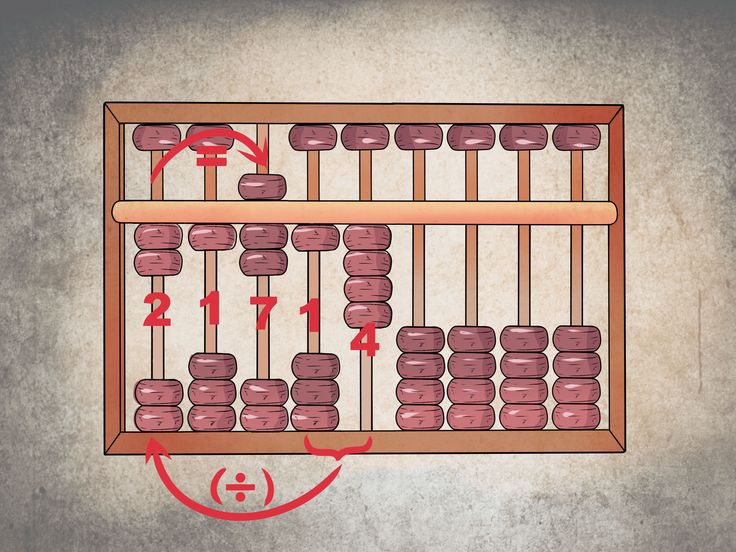

Принцип системного подхода — для освоения и развития полученного навыка ментального счета при помощи воображаемого абакуса (соробана) необходима четко выстроенная система занятий и тренировок. Регулярность крайне важна, так как навык ментального счета, словно мышцу, важно держать в тонусе.

Занятия ментальной арифметикой должны проходить не менее одного раза в неделю, а между встречами с преподавателем важно заниматься самостоятельно по специализированным тетрадям. Будет лучше, если тетради, по которым занимается ваш ребенок, были

Уже занимаетесь ментальной арифметикой и хотите в перерывах тренироваться самостоятельно?

Вот наш бесплатный онлайн-тренажер (https://siriusfuture.ru/train-numbers). Выбирайте в настройках уровень сложности и повышайте навык ментального счета =)

Делитесь интересным c друзьями:

Читать еще

На главную

Онлайн-тренажер

Запишите Ребенка на пробное занятие прямо сейчас!

Узнайте о современном детских занятиях, проверьте эффективность и получите новые знания!

Главные принципы ментальной арифметики | Дефектология Проф

За последнее время в школьном образовании сложилась тенденция постоянного повышения требований и усложнения программ. Из-за этого детям все труднее справляться с нагрузкой, в результате чего на полноценную подготовку ко всем урокам не всегда хватает времени. Однако принципы ментальной арифметики обеспечивают школьнику быстрое усвоение знаний и повышенную успеваемость уже с первого класса.

ИСТОРИЯ ВОЗНИКНОВЕНИЯ

История ментальной арифметики берёт своё начало в Древней Греции и Месопотамии (около 5 000 тысяч лет назад). Именно тогда появился невероятный способ, который стимулирует развитие обоих полушарий головного мозга, позволяет развить память, внимание и устный счет до фантастических результатов.

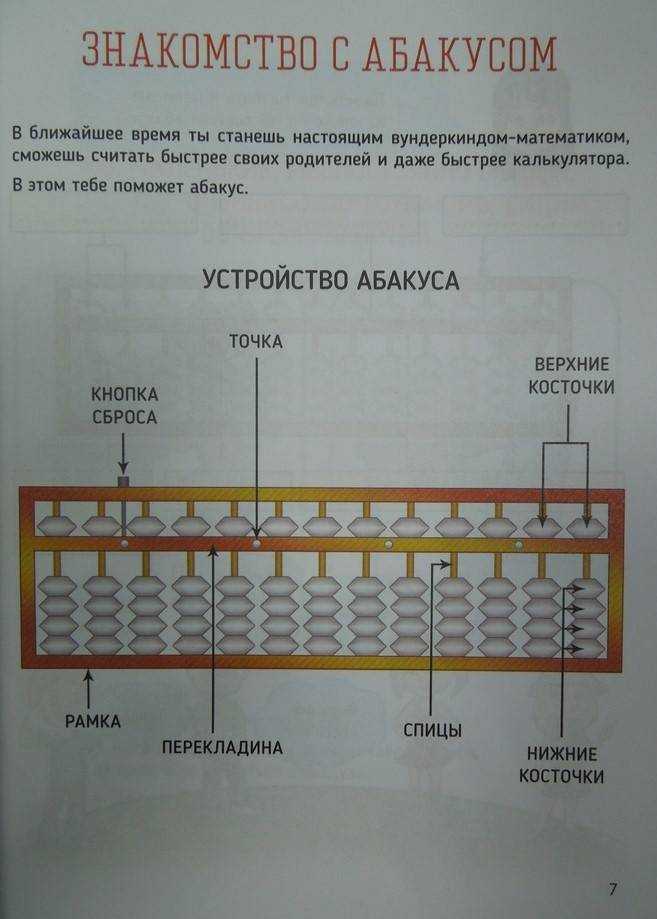
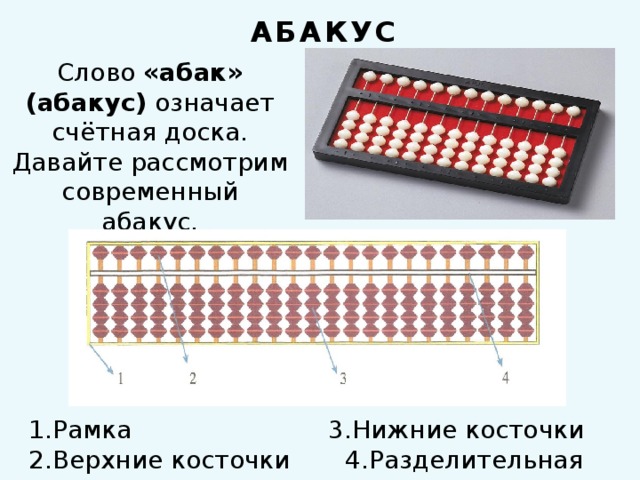
В основе методики лежат древние счеты-абакус. В Китае они называются суаньпань, а в Японии – соробан. Это самый главный инструмент, который был придуман для того, чтобы люди научились быстро и правильно считать. Можно сказать, что абакус — это прародитель современного калькулятора. Только калькулятор не развивает интеллект и не заставляет человека думать, а вот абакус устроен таким образом, что умение считать на нем тренирует мозг, развивает нейронные связи между обоими полушариями, творческие способности и интеллект.

Во многих странах Азии ментальная арифметика является обязательным предметом, с которого дети начинают обучение в школе. Очень активно применяют техники ментальной арифметики в Турции, Казахстане, Малайзии и странах Северной Америки. А, например, в Беларуси уже несколько лет активно распространяется франшиза детского развивающего центра SMARTUM, благодаря которой тысячи детей по всей стране получили возможность доступно заниматься ментальной арифметикой и развивать свой интеллект.

Ментальная арифметика и принцип ее работы состоит в том, чтобы обеспечить одновременное развитие обоих полушарий головного мозга ребенка, благодаря чему он станет личностью с огромным количеством талантов. Для этого применяются специальные методики развития памяти и мышления. Достигается все это путем систематических занятий со счетами-абакусом, вследствие чего школьник приобретает навыки быстрого счета в уме.

 

КАК ПРОИСХОДИТ ОБУЧЕНИЕ МЕНТАЛЬНОЙ АРИФМЕТИКЕ?

Главный принцип ментальной арифметики – это работа со счетами абакус. Дети начинаются учиться с самого простого. Сначала они складывают и вычитают. Этот процесс занимает около года. Затем они учатся умножать и делить. Это ещё год. Потом начинается высшая техника – это извлечение степеней и корней на счетах.

При вычислениях на абакусе необходимо правильно его держать и двигать косточки. Счёты должны лежать на горизонтальной плоскости, например, на столе. Чтобы он крепко лежал, нужно придерживать его тремя пальцами левой руки: большим, безымянным и мизинцем. Остальными двумя пальцами мы считаем.

Правую руку мы сжимаем в кулак и держим там карандаш или ручку грифелем вниз. Большим и указательным пальцем мы считаем, а средним, безымянным и мизинцем держим карандаш или ручку. Пишущий предмет нужен нам, чтобы мы записывали ответы на арифметические примеры. 

После того, как дети сумели вычислить примеры на абакусе, они убирают его со стола и начинают воображать его в уме, то есть считают ментально. Благодаря тому, что у ребёнка одновременно работает образное мышление и моторика рук, весь мозг развивается у малыша очень активно.

ПОЛЬЗА МЕНТАЛЬНОЙ АРИФМЕТИКИ

Многие родители спрашивают, как работает ментальная арифметика и в чем ее польза. Считается, что каждое из полушарий человеческого мозга отвечает за свои направления. Так, правое из них позволяет развить творчество, образное восприятие и мышление. Левое же в ответе за логическое мышление.

Деятельность полушарий активизируется в тот момент, когда человек начинает работать руками. Если активна правая из них, то начинает работать левое полушарие. И наоборот. Человек, работающий левой рукой, способствует активизации работы правого полушария.

Освоение ментальной арифметики способствует следующему:

• активизации зрительной и слуховой памяти;
• умению концентрации внимания;
• совершенствованию смекалки и интуиции;
• креативному мышлению;
• проявлению уверенности в себе и самостоятельности;
• быстрому освоению иностранных языков;
• реализации способностей в будущем.

 

  Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста, напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.

Роль оценивания и принципа коммутативности в развитии умственного умножения третьеклассников

. 1999 ноябрь; 74(3):157-93.

doi: 10.1006/jecp.1999.2524.

Эй Джей Баруди ¹

принадлежность

• ¹ Университет Иллинойса в Урбана-Шампейн, 61820-6990, США.

• PMID: 10527553
• DOI: 10. 1006/jecp.1999.2524

Эй Джей Баруди. J Exp Детская психология. 1999 ноябрь

. 1999 ноябрь; 74(3):157-93.

дои: 10.1006/jecp.1999.2524.

Автор

Эй Джей Баруди ¹

принадлежность

• ¹ Университет штата Иллинойс в Урбана-Шампейн, 61820-6990, США.

• PMID: 10527553
• DOI: 10.1006/jecp.1999,2524

Абстрактный

В этом обучающем эксперименте предварительное тестирование выявило 36 третьеклассников (средний возраст = 8 лет 5 месяцев, SD = 4 месяца) с незначительным владением комбинациями умножения, включающими множители от 3 до 9. Участников случайным образом распределили на 2 группы, которые практиковали разные подмножества комбинации, а затем были повторно протестированы. Результаты не согласовывались с результатами Р. С. Зиглера (1988) предложение о том, что необходима вычислительная практика для конкретных элементов, чтобы способствовать изменениям в шаблонах ошибок и мастерству комбинаций. Результаты согласуются с гипотезой о том, что дети разрабатывают все более гибкие и точные стратегии оценки и используют реляционные знания, такие как принцип коммутативности, для освоения комбинаций. Поскольку даже быстрые ментальные арифметические ошибки и правильные ответы могут быть вызваны стратегиями, отличными от поиска, исследователям необходимо разработать способы различения стратегий поиска и невоспроизведения.

Copyright 1999 Академическая пресса.

Похожие статьи

• Содействие формальным знаниям коммуникативности с помощью приближенной арифметики.

  Хансен С.М., Хайдер Х., Эйхлер А., Годау С., Френш П.А., Гашлер Р. Хансен С.М. и др. ПЛОС Один. 2015 11 ноября; 10 (11): e0142551. doi: 10.1371/journal.pone.0142551. Электронная коллекция 2015. ПЛОС Один. 2015. PMID: 26560311 Бесплатная статья ЧВК.

• Простое умственное сложение у детей с легкой умственной отсталостью и без нее.

  Янссен Р., Де Боек П., Виэне М., Валлейс Л. Янссен Р. и соавт. J Exp Детская психология. 1999 ноябрь; 74(3):261-81. doi: 10.1006/jecp.1999.2527. J Exp Детская психология. 1999. PMID: 10527557

• Изучение фактов умножения: исследование детей, обучаемых методами открытия в Англии.

  Сталь S, Воронка E. Стил С и др. J Exp Детская психология. 2001 г. , май; 79 (1): 37–55. doi: 10.1006/jecp.2000.2579. J Exp Детская психология. 2001. PMID: 11292310

• Микрогенетическое исследование простого деления.

  Робинсон К.М., Дубе А.К. Робинсон К.М. и др. Может ли J Exp Psychol. 2008 г., сен; 62 (3): 156–62. дои: 10.1037/1196-1961.62.3.156. Может ли J Exp Psychol. 2008. PMID: 18778144

• Корейские дети понимают сложение и вычитание многозначных чисел.

  Фьюсон К.С., Квон Ю. Фьюсон К.С. и др. Детский Дев. 1992 г., апрель 63(2):491-506. Детский Дев. 1992. PMID: 1611949

Посмотреть все похожие статьи

Цитируется

• Содействие формальным знаниям коммуникативности с помощью приближенной арифметики.

  Хансен С.М., Хайдер Х., Эйхлер А., Годау С., Френш П.А., Гашлер Р. Хансен С.М. и др. ПЛОС Один. 2015 11 ноября; 10 (11): e0142551. doi: 10.1371/journal.pone.0142551. Электронная коллекция 2015. ПЛОС Один. 2015. PMID: 26560311 Бесплатная статья ЧВК.

• Подключение нейронного кодирования к познанию чисел: вычислительный счет.

  Пратер РВ. Пратер РВ. Dev Sci. 2012 июль; 15 (4): 589-600. doi: 10.1111/j.1467-7687.2012.01156.x. Dev Sci. 2012. PMID: 22709407 Бесплатная статья ЧВК.

• Умножение ядра в детстве.

  МакКринк К., Спелке Э.С. Маккринк К. и др. Познание. 2010 авг.; 116(2):204-16. doi: 10.1016/j.cognition.2010.05.003. Epub 2010 26 мая. Познание. 2010. PMID: 20537618 Бесплатная статья ЧВК.

• Взаимодействующие соседи: коннекционистская модель поиска в однозначном умножении.

  Вергутс Т., Фиас В. Вергутс Т. и соавт. Мем Когнит. 2005 Январь; 33 (1): 1-16. дои: 10.3758/bf03195293. Мем Когнит. 2005. PMID: 15915789

Типы публикаций

термины MeSH

Умственная арифметика и расчеты по календарю

В этом предыдущем посте я вспомнил нашу дискуссию с Джоном Конвеем о плюсах и минусах различных систем мысленного вычисления дня недели для любой заданной даты. В этом посте я представлю две самые популярные системы для этого: «Апокрифический метод» [

Примечание добавлено 03.05.20 но его корни уходят даже дальше, чем Гаусс] и метод судного дня Конвея. Лично я использую модифицированную версию апокрифического метода. Я представлю обе системы таким образом, чтобы можно было непосредственно сравнить их относительные достоинства, и позволить вам, дорогой читатель, решить для себя, какую из них изучать.

Модульная арифметика

Основным условием для понимания этих двух алгоритмов является элементарное знание модульной арифметики. Когда мы выполняем арифметику по модулю m , это означает, что мы можем складывать или вычитать кратные m по желанию без изменения ответа. Например, арифметика по модулю 12 часто называется

арифметика часов : 13 часов совпадает с 1 часом, поэтому 13 и 1 конгруэнтны по модулю 12 . Точно так же, когда мы работаем по модулю 12, 5 сравнимо с 17, что также сравнимо с 29.. Мы также можем пойти назад: например, вычитая 12, мы видим, что 5 сравнимо с -7. (Это должно иметь интуитивно понятный смысл: если сейчас 12 часов, то через 5 часов будет 5 часов, а 7 часов назад также было 5 часов.)

Для календарных вычислений нам нужно работать по модулю 7. (потому что в неделе 7 дней) и по модулю 4 (потому что каждые 4 года бывает високосный год). Так, например, работая по модулю 7, мы обнаруживаем, что 37 сравнимо с 2, поскольку 35 кратно 7 и 37 – 35 = 2.0137 остаток , когда мы делим 37 на 7.) И когда мы работаем по модулю 4, 19 сравнимо с 3 (поскольку мы получаем остаток от 3 при делении 19 на 4).

Одна из замечательных особенностей модульной арифметики заключается в том, что не имеет значения, складываете ли вы сначала, а затем упрощаете по модулю m, или же вы упрощаете по ходу дела. Например, чтобы вычислить 4 + 8 + 11 по модулю 7, вы можете либо вычислить 4 + 8 + 11 = 23, а затем упростить, чтобы получить 23 = 2 (по модулю 7), либо вы можете сделать 4 + 8 = 12 = 5 (по модулю 7). ), а затем добавьте 11, чтобы получить 5+11 = 16 = 2 (по модулю 7). Или вы могли бы признать, что 11 = 4 (по модулю 7) и вместо добавления 11 просто добавить 4, чтобы получить 5 + 4 = 9= 2 (по модулю 7). Видеть? Это не имеет значения.

Кодирование дней недели

Для апокрифического метода и метода Судного дня мы будем использовать следующее числовое кодирование дней недели:

• Воскресенье = 0
• Понедельник = 1
• Вторник = 2
• Среда = 3
• Четверг = 4
• Пятница = 5
• Суббота = 6

Лучше всего запомнить эту корреспонденцию, а не просто иметь возможность разобраться.

Джон Конвей предлагает в качестве мнемонического приема думать о днях недели как «ни дня», «один день», «два дня», «тройной день», «четыре дня», «пять дней» и «шесть дней». ».

Кроме того, в последующих вычислениях лучше думать об этих числовых значениях как о заданных по модулю 7 . Так, например, 3 дня после субботы — это вторник, а 6 (суббота) + 3 эквивалентны 2 (вторник) по модулю 7. рассматриваемый год как CCYY, последние 2 цифры YY будут определять код года, а первые 2 цифры CC будут определять поправку на век. Код года, который одинаков в обеих системах, является наиболее сложным из всех вычислений, которые нам нужно сделать, поэтому мы можем начать с него.

Чтобы найти код года, мы сначала вычисляем, сколько раз 4 входит в YY, отбрасывая любой остаток. Затем мы добавляем этот результат к YY и берем результат по модулю 7; это дает код года. (В математических терминах: код года равен модулю 7.)

Например, если год 1963, то CC = 19 и YY = 63. Мы вычисляем:

• 63 разделить на 4 равно 15 с остатком 3 (остальное игнорируем).
• 63 + 15 = 78.
• 78 сравнимо с 1 по модулю 7, поэтому код года равен 1,9.0018

На практике существует несколько способов упростить или ускорить вычисление кода года. Мы объясним один сейчас, а некоторые обсудим в конце этого поста.

В любом столетии григорианский календарь повторяется каждые 28 лет. Это означает, что мы можем вычесть из YY числа, кратные 28 (если это не даст отрицательного ответа), и результат будет таким же. Чтобы сделать это быстро, я считаю полезными следующие правила:

• Чтобы вычесть 28, вычтите 30, а затем прибавьте 2.
• Чтобы вычесть 56, вычтите 60, а затем прибавьте 4.
• Чтобы вычесть 84, вычтите 90 и затем прибавьте 6. вычитается, например, 60 = 4 * 15.)

  Таким образом, другим способом вычисления кода года для 1963 года может быть следующее:

  • ГГ=63.
  • 63 – 60 + 4 = 7.
  • 7 разделить на 4 равно 1 с остатком 3 (остаток не учитывать).
  • 7 + 1 = 8,
  • 8 сравнимо с 1 по модулю 7, поэтому код года равен 1.

  Поправка на век

  Григорианский календарь повторяется каждые 400 лет. В результате корректировка века зависит только от CC по модулю 4. А именно:

  Апокрифическая система

  Мнемоника: 31 & -12 (31 = количество дней в типичном месяце, 12 = количество месяцев в году)

  Формула: Поправка на век = 5*CC – 2 (по модулю 7)

  Вы можете запомнить 6 и 5 вместо -1 и -2, если хотите, так как они одинаковы по модулю 7.

  Система Судного Дня

  Мнемоника: Если вы знакомы с Большой Системой, вы можете легко запомнить «0532», используя мнемонику «Соломон». Конвей перефразирует Поправки века в терминах того, что он называет «якорными днями», и у него есть мнемоники для них, о которых вы можете прочитать здесь.

  Если вы уже знакомы с апокрифическими корректировками века, то вы можете просто добавить 4 (по модулю 7), чтобы получить соответствующие корректировки Судного дня.

  Формула: Корректировка века = 5*CC – 5 (по модулю 7)

  Апокрифический алгоритм

  В апокрифической системе каждый месяц имеет код месяца , заданный следующим образом: вопрос високосный год , нам нужно вычесть 1 из кода месяца в январе или феврале.

  Хорошая мнемоника для этого состоит в том, что, читая список, мы имеем последовательности 144, 025, 036, 146. Первые три из них (144, 025, 036) являются полными квадратами (а последняя триада состоит из первые 2 цифры и последняя цифра предыдущих 9числа).

  Однако, если вы хотите по-настоящему быстро разобраться с апокрифической системой, то, как и в случае с днями недели, вам нужно иметь возможность сразу же вспомнить код месяца, указанный месяцу, не просто «идя вниз по списку». Я сам просто запоминал коды месяцев путем повторения и заучивания, но если вы предпочитаете мнемонику, то я придумал следующее:

  • Январь = 1 (1-й месяц года)
  • Февраль = 4 («Четверофевраль»)
  • Март = 4 (В «Маленьких женщинах» 4 сестры Марш)
  • Апрель = 0 (Дураки ничего не знают)
  • Май = 2 (В слове MAYDAY два слога)
  • Июнь = 5 (камень рождения июня — ЖЕМЧУЖИНА, в котором 5 букв)
  • Июль = 0 (Америке в этом месяце исполнилось 0 июля)
  • август = 3 (Август Цезарь входил в состав триумвирата)
  • сентябрь = 6 ( S сентябрь = S ix)
  • октябрь = 1 ( O ctober = One 8
  • Ноябрь = 4 (NOVA имеет 4 буквы)
  • Декабрь = 6 (Рождество через 6 дней после окончания года)

  Апокрифическая формула: День недели = код месяца + день + код года + поправка на век (по модулю 7). Код месяца = 0 = -1 (поскольку 19 = 3 по модулю 4)

• День недели = 0 + 0 + 1 – 1 = 0 <—> Воскресенье

Пример 2: 9 марта 1840

• Код месяца = 4 (без коррекции високосного года)
• День = 9 (= 2 по модулю 7)
• Код года = 40 + 10 = 50 (= 1 по модулю 7)
• Коррекция века = 1 (поскольку 18 = 2 по модулю 4)
• День недели = 4 + 2 + 1 + 1 = 1 (по модулю 7) <–> Понедельник

Пример 3: 25 февраля 2016 г.

4 Код месяца = 4 – 1 = 3 (-1 для поправки на високосный год)

День = 25 (= 4 по модулю 7)

Код года = 16 + 4 = 20 (= 6 по модулю 7)

Поправка на век = -2 (поскольку 20 = 0 по модулю 4)

День недели = 3 + 4 + 6 – 2 = 11 = 4 по модулю 7 <–> Четверг

Алгоритм Судного дня Конвея

В методе Конвея вместо запоминания кода для каждого месяца мы запоминаем определенные даты, называемые Судными днями, которые всегда приходятся на один и тот же день недели в любом данном году . Мы используем код года и поправку на столетие, чтобы выяснить, какой день недели приходится на Судный день в данном году, а затем мы выполняем корректировку вперед или назад от соответствующего Судного дня, чтобы определить день недели для данной даты.

Некоторые даты, выпадающие на Судный день:

• 1/3*, 2/28*, 3/14 (мнемоника: Pi = 3,14)
• 4/4, 6/6, 8/8, 10/10, 12/12
• 5/9, 9/5, 7/11, 11/7 (мнемоника: «Работа с 9 до 5 в 7-Eleven»)

Одна из замечательных особенностей алгоритма Конвея — его простота. это запомнить этот список!

Звездочки здесь потому, что в високосный год Судный день будет 1/4, а не 1/3, и 2/29 вместо 2/28. В качестве мнемоники для них Конвей предлагает запомнить, что для января это 9-е число.0137 третий день 3 года из 4, а четвертый день каждые 4 года. А судный день всегда последний день февраля.

Правило Судного дня: День недели для Судного дня = Код года + Поправка на век (по модулю 7)

В следующих примерах мы используем упрощение «кратное 28» при расчете кода года.

Пример 1: 14 апреля 1963 г.

• YY = 63 (= 63 – 60 + 4 = 7 по модулю 28)
• Код года = 7 + 1 = 8 (= 1 по модулю 7)
• Поправка на век = 3 (поскольку 19 = 3 по модулю 4)
• Код года + поправка на век = 1 + 3 = 4 <—> Четверг . Итак, судный день был четвергом в 1963 году. Но лучше просто запомнить число 4, а не преобразовывать его прямо сейчас в четверг.
• Ближайшая ссылка Судный день = 4/4. Поскольку 4/4 был четвергом, 14/4 было воскресеньем (4 + 10 = 14 = 0 по модулю 7).

Пример 2: 9 марта 1840 г.

• ГГ = 40 (= 40 – 30 + 2 = 12 по модулю 28)
• Код года = 12 + 3 = 15 (= 1 по модулю 7)
• Поправка на век = 5 (поскольку 18 = 2) по модулю 4)
• Код года + Корректировка века = 1 +5 = 6 <—> Суббота . Запомните цифру 6.
• Ближайшая ссылка Судный день = 3/14. Таким образом, 3/9 было в понедельник (6 – 5 = 1 по модулю 7).

Пример 3: 25 февраля 2016 г.

• ГГ = 16
• Код года = 16 + 4 = 20 (= 6 по модулю 7)
• Поправка на век = 2 (поскольку 20 = 0 по модулю 4)
• Код года + поправка на век = 6 +2 = 8 (= 1 по модулю 7) <— > Понедельник . Запомните число 1.
• Ближайшая ссылка Судный день = 2/29 (корректировка високосного года). Таким образом, 2/25 было четверг (1 – 4 = -3 = 4 по модулю 7).

Примечание о високосных годах

Чтобы правильно определять дни недели в таких годах, как 1900 или 2000, которые делятся на 100, необходимо понимать менее известные особенности григорианского календаря. (Для целей наших календарных расчетов это влияет только на даты в январе и феврале.)

Общее правило для високосных лет: каждый год, который делится на 4, является високосным, если только этот год не делится на 100, но не на 400. Так, например, 1900 год был , а не , а 2000 год был високосным.

Пример 1: 30 января 1900 г.

Апокрифический метод: Код года = 0, корректировка века = -1, код месяца = 1 (не вычитайте 1, как в високосном году), день = 30.

0 – 1 + 1 + 30 = 2 (по модулю 7) <—> вторник

Метод Судного дня: Код года = 0, корректировка века = 3, поэтому Судный день был средой в 1900 году. Ближайший Судный день = 3 января (поскольку 1900 год не високосный), поэтому 30 января (27 = 28 – 1 день). позже) был вторник.

Пример 2: 30 января 2000 г.

Апокрифический метод: Код года = 0, корректировка века = -2, код месяца = 0 (вычтите 1 для високосного года), день = 30.

0 – 2 + 0 + 30 = 0 (по модулю 7) <—> воскресенье

Метод судного дня: Код года = 0, корректировка века = 2, поэтому Судный день был вторником в 1900 году. Ближайший Судный день = 4 января (поскольку 2000 год високосный), поэтому 30 января (26 = 28 — 2 дня спустя) было воскресенье.

Вопрос с подвохом

Джордж Вашингтон родился 11 февраля 1731 года. Какой это был день недели?

Если мы будем следовать нашему методу, мы получим (неправильный) ответ Sunday.

Проблема в том, что Англия и ее колонии не принимали григорианский календарь до 1752 года; дата 11 февраля 1731 года по юлианскому календарю. По григорианскому календарю Джордж Вашингтон родился 22 февраля 1732 года, то есть в пятницу (правильный ответ).

См. https://www.mountvernon.org/george-washington/celebrating-his-birthday/celebrating-george-washingtons-birthday/

Альтернативные методы получения кода года

Расчет кода года в быстрый способ является одним из основных препятствий для быстрого выполнения любой из двух систем, которые мы обсуждали. Вот несколько альтернативных методов, которые были предложены (см. эту страницу Википедии для ссылок):

• Метод Льюиса Кэрролла: Разделить YY на 12; скажем, он входит в A раз с остатком B. Пусть C будет число раз, когда 4 входит в B (отбрасывая остаток). Тогда код года будет A+B+C (по модулю 7). (В собственной прозе Конвея вы складываете: «Количество десятков; остаток после этого; и количество четверок в остатке».) Например, если YY=63, то A=5, B=3, C= 0 и код года 5+3+0 = 1 (по модулю 7), а если YY=16, то A=1, B=4, C=1 и код года 1+4+1 = 6 (по модулю 7). ).
• Метод Майка Уолтерса «Легкий судный день»: Если YY еще не кратен 4, добавьте 11, 22 или 33 в зависимости от того, равен ли YY по модулю 4 1, 2 или 3. Теперь разделите на 2, возьмите результат по модулю 7 и вычтите из 7, чтобы получить код года. Например, если YY=63, мы прибавляем 33, чтобы получить 96, делим на 2, чтобы получить 48, и возьмем это по модулю 7, чтобы получить 6. Вычитание из 7 дает 7 – 6 = 1 для кода года. А если YY=16, то мы делим на 2, чтобы получить 8, что сравнимо с 1 по модулю 7. Вычитание из 7 дает 7 – 1 = 6 для кода года.
• Метод «Нечет + 11» (модификация метода «Легкий судный день» Фонга и Уолтерса): если YY нечетно, прибавьте 11 и разделите на 2; в противном случае просто разделите на 2. Если новое число нечетное, добавьте 11; иначе ничего не делать. Возьмите полученное по модулю 7 и вычтите из 7, чтобы получить код года. Например, если YY=63, мы прибавляем 11, чтобы получить 74, и делим на 2, чтобы получить 37. Прибавление 11 дает 48, что равно 6 по модулю 7, что дает 7 – 6 = 1 в качестве кода года. А если YY=16, то мы делим на 2, чтобы получить 8, что сравнимо с 1 по модулю 7. Вычитание из 7 дает 7 – 1 = 6 для кода года.

Другие умственные сокращения

Как и в случае с кубиком Рубика, лучший способ (помимо частой практики и повторения) улучшить свою способность быстро выполнять умственные календарные вычисления — это изучить дополнительные сокращения. Например, для ускорения метода Судного дня полезно выучить дополнительные даты, кроме перечисленных выше, которые всегда приходятся на Судный день. Дополнительные легко запоминающиеся примеры включают 4 июля и 31 октября (Хэллоуин). Чем больше из них вы знаете (не задумываясь об этом), тем быстрее вы освоите метод Судного дня. Вы можете найти полный список Судных дней здесь.

Для кода года можно избежать чрезмерных вычислений, запомнив код года для определенного числа целевых лет, а затем просто работая в обратном или прямом направлении. Например, предположим, что вам удалось запомнить следующие два списка:

Код года 0: 00, 06, 17, 23

Код года 3: 03, 08, 14, 25

Тогда вы можете получить любой год, сначала вычитая кратные 28 из YY, чтобы попасть в диапазон от 00 до 27, а затем считая в большую или меньшую сторону не более 3 лет от одного из исходных лет (с учетом високосных лет, если это необходимо). Например:

• ГГ = 78 ==> 78 – 60 + 4 = 22, что на единицу меньше 23, поэтому код года для ’78 0-1=6.
• ГГ = 52 ==> 52 – 30 + 2 = 24, что на 1 больше, чем 23. Поскольку годы, оканчивающиеся на 24, являются високосными, мы должны добавить 2 (а не 1), чтобы получить код года для ’24 из что 23 года. Таким образом, код года для 52 года — 0+2=2.
• ГГ = 94 ==> 94 – 90 + 6 = 10, что на 2 больше, чем 08. Поскольку при переходе с ’08 на ’10 мы не перемещаемся по високосным годам, мы добавляем 2 к коду года для ’08, чтобы получить код года 3+2=5 для ’94.

Конечно, можно пойти еще дальше и запомнить все года с кодом года 0 (00, 06, 17, 23, 28, 34, 45, 51, 56, 62, 73, 79, 84). , 90). Лично я использую следующие мнемоники:

• 00, 28, 56, 84: кратные 28
• 19 06 : Землетрясение в Сан-Франциско
• 19 17 : США вступают в Первую мировую войну 19 45 : Вторая мировая война закончилась
• 19 51 : Розенберги казнены; 19 62 : Кубинский ракетный кризис
• 19 73 : Роу против Уэйда (также год моего рождения)
• 19 79 : Россия вторгается в Афганистан; 19 90 : Ирак вторгается в Кувейт

(Остается только 23 и 34, которые я помню с точки зрения числовых моделей. )

Если вы также запомните 03, 08, 14, 31, 36, 42, 64, 70, 92, 98 как имеющие код года 3, то вы можете перейти к любому данному году из базисного года с кодом 0 или 3, считая вверх или вниз не более 3 лет. Если вы можете освоить необходимое запоминание, этот метод будет значительно быстрее, чем вычисление кода года по формуле. Вот некоторые мнемоники (я использую известные даты в 1900 для кода года 0 и известные даты 1800-х годов для кода года 3):

• 18 03 : покупка Луизианы
• 18 08 : африканская работорговля закончилась в США
3 0 1 9 0 9 0 2 1 1 8 down by British troops
• 18 31 : Nat Turner’s rebellion
• 18 36 : Battle of the Alamo
• 18 64 : General Sherman burns down Atlanta
• 18 70 : Franco-Prussian War
• 18 98 : Парижский договор подписан, положивший конец испано-американской войне

(Остается только 42 и 92, которые можно запомнить отдельно).

Если вы еще не знаете эти даты, ваши навыки в пустяках улучшатся, если вы их узнаете, независимо от того, используете ли вы их для расчетов календаря или нет.

Сравнение двух методов

Возвращаясь к началу этого поста (где я вспомнил собственный разговор с Конвеем на эту тему): как соотносятся эти два метода?

Короче говоря, лично я считаю, что апокрифический метод проще, если пристегнуться и запомнить код месяца. Если вы умеете выполнять арифметические операции по модулю 7 в уме, то единственным реальным узким местом для скорости является определение кода года (что является общим для обоих методов).

С другой стороны, (основные) судные дни легче запомнить, чем коды месяцев, благодаря изящной мнемонике Конвея. И если вы зафиксируете в памяти дополнительные Судные дни, это соответственно ускорит процесс (апокрифический метод не допускает такой дополнительной гибкости).

Метод Конвея можно объяснить в более элементарных терминах, так как на самом деле не нужно знать модульную арифметику, чтобы понять метод. В сочетании с тем фактом, что основные Судные дни так легко запоминаются, это дает сильный педагогический аргумент в пользу метода Конвея. С другой стороны, я преподаю модульную арифметику в своем курсе теории чисел с использованием календарных вычислений, и апокрифический метод является прекрасной иллюстрацией его применения к реальным задачам (еще одним примером является квинтовый круг в теории музыки).

Альтернативный способ кодирования дней недели

На самом деле я использую несколько иное кодирование дней недели, чем то, что я объяснил выше. (Я узнал об этом из книги Уильяма Саймона «Математическая магия», когда был ребенком.) Соответствие, которое я использую:

• Суббота = 0
• Воскресенье = 1
• Понедельник = 2
• Вторник = 3
• Среда = 4
• Четверг = 5
• Пятница = 6

(Для меня это естественно, т.к. я еврей и вместо седьмого дня (Sabbath = Day of Rest) воскресенья, в моей системе это суббота. 😊 )

Если использовать это соответствие, то единственная модификация необходимым для апокрифического метода, как описано выше, является добавление 1 (по модулю 7) к поправке на век. Поэтому вместо

3 1 -1 -2,

я использую

4 2 0 -1.

Одним из преимуществ этой кодировки является то, что для дат в 20-м веке (именно тогда я изучил систему) корректировка века не требуется (т. е. корректировка века для 19-го века).** равно 0).

Если вы хотите использовать это кодирование дней недели с методом Doomsday, снова единственной необходимой корректировкой будет добавление 1 (по модулю 7) к корректировке века. Таким образом, вместо

0 5 3 2,

мы получаем модифицированный Century Adjustments

+1 -1 +4 -4,

, который достаточно легко запомнить.

Задача-вызов

Используйте любую из вышеперечисленных систем для решения следующей задачи:

На какой день недели чаще всего приходится 13-е число месяца?

Мысли на прощание

Если вы изучите любой из этих методов и воспользуетесь некоторыми из приведенных здесь советов, вы обнаружите, что с практикой вы можете довольно быстро вычислять день недели для любой заданной даты. Однако для достижения мастерства, подобного Конвею, потребуется невероятная самоотверженность.

Когда New York Times рассказала о Джоне Конвее в статье Джины Колаты 1993 года, статья начиналась так:

ДР. ДЖОН Х. КОНВЭЙ садится за свой компьютер и готовится войти в систему. Но прежде чем компьютер позволит ему начать работу, он быстро выдает 10 случайно выбранных дат из прошлого и будущего, вроде 15 марта 2005 года или 29 апреля 1803 года. Доктор Конвей должен мысленно рассчитать каждый день недели, прежде чем его компьютер позволит ему открыть файл и приступить к работе.

Это игра, которую он придумал, чтобы играть с самим собой. «Я думаю, что я самый быстрый человек в мире в этом», — говорит он. Его рекорд 15,9.2 секунды, чтобы рассчитать все 10 дней.

Ссылки

Для получения дополнительной информации см. следующие источники:

• Обзор различных методов (Википедия)
• Метод Судного дня (Википедия)
• Если вы хотите узнать о методе Судного дня, см.