Конспект урока по математике в 3 классе по теме : Внетабличное умножение и деление.

Урок математики в 3 классе .

Тема: Внетабличное умножение и деление.

Тип урока: закрепление изученного материала.

Цель: отработать устные приёмы умножения и деления однозначного числа на двузначное, деления с остатком. Развивать коммуникативные навыки, умение анализировать, обобщать, решать задачи.

Задачи:

-образовательные: повторить таблицу умножения и деления, закрепить умение выполнять внетабличное умножение и деление, совершенствовать вычислительные навыки.

-воспитательные: воспитывать точность, аккуратность, самоконтроль.

-развивающие: развивать логическое мышление, гибкость мышления, внимание, память.

Оборудование: компьютер, проектор, интерактивная доска, учебник «Математика» 3 класс под редакцией М. И. Моро.

Ход урока:

I . Организационный момент. Приветствие обучаемых, проверка готовности к уроку.

II. Актуализация знаний.

— Скажите мне пожалуйста, что нужно хорошо знать и уметь для того, чтобы быстро считать? (Таблицу умножения)

Я предлагаю Вам решить примеры на листах, а результаты записать в таблицу внизу, расшифровав запись.

36:3(О) 19·4(В) 70:10(Р)

42:3(П) 72:3(Е) 30·3(У)

23·4(Ч) 80:40(А) 88:4(М)

45:15(Ь) 43·2(Т)

40:2(Я) 63:3(Н)

14	12	76	86	12	7	24	21	3	24		22	2	86	3
п	о	в	т	о	р	е	н	ь	е	—	м	а	т	ь

90	92	24	21	3	20
у	ч	е	н	ь	я

Что у вас получилось? (пословица: Повторенье-мать ученья. )

Давайте из этой пословицы определим тему сегодняшнего урока: повторять, закреплять, способы внетабличного умножения и деления.

Какие вычислительные приёмы мы будем закреплять? (метод подбора, метод разложения на удобные слагаемые или на разрядные слагаемые). Какие приёмы умножения и деления нам в этом помогут? (умножение и деление суммы на число).

III.Работа по теме урока.

А теперь давайте повторим, вспомним изученные случаи внетабличного умножения и деления.

12∙6=10∙6+2∙6=60+12=72

Чтобы умножить двузначное число на однозначное, надо двузначное число разложить на разрядные слагаемые.

84:3= (60+24):3= 60:3+24:3=20+8=28

Чтобы разделить двузначное число на однозначное, надо двузначное число разложить на удобные слагаемые.

87:29=3

Чтобы разделить двухзначное число на двухзначное, надо найти такое число, которое бы при умножении на делитель давало бы делимое.

Будем находить частное подбором.

Пробуем в частном 2 и проверяем: 29∙2=58, 58<87. Число 2 не подходит.

Пробуем в частном 3 и проверяем: 29∙3=87, 87=87, значит, 87:29=3

IV. Физкультминутка.

Руки подняли и покачали

Это деревья в лесу.

Руки согнули, кисти встряхнули-

Ветер сбивает росу.

В стороны руки, плавно помашем-

Это к нам птицы летят.

Как они тихо садятся, покажем-

Крылья сложили назад.

V. Закрепление изученного материала.

Работа по учебнику.

Запись в тетради: число, классная работа.

№1 (стр.24) -взаимопроверка.

№9 (стр.21)

Прочитайте условие задачи.

Что надо узнать в задаче? (сколько часов экономит самолет для пассажира).

Что это значит? (на самолёте быстрее добраться от Москвы до Ставрополя).

Как можно по –другому сформулировать главный вопрос? (на сколько меньше летит самолёт, чем идёт поезд?)

Запишем задачу кратко.

Что значит «в 14 раз меньше»? Какое действие нужно выполнить? (Деление.)

Как узнать, на сколько часов в пути самолёт был меньше? (вычитанием).

Запишите решение задачи по действиям.

Решение:

28:14=2(ч)-летит самолёт.

28-2=26(ч)

Ответ: самолёт экономит для пассажира 26 часов.

VI. Рефлексия.

Работа по карточкам в парах.

-Решите уравнения. Решение уравнения впишите в пустую клетку следующего уравнения. Расположите ответы в порядке убывания и расшифруйте слово.

х:12=6(!) х ∙ ….=48(А) …∙ х=30(Р) …. : х=3(У)

Ответ: ура!

Оцените свою работу на уроке.

VII. Итог урока, домашнее задание.

Какую цель мы ставили в начале урока? С чего начался урок?

Какое задание было самым интересным?

Кто доволен своей работой?

Дома выполнить: учебник стр. 24 №3, №4.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/133943-konspekt-uroka-po-matematike-v-3-klasse-po-te

2. Внетабличное умножение и деление в пределах 100

К внетабличным случаям умножения и деления в пределах 100 относят случаи умножения двузначного числа на однозначное (20-3, 18-3),а также случаи деления двузначного числа на однозначное, не входящие в число табличных (80 : 4, 96 : 6) и случаи деления двузначного числа на двузначное в пределах 100 (80 : 40, 96 : 16). Эти случаи рассматриваются как случаи устных вычислений, и предполагается, что ребенок выполняет их без обращения к письменным алгоритмам вычислений, а лишь используя известные ему правила и законы арифметических действий и знание табличного умножения и деления.

Используемые математические законы и правила

Для подготовки к изучению внетабличного умножения и деления необходимо рассмотреть следующие правила арифметических действий:

1) правило умножения суммы на число и правило умножения числа на сумму;

2) правило деления суммы на число;

3) правило группировки множителей (сочетательное свойство умножения).

Рассмотрим каждое из этих правил и обоснуем их использование при устных внетабличных вычислениях.

Правило умножения суммы на число и правило умножения числа на сумму

Эти два правила являются двумя вариантами раскрытия смысла распределительного свойства умножения относительно сложения. В буквенном виде эти варианты могут быть записаны следующим образом:

(a+b) •c=a•c+b•c с•(a+b)=с•a+с•b

Реально знакомство детей с этими двумя вариантами одного и того же правила разведено во времени почти на целый год: первое правило лежит в основе обучения детей умножению двузначных чисел на однозначные в теме «Внетабличное умножение и деление» в 3 классе, а второе правило лежит в основе способа действия при умножении двузначного числа на двузначное при умножении в столбик в 4 классе.

В основе разъяснения правила умножения суммы на число лежит опора на знание конкретного смысла действия умножения.

Рассматривая два способа вычисления результатов с опорой на анализ рисунка, дети убеждаются в том, что результат при обоих способах вычислений одинаков.

Следует отметить, что первый способ вычислений не требует специальных объяснений и введения нового правила, поскольку он подчиняется общим требованиям к порядку выполнения действий в выражениях со скобками: действия в скобках выполняются первыми.

Особо следует оговорить второй способ, поскольку при таких вычислениях фактически нарушается установка на выполнение действия в скобках первым. Именно поэтому при знакомстве детей с этим правилом в 3 классе снова возвращаются к предметным картинкам, позволяющим получить результаты действий пересчетом. В данном случае пересчет фигурок является тем единственным аргументом, который учитель может привести в подкрепление правомочности такого нарушения устоявшегося правила (действие в скобках выполняется первым).

Введение правила таким образом является нестрогим, эмпирическим (т. е. опирающимся на непосредственный практический опыт). Более общие способы доказательства этого закона требуют привлечения сложного математического аппарата и нецелесообразны в начальной школе. Безусловно, такое введение правила не формирует у детей обобщенных представлений о способах раскрытия скобок при вычислениях, однако в начальной школе это и не предполагается. Более того, терминология, содержащая слова «раскрываем скобки», не употребляется в начальной школе вообще. Хотя дети и знакомятся с правилом умножения суммы на число, но применять они его могут только на ограниченном количестве случаев, связанных с внетабличным умножением двузначных чисел на однозначное. Применение того же правила в других обстоятельствах (например, при решении уравнений) не предусмотрено. Так при решении уравнения вида

(х + 2 ) • 3 = 15 дети не будут применять правило умножения суммы на число (это не предусмотрено ни учебником, ни программой, ни методикой) не только в начальной школе, но и в 5—6 классе, а будут использовать правила взаимосвязи компонентов действий умножения и сложения.

Способ решения: х + 2 = 15 : 3 х+2 = 5х = 5 — 2 х = 3.

Правило умножения суммы на число:

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и полученные результаты сложить.

Используя аналогичный предметный рисунок, рассматривают правило умножения числа на сумму:

4-(3 + 2) = 4- 5 = 20 4-(3 + 2) = 4-3 + 4- 2 = 12 + 8 = 20

Анализ предметного рисунка и подсчет фигурок на нем помогает ребенку убедиться в том, что результаты вычислений совпадают, несмотря на разные способы вычислений. Этот способ знакомства с правилом используется в 4 классе также как и в 3 классе использовался предыдущий вариант. Точно также, речь идет не о формировании у ребенка обобщенных представлений о способах действий в выражениях со скобками, а только об использовании данного способа вычислений при письменных вычислениях в столбик.

Правило умножения числа на сумму:

Чтобы умножить число на сумму можно умножить это число на каждое слагаемое и полученные произведения сложить.

Правило деления суммы на число

Это правило является вариантом раскрытия смысла распределительного свойства деления относительно сложения. В буквенном виде это правило может быть записано следующим образом:

(a + b) : с = a : с + b : с

В основе разъяснения правила деления суммы на число лежит опора на знание конкретного смысла действия деления. Например:

(8 + 6): 2 = 14:2 = 7 (8 + 6): 2 = 8: 2+ 6: 2 = 4+ 3 = 7

Рассматривая два способа вычисления результатов с опорой на анализ рисунка, дети убеждаются в том, что результат при обоих способах вычислений одинаков.

Следует отметить, что первый способ вычислений не требует специальных объяснений и введения нового правила, поскольку он подчиняется общим требованиям к порядку выполнения действий в выражениях со скобками:

действия в скобках выполняются первыми.

Особо следует оговорить второй способ, поскольку при таких вычислениях фактически нарушается установка на выполнение действия в скобках первым. Именно поэтому при знакомстве детей с этим правилом в 3 классе снова возвращаются к предметным картинкам, позволяющим получить результаты действий пересчетом. В данном случае пересчет фигурок является тем единственным аргументом, который учитель может привести в подкрепление правомочности такого нарушения устоявшегося правила (действие в скобках выполняется первым).

Такое введение правила является нестрогим, эмпирическим. Более общие способы доказательства этого закона требуют привлечения сложного математического аппарата и нецелесообразны в начальной школе. Такое введение правила не формирует у детей обобщенных представлений о способах раскрытия скобок при вычислениях, что в начальной школе и не предполагается. Хотя дети и знакомятся с правилом деления суммы на число, но применять они его могут только на ограниченном количестве случаев, связанных с внетабличным делением двузначных чисел на однозначные.

Применение того же правила в других обстоятельствах (например, при решении уравнений) не предусмотрено. Так при решении уравнения вида (х + 6) : 3 = 5 дети не будут применять правило деления суммы на число (это не предусмотрено ни учебником, ни программой, ни методикой) не только в начальной школе, но и в 5—6 классе, а будут использовать правила взаимосвязи компонентов действий умножения и сложения.

Способ решения: х + 6 = 5 • 3 д: + 6=15 х=15-6 х = 9

Правило деления суммы на число:

Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и полученные результаты сложить.

Правило группировки множителей (сочетательное свойство умножения)

Правило группировки множителей (сочетательное свойство умножения) представлено в учебнике как правило умножения числа на произведение. Это правило позволяет научить детей новым способам действия при выполнении устных внетабличных вычислений. В буквенном виде правило может быть представлено следующим образом:

(а • b) • с = а • (b • с) ~ (а • с) • b

В основе его разъяснения лежит конкретный смысл действия умножения и правило перестановки множителей.

Рассматривая три способа вычисления результатов с опорой на анализ рисунка, дети убеждаются в том, что результат при всех способах вычислений одинаковый. Формулируется правило:

Умножить число на произведение можно разными способами:

1) Вычислить произведение и умножить на него число: 6-(3-4) =612 = 72

Что такое коэффициент? Определение, пример, факты

Частное — это ответ, который получается при делении одного числа на другое. Например, если мы разделим число 6 на 3, мы получим результат как 2, то есть частное. Частное может быть целым или десятичным числом. Для точных делений, таких как 10 ÷ 5 = 2, у нас есть целое число в качестве частного, а для таких делений, как 12 ÷ 5 = 2,4, частное представляет собой десятичную дробь. Частное может быть больше делителя, но всегда меньше делимого. Давайте изучим и узнаем больше о частном и методах его нахождения.

1.	Что такое частное в делении?
2.	Определение коэффициента
3.	Как найти частное?
4.	Термины, относящиеся к коэффициенту
5.	Частное и остаток
6.	Часто задаваемые вопросы о факторе

Что такое частное в делении?

Частное — это окончательный ответ, который мы получаем при делении числа. Деление — это метод равномерного распределения предметов по группам, обозначаемый математическим символом (÷). Например, есть 15 шариков, которые нужно разделить поровну на 3 группы. Итак, когда мы делим эти шары на 3 равные группы, утверждение о делении может быть выражено как 15 ÷ 3 = 5. Здесь 5 — это частное. Это значит, что в каждой группе будет по 5 мячей.

Определение коэффициента

Частное в математике может быть определено как результат деления числа на любой делитель. Это количество раз, когда делитель содержится в делимом. На следующем рисунке показано выражение деления, которое отмечает делитель, делимое и частное. Делитель 2 содержится 6 раз в делимом 12. Частное больше или меньше делителя, но всегда меньше делимого.

Как найти частное?

Частное получается после завершения процесса деления. Это означает, что когда делитель делит делимое, ответ, который мы получаем, является частным. Деление — одна из четырех основных математических операций, остальные три — сложение, вычитание и умножение. Частное является результатом процесса деления. После того, как мы полностью разделим число, мы получим частное. В некоторых случаях, когда мы делим число, оно не делится полностью, и мы получаем остаток. Однако даже в этом случае в качестве ответа остается частное, а остаток мы упоминаем отдельно.

Когда мы делим число, помимо частного в процессе деления используются и другие термины. Давайте разберемся в этом с помощью примера. Например, есть плитка шоколада на 12 штук. Можно ли разделить бар поровну между двумя друзьями? Ответ: да, если плитку шоколада разделить поровну между двумя друзьями, каждый из них получит по 6 кусочков шоколада. Вы замечали, что ни один кусочек шоколада не остается нераспределенным. Следовательно, остатка нет. Мы можем записать оператор деления для этого примера как 12 ÷ 2 = 6. Здесь каждое из чисел в делении может быть обозначено специальными терминами. Проверим следующие члены, тесно связанные с частным.

Условия	Описания	Значения
Дивиденд	Общее количество частей, которые должны быть разделены.	12
Делитель	Количество равных групп, которые необходимо создать.	2
Частное	Количество штук в каждой группе.	6
Остаток	Оставшаяся часть, не входящая ни в одну группу.	0

Этот пример также может быть математически представлен следующим образом:

Частное и остаток

Когда мы делим число и если оно не делится полностью, у нас остается остаток. Давайте разберемся в этом с помощью примера. Частное можно вычислить, разделив делимое на делитель. Частное = Дивиденд ÷ Делитель. Решим 435 ÷ 4. Здесь 435 — делимое, а 4 — делитель.

Следующие шаги помогут понять процесс деления и найти частное и остаток.

• Шаг 1: Возьмите первую цифру делимого. Если эта цифра больше или равна делителю, то разделите ее на делитель и сверху запишите ответ как часть частного. Умножьте это число на делитель и запишите произведение под первой цифрой делимого. Вычтите результат из цифры и запишите его под этим числом. Здесь первая цифра 4 и она равна делителю. Итак, 4 ÷ 4 = 1 написано сверху на черте. Произведение 4 × 1 = 4 вычитается из цифры и ниже записывается 0. Теперь сократите следующее число делимого, равное 3, и поместите его рядом с 0,9.0138
• Шаг 2: Мы видим, что в результате шага 1 у нас есть 3. Повторите тот же шаг, чтобы проверить, больше или меньше это число, чем делитель. Поскольку 3 меньше 4, мы не можем разделить это число. Следовательно, мы записываем 0 сверху и записываем произведение 4 × 0 = 0 под цифрой 3, затем вычитаем 3 — 0 = 3. Следующим шагом является уменьшение следующего числа из делимого и размещение его рядом с 3. Получается 35. Поскольку 35 > 4, мы можем разделить это число на 4. После записи 8 сверху мы записываем произведение 4 × 8 = 32 под 35, как показано на рисунке. Вычтите 35 — 32 = 3. Теперь эта 3 меньше, чем делитель 4, и из делимого не осталось числа, которое можно было бы уменьшить. Это означает, что мы оставим 3 в качестве остатка и завершим деление. Таким образом, 3 известен как 9Остаток 0049 и 108 называется частным .

Проверка результата деления

Мы можем легко проверить, верен ли ответ, который мы получили при делении в большую сторону. Поскольку процесс деления является обратным умножению, давайте выясним, как мы можем проверить наш ответ, используя эту информацию. Мы используем формулу: Дивиденд = (Делитель × Частное) + Остаток. Это означает, что если мы умножим делитель на частное и добавим остаток, мы должны получить число как делимое. Если числа удовлетворяют этому уравнению, то ответ считается правильным, в противном случае нужно проверить наше деление. Давайте еще раз рассмотрим рассмотренный выше пример. Здесь делимое равно 435, делитель равен 4, частное равно 108, а остаток равен 3. Подставляя значение в формулу, получаем 435 = (4 × 108) + 3. Это доказывает, что ответ правильный. Возьмем другой пример. Если мы разделим 6 ÷ 2 = 3, мы получим остаток как 0. Теперь давайте подставим эти значения в формулу, 6 = (2 × 3) + 0. Это означает, что ответ правильный.

☛ Похожие статьи

• Формула остатка делителя дивиденда
• Калькулятор коэффициентов

 

Примеры на частное

1. Пример 1: 4000 долларов распределяются между 25 рабочими за работу, выполненную ими на строительной площадке. Подсчитайте сумму, которую дали каждому работнику.

   Решение:

   Общая распределяемая сумма = 4000 долларов. Количество рабочих = 25. Нам нужно рассчитать сумму, отдаваемую каждому рабочему. Для этого мы разделим 4000 на 25, используя метод деления в длинную сторону, и найдем частное.

   Полученное частное равно 160. Следовательно, сумма, выдаваемая каждому рабочему, составляет 160 долларов.

2. Пример 2: Разделите 66 ÷ 7 и найдите частное.

   Решение:

   Мы будем использовать метод деления в длину, чтобы найти частное.

   После деления 66 на 7 мы получим 9 в частном и 3 в остатке.

3. Пример 3: Состояние истинное или ложное

   а.) Частное — это окончательный ответ, который мы получаем при делении числа.

   б.) Когда мы делим число и если оно не делится полностью, у нас остается остаток.

   Решение:

   а.) Верно, частное — это окончательный ответ, который мы получаем при делении числа.

   б.) Правда, когда мы делим число и если оно не делится полностью, у нас остается остаток.

перейти к слайдуперейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по Quotient

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о коэффициенте

Что такое частное в математике?

Частное — это окончательный ответ, который мы получаем при делении числа.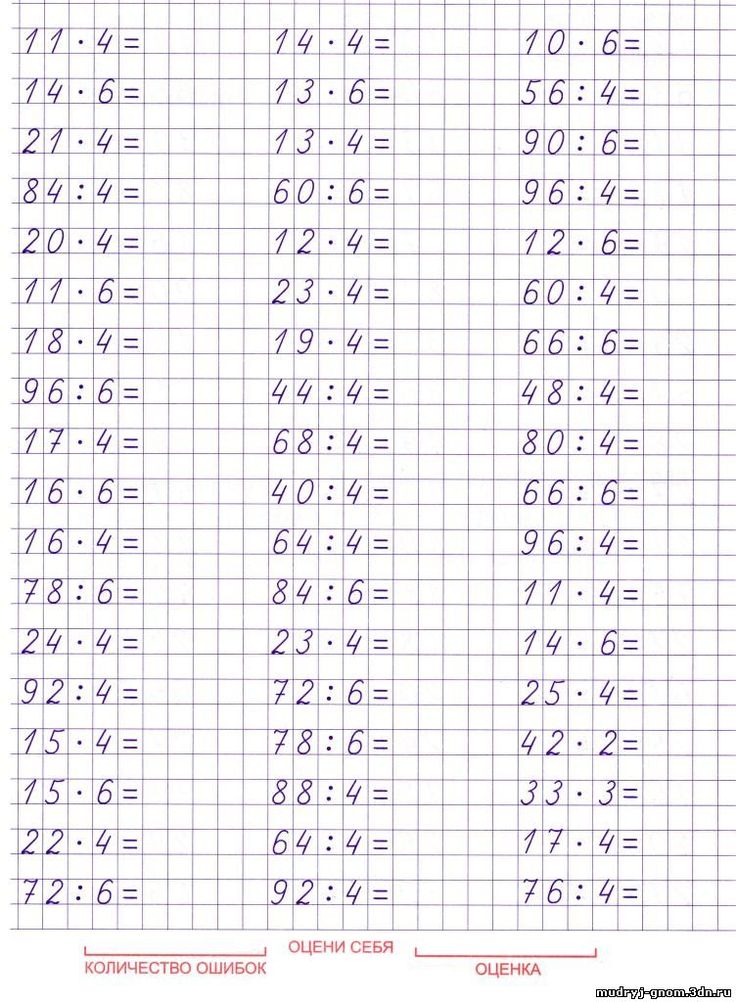 Например, если мы разделим 63 ÷ 9, мы получаем ответ как 7. Здесь 7 называется частным. Следует отметить, что частное может быть больше или меньше делителя, но всегда меньше делимого.

Как найти частное при делении?

Частное получается после завершения процесса деления. Это означает, что когда делитель делит делимое, ответ, который мы получаем, является частным. Другими словами, частное можно найти по формуле Дивиденд ÷ Делитель = Частное. Поясним это на простом примере 12 : 4 = 3. Здесь 12 — делимое, 4 — делитель, а 3 — частное.

Всегда ли частное является целым числом?

Нет, частное не всегда может быть целым числом. Частное может быть целым или десятичным числом. Для совершенного деления, такого как 16 ÷ 2 = 8, частное представляет собой целое число, а для чисел, в которых у нас остался остаток, мы делим число дальше, помещая десятичную дробь в частное. Следовательно, в этих случаях частное становится десятичным числом. Например, если мы разделим 16 ÷ 5, мы получим 3,2 как частное, которое является десятичным числом.

В чем разница между частным и остатком?

Частное — это ответ, который мы получаем при делении числа. Число, оставшееся после окончания деления, называется остатком. Это относится к оставшейся части после завершения процесса деления. Например, если нам нужно распределить 7 мячей между 2 детьми поровну, мы даем каждому ребенку по 3 мяча и у нас остается 1 мяч. Этот 1 шар является остатком. Математически число 7 нельзя полностью разделить на число 2. После деления в остатке остается число 1. Для совершенных делений частное равно целому числу, а остаток равен нулю.

Как проверить частное при делении?

Деление также известно как обратное умножение. Мы можем проверить частное, используя следующую формулу:

Делимое = (Делитель × Частное) + Остаток

Это означает, что если мы умножим делитель на частное и добавим остаток, мы должны получить число как делимое. Если числа удовлетворяют этому уравнению, то ответ считается правильным, в противном случае нужно проверить наше деление.

Как найти частное, если известны остаток и делитель?

Если известны остаток, делитель и делимое, мы можем легко найти частное, подставив значения в формулу Делимое = (Делитель × Частное) + Остаток. После подстановки известных значений мы можем получить значение частного.

Чему равно частное 21 при делении на 7?

При делении 21 на 7 в частном получается 3. Число 21 является делимым, число 7 — делителем, а 3 — частным.

В чем разница между частным и произведением?

«Частное» — это результат деления, а «произведение» — это результат умножения. Частное меньше делимого и делителя. Произведение больше, чем числа, которые умножаются.

Скачать БЕСПЛАТНО учебные материалы

Рабочие листы по частному

Базовая математика | Раздел Объяснение

Поиск по моему сайту:

Поделись этой страницей!

Деление как повторное вычитание

Деление — это действие, обратное умножению.

При умножении мы хотим узнать сумму групп чисел .

В приведенном ниже примере мы хотим узнать общее количество 4 группы по 8 .

При делении мы хотим разделить сумму на несколько групп и узнать, сколько человек в каждой группе.

В приведенном ниже примере мы хотим узнать, сколько человек в каждой группе, если мы разделим 72 на 4 равные группы?

(Часть 2) Подробнее о Division

Словарь Division

Division с остатком

Long Division

Посмотрите видео с обзором Division.

Деление также можно объяснить следующим образом: мы хотим разделить сумму на группы определенного числа и хотим знать, сколько существует групп.

В приведенном ниже примере мы хотим узнать, сколько групп по 4 можно получить из 36?

Распечатайте и вырежьте эти карточки.

Содержание

Разделить на равные группы

Вот как вы научите своего ребенка делить число на равные группы.

Разделим 12 на 3 равные группы. Сколько в каждой группе?

Дайте ребенку 12 фишек (для иллюстрации я буду использовать морские ракушки) и разделите их следующим образом:

1. Начните с 12.

(Выстраивать их не обязательно.)

2. Возьмите одну часть и отложите ее в сторону.

3. Возьмите еще один кусок и положите его во вторую стопку.

4. Возьмите следующий кусок и положите его в третью стопку.

Теперь у нас есть 3 стопки или группы.

5. Положите четвертую часть обратно в первую стопку.

Продолжайте помещать по фишке в каждую группу, пока не будут израсходованы все 12 жетонов.

В итоге у вас будет 4 жетона в каждой группе, поэтому 12 разделить на 3 равно 4.

Запишите это так: 12 ÷ 3 = 4

Содержание

Разделить число на группы

Вот еще один способ разделения.

Разделите 12 на группы по 3 человека. Сколько групп я получу? Другими словами, сколько троек входит в число 12?

Дайте ребенку 12 фишек и разделите их следующим образом:

1. Начните с 12.

2. Сгруппируйте их по три.

Вы получите 4 группы.

Опять же, 12 разделить на 3 равно 4. Или 4 группы по 3 составляют 12.

Запишите это так: 12 ÷ 3 = 4

Деление как многократное вычитание

Другой способ думать о делении — это многократное вычитание.

Например, 12 ÷ 4 означает, сколько раз можно вычесть 4 из 12?

Сводка

Подробнее о делении

Словарь деления

Деление с остатком

Длинное деление

Общие множители0242 Игра на деление

Вот несколько карточек с заданиями на деление, в которые можно поиграть с ребенком. Распечатайте и вырежьте эти карточки. Держите под рукой набор жетонов, которыми может пользоваться ваш ребенок.

Перемешайте карты и положите их стопкой лицевой стороной вниз в центре стола.
Откройте верхнюю карту. Каждый пишет свою работу. Затем по очереди объясните, как они получили ответ.