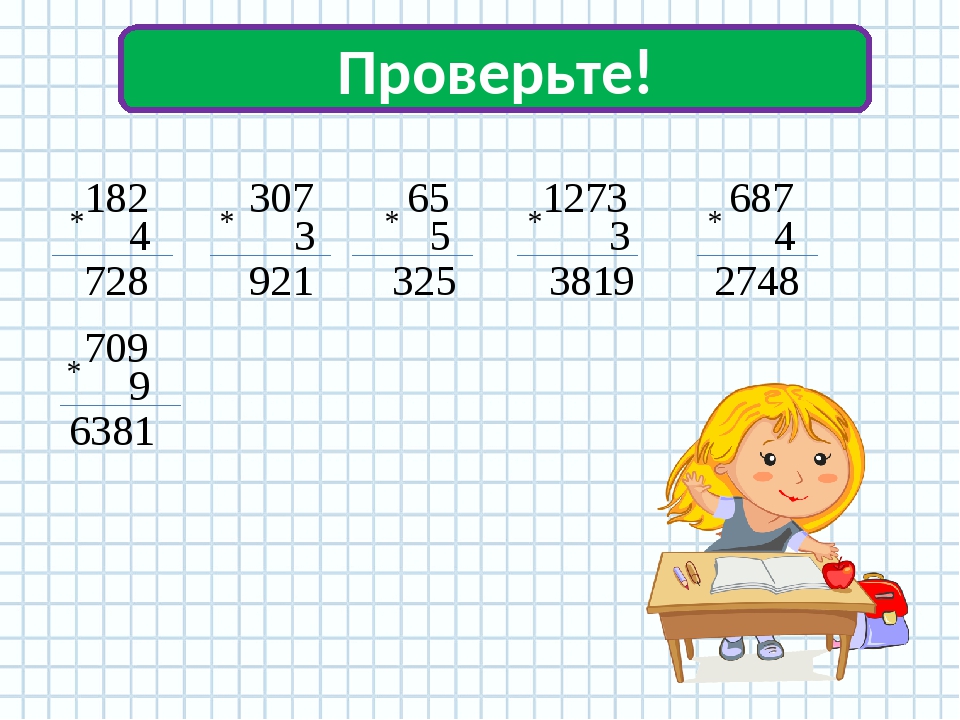
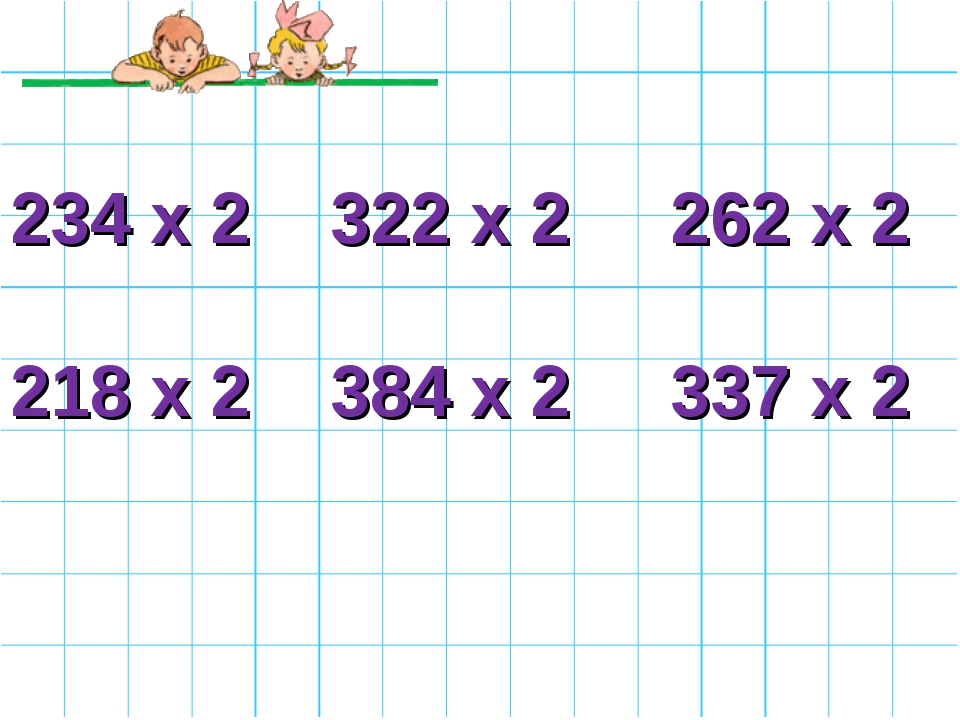Умножение в столбик Арифметика
Привет, мой друг, тебе интересно узнать все про умножение в столбик, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое умножение в столбик , настоятельно рекомендую прочитать все из категории Арифметика
Решим пример:
- Запишем числа столбиком (одно под другим). В верхней строчке — большее число , в нижней — меньшее.
Самая правая цифра (знак) верхнего числа должна стоять над самой правой цифрой нижнего числа. Сбоку между числами ставим знак действия. У нас это «×» (знак умножения). умножение в столбик » />
- Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа . Об этом говорит сайт https://intellect.icu . Результат записывается под чертой под самой правой цифрой.
Умножаем число сверху по цифре (знаку) справа налево. 7 · 6 = 42. У нас получилось число большее или равное 10.
Поэтому под черту идет только последняя цифра результата.

- Умножаем 2 на 6. 2 · 6 = 12. Не забудем, что над 2 стоит 4. Это значит, что к результату умножения (произведению) надо прибавить 4. 12 + 4 = 16.
6 записываем под чертой и 1 записываем над 4.
- Умножаем 4 на 6. 4 · 6 = 24. К произведению добавляем 1. 24 + 1 = 25.
- Переходим к умножению числа 427 на 3. Умножаем по тем же правилам, что и на 6.
Результат умножения на вторую цифру необходимо записывать под второйцифрой результата первого действия умножения.
- Полученные числа под чертой складываем по правилам сложения в столбик.
Теперь освоив умножение столбиком, вы сможете перемножать сколь угодно большие числа.
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про умножение в столбик Надеюсь, что теперь ты понял что такое умножение в столбик
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу.
Умножение столбиком — Играем и учимся сами
Онлайн игра-тренажёр «Умножение столбиком» помогает научиться умножать двух- и трёхзначные числа. Эта игра ориентирована на детей от 7 до 10 лет. Умножение чисел столбиком — это программа математики за 3 класс школы. Но в этом действии нет ничего сложного, поэтому освоить умножение в столбик можно и раньше.
Как научиться умножать столбиком?
В игре представлены три уровня: умножение двузначного числа на двузначное (числа от 10 до 99), умножение трёхзначного числа на трёхзначное (числа от 100 до 999) и микс. В миксе трёхзначное число умножается на двузначное или двузначное умножается на трёхзначное.
Чтобы правильно умножать двух- и трёхзначные числа надо хорошо знать сложение чисел и таблицу умножения.
Надеюсь, ты помнишь, что числа, которые умножаются друг на друга называются множителями: первый множитель, второй множитель и так далее. Результат умножения называется произведением. Также полагаю, что тебе известно, что в числах есть разряды: единицы (самый маленький), десятки, сотни, тысячи…
Итак, приступим. Начать умножение в столбик надо с того, что расположить множители таким образом, чтобы друг под другом оказались числа одинаковых разрядов: единицы под единицами, десятки под десятками и так далее. На следующем шаге берём цифру из разряда единиц второго множителя и умножаем её по очереди на каждую цифру первого множителя. Результат умножения каждой пары цифр записываем в верхнюю строку под соответствующим разрядом.
За каждый правильный ответ начисляется 1 балл. За неправильный — отнимается 3 балла.
Если тебе понравилась эта игра, обязательно поделись ею со своими друзьями. Ведь им она тоже может понравиться:-)
Эта игра предназначена и чрезвычайно полезна для мальчиков и девочек от 7 до 10 лет.
Создатель сайта будет благодарен Вам, если оцените данную игру. (Это можно сделать вверху страницы.) Ну а Вашим комментариям будет рад вдвойне:-)
Урок 38. письменные приёмы умножения вида 243 ∙ 20, 532 ∙ 300 — Математика — 4 класс
Математика, 4 класс
Урок № 38. Письменные приемы умножения вида 243 · 20, 552 · 300
Перечень вопросов, рассматриваемых в теме:
— как письменно умножать и делить на числа, оканчивающиеся нулями?
— какой алгоритм письменного умножения и деления на числа, оканчивающиеся нулями?
Глоссарий по теме:
Алгоритм — последовательность действия (шагов)
Умножение — действие, при котором одно число повторяется столько раз, сколько в другом содержится единиц, и находится сумма этих слагаемых.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2015. – с.13.
и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2015. – с.13.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.10-12.
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.60.
Теоретический материал для самостоятельного изучения
Вспомним устные приемы умножения на круглое число.
18 ∙ 20Заменили число двадцать произведением чисел два и десять. Число двадцать заменили произведением удобных множителей, так как легко умножать на десять.
20 = 2 ∙ 10
Получили выражение: восемнадцать умножить на произведение двух и десяти. Удобнее сначала восемнадцать умножить на два, и полученный результат тридцать шесть умножить на десять, получится триста шестьдесят.
18 ∙ (2 ∙ 10) = 18 ∙ 2 ∙ 10 = 36 ∙ 10 = 360
Рассмотрим еще одно выражение:
154 ∙ 200
Заменили число двести произведением чисел два и сто. Число двести заменили произведением удобных множителей, так как легко умножать на сто.
Число двести заменили произведением удобных множителей, так как легко умножать на сто.
200 = 2 ∙ 100
Получили выражение: сто пятьдесят четыре умножить на произведение двух и ста. Удобнее сначала сто пятьдесят четыре умножить на два, и полученный результат триста восемь умножить на сто, получится тридцать тысяч восемьсот.
154 ∙ 200 = 154 ∙ (2 ∙ 100) = 154 ∙ 2 ∙ 100 = 30 800
Устно выполнить подобные вычисления бывает трудно, поэтому предлагается записать в столбик, то есть использовать письменные приемы вычислений.
Познакомимся с алгоритмом умножения на числа, оканчивающиеся нулями
Решим письменно выражение двести сорок три умножить на двадцать
243 ∙ 20
Вы уже умеете выполнять в столбик умножение числа двести сорок три на два. Умножаем единицы: три умножить на два, получилось шесть. Умножаем десятки: четыре умножаем на два, получилось восемь. Умножаем сотни: два на два, получилось четыре. Читаем результат: четыреста восемьдесят шесть.
А как умножить двести сорок три на двадцать?
Надо представить множитель двадцать в виде произведения чисел два и десять.
243 ∙ 20 = 243 ∙ (2 ∙ 10)
Произведение чисел двести сорок три и два мы уже вычислили в столбик.
Посмотрим, как нужно изменить эту запись, чтобы получилось умножение числа двести сорок три на на два, а на двадцать.Дописываем ноль после цифры два, а также в записи результата умножения на два. В результате получилось число четыре тысячи восемьсот шестьдесят.
Обратите внимание, что цифра ноль, обозначающая количество единиц в числе двадцать, смещена вправо. Она не записывается под цифрой три, обозначающей количество единиц в первом множителе. На первом этапе на этот ноль можно не обращать внимание, но на втором этапе, когда получен результат умножения числа двести сорок три на два, надо приписать к результату столько нулей, сколько их было у второго множителя. В нашем случае один ноль.
Рассмотрим еще один пример: пятьсот тридцать два умножить на триста.
532 ∙ 300
Представим множитель триста в виде произведения чисел три и сто.
532 ∙ 300 = 532 ∙ (3 ∙ 100)
Умножим в столбик число пятьсот тридцать два на три. Умножаем единицы: два умножить на три получилось шесть. Умножаем десятки: три умножаем на три, получилось девять.
Умножаем сотни: пять умножить на три — получилось пятнадцать. Читаем результат: одна тысяча пятьсот девяносто шесть.
Но мы умножаем не на три, а на триста, поэтому дописываем два ноля после цифры три, а также в записи результата умножения на три. В результате получилось число сто пятьдесят девять тысяч шестьсот.
Задания тренировочного модуля:
1. Запишите столбиком и найдите значения выражений
588 ∙ 70 647 ∙ 300
Правильный ответ: 41160, 194100.
2. Выберите знак «∙» или «:» так, чтобы равенства стали верными.
220….4 = 880
100…4 = 400
450…3 = 150
770…10 = 77
25…10 = 250
640…2 = 320
Правильный вариант:
220 ∙ 4 = 880
100 ∙ 4 = 400
450 : 3 = 150
770 : 10 = 77
25 ∙ 10 = 250
640 : 2 = 320
|
|
|
|
| Устный счёт (повторяем таблицу умножения):
I — вариант: 2х8 7х3 5х8 3х9 5х5 2х6 8х4 5х3 6х9 9х9 (16, 21, 40, 27, 25, 12, 32, 15, 54, 81) |
Вычисляют |
|
| — Вы повторили таблицу умножения. А теперь посмотрите на следующее задание, здесь тоже умножаются числа. Кто вспомнит, как они называются? (Круглые). 32х10=320 20х3=60 4х100=400 40х3=120 10х72=720 30х5=150 — Давайте с вами вспомним, как нужно умножать круглые числа? Выполняется устно. |
|
|
| — На следующем слайде вы видите выражения. Посмотрите внимательно и распределите их в два столбика. 42х3 5х3 16х4 8х9 7х2 27х5 35х6 6х4 42х3 5х3 16х4 8х9 27х5 7х2 35х6 6х4 — Чем похожи и чем отличаются данные выражения? (Все примеры на нахождение произведения.
— Молодцы! Но это только первая часть нашей темы. О второй части мы поговорим позже. — Чтобы решить примеры первого столбика нам достаточно знать таблицу умножения. А как же решать примеры второго столбика? — Какой способ решения вы предложите? (Чтобы умножить двузначное число на однозначное, нужно представить число в виде суммы разрядных слагаемых. Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и полученные результаты сложить). Решение примеров в тетради, по алгоритму, несколько учеников у доски. 42х3=126 16х4=64 27х5=135 35х6=210 — Все очень хорошо справились с заданием. |
Тема урока: Умножение двузначных чисел. | |
| — Удобен ли приём вычисления, разобранный нами в предыдущем случае? — Как мы складывали многозначные числа, если у нас возникали трудности, сложения их в строчку? — Можно ли умножить двузначные числа по другому? Как вы думаете, какой приём можно использовать? — Совершенно верно. Сегодня на уроке нам и предстоит поработать над этим приёмом. — Вот мы и подошли ко второй части темы нашего урока. Итак, какую цель мы поставим перед собой? |
Письменный приём, решение столбиком
цель нашего урока: отработка письменного приёма умножения на двузначное число |
|
|
| План урока: 1.Открыть алгоритм письменного умножения двузначного числа на однозначное. 2.Поупражняться в умножении двузначного числа на однозначное 3.Учиться самостоятельно применять алгоритм письменного умножения двузначного числа на однозначное 4. Оценка. |
|
| — Давайте с вами попробуем с вами открыть алгоритм письменного умножения 14х6=84 — Как мы будем записывать числа в столбик? (Единицы под единицами, десятки под десятками). — Начинаем умножать с разряда единиц. Запишем первое неполное произведение, единицы под единицами, десятки под десятками. Затем умножим на число десятков. Получим второе неполное произведение и начнем запись под десятками. Сложим неполные произведения и прочитаем ответ. (Выполнили 1 задачу). 43х4=172 35х2=70 Скажите, мы справились со второй задачей? Поднимите руку кто освоил алгоритм вычисления столбиком? Кому еще нужна помощь? А кто может объяснить другому? |
|
|
|
Оценка. |
Оценка своих действий по критерию — умножение двузначного числа на однозначное число. |
|
|
|
|
|
Как умножают в столбик в разных странах
Начало тут
Рабочая тетрадь по-индийски
Если присмотреться — понятно, что в клеточках тот же наш столбик,
только то, что у нас «в уме» — записывается рядом, через косую черту. Не запутаешься.
Не запутаешься.
В примере справа аналогия еще более очевидна,
кст израильские школьники умножают именно так —
строчки в обратно порядке по сравнению с нашим способом
(и то что «в уме» тоже записывают явно, дополнительной строкой).
Индийская система — похоже, что самая удобная,
в итоговой табличке между косыми направляющими числа группируются по разрядам и
удобно складываются все разом — десятки с десятками, сотни с сотнями,
ничего не потеряется при переходе через разряд.
Латиноамериканское умножение на тот же манер
В чертеже справа, развернутом на уголок, просматривается определенное сходство с
японо-китайской системой из предыдущего поста:
Как вообще получается, что счет на пересекающихся линиях дает верный результат?
Умножим 34 х 25 по-китайски и обычным способом(только запишем промежуточный результат
по-индийски, то что должно быть «в уме» — через косую черту)
Из сопоставления примеров можно убедиться,
что метод «на палочках» — не какой-то магический трюк, а графическое представление
того же поразрядого умножения в столбик.
(Это по поводу вчерашнего — на «Малышах» разместила «2х2 по-китайски»,
там частью даже перепугались — что, дескать, за фокус, как можно такое давать детям =)
АПД
Видео, где как раз раскрыт момент перехода к использованию таблицы умножения —
субтитры на разных языках
скептики сомневаются, работает ли метод кроме как в приделах первых трех-четырех десятков,
дескать попробуйте 72 на 89 умножить —
китаянка уверенной рукой чертит пучок линеек, и точечки — тюк-тюк-тюк,
по ходу рассказывает, что как раз тут-то детям и предлагают не пересчитывать,
а воспользоваться табличным значением для 8х7 и тд:
восемь рядов по семь, семь столбцов по девять.
Офф — помню еще когда в бухгалтериях пользовались счетами. Была одна дама — умножала на костяшках с пулеметной скоростью, туда-сюда, щелк-щелк.
так что и китайцам не удивляюсь, наловчились и считают, быстрей, чем мы в столбик.
А еще мимоходом нашлось удивительное —
древние майя пользовались такой же схемой умножения,
как современные китайцы в начальной школе:
http://www. taringa.net
taringa.net
| № п/п | Этап урока |
Деятельность учителя |
Деятельность обучающихся |
Формируемые УУД |
||||||||||||||||||
| 1 | Мотивация к учебной деятельности | Долгожданный дан звонок, Начинается урок. Тут затеи и задачи, Игры, шутки, – Всё для вас! Пожелаю вам удачи– За работу, в добрый час! |
Настраиваются на урок. | Интерес к уроку, самооценка своих возможностей |
||||||||||||||||||
| 2 | Актуализация и фиксирование индивидуального затруднения в пробном учебном действии | – Перед вами ребус, какое слово
зашифровано?
– Давайте вспомним правило умножения на
0 и 1. Демонстрация на интерактивной доске таблицы Урок 4 (6) учебное пособие «Наглядная школа» |
(Умножение)
Дети читают правила умножения на 1 и 0. |
Познавательные УУД: работа с информацией | ||||||||||||||||||
| 3 | Постановка учебной задачи | – Как вы считаете, чем мы будем
заниматься на уроке? – Какие знания для этого нам пригодятся в первую очередь? – Вот и давайте-ка повторим табличное умножение ещё раз. Устный счёт( табличное умножение карточки-«сорбонки»: (учитель показывает карточку) – Полученные ответы представьте в виде суммы разрядных слагаемых – Назовите слагаемое, которое показывает
десятки в каждой сумме, как мы называем такие
числа? |
Читают тему урока в учебнике. Таблица умножения. В строчку записывают ответы:
Работа в парах: 1 ученик выписывает чётные
числа, 2 ученик –нечётные.
Умеем. Работа в парах. |
Регулятивные УУД:
целеполагание– постановка ученой задачи на
основе соотнесение того, что уже известно
учащимся, и того, что еще неизвестно.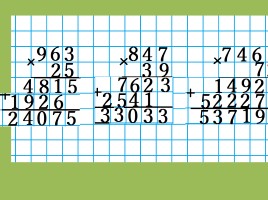
Коммуникативные УУД: |
||||||||||||||||||
| 4 | Проблемная ситуация ЭОР 1 23 умножить на 4 (анимация) http://files.school-collection.edu.ru/dlrstore/26e87d9e-5e10-486e-ac8c-35805c4d1cdc/ResFile.SWF (Приложение 1) |
Игра «Математические гонки». – Решение какого примера вызвало затруднение? – Почему? – Давайте вспомним, как можно решить такой пример |
У каждой пары на столе карточки с
заданием. Какая пара быстрее выполнит задание и
запишет свои ответы?
В таблице нет такого случая Дети слушают и записывают в тетрадь. |
Познавательные УУД: формулирование проблемы Познавательные УУД:Логические УУД: анализ объекта с выделением существенных признаков. Построение логической цепи рассуждения. Выдвижение гипотез. |
||||||||||||||||||
| 5 | Открытие нового знания ЭОР 2 Рождение алгоритма умножения http://files.school-collection.edu.ru/dlrstore/7583fbdb-0064-4f9c-9440-10118e3b6f04/ResFile.SWF (Приложение 1) |
– Можно выполнить умножение ещё
одним способом (письменно) Давайте на примере
разберём, как нужно выполнить умножение
многозначных чисел на однозначное. |
Дети слушают и записывают в тетрадь. | Познавательные УУД | ||||||||||||||||||
| 6 | Физминутка для глаз | 1. Быстро поморгать, закрыть глаза
и посидеть спокойно, медленно считая до 5.
Повторять 4-5 раз. 2. Крепко зажмурить глаза (считать до 3, открыть их и посмотреть вдаль (считать до 5). Повторять 4-5 раз. 3. Вытянуть правую руку вперед. Следить глазами, не поворачивая головы, за медленными движениями указательного пальца вытянутой руки влево и вправо, вверх и вниз. Повторять 4-5 раз. |
Дети выполняют движения | |||||||||||||||||||
| 7 | Построение проекта выхода из затруднений | Построение алгоритма
действия умножения в столбик. 157 ?3 157 ?3– Какие действия нужно совершить, что бы вычислить произведение в столбик? 1. Прочитать
выражение. |
Проговаривают алгоритм умножения. | Коммуникативные УУД: планирование учебного сотрудничества со сверстниками. Умение с достаточной полнотой и точностью выражать свои мысли. Познавательные УУД: Построение логической цепи рассуждения. |
||||||||||||||||||
| 8 | Реализация построенного проекта | Решите примеры с объяснением. | Выполняют умножение столбиком у
доски с объяснением.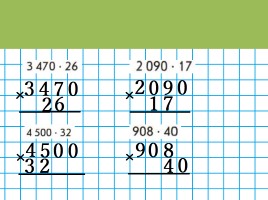 |
Коммуникативные УУД: Умение с достаточной полнотой и точность выражать свои мысли | ||||||||||||||||||
| 9 | Физ.минутка | Если я показываю 1-х значное число, вы 1 раз подпрыгиваете на месте. 2-х значное –2 раза прогибаетесь назад. 3-хзначное –3 раза наклоняетесь вперед. | Выполняют упражнения | |||||||||||||||||||
| 10 | Самостоятельная работа Дифференцированное письменное решение задачи – с проверкой у доски. Стр. 69 №6. Дети самостоятельно выбирают задание. |
1 уровень – Заполни таблицу и
реши задачу. (Таблица на карточках)
1-й уровень – реши задачу и запиши
решение выражением. 2-й уровень – измени вопрос задачи так, что бы она решалась сложением. |
1 Уровень.
1) 65 х 7 = 455км – пролетели журавли 513 – 455 = 58 км Ответ: гуси пролетели больше на 58 км. 2 Уровень. 57 х 9 – 65 х 7 = 58 км 3 Уровень. Что бы задача решалась сложением, нужно
изменить вопрос задачи. В задаче нужно найти
какое расстояние всего пролетели птицы. 1) 65 х 7 = 455 км – пролетели журавли Ответ: 968 км пролетели птицы. |
Общеучебные УУД: Моделирование таблицы, Умение решать задачи разными способами. Регулятивные
УУД: Познавательные УУД:Анализ, синтез |
||||||||||||||||||
| Проверка | Учитель фиксирует , кто неправильно решил задачу. | 1 уровень – проверяют ответ. 2 уровень – записывают выражение на доске. 3 уровень – читают составленный вопрос к задаче и называют ответ. |
Регулятивные УУД: Контроль, коррекция и оценка |
|||||||||||||||||||
| 11 | Домашнее задание | № 4 задача, записать решение по
выбору: 1 – по действиям, 2 – выражением. № 5 объясни вычисления и закончи. |
Дети читают задачу и задают вопросы по содержанию, если возникнут. | Познавательные УУД: Общеучебные УУД Структурирование знаний |
||||||||||||||||||
| 12 | Рефлексия учебной деятельности | Что нового вы узнали на уроке? Что вам еще было бы интересно узнать? За что вы можете себя похвалить на этом уроке? |
Как записать умножение в столбик. Алгоритм письменного умножения. Научились умножать двузначное число на однозначное. Дети высказывают своё мнение |
Регулятивные УУД: оценка |
Умножение в столбик worksheet
Advanced searchContent:
Language: AfarAbkhazAvestanAfrikaansAkanAmharicAragoneseArabicAssameseAsturianuAvaricAymaraAzerbaijaniBashkirBelarusianBulgarianBihariBislamaBambaraBengali, BanglaTibetan Standard, Tibetan, CentralBretonBosnianCatalanChechenChamorroCorsicanCreeCzechOld Church Slavonic, Church Slavonic,Old BulgarianChuvashWelshDanishGermanDivehi, Dhivehi, MaldivianDzongkhaEweGreek (modern)EnglishEsperantoSpanishEstonianBasquePersian (Farsi)Fula, Fulah, Pulaar, PularFinnishFijianFaroeseFrenchWestern FrisianIrishScottish Gaelic, GaelicGalicianGuaraníGujaratiManxHausaHebrew (modern)HindiHiri MotuCroatianHaitian, Haitian CreoleHungarianArmenianHereroInterlinguaIndonesianInterlingueIgboNuosuInupiaqIdoIcelandicItalianInuktitutJapaneseJavaneseGeorgianKongoKikuyu, GikuyuKwanyama, KuanyamaKazakhKalaallisut, GreenlandicKhmerKannadaKoreanKanuriKashmiriKurdishKomiCornishKyrgyzLatinLuxembourgish, LetzeburgeschGandaLimburgish, Limburgan, LimburgerLingalaLaoLithuanianLuba-KatangaLatvianMalagasyMarshalleseMāoriMacedonianMalayalamMongolianMarathi (Marāṭhī)MalayMalteseBurmeseNauruanNorwegian BokmålNorthern NdebeleNepaliNdongaDutchNorwegian NynorskNorwegianSouthern NdebeleNavajo, NavahoChichewa, Chewa, NyanjaOccitanOjibwe, OjibwaOromoOriyaOssetian, OsseticEastern Punjabi, Eastern PanjabiPāliPolishPashto, PushtoPortugueseQuechuaRomanshKirundiRomanianRussianKinyarwandaSanskrit (Saṁskṛta)SardinianSindhiNorthern SamiSangoSinhalese, SinhalaSlovakSloveneSamoanShonaSomaliAlbanianSerbianSwatiSouthern SothoSundaneseSwedishSwahiliTamilTeluguTajikThaiTigrinyaTurkmenTagalogTswanaTonga (Tonga Islands)TurkishTsongaTatarTwiTahitianUyghurUkrainianUrduUzbekValencianVendaVietnameseVolapükWalloonWolofXhosaYiddishYorubaZhuang, ChuangChineseZulu Subject:
Grade/level: Age: 3456789101112131415161718+
Search: All worksheetsOnly my followed usersOnly my favourite worksheetsOnly my own worksheets
Умножение методом столбцов— определение, примеры
Вас не смущает умножение методом столбцов? вы попали на нужную страницу, где получите полную информацию об умножении методом столбцов. Это включает определение умножения метода столбца, шаги, чтобы следовать умножению метода столбца. Вы также можете найти примеры умножения методом столбцов, полностью прочитав эту статью.
Это включает определение умножения метода столбца, шаги, чтобы следовать умножению метода столбца. Вы также можете найти примеры умножения методом столбцов, полностью прочитав эту статью.
Обратитесь: метод расширения умножения
Умножение методом столбца | Длинное умножение
При умножении методом столбца одно число пишется под другим числом, и числа умножаются вместе.Это также называется умножением методом длинного метода.
Например 3 5
* 2 5
——–——–——–
8 7 5
——–——–——–
Метод столбца Умножение 3-х цифр на 2-х разряды
Шаги, которые необходимо выполнить для метода столбца умножения трехзначного числа на двузначное число, следующие:
- Умножьте одну цифру числа на одну цифру множителя.
- Умножьте цифру десятков числа на одну цифру числа.
- Умножьте сотую цифру числа на одну цифру множителя.
- Умножьте единицу числа на цифру десятков множителя.
- Умножьте цифру десятков числа на цифру десятков числа.

- Умножьте сотую цифру числа на десятки множителя.
- Добавьте товары.
Та же процедура должна выполняться для умножения двузначного числа на двузначное число.
Примеры умножения методом столбцов
Пример 1:
Умножьте 53, 23 на умножение методом столбца.
Решение:
1. Умножьте множимое на единицу множителя.
5 3
* 3 шт.
——–——–—
1 5 9
——–——–—
2. Умножьте множимое на разряд десятков множителя.
5 3
* 2тенс
——–——–——–
1 0 6
——–——–——–
3.Добавьте продукты.
159 единиц + 106 десятков
= 159 * 1 + 106 * 10
= 159 + 1060
= 1219.
Произведение 53,23 равно 1,219.
Значит 5 3
* 2 3
——–——–——––—–
1 5 9 —-> 53 * 3 = 159
1 0 6 0 —-> 53 * 20 = 1060
1
——–——–——–——–——–
1 2 1 9 ——> 53 * 23 = 1219
——–——–——–——–——–
Пример 2:
Найти умножение 455,32 методом умножения по столбцам?
Решение:
1. Умножьте множимое на единицу множителя.
Умножьте множимое на единицу множителя.
4 5 5
* 2 единицы
——–——–——––—–
9 1 0
——–——–——––—–
2. Умножьте множимое на разряд десятков множителя.
4 5 5
* 3tens
——–——–——––—–
1 3 6 5
——–——–——––—–
3. Добавьте товары.
910 шт. + 1365тенс
= 910 * 1 + 1365 * 10
= 910 + 13650
= 14560.
Умножение 455,32 дает 14560.
Значит
4 5 5
* 3 2
——–——–——–
9 1 0 —-> 455 * 2 = 910
1 3 6 5 0 —–> 455 * 30 = 13650
1
——–——–——––—–
1 4 5 6 0 —–> 455 * 32 = 14560
——–——–——–——–——–
Пример 3:
Найдите произведение 1234,34 по столбцу Умножение.
Решение:
1. Умножьте множимое на единицу множителя.
1 2 3 4
* 4 шт.
——–——–——––—–
4 9 3 6
——–——–——––—–
2. Умножьте множимое на разряд десятков множителя.
Умножьте множимое на разряд десятков множителя.
1 2 3 4
* 3 десятка
——–——–——––—–
3 7 0 2
——–——–——––—–
3. Добавьте товары.
1234 * 4ones + 1234 * 3tens
= 1234 * 4 + 1234 * 30
= 4936 + 37020
= 41 956.
Аналогичным образом мы можем произвести умножение четырехзначного числа, умножение пятизначного числа на двузначные числа.
Метод столбцов Умножение 4-значного числа на 2-значное Примеры
Пример 1:
Найти произведение умножения 34251,62 методом столбца умножения?
Решение:
1. Умножьте множимое на одну цифру множителя.
3 4 2 5 1
* 2
——–——–——––—–
6 8 5 0 2
——–——–——––—–
2.Умножьте множимое на цифру десятков множителя.
3 4 2 5 1
* 6 десятков
——–——–——––—–
2, 0 5, 5 0 6
——–——–——–——–——–
3. Добавьте товары.
Добавьте товары.
3425 * 2 единицы + 3425 * 6 десятков
= 3425 * 2 + 3425 * 60
= 68502 + 2055060
= 2 123 562.
Умножение числового столбца на такое же число
Предположим, вы хотите умножить числовой столбец на такое же число в другой ячейке.Уловка умножения столбца чисел на одно число заключается в добавлении символов $ к адресу ячейки этого числа в формуле перед копированием формулы.
В нашем примере таблицы ниже мы хотим умножить все числа в столбце A на число 3 в ячейке C2. Формула = A2 * C2 даст правильный результат (4500) в ячейке B2. Но копирование формулы в столбец B не сработает, потому что ссылка на ячейку C2 изменится на C3, C4 и т. Д. Поскольку в этих ячейках нет данных, результат в ячейках с B3 по B6 будет нулевым.
Чтобы умножить все числа в столбце A на ячейку C2, добавьте символы $ к ссылке на ячейку следующим образом: $ C $ 2 , что вы можете увидеть в примере ниже.
Использование символов $ сообщает Excel, что ссылка на C2 является «абсолютной», поэтому при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Для создания формулы:
В ячейке B2 введите знак равенства (=).
Щелкните ячейку A2, чтобы ввести ячейку в формулу.
Введите звездочку (*).
Щелкните ячейку C2, чтобы ввести ячейку в формулу.
Теперь введите символ $ перед C и символ $ перед 2: $ C $ 2 .
Нажмите Enter.
Совет: Вместо того, чтобы вводить символ $, вы можете поместить точку вставки либо до, либо после ссылки на ячейку, которую вы хотите сделать «абсолютной», и нажать клавишу F4, которая добавляет символы $.
Теперь мы вернемся немного назад, чтобы увидеть простой способ скопировать формулу вниз по столбцу после того, как вы нажмете Enter в ячейке B2.
Выберите ячейку B2.
org/ListItem»>
Дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки.
Формула автоматически копируется до ячейки B6.
После копирования формулы столбец B возвращает правильные ответы.
Умножение матриц— ChiliMath
Умножение матриц — это «беспорядочный тип», потому что вам нужно будет следовать определенному набору процедур, чтобы сделать это правильно. Это «беспорядочный тип», потому что процесс более сложен.Однако позже, пройдя процедуру и несколько примеров, вы поймете, что необходимые шаги можно выполнить. Не волнуйтесь, я помогу вам в этом!
Это «беспорядочный тип», потому что процесс более сложен.Однако позже, пройдя процедуру и несколько примеров, вы поймете, что необходимые шаги можно выполнить. Не волнуйтесь, я помогу вам в этом!
Но сначала мы должны убедиться, что две матрицы «разрешено» умножать вместе. В противном случае данные две матрицы «несовместимы» для умножения. В этом случае мы говорим, что решение не определено.
Умножение матрицы на матрицу, также известное как «Беспорядочный тип»
Всегда помните об этом!
Чтобы умножение матриц работало, количество столбцов левой матрицы ДОЛЖНО РАВНО количеству строк правой матрицы.
Предположим, нам даны матрицы A и B, найдите AB (произведите умножение матриц, если применимо). Определите, какая из них левая и правая матрицы, в зависимости от их расположения. Это очень важный шаг.
Чтобы определить, могу ли я умножить две заданные матрицы, мне нужно обратить внимание на количество столбцов матрицы A и количество строк матрицы B. Если они равны, я могу продолжить умножение матрицы. В противном случае сделаю вывод, что ответ неопределенный!
Если они равны, я могу продолжить умножение матрицы. В противном случае сделаю вывод, что ответ неопределенный!
Поскольку матрица A имеет количество столбцов 2 , а матрица B имеет количество строк 3 , и они не равны (2 ≠ 3), я заключаю, что AB = undefined .Это означает, что их продукт невозможно найти.
Примеры умножения матриц, также известного как «Беспорядочный тип»
Указания : Для следующих матриц выполните указанную операцию.
Пример 1 : Вычислить, если возможно, произведение B и E.
Чтобы матрицы B и E имели произведение, количество столбцов левой матрицы B должно равняться количеству строк правой матрицы E.
количество столбцов = 3
количество строк = 3
В этом случае их можно перемножить.Теперь это шаги:
Шаг 1: Поместите их рядом.
Шаг 2: Умножьте строки B на столбцы E, умножив соответствующие элементы каждой строки на каждый элемент столбца, а затем сложите их вместе.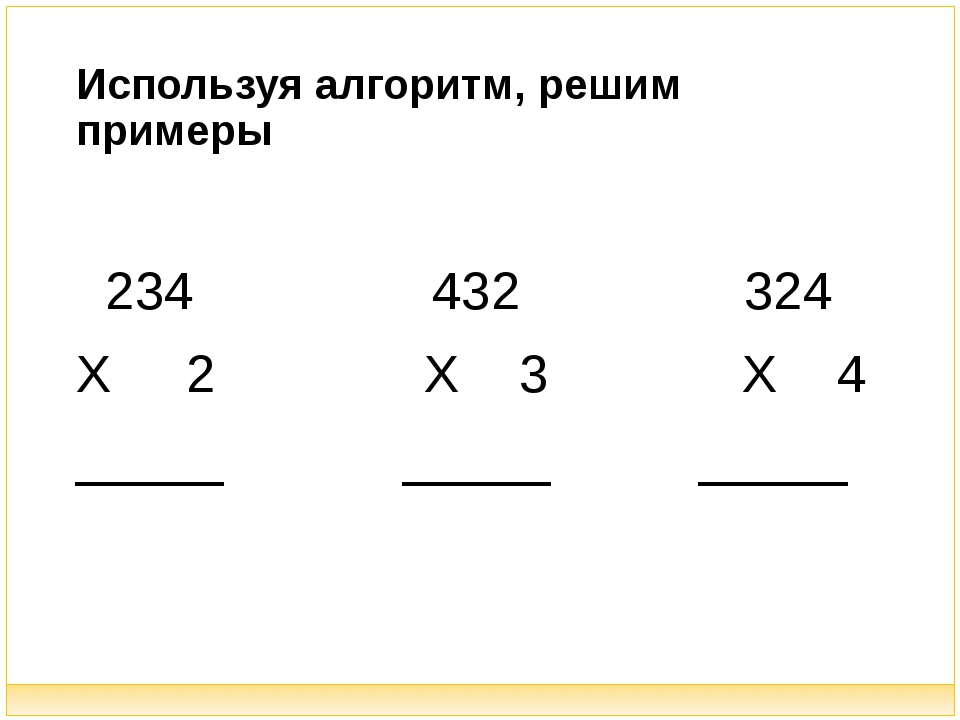
Внимательно посмотрите анимированное решение.
Если у вас нет терпения при просмотре приведенного выше анимированного решения о том, как выполнять матричное умножение, вы можете просмотреть обычное решение, которое я включил ниже.
Пример 2 : Вычислить, если возможно, произведение E и F.
Сначала проверьте, существует ли произведение двух матриц, убедившись, что количество столбцов левой матрицы E равно количеству строк правой матрицы F.
количество столбцов = 2
количество строк = 2
Это замечательно, поскольку количество столбцов матрицы E равно количеству строк матрицы F. Это означает, что произведение EF определено, поэтому мы можем продолжить и выполнить умножение матриц.См. Ниже анимированное пошаговое решение умножения матриц.
Пример 3 : Рассчитайте, если возможно, произведение F и E.
В нашем предыдущем примере мы успешно получили продукт EF. На этот раз мы хотим выяснить, сможем ли мы найти произведение E [латекс] и [латекс] F в указанном порядке.
Напомню, что действительные числа коммутативны при операции умножения, что означает, что порядок умножения не влияет на конечный результат.Например …
Таким образом, возникает большой вопрос, работает ли это также при умножении матриц?
Проверим, равно ли количество столбцов матрицы F количеству строк матрицы E.
количество столбцов = 2
количество строк = 3
Очевидно, что количество столбцов Matrix F не равно количеству строк Matrix E. Подразумевается, что произведение FE не может быть вычислено, поэтому оно не определено!
В общем случае умножение матриц не коммутативно.
Пример 4 : Рассчитайте, если возможно, произведение AE.
Стандартный способ описать размер или размерность матрицы — это . ..
..
(указать количество строк) x (указать количество столбцов)
… читается как «количество строк по количеству столбцов».
3 x 3 (матрица три на три)
3 x 2 (матрица три на два)
Поскольку количество столбцов матрицы A равно количеству строк матрицы E , мы заключаем, что произведение AE определено.
Давайте разберемся. См. Анимированное решение ниже.
Пример 5 : Рассчитайте, если возможно, произведение E и A.
3 x 2 (матрица три на два)
3 x 3 (матрица три на три)
Очевидно, что количество столбцов матрицы E не равно количеству столбцов матрицы A. Следовательно, произведение EA не может быть вычислено или не определено.
Пример 6 : Рассчитайте, если возможно, произведение D и F.2}. Другими словами, мы возводим в квадрат матрицу C.
Здесь нужно проявлять осторожность. Обратите внимание, что возвести в квадрат можно только квадратную матрицу. Напомним, квадратная матрица — это матрица, в которой номер строки равен номеру столбца.
Я предоставлю вам возможность проверить правильность приведенного ниже решения. Такие математические задачи, как эта, хотя и утомительны, я всегда рекомендую решать их вручную, используя карандаш и бумагу.
Практика с рабочими листами
Возможно, вас заинтересует:
Сложение и вычитание матриц
Скалярное умножение
Как умножить два столбца в SQL
База данных:
Операторы:
Умножение двух столбцов, СОЕДИНЕНИЕ, псевдонимЗадача:
хочет умножить значения из двух столбцов таблицы.
Пример:
В нашей базе данных есть таблица с именем покупка с данными в следующих столбцах: id , name , price , количество и Discount_id .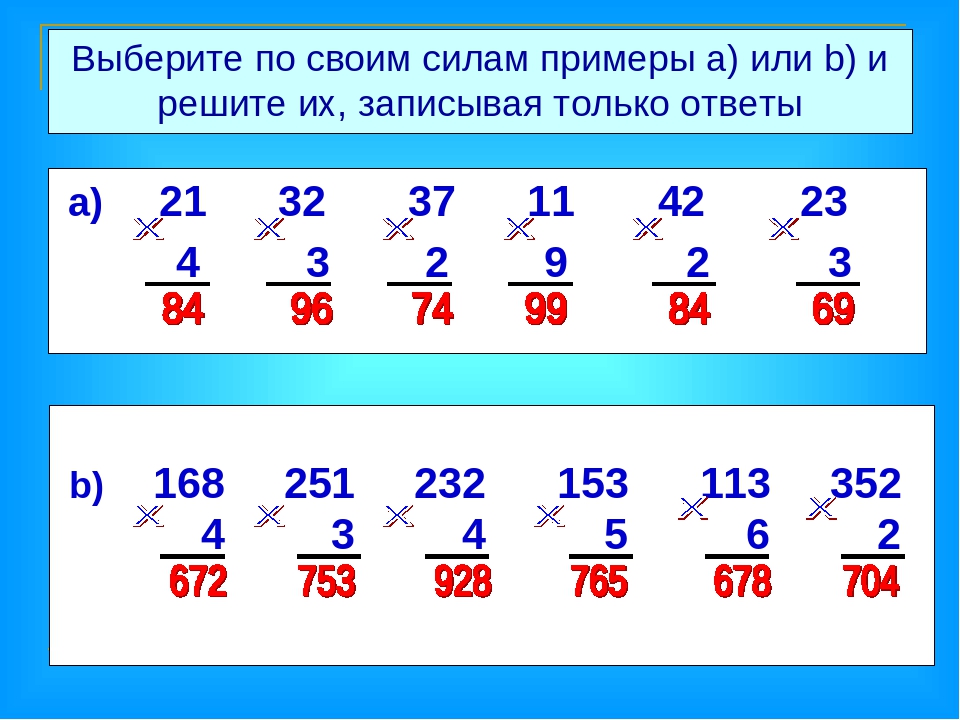
| id | имя | цена | количество | Discount_id |
|---|---|---|---|---|
| 1 | ручка | 7 | 3 | 1 |
| 2 | ноутбук | 5 | 8 | 2 |
| 3 | резина | 11 | 3 | 1 |
| 4 | пенал | 24 | 2 | 3 |
Давайте умножим цену на количество товаров, чтобы узнать, сколько вы заплатили за каждый товар в своем заказе.
Решение:
ВЫБЕРИТЕ имя, цена * количество AS total_price ОТ покупки;
Этот запрос возвращает записи с названием продукта и его общей ценой:
| имя | total_price |
|---|---|
| ручка | 21 |
| ноутбук | 40 |
| резина | 33 |
| пенал | 48 |
Обсуждение:
Вам нужно выбрать имя каждой записи (в нашем случае имя ) и вычислить для него результат умножения одного числового столбца на другой ( цена и количество )? Все, что вам нужно сделать, это использовать оператор умножения (*) между двумя столбцами множимого ( цена * количество ) в простом запросе SELECT . Этому результату можно присвоить псевдоним с ключевым словом
Этому результату можно присвоить псевдоним с ключевым словом AS ; в нашем примере мы присвоили столбцу умножения псевдоним total_price .
Обратите внимание, что вы также можете использовать данные из двух столбцов из разных таблиц. В нашей базе данных есть еще одна таблица с именем Discount , в которой есть столбцы с именами id и value ; последний представляет собой процентную скидку на товар с данным идентификатором.
Посмотрите на пример ниже.
Решение:
ВЫБЕРИТЕ p.name, п.цена * п.количество * (100-дневное значение) / 100 AS total_price ОТ покупки p ПРИСОЕДИНЯЙТЕСЬ скидка d НА d.id = p.discount_id;
Вот результат:
| имя | total_price |
|---|---|
| ручка | 18.90 |
| блокнот | 32.00 |
| резина | 29,70 |
| пенал | 33. 60 60 |
Как видите, перемножать значения из разных объединенных таблиц довольно просто. В нашем примере выше мы умножили цену каждого продукта на его количество из одной таблицы ( покупка ), а затем умножили эту общую цену на процентную скидку, используя таблицу скидка .
Умножающие матрицы — MathBootCamps
Хотя сложение или вычитание матриц относительно несложно, умножение матриц сильно отличается от большинства математических операций, которые вы усвоили заранее.Здесь мы рассмотрим хороший способ умножения двух матриц и некоторые важные свойства, связанные с ним. Вы также узнаете, как определить, когда умножение не определено.
реклама
Содержание:
- Умножение двух матриц: «строки попадают в столбцы» (анимация)
- Умножение матриц не всегда определяется
- Умножение матриц некоммутативно
- Примеры умножения матриц
- Обзор свойств
Умножение двух матриц: «строки попадают в столбцы»
Чтобы понять общую схему умножения двух матриц, представьте, что «строки попадают в столбцы и заполняются строками». Рассмотрим следующий пример.
Рассмотрим следующий пример.
Первая строка «попадает» в первый столбец, давая нам первую запись продукта. Обратите внимание, что, поскольку это произведение двух матриц 2 x 2 (количество строк и столбцов), результатом также будет матрица 2 x 2. Как на это влияет размер матрицы, мы рассмотрим позже в статье.
Теперь первая строка «попадает» во второй столбец, заполняя строку продукта.
Закончились столбцы для «попадания», теперь мы работаем со второй строкой.
Осталась одна последняя запись для расчета. Вторая строка теперь «попадает» во второй столбец.
Наконец, нам просто нужно выполнить арифметику, чтобы получить окончательный ответ.
Анимация этого процесса
Здесь вы можете увидеть анимацию этого процесса. Нет звука — не беспокойтесь о поиске наушников!
Вскоре мы увидим еще пару примеров, но сначала нам нужно обсудить, как размер матрицы влияет на результат при умножении. Фактически, бывают случаи, когда из-за размера матрицы умножение не определено.
Фактически, бывают случаи, когда из-за размера матрицы умножение не определено.
Умножение матриц не всегда определяется
При умножении матриц размер двух задействованных матриц определяет, будет ли определен продукт. Вы также можете использовать размеры, чтобы определить результат умножения двух матриц. Напомним, что размер матрицы — это количество строк по количеству столбцов. Матрицы выше были 2 x 2, так как каждая из них имела 2 строки и 2 столбца.
Как видите, размеры матриц не обязательно должны быть одинаковыми, вам просто нужно сопоставить два средних числа, когда вы пишете размеры рядом. В противном случае продукт не определен.
Подумайте об этом: например, если матрица A имеет размер 3 x 4, то произведение A и самого себя не будет определено, поскольку внутренние числа не будут совпадать. Это всего лишь один пример того, как умножение матриц ведет себя не так, как вы могли бы ожидать.
Умножение матриц некоммутативное
Из начальной школы вы знаете, что произведение (2) (3) = (3) (2). Неважно, в каком порядке вы умножаете числа, результат тот же. В общем случае это не работает для матриц. Только в особых случаях можно сказать, что AB = BA. Итак, в общем, вы должны предполагать, что они не равны. Может даже случиться так, что AB определен, а BA не определен!
Неважно, в каком порядке вы умножаете числа, результат тот же. В общем случае это не работает для матриц. Только в особых случаях можно сказать, что AB = BA. Итак, в общем, вы должны предполагать, что они не равны. Может даже случиться так, что AB определен, а BA не определен!
Даже если продукт определен, опять же, маловероятно, что результаты будут одинаковыми для AB и BA.
Примеры умножения матриц
Теперь, когда мы рассмотрели некоторые важные свойства умножения матриц, давайте рассмотрим пару примеров.
Пример
Найдите продукт AB, где:
\ (A = \ left [\ begin {array} {cc} -5 & 3 \\ -4 & -1 \\ \ end {array} \ right] \)
and
\ ( B = \ left [\ begin {array} {cc} 1 & -1 \\ 2 & 6 \\ \ end {array} \ right] \)
Решение
Помните, что строки попадают в столбцы и заполняют строки. Здесь каждая из матриц имеет размер 2 x 2, поэтому результатом будет матрица 2 x 2.
\ (\ begin {align} AB & = \ left [\ begin {array} {cc} -5 & 3 \\ -4 & -1 \\ \ end {array} \ right] \ left [\ begin {array} {cc} 1 & -1 \\ 2 & 6 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} -5 (1) + 3 (2) & -5 (-1) + 3 (6) \\ -4 (1) + (- 1) (2) & (-4) (- 1) + (- 1) (6) \\ \ end {array} \ right ] \\ & = \ boxed {\ left [\ begin {array} {cc} 1 & 23 \\ -6 & -2 \\ \ end {array} \ right]} \ end {align} \)
Пример
Найдите продукт AB где:
\ (A = \ left [\ begin {array} {cccc} -2 & -1 & 0 & 0 \\ 1 & 2 & 1 & 1 \\ \ end {array} \ right] \)
и
\ (B = \ left [\ begin {array} {cccc} 3 & 1 & 1 & 2 \\ -1 & -1 & 0 & 1 \\ \ end {array} \ right] \)
Решение
Здесь матрица 2 x 4 умножена на матрицу 2 x 4.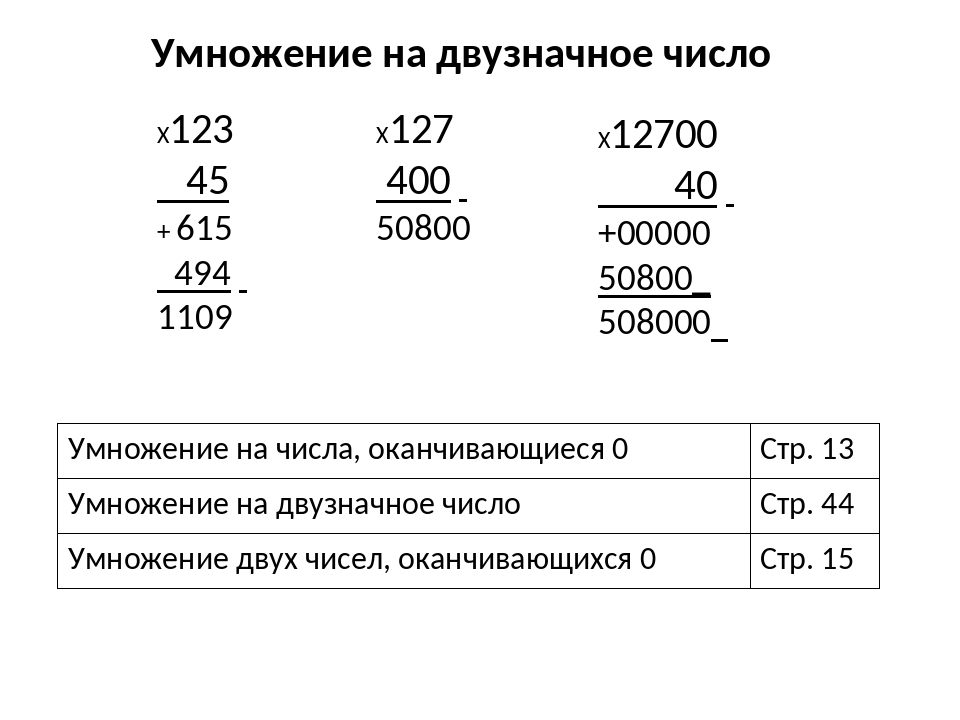 Внутренние числа этих размеров не совпадают, поэтому:
Внутренние числа этих размеров не совпадают, поэтому:
\ (\ boxed {AB \ text {не определено}} \)
Пример
Найдите продукт AB, где:
\ (A = \ left [\ begin {array} {cc} 1 & 2 \\ -2 & 0 \\ 3 & 1 \\\ end {array} \ right] \)
и
\ (B = \ left [\ begin {array} {cc} 4 & 0 \\ 0 & 1 \\ \ end {array} \ right] \)
Решение
Это произведение матрицы 3 x 2 и матрицы 2 x 2. Внутренние числа совпадают, поэтому продукт определен.Результатом будет матрица 3 x 2.
\ (\ begin {align} AB & = \ left [\ begin {array} {cc} 1 & 2 \\ -2 & 0 \\ 3 & 1 \\\ end {array} \ right] \ left [\ begin {массив} {cc} 4 & 0 \\ 0 & 1 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 1 (4) + 2 (0) & 1 (0) + 2 (1) \\ -2 (4) + 0 (0) & -2 (0) + 0 (1) \\ 3 (4) + 1 (0) & 3 (0) + 1 ( 1) \\\ end {array} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 4 & 2 \\ -8 & 0 \\ 12 & 1 \\\ end {массив } \ right]} \ end {align} \)
реклама
Сводка
Помните следующее всякий раз, когда вы умножаете две или более матриц.
- Строки попадают в столбцы и заполняют строки.
- Умножение матриц не всегда определяется — сначала проверьте размеры матрицы!
- Умножение матриц в общем случае не коммутативно.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
СвязанныеКак умножать в Google Таблицах (числа, ячейки или столбцы)
Большинство людей используют Google Таблицы для двух основных целей — создания базы данных записей или выполнения простых вычислений, таких как умножение ячеек или столбцов.
Существует множество способов умножения столбцов (или ячеек, или чисел) в Google Таблицах, и вы можете использовать любой из методов в зависимости от того, как структурированы ваши данные.
В этом уроке я покажу вам различные методы умножения на в Google Таблицах .
Умножение двух чисел в Google Таблицах
Если у вас есть два числа или две ячейки с числами, которые вы хотите умножить, есть несколько способов сделать это.
Использование функции MULTIPLY
Поскольку умножение чисел является такой распространенной задачей, в Google Таблицах было решено включить в него специальную формулу MULTIPLY (ее нет в MS Excel, если вам интересно).
Предположим, вы хотите умножить два числа (12 и 14), вы можете использовать следующую формулу:
= MULTIPLY (12,14)
Эта формула MULTIPLY отлично подходит для использования, когда у вас есть только два числа и вы хотите быстро получить результат.
Хотя я жестко запрограммировал числа в формуле в приведенном выше примере, вы также можете использовать ссылку на ячейки, которые имеют эти значения.
Например, если в ячейке A1 12, а в A2 14, вы можете использовать следующую формулу, чтобы получить результат:
= MULTIPLY (A1, A2)
Формула MULTIPLY может работать только с двумя аргументами, но если вы если их больше двух, то эта формула выдаст вам ошибку. Кроме того, вы можете умножить два результата формулы или именованные диапазоны, которые относятся к ячейке
Кроме того, вы можете умножить два результата формулы или именованные диапазоны, которые относятся к ячейке
Использование оператора MULTIPLY
Вы также можете использовать оператор умножения (знак звездочки) для быстрого умножения двух или более ячеек / чисел в Google Таблицах.
Предположим, вы хотите умножить два числа (12 и 14), вы можете использовать следующую формулу:
= 12 * 14
Если эти значения находятся в ячейках A1 и A2, вы можете использовать следующую формулу:
= A1 * A2
С помощью оператора умножения вы можете умножить более двух значений.Просто используйте оператор умножения между всеми значениями, которые вы хотите умножить.
Например, если у вас есть значения в ячейках A1, A2 и A3, вы можете использовать следующую формулу:
= A1 * A2 * A3
Кроме того, помните, что если любая из этих ячеек пуста, формула даст вам 0.
Одна важная вещь, которую нужно знать при использовании оператора умножения, — это соблюдать порядок приоритета. Например, если вы используете приведенную ниже формулу, она даст вам 170 (поскольку сначала выполняется умножение, а затем добавляется 2 к результату):
Например, если вы используете приведенную ниже формулу, она даст вам 170 (поскольку сначала выполняется умножение, а затем добавляется 2 к результату):
= 12 * 14 + 2
В случае, если вы хотите добавить Сначала от 2 до 14, а затем умножьте, вам нужно использовать приведенную ниже формулу (где скобки используются для четкого разделения разделов, которые необходимо вычислить в первую очередь):
= 12 * (14 + 2)
Также прочтите: Как разделить в Google Таблицах
Умножение двух столбцов в Google Таблицах
Хотя в приведенных выше примерах рассматривается умножение отдельных значений или ячеек, в этом разделе я покажу вам, как умножить два столбца (или умножить более двух столбцов) на простая формула.
Предположим, у вас есть набор данных, как показано ниже, и вы хотите получить умноженное значение ячеек в строке в столбце C.
Ниже приведена формула, которая будет делать это:
= ARRAYFORMULA (A1: A10 * B1 : B10)
Поскольку это формула массива, вам нужно только ввести ее в ячейку C1, и она автоматически заполнит остальные ячейки столбца.
Также с помощью формул массива нельзя удалить или отредактировать часть результирующего массива.Однако вы можете удалить весь массив, если хотите.
Вы также можете использовать приведенную ниже формулу, чтобы сначала умножить ячейки в строке, а затем скопировать формулу для всех ячеек в столбце.
Поскольку приведенная выше формула не является формулой массива, вы можете изменять или редактировать отдельные ячейки по своему усмотрению.
Если вы хотите получить сумму всех значений умножений в одной ячейке, вы можете использовать приведенную ниже формулу СУММПРОИЗВ:
= СУММПРОИЗВ (A1: A10 * B1: B10)
Итак, есть несколько способов вы можете умножать в Google Таблицах.В зависимости от того, хотите ли вы использовать несколько ячеек или столбцов, вы можете выбрать функцию НЕСКОЛЬКО или оператор.
Надеюсь, вы нашли это руководство полезным.
Другие руководства по Google Таблицам, которые могут вам понравиться:
Как умножить в Excel
Чтобы на умножить числа в Excel, используйте символ звездочки (*) или функцию ПРОИЗВОД. Узнайте, как умножить столбцы и как умножить столбец на константу.
Узнайте, как умножить столбцы и как умножить столбец на константу.
1. Приведенная ниже формула умножает числа в ячейке.Просто используйте символ звездочки (*) в качестве оператора умножения. Не забывайте, всегда начинайте формулу со знака равенства (=).
2. Приведенная ниже формула умножает значения в ячейках A1, A2 и A3.
3. Как вы понимаете, эта формула может быть довольно длинной. Используйте функцию ПРОИЗВОД, чтобы сократить формулу. Например, приведенная ниже функция ПРОИЗВОД умножает значения в диапазоне A1: A7.
4. Еще один пример.
Объяснение: = A1 * A2 * A3 * A4 * A5 * A6 * A7 * B1 * B2 * B3 * B4 * C1 * 8 дает точно такой же результат.
Посмотрите на снимок экрана ниже. Чтобы умножить два столбца вместе, выполните следующие шаги.
5а. Сначала умножьте значение в ячейке A1 на значение в ячейке B1.
5б. Затем выберите ячейку C1, щелкните в правом нижнем углу ячейки C1 и перетащите ее в ячейку C6.
Посмотрите на снимок экрана ниже.Чтобы умножить столбец чисел на постоянное число , выполните следующие шаги.
6а. Сначала умножьте значение в ячейке A1 на значение в ячейке A8. Исправьте ссылку на ячейку A8, поместив символ $ перед буквой столбца и номером строки ($ A $ 8).
6б. Затем выберите ячейку B1, щелкните в правом нижнем углу ячейки B1 и перетащите ее в ячейку B6.
Объяснение: когда мы перетаскиваем формулу вниз, абсолютная ссылка ($ A $ 8) остается неизменной, а относительная ссылка (A1) изменяется на A2, A3, A4 и т. Д.
Если вы не являетесь героем формул, используйте Специальную вставку для умножения в Excel без использования формул!
7. Например, выберите ячейку C1.
8. Щелкните правой кнопкой мыши, а затем щелкните Копировать (или нажмите CTRL + c).
9. Выберите диапазон A1: A6.
10. Щелкните правой кнопкой мыши и выберите «Специальная вставка».

 Организационно-мотивационный
Организационно-мотивационный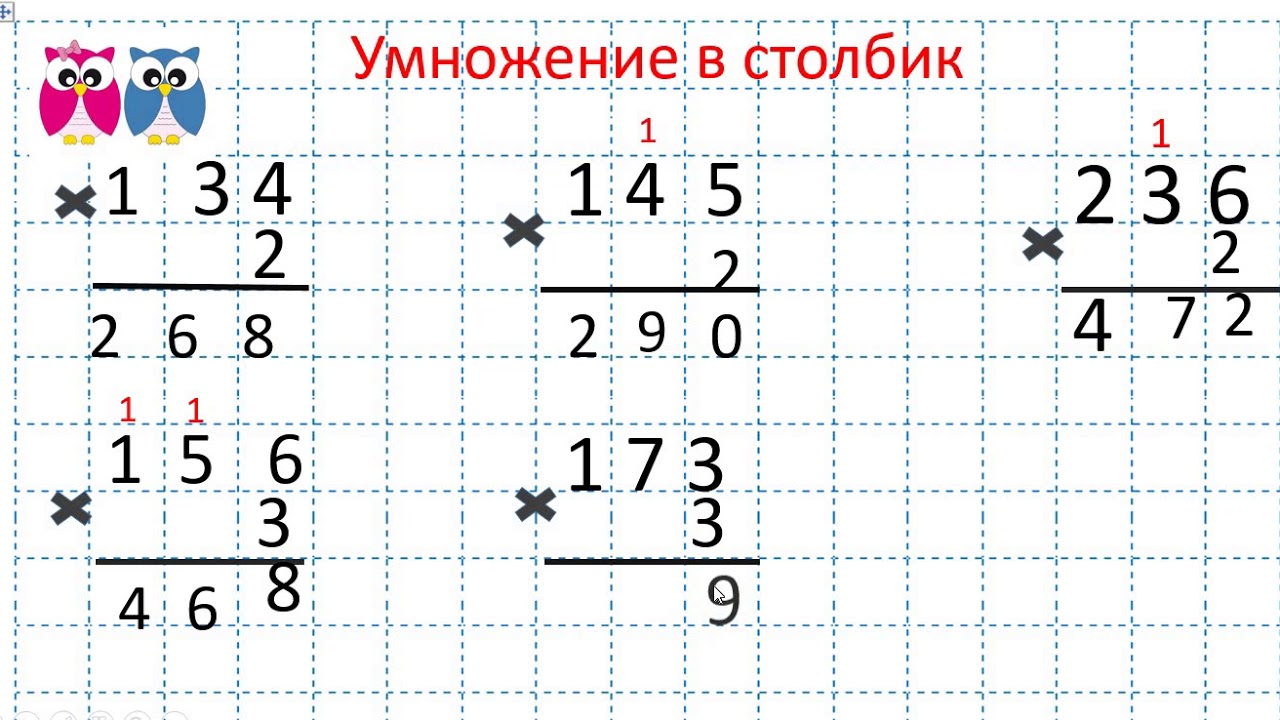
 2 столбик — табличное умножения, 1 столбик – умножение двузначных чисел).
2 столбик — табличное умножения, 1 столбик – умножение двузначных чисел).
 ) Личностные УУД: смыслообразование (учебная мотивация)
) Личностные УУД: смыслообразование (учебная мотивация) Первичное восприятие и усвоение нового учебного материала
Первичное восприятие и усвоение нового учебного материала Работа с информацией, поиск информации. Коммуникативные УУД: умение работать в паре, в группе, высказывать свое мнение. Регулятивные УУД: удержание цели и задач урока.
Работа с информацией, поиск информации. Коммуникативные УУД: умение работать в паре, в группе, высказывать свое мнение. Регулятивные УУД: удержание цели и задач урока.