Математика, 6 класс: 19-22. Деление десятичных дробей
Устный счет
Это надо знать
Деление десятичной дроби на 10, 100, 1000 и так далее
При делении десятичной дроби на 10, 100, 1000 и так далее запятую надо перенести влево на столько знаков, сколько нулей имеется в разрядной единице.
Примеры:
56,1 : 10 = 5,61;
56,1 : 100 = 0,561;
56,1 : 1000 = 0,0561.
Деление десятичной дроби на 0,1; 0,01; 0,001 и так далее
При делении десятичной дроби на 0,1; 0,01; 0,001 и так далее запятую надо перенести вправо на столько знаков, сколько цифр имеется после запятой в 0,1; 0,01; 0,001 и т.д..
Примеры:
5,61 : 0,1 = 56,1;
5,61 : 0,01 = 561;
5,61 : 0,001 = 5610.
Деление на натуральное число
При делении на натуральное число надо:
1.
Выполнить деление, не обращая внимания на запятую;
2. В полученном частном поставить запятую сразу, как только закончено деление целой части.
Пример:
31,2 : 5 = 6,24
Деление на десятичную дробь
При делении на десятичную дробь надо:
1. Перенести в делимом и делителе запятую вправо на столько цифр, сколько их после запятой в делителе;
2. Выполнить деление на натуральное число.
Пример:
8, 255 : 0,04 = 825,5 : 4 =
Видеоурок
Домашнее задание
К уроку 19 (на 28.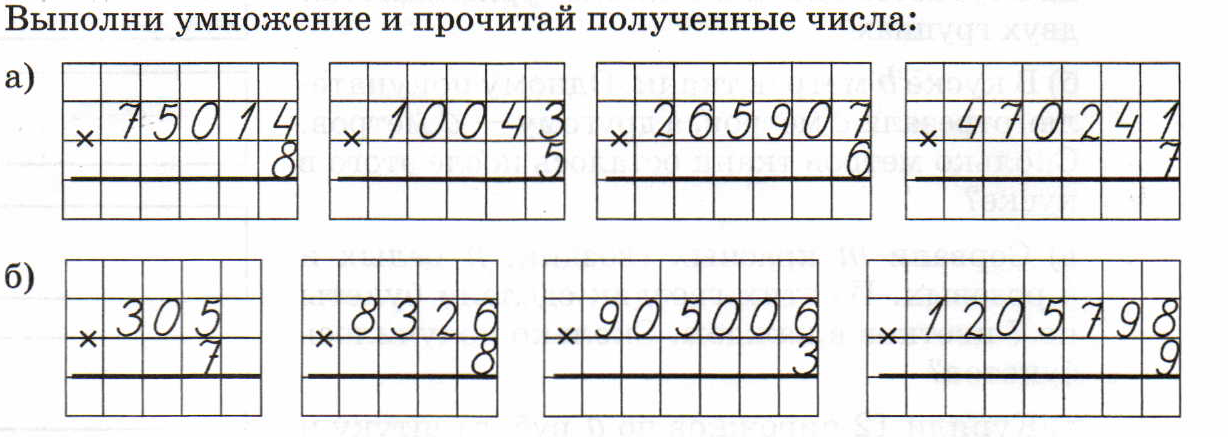
09)
П. 4.1
1 уровень (учебник)
№ 4.3
№ 4.8
2 уровень (сборник)
№ 1.67 стр. 16
Вычислите:
1) 48 : 10; 2) 75 : 100; 3) 12 : 100; 4) 305 : 10; 5) 7803 : 100; 6) 57057 : 1000.
№ 1.70 стр. 16
Найдите частное от деления числа 261 на число:
1) 0,001; 2) 0,01; 3) 0,000001.
№ 1.72 стр. 16
Найдите частное от деления на 0,0001 числа:
1) 52; 2) 462; 3) 15; 4) 3,87; 5) 1,008; 6) 4,9; 7) 0,004; 8) 0,023.
К уроку 20 (на 29.09)
П. 4.2
1 уровень (учебник)
№ 4.25
№ 4.28
2 уровень (сборник)
№ 1.
73 стр. 17
Выполните деление:
1) 32 : 800; 2) 56 : 70; 3) 26 : 1300; 4) 96 : 32000; 5) 1500 : 6000; 6) 25 : 1250.
№ 1.75 стр. 17
Найдите частное чисел:
1) 16,75 : 50; 2) 6,942 : 25; 3) 72,18 : 360; 4) 22,5 : 45; 5) 1,75 : 17500; 6) 6,6645 : 36.
К уроку 21 (на 30.09)
П. 4.3
1 уровень (учебник)
№ 4.63
№ 4.65 (1, 2)
2 уровень (сборник)
№ 1.78 стр. 17
Пользуясь верным равенством 794 ∙ 325 = 258 050, найдите значение выражения:
1) 25,805 : 3,25; 2) 2580,5 : 32,5; 3) 258,05 : 0,0325; 4) 258,05 : 0,794;
5) 0,025805 : 0,00794; 6) 0,25805 : 0,000794.
№ 1.76 стр. 17
Выполните деление:
1) 37,563 : 6,59; 2) 219,975 : 4,19; 3) 22,411 : 0,73;
4) 229,04 : 5,6; 5) 19,152 : 6,3; 6) 199,43 : 0,49.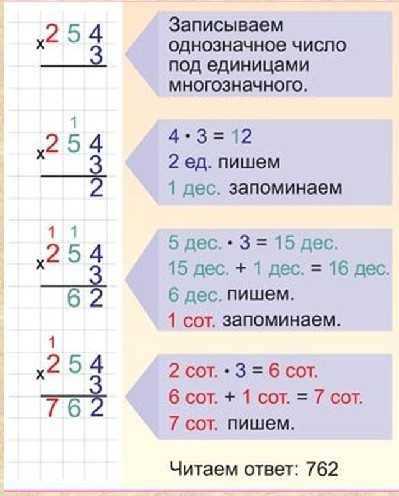
К уроку 22 (на 03.10)
П. 4.3
1 уровень (учебник)
№ 4.68
№ 4.76 (1-4)
2 уровень (сборник)
№ 1.100 стр. 20
Уменьшите значение величины 329,4 км в:
1) 3 раза; 2) 4 раза; 3) 5 раз; 4) 12 раз.
№ 1.102 ( 5-8) стр. 21
Обратите каждую обыкновенную дробь в десятичную и выполните действие:
№ 3.14 (4-7) стр. 78
Решите уравнение:
4) 6,78 : y = 6780; 5) 2,95 : y = 0,0295; 6) 0,01 : x = 100; 7) y : 0,01 = 168.
Деление в столбик — объяснение (3 класс)
Сегодня мы рассмотрим деление в столбик — объяснение (3 класс).
Бывают небольшие числа, и с ними можно работать в уме.
Бывают очень большие числа, для таких чисел люди нашли разные способы умножения и деления. Есть умножение в столбик. Это замечательно, там сразу видно что куда необходимо переносить и куда добавлять. Конечно, если аккуратно записывать. Но если есть умножение в столбик, тогда должно быть и деление в столбик.
Люди нашли удобный способ представления деления больших чисел, чтобы ничего не забыть.
Пример:
Это удобно, но почему так?
Сегодня в этом разбираются Бом, Бим и ребята.
Содержание статьи:
Деление — это действие обратное умножениюДеление двух чисел — это действие обратное к умножению. Используется для нахождения одного из неизвестных (первого или второго множителя) в операции умножения. Делить на ноль — нельзя.
Деление в столбик — объяснение (3 класс)Деление в столбик — это удобный способ представления деления одного числа на другое.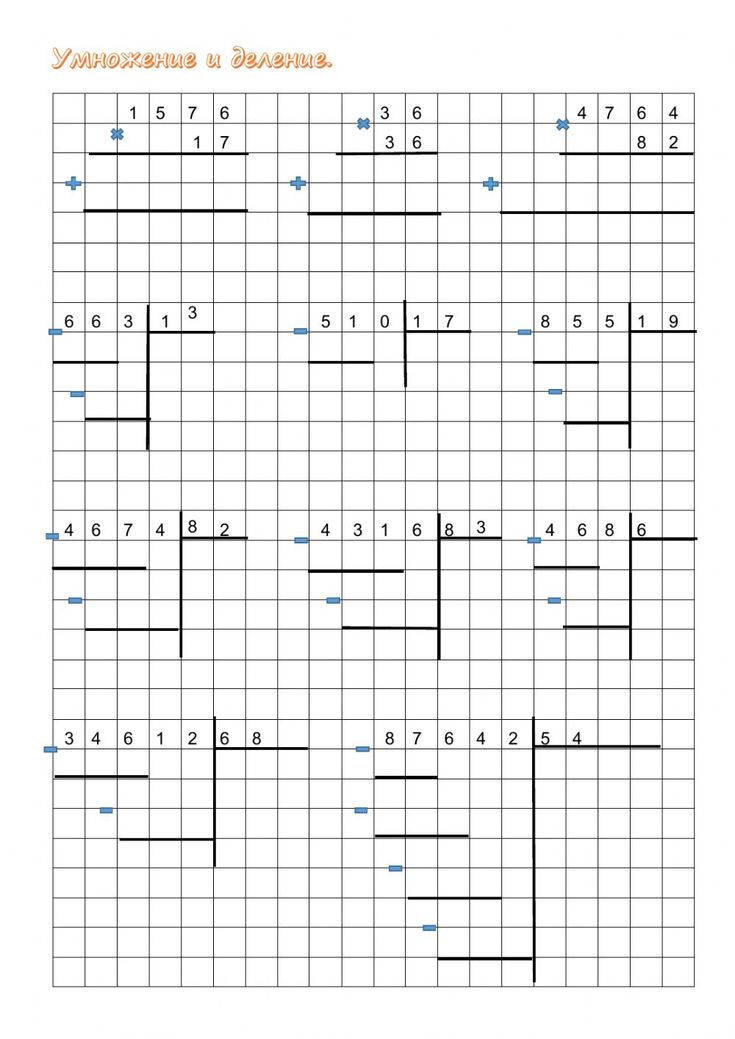
Сегодня ребята пришли раньше на представление и пошли осматривать цирк. По дороге им встретился Бим, который вез тележку с тремя коробками.
— Здравствуйте, ребята! — обрадовался. Бим. — Пойдемте за кулисы, поможете мне и Бому!
Бим и ребята пошли к Бому. В трех коробках находились бананы: в первой большой коробке лежали два больших пакета, в каждом большом пакете лежало по 100 бананов. Во второй, средней коробке, лежали два средних пакета; и здесь в каждом среднем пакете лежало по 10 бананов. В третьей маленькой коробке лежало четыре банана.
— Давайте посчитаем сколько всего бананов получается, — предложил Бим. — В большом пакете 100 бананов. Всего 2 больших пакета. В двух больших пакетах будет:
2 х 100 = 200 бананов.
Всего в большой коробке лежит 200 бананов. Теперь считаем сколько бананов в средней коробке: два пакета по 10 бананов,
2 х 10 = 20 бананов.
В маленькой коробке 4 банана. Получается, что во всех трех коробках будет:
200 + 20 + 4 = 224 банана.
Мне буфетчица сказала, что надо поделить эти бананы на 14 представлений и дать тебе, Бом, для твоих подопечных. Вот, что я придумал. Давайте все бананы высыплем в одну коробку и будем раскладывать по одному банану на 14 подносов пока все бананы не закончатся.
Бим начал высыпать все бананы в маленькую коробку.
— Здесь, конечно, бананов немного, а если бы бананов была тонна, то ты тоже по одному банану раскладывал бы? — поинтересовался Бом. — Очень легко запутаться. Давай придумаем другой способ.
— Ребята, — обратился Бом к школьникам, — помогите Биму все бананы сложить на место. В большой коробке должно быть два больших пакета по 100 бананов, всего в большой коробке будет 200 бананов. В средней коробке два средних пакета по 10 бананов в каждом пакете, всего в средней коробке будет 20 бананов. В маленькой коробке будет четыре банана.
И давай, Бим, договоримся, что в большой коробке будут лежать только большие пакеты по 100 бананов, в средней только средние пакеты по 10 бананов, в маленькой коробке только оставшиеся бананы без никаких пакетиков.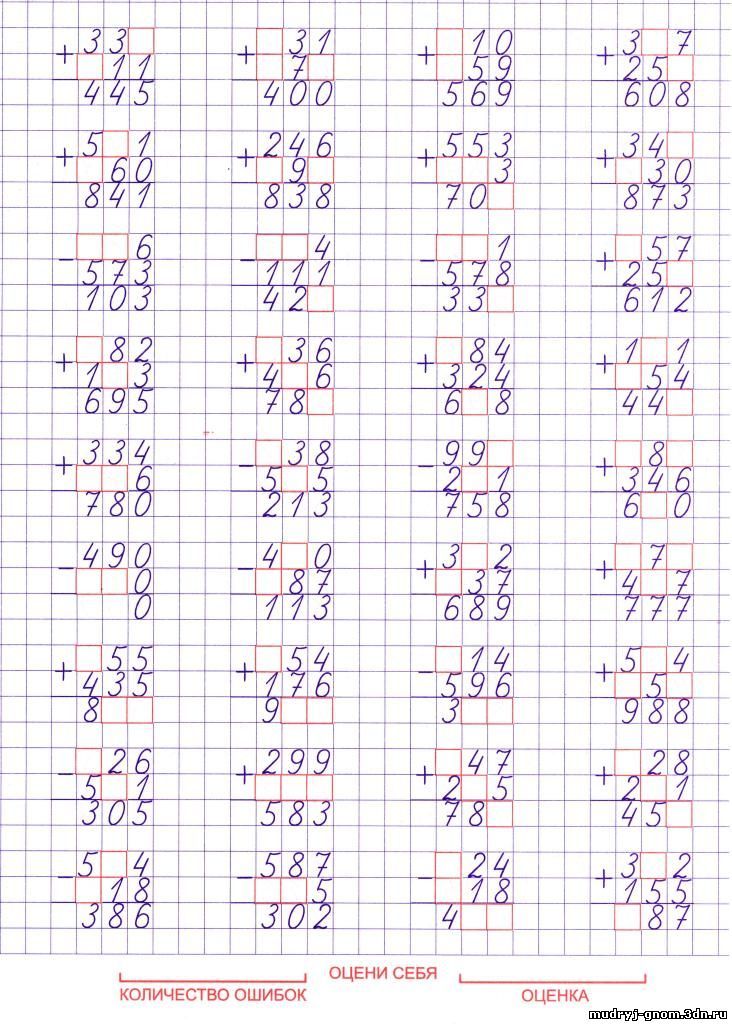
Ребята быстро помогли Бому и Биму.
— Вот теперь всё на месте, — подытожил Бом. — Давайте теперь будем делить так, чтобы бананов хватило на 14 представлений. В большой коробке два больших пакета, два на 14 не делится. А что, если мы бананы переложим из большой коробки в среднюю? Но для этого нужно достать каждый большой пакет и выложить из него бананы по 10 штук в средние пакети, и тогда мы можем бананы из большой коробки переложить в среднюю коробку.
Бом достал большой пакет из большой коробки. Ребята переложили бананы в средние пакеты и начали считать:
— Из одного большого пакета получается 10 средних пакетов по 10 бананов.
— У нас два больших пакета, значит из двух больших пакетов у нас получается 20 средних пакетов по 10 бананов, продолжил Бом. — Мы все средние пакеты помещаем в среднюю коробку.
Ого! В средней коробке уже 22 средних пакета. Такое количество уже делится на 14, это у нас неполное деление с остатком. Получается, на каждое представление будет по одному среднему пакету.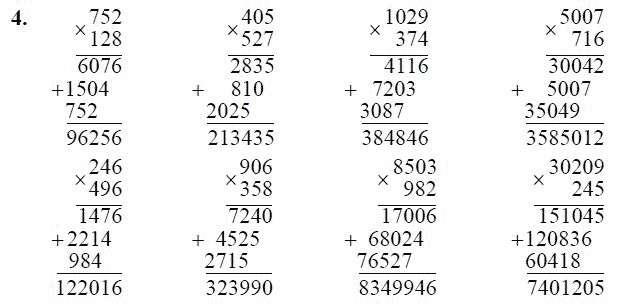
Бом взял 14 подносов и разложил по 1 среднему пакетику на каждый поднос:
— У нас было 22 средних пакетика, 14 мы разложили по местам, остаток 8 средних пакетиков в средней коробке и 4 банана в маленькой. Восемь на четырнадцать не делится. Но если мы оставшиеся в средней коробке бананы в восьми средних пакетах высыплем в маленькую коробочку, то получится в маленькой коробочке 84 банана:
8 х 10 + 4 = 84.
84 банана делятся на 14, получается по 6 бананов, то есть мы на каждый поднос должны добавить еще по 6 бананов. У нас всего 14 подносов, и на каждом подносе лежит одинаковое количество бананов. Значит мы поделили поровну все бананы, которые у нас были. На каждом подносе 1 средний пакет и 6 бананов. Выходит, что всего на каждом подносе по 16 бананов.
— Неужели всякий раз придется по разным пакетикам раскладывать, чтобы правильно поделить? — озадаченно спросил Бим.
— Совсем не обязательно, — ответил Коля. — Люди вместо коробок и пакетиков договорились, как будет называться каждая из цифр в числе.
Цифра, которая стоит в числе самой правой, называется разрядом единиц. У нас в маленькой коробке 4 банана, значит число единиц — 4.
— Следующая цифра, которая находится левее разряда единиц называется разрядом десятков, — продолжила Оля. — У нас в средней коробке 2 пакета, значит число десятков равно 2. И мы знаем, что 2 десятка — это 20, и у нас в средней коробке как раз 2 пакетика по 10 бананов, всего 20 бананов.
— Следующая цифра, которая находится левее разряда десятков называется разрядом сотен. У нас это самая большая коробка, в ней два больших пакета, значит число бананов 200, — закончил Вася. — И мы знаем, что 2 сотни — это число 200.
— А какие еще числа могут стоять … в разрядах? — поинтересовался Бим.
— Число в каждом из разрядов может быть любой цифрой от 0 до 9, — ответил Биму Коля. — Еще левее от разряда сотен стоит разряд тысяч. У нас нет еще большей коробки, в которой лежали бы пакеты с количеством бананов по 1000 в каждом, поэтому мы ничего не пишем.
— Мы разложили бананы, у нас общее число бананов 224: 4 банана в маленькой коробке, 2 средних пакета по 10 бананов в средней коробке, — всего 20, и 2 больших пакета из 100 бананов в большой коробке, — подытожил Бом. — Число единиц у нас 4, число десятков 2, число сотен 2. Записываем: 4 стоит справа, левее стоит число десятков 2, еще левее число сотен 2. Теперь это число 224 будем делить на 14.
— Давайте теперь запишем деление 224 на 14 в столбик, — предложил Коля. — Делимое у нас 224, делитель 14. Смотрим: первая цифра слева 2 (число сотен) на 14 не делится, значит надо к ней справа приписать следующую за “2” цифру 2. Читаем число, которое получилось — 22. Число 22 уже делится на 14. Число 14 помещается в числе 22 по одному (1) разу, вот это число “1” и записываем в ответ для частного первым, потом надо из 22 вычесть 14 х 1:
22
—
14
____
8
Мы при делении 22 на 14 находим неполное частное 1 и остаток 8.
Неполное частное записываем в частное результата, остаток пишем как при обычном вычитании чисел в столбик.
Теперь смотрим, есть ли еще цифры справа, в делимом 224. Да такая цифра есть, после 22 стоит цифра 4, мы её записываем справа от остатка 8. Эта четверка будет стоять на том же месте в строке, где стоит 4 в числе 224, но только ниже возле “8”. У нас внизу получается число “84”. Смотрим, делится ли оно на делитель “14”. Делится. В результате деления 84 на 14 получаем “6”, его записываем справа от “1” в частном. А внизу после того, как умножим 14 х 6 = 84 мы пишем опять обыкновенное вычитание в столбик:
84
—
84
___
0
Ура! Еще и остаток в конце равен 0. В числе 224 нет справа больше цифр, сносить на более нижние строки нечего. Значит, мы закончили деление. Частное — 16.
— Смотрите, получилось такое же число, как и количество бананов на каждом подносе, — обрадовалась Оля.
— Проверка, что деление выполнено правильно, делается также как и для обычного деления: частное умножается на делитель, должно получиться делимое, — добавил Вася.
— Сейчас каждый из нас еще по одному примеру деления в столбик запишет, — продолжил Коля.
Коля 1000 : 25 = 40. Оля 1025 : 25 = 41. Вася 10025 : 25 =401.
— Жалко, что у нас нет бананов в остатке, я бы его съел, огорчился Бим.
— Делаем вывод, — продолжил Коля. — Все деление в столбик состоит из неполных делений чисел, пока в числе не окончатся все разряды, но если после того, как мы снесли последний разряд (число единиц) остался остаток, то все деление у нас неполное, и результат будет состоять из частного-результата и остатка-результата. Если в конце деления остаток 0, то так и говорят, что делимое делится на делитель без остатка.
Можно и так определить деление в столбик, — подытожил Бом:
Деление в столбик — это ряд неполных делений чисел (неполных делимых), составленных из остатков от деления и цифр делимого, на делитель.
В результате деления в столбик должны быть использованы все цифры делимого.
Вначале в делимом выделяем первое неполное делимое из цифр делимого, начиная с левой цифры делимого, пока неполное делимое не будет делиться не делитель. Частное от неполного деления записываем первой цифрой в частном.
К остатку от неполного деления сносим следующие цифры из делимого, пока новое неполное делимое не будет делится на делитель. При этом, если после снесенной цифры, неполное делимое не делится на делитель, то в частное ставится справа 0. После деления нового неполного делителя на делимое неполное частное записывается справа от уже найденных цифр частного, а к полученному неполному остатку опять сносятся последующие цифры из делимого. Действия повторяются, пока не будут снесены все цифры делимого.
Неполное частное при делении в столбик — это частное от деления в столбик, при котором имеется остаток после использования последнего разряда в операции деления в столбик.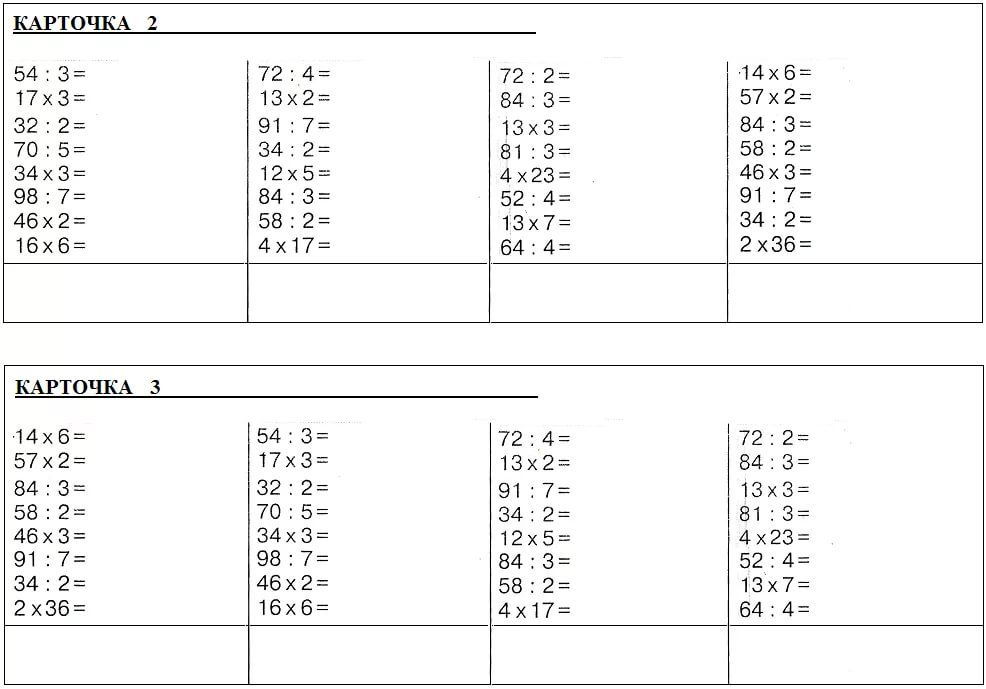
— Получается, — подхватил Вася, — что при делении в столбик тоже может быть неполное деление, когда есть остаток в самом конце деления. И результат тогда пишут, как при обычном неполном делении: частное-результат или как обычно говорят “частное”, а в конце в скобочке пишут остаток.
Пример:
— Спасибо ребята, что помогли нам сегодня разобраться с делением в столбик, — поблагодарил зрителей Бом. — Вот вам 315 конфет. Поделите в столбик 315 на 15 и разложите по 15 конфет в каждый кулечек. Три пакетика заберите себе, а остальные я раздам другим ребятам. Сколько всего получится пакетиков и сколько пакетиков мне останется раздать ребятам пусть посчитают ребята, которые научились делению в столбик.
— Подсказка. В ответе должен быть 21 кулечек, три из которых получили Коля, Оля и Вася, — добавил Бим. — Теперь напишите, пожалуйста, вопросы и ответы для ребят с Бомом, а я побежал одеваться, мой выход в самом начале представления, а выход Бома с обезьянками будет позже.
Бим убежал.
— До начала представления еще есть время, — посмотрел на часы Бом. — Ребята, давайте запишем вопросы:
- Что такое деление?
- Деление в столбик — это …
- Деление в столбик с остатком — это …
И как обычно, ответы:
- Деление двух чисел — это действие обратное к умножению, используется для нахождения одного из неизвестных (первого или второго множителя) в операции умножения. Делить на ноль — нельзя.
- Деление в столбик — это удобный способ представления обыкновенного деления. Деление — это действие обратное к умножению.
- Неполное частное при делении в столбик — это частное от деления в столбик, при котором имеется остаток после использования последнего разряда в операции деления в столбик
— Спасибо, ребята! — обрадовался Бом. — Вы очень помогли нам с Бимом. А теперь бегите на представление.
Сегодня мы постарались в игровой форме рассмотреть тему: «Деление в столбик — объяснение (3 класс)».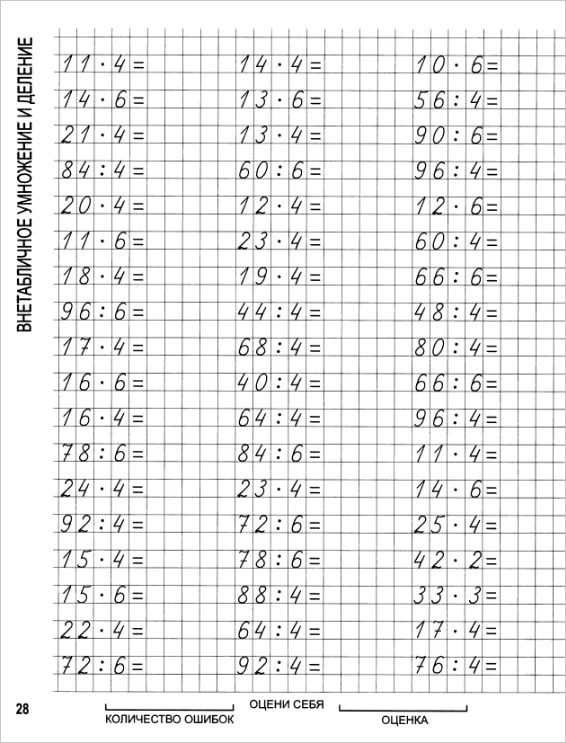
Надеемся, что ребята выучат деление в столбик и оно им еще не один раз пригодится.
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания! Комментарии приветствуются. По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))
Деление натуральных чисел — Бесплатные рабочие листы по математике
Деление — одно из четырех основных арифметических действий в математике. Это операция, обратная умножению, означает разделение чего-то на равные группы. Символы деления: «$/$», «$÷$» и «$:$».
Деление двух чисел имеет следующий вид:
« делимое $:$ делитель = частное» .
Первое число называется делимым , секунды — это делитель , а результат называется частным .
Мы можем разделить любое число на любое число , кроме нуля . Деление на ноль не определено.
Чтобы хорошо делить числа, вам нужно хорошо знать таблицу деления . Таблица деления похожа на таблицу умножения в обратном порядке .
Изображение предоставлено: math-refresher.com
Деление натуральных чисел
Теперь мы рассмотрим деление натуральных чисел. Если вы будете придерживаться принципов, описанных в следующей части этого урока, у вас не возникнет проблем с делением любого числа на любое число. Лучший способ узнать что-то — это посмотреть на примеры проблемы.
Проверка 1.
Мы собираемся разделить число $117$ на число $9$:
Деление в приведенном выше примере выполняется в следующие шаги:
-> Мы начинаем с деления старшая цифра с делителем. В нашем примере самая значащая цифра — $1$. Цифра $1$ не делится на цифру $9$. Если мы не можем разделить цифру на делитель, мы объединяем эту цифру со следующей значащей цифрой и получаем двузначное число.
В нашем случае это цифра $1$, поэтому мы получаем число $11$. Делим число $11$ на число $9$. Результатом является число $1$. В полученном результате запишите число $1$.
-> На этом шаге мы умножаем число $1$ на число $9$ и пишем под номером $11$. После этого мы должны вычесть эти числа.
->Число $11$ минус число $9$ равно числу $2$. Запишите число $2$ в результате вычитания. Теперь нам нужно добавить следующую цифру из делимого рядом с числом $2$. Это число $7$. Теперь у нас есть $27$.
-> Теперь нам нужно разделить число $27$ на число $9$, чтобы получить следующую цифру в полученном числе. Число $27$ разделить на $9$ – это число $3$. Впишите в результат число $3$.
-> После этого $3 \cdot 9 = 27$. Мы пишем число $27$ под $27$ и вычитаем эти числа. Результат равен $0$. Вычитание выполняется, когда остаток от деления не может делиться на делитель.
-> Окончательный результат — число $13$. Это означает, что $13 \cdot 9 = 117$.
Проверить 2 .
Следующий пример будет более сложным. Мы собираемся разделить число $1736$ на число $14$.
Деление должно выглядеть так:
-> Опять же, цифра $1$ меньше, чем цифра $14$, поэтому мы не можем делить. Возьмите следующую цифру и сформируйте $17$. Число $17$, разделенное на число $14$, равно числу $1$. Запишите число $1$ в результате.
->Теперь у нас $1 \cdot 14 = 14$. Запишите число $14$ под номером $17$ и вычтите эти числа. После этого у нас есть $17\cdot 14 = 3$. Запишите число $3$ в результате вычитания.
-> Добавить одну цифру из делимого. Следующая цифра $3$. Теперь у нас есть число $33$. Число $33$, разделенное на число $14$, равно числу $2$.
->Теперь у нас $2 \cdot 14 = 28$. Запишите число $28$ под числом $33$ и вычтите его. Результатом является число $5$.
-> Добавить одну цифру из делимого. Эта цифра — цифра $6$. Теперь у нас есть число $56$.Число $56$ разделить на число $14$ равно числу $4$.
-> У нас есть $4 \cdot 14 = 56$.
Запишите число $56$ под числом $56$ и вычтите. Результат вычитания — число $0$.
Словарь разделов — лучшие классы GED
Чтобы успешно сдать любой тест по математике, важно понимать язык математики.
В этом посте мы поговорим о словах, терминах и выражениях, с которыми вы можете столкнуться, когда речь заходит о Дивизионе.
Выражения, используемые в делении, аналогичны выражениям, используемым в умножении. Чтобы сдать любой экзамен по математике, очень важно убедиться, что вы понимаете и используете правильный словарный запас.
Мы также объясним наиболее часто используемые слова и выражения, используемые в математическом отделе.
Ключевые математические слова
Вам нужно будет понять, что обозначают такие слова, как множитель, произведение, делимое, делитель, частное, остаток, остаток и т. д., и как их использовать. Начнем с нескольких примеров:
Допустим, у нас есть 4 x 6 = 24. 4 и 6 называются «множителями», а 24 — «произведением».
Таким образом, числа, которые мы перемножаем вместе, являются множителями, а ответом на умножение является произведение. Поэтому мы говорим, что «множитель, умноженный на фактор, равен произведению».
Теперь давайте рассмотрим еще один пример. Давайте посмотрим на 56 / 7 = 8. Мы называем число 56 «дивидендом». Число 7 называется «делителем», а число 8 — «частным».
Таким образом, число, которое разбивается или делится, является нашим дивидендом. Делитель — это число, на которое мы делим, а наш ответ на задачу о делении называется частным. Поэтому мы говорим, что «деленное на делитель равно частному». Звучит сложно? Ну не совсем. Вы привыкнете к этому достаточно быстро!
Онлайн-курсы GED — быстро, просто и дешево
Получите диплом GED за 2 месяца.
Индивидуальный план, который поможет вам быстро и легко получить диплом.
Начало работы
Еще одно слово, которое вам нужно знать в задачах на деление, это «остаток». Это «остаточное» число, которое больше нельзя разделить на делитель.
Таким образом, мы можем сказать, что если в задаче на деление нет остатка (если остаток равен нулю), делитель делит делимое нацело.
Однако, если есть остаток, мы используем обычное обозначение: сначала записывается частное, затем « R», и затем оставшееся значение. Таким образом, 8/5 (8 разделить на 5) дает 1 R 3. Проще говоря, число 5 входит в наше число 8 один раз, с остатком 3.
Деление и умножение
Ну, как вы, вероятно, Знаете, в математике деление связано с умножением. Мы можем сказать, что 63 / 7 = 9, поскольку 9 x 7 = 63. Это говорит нам о том, что деление противоположно умножению (или отменяет его).
Однако, когда мы используем это правило, мы должны помнить об одном ограничении. Деление на самом деле единственная основная арифметическая операция с ограничением!
Давайте объясним это. Посмотрите на восемь, деленное на ноль, или 8/0. Если мы скажем, что 8/0 = а, наше определение говорит, что это эквивалентно утверждению, что а x 0 = 8.
Однако 0, умноженное на любое число, всегда даст нам 0, так что говоря a x 0 = 8 невозможно! Итак, деление на 0 (ноль) не определено. Его просто не существует! Это наше ограничение.
Имейте в виду, однако, что ноль вполне можно разделить на ненулевые числа. Просто посмотрите на 0 / 8 = 0. Это верно, поскольку 8 x 0 = 0. Таким образом, число ноль вполне может быть частным или делимым. Однако он не может быть делителем.
Итак, теперь давайте рассмотрим некоторые из наиболее часто встречающихся терминов, слов и выражений при работе со словарем Math Division. Включены также выражения, связанные с умножением, поскольку деление и умножение связаны. Вот так:
Словарь математического отдела
Дробь: Дробь — это частное двух (2) рациональных чисел. Дроби — это задачи на деление
Основание: Число, на которое умножается
Показатель степени: Показатель степени говорит нам, во сколько раз умножается основание
Фактор: Факторы — это числа, которые умножаются вместе, чтобы получить произведение.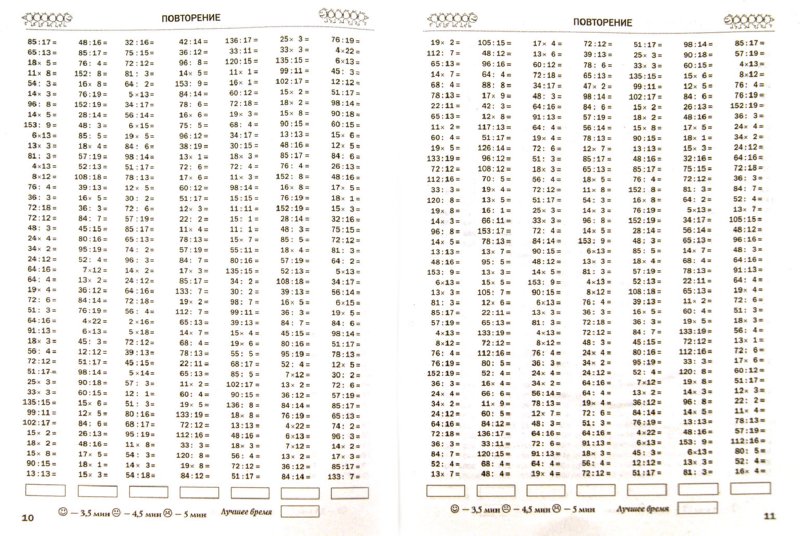
Числитель: Верхнее число дробей, делимое дроби
Делимое: Делимыми являются числа, которые делятся
Делители: числа делим на
Произведение: Произведения — это ответы на задачи на умножение. Таким образом, продукты — это количества, которые мы получаем, когда умножаем
Распределительное свойство (умножения): изменяется только порядок множителей
Ассоциативное свойство (умножения): Изменяются только группы множителей
Идентификационное свойство (умножения): Умножение на единицу (1) не изменяет множители
Обратные операции: Выполнение противоположных действий (например, деление на 4 и умножение на 4)
Множественное: Например, 24 кратно 4, потому что 4 идет равномерно в 24).
Таким образом, кратные являются произведением числа (4 в нашем примере) и другого целого числа (6 в нашем примере, так как 4 x 6 = 24) По: За каждый. Например, 12 долларов в час
Частное: Частное — это ответы на задачи на деление. Частные S0 — это числа, которые мы получаем делением
Остаток: Остаток — это числа, оставшиеся после того, как мы нашли частные
Плюс: Это арифметическая операция сложения (или суммирования)
Разность: число, оставшееся после вычитания
Объединить: Сложение или складывание
Раздельно: Взять, потянуть или разделить (разрезать)
Вместе: Собрать или добавить в одном месте
Сдача: В математике или финансах сдача – это остаток полученных денег, поэтому она делать с вычитанием
раз: раз умножение. Арифметическая операция, обратная делению
Остаток: При вычитании, не израсходовано
Увеличение: Увеличение, добавление или увеличение в количестве, степени или размере
Уменьшенный: Уменьшенный по количеству или размеру
Итого: Кроме того, целое количество или количество
Половина: Половина — это 1 (одна) из 2 (двух) равных частей (частей) целого, когда деленная на 2
Четверть: Четверть равна 1 (одной) из 4 (четырех) равных частей целого при делении на 4
Общий: Это означает наличие, опыт или общее.
В равных долях находится 9-й дивизион.0021 Разделить: При делении разделить означает разделить на части или части Сумма: Сумма – это количество, которое мы получаем, складывая группу чисел
Остаток: При вычитании остаток – это то, что не израсходовано
Больше: Больше или больше по количеству, степени, размеру или протяженности
Меньше: В математике меньше означает меньше. Например, 12 меньше 5 означает 12 – 5 = 7. Но имейте в виду, что 12 меньше 5 – это совершенно другое: 5 – 12 = -7!
Меньше: В математике меньше — это квантификатор вычитания, означающий «меньшее количество» или «меньше». Например, у Джона на 3 книги меньше, чем у Джанет, у которой 8 книг. Сколько книг у Джона?
Квадрат: В математике слово «квадрат» может иметь два значения. Во-первых, в геометрии квадраты — это многоугольники с 4 (четырьмя) прямыми углами и 4 (четырьмя) равными сторонами.
Во-вторых, квадрат также может относиться к числу, умноженному само на себя Сложение: Сложение — это числа, которые комбинируются с другими числами. Например. в 8 + 4 = 12, 8 и 4 являются слагаемыми
Среднее значение: Речь идет о сложении и делении. Вы получаете среднее значение по оценочной шкале, складывая все значения и затем разделив это число на общее количество значений.
Выражение: Выражения — это группы символов, которые составляют математические утверждения. Выражения НЕ имеют знаков равенства
Оценка: Оценки являются приблизительными вычислениями величин, степеней, значений или стоимости
Целое число: Целые числа представляют собой натуральные числа, их отрицательные значения или ноль. Таким образом, целые числа — это положительные или отрицательные целые числа.
