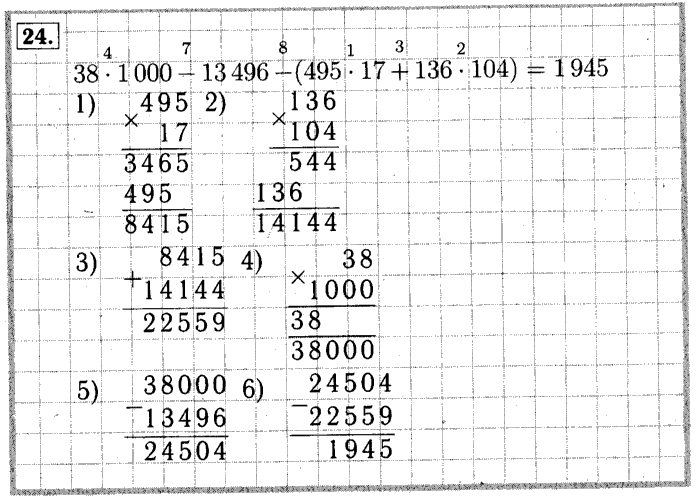
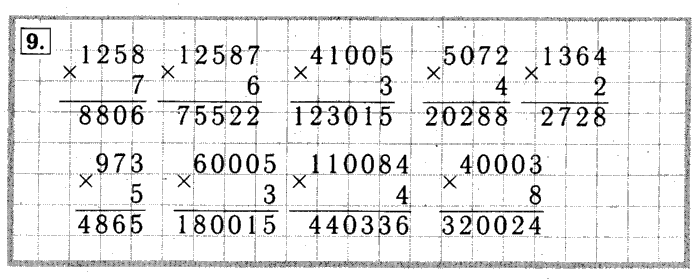
Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.
Калькулятор вычисления суммы, разности, произведения и частного столбиком отобразит все этапы решения примера и даст подробное решение. Калькулятор может сложить, вычесть, умножить и разделить столбиком десятичные дроби и целые числа. Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12).
Введите числа
+−×÷
Вам так же пригодится калькулятор деления столбиком с остатком
Как складывать столбиком
Для того, чтобы сложит два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное сложение справа на лево, например, сложим столбиком 345 и 67.
345 + 67 = 412
110
+345
67
412
1) 5 + 7 = 12; 2 пишем, число 1 запишем над числом 4.
2) 4 + 6 = 10; 10 + 1 = 11; 1 пишем, 1 запишем над числом 3.
3) Под числом 3 нет слагаемого, поэтому просто прибавим 3 + 1 = 4
Получилось 412
Приведем еще один пример: 1567 + 761
1567 + 761 = 2328
1100
+1567
761
2328
1) 7 + 1 = 8, запишем 8.
2) 6 + 6 = 12; 2 пишем, 1 запишем над числом 5.
3) 5 + 7 = 12; 12 + 1 = 13; 3 пишем, 1 запишем над числом 1.
Как складывать столбиком десятичные дроби
Для того, чтобы сложить две десятичные дроби, необходимо записать одну десятичную дробь над другой, совместив их точки. Приведем пример: 123.345 + 46.02
123.345 + 46.02 = 169.365
+123.345
46.020
169.365
1) Запишем число 123.345 над числом 46.02
2) Под числом 5 нет слагаемого, поэтому просто запишем его внизу.
2) Далее сложим 2 и 4; 2 + 4 = 6; запишем 6 внизу.
3) 3 + 0 = 3; записываем 3.
4) Ставим точку
5) 3 + 6 = 9; записываем 9 внизу.
6) 2 + 4 = 6; записываем 6 внизу.
7) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Итак, у нас получилось 169.365
Приведем следующий пример: 123.99 + 12.99
123.99 + 12.99 = 136.98
001010
+123.99
12.99
136.98
1) 9 + 9 = 18; 8 пишем, 1 запишем над числом 9.
2) 9 + 9 = 18; 18 + 1 = 19; 9 пишем, 1 запишем над числом 3.
3) Ставим точку.
4) 2 + 3 = 5; 5 + 1 = 6; 6 запишем внизу
5) 2 + 1 = 3; 3 запишем внизу.
6) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Ответ: 136.98
Для того чтобы сложить десятичную дробь с целым числом, необходимо сложить целую часть десятичной дроби с целым числом. Сложим, например, 23 и 0.34. У числа 23, после точки поставим столько нолей, сколько чисел после точки у десятичной дроби.
23 + 0.34 = 23.34
+23.00
0.34
23.
 34
341) 0 + 4 = 4. Запишем 4.
2) 0 + 3 = 3. Запишем 3.
3) Ставим точку
5) Под числом 2 нет слагаемого, поэтому просто сносим его вниз.
Ответ: 23.34
Как вычитать столбиком
Для того, чтобы вычесть два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное вычитание, например, вычтем столбиком 456 и 89.
456 — 89 = 367
..0
—456
89
367
1) Из 6-ти вычесть число 9 не получится, так как 6 меньше девяти, поэтому займем 1 у числа 5 и поставим над ним точку, получим вместо числа 6 число 16. Отнимем от 16 число 9; 16 – 9 = 7; запишем 7.
2) Так как мы заняли число 1 у числа 5, то теперь осталось число 4. Из числа 4 вычесть число 8 не получится, поэтому займем 1 у соседнего числа 4 и поставим над ним точку, получим вместо числа 4 число 14. Отнимем от числа 14 число 8 = 6. Запишем 6.
3) Под числом 4 нет вычитаемого, поэтому отнимем от числа 4 число 1 (так как мы занимали 1-цу): 4 -1 = 3; запишем число 3.
Получилось 367.
Приведем еще один пример: 307 – 58
307 — 58 = 249
..0
—307
58
249
1) Из числа 7 вычесть число 8 не получится, так как 7 меньше 8, поэтому займем 1 у ноля. Поставим над нолем точку. Когда мы занимаем 1-цу у нуля, ноль становится числом 9! получим вместо 0 число 9. Однако у ноля не получится взять единицу, поэтому двигаемся влево и занимаем единицу у числа 3 и ставим над ним точку; отнимем от 17 число 8; 17 – 8 = 9; запишем 9.
2) Так как мы заняли число 1 у ноля, то теперь осталось число 9. Отнимем от числа 9 число 5 = 4. Запишем 4.
3) Под числом 3 нет вычитаемого, но мы помним, что мы заняли единицу у числа 3, поэтому 3-1 = 2. Запишем число 2.
Получилось 249.
Как вычитать столбиком десятичные дроби
Для того, чтобы отнять из десятичной дроби целое число, либо из целого числа вычесть десятичную дробь нужно у целого числа после точки записать столько нолей, сколько чисел после точки у десятичной дроби, затем записать большее число над меньшим.
Например вычтем столбиком из десятичной дроби 123.478 целое число 56
123.478 — 56 = 67.478
..00000
—123.478
56.000
67.478
Начинаем последовательно вычитать справа налево
1) 8 – 0 = 8. Запишем 8.
2) 7 – 0 = 7. Запишем 7.
3) 4 – 0 = 4. Запишем 4.
4) Ставим точку.
5) Из числа 3 не вычесть число 6, поэтому занимаем единицу у числа 2 и ставим над ним точку. 13 – 6 = 7. Запишем число 7.
6) Над числом 2 стоит точка, значит теперь там уже не число 2, а число 1. Из единицы число 5 не вычесть, поэтому занимаем единицу у числа 1 и ставим над ним точку. 11 – 5 = 6. Запишем число 6.
Ответ: 67.478
Еще один пример на вычитание столбиком десятичной дроби из целого числа.
432 — 2.95
432 — 2.95 = 429.05
0..0.0
—432.00
2.95
429.
 05
051) Из ноля число 5 не вычесть, поэтому займем единицу у ноля и поставим над ним точку, далее, как мы уже знаем ставим точку над числом 2 и занимаем единицу. 10 – 5 = 5. Запишем число 5.
2) Над числом 0 стоим точка, следовательно, 0 превратился в число 9. 9 – 9 = 0. Запишем 0.
3) Над числом два стоит точка значит 2-1 = 1. Из числа 1 число 2 не отнять, поэтому занимаем единицу у числа 3 и ставим над ним точку. 11 – 2 = 9. Запишем число 9.
4) Над числом 3 стоит точка, 3 – 1 = 2. Так как нет вычитаемого, просто сносим число 2 вниз, тоже делаем и с числом 4.
Правила вычитания десятичной дроби из десятичной дроби, такие же как при сложении. Нам так же необходимо сначала совместить точки десятичных дробей и затем выполнить последовательное вычитание справа налево. Вот несколько примеров на вычитание десятичных дробей:
378.326 — 26.57 = 351.756
00.0.00
—378.326
26. 570
570
351.756
0.07 — 0.009 = 0.061
000.0
—0.070
0.009
0.061
Как умножать столбиком
Для того, чтобы умножить одно число на другое необходимо записать первый множитель над вторым, причем не важно какой множитель больше первый или второй, но удобнее чтобы записать более компактное решение записать большее число над меньшим. Затем необходимо каждое число нижнего множителя умножить на каждое число верхнего справа налево, затем суммировать произведения.
На примере будет намного понятнее. Итак, умножим 367 на 12
367 × 12 = 4404
×367
12
734
3670
4404
1. Умножим число 2 на 367 и результат запишем с справа налево от числа 2.
1) 2 × 7 = 14. Запишем число 4, число 1 в уме.
2) 2 × 6 = 12; 12 + 1 = 13. Запишем 3, число 1 в уме.
3) 2 × 3 = 6; 6 + 1 = 7. Запишем число 7. На этом этапе мы получили число 734.
2. Умножим число 1 на 367 и результат запишем справа на лево начиная уже от числа 1 под первой строкой.
1) 1 × 7 = 7. Запишем число 7.
2) 1 × 6 = 6. Запишем число 6.
3) 1 × 3 = 3. Запишем число 3. На этом этапе мы получили число 367
3. Теперь нам необходимо сложить получившиеся два числа 734 и 367
1) Под числом 4 нет слагаемого, поэтом просто снесем его вниз. Запишем число 4.
2) 3 + 7 = 10. Запишем 0 и запомним число 1.
3) 7 + 6 + 1 = 14. Запишем число 4, число 1 в уме.
4) У числа три нет слагаемого, поэтому просто запишет число 3.
На этом решение закончено, получилось 4404.
Как умножать столбиком десятичные дроби
Десятичные дроби столбиком умножать очень просто. Прежде всего, уберем точки из десятичных дробей. Затем произведем умножение уже получившихся целых чисел, далее посчитаем количество чисел в первом и во втором множителе, сложим эти значения, результатом будет число равное количеству чисел после точки в получившемся произведении.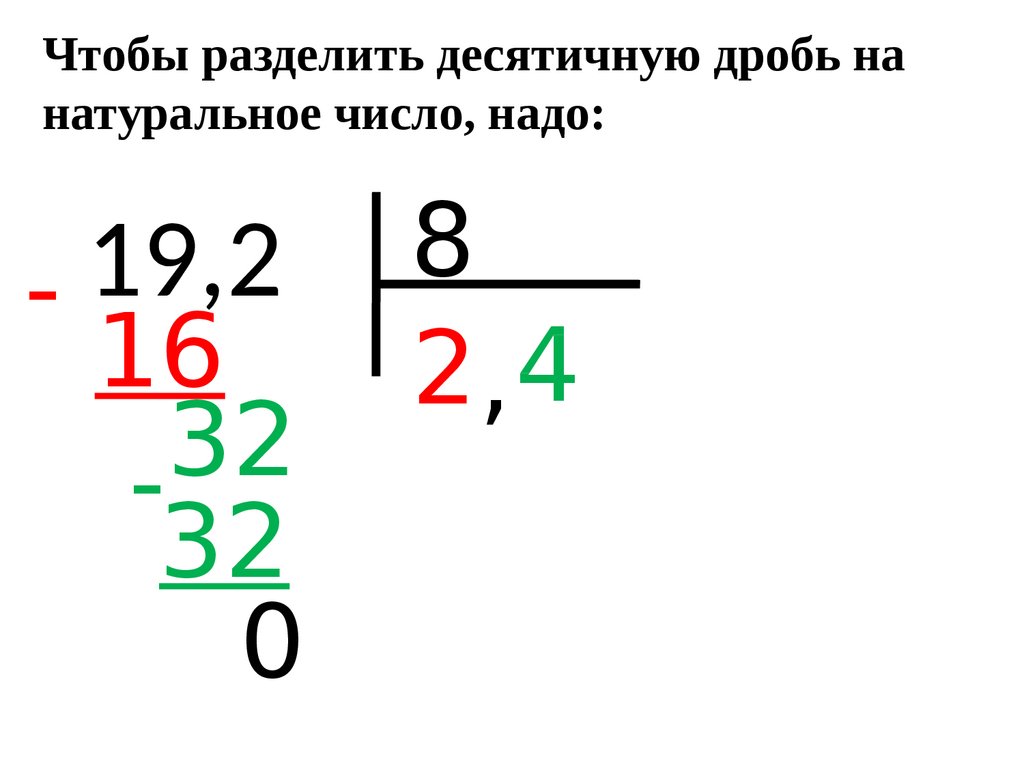 На примерах все станет намного понятнее.
На примерах все станет намного понятнее.
Умножим 0.2354 на 12.3997
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×123997
2354
495988
6199850
37199100
247994000
291888938
Теперь добавим точку в получившейся ответ. Так как в первом множителе 12.3997 после точки стоит 4 числа, и во втором множителе 0.2354 стоит 4 числа, тогда 4 + 4 = 8. Сдедовательно в ответе после точки будет 8 чисел.
2.91888938
×12.3997
0.2354
2.91888938
Умножим 49.265 на 0.0045
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×49265
45
246325
1970600
2216925
Теперь добавим точку в получившейся ответ. Так как в первом множителе 49.265 после точки стоит 3 числа, а во втором множителе 0.0045 стоит 4 числа, тогда 3 + 4 = 7.
0.2216925
×49.265
0.0045
0.2216925
Как делить столбиком
Как делить столбиком целые числа.
Деление столбиком с остатком, в данном материале рассматриваться не будет, если интересно, есть много информации по остатку от деления тут.
Разберем для начала как разделить большее число на меньшее в столбик (когда делимое больше делителя).
На примере будет намного нагляднее изучить данную тему. Итак, разделим 12 на 5
12 : 5 = 2.4
01205
01002.4
0020
0020
0000
При делении числа 12 на число 5 у нас получится конечная десятичная дробь. Кому интересно почитать что такое десятичные дроби — это можно сделать здесь.
1) Сколько раз число 5 помещается в числе 12? Правильно 2 раза. Поэтому первым делом умножим 2 на 5 получим 10.
Поэтому первым делом умножим 2 на 5 получим 10.
2) Теперь отнимем из числа 12 число 10; 12 – 10 = 2. Запишем число 2.
3) В числе 12 нет больше чисел, поэтому поле числа 2 в ответе необходимо поставить точку. Целую часть ответа мы уже нашли! Двигаемся дальше.
4) Теперь будем находить дробную часть нашей десятичной дроби. Поставим ноль рядом с разностью. Получим число 20. Теперь снова думаем, сколько раз число 5 содержится в числе 20? Правильно 4 раза. 5 × 4 = 20.
5) Отнимем от числа 20 число 20; 20 – 20 = 0. Разность равна нулю, следовательно, результатом деления является конечная десятичная дробь.
Ответ: 2.4
Возьмем другой пример, где уже ответом будет являться бесконечная периодическая десятичная дробь. Разделим 7 на 3
7 : 3 = 2.(3)
0703
0602.3
010
009
001
1) В числе 7 число 3 содержится 2 раза. То есть неполное частное деления числа 7 на число 3 равно числу 2. Умножим число 2 на делитель. 2 × 3 = 6.
Умножим число 2 на делитель. 2 × 3 = 6.
2) Отнимем от числа 7 число 6; 7 — 6 = 1; В делимом больше нет чисел, поэтому ставим точку.
3) Начинаем вычислять ответ для дробной части. Для этого к получившейся разности добавим ноль, получим число 10. Неполное частное деления числа 10 на число 3 равно числу 3. Запишем число 3 после точки.
4) 3 × 3 = 9. Из числа 10 отнимем число 9; 10 – 9 = 1. На этом этапе необходимо завершить деление, так как мы уже получали число 1 при вычитании числа 6 из числа 7, следовательно, при дальнейшем решении примера мы снова и снова будем получать число три в виде неполного частного и этот процесс будет продолжаться бесконечно (2.333333333333333333333333333…). Такое повторение называется периодом бесконечной периодической десятичной дроби. Для краткости период записывают в скобках 2.(3)
Деление десятичных дробей в столбик примеры
Разделим 3.12 на 3.6
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 100
7. 12 12 | = | |
| 3.6 |
| 7.12 × 100 | = | |
| 3.6 × 100 |
| 712 | = | |
| 360 |
| 1.9(7) | ||
07120360
036001.97
03520
03240
002800
002520
000280
Разделим 9.4 на 45.1
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 10
| 9.4 | = | |
| 45.1 |
9. 4 × 10 4 × 10 | = | |
| 45.1 × 10 |
| 94 | = | |
| 451 |
| 0.(2084257206) | ||
0940451
00000.2084257206
0940
0902
003800
003608
0001920
0001804
00001160
00000902
000002580
000002255
0000003250
0000003157
00000000930
00000000902
0000000002800
0000000002706
0000000000094
Вам так же пригодится калькулятор деления столбиком с остатком
| Вам могут также быть полезны следующие сервисы |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Показать больше |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона.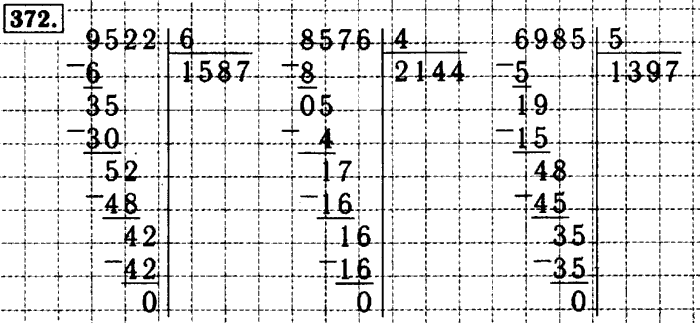 Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Решение длинных примеров в столбик. Как делить в столбик? Как объяснить ребенку деление столбиком? Деление на однозначное, двузначное, трехзначное число, деление с остатком
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
- Цифры.

- Знаки арифметических действий.
- Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
- умножение;
- деление;
- сложение;
- вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
- Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
- Очень простой, интуитивно понятный интерфейс для каждого пользователя.

- Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
- Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах.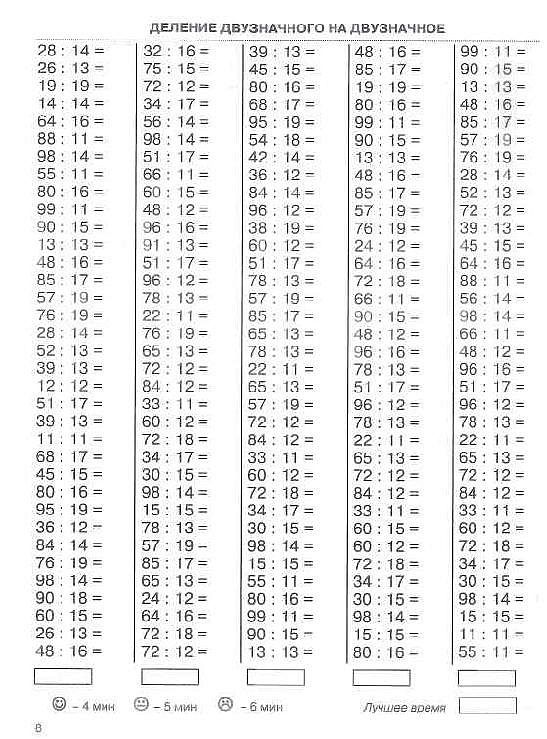 Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.

- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.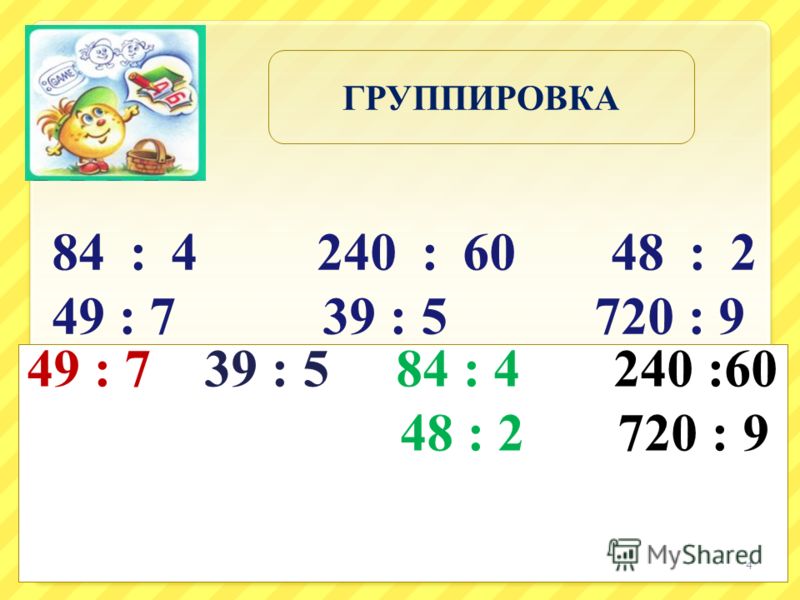
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль.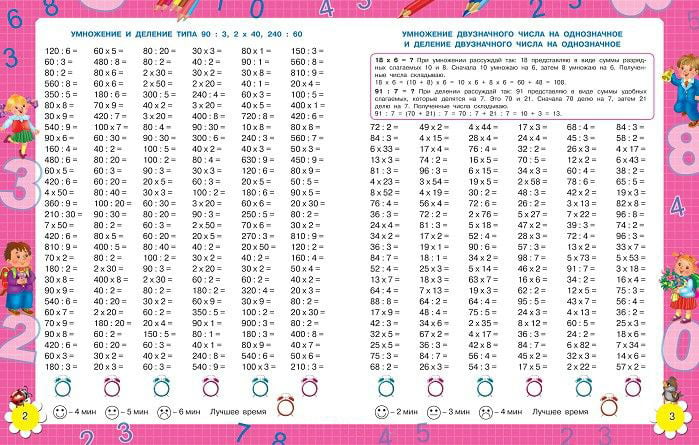 Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.

- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом.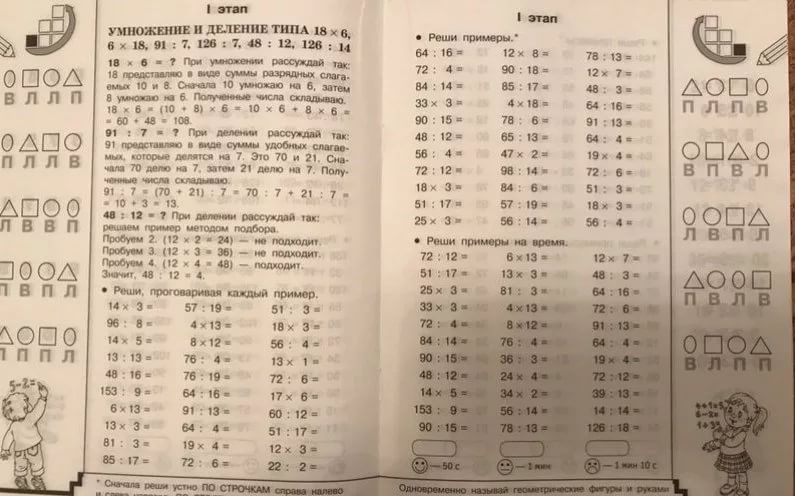 То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.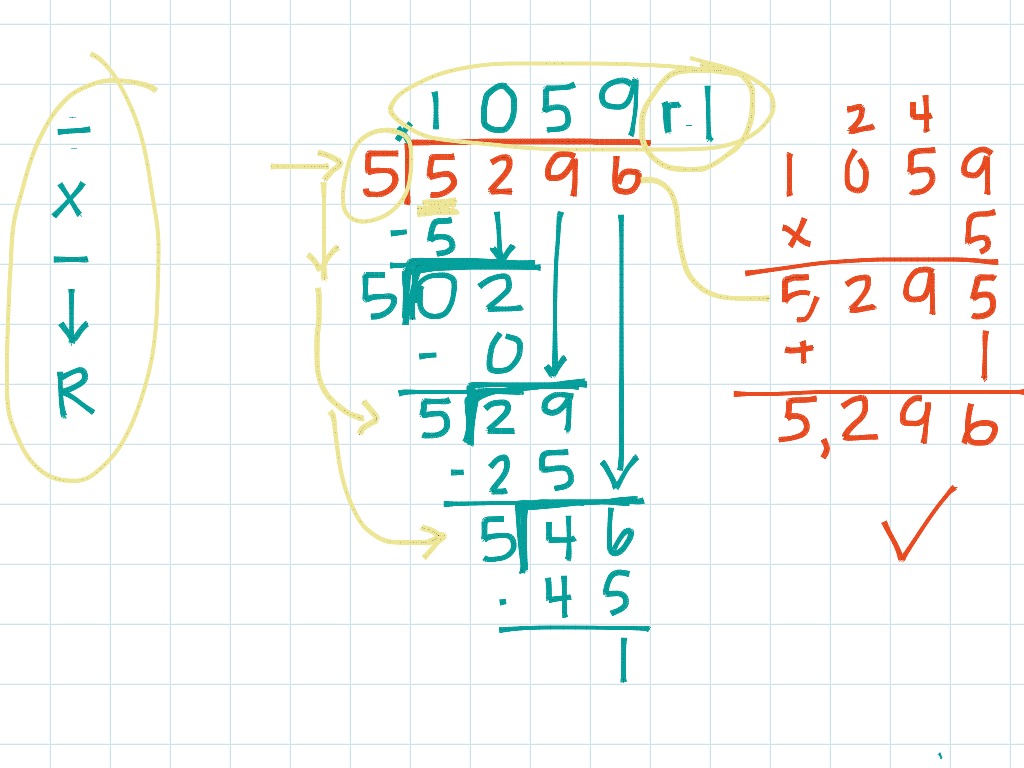
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8 на 2 .
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0
, 1
, 2
, 3
, … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.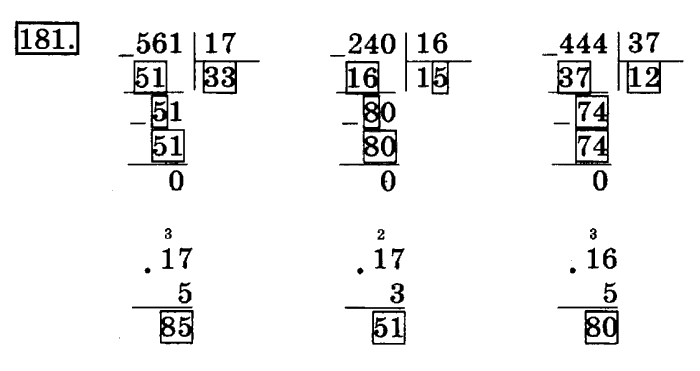
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).
Ответ:
8:2=4 .
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7 на 3 .
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Ответ:
7:3=2 (ост. 1) .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288
на однозначное натуральное число 4
. Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x
). Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=014
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2
по 4
пункты алгоритма.
Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2
по 4
пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=02
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288
на однозначное натуральное число 4
, мы видим, что частным является число 35 072
, (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Пример.
Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .
Решение.
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136
и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
Ответ:
7 136:9=792 (ост. 8) .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Пример.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Решение.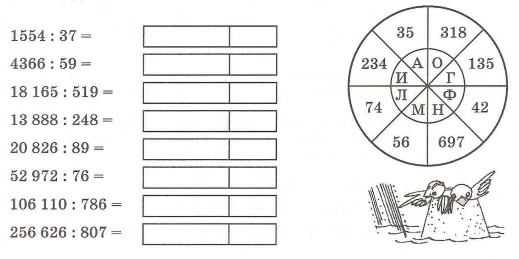
Удобнее всего выполнить деление столбиком.
Ответ:
7 042 035:7=1 006 005 .
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2
, 3
и 4
пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
- Математика.
 Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений. - Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами.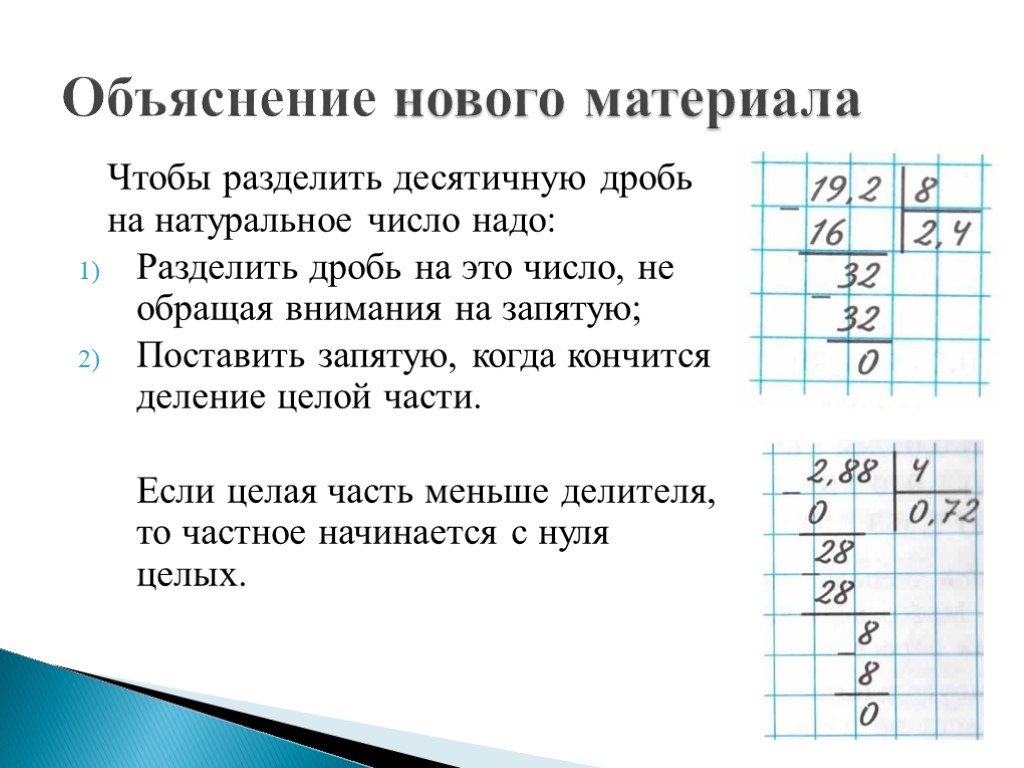 Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.

- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.

- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления.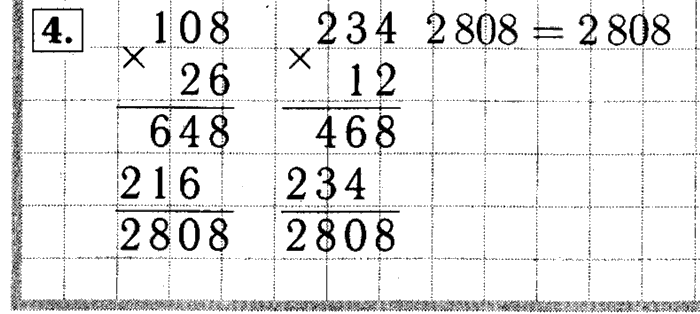 А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Деление столбиком
Правила деления в столбик
Деление в столбик позволяет разделить любое число без использования калькулятора или иных средств, которые автоматически показывают результат.
Для деления в столбик потребуется только листок и ручка (карандаш), в отличие от обычного деления, деление в столбик имеет свои особенности:
- Особую запись примера, при делении в столбик решение записывается не строку, а в столбик.

- При делении в столбик может остаться «остаток» — число которое нельзя разделить, например, при делении 10 на 4 остаток будет 2, таким образом, ответ будет: 10/4=2 (остаток 2), при нормальном делении 10 на 4 результат будет 2,5.
- Нельзя проводит операции с дробями, при делении в столбик можно делить только целые числа, то есть число 2,4 (две целы четыре десятых) разделить не получится.
Понятия: делимое, делитель, частное
При делении в столбик, как и при обычном делении каждое число имеет своё название:
- Делимое – то число, которое необходимо разделить.
- Делитель – то число, на которое необходимо разделить.
- Частное – итог, получившейся результат.
Примеры деления различных цифр (двузначных, трехзначных, четырехзначных) на (двузначные, трехзначные, четырехзначные)
Рассмотрим примеры деления в столбик различных чисел, наиболее простым является деление двузначных (от 10 до 99).
Деление единиц (цифр от 0 до 9) в столбик не целесообразно так как разделить, например, 8 на 2 можно в уме.
Пример деления в столбик двузначных чисел без остатка
Пример 1.
Требуется разделить 81 на 3.
Для наглядности ход решения будет представлен также при от руки.
Шаг 1. Запишем данный пример для деления в столбик:
Шаг 2. Деление цифр начинаем слева направо, сначала проверяем возможность разделить на 3 первую цифру (в примере это 8), для этого следует сравнить цифры если цифра на которую необходимо разделить (в примере это 3) меньше чем первая цифра (в примере это 8), то цифру разделить можно, после того как цифра из делимого выбрана следует умножая делитель (в примере – 3) на цифры начиная с 1 заканчивая 9 найти наиболее близкую к выбранной цифре (в примере 8), рассмотрим алгоритм:
3 * 1 = 3 сравниваем 3 с 8 – 3 меньше 8, значит, продолжаем
3 * 2 = 6 сравниваем 6 с 8 – 6 меньше 8, значит, продолжаем
3 * 3 = 9 сравниваем 9 с 8 – 9 больше 8, значит, 9 не подходит, возвращаемся к предыдущей цифре (у нас это 6).
Первая цифра найдена, необходимо добавить её в запись деления столбиком (так же как это делятся при вычитании в столбик), пример приведён ниже:
Шаг 3. После того как 6 была записана в пример, следует от 8, от того числа с которым ранее проводилось сравнение отнять её (цифру 6), если в ходе вычитания был получен остаток его следует записать (так же как это делятся при вычитании и сложении в столбик), пример приведён ниже:
Шаг 4. Если в ходе вычитания был получен остаток к нему, необходимо добавить (не сложить, а приписать справа) следующее в делимом число (в примере это 1), пример приведён ниже:
Шаг 5. С полученным в ходе объединения цифр числом необходимо проделать ту же операцию, которую была выполнена на Шаге 2, рассмотрим подробнее:
3 * 1 = 3 сравниваем: 3 меньше 21 продолжаем расчёт
3 * 2 = 6 сравниваем: 6 меньше 21 продолжаем расчёт
3 * 3 = 9 сравниваем: 9 меньше 21 продолжаем расчёт
3 * 4 = 12 сравниваем: 12 меньше 21 продолжаем расчёт
3 * 5 = 15 сравниваем: 15 меньше 21 продолжаем расчёт
3 * 6 = 18 сравниваем: 18 меньше 21 продолжаем расчёт
3 * 7 = 21 сравниваем: 21 равно 21 продолжать расчёт не имеет смысла
Вторая цифра найдена её необходимо добавить в частное (результат) (не сложить, а записать рядом).
Полученную в ходе умножения цифру (в пример 21) также следует записать, как это было сделано выше.
Шаг 6. Необходимо провести операцию вычитания, в примере требуется от 21 отнять результат умножения (число 21), если итог равен 0 и больше в делимом нет цифр (в примере их нет), то пример решён, если в результате вычитания цифра больше 0, то это остаток, если цифра больше делителя (в примере 3), то пример решён неверно.
Решение пример в столбик представлен ниже:
Ответ: 27.
Деление сотен в столбик (чисел от 100 до 999)
Деление в столбик не зависит от количества цифр в делимом, отличается лишь количество необходимых операций, то есть чем больше цифр в делимом и меньше в делителе, тем больше будет этапов для нахождения частного (ответа или результата деления цифр).
Но также при делении чисел из 3 цифр существуют особенности, для примера возьмём 525 и разделим его на 25:
Шаг 1. Запишем пример для деления в столбик:
Шаг 2. Деление числа начинается слева направо, но так как у нас делитель состоит из 2 цифр (25), то можно сразу начинать проверку возможности деления первых 2 цифр, алгоритм поиска при делении в столбик всегда одинаков:
Деление числа начинается слева направо, но так как у нас делитель состоит из 2 цифр (25), то можно сразу начинать проверку возможности деления первых 2 цифр, алгоритм поиска при делении в столбик всегда одинаков:
25 * 1 = 25 сравниваем 25 меньше чем 52, продолжаем
25 * 2 = 50 сравниваем 50 меньше 52, если неуверены можно продолжать расчёт и сравнивать, но в примере этого делать не будем, так как понятно, что дальнейший расчёт не имеет смысла.
Если делимое состоит из 3 цифр а делитель из 2, то вначале всегда можно брать 2 первые цифры и искать первую цифру в частное.
Шаг 3. Из 52 необходимо вычесть полученный результат то есть 50, а цифру 2 необходимо зависать в частное.
Шаг 4. После вычитания полученную цифру (в примере 2) необходимо записать и к ней добавить цифру из делимого, получаем 25, с этим числом необходимо повторить расчёт:
25 * 1 = 25 сравниваем 25 равно 25, продолжать расчёт не нужно.
Шаг 5. Записываем полученные цифры.
Ответ: 21.
Деление в столбик с остатком
Ещё одной особенностью деления в столбик является возможность появления остатка, рассмотрим такой пример.
Необходимо разделить 311 на 3.
Шаг 1. Записываем цифры для деления в столбик.
Шаг 2. Деление начинаем слева направо, проверяем возможность деления первой цифры, для этого необходимо сравнить цифру, с которой хотим начинать расчёт (в примере это 3) и делитель (в примере это также 3), если эти цифры равны или делитель меньше, то можно продолжать расчёт, если же делитель больше, то следует для расчёт взять ещё одну цифру из делимого, в примере 3 равно 3, значит, можно проводить расчёт:
3 * 1 = 3 сравниваем 3 равно 3 первая цифра в частное найдена
Шаг 3. Проводим операцию вычитания 3 из 3, в частное записываем 1, как показано на рисунке:
Шаг 4.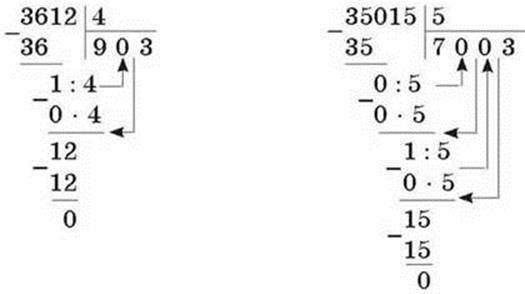 При вычитании был получен 0, но это не меняет процесс деления в столбик, также требуется записать следующую после взятой ранее цифры из делимого (в примере это 1), после того как цифра была записана необходимо проверить возможность использовать данную цифру для расчёта, для этого сравниваем 1 и 3 (3 – это делитель), так как 1 меньше 3 проводить расчёт нельзя, следует взять ещё одну цифру из делимого, но при этом требуется в частное (в ответ) добавить 0, как показана на рисунке:
При вычитании был получен 0, но это не меняет процесс деления в столбик, также требуется записать следующую после взятой ранее цифры из делимого (в примере это 1), после того как цифра была записана необходимо проверить возможность использовать данную цифру для расчёта, для этого сравниваем 1 и 3 (3 – это делитель), так как 1 меньше 3 проводить расчёт нельзя, следует взять ещё одну цифру из делимого, но при этом требуется в частное (в ответ) добавить 0, как показана на рисунке:
Шаг 5. Проводим расчёт с полученным числом (в примере 11):
3 * 1 = 3 сравниваем 3 меньше 11, продолжаем
3 * 2 = 6 сравниваем 6 меньше 11, продолжаем
3 * 3 = 9 сравниваем 9 меньше 11, неуверены можно продолжить, но в примере этого делать не будем, так как не имеет смысла.
Шаг 5. В частное записываем 3, далее проводим операцию вычитания из 11 вычитаем 9 получаем 2, так как 2 меньше 3 то проводить дальнейший расчёт делением в столбик невозможно, это и будет остаток.
Ответ: 103 (остаток 2).
Примеры в столбик 5. Как делить десятичные дроби
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3.
 Записываем 3 в ответ под чертой справа
Записываем 3 в ответ под чертой справа - Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6.
 Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4 - Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30.
 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6 - Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).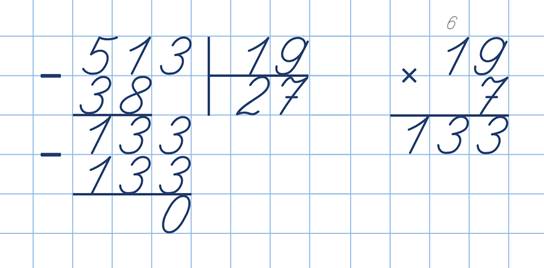
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении.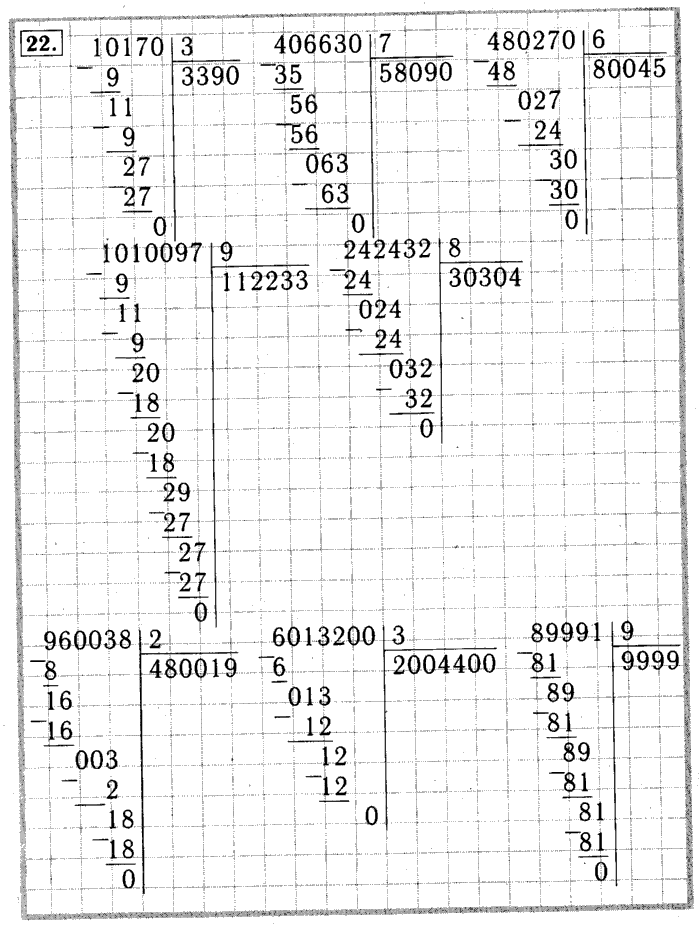 Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.

Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.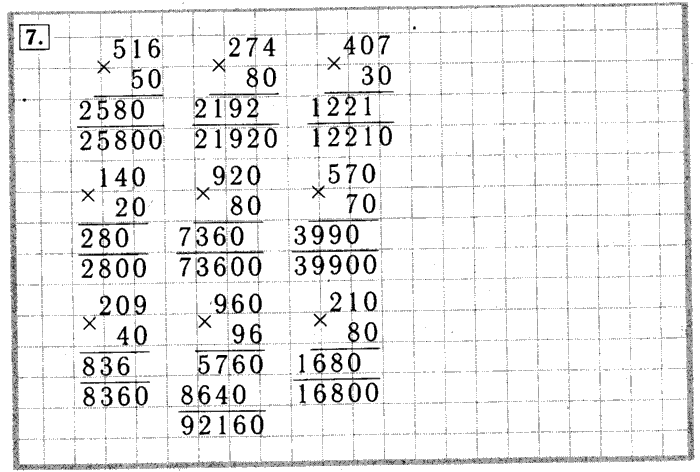
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа.
 Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления.
 Обычно оно состоит из одной цифры, максимум из двух.
Обычно оно состоит из одной цифры, максимум из двух. - Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель.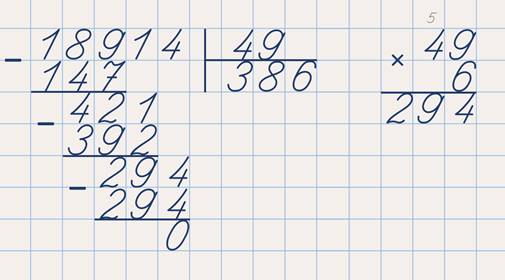 Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра.
 Умножение даст 284 и 32.
Умножение даст 284 и 32. - Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.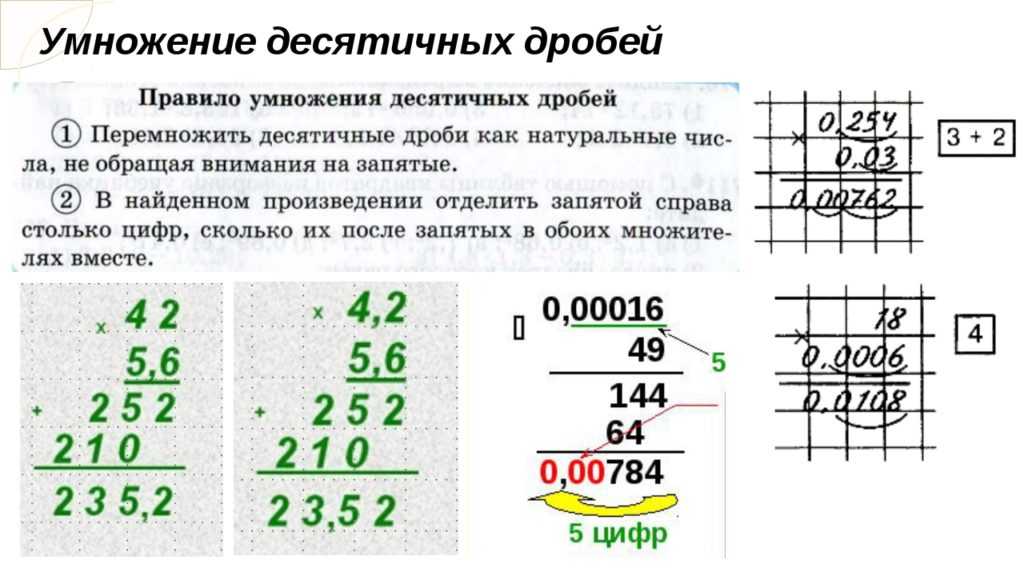
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей.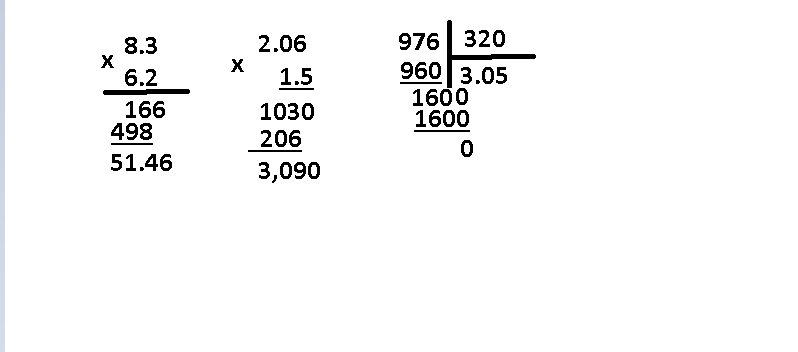 Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.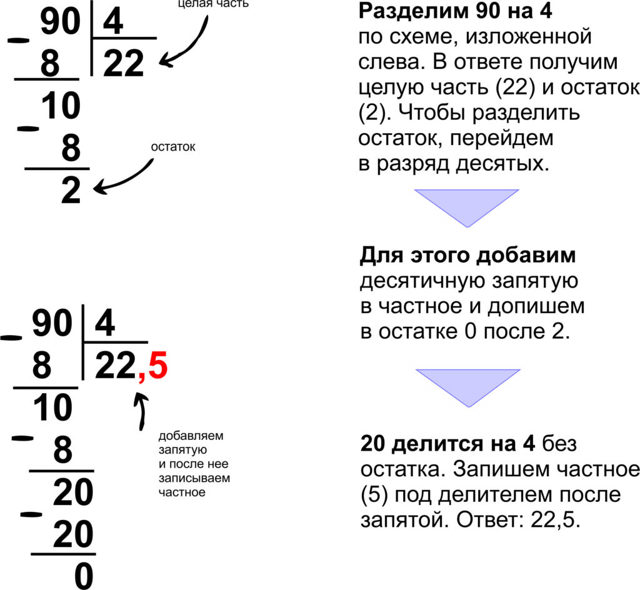 д.) во время конструирования, игр и наблюдений за природой.
д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление десятичных в столбик калькулятор. Как научиться делить столбиком: примеры и решения
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134.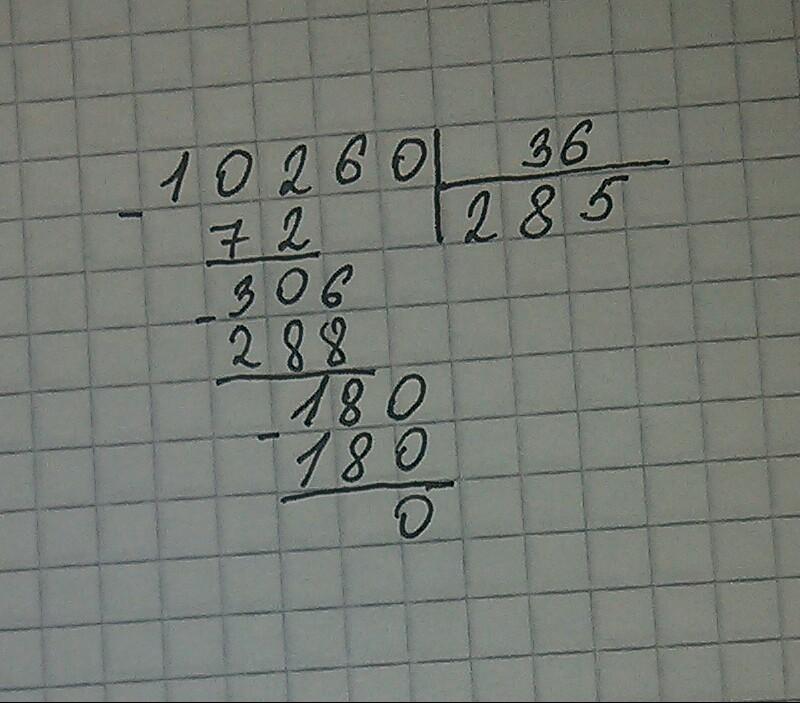 Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах.
 Возьмите счетные палочки, например, 8 штук
Возьмите счетные палочки, например, 8 штук - Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25.
 Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа - Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий.
Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да.
 Получается 2, записываем эту цифру в ответ
Получается 2, записываем эту цифру в ответ - Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4.
 Умножаем 4 на 716, получается 2864
Умножаем 4 на 716, получается 2864 - Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0.
 Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4 - К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным.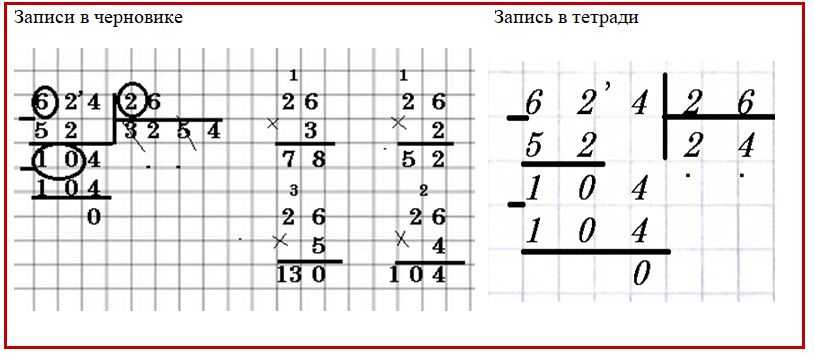 Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления.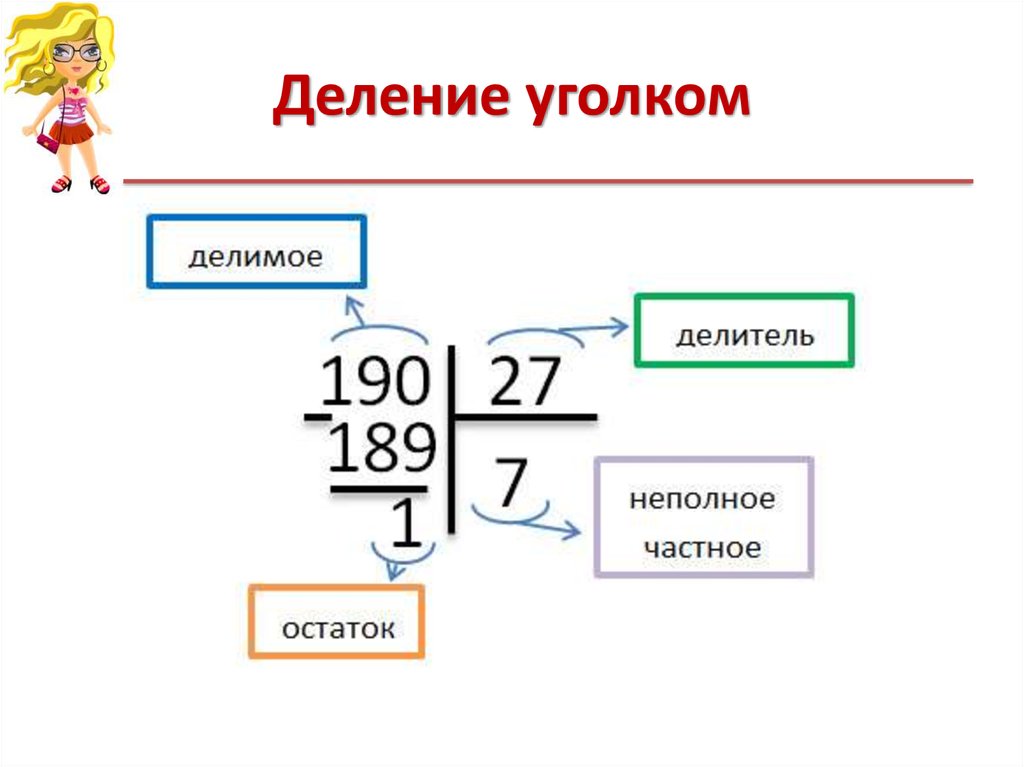 Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта.
 Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8 на 2 .
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0
, 1
, 2
, 3
, … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8
на 2
. Мы видим, что частное 8:2
равно 4
(и остаток равен 0
).
Мы видим, что частное 8:2
равно 4
(и остаток равен 0
).
Ответ:
8:2=4 .
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7 на 3 .
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Ответ:
7:3=2 (ост. 1) .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше.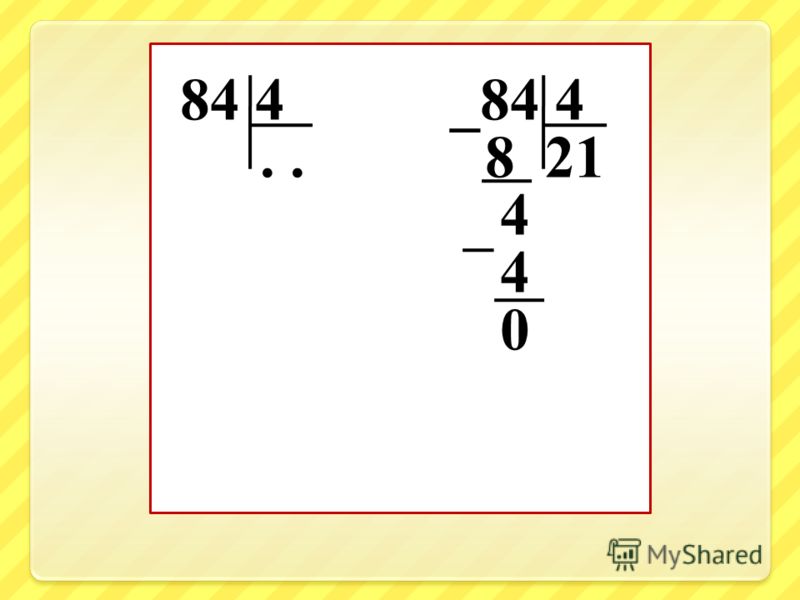 Выделяем это число в записи делимого.
Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x
). Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
(Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=014
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=02
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Пример.
Выполните деление в столбик, если делимое равно 7 136
, а делителем является однозначное натуральное число 9
.
Решение.
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136
и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
Ответ:
7 136:9=792 (ост. 8) .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Пример.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Решение.
Удобнее всего выполнить деление столбиком.
Ответ:
7 042 035:7=1 006 005 .
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2
по 4
этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
Это действительно так, так как со 2
по 4
этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие.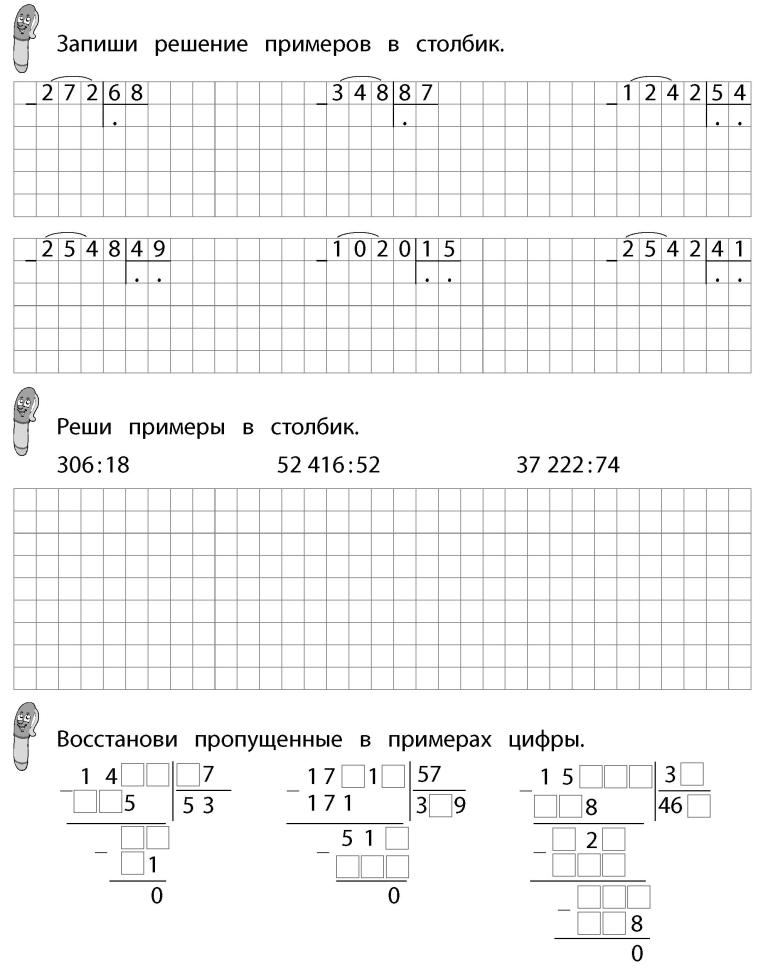 Что же такое деление в столбик? Ответ можете найти ниже:
Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.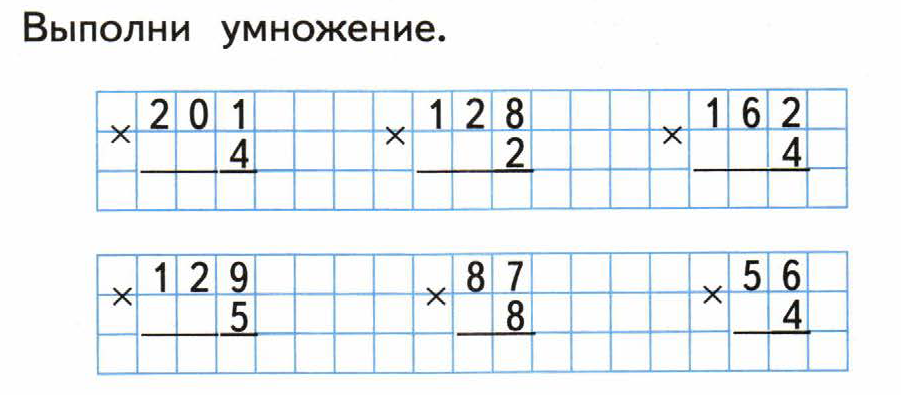
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление столбиком. Онлайн калькулятор | Математика
- Как записывать деление в столбик
- Как делить столбиком
- Деление столбиком с остатком
- Калькулятор деления столбиком
Как записывать деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно.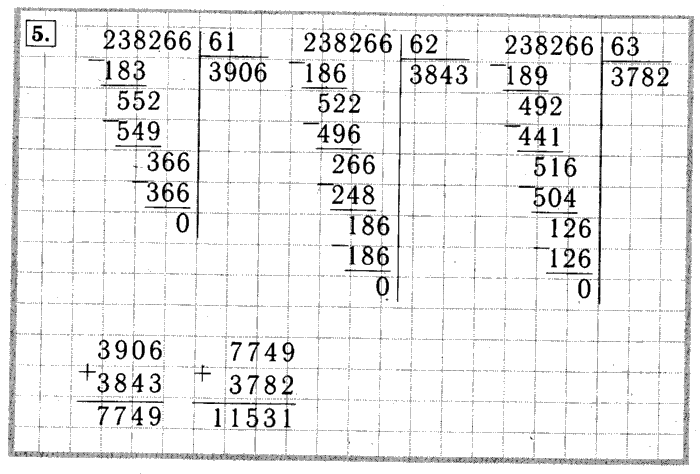 Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело.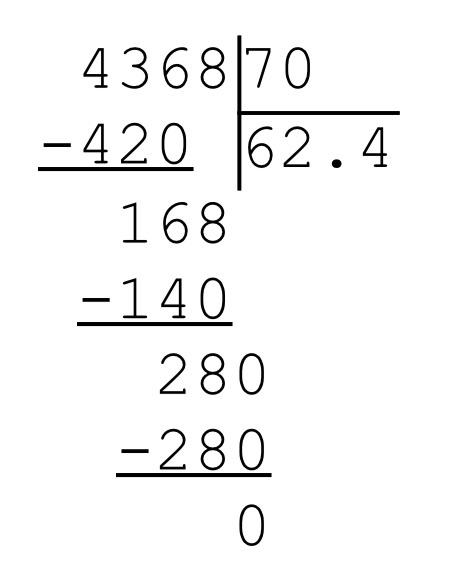 В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
780 : 12 = 65.
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27.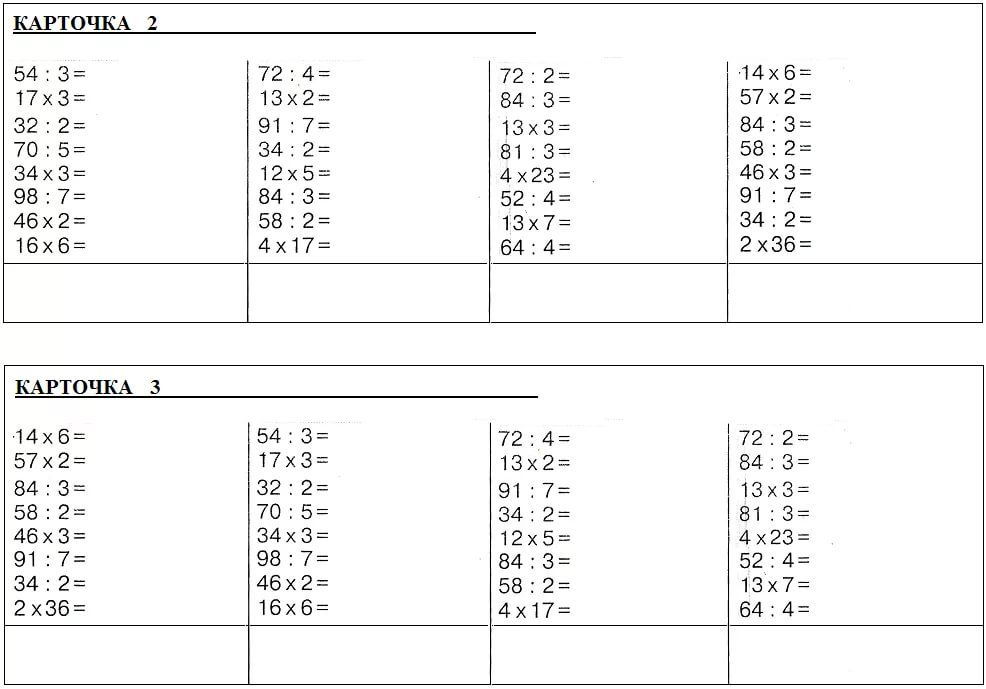 Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
9027 : 9 = 1003.
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
3000 : 6 = 500.
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340 : 23 = 58 (остаток 6).
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3 : 10 = 0 (остаток 3).
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку
Просто введите делимое и делитель и нажмите кнопку Вычислить
.
шагов к задаче на длинное деление (с примерами)
Математика может быть сложной. Упростите задачу, разбив такую сложную тему, как деление, на простые для выполнения длинные этапы деления. Вот что такое длинное деление. Это способ разбить деление больших чисел на простые шаги. Изучите шаги на нескольких примерах с длинным делением.
части задачи на деление в длину
Реклама
Что такое длинное деление?
Разделение 543 439к 31 было бы сложно сделать в вашей голове. Таким образом, вместо того, чтобы сосредотачивать все свои умственные способности на делении, вы можете использовать метод длинного деления, который разбивает числа на шаги. Эти шаги позволяют вам брать одну часть числа за раз, делая математику настолько простой, что с ней справится даже четвероклассник.
Термины, используемые в делении в длинное число
Прежде чем вы научитесь выполнять деление в длинное число, необходимо ознакомиться с несколькими важными математическими терминами. Вы можете встретить задачу на деление, записанную по-разному, например, с использованием ÷ или / для обозначения «делится на».
Вы можете встретить задачу на деление, записанную по-разному, например, с использованием ÷ или / для обозначения «делится на».
- Dividend — число, которое требует деления
- Divisor — Число, которое вы делите на
- Коэффициент — Ответ
- Остальная
Следовательно, в уравнении 1327 / 25 = 53 R2 1327 — делимое, 25 — делитель, 53 — частное, а 2 — остаток. Хорошо, теперь, когда у вас есть основы, пришло время погрузиться в то, как делить.
Простые шаги длинного деления
Как правило, длинное деление разбивается на пять различных шагов. Исследуйте каждый отдельный шаг, используя уравнение:
1579 / 6 = x.
Шаг 1: Разделить
Полное деление состоит в том, чтобы разбить уравнение на разные части. Поэтому вместо того, чтобы смотреть на все уравнение, вы смотрите на первое число делимого, которое в уравнении 1579/6 является числом 1.
 Спросите себя: сколько 6 в 1? Поскольку 1 меньше 6, ваш ответ будет 0,9.0003
Спросите себя: сколько 6 в 1? Поскольку 1 меньше 6, ваш ответ будет 0,9.0003Реклама
Шаг 2: Умножение
Теперь, когда вы знаете, что 6 превратится в 1 ноль раз, вам нужно умножить (6 * 0 = 0). Поместите ноль под 1 в уравнении.
Реклама
Шаг 3: Вычтите
Теперь пришло время вычесть числа одно из другого (1 — 0 = 1). Вы запишите разницу под чертой в своем уравнении.
Реклама
Шаг 4: Уменьшите число
После завершения вычитания вы уменьшаете следующее число в уравнении. В нашем дивиденде вам нужно было бы уменьшить 5.
Advertisement
Шаг 5: Повторите
Как только вы поймете шаги 1-4, вам просто нужно повторять деление, умножение, вычитание и уменьшение числа до тех пор, пока не останется больше чисел, которые вы можете записать. Итак, для нашего уравнения вы обнаружите, что 1579 / 6 = 263 R1.
Реклама
Примеры деления на длинное деление
Теперь, когда вы знаете, как решить задачу на деление на длинное, пора попробовать самостоятельно выполнить несколько примеров.
 Вам нужно будет записать их, используя стандартное форматирование для задачи на деление.
Вам нужно будет записать их, используя стандартное форматирование для задачи на деление.- 1204 / 4
4 переходит в 1 ноль раз
1 — 0 = 1, 2 выпадает
4 переходит в 12 три раза (первое число в ответе 3)
12 — 12 = 0, 0 выпадает вниз
4 переходит в 0 ноль раз (второе число в ответе 0)
0 — 0 = 0, 4 выпадает вниз
4 переходит в 4 один раз (третье число в ответе 1), ответ 301
Проверьте свой ответ: 301 * 4 = 1204
- 3024 / 24
24 входит в число 3, умноженное на 9.0011 3 — 0 = 3, 0 выпадает
24 входит в число 30 один раз (первое число в ответе равно 1)
30 — 24 = 6, 2 выпадает, образуя 62
24 входит в число 62 два раза (второе число в ответе ответ 2)
62 — 48 = 14, 4 выпадает, чтобы получить 144
24 входит в 144 шесть раз (последнее число 6), ответ 126
Проверьте свой ответ 24 * 126 = 3024 - 675 / 5
5 входит в число 6 один раз (первое число в ответе 1)
6 — 5 = 1, 7 выпадает
5 входит в число 17 три раза (второе число в ответе равно 3)
17 — 15 = 2, 5 выпадает
5 входит в 25 пять раз (последнее число в ответе 5), ответ 135
Проверьте свой ответ 5 * 135 = 675 - 679 / 5
5 входит в число 6 один раз (первое число в ответе равно 1)
6 — 5 = 1, 7 выпадает
5 входит в число 17 три раза (второе число в ответе равно 3)
17 — 15 = 2, 9 выпадает
5 входит в 29 пять раз (последнее число в ответе 5)
у вас есть остаток 4, ответ 135 R4
Проверьте свою работу (5 * 135) + 4 = 679
Почему в некоторых уравнениях есть остаток
Не каждый делитель, который у вас есть при делении на две части, делится поровну.
 Поэтому в большинстве случаев у вас есть оставшийся бит, который нельзя разделить на число дальше. Это называется вашим остатком. Это представлено в математическом уравнении с буквой R. Как только вы немного углубитесь в рациональные числа, вы увидите, как вписывается остаток!
Поэтому в большинстве случаев у вас есть оставшийся бит, который нельзя разделить на число дальше. Это называется вашим остатком. Это представлено в математическом уравнении с буквой R. Как только вы немного углубитесь в рациональные числа, вы увидите, как вписывается остаток!Реклама
Как делить десятичные дроби с помощью длинного деления
При делении десятичных дробей в длинном делении вы используете те же пять шагов, что и в примере задачи на длинное деление. Однако вам нужно поставить десятичную дробь от делителя на ту же позицию в частном.
Упростите этапы деления в длинное число
Деление в длинное не сложно, так как оно разбивает большое число на несколько меньших чисел. Тем не менее, это может стать немного сложнее, чем больше число. Пока вы следуете своим основным пяти шагам, вы уже на пути к тому, чтобы стать мастером длинного дивизиона. Если деление в длинных числах было проще простого, то вам, возможно, захочется углубиться в глубокие воды квадратных уравнений.
 Это может заставить вас желать простоты деления на длинные.
Это может заставить вас желать простоты деления на длинные.Штатный писатель
Длинная дивизия — Шаги | Метод
Длинное деление — это метод деления больших чисел, который разбивает задачу деления на несколько последовательных шагов. Как и в обычных задачах на деление, делимое делится на делитель, который дает результат, известный как частное, а иногда и остаток. Давайте узнаем больше о методе длинного деления вместе с его шагами и примерами в этой статье.
1. Что такое метод длинного деления? 2. Части длинной дивизии 3. Как сделать длинное деление? 4. Часто задаваемые вопросы о Long Division Что такое метод длинного деления?
В математике длинное деление — это метод деления больших чисел на шаги или части, разбивающий задачу деления на последовательность более простых шагов.
 Это наиболее распространенный метод, используемый для решения задач, основанных на делении. Обратите внимание на следующее длинное деление, чтобы увидеть делитель, делимое, частное и остаток.
Это наиболее распространенный метод, используемый для решения задач, основанных на делении. Обратите внимание на следующее длинное деление, чтобы увидеть делитель, делимое, частное и остаток.Части длинной дивизии
При выполнении деления в длинное число нам необходимо знать важные части деления в длинное число. Основные части длинного деления могут быть перечислены следующим образом:
- Дивиденд
- Делитель
- Коэффициент
- Остаток
В следующей таблице описаны части длинного деления со ссылкой на приведенный выше пример.
Дивиденд Число, которое необходимо разделить. 75 Делитель Число, на которое делится делимое. 4 Частное Результат деления. 18 Остаток Оставшаяся часть или число, оставшееся после деления, которое нельзя разделить дальше. 
3 Как сделать длинное деление?
Деление — одна из четырех основных математических операций, три другие — сложение, вычитание и умножение. В арифметике длинное деление — это стандартный алгоритм деления больших чисел, разбивающий задачу деления на ряд более простых шагов. Давайте узнаем о шагах, которые выполняются в длинном делении.
Длинные шаги деления
Чтобы выполнить деление, нам нужно понять несколько шагов. Делимое отделяется от делимого правой скобкой 〈)〉 или вертикальной чертой 〈|〉, а делимое отделяется от частного винкулумом (чертой чертой). Теперь давайте выполним шаги длинного деления, приведенные ниже, чтобы понять процесс.
- Шаг 1: Возьмите первую слева цифру делимого. Проверьте, больше ли эта цифра делителя или равна ему.
- Шаг 2: Затем разделите на делитель и запишите ответ сверху как частное.
- Шаг 3: Вычтите результат из цифры и запишите разницу ниже.

- Шаг 4: Запишите следующую цифру делимого (если она есть).
- Шаг 5: Повторите тот же процесс.
Давайте взглянем на приведенные ниже примеры для лучшего понимания концепции. При делении в длинное мы можем столкнуться с проблемами, когда остатка нет, а в некоторых вопросах есть остаток. Итак, сначала научимся делению, при котором мы получаем остаток.
Деление с остатком
Случай 1: Когда первая цифра делимого больше или равна делителю.
Пример: Деление 435 ÷ 4
Решение: Шаги этого длинного деления приведены ниже:
- Шаг 1: Здесь первая цифра делимого равна 4 и равна делителю. Итак, 4 ÷ 4 = 1. Итак, 1 записывается сверху как первая цифра частного.
- Шаг 2: Вычесть 4 — 4 = 0. Уменьшить вторую цифру делимого и поместить ее рядом с 0.
- Шаг 3: Теперь 3 < 4.
 Следовательно, мы пишем 0 как частное и записываем следующую цифру делимого и ставим ее рядом с 3.
Следовательно, мы пишем 0 как частное и записываем следующую цифру делимого и ставим ее рядом с 3. - Шаг 4: Итак, у нас есть 35 в качестве нового делимого. 35 > 4, но 35 не делится на 4, поэтому мы ищем число чуть меньше 35 в таблице 4. Мы знаем, что 4 × 8 = 32, что меньше 35, поэтому мы идем на это.
- Шаг 5: Запишите 8 в частном. Вычесть: 35 — 32 = 3.
- Шаг 6: Теперь 3 < 4. Таким образом, 3 — остаток, а 108 — частное.
Случай 2: Когда первая цифра делимого меньше делителя.
Пример: Разделить 735 ÷ 9
Решение: Разделим это, используя следующие шаги.
- Шаг 1: Так как первая цифра делимого меньше делителя, в частном поставьте ноль и запишите следующую цифру делимого. Теперь рассмотрим первые 2 цифры, чтобы продолжить деление.
- Шаг 2: 73 не делится на 9, но мы знаем, что 9 × 8 = 72, так что действуем.

- Шаг 3: Запишите 8 в частном и вычтите 73 — 72 = 1.
- Шаг 4: Сбросьте 5. Число, которое будет рассматриваться сейчас, равно 15.
- Шаг 5: Поскольку 15 не делится на 9, но мы знаем, что 9 × 1 = 9, берем 9.
- Шаг 6: Вычесть: 15 — 9 = 6. Запишите 1 в частном.
- Шаг 7: Теперь 6 < 9. Таким образом, остаток = 6 и частное = 81.
Случай 3: Это случай деления в большую сторону без остатка.
Деление без остатка
Пример: Разделить 900 ÷ 5
Решение: Разделим это, используя следующие шаги.
- Шаг 1: Будем считать первую цифру делимого и ее на 5. Здесь это будет 9 ÷ 5.
- Шаг 2: Теперь 9 не делится на 5, а 5 × 1 = 5, поэтому запишите 1 как первую цифру в частном.
- Шаг 3: Запишите 5 под 9 и вычтите 9 — 5 = 4.

- Шаг 4: Поскольку 4 < 5, мы уменьшим 0 из делимого до 40.
- Шаг 5: 40 делится на 5, а мы знаем, что 5 × 8 = 40, поэтому запишите 8 в частном.
- Шаг 6: Запишите 40 под 40 и вычтите 40 — 40 = 0.
- Шаг 7: Снизьте следующий 0 из делимого. Поскольку 5 × 0 = 0, мы пишем 0 как оставшееся частное.
- Шаг 9: Следовательно, частное = 180 и после деления не остается остатка, то есть остаток = 0.
Задачи на деление в длинное число также включают задачи, связанные с многочленами в длинное деление и делением в длинное с десятичными дробями.
Длинное деление многочленов
Если нет общих множителей между числителем и знаменателем или если вы не можете найти множители, вы можете использовать процесс длинного деления, чтобы упростить выражение. Для получения дополнительной информации о полиномах деления в длину посетите страницу Полиномы деления.

Деление в длинное с десятичными дробями
Деление в длинное с десятичными дробями можно легко выполнить так же, как и обычное деление. Для получения дополнительной информации о делении в длинное с десятичными дробями посетите страницу Деление десятичных дробей.
Советы и рекомендации по делению в длину:
Ниже приведены несколько важных советов и рекомендаций, которые помогут вам при работе с делением в длину:
- Остаток всегда меньше делителя.
- При делении делитель не может быть равен 0,
- Деление — это повторное вычитание, поэтому мы можем проверить наше частное повторными вычитаниями.
- Мы можем проверить частное и остаток от деления, используя формулу деления: Делимое = (Делитель × Частное) + Остаток.
- Если остаток равен 0, то мы можем проверить наше частное, умножив его на делитель. Если произведение равно делимому, то частное верно.
☛ Статьи по теме
- Формула длинного дивизиона
- Длинное деление многочленов
- Длинное деление с остатками Рабочие листы
- Полное деление без остатка Рабочие листы
- Длинное деление с двузначными делителями Рабочие листы
- Калькулятор длинного деления
Часто задаваемые вопросы о длинном дивизионе
Что такое длинное деление в математике?
Длинное деление — это процесс деления больших чисел удобным способом.
 Число, которое делится на более мелкие группы, называется делимым, число, на которое мы делим его, называется делителем, значение, полученное после выполнения деления, называется частным, а число, оставшееся после деления, называется остатком.
Число, которое делится на более мелкие группы, называется делимым, число, на которое мы делим его, называется делителем, значение, полученное после выполнения деления, называется частным, а число, оставшееся после деления, называется остатком.Как сделать длинное деление?
Следующие шаги объясняют процесс деления в большую сторону:
- Запишите делимое и делитель на соответствующих позициях.
- Возьмите первую слева цифру делимого.
- Если эта цифра больше или равна делителю, то разделите ее на делитель и сверху запишите ответ как частное.
- Запишите произведение под делимым и вычтите результат из делимого, чтобы получить разницу. Если эта разность меньше делителя, а в делимом не осталось чисел, то это считается остатком и производится деление. Однако, если в делимом больше цифр, которые нужно перенести вниз, мы продолжаем тот же процесс, пока в делимом не останется больше цифр.
Каковы этапы длинного деления?
Ниже приведены 5 основных шагов деления в большую сторону.
 Например, давайте посмотрим, как мы делим 52 на 2.
Например, давайте посмотрим, как мы делим 52 на 2.- Шаг 1: Рассмотрим первую цифру делимого, которая в этом примере равна 5. Здесь 5 > 2. Мы знаем, что 5 не делится на 2.
- Шаг 2: Мы знаем, что 2 × 2 = 4, поэтому запишем 2 как частное.
- Шаг 3: 5 — 4 = 1 и 1 < 2 (Записав произведение 4 под делимым, мы их вычтем).
- Шаг 4: 1 < 2, поэтому мы уменьшаем 2 из делимого и теперь получаем 12 в качестве нового делимого.
- Шаг 5: Повторяйте процесс до тех пор, пока не получите остаток меньше делителя. 12 делится на 2, так как 2 × 6 = 12, поэтому мы пишем 6 в частном, а 12 — 12 = 0 (остаток).
Следовательно, частное равно 26, а остаток равен 0.
Как выполнить длинное деление с двумя цифрами?
При длинном делении на 2 цифры считаем обе цифры делителя и проверяем на делимость первых двух цифр делимого. Если первые 2 цифры делимого меньше делителя, то учитывают первые три цифры делимого.
 Продолжайте деление так же, как мы делим обычные числа.
Продолжайте деление так же, как мы делим обычные числа.Что такое длинное деление многочленов?
В алгебре длинное деление многочленов — это алгоритм деления многочлена на другой многочлен той же или меньшей степени. Например, (4x 2 — 5x — 21) является многочленом, который можно разделить на (x — 3) по определенным правилам, что даст в результате 4x + 7 в качестве частного.
Как выполнить длинное деление с десятичными дробями?
Длинное деление с десятичными знаками выполняется так же, как и обычное деление. Это следует шагам, указанным ниже:
- Запишите деление в стандартной форме.
- Начните с деления целой части числа на делитель.
- Поместите десятичную запятую в частном над десятичной запятой делимого.
- Опустить цифры до десятых долей, т. е. цифру после запятой.
- Разделите и запишите другую цифру по порядку.
- Деление до тех пор, пока не закончатся все цифры делимого и в остатке не получится число меньше делителя или 0.

Дивиденд в делении – значение, формула, примеры
Дивиденд – это целое число или количество вещей, которые необходимо разделить на определенные равные части. Деление — это процесс деления числа на равные части с остатком, если данное число не может быть разделено на части поровну. Дивиденды являются важной частью операции деления.
1. Что такое Дивиденды в разделе Значение? 2. Как определить дивиденд? 3. Формула дивидендов 4. Дивиденд в дробях 5. Разница между дивидендом и делителем 6. Часто задаваемые вопросы о дивидендах Что такое Дивиденды в разделе Значение?
Когда мы делим любое число p на число q (p ÷ q), здесь в этом делении факт ‘p’ относится к делимому.
 Давайте разберемся в этом на примере. Разделите число 20 на 5. Запишем факт деления для данного примера.
Давайте разберемся в этом на примере. Разделите число 20 на 5. Запишем факт деления для данного примера.
Факт деления = 20 ÷ 5. Здесь 20 — делимое.Определение дивиденда
В процессе деления делимое — это число, которое полностью делится на делитель, оставляя результат в виде остатка. Другими словами, это целое, которое нужно разделить на части. Например, 15 яблок нужно разделить между 3 детьми. Здесь 15 — делимое. Деление может быть выполнено в различных формах. Разберемся, как идентифицировать делимое в разных представлениях.
Как определить дивиденд?
При делении делимое делится на равные группы по делителю. Число, которое делится в задаче на деление, называется делимым , а число, на которое делится делимое, называется делителем . Существует 3 различных способа представления факта деления. Во всех соответствующих формах результаты остаются одинаковыми. Давайте в общих чертах посмотрим на изображение ниже, на котором показаны различные методы записи дивидендов.

На изображении выше 32 — это делимое, представленное в трех разных формах.
Формула дивидендов
Без дивидендов операция деления невозможна. Предположим, нам нужно разделить число 75 на 5. Математически это можно представить как факт деления, например, 75 ÷ 5 = 15. В этом факте деления:
- Число 75 является делимым. Это число, которое нужно разделить.
- Число 5 это Делитель. Это число, которое делит делимое.
- Число 15 — это частное.
- Остаток для вышеуказанного случая равен нулю.
Чтобы провести тщательную проверку деления, мы можем использовать формулу для нахождения дивидендов или, другими словами, формулу деления. Посмотрите на формулу, упомянутую ниже.
Дивиденд = (Делитель × Частное) + Остаток.
Рассмотрим еще один пример, где мы найдем делимое по указанной формуле.
- делимое = х
- делитель = 6
- частное = 6
- остаток = 0
Подставив значение в формулу, получим x = (6×6)+0 = 36.
 Следовательно, значение делимого равно 36.
Следовательно, значение делимого равно 36.Разберемся с формулой нахождения дивидендов, когда остаток равен нулю. Для этого конкретного случая формула будет такой:
- Если остаток равен 0, то Дивиденд = (Делитель × Частное).
Дивиденд в дробях
Дроби — это числа, представленные в виде p/q. Например, ¼, ½, ¾ и т. д. Когда группа предметов или коллекция разбита на равные части или части, мы называем это частью целого. Все дроби состоят из числителя и знаменателя.
- Числитель дроби является делимым.
- Знаменатель дроби является делителем.
Разница между дивидендом и делителем
Дивиденд и делитель являются основными частями факта деления. Без делителя мы не можем разделить делимое, а без делимого мы не можем выполнить деление. Делитель делит делимое на равные части, тогда как делимое делится поровну на делитель. Поясним этот факт с помощью иллюстрации.
Пример: разделить 52 на 4
Факт деления = 52 ÷ 4
Здесь 52 — делимое, а 4 — делитель. Если какой-либо член отсутствует, мы не можем выполнить деление с одним термином. Следовательно, 52 ÷ 4 = 13. Здесь 13 — частное.
Если какой-либо член отсутствует, мы не можем выполнить деление с одним термином. Следовательно, 52 ÷ 4 = 13. Здесь 13 — частное.Факты о дивидендах
Ниже приведены факты, связанные с дивидендами в подразделении.
- Когда делимое и делитель равны в задаче на деление, результат такой задачи на деление всегда равен 1. Например, 75 ÷ 75 = 1
- Когда остаток равен нулю, это означает, что делимое полностью делится на делитель.
- Если делимое и частное факта деления равны, то значение делителя равно 1. Например, 75 ÷ 1 = 75
- Если делитель больше делимого, то результирующее число будет десятичным числом. Например, 75 ÷ 1000 = 0,075· .
☛Статьи по теме
Ознакомьтесь с интересными темами, чтобы узнать больше о дивидендах.
- Длинная часть
- Остаток
- Дивизион Формула
- Коэффициент
Часто задаваемые вопросы о дивидендах
Что такое дивиденд в математике?
Число, которое делится на другое число (делитель), называется делимым.
 Например, разделите 24 на 4. Здесь 4 — это число, на которое делится число 24, поэтому 24 называется делимым, а 4 — делителем.
Например, разделите 24 на 4. Здесь 4 — это число, на которое делится число 24, поэтому 24 называется делимым, а 4 — делителем.Как рассчитать дивиденды в подразделении?
Если известны другие части факта деления, такие как делитель, частное и остаток, то мы можем найти делимое, используя данную формулу:
Дивиденд = делитель x частное + остаток.
Какая формула для нахождения дивиденда, когда остаток равен нулю?
Если в остатке 0, то формула нахождения Дивиденда = (Делитель × Частное).
Куда мы пишем дивиденды в подразделении?
При выполнении длинного деления делимое записывается внутри знака деления, а делитель вне его, слева.
Что такое дивиденд в дроби?
Дробь представлена в виде p/q,(q не равно 0). Все дроби состоят из двух частей: числителя и знаменателя. Здесь числитель — делимое. Например, 8/2, числитель 8 — это делимое.
Что такое Дивиденд в разделе?
Когда любой общий факт деления представлен как A ÷ B = C, в таком случае A является дивидендом соответствующего факта деления.

Чему равно число 24, разделенное на 3?
Данный пример можно представить как 24 ÷ 3. В этом случае 24 — делимое, а 3 — делитель.
Какой дивиденд в 72/8?
72/8 записывается в форме дроби, здесь числитель равен 72, а в форме дроби часть числителя известна как делимое.
Каков дивиденд деления Факт 45 ÷ 15 дает 3?
Делимое — это число, которое делится поровну на делитель. Здесь 45 делится на 15. Следовательно, 45 — делимое.
Деление десятичных дробей — Как делить десятичные дроби?
Деление десятичных дробей аналогично делению целых чисел с учетом положения десятичной точки. При делении десятичных чисел нам нужно следовать определенному набору правил, но основной процесс деления остается прежним. Давайте узнаем о длинном делении с десятичными дробями, как делить десятичные дроби на целые числа и как делить десятичные дроби на десятичные дроби в этой статье.
1. 
Как делить десятичные дроби? 2. Деление десятичных дробей на целые числа 3. Деление десятичных дробей на десятичные дроби 4. Часто задаваемые вопросы о делении десятичных дробей Как делить десятичные дроби?
Процесс деления десятичных дробей аналогичен обычному процессу деления, но нам просто нужно помнить о десятичной точке, которая должна быть правильно помещена в частное. Десятичное число состоит из целой части числа и дробной части, разделенных точкой, которая является десятичной запятой. Цифры после запятой имеют значение меньше 1. Например, 24,15 — это десятичное число, в котором 24 — целая часть числа, а 15 — дробная часть. Для деления десятичных чисел мы можем встретить 2 сценария: один, в котором нам нужно разделить десятичные дроби на целое число, и другой, в котором мы делим десятичные дроби на десятичные дроби.
 Подробнее об этом читайте в следующих разделах .
Подробнее об этом читайте в следующих разделах . Деление десятичных дробей на целые числа
Деление десятичных дробей на целые числа аналогично обычному делению. Здесь делимое — это десятичное число, а делитель — целое число, поэтому десятичная точка в частном будет располагаться в соответствии с десятичной точкой делимого. Мы можем понять это с помощью длинного деления десятичных дробей.
Деление десятичных дробей в длинное
Деление десятичных дробей в длинное можно легко выполнить так же, как и обычное десятичное деление. Давайте разберемся в этом на примере.
Пример: Разделить 338,56 ÷ 23
Решение:
- Шаг 1: Сначала запишите деление в стандартной форме. Начните с деления целой части числа на делитель.
- Шаг 2: Поставьте десятичную точку в частном над десятичной точкой делимого. Запишите десятую цифру.
- Шаг 3: Разделите и запишите другую цифру по порядку.
 Делим до тех пор, пока в остатке не получится 0. Таким образом, десятичная дробь в частном ставится в соответствии с десятичной дробью в делимом.
Делим до тех пор, пока в остатке не получится 0. Таким образом, десятичная дробь в частном ставится в соответствии с десятичной дробью в делимом.
Теперь давайте научимся делить десятичные дроби на десятичные дроби.
Деление десятичных дробей на десятичные дроби
Для деления десятичной дроби на другую десятичную дробь нам нужно преобразовать делитель в целое число, а затем продолжить деление. Давайте разберемся с условиями и правилами этого метода на примере.
Пример: Разделить 48,65 ÷ 3,5
Решение: В этом делении делимое и делитель являются десятичными дробями, поэтому нам нужно преобразовать делитель в целое число, выполнив следующие шаги.
- Шаг 1: Делимое равно 48,65, а делитель 3,5. Нам нужно изменить делитель на целое число, и поэтому мы умножим его на 10, чтобы десятичная точка сместилась вправо, и оно стало целым числом. Это означает, что 3,5 × 10 = 35, .
- Шаг 2: Нам нужно обращаться с делимым так же, как мы обращались с делителем. Значит, делимое тоже умножим на 10. Это означает, что это будет 48,65 × 10 = 486,5. Другими словами, нам нужно переместить обе десятичные точки вправо, пока делитель не станет целым числом.
- Шаг 3: Теперь у нас есть 486,5 в качестве делимого и 35 в качестве делителя. Это можно разделить, как мы делаем обычное деление, и мы получим 13,9 как частное.

Важные советы по делению десятичных дробей
Теперь давайте рассмотрим следующие полезные советы при делении десятичных дробей.
- Преобразуйте делитель в целое число путем умножения на 10. Умножьте делимое на те же степени 10.
- Чтобы разделить десятичное число на 10, переместите запятую влево на один разряд. Например, если нам нужно разделить 45,67 ÷ 10, то это легко сделать, сдвинув запятую влево, и ответ будет 4,567 .
- Чтобы разделить десятичное число на 100, переместите запятую влево на два знака.
 Например, если нам нужно разделить 324,6 ÷ 100, то это легко сделать, сдвинув запятую влево и ответ будет 3,246
Например, если нам нужно разделить 324,6 ÷ 100, то это легко сделать, сдвинув запятую влево и ответ будет 3,246 - Чтобы разделить десятичное число на 1000, переместите запятую влево на три знака. Например, если нам нужно разделить 8934,5 ÷ 1000, то это легко сделать, сдвинув запятую влево и ответ будет 8,9345
☛ Похожие темы
- Сложение десятичных знаков
- Вычитание десятичных дробей
- Умножение десятичных дробей
- Сложение и вычитание десятичных знаков
- Сравнение десятичных дробей
- Десятичное разрядное значение
- Связь между дробями и десятичными знаками
- Десятичные числа и дроби
Часто задаваемые вопросы о делении десятичных дробей
Что такое деление десятичных дробей?
Деление десятичных дробей означает деление десятичного числа на другое десятичное число или деление целого числа на десятичное число в зависимости от обстоятельств.
 Он включает в себя деление, в котором используются десятичные числа. Мы знаем, что десятичное число — это число, состоящее из целой части числа и дробной части, разделенных точкой, известной как десятичная точка. Например, 56,34. Итак, когда мы говорим о делении десятичных дробей, это может означать 32,16 ÷ 2,3, или 56,8 ÷ 4, или 2387 ÷ 9..2 и так далее.
Он включает в себя деление, в котором используются десятичные числа. Мы знаем, что десятичное число — это число, состоящее из целой части числа и дробной части, разделенных точкой, известной как десятичная точка. Например, 56,34. Итак, когда мы говорим о делении десятичных дробей, это может означать 32,16 ÷ 2,3, или 56,8 ÷ 4, или 2387 ÷ 9..2 и так далее.Как делить десятичные числа на 10, 100, 1000?
Чтобы разделить десятичные числа на 10, 100 или 1000, нам нужно использовать следующие правила:
- Когда мы делим десятичное число на 10, мы должны переместить десятичную точку на одно место влево. Например, если нам нужно разделить 12,87 ÷ 10, то это легко сделать, сдвинув запятую влево и ответ будет 1,287
- Когда мы делим десятичное число на 100, мы должны переместить десятичную точку влево на два знака. Например, если нам нужно разделить 753,8 ÷ 100, то это легко сделать, сдвинув запятую влево и ответ будет 7,538
- Когда мы делим десятичное число на 1000, мы должны переместить десятичную точку влево на три знака.
 Например, если нам нужно разделить 432,7 ÷ 1000, то это легко сделать, сдвинув запятую влево и ответ будет 0,4327 .
Например, если нам нужно разделить 432,7 ÷ 1000, то это легко сделать, сдвинув запятую влево и ответ будет 0,4327 .
Как выполнить длинное деление с десятичными дробями?
Длинное деление десятичных дробей выполняется так же, как и обычное длинное деление целых чисел. Нам просто нужно проверить, является ли делитель целым числом или десятичным числом.
- Если делитель — целое число, а делимое — десятичное число, мы можем разделить обычным способом и сохранить десятичную точку в частном согласно делимому. Другими словами, при делении, когда мы встречаем десятичную точку в делимом, мы ставим десятичную точку в частное на этом конкретном шаге и продолжаем деление.
- Если делитель представляет собой десятичное число, нам нужно преобразовать его в целое число, сдвигая десятичную дробь вправо, пока она не станет целым числом. Затем важно сдвинуть десятичную дробь делимого на такое же количество знаков. Это можно сделать, умножив делитель на степени 10 и затем соответственно умножив делимое также на ту же степень 10.
 Например, если нам нужно разделить 54,79÷ 1,5, мы умножим делитель на 10, чтобы удалить десятичную точку. это будет 1,5 × 10 = 15. Теперь нам нужно умножить делимое на то же число 10, так что мы получим 54,79 × 10 = 547,9. После этого шага мы можем разделить 547,9 ÷ 15 обычным способом и получить 36,52 в качестве частного.
Например, если нам нужно разделить 54,79÷ 1,5, мы умножим делитель на 10, чтобы удалить десятичную точку. это будет 1,5 × 10 = 15. Теперь нам нужно умножить делимое на то же число 10, так что мы получим 54,79 × 10 = 547,9. После этого шага мы можем разделить 547,9 ÷ 15 обычным способом и получить 36,52 в качестве частного.
Как делить десятичные дроби на десятичные дроби?
Когда нам нужно разделить десятичную дробь на десятичную, нам нужно преобразовать делитель в целое число, а затем выполнить обычное деление. Мы преобразуем делитель в целое число, сдвигая десятичную дробь вправо, пока она не станет целым числом. Это можно сделать, умножив делитель на степени 10 и затем соответственно умножив делимое также на ту же степень 10. Например, если нам нужно разделить 78,91 ÷ 3,7, мы умножим делитель на 10, чтобы удалить десятичную точку. Это будет 3,7 × 10 = 37. Теперь нам нужно умножить делимое на 10, так что мы получим 78,91 × 10 = 789,1. После этого шага мы можем разделить 789,1 ÷ 37 в длинное деление и получить частное как 21,32
Как разделить десятичную дробь на 100?
Десятичная точка десятичного числа смещается на два знака влево, если мы делим его на 100.
 Например, 34,286 ÷ 100 = 34,286/100 = 0,34286, а 678,37 ÷ 100 = 678,37/100 = 6,7837. Здесь мы перемещаем десятичную точку делимого влево на 2 знака.
Например, 34,286 ÷ 100 = 34,286/100 = 0,34286, а 678,37 ÷ 100 = 678,37/100 = 6,7837. Здесь мы перемещаем десятичную точку делимого влево на 2 знака.Как делить десятичные дроби на целые числа?
Деление десятичной дроби на целое такое же, как и обычное деление. Десятичная дробь помещается в частное в соответствии с десятичной дробью делимого. Давайте разберемся в этом на простом примере. Деление 42,7 на 7 дает в частном 6,1.
Может ли десятичная дробь быть целым числом?
Нет, любое число справа от запятой имеет значение меньше 1, поэтому оно не может быть целым числом. Однако целые числа, такие как 5, 11 и 22, можно записать в виде десятичных чисел, таких как 5,0, 11,0, 22,0
Что такое первый шаг в делении десятичных дробей?
Первым шагом в делении десятичных дробей является удаление десятичной точки делителя путем умножения его на 10-ю степень. Затем делимое также обрабатывается таким же образом и умножается на ту же 10-ю степень. Давайте разберемся в этом.
 с примером. Например, чтобы разделить 12,5 ÷ 0,5, нам нужно умножить делитель 0,5 на 10, чтобы он стал целым числом. Это даст 0,5 × 10 = 5. Затем мы умножим делимое также на 10, чтобы получить 12,5. × 10 = 125. После этого шага мы можем разделить 125 ÷ 5 = 25,
с примером. Например, чтобы разделить 12,5 ÷ 0,5, нам нужно умножить делитель 0,5 на 10, чтобы он стал целым числом. Это даст 0,5 × 10 = 5. Затем мы умножим делимое также на 10, чтобы получить 12,5. × 10 = 125. После этого шага мы можем разделить 125 ÷ 5 = 25,В чем разница между умножением и делением десятичных дробей?
При умножении десятичных дробей мы складываем количество десятичных знаков множимого и множителя, а затем ставим десятичную точку в произведении в соответствии с этим количеством знаков. Например: 0,0020 × 0,005 = 0,0000100. В этом случае 0,0020 имеет 4 цифры после запятой, а 0,005 имеет 3 цифры после запятой. Это дает нам 3 + 4 = 7. Итак, мы будем умножать числа как обычно и ставить десятичную точку в произведении через 7 знаков справа. При делении мы вычитаем количество знаков после запятой делимого и делителя. Например, 0,0020 ÷ 0,005 = 0,4. В этом случае 4 — 3 = 1, поэтому мы будем делить числа как обычно (без учета десятичных знаков), а затем ставить десятичную точку после 1 знака справа.

Деление многочленов — определение, синтетическое деление, длинное деление, примеры
Деление многочленов — это арифметическая операция, при которой мы делим многочлен на другой многочлен, как правило, с меньшей степенью по сравнению с делимым. Деление двух многочленов может привести к полиному, а может и не получиться. Давайте узнаем о делении многочленов в этой статье подробно.
1. Что такое деление многочленов? 2. Деление многочленов на одночлены 3. Деление многочленов на двучлены 4. Деление полиномов с помощью синтетического деления 5. Часто задаваемые вопросы о полиномах деления Что такое деление многочленов?
Полиномы — это алгебраические выражения, состоящие из переменных и коэффициентов.
 Записывается в следующем формате: 5х 2 + 6x — 17. Этот многочлен имеет три члена, которые расположены в соответствии с их степенями. Сначала ставится термин с высшей степенью, затем с низшей. Разделение многочленов — это алгоритм решения рационального числа, представляющего собой многочлен, разделенный на одночлен или другой многочлен. Делитель и делимое располагаются точно так же, как и при обычном делении. Например, если нам нужно разделить 5х 2 + 7х + 25 на 6х — 25, запишем это так: 92+7 x+25)}{(6 x -25)}\]
Записывается в следующем формате: 5х 2 + 6x — 17. Этот многочлен имеет три члена, которые расположены в соответствии с их степенями. Сначала ставится термин с высшей степенью, затем с низшей. Разделение многочленов — это алгоритм решения рационального числа, представляющего собой многочлен, разделенный на одночлен или другой многочлен. Делитель и делимое располагаются точно так же, как и при обычном делении. Например, если нам нужно разделить 5х 2 + 7х + 25 на 6х — 25, запишем это так: 92+7 x+25)}{(6 x -25)}\]Многочлен, написанный над чертой, является числителем ( 5x 2 + 7x + 25), а многочлен, написанный под чертой, равен знаменатель (6x — 25). Это можно понять из следующего рисунка, который показывает, что числитель становится делимым, а знаменатель становится делителем.
Деление многочленов на одночлены
При делении многочленов на одночлены деление может производиться двумя способами. Один из них заключается в простом разделении знаков оператора «+» и «-».
 То есть мы отрываем многочлен от знака оператора и решаем каждую часть отдельно. Другой метод заключается в простой факторизации и дальнейшем упрощении. Давайте посмотрим на оба метода подробно.
То есть мы отрываем многочлен от знака оператора и решаем каждую часть отдельно. Другой метод заключается в простой факторизации и дальнейшем упрощении. Давайте посмотрим на оба метода подробно.Метод разделения членов
Разделить члены полинома, разделенные оператором ( ‘+’ или ‘-‘ ), между ними и упростить каждый член. Например, (4x 2 — 6x) ÷ (2x) можно решить, как показано здесь. Сначала мы берем общие термины из числителей и знаменателей обоих терминов, мы получаем [(4x 2 ) / (2x)] — [(6x) / (2x)]. Сократив общий член 2x из числителя и знаменателя, получим 2x — 3.
Метод факторизации
Когда вы делите многочлены, вам может потребоваться разложить многочлен на множители, чтобы найти общий множитель между числителем и знаменателем. Например: Разделите следующий многочлен: (2x 2 + 4x) ÷ 2x. И числитель, и знаменатель имеют общий делитель 2х. Таким образом, выражение можно записать как 2x(x + 2)/2x. Сократив общий член 2x, мы получим в качестве ответа x+2.

Деление многочленов на двучлены
Для деления многочленов на двучлены или многочлены любого другого типа наиболее распространенным и общим методом является метод деления в длину. Если между числителем и знаменателем нет общих множителей или если вы не можете найти множители, вы можете использовать процесс длинного деления, чтобы упростить выражение.
Деление многочленов с помощью длинного деления
Рассмотрим алгоритм деления многочленов на двучлены на примере: Разделить: (4x 2 — 5x — 21) ÷ (x — 3). Здесь (4x 2 — 5x — 21) — делимое, а (x — 3) — делитель, который является биномом. Обратите внимание на разделение, показанное ниже, а затем на шаги.
Шаг 1. Разделите первое слагаемое делимого (4x 2 ) на первое слагаемое делителя (x) и поставьте его как первое слагаемое в частном (4x).
Шаг 2. Умножьте делитель на этот ответ, поместите произведение (4x 2 — 12x) под делимым.

Шаг 3. Вычтите, чтобы создать новый полином (7x — 21).
Шаг 4. Повторите тот же процесс с новым многочленом, полученным после вычитания.
Итак, когда мы делим многочлен (4x 2 — 5x — 21) на двучлен (x — 3), частное равно 4x+7, а остаток равен 0.
Деление полиномов с помощью синтетического деления
Синтетическое деление — это метод деления многочлена на линейный двучлен с учетом только значений коэффициентов. В этом методе мы сначала записываем полиномы в стандартной форме от члена высшей степени к члену низшей степени. При записи в убывающей степени используйте 0 в качестве коэффициентов пропущенных терминов. Например, x 3 +3 нужно записать как x 3 + 0x 2 + 0x + 3. Для деления многочленов методом синтетического деления выполните следующие действия:
Разделим x 2 + 3 на x — 4.
Шаг 1: Запишите делитель в виде x — k и запишите k в левой части деления.
 Здесь делитель равен x-4, поэтому значение k равно 4.
Здесь делитель равен x-4, поэтому значение k равно 4.Шаг 2: Установите деление, записав коэффициенты делимого справа и k слева. [Примечание: используйте 0 для отсутствующих членов дивиденда]
Шаг 3: Теперь уменьшите коэффициент члена наивысшей степени дивиденда, как он есть. Здесь старший коэффициент равен 1 (коэффициент x 2 ).
Шаг 4: Умножьте k на этот старший коэффициент и запишите произведение под вторым коэффициентом слева от делимого. Итак, мы получаем, 4×1=4, что мы запишем ниже 0.
Шаг 5: Складываем числа, написанные во втором столбце. Здесь, сложив, мы получаем 0+4=4.
Шаг 6: Повторите тот же процесс умножения k на число, полученное в шаге 5, и запишите произведение в следующем столбце справа.
Шаг 7: Наконец, запишем окончательный ответ, который будет на одну степень меньше делимого. Итак, здесь в нашем делимом член высшей степени равен x 2 , следовательно, в частном член высшей степени будет x.
 Следовательно, полученный ответ равен х+4+(19/х-4).
Следовательно, полученный ответ равен х+4+(19/х-4).Темы, связанные с делением многочленов
Ознакомьтесь с этими статьями, чтобы узнать больше о концепции деления многочленов и связанных с ней темах.
- Длинное деление многочленов
- Синтетическое деление многочлена
- Алгоритм деления многочленов
- Деление двух многочленов
- Деление многочлена на линейный множитель
Примеры деления многочленов
Пример 1: Алекс застрял на задаче, работая над делением многочленов. Можете ли вы помочь ему получить частное: (x 4 — 10x 3 + 27x 2 — 46х + 28) ÷ (х — 7).
Решение:
Следовательно, частное равно x 3 — 3x 2 + 6x — 4.
Пример 2: Стейси нужна помощь в нахождении остатка при делении многочленов. Вы можете помочь ей решить эту проблему?
(4x 3 + 5x 2 + 5x + 8) ÷ (4x + 1)
Решение: Используя метод деления многочленов в длину, получаем,
Следовательно, остаток равен 7.

перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по делению многочленов
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о полиномах деления
Что такое деление многочленов?
Деление многочленов — это одна из арифметических операций, выполняемых над двумя заданными многочленами. При этом делимое обычно имеет более высокую степень, а делитель является полиномом более низкой степени.
Почему деление многочленов важно?
Деление полиномов важно, потому что оно предоставляет алгоритм для решения рационального числа, представляющего многочлен, разделенный на одночлен или другой многочлен.
Как проще всего делить многочлены?
Самый простой способ разделить многочлены — это использовать метод деления в длину.
 Однако в случае деления многочленов на моном его можно решить непосредственно путем расщепления членов или факторизации.
Однако в случае деления многочленов на моном его можно решить непосредственно путем расщепления членов или факторизации.Какие существуют два метода деления многочленов?
Ниже приведены два метода деления многочленов:
- Метод синтетического деления
- Метод длинного деления
Для чего в реальной жизни используется полиномиальное деление?
Мы используем полиномиальное деление для различных аспектов нашей повседневной жизни. Нам это нужно для кодирования, проектирования, проектирования, архитектуры и многих других областей реальной жизни.
Какой метод деления многочленов на одночлен лучше всего?
В случае деления многочленов на моном его можно решить непосредственно путем расщепления членов или факторизации. Мы можем разделить каждый член делимого на заданный моном и найти результат.
Длинное полиномиальное деление: Примеры | Purplemath
SimplificationLong Division
Purplemath
В отличие от примеров на предыдущей странице, почти все полиномиальные деления не «выходят четными»; обычно у вас остается остаток.

Я начну с деления деления:
Глядя только на первые члены, я делю 3 x 3 на 3 x , чтобы получить x 2 . Это то, что я поставил сверху:
Содержание продолжается ниже
Mathhelp.com
I Умножьте это x 2 на 3 x +1, чтобы получить 3 x 3 +1 x 3 +1 x 2 3 +1 x 3 +1 x 3 +1 x 3 +1 x 3 +1 x внизу:
Затем я меняю знаки, прибавляю и не забываю перенести «+10 x — 3″ из исходного делимого, что дает мне новую нижнюю строку −6 x 2 + 10 x — 3:
Деление нового старшего члена, -6 x 2 , по старшему члену делителя, 3 x , я получаю −2 x , поэтому я помещаю это сверху:
Затем я умножаю −2 x на 3 x 9125 чтобы получить -6 x 2 — 2 x , которое я поместил ниже.
 Я меняю знаки, добавляю вниз и не забываю переносить «-3» из делимого:
Я меняю знаки, добавляю вниз и не забываю переносить «-3» из делимого:Моя новая последняя строка «12 x — 3. Деление нового старшего члена 12 x на старший член делителя из 3 x , получаю +4, которые ставлю сверху. Я умножаю 4 на 3 x + 1, чтобы получить 12 x + 4. Я меняю знаки и прибавляю. У меня получается остаток −7:
Это деление не вышло даже. Что мне делать с остатком?
Вспомните, как вы делили простые числа в длинное. Иногда оставался остаток; например, если вы разделите 132 на 5:
… в остатке будет 2. Помните, как вы справились с этим? Вы составили дробь, положив остаток на делитель, и записали ответ как «двадцать шесть и две пятых»:
Первая форма, без «плюса» в середине, — это то, как пишутся «смешанные числа», но смысл смешанного числа — это на самом деле форма с добавлением.
То же самое делаем с полиномиальным делением. Поскольку остаток в этом случае равен −7, а делитель равен 3 x + 1, то я превращу остаток в дробь (остаток, разделенный на исходный делитель), и добавлю эту дробь к многочлену через над символом деления.
 Тогда мой ответ таков:
Тогда мой ответ таков:Предупреждение: , а не записывать многочлен «смешанное число» в том же формате, что и числовые смешанные числа! Если вы просто добавите дробную часть к полиномиальной части, это будет интерпретировано как полиномиальное умножение, то есть , а не , что вы имеете в виду!
Примечание. В разных книгах длинный раздел форматируется по-разному. При написании выражений в верхней части раздела в некоторых книгах термины помещаются над термином той же степени, а не над термином, над которым ведется работа. В таком тексте длинное деление выше было бы представлено, как показано здесь:
Единственное отличие состоит в том, что термины в верхней части сдвинуты вправо. В остальном все точно так же; в частности, все вычисления точно такие же. Если вы сомневаетесь, используйте форматирование, которое использует ваш преподаватель.
Вам может быть интересно, откуда я знал, что надо остановиться, когда дошел до остатка -7.
 Это очень похоже на то, как вы знали, когда остановиться при делении в большую сторону (до того, как вы узнали о десятичных разрядах). Как только вы добрались до чего-то, на что делитель был слишком велик, чтобы разделить его, вы зашли так далеко, как только могли, поэтому остановились; все, что осталось, если что, было вашим остатком. То же самое касается полиномиального длинного деления. −7 — это просто постоянный член; 3 x «слишком велико», чтобы в него входить, точно так же, как 5 было «слишком велико», чтобы входить в 2 в приведенном выше примере с числовым делением. Как только вы получите остаток, который «меньше» (в полиномиальной степени), чем делитель, все готово.
Это очень похоже на то, как вы знали, когда остановиться при делении в большую сторону (до того, как вы узнали о десятичных разрядах). Как только вы добрались до чего-то, на что делитель был слишком велик, чтобы разделить его, вы зашли так далеко, как только могли, поэтому остановились; все, что осталось, если что, было вашим остатком. То же самое касается полиномиального длинного деления. −7 — это просто постоянный член; 3 x «слишком велико», чтобы в него входить, точно так же, как 5 было «слишком велико», чтобы входить в 2 в приведенном выше примере с числовым делением. Как только вы получите остаток, который «меньше» (в полиномиальной степени), чем делитель, все готово.Прежде всего отмечу, что имеется разрыв в степенях членов делимого: полином 2 x 3 − 9 x 2 + 15 не имеет члена x . Моя работа может усложниться внутри символа деления, поэтому важно, чтобы я оставил место для 9.1253 x — столбец терминов, на всякий случай.
 (Это похоже на ноль, скажем, в разряде сотен делимого, удерживая этот столбец открытым для вычитания под символом длинного деления). x 2 + 0 x + 15.
(Это похоже на ноль, скажем, в разряде сотен делимого, удерживая этот столбец открытым для вычитания под символом длинного деления). x 2 + 0 x + 15.(Это допустимый математический шаг. Я только добавил ноль, поэтому на самом деле ничего не изменил в значении.)
Теперь, когда я есть все «комнаты», которые мне могут понадобиться для моей работы, я сделаю разделение. Начну, как обычно, с расстановки на длинное деление:
Разделив 2 x 3 на 2 x , я получаю x 2 , поэтому я помещаю это сверху. Затем я умножаю x 2 на 2 x — 5, чтобы получить 2 x 3 — 5 x 2 , которое я помещаю ниже. Затем я меняю знаки, прибавляю и переношу 0 x + 15 от исходного делимого. Это дает мне −4 91 253 x 91 254 90 530 2 90 531 + 0 91 253 x 91 254 + 15 в качестве моей новой итоговой строки:
Разделив −4 x 2 на 2 x , я получаю −2 x , которое я положил сверху.
 Умножая это -2 x на 2 x — 5, я получаю -4 x 2 + 10 x , которое я помещаю ниже. Затем я меняю знаки, прибавляю и опускаю +15 от предыдущего делимого. Это дает мне -10 x + 15 в качестве моей новой итоговой строки:
Умножая это -2 x на 2 x — 5, я получаю -4 x 2 + 10 x , которое я помещаю ниже. Затем я меняю знаки, прибавляю и опускаю +15 от предыдущего делимого. Это дает мне -10 x + 15 в качестве моей новой итоговой строки:Разделив -10 x на 2 x , я получаю -5, которое я помещаю сверху. Умножение −5 на 2 · x − 5, я получаю 10 x + 25, которые помещаю ниже. Затем я меняю знаки и прибавляю вниз, в результате чего у меня остается остаток −10:
Мне нужно помнить, что к прибавляю остаток к полиномиальной части ответа:
Во-первых, я переставлю
4 х 4 + 3 х 3 + 2 х + 1
Я замечаю, что нет x 2 член в делимом, поэтому я создам его, добавив член 0 x 2 к делимому (внутри символа деления), чтобы освободить место для моей работы.

Тогда я сделаю деление в обычном порядке. Разделив 4 x 4 на x 2 , я получаю 4 x 2 , которые я положил сверху. Затем я умножаю и так далее, что приводит к новой нижней строке:
Деление − x 3 на x 2 , я получаю − x , которое ставлю сверху. Затем я умножаю, и т.д., и т.п.:
Разделив −7 x 2 на x 2 , я получаю −7, который я кладу сверху. Затем я умножаю и т. д. и т. д.:
И затем я закончил деление, потому что остаток линейный (11 x + 15), а делитель квадратичный. Квадратичный не может делиться на линейный многочлен, поэтому я зашел так далеко, как только мог.
Тогда мой ответ:
Чтобы добиться успеха в полиномиальном длинном делении, вам нужно писать аккуратно, не забывать менять знаки при вычитании и работать осторожно, выстраивая столбцы правильно.

- 1204 / 4



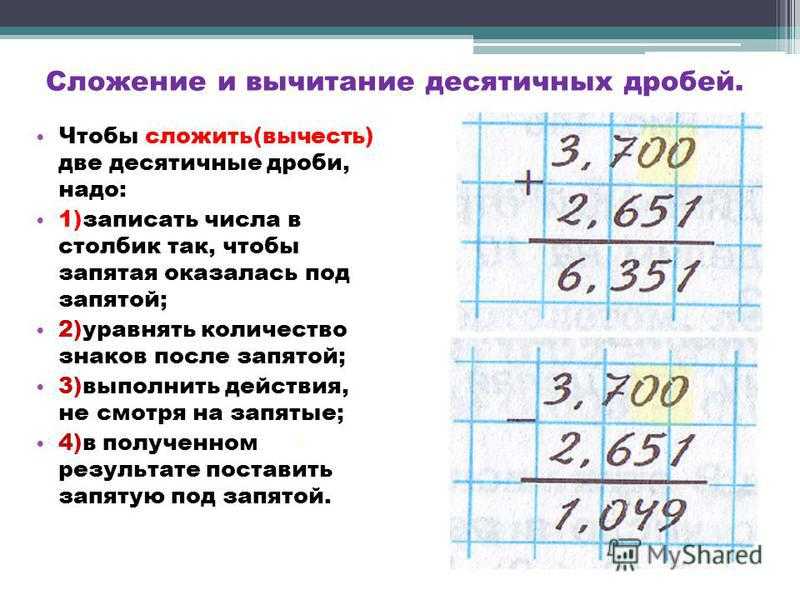
 Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.







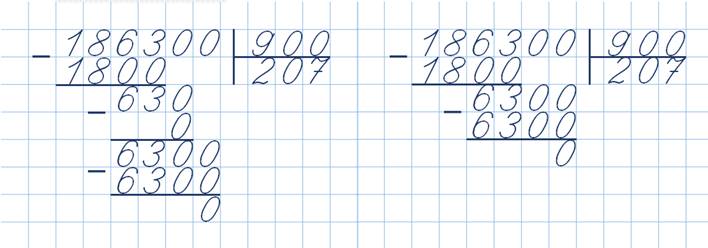 Записываем 3 в ответ под чертой справа
Записываем 3 в ответ под чертой справа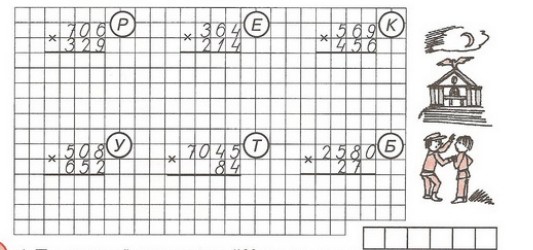 Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
 Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.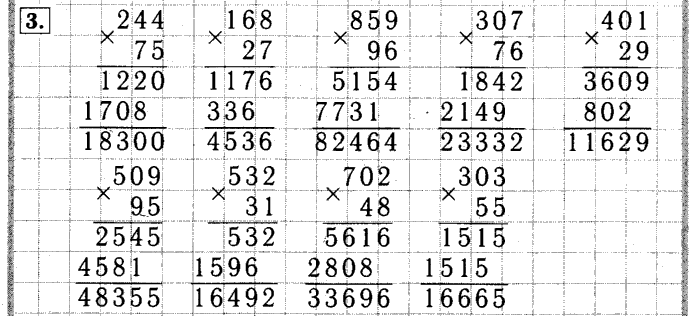 Обычно оно состоит из одной цифры, максимум из двух.
Обычно оно состоит из одной цифры, максимум из двух. Умножение даст 284 и 32.
Умножение даст 284 и 32.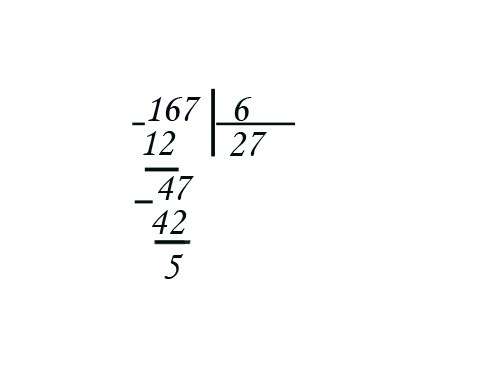 Возьмите счетные палочки, например, 8 штук
Возьмите счетные палочки, например, 8 штук Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа. Получается 2, записываем эту цифру в ответ
Получается 2, записываем эту цифру в ответ Умножаем 4 на 716, получается 2864
Умножаем 4 на 716, получается 2864 Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4 Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. Спросите себя: сколько 6 в 1? Поскольку 1 меньше 6, ваш ответ будет 0,9.0003
Спросите себя: сколько 6 в 1? Поскольку 1 меньше 6, ваш ответ будет 0,9.0003 Вам нужно будет записать их, используя стандартное форматирование для задачи на деление.
Вам нужно будет записать их, используя стандартное форматирование для задачи на деление. Поэтому в большинстве случаев у вас есть оставшийся бит, который нельзя разделить на число дальше. Это называется вашим остатком. Это представлено в математическом уравнении с буквой R. Как только вы немного углубитесь в рациональные числа, вы увидите, как вписывается остаток!
Поэтому в большинстве случаев у вас есть оставшийся бит, который нельзя разделить на число дальше. Это называется вашим остатком. Это представлено в математическом уравнении с буквой R. Как только вы немного углубитесь в рациональные числа, вы увидите, как вписывается остаток!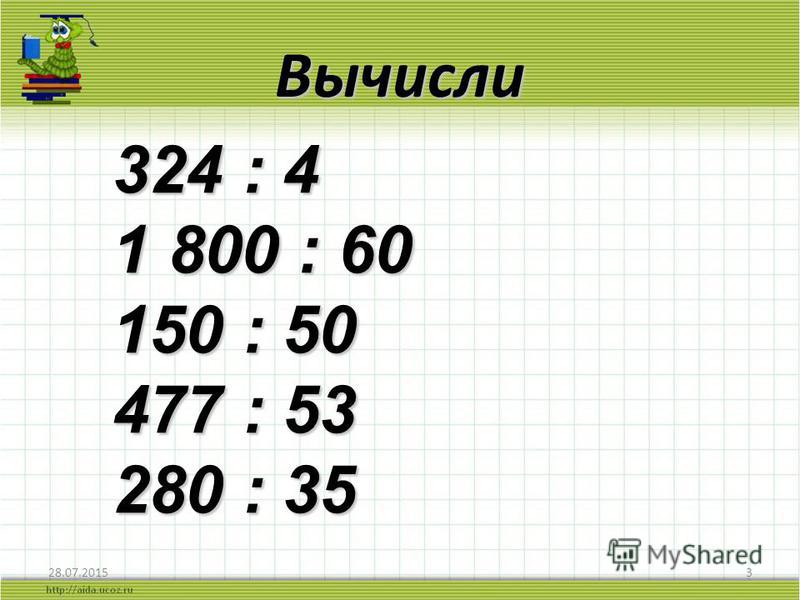 Это может заставить вас желать простоты деления на длинные.
Это может заставить вас желать простоты деления на длинные. Это наиболее распространенный метод, используемый для решения задач, основанных на делении. Обратите внимание на следующее длинное деление, чтобы увидеть делитель, делимое, частное и остаток.
Это наиболее распространенный метод, используемый для решения задач, основанных на делении. Обратите внимание на следующее длинное деление, чтобы увидеть делитель, делимое, частное и остаток.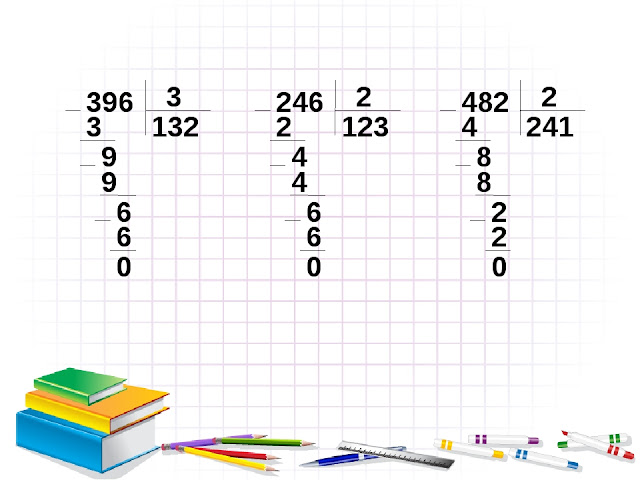

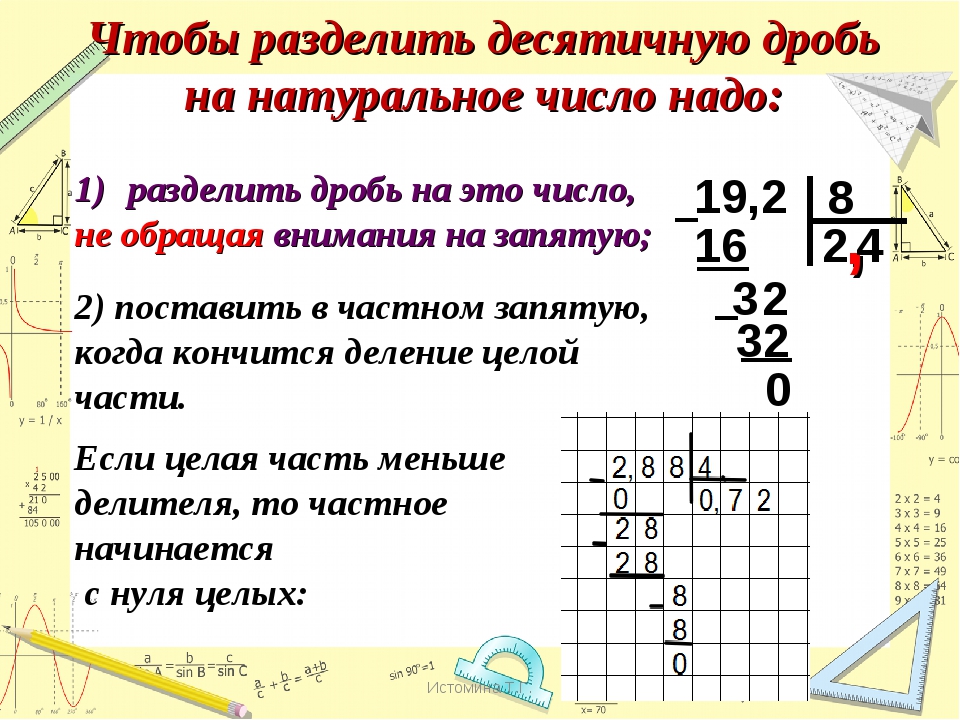 Следовательно, мы пишем 0 как частное и записываем следующую цифру делимого и ставим ее рядом с 3.
Следовательно, мы пишем 0 как частное и записываем следующую цифру делимого и ставим ее рядом с 3.
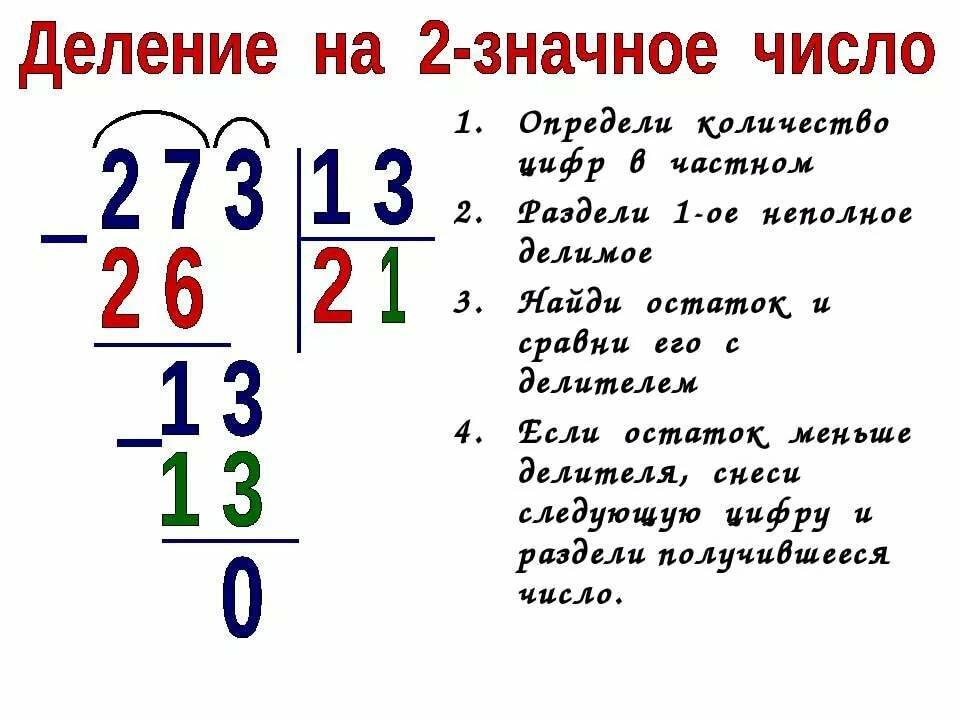

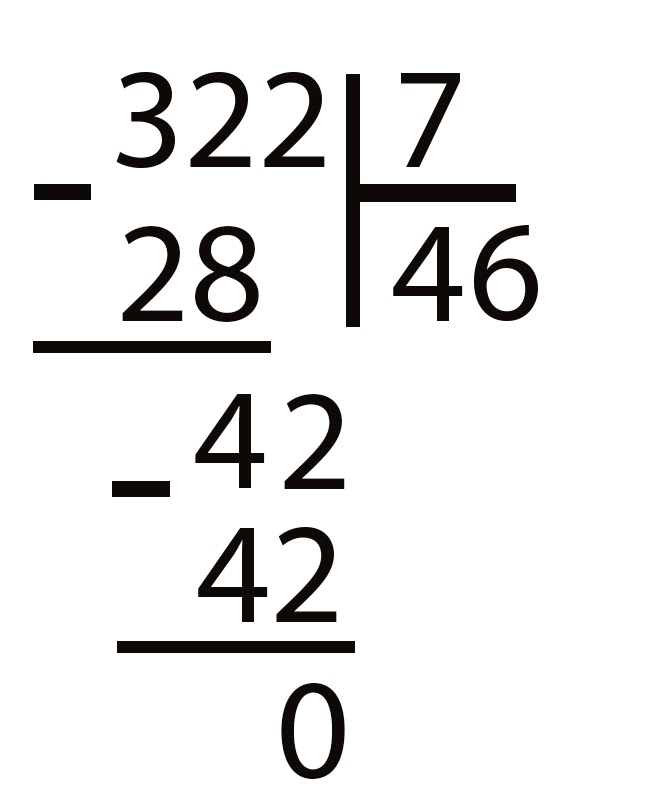 Число, которое делится на более мелкие группы, называется делимым, число, на которое мы делим его, называется делителем, значение, полученное после выполнения деления, называется частным, а число, оставшееся после деления, называется остатком.
Число, которое делится на более мелкие группы, называется делимым, число, на которое мы делим его, называется делителем, значение, полученное после выполнения деления, называется частным, а число, оставшееся после деления, называется остатком. Например, давайте посмотрим, как мы делим 52 на 2.
Например, давайте посмотрим, как мы делим 52 на 2. Продолжайте деление так же, как мы делим обычные числа.
Продолжайте деление так же, как мы делим обычные числа.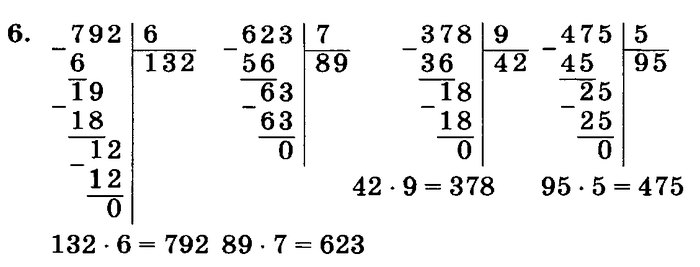
 Давайте разберемся в этом на примере. Разделите число 20 на 5. Запишем факт деления для данного примера.
Давайте разберемся в этом на примере. Разделите число 20 на 5. Запишем факт деления для данного примера. 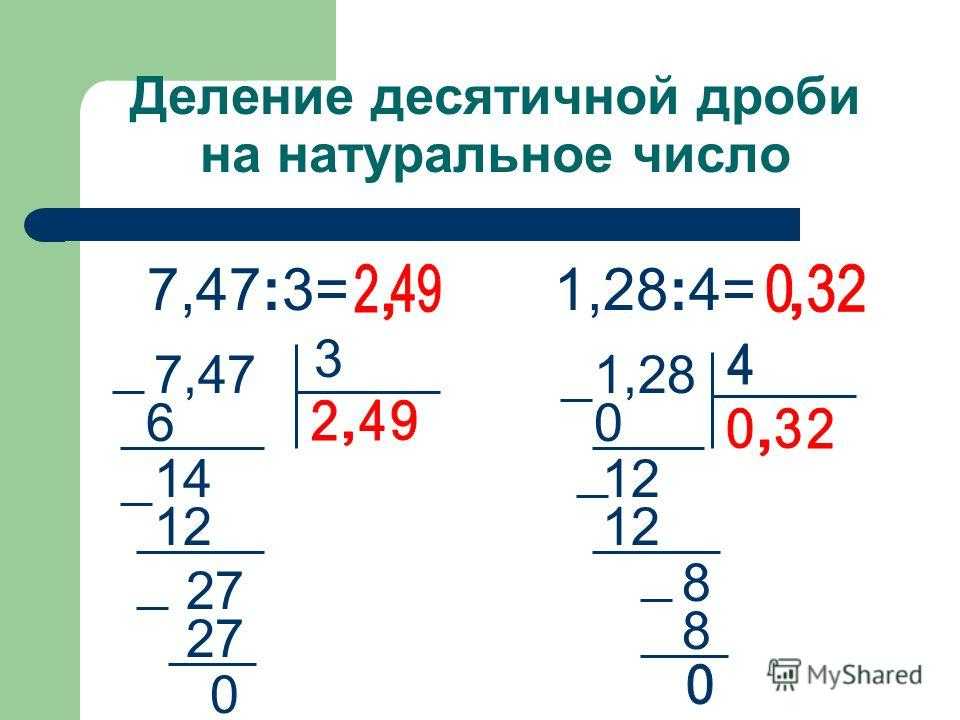
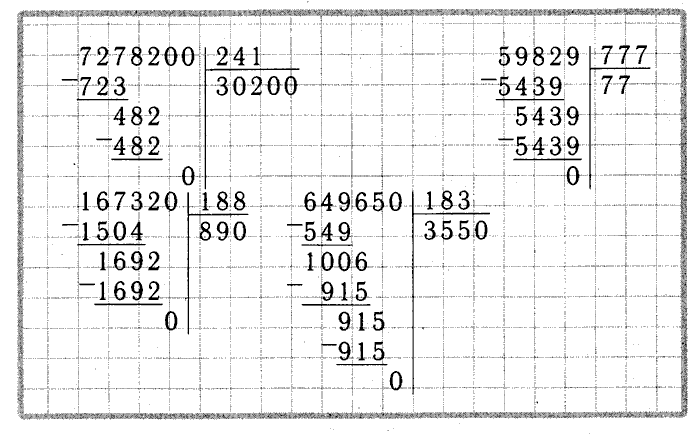 Следовательно, значение делимого равно 36.
Следовательно, значение делимого равно 36.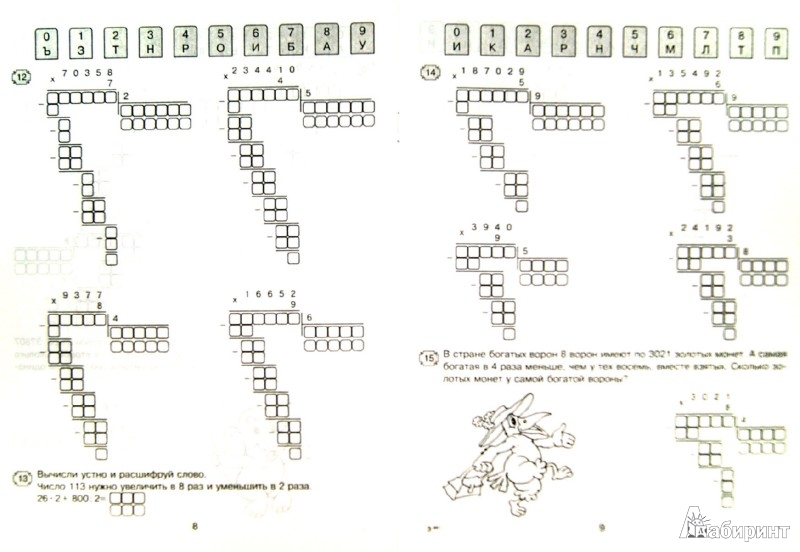 Если какой-либо член отсутствует, мы не можем выполнить деление с одним термином. Следовательно, 52 ÷ 4 = 13. Здесь 13 — частное.
Если какой-либо член отсутствует, мы не можем выполнить деление с одним термином. Следовательно, 52 ÷ 4 = 13. Здесь 13 — частное. Например, разделите 24 на 4. Здесь 4 — это число, на которое делится число 24, поэтому 24 называется делимым, а 4 — делителем.
Например, разделите 24 на 4. Здесь 4 — это число, на которое делится число 24, поэтому 24 называется делимым, а 4 — делителем.

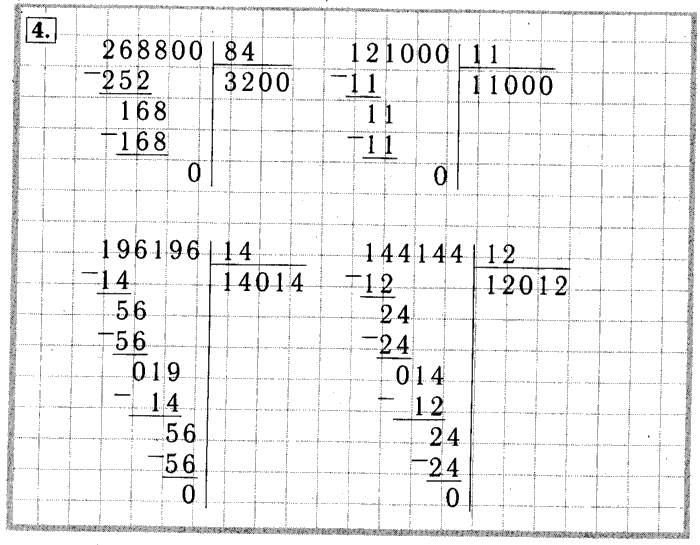 Подробнее об этом читайте в следующих разделах .
Подробнее об этом читайте в следующих разделах .  Делим до тех пор, пока в остатке не получится 0. Таким образом, десятичная дробь в частном ставится в соответствии с десятичной дробью в делимом.
Делим до тех пор, пока в остатке не получится 0. Таким образом, десятичная дробь в частном ставится в соответствии с десятичной дробью в делимом.
 Например, если нам нужно разделить 324,6 ÷ 100, то это легко сделать, сдвинув запятую влево и ответ будет 3,246
Например, если нам нужно разделить 324,6 ÷ 100, то это легко сделать, сдвинув запятую влево и ответ будет 3,246 Он включает в себя деление, в котором используются десятичные числа. Мы знаем, что десятичное число — это число, состоящее из целой части числа и дробной части, разделенных точкой, известной как десятичная точка. Например, 56,34. Итак, когда мы говорим о делении десятичных дробей, это может означать 32,16 ÷ 2,3, или 56,8 ÷ 4, или 2387 ÷ 9..2 и так далее.
Он включает в себя деление, в котором используются десятичные числа. Мы знаем, что десятичное число — это число, состоящее из целой части числа и дробной части, разделенных точкой, известной как десятичная точка. Например, 56,34. Итак, когда мы говорим о делении десятичных дробей, это может означать 32,16 ÷ 2,3, или 56,8 ÷ 4, или 2387 ÷ 9..2 и так далее. Например, если нам нужно разделить 432,7 ÷ 1000, то это легко сделать, сдвинув запятую влево и ответ будет 0,4327
Например, если нам нужно разделить 432,7 ÷ 1000, то это легко сделать, сдвинув запятую влево и ответ будет 0,4327 Например, если нам нужно разделить 54,79÷ 1,5, мы умножим делитель на 10, чтобы удалить десятичную точку. это будет 1,5 × 10 = 15. Теперь нам нужно умножить делимое на то же число 10, так что мы получим 54,79 × 10 = 547,9. После этого шага мы можем разделить 547,9 ÷ 15 обычным способом и получить 36,52 в качестве частного.
Например, если нам нужно разделить 54,79÷ 1,5, мы умножим делитель на 10, чтобы удалить десятичную точку. это будет 1,5 × 10 = 15. Теперь нам нужно умножить делимое на то же число 10, так что мы получим 54,79 × 10 = 547,9. После этого шага мы можем разделить 547,9 ÷ 15 обычным способом и получить 36,52 в качестве частного. Например, 34,286 ÷ 100 = 34,286/100 = 0,34286, а 678,37 ÷ 100 = 678,37/100 = 6,7837. Здесь мы перемещаем десятичную точку делимого влево на 2 знака.
Например, 34,286 ÷ 100 = 34,286/100 = 0,34286, а 678,37 ÷ 100 = 678,37/100 = 6,7837. Здесь мы перемещаем десятичную точку делимого влево на 2 знака. с примером. Например, чтобы разделить 12,5 ÷ 0,5, нам нужно умножить делитель 0,5 на 10, чтобы он стал целым числом. Это даст 0,5 × 10 = 5. Затем мы умножим делимое также на 10, чтобы получить 12,5. × 10 = 125. После этого шага мы можем разделить 125 ÷ 5 = 25,
с примером. Например, чтобы разделить 12,5 ÷ 0,5, нам нужно умножить делитель 0,5 на 10, чтобы он стал целым числом. Это даст 0,5 × 10 = 5. Затем мы умножим делимое также на 10, чтобы получить 12,5. × 10 = 125. После этого шага мы можем разделить 125 ÷ 5 = 25,
 Записывается в следующем формате: 5х 2 + 6x — 17. Этот многочлен имеет три члена, которые расположены в соответствии с их степенями. Сначала ставится термин с высшей степенью, затем с низшей. Разделение многочленов — это алгоритм решения рационального числа, представляющего собой многочлен, разделенный на одночлен или другой многочлен. Делитель и делимое располагаются точно так же, как и при обычном делении. Например, если нам нужно разделить 5х 2 + 7х + 25 на 6х — 25, запишем это так: 92+7 x+25)}{(6 x -25)}\]
Записывается в следующем формате: 5х 2 + 6x — 17. Этот многочлен имеет три члена, которые расположены в соответствии с их степенями. Сначала ставится термин с высшей степенью, затем с низшей. Разделение многочленов — это алгоритм решения рационального числа, представляющего собой многочлен, разделенный на одночлен или другой многочлен. Делитель и делимое располагаются точно так же, как и при обычном делении. Например, если нам нужно разделить 5х 2 + 7х + 25 на 6х — 25, запишем это так: 92+7 x+25)}{(6 x -25)}\] То есть мы отрываем многочлен от знака оператора и решаем каждую часть отдельно. Другой метод заключается в простой факторизации и дальнейшем упрощении. Давайте посмотрим на оба метода подробно.
То есть мы отрываем многочлен от знака оператора и решаем каждую часть отдельно. Другой метод заключается в простой факторизации и дальнейшем упрощении. Давайте посмотрим на оба метода подробно.

 Здесь делитель равен x-4, поэтому значение k равно 4.
Здесь делитель равен x-4, поэтому значение k равно 4. Следовательно, полученный ответ равен х+4+(19/х-4).
Следовательно, полученный ответ равен х+4+(19/х-4).
 Однако в случае деления многочленов на моном его можно решить непосредственно путем расщепления членов или факторизации.
Однако в случае деления многочленов на моном его можно решить непосредственно путем расщепления членов или факторизации.
 Я меняю знаки, добавляю вниз и не забываю переносить «-3» из делимого:
Я меняю знаки, добавляю вниз и не забываю переносить «-3» из делимого: Тогда мой ответ таков:
Тогда мой ответ таков: Это очень похоже на то, как вы знали, когда остановиться при делении в большую сторону (до того, как вы узнали о десятичных разрядах). Как только вы добрались до чего-то, на что делитель был слишком велик, чтобы разделить его, вы зашли так далеко, как только могли, поэтому остановились; все, что осталось, если что, было вашим остатком. То же самое касается полиномиального длинного деления. −7 — это просто постоянный член; 3 x «слишком велико», чтобы в него входить, точно так же, как 5 было «слишком велико», чтобы входить в 2 в приведенном выше примере с числовым делением. Как только вы получите остаток, который «меньше» (в полиномиальной степени), чем делитель, все готово.
Это очень похоже на то, как вы знали, когда остановиться при делении в большую сторону (до того, как вы узнали о десятичных разрядах). Как только вы добрались до чего-то, на что делитель был слишком велик, чтобы разделить его, вы зашли так далеко, как только могли, поэтому остановились; все, что осталось, если что, было вашим остатком. То же самое касается полиномиального длинного деления. −7 — это просто постоянный член; 3 x «слишком велико», чтобы в него входить, точно так же, как 5 было «слишком велико», чтобы входить в 2 в приведенном выше примере с числовым делением. Как только вы получите остаток, который «меньше» (в полиномиальной степени), чем делитель, все готово. (Это похоже на ноль, скажем, в разряде сотен делимого, удерживая этот столбец открытым для вычитания под символом длинного деления). x 2 + 0 x + 15.
(Это похоже на ноль, скажем, в разряде сотен делимого, удерживая этот столбец открытым для вычитания под символом длинного деления). x 2 + 0 x + 15.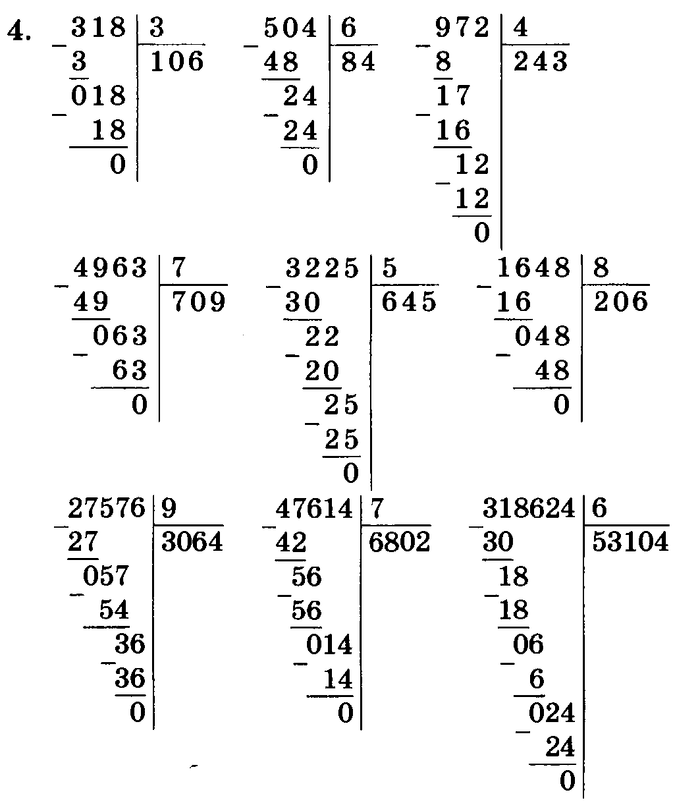 Умножая это -2 x на 2 x — 5, я получаю -4 x 2 + 10 x , которое я помещаю ниже. Затем я меняю знаки, прибавляю и опускаю +15 от предыдущего делимого. Это дает мне -10 x + 15 в качестве моей новой итоговой строки:
Умножая это -2 x на 2 x — 5, я получаю -4 x 2 + 10 x , которое я помещаю ниже. Затем я меняю знаки, прибавляю и опускаю +15 от предыдущего делимого. Это дает мне -10 x + 15 в качестве моей новой итоговой строки:
