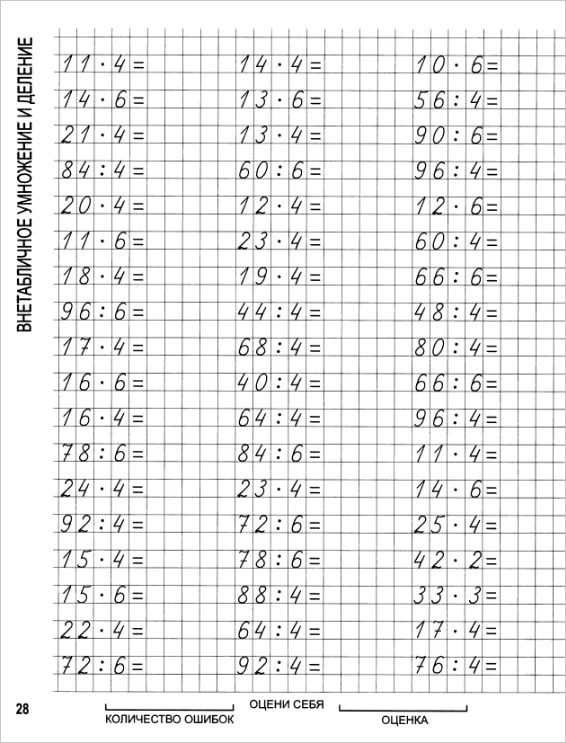
Умножение натуральных чисел в столбик: правила, примеры

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Арифметика Умножение двузначных, трехзначных и многозначных чисел столбиком

В данной публикации мы рассмотрим правила и практические примеры того, каким образом можно умножать столбиком натуральные числа (двузначные, трехзначные и многозначные).

• Правила умножения в столбик
• Примеры умножения в столбик

Правила умножения в столбик

Чтобы найти произведение двух натуральных чисел с любым количеством разрядов можно выполнить умножение в столбик. Для этого:

1. Пишем первый множитель (начинаем с того, у которого больше разрядов).
2. Под ним записываем второй множитель (с новой строки). При этом важно, чтобы одинаковые разряды обоих чисел были расположены строго друг под другом (десятки под десятками, сотни под сотнями и т. д.)
3. Под сомножителями чертим горизонтальную линию, которая будет отделять их от результата.
4. Начинаем выполнять умножение:
   • Крайнюю правую цифру второго множителя (разряд – единицы) поочередно умножаем на каждую цифру первого числа (справа налево). При этом если ответ оказался двузначным, в текущем разряде оставляем последнюю цифру, а первую переносим в следующий, сложив со значением, полученным в результате умножения. Иногда в результате такого переноса в ответе появляется новый разряд.
   • Затем переходим к следующей цифре второго множителя (десятки) и выполняем аналогичные действия, записывая результат со сдвигом на один разряд влево.
5. Получившиеся числа складываем и получаем ответ. Правила и примеры сложения чисел в столбик мы рассмотрели в отдельной публикации.

Примеры умножения в столбик

Пример 1

Умножим двузначное число на однозначное, например 32 на 7.

Пояснение:

В данном случае второй множитель состоит только из одного разряда – единицы. Поочередно умножаем 7 на каждую цифру первого множителя. При этом произведение чисел 7 и 2 равняется 14, следовательно, в ответе цифру 4 оставляем в текущем разряде (единицы), а один прибавляем к результату умножения 7 на 3 (7⋅3+1=22).

Пример 2

Найдем произведение двузначного и трехзначного чисел: 416 и 23.

Пояснение:

• Записываем множители друг под другом (в верхней строке – 416).
• Поочередно умножаем цифру 3 числа 23 на каждый разряд числа 416, получаем – 1248.
• Теперь умножаем 2 на каждую цифру 416, и полученный результат (832) записываем под числом 1248 со смещением на один разряд влево.
• Остается только сложить числа 832 и 1248, чтобы получить ответ, который равняется 9568.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Mathway | Популярные задачи

1	Множитель	x^2-4
2	Множитель	4x^2+20x+16
3	График	y=-x^2
4	Вычислить	2+2
5	Множитель	x^2-25
6	Множитель	x^2+5x+6
7	Множитель	x^2-9
8	Множитель	x^3-8
9	Вычислить	квадратный корень из 12
10	Вычислить	квадратный корень из 20
11	Вычислить	квадратный корень из 50
12	Множитель	x^2-16
13	Вычислить	квадратный корень из 75
14	Множитель	x^2-1
15	Множитель	x^3+8
16	Вычислить	-2^2
17	Вычислить	квадратный корень из (-3)^4
18	Вычислить	квадратный корень из 45
19	Вычислить	квадратный корень из 32
20	Вычислить	квадратный корень из 18
21	Множитель	x^4-16
22	Вычислить	квадратный корень из 48
23	Вычислить	квадратный корень из 72
24	Вычислить	квадратный корень из (-2)^4
25	Множитель	x^3-27
26	Вычислить	-3^2
27	Множитель	x^4-1
28	Множитель	x^2+x-6
29	Множитель	x^3+27
30	Множитель	x^2-5x+6
31	Вычислить	квадратный корень из 24
32	Множитель	x^2-36
33	Множитель	x^2-4x+4
34	Вычислить	-4^2
35	Множитель	x^2-x-6
36	Множитель	x^4-81
37	Множитель	x^3-64
38	Вычислить	4^3
39	Множитель	x^3-1
40	График	y=x^2
41	Вычислить	2^3
42	Вычислить	(-12+ квадратный корень из -18)/60
43	Множитель	x^2-6x+9
44	Множитель	x^2-64
45	График	y=2x
46	Множитель	x^3+64
47	Вычислить	(-8+ квадратный корень из -12)/40
48	Множитель	x^2-8x+16
49	Вычислить	3^4
50	Вычислить	-5^2
51	Множитель	x^2-49
52	Вычислить	(-20+ квадратный корень из -75)/40
53	Множитель	x^2+6x+9
54	Множитель	4x^2-25
55	Вычислить	квадратный корень из 28
56	Множитель	x^2-81
57	Вычислить	2^5
58	Вычислить	-8^2
59	Вычислить	2^4
60	Множитель	4x^2-9
61	Вычислить	(-20+ квадратный корень из -50)/60
62	Вычислить	(-8+ квадратный корень из -20)/24
63	Множитель	x^2+4x+4
64	Множитель	x^2-10x+25
65	Вычислить	квадратный корень из -16
66	Множитель	x^2-2x+1
67	Вычислить	-7^2
68	График	f(x)=2^x
69	Вычислить	2^-2
70	Вычислить	квадратный корень из 27
71	Вычислить	квадратный корень из 80
72	Множитель	x^3+125
73	Вычислить	-9^2
74	Множитель	2x^2-5x-3
75	Вычислить	квадратный корень из 40
76	Множитель	x^2+2x+1
77	Множитель	x^2+8x+16
78	График	y=3x
79	Множитель	x^2+10x+25
80	Вычислить	3^3
81	Вычислить	5^-2
82	График	f(x)=x^2
83	Вычислить	квадратный корень из 54
84	Вычислить	(-12+ квадратный корень из -45)/24
85	Множитель	x^2+x-2
86	Вычислить	(-3)^3
87	Множитель	x^2-12x+36
88	Множитель	x^2+4
89	Вычислить	квадратный корень из (-8)^2
90	Множитель	x^2+7x+12
91	Вычислить	квадратный корень из -25
92	Множитель	x^2-x-20
93	Вычислить	5^3
94	Множитель	x^2+8x+15
95	Множитель	x^2+7x+10
96	Множитель	2x^2+5x-3
97	Вычислить квадратный корень	квадратный корень из 116
98	Множитель	x^2-x-12
99	Множитель	x^2-x-2
100	Вычислить	2^2

Что такое длинное умножение? | TheSchoolRun

Мы объясним, что такое метод длинного умножения, и рассмотрим, как навыки умножения формируются в течение каждого года обучения в начальной школе.

или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам

Что такое длинное умножение?

Длинное умножение (или умножение в столбик ) — письменный способ умножения чисел (обычно дву- или трехзначного числа на другое большое число).

Обычно используется в 5-м и 6-м классах после того, как дети освоят метод сетки . Преимущество метода сетки заключается в том, что он побуждает детей думать о разряде и умножать числа, кратные десяти и сотням. Как только они освоятся с этим, длинное умножение станет более быстрой и эффективной техникой для использования.

Как умножать методом длинного умножения

Как и при сложении и вычитании столбцов, числа располагаются в столбце следующим образом:

Умножение в начальной школе

Навыки умножения у детей формируются во время обучения в начальной школе следующим образом.

Год 1

• Счет вперед или назад единицами, двойками, пятерками и десятками.
• Решите одношаговые задачи на умножение с использованием объектов и массивов при поддержке учителя.

Вот пример массива для демонстрации 5 x 3 или 3 x 5:

Год 2

• Вызов фактов умножения для таблиц умножения на 2, 5 и 10 и соответствующих фактов деления.
• Используйте многократное сложение (представляющее 4 партии по 3 как 3 + 3 + 3 + 3) и массивы для решения вопросов на умножение.
• Распознавать числа, кратные 2, 5 и 10.
• Используйте знаки x и = при написании предложений с числами умножения.
• Решите задачи на умножение с использованием объектов и массивов (см. схему выше).

Год 3

• Вызов фактов умножения для таблиц умножения на 2, 3, 4, 5, 8 и 10 и соответствующих фактов деления.
• Используйте письменные методы для умножения двузначных чисел на однозначные числа (например: 13 x 4).

Год 4

• Вспомнить факты умножения до 12 x 12 и соответствующие факты деления.
• Распознавание и использование пар факторов.
• Умножение двузначных и трехзначных чисел на однозначное с использованием формальной письменной схемы.

Год 5

• Определение кратных и коэффициентов.
• Распознавать простые числа, имеющие только два делителя, и определять простые числа меньше 100.
• Понимать квадратные и кубические числа.
• Умножение чисел до четырех цифр на однозначное или двузначное число с использованием формальных методов, включая длинное умножение.

Как видно из приведенных выше задач, детям не нужно умножать двузначные числа на трехзначные числа до 6-го класса, поэтому методу длинного умножения, вероятно, не будут обучать до тех пор (хотя способные дети 5-го класса могут используйте и его).

Год 6

• Умножение чисел до четырех цифр на двузначное с использованием длинного умножения.
• Определите общие делители, общие кратные и простые числа.
• Умножение однозначных чисел, содержащих до двух знаков после запятой, на целые числа.

Длинное умножение — определение, методы, шаги, примеры

Длинное умножение считается специальным методом умножения больших двузначных и более чисел. Метод умножения чисел больше 10 известен как метод длинного умножения. Для этого метода необходимо знание таблицы умножения от 1 до 10. В этом разделе мы узнаем о длинном умножении, поняв умножение больших чисел, метод умножения столбцом и то, как их применять при решении задач.

1.	Что такое длинное умножение?
2.	Метод длинного столбца умножения
3.	Длинное умножение с десятичными дробями
4.	Горизонтальный метод длинного умножения
5.	Длинное умножение с отрицательными числами
6.	Часто задаваемые вопросы о длинном умножении

Что такое длинное умножение?

Длинное умножение — это метод умножения двух или более чисел. Учтите, что нам нужно умножить любые два числа больше 10 или 100, мы обычно выполняем длинное умножение. Другое название длинного умножения — столбцовый метод умножения, поскольку числа также можно умножать в столбце. Обычно нахождение произведения двух чисел не может быть простым, то есть когда мы используем метод длинного умножения.

Давайте посмотрим на этот пример, рассмотрим 31 × 49. Здесь мы умножаем 31 на 49 напрямую, записывая одно из этих чисел в расширенной форме, т. е. 31 = 30 + 1. 30 — десятая часть, а 1 — единица. . Таким образом, 31 × 49 можно записать как 30 × 49 + 1 × 49. Сначала мы умножаем 49 на 30, затем 49 умножаем на 1, а затем складываем их. Итак, вместо прямого умножения мы выполнили длинное умножение, что делает процесс простым и точным.

Метод длинного столбца умножения

Метод умножения в столбик почти такой же, как и метод длинного умножения, с той лишь разницей, что в методе длинного умножения мы выполняем умножение по горизонтали, а в методе умножения в столбик мы выполняем умножение по вертикали. Как и длинное умножение, метод столбца также имеет пошаговую процедуру. Вот они:

• Шаг 1: Расположите числа в столбце в соответствии с их разрядностью. Большее число обычно пишется сверху.
• Шаг 2: После упорядочивания начните с умножения нижнего числа в разряде единиц на верхнее число.
• Шаг 3: Всегда помните о движении справа налево, поэтому, когда результат будет получен, расположите его под двумя числами. Начните умножать число десятков в нижнем числе на верхнее число. Поместите результат, оставив место единицы пустым или поставив ноль.
• Шаг 4: После получения чисел используйте метод сложения для получения окончательного решения.

Давайте рассмотрим пример для лучшего понимания. Умножьте 52 × 11.

Шаг 1: Расположите числа вертикально, как показано ниже.

Шаг 2: Сначала умножьте 52 на 1.

Шаг 3: Теперь умножьте 52 на 1 на десятом месте, здесь мы на самом деле умножаем 52 Шаг 40 20 20 9 на 10.

3 900 : Теперь добавьте 52 и 520.

Следовательно, 52 × 11 = 572,

Длинное умножение с десятичными дробями

Метод длинного умножения можно использовать и для десятичных чисел. Давайте рассмотрим пример: умножьте 4,1 × 2,7.

При умножении держите меньшее число справа.

Шаг 1: Удалите десятичную дробь и преобразуйте десятичное число в дробь.

4,1 × 2,7 = 41/10 × 27/10

Шаг 2: Теперь оставьте 10 в знаменателе.

41/10 × 27/10 = (41 × 27) / (10 × 10)

Шаг 3: Выполните длинное умножение числителей и некоторое время отложите знаменатель.

Шаг 4: Теперь разделите результат умножения на знаменатель, который мы оставили в стороне. Чтобы получить десятичное число, мы преобразуем 1107, учитывая два нуля в знаменателе и считая десятичную точку от последнего числа, т.е. 7, к следующему числу, т.е. 0. Следовательно, десятичная точка ставится через два числа после последнего числа.

(1107) / (10 × 10) = 1107 / 100 = 11,07

Следовательно, 4,1 × 2,7 = 11,07

Горизонтальный метод длинного умножения

В длинном умножении одним из методов, помимо метода столбца, является горизонтальный метод. Этот метод в основном используется для однозначных и двузначных чисел. Давайте рассмотрим пошаговую процедуру решения длинного умножения горизонтальным методом:

• Шаг 1: Расположите числа горизонтально рядом друг с другом в обычном формате умножения.
• Шаг 2: Начните с умножения первого числа, стоящего на месте единицы, на другое число.
• Шаг 3: Всегда двигайтесь справа налево при длинном умножении. Как только первое число будет сделано, умножьте число в разряде десятков на другое число.
• Шаг 4: Как только результат получен и записан в формате столбца, используйте метод сложения, чтобы найти окончательное решение.

Давайте воспользуемся приведенным выше примером для лучшего понимания умножения двухзначных чисел. Умножить 31 × 49

Шаг 1: Расположите числа горизонтально и начните с умножения 49 на 1.

Шаг 2: Теперь умножьте 49 на 3 и поставьте крестик чуть ниже 9 (место единицы числа 49) , этот крестик представляет 0.

Шаг 3: Напишите нули перед числом 49, чтобы оно покрывало число 1 из 147, напишите числа сразу под другим числом, чтобы сложение было легким.

Шаг 4: Добавьте эти два числа 0049и 1470.

Следовательно, 31 × 49 = 1519. В длинном умножении крестик представляет ноль. Кроме того, при умножении чисел до 3-значных мы должны добавить два креста, пока мы умножаем до стозначного числа.

Длинное умножение с отрицательными числами

Длинное умножение отрицательных чисел следует тому же правилу, что и положительные числа, с той лишь разницей, что используются знаки. Мы должны помнить правила знаков при умножении чисел. При умножении положительного числа на отрицательное получается отрицательное число.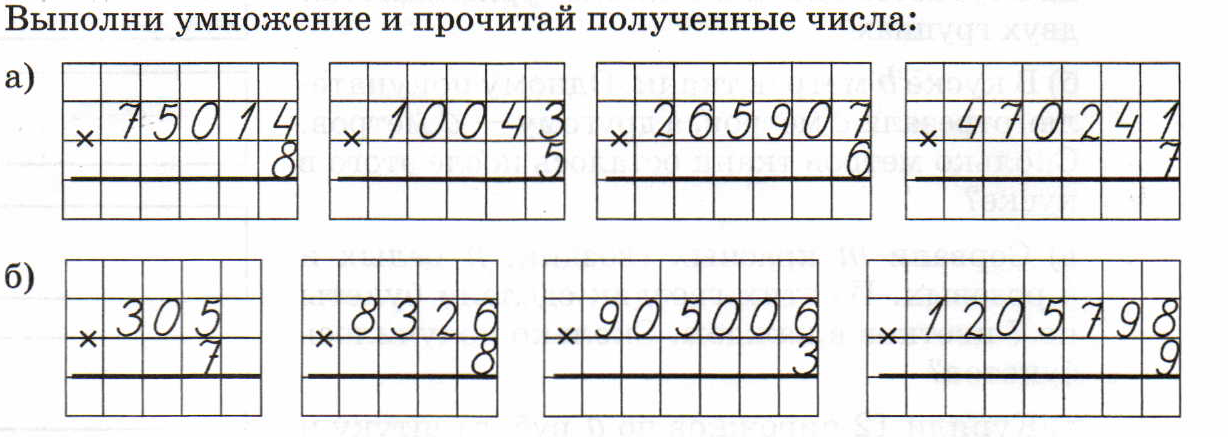 Принимая во внимание, что когда два отрицательных числа умножаются друг на друга, решение является положительным числом.

Часто задаваемые вопросы о длинном умножении

Что означает длинное умножение?

Длинное умножение — это метод умножения, используемый для умножения чисел до двух и более цифр. Длинное умножение можно выполнить двумя способами — числа, записанные горизонтально, и числа, записанные столбцом. Большие числа, состоящие более чем из 3 цифр, умножаются методом длинного умножения. Умножение двух чисел также называется произведением двух чисел. Длинное умножение также известно как столбцовый метод умножения.

Каковы шаги горизонтального метода длинного умножения?

Для выполнения длинного умножения больших чисел требуется 4 шага:

• Расположите числа горизонтально.
• Начните с умножения первого числа, стоящего на месте единицы, на другое число.
• Всегда двигаться справа налево при длинном умножении. Как только первое число будет завершено, умножьте число в разряде десятков на другое число.
• После того, как результат получен и записан в виде столбца, используйте метод сложения, чтобы найти окончательное решение.

Каковы шаги для метода длинного столбца умножения?

Шаги длинного умножения по столбцам очень похожи на обычное длинное умножение. Метод столбца выполняется вертикально и состоит из 4 шагов:

• Расположите числа в формате столбца в соответствии с их разрядностью.
• Начните с умножения нижнего числа в разряде единиц на верхнее число.
• После получения результата расположите его под двумя числами. Начните умножать число десятков в нижнем числе на верхнее число.
• После того, как числа получены, используйте метод сложения, чтобы прийти к окончательному решению.

Можно ли использовать длинное умножение для десятичных чисел?

Да, метод длинного умножения можно использовать и для десятичных чисел. При умножении десятичных чисел всегда держите меньшее число справа. Для десятичных чисел можно использовать как горизонтальные, так и вертикальные методы умножения.

Можно ли использовать длинное умножение для отрицательных чисел?

Да, метод длинного умножения можно использовать для отрицательных чисел с помощью нескольких правил, таких как:

• Положительное число, умноженное на положительное число, даст положительное число.
• Умножение отрицательного числа на положительное или наоборот даст отрицательное число.
• При умножении отрицательного числа на отрицательное число получается положительное число.

Как решать длинные задачи на умножение?

Задачи на длинное умножение можно решить двумя способами: методом длинного умножения и методом столбца. Метод длинного умножения требует, чтобы числа были написаны горизонтально, тогда как метод столбца требует, чтобы числа были написаны вертикально. Оба метода помогают в решении задач с большими числами.