Умножение на 4 | Таблица умножения
На этой странице представлены примеры, описывающие умножение на 4 и умножение числа 4, деление, некоторые способы произношения и записи, таблица умножения на 4 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать часть таблицы. Умножение на 4:
1 x 4 = 4
2 x 4 = 8
3 x 4 = 12
4 x 4 = 16
5 x 4 = 20
6 x 4 = 24
7 x 4 = 28
8 x 4 = 32
9 x 4 = 36
10 x 4 = 40
Первый вариант произношения:
1 x 4 = 4 (1 умножить на 4, равно 4)
2 x 4 = 8 (2 умножить на 4, равно 8)
3 x 4 = 12 (3 умножить на 4, равно 12)
4 x 4 = 16 (4 умножить на 4, равно 16)
5 x 4 = 20 (5 умножить на 4, равно 20)
6 x 4 = 24 (6 умножить на 4, равно 24)
7 x 4 = 28 (7 умножить на 4, равно 28)
8 x 4 = 32 (8 умножить на 4, равно 32)
9 x 4 = 36 (9 умножить на 4, равно 36)
10 x 4 = 40 (10 умножить на 4, равно 40)
Второй вариант произношения:
1 x 4 = 4 ( по 1 взять 4 раза, получится 4)
3 x 4 = 12 ( по 3 взять 4 раза, получится 12)
4 x 4 = 16 ( по 4 взять 4 раза, получится 16)
5 x 4 = 20 ( по 5 взять 4 раза, получится 20)
6 x 4 = 24 ( по 6 взять 4 раза, получится 24)
7 x 4 = 28 ( по 7 взять 4 раза, получится 28)
8 x 4 = 32 ( по 8 взять 4 раза, получится 32)
9 x 4 = 36 ( по 9 взять 4 раза, получится 36)
10 x 4 = 40 ( по 10 взять 4 раза, получится 40)
От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 4, можно легко найти результаты умножения числа 4.
В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки ( ∙ )
Умножение числа 4:
4 ∙ 1 = 4
4 ∙ 2 = 8
4 ∙ 3 = 12
4 ∙ 4 = 16
4 ∙ 5 = 20
4 ∙ 6 = 24
4 ∙ 7 = 28
4 ∙ 8 = 32
4 ∙ 9 = 36
4 ∙ 10 = 40
Варианты произношения:
4 ∙ 1 = 4 (по 4 взять 1 раз, получится 4)
4 ∙ 2 = 8 (по 4 взять 2 раза, получится 8)
4 ∙ 3 = 12 (по 4 взять 3 раза, получится 12)
4 ∙ 4 = 16 (по 4 взять 4 раза, получится 16)
4 ∙ 5 = 20 (по 4 взять 5 раз, получится 20)
4 ∙ 6 = 24 (по 4 взять 6 раз, получится 24)
4 ∙ 7 = 28 (по 4 взять 7 раз, получится 28)
4 ∙ 8 = 32 (по 4 взять 8 раз, получится 32)
4 ∙ 9 = 36 (по 4 взять 9 раз, получится 36)
4 ∙ 10 = 40 (по 4 взять 10 раз, получится 40)
4 ∙ 1 = 4 (4 умножить на 1, равно 4)
4 ∙ 2 = 8 (4 умножить на 2, равно 8)
4 ∙ 3 = 12 (4 умножить на 3, равно 12)
4 ∙ 4 = 16 (4 умножить на 4, равно 16)
4 ∙ 5 = 20 (4 умножить на 5, равно 20)
4 ∙ 6 = 24 (4 умножить на 6, равно 24)
4 ∙ 7 = 28 (4 умножить на 7, равно 28)
4 ∙ 8 = 32 (4 умножить на 8, равно 32)
4 ∙ 9 = 36 (4 умножить на 9, равно 36)
4 ∙ 10 = 40 (4 умножить на 10, равно 40)
Деление на 4:
4 ÷ 4 = 1
8 ÷ 4 = 2
16 ÷ 4 = 4
20 ÷ 4 = 5
24 ÷ 4 = 6
28 ÷ 4 = 7
32 ÷ 4 = 8
36 ÷ 4 = 9
40 ÷ 4 = 10
4 ÷ 4 = 1 (4 разделить на 4, равно 1)
8 ÷ 4 = 2 (8 разделить на 4, равно 2)
12 ÷ 4 = 3 (12 разделить на 4, равно 3)
16 ÷ 4 = 4 (16 разделить на 4, равно 4)
20 ÷ 4 = 5 (20 разделить на 4, равно 5)
24 ÷ 4 = 6 (24 разделить на 4, равно 6)
28 ÷ 4 = 7 (28 разделить на 4, равно 7)
32 ÷ 4 = 8 (32 разделить на 4, равно 8)
36 ÷ 4 = 9 (36 разделить на 4, равно 9)
40 ÷ 4 = 10 (40 разделить на 4, равно 10)
Картинка:
Деление.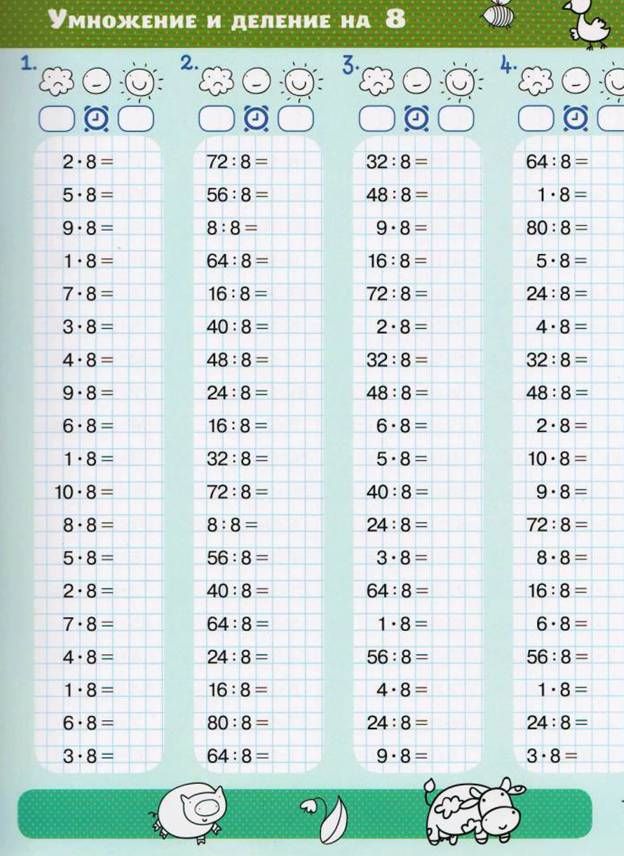
Картинка:
Таблица умножения и деления на 4 без ответов (по порядку и вразброс):
| 1 ∙ 4 = | 3 ∙ 4 = | 4 ÷ 4 = | 36 ÷ 4 = |
| 2 ∙ 4 = | 6 ∙ 4 = | 8 ÷ 4 = | 32 ÷ 4 = |
| 3 ∙ 4 = | 1 ∙ 4 = | 12 ÷ 4 = | 28 ÷ 4 = |
| 4 ∙ 4 = | 4 ∙ 4 = | 16 ÷ 4 = | 24 ÷ 4 = |
| 5 ∙ 4 = | 2 ∙ 4 = | 20 ÷ 4 = | 16 ÷ 4 = |
| 6 ∙ 4 = | 7 ∙ 4 = | 24 ÷ 4 = | 20 ÷ 4 = |
| 7 ∙ 4 = | 10 ∙ 4 = | 28 ÷ 4 = | 12 ÷ 4 = |
| 8 ∙ 4 = | 5 ∙ 4 = | 32 ÷ 4 = | 8 ÷ 4 = |
| 9 ∙ 4 = | 9 ∙ 4 = | 36 ÷ 4 = | 4 ÷ 4 = |
| 10 ∙ 4 = | 8 ∙ 4 = | 40 ÷ 4 = | 40 ÷ 4 = |
Способы записи таблицы умножения на 4:
| x | Приподнятая точка | * | Знак не указан |
|---|---|---|---|
| 1 x 4 = 4 | 1 ∙ 4 = 4 | 1 * 4 = 4 | 1 __ 4 = 4 |
| 2 x 4 = 8 | 2 ∙ 4 = 8 | 2 * 4 = 8 | 2 __ 4 = 8 |
| 3 x 4 = 12 | 3 ∙ 4 = 12 | 3 * 4 = 12 | 3 __ 4 = 12 |
| 4 x 4 = 16 | 4 ∙ 4 = 16 | 4 * 4 = 16 | 4 __ 4 = 16 |
| 5 x 4 = 20 | 5 ∙ 4 = 20 | 5 * 4 = 20 | 5 __ 4 = 20 |
| 6 x 4 = 24 | 6 ∙ 4 = 24 | 6 * 4 = 24 | 6 __ 4 = 24 |
| 7 x 4 = 28 | 7 ∙ 4 = 28 | 7 * 4 = 28 | 7 __ 4 = 28 |
| 8 x 4 = 32 | 8 ∙ 4 = 32 | 8 * 4 = 32 | 8 __ 4 = 32 |
| 9 x 4 = 36 | 9 ∙ 4 = 36 | 9 * 4 = 36 | 9 __ 4 = 36 |
| 10 x 4 = 40 | 10 ∙ 4 = 40 | 10 * 4 = 40 | 10 __ 4 = 40 |
Способы записи таблицы деления на 4:
| / | : | ÷ | Знак не указан |
|---|---|---|---|
| 4 / 4 = 1 | 4 : 4 = 1 | 4 ÷ 4 = 1 | 4 __ 4 = 1 |
| 8 / 4 = 2 | 8 : 4 = 2 | 8 ÷ 4 = 2 | 8 __ 4 = 2 |
| 12 / 4 = 3 | 12 : 4 = 3 | 12 ÷ 4 = 3 | 12 __ 4 = 3 |
| 16 / 4 = 4 | 16 : 4 = 4 | 16 ÷ 4 = 4 | 16 __ 4 = 4 |
| 20 / 4 = 5 | 20 : 4 = 5 | 20 ÷ 4 = 5 | 20 __ 4 = 5 |
| 24 / 4 = 6 | 24 : 4 = 6 | 24 ÷ 4 = 6 | 24 __ 4 = 6 |
| 28 / 4 = 7 | 28 : 4 = 7 | 28 ÷ 4 = 7 | 28 __ 4 = 7 |
| 32 / 4 = 8 | 32 : 4 = 8 | 32 ÷ 4 = 8 | 32 __ 4 = 8 |
| 36 / 4 = 9 | 36 : 4 = 9 | 36 ÷ 4 = 9 | 36 __ 4 = 9 |
| 40 / 4 = 10 | 40 : 4 = 10 | 40 ÷ 4 = 10 | 40 __ 4 = 10 |
Умножение на:
‹ Умножение на 3 Вверх Умножение на 5 ›
32Методика изучения табличного умножения и деления
32 Методика
изучения табличного умножения и деления.
При изучении
таблицы умножения во II классе, как
показывает опыт, целесообразно
пользоваться следующими основными
положениями. Таблица умножения изучается
в порядке натурального ряда чисел:
умножение числа 2, числа 3, числа 4 и т.д.
Таблица умножения каждого числа
располагается по постоянному множимому,
это обеспечивает понимание умножения
как сложения одинаковых слагаемых.
Наизусть и твердо усваивается только
таблица умножения. Таблица деления
специально не изучается и не заучивается.
Результаты табличного деления ученик
находит по таблице умножения. Например,
36 разделить на 4, будет 9, потому что,
если9умножить на четыре, то получится
36. С самого начала изучения таблицы
умножения широко и последовательно
используется переместительный закон
умножения. Каждый пример из таблицы,
допустим 3 x 8 = 24, может быть прочитан
двояко: 3 умножить на 8, получится 24 и 8
умножить на 3, получится 24. Так ученики
читают один и тот же пример на основании
переместительного закона умножения. В
каждом табличном примере первое число
можно рассматривать как множимое и как
множитель.
Табличное умножение и деление изучаются совместно: из каждого случая умножения вытекают два случая деления. Например: 3 x 9 = 27. Отсюда 27 : 3 = 9; 27 : 9 = 3. Таким образом, результаты табличного деления всегда берутся из таблицы умножения.
Изучение таблицы умножения и табличного деления все время сопровождается решением задач, в которых эти действия находят практическое применение, что способствует твердому усвоению таблицы умножения и быстрому нахождению по этой таблице результатов, деления.
На первом уроке таблица умножения составляется, и проводятся первоначальные упражнения в ее усвоении. Примерный план этого урока.
1. Счет
четверками в пределах 40. Этот счет идет
сначала на наглядном пособии, например
на классных счетах, а потом отвлеченно.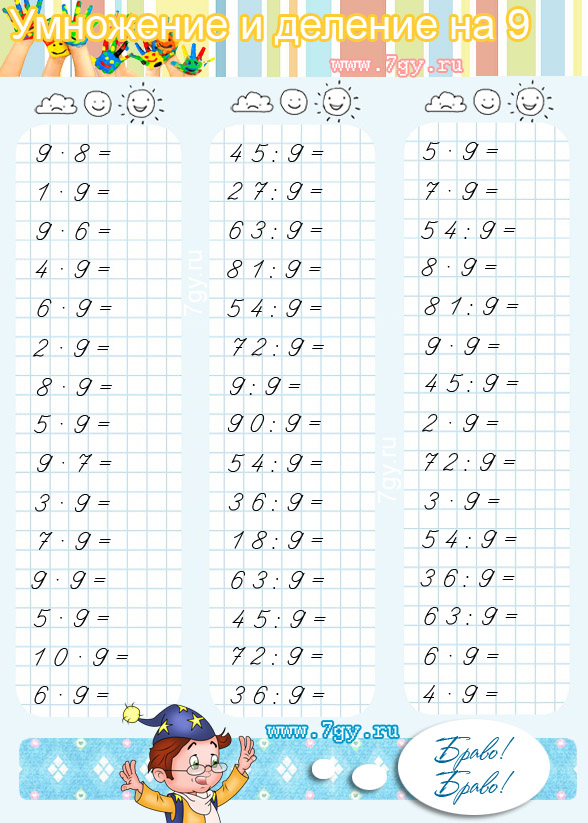
Очень важно, чтобы ученики запомнили
результаты этого счета, составляющие
числовой ряд: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40 — и
могли бы по памяти быстро и правильно
воспроизвести числа этого ряда в прямом
и обратном порядке.
3. Чтение таблицы, упражнения в ее запоминании. Составленная таблица читается хором и отдельными учениками, подряд и вразбивку, с открытыми результатами и закрытыми. Детям сразу дается установка на запоминание таблицы: «Таблицу нужно знать наизусть, твердо. Читая, старайтесь ее запомнить». При этом обращается внимание детей на способ набора четверок: четверки можно набирать по одной и группами. Например, чтобы набрать 6 четверок, можно взять 3 четверки и еще 3, или 5 четверок и еще одну четверку.
Ученики скорее и лучше запомнят таблицу, если усвоение ее будет опираться на различные восприятия и анализаторы: зрительные, слуховые, кинестезические (проговаривание), моторные.
4. Применение
знания таблицы умножения при решении
задач. Детям предлагают преимущественно
простые задачи на умножение: 1.
В одном
литре 4 стакана молока. Сколько стаканов
молока в 6, 7, 8, 9, 10 литрах? 2. Для одной
автомашины требуется 4 колеса. Сколько
колес требуется для 5, 6, 7, 8, 9, 10 автомашин?
5. Задание на дом:
1. Усвоить таблицу умножения числа 4 наизусть.
2. Решить несколько примеров и задач, в которых применяется знание таблицы умножения 4 и ранее изученных таблиц.
На втором уроке продолжаются упражнения в закреплении знания таблицы умножения числа 4 путем решения примеров и.задач на умножение. Кроме того, на этом уроке учитель знакомит детей с табличным делением, показывая им, как можно получить результат деления на 4, зная таблицу умножения четырех.
Когда все случаи табличного умножения и деления будут пройдены, полезно в целях повторения выписать все табличные результаты, большие 20, и поупражнять детей в подборе к каждому из них сомножителей и делителей:
21; 24; 25; 27; 28; 30;
32; 35; 36; 40; 42; 45; 48; 49; 50;
54; 56; 60; 64; 70;
72; 80; 81; 90.
При такой системе изучения табличного умножения и деления сокращаются сроки изучения этого раздела и устраняются многие трудности.
При изучении табличного умножения в пределах ста используются переместительный и распределительный законы умножения. Применение переместительного закона проиллюстрировано выше. Использование же распределительного закона поясним на примере умножения числа 6 (рис, 45).
При изучении табличного деления нет необходимости раскрывать свойства этого действия. Дело ограничивается установлением взаимосвязи между делением и умножением, различением двух видов деления и обобщением их в одно действие деления.
32. Методика изучения табличного умножения и деления.
1. сложение, повторение одинаковых слагаемых , счет равными группами
2. распределительное свойство умножения относительно суммы – множителя. 6*7=6*5+6*2
3. сочетательное свойство умножения. 7*6= (7*3)*2
4. переместительное свойство умножения. 7*6=6*7
5.
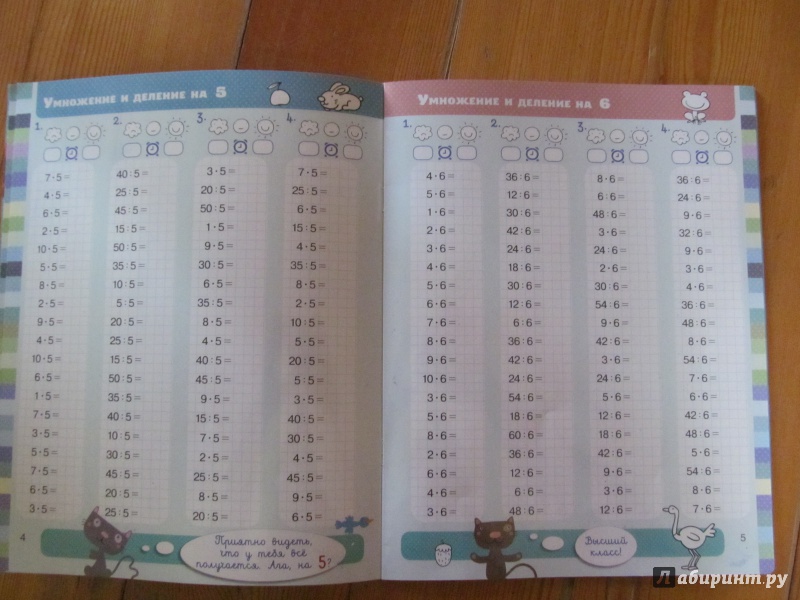распределительное
свойство умножения относительно разности
множителя. 7*8=7*10 – 7*2
6. распределительное свойство умножения относительно суммы – множимого. 8*4= 5*4+3*4
7. распределительное свойство умножения относительно разности – множимого. 8*6=10*6-2*6
Прием изучения табличного деления.
Применение таблицы умножения. Чтобы 21/7. Если 21 разделить на 7 равных частей сколько должно получиться?
Division 4 in a Row — математическая игра Division
Division 4 in a Row — математическая игра Division
Content Skill: Division
Common Core State Standards: CCSS.Math.Content.3.OA.C.7 — Свободно делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
Описание
Раздел 4 в ряд — это фантастический способ выучить факты умножения. В этой многопользовательской математической игре уравнения сочетаются со стратегией.
Дети просто не могут насытиться этой игрой. Либо играйте против компьютера, либо играйте против других игроков по всему миру.
Мы должны предупредить вас, что эту игру трудно бросить! Держись! Не сдавайся. Вы можете победить компьютер!
Инструкции
Экран приветствия
Экран приветствия служит отправной точкой игры. Отсюда вы можете отключить все звуки игры. Нажмите пульсирующую кнопку воспроизведения, чтобы начать игру в одиночном или многопользовательском режиме.
Выберите игровой режим
Выберите режим одиночной игры или игру против других игроков. Кнопка слева немедленно начнет одиночную игру. Кнопка справа приведет вас либо к экрану входа в систему, либо к экрану начала матча. Если вы уже являетесь студентом, вошедшим в систему управления студентами Multiplication.com, вы уже вошли в систему. Если нет, вам нужно будет указать имя пользователя для входа.
Одиночная игра
В одиночной игре компьютер сразу выбирает ход. Каждый раз, когда подходит ваша очередь, вам будет предложено ответить на один вопрос.
После того, как вы ответили на уравнение, вы также сможете выбрать ход. Будьте осторожны, компьютер — очень хороший противник.
Одиночная игра окончена
Когда одиночная игра закончится, вы увидите этот экран. Кнопка «Домой» вернет вас на экран приветствия. Кнопка обновления запустит новую одиночную игру.
Экран входа в систему
Если вы не вошли в систему как студент multiplication.com, вам необходимо войти в игру, чтобы иметь возможность играть против других игроков. Введите имя пользователя, которое вы хотите использовать. Убедитесь, что ваше имя пользователя соответствует.
Экран начала матча
После успешного входа в систему вы увидите экран начала матча. На данный момент вы вошли в систему и готовы играть в многопользовательскую игру. Если вы решите, что не хотите играть в многопользовательском режиме, вы можете нажать кнопку отмены, чтобы вернуться на экран приветствия. В противном случае нажмите кнопку битвы.
Экран ожидания противника
В течение 15 секунд мы будем искать другого игрока, готового начать многопользовательскую игру, чтобы сразиться с вами.