Примеры умножение столбиком 4 класс: 4 класс. Примеры на умножение многозначных чисел в столбик. Примеры с ответами. Скачать pdf или jpg.

admin

Содержание

😃 Умножение — правила, секретные примеры, упражнения, игры

Основа математики – это четыре операции с числами и переменными: сложение, вычитание, деление и умножение. Как раз об операции умножения и пойдет речь в этой статье.

  • Формулы умножения
  • Сокращенное умножение
  • Умножение дробей
  • Таблица умножения
  • Игры на развитие счета
  • Развитие феноменального устного счета

Умножение чисел

Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.

Пример 2*5. Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.

Пример 4*3. Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.

Пример 5*3. Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Записаться на курсПодробнее

Формулы умножения

Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:

a1+a2+…+an=n*a.

Где, а – любое число, n – число слагаемых а. Допустим, а=2, тогда 2+2+2=6, тогда n=3 умножая 3 на 2, получаем 6.Рассмотрим в обратном порядке. Например, дано: 3 * 3, то есть. 3 умножить на 3 – это значит, что тройку надо взять 3 раза: 3 + 3 + 3 = 9. 3 * 3=9.

Сокращенное умножение

Сокращенное умножение – сокращение операции умножения в определенных случаях, и специально для этого выведены формулы сокращенного умножения. Которые помогут сделать вычисления наиболее рациональными и быстрыми:

Формулы сокращенного умножения

Пусть a, b принадлежат R, тогда:

  1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения. 2)

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Записаться на курсПодробнее

Умножение дробей

Рассматривая сложение и вычитание дробей, прозвучало правило, приведения дробей к общему знаменателю, чтобы выполнить расчет. При умножении этого делать не надо! При умножении двух дробей, умножается знаменатель на знаменатель, а числитель на числитель.

Например, (2/5) * (3 * 4). Умножим две трети на одну четверть. Умножаем знаменатель на знаменатель, а числитель на числитель: (2 * 3)/(5 * 4), тогда 6/20, совершаем сокращение, получаем 3/10.

Умножение 2 класс

Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения.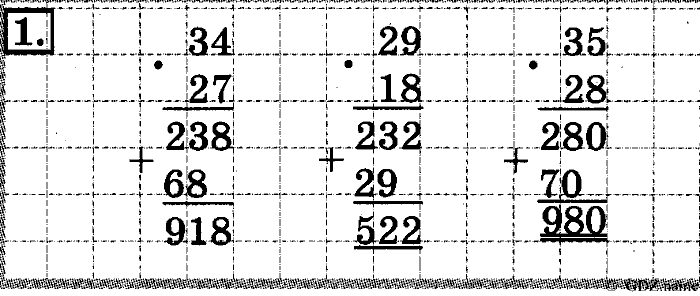 Давайте рассмотрим задачи на умножение уровня второго класса:

  1. Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?

  2. В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?

  3. Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?

  4. В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?

  5. Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?

  6. В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?

  7. Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?

  8. В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?

Умножение 3 класс

В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление.

Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.

Умножение столбиком:

Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.

1 шаг. Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.

2 шаг. Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.

Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.

3 шаг. Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.

4 шаг. Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.

Итак, умножив 427 на 6, получился ответ 2562

ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!

5 шаг. Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281

6 шаг. Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.

Умножение 4 класс

Четвертый класс – это уже умножение только больших чисел. Вычисление выполняются методом умножения в столбик. Метод описан выше доступным языком.

Например, найти произведение следующих пар чисел:

  1. 988 * 98 =
  2. 99 * 114 =
  3. 17 * 174 =
  4. 164 * 19 =

Презентация на умножение

Скачайте презентацию на умножение с простейшими заданиями для второклассников. Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!

Презентация

Таблица умножения

Таблица умножения учится каждым школьником во втором классе. Ее обязан знать каждый!

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Записаться на курсПодробнее

Примеры на умножение

Умножение на однозначное

  1. 9 * 5 =
  2. 9 * 8 =
  3. 8 * 4 =
  4. 3 * 9 =
  5. 7 * 4 =
  6. 9 * 5 =
  7. 8 * 8 =
  8. 6 * 9 =
  9. 6 * 7 =
  10. 9 * 2 =
  11. 8 * 5 =
  12. 3 * 6 =

Умножение на двузначное

  1. 4 * 16 =
  2. 11 * 6 =
  3. 24 * 3 =
  4. 9 * 19 =
  5. 16 * 8 =
  6. 27 * 5 =
  7. 4 * 31 =
  8. 17 * 5 =
  9. 28 * 2 =
  10. 12 * 9 =

Умножение двузначное на двузначное

  1. 24 * 16 =
  2. 14 * 17 =
  3. 19 * 31 =
  4. 18 * 18 =
  5. 10 * 15 =
  6. 15 * 40 =
  7. 31 * 27 =
  8. 23 * 25 =
  9. 17 * 13 =

Умножение трехзначных чисел

  1. 630 * 50 =
  2. 123 * 8 =
  3. 201 * 18 =
  4. 282 * 72 =
  5. 96 * 660 =
  6. 910 * 7 =
  7. 428 * 37 =
  8. 920 * 14 =

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.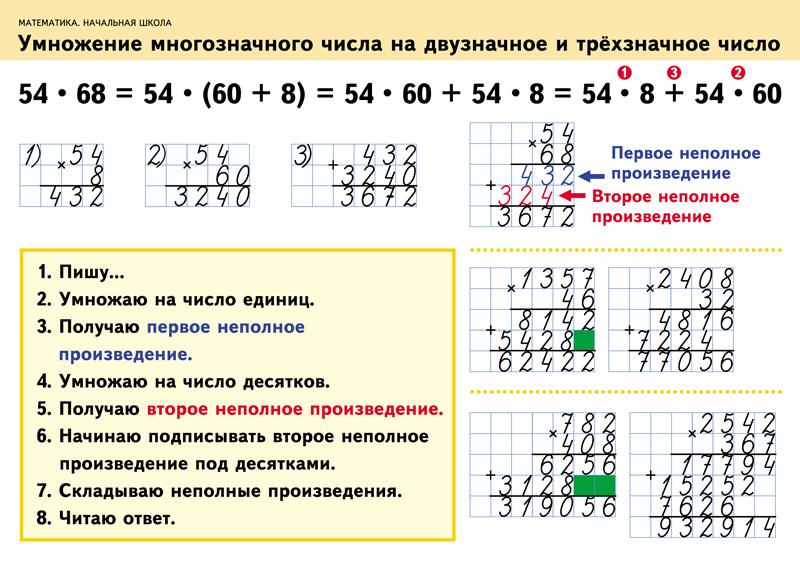

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Играть сейчас

Игра «Математические матрицы»

«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Играть сейчас

Игра «Числовой охват»

Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.

Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.

Играть сейчас

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра «Математические сравнения»

Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Записаться на курсПодробнее

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Записаться на курсБесплатный урок

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.

После прохождения курса ребенок сможет:

  1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
  2. Научится запоминать на более длительный срок
  3. Увеличится скорость воспоминания нужной информации

Записаться на курсПодробнее

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Записаться на курсПодробнее

Как улучшить память и развить внимание

Бесплатное практическое занятие от advance.

Записаться бесплатноПодробнее

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Записаться на курсПодробнее

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Записаться на курсПодробнее

Калькулятор уравнений, интегралов, производных, пределов и пр.

Пояснения к калькулятору

  1. Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
  2. Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
  3. ⌫ — удалить в поле ввода символ слева от курсора.
  4. C — очистить поле ввода.
  5. При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
  6. Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
  7. Ввод числа в n-ой степени и квадратного корня
    прозводится кнопками ab и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей →.

Упрощение выражений, раскрытие скобок, разложение многочленов на множители

Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. Результат выводится в нескольких вариантах упрощения/разложения/раскрытия скобок и пр. 2+4x+4}{x+2}\le 9 \\ 2x+9>1 \end{cases}$$ (решить систему неравенств)

Вычисление выражений с логарифмами

В калькуляторе кнопкой loge(x) возможно задать натуральный логарифм, т.е логарифм с основанием «e»: loge(x) — это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$\log_a \left(b\right) = \frac{\log \left(b\right)}{\log \left(a\right)}$$ Например, $$\log_{3} \left(5x-1\right) = \frac{\log \left(5x-1\right)}{\log \left(3\right)}$$

$$\log _3\left(5x-1\right)=2$$ преобразуем в $$\frac{\log \left(5x-1\right)}{\log \left(3\right)}=2$$ (решить уравнение)

$$\log _2\left(x\right)=2\log _x\left(2\right)-1$$ преобразуем в $$\frac{\log \left(x\right)}{\log \left(2\right)}=2\cdot \frac{\log \left(2\right)}{\log \left(x\right)}-1$$ (найти x в уравнении)

Вычисление пределов функций

Предел функции задается последовательным нажатием групповой кнопки f(x) и функциональной кнопки lim. 7}{\left(4-5i\right)\left(-3+i\right)}-\frac{4+4i}{-2-5i}$$ (выполнить действия над комплексными числами)

Длинное умножение | Методы, примеры, 10,100 и 1000

Мы знаем, что умножение — это форма многократного сложения. Хотя легко умножить два однозначных или двузначных числа с помощью таблицы умножения, то же самое нельзя сказать о больших числах. Умножение больших чисел, где либо множимое представляет собой двухзначное число или более, либо множитель представляет собой двузначное число или более, включает другой метод умножения, известный как длинное умножение.

Помните, что способ умножения чисел остается прежним, это всего лишь способ расположить числа таким образом, чтобы сделать процесс умножения проще и быстрее.

В этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.

Давайте разберем их один за другим

Этот метод вступает в силу, когда у нас есть числа, которые не требуют переноса каких-либо чисел на разряд следующего разряда. Давайте разберемся на примере.

Например, умножьте 1021 на 3

Решение:

Мы будем использовать следующие шаги, чтобы получить наш результат.

Шаг 1: Сначала мы записываем множимое и множитель в столбцах.

Шаг 2: Теперь умножаем число в разряде единиц на 3. Получаем

Шаг 3: Теперь умножаем число в разряде десятков на 3. Получаем

Шаг 4: Далее умножаем число в разряде сотен на 3. Получаем

Шаг 5: Наконец, умножаем число в разряде тысяч на 3. Получаем

Следовательно, 1021 x 3 = 3063

В приведенном выше случае у нас есть небольшие умножения, которые ни на одном шаге не включали двузначные результаты. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.

Например, умножьте 5092 на 5

Решение

Мы будем использовать следующие шаги, чтобы получить наш результат.

Шаг 1: Сначала мы записываем множимое и множитель в столбцах.

Шаг 2: Умножьте цифру единиц на 5. У нас 2 x 5 = 10. Запишите 0 в колонке единиц и перенесите 1 в колонку десятков.

Шаг 3: Умножьте цифру десятков на 5. Получаем 9 x 5 = 45. Прибавьте к ней перенесенную 1, чтобы получить 45 + 1 = 46. Теперь запишите 6 в столбце десятков и перенесите 4 в разряд сотен. столбец.

Шаг 4: Умножьте цифру сотен на 5. Получаем 0 x 5 = 5. Теперь прибавьте к ней перенесенное 4, и получится 4. Запишите 4 в столбце сотен.

Шаг 5: Умножьте 5 на цифру тысячи. Получаем 5 x  = 25. Запишите 5 в столбце тысяч и 2 в столбце десятков тысяч.

Следовательно, конечный продукт равен 25460.

Просмотреть все НОВЫЕ математические рабочие листы

Метод длинного умножения, когда множитель представляет собой двузначное число, т. е. когда множитель больше 9, включает следующие шаги:

  1. Сначала запишем множимое и множитель столбцами.
  2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
  3. Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
  4. Теперь перейдите к следующей строке.
  5. Поставьте 0 на месте единицы в этой строке.
  6. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0068
  7. Поскольку множитель был двузначным числом, вы достигли конца множителя.
  8. Сложите числа по вертикали в соответствии с их разрядностью.
  9. Полученное таким образом число и есть ваш результат.

Разберем это на примере

Например, умножим 132 на 13

Решение

1. Сначала запишем множимое и множитель столбцами.

2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.

3. Поставьте 0 на месте единицы следующей строки

4. Теперь найдите цифру в разряде десятков множителя. Умножьте число в десятом разряде множителя на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.

5. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.

6. Окончательный ответ: 1716. Следовательно, 132 x 13 = 1716

Метод длинного умножения, когда множитель представляет собой трехзначное число, т. е. когда множитель больше 99, включает следующие шаги:

  1. Во-первых, мы записываем множимое и множитель в столбцах.
  2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
  3. Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
  4. Теперь перейдите к следующей строке.
  5. Поставьте 0 на месте единицы в этой строке.
  6. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0.
  7. Снова переходите на следующую строку.
  8. Поставьте 0 на месте единиц и десятков в этой строке.
  9. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
  10. Поскольку множитель представляет собой трехзначное число, вы достигли конца множителя
  11. Сложите числа по вертикали в соответствии с их разрядами.
  12. Полученное таким образом число и есть ваш результат.

Например, умножьте 364 на 123

Решение

1. Сначала запишем множимое и множитель в столбцы

2. Теперь умножим все числа множителей с разрядом единицы множимого и запишите их горизонтально.

3. Поставьте 0 на месте единицы следующей строки

4. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в разряде десятков множителя, на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.

5. Поставьте 0 в разрядах единиц и десятков следующей строки.

6. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.

7. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.

8. Следовательно, конечный продукт равен 44 772. Мы можем сказать, что 364 x 123 = 44772

Давайте теперь суммируем шаги, связанные с длинным умножением, независимо от количества цифр множителя. Шаги:

  1. Сначала мы записываем множимое и множитель в столбцах.
  2. Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
  3. Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
  4. Теперь перейдите к следующей строке.
  5. Поставьте 0 на месте единицы в этой строке.
  6. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0.
  7. Снова переходите на следующую строку.
  8. Поставьте 0 на месте единиц и десятков в этой строке.
  9. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
  10. Продолжайте в том же духе, добавляя дополнительный ноль в каждую строку, пока не дойдете до конца множителя
  11. Сложите числа по вертикали в соответствии с их разрядами.
  12. Полученное таким образом число и есть ваш результат.

Например, умножьте 49568 на 7094

Решение

1. Сначала запишем множимое и множитель в столбцы

2. Теперь умножим все числа на место единиц числа множимого и запишите их горизонтально.

3. Поставьте 0 на место единиц следующей строки

4. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0003

5. Снова перейти на следующую строку. Поставьте 0 на месте единиц и десятков в этой строке.

6. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.

7. Снова перейти на следующую строку. Поставьте 0 на месте единиц, десятков и сотен в этой строке.

8. Теперь найдите цифру в тысячном разряде множителя. Умножьте число, стоящее в тысячном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили три нуля.

9. Поскольку множитель представляет собой четырехзначное число, вы достигли конца множителя. Сложите числа по вертикали в соответствии с их разрядностью.

10. Полученное таким образом число и есть ваш результат. Следовательно, 49568 x 7094 = 351635392

  • Чтобы умножить число на 10, нужно поставить 0 справа от числа. Например, 435 x 10 = 4350
  • Чтобы умножить число на 100, нужно поставить два нуля справа от числа. Например, 435 х 100 = 43500
  • Чтобы умножить число на 1000, поставьте справа от числа три нуля. Например, 435 х 1000 = 435000
  • Чтобы умножить число на произведение 10, 100 и 1000 на счетные числа, умножьте числа на ненулевые числа, а затем добавьте к результату количество нулей. Например, умножим 45 на 200. Чтобы решить эту проблему, сначала умножим 45 на 200. Получим 45 х 2 = 90. Теперь добавим 2 нуля (так как у 200 было 2 нуля) справа от 90. Получим 9000.
  • Следовательно, 45 х 20 = 9000

1. Умножение коммуникативно, так же как и ассоциативно. Таким образом, из двух чисел не имеет значения, какое из них вы отмечаете как множитель, а какое число как множимое. Поэтому всегда полезно использовать более короткое число в качестве множителя, так как это облегчит ваши вычисления. Например, если мы хотим умножить 125 на 45612, обратите внимание, что мы должны использовать 125 в качестве множителя вместо 45612, так как это более короткое число. Следовательно,

2. Из двух чисел, которые необходимо умножить, проверьте, какое число имеет максимальное количество нулей. В качестве множителя следует использовать число, в котором больше нулей.

Пример 1     

Туристическое агентство взимает 80 563 фунтов стерлингов за 7-дневную поездку в Европу на одного пассажира. Если 8790 пассажиров совершают поездку за год, сколько заработает туристическое агентство за этот год?

Решение : Нам сообщили, что туристическое агентство взимает 80 563 фунта стерлингов за 7-дневную поездку в Европу с пассажира.

SO, стоимость одного пассажира за 7-дневную поездку = £ 80563

Общее количество пассажиров за год = 8790

Мы обязаны выяснить прибыль туристического агентства в этом году. Чтобы найти это, нам нужно умножить 80 563 фунтов стерлингов на 8 790. 90 003 90 002 (Примечание: мы выбрали меньшее число в качестве множителя) 90 003 90 002 Таким образом, используя шаги, описанные выше для умножения в длину, мы получаем 90 003

Следовательно, туристическое агентство зарабатывает 70,81,48,770 фунтов стерлингов в этом году.

Пример 2   

На заводе в одну коробку можно упаковать 144 мяча для крикета. Таких коробок на фабрике 675 штук. Сколько мячей можно упаковать в эти коробки?

Решение: Нам дано, что –

                                Количество мячей для крикета, которые можно упаковать в одну коробку = 1440003

Нам нужно выяснить, сколько мячей можно упаковать в 675 коробок. Чтобы найти это, нам нужно умножить 675 на 144

(Примечание: мы выбрали меньшее число в качестве множителя)

Итак, используя шаги, описанные выше для длинного умножения, мы получаем

Пример 3   

В в городе 146 рядов домов. Сколько домов в городе, если в каждом ряду 25 домов?

Решение : Нам известно, что в городе 146 рядов домов.

Количество домов в каждом ряду равно 25.

Нам нужно найти общее количество домов в городе. Чтобы найти это, нам нужно будет умножить 146 на 25.

Примечание: мы возьмем 25 в качестве множителя по двум причинам; во-первых, оно кратно 5, что облегчает умножение, а во-вторых, это меньшее число, чем 146.

Таким образом, умножив 146 на 25, мы получим –

Следовательно, общее количество домов в городе равно 3650

Пример 4   

У Марии есть пекарня, которая может производить 2435 больших упаковок печенья в месяц. Каждый пакет файлов cookie содержит 35 файлов cookie. Сколько печенья выпекается в пекарне в месяц?

Решение: нам было дано, что —

Количество больших пакетов печенья, которые могут быть произведены за месяц в пекарне Марии — 2435

Количество печенья в каждом пакете = 35

Мы обязаны Найдите общее количество печенья, которое можно приготовить в пекарне Марии за месяц. Чтобы найти это, нам нужно будет умножить 2435 на 35.

Примечание. Мы возьмем 35 в качестве множителя по двум причинам. во-первых, оно кратно 5, что облегчает умножение, а во-вторых, это меньшее число, чем 2435.

Таким образом, умножая 2435 на 35, мы получаем –

Следовательно, общее количество печенья, которое может быть произведено в пекарни в месяц = ​​85225

Мультипликативные сравнения и уравнения Рабочие листы по математике для 4-го класса
Умножение и деление многозначных целых чисел Рабочие листы по математике для 5-го класса
Порядок работы (PEMDAS) (Тема работы на дому) Рабочие листы

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

Четыре метода умножения, которые вы могли не знать в школе | Эндрю Джеймисон

Когда мы учимся умножать, мы учимся разбивать уравнение на части. Во-первых, мы находим продукт, используя значение разряда единиц. Затем переходим к десяткам, а затем к сотням. Наконец, мы суммируем все и приходим к нашему ответу. Этот метод отлично работает, но не всегда самый эффективный. Вот еще несколько методов, которые могут ускорить процесс.

В этих примерах я использую двух- и трехзначные числа. Эти методы также работают с большими числами.

Фото Лукаса ван Оорта на Unsplash

Нарисуйте сетку и разделите каждый квадрат диагональной линией. Напишите одно число сверху, а другое справа, по одной цифре в столбце или строке.

586 х 45 =

586 х 45: 586 сверху, 45 справа

В каждой ячейке умножьте строку на столбец.

Разделите продукт на разряд десятков и разряд единиц. Запишите цифру десятков над диагональной линией и цифру единиц под диагональной линией.

5 x 4 = 20. Ставим двойку над чертой, ноль под чертой. Сетка завершена

Теперь посмотрим на сетку по диагоналям. Сложите цифры по диагоналям. Если сумма больше девяти, перенесите разряд десятков в следующий столбец.

Сумма по синей и белой диагоналям
 586 x 45 
 -> 2, (2+0+3), (5+4+2+2), (0+3+4), 0 
 -> 2, 5 , 13, 7, 0 
 -> 2, 6, 3, 7, 0 
 =  26370

Наконец, запишите сумму по диагоналям цифрами, и вы получите ответ.

586 x 45 = 26 370

Фото Photoholgic на Unsplash

Этот метод работает невероятно хорошо для 2- и 3-значных чисел, когда цифры маленькие. Это может стать немного беспорядочным, когда у вас много пересекающихся линий.

Нарисуйте серию параллельных линий, представляющих каждую цифру первого числа. Линии должны располагаться примерно под углом 45 градусов и иметь зазор между каждой цифрой.

В этом примере мы будем работать с 223 x 52

223, представленными строками

Значение разряда сотен равно двум; две верхние линии представляют его. Следующие две строки представляют десятки, а последние три строки представляют разряд единиц.

Далее рисуем второе число, на которое умножаем. Мы делаем это, рисуя новый набор параллельных линий, которые пересекают первый набор.

223 (оранжевый) x 52 (синий)

На этот раз нижний набор строк представляет пять десятков, а две верхние строки представляют единицы. Обратите внимание, что строки с более высоким разрядом всегда находятся слева.

Теперь рисуем точки в местах пересечения линий.

Точки в точках пересечения

Далее мы группируем точки по положению вдоль оси x. Каждая группа точек представляет цифру в нашем окончательном ответе. Суммируем точки в каждой группе. Если сумма больше девяти, перенесите значение десятков в следующий столбец.

Каждая группа точек представляет цифру. Сумма точек

В качестве ответа запишите общую сумму групп.

 223 x 52 
 -> 10 ,(4 + 10) ,(4 + 15) , 6 # сумма точек 
 -> 10, 14, 19, 6 # 14 и 19 больше девяти 
 -> 10+1, 4+1, 9, 6 # переносят 1 из 14 и 19 
 ->  11596

223 x 52 = 11 596

Фото Райана Шрама на Unsplash

В этом методе вы перемещаетесь по уравнению справа налево. На первом этапе мы умножаем единицы на единицы. Затем мы переходим в столбец десятков и умножаем десятки на единицы и единицы на десятки и суммируем эти два вычисления. Продолжаем двигаться по уравнению. Общая схема выглядит так.

Узор крест-накрест

Да, это выглядит сложно. Это имеет больше смысла, когда мы смотрим на это шаг за шагом.

Процесс симметричный. У нас есть только одно вычисление на краях (единицы x единицы или сотни x сотни). В середине у нас есть три вычисления.

Самое сложное — убедиться, что вы перенесли правильное значение разряда в следующий столбец.

 125 x 648 
 -> 6, 16, 46, 36, 40 
 -> 6+1, 6+4, 6+3, 6+4, 0 
 -> 7, 10, 9, 10, 0 
 -> 7+1, 0, 9+1, 0, 0 
 -> 8, 0+1, 0, 0, 0 
 =  81000

125 x 648 = 81 000

Фото Zachary Kadolph на Unsplash

Этот метод почти волшебный. Вы начинаете с того, что делаете противоположное ожидаемому — меняете местами цифры одного из множителей.

Этот перевернутый номер действует как окно. Он перемещается по уравнению на одно разрядное значение за раз.

424 x 83 =

Начните с окна как можно дальше влево. Значение первого разряда окна должно быть ниже наибольшего разрядного значения другого множителя. Умножьте эти числа вместе

Шаг 1: 83 в обратном порядке становится 38. Умножение 4 x 8

Сдвиньте окно на одну позицию вправо. Умножьте оба столбца и просуммируйте произведения.

Шаг 2: Сдвиньте вправо, умножьте и просуммируйте столбцы.

Продолжайте перемещать окно вправо.

Шаг 3: Сдвигай, умножай, суммируй.

admin

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *