Урок в 5 классе по теме «Умножение дробей. Умножение смешанных чисел» | План-конспект урока по алгебре (5 класс) на тему:
Урок математики
на тему «Умножение смешанных чисел»
2 * 3 = ?
Составитель : Вакутина Л.С.
Учитель математики
Высшей квалификационной категории
МБОУ СОШ №2 с.Аскино
Аскинского района
Республики Башкортостан
Стаж работы 31 год
Урок математики в 5 классе
Технологическая карта урока математики по теме «Умножение смешанных чисел»
составлена на основе требований Федерального государственного образовательного стандарта по математике.
УМК под редакцией Дорофеева Г.В., Петерсон Л.Г.
Тема: «Умножение смешанных чисел».
Цели урока: Получить алгоритм умножения смешанных чисел, способствовать к его практическому использованию при решении примеров и задач.
Обучающая: вывести алгоритм умножения смешанных чисел и сформировать способность к его практическому использованию при решении примеров и задач.
Развивающая: развитие аналитического мышления учащихся, формирование умения у обучающихся выделять главное и обобщать. Воспитательная: содействовать воспитанию интереса к математике, аккуратности.
Задачи урока:
- повторить, обобщить знания и умения связанные с умножением дроби на число, дроби на дробь;
- получить алгоритм умножения смешанных чисел, способствовать к его практическому использованию;
- способствовать формированию умений применять приемы анализа, сравнения, переноса знаний в новую ситуацию, развитию творческих способностей учеников;
- побуждать учащихся к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.
Предметные результаты: алгоритм умножения смешанных дробей .
Метапредметные и личностные результаты :
- Регулятивные УУД: постановка цели; план, получение результата
- Познавательные УУД: общеучебные, логические, постановка и решение проблемы
- Коммуникативные УУД: работа в парах
Оборудование: учебник математики 5 класс автор Г.
В.Дорофеев, Л.Г.Петерсон, раздаточный материал, проектор.
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Этапы урока | Формируемые УУД | Деятельность учителя | Деятельность учащихся |
Самоопределение к деятельности Цели: – психологический настрой уч-ся на работу; | Личностные: осмысление внутренней позиции ученика на уровне положительного отношения к уроку. Регулятивные: самоорганизация и организация своего рабочего места. | Девиз нашего урока такой: «О, сколько нам открытий чудных готовит просвещения дух». (На экране ) | Проявляют психологическую готовность к познавательной деятельности.
– Открытию нового знания. Если человек своим трудолюбием, упорством достигает истины в чем-либо, то это и есть его открытие. Ребята с места отвечают на вопросы |
Актуализация знаний Цель: повторение изученного материала необходимого для «открытия нового знания» и выявление затруднений. | Личностные: осознание своих эмоций, интереса к изучению математике. Познавательные: актуализация изученных способов действий, развитие мыслительных операций; умение из предложенной информации выделять главное. Регулятивные: учатся работать по предложенному учителем плану; умение разбивать на группы, делать выводы, мотивация к учебной деятельности. Коммуникативные:планирование учебного сотрудничества с учителем и со сверстниками; уметь выслушивать и понимать речь других. | Фронтальный опрос: | Отвечают с места. 1.= 2.Например: 3. = 4. -правильная дробь, — неправильная дробь. 5. = 1 6.3 ==; 7. * 4= ; 8.* = ; 9. * 0 = 0. |
Постановка учебной проблемы | Познавательные: уметь ориентироваться в своей системе знаний; отличать новое от уже известного с помощью учителя. Регулятивные: подготовка к самостоятельной формулировки темы урока. Коммуникативные:формирование способности сохранять доброжелательное отношение друг к другу в учебной деятельности. | – Теперь, ребята, мы с вами поработаем в парах. | Выслушивать друг друга, не перебивая. |
– Итак, у Вас на столах лежат карточки с примерами. Вам необходимо решить их. Вычислите:
После решения выполнить проверку, на слайде появились ответы. | Решают в группах. | ||
– Какое задание вызвало затруднение? | 4 *2 | ||
– Почему? | – Мы еще не умеем умножать такие примеры. | ||
1.– Как называются числа4 2? | – Смешанные числа | ||
– Как вы думаете какова тема нашего сегодняшнего урока? | – Умножение смешанных чисел. | ||
– Какие цели на сегодняшний урок вы перед собой ставите? | Формулируют цели урока: научиться умножать смешанные числа. | ||
Открытие уч-ся нового знания Цель: организовать устранение и фиксирование преодоления затруднения. | Познавательные: активизация мыслительной деятельности через проблемное задание; Регулятивные: определение и формулирование цели деятельности на уроке с помощью учителя; Коммуникативные:оформление своих мыслей согласно заданным рамкам обсуждения, аргументация своих суждений; Личностные: понимать свои желания и цели по отношению к общим учебным задачам. | – Давайте вспомним, как мы складывали и вычитали смешанные числа? – Можем ли мы перемножать неправильные дроби? – Попробуйте составить алгоритм умножения смешанных чисел? _ Составить алгоритм умножения дроби на натуральное число. Параллельно ответам появляется алгоритм на доске. | – Мы для этого переводили смешанные числа в неправильные дроби. – Да 1. Перевести смешанные числа в неправильную дробь. 5. * n = |
Первичное закрепление Цель: зафиксировать новое знание в речи и знаках; уточнить тему урока. | Познавательные: умение следовать образцу и правилу. Регулятивные: проявление самостоятельности и инициативы в разных видах деятельности. Коммуникативные: умение вести диалог, выполнять различные роли (продавец, покупатель). | Давайте на практике попробуем применить данный алгоритм. Д ля этого решим следующие примеры. № 300(а ,б, в, г), стр. 60 | На доске 4 ученика решают примеры. |
Физкультминутка | Личностные: умение применять правила охраны своего здоровья. | Зарядка для глаз. (На экране знак бесконечности). Нужно 5 раз глазами пройти по знаку. | Выполняют зарядку для глаз . |
Самостоятельная работа с самопроверкой по образцу Цель: организовать выполнение учащимися самостоятельной работы на новое знание; | Познавательные: понимание смысла задания; Коммуникативные: осуществление взаимоконтроля по ходу выполнения задания. | – А сейчас, ребята вы будете работать самостоятельно с последующей проверкой
Проверка по образцу (презентация) – Кто решил всё правильно? «Давайте по рассуждаем…» “Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что он есть на самом деле” (Л.Н. Толстой).Задумай тесь над этими словами. |
|
Включение нового знания в систему знаний и повторение Цель: включить новое знание в систему уже имеющихся. | Познавательные: находить ответы на вопросы используя учебник, свой жизненный опыт и информацию, полученную на уроке. Коммуникативные: слушать и понимать речь других. | – А сейчас откроем учебник стр.61,№ 303 (1; 2). Что нам нужно сделать? – Прочитайте задачу. 1.Сколько литров воды в двух бочках? 2.Как найти вес воды в двух бочках? 3.Сколько килограммов соли в двух бочках морской воды? | – Решить задачу 1. 5 * 2 = =12(см3) 2. 1) 500+500= 1000(кг) 2) 1000*1 = 8*137; 3) 8*137 *= = 27(кг). Ответ: 27(кг). |
Реши уравнения №306 (свойства умножения числа на нуль, на единицу) | Ответы: а) х=1 б) х=0 в) х=1 г) х=0 | ||
№307(1) Великий древнегреческий математик Архимед (3 век до н.э.) установил, что длина окружности примерно в 3 раза больше её диаметра. Какова длина беговой дорожки ипподрома, имеющей форму круга радиусом км? | * 3 = = (км) | ||
Решите задачу. Какое расстояние пройдут туристы за ч со скоростью км/час? Как найти расстояние? | Нужно скорость умножить на время. * = * =12км. | ||
| |||
Рефлексия Цели: | Регулятивные: формирование умения адекватно оценивать свою деятельность. Личностные: оценивание разного вида деятельности на уроке. | – Итак, каждый ставил перед собой цель, поднимите руки, кто достиг ее. Домашнее задание:/№342; №344(1). | Ответы учеников. |
Для этого надо быть настойчивым и внимательным. 
Находить и формулировать решение задачи с помощью простейшей модели(рисунка).
Алгебра. Учебник для 6-8 классов
Алгебра. Учебник для 6-8 классов
ОглавлениеГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.§ 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА.  § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов.  § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений. § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители.  § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. § 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76.  (1/3)§ 130. Примеры графического решения уравнений и систем уравнений. |
Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с.
Умножение дробей | Магазин развивающей математики
Результаты обучения
- Умножение двух или более дробей
- Умножить дробь на целое число
Модель может помочь вам понять умножение дробей. Мы будем использовать дробные плитки для моделирования [латекс]\большой\фрак{1}{2}\cdot \фрак{3}{4}[/латекс]. Чтобы умножить [латекс]\большой\фракция{1}{2}[/латекс] и [латекс]\большой\фракция{3}{4}[/латекс], подумайте [латекс]\большой\фракция{1}{ 2}[/latex] из [latex]\Large\frac{3}{4}[/latex].
Начните с тайлов дроби на три четверти. Чтобы найти половину от трех четвертей, нам нужно разделить их на две равные группы. Поскольку мы не можем разделить три плитки [latex]\Large\frac{1}{4}[/latex] поровну на две части, мы обмениваем их на плитки меньшего размера.
Мы видим, что [latex]\Large\frac{6}{8}[/latex] эквивалентен [latex]\Large\frac{3}{4}[/latex].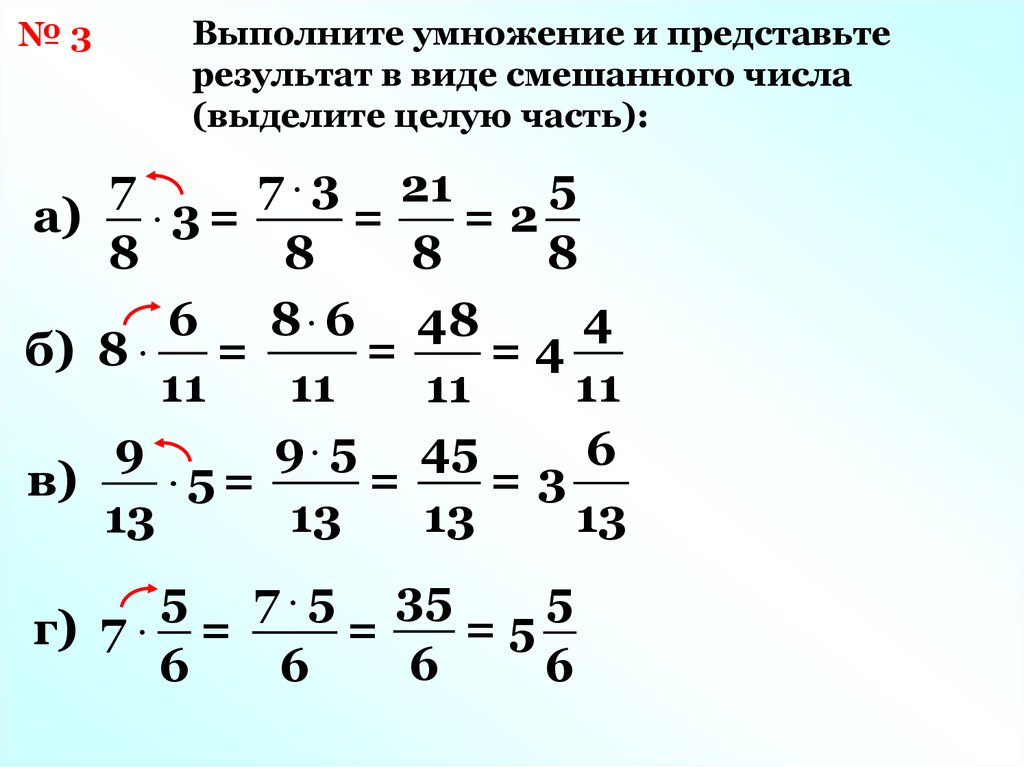
Следовательно,
[латекс]\Large\frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}[/latex]
Пример
Используйте диаграмму к модели [латекс]\Большой\фрак{1}{2}\cdot \фрак{3}{4}[/латекс]
Решение:
Первый оттенок в [латекс]\Большой\фрак{3}{4} [/latex] прямоугольника.
Мы возьмем [латекс]\Большой\фрак{1}{2}[/латекс] из этого [латекса]\Большой\фрак{3}{4}[/латекс], поэтому сильно заштрихуем [латекс] \Large\frac{1}{2}[/latex] заштрихованной области.
Обратите внимание, что [латекс]3[/латекс] из [латекс]8[/латекс] сильно затенены. Это означает, что [latex]\Large\frac{3}{8}[/latex] прямоугольника сильно затенены.
Следовательно, [latex]\Large\frac{1}{2}[/latex] из [latex]\Large\frac{3}{4}[/latex] равно [latex]\Large\frac{3}{ 8}[/латекс], или [латекс]{\большой\гидроразрыв{1}{2}\cdot \гидроразрыва{3}{4}}={\большой\гидроразрыва{3}{8}}[/латекс] .
Посмотрите на результат, который мы получили от модели в примере выше. Мы обнаружили, что [latex]\Large\frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}[/latex]. Вы заметили, что мы могли бы получить один и тот же ответ, перемножив числители и умножив знаменатели?
| [латекс]\Большой\фракция{1}{2}\cdot \фракция{3}{4}[/латекс] | |
| Умножьте числители и умножьте знаменатели. | [латекс]\Большой\фракция{1}{2}\cdot \фракция{3}{4}[/латекс] |
| Упрощение. | [латекс]\большой\фрак{3}{8}[/латекс] |
Это приводит к определению дробного умножения. Чтобы умножить дроби, мы умножаем числители и умножаем знаменатели. Тогда запишем дробь в упрощенной форме.
Умножение дроби
Если [latex]a,b,c,\text{ и }d[/latex] являются числами, где [latex]b\ne 0\text{ и }d\ne 0[/latex], затем
[latex]\Large\frac{a}{b}\cdot \frac{c}{d}=\frac{ac}{bd}[/latex]
Пример
Умножьте и запишите ответ в упрощенной форме: [latex]\Large\frac{3}{4}\cdot \frac{1}{5}[/latex]
Показать решение
Попробуйте
youtube.com/embed/f_L-EFC8Z7c?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Чтобы умножить более двух дробей, у нас есть аналогичное определение. Мы по-прежнему умножаем числители и умножаем знаменатели. Тогда запишем дробь в упрощенной форме.
Умножение более двух дробей
Если [latex]a,b,c,d,e \text{ и }f[/latex] числа, где [latex]b\ne 0,d\ne 0\text{ и }f\ne 0[/latex], затем
[латекс]\Large\frac{a}{b}\cdot\Large\frac{c}{d}\cdot\Large\frac{e}{f }=\Large\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex]
Подумайте об этом
Умножьте [латекс]\Large\frac{2}{3 }\cdot\Large\frac{1}{4}\cdot\Large\frac{3}{5}[/latex]. Упростите ответ.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы умножили три дроби.
Показать решение
При умножении дробей сохраняются свойства положительных и отрицательных чисел.
В качестве первого шага рекомендуется определить знак произведения. В следующем примере мы умножим два отрицательных значения, поэтому произведение будет положительным.
Пример
Умножьте и запишите ответ в упрощенной форме: [латекс]\большой-\frac{5}{8}\left(-\frac{2}{3}\right)[/latex]
Показать решение
Попробуй
Пример
Умножьте и запишите ответ в упрощенной форме: [latex]\Large-\frac{14}{15}\cdot \frac{20}{21}[/latex]
Показать решение
Попробуйте
В следующем видео показан еще один пример умножения отрицательных дробей.
При умножении дроби на целое число может быть полезно записать целое число в виде дроби. Любое целое число, [латекс]а[/латекс], может быть записано как [латекс]\большой\фрак{а}{1}[/латекс].
Например, [latex]3=\Large\frac{3}{1}[/latex].
пример
Умножьте и запишите ответ в упрощенной форме:
- [латекс]\Large{\frac{1}{7}}\normalsize\cdot 56[/latex]
- [латекс]\Large{\frac{12}{5}}\normalsize\left(-20x\right)[/latex]
Показать раствор
Попробуйте
Посмотрите следующее видео, чтобы увидеть больше примеров умножения дроби и целого числа.
У вас была идея улучшить этот контент? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Работа с дробями: умножение дробей
Дроби — горячая тема в большинстве наших школ, особенно в связи с тем, что большинство школ проекта M3 приближаются к весеннему государственному тестированию!
Большинство фракций расположены в течение учебного года, чтобы учащиеся могли как можно больше познакомиться с фракциями.
Развитие четкого понимания дробей так же важно, как и развитие этого основополагающего чувства целых чисел. Учащиеся должны хорошо понимать концепцию дробей в целом, чтобы они могли успешно начать изучение различных аспектов дробей: эквивалентность, сравнение, сложение/вычитание, умножение/деление и т. д.
Большой вопрос для нас, учителей: Как нам учить детей дробям? Мы хотим, чтобы они поняли это быстро, но как мы можем сделать это с концептуальным пониманием вместо того, чтобы просто учить их запоминать правила или трюки?
Я часто задаюсь вопросом, почему преподавание дробей так сложно для многих учителей, и я обнаружил, что многие из учителей, с которыми я работаю, сами не чувствовали себя комфортно с дробями, будучи учениками. Их чувство целых чисел не было хорошо развито, и у них есть пробелы в собственном понимании операций, округления, оценки и других вещей с целыми числами. Итак, когда вы начинаете говорить о том, чтобы делать эти вещи с частями целого, это становится еще более запутанным.
Поскольку образование все больше склоняется к концепции перевернутого класса, где учащиеся смотрят ролики о том, как что-то делать в качестве предшественника перехода на станцию «Математика с учителем», я хотел посвятить март месяцу визуальному ответу на вопрос как мы учим дроби.
По мере того, как мы продолжаем создавать нашу видеотеку и канал YouTube, у вас будет доступ по запросу к видео, который вы сможете использовать различными способами. Вы можете предложить учащимся посмотреть видео самостоятельно перед встречей с вами в математической группе с гидом, вы можете использовать его, чтобы помочь начать урок всей группе, а затем вовлечь учащихся в модель семинара, или вы можете сделать его теплым. -до, чтобы получить мозги детей собирается.
Как бы вы ни планировали использовать эти видео, воспользуйтесь преимуществами технологий и цифровых медиа! Исследования Horizontals по развитию мозга показывают, что когда дети учатся с помощью технологий, они учатся намного быстрее.
Мы определенно не хотим превращаться в «вау-вау» учителя Чарли Брауна и получать информацию, которую мы передаем, в одно ухо через другое. С помощью видео у студентов есть возможность по-настоящему переварить контент — поставить видео на паузу, вернуться, чтобы пересмотреть все, что не имеет смысла, чтобы они действительно поняли. Это может повысить уровень вовлеченности, и, особенно если вы используете CPA для конкретных графических рефератов, может привлечь больше учащихся!
Я всегда ловлю себя на том, что ввожу понятие умножения, спрашивая класс о том, что они знают об умножении в пределах целого числа. Я напишу на доске задачу — 5 х 6 — и спрошу — что это значит? Как правило, учащиеся говорят что-то вроде «умножить», «умножить» или «ответ равен 30». Поэтому я продолжаю задавать вопрос — что означает ? Мы надеемся, что по мере того, как студенты будут углубляться и копать глубже, они в конце концов придут к тому факту, что 5 x 6 на самом деле означает «5 групп по 6».
Мы также знаем, что если бы мы изменили его на 6 x 5, это было бы «6 групп по 5». Если ваши ученики делают журналы умножения и играют в Speed! В игре эта концепция «группы» вбита в их головы, даже если им потребуется немного подсказок, чтобы сказать это.
Теперь мы можем перейти к более серьезной проблеме. Я напишу на доске что-то вроде 89 x 12. Что означает это ? Это означает, что у нас есть 89 групп по 12 человек, так сколько у нас всего вместе? Мы действительно хотим, чтобы дети поняли этот шаблон и фразы с целыми числами, потому что, когда мы переходим к умножению дробей, это сделает этот переход более плавным.
Умножение целого числа на дробьИтак, далее мы пишем на доске задачу с дробью – 4 x ½. Что это значит сейчас? Внезапно одно из наших чисел оказалось дробью! В этом случае мы могли бы действительно сказать, что это означает «4 группы по ½». Если бы у меня было ½, ½, ½ и ½, это было бы 2. Таким образом, 4 группы по ½ равняются 2.
Использование этой последовательности заданий, основанных на запросах, действительно помогает пробудить интерес учащихся, помогая им понять принципы, лежащие в основе умножения.
Обычно с дробями мы начинаем с процедуры — делаем этот шаг, этот шаг, этот шаг и этот шаг. Затем мы предлагаем учащимся выполнить процедуру вместе с нами, а затем они самостоятельно выполняют задание, чтобы убедиться, что они запомнили процедуры. На самом деле это не тот уровень вовлеченности, который нужен студентам 21 века. Им нужно участвовать в разговоре и решать такие вопросы, как что на самом деле означает этот символ?
Здесь есть множество различных заданий, которые вы можете использовать, чтобы помочь учащимся углубить свое конкретное понимание. Им нужно много практики! Если бы я был в 4-м классе, я мог бы остановиться на этом, начать вводить манипуляции, которые могут способствовать развитию понимания учеников.
Знакомство с манипуляторами (4 класс)В этом видео я покажу вам, как использовать два моих любимых манипулятора: шаблоны и листы бумаги для моделей.
youtube.com/embed/oWaU7UCc0EU» frameborder=»0″ allowfullscreen=»allowfullscreen»>Мне нравится начинать с шаблонов, потому что они, вероятно, уже знакомы с шаблонами из предыдущих классов.
Если бы я использовал плитки дробей для моделирования этой задачи, мне пришлось бы получить два набора плиток дробей, потому что мне понадобилось бы 4 части по ½, поэтому, поскольку блоки шаблона поставляются в большом ведре, у нас нет этот вызов! Кроме того, фрагменты фрагментов также отпечатаны с частью, которую они представляют, поэтому нет гибкости для использования этих фрагментов для представления другого значения, как в случае с блоками шаблонов.
Еще одно преимущество использования шаблонов состоит в том, что, когда мы будем готовы говорить о делении целого числа на дробь, дети уже будут знакомы с процессом и смогут увидеть, как умножение и деление дробей идут вместе. Это похоже на семейство фактов сложения и вычитания, и как, когда мы учим отсутствующее сложение, мы видим, что сложение и вычитание идут рука об руку.
Используя блоки шаблонов, я смоделирую, как решать задачу на целое число, умноженное на дробь. Если мы используем правильный язык для этого, «четыре группы пополам», это будет иметь большой смысл. Давайте воспользуемся шестиугольником целиком, тогда у нас будет красная трапеция в качестве ½, синий ромб будет ⅓, а затем мы можем просто использовать треугольник в качестве ⅙.
Для начала мы хотели увидеть 4 группы по ½, чтобы дети могли тянуть свои ½ части, трапеции, пока у них не будет 4 трапеции. Затем дети могут легко увидеть, используя один целый шестиугольник в качестве эталона, что 4 группы по ½, 4 трапеции — это то же самое, что 2 целых шестиугольника. Для некоторых детей из группы риска они могут захотеть на самом деле сопоставить трапеции поверх шестиугольников, чтобы укрепить эту концепцию количества. Затем дети могут разыграть несколько других примеров, изучая умножение дробей.
Мы всегда хотим начинать с бетона, потому что он дает учащимся то, что называется импринтом, к которому они могут вернуться позже.
Этим отпечатком может быть ваше моделирование под камерой для документов или моя демонстрация на видео на YouTube. Это может быть воспоминание о том, как они построили его с партнером по классу. Независимо от того, как они это получили, теперь у них есть память о том, о чем мы говорили.
Итак, для наших четвероклассников все начинается с правильного изучения языка, чтобы понять, что мы на самом деле делаем с дробями — «группами», — а затем начинаем с целых чисел и переходим к целым числам, умноженным на дроби. Это подготовит их к стандартам 5-го класса, где они будут умножать две дроби.
Умножение двух дробей (5-й класс)
Опять же, важно создать как можно более прочную основу концептуальных знаний, чтобы у детей был план того, что они делают. Мы хотим избежать обучения процедурам, которые дети должны запоминать, не понимая, что происходит.
В этом видео мы рассмотрим, как концептуально пройтись по примеру умножения дроби на дробь.
Возьмем ⅓ х ½. Что это на самом деле спрашивает нас? Наших учеников уже не запугать! Они должны чувствовать себя уверенно, зная, что просят ⅓ от ½.
Вы определенно можете использовать для этого примера бумагу для моделирования площадей, или шаблоны, или другие материалы, просто убедитесь, что выбранные вами манипуляции соответствуют дробям в примерах, которые вы используете.
Итак, что такое ⅓ от ½? Я начну с половины — красной трапеции. Глядя на этот фрагмент, мне нужно подумать о том, как я разобью его на терции или группу из ⅓. Однако они не могут думать о зеленом треугольнике как о ⅙, потому что мы не говорим о целом куске, мы смотрим на часть целого. Но, глядя на трапецию, учащиеся должны увидеть, что мы можем поместить три треугольника на трапецию и разбить эту ½ на три ⅓ части. Затем, глядя на ⅓ частей по отношению к целому, мы можем видеть, что ⅓ от ½ представляет ⅙.
На протяжении всего этого процесса мне нравится, чтобы весь блок узора, шестиугольник, был виден учащимся, чтобы они знали, что могут связать его с целым. Когда я разбиваю трапецию, треугольники составляют ⅓ трапеции, но когда я даю свой окончательный ответ, он находится в отношении к целому, что снова делает треугольники ⅙.
После того, как мы смоделировали этот процесс нахождения ⅓ из ½, мы можем спросить учащихся, что бы они сделали, если бы мы попросили их найти ½ из ⅓? Это заставляет учащихся задуматься о свойстве коммутативности. Мы знаем, что вы, вероятно, все еще получите тот же ответ ⅙, но выглядит ли модель так же? Нет, это не так. Точно так же, как если бы у вас была проблема с умножением целых чисел, например 5 x 6, и вы построили массив. Если я изменю его на 6 x 5, свойство коммутативности говорит, что ответ останется тем же, но картина будет другой.
Если мы хотим узнать, что такое ½ от ⅓, мы должны начать с синего ромба, ⅓ части. Когда я смотрю на это, я могу взять свой треугольник и положить его поверх ромба, чтобы увидеть, что он действительно представляет ½ части.