Сложение чисел столбиком. Онлайн калькулятор
Сложение однозначных чисел
Однозначные числа складывают, используя таблицу сложения. Таблицу сложения, а точнее результаты сложения однозначных чисел, нужно помнить наизусть.
Пример. Сложим однозначные числа 4 и 9:
4 + 9 = 13.
Сложение многозначных чисел
Многозначные числа складывают по разрядам, используя переместительный и сочетательный законы сложения.
Пример. Сложим двузначные числа 26 и 48:
26 + 48 = (20 + 6) + (40 + 8) = 20 + 6 + 40 + 8 = (20 + 40) + (6 + 8) = 60 + 14 = 60 + (10 + 4) = 60 + 10 + 4 = (60 + 10) + 4 = 70 + 4 = 74.
Сначала мы разложили слагаемые на разряды, затем сгруппировали в одну группу десятки, в другую — единицы и выполнили сложение по разрядам, т. е. сложили десятки с десятками и единицы с единицами, затем один десяток, получившийся от сложения единиц, прибавили к десяткам, которых у нас было 6 от сложения десятков, и в конце сложили десятки с единицами.
Форма записи сложения, которую мы использовали, слишком длинная и потому неудобная, поэтому при сложении многозначных чисел обычно используется другая, более удобная форма записи, которая называется сложением столбиком.
Сложение столбиком
Сложение многозначных натуральных чисел удобней выполнять в столбик.
Сложение столбиком — это форма записи и способ сложения, используемый при сложении многозначных чисел. Сложение столбиком иначе ещё называют сложением в столбик.
Рассмотрим сложение столбиком на примере сложения чисел 7056 и 483.
Сложение в столбик записывается так: одно слагаемое записывается под другим так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства обычно меньшее число записывают под большим. Слева между слагаемыми ставится знак плюс, а под нижним слагаемым проводится горизонтальная черта:
Полученную запись можно мысленно разбить на столбики так, как это показано на рисунке:
Все дальнейшие действия сводятся к сложению однозначных чисел, которые находятся в одном столбике. Вычисление выполняется поразрядно справа налево, начиная с разряда единиц.
Вычисление выполняется поразрядно справа налево, начиная с разряда единиц.
Если в результате сложения получается число меньшее 10, то оно записывается под чертой в этом же разряде.
Начинаем вычисление с разряда единиц: складываем числа 6 и 3. В результате имеем число 9. Так как 9 < 10, то записываем это число под чертой, в том же разряде:
Если в результате сложения получается число, равное 10 или большее 10, то под чертой в этом же разряде записывается значение разряда единиц полученного числа, а значение разряда десятков полученного числа запоминается (оно используется на следующем шаге).
Переходим к сложению чисел в следующем разряде, то есть к сложению значений разряда десятков. Складываем числа 5 и 8, получаем число 13. Так как 13 > 10, то под чертой, в том же разряде, записываем число 3 (это значение разряда единиц числа 13), а число 1 запоминаем (это значение разряда десятков числа 13), при этом говорят три пишем, а один в уме
. Чтобы не забыть о запомненном числе, его обычно записывают сверху над следующим (слева) разрядом:
Чтобы не забыть о запомненном числе, его обычно записывают сверху над следующим (слева) разрядом:
Запомненное число прибавляется к сумме чисел следующего разряда.
Переходим к следующему разряду и складываем числа 0 и 4. В результате имеем 4. К полученному числу прибавляем запомненное число 1, получаем 5. Так как 5 < 10, то под чертой, в том же разряде, записываем число 5:
После этого происходит переход на один разряд влево и действия повторяются. Данный процесс продолжается до тех пор, пока числа не закончатся.
Если в столбике содержится только одно число, и у нас нет запомненного числа (от предыдущего сложения), в этом случае мы просто записываем это число под чертой, в том же разряде.
Так как в следующем столбике находится лишь одно число — 7, и в памяти у нас нет запомненного числа, то мы просто записываем 7 под чертой, в том же разряде:
Дальше никаких чисел нет и в памяти тоже чисел нет.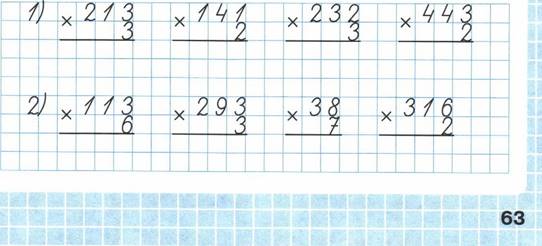 На этом процесс сложения можно считать завершённым. Натуральное число, получившееся под чертой, является результатом сложения данных чисел. Теперь можно записать сумму данных чисел в обычном виде:
На этом процесс сложения можно считать завершённым. Натуральное число, получившееся под чертой, является результатом сложения данных чисел. Теперь можно записать сумму данных чисел в обычном виде:
7056 + 483 = 7539.
Рассмотрим ещё пару примеров сложения столбиком, чтобы разобраться с оставшимися нюансами.
Пример 1. Сложим числа 29 и 6 столбиком.
Складываем 9 и 6, в результате получаем число 15. Так как 15 > 10, то число 5 записываем, а число 1 запоминаем:
Если в столбике содержится только одно число, и у нас имеется запомненное число (от предыдущего сложения), то запомненное число просто прибавляется к этому одному числу.
В следующем столбике находится лишь одно число — 2. Так как у нас в памяти имеется число 1, то его нужно прибавить к 2. В результате получаем число 3:
Дальше никаких чисел нет и запомненного числа тоже нет, следовательно, сложение столбиком завершено.
Пример 2. Сложим столбиком числа 43 и 94.
Складываем 3 и 4. В результате имеем число 7. Так как 7 < 10, то записываем это число под чертой, в том же разряде:
Если в последнем разряде в результате сложения получается число, равное 10 или большее 10, то под чертой в этом же разряде записывается значение разряда единиц полученного числа, а значение разряда десятков полученного числа записывается под чертой в следующий разряд.
В следующем разряде складываем числа 4 и 9, получаем число 13. Так как 13 > 10, то под чертой, в том же разряде, записываем число 3, а число 1 записываем под чертой в следующий разряд:
Дальше никаких чисел нет и в памяти числа тоже нет, следовательно, сложение в столбик завершено.
Удобство сложения в столбик заключается в том, что сложение многозначных натуральных чисел фактически сводится к сложению однозначных чисел и запись процесса сложения занимает меньше места.
Калькулятор сложения столбиком
Данный калькулятор поможет вам выполнить сложение столбиком. Просто введите слагаемые и нажмите кнопку Вычислить
.
Тест Сложение и вычитание столбиком по математике онлайн
Сложность: знаток.Последний раз тест пройден более 24 часов назад.
Перед прохождением теста рекомендуем прочитать:Вопрос 1 из 10
Перенос числа вправо по числовой прямой имеет название…
- Правильный ответ
- Неправильный ответ
- Вы и еще 69% ответили правильно
- 69% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
Есть ли особенности записывания чисел столбиком для сложения или вычитания?
- Правильный ответ
- Неправильный ответ
- Вы и еще 70% ответили правильно
- 70% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Записывать числа в столбик по разрядам, это правило действительно только для сложения?
- Правильный ответ
- Неправильный ответ
- Вы и еще 83% ответили правильно
- 83% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Можно ли при сложении единицы прибавлять к десятками или сотням?
- Правильный ответ
- Неправильный ответ
- Вы и еще 54% ответили правильно
- 54% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Можно ли при вычитании из сотен вычитать единицы?
- Правильный ответ
- Неправильный ответ
- Вы и еще 73% ответили правильно
- 73% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
Что делать, если при сложении получилось больше десятка?
- Правильный ответ
- Неправильный ответ
- Вы и еще 69% ответили правильно
- 69% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Что делать при вычитании, если в разряде единиц уменьшаемо недостаточное число для вычитания?
- Правильный ответ
- Неправильный ответ
- Вы и еще 87% ответили правильно
- 87% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Решить пример: 89045+5982=
- Правильный ответ
- Неправильный ответ
- Вы и еще 76% ответили правильно
- 76% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Решить пример: 10486-3482=…
- Правильный ответ
- Неправильный ответ
- Вы и еще 87% ответили правильно
- 87% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Решить пример: 34980-38750=…
- Правильный ответ
- Неправильный ответ
- Вы и еще 53% ответили правильно
- 53% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Анна Ножеева
9/10
Evgeniy Morozov
10/10
Лира Нургалиева
10/10
Светлана Быкова
8/10
Стас Богданов
9/10
Вероника Калачёва
10/10
Артём Мещеряков
6/10
Рейтинг теста
Средняя оценка: 4.1. Всего получено оценок: 203.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Конспект урока по математике на тему :» Решение примеров столбиком» (2 класс)
Конспект урока по математике на тему: Решение примеров столбиком.
Цель: научить учеников складывать и вычитать примеры столбиком. Закрепить знание разрядов чисел, совершенствовать приемы сложения и вычитания.
Задачи:
1.Повторить разряд чисел (десятки, единицы).
2.Познакомить с вычислениями, производимые методом столбика.
3. Закрепить знания арифметических действий.
4. Прививать любовь к математике.
Ход урока:
1.Оргмомент.
Проверка готовности к уроку.
— Прозвенел звонок!
Начинается урок!
2.Чистописание.
— Ребята открываем тетради, записываем: число, месяц, классная работа.
Проведем минутку чистописания: прописываем числа 17, 174, 749.
Продолжим ряд: 11, 21, 31…
Давайте вспомним разряд числа, разберем по разрядам числа:
82=8 дес.+ 2 ед. 93=9 дес.+ 3ед.
65= 6дес. + 5 ед. 44= 4дес.+4 ед.
74= 7 дес.+ 4ед. 99= 9дес.+9 ед.
2.Актуализация знаний:
Ребята давайте решим примеры и проведем проверку:
23+34 61-11
35+33 28-12
42+51
3.Подводка новой темы:
Ребята сегодня мы с вами будем решать примеры, используя новый метод вычисления столбиком.
Записываю число 62.
Клетка под клеткой записываю следующее слагаемое 21.
Посередине ставим знак +.
Проводим линию, считаем:
Складываем единицы 2+1=3, пишу 3.
Складываем десятки 6+2=8, пишу 8.
Читаем ответ 83.
Решим еще примеры таким же способом:
23+42, 34+25, 17+31, 44+25, 34+52.
4.Работа по решению задач.
На рыбалке Вова поймал 28 карасей, а Дима на 7 меньше. Сколько карасей поймали мальчики вместе?
В магазин завезли 12 кг яблок, а апельсинов на 2кг меньше.
Сколько всего кг фруктов завезли в магазин.
5.Рефлексия.
Чего нового мы узнали на уроке?
Что было сложно?
Оцените свою работу с помощью круга: начертите красный- если плохо, желтый – буду тренироваться дома, зеленый – хорошо.
Сложение столбиком. Сложение чисел столбиком. Математика сложение столбиком.
Когда вы хотите сложить два числа, вы можете сложить их столбиком.
Как правильно записать цифры в столбик?
Десятки цифр выстраиваются под десятками, сотни под сотнями и так далее. Затем складываем по столбцам, начиная со столбца справа.
Затем складываем по столбцам, начиная со столбца справа.
Пример 1. Сложите два числа: \(55 + 31\) в столбик.
Решение:
\(5+1=6\)
\(5+3=8\)
Ответ: \(86.\)
В этом случае мы складывали два двузначных числа. Давайте сложим двузначное с трехзначным, здесь надо обратить внимание на правильную запись: десятки под десятками и сотни под сотнями.
Пример 2. Сложите два числа: \(523 + 31\) в столбик.
Решение:
\(3+1=4\)
\(2+3=5\)
Ответ: \(554\).
Если при сложении образуется число больше 9: обычно это 10-18, то мы запоминаем десяток и прибавляем его к разряду выше, например если при сложении цифр 2 и 9 результат сложения равен 11, 1 мы записываем в сотни , а вторую еденицу прибавляем к тысячным.
Пример 3. Сложите два числа: \(523 + 91\) в столбик.
Решение:
\(3+1=4\)
\(2+9=11\) записываем \(1\)
\(5+1=6\)
Ответ: \(614\).
И еще пару примеров для лучшего понимания.
Пример 4. Сложите два числа: \(523 + 98\) в столбик.
Решение:
\(3+8=11\)
\(2+9+1\)
\(5+1=6\)
Ответ: \(621.\)
Пример 5. Сложите два числа: \(224 + 98\) в столбик.
Решение:
\(4+8=12\) записываем \(2\)
\(2+9+1=12\) записываем \(2\)
\(2+1=3\)
Ответ: \(322.\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
«Сложение и вычитание столбиком» — задание по математике для 2 класса
Задание по математике для 2 класса — «Сложение и вычитание столбиком»
Лимит времени: 0
Информация
Выполните задание онлайн олимпиады и узнайте результат.
Для зарегистрированных участников, результаты отправляются на электронную почту.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 10
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Поздравляем!
Вы отлично справились с заданием.
Ваш результат соответствует 1 месту.Оформить диплом
Поздравляем!
Вы хорошо справились с заданием.
Ваш результат соответствует 2 месту.Оформить диплом
Поздравляем!
Вы выполнили задние допустив незначительное количество ошибок.
Ваш результат соответствует 3 месту.Оформить диплом
Сделайте работу над ошибками.
Попробуйте пройти тестирование еще раз и добиться хорошего результата.
Ваш результат может стать значительно лучше.
- С ответом
- С отметкой о просмотре
Урок математики в 3 классе «Записываем вычитание в столбик»
Урок математики в 3 классе
УМК «Планета знаний»
М. И. Башмаков, М. Г. Нефёдова
Тема: «Записываем вычитание в столбик»
Составила: учитель начальных классов
МБОУ «Тиксинская СОШ №2»
Огурцова Наталья Николаевна
Место в системе уроков:
Первый урок по теме: «Вычитаем числа».
Цель: сформировать умение вычитания чисел с переходом через разряд.
Задачи:
Образовательные:
познакомиться с алгоритмом письменных приёмов вычитания трёхзначных чисел, аналогичных таким же приёмам при вычитании двузначных чисел;
закрепить навык применения алгоритма письменного сложения и вычитания;
закрепить умение решать составные задачи;
Развивающие:
развивать навык устного счёта;
совершенствовать мыслительные операции: анализа, сопоставления;
развитие умения аргументировать своё мнение;
развивать интерес детей к математике, их математические способности;
развитие мыслительной деятельности, познавательной активности, мышления, наблюдательности, внимания, памяти;
развитие умения давать самооценку своей деятельности;
Воспитывающие:
воспитывать дисциплинированность, ответственность, способность сопереживать, самоуважение; активность, усидчивость, прилежание, любознательность, заинтересованность и пытливость в процессе учения;
воспитывать взаимопомощь, взаимовыручку;
воспитание и укрепление интереса к математике;
создание благоприятного психологического климата для возможности раскрытия потенциала каждого ребенка.
Планируемые результаты.
Предметные:
изучить способ вычитания чисел с переходом через разряд столбиком;
повторить разрядный состав двузначного и трехзначного числа.
Метапредметные:
определять цель деятельности на уроке с помощью учителя и самостоятельно.
высказывать свою версию, пытаться предлагать способ её проверки (на основе продуктивных заданий в учебнике).
развивать коммуникативные навыки (корректно излагать свое мнение, аргументировать свою позицию, уважать мнение партнера).
Личностные:
формирование познавательного интереса к новому учебному материалу;
определять успешность выполнения своего задания в диалоге с учителем.
самостоятельно определять и высказывать самые простые, общие для всех людей правила поведения при совместной работе и сотрудничестве (этические нормы).
Тип урока: урок «открытия» нового знания.
Оборудование, наглядность: учебник «Математика» (стр.46-47), тетрадь на печатной основе, персональный компьютер, проектор, раздаточный материал с заданиями, карточки для рефлексии.
Используемые методы и приемы:
метод эмоционального стимулирования,
словесный метод,
наглядный метод,
проблемно-поисковые методы,
практические методы,
самостоятельная работа,
элементы технологии коллективного взаимодействия.
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Этап урока | Деятельность учителя | Деятельность учащихся | Формируемые УУД |
Осуществляемые действия | Осуществляемые действия | ||
I. Цель: Осознанный переход обучающихся из внеурочной жизнедеятельности в пространство учебной деятельности. | Эмоциональный настрой. Слайды 2- 3 Проговаривание стихотворения: Начинаем ровно в срок Мы – умные! Мы — дружные! Мы — внимательные и старательные! Будем слушать, отвечать, И пятёрки получать! Я желаю вам хорошего настроения и удачи на уроке. — Повернитесь друг к другу, улыбнитесь и скажите: «Я желаю тебе удачи». — Подумайте, что пригодится для успешной работы на уроке? — Предлагаю вам прочитать девиз нашего урока. Ребята, у вас на партах листы самооценки. На протяжении всего урока вы их будете заполнять. -Откройте тетради, запишите дату, классная работа. | Приготовление к уроку. Проговаривание стихотворения: — Вера в успех, внимание, трудолюбие, усердие, старание, знания. — «Мы пришли сюда учиться Не лениться, а трудиться, Только тот, кто много знает В жизни что-то достигает». | Личностные: Личностные Регулятивные |
II. Цель: Повторение изученного материала, необходимого для «открытия нового знания» и выявление затруднений в индивидуальной деятельности каждого учащегося. | СЛАЙД 5 (математическая разминка) Для начала проведём математическую разминку. Она нам поможет в нашей дальнейшей работе. 1.Таблица умножения Тренажер-презентация 2.Покажите числа, в которых: 4 сотни, 2 десятка 420 5 сотен 500 8 десятков, 3 сотни 380 4 сотни, 1 десяток 410 4 сотни, 2 десятка, 6 единиц 426 6 сотен, 7 десятков, 8 единиц 678 1 единица, 5 сотен, 3 десятка 531 3 десятка, 5 сотен, 4 единицы 534 (Числа записываются учениками на доске). Что объединяет эти числа? (Они трёхзначные). Из каких разрядов они состоят? (Единицы, десятки, сотни). Где пишутся единицы? Десятки? Сотни? Назовите числа, в которых отсутствуют единицы, десятки. Запишите ответы в тетрадях Увеличьте число 380 на 1 сотню. (480) Уменьшите число 531 на 1 единицу. (532) Увеличьте число 426 на 3 десятка. (456) Назовите наименьшее их этих чисел. (456) Назовите наибольшее из этих чисел. (532) Расположите данные числа в порядке возрастания. Откройте тетради, запишите там полученный ряд. (1 человек работает у доски) ПРОВЕРИМ! Устные вычисления Слайд 6 420+80=500 380+50=430 500-60=440 410-30=380 Прочитайте 1 выражение. Проверим. Слайд 7 Объясните, как вы считали. Какое правило помнили? Трёхзначные числа складываем и вычитаем по разрядам. Кто считал по-другому? — Молодцы! Вы хорошо потрудились. Оцените себя в листе самооценки. ПОКАЖИТЕ НАСТРОЕНИЕ | Показывают смайлики | |
III. Выявление места и причины затруднения. Цель: Обсуждение затруднений. 1 мин | СЛАЙД 8. Открытие новых знаний Слайд 63 -7 42-14 134-9 176 — 28 325-154 Прочитайте следующие выражения. Удобны ли известные вам приёмы вычисления при выполнении этого задания? Почему? Что же делать? Какой приём надо использовать, если трудно вычесть трёхзначные числа устно? — Умеем ли мы выполнять эти вычисления? | 176-28 325 -154 -Трудные случаи вычислений — Мы не умеем вычитать числа с переходом через разряд (Письменный приём, решение столбиком). | |
IV. Целеполагание и построение проекта выхода из затруднения. Цель: Обсуждение проекта выхода из затруднений. 2 мин. | Определите тему сегодняшнего урока. — Какое новое знание нам необходимо для дальнейшей работы? — Какую цель мы поставим? | «Записываем вычитание в столбик» — Научиться записывать и производить вычисления в столбик | |
V. | (Слайд 9) Повторение алгоритма письменного вычитания А сможете ли вы самостоятельно объяснить, как вычитать эти числа столбиком? Отработка алгоритма письменного вычитания. 1)устная работа №1 , стр. 46 | Да, как вычитали двузначные числа. Будем учиться строить алгоритм вычитания чисел — По аналогии с алгоритмом вычитания двухзначных чисел — Так же, как и раньше: единицы под единицами, десятки под десятками, сотни под сотнями. Так же по разрядам. 2-й шаг – вычитаем единицы… 3-й шаг – вычитаем десятки… 4-й шаг – вычитаем сотни… 5-й шаг – читаем ответ. — Записываем единицы под единицами, десятки под десятками, сотни под сотнями… | Личностные: |
Физминутка. 1 мин | Музыкальная физминутка Слайд 10 | ||
VI. Первичное закрепление с комментированием во внешней речи. Цель: Проговаривание нового знания, запись в виде опорного сигнала (фронтальная работа, работа в парах). | Учебник с. 46 Сравните его с выводом, который мы составили сами. — Значит мы с вами вывели правильный алгоритм. — А научились мы им пользоваться? — Давайте будем совершенствовать новые знания Слайд 11 Пользуясь выведенным алгоритмом, выполним Задание №2 учебника. (с объяснением) — Объясни вычисления и выполни вычитание чисел (Один ученик у доски.) Два последних примера – самостоятельно. (Взаимопроверка.) ПОКАЖИТЕ НАСТРОЕНИЕ — Молодцы! Вы хорошо потрудились. Оцените друг друга в листе самооценки. | — Они одинаковы. — Нет, нужно потренироваться. Работаем в тетради. Используем таблицу алгоритм. Работа в парах | Познавательные УУД- построение логической цепи рассуждений. Коммуникативные — умение слушать, вступать в диалог Личностные: |
VII. Самостоятельная работа (работа в парах). Цель: Каждый для себя должен сделать вывод о том, что он уже умеет. | Самостоятельная работа (тест) Слайд 12 — Каким алгоритмом пользовались? Самопроверка Слайд 13 — Молодцы! Вы хорошо потрудились. Оцените себя в листе самооценки ПОКАЖИТЕ НАСТРОЕНИЕ | ||
Физминутка | Гимнастика для глаз | ||
VIII. | Где мы сможем применить полученные сегодня знания? Отправляемся в магазин за покупками. Стр. 47 № 4 (а) Задача Слайд 14 Разбор задачи. Прочитайте задачу. Покупатель купил шляпу за 448р. и шарф. У него было 975 р., а осталось 177р. Сколько он заплатил за шарф? Прочитайте условие задачи. Прочитайте вопрос задачи. Составим схему. — Слайд 15 Пригодились ли новые знания? — Молодцы! Оцените себя в листе самооценки ПОКАЖИТЕ НАСТРОЕНИЕ Игра «Волшебный квадрат» Ну а теперь проверим, какие вы трудолюбивые и внимательные. Решите данные на карточке примеры, если потребуется решить столбиком, вычисления выполните в тетрадях. Закрасьте ответы в волшебном квадрате, и вы узнаете, как вы потрудились. Проверка. СЛАЙД 17 | Было – 975р Купил -? 448р. и? р. Осталось – 177р. Было – Шляпа – Шарф = Осталось 975 – 448 -? =177 547 -? = 177 ? = 547 -177 Решают примеры ,закрашивают соответствующий квадратик в волшебном квадрате | |
IX. Рефлексия учебной деятельности (итог урока). Цель: Осознание учащимися учебной деятельности, самооценка результатов деятельности своей и всего класса. | СЛАЙД 18 -21 Завершается урок, Он пошёл ребятам впрок? Постарались всё понять? Учились тайны открывать? Ответы полные давали? На уроке не зевали? — Какую задачу ставили в начале урока? — Удалось ли решить поставленную задачу? — Каким способом? — Следовали составленному плану? Каким образом? — Какие получили результаты? — Что нужно сделать ещё? — Где можно применить новые знания? — Что на уроке у вас хорошо получилось? — Над чем ещё надо поработать? В листе самооценки выставите себе оценку за весь урок (критерии те же), вложите в тетрадь. ПОКАЖИТЕ НАСТРОЕНИЕ | — Научится решать примеры на сложение двух и трёхзначных чисел с переходом через разряд. — Да — Составили новый алгоритм. — Да. Мы сначала наблюдали, потом сравнивали, потом выводили алгоритм. — Закрепили умение применять новые знания на практике при решении примеров, задач. — Повторили единицы измерений и сложение именованных чисел. — Применяли логику, анализировали, сравнивали, оценивали себя и товарищей. — Потренироваться в решении примеров с переходом через разряд. — На уроке математике, в жизни при покупках и т.д. | |
Домашнее задание: | Домашнее задание: | Стр. |
Сложение натуральных чисел столбиком: правило, примеры
Сложение столбиком, или как еще говорят, сложение в столбик — это метод, широко используемый для сложения многозначных натуральных чисел. Суть этого метода в том, что сложение двух и более многозначных чисел сводится к нескольким простым операциям сложения однозначных чисел.
В статье подробно расписано, как выполнять сложение двух и большего количества многозначных натуральных чисел. Дано правило сложения чисел в столбик и примеры решения с разбором всех самых характерных ситуаций, возникающих при сложении чисел в столбик.
Сложение двух чисел в столбик: что нужно знать?
Прежде чем мы перейдем непосредственно к операции сложения в столбик, рассмотрим некоторые важные моменты. Для быстрого освоения материала желательно:
- Знать и хорошо ориентироваться в таблице сложения.
 Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения.
Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения. - Помнить свойства сложения натуральных чисел. Особенно свойства, связанные со сложением нулей. Напомним их кратко. Если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому. Сумма двух нулей есть нуль.
- Знать правила сравнения натуральных чисел.
- Знать, что такое разряд натурального числа. Напомним, что разряд — это позиция и значение цифры в записи числа. Разряд определяет значение цифры в числе — единицы, десятки, сотни, тысячи и т.д.
Сложение двух натуральных чисел в столбик
Опишем алгоритм сложения чисел столбиком с использованием конкретного примера. Пусть мы складываем числа 724980032 и 30095. Сначала следует записать эти числа по правилам записи сложения в столбик.
Числа записываются одно под другим, цифры каждого разряда располагаются, соответственно, одна под другой. Слева ставим знак «плюс», а под числами проводим горизонтальную линию.
Теперь мысленно разбиваем запись на столбики по разрядам.
Все, что остается сделать — сложить однозначные числа в каждом столбике.
Начинаем с крайнего правого столбика (разряд единиц). Складываем числа, и под чертой записываем значение единиц. Если при сложении значение десятков в результате получилось отличным от нуля, запоминаем это число.
Складываем цифры второго столбика. К результату прибавляем число десятков, которое мы запомнили на предыдущем шаге.
Повторяем весь процесс с каждым столбиком, вплоть до крайнего левого.
Данное изложение — упрощенная схема алгоритма сложения натуральных чисел столбиком. Теперь, когда мы разобрались с сутью метода, рассмотрим каждый шаг подробно.
Сначала складываем единицы, то есть числа в правом столбце. Если у нас получилось число, меньшее чем 10, записываем его в том же столбике и переходим к следующему. Если же результат сложения больше или равен 10, то под чертой в первом столбике записываем значение разряда единиц, а значение разряда десятков — запоминаем. Например, получилось число 17. Тогда записываем число 7 — значение единиц, а значение десятков — 1 — запоминаем. Обычно говорят: «семь пишем, один в уме».
Например, получилось число 17. Тогда записываем число 7 — значение единиц, а значение десятков — 1 — запоминаем. Обычно говорят: «семь пишем, один в уме».
В нашем примере, при сложении чисел первого столбика, мы получаем число 7.
7<10, поэтому записываем это число в разряд единиц результата, а запоминать нам ничего не нужно.
Далее складываем числа в следующем столбце, то есть в разряде десятков. Проводим те же действия, только к сумме нужно прибавить число, которое мы держали в уме. Если сумма получилась меньше 10, просто записываем число под вторым столбиком. Если же результат больше или равен 10, записываем во втором столбике значение единиц этого числа, а цифру из разряда десятков запоминаем.
В нашем случае мы складываем числа 3 и 9, в результате имеем 3+9=12. На предыдущем шаге мы ничего не запоминали, поэтому к этому результату ничего прибавлять не нужно.
12>10, поэтому во втором столбике записываем цифру 2 из разряда единиц, а цифру 1 из разряда десятков держим в уме.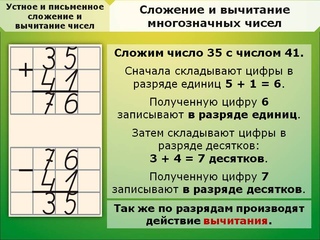 Для удобства можно записать это число над следующим столбиком другим цветом.
Для удобства можно записать это число над следующим столбиком другим цветом.
Переходя к третьему, четвертому и так далее столбику повторяем действие, пока столбики не закончатся.
В третьем столбике сумма цифр равна нулю (0+0=0). К этой сумме прибавляем то число, которое ранее держали в уме, и получаем 0+1=1. записываем:
Переходя к следующему столбцу также складываем 0+0=0 и записываем в результате 0, так как на предыдущем шаге мы ничего не запоминали.
Следующий шаг дает 8+3=11. В столбике записываем цифру 1 из разряда единиц. Цифру 1 из разряда десятков держим в уме и переходим к следующему столбцу.
Этот столбик содержит только одно число 9. Если бы у нас не было в памяти числа 1, мы бы просто переписали число 9 под горизонтальную черту. Однако, учитывая, что не предыдущем шаге мы запомнили число 1, нужно сложить 9+1 и записать результат.
9+1=10
Поэтому, под горизонтальной чертой мы записываем 0, а единицу снова держим в уме.
Переходя к следующему столбику складываем 4 и 1, результат пишем под чертой.
Следующий столбик содержит только число 2. Так на предыдущем шаге мы ничего не запоминали, просто переписываем это число под черту.
Также поступаем и с последним столбиком, содержащим число 7.
Столбцов более нет, и в памяти также ничего нет, поэтому можно сказать, что операция сложения в столбик окончена. Число, записанное под чертой — результат сложения двух верхних чисел.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЧтобы разобраться со всеми возможными нюансами, рассмотрим еще несколько примеров.
Пример 1. Сложение натуральных чисел столбикомСложим два натуральных числа: 21 и 36.
Сначала запишем эти числа по правилу записи при сложении столбиком:
Начав с правого столбика, приступаем к сложению чисел.
1+6=7
Так как 7<10, записываем 7 под чертой.
Складываем числа во втором столбике.
2+3=5
Так как 5<10, а в памяти с предыдущего шага ничего нет, записываем результат
В памяти и в следующем столбике чисел более нет, сложение закончено. 21+36=57
Пример 2. Сложение натуральных чисел столбикомСколько будет 47+38?
Запишем:
7+8=15, поэтому запишем 5 в первом столбике под чертой, а 1 будем держать в уме.
Теперь складываем значения из разряда десятков: 4+3=7. Не забываем о единице и прибавляем ее к результату:
7+1=8. Полученное число записываем под чертой.
Это и есть результат сложения.
47+38=85
Пример 3. Сложение натуральных чисел столбикомТеперь возьмем два трехзначных числа и выполним их сложение.
3+9=12; 12>10
Записываем 2 под чертой, 1 держим в уме.
8+5=13; 13>10
Складываем 13 и запомненную единицу, получаем:
13+1=14; 14>10
Записываем 4 под чертой, 1 держим в уме.
7+2=9
Не забываем, что на предыдущем шаге мы запомнили 1.
9+1=10
Записываем 0 под чертой, 1 держим в уме.
В последнем столбике переносим единицу, которую мы запомнили ранее, под черту, и получаем окончательный результат сложения.
783+259=1042
Пример 4. Сложение натуральных чисел столбикомНайдем сумму чисел 56927 и 90.
Как всегда, сначала записываем условие:
7+0=7; 7<10
Записываем 7 под чертой и переходим к следующему столбику.
2+9=11; 11>10
Записываем 1 под чертой, 1 держим в уме и переходим к следующему столбику.
9+1=10
Записываем 0 под чертой, 1 держим в уме и переходим к следующему столбику.
Столбик содержит одно число 6. Складываем его с запомненной единицей.
6+1=7; 7<10
Записываем 7 под чертой и переходим к следующему столбику.
Столбик содержит одно число 5. Переносим его под черту и заканчиваем операцию сложения.
56927+90=57017
Следующий пример приведем без промежуточных результатов и пояснений, как образец записи сложения в столбик на практике.
Пример 5. Сложение натуральных чисел столбиком5807+4137502=?
Ответ: 5807+4137502=4143309
Сложение столбиком трех и более чисел. Что нужно знать?
Во первых, нужно усвоить всю информацию, уже изложенную в этой статье. Во вторых, также помним, что нули не влияют на результат сложения, и сколько бы не было в выражении слагаемых нулей, их сумма будет равна нулю.
Этапы сложения в столбик трех и более чисел аналогичны этапам из уже рассмотренных примеров с двумя числами. Обратимся к практике и поясним ход решения.
Пример 5. Сложение трех натуральных чисел столбикомСложим столбиком числа 274, 3082 и 201297.
Сначала делаем запись:
Начинаем с первого столбика, справа налево.
4+2+7=13; 13>10
3 пишем, 1 в уме. Переходим ко второму столбику.
7+8+9=24; 24+1=25; 25>10
5 пишем, 2 в уме. Переходим к третьему столбику.
2+0+2=4; 4+2=6; 6<10
6 пишем, и ничего не запоминаем. Переходим к четвертому столбику.
3+1=4; 4<10
4 пишем, и ничего не запоминаем. Переходим к пятому столбику. Пятый и шестой столбики содержат по одному числу, в уме с предыдущих шагов мы ничего не держим, поэтому просто переносим числа из последних двух столбиков под черту.
Ответ: 274+3082+201297=204653
Совет: при сложении трех и большего количества чисел в столбик, если вычисления выходят слишком громоздкими, бывает удобнее последовательно сложить два числа, затем еще два и так далее.
Матрица столбцовМатрица, которая состоит из всех элементов только в одном столбце, называется матрицей столбцов.
Введение
Матрица-столбец — это один из типов матриц. В этой матрице элементы расположены в несколько строк, но в один столбец. Следовательно, он называется матрицей-столбцом, а также вектор-столбцом.
Например, у нас есть несколько элементов, но все они расположены только в одном столбце. На самом деле элементы расположены в разных рядах для их разделения.Предположим, что в этом случае все элементы расположены в $ m $ строк. Таким образом, элементы располагаются в $ m $ строке и $ 1 $ столбце.
Формируется матрица $ M $ порядка $ m \ times 1 $, которую математически можно записать в следующем виде.
$ M $ $ \, = \, $ $ {\ begin {bmatrix} e_ {11} \\ e_ {21} \\ e_ {31} \\ \ vdots \\ е_ {m1} \ конец {bmatrix}} _ {\ displaystyle m \ times 1} $
Расположение элементов в этой матрице представляет собой прямоугольник.Итак, матрица столбцов на самом деле представляет собой прямоугольную матрицу, и ее просто выражают следующим образом.
млн $ = {\ begin {bmatrix} е _ {\ displaystyle ij} \ конец {bmatrix}} _ {\ displaystyle m \ times n} $
В случае вектора-столбца количество столбцов $ j = 1 $. Итак, $ n = 1 $, но $ i = m $. Следовательно, простая форма матрицы столбцов может быть записана в следующей форме матрицы.
млн $ = {\ begin {bmatrix} е _ {\ displaystyle i1} \ конец {bmatrix}} _ {\ displaystyle m \ times 1} $
Примеры
Следующие ниже матрицы являются лучшими примерами столбцовой матрицы.
$ (1). \, \, \, \, $ А = \ begin {bmatrix} 7 \ end {bmatrix} $
$ A $ — матрица-столбец порядка $ 1 \ times 1 $. В этой матрице столбцов единственный элемент отображается в одной строке и одном столбце.
$ (2). \, \, \, \, $ В = \ begin {bmatrix} -1 \\ 4 \ end {bmatrix} $
$ B $ — это матрица столбцов порядка $ 2 \ times 1 $, и в этой матрице два элемента расположены в две строки и один столбец.
$ (3). \, \, \, \, $ C = \ begin {bmatrix} 6 \\ 0 \\ 9 \ end {bmatrix} $
$ C $ — матрица-столбец порядка $ 3 \ times 1 $.Три элемента расположены в матрице в три строки и один столбец.
$ (4). \, \, \, \, $ D = \ begin {bmatrix} -5 \\ 8 \\ 2 \\ 3 \ end {bmatrix} $
$ D $ — матрица-столбец порядка $ 4 \ times 1 $. Четыре элемента расположены в матрице в четыре строки и один столбец.
Во всех приведенных выше четырех примерах элементы расположены только в одном столбце, но количество строк разное. Фактически расположение элементов во всех матрицах образует прямоугольную форму.Итак, матрица столбцов всегда является прямоугольной матрицей.
Определение и примеры матрицы, ее записей, строк, столбцов, матричной нотации. Матрица — это просто …
Матрица — это способ организации данных в столбцы и строки. В скобках [] пишется матрица. Посмотрите на картинку ниже, чтобы увидеть пример.
Каждый элемент в матрице называется записью.
Матрица, изображенная ниже, состоит из двух строк и трех столбцов.
- Его размеры 2 × 3
- Элементы матрицы ниже: 2, -5, 10, -4, 19, 4.
Размер матрицы
Размеры матрицы относятся к количеству строк и столбцов данной матрицы. По соглашению размер матрицы определяется числом строк • числом столбцов
Один из способов, которым некоторые люди помнят, что обозначение размеров матрицы — это строки за столбцами (а не столбцы за строками), — это вспомнить некогда популярное слово:
RC Cola - строки перед столбцами!
Ниже вы можете увидеть два изображения одной и той же матрицы с выделенными строками и столбцами.
Размеры данной матрицы
- размеры: 2 × 3
- 2 строки × 3 столбца
Матричное обозначение
Чтобы идентифицировать запись в матрице, мы просто пишем нижний индекс строки соответствующей записи, за которой следует столбец.
В матрице A слева мы пишем 23 для обозначения записи во второй строке и третьем столбце.
Один из способов запомнить, что в этой нотации на первом месте строки, а на втором — столбцы, — это думать об этом как о чтении книги. Вы всегда сначала читаете сбоку, так же как всегда сначала пишете строки. Продолжая аналогию, когда вы заканчиваете читать строку в книге, ваши глаза опускаются, как столбцы после строк. 23 указывает сначала номер строки, 2, затем номер столбца 3.
Практика определения записей
Практика 1
Шаг 1 Габаритные размеры
Размеры матрицы 3 × 3 (3 строки × 3 столбца)
Шаг 2Найдите запись G 23 в матрице G слева.
ВходG 23 — запись во второй строке и третьем столбце: 55.
Шаг 3 Габаритные размерыРазмеры 3 × 5 (3 строки × 5 столбцов)
Практика 2
Шаг 1 Отвечать
Запись j 34 — это запись в третьей строке и четвертом столбце.
Шаг 2 ОтвечатьJ 12 — это число в первой строке и втором столбце: -5
Практика 3
Шаг 1 Отвечать
Размеры матрицы 4 × 5 (4 строки × 5 столбцов)
Шаг 2 ОтвечатьЗапись 31 (строка 1 и столбец 4)
Шаг 3 Отвечатьv 45 обозначает запись в четвертой строке и пятом столбце, число 15 в правом нижнем углу.
Сложение и вычитание матриц
Вы можете складывать или вычитать матрицы, если каждая матрица имеет одинаковые размеры (другими словами, каждая матрица должна иметь одинаковое количество столбцов и строк).
Чтобы сложить или вычесть матрицы, вы просто добавляете или вычитаете соответствующие записи (записи или числа, которые находятся в одном месте).
Почему для сложения и вычитания требуются одинаковые размеры?
Подумайте об этом: Поскольку добавление / вычитание матриц включает добавление / вычитание соответствующих записей. Что бы вы сделали с записями в одной матрице, которым нет соответствующей записи в другой?)
Рассмотрим пример, изображенный выше.. Матрица №1 имеет на один столбец больше, чем Матрица №2. Как бы вы сопоставили, не говоря уже о добавлении, записи в столбце 3 №1 с соответствующими записями в столбце №2. Что ж, ответ — вы не можете, поскольку вы не можете добавлять матрицы, если они не имеют одинакового количества строк и столбцов.
Вектор-столбец — объяснение и примеры
Вектор-столбец — это матрица с 1 столбцом. Давайте посмотрим на формальное определение вектора-столбца.
Вектор-столбец — это матрица размером $ m \ times 1 $, состоящая из одного столбца с m элементами.
В этой статье мы рассмотрим, что такое вектор-столбец, их примеры и матричные операции с векторами-столбцами.
Что такое вектор-столбец?
Как упоминалось ранее, вектор-столбец — это тип матрицы с только $ 1 $ столбцом. Векторы-столбцы также известны как матрицы столбцов . Может быть $ 1 $ строки, $ 2 $ строк, $ 3 $ строк или $ n $ строк. Но номер столбца всегда 1 $! Ниже показано следующее:
Здесь показан вектор-столбец $ A $ с $ 1 $ столбцом и $ n $ строками.Первым элементом матрицы является $ a_1 $, вторым элементом является $ a_2 $, и так далее до последнего элемента, $ a_n $. Давайте посмотрим на несколько векторов-столбцов ниже :
$ \ begin {bmatrix} 5 \ end {bmatrix} $
Это простейший вектор-столбец с $ 1 $ столбцом и $ 1 $ строкой. Единственный элемент в этой матрице — 5 долларов.
$ \ begin {bmatrix} {- 3} \\ {- 5} \ end {bmatrix} $
Это матрица размером $ 2 \ times 1 $. Есть $ 2 $ строки и $ 1 $ столбец.
$ \ begin {bmatrix} {- 3} \\ {- 5} \\ 4 \ end {bmatrix} $
Это матрица размером 3 \ times 1 $.Есть $ 3 $ строки и $ 1 $ столбец. Это вектор-столбец.
Конечно, мы можем иметь столько строк, сколько захотим, но количество столбцов должно составлять 1 доллар. Это то, что делает матрицу вектором-столбцом !
Транспонирование вектора-столбца
Напомним, что транспонирование матрицы означает замену строк и столбцов. Строки становятся столбцами, а столбцы становятся строками.
Что происходит, когда мы транспонируем вектор-столбец?
Поскольку существует только столбец $ 1 $, транспонирование вектора столбца делает его вектором-строкой ! Предположим, у нас есть вектор-столбец $ A $:
$ A = \ begin {bmatrix} {- 2} \\ {- 1} \\ 13 \ end {bmatrix} $
Если мы транспонируем его , мы есть вектор-строка, показанный ниже (назовем его матрицей $ B $):
$ B = \ begin {bmatrix} {- 2} & {- 1} & 13 \ end {bmatrix} $
Чтобы узнать больше о векторы строк, перейдите сюда.
Как найти вектор-столбец
Как и в случае с матрицами, мы можем выполнять арифметические операции и с векторами-столбцами. Мы рассмотрим сложение, вычитание и скалярное умножение.
Добавление
Перед добавлением векторов столбцов $ 2 $ мы должны проверить, имеют ли они одинаковые размеры. Если их нет, мы не сможем их добавить. Если они есть, мы просто добавляем соответствующие элементы каждого вектора-столбца. Рассмотрим матрицы $ A $ и $ B $, показанные ниже:
$ A = \ begin {bmatrix} {- 2} \\ 3 \ end {bmatrix} $
$ B = \ begin {bmatrix} 8 \\ 4 \ end {bmatrix} $
Матрицы $ A $ и $ B $ являются матрицами размером $ 2 \ times 1 $.Мы складываем два вектора-столбца, добавляя соответствующие записи. Показано ниже:
$ A + B = \ begin {bmatrix} {- 2 + 8} \\ 3 + 4 \ end {bmatrix} $
$ A + B = \ begin {bmatrix} {6} \\ 7 \ end {bmatrix} $
Вычитание
Вычитание выполняется по тому же правилу, что и сложение. Мы просто вычитаем каждую соответствующую запись. Рассмотрим матрицы $ C $ и $ D $, показанные ниже:
$ C = \ begin {bmatrix} {- 5} \\ 5 \ end {bmatrix} $
$ D = \ begin {bmatrix} {- 1} \ \ {- 6} \ end {bmatrix} $
Матрицы $ C $ и $ D $ являются матрицами $ 2 \ times 1 $.Мы вычитаем два вектора-столбца, вычитая соответствующие записи. Показано ниже:
$ C — D = \ begin {bmatrix} {- 5 — (-1)} \\ 5 — (-6) \ end {bmatrix} $
$ C — D = \ begin {bmatrix} {-5 + 1} \\ 5 + 6 \ end {bmatrix} $
$ C — D = \ begin {bmatrix} {- 4} \\ 11 \ end {bmatrix} $
Скалярное умножение
Когда мы хотим умножить вектор-столбец на скаляр, мы просто умножаем каждый элемент матрицы-столбца на скаляр.Рассмотрим матрицу $ A $, показанную ниже:
$ A = \ begin {bmatrix} {- 2} \\ 3 \\ {- 6} \ end {bmatrix} $
Если мы хотим умножить эту матрицу столбца на скаляр $ 6 $, мы сделаем это, умножив каждую из его записей на $ 6 $. Показано ниже:
$ 6A = 6 \ times \ begin {bmatrix} {- 2} \\ 3 \\ {- 6} \ end {bmatrix} $
$ = \ begin {bmatrix} {6 \ times — 2 } \\ 6 \ times 3 \\ {6 \ times — 6} \ end {bmatrix} $
$ = \ begin {bmatrix} {-12} \\ 18 \\ {-36} \ end {bmatrix} $
Давайте рассмотрим несколько примеров, чтобы прояснить наше понимание.
Пример 1Из 4-х матриц, показанных ниже, определите, какие из них являются векторами-столбцами.
$ A = \ begin {bmatrix} {-2} \\ 6 \\ {-2} \ end {bmatrix} $
$ B = \ begin {bmatrix} {0} \\ 0 \\ {0 } \\ 1 \\ 0 \ end {bmatrix} $
$ C = \ begin {bmatrix} {-12} & 6 \ end {bmatrix} $
$ D = \ begin {bmatrix} {- 43} \ end {bmatrix} $
Решение
- Матрица $ A $ — это матрица размером $ 3 \ times 1 $.Он имеет $ 3 $ строк и $ 1 $ столбец. Таким образом, это вектор-столбец .
- Матрица $ B $ — это матрица s $ 5 \ times 1 $. Он имеет 5 $ строк и 1 $ столбец. Большинство записей — нули, но это не имеет значения. Поскольку он имеет один столбец, он является вектор-столбцом .
- Матрица $ C $ — это матрица размером $ 1 \ times 2 $. У него есть строка $ 1 $ и столбец $ 2 $. Это не вектор-столбец , а вектор-строка.
- Матрица $ D $ — это матрица размером $ 1 \ times 1 $.Это простейшая форма матрицы. У него есть строка $ 1 $ и столбец $ 1 $. Это простейшая матрица-столбец. Это вектор-столбец .
Каково транспонирование следующего вектора-столбца?
$ \ begin {bmatrix} {- 6} \\ 0 \\ 9 \\ {-1} \ end {bmatrix} $
Решение
Напомним, что транспонированный вектор-столбец является вектором-строкой. Мы просто записываем те же записи в виде «строки», а не столбца.Таким образом, транспонирование :
$ \ begin {bmatrix} {- 6} & 0 & 9 & {- 1} \ end {bmatrix} $
Пример 3Добавить матрицу $ F $ и $ G $.
$ F = \ begin {bmatrix} -3 \\ 0 \\ -2 \ end {bmatrix} $
$ G = \ begin {bmatrix} 0 \\ -3 \\ 6 \ end {bmatrix} $
Решение
Матрица $ F $ и $ G $ являются матрицами размером $ 3 \ times 1 $. У них такое же измерение. Таким образом, их можно добавлять, добавляя друг к другу соответствующие элементы.Показано ниже:
$ F + G = \ begin {bmatrix} {- 3+ 0} \\ 0 + -3 \\ -2 + 6 \ end {bmatrix} $
$ F + G = \ begin {bmatrix } {- 3} \\ {- 3} \\ 4 \ end {bmatrix} $
Практические вопросы- Найдите транспонирование:
- $ \ begin {pmatrix} a \\ b \ \ c \\ e \\ g \ end {pmatrix} $
- $ \ begin {pmatrix} z \ end {pmatrix} $
- Выполните указанную операцию для матриц, показанных ниже:
$ A = \ begin { pmatrix} 1 \\ {0} \\ {- 2} \\ 8 \ end {pmatrix} $$ B = \ begin {pmatrix} 3 \\ {4} \\ 3 \ end {pmatrix} $
$ C = \ begin {pmatrix} -9 \\ {1} \\ {1} \ end {pmatrix} $
$ D = \ begin {pmatrix} 2 & {3} & {- 2} & 9 \ end { pmatrix} $
- $ -3A $
- $ A + D $
- $ B — C $
- Чтобы найти транспонирует вектора-столбца, записывает столбец в виде строк, вот и все!
- $ \ begin {pmatrix} a & b & c & e & g \ end {pmatrix} $
- $ \ begin {pmatrix} z \ end {pmatrix} $
Обратите внимание, транспонирование $ 1 \ times 1 $ матрица сама по себе!
- Часть (a) — это скалярное умножение.Умножаем каждый элемент матрицы $ A $ на скаляр $ {- 3} $.
Часть (б) является дополнением. Поскольку размерность матрицы $ A $ не совпадает с размерностью матрицы $ D $, мы не можем выполнить сложение.
Часть (c) — это вычитание. Обе матрицы $ B $ и $ C $ являются матрицами размером $ 3 \ times 1 $. Таким образом, можно выполнять вычитание.
Все ответы показаны ниже:
- $ -3A = {- 3} \ times \ begin {pmatrix} 1 \\ {0} \\ {- 2} \\ 8 \ end {pmatrix} $
$ = \ begin {pmatrix} -3 \ times 1 \\ {-3 \ times 0} \\ {-3 \ times — 2} \\ -3 \ times 8 \ end {pmatrix} $
$ = \ begin { pmatrix} -3 \\ 0 \\ 6 \\ -24 \ end {pmatrix} $ - Добавление невозможно!
- $ B — C = \ begin {pmatrix} 3 \\ {4} \\ 3 \ end {pmatrix} — \ begin {pmatrix} -9 \\ 1 \\ 1 \ end {pmatrix} $
$ B — C = \ begin {pmatrix} 3 — — 9 \\ 4-1 \\ 3-1 \ end {pmatrix} $
$ B — C = \ begin {pmatrix} 12 \\ 3 \\ 2 \ end { pmatrix} $
- $ -3A = {- 3} \ times \ begin {pmatrix} 1 \\ {0} \\ {- 2} \\ 8 \ end {pmatrix} $
Матрица (математика) — Простая английская Википедия, бесплатная энциклопедия
Для ссылок на конкретные элементы матрицы часто используются пары нижних индексов для чисел в каждой из строк и столбцов .В математике матрица (множественное число: матрицы ) представляет собой прямоугольник чисел, расположенный в строках и столбцах . Каждая строка располагается слева направо (по горизонтали), а столбцы идут сверху вниз (по вертикали). Левая верхняя ячейка находится в строке 1, столбце 1 (см. Диаграмму справа) .
Матрицы часто представлены заглавными латинскими буквами, такими как A {\ displaystyle A}, B {\ displaystyle B} и C {\ displaystyle C}, [1] , и существуют правила сложения, вычитания и «умножения» матрицы вместе, но правила другие, чем для чисел. [2] Например, произведение AB {\ displaystyle AB} не всегда дает тот же результат, что и BA {\ displaystyle BA}, как в случае умножения обычных чисел. [3] Матрица может иметь более двух измерений, например трехмерная матрица. Кроме того, матрица может быть одномерной, в виде одной строки или одного столбца.
Матрицы используются во многих естественных науках. Во многих университетах курсы по матрицам (обычно называемые линейной алгеброй) преподаются очень рано, иногда даже на первом году обучения.Матрицы также очень распространены в информатике, инженерии, физике, экономике и статистике. [4]
Горизонтальные линии в матрице называются строками , а вертикальные линии называются столбцами . Матрица с м строк и n столбцов называется матрицей м на n (или матрицей м × n ), а м и n называются ее размерами .
Места в матрице, где находятся числа, называются записями . [2] Запись матрицы A , которая находится в строке номер i и номер столбца j , называется записью i, j в A . Это записывается как A [ i, j ] или a i, j .
Мы пишем A: = (aij) m × n {\ displaystyle A: = (a_ {ij}) _ {m \ times n}}, чтобы определить матрицу m × n A , с каждым Запись в матрице называется a i, j для всех 1 ≤ i ≤ m и 1 ≤ j ≤ n .
Пример [изменение | изменить источник]
Матрица
- [123127492615] {\ displaystyle {\ begin {bmatrix} 1 & 2 & 3 \\ 1 & 2 & 7 \\ 4 & 9 & 2 \\ 6 & 1 & 5 \ end {bmatrix}}}
— это матрица 4 × 3. Эта матрица имеет m = 4 строки и n = 3 столбца.
Элемент A [2,3] или a 2,3 равен 7.
Дополнение [изменение | изменить источник]
Сумма двух матриц — это матрица, которая ( i , j ) -й элемент равна сумме ( i , j ) -го элементов двух матриц:
- [132100122] + [005750211] = [1 + 03 + 02 + 51 + 70 + 50 + 01 + 22 + 12 + 1] = [137850333] {\ displaystyle {\ begin {bmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \ end {bmatrix}} + {\ begin {bmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \ end {bmatrix}} = {\ begin {bmatrix}} 1 + 0 & 3 + 0 & 2 + 5 \\ 1 + 7 & 0 + 5 & 0 + 0 \\ 1 + 2 & 2 + 1 & 2 + 1 \ end {bmatrix}} = {\ begin {bmatrix} 1 & 3 & 7 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \ end {bmatrix}}}
Две матрицы имеют одинаковые размеры.Здесь A + B = B + A {\ displaystyle A + B = B + A} верно (и верно в целом для матриц одинаковых размеров).
Умножение двух матриц [изменить | изменить источник]
Умножение двух матриц немного сложнее:
- [a1a2a3a4] ⋅ [b1b2b3b4] = [(a1⋅b1 + a2⋅b3) (a1⋅b2 + a2⋅b4) (a3⋅b1 + a4⋅b3) (a3⋅b2 + a4⋅b4)] {\ displaystyle {\ begin {bmatrix} a1 & a2 \\ a3 & a4 \\\ end {bmatrix}} \ cdot {\ begin {bmatrix} b1 & b2 \\ b3 & b4 \\\ end {bmatrix}} = {\ begin {bmatrix} (a1 \ cdot b1 + a2 \ cdot b3) & (a1 \ cdot b2 + a2 \ cdot b4) \\ (a3 \ cdot b1 + a4 \ cdot b3) & (a3 \ cdot b2 + a4 \ cdot b4) \\\ end {bmatrix }}}
Итак с числами:
- [3514] ⋅ [2350] = [(3⋅2 + 5⋅5) (3⋅3 + 5⋅0) (1⋅2 + 4⋅5) (1⋅3 + 4⋅0)] = [ 319223] {\ displaystyle {\ begin {bmatrix} 3 & 5 \\ 1 & 4 \\\ end {bmatrix}} \ cdot {\ begin {bmatrix} 2 & 3 \\ 5 & 0 \\\ end {bmatrix}} = {\ begin {bmatrix} (3 \ cdot 2 + 5 \ cdot 5) & (3 \ cdot 3 + 5 \ cdot 0) \\ (1 \ cdot 2 + 4 \ cdot 5) & (1 \ cdot 3 + 4 \ cdot 0) \\ \ end {bmatrix}} = {\ begin {bmatrix} 31 & 9 \\ 22 & 3 \\\ end {bmatrix}}}
- Две матрицы могут быть умножены друг на друга, даже если они имеют разные размеры, при условии, что число столбцов в первой матрице равно количеству строк во второй матрице. [3]
- Результатом умножения, называемым произведением, является другая матрица с тем же количеством строк, что и первая матрица, и тем же количеством столбцов, что и вторая матрица.
- Умножение матриц не коммутативно, что означает, что в общем случае AB ≠ BA {\ displaystyle AB \ neq BA}. [4]
- Умножение матриц ассоциативно, что означает, что (AB) C = A (BC) {\ displaystyle (AB) C = A (BC)}. [4]
Есть несколько специальных матриц.
Квадратная матрица [изменить | изменить источник]
Квадратная матрица имеет такое же количество строк, что и столбцы, поэтому m = n. [5]
Пример квадратной матрицы:
- [5-24091-768] {\ displaystyle {\ begin {bmatrix} 5 & -2 & 4 \\ 0 & 9 & 1 \\ — 7 & 6 & 8 \\\ end {bmatrix}}}
В этой матрице 3 строки и 3 столбца: m = п = 3.
Личность [изменение | изменить источник]
Каждый квадратный набор размеров матрицы имеет специальный аналог, называемый «единичной матрицей», представленный символом I {\ displaystyle I}. [1] В единичной матрице нет ничего, кроме нулей, кроме главной диагонали, где все единицы. Например:
- [100010001] {\ displaystyle {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\\ end {bmatrix}}}
— это единичная матрица. Для каждого квадратного набора размерностей существует ровно , одна единичная матрица . Идентификационная матрица является особенной, потому что при умножении любой матрицы на единичную матрицу результатом всегда будет исходная матрица без изменений.
Обратная матрица [изменить | изменить источник]
Обратная матрица — это матрица, которая при умножении на другую матрицу равна единичной матрице. Например:
- [7867] ⋅ [7-8-67] = [1001] {\ displaystyle {\ begin {bmatrix} 7 & 8 \\ 6 & 7 \\\ end {bmatrix}} \ cdot {\ begin {bmatrix} 7 & -8 \ \ -6 & 7 \\\ end {bmatrix}} = {\ begin {bmatrix} 1 & 0 \\ 0 & 1 \\\ end {bmatrix}}}
[7-8-67] {\ displaystyle {\ begin {bmatrix} 7 & -8 \\ — 6 & 7 \\\ end {bmatrix}}} является обратным [7867] {\ displaystyle {\ begin {bmatrix} 7 & 8 \\ 6 & 7 \\\ end {bmatrix}}}.
Формула, обратная матрице 2×2, [xyzv] {\ displaystyle {\ begin {bmatrix} x & y \\ z & v \ end {bmatrix}}}:
(1det) [v − y − zx] {\ displaystyle \ left ({\ frac {1} {\ det}} \ right) {\ begin {bmatrix} v & -y \\ — z & x \ end {bmatrix} }}
Где det {\ displaystyle \ det} — определитель матрицы. В матрице 2×2 определитель равен:
xv − yz {\ displaystyle {xv-yz}}
Матрица с одним столбцом [изменение | изменить источник]
Матрица, в которой много строк, но только один столбец, называется вектором-столбцом.
Определитель берет квадратную матрицу и вычисляет простое число, скаляр. Чтобы понять, что означает это число, возьмите каждый столбец матрицы и нарисуйте его как вектор. Параллелограмм, нарисованный этими векторами, имеет площадь, которая является определяющим фактором. Для всех матриц 2×2 формула очень проста: det ([abcd]) = ad − bc {\ displaystyle \ det \ left ({\ begin {bmatrix} a & b \\ c & d \\\ end {bmatrix}} \ right) = ad-bc}
Для матриц 3×3 формула более сложная: det ([a1b1c1a2b2c2a3b3c3]) = a1 (b2c3 − c2b3) −a2 (b1c3 − c1b3) + a3 (b1c2 − c1b2) {\ displaystyle \ det \ left ({\ begin {bmatrix} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ {3} & b_ {3} & c_ {3} \\\ end {bmatrix}} \ right) = a_ {1} (b_ { 2} c_ {3} -c_ {2} b_ {3}) — a_ {2} (b_ {1} c_ {3} -c_ {1} b_ {3}) + a_ {3} (b_ {1} c_ {2} -c_ {1} b_ {2})}
Нет простых формул для определителей больших матриц, и многие программисты изучают, как заставить компьютеры быстро находить большие детерминанты.
Свойства определителей [изменить | изменить источник]
Есть три правила, которым следуют все детерминанты. Эти:
- Определитель единичной матрицы 1
- Если две строки или два столбца матрицы меняются местами, то определитель умножается на -1. Математики называют это чередующимся .
- Если все числа в одной строке или столбце умножаются на другое число n , то определитель умножается на n .Кроме того, если матрица M имеет столбец v , который является суммой двух матриц столбцов v1 {\ displaystyle v_ {1}} и v2 {\ displaystyle v_ {2}}, то определитель M будет сумма определителей M с v1 {\ displaystyle v_ {1}} вместо v и M с v2 {\ displaystyle v_ {2}} вместо v . Эти два условия называются мультилинейностью .
- ↑ 1.0 1.1 «Полный список символов алгебры». Математическое хранилище . 2020-03-25. Проверено 19 августа 2020.
- ↑ 2,0 2,1 «Матрицы». www.mathsisfun.com . Проверено 19 августа 2020.
- ↑ 3,0 3,1 «Как умножать матрицы». www.mathsisfun.com . Проверено 19 августа 2020.
- ↑ 4,0 4,1 4,2 «Матрица | математика». Британская энциклопедия . Проверено 19 августа 2020.
- ↑ Вайсштейн, Эрик В. «Матрица». mathworld.wolfram.com . Проверено 19 августа 2020.
| Викискладе есть медиафайлы, связанные с Matrix . |
- История
- Электронные книги
Двухколоночная проба в геометрии (определение, примеры и видео)
Доказательство с двумя столбцами в геометрии — это только один из трех способов продемонстрировать истинность некоторого математического утверждения.Тем не менее, это один из самых надежных методов, поскольку он заставляет геометрического специалиста или, по крайней мере, изучающего геометрию подкреплять каждое утверждение реальными доказательствами.
Что вы узнаете:
- Определение двухколоночного доказательства
- Структура в двухколоночных пробах
- Как решить двухколоночное доказательство
- Как написать двухколоночное доказательство
- Доказательства и рассуждения в две колонки
Определение двухколоночного доказательства
Среди множества методов, доступных математикам, есть доказательств, или логические аргументы, которые начинаются с посылки и приводят к выводу, очерчивая факты.
Написать доказательство — непростая задача, потому что вам нужно подогнать каждую деталь в правильном порядке. Большая часть геометрии работает с тремя типами доказательства:
- Подтверждение абзаца
- Блок-схема доказательства
- Двухстоечный пробой
В абзацах и блок-схемах можно достаточно хорошо изложить различные этапы, но для чистоты и ясности ничто не сравнится с доказательством в две колонки.
Проверка с двумя столбцами использует таблицу для представления логического аргумента и назначает каждый столбец для выполнения одной работы, а затем два столбца работают синхронно, чтобы провести читателя от предпосылки к выводу.
Структура в двухколоночных доказательствах
Доказательство абзаца рассказывает историю, в которой каждый факт и причина изложены в хронологическом порядке. Это означает, что вам нужно быть предельно организованным и, возможно, переписать абзац несколько раз, прежде чем он станет правильным. За доказательством блок-схемы может быть трудно следовать, но, по крайней мере, она четко отделяет математику от рассуждений.
Только двухколоночное доказательство явно помещает математику на одну сторону (первый столбец), а рассуждения — на другую сторону (второй или правый столбец).Пока вы держите две стороны в ряд, вы не сможете не переместить читателя от одной посылки к другой и, наконец, к заключению.
Структура двухколоночного доказательства должна соответствовать четырем основным принципам:
- В первом или левом столбце содержатся только математические утверждения, например «четырехугольник РОЗОВЫЙ — параллелограмм» или «сторона PI = сторона NK».
- Во втором или правом столбце указаны только причины, подтверждающие справедливость этих математических утверждений, например «Дано» или «Если противоположные стороны четырехугольника имеют одинаковую длину, тогда фигура представляет собой параллелограмм.«
- Каждый логический упорядоченный шаг пронумерован в обоих столбцах, поэтому первый шаг слева поддерживается первым шагом справа.
- Вы заканчиваете, когда доказываете свою концепцию.
Как решать двухколоночные доказательства
Доказательство из двух столбцов — это всего лишь структура, подобная скелету. У вас должно быть под рукой пять инструментов, чтобы пройти от предпосылки к выводу и завершить доказательство в две колонки:
- Givens — Укажите, что дано вам и читателю на схеме или постановке задачи
- Диаграмма — Диаграмма поясняет, что такое геометрическая фигура; если диаграммы нет, нарисуйте ее!
- Базовые знания — Вы должны глубоко разбираться в теоремах и постулатах, чтобы применять их быстро и логично; без понимания определений, словаря и отношений между геометрическими фигурами вы не можете перейти от аргумента к аргументу
- Рассуждения и навыки мышления — Это не королевская дорога; вы можете начать, натолкнуться на ментальную стену, и вам придется начинать заново; логическое мышление — это усвоенный и сложный навык, так что наберитесь терпения и дайте себе время подумать
- Заказ — Доказательства в две колонки переходят от одной идеи к другой логичным, ясным и кратким образом, приходят к выводу и затем останавливаются.
Как писать доказательства в две колонки
Вы можете написать пробу из двух столбцов, нарисовав горизонтальную линию вверху листа бумаги и вертикальную линию посередине.Назовите левую часть «Утверждение», а правую — «Причина». Допустим, вас просят доказать теорему о равнобедренном треугольнике, которая гласит, что если две стороны треугольника совпадают, их противоположные углы совпадают.
Вам будет предоставлена некоторая информация, например △ WHZ имеет Side HW ≅ Side HZ, что делает его равнобедренным треугольником.
Вас просят доказать ∠W ≅ ∠ Z.
| Выписки | Причины |
|---|---|
| HW ≅ HZ | Дано |
| Постройте биссектрису ∠H до точки I на стороне WZ | В каждом внутреннем ∠ есть ровно одна ∠ биссектриса |
| ∠WHI ≅ ∠ZHI | Определение, биссектриса |
| HI ≅ HI | Рефлексивное свойство равенства |
| HWI ≅ △ HZI | Боковой угол-боковой постулат |
| ∠W ≅ ∠ Z | Соответствующие части конгруэнтных треугольников равны (CPCTC) |
Это было пятиступенчатое доказательство.Большинство геометрических доказательств можно выполнить менее чем за 10 шагов. Если вы обнаружите, что проходите, скажем, семь или восемь шагов, возможно, вы идете по неэффективному или неправильному пути. Как ты можешь помочь себе?
Доказательства и рассуждения в две колонки
Одна из стратегий проработки двухстолбцового доказательства — сначала рассмотреть конец: что вас просят доказать? Не учитывая пронумерованный элемент, запишите это как утверждение для последней позиции. Обдумайте причину этого утверждения; что вам нужно, чтобы это доказать?
Еще одна важная деталь — нарисовать диаграмму или картинку, которая точно соответствует заданной информации.Посмотрите, что еще раскрывается данной информацией, например, дополнительные или дополнительные углы, прямые углы, которые вы, возможно, не заметили, или равенство углов или сторон.
Держите свои доводы под рукой, особенно если вы не выучили наизусть огромную коллекцию аксиом и теорем. Это могут быть постулаты, другие теоремы, определения или свойства. Помните, что свойства могут быть и вне геометрии, например, свойства равенства.
Будьте готовы изменить порядок. Не привязывайтесь к своему доказательству настолько, что вы упорно пытаетесь «заставить его работать», если оно привело вас по слепому пути.
Начни с простого. Если вы боретесь со сложным доказательством серьезной проблемы, посмотрите, сможете ли вы найти в нем более мелкие, более легко доказуемые фрагменты.
Самый верный способ научиться создавать доказательства из двух столбцов — это попрактиковаться в их написании.
демонстрируя
Если вы действительно уверены в своей способности писать доказательства из двух столбцов, вы можете немного похвастаться, написав Q.E.D. в конце — сокращение от латинского словосочетания quod erat manifestrandum , «то, что было продемонстрировано».»Это сигнализирует вашему учителю математики и другим, что вы закончили, вы выполнили доказательство.
Краткое содержание урока
Теперь, когда вы просмотрели обе колонки сверху вниз в этой части, вы можете понять и оценить ценность доказательств в математических рассуждениях. Вы также можете распознать и назвать три вида математических доказательств, определить элементы доказательств с двумя столбцами и даже написать собственное доказательство с двумя столбцами.
Следующий урок:
Поперечные сечения в геометрии
Серия умножения: числовые массивы
Использование массивов для исследования чисел
Массивы — это полезные модели для умножения, которые можно использовать по-разному, от высоко структурированных уроков до игр и открытых исследований.Массив формируется путем размещения набора объектов в строки и столбцы. Каждый столбец должен содержать такое же количество объектов, что и другие столбцы, и каждая строка должна иметь то же количество объектов, что и другие строки.
Следующий массив, состоящий из четырех столбцов и трех строк, может использоваться для представления числового предложения 3 x 4 = 12.
Номер здания Факты
Массивы можно использовать для конструктивного построения фактов умножения. Прежде чем сверлить и запоминать таблицы, дети должны понять, как эти факты выводятся.Например, постепенно добавляя еще один столбец из трех объектов, дети могут построить себе трехкратные таблицы. Это представление не только помогает понять процесс, но и дает визуальное изображение для детей, на которых можно рисовать, когда они начнут использовать и запоминать основные числовые факты.
Шансы и эвены
Понятия нечетных и четных чисел несколько сбивают с толку многих маленьких детей, поэтому крайне важно иметь метод моделирования чисел, который ясно показывает разницу между шансами и четными числами.Четные числа можно преобразовать в двухстрочные массивы, а нечетные — нельзя — всегда остается один элемент. Составление двух строк подчеркивает тот факт, что четные числа всегда делятся на два.
Факторы исследования
Другой подход к обнаружению множителей чисел — начать с определенного целого числа и создать как можно больше различных прямоугольных массивов — см. Задачу «Создание фигур». (Прямоугольники включают квадраты.) Например, для числа 12 возможными прямоугольными массивами являются:Таким образом, мы находим, что делители 12 равны: 3, 4, 2, 6, 1 и 12.
Подобное изучение факторов приведет к открытию того, что некоторые числа могут быть преобразованы в несколько массивов (то есть составные числа), а некоторые числа могут быть представлены только однострочными массивами (то есть простыми числами).
Еще одно исследование факторов с использованием массивов — это поиск чисел, которые могут образовывать квадратные массивы; а именно квадратные числа.
Сетка может быть полезна для записи результатов таких исследований. Задачи, подобные приведенным ниже, могут закрепить открытия, сделанные маленькими детьми.
Матрицы и матричная алгебра — Статистика Как к
Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):
- Матричная алгебра: введение
- Добавление матрицы: больше примеров
- Умножение матриц
- Определение сингулярной матрицы
- Матрица идентичности
- Что такое обратная матрица?
- Собственные значения и собственные векторы
- Расширенные матрицы
- Определитель матрицы
- Диагональная матрица
- Что такое симметричная и кососимметричная матрицы?
- Что такое матрица транспонирования?
- Что такое матрица дисперсии-ковариации?
- Корреляционные матрицы
- Идемпотентная матрица.
Матрица — это прямоугольный массив чисел, упорядоченный по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:
Преобразование в матричную алгебру в основном просто включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, которые появляются в матрице, называются элементами матрицы .
: Обозначение
Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список вроде этого: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы соблюсти соглашение.
Некоторые из наиболее распространенных терминов, с которыми вы столкнетесь при работе с матрицами:
- Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, в которой есть единицы.
- Скаляр : любое действительное число.
- Матрица Функция: скаляр, умноженный на матрицу, чтобы получить другую матрицу.
Матрицы идентичности. Изображение: Википедия.com.
Матричная алгебра: сложение и вычитание
Размер матрицы (т. Е. 2 x 2) также называется размером матрицы или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размерность должна быть точно так же . Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одном и том же месте (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Примечание к обозначениям: рабочий лист (например, в Excel) использует буквы столбцов (ABCD) и номера строк (123), чтобы указать местоположение ячейки, например A1 или D2. Для матриц типично использовать обозначение типа g ij , что означает i-ю строку и j-й столбец матрицы G.
Матричное вычитание работает точно так же.
В начало
Матричное дополнение — это всего лишь серия дополнений. Для матрицы 2 × 2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом положении.
- Сложите верхние правые числа и запишите сумму в верхнем правом углу.
- Сложите нижние левые числа вместе и запишите сумму в нижнем левом углу.
- Сложите нижние правые числа вместе и запишите сумму в правом нижнем углу:
Используйте ту же процедуру для матрицы 2 × 3:
Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Вышеупомянутый метод иногда называют «начальным суммированием», поскольку вы просто складываете записи и фиксируете результат.
Другой способ подумать об этом…
Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z. И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.
Сложение матрицы для неравных размеров
Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод.Один из таких приемов — прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q является матрицей размера (m + p) × (n + q):
Например:
В начало
Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14
Результат четырех умножений дает числа в новой матрице справа.
Умножение матриц: две матрицы
Когда вы хотите перемножить две матрицы, процесс становится немного сложнее. Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Если все это звучит немного сложно, в этом (очень коротком) видео показано, как это делается:
Вы можете выполнить матричное умножение двух матриц, только если количество столбцов в первой матрице равно количеству строк в вторая матрица.Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете умножить несколько матриц вместе.
Microsoft Excel также может выполнять умножение матриц с помощью функций «массива».Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
В начало
Быстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):
Существуют и другие типы сингулярных матриц, некоторые из которых не так-то легко обнаружить.Следовательно, необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет инверсии.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов. Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Особая матрица — это квадратная матрица, но не все квадратные матрицы сингулярны.
Необратимые матрицы
Если квадратная матрица не имеет обратной, то это особая матрица.
Обратная матрица — это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, получится единичная матрица , , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.
Матрицы идентичности. Изображение: Wikipedia.com.
Если вы не знакомы с поиском инверсий, вы можете посмотреть это короткое видео:
Определитель нуля
Определитель — это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc.
Эта простая матрица 2 × 2 сингулярна, потому что ее определитель равен нулю:
В начало
Единичная матрица — это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева направо снизу и нулями в остальных местах. Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным.Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т. Е. 10 * 1 = 10 ). Говоря более формально, если x — действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x. По той же логике матрица идентичности I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n . На главной диагонали всегда будут единицы, а оставшиеся пробелы — нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Дополнительная идентификационная матрица
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности.Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули. Поэтому их иногда называют нулевой матрицей .
Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началу
Обратные матрицы — это то же самое, что и обратные. В элементарной алгебре (а может быть, и раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.
Изображение предоставлено LTU
Если вы умножите одну матрицу на ее обратную, вы получите матричный эквивалент 1: Identity Matrix , которая в основном представляет собой матрицу с единицами и нулями.
Поиск обратной матрицы состоит из нескольких шагов. Посмотрите это короткое видео о том, как найти обратную матрицу, или выполните следующие действия:
Шаг 1: Найдите адъюгат матрицы. Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:
Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) — (b * c).
Шаг 3: Умножить 1 / определитель * адъюгат. .
Проверка ответа
Вы можете проверить свой ответ с помощью умножения матриц. Умножьте свою матрицу ответов на исходную матрицу, и вы получите единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
В начало
Собственное значение (λ) — это специальный скаляр, используемый при матричном умножении и имеющий особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем.Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением . Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его по вектору x .
Пример собственного значения
В следующем примере 5 — собственное значение A, а (1,2) — собственный вектор:
Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что если бы вместо новой матрицы nx 1 можно было получить ответ с тем же вектором, который вы умножили на вместе с новым скаляром?
Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр — собственным значением.Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в так называемом разложении по собственным значениям . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:
Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:
Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) — (3) (3)
Упрощая, получаем:
-5 — 5λ + λ + λ 2 — 9
= λ 2 — 4λ — 14
Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ 2 — 4λ — 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором.Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2
Ответ : 2 + 3√2 и 2-3√2
Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.
В начало
На изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений и, собственно, именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11
Можно поместить в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.
У вас нет , есть , чтобы использовать вертикальную черту в расширенной матрице. Обычно матрицы вообще не содержат линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.
Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно укажите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, а затем укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, а затем укажите «z.«Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y — 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце, поставив перед знаком равенства.
-1x + 7y + 3 = 0
2x + 4y — 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом шаге стоит отрицательный знак, просто сделайте константу отрицательным числом.
В начало
Определитель матрицы — это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:
- Это действительное число. Сюда входят отрицательные числа.
- Определители существуют только для квадратных матриц.
- Обратная матрица существует только для матриц с ненулевыми определителями.
Символ для определителя матрицы A — это | A |, который также является тем же символом, который используется для абсолютного значения, хотя эти два символа не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2 × 2
Формула определителя матрицы 2 × 2 — ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3 × 3
Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:
= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
В основном здесь происходит умножение a, b и d на детерминанты меньших 2×2 в матрице 3×3. Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Определитель матрицы 4 × 4
Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые находятся в матрице 4 × 4.В виде формулы:
Вернуться к началу
Диагональная матрица — это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.
Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.
Единичная матрица, которая содержит все единиц по диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е.2,2,2 или 9,9,9), является скалярным кратным единичной матрицы и также может быть классифицировано как диагональное.
Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n — порядок матрицы. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Обозначение
Обозначение, обычно используемое для описания диагональной матрицы: diag (a, b, c) , где abc представляет собой числа в первой диагонали.Для приведенной выше матрицы это обозначение будет diag (3,2,4). .
Верхняя и нижняя треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. Нижнетреугольная матрица имеет числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.
Диагональная матрица — это матрица с нижней диагональю и матрица с нижней диагональю.
Прямоугольные диагональные матрицы
Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n . Существуют и другие формы, которые обычно не используются, например, прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
В начало
Транспонирование матрицы (или транспонирование матрицы) — это как раз то место, где вы переключаете все строки матрицы в столбцы.Матрицы транспонирования полезны при комплексном умножении.
Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r». Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица — это частный случай транспонированной матрицы; он равен своей транспонированной матрице.
Говоря более формально, A = A T .
Символы для транспонированной матрицы
Обычный символ для транспонированной матрицы — A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и.
Свойства матриц транспонирования
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным). Основные свойства матриц:
- (A T ) T = A: транспонированная матрица транспонирования является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.
- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент — это величина, которая может умножать матрицу).
- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, совпадает с произведением их матриц транспонирования в обратном порядке.
- (A -1 ) T = (A T ) -1 : транспонирование и инверсия матрицы могут выполняться в любом порядке.
В начало
Симметричная матрица — это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо. Представьте себе складку в матрице по диагонали (не включайте числа в действительную диагональ). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом по линии симметрии ( всегда ведущая диагональ), как в примере справа , у вас симметричная матрица.
Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной. В случае транспонирования матрицы первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда альтернативное определение, что симметричная матрица равна ее транспонированию.С математической точки зрения, M = M T , где M T — транспонированная матрица.
Максимальное количество номеров
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ — это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.
Диагональные матрицы
Диагональная матрица — это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.
Что такое асимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:
Математически асимметричная матрица удовлетворяет условию a ij = -a ji .Например, возьмите запись в строке 3, столбце 2, которая равна 4. Его симметричным аналогом является -4 в строке 2, столбце 3. Это условие также можно записать в терминах его транспонированной матрицы: A T = — А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T это транспонированная матрица.
Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми. Это потому, что из i, i = −a i, i следует i, i = 0.
Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:
Добавление двух кососимметричных матриц все вместе.
Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг — убедиться, что все элементы на главной диагонали равны нулю (то, что невозможно «доказать» математически!).Второй шаг — сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a ij = — a ji .
Косоэрмитский
Косоэрмитова матрица по сути такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.
Косоэрмитова матрица, показывающая комплексные числа.
Фактически, кососимметричный и косоэрмитовый эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началу
Матрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) — это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Разница — это мера того, насколько разбросаны данные. Ковариация — это мера того, насколько две случайные величины перемещаются вместе в одном направлении.
Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариантной матрицы, потому что, по сути, эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках.Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Создание матрицы дисперсии-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1).Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Если вы хотите сделать один вручную:
Шаг 1: Вставьте отклонения для ваших данных в диагонали матрицы.
Шаг 2: Рассчитайте ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A).


 Мотивация к учебной деятельности.
Мотивация к учебной деятельности.
 Актуализация знаний и фиксирование затруднений в пробном учебном материале.
Актуализация знаний и фиксирование затруднений в пробном учебном материале.
 Выражения читайте по-разному.
Выражения читайте по-разному.
 Реализация построенного проекта.
Реализация построенного проекта.


 Включение в систему знаний и повторение (предложить из набора заданий выбрать те, которые содержат новый алгоритм или новые понятия).
Включение в систему знаний и повторение (предложить из набора заданий выбрать те, которые содержат новый алгоритм или новые понятия). СЛАЙД 16.
СЛАЙД 16. Я проверю, поставлю свою оценку. Если оценки совпадут, то вы научились правильно оценивать себя.
Я проверю, поставлю свою оценку. Если оценки совпадут, то вы научились правильно оценивать себя. 47 № 4(б), 6
47 № 4(б), 6 Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения.
Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения.