«Сложение и вычитание в пределах 1000». 3 класс
ПОДГОТОВИТЕЛЬНЫЙ ВАРИАНТ № 1 ПРОВЕРОЧНОЙ РАБОТЫ
Реши примеры столбиком.
737 + 246 547 + 337
134 + 628 238 + 548
Реши примеры столбиком.
794 – 265 542 – 113
971 – 632 896 – 549
Реши примеры.
560 + 40 670 + 30
500 – 40 600 – 30
Запиши число, в котором:
9 ед. 3 разряда 1 ед. 2 разряда 8 ед. 1 разряда
2 ед. 3 разряда 8 ед. 1 разряда
1 ед. 1 разряда 8 ед. 2 разряда 6 ед. 3 разряда
6 ед. 3 разряда 4 ед. 1 разряда
ПОДГОТОВИТЕЛЬНЫЙ ВАРИАНТ № 1 ПРОВЕРОЧНОЙ РАБОТЫ
Реши примеры столбиком.
737 + 246 547 + 337
134 + 628 238 + 548
Реши примеры столбиком.
794 – 265 542 – 113
971 – 632 896 – 549
Реши примеры.
560 + 40 670 + 30
500 – 40 600 – 30
Запиши число, в котором:
9 ед. 3 разряда 1 ед. 2 разряда 8 ед. 1 разряда
2 ед. 3 разряда 8 ед. 1 разряда
1 ед. 1 разряда 8 ед. 2 разряда 6 ед. 3 разряда
6 ед. 3 разряда 4 ед. 1 разряда
ПОДГОТОВИТЕЛЬНЫЙ ВАРИАНТ № 2 ПРОВЕРОЧНОЙ РАБОТЫ
Реши примеры столбиком.
238 + 624 316 + 376
636 + 157 148 + 149
Реши примеры столбиком.
653 – 515 694 – 359
763 – 119 983 – 263
Реши примеры.
300 – 90 500 – 70
340 + 60 210 + 90
Запиши число, в котором:
5 ед. 3 разряда
3 ед. 3 разряда 6 ед. 2 разряда 4 ед. 1 разряда
1 ед. 3 разряда 6 ед. 2 разряда
8 ед. 1 разряда 5 ед. 2 разряда 1 ед. 3 разряда
ПОДГОТОВИТЕЛЬНЫЙ ВАРИАНТ № 2 ПРОВЕРОЧНОЙ РАБОТЫ
Реши примеры столбиком.
238 + 624 316 + 376
636 + 157 148 + 149
Реши примеры столбиком.
653 – 515 694 – 359
763 – 119 983 – 263
Реши примеры.
300 – 90 500 – 70
340 + 60 210 + 90
Запиши число, в котором:
5 ед. 3 разряда
3 ед. 3 разряда 6 ед. 2 разряда 4 ед. 1 разряда
1 ед. 3 разряда 6 ед. 2 разряда
8 ед. 1 разряда 5 ед. 2 разряда 1 ед. 3 разряда
Оценивание | |||
«5» | «4» | «3» | «2» |
выполнена без ошибок | 1-2 вычислительные ошибки | 3-4 вычислительные ошибки | 5 и более вычислительных ошибок |
Оценивание | |||
«5» | «4» | «3» | «2» |
выполнена без ошибок | 1-2 вычислительные ошибки | 3-4 вычислительные ошибки | 5 и более вычислительных ошибок |
Урок математики «Сложение и вычитание трёхзначных чисел в столбик»; 3 класс — Математика — Начальные классы
Учитель начальных классов
высшей квалификационной категории
МОУ
СОШ № 25 г.
о. Саранск
Республики Мордовия
Кулагина Г.И.
Конспект урока математики по теме « Сложение и вычитание трёхзначных чисел в столбик»
Цели: 1. Познакомить с алгоритмами письменных приёмов сложения и вычитания трёхзначных чи-
сел, аналогичных таким же приёмам при сложении и вычитании двузначных чисел.
2.Осуществлять проверку вычислений на основе знания о взаимосвязи действий сложения
и вычитания.
3. Решать на новом числовом концентре текстовые задачи изученного вида.
4. Систематическое повторение и закрепление ранее изученного.
Ход урока.
I. Мотивация к деятельности. Актуализация знаний.
( слайд 1)
1.Организационный момент.
Начинается урок, ( слайд 2)
Он пойти вам должен впрок.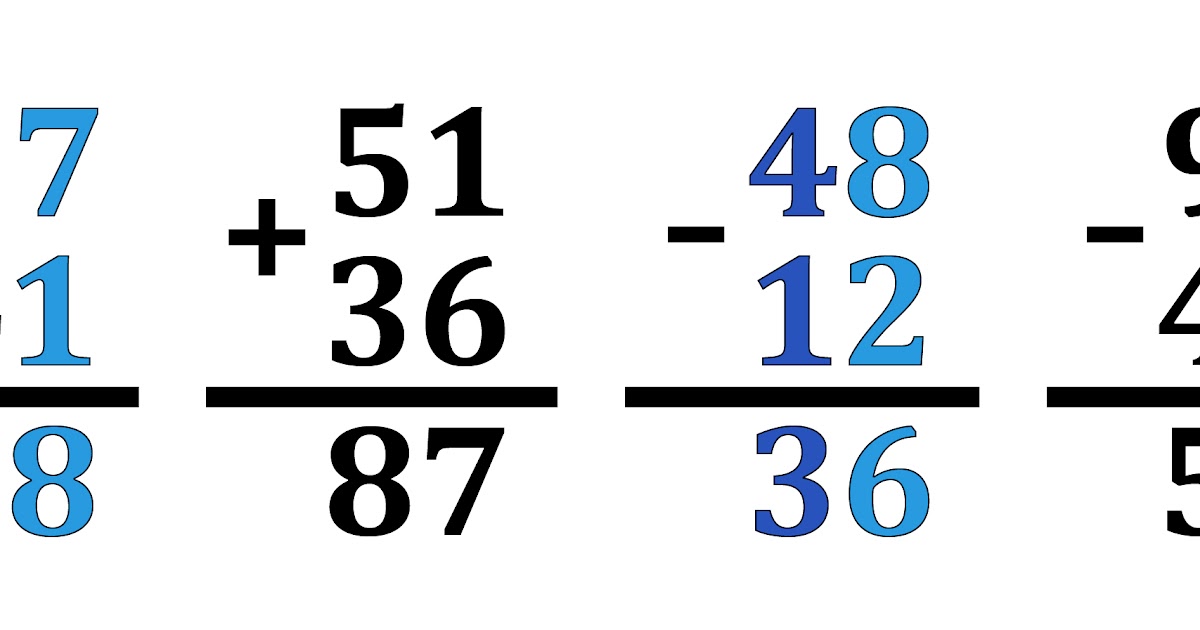
Постарайтесь всё понять,
Учитесь тайны открывать,
Ответы полные давайте
И на уроке не зевайте.
-Начинаем урок математики. На нашем уроке присутствуют гости. Поприветствуйте их. Настройтесь на отличную работу.
Сегодня мы будем совершать открытия, решать примеры, задачи, развивать внимание, память, логическое мышление. Дадим себе установку на урок (дети произносят хором):
-Будем открывать новые знания, стараться выполнять все задания правильно и красиво.
— Сегодня вы продолжаете путешествие по стране трёхзначных чисел. Что вы умеете делать с трёхзначными числами? ( Читать, записывать, изображать с помощью графической модели, представлять в виде суммы разрядных слагаемых, сравнивать, выполнять устные приёмы сложения и вычитания)
— Можете ли вы назвать себя знатоками трёхзначных или вам не хватает каких-то знаний?(Не хватает)
—
—Для чего? ( Они могут пригодиться при открытии нового)
-Приступим?
2.
Фронтальная работа.
-Ребята, сегодня я нашла на столе письмо.( слайд 3) Оно адресовано нашему классу. Давайте прочтём его.
-« Здравствуйте, ребята. Я знаю, что вы большие молодцы и всегда помогаете всем в трудную минуту. Так вот, она у меня настала. Помогите, пожалуйста, мне сделать новое открытие и
выполнить все задания, которые приготовили для меня Витя и Костя. Иначе они не возьмут меня с собой в цирк, а я так об этом мечтала. Лика».
А кто такие Лика, Витя и Костя?( Наши друзья, вместе с которыми мы совершаем пятое путешествие по стране Математика.
-Ну что, ребята, поможем Лике? (Да)
-Посмотрите на слайд ( Даны ряды чисел)( слайд 4)
76, 53, 458 , 27, 99, 31, 52, 48.
548, 460, 752, 300, 76, 600, 953.
300, 100, 542, 700, 900, 200, 800.
854, 246, 927, 400, 299, 762, 127.
325, 121, 102, 534, 873, 689.
-Как вы думаете, какое задание можно выполнить с данными рядами чисел? (Найти лишнее число в каждой группе чисел)
-Найдём эти числа и объясним, почему они лишние.
458, 76, 542, 400, 102. ( слайд 5)
О В Н С О
— Посмотрите на оставшийся ряд чисел, он не обычен. Здесь какая-то зашифрованная запись. Расположите числа в порядке убывания, запишите в тетради, угадайте зашифрованное слово.
-Прочитайте хором, какое слово получилось. (Носов) Молодцы.
-Что же мы смогли расшифровать?( Николай Носов – автор повести «Витя Малеев в школе и дома», героями которой являются Витя, Костя и Лика.
_ Придумайте задания для этого ряда.( слайд 6) (Расположить числа в порядке возрастания, сравнить числа, назвать самое большое( самое маленькое число), рассказать о каждом числе( сколько в нём разрядных единиц. Назвать предыдущее, последующее число) (Учащиеся дают друг другу задания и контролируют полученный результат)
-А теперь запишите все трёхзначные числа
этого ряда в виде суммы разрядных
слагаемых.
( 1 уч- ся выполняет на доске,
а остальные в тетради) ( слайд 7)
— Сколько разрядов в каждом числе?( три- сотни, десятки, единицы)
( Учитель выставляет опорный сигнал обозначения трёхзначных чисел- С Д Е )
-Сколько слагаемых в каждой сумме?( 3,2,1) Почему не везде одинаковое количество слагаемых?( отсутствуют разряды)
-Итак, мы с вами повторили нумерацию и разрядные слагаемые трёхзначных чисел.
II. Формулирование темы и целей урока.
Самостоятельная работа.
(Во время выполнения задания дети фиксируют затруднение при решении примеров последнего столбика).
–На предыдущих уроках вы решали много примеров на сложение и вычитание. Давайте решим несколько выражений.( № 1, с.58).Вы видите их на слайде.( 2 примера проговорим вслух, остальные решите самостоятельно) ( слайд 8)
426+231( 4с.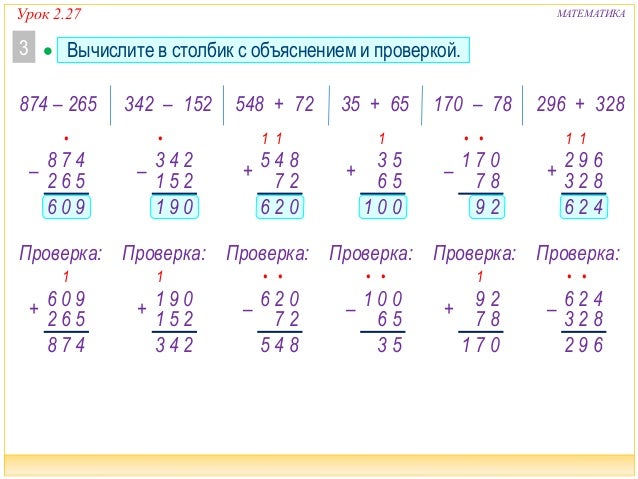
+2с., 2д.+3д., 6 ед.+ 1ед. 420+80
380+ 50 531+19!
678- 345 500-600 410- 30 534-19!
-Справились ли вы с решением всех примеров? (нет) А что же вызвало затруднение? ( Мы умеем решать примеры на сложение и вычитание трёхзначных чисел, сводимых к вычислениям в пределах100, где не было перехода через разрядную единицу, а выражения последнего столбика мы не умеем решать)
— Прочитайте ответы, которые у вас получились во 2, 3 столбиках. ( чтение ответов «цепочкой»)
А, кто справился с последним столбиком назовите свои ответы. ( Учитель на доске фиксирует все ответы и обводит правильный ответ и просит обосновать свое решение тех, у кого результат верный ( сослаться на правило) (Не могут этого сделать)
— Что надо сделать?( Остановиться и подумать)
2. – Если устно трудно выполнить
сложение и вычитание чисел такого вида,
как вы предлагаете найти значение этих
выражений?( Письменно.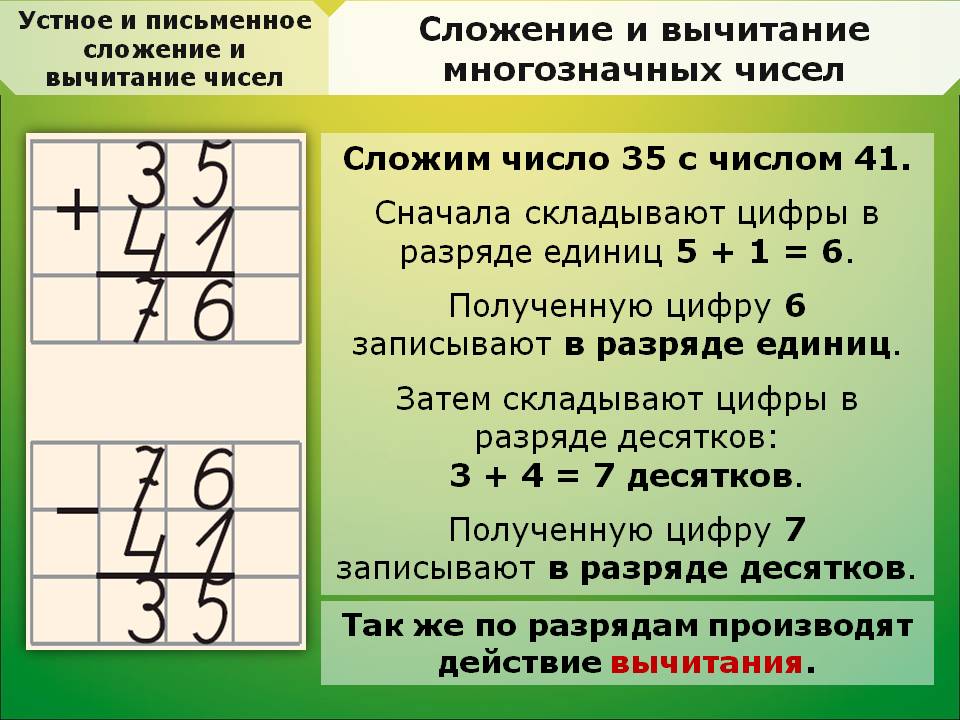
-Какие числа мы умеем складывать и вычитать в столбик?( двузначные)
-Объясните , как наши знакомые Витя и Костя складывали и вычитали числа?
С лайд – 31 31 ( слайд 9)
1 9
1 2
— Каким алгоритмом мы пользуемся при записи и вычислениях ? (Единицы пишу под единицами…, Начинаем с единиц…
(Учитель вывешивает на доску опорный сигнал сложения и вычитания двузначных чисел )
-А умеем ли мы складывать и вычитать трёхзначные числа в столбик? (Нет)
-Значит, чему же мы с вами должны научиться сегодня на уроке? ( Складывать и вычитать трёхзначные числа в столбик).
На слайде появляется тема: Сложение и вычитание трёхзначных чисел в столбик
III. Открытие нового знания.
1.
— Мы выведем алгоритм сложения и
вычитания трёхзначных чисел в столбик
и научимся им пользоваться.
-Вы будете открывать новый алгоритм или уточнять уже известный? ( Уточнять)
— Как звучит первый шаг в алгоритме сложения двузначных чисел? ( Пишу единицы под единицами, десятки под десятками).
-Нужно ли дополнить этот шаг для трёхзначных чисел? (Да)
— Как?( Пишу единицы под единицами, десятки под десятками, сотни под сотнями).
— Что вы будете делать дальше?( Складывать единицы) А затем? ( Десятки)
_ А следующий шаг вы сформулируете самостоятельно.
-Давайте составим план вашей дальней шей работы:
1. Записать выражение 531+ 19 в столбик и вычислить.2.Сформулировать недостающий шаг.
3.Составить опорный сигнал для сложения трехзначных чисел.
( Учитель фиксирует план на слайде) ( слайд 11)
Реализация построенного плана ( работа в группах)
— Работать вы будете в группах.
( Учащимися должен быть получен опорный сигнал: ( слайд 12)
С
Д
Е
-Представьте свои результаты. Объясните свои действия.( У доски отвечают по одному представителю от группы).
-Итак, какой же шаг добавляется третьим. ( Учащимися должен быть устно сформулирован шаг: « Складываю сотни, результат пишу под сотнями) ( слайд)
-Ребята. скажите, а для вычитания трёхзначных чисел подойдёт составленный вами опорный сигнал7 Как его можно изменить, чтобы он подошёл и для вычитания?( Добавить в сигнал минус)
( Слайд с общей опорной схемой : ( слайд 13)
С
Д
Е
-А теперь сформулируйте общий алгоритм сложения и вычитания трёхзначных чисел.
( Дети называют каждый шаг, учитель фиксирует его на слайде) ( слайд 14)
Алгоритм сложения и вычитания
трёхзначных чисел..jpg)
1.Пишу единицы…
2.Складываю (вычитаю) единицы…
Результат пишу под единицами.
3.Складываю ( вычитаю) десятки…
Результат пишу под десятками.
4.Складываю ( вычитаю) сотни…
Результат пишу под сотнями.
5.Читаю ответ…
-Сравните полученный алгоритм с выводами в учебнике. Прочитайте их самостоятельно на с.58, в № 2, № 3.
_ Мы всё сделали правильно?( Да) Скажите, знаете ли вы теперь, как правильно складывать и вычитать трёхзначные числа в столбик? ( да).
IV. Физкультминутка.
-Вот пришла пора отдохнуть и нашим глазам. ( Презентация с музыкой физкультминутки для глаз)
V. Первичное закрепление с проговариванием во внешней речи.
1. —Можно ли сказать, что мы уже всё сделали на уроке? (нет)
— Какую цель вы поставите на оставшиеся этапы? ( Научиться складывать и вычитать трёхзначные числа в столбик)
-Что для этого надо сделать? ( Потренироваться
в использовании нового алгоритма).
-Сделаем это, решая примеры № 4( с. 58)
2 примера на доске 1 уч-ся;
2 примера с места с комментированием с места по одному примеру;
2. — Вы поработали все вместе, теперь давайте поработаем в парах. ( следующие 2 примера)
-В парах вы будете работать следующим образом:1-ое выражение объясняют своему соседу по парте ученики первого варианта, 2-ое – ученики второго варианта, пишут оба варианта)
( Проверка по образцу- эталону на слайде) (слайд 15)
— Те ребята, которые допустили ошибку, найдите место ошибки, проанализируйте и исправьте её.
Самостоятельная работа с самопроверкой по эталону.
— Вы поработали вместе, в парах, а что теперь необходимо сделать? ( Поработать самостоятельно)
— Выполните №4 (7,8 примеры)
— Проверьте.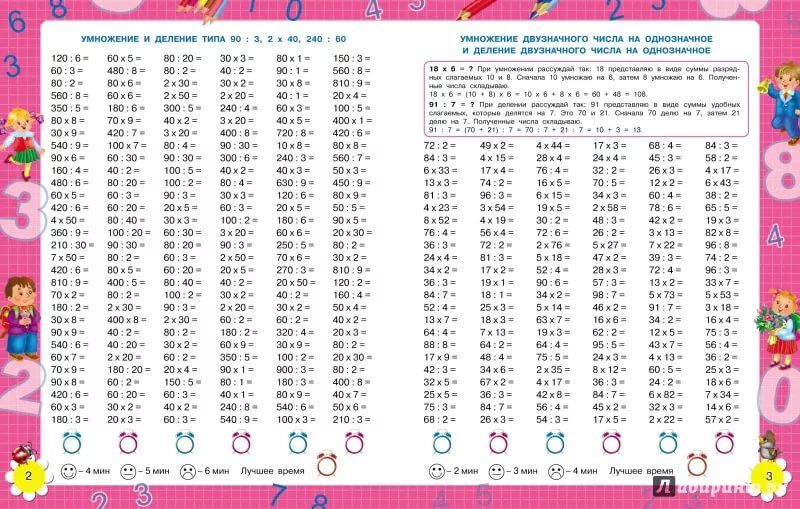
( На экране эталон для
самопроверки: ( слайд 16)
У кого есть ошибки, исправьте их пожалуйста.
— Молодцы. Ребят, которые допустили ошибку, я тоже могу похвалить. Ведь вы сами нашли свою ошибку и знаете, над чем вам ещё нужно поработать.
VI. Повторение и закрепление изученного ранее.
—Можете ли вы использовать умения, приобретенные на уроке при решении задач? Я предлагаю вам решить задачу.
Решение задач №5 ( а) – решение на доске и в тетрадях после предварительного анализа.
— Прочитайте задачу. Подчеркните числа и слова, которые к ним относятся. Найдите вопрос.
«Оденьте» схему.( На доске 1 уч-ся)
а
выдали осталось ( слайд 17)
b * 30 ?
-Запишите решение. ( 1 уч-ся на доске, остальные в тетради)
— Решите задачу под буквой в самостоятельно в парах.
( Запись
вариантов решения задачи на доске — по
одному учащемуся от ряда. Сравнение и
выбор правильного варианта решения).
VII. Рефлексия учебной деятельности на уроке.
—Какие цели вы сегодня ставили? Достигли вы этих целей? У кого остались затруднения по теме?
— Какой же новый способ сложения и вычитания трёхзначных чисел живёт в стране Математика? ( В столбик)
Можно ли сказать, что вы сегодня были настоящими учениками? ( слайд 18)
— Оцените цветом свою работу на уроке. Зелёный цвет показывает, что ваша работа была успешной и дорога к следующим знаниям для вас открыта. Если у вас ещё есть небольшие затруднения и вам нужно немного поработать над новым алгоритмом – покажите жёлтую карточку. Красный покажет, что путь к новым знаниям пока закрыт.
Помогли ли мы Лике ?(Да) Молодцы.
VIII. Домашнее задание.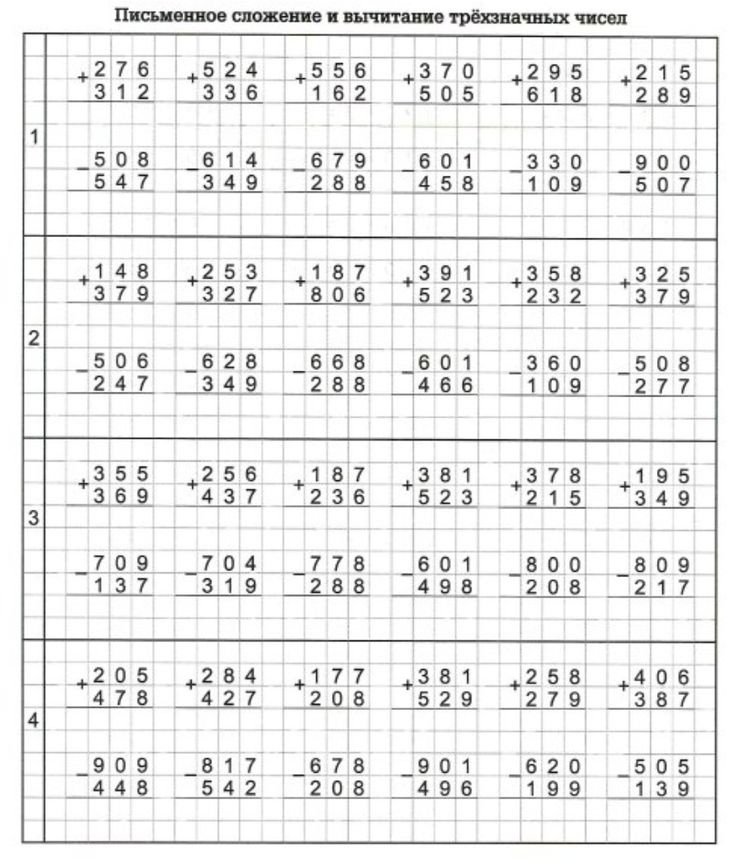
С. 59,№4 ( последний столбик),№6 – инвариант;
№7 – по желанию- вариант. ( слайд 19)
Завершается урок, ( слайд 20)
Он пошёл ребятам впрок?
Постарались всё понять?
Учились тайны открывать?
Ответы полные давали?
На уроке не зевали?
— Спасибо за урок. ( слайд 21)
Вычитание целых чисел: операция, обратная сложению
Результаты обучения
- Вычитание однозначных чисел и проверка решения с помощью сложения
- Использовать столбцы, представляющие разрядность, для вычитания многозначных чисел
Сложение и вычитание являются обратными операциями. Сложение отменяет вычитание, а вычитание отменяет сложение.
Мы знаем [латекс]7 — 3=4[/латекс], потому что [латекс]4+3=7[/латекс]. Знание всех фактов сложения чисел поможет с вычитанием. Затем мы можем проверить вычитание, сложив.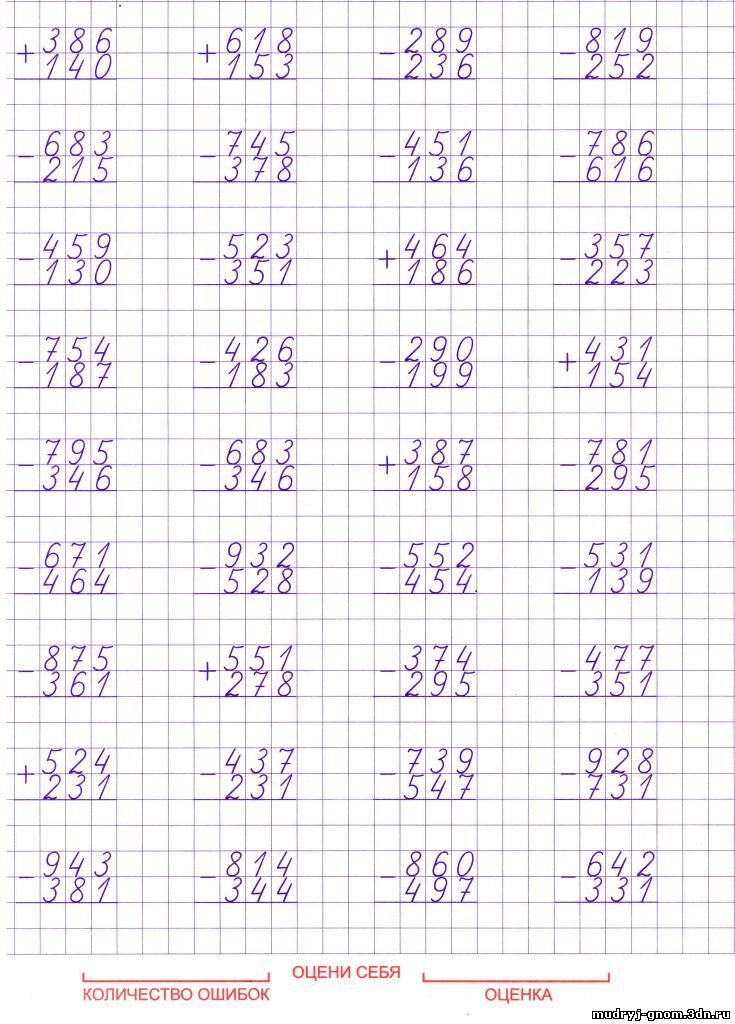
В приведенных выше примерах наши вычитания можно проверить сложением.
| [латекс]7-3=4[/латекс] | потому что | [латекс]4+3=7[/латекс] |
| [латекс]13-8=5[/латекс] | потому что | [латекс]5+8=13[/латекс] |
| [латекс]43-26=17[/латекс] | потому что | [латекс]17+26=43[/латекс] |
Пример
Вычтите и затем проверьте, добавив:
- [латекс]9 — 7[/латекс]
- [латекс]8 — 3[/латекс]
Решение
| 1. | |
| [латекс]9 — 7[/латекс] | |
| Вычесть 7 из 9. | [латекс]2[/латекс] |
| Проверить с дополнением. [латекс]2+7=9\четверка\галочка [/латекс] |
| 2. | |
| [латекс]8 — 3[/латекс] | |
Вычесть 3 из 8.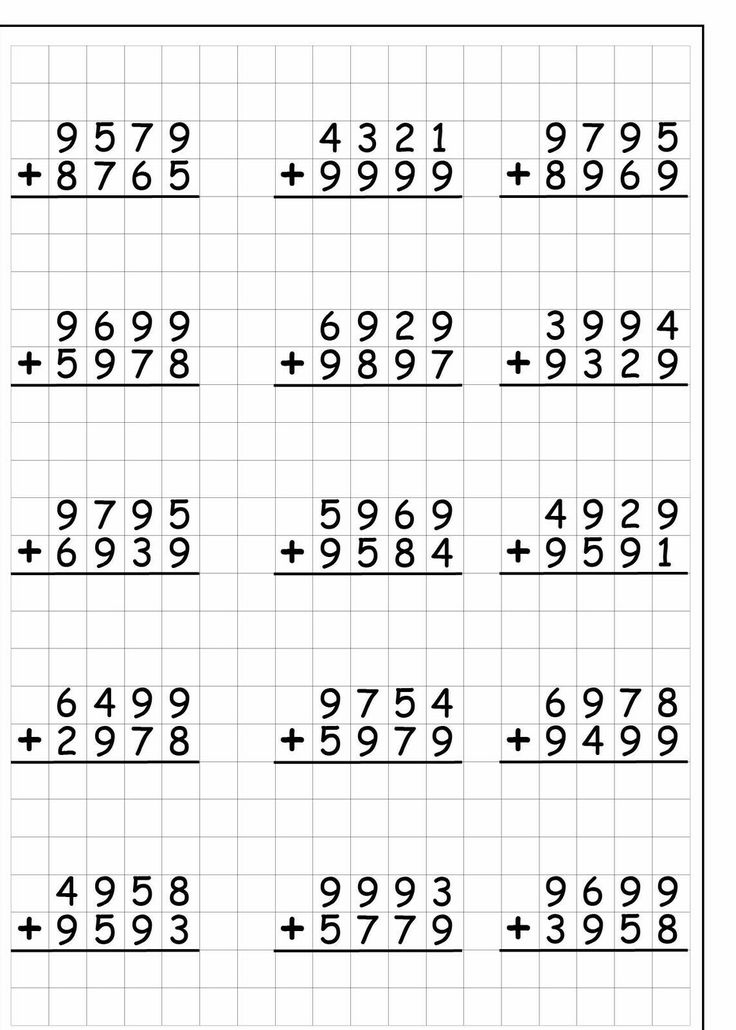 | [латекс]5[/латекс] |
| Проверить с дополнением. [латекс]5+3=8\четверка\галочка [/латекс] |
ПОПРОБУЙТЕ
Чтобы вычесть числа, состоящие из более чем одной цифры, обычно проще писать числа вертикально в столбцах, как мы это делали для сложения. Выровняйте цифры по разрядности, а затем вычтите каждый столбец, начиная с единиц, и затем работайте влево.
Пример
Вычтите, а затем проверьте, добавив: [латекс]89 — 61[/латекс].
Показать решение
ПОПРОБУЙТЕ
Когда мы моделировали вычитание [латекс]26[/латекс] из [латекс]43[/латекс], мы обменивали [латекс]1[/латекс] десять на [латекс]10[/ латекс]. Когда мы делаем это без модели, мы говорим, что заимствуем [латекс]1[/латекс] из разряда десятков и добавляем [латекс]10[/латекс] к разряду единиц.
Найдите разность целых чисел
- Запишите числа так, чтобы каждый разряд располагался вертикально.
- Вычтите цифры из каждого разряда. Работайте справа налево, начиная с места единиц. Если цифра сверху меньше, чем цифра снизу, заимствуйте по мере необходимости.
- Продолжайте вычитать значение каждого разряда справа налево, при необходимости заимствуя.
- Проверить добавлением.
упражнение
Вычесть: [латекс]43 — 26[/латекс].
Показать раствор
попробуйте
Пример
Вычтите, а затем проверьте, добавив: [латекс]207 — 64[/латекс].
Показать раствор
попробуйте
Вычтите, а затем проверьте, добавив: [латекс]439- 52[/латекс].
Показать раствор
Вычтите, а затем проверьте, добавив: [латекс]318 — 75[/латекс].
Показать раствор
Пример
Вычтите, а затем проверьте, добавив: [латекс]910 — 586[/латекс].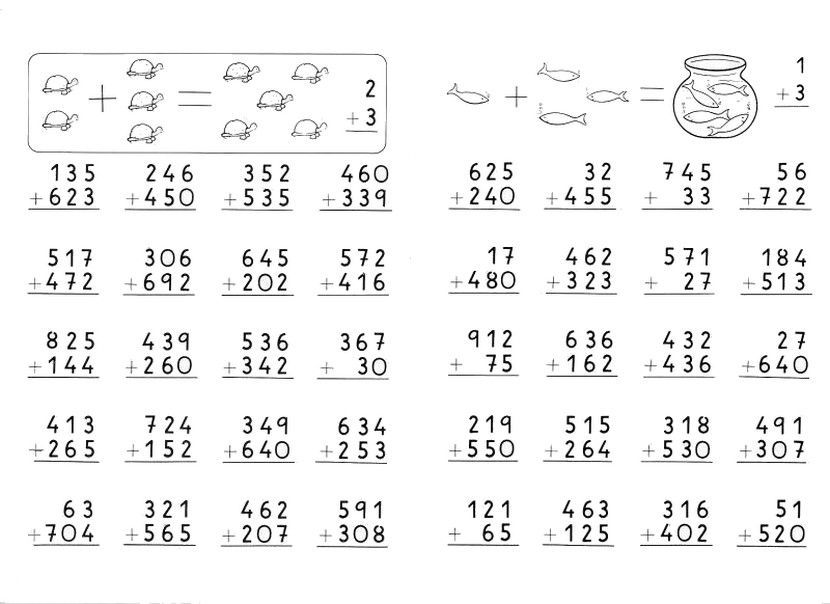
Показать раствор
попробуйте
Пример
Вычтите и затем проверьте, добавив: [латекс]2,162 — 479[/латекс].
Показать раствор
попробовать
4.5: Алгоритмы вычитания — математика Libretexts
Вам понадобится: Базовые блоки (Материальные карты 4-15)
Самая распространенная подраздел Algorithm — 904 904. Алгоитм , когда вы начинаете в столбце единиц и вычитаете, затем перемещаетесь влево и вычитаете в каждом столбце. Проблема, конечно, когда верхняя цифра меньше нижней и приходится перегруппировываться. Выньте свои блоки Base Ten сейчас, чтобы увидеть, что происходит на самом деле.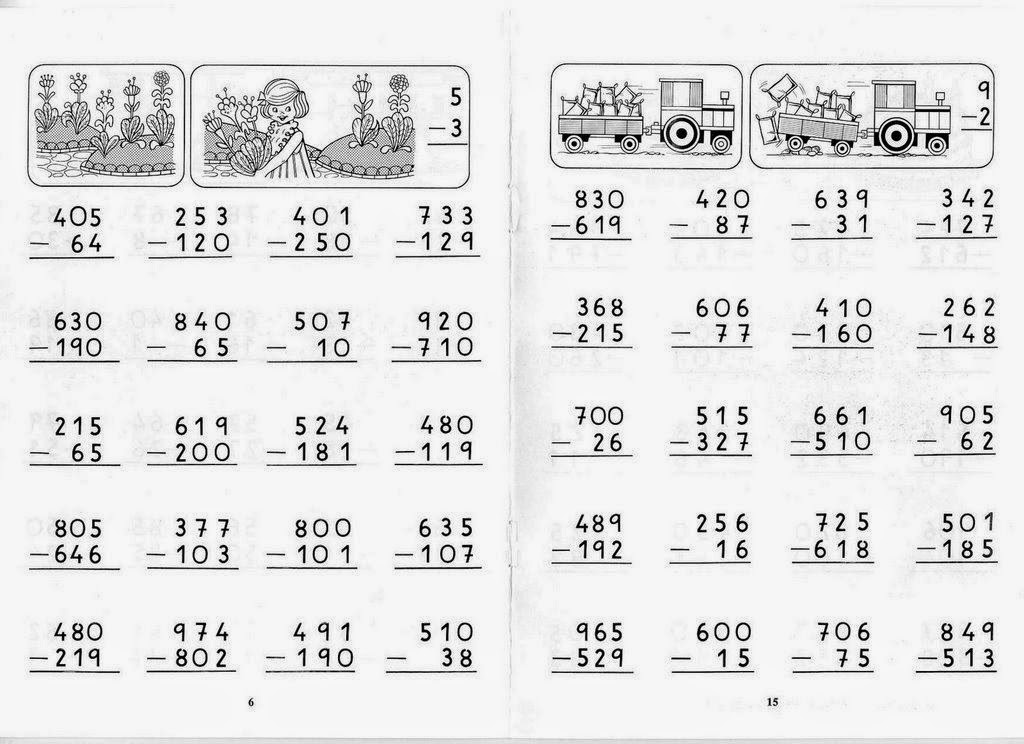
Рассмотрим задачу на вычитание 425 –158. Из наших знаний о разрядности мы знаем, что 425 равно 4 \(\times\) 100 + 2 \(\times\) 10 + 5 (или 400 + 20 + 5), а 158 равно 1 \(\times\) 100 + 5 \(\раз\) 10 + 8 (или 100 + 50 + 8). Используя блоки Base Ten, 425 будет представлено 4 плоскими, 2 длинными и 5 единицами, тогда как 158 будет представлено 1 плоским, 5 длинными и 8 единицами. Итак, задачу вычитания можно представить следующим образом:
Используя базовые блоки \[\begin{aligned} (4 \text{ flat(s) } + 2 \text{ long(s) } + 5 \text { единица(ы) }) \\ \underline{– (1 \text{ плоская(ые) } + 5 \text{ длинная(ая) } + 8 \text{ единица(ы) })} \end{выровненная} \номер\]
Используя блоки, задача на вычитание показана ниже:
Мы не можем вычесть 8 единиц из 5 единиц, поэтому длинная заменяется на десять единиц, что дает 4 бемоля, 1 длинную и 15 единиц в уменьшении. Теперь мы также не можем вычесть 5 длинных из 1 длинной, поэтому 1 плоская грань обменивается на десять длинных, что дает 3 плоских, 11 длинных и 15 единиц в уменьшении.
Теперь мы можем вычитать в каждом столбце, как показано на следующей странице. Для вычитания можно использовать либо подход на вычет, либо подход с отсутствующими сложениями. Используйте свои базовые блоки, чтобы решить эти проблемы.
Использование базовых блоков \[\begin{aligned} &(3 \text{ flat(s) } + 11 \text{ long(s) } + 15 \text{ unit(s)}) \\ -& ( 1 \text{ плоские(ые) } + 5 \text{длинные(ые) } + 8 \text{единицы(и)}) \\ \hdashline &2 \text{ плоские(ые) } + 6 \text{ длинные( s) } + 7 \text{ unit(s)}) = \underline{267} \end{aligned} \nonumber \]
Задача на вычитание с использованием блоков показана ниже:
Поскольку мы работаем в десятичной системе счисления, ответ (разность) равен 267. Итак, 425 – 158 = 267,
Задача может быть решена с помощью таблицы, в которой между уменьшаемым и вычитаемым остается достаточно места, чтобы можно было произвести обмен в уменьшаемом. Обратите внимание на показанные шаги, если вы решаете эту проблему с помощью базовой диаграммы, как показано ниже.
Теперь мы выполним этот базовый алгоритм на разных основаниях. При вычитании обращайте внимание на основание! Например, в первом примере ниже вы должны обменять квартиру еще на 9 лонгов (поскольку это базовая девятка). Один из способов показать это — добавить 9(основание) к количеству уже имеющихся длин, поэтому я вычеркиваю 5 и добавляю 9, чтобы получить 14. Если вы пишете это таким образом, помните, что число, которое вы пишете, находится в базе десяти, а не в базе, в которой вы находитесь. работать в. Написать это, вероятно, проще всего, когда вы впервые начинаете вычитать. Более элегантный способ — записать его так же, как вы делаете это при работе с десятичным числом, то есть поставить 1 перед 5 в столбце длинных чисел, чтобы оно выглядело как 15 (это не означает пятнадцать), что в Базовая девятка представляет 14 длинных чисел (5 длинных + 9еще от обмена)! Показаны оба способа написания. Возможно, вы захотите использовать свои базовые блоки, чтобы помочь визуализировать фактические обмены.
Изучите следующие примеры. Проверьте каждый ответ, добавив ответ к вычитаемому, и убедитесь, что вы получили уменьшаемое!
Пример 1
| \(\begin{align} 253_{\text{девять}} \\ \underline{-182_{\text{девять}}} \end{выровнено}\) |
Пример 2
| \(\begin{align} 3\text{E}1_{\text{двенадцать}} \\ \underline{-14\text{T}_{\text{двенадцать }}} \end{выровнено}\) |
Пример 3
| \(\begin{align} 402_{\text{five}} \\ \underline{-233_{\text{five}}} \end{aligned}\) |
Пример 4
| \(\begin{align} 1010_{\text{two}} \\ \underline{-111_{\text{two}}} \end{aligned}\) |
Проверить: \(\begin{align} 11_{\text{two}} \\ \underline{+111_{\text{two}}} \\ 1010_{\text{two}} \end{align }\)
В примерах 3 и 4, когда мне нужно было произвести обмен, а в разрядном значении слева был ноль, сначала нужно было произвести обмен на более высокое разрядное значение.
Затем производится обмен по линии до тех пор, пока вы не сможете вычесть. Этот случай происходит с основанием десять все время, когда вы вычитаете число из 100, 1000, 10000 и т. д. Большинство людей просто начинают вычеркивать каждый нуль и прибавлять 9.над ними по привычке, не имея ни малейшего представления, зачем они это делают. Чтобы из 1000 вычесть 235, сначала нужно вычеркнуть единицу, поставить над ней ноль и поставить единицу перед нулем на месте сотен (что меняет 1000 на 10 сотен), затем следует вычеркнуть эти 10. в разряде сотен поставьте над ним девятку и поставьте 1 перед нулем в разряде десятков (что означает обмен 10 сотен на 9 сотен и 10 десятков), затем вы должны вычеркнуть эту 10, поставить над ней 9 и 1 перед нулем вместо единиц (что означает обмен 10 десятков на 9).десятки и 10 единиц). Затем вы можете вычесть, как показано в примере справа. Важно действительно понять, что здесь происходит, потому что детям обычно очень тяжело, когда нужно вычеркнуть ноль.
Упражнение 1
Решите следующие задачи на вычитание..jpg)
Вы можете использовать блоки или диаграммы, чтобы помочь визуализировать проблему, но в конечном итоге вы хотите работать над тем, чтобы иметь возможность делать это без манипулятивных действий. Под каждой задачей проверьте, добавив разность (ответ) к вычитаемому (вычитаемое число) и посмотрите, является ли сумма уменьшаемым (число сверху). Используйте любой алгоритм добавления, который вы предпочитаете.
| а. \(\begin{выровнено} 4 5 2_{\text{тринадцать}} \\ \underline{-1 3 \text{E}_{\text{тринадцать}}} \end{выровнено}\) | б. \(\begin{выровнено} 8 3 1 _{\text{девять}} \\ \underline{-6 7 0 _{\text{девять}}} \end{выровнено}\) | в. \(\begin{выровнено} 2 0 0 4_{\text{шесть}} \\ \underline{-3 3 5_{\text{шесть}}} \end{выровнено}\) | д. \(\begin{выровнено} 4 2 1 _{\text{пять}} \\ \underline{-2 3 2 _{\text{пять}}} \end{выровнено}\) | эл. \(\begin{выровнено} 1 0 0_{\text{три}} \\ \underline{-1 1_{\text{три}}} \end{выровнено}\) |
Проверьте каждую проблему здесь:
| a. | б. | в. | д. | эл. |
Традиционный стандартный алгоритм вычитания не обязательно лучший, и есть много других, которые вы изучите в оставшейся части этого набора упражнений.
Следующий алгоритм был изучен многими людьми до появления «новой математики», поэтому я называю его Алгоритмом Старожилов . Он похож на стандартный алгоритм в том, что вы начинаете справа и двигаетесь влево. Но вы не перегруппировываетесь (формально известное как заимствование). Сначала снова взгляните на пример использования стандартного алгоритма для вычитания 95–28. Поскольку вы не можете вычесть 8 из 5, вы перегруппируете 9, зачеркнув 9 и написав 8, чтобы вы могли поставить 1 перед 2. Теперь в столбце единиц 15 – 8 = 7, а в столбце десятков 8 – 2 = 6. Ответ 67. Этот новый метод начинается так же. Вы не можете вычесть 8 из 5, но вместо того, чтобы перегруппировать из 9, вы добавляете 1 к числу под 9, и ставите 1 перед 5. Обратите внимание, что в столбце единиц 15 — 8 = 7, а в столбце десятков вместо 8 -2 у вас есть 9 –3, что соответствует ответу 6. Преимущество этого метода в том, что если вы ставите 1 вверху одного столбца, вы компенсируете это, добавляя 1 внизу следующего столбца. Вам не нужно беспокоиться о том, чтобы зачеркнуть что-то и создать беспорядок, и вам не нужно думать о цифре в столбце слева, пока вы не перейдете к этому столбцу для вычитания — не нужно пытаться перегруппироваться и зацикливаться на этом. ! Посмотрите на два метода рядом. Если вы используете новый метод, вы должны оставить место между вычитаемым и чертой вычитания на случай, если вам нужно поставить там 1.
Что мне действительно нравится в методе Oldtimer, так это то, что его гораздо проще проверить. Просто добавьте каждый столбец. Переноски нет: 7 + 8 = 15 и 6 + 1 + 2 = 9. Это проще простого. Чтобы проверить стандартный алгоритм, это что-то вроде беспорядка, и вам нужно записать его где-нибудь еще и проверить. Изучите следующие примеры.
Вы все еще должны быть очень осторожны, чтобы уделить пристальное внимание базе. Когда вы ставите 1 перед цифрой, помните, что она обозначает число, которое является основанием. Другой способ указать то же самое — написать, что это означает, как показано ниже. Те же пять примеров снова проиллюстрированы таким образом. Это не так элегантно, но если это помогает понять, что происходит на самом деле, сделайте это так.
Упражнение 2
Вычтите следующее, используя алгоритм Олдтаймера. Проверьте свои ответы, сложив.
| а. \(\begin{align} 5 0 3 6 \\ \underline{-3 4 1 8} \end{align}\) | б. \(\begin{выровнено} 314 _{\text{четыре}} \\ \underline{-221 _{\text{четыре}}} \end{выровнено}\) | в. \(\begin{выровнено} 5 \text{T} 2 _{\text{двенадцать}} \\ \underline{-2 3 \text{E}_{\text{двенадцать}}} \end{выровнено}\) | д. \(\begin{выровнено} 4 1 3_{\text{шесть}} \\ \underline{-3 2 4_{\text{шесть}}} \end{выровнено}\) | эл. \(\begin{выровнено} 1 1 0 0 _{\text{два}} \\ \underline{-1 0 1 _{\text{два}}} \end{выровнено}\) |
| ф. \(\begin{выровнено} 537 _{\text{девять}} \\ \underline{-273 _{\text{девять}}} \end{выровнено}\) | г. \(\begin{выровнено} 312_{\text{пять}} \\ \underline{-224_{\text{пять}}} \end{выровнено}\) | час. \(\begin{выровнено} 502 _{\text{семь}} \\ \underline{-235 _{\text{семь}}} \end{выровнено}\) | я. \(\begin{align} 200_{\text{three}} \\ \underline{-121_{\text{three}}} \end{align}\) | Дж. \(\begin{выровнено} 523_{\text{восемь}} \\ \underline{-265_{\text{восемь}}} \end{выровнено}\) |
Теперь, когда вы освоили этот алгоритм, вот еще один для вас. Это алгоритм слева направо , в котором перегруппировка не происходит до конца задачи — вы перегруппировываетесь из ответа! Вот как это работает. Начните с самого левого столбца и вычтите. Перейти к следующему столбцу. Вычесть, если можно. Если вам нужно перегруппироваться, поставьте 1 перед старшей цифрой, как обычно, и перечеркните предыдущую цифру в ответе. В конце концов, вы уйдете от ответа. Переходите к следующему столбцу, пока не закончите столбец единицы. Затем вернитесь назад и вычтите единицу из всех цифр с косой чертой через них. Изучите следующий пример, который показан шаг за шагом.
Вот несколько примеров в других базах. Если вы предпочитаете, вместо того, чтобы ставить 1 перед цифрой при перегруппировке, вы можете поставить, например, +4, если она находится в основании четыре, как было показано для предыдущего алгоритма внизу последней страницы.
Упражнение 3
Проверьте приведенные выше примеры, решив следующие задачи на сложение.
| \(\begin{выровнено} 213 _{\text{шесть}} \\ \underline{+215_{\text{шесть}}} \end{выровнено}\) | \(\begin{align} 101_{\text{two}} \\ \underline{+101_{\text{two}}} \end{align}\) | \(\begin{выровнено} 2 7 \text{E}_{\text{двенадцать}} \\ \underline{+1 \text{T} 3_{\text{двенадцать}}} \end{выровнено}\ ) | \(\begin{align} 202_{\text{three}} \\ \underline{+1212_{\text{three}}} \end{align}\) |
Упражнение 4
Вычтите следующее, используя алгоритм слева направо.
| a. \(\begin{align} 8 0 4 2 \\ \underline{-1 3 2 5} \end{align}\) | б. \(\begin{выровнено} 4132_{\text{пять}} \\ \underline{-2413_{\text{пять}}} \end{выровнено}\) | в. \(\begin{выровнено} 7210 _{\text{восемь}} \\ \underline{-5564_{\text{восемь}}} \end{выровнено}\) | д. \(\begin{выровнено} \text{T} 3 7_{\text{тринадцать}} \\ \underline{-569_{\text{тринадцать}}} \end{выровнено}\) | эл. \(\begin{выровнено} 1 1 0 1 _{\text{два}} \\ \underline{-1 1 _{\text{два}}} \end{выровнено}\) |
Упражнение 5
Проверьте ответы на Упражнение 4, решив соответствующую задачу на сложение
В этом алгоритме есть еще одна маленькая деталь. Если вы вычеркиваете ноль, вы должны продолжать вычеркивать цифру слева от нуля. Если в строке влево больше одного нуля, вычеркивайте каждый ноль, пока не дойдете до цифры, отличной от нуля. Затем вычтите 1 из каждого вычеркнутого числа, как и раньше. Обратите внимание на основание: во втором примере ниже число до 40five равно 34five. В третьем примере число перед 100two равно 11two. Изучите следующие примеры.
Упражнение 6
Вычтите следующее, используя алгоритм слева направо.
| а. \(\begin{align} 8 0 4 2 \\ \underline{-1 3 4 5} \end{align}\) | б. \(\begin{выровнено} 4132 _{\text{пять}} \\ \underline{-2433_{\text{пять}}} \end{выровнено}\) | в. \(\begin{выровнено} 7210 _{\text{восемь}} \\ \underline{-5214_{\text{восемь}}} \end{выровнено}\) | д. \(\begin{align} \text{T} 3 7_{\text{тринадцать}} \\ \underline{-539_{\text{тринадцать}}} \end{выровнено}\) | эл. \(\begin{выровнено} 1 1 0 0 _{\text{два}} \\ \underline{-10 1 _{\text{два}}} \end{выровнено}\) |
Упражнение 7
Проверьте ответы на упражнение 6, решив соответствующую задачу на сложение.
Алгебра поможет вам понять следующий алгоритм:
M – S = M – S + x – x = M + x – S – x = (M + x) – (S + x)
M – S = М – S + х – х = М – х – S + х = (М – х) – (С – х)
По сути, здесь говорится, что при вычитании двух чисел, М (уменьшаемое) и S (вычитаемое), вы получите один и тот же ответ, если сначала прибавите (или вычтете) одно и то же число к М и S перед вычитанием. Алгоритм Олдтаймера работает из-за этого факта. Например, когда вы ставите 1 перед цифрой единицы уменьшаемого и 1 перед цифрой десятки вычитаемого, вы добавляете 10 как к уменьшаемому, так и к вычитаемому; то вы вычитаете.
Этот алгоритм особенно полезен, если уменьшаемое число имеет в конце строку нулей. Сначала вычтите 1 из уменьшаемого и вычитаемого, а затем выполните вычитание. Посмотрите, как это работает:
| \(\begin{align} 100000 && && 99999 \\ \underline{–65378} && && \underline{–65377} \\ 34622 &&= && 34622 \end{align}\) | \(\begin{align} 3000 && && 2999\\ \underline{–1264} && && \underline{–1263} \\ 1736 && = && 1736 \end{align}\) |
Ну, что вы думаете? Разве второе вычитание, показанное в каждой паре, не легче сделать, чем первое? Я только что вычел 1 из уменьшаемого и сначала вычитаемого!
Упражнение 8
Придумайте две собственные задачи на вычитание, используя этот метод для вычитания.
Этот алгоритм также хорошо работает, если вычитаемое близко к степени основания, например 100, 1000 и т. д. Например, для задачи на вычитание 4503–997 добавьте 3 к уменьшаемому и вычитаемому, чтобы задача приняла вид 4506. – 1000 = 3506. В задаче с основанием четыре, \(2302 _{\text{четыре}} – 333 _{\text{четыре}}\), прибавьте 1 к обоим, чтобы получить \(2303 _{\text{четыре}} – 1000 _ {\ text {четыре}} = 1303 _ {\ text {четыре}} \)
Упражнение 9
Составьте две собственные задачи на вычитание, используя этот метод для вычитания. Используйте основание, отличное от 10.
Описанный выше метод иногда называют Дополнительным методом . Существует еще более специфический подход, называемый Дополнительным Алгоритмом . Он основан на идее дополнений, которую мы определили в предыдущем наборе упражнений. В системе счисления с основанием десять парами дополнений были 1 и 9, 2 и 8, 3 и 7, 4 и 6 и 5 и 5. Для дополнительного метода вы находите очень специфическое дополнение вычитаемого и добавляете его как к уменьшаемому, так и к уменьшаемому. вычитаемое перед вычитанием. Дополнение в этом случае представляет собой 1, за которой следуют только нули, так что количество нулей равно количеству цифр в уменьшаемом конце. Во-первых, вам придется придумать простой способ найти дополнение заданного числа.
Ниже приведены примеры, показывающие, как найти дополнение (C) заданного числа (A), если вы хотите, чтобы A + C в сумме давали число B.
Пример 1
A = 74 и B = 1000.
Решение
Чтобы найти C, прибавьте 6 к 74, чтобы получить 80, затем 20, чтобы получить 100, и 900, чтобы получить 1000. C = 926.
Пример 2
}}\) и B = \(1000_{\text{шесть}}\).
Решение
Чтобы найти C, добавьте 2 единицы, чтобы получить 3 длинных, затем 3 длинных, чтобы получить 1 плоскость, и 5 граней, чтобы получить 1 блок. Тогда C = \(532_{\text{шесть}}\).
Есть и другие способы вычислить дополнение. Например, в системе счисления с основанием 10, если A равно 28403, и вы хотите C, такое что A + C = 1000000, вы можете найти ответ, написав фактическое дополнение 3, что равно 7, для цифры единицы. Двигайтесь влево. Вам нужна цифра для каждого разряда, которая при добавлении к цифре дает сумму 9. Делайте это до тех пор, пока в числе не будет столько цифр, сколько нулей в 1000000. В этом случае ответ будет 971597. Это сложнее объяснить. чем делать! Если у вас есть свой способ определения дополнения, это здорово! Не держите это в секрете.
Упражнение 10
Найдите дополнение (C) к данному числу (A), такое что A + C = B.
a. А = 538 и В = 10000
б. A = \(212_{\text{четыре}}\) и B = \(1000_{\text{четыре}}\)
c. A = \(1011 _{\text{два}}\) и B = \(10000 _{\text{два}}\)
Вот как работает этот дополнительный метод. Рассмотрим задачу 452 – 74. Нам нужно найти число, которое при прибавлении к 74 равно 1000. Как выбрать, что должно получиться в сумме, как в 1000? Если первое число (уменьшаемое) — это 2-значное число, вам нужна 1 с 2 нулями (100). Если первое число (уменьшаемое) представляет собой трехзначное число, вам нужна единица с тремя нулями (1000) и так далее. Этот шаг одинаков для всех баз. Вернемся к задаче: 452 – 74: 926 – это то, что нужно прибавить к 74, чтобы получить 1000 (из примера 1). Добавьте 926 к уменьшаемому и вычитаемому, чтобы получить новую задачу на вычитание: 1378 – 1000 = 378. Ответ – новое уменьшаемое без первой цифры: 378. Довольно дико! Посмотрите на \(402_{\text{шесть}} –24_{\text{шесть}}\). Нам нужно найти число, которое при добавлении к \(24_{\text{шесть}}\) равно \(1000_{\text{шесть}}\)., то есть \(532_{\text{шесть}}\ ) из примера 2. Добавьте \(532_{\text{шесть}}\) к уменьшаемому и вычитаемому, чтобы получить новую задачу на вычитание, которая имеет вид \(1304 — 1000_{\text{шесть}} = 304_{\text{шесть} }}\). Опять же, ответ представляет собой новое уменьшаемое без первой цифры: \(304 _{\text{шесть}}\). Вот в чем прикол — Просто добавьте дополнение к уменьшаемому, уберите первую цифру и вот ответ! Вычитания нет.
Пример 3
Вычесть по дополнительному методу: 912 – 573
Решение
427 – это число, которое при прибавлении к 573 равно 1000. Прибавляем к уменьшаемому: 427 + 1 392. Вычитаем первое
Пример 4
Вычтите \(301_{\text{четыре}} – 212_{\text{четыре}}\), используя дополнительный алгоритм.
Решение
Из 10.b. дополнение равно \(122_{\text{четыре}}\). \(301 _ {\ text {четыре}} + 122 _ {\ text {четыре}} = 1023 _ {\ text {четыре}} \).
Таким образом, ответ равен \(23_{\text{четыре}}\).
Упражнение 11
Вычтите \(1100_{\text{два}} – 1011_{\text{два}}\), используя дополнительный алгоритм, и ваш ответ из 10.c.
Упражнение 12
Решите следующие задачи на вычитание, используя дополнительный метод.
| а. \(\begin{выровнено} 5034 \\ \underline{–357} \end{выровнено}\) | б. \(\begin{выровнено} 420_{\text{пять}} \\ \underline{–231_{\text{пять}}} \end{выровнено}\) |
Дополнительный метод на самом деле проще сделать с блоками – как только вы освоите его. Выньте свои блоки Base Three, чтобы выполнить следующий пример и задачи.
Чтобы вычислить \(212_{\text{три}} – 120_{\text{три}}\), представить \(212_{\text{три}}\) и \(120_{\text{три}} \) с блоками, как показано ниже.
Уменьшаемый конец показан слева. Поскольку его самый большой «блок» — это квартира, следующее «значение места» вверх по блоку. Таким образом, проблема состоит в том, чтобы выяснить, что нужно добавить к вычитаемому (показанному справа), чтобы получился блок. Это будет еще 1 длинный и еще 1 плоский. Другими словами, если вы добавите к вычитаемому долгую и бемоль, у вас будет блок, верно? Добавьте такое же количество к уменьшаемому, как показано слева выше. Это должно выглядеть так:
Если вычесть сейчас, ответом будет новое уменьшаемое число с удаленным самым большим блоком. Таким образом, ответ — 2 длинных и 2 единицы, или \(22_{\text{три}}\). Важный шаг — выяснить, что нужно добавить к вычитаемому, чтобы получился блок. Затем также добавьте его к уменьшаемому, удалите самый большой блок из нового уменьшаемого и вот ответ! Та да!
Поскольку рисование блоков иногда бывает громоздким, еще один способ графически показать, что происходит, — это использовать сокращенные изображения для блоков, плоских, длинных и единиц (3B, 3F, 3L, U), как показано ниже.
Упражнение 13
На следующей странице используйте соответствующие базовые блоки для вычитания \(120_{\text{три}} — 12_{\text{три}}\) и \(213_{\text{четыре}} — 133_{\text{четыре}}\) с использованием дополнительного метода . Объясните как это сделать и покажите полные или сокращенные картинки с базовыми блоками.
а. Используйте базовые три блока и дополнительный метод, чтобы вычесть \(120 _ {\ text {три}} — 12 _ {\ text {три}} \).
б. Используйте блоки с основанием четыре и дополнительный метод, чтобы вычесть \(213 _ {\ text {четыре}} — 133 _ {\ text {четыре}} \).
Упражнение 14
Объясните, как каждый учащийся решает задачу на вычитание 634 – 152.
a. Мэри делает вычитание в уме, думая вслух «534, 484, 482». Каковы ее рассуждения?
б. Педро выполняет вычитание, думая вслух: «634 и 48 — это 682, отнять 200 — это 482». Каковы его рассуждения? 9{14} \\ \cancel{5} &&\cancel{3}&&4 \\ -2&&5&&6 \\ \hline 2&&7&&8 \end{выровнено}\)
Используя метод вычитания из основания, если у вас есть место, где нижнее число больше, чем верхнее, перегруппируйте, как в традиционном методе, затем вычтите нижнее число из основания и прибавьте результат к верхнему числу. Преимущество этого метода в том, что вы никогда не вычитаете число из числа, превышающего основание. Это хороший метод для людей, которым нужно использовать пальцы для вычитания.
Алгоритм вычитания из базы:
При использовании этого метода в других базах обведите номер базы при перегруппировке. Например, при работе с основанием шесть число 6 не существует, и запись числа 10 может сбивать с толку, хотя это правильно.
Упражнение 15
Вычтите следующее, используя алгоритм вычитания из базового. Это те же проблемы, что и в №6. Не забудьте обвести базовый номер при перегруппировке.
| а. \(\begin{align} 8 0 4 2 \\ \underline{-1345} \end{align}\) | б. \(\begin{выровнено} 4 1 3 2 _{\text{пять}} \\ \underline{-2433_{\text{пять}} } \end{выровнено}\) | в. \(\begin{выровнено} 7 2 1 0_{\text{восемь}} \\ \underline{-5214 _{\text{восемь}}} \end{выровнено}\) | д. \(\begin{выровнено} \text{T} 3 7_{\text{тринадцать}} \\ \underline{-539 _{\text{тринадцать}}} \end{выровнено}\) | эл. |