Этапы урока. Цель | Виды работы | Содержание взаимодействия с учащимися. | Деятельность учителя | Деятельность учащихся |
I. Организационный момент Цель: приветствие; эмоциональный настрой; проверка готовности учащихся к уроку. | 1.Приветствие учащихся. | — Здравствуйте, ребята! Меня зовут Маргарита Мусаевна, сегодня урок математики проведу у вас я. | Приветствует учащихся; эмоционально настраивает их на работу; проверяет готовность к уроку. | Приветствуют учителя; эмоционально настраиваются на урок; проверяют наличие учебных принадлежностей на столе. |
2.Эмоциональный настрой. | Все друг к другу повернитесь, И друг другу улыбнитесь, И удачи вам во всём, А теперь урок начнём! | |||
3.Проверка готовности к уроку. | — Проверьте готовность к уроку. — На партах у вас должен лежать учебник «Математика», рабочая тетрадь и пенал. | |||
II. Актуализация знаний Цель: подготовка учащихся к восприятию новых знаний. III. Целеполагание. Цель: обеспечить мотивацию учения школьников. Принятия ими целей урока. | 1. Работа с математической цепочкой. | — Ребята, посмотрите внимательно на слайд, Слайд 1 на нем вы видите математическую цепочку, решим её. 9 0:6=15 15·4 = 60 60:3=20 20+80=100 100=100 | Организуют работу обучающихся с математической цепочкой, с целью развития вычислительных навыков. | Внимательно слушают учителя, выполняют предложенное им задание, отвечают на вопросы. |
2. Работа с геометрическими фигурами. | -Посмотрите на доску. Слайд 2 -Кто изображен на слайде? (кошка из геометрической фигуры — треугольников) —Посчитайте и скажите, из скольких треугольников состоит кошка? (20 треугольников) -Теперь вместе посчитаем составные части нашей геометрической кошки. —Начнем с самого большого – головы. Сколько треугольников находится в верхней части кошки? (10 треугольников). —Теперь посчитаем треугольники на теле кошки. Из какого количества треугольников состоит туловище кошки? (3 треугольника). —Остался хвост кошки. Сколько здесь треугольников? (7 треугольников). —Сколько всего треугольников получилось? (20 треугольников). | Организуют работу обучающихся с геометрическим материалом. | Работают с геометрическим материалом. | |
3.Логическая задача. | Сл. 3 — Петя записывал рост своего щенка каждый год. Когда щенка подарили, его рост был ровно 20 см. Через год — 36 см, через два года — 44 см, через три года — 48 см. Какой рост (в см) будет у Петиного щенка через пять лет после дарения, если закономерность изменения роста сохранится? (каждый год прирост уменьшается в 2 раза по сравнению с предыдущим. Следовательно, за четвертый год щенок вырастет на 2 см, а за пятый — еще на 1 см. Рост щенка через пять лет составит 48 см + 2 см + 1 см = 51 см). | Организуют работу обучающихся над решением логической задачи. | Решают логическую задачу. | |
1.Подведение к теме урока. 2.Формулировка темы и целей урока. | — Ребята, обратите внимание на пример, изображенный на слайде: Слайд 4 — Как мы можем решить этот пример? (устно) — Решим этот пример, используя устные приёмы вычисления. 34×2=(30+4)×2= 30×2+4×2=60+8=68 — А теперь, посмотрите на следующий пример: 234×2 — Что изменилось во втором примере? (первый множитель – трехзначное число) — Можем ли мы решить данный пример устно? (да) 234×2=(200+30+4)×2=200×2+30×2+4×2=400+60+8=468 — А как нам решить этот пример, используя более краткую запись? (в столбик) — Кто догадался, какова тема нашего урока? (умножение трехзначного числа на однозначное в столбик) — А какие цели мы поставим перед собой? (познакомиться с письменным приемом умножения трехзначного на однозначное число, решать примеры данного вида) | Предлагает решить примеры, тем самым подводит учащихся к теме урока. Задает вопросы для определения темы урока. | Отвечают на вопросы учителя. Отвечают на вопросы, определяют тему урока. | |
IV. Изучение нового материала. Цель: создать условия для осознанного применения полученных знаний. | 1. Работа с правилом. | — Откройте страницу 88-ую учебника и обратите внимание на правило. — Прочитайте его про себя. — Итак, почему же используются письменные приемы вычислений? (потому что устно выполнить умножение трудно) — Как удобнее записать решение? (в столбик, используя знак ×) Повторим алгоритм — С чего начинают письменное умножение на однозначное число? (Записываем второй множитель под единицами первого множителя) — Что зачем нужно умножать? (сначала единицы, потом десятки, затем сотни) Разберем пример, решенный на странице учебника. — Запишем данный пример в столбик, используя знак ×. — Записываем второй множитель под единицами первого множителя. — Умножаем единицы: 4×2 = 8, записываем под единицами. — Умножаем десятки: 3×2=6, записываем под десятками. — Умножаем сотни: 2×2=4, записываем под сотнями. — Читаем ответ: произведение 234 и 2 равно 468. — Молодцы, ребята! | Организует работу с правилом. Задает вопросы. | Работают с правилом. Отвечают на вопросы учителя. |
2. Решение примеров. (№1, стр. 88) 3. Решение примеров, №1 стр.89 | — Откройте тетради и запишите сегодняшнее число – 22 апреля и «Классная работа», не забывая о том, что «классная» пишется с удвоенной сс. — Для отработки вычислений, выполним номер 1-ый. Первый пример учитель выполняет совместно с обучающимися, с комментированием у доски. — Итак, первый пример: 123 × 3 — Назовите первый множитель? (123) — Назовите второй множитель? (3) — Запишем решение столбиком, используя знак × — Записываем второй множитель под единицами первого множителя. — Умножаем единицы: 3×3=9, записываем под единицами. — Умножаем десятки: 2×3 = 6, записываем под десятками. — Умножаем сотни: 1×3=3, записываем под сотнями. — Читаем ответ: Произведение чисел 123 и 3 равно 369. Далее выполняется по аналогии. 433×2= 866 122×4=488 — А теперь давайте решим по такому же алгоритму примеры посложнее. № 1 стр.89 Первый пример учитель выполняет совместно с обучающимися, с комментированием у доски. — Умножаем единицы: 6×2=12, 2 единицы записываем под единицами, а 1 десяток запоминаем. — Умножаем десятки: 4×2 = 8, да ещё 1 десяток запоминали, получаем 9, записываем под десятками. — Умножаем сотни: 4×2=8, записываем под сотнями. — Читаем ответ: Произведение чисел 446 и 2 равно 892. Далее выполняется по аналогии. 283×3=849 151×7=1057 — Чем отличаются эти примеры? (есть переход через разряд) | Организует оформление рабочей страницы в тетради. Организует работу учащихся по решению примеров. Задаёт вопросы | Оформляют рабочую страницу в тетради. Вопросы учителя. Решают примеры. Отвечают на вопросы. | |
4. Работа над задачей. (№3, стр.88) | — Ребята, обратите внимание на задачу 3-юю. — Прочитайте её про себя. — О чём говорится в задаче? (О рулонах пленки) — Что известно? (Что купили 5 рулонов пленки по 20 метров в каждом) — Что надо узнать? (Хватит ли этой пленки на 4 теплицы, если на каждую идет 16 метров пленки? 25 метров пленки?) — В виде чего составим краткую запись? (В виде опорных слов) — Какие слова возьмём для краткой записи? Что известно о купленных рулонах? (Мы не знаем, сколько всего метров купили, но знаем, что 5 рулонов по 20 метров в каждом) Что известно о расходе на теплицы в 1 раз? (Что в первый раз на 4 теплицы нужно потратить по 16 метров) Что известно о расходе на теплицы во 2 раз? (Что во второй раз на 4 теплицы нужно потратить по 25 метров) Что необходимо узнать? (Хватит ли купленной пленки на теплицы) — Повторим задачу по краткой записи. — Можем ли мы сразу ответить на главный вопрос задачи? (Нет) — Почему? (Потому что не знаем, сколько метров пленки находится в 5 рулонах) — А можем узнать? (Да) — Почему? (Потому что знаем количество рулонов и сколько метров содержится в каждом рулоне) — Каким действием? (Умножением) — Почему? (Потому что сказано, что 5 рулонов ПО 20 метров в каждом) — Теперь можем ответить на главный вопрос задачи? (Нет) — Почему? (Потому что не знаем, сколько пленки уйдет на 4 теплицы) — А можем узнать? (Да) — Почему? (Потому что знаем количество теплиц и сколько метров пленки уйдет на каждую) — Каким действием? (Умножением) — Почему? (Потому что сказано, что на каждую из 4 теплиц уходит ПО 16 метров плёнки) — А теперь можем ответить на главный вопрос задачи? (Да) — Почему? (Потому что знаем, сколько всего плёнки купили, и сколько уйдет на 4 теплицы) — Как? (сравним 2 полученных результата) 64˂100 Плёнки хватит. — Ответим на второй вопрос задачи. — Можем ли мы сразу на него ответить? (Нет) — Почему? (Потому что не знаем, сколько пленки по 25 метров уйдет на 4 теплицы) — А можем узнать? (Да) — Почему? (Потому что знаем количество теплиц и сколько метров пленки уходит на 1 теплицу) — Каким действием? (умножением) — Почему? (Потому что сказано, что на каждую из 4 теплиц уходит ПО 25 метров). — Как? (сравним 2 полученных результата) 100=100 Плёнки хватит. — Сколько действий в задаче? (3) — Что найдем первым действием? (Общее количество пленки) — Что найдем вторым действием? (сколько пленки по 16 метров уйдет на 4 теплицы) — Что найдем третьим действием? (сколько пленки по 25 метров уйдет на 4 теплицы) — Запишем решение задачи и ответ с комментированием. 1) 20·5 = 100 (м) – купили всего. 2) 16·4 = 64 (м) – расходовали на теплицы в 1 раз. 3) 25·4 = 100 (м) – расходовали на теплицы во 2 раз. Ответ: Плёнки хватит. | Организует работу учащихся по решению задачи. Контролирует работу учащихся. Задает вопросы. | Решают задачу. Отвечают на вопросы учителя. | |
Физкультминутка | В понедельник я купался, (Изображаем плавание.) Целый день я отдыхал. (Присаживаются за парты) | Проводит физкультминутку, проводит профилактику переутомления учащихся. | Повторяют движения за учителем для профилактики переутомления. | |
5. Работа над задачей. (№2, стр.89) | — Обратите внимание на задачу 2-ую на странице 89-ой. — Прочитайте её про себя. — Прочитайте задачу вслух. — О ком говорится в задаче? (О школьниках, которые поехали на экскурсию) — Что известно? (Что на экскурсию поехали 100 школьников, что в большой автобус сели 40 школьников, а остальные – поровну в 3 маленьких автобуса) — Что надо узнать? (Сколько школьников было в 1 маленьком автобусе?) — В виде чего составим краткую запись? (В виде опорных слов) — Какие слова возьмём для краткой записи? Что известно об общем количестве школьников, которые поехали на экскурсию? (Что на экскурсию поехали 100 школьников) Что известно о количестве школьников, которые сели в большой автобус? (Что в большой автобус сели 40 школьников) Что известно о количестве школьников, которые сели в маленькие автобусы? (Известно, что остальные школьники сели поровну в 3 маленьких автобуса) Что нужно узнать? (Сколько школьников было в 1 маленьком автобусе) — Повторим задачу по краткой записи. — Можем ли мы сразу ответить на главный вопрос задачи? (Нет) — Почему? (Потому что не знаем, сколько школьников село в маленькие автобусы) — А можем узнать? (Да) — Почему? (Потому что знаем, сколько всего школьников поехало на экскурсию и сколько школьников село в большой автобус) — Каким действием? (вычитанием) — Почему? (Потому что нужно найти оставшихся школьников) — Теперь можем ответить на главный вопрос задачи? (Да) — Почему? (Потому что знаем, сколько школьников село в маленькие автобусы и количество автобусов) — Каким действием? (Делением) — Почему? (Потому что сказано, что оставшиеся школьники сели в 3 одинаковых автобуса) — Сколько действий в задаче? (2) — Что найдем первым действием? (сколько школьников сели в маленькие автобусы) — Что найдем вторым действием? (сколько школьников сели в 1 маленький автобус) — Запишем решение задачи и ответ с комментированием. 1) 100 – 40 = 60 (шк.) – сели в 3 маленьких автобуса. 2) 60 3 = 20 (шк.) – было в 1 маленьком автобусе. Ответ: 20 школьников было в одном маленьком автобусе. | Организует работу учащихся по решению задачи. Контролирует работу учащихся. Задает вопросы. | Решают задачу. Отвечают на вопросы учителя. | |
V. Закрепление изученного материала. Цель: создать условия для осознанного применения полученных знаний. | 1. Решение примеров. (№2, стр.88) | — Обратите внимание на номер 2-ой. — Решим примеры первой строчки. Учащиеся решают примеры в тетради, с комментированием. 483+257=740 820-164=656 15× 8:3=40 15×8 = 120, 120:3=40 6×16 : 8 – 2=10 6×16=96, 96:8=12, 12-2=10 | Организует работу учащихся по решению примеров | Решают примеры. |
VII. Подведение итогов урока. Цель: провести анализ проделанной работы, рефлексия и самооценка учащимися собственной учебной деятельности. | 1. Обобщающая беседа. 2. Рефлексия. 3. Выставление оценок 4. Домашнее задание | — С каким вычислительным приемом сегодня работали? (Умножение на однозначное число в столбик) — Какой алгоритм изучили? (Алгоритм письменного умножения на однозначное число) — Оцените свою деятельность на уроке с помощью смайликов. — Сегодня на уроке хорошо поработали… (Имена детей, комментарий учителя) — Запишите домашнее задание… | Подводит итоги, рефлексию, выставляет оценки | Соотносят цель учебной деятельности и ее результаты, записывать |
«Умножение на трёхзначные числа. Планеты Солнечной системы». 3-й класс
Ключевые слова: математика, окружающий мир, умножение на трехзначное число
Основные цели
Метапредметные
- Тренировать умение проводить самооценку своей деятельности по построенному алгоритму.

Предметные
- Сформировать умение умножать многозначное числа на трёхзначное число.
- Тренировать умение письменно умножать на двухзначное число, используя распределительное свойство умножения.
- Тренировать устные вычислительные навыки табличного умножения.
- Дать первичное представление о планетах Солнечной системы.
Алгоритм умножения многозначного числа на трехзначное вводится на уроке 18 аналогично алгоритму умножения на двузначное число, однако распределительное свойство умножения, лежащее в основе этого введения, распространяется на три слагаемых.
На уроке учащиеся выполняют следующие виды математических действий:
- строят и применяют алгоритмы умножения на трехзначное число, записывают умножение на трехзначное число в столбик, проверяют правильность выполнения действий с помощью алгоритма и вычислений на калькуляторе;
- решают вычислительные примеры, уравнения, простые и составные задачи изученных типов;
- исполняют вычислительные алгоритмы, заданные в виде схем и блок-схем, фиксируют результаты вычислений в таблице, записывают заданную программу действий с помощью числового выражения;
- выполняют задания поискового и творческого характера.

Основные структурные элементы урока:
1. Новое знание: алгоритм умножения числа на трехзначное число.
2. Пробное действие: № 2 (а), стр. 33 (РТ).
3. Фиксация затруднения: я пока не могу вычислить произведение на трехзначное число в столбик.
4. Фиксация причины затруднения: пока не знаю алгоритма умножения на трехзначное число в столбик.
5. Цель деятельности учащихся: узнать алгоритма умножения на трехзначное число в столбик.
6. Фиксация нового знания: алгоритма умножения на трехзначное число в столбик.
Оборудование.
1) Демонстрационный материал
- Д-18.1
- Д−18.
 2 Карточки с числами для этапа мотивации.
2 Карточки с числами для этапа мотивации. - Д−18.3 Распределительное свойство для двух чисел.
- Д−18.4 Алгоритм умножения на двузначное число.
- Д−18.5 Алгоритм умножения на круглое многозначное число.
- Д−18.6 Алгоритм умножения на трёхзначное число.
- Д−18.7 Подробный образец выполнения задания в парах.
2) Раздаточный материал
- Р−18.1 Эталон для самопроверки.
- Презентация к уроку 18: слайды 1−14.
- Печатная форма учебника (3 класс, часть 3).
- Рабочая тетрадь к учебнику (3 класс, часть 3).
Ход урока
1. Мотивация к учебной деятельности
Мотивация к учебной деятельности— Какой праздник мы отмечали совсем недавно? (День космонавтики)
Мчатся ракеты
к дальним мирам,
К подвигу сердце рвётся…
Кто верит крылатым,
как песня, мечтам,
Тот цели своей добьётся!
— Вы готовы сегодня открывать новые знания и добиться цели?
Загадка про солнце.
— Как называется планетная система?
— Итак, наша ракета готова отправиться в космическое путешествие.
— Отгадайте, на какую планету мы прилетели (Меркурий)
Сколько звёзд на небе?
А травинок в поле?
Сколько крошек в хлебе?
Сколько капель в море?
На вопросы эти
Не найти ответ,
Но сейчас вам, дети,
Дам один совет.
Если попытаться
С числами дружить,
Можно не бояться,
Жить и не тужить.
108, 2, 57, 59, 61
(За 108 мин Гагарин облетел Землю; 2 года назад открыта Школа космонавтики во Владикавказе; 57 лет как первый раз человек вышел в открытый космос — Леонов; 59 лет назад в космосе побывала первая женщина — В. Терешкова; 61 год назад Ю.Гагарин полетел в космос.)
Терешкова; 61 год назад Ю.Гагарин полетел в космос.)
— Что вы можете сказать об этих числах? — Какие операции с многозначными числами вы умеете выполнять? (Сравнивать, складывать, вычитать, умножать.)
— Назовите пары чисел, произведение которых вы можете найти.
— Расположите числа в порядке возрастания.
— Наше путешествие тоже будет к планетам в порядке возрастания их массы.
— Сегодня на уроке вы продолжите работу с многозначными числами.
2. Актуализация знаний и фиксация индивидуального затруднения в пробном действииПродолжим наш полёт.
— Отгадайте, на какой мы планете? (Марс)
— Назовите, по какому плану мы обычно работаем при открытии нового знания?
— Вначале повторим то, что нам может пригодиться при открытии нового знания.
1. — Какой последний случай умножения мы изучали? (На двузначное число)
Учащиеся в парах выполняют задание и показывают результат работы учителю. Если выясняется, что у кого-то из учащихся есть ошибки, то предлагается им озвучить, как они находили результат.
Если выясняется, что у кого-то из учащихся есть ошибки, то предлагается им озвучить, как они находили результат.
2. Действие умножение используется в различных формулах, которые помогут открыть новое знание.
Соотнесите формулы с их названиями.
3. — Для того чтобы подготовится к открытию нового я вам предлагаю выполнить задание № 1 (РТ), стр. 33.
Задание выполняется поэтапно с последовательной проверкой: 1) дописывается распределительное свойство умножения для трех чисел; 2) находится произведение многозначных чисел с использованием распределительного свойства умножения.
Решение задания:
a • (b + c + d) = a • b + a • c + a • d
156 • 324 = 156 • (300 + 20 + 4) =
= 156 · 300 + 156 ∙ 20 + 156 ∙ 4 =
= 46 800 + 3120 + 624 = 50 544.
— Что вы повторили? (…)
— Какое следующее задание?
— Вам надо выполнить задание № 2 (а) (РТ), стр. 33. Является ли это задание пробным, обоснуйте свой ответ. (Да, является пробным, т.к. надо выполнить умножение в столбик.)
Учащиеся выполняют задание на планшетках.
— У кого нет результата?
— Что вы пока не можете сделать?
— Поднимите планшетки с результатами. Как вы можете доказать, что действовали правильно, каким эталоном вы могли воспользоваться?
— Что вы пока не можете сделать? (Мы пока не можем доказать, что действовали правильно, не можем назвать эталон, которым пользовались.)
3. Выявление места и причины затруднения— Отгадайте, на какой мы планете?
Уч-ся отгадывают загадку (Венера), а затем читают краткую информацию о планете.
— Она очень горячая и мы не будем долго на ней задерживаться.
— Что необходимо сделать? (Остановиться и определить причину возникшего затруднения.
— Какое задание выполняли? (Находили произведение на трёхзначное число в столбик.)
— Как пробовали выполнять задание? (…)
— Почему не смогли выполнить задание или не можете обосновать свои действия? (У нас пока нет способа умножения на трёхзначное число в столбик.)
4. Построение проекта выхода из затруднения— Сейчас вам предстоит отгадать, к какой планете мы приблизились?
Уч-ся отгадывают загадку (Нептун), а затем читают краткую информацию о планете.
— Сформулируйте цель сегодняшнего урока. (Построить правило умножения на трёхзначное число в столбик и научиться умножать на трёхзначные числа в столбик.)
— Сформулируйте тему урока. (Умножение на трёхзначные числа в столбик.)
Учитель записывает на доске тему урока.
— Прочтите задание № 2 (б) (РТ), стр. 33 и составьте план своей работы. (Дописать равенства на схеме, предложить свой способ умножения в столбик на трёхзначное число, проверить себя по учебнику.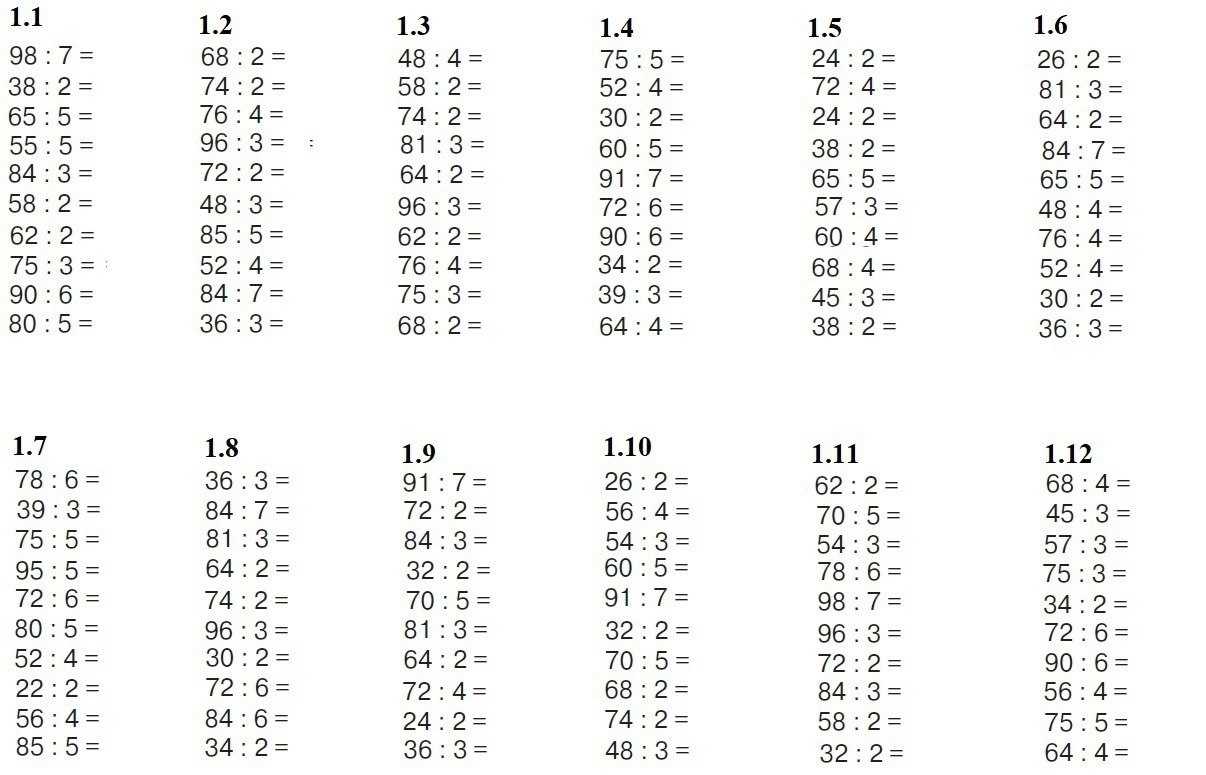 )
)
— Отгадайте, к какой планете мы приблизились?
Уч-ся отгадывают загадку (Уран), а затем читают краткую информацию о планете.
Учащиеся работают в группах 5 минут, обсуждаются итоги работы групп. Учитель может организовать подводящий диалог. В результате обсуждения на доске фиксируется эталон умножения на трехзначное число (Д−18.6):
— Сравните полученный алгоритм с правилом в учебнике на стр. 36.
Дети читают правило про себя, затем один ученик вслух.
— Справились с затруднением? — Молодцы!
— Какие задания вы теперь можете выполнять? (Мы теперь можем умножать любые числа на трёхзначные.)
6. Первичное закрепление с проговариванием во внешней речи— Итак, следующая планета.
Уч-ся отгадывают загадку (Сатурн), а затем читают краткую информацию о планете.
— А теперь что необходимо в дальнейшей работе на уроке? (Научиться применять новый эталон.)
На этапе предлагается фронтально выполнить третий пример из № 3 (РТ), стр. 33, а первый и второй пример — в парах. После выполнения задания учащиеся проводят самопроверку по подробному образцу (Д−18.7, слайд 3):
— У кого задание вызвало затруднение?
— На каком шаге алгоритма вы допустили ошибку?
— Кто задание выполнил правильно?
7. Самоконтроль с самопроверкой по эталонуУч-ся отгадывают загадку про очередную планету (Юпитер), а затем читают краткую информацию о планете.
Для самостоятельной работы предлагается выполнить № 4 (а) (У), стр. 39. Выполнение задания сопоставляется с эталоном для самопроверки (Р−18.1):
— Кто действовал так же и получил тот же результат — поставьте «+».
— Молодцы!
— У кого получился другой ответ — поставьте «?», найдите по шагам место, где допущена ошибка, обведите её. — Обратите внимание на это место. — Молодцы в том, что сумели найти место, в котором допущена ошибка. — Поставьте рядом «+».
8. Включение в систему знаний и повторение— А эту планету с 2006 года уже не считают планетой.
— Отгадайте. Как она называется?
Уч-ся отгадывают загадку про очередную планету (Плутон), а затем читают краткую информацию о планете.
— Где нам могут пригодиться полученные знания? (При решении задач.)
1. № 3 (У), стр. 39.
— Прочитайте текст задачи.
— На какие вопросы можно ответить по данной записи примеров?
— Запишите решение задачи:
485*365=177025(авт.)
Ответ: за год завод выпускает 177025 автомобилей.
9. Рефлексия деятельности на уроке Но вот наше виртуальное путешествие подошло к концу.
— Чему мы сегодня учились на уроке?
— Мы достигли своей цели?
— Сегодня вы ещё на один шаг продвинулись в своём обучении.
— Назовите учеников, чья работа вам больше всего понравилась?
— А теперь оцените самих себя.
— Ребята, у каждого из вас по 3 прямоугольника: зелёного, жёлтого, красного цвета. Оцените свою работу на уроке по следующим критериям:
1) если вам было сложно, вы не справились с самостоятельной работой и трудности остались в конце урока — возьмите прямоугольник красного цвета и вырежете из него ракету
2) если в процессе самостоятельной работы вы смогли преодолеть свои затруднения, но что-то ещё осталось не совсем понятным или были недочёты в работе — ракету жёлтого цвета;
3) если вам всё ясно и понятно, а самостоятельная работа не вызвала никаких затруднений и вы были активным участником урока — ракету зелёного цвета.
Д/з: (У.) Стр.39. №4 (б, ж), №7.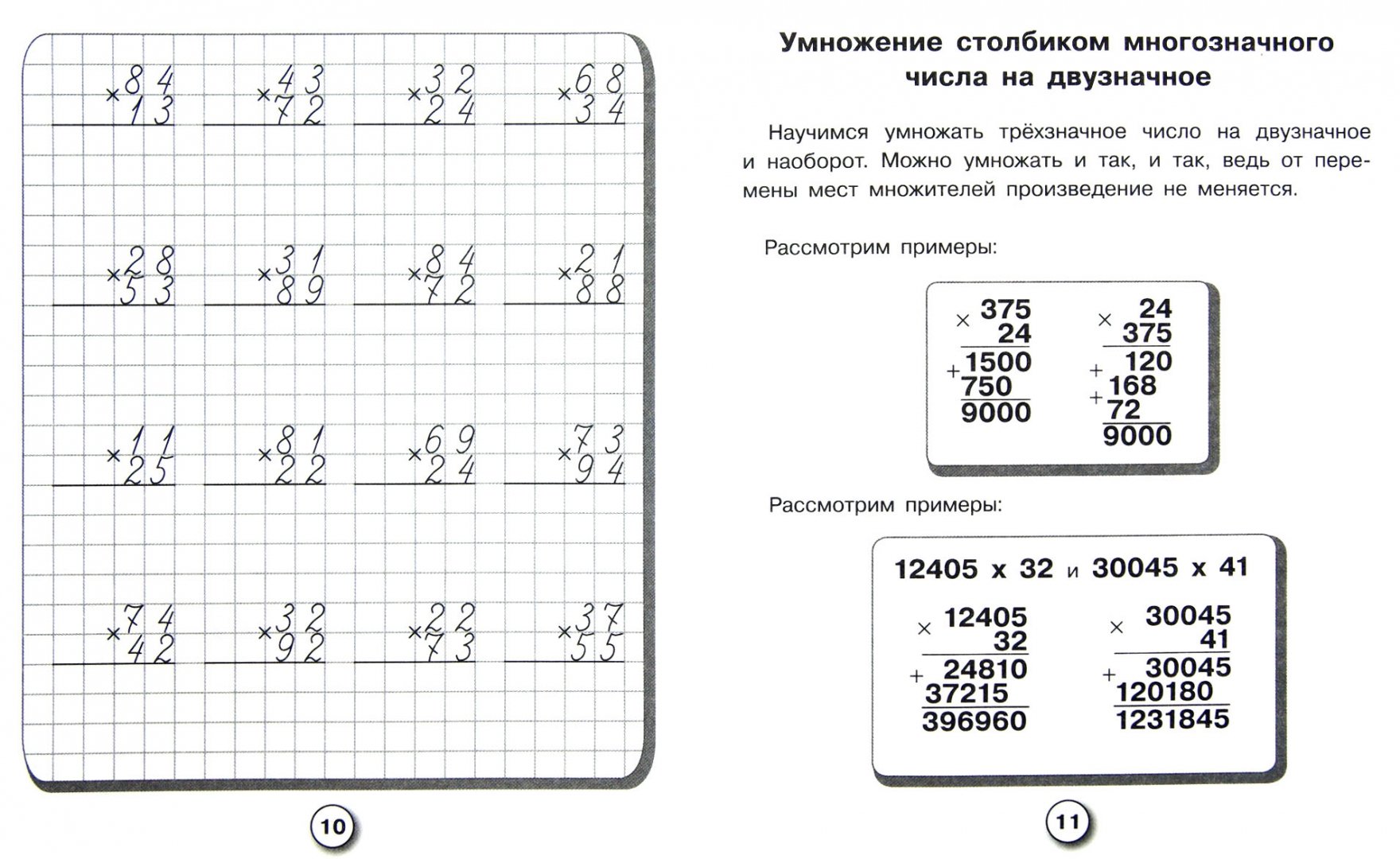
Умножение двузначных чисел на трехзначные | Математика 4 класса
Теперь умножьте на 413 × 2.
Молодец! 👍
Теперь давайте умножим на 413 × 30.
Поскольку 30 является кратным 10, мы можем просто найти 413 × 3 и ставят «0» в конце продукт.
Давайте сначала поместим ‘0’ .
А теперь умножим на 413 × 3.
Очень хорошо! Сделайте паузу и медленно просмотрите эти шаги, если вам нужно.
Наконец, давайте добавим два продукта , чтобы получить окончательный ответ.
Итак,
413 × 32 = 13 216 ✅
Хорошая работа. 👏
Пример 2
895 × 57 = ?
Повторим шаги еще раз.
Во-первых, запишем числа в столбце формы , начиная с большего числа.
Теперь давайте умножим на 895 × 7.
Затем давайте поместим ‘0’ на разряд единиц следующего продукта.
Также давайте удалим все предыдущие переносы, чтобы избежать путаницы.
Теперь давайте умножим на 895 × 5.
Наконец, давайте сложим два произведения , чтобы получить окончательный ответ.
Итак,
895 × 57 = 51 015
Вперед!
Давайте рассмотрим
Вот шаги еще раз:
✅ ШАГ 1: Напишите числа в столбце формы , одно под другим, начиная с большего числа.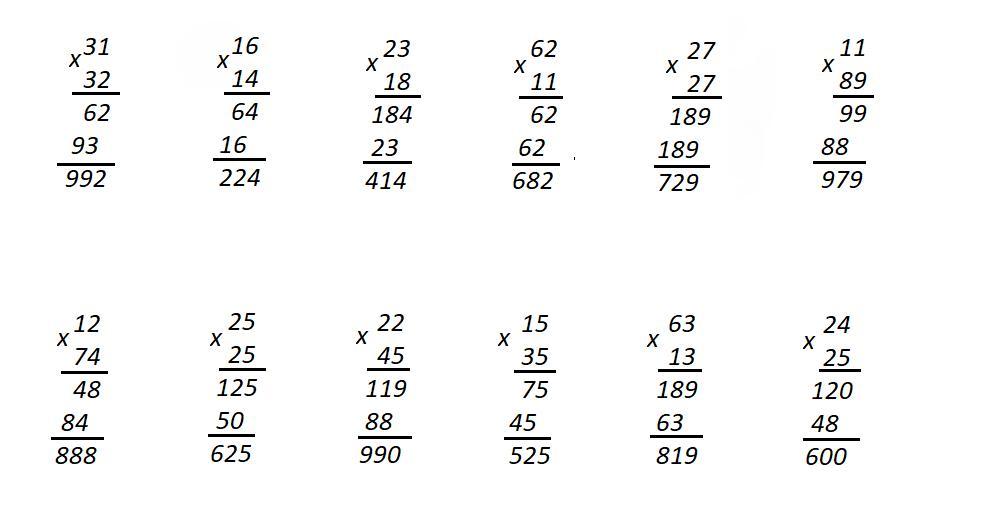
✅ ШАГ 2: Умножьте верхний множитель на Единицы, поместите цифру нижнего множителя и запишите произведение.
✅ ШАГ 3: Поставьте «0» на разряд единиц следующего продукта. Кроме того, очистить все предыдущие переносы, , чтобы избежать путаницы.
✅ ШАГ 4: Умножьте верхний коэффициент на разряд десятков нижнего множителя и запишите произведение.
✅ ШАГ 5: Сложите два продукта вместе, чтобы получить окончательный ответ.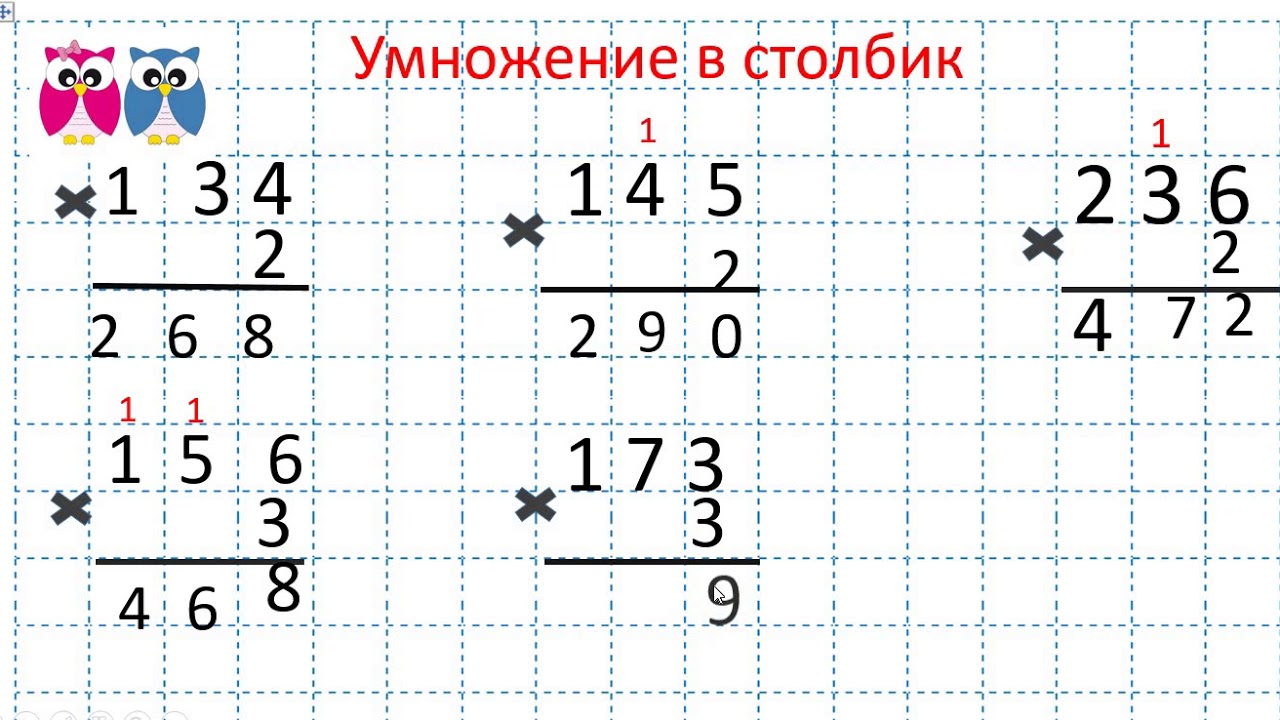
Поздравляем! 🎉 Теперь вы знаете, как умножать двузначные числа на трехзначные числа.
Теперь потренируемся.
Умножение предложений — Математика с мамой
Что такое умножение предложений?
Предложение умножения состоит из 3 чисел. Первое число перед знаком умножения говорит нам, сколько у нас равных групп. Второе число после знака умножения говорит нам, сколько их в каждой группе. Третье число идет после знака равенства и показывает, сколько их всего.
Пример предложения умножения: 3 × 5 = 15. Предложение умножения состоит из 3 чисел. 2 рядом со знаком умножения и один в конце, после знака равенства.
Это предложение умножения означает, что 3 лотов из 5 составляют в общей сложности 15.
Полезно помнить, что при написании предложений на умножение целых чисел наибольшее число ставится в конце после знака равенства.
Предложение умножения — это математический способ записать общее количество объектов, находящихся в равных группах.
Например, ниже у нас есть 3 бабочки.
У каждой бабочки по 2 крыла.
Чтобы найти общее количество крыльев, мы прибавляем 2 крыла первой бабочки к 2 крыльям второй бабочки и к 2 крыльям третьей бабочки.
Если мы сложим 2 + 2 + 2, то получим 6. Всего 6 крыльев.
Легче представить это как 3 группы по 2 крыла. У каждой бабочки 2 крыла, а бабочек 3.
Можно сказать, что у нас есть 3 лотов из 2 , что всего 6.
Знак умножения — ×. Знак умножения используется вместо записи «много» или «равные группы» .
Итак, мы можем написать 3 × 2 = 6, что означает, что 3 лота по 2 равны 6. Это быстрее, проще и занимает меньше места для записи по сравнению с записью предложения умножения словами.
Написание предложений умножения для массивов
Для массива можно записать 2 предложения на умножение. Чтобы написать предложение умножения для массива, выполните следующие действия:
Чтобы написать предложение умножения для массива, выполните следующие действия:
- Подсчитайте количество рядов и запишите это число.
- Запишите знак умножения, ×.
- Подсчитайте количество столбцов и запишите это число после знака умножения.
- Напишите знак равенства, =.
- Подсчитайте общее количество объектов в массиве и запишите это число после знака равенства.
- Чтобы найти другое предложение умножения, поменяйте местами два числа по обе стороны от знака умножения.
Массивы часто используются для обучения умножению. Массив представляет собой прямоугольный набор объектов (обычно счетчиков), расположенных в равных строках и столбцах.
Вот пример массива умножения.
У нас есть 5 счетчиков в каждом ряду.
У нас есть 3 строки по 5 в массиве. В каждом ряду по 5 фишек.
Мы можем сказать, что у нас есть 3 строки по 5. Поскольку каждая строка в массиве имеет одинаковое количество счетчиков, мы можем сказать, что у нас есть 3 «равных групп» 5 или просто 3 «много» 5 .
При написании предложения умножения для этого массива мы можем заменить слова ‘много’ со знаком умножения, ×.
Мы можем написать 3 × 5, чтобы обозначить 3 равных партии по 5 штук.
Число после знака равенства говорит нам, сколько всего счетчиков у нас есть в массиве. Если мы посчитаем все счетчики, мы увидим, что у нас их 15.
Предложение умножения для этого массива записывается как 3 × 5 = 15.
Это предложение умножения означает, что 3 лота по 5 дают в общей сложности 15.
При написании предложения об умножении с целыми числами два меньших числа идут первыми и идут после знака умножения. Большее число идет последним после знака равенства.
В предложении умножения два числа по обе стороны от знака умножения называются множителями, а число после знака равенства называется кратным.
Если вы записали два меньших числа наоборот, как 5 × 3 = 15 вместо 3 × 5 = 15, это не имеет значения, когда речь идет об этом массиве.
Это будет означать 5 лотов по 3. Мы все еще можем думать об этом массиве как представляющем 5 лотов по 3, потому что у нас есть 5 столбцов, каждый из которых содержит 3 счетчика.
У нас есть 3 строки, содержащие 5 счетчиков или 5 столбцов, каждый из которых содержит 3 счетчика.
Итак, для этого массива предложения умножения:
3 × 5 = 15 или
5 × 3 = 15.
Сумма должна стоять после знака равенства.
Вот еще один пример написания предложения умножения для массива.
В этом массиве у нас есть 4 счетчика в каждом столбце.
У нас есть 6 столбцов.
Есть 6 столбцов по 4. Поскольку в каждом столбце равное количество счетчиков, мы можем записать это как умножение.
У нас есть 6 лотов 4. Помните, что мы можем заменить слова лотов знаком умножения.
Мы можем записать предложение умножения для этого массива как 6 × 4 = 24.
Всего 24 счетчика. Мы можем считать счетчики по отдельности, многократно добавляя 4 + 4 + 4 + 4 + 4 + 4, чтобы получить 24.
Мы можем считать счетчики по отдельности, многократно добавляя 4 + 4 + 4 + 4 + 4 + 4, чтобы получить 24.
6 × 4 = 24 означает, что 6 лотов по 4 дают в сумме 24.
Первое число говорит нам, сколько у нас групп. Второе число говорит нам, сколько человек в каждой группе, а последнее число говорит нам, сколько их всего.
Два перемножаемых числа называются множителями, а число, стоящее после знака равенства, называется кратным.
Факторы умножаются вместе, чтобы получить кратное.
Помните, что при написании предложения умножения для массива возможны два варианта.
У нас 6 столбиков по 4 или 4 ряда по 6.
Мы можем поменять местами два числа по обе стороны от знака умножения.
У нас есть 6 × 4 = 24 или
4 × 6 = 24.
Как писать предложения с умножением
Чтобы написать предложение с умножением, выполните следующие действия:
- Подсчитайте количество одинаковых групп и запишите это число.

- Запишите знак умножения.
- Подсчитайте количество предметов в каждой группе и запишите это число после знака умножения.
- Напишите знак равенства.
- Подсчитайте общее количество объектов и запишите это число после знака равенства.
Вот пример написания предложения с умножением для описания проблемы.
У нас 2 божьи коровки и у каждой божьей коровки по 6 лапок.
Всего 12 ножек.
Нас просят написать предложение на умножение, чтобы показать, сколько всего ног.
Первый шаг – подсчитать количество равных групп. Ноги в двух группах. Каждая божья коровка представляет собой группу ножек.
У нас 2 группы, поэтому пишем 2.
У каждой божьей коровки по 6 ног, значит, по 6 ног в каждой группе.
2 лота по 6 ножек можно записать как 2 × 6.
Если мы посчитаем общее количество ножек, то увидим, что их 12.
Это общее число идет после знака равенства.
Предложение умножения для описания этой задачи: 2 × 6 = 12.



 234·2 (устно)
234·2 (устно)









 2 Карточки с числами для этапа мотивации.
2 Карточки с числами для этапа мотивации.