Состав числа в пределах 10
Описание
Состав числа в пределах 10 – это первые примеры, с которыми знакомится ребенок. Работать с голыми цифрами после подсчета картинок, палочек или собачек часто оказывается сложно. Простое заучивание наизусть не всегда дает быстрый и прочный результат. Именно поэтому нужна практика, которая поможет развить внимательность и закрепить навыки устного счета у детей. Для этого достаточно заниматься 10-15 минут в день.
Генератор примеров будет полезен как для подготовки дошкольников, так и для закрепления состава числа учеников 1 класса. Также программа помогает развить внимательность и закрепить навыки счета.
Программа представляет собой тренажер состава числа до 10. Программа написана в Excel с помощью макросов. Формируются таблицы в виде домиков на листе формата А4. Задания генерируются случайным образом, количество генераций не ограничено.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей, так как не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения примеров в пределах 10, затем перейти к более сложным примерам в пределах 20 и т. д. до 100.
д. до 100.
На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
I этап. Мотивация Цель – активизация учащихся. | Формулировать правила поведения на уроке. | Настраивать детей на работу. | I этап. Мотивация. -Прозвенел звонок. Начинаем наш урок. Математика — особая страна, Для путешествия смекалка нам нужна, Будем много думать и считать, И примеры не забудем мы решать. -Сегодня на уроке мы с вами отправимся в путешествие по планетам знаний вместе с Маленьким принцем, который жил на маленькой планете. Он трудился, любил любоваться закатом. Однажды он решил отправиться в путешествие по планетам вместе с перелётными птицами. -У каждого из вас на парте по 3 звёздочки удачи -зелёная, жёлтая, красная. По ходу путешествия, и в конце путешествия, вы проанализируете свою работу на уроке и дадите ей оценку с помощью этих звёздочек. Конечно, у зелёной звёздочки удача больше. -Кто играет дружно, Считает умело, Тот и в путешествие отправится смело. -Вместе с Маленьким принцем мы отправляемся на первую планету . Планета «Разминка». | I этап. Мотивация. Эмоциональный настрой на предстоящую деятельность; | II этап. Актуализация знаний и мотивация. Цель – — упражняться, в умении находить по общему признаку фигуры; -развивать мышление и память; — обогащать словарный запас, развивать речь. | Работать с информацией, формулировать собственное мнение и аргументировать его. | Организовать фронтальную работу по нахождению ответов на вопросы, создать условия для повторения , включить учащихся в обсуждение вопросов. | II этап. Актуализация знаний и мотивация. -На этой планете мы посчитаем устно. (Слайд1) Рассмотрите внимательно геометрические фигуры. По какому признаку фигуры можно разбить на группы, чтобы не было лишних? (по цвету и форме) -Какие фигуры будут в каждой группе? (квадрат, круг, треугольник) -У вас на парте выложен числовой ряд. Произнесём его хором. (ряд от 1 до 9) -Будем считать устно, используя карточки с цифрами. 1. Найдите значение суммы чисел 7 и 2 (9) Возьмите карточку с ответом, выложите перед собой. 2. Найдите значение разности чисел 8и 3 (5) Возьмите карточку с ответом, выложите перед собой. 3. Укажите предыдущее число 5 (4) Возьмите карточку с ответом, выложите перед собой. 4. Какое число стоит между числами 5 и 7 (6) Возьмите карточку с ответом, выложите перед собой. -Кто выполнил задание верно, тот получил ряд чисел: 9,5,4,6. (Слайд 2) -Оцените свою работу с помощью звёздочек. Поднимите их. Кто всё выполнил верно зелёную звёздочку, кто допустил одну ошибку жёлтую, кто допустил больше ошибок красную. -Расположите эти числа в порядке возрастания. -Кто выполнил задание верно, тот получил ряд чисел: 4, 5, 6, 9. (Слайд 3) -Оцените свою работу с помощью звёздочек. Поднимите их. Кто всё выполнил верно зелёную звёздочку, кто допустил одну ошибку жёлтую, кто допустил больше ошибок красную. -Какие из чисел можно представить в виде суммы двух одинаковых слагаемых? (4,6) Расскажите как это можно сделать. -Теперь верните карточки с цифрами на свои места. | II этап. Актуализация знаний и мотивация. Помочь учащимся целостно представить проект по обобщению, систематизации знаний в рамках темы. | III этап. Постановка учебной задачи. Цель – — сформировать знание о числе 10 — развивать творческое воображение; -создать условия для успешного изучения нового материала. 4 этап. Открытие детьми нового знания. Цель: сформировать представление детей о составе числа 10 5этап. Первичное закрепление. Цель: закрепить полученные знания 6этап Самостоятельная работа. Цель: проверить полученные знания на практике. 7этап. Включение в систему знаний и повторение. Цель: закрепить и повторить полученные знания. 8этап. Итог урока. Цель: подвести итог урока. 9этап.Рефлексия Цель: настрой учащихся на завершение работы. | Участвовать в практической работе по составлению состава числа 10 Осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь Оценивать правильность выполнения заданий. Участвовать в обсуждении проблемных вопросов, формулировать собственное мнение и аргументировать его. Работать с информацией. Формулировать собственное мнение и аргументировать его. | Организовать фронтальную работу по нахождению состава числа 10 обеспечить контроль за выполнением задания. Включить учащихся в обсуждение проблемных вопросов. Организовать фронтальную работу. | -У Самуила Яковлевича Маршака есть стихотворение «Весёлый счёт». Цифра вроде буквы О- Это ноль иль ничего Этот ноль такой хорошенький Но не значит ничегошеньки. Если ж слева рядом с ним Единицу примостим, Он побольше станет весить Потому, что это- десять. (Слайд 4) -Чем число 10 при записи отличается от остальных? (при записи его используется два знака- цифра 1 и 0) -Как называются числа от 0 до 9? (однозначное) -Каким будет число 10? (двузначным) -Где вы встречаетесь с числом 10 в жизни? (календарь, часы, деньги и др.) -Что есть у человека в количестве 10? (пальцы рук) Физкультминутка -Ребята, мы отправляемся на следующую планету. Планета «Проблемная». Жители этой планеты плачут, у них не получается заселиться в этот домик. На каждом этаже должно жить два человечка, и сумма их должна составлять 10. Ребята, а все ли из вас могут прямо сейчас помочь жителям заселиться в этот домик? (нет) -Значит, что мы сегодня должны сделать на уроке, какую задачу поставим на сегодняшний урок? -У нас задача на урок , как получить число 10. Состав числа 10. -А кто поможет нам в этом , мы сейчас узнаем разгадав загадку в учебнике. Стр.94 зад.1 -Прочитаем загадку. -Что это? (пальцы) -Ребята, сколько пальцев на одной руке? (5) -На второй? (5) — В сумме это? (10) -Давайте заселим этих жителей. -Ребята, давайте ещё немного поработаем с нашими пальчиками и расселим остальных жителей этого домика. -Сколько пальцев нужно загнуть, чтобы осталось 2 пальца? (8) 10 это? (8 и 2) Давайте заселим этих жителей. Следующий этаж домика. Сколько пальцев нужно загнуть, чтобы осталось 3 пальца? (7) 10 это? (7 и 3) Давайте заселим этих жителей. Следующий этаж домика. Сколько пальцев нужно загнуть, чтобы осталось 4 пальца? (6) 10 это? (4 и 6) Давайте заселим этих жителей. — Ребята, теперь жители рады, что вы им помогли, и говорят вам- » Спасибо!» — А теперь с Маленьким принцем отправляемся на следующую планету. Планета «Практическая». Стр. 94 зад.3 -Ребята, что видим на первом рисунке?(шары) Сколько их? Сколько шаров нужно добавить, чтобы их стало 10? -Что видим на втором рисунке? (флажки) Сколько их? Сколько флажков нужно добавить, чтобы их стало 10? -Что видим на следующем рисунке? (игрушки) Сколько их? Сколько игрушек нужно добавить, чтобы их стало 10? -Что видим на следующем рисунке? (звёзды) Сколько их? Сколько звёзд нужно добавить, чтобы их стало 10? -Молодцы! И с этим заданием вы справились. Теперь можем отправляться на следующую планету. Планета «Самостоятельная» -Ребята, Маленький принц очень любит стрелять. Давайте поможем ему в следующем задании набрать 10 очков. Стр.95 зад. 5 Первый выстрел устно, а остальные самостоятельно в рабочей тетради. -Проверим, верно ли выполнено задание. Каждый оцените свою работу в тетради. Кто выполнил задание верно нарисуйте зелёный кружок, кто допустил 1-2 ошибки жёлтый, кто допустил больше ошибок красный. -Ребята, Маленький принц очень доволен вашей работой. И предлагает вам отправиться на следующую планету. -Жителям этой планеты тоже нужна ваша помощь. Нужно разложить блоки на машины, чтобы машины не были перегружены. Поможем жителям? -Сколько может увезти первая машина? (9) Попробуем разложить блоки на машину. (1 ученик у доски) Сколько может увезти вторая машина? (10) Попробуем разложить блоки на машину. (1 ученик у доски) -Ребята, можно ли блоки увезти все за один раз? (нет) -Давайте проверим, помогли ли мы жителям этой планеты выполнить это задание. -Молодцы! Маленький принц вами очень доволен. -Подходит к концу наше путешествие. Давайте вспомним, какую задачу мы ставили в начале урока. Чему мы должны были научиться на уроке? -Мы знаем как получить число 10? С планетами пришла пора проститься, На землю всем нам надо торопиться. Кому из вас понравилось в пути? Кто ж смог звезду удачи обрести. -Оцените свою работу за весь урок. Возьмите свою звезду удачи и прикрепите её на звёздное небо на доске. Кто понял и может объяснить другому новый материал, прикрепите зелёную звезду, кто понял, но пока не может объяснить другому жёлтую звезду, кто пока не понял сегодняшний материал красную. Посмотрите на наше звёздное небо. Сколько здесь разных звёзд. -Всем спасибо за урок. Вы хорошо поработали. -Урок окончен. | III этап. Постановка учебной задачи. Сформировать представление учащихся о составе числа 10. 4 этап. Открытие детьми нового знания. Познакомить учащихся как можно получить число 10. 5этап. Первичное закрепление. Проверить и закрепить знания по новой теме. 6этап Самостоятельная работа. Самостоятельная работа : состав числа 10, решение выражений Делается вывод: Как получить число 10. 7этап. Включение в систему знаний и повторение. Повторение изученного материала. 8этап. Итог урока. Подведение итогов. 9этап.Рефлексия Эмоциональный настрой на окончание урока. |
«Состав числа 10. Решение задач»
Тема: «Состав числа 10. Решение задач.» (урок закрепления знаний)
Тип урока: урок-путешествие, урок-закрепление.
Формы организации: (фронтальная, индивидуальная
Материалы и оборудование: учебник «Математика» Моро М. И., 1 класс
сказка «Колобок», иллюстрации героев сказки «Колобок»,
оформление доски в соответствии с сюжетом сказки «Колобок»,
проектор, презентация к уроку
Цель – создание условий для закрепления знаний учащихся по теме «Состав числа 10. Решение задач.».
Задачи:
Обучающие:
Уметь выполнять сложение и вычитание в пределах 10 при решении числовых выражений, задач.
Закрепить знание состава числа 10,навык счета в пределах 10, умение решать текстовые составные задачи изученных видов.
Повторение порядкового счета в пределах 10, состав чисел первого десятка.
Развивающие:
Развивать логическое мышление, внимание учащихся, математическую речь.
Воспитывающие:
Воспитывать интерес к сказкам своего народа.
Формирование УУД
ПознавательныеУУД:
общеучебные: умение структурировать знания, контроль и оценка процесса и результатов деятельности; составление задачи на основе простейших математических моделей, выявлять и корректировать причины собственного затруднения.
логические:анализ, синтез, выбор оснований для сравнения.
Коммуникативные УУД: работать в паре, осуществлять конструктивное взаимодействие друг с другом; уметь слушать и вступать в диалог, умение выражать свои мысли.
Личностные УУД: формировать положительное отношение к учёбе и своим знаниям.
Регулятивные УУД: контролировать свою работу и своего товарища, планировать работу в парах, учиться совместно с учителем и другими учениками давать эмоциональную оценку своей деятельности и деятельности класса на уроке, воспитывать умение преодолевать трудности.
Планируемые результаты
Личностные
1. Формируем эмоциональное отношение к школе и учебной деятельности.Формируем общее представление о моральных нормах поведения.
Формируем чувство сострадания и сопереживания.
Формируем интерес к устному народному творчеству.
Метапредметные.
1 Умение анализировать, синтезировать и обобщать полученные ранее знания;
2. Умение концентрировать внимание на различных объектах урока;
3. Умение правильно составлять высказывания.
Предметные
Умение считать в пределах 10;
2. Умение решать задачи изученных видов;
3. Знание порядкового и количественного счета;
4. Знание геометрического материала
Ход урока:
1. Орг.момент
Цель: Организация учащихся к работе на уроке. СЛАЙД 1
Прозвенел и смолк звонок,
Чудесным пусть будет у вас настроение,
Легко и свободно даётся учение.
2. Введение в урок
Цель: Закреплять знания состава чисел, решать примеры на сложение и вычитание чисел, развивать логику и смекалку.
Сегодня мы не просто будем считать и решать, мы отправимся в путешествие. Путешествовать одним скучно и неинтересно, поэтому нужно брать с собой друзей. А вот кого мы возьмём в путешествие, вы узнаете, отгадав загадку.
Из муки его слепили,
После в печку посадили,
На окошке он студился,
По дорожке он катился.
Был он весел, был он смел,
И в пути он песню пел.(Колобок) ( Вывешиваю портрет Колобка на доску.)
– Ребята, я как-то читала сказку про колобка и вдруг поняла, что эта сказка не совсем правильная. В сказках всегда действуют две силы. Какие? (добро и зло).
– И что обычно побеждает в сказках? ( Добро.)
– А в сказке «Колобок»? ( Зло.)
– Как вы думаете, почему?
– Правильно, Колобок был доверчивым, не учился в школе, мало знал, не успел завести себе друзей.
– Давайте предложим Колобку дружбу и пригласим к нам на урок, изменим сказку и поможем спастись Колобку от зубов хитрой лисы.
3. Актуализация знаний. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Вспомним, с каких слов начинается эта сказка? ( «Жили-были дед и баба…»)
Так, так, а в чём они жили?( В доме)
А дома то у нас нет. Сейчас построим математический дом для деда и бабы.
(Повторяем состав числа 10.На доску вывесить крышу домика с числом 10 ) На доске цифры, дети выходят к доске и составляют состав числа 10. Все остальные ученики проверяют правильность с помощью светофоров.
Какой математический приём использовали ? (Перестановку слагаемых).
Первичное закрепление — в знакомой ситуации (типовые) — в изменённой ситуации (конструктивные)
Бабка колобок взяла,
На окошко понесла.
Колобок лежит, мечтает,
Звезды на небе считает.
— Посчитаем вместе с ним
а) Решение примеров у доски (2 ученика):
10 — = 5 2 + = 10
4 + = 10 10 — = 4
3 + = 10 1 + = 10
Решение примеров «цепочкой» по рядам
«Зарядка для ума» (3 карточки на 3 ряда)
10 – 8 = ___ +6 = ____-5 = ____+4 = ____ -1 =_____-2 = _____
ИЛИ
10 – 8 = ___ +6 = ____-5 = ____+4 = ____ -1
Дети решили, поднимают веер с получившимся ответом.
А теперь проверим! Если вы решили правильно, то в сумме получите число 10. Кто получил, поднимите руки в замок.
У: Какой математический приём использовали при решении примеров?
Д: Перестановку слагаемых.
– Как вы думаете, помогли мы Колобку научиться считать?
Определение темы урока. Постановка целей
– Проанализируйте выполненные задания и попробуйте определить тему урока. О чем мы будем говорить сегодня? (О составе числа 10)
– Какие цели мы поставим на сегодняшний урок? Дерево целей СЛАЙД 3
Что будем повторять? Повторим состав числа 10;
Какие знания и умения будем закреплять? закрепим навык счёта в пределах 10
— умение сравнивать числа и выражения, решать задачи.
Творческое применение и добывание знаний в новой ситуации (проблемные задания)
Колобок лежал, лежал на окошке , да и заскучал.
И решил колобок узнать, что там за окном. Но на окне замок. СЛАЙД 4. Поможем Колобку его открыть. Откройте тетради на печатной основе на странице 11,задание №2. Опираясь на знание состава числа, найдите значения выражений.
Самостоятельная работа учащихся.
Взаимопроверка. Поменяйтесь тетрадями и проверьте , правильно ли выполнено задание. Если не уверены, посмотрите на слайд. СЛАЙД 5.Если правильно, нарисуйте зелёный кружок, есть ошибки – жёлтый. У кого без ошибок? МОЛОДЦЫ!
Замок открылся, окно распахнулось, и колобок увидел дорожку. СЛАЙД 6 . Вот какая она. Ломаная, прямая, волнистая. По какой дорожке он покатится? (по прямой) Давайте её начертим у себя в тетрадях.
Какое расстояние необходимо пройти колобку до калитки?
Отрезок 5 см. А чем отличается отрезок от прямой линии? (имеет начало и конец)
Открыли рабочие тетради. Записываем число. Сколько клеточек вниз и вправо?. Взяли линейки и карандаши, чертим отрезок длиной 5 см. Подпишите длину отрезка. Ниже начертите отрезок на 2 см меньше.
Ниже начертите отрезок на 2 см меньше.
Что значит на 2 см меньше? Какой длины начертим отрезок? (3см) Как узнали его длину? (5-2=3см)
По тропинке он бежит,
Заяц на тропе сидит. РИСУНОК ЗАЙЦА НА ДОСКУ К ЗАДАНИЮ. В РУКАХ ЗАДАНИЕ < > =
Говорит ему Косой:
«Колобок, а ну постой.
Я тебя бы сразу съел,
Да ведь ты же поумнел.
-Если ты решишь заданье,
Я тебя без наказанья
В путь дорожку опущу
И морковкой угощу!»
Надо ребята Колобочку помочь, чтоб от Зайчишки сбежать он смог.
Сравнение чисел и выражений.
Выполняем на доске и в тетради задание из учебника на с.18(под чертой)
К доске по одному ученику. Решают с комментированием.
8>5 , 6<9, сумма чисел 6+2 > 8, разность чисел 8 и 1 < 8, 9+1>9, 9-1<9
Покатился Колобок дальше.
Вот навстречу серый волк, РИСУНОК ВОЛКА НА ДОСКУ К ЗАДАНИЮ.
В колобках он знает толк.
Испугался Колобок:
«Ты меня послушай, Волк,
Песню я тебе спою…»
Волк сердито: «Не велю! Отгадай загадку!
Есть у меня работники,
Во всем помочь охотники.
Целый десяток верных ребяток. (Пальцы.)
А сколько их? 5 и 5.А на двух руках?
Отгадал Колобок загадку и покатился дальше. Катится и песенку поёт. СЛАЙД 7
Песня «Две руки».
Физминутка
Цель: снять усталость и мышечное напряжение
Постановка проблемы. Открытие нового знания.
Колобок вперед бежит,
А на пне медведь сидит. РИСУНОК МЕДВЕДЯ НА ДОСКУ.
Колобка он увидал,
Облизнулся и сказал.
Будет мне обед! Удача!
Если не решишь задачу.
Работа с учебником .
— Давайте, ребята, выручать Колобка. Прочитаем задачу№3 на с.18.
Из каких частей состоит задача?
О чём говорится в условии? О чём задаче спрашивается?
Сколько вопросов в задаче? Значит, сколько будет действий?
Какое действие следует выполнить, чтобы ответить на первый вопрос задачи7 (вычитание)
Почему? (т. к. в условии сказано, что российских марок на 3 меньше)
к. в условии сказано, что российских марок на 3 меньше)
Запишите решение. У доски….(6-3=3 (м.)
Какое действие необходимо выполнить, чтобы ответить на второй вопрос задачи? (сложение)
Почему? (т.к. спрашивается, сколько всего марок).
Запишите решение У доски …(6+3=9 (м.)
Ответ: Ответьте на поставленные вопросы задачи. Записываем Ответ: 3м., 9м.
-Молодцы, снова мы выручили Колобка и покатился Колобок дальше.
Катится и по сторонам смотрит. Давайте и мы посмотрим.
Физминутка Гимнастика для глаз
Ах, как долго мы писали, Глазки у ребят устали. (Поморгать глазами.)
Посмотрите все в окно,
(Посмотреть в окно в даль.)
Солнце в небе высоко.
(Посмотреть на небо.)
Руки за спину, головки назад.
(Закрыть глаза, расслабиться.)
Глазки пускай в потолок поглядят. (Открыть глаза, посмотреть вверх.)
Головки опустим — на парту гляди. (Вниз.)
И снова наверх — где там лампа висит? (Вверх.)
Мы глаза сейчас закроем,
(Закрыть глаза ладошками.)
В классе радугу построим, Вверх по радуге пойдем,
(Посмотреть по дуге вверх, вправо и вверх — влево.)
Вправо, влево повернем.
И на доску все взглянули…
Наши глазки отдохнули.
Посмотрите, всё что вы нарисовали своими глазками, появилось на нашем экране.
Что видим ? (геометрические фигуры?СЛАЙД 10
Какой фигуры недостаёт на каждой карточке?
СЛАЙД 11
Закрепление.
Цель: выявит качество и уровень усвоения учащимися знаний и способы деятельности.
— Пока мы выполняли задания, Колобок соскучился по бабушке и решил вернуться домой. Катится по дороге, вдруг из-за елки Лиса. РИСУНОК ЛИСЫНА ДОСКУ.
РИСУНОК ЛИСЫНА ДОСКУ.
— Хитро, ласково так заговорила: “Здравствуй, колобок, румяненький бок. Слышала – гуляешь, зверушкам помогаешь, задачки решаешь. А вот сможешь ли моё задание выполнить? Я ведь в лесу лучший математик. А не выполнишь я тебя съем”. Делать нечего, пришлось ему соглашаться. СЛАЙД 12
Лиса хитрая и задачи у неё хитрые.
1. В пакете 5 лисичек, а в корзине два раза по столько же лисичек. Сколько лисичек в корзине?5+5=10
Ребята, а о каких лисичках идёт речь?
Какие это грибы? (съедобные)
2.По дороге идут 5 детей. За каждым мальчиком, кроме последнего, идет девочка. Сколько девочек идет по дороге?
Задание на внимание СЛАЙД 17-18
— Молодец колобок, справился с заданием. Делать нечего пришлось лисе отпустить колобка, осталась она ни с чем.
Цель: выявит качество и уровень усвоения учащимися знаний и способы деятельности.
— Прикатился Колобок домой, а бабушка хоть и обрадовалась, но все же решила немного проучить его за непослушание.
— Ребята, за что бабушка ругала колобка?
— Нужно слушать взрослых, без разрешения нельзя уходить. Если вы хотите идти куда-то, то надо обязательно отпрашиваться у взрослых.
Итог урока.
Цель: умение учащихся оценивать себя, границы своего знания и незнания. -Ребята, вспомните, с какими сказочными персонажами встретился Колобок во время своего путешествия.
-Где живут эти животные?
— Как вы думаете, зверям трудно зимой?
— Зверям трудно зимой во время снегопадов, метелей, в сильные морозы. В такую погоду они часто погибают от голода. Поэтому зверей, так же как и птиц, зимой нужно подкармливать.
А что помогло Колобку сегодня на нашем уроке?
-Только настоящие друзья придут быстро на помощь. Давайте всегда помогать друг другу и своим близким.
Колобок рассказал своим бабушке и дедушке, чему он научился во время своего путешествия. И мы сейчас тоже скажем. СЛАЙД 13
Продолжите предложения.
Я узнал…
Я научился…
Мне было интересно…
Мне было трудно…
11. Рефлексия
Рефлексия
– Вспомните сегодняшний урок. Если он принёс вам знания и поможет в дальнейшем и у вас хорошее настроение, возьмите зелёный колобочек; Если не всё на уроке получалось, то возьмите жёлтый колобочек.если вам было трудно, многое не получалось, то возьмите красный колобочек.
– Посмотрите, сколько зелёных колобочков! Думаю, что урок удался!
Домашнее задание : в тетради на печатной основе на с.11 №1,№3
12. Награждение медалями «За спасение Колобка». За активную работу на уроке Колобок вам вручает вот такие медали…
— За ударный труд – награда – медаль «За спасение Колобка»
1
Орг.момент
СЛАЙД 1
-Прозвенел и смолк звонок,
Вас ждёт интересный, полезный урок.
Чудесным пусть будет у вас настроение,
Легко и свободно даётся учение.
-Сегодня мы не просто будем считать и решать, мы отправимся в путешествие. Путешествовать одним скучно и неинтересно, поэтому нужно брать с собой друзей. А вот кого мы возьмём в путешествие, вы узнаете, отгадав загадку.
-Из муки его слепили,
После в печку посадили,
На окошке он студился,
По дорожке он катился.
Колобок) ( Вывешиваю портрет Колобка на доску.)СЛАЙД 2
2
– Ребята, я как-то читала сказку про колобка и вдруг поняла, что эта сказка не совсем правильная. В сказках всегда действуют две силы. Какие? (добро и зло).
– И что обычно побеждает в сказках? ( Добро.)– А в сказке «Колобок»? ( Зло.)– Как вы думаете, почему?
– Правильно, Колобок был доверчивым, не учился в школе, мало знал, не успел завести себе друзей.
– Давайте предложим Колобку дружбу и пригласим к нам на урок, изменим сказку и поможем спастись Колобку от зубов хитрой лисы.
-Вспомним, с каких слов начинается эта сказка? ( «Жили-были дед и баба…»)Так, так, а в чём они жили?( В доме)
А дома то у нас нет. Сейчас построим математический дом для деда и бабы.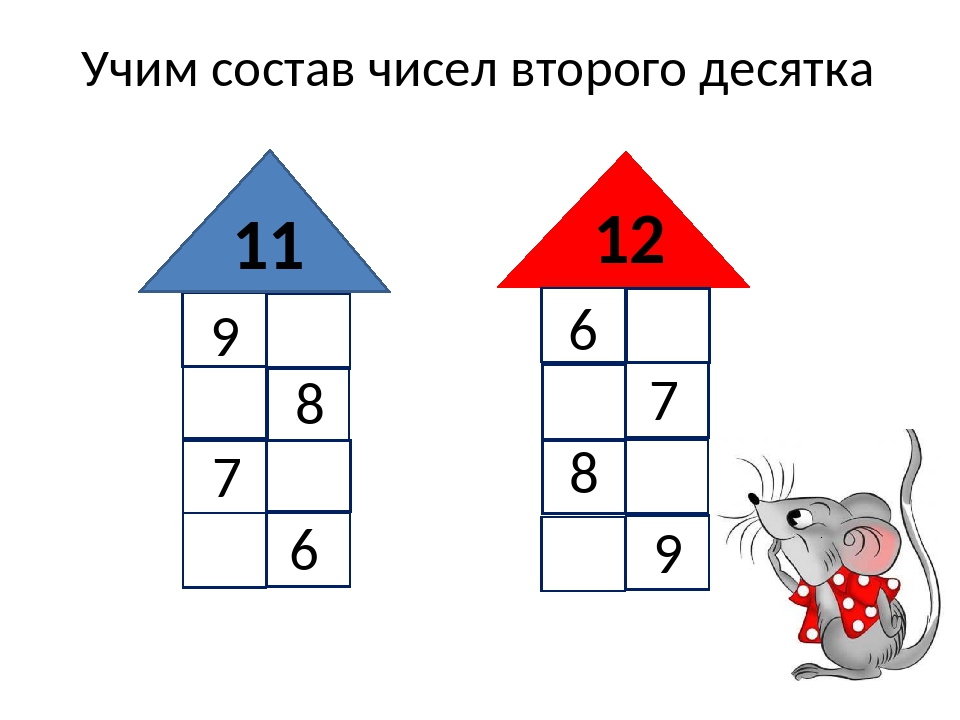 ( На доску вывесить крышу домика с числом 10 ) _ Начинаем строительство дома. На доске цифры, дети выходят к доске и составляют состав числа 10. Все остальные ученики проверяют правильность с помощью светофоров.
( На доску вывесить крышу домика с числом 10 ) _ Начинаем строительство дома. На доске цифры, дети выходят к доске и составляют состав числа 10. Все остальные ученики проверяют правильность с помощью светофоров.
Какой математический приём использовали ? (Перестановку слагаемых).
3 Бабка колобок взяла,
На окошко понесла.
Колобок лежит, мечтает,
Звезды на небе считает.
— Посчитаем вместе с ним
а) к ДОСКЕ:_2 УЧ._________________________________________
10 — = 5 2 + = 10
4 + = 10 10 — = 4
3 + = 10 1 + = 10
Все остальные решаем цепочку примеров.
Взяли карточку. НАЧАЛИ!
«Зарядка для ума» (3 карточки на 3 ряда)
10 – 8 = ___ +6 = ____-5 = ____+4 = ____ -1 =_____-2 = _____
ИЛИ
10 – 8 = ___ +6 = ____-5 = ____+4 = ____ -1
Дети решили, поднимают веер с получившимся ответом.
А теперь проверим! Если вы решили правильно, то в сумме получите число 10. Кто получил, поднимите руки в замок.
Что повторили? (Состав числа 10). Какой математический приём использовали при решении примеров?
Д: Перестановку слагаемых.
– Как вы думаете, помогли мы Колобку научиться считать?
4
– Проанализируйте выполненные задания и попробуйте определить тему урока. О чем мы будем говорить сегодня? (О составе числа 10)ОТКРЫТЬ ТЕМУ УРОКА
– Какие цели мы поставим на сегодняшний урок? Дерево целей СЛАЙД 3
Что будем повторять? Повторим состав числа 10;
Какие знания и умения будем закреплять? закрепим навык счёта в пределах 10
— умение сравнивать числа и выражения, решать задачи.
Колобок лежал, лежал на окошке , да и заскучал.
И решил колобок узнать, что там за окном. Но на окне замок. СЛАЙД 4. Поможем Колобку его открыть. Откройте тетради на печатной основе на странице 11,задание №2. Опираясь на знание состава числа, найдите значения выражений.
Самостоятельная работа учащихся.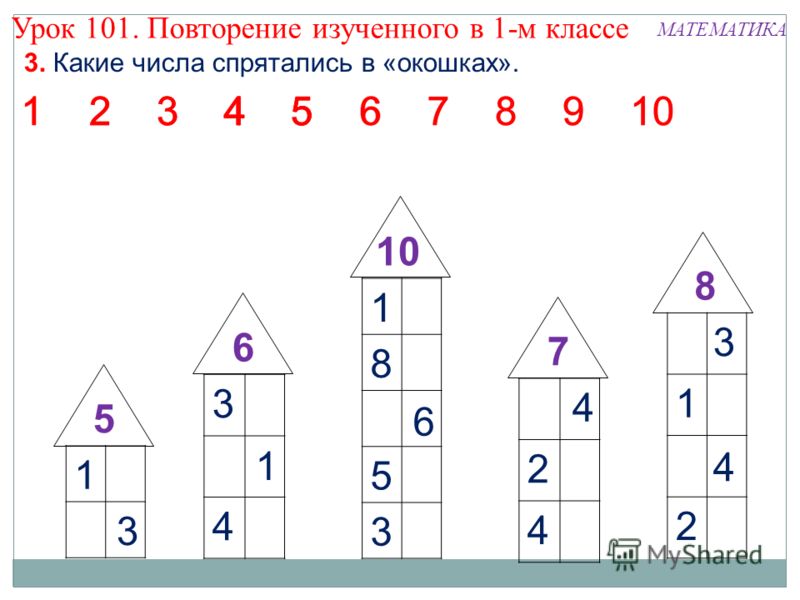 Взаимопроверка.
Взаимопроверка.
5 Поменяйтесь тетрадями и проверьте , правильно ли выполнено задание. Если не уверены, посмотрите на слайд. СЛАЙД 5.Если правильно, нарисуйте зелёный кружок, есть ошибки – жёлтый. У кого без ошибок? МОЛОДЦЫ!
Замок открылся, окно распахнулось, и колобок увидел дорожку. СЛАЙД 6 . Вот какая она. Ломаная, прямая, волнистая. По какой дорожке он покатится? (по прямой) Давайте её начертим у себя в тетрадях.
Какое расстояние необходимо пройти колобку до калитки?
Отрезок 5 см. А чем отличается отрезок от прямой линии? (имеет начало и конец)
Открыли рабочие тетради. Записываем число. Сколько клеточек вниз и вправо?. Взяли линейки и карандаши, чертим отрезок длиной 5 см. Подпишите длину отрезка. Ниже начертите отрезок на 2 см меньше.
Что значит на 2 см меньше? Какой длины начертим отрезок? (3см) Как узнали его длину? (5-2=3см)
6 По тропинке он бежит,
Заяц на тропе сидит. РИСУНОК ЗАЙЦА НА ДОСКУ К ЗАДАНИЮ. Около задания нарисовать < > =
Говорит ему Косой:
«Колобок, а ну постой.
Я тебя бы сразу съел,
Да ведь ты же поумнел.
-Если ты решишь заданье,
Я тебя без наказанья
В путь дорожку опущу
И морковкой угощу!»
Надо ребята Колобочку помочь, чтоб от Зайчишки сбежать он смог.
Сравнение чисел и выражений. Выполняем на доске и в тетради задание из учебника на с.18(под чертой)
К доске по одному ученику. Решают с комментированием.
8>5 , 6<9, сумма чисел 6+2 > 8, разность чисел 8 и 1 < 8, 9+1>9, 9-1<9
7 Покатился Колобок дальше.
Вот навстречу серый волк, РИСУНОК ВОЛКА НА ДОСКУ К ЗАДАНИЮ.
В колобках он знает толк.
Испугался Колобок:
«Ты меня послушай, Волк,
Песню я тебе спою…»
Волк сердито: «Не велю! Отгадай загадку!
Есть у меня работники,
Во всем помочь охотники.
Целый десяток верных ребяток. (Пальцы. )
)
А сколько их? 5 и 5.А на двух руках?
Отгадал Колобок загадку и покатился дальше. Катится и песенку поёт. СЛАЙД 7
Песня «Две руки».
Физминутка
Цель: снять усталость и мышечное напряжение
Постановка проблемы. Открытие нового знания.
Колобок вперед бежит,
А на пне медведь сидит. РИСУНОК МЕДВЕДЯ НА ДОСКУ.
Колобка он увидал,
Облизнулся и сказал.
Будет мне обед! Удача!
Если не решишь задачу.
8 Работа с учебником .
— Давайте, ребята, выручать Колобка. Прочитаем задачу№3 на с.18.
Из каких частей состоит задача?
О чём говорится в условии? О чём задаче спрашивается?
Сколько вопросов в задаче? Значит, сколько будет действий?
Какое действие следует выполнить, чтобы ответить на первый вопрос задачи7 (вычитание)
Почему? (т.к. в условии сказано, что российских марок на 3 меньше)
Запишите решение. У доски….(6-3=3 (м.)
Какое действие необходимо выполнить, чтобы ответить на второй вопрос задачи? (сложение)
Почему? (т.к. спрашивается, сколько всего марок).
Запишите решение У доски …(6+3=9 (м.)
Ответ: Ответьте на поставленные вопросы задачи. Записываем Ответ: 3м., 9м.
9 -Молодцы, снова мы выручили Колобка и покатился Колобок дальше.
Катится и по сторонам смотрит. Давайте и мы посмотрим.
Физминутка Гимнастика для глаз
Ах, как долго мы писали, Глазки у ребят устали. (Поморгать глазами.)
Посмотрите все в окно,
(Посмотреть в окно в даль.)
Солнце в небе высоко.
(Посмотреть на небо.)
Руки за спину, головки назад.
(Закрыть глаза, расслабиться.)
Глазки пускай в потолок поглядят. (Открыть глаза, посмотреть вверх.)
Головки опустим — на парту гляди. (Вниз.)
И снова наверх — где там лампа висит? (Вверх.)
Мы глаза сейчас закроем,
(Закрыть глаза ладошками.)
В классе радугу построим, Вверх по радуге пойдем,
(Посмотреть по дуге вверх, вправо и вверх — влево. )
)
Вправо, влево повернем.
И на доску все взглянули…
Наши глазки отдохнули.
10 Посмотрите, всё что вы нарисовали своими глазками, появилось на нашем экране.
Что видим ? (геометрические фигуры?СЛАЙД 10
Какой фигуры недостаёт на каждой карточке?
СЛАЙД 11
— Пока мы выполняли задания, Колобок соскучился по бабушке и решил вернуться домой. Катится по дороге, вдруг из-за елки Лиса. РИСУНОК ЛИСЫ НА ДОСКУ.
— Хитро, ласково так заговорила: “Здравствуй, колобок, румяненький бок. Слышала – гуляешь, зверушкам помогаешь, задачки решаешь. А вот сможешь ли моё задание выполнить? Я ведь в лесу лучший математик. А не выполнишь я тебя съем”. Делать нечего, пришлось ему соглашаться. СЛАЙД 12
11 Лиса хитрая и задачи у неё хитрые.
1. В пакете 5 лисичек, а в корзине два раза по столько же лисичек. Сколько лисичек в корзине?5+5=10
Ребята, а о каких лисичках идёт речь?
Какие это грибы? (съедобные)
2.По дороге идут 5 детей. За каждым мальчиком, кроме последнего, идет девочка. Сколько девочек идет по дороге?
— Молодец колобок, справился с заданием. Делать нечего пришлось лисе отпустить колобка, осталась она ни с чем.
12 — Прикатился Колобок домой, а бабушка хоть и обрадовалась, но все же решила немного проучить его за непослушание.
— Ребята, за что бабушка ругала колобка?
— Нужно слушать взрослых, без разрешения нельзя уходить. Если вы хотите идти куда-то, то надо обязательно отпрашиваться у взрослых.
Итог урока.
Цель: умение учащихся оценивать себя, границы своего знания и незнания. -Ребята, вспомните, с какими сказочными персонажами встретился Колобок во время своего путешествия.
-Где живут эти животные?
— Как вы думаете, зверям трудно зимой?
— Зверям трудно зимой во время снегопадов, метелей, в сильные морозы. В такую погоду они часто погибают от голода. Поэтому зверей, так же как и птиц, зимой нужно подкармливать.
А что помогло Колобку сегодня на нашем уроке?
-Только настоящие друзья придут быстро на помощь. Давайте всегда помогать друг другу и своим близким.
Колобок рассказал своим бабушке и дедушке, чему он научился во время своего путешествия. И мы сейчас тоже скажем. СЛАЙД 13
13 Продолжите предложения.
Я узнал…
Я научился…
Мне было интересно…
Мне было трудно…
14 Рефлексия
– Вспомните сегодняшний урок. Если он принёс вам знания и поможет в дальнейшем и у вас хорошее настроение, возьмите зелёный колобочек; Если не всё на уроке получалось, то возьмите жёлтый колобочек.если вам было трудно, многое не получалось, то возьмите красный колобочек.
– Посмотрите, сколько зелёных колобочков! Думаю, что урок удался!
Домашнее задание : в тетради на печатной основе на с.11 №1,№3
15. Награждение медалями «За спасение Колобка». За активную работу на уроке Колобок вам вручает вот такие медали…
— За ударный труд – награда – медаль «За спасение Колобка»
«Число 10. Состав числа 10»
Тема: Число 10. Состав числа 10.
Тип урока: Ознакомление с новым материалом.
Задачи:
- Познакомить с числом 10 и его составом.
- Учить операциям сложения и вычитания в пределах 10 с опорой на его состав.
- Закрепить знания составов чисел до 9, действий в пределах 9.
- Учить самостоятельности и умению слушать других.
- Развивать речь, память, внимание и логическое мышление.
Ход урока
I. Орг. момент.
— Прозвенел звонок, начинается урок.
II. Актуализация знаний.
— Ребята, посмотрите на доску.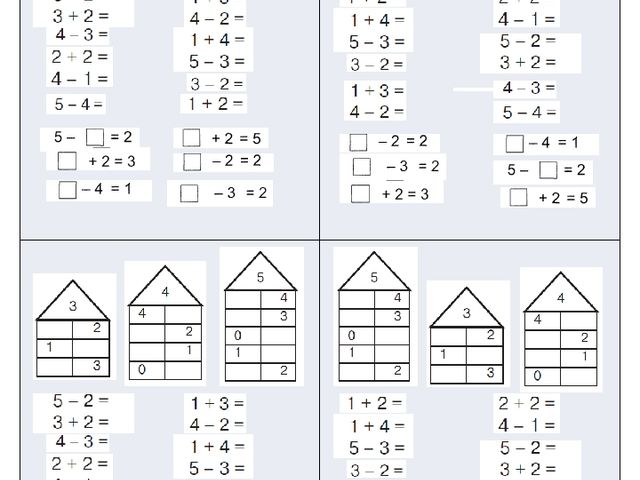 В домиках № 7 и № 9
некоторые жильцы получили странное послание.
Хотите узнать какое?
В домиках № 7 и № 9
некоторые жильцы получили странное послание.
Хотите узнать какое?
— Тогда в тетрадях запишите этих жильцов – пропущенные числа в парах состава чисел 7 и 9, а на доске работают двое.
— Сейчас расположите числа в порядке убывания, и в соответствии с буквенным кодом прочитайте им послание. Что у вас получилось?
— Что такое клад?
— Хотите найти математический клад?
— Какими качествами должны обладать кладоискатели?
— А кто ещё всегда ищет клады?
— Откроем учебник на стр. 35 № 8. Посмотрите, пираты нас хотят опередить, они уже на острове. Давайте узнаем, найдут ли они клад, для этого вычислим примеры по стрелкам. Что у вас получилось?
— Что заметили? Верно, ответ предыдущего примера становится началом следующего. Такие примеры называются “круговыми”. Ответ последнего должен быть началом всей цепочки:
— Где можно было ещё замкнуть круг?
— Это нам позволит обогнать пиратов. Пусть они ходят по кругу, а мы пойдём вперёд к цели. Вот и нужное место. Надо копать.
III. Физкультминутка.
Копаем землю и её выбрасываем их ямы (имитация движений под счёт до 9).
IV. Новый материал.
— Ну, вот и заветный сундук, но на нём замок. На замке числа. Какие, узнаем, выполнив математический диктант. Все пишут в тетради, а на двое доске. Внимание:
— запишите число, следующее за 7 (8)
— запишите число, предыдущее 5 (4)
— запишите число, стоящее между 6 и 8 (7)
— запишите соседей числа 2 (1 и 3)
— запишите число, стоящее справа от 8 (9)
— запишите число, стоящее слева от 6 (5)
— я задумала число, оно предшествует 3 (2)
— Елена Илларьевна задумала число, оно следует за 5 (6)
— Проверяем (взаимопроверка) работу на доске.
— У нас получился числовой ключ, чтобы им открыть замок, надо числа расположить в порядке возрастания. Пишите и диктуйте: (учитель на доске)
1, 2, 3, 4, 5, 6, 7, 8, 9.
— Какое число следует в ряду чисел за 9?
— Вот он и наш клад – число 10!
— Какая же тема нашего урока?
— Чему будем учиться?
— Что знаете про число 10?
— Число 10 – самое маленькое двузначное число, в записи берутся 2 цифры. Что обозначает цифра 1? Что у человека есть в количестве 1 десятка?
— В тетради запишем строчку числа 10. сколько получилось десятков? Кто знает, какое это число?
— Нам надо разложить 10 алмазов из нашего клада в 2 мешочка. Как можно это сделать? (В тетради – дети, учитель – на доске)
— Что у нас получилось? Какие случаи лишнее? Почему? (По переместительному свойству сложения)
— Что будем запоминать? (Хором, по одиночке, с закрытыми глазами)
— Кто сможет закончить состав 10 в разбивку? (Учитель – 10 это 8 — ученик – 2,
— У дружных кладоискателей всё делится как? Какой случай из состава подойдёт?
V. Физкультминутка
“5 на 5” (5 – прыжков, 5 — хлопков)
VI. Закрепление изученного.
— А сейчас, давайте возьмём другие пары из состава 10. Запишите все взаимосвязанные равенства с: 8 + 2 = 10 (I ряд)
7 + 3 = 10 (II ряд)
6 + 4 = 10 (III ряд)
— Если затрудняетесь, консультируетесь в паре с соседом. Что у вас получилось?
8 + 2 = 10
2 + 8 = 10
10 – 8 = 2
10 – 2 = 8
— Что же за взаимосвязанные равенства должны быть? (Переместительное свойство сложения обратные случаи вычитания)
— Откроем учебник на стр. 39 № 5. Что нужно сделать? Сравним с объяснением:
1 столбик – с опорой на числовой отрезок.
(10 больше 8, т.к. на числовом отрезке стоит справа, 7 меньше 10, т.к. на числовом отрезке стоит слева)
2 столбик – не вычисляя
(10 + 0 = 10 – 0, т.к. нуль есть ничего,
10 – 2 > 10 – 5, т.к. при одинаковом уменьшаемом чем меньше убираем, тем больше остаётся)
3 столбик – не вычисляя
(3 + 7 = 2 + 8, т.к. первое слагаемое убыло на 1, а второе уменьшилось тоже на 1,
1 + 9 > 5 – 5, т.к. справа число самоуничтожается в 0)
— Решим уравнения № 6 (стр 39, по вариантам). Что получилось? Что такое Х?
— В тетрадь решим задачи № 7 (стр. 39). Читаем задачу (а). Какая схема на доске подойдёт к этой задаче? Что подпишем? Ведёт решение ученик на доске. (Аналогичная работа над двумя другими задачами.)
VII. Рефлексия.
— Что сегодня изучали?
— Игра “Часики”: за 1 минуту вы должны восстановить соседей числа 10 на песочных часиках (у каждого ученика – листок с заданием). Приготовились. Начали. Что получилось?
— Встаньте, у кого верные часики.
— Хлопните в ладоши, кому было легко выполнить это задание.
— Подпрыгните 10 раз, кому было интересно сегодня на уроке.
VIII. Домашнее задание.
— В дневниках д/з – стр. 36.
Урок 15. состав чисел от 2 до 10. числа в загадках, пословицах, поговорках — Математика — 1 класс
Математика
1 класс
Урок 15
Состав чисел от 2 до 10.
Числа в загадках, пословицах, поговорках
Перечень вопросов, рассматриваемых на уроке:
- Состав чисел от 2 до 10.
- Сравнение чисел от 2 до10.
- Запись сравнения чисел при помощи знаков «больше», «меньше», «равно».
- Составление и чтение неравенств.
- Создание проекта «Математика вокруг нас».
Глоссарий по теме
Формирование вычислительных навыков в пределах 10. Математические представления в количественном и пространственном отношении. Составление из двух чисел числа от 2 до 10. Сравнение любых двух чисел. Запись результата сравнения, используя знаки сравнения «>», «<», «=».
Математические представления в количественном и пространственном отношении. Составление из двух чисел числа от 2 до 10. Сравнение любых двух чисел. Запись результата сравнения, используя знаки сравнения «>», «<», «=».
Ключевые слова
Состав чисел; сравнение чисел; знаки сравнения «больше», «меньше», «равно»; равенства; неравенства.
Основная и дополнительная литература:
1. Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. Ч. 1.– М.: Просвещение, 2017. – С. 62 – 65.
2. Моро М. И., Волкова С. И. Математика рабочая тетрадь. 1 кл. 1 ч.– М.: Просвещение, — С. 23.
3. Моро М. И., Волкова С. И. Для тех, кто любит математику. 1 класс., с.24-25
4. Кац Е. М. Необычная математика. Тетрадь логических заданий для детей 6 – 7лет. – М.: МЦНМО, 2018. – С. 21-23.
5. Кац Е. М. Необычная математика. Тетрадь логических заданий для детей 7 – 8 лет. – М.: МЦНМО, 2018. – С. 4.
На уроке мы узнаем о том, как можно получать изученные числа разными способами. Научимся применять навыки счёта и знание состава числа. Сможем, с помощью математических знаков сравнивать любые два числа от 2 до 10.
Основное содержание урока
Сегодня мы с вами повторим состав чисел. А разве числа из чего-то состоят? Конечно, если число больше единицы, то его можно разложить на слагаемые.
Мы с вами отправляемся на лесную прогулку и повстречаем там много сказочных друзей. Но как же встречаться с друзьями без подарков? Для лесных жителей мы сегодня соберём корзинки с овощами и фруктами.
В первую корзинку мы соберём подарок для лосёнка.
Ему нужно положить 2 предмета. Что любят лоси? Грибы, особенно мухоморы, и соль. Значит два – это …. Один и один.
Для ёжика в корзинку нужно положить три предмета. Что любят ёжики? Грибы и яблоки.
Как мы можем это сделать? Положить два гриба и одно яблоко или наоборот, один гриб и два яблока. Значит три – это один и два или два и один. Ведь от перестановки слагаемых сумма не меняется
.
Для белочек в корзинке должно лежать четыре предмета. Что любят белки? Это будут орехи и грибочки. Как мы можем это сделать? Положить один орех и три грибочка или наоборот, три ореха и один грибочек, а ещё можно разложить по два.
Для зайчиков в корзинке должно лежать пять предметов. Что любят зайцы? Морковь и капусту. Как мы можем это сделать? Положить одну морковь и четыре кочана капусты или наоборот, четыре морковки и один кочан капусты. А как по-другому? Две морковки и три кочана капусты или наоборот, три морковки и два кочана капусты.
Для детёнышей кабана, маленьких поросят нужно положить шесть предметов. Что любят кабаны? Жёлуди и яблоки. Как разложить? Один жёлудь и пять яблок или наоборот, пять желудей и одно яблоко. Два жёлудя и четыре яблока или наоборот, четыре жёлудя и два яблока. А можно положить поровну, по три.
Для маленьких медвежат мы положим семь предметов. Что любят медведи? Мёд и малину. Как разложить? Одна баночка мёда и шесть баночек малинового варенья или наоборот, шесть баночек мёда и одну малинового варенья. Две мёда и пять варенья или наоборот, пять мёда и две варенья. Три мёда и четыре варенья или наоборот, четыре мёда и три варенья.
Теперь, когда вы знаете состав чисел, вам будет легче решать примеры. Вы знаете, что семь – это 3 и 4, получается, что к трём прибавить четыре получается семь. А если из семи вычесть четыре, то останется три. И наоборот, если из семи вычесть три, то получится четыре. Главное, запомнить состав чисел.
Назовите соседей чисел:
Ответ:
Какие числа надо переставить, чтобы они шли в порядке возрастания: 1, 3, 2, 5, 4, 6, 7, 9, 8?
Ответ: 3 и 2, 5 и 4, 9 и 8.
Разбор тренировочных заданий
Выделите жёлтым цветом все равенства, а зелёным цветом все неравенства:
Ответ:
Найдите неверные неравенства и равенства. Замените в них знак, чтобы они стали верными.
Ответ:
Вставьте недостающие числа:
Ответ:
Рассмотрите рисунок. Сравните чего больше, чего меньше. Заполните пропуски цифрами.
Ответ:
|
Мотивация к учебной деятельности
|
ХОД УРОКА К нам на урок должен прийти необыкновенный гость. |
Каждый день, всегда, везде, |
Актуализация знаний и фиксация затруднений в деятельности.
Повторение названий компонентов при вычитании
Физ.минутка
Запись числа в тетради
Выявление причин затруднений и постановка цели деятельности
|
На доске (слайд 1)
Вопрос: Что вы видите на доске?
Загадка: Получился математический снеговик, а на урок к нам придёт снеговик сказочный (слайд 3) Задание: Чей ряд быстрее приготовится к встрече гостя и наведёт порядок на столах? Учитель: А вот и наш гость пожаловал (слайд 4) Нравится он вам? Занимательный момент. Появление снеговика Учитель: Снеговик принёс интересные математические задания, но все они связаны с зимой, с холодом. Догадались почему? Снеговик – зимний житель, в тепле он боится растаять, поэтому он решил подстраховаться и принёс “ холодные” задания. Не боитесь замёрзнуть? Тогда вперед. А за каждый правильный ответ снеговик будет вручать вот такую фишку.
Учитель: Вы справились с заданием, но снег продолжает падать. Лёгкие, пушистые снежинки кружатся в воздухе и тихо опускаются на землю.
(слайды 5,6,7,8,9) Снеговик снова предлагает вам поиграть, но теперь в снежки. |
Геометрические фигуры.
Да
Нет
Математические выражения Два. Уменьшаемое, вычитаемое, разность. Из 9 вычесть 3 получится 6. Уменьшаемое 9, вычитаемое3, разность 6. Разность чисел 9и 3 равна 6.
Мы повторили, из каких чисел состоит число 10. Молодцы! Кто может с уверенностью сказать, что хорошо знает состав числа 10.Ответы детей. |
Построение проекта выхода из затруднения Реализация построенного проекта
|
(слайд 10)Запишем в тетрадях, из каких двух чисел состоит число 10 и составим примеры на вычитание. В этом нам помогут снежки, если вы с заданием справились правильно, значит, снеговик промахнулся, ну, а если неверно,… (значит, снежок угодил прямо в вас) Руки? 10=7+3 Чему учились выполняя это задание ? Что нужно знать для решения таких выражений на вычитание? Кто может быстро рассказать из каких чисел состоит число 10? |
“На месте!”
Составлять выражения на сложение и вычитание и решать их. Состав числа 10 Ответы учеников |
Первичное закрепление во внешней речи.
Самостоятельная работа с самопроверкой по эталону.
|
(слайд 11)Ребята, мне кажется, со снеговиком, что — то происходит. Он начал таять. Не помогли ему его “холодные” задания, тепло от вашей дружной работы оказалось сильнее. Но есть средство, которое может спасти снеговика. Вот эти льдинки. Если их расколдовать, а это сможете сделать только вы, снеговик не растает. (слайд 12)Посмотрите, какой сугроб намело. Что же это такое? Что мы знаем? Что нужно узнать? Вопрос задачи. Какое решение запишем? Почему решаем вычитанием? Получился ответ. Индивидуальные задания. |
Выражения 10-5= 10-4= 10-6= 10-7= 10-9= 10-8= Рассуждают 10-это 5 и 5.10 минус 5 , получится 5.(и снова работаем с линеечками роста) Задача Я знаю, что было на горке 10 ребят. Я знаю что, два скатилось. Надо узнать ск-ко осталось. 10-2=8(р.) Надо узнать ск-ко осталось. Молодцы! |
Состав числа. Занятия по математике для детей подготовительной группы
1. Презентация занятия по математике для детей подготовительной группы на тему: «Состав числа 10».
Подготовилавоспитатель первой
квалификационной
категории Линник
Анна Сергеевна
2. Цель: усвоить знания о составе числа 10, повторить и закрепить ранее усвоенные знания.
Задачи:1. Обучающие:
• Познакомить с составом числа 10.
2. Развивающие:
• Продолжать учить находить предыдущее число к названному,
последующее число к названному.
• Уточнить представления о весе предметов и относительности веса
при их сравнении.
• Продолжать формировать представления о временных отношениях и
учить обозначать их словами: сначала, потом, до, после, раньше, позже.
3. Воспитательные:
• Совершенствовать морально-волевые качества воспитанников
посредством развития усидчивости, самостоятельности.
3. — Здравствуйте, ребята вы любите математику? Уверены в своих силах и знаниях? Тогда для начала я предлагаю вам провести
небольшуюразминку.
• Сколько носов у трех
котов?
• Сколько ушей у двух
мышей?
• Какая цифра спряталась в
слове “семь-я”?
• Сколько пальцев на одной
руке?
• Какой сегодня день
недели?
• Сколько раз в году бывает
день рождения?
• Какое сейчас время года?
• Сколько углов в
треугольнике?
• Сколько дней в одной
неделе?
• Что бывает раньше: утро
или вечер?
• Сколько спинок у трех
свинок?
• Сколько животиков у пяти
бегемотиков?
Следующая игра «Назовите числа,
которые
стоят между»
и
и
и
и
5. Следующее задание для самых внимательных. Найди числа, которое потерялись.
16
2
3
8
5
9
10
-Следующая игра называется «Какое
число называют
при счёте после…»
7
6
-Ребята, а теперь давайте
посчитаем от 1 до 10.
9
8
7
6
5
4
3
2
1
-Ребята, а теперь давайте
посчитаем от 10 до 1.
9
8
7
6
5
4
3
2
1
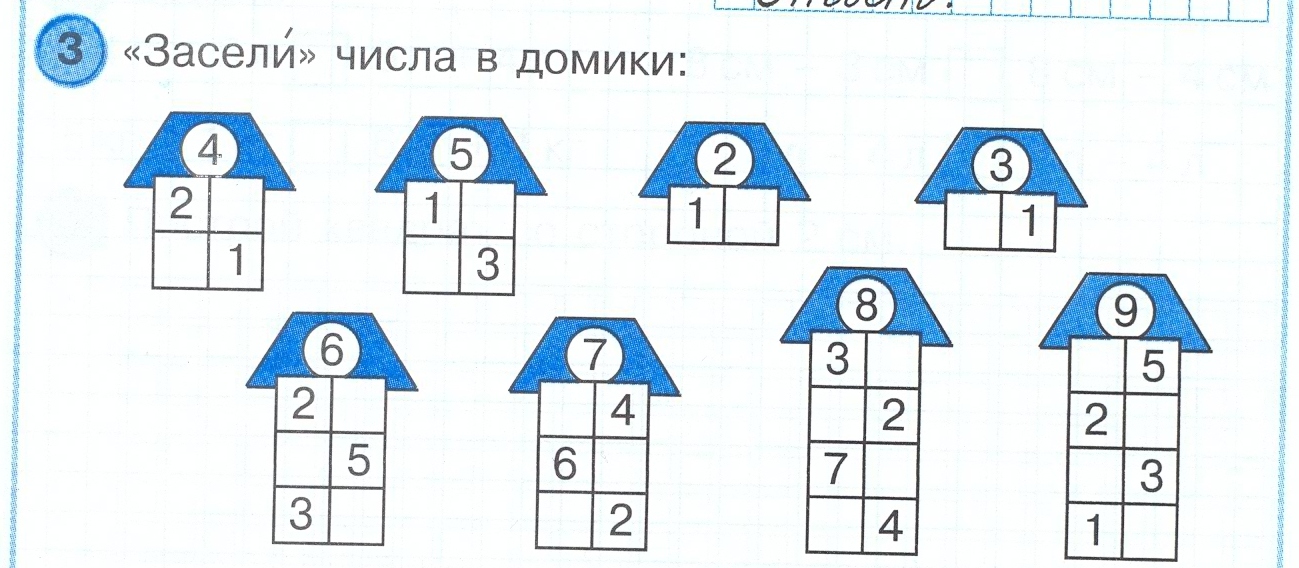
Игра «Засели домик»
Дом
№ 10
5
3
10
10
5
1
5
10
10
7
9
3
8
10
4
6
2
11. — Так цифра 10 пишется! Запомни!
13. -Следующее задание «Составь и реши задачу».
5+5=1018. -Ребята, помогите Винни Пуху решить примеры.
9 + 1 = 108 + 2 = 10
7 + 3 = 10
6 + 4 =10
5 + 5 =10
-Молодцы, ребята! Отлично справились со всеми
заданиями. Дома в свободное время постарайтесь
выполнить задания, которые я вам предлагаю.
До свидания!
19. Вспомни, из каких чисел состоит цифра 10.
20. Заполни пустые окошки.
Молодцы !Состав функций: составление функций с функциями
Состав
функций:
Составление функций с
Функции (стр.
3 из 6)
Разделы: Составление функции, которые являются наборами точек, Составление функции в точках, Составление функций с другими функциями, Word задачи с использованием композиции, обратные функции и состав
Также можно оценивать композиции символически.Проще оценить композицию в точке, потому что вы можете упростить по ходу дела, так как вы всегда будете просто вставлять числа и упрощение. Оценивая символическую композицию, вы в первую очередь заглушка x в какую-то функцию, а затем подключить эту функцию к другой функции, может быть намного сложнее. Но процесс работает так же, как и композиция по номеру. делает, и использование круглых скобок, чтобы быть точным на каждом этапе, приведет к быть еще более полезным.
- Дано f ( x ) = 2 x + 3 и г ( x ) = x 2 + 5, найти ( f о г ) ( х ).
В данном случае я не пытаясь найти определенное числовое значение. Вместо этого я пытаюсь найти формула, полученная в результате подстановки формулы для г ( x ) в формулу для f ( x ).Я буду писать формулы на каждом этапе, используя круглые скобки для обозначения куда должны идти входы:
( ф о г ) ( x ) = г ( г ( x ))
= f ( x 2 + 5)
=
2 (
) + 3 …
настройка для вставки входной формулы
=
2 ( х 2 + 5) + 3
=
2 х 2 + 10 + 3
= 2 х 2 + 13
Если подключить «1» для x в приведенном выше примере вы получите ( f o г ) (1) = 2 (1) 2 + 13 = 2 + 13 = 11, это тот же ответ, который мы получили раньше.Раньше мы вставляли номер в g ( x ), нашел новое значение, вставил это значение в f ( x ), и упростил результат. На этот раз мы подключили формулу к f ( x ), упростил формулу, включил то же число, что и раньше, и упростил результат. Окончательные числовые ответы были такими же. Если вы сделали символическая композиция (композиция с формулами) правильно, вы получите одинаковые значения в любом случае, независимо от того, какое значение вы выберете для x .Это может быть удобный способ проверить свою работу.
Вот еще символический пример: Авторские права Элизабет Стапель 2002-2011 Все права защищены
Есть кое-что, что вы Следует отметить из этих двух символических примеров. Посмотрите, что у меня получилось:
То есть ( f o г ) ( x ) есть не то же самое как ( г о f ) ( x ).Этот верно в целом; следует предположить, что композиции ( f o г ) ( x ) и ( г о f ) ( x ) собираются быть разными. В частности, композиция — это не то же самое, что и умножение. Открытая точка «о» не то же самое, что точка умножения «», и не означает тоже самое. Хотя верно следующее:
…вы не можете так сказать:
То есть реверсировать нельзя порядок в композиции и ожидайте в конечном итоге правильного результата. Композиция не такая гибкая, как умножение, и представляет собой совершенно другое процесс. Не пытайтесь умножать функции, когда вы должны вставляя их друг в друга.
Вы можете использовать виджет Mathway ниже, чтобы практиковать композицию функций. Попробуйте выполнить указанное упражнение или введите свое собственное.Затем нажмите кнопку «бумажный самолетик», чтобы сравнить свой ответ с ответом Матвея. (Или пропустите виджет и продолжите с уроком.)
(Нажав на «Нажмите, чтобы просмотреть шаги» на экране ответа виджета приведет вас на сайт Mathway для платного обновления .)
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | Возвращаться к указателю Вперед >>
Цитируйте эту статью как: | Стапель, Елизавета.«Составление функций с функциями». Пурпурная математика .
Доступно по номеру |
Составные функции — объяснение и примеры
В математике функция — это правило, которое связывает данный набор входов с набором возможных выходов. Важно отметить, что каждый вход связан ровно с одним выходом.
Процесс присвоения имен функциям известен как обозначение функций. Чаще всего используются следующие символы обозначения функций: «f (x) =…», «g (x) =…», «h (x) =…» и т. Д.
В этой статье мы узнаем, какой составной есть функции и способы их решения.
Что такое составная функция?
Если нам даны две функции, мы можем создать другую функцию, составив одну функцию в другую. Шаги, необходимые для выполнения этой операции, аналогичны тем, когда любая функция решается для любого заданного значения.Такие функции называются составными функциями.
Составная функция — это обычно функция, написанная внутри другой функции. Композиция функции выполняется путем замены одной функции другой функцией.
Например, , f [g (x)] — это составная функция от f (x) и g (x). Составная функция f [g (x)] читается как «f of g of x ». Функция g (x) называется внутренней функцией, а функция f (x) называется внешней функцией.Следовательно, мы также можем читать f [g (x)] как «функция g является внутренней функцией внешней функции f ».
Как решать составные функции?
Решение составной функции означает нахождение композиции двух функций. Мы используем маленький кружок (∘) для композиции функции. Вот шаги по решению составной функции:
- Перепишите композицию в другой форме.
Например:
(f ∘ g) (x) = f [g (x)]
(f ∘ g) (x) = f [g (x)]
(f ∘ g) (x² ) = F [g (x²)]
- Замените переменную x, которая находится во внешней функции, на внутреннюю функцию.
- Упростите функцию.
Примечание: Порядок в композиции функции важен, потому что (f ∘ g) (x) НЕ то же самое, что (g ∘ f) (x).
Давайте рассмотрим следующие задачи:
Пример 1
Учитывая функции f (x) = x 2 + 6 и g (x) = 2x — 1, найти (f ∘ g ) (Икс).
Решение
Замените x на 2x — 1 в функции f (x) = x 2 + 6.
(f ∘ g) (x) = (2x — 1) 2 + 6 = (2x — 1) (2x — 1) + 6
Применить FOIL
= 4x 2 — 4x + 1 + 6
= 4x 2 — 4x + 7
Пример 2
Учитывая функции g (x) = 2x — 1 и f (x) = x 2 + 6, найдите (g ∘ f) ( Икс).
Решение
Заменить x на x 2 + 6 в функции g (x) = 2x — 1
(g ∘ f) (x) = 2 (x 2 + 6) — 1
Используйте свойство distributive, чтобы убрать круглые скобки.
= 2x 2 + 12-1
= 2x 2 + 11
Пример 3
Учитывая f (x) = 2x + 3, найдите (f ∘ f) (x).
Решение
(f ∘ f) (x) = f [f (x)]
= 2 (2x + 3) + 3
= 4x + 9
Пример 4
Найдите (g ∘ f) (x), учитывая, что f (x) = 2x + 3 и g (x) = –x 2 + 5
⟹ (g ∘ f) (x) = g [f (x )]
Заменить x в g (x) = –x 2 + 5 на 2x + 3
= — (2x + 3) 2 + 5
= — (4x 2 + 12x + 9) + 5
= –4x 2 — 12x — 9 + 5
= –4x 2 — 12x — 4
Пример 5
Оценить f [g (6)] с учетом того, что f (x) = 5x + 4 и g (x) = x — 3
Решение
Сначала найдите значение f (g (x)).
⟹ f (g (x)) = 5 (x — 3) + 4
= 5x — 15 + 4
= 5x — 11
Теперь замените x в f (g (x)) на 6
⟹ 5 (6) — 11
⟹ 30 — 11
= 19
Следовательно, f [g (6)] = 19
Пример 6
Найдите f [g (5)], учитывая, что , f (x) = 4x + 3 и g (x) = x — 2.
Решение
Начните с определения значения f [g (x)].
⟹ f (x) = 4x + 3
⟹ g (x) = x — 2
f [g (x)] = 4 (x — 2) + 3
= 4x — 8 + 3
= 4x - 5
Теперь вычислим f [g (5)], заменив x в f [g (x)] на 5.
f [g (x)] = 4 (5) — 5
= 15
Следовательно, f [g (5)] = 15.
Пример 7
Учитывая g (x) = 2x + 8 и f (x) = 8x², Найти (f ∘ g) (x)
Решение
(f ∘g) (x) = f [g (x)]
Заменить x в f ( x) = 8x² с (2x + 8)
⟹ (f ∘g) (x) = f [g (x)] = 8 (2x + 8) ²
⟹ 8 [4x² + 8² + 2 (2x) (8)]
⟹ 8 [4x² + 64 + 32x]
⟹ 32x² + 512 + 256 x
⟹ 32x² + 256 x + 512
Пример 8
Найти (g ∘ f) ( x) if, f (x) = 6 x² и g (x) = 14x + 4
Решение
⟹ (g ∘ f) (x) = g [f (x)]
Заменить x на g (x) = 14x + 4 с 6 x²
⟹g [f (x)] = 14 (6 x²) + 4
= 84 x² + 4
Пример 9
Вычислить (f ∘ g ) (x) с использованием f (x) = 2x + 3 и g (x) = -x 2 + 1,
Решение 9 0182
(f ∘ g) (x) = f (g (x))
= 2 (g (x)) + 3
= 2 (-x 2 + 1) + 3
= — 2 x 2 + 5
Пример 10
Учитывая f (x) = √ (x + 2) и g (x) = ln (1 — x 2 ), найдите область (g ∘ f) (Икс).
Решение
⟹ (g ∘ f) (x) = g (f (x))
⟹ ln (1 — f (x) 2 ) = ln (1 — √ (x + 2) 2 )
⟹ ln (1 — (x + 2))
= ln (- x — 1)
Установить x + 2 на ≥ 0
Следовательно, домен: [-2, -1]
Пример 11
Даны две функции: f = {(-2, 1), (0, 3), (4, 5)} и g = {(1, 1), (3, 3), (7 , 9)}, найти (g ∘ f) и определить его область определения и диапазон.
Решение
⟹ (g ∘ f) (-2) = g [f (-2)] = g (1) = 1
⟹ (g ∘ f) (0) = g [f (0) ] = g (3) = 3
⟹ (g ∘ f) (4) = g [f (4)] = g (5) = undefined
Следовательно, g ∘ f = {(-2, 1), ( 0, 3)}
Следовательно, домен: {-2, 0} и диапазон: {1, 3}
Практические вопросы- Найдите составную функцию ( f ∘ f ):
f (x) = -9x 2 + 7x — 3
- Выполнить функциональную композицию, f ∘ g ∘ h .
f (x) = 1 / (2x + 3), g (x) = √ (x + 2) / x и h (x) = x 3 — 3
- Найдите композиционную функцию, если внутренняя функция — это функция извлечения квадратного корня, заданная как √ (-12x — 3), а внешняя функция — как 3x 2 + 5.
Разложение чисел — Почему мы учим этому в детском саду — KindergartenWorks
Разложение чисел означает разбиение чисел на части. Common Core В стандарте учащиеся детского сада могут разложить числа двумя способами.
Первый — разложить числа на десятки и единицы (внимание к числам 11-19), а второй — показать, как любое число 1-10 может быть создано с помощью различных слагаемых.
Я хочу вместе с вами сосредоточиться на стандарте NBT.1 Common Core, который касается аспекта разрушения и создания чисел с десятками и единицами (или разрядными значениями).
Давайте посмотрим на:
- как он развивается
- как мы можем регулярно практиковаться
- как мы расширяем его для наших продвинутых или ускоренных киндеров
Поскольку есть так много всего, что нужно покрыть — я разбил его на три части.Это часть 1 — зачем нам преподавать этот стандарт в детском саду и почему я вообще так много говорю об этом в этом блоге?
Понимание декомпозиции / составления чисел как учителей
Хорошо, учителя — давайте разберемся. Этот стандарт состоит из двух основных частей:
Когда я впервые столкнулся с этим стандартом, я был сбит с толку и почувствовал, что действительно не понимаю ценности его преподавания. Я мало знал, что найду, когда буду преподавать это ежедневно в рамках нашего календаря и уроков математики в небольших группах.
Почему мы ожидаем, что они будут разлагать и составлять числа?
{И почему я все время об этом пишу?}
Давайте посмотрим на долгосрочную перспективу. Простой ответ заключается в том, что есть у учащихся значение , которые могут видеть группировки, отношения и закономерности в числах. Мы закладываем основу для того, чтобы студенты могли в конечном итоге решить 53 + 12 и увидеть, что они могут манипулировать этим:
50 + 15
или 60 + 5
или 50 + 10 + 3 + 2
или любой другой множество способов увидеть количество, поскольку оно имеет для них смысл .
Теперь это более широкая картина, которая переносит нас к стандартам Common Core на более старом уровне класса … так что давайте вернемся к уровню нашего детского сада.
Мы работаем над пониманием того, что числа 11-19 имеют группу из десяти, а затем и единиц.
Если мы увидим чисел, разбитых на последовательность их групп десятков, а затем добавив несколько единиц , эти числа станут приятными и простыми .
Изучение того, как составлять и разлагать числа таким образом, дает им «визуальное» (особенно если вы представляете десятью кадрами) то, как 6, 16 или 67 действительно выглядят и есть.
Соединение визуального образа и числа
Замечательно то, что, обучая этому основанию того, как составлять и разлагать числа 11-19 (и далее) на их группы из десятков и единиц, они начинают понимать, почему 16 имеет один, затем шесть.
Когда это щелкает, они так взволнованы, что не могут дождаться, чтобы увидеть, применимо ли их новое понимание к «большим числам». И когда они начинают работать над числами до 99, происходит какое-то серьезное волшебство.
В принципе, этот стандарт огромен!
Он придает смысл числовой форме и полностью переносится во все другие математические концепции.Я не шучу. Я никогда не встречал стандарта (кроме счета 1: 1), который так сильно влиял бы на другие стандарты и являлся отправной точкой для того, чтобы увидеть, как дети стремительно растут в своих математических навыках!
Вот несколько планов уроков, о которых я написал, чтобы вы могли увидеть их в действии —
, но не забудьте прочитать следующий пост из этой серии, чтобы вы могли найти простые способы поработать над этим ключевым навыком!
Состав функций
«Функциональная композиция» применяет одну функцию к результатам другой:
Результат f () отправляется через g ()
Записано: (g º f) (x)
Что означает: g (f (x))
Пример:
f (x) = 2x + 3 и g (x) = x 2«x» — это просто заполнитель .Во избежание путаницы назовем его просто «ввод»:
f (ввод) = 2 (ввод) +3
г (ввод) = (ввод) 2
Начнем:
(g º f) (x) = g (f (x))
Сначала мы применяем f, затем применяем g к этому результату:
(g º f) (x) = (2x + 3) 2
Что, если мы перевернем порядок f и g?
(f º g) (x) = f (g (x))
Сначала мы применяем g, затем применяем f к этому результату:
(f º g) (x) = 2x 2 +3
Получаем другой результат!
Когда мы меняем порядок, результат редко бывает одинаковым.
Так что будьте осторожны, какая функция стоит первой.
Символ
Обозначение композиции — маленький кружок:
(г º f) (x)
Это , а не , а заполненная точка: (g · f) (x), так как это означает умножить на .
Состоит из самого себя
Мы даже можем составить функцию сама с собой!
Пример:
f (x) = 2x + 3(f º f) (x) = f (f (x))
Сначала мы применяем f, затем применяем f к этому результату:
(f º f) (x) = 2 (2x + 3) +3 = 4x + 9
Мы могли бы обойтись без красивой диаграммы:
(f º f) (x) = f (f (x))
= е (2x + 3)
= 2 (2x + 3) +3
= 4x + 9
Домены
До сих пор это было легко, но теперь мы должны рассмотреть доменов функций.
Область — это набор всех значений, которые входят в функцию.
Функция должна работать для всех значений, которые мы ей даем, так что зависит от нас, , чтобы убедиться, что мы получили правильный домен!
Пример: домен для √x (квадратный корень из x)
У нас не может быть квадратного корня из отрицательного числа (если мы не используем мнимые числа, но это не так), поэтому мы должны исключить отрицательных чисел:
Область √x — все неотрицательные действительные числа
В числовой строке это выглядит так:
В нотации конструктора множеств записано:
{x | x ≥ 0}
Или, используя обозначение интервала, это:
[0, + ∞)
Важно правильно оформить домен, иначе мы получим плохие результаты!
Область составной функции
Мы должны получить для обоих Доменов правильно (составная функция и — первая использованная функция).
При выполнении, например, (g º f) (x) = g (f (x)):
- Убедитесь, что мы получили домен для f (x) правильно,
- Затем также убедитесь, что g (x) получает правильный домен
Пример:
f (x) = √x и g (x) = x 2Область f (x) = √x — все неотрицательные действительные числа
Область g (x) = x 2 — это все действительные числа
Составная функция:
(g º f) (x) = g (f (x))
= (√x) 2
= х
Итак, «x» обычно имеет Домен всех действительных чисел…
… но поскольку это составная функция , мы должны также учитывать f (x) ,
Таким образом, домен состоит из неотрицательных вещественных чисел
Почему оба домена?
Ну, представьте, что функции — это машины … первая плавит отверстие пламенем (только для металла), вторая просверливает отверстие немного больше (работает с деревом или металлом):
То, что мы видим в конце, — это просверленное отверстие, и мы можем подумать, что «это должно работать для дерева или металла ». Но если мы поместим дрова в g º f, то первая функция f разожжет огонь и сожжет все дотла! |
Поэтому важно то, что происходит «внутри машины».
Функция разложения
Мы можем пойти другим путем и разбить функцию на набор других функций.
Пример:
(x + 1 / x) 2Эту функцию можно выполнить с помощью этих двух функций:
f (х) = х + 1 / х
г (x) = x 2
И получаем:
(g º f) (x) = g (f (x))
= г (х + 1 / х)
= (x + 1 / x) 2
Это может быть полезно, если исходная функция слишком сложна для работы.
Сводка
- «Функциональная композиция» применяет одну функцию к результатам другой.
- (g º f) (x) = g (f (x)) , сначала примените f (), затем примените g ()
- Мы также должны уважать область определения первой функции
- Некоторые функции можно разделить на две (или более) более простые функции.
Композиция функций — ChiliMath
В этом уроке я рассмотрю восемь (8) рабочих примеров, чтобы проиллюстрировать процесс, участвующий в композиции функций.
Если нам даны две функции, можно создать или сгенерировать «новую» функцию, объединяя одну в другую. Этот шаг аналогичен, когда функция оценивается для заданного значения. Например, оцените функцию ниже для x = 3.
Очевидно, что мне нужно заменить каждый x заданным значением, а затем упростить.
Ключевая идея в композиции функций состоит в том, что входом функции является , а не числовое значение, вместо этого вход также другая функция .
Общее правило композиции функции
Предположим, что две заданные функции — это f и g, состав f \ circ g определяется
Кроме того, состав g \ circ f определяется
Несколько замечаний о символической «формуле» выше :
- Порядок в функциональной композиции имеет значение! Вы всегда составляете функции справа налево . Следовательно, для данной функции вход всегда находится справа от нее.Другими словами, правая функция входит в левую.
- Обратите внимание, что в f \ circ g = f \ left [{g \ left (x \ right)} \ right] вход или «внутренняя функция» — это функция g, потому что она находится справа от функции f, которая является основная или «внешняя функция».
- Что касается порядка композиции, видите ли вы тот же узор в g \ circ f = g \ left [{f \ left (x \ right)} \ right]? Верно! Функция f является внутренней функцией внешней функции g.
Давайте рассмотрим несколько примеров, чтобы увидеть, как работает композиция функций.Позже вы поймете, что это просто упражнение по алгебраической подстановке и упрощению.
Примеры создания функций
Пример 1 : Выполните указанную композицию функций:
Порядок композиции важен. Обратите внимание, что в f \ circ g мы хотим, чтобы функция g \ left (x \ right) была входом основной функции {f \ left (x \ right)}.
Это должно выглядеть так:
Я начинаю с записи основной или внешней функции f \ left (x \ right), и в каждом экземпляре x я заменяю полное значение g \ left (x \ right ).
Затем я сделаю все необходимое, чтобы упростить выражения, например возведение бинома в квадрат, применение свойства распределения и объединение подобных терминов. Кроме этого, на самом деле в этом нет ничего особенного.
Позвольте мне показать вам, что я имел в виду под этим.
Пример 2 : Выполните указанную композицию функций:
Мне нужно найти составную функцию g \ circ f, что означает, что функция f является входом функции g.
Пример 3 : Выполните указанную композицию функций:
Это пример композиции функций, где входными данными является функция квадратного корня .Посмотрим, как это работает.
Опять же, в f \ circ g мы хотим вставить функцию g в функцию f.
Пример 4 : Выполните указанную композицию функций:
Эта композиция функций весьма интересна. Я надеюсь, вы понимаете, что у нас будет ситуация, когда функция извлечения квадратного корня входит в другую функцию извлечения квадратного корня.
Ключом к правильному составлению этой функции является понимание того, что символ квадратного корня может быть выражен как экспоненциальное выражение с дробной экспонентой, равной {1 \ over 2} .{{1 \ over 2}}}.
Пример 5 : Выполните указанную композицию функций:
До сих пор в наших предыдущих примерах мы выполняли композиции функций, используя две различные функции. Однако также возможно составить функцию с самой собой.
Пример 6 : Выполните указанную композицию функций:
Давайте разработаем пример композиции функции, которая имеет дело с рациональными функциями. Используемая алгебра немного утомительна, однако с вами все будет в порядке, если вы будете осторожны в упрощении выражений на каждом этапе.
В этом примере вы примените процедуры сложения или вычитания рациональных выражений, а также умножения рациональных выражений.
Ну вот …
Это было неплохо, правда?
Пример 7 : Выполните указанную композицию функций:
Если вы думаете, что наш последний пример композиции рациональных функций был беспорядочным, подождите, пока вы не увидите следующий пример. Это может быть немного сложнее, но все же очень управляемо. Так что не волнуйтесь! Всегда имейте этот «лазерный» фокус в каждом процессе упрощения, чтобы успешно решить эту проблему.
Входная функция f будет подставлена в каждый x основной функции g.
Это было легко, не правда ли? 😀
Для большей практики я предлагаю вам попробовать изменить порядок композиции функций на обратный. Другими словами, найдите f \ circ g.
У вас тоже получится?
Если это так, когда g \ circ f = f \ circ g = x, то мы заключаем, что функции g и f являются обратными друг другу. У меня есть отдельное руководство о том, как доказать или проверить, являются ли две функции обратными друг другу.
Пример 8 : Найдите составную функцию:
В этом примере мы собираемся составить три функции. Соблюдая обозначения искомой составной функции f \ circ g \ circ h, мы собираемся вычислить ее от справа налево .
Сначала мне нужно вставить функцию h в функцию g, а затем упростить, чтобы получить новую функцию.
Результат предыдущего шага будет подставлен в основную функцию f для получения окончательного ответа.2} + 1}}}} становится входом функции f
Практика с рабочими листами
Составление и разложение чисел | Study.com
Составление числа
Давайте снова рассмотрим деньги, чтобы представить эту концепцию. Предположим, я даю вам 1 стодолларовую купюру, 3 купюры по 10 долларов, 8 однодолларовых купюр и 7 пенсов, а затем я спрашиваю вас, сколько денег у вас все вместе. Чтобы найти это, вы должны сложить разные суммы каждой деноминации, которую я вам дал.То есть у вас есть 1 стодолларовая купюра на 100 долларов, 3 десятидолларовых купюры на 30 долларов, 8 однодолларовых купюр на 8 долларов и 7 пенни на 0,07 доллара. Если сложить все это вместе, получится следующее.
100 долларов США + 30 долларов США + 8 долларов США + 0,07 доллара США = 138,07 доллара США
Таким образом, вы выясняете, что у вас всего 138,07 долларов США. Теперь давайте представим это в виде обычных чисел. Предположим, я спросил, какое число получится из 2 сотен, 5 десятков, 1 единицы и 7 десятых. Точно так же, как мы вычислили, сколько денег у нас было на основе различных номиналов, мы собираемся вычислить это число на основе заданных значений разряда.Две сотни стоят 200, 5 десятков — 50, 1 — 1, а 7 десятых — 7/10 или 0,7. Чтобы найти число, мы складываем все эти разрядные значения вместе.
200 + 50 + 1 + 0,7 = 251,7
Описанное число — 251,7. Складывание заданных значений разряда, как мы это делали, называется , составляя числа. Композицию можно определить как создание целого из частей. Например, музыкальный композитор сочиняет музыкальное произведение из нот. Музыкальное произведение — это цельное произведение, а музыкальные ноты — это составляющие его части.Определение compose позволяет легко запомнить, что составление числа — это просто сложение числа из его частей.
Декомпозиция числа
Теперь давайте посмотрим на обратную сторону компоновки. В последний раз давайте рассмотрим деньги. Предположим, я говорю вам, что у меня есть 38,19 доллара, а деньги состоят из купюр и монет, соответствующих номиналу каждой цифры. Например, тройка попадает в разряд десятков, поэтому у меня есть 3 десятидолларовых купюры. Точно так же восьмерка находится на одном месте, поэтому у меня есть 8 однодолларовых купюр.1 находится на отметке в десять центов, поэтому у меня 1 цент, а 9 — в месте в один цент, поэтому у меня 9 пенни. Таким образом, у меня есть 3 десятки на 30 долларов, 8 на 8 долларов, 1 цент на 0,10 доллара и 9 пенни на 0,09 доллара. Собирая все вместе, я вижу, что моя долларовая сумма в 38,19 доллара может быть разбита следующим образом.
38,19 $ = 30 $ + 8 $ + 0,10 $ + 0,09 $
А теперь подумайте о том, чтобы сделать это для обычного номера. То есть разбейте число на сумму его разрядов. Для этого рассмотрим число 4771.Имеем следующее.
- Четверка из тысяч имеет разрядную стоимость 4000.
- Число 7 в сотнях имеет значение 700.
- Семерка в разряде десятков имеет значение 70.
- 1 в одном месте имеет значение 1.
Таким образом, мы можем разбить число 4 771 следующим образом.
4,771 = 4,000 + 700 + 70 + 1
Разбиение числа на сумму его значений разряда называется разложением числа.Разложение можно определить как разрушение. Например, некоторые соединения разлагаются в присутствии света. То есть они химически распадаются на разные части. Это определение позволяет легко запомнить, что разложение числа — это его разбиение на сумму его разрядов.
Краткое содержание урока
Разрядное значение цифры в числе связано с тем, где цифра располагается по отношению к десятичной запятой. Мы можем разложить число, разбив его на сумму его разрядных значений, и мы можем составить число, сложив его разрядные значения вместе (или суммируя их).Знакомство с разрядами, разложением чисел и составлением чисел позволяет нам лучше понять систему счисления и то, как числа работают вместе.
1.4 Состав функций — Precalculus
Цели обучения
В этом разделе вы:
- Комбинируйте функции, используя алгебраические операции.
- Создать новую функцию путем композиции функций.
- Оценивать составные функции.
- Найдите область определения составной функции.
- Разложите составную функцию на ее составные функции.
Предположим, мы хотим подсчитать, сколько стоит отапливать дом в определенный день года. Стоимость отопления дома будет зависеть от средней дневной температуры, а средняя дневная температура, в свою очередь, зависит от конкретного дня в году. Обратите внимание, как мы только что определили два отношения: стоимость зависит от температуры, а температура зависит от дня.
Используя описательные переменные, мы можем записать эти две функции.Функция C (T) C (T) дает стоимость CC отопления дома для данной средней дневной температуры в TT градусах Цельсия. Функция T (d) T (d) дает среднесуточную температуру в день dd года. Для любого дня Cost = C (T (d)) Cost = C (T (d)) означает, что стоимость зависит от температуры, которая, в свою очередь, зависит от дня в году. Таким образом, мы можем оценить функцию стоимости при температуре T (d) .T (d). Например, мы могли бы оценить T (5) T (5), чтобы определить среднесуточную температуру на 5-й день года.Затем мы могли бы оценить функцию стоимости при этой температуре. Мы бы написали C (T (5)). C (T (5)).
Объединив эти два отношения в одну функцию, мы выполнили композицию функций, которой и посвящен этот раздел.
Объединение функций с помощью алгебраических операций
Композиция функций — это только один из способов объединения существующих функций. Другой способ — выполнять обычные алгебраические операции над функциями, такие как сложение, вычитание, умножение и деление.Мы делаем это, выполняя операции с выходами функции, определяя результат как выход нашей новой функции.
Предположим, нам нужно добавить два столбца чисел, которые представляют отдельные годовые доходы мужа и жены за период лет, в результате чего получится их общий семейный доход. Мы хотим делать это для каждого года, добавляя только доходы за этот год, а затем собирая все данные в новом столбце. Если w (y) w (y) — доход жены, а h (y) h (y) — доход мужа в год y, y, и мы хотим, чтобы TT представляло общий доход, то мы можем определить новую функцию.
T (y) = h (y) + w (y) T (y) = h (y) + w (y).Если это верно для каждого года, то мы можем сосредоточиться на связи между функциями без привязки к году и написать
Так же, как и для этой суммы двух функций, мы можем определить функции разности, произведения и отношения для любой пары функций, которые имеют одинаковые типы входов (не обязательно числа), а также одинаковые виды выходов (которые должны быть числа, так что обычные операции алгебры могут применяться к ним, и которые также должны иметь те же единицы или не иметь единиц, когда мы складываем и вычитаем).Таким образом, мы можем думать о сложении, вычитании, умножении и делении функций.
Для двух функций f (x) f (x) и g (x) g (x) с выходами вещественных чисел мы определяем новые функции f + g, f − g, fg, f + g, f − g, fg, и fgfg соотношениями
(f + g) (x) = f (x) + g (x) (f − g) (x) = f (x) −g (x) (fg) (x) = f (x) g (x ) (Fg) (x) = f (x) g (x) (f + g) (x) = f (x) + g (x) (f − g) (x) = f (x) −g ( x) (fg) (x) = f (x) g (x) (fg) (x) = f (x) g (x)Пример 1
Выполнение алгебраических операций над функциями
Найдите и упростите функции (g − f) (x) (g − f) (x) и (gf) (x), (gf) (x), если f (x) = x − 1f (x) = x − 1 и g (x) = x2−1.д (х) = х2−1. У них одна и та же функция?
Решение
Начните с написания общей формы, а затем замените заданные функции.
(g − f) (x) = g (x) −f (x) (g − f) (x) = x2−1− (x − 1) (g − f) (x) = x2 − x (g −f) (x) = x (x − 1) (gf) (x) = g (x) f (x) (gf) (x) = x2−1x − 1 (gf) (x) = (x + 1) (x − 1) x − 1, где x ≠ 1 (gf) (x) = x + 1 (g − f) (x) = g (x) −f (x) (g − f) (x) = x2−1− (x − 1) (g − f) (x) = x2 − x (g − f) (x) = x (x − 1) (gf) (x) = g (x) f (x ) (gf) (x) = x2−1x − 1 (gf) (x) = (x + 1) (x − 1) x − 1, где x ≠ 1 (gf) (x) = x + 1Нет, функции не совпадают.
Примечание. Для (gf) (x), (gf) (x) условие x ≠ 1x ≠ 1 необходимо, потому что, когда x = 1, x = 1, знаменатель равен 0, что делает функцию неопределенной.
Попробуй # 1
Найдите и упростите функции (fg) (x) (fg) (x) и (f − g) (x). (F − g) (x).
f (x) = x − 1 и g (x) = x2−1f (x) = x − 1 и g (x) = x2−1Они выполняют одну и ту же функцию?
Создание функции с помощью композиции функций
Выполнение алгебраических операций над функциями объединяет их в новую функцию, но мы также можем создавать функции, составляя функции. Когда мы хотели вычислить стоимость отопления для одного дня в году, мы создали новую функцию, которая принимает день в качестве входных данных и дает стоимость в качестве выходных данных.Процесс объединения функций таким образом, что выход одной функции становится входом другой, известен как композиция функций . Результирующая функция известна как составная функция . Представим эту комбинацию следующими обозначениями:
(f∘g) (x) = f (g (x)) (f∘g) (x) = f (g (x))Мы читаем левую часть как «f« f, составленную с gg в x , «X», а в правой части — «f« f of gg of x. »X.» Две части уравнения имеют одинаковый математический смысл и равны.Символ открытого круга ∘∘ называется оператором композиции. Мы используем этот оператор в основном, когда хотим подчеркнуть взаимосвязь между самими функциями, не обращаясь к какому-либо конкретному входному значению. Композиция — это бинарная операция, которая принимает две функции и формирует новую функцию, подобно тому, как сложение или умножение принимает два числа и дает новое число. Однако важно не путать композицию функций с умножением, потому что, как мы узнали выше, в большинстве случаев f (g (x)) ≠ f (x) g (x).f (g (x)) ≠ f (x) g (x).
Также важно понимать порядок операций при оценке составной функции. Мы следуем обычному соглашению с круглыми скобками, начиная сначала с самых внутренних скобок, а затем перейдя к внешним. В приведенном выше уравнении функция gg сначала принимает вход xx и дает выход g (x) .g (x). Затем функция ff принимает g (x) g (x) в качестве входа и дает выход f (g (x)). F (g (x)).
В общем, f∘gf∘g и g∘fg∘f — это разные функции.Другими словами, во многих случаях f (g (x)) ≠ g (f (x)) f (g (x)) ≠ g (f (x)) для всех x.x. Мы также увидим, что иногда две функции могут быть составлены только в одном определенном порядке.
Например, если f (x) = x2f (x) = x2 и g (x) = x + 2, g (x) = x + 2, то
f (g (x)) = f (x + 2) = (x + 2) 2 = x2 + 4x + 4f (g (x)) = f (x + 2) = (x + 2) 2 = x2 + 4x + 4но
g (f (x)) = g (x2) = x2 + 2g (f (x)) = g (x2) = x2 + 2Эти выражения не равны для всех значений x, x, поэтому две функции не равны.Неважно, что выражения совпадают для единственного входного значения x = −12.x = −12.
Обратите внимание, что диапазон внутренней функции (первая функция, которая должна быть оценена) должен находиться в пределах области внешней функции. Менее формально композиция должна иметь смысл с точки зрения входов и выходов.
Состав функций
Когда вывод одной функции используется как ввод другой, мы называем всю операцию композицией функций.Для любого входа xx и функций ff и g, g это действие определяет составную функцию, которую мы записываем как f∘gf∘g, такую, что
(f∘g) (x) = f (g (x)) (f∘g) (x) = f (g (x))Область определения составной функции f∘gf∘g — это все xx такие, что xx находится в области определения gg, а g (x) g (x) находится в области определения f.f.
Важно понимать, что произведение функций fgfg не то же самое, что композиция функций f (g (x)), f (g (x)), потому что, как правило, f (x) g (x) ≠ f (g (x)). f (x) g (x) ≠ f (g (x)).
Пример 2
Определение, является ли композиция функций коммутативной
Используя указанные функции, найдите f (g (x)) f (g (x)) и g (f (x)).g (f (x)). Определите, является ли композиция функций коммутативной.
f (x) = 2x + 1g (x) = 3 − xf (x) = 2x + 1g (x) = 3 − xРешение
Начнем с замены g (x) g (x) в f (x) .f (x).
f (g (x)) = 2 (3 − x) +1 = 6−2x + 1 = 7−2xf (g (x)) = 2 (3 − x) +1 = 6−2x + 1 = 7− 2xТеперь мы можем заменить f (x) f (x) на g (x) .g (x).
g (f (x)) = 3− (2x + 1) = 3−2x − 1 = −2x + 2g (f (x)) = 3− (2x + 1) = 3−2x − 1 = −2x + 2Мы находим, что g (f (x)) ≠ f (g (x)), g (f (x)) ≠ f (g (x)), поэтому операция композиции функций не коммутативна.
Пример 3
Интерпретация составных функций
Функция c (s) c (s) дает количество калорий, сожженных при выполнении приседаний ss, а s (t) s (t) дает количество приседаний, которые человек может выполнить за tt минут. Интерпретируйте c (s (3)). C (s (3)).
Решение
Внутреннее выражение в композиции — s (3) .s (3). Поскольку входом для функции s является время, t = 3t = 3 представляет 3 минуты, а s (3) s (3) — количество приседаний, выполненных за 3 минуты.
Использование s (3) s (3) в качестве входных данных для функции c (s) c (s) дает нам количество калорий, сожженных за количество приседаний, которые можно выполнить за 3 минуты, или просто количество калорий, сожженных за 3 минуты (делая приседания).
Пример 4
Исследование порядка функциональной композиции
Предположим, что f (x) f (x) дает мили, которые можно проехать за xx часов, а g (y) g (y) дает галлоны бензина, использованные для движения yy миль. Какое из этих выражений имеет смысл: f (g (y)) f (g (y)) или g (f (x))? G (f (x))?
Решение
Функция y = f (x) y = f (x) — это функция, выходом которой является количество пройденных миль, соответствующее количеству пройденных часов.
количество миль = f (количество часов) количество миль = f (количество часов)Функция g (y) g (y) — это функция, выходом которой является количество использованных галлонов, соответствующее количеству пройденных миль. Это означает:
количество галлонов = g (количество миль) количество галлонов = g (количество миль)Выражение g (y) g (y) принимает мили в качестве входных данных и количество галлонов в качестве выходных данных. Функция f (x) f (x) требует ввода количества часов. Пытаться ввести количество галлонов не имеет смысла.Выражение f (g (y)) f (g (y)) не имеет смысла.
Выражение f (x) f (x) принимает часы в качестве входных данных и количество пройденных миль в качестве выходных данных. Функция g (y) g (y) требует ввода количества миль. Использование f (x) f (x) (пройденные мили) в качестве входного значения для g (y), g (y), где галлоны бензина зависят от пройденных миль, имеет смысл. Выражение g (f (x)) g (f (x)) имеет смысл и даст количество использованных галлонов газа, g, g, на проезд определенного количества миль, f (x), f (x) , через xx часов.
Вопросы и ответы
Существуют ли ситуации, когда f (g (y)) f (g (y)) и g (f (x)) g (f (x)) оба будут значимыми или полезными выражениями?
Да.Для многих чисто математических функций обе композиции имеют смысл, хотя обычно они создают разные новые функции. В реальных задачах функции, входы и выходы которых имеют одинаковые единицы, также могут давать композиции, значимые в любом порядке.
Попробуй # 2
Гравитационная сила на планете на расстоянии r от Солнца задается функцией G (r) .G (r). Ускорение планеты, подверженной действию любой силы FF, задается функцией a (F).а (F). Сформируйте осмысленную композицию из этих двух функций и объясните, что это означает.
Оценка составных функций
После того, как мы составим новую функцию из двух существующих функций, нам нужно иметь возможность оценивать ее для любого ввода в ее домене. Мы сделаем это с помощью конкретных числовых входных данных для функций, выраженных в виде таблиц, графиков и формул, и с переменными в качестве входных данных для функций, выраженных в виде формул. В каждом случае мы оцениваем внутреннюю функцию, используя начальный ввод, а затем используем вывод внутренней функции как ввод для внешней функции.
Оценка составных функций с помощью таблиц
При работе с функциями, заданными в виде таблиц, мы считываем входные и выходные значения из записей таблицы и всегда работаем изнутри наружу. Сначала мы оцениваем внутреннюю функцию, а затем используем вывод внутренней функции как вход для внешней функции.
Пример 5
Использование таблицы для вычисления составной функции
Используя таблицу 1, оцените f (g (3)) f (g (3)) и g (f (3)). G (f (3)).
| xx | е (х) е (х) | г (x) г (x) |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 8 | 5 |
| 3 | 3 | 2 |
| 4 | 1 | 7 |
Таблица 1
Решение
Чтобы оценить f (g (3)), f (g (3)), мы начинаем изнутри с входного значения 3.Затем мы вычисляем внутреннее выражение g (3) g (3), используя таблицу, которая определяет функцию g: g: g (3) = 2.g (3) = 2. Затем мы можем использовать этот результат в качестве входных данных для функции f, f, поэтому g (3) g (3) заменяется на 2, и мы получаем f (2) .f (2). Затем, используя таблицу, определяющую функцию f, f, находим, что f (2) = 8. f (2) = 8.
g (3) = 2f (g (3)) = f (2) = 8g (3) = 2f (g (3)) = f (2) = 8Чтобы оценить g (f (3)), g ( f (3)), мы сначала вычисляем внутреннее выражение f (3) f (3), используя первую таблицу: f (3) = 3.f (3) = 3. Затем, используя таблицу для g, g, мы можем оценить
g (f (3)) = g (3) = 2g (f (3)) = g (3) = 2Таблица 2 показывает составные функции f∘gf∘g и g∘fg∘f в виде таблиц.
| xx | г (х) г (х) | f (g (x)) f (g (x)) | f (x) f (x) | г (f (x)) g (f (x)) |
| 3 | 2 | 8 | 3 | 2 |
Таблица 2
Попробуй # 3
Используя таблицу 1, оцените f (g (1)) f (g (1)) и g (f (4)). G (f (4)).
Оценка составных функций с помощью графиков
Когда нам даются отдельные функции в виде графиков, процедура оценки составных функций аналогична процессу, который мы используем для оценки таблиц.Мы считываем входные и выходные значения, но на этот раз по осям x-x и y-y графиков.
Как к
Для составной функции и графиков ее отдельных функций оцените ее, используя информацию, представленную на графиках.
- Найдите входные данные внутренней функции на оси x-x ее графика.
- Считайте выходные данные внутренней функции по оси ординат ее графика.
- Найдите выход внутренней функции на оси x-x графика внешней функции.
- Считайте результат внешней функции по оси ординат ее графика. Это результат составной функции.
Пример 6
Использование графика для вычисления составной функции
Используя рисунок 1, оцените f (g (1)). F (g (1)).
Рисунок 1
Решение
Чтобы оценить f (g (1)), f (g (1)), мы начинаем с внутренней оценки. См. Рисунок 2.
Рисунок 2
Мы оцениваем g (1) g (1), используя график g (x), g (x), находя вход 1 на оси x-x и находя выходное значение графика на этом входе.Здесь g (1) = 3.g (1) = 3. Мы используем это значение в качестве входных данных для функции f.f.
Затем мы можем оценить составную функцию, посмотрев на график f (x), f (x), найдя входное значение 3 на оси x-x и прочитав выходное значение графика на этом входе. Здесь f (3) = 6, f (3) = 6, поэтому f (g (1)) = 6. f (g (1)) = 6.
Анализ
На рисунке 3 показано, как мы можем пометить графики стрелками, чтобы проследить путь от входного значения к выходному значению.
Рисунок 3
Попробовать # 4
Используя рисунок 1, оцените g (f (2)).g (f (2)).
Оценка составных функций с помощью формул
При оценке составной функции, в которой мы либо создали, либо получили формулы, правило работы изнутри остается неизменным. Входное значение внешней функции будет выходом внутренней функции, которое может быть числовым значением, именем переменной или более сложным выражением.
Хотя мы можем составлять функции для каждого отдельного входного значения, иногда бывает полезно найти единую формулу, которая будет вычислять результат композиции f (g (x)).f (g (x)). Для этого мы расширим наше представление об оценке функций. Напомним, что, когда мы оцениваем функцию типа f (t) = t2 − t, f (t) = t2 − t, мы подставляем значение внутри круглых скобок в формулу везде, где видим входную переменную.
Как к
Получив формулу для составной функции, вычислите функцию.
- Оцените внутреннюю функцию, используя предоставленное входное значение или переменную.
- Используйте полученный результат как вход для внешней функции.
Пример 7
Оценка композиции функций, выраженных в виде формул, с числовым вводом
Дано f (t) = t2 − tf (t) = t2 − t и h (x) = 3x + 2, h (x) = 3x + 2, вычислить f (h (1)). F (h (1 )).
Решение
Поскольку внутреннее выражение — это h (1), h (1), мы начинаем с вычисления h (x) h (x) как 1.
h (1) = 3 (1) + 2h (1) = 5h (1) = 3 (1) + 2h (1) = 5Тогда f (h (1)) = f (5), f (h (1)) = f (5), поэтому мы вычисляем f (t) f (t) на входе 5.
f (h (1)) = f (5) f (h (1)) = 52−5f (h (1)) = 20f (h (1)) = f (5) f (h (1)) = 52−5f (h (1)) = 20Анализ
Не имеет значения, какие входные переменные tt и xx были вызваны в этой задаче, потому что мы вычисляли конкретные числовые значения.
Попробуй # 5
Учитывая f (t) = t2 − tf (t) = t2 − t и h (x) = 3x + 2, h (x) = 3x + 2, оцените
- ⓐ h (f (2)) h (f (2))
- ⓑ ч (f (−2)) h (f (−2))
Нахождение области составной функции
Как мы обсуждали ранее, область определения составной функции, такой как f∘gf∘g, зависит от области определения gg и области определения f.f. Важно знать, когда мы можем применить составную функцию, а когда нет, то есть знать область определения функции, такой как f∘g.f∘g. Предположим, что нам известны области определения функций ff и gg по отдельности. Если мы запишем составную функцию для входа xx как f (g (x)), f (g (x)), мы сразу увидим, что xx должен быть членом домена gg, чтобы выражение было имеет смысл, потому что в противном случае мы не сможем завершить оценку внутренней функции. Однако мы также видим, что g (x) g (x) должен быть членом области определения f, f, иначе вторая оценка функции в f (g (x)) f (g (x)) не может быть завершена, и выражение все еще не определено.Таким образом, область f∘gf∘g состоит только из тех входов в области gg, которые производят выходные данные из gg, принадлежащих области f.f. Обратите внимание, что область определения ff, составленная из gg, — это множество всех xx, таких что xx находится в области gg, а g (x) g (x) находится в области f.f.
Область составной функции
Область определения составной функции f (g (x)) f (g (x)) — это набор тех входов xx в области определения gg, для которых g (x) g (x) находится в области определения f.f.
Как к
По заданной композиции функций f (g (x)), f (g (x)) определите ее область определения.
- Найдите домен g.g.
- Найдите домен f.f.
- Найдите те входы xx в области gg, для которых g (x) g (x) находится в области f.f. То есть исключить те входы xx из области gg, для которых g (x) g (x) не находится в области f.f. Результирующий набор является доменом f∘g.f∘g.
Пример 8
Нахождение области составной функции
Найдите домен
(f∘g) (x), где f (x) = 5x − 1 и g (x) = 43x − 2 (f∘g) (x), где f (x) = 5x − 1 и g (x) = 43x − 2Решение
Область определения g (x) g (x) состоит из всех действительных чисел, кроме x = 23, x = 23, поскольку это входное значение заставит нас разделить на 0.Аналогично, область определения ff состоит из всех действительных чисел, кроме 1. Таким образом, нам нужно исключить из области определения g (x) g (x) то значение xx, для которого g (x) = 1.g (x) = 1 .
43x − 2 = 14 = 3x − 26 = 3xx = 243x − 2 = 14 = 3x − 26 = 3xx = 2Таким образом, домен f∘gf∘g — это набор всех действительных чисел, кроме 2323 и 2.2. Это означает, что
x ≠ 23orx ≠ 2x ≠ 23orx ≠ 2Мы можем записать это в обозначении интервала как
(−∞, 23) ∪ (23,2) ∪ (2, ∞) (- ∞, 23) ∪ (23,2) ∪ (2, ∞)Пример 9
Нахождение области составной функции, включающей радикалы
Найдите домен
(f∘g) (x), где f (x) = x + 2 и g (x) = 3 − x (f∘g) (x), где f (x) = x + 2 и g (x) = 3 − xРешение
Поскольку мы не можем извлечь квадратный корень из отрицательного числа, область определения gg равна (−∞, 3].(−∞, 3]. Теперь проверим область определения составной функции
(f∘g) (x) = 3 − x + 2 (f∘g) (x) = 3 − x + 2Для (f∘g) (x) = 3 − x + 2,3 − x + 2 ≥0, (f∘g) (x) = 3 − x + 2,3 − x + 2≥0, так как подкоренное выражение квадратного корня должно быть положительным. Поскольку квадратные корни положительны, 3 − x≥0,3 − x≥0 или 3 − x≥0,3 − x≥0, что дает область определения (-∞, 3] (- ∞, 3].
Анализ
Этот пример показывает, что знание диапазона функций (в частности, внутренней функции) также может быть полезно при поиске области определения составной функции.Это также показывает, что домен f∘gf∘g может содержать значения, которые не находятся в области определения f, f, хотя они должны быть в области g.g.
Попробуйте # 6
Найдите домен
(f∘g) (x), где f (x) = 1x − 2 и g (x) = x + 4 (f∘g) (x), где f (x) = 1x − 2 и g (x) = x + 4Разложение составной функции на ее составные функции
В некоторых случаях необходимо разложить сложную функцию. Другими словами, мы можем записать его как композицию двух более простых функций.Может существовать более одного способа разложения составной функции, поэтому мы можем выбрать такое разложение, которое кажется наиболее целесообразным.
Пример 10
Разложение функции
Запишем f (x) = 5 − x2f (x) = 5 − x2 как композицию двух функций.
Решение
Мы ищем две функции, gg и h, h, поэтому f (x) = g (h (x)). F (x) = g (h (x)). Для этого мы ищем функцию внутри функции в формуле для f (x) .f (x). В качестве одной из возможностей мы могли бы заметить, что выражение 5 − x25 − x2 является внутренней частью квадратного корня.Затем мы могли бы разложить функцию как
h (x) = 5 − x2 и g (x) = xh (x) = 5 − x2 и g (x) = xМы можем проверить наш ответ, перекомпоновав функции.
g (h (x)) = g (5 − x2) = 5 − x2g (h (x)) = g (5 − x2) = 5 − x2.Попробуй # 7
Запишем f (x) = 43−4 + x2f (x) = 43−4 + x2 как композицию двух функций.
1,4 Упражнения по разделам
Устные
1.Как найти область частного отношения двух функций, fg? Fg?
2.Какова композиция двух функций, f∘g? F∘g?
3.Если при составлении двух функций порядок обратный, может ли результат быть таким же, как ответ в исходном порядке композиции? Если да, приведите пример. Если нет, объясните, почему нет.
4.Как найти область для композиции двух функций, f ,g? F∘g?
Алгебраические
5.Дано f (x) = x2 + 2xf (x) = x2 + 2x и g (x) = 6 − x2, g (x) = 6 − x2, найти f + g, f − g, fg, f + g , f − g, fg и fg.fg. Определите область для каждой функции в интервальной нотации.
6.Дано f (x) = — 3×2 + xf (x) = — 3×2 + x и g (x) = 5, g (x) = 5, найдите f + g, f − g, fg, f + g, f −g, fg и fg.fg. Определите область для каждой функции в интервальной нотации.
7.Дано f (x) = 2×2 + 4xf (x) = 2×2 + 4x и g (x) = 12x, g (x) = 12x, найдите f + g, f − g, fg, f + g, f − g. , fg и fg.fg. Определите область для каждой функции в интервальной нотации.
8.Дано f (x) = 1x − 4f (x) = 1x − 4 и g (x) = 16 − x, g (x) = 16 − x, найти f + g, f − g, fg, f + g , f − g, fg и fg.fg. Определите область для каждой функции в интервальной нотации.
9.Дано f (x) = 3x2f (x) = 3×2 и g (x) = x − 5, g (x) = x − 5, найти f + g, f − g, fg, f + g, f − g. , fg и fg.fg. Определите область для каждой функции в интервальной нотации.
10.Для заданных f (x) = xf (x) = x и g (x) = | x − 3 |, g (x) = | x − 3 | найдите gf.gf. Определите область определения функции в интервальной записи.
11.Дано f (x) = 2×2 + 1f (x) = 2×2 + 1 и g (x) = 3x − 5, g (x) = 3x − 5, найдите следующее:
- ⓐ f (г (2)) f (г (2))
- ⓑ f (g (x)) f (g (x))
- ⓒ г (f (x)) g (f (x))
- ⓓ (g∘g) (x) (g∘g) (x)
- ⓔ (f∘f) (- 2) (f∘f) (- 2)
Для следующих упражнений используйте каждую пару функций, чтобы найти f (g (x)) f (g (x)) и g (f (x)).g (f (x)). Упростите свои ответы.
12.f (x) = x2 + 1, g (x) = x + 2f (x) = x2 + 1, g (x) = x + 2.
13.f (x) = x + 2, g (x) = x2 + 3 f (x) = x + 2, g (x) = x2 + 3.
14.f (x) = | x |, g (x) = 5x + 1f (x) = | x |, g (x) = 5x + 1.
15.f (x) = x3, g (x) = x + 1×3 f (x) = x3, g (x) = x + 1×3
16.f (x) = 1x − 6, g (x) = 7x + 6f (x) = 1x − 6, g (x) = 7x + 6.
17.f (x) = 1x − 4, g (x) = 2x + 4f (x) = 1x − 4, g (x) = 2x + 4.
В следующих упражнениях используйте каждый набор функций, чтобы найти f (g (h (x))). F (g (h (x))). Упростите свои ответы.
18.f (x) = x4 + 6, f (x) = x4 + 6, g (x) = x − 6, g (x) = x − 6 и h (x) = xh (x) = x
19.f (x) = x2 + 1, f (x) = x2 + 1, g (x) = 1x, g (x) = 1x и h (x) = x + 3h (x) = x + 3.
20.Дано f (x) = 1xf (x) = 1x и g (x) = x − 3, g (x) = x − 3, найдите следующее:
- ⓐ (f∘g) (x) (f∘g) (x)
- ⓑ область определения (f∘g) (x) (f∘g) (x) в обозначении интервала
- ⓒ (g∘f) (x) (g∘f) (x)
- ⓓ область (g∘f) (x) (g∘f) (x)
- ⓔ (фг) x (фг) x
Дано f (x) = 2−4xf (x) = 2−4x и g (x) = — 3x, g (x) = — 3x, найдите следующее:
- ⓐ (g∘f) (x) (g∘f) (x)
- ⓑ область определения (g∘f) (x) (g∘f) (x) в обозначении интервала
Учитывая функции f (x) = 1 − xxandg (x) = 11 + x2, f (x) = 1 − xxandg (x) = 11 + x2, найти следующее:
- ⓐ (g∘f) (x) (g∘f) (x)
- ⓑ (g∘f) (2) (g∘f) (2)
Для заданных функций p (x) = 1xp (x) = 1x и m (x) = x2−4, m (x) = x2−4 укажите область определения каждой из следующих функций, используя интервальную нотацию:
- ⓐ p (x) m (x) p (x) m (x)
- ⓑ p (m (x)) p (m (x))
- ⓒ м (p (x)) m (p (x))
Для заданных функций q (x) = 1xq (x) = 1x и h (x) = x2−9, h (x) = x2−9 укажите область определения каждой из следующих функций, используя интервальную нотацию.
- ⓐ q (x) h (x) q (x) h (x)
- ⓑ q (h (x)) q (h (x))
- ⓒ ч (q (x)) h (q (x))
Для f (x) = 1xf (x) = 1x и g (x) = x − 1, g (x) = x − 1 запишите область определения (f∘g) (x) (f∘g) ( x) в интервальной записи.
Для следующих упражнений найдите функции f (x) f (x) и g (x) g (x), чтобы данная функция могла быть выражена как h (x) = f (g (x)). H (x) = f (g (x)).
27.h (x) = (x − 5) 3h (x) = (x − 5) 3.
31.h (x) = 12x − 33h (x) = 12x − 33
32.h (x) = 1 (3×2−4) −3h (x) = 1 (3×2−4) −3
33.h (x) = 3x − 2x + 54h (x) = 3x − 2x + 54
34.h (x) = (8 + x38 − x3) 4h (x) = (8 + x38 − x3) 4
36.h (x) = (5x − 1) 3h (x) = (5x − 1) 3
39.h (x) = 1 (x − 2) 3h (x) = 1 (x − 2) 3
40.h (x) = (12x − 3) 2h (x) = (12x − 3) 2
41.h (x) = 2x − 13x + 4h (x) = 2x − 13x + 4
Графический
Для следующих упражнений используйте графики f, f, показанные на рисунке 4, и g, g, показанные на рисунке 5, чтобы оценить выражения.
Рисунок 4
Рисунок 5
Для следующих упражнений используйте графики f (x), f (x), показанные на рисунке 6, g (x), g (x), показанные на рисунке 7, и h (x), h (x), показанный на рисунке 8, чтобы оценить выражения.
Рисунок 6
Рисунок 7
Рисунок 8
57.f (g (f (−2))) f (g (f (−2)))
Числовой
В следующих упражнениях используйте значения функций для f, gf и g, показанные в таблице 3, чтобы оценить каждое выражение.
| хх | f (x) f (x) | г (x) г (x) |
| 0 | 7 | 9 |
| 1 | 6 | 5 |
| 2 | 5 | 6 |
| 3 | 1 | |
| 5 | 0 | 8 |
| 6 | 2 | 7 |
| 7 | 1 | 3 |
| 9 | 3 | 0 |
Таблица 3
В следующих упражнениях используйте значения функций для f, gf и g, показанные в таблице 4, чтобы оценить выражения.
| хх | f (x) f (x) | г (x) г (x) |
| -3 | 11 | -8 |
| -2 | 9 | -3 |
| -1 | 7 | 0 |
| 9117 1 9017 1 9017 1 9017 | ||
| 1 | 3 | 0 |
| 2 | 1 | -3 |
| 3 | -1 | -8 |
Таблица 4
Для следующих упражнений используйте каждую пару функций, чтобы найти f (g (0)) f (g (0)) и g (f (0)).g (f (0)).
72.f (x) = 4x + 8, g (x) = 7 − x2f (x) = 4x + 8, g (x) = 7 − x2.
73.f (x) = 5x + 7, g (x) = 4−2x2f (x) = 5x + 7, g (x) = 4−2×2
74.f (x) = x + 4, g (x) = 12 − x3f (x) = x + 4, g (x) = 12 − x3.
75.f (x) = 1x + 2, g (x) = 4x + 3f (x) = 1x + 2, g (x) = 4x + 3.
Для следующих упражнений используйте функции f (x) = 2×2 + 1f (x) = 2×2 + 1 и g (x) = 3x + 5g (x) = 3x + 5. чтобы оценить или найти составную функцию, как указано.
Добавочные номера
Для следующих упражнений используйте f (x) = x3 + 1f (x) = x3 + 1 и g (x) = x − 13.г (х) = х-13.
80.Найдите (f∘g) (x) (f∘g) (x) и (g∘f) (x). (G∘f) (x). Сравните два ответа.
81.Найдите (f∘g) (2) (f∘g) (2) и (g∘f) (2). (G∘f) (2).
82.Какова область определения (g∘f) (x)? (G∘f) (x)?
83.Какова область определения (f∘g) (x)? (F∘g) (x)?
84.Пусть f (x) = 1x.f (x) = 1x.
- ⓐ Найдите (f∘f) (x). (F∘f) (x).
- ⓑ Является ли (f∘f) (x) (f∘f) (x) для любой функции тем же результатом, что и ответ на часть (a) для любой функции? Объяснять.
Для следующих упражнений пусть F (x) = (x + 1) 5, F (x) = (x + 1) 5, f (x) = x5, f (x) = x5 и g (x) = х + 1.g (х) = х + 1.
85.Верно или неверно: (g∘f) (x) = F (x). (G∘f) (x) = F (x).
86.Верно или неверно: (f∘g) (x) = F (x). (F∘g) (x) = F (x).
Для следующих упражнений найдите композицию, когда f (x) = x2 + 2f (x) = x2 + 2 для всех x≥0x≥0 и g (x) = x − 2.g (x) = x − 2. .
87.(f∘g) (6); (g∘f) (6) (f∘g) (6); (g∘f) (6)
88.(g∘f) (a); (f∘g) (a) (g∘f) (a); (f∘g) (a)
89.(f∘g) (11); (g∘f) (11) (f∘g) (11); (g∘f) (11)
Реальные приложения
90.Функция D (p) D (p) дает количество товаров, которые будут востребованы при цене п.п. Стоимость производства C (x) C (x) — это стоимость производства xx единиц продукции. Что бы вы сделали, чтобы определить стоимость производства при цене 6 долларов?
- ⓐ Оцените D (C (6)). D (C (6)).
- ⓑ Оцените C (D (6)). C (D (6)).
- ⓒ Решить D (C (x)) = 6. D (C (x)) = 6.
- ⓓ Решить C (D (p)) = 6.С (D (p)) = 6.
Функция A (d) A (d) дает уровень боли по шкале от 0 до 10, который испытывает пациентка с dd миллиграммами обезболивающего препарата в ее организме. Миллиграммы лекарства в организме пациента через tt минут моделируются с помощью m (t) .m (t). Что из следующего вы бы сделали, чтобы определить, когда у пациента будет уровень боли 4?
- ⓐ Вычислить A (m (4)). A (m (4)).
- ⓑ Оценить m (A (4)). M (A (4)).
- ⓒ Решить A (m (t)) = 4.А (m (t)) = 4.
- ⓓ Решить m (A (d)) = 4. m (A (d)) = 4.
Магазин предлагает покупателям скидку 30% от цены xx выбранных товаров. Затем магазин снимает на кассе дополнительные 15%. Напишите функцию цены P (x) P (x), которая вычисляет окончательную цену товара в единицах исходной цены x.x. (Подсказка: используйте композицию функций, чтобы найти свой ответ.)
93.Капля дождя, падающая на озеро, вызывает круговую рябь. Если радиус в дюймах увеличивается как функция времени в минутах согласно r (t) = 25t + 2, r (t) = 25t + 2, найдите площадь пульсации как функцию времени.Найдите площадь пульсации при t = 2, t = 2.
94.Лесной пожар оставляет после себя участок травы, выгоревший по расширяющейся круговой схеме. Если радиус круга горящей травы увеличивается со временем по формуле r (t) = 2t + 1, r (t) = 2t + 1, выразите площадь сожженной травы как функцию времени tt (минуты).
95.Воспользуйтесь функцией, которую вы нашли в предыдущем упражнении, чтобы определить общую площадь ожога через 5 минут.
96.Радиус r, r в дюймах сферического шара связан с объемом V, V соотношением r (V) = 3V4π3.г (В) = 3V4π3. Воздух закачивается в баллон, поэтому объем через tt секунд определяется как V (t) = 10 + 20t.

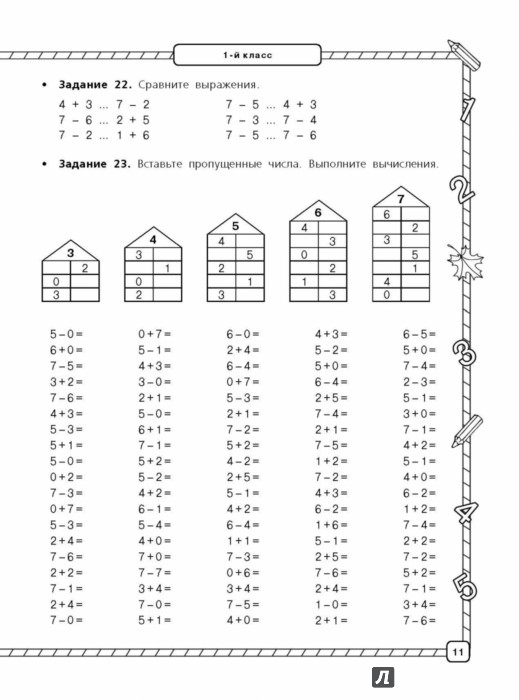
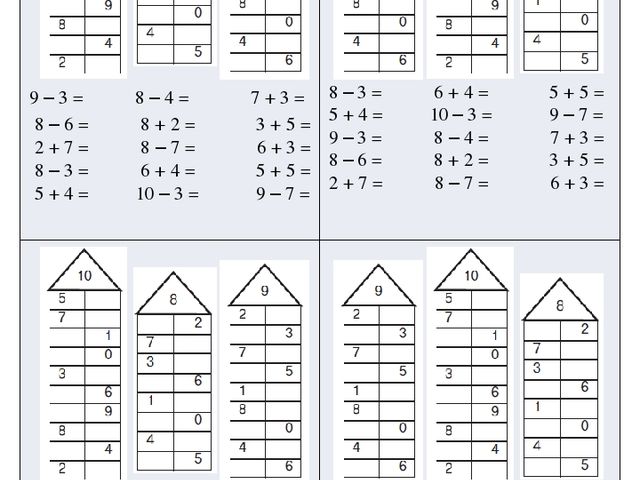
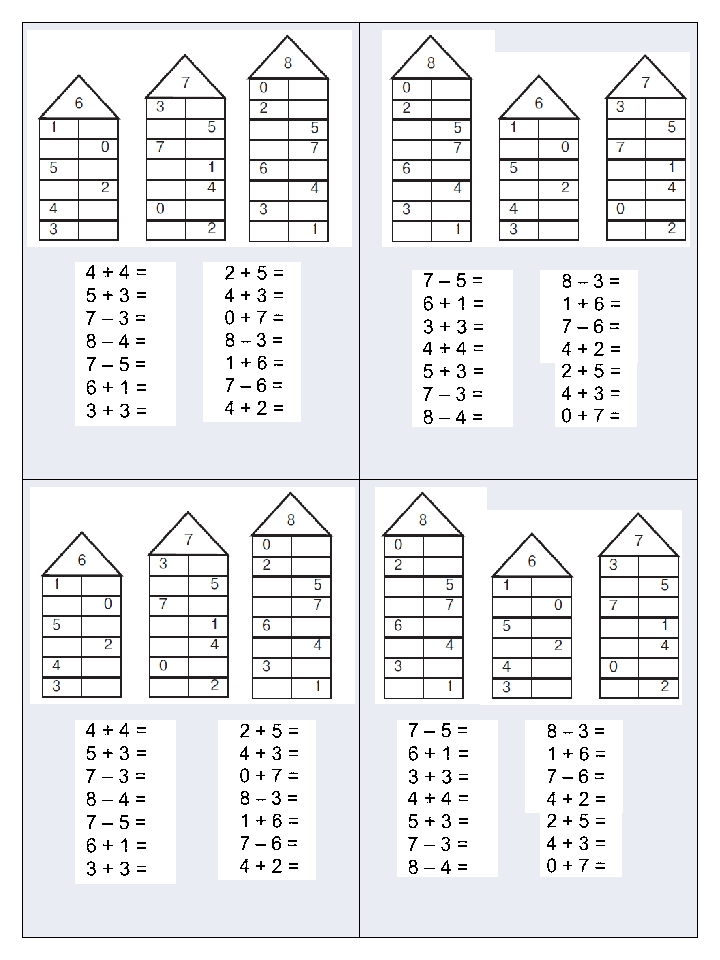
 Планета «Завершающая».
Планета «Завершающая».