Порядок выполнения действий в выражениях без скобок и со скобками — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Раздаточный материал. Карточка- тренажёр «Порядок действий в числовом выражении» | Тренажёр по математике (3 класс) на тему:
ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ В ЧИСЛОВОМ ВЫРАЖЕНИИ
1. Запиши выражение.
2. Определи порядок действий.
3. Найди значение этого выражения. В выражениях без скобок умножение и деление выполняются по порядку, слева направо. В выражениях без скобок, сначала выполняются действия умножения и деления, а затем действия сложения и вычитания.
В выражениях со скобками сначала выполняются действия в скобках, затем действия умножения и деления по порядку, потом действия сложения и вычитания по порядку.
Решить в отдельной тетради :
1. Реши выражения.
90 – 27 : 9 • 6 + 2 • 4
40 – 10 : 5 • 3 : 2 : 3 + 10
20 – 24 : 3 + 18 – 2 • 6
7 • 3 + 21 : 7 • 5 – 16 : 2 : 4 • 3
2. Реши выражения.
60 – (8 • 3 – 18 : 2) : 5 • 3 + 3 • 9
40 – 15 : 3 + 27 : 3 – 3
10 + 21 : 3 – 15 : 5 + 9 • 3 + 9 • 2
(27 – 19) • 3 + 18 : 3 + (8 + 7) : 5 – 17
3. Реши выражения.
50 + 15 : 5 + 16 : 2 – 3
9 • 3 – 19 + 6 • 3 – 3 • 5
9 • (6 : 2) – 24 : 8 • 3 + 7 • 3 – 34
90 – 7 • 3 – 24 : 8 • 5
4. Реши выражения.
50 – 3 • 8 – 2 • 7 + 13 – 11
3 • 6 + 16 : 2 : 4 • 7 – 19
(7 • 3 + 33) – 3 • 6 : 2
3 • (12 – 8) : 2 + 3 • 9 – 33
5. Реши выражения.
50 – 15 : 5 • 3 + 16 : 8 • 5
60 – (13 + 2) : 5 – 6 • 3 + 25
3 • 8 – 4 • 3 + 2 • 8 – 11
6. Реши выражения.
6 • 3 + 18 : 2 : 3 • 7 – 9 • 2
16 : 2 : 2 • 3 : 2 • 3
9 • 3 – 12 : 2 • 3 + 49
7. Реши выражения.
8 • 2 + 23 – 24 : 8 • 3 + 17
2 • 4 + 24 : 3 + 18 : 6 • 9
90 – (20 – 24 : 3) : 4 • 6 + 3 • 5
(82 – 74) : 2 • 3 + 7 • 3 – 19 + (64 – 36) : 4
8. Реши выражения.
3 • 4 + 9 • 3 – (15 + 9) : 8 • 5
(50 – 23) : 3 + 8 • 3 – 6 • 2 + (6 + 15) : 3
3 • 6 + 9 • 2 – (2 • 7 + 12 : 6 • 5)
(5 • 3 – 3 • 2 + 18 : 3) + (82 – 79) • 7 – 13
» Порядок выполнения действий в выражениях со скобками и без скобок»
Луханина Ирина Александровна, учитель начальных классов ГБОУ РК «Лозовская специальная школа-интернат»
Урок математики в 3 классе
Тема урока : « Порядок выполнения действий в выражениях со скобками и без скобок».
Цель урока: создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.
Задачи урока:
Образовательные:
— закрепить знания учащихся о правилах выполнения действий в выражениях без скобок и со скобками; формировать у них умение пользоваться этими правилами при вычислении конкретных выражений; совершенствовать вычислительные навыки; повторить табличные случаи умножения и деления;
Развивающие:
— развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,коммуникативные навыки;
Воспитательные:
— воспитывать толерантное отношение друг к другу, взаимное сотрудничество,
культуру поведения на уроке, аккуратность, самостоятельность, воспитывать интерес к занятиям математикой.
Формируемые УУД:
Регулятивные УУД:
-работать по предложенному плану, инструкции;
-выдвигать свои гипотезы на основе учебного материала;
— осуществлять самоконтроль.
Познавательные УУД:
-знать правила порядка выполнения действий:
-уметь разъяснить их содержание;
-понимать правило порядка выполнения действий;
-находить значения выражений согласно правилам порядка выполнения
действий, используя для этого текстовые задачи;
— записывать решение задачи выражением;
— применять правила порядка выполнения действий;
-уметь применять полученные знания при выполнении контрольной работы.
Коммуникативные УУД:
-слушать и понимать речь других;
— выражать свои мысли с достаточной полнотой и точностью;
— допускать возможность различных точек зрения, стремиться понимать позицию собеседника;
-работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;
Личностные УУД:
-устанавливать связь между целью деятельности и её результатом;
-определять общие для всех правила поведения;
— уметь осознанно и внимательно читать задания;
-выражать способность к самооценке на основе критерия успешности учебной деятельности.
Планируемый результат:
Предметные:
-Знать правила порядка выполнения действий.
-Уметь разъяснить их содержание.
-Уметь решать задачи с помощью выражений.
Личностные:
—Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные: регулятивные УУД-
-Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
Коммуникативные УУД:
-Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им .
Познавательные УУД:
-Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке .
Тип урока : Комплексное применение знаний и способов действий.
Методы и формы обучения: методы- словесный, наглядный, практический. Формы- фронтальная, индивидуальная.
Оборудование: интерактивная доска, компьютер, проектор, листы с числами
Ход урока
1. Организационный момент. Эмоционально-психологическая и мотивационная подготовка к усвоению материала.
Давайте, ребята, учиться считать,
Делить, умножать,
Прибавлять, вычитать.
Запомните все,
Что без точного счета,
Не сдвинется с места
Любая работа.
— Займите свои рабочие места.
Открыли тетради, записали число и классная работа.
2. Актуализация знаний.
— На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.
2.1.Устный счёт.
Игра «Молчанка»
3 х
Игра «Найди правильный ответ».
( У каждого ученика лист с числами)
Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)
— Соедините полученные результаты.
— Какую геометрическую фигуру вы получили? ( Треугольник)
— Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)
— Продолжаем работать по карточке.
Найдите разность чисел 100 и 22.
 (78)
(78)Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
Возьмите число 25 4 раза. (100)
— Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.
— Сколько треугольников получилось? (5)
3. Работа над темой урока.
(Наблюдение за изменением значения выражения от порядка выполнения арифметических действий )
— В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
— А в математике обязательно ли выполнять арифметические действия в определенном порядке?
— Давайте проверим:
Сравним выражения:
8-3+4 и 8-3+4
-Видим, что оба выражения совершенно одинаковы.
-Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий ( выведено на экран)
Порядок действий
-В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
-Запишем.
8-3+4=5+4=9
-Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
8-3+4=8-7=1
— Почему результаты получились разные ?
— Отчего зависит порядок действий?
— Давайте сделаем вывод: порядок выполнения арифметических действий менять нельзя.
— Каков же порядок выполнения действий в выражениях без скобок ?
— Узнаем правило выполнения арифметических действий в выражениях без скобок.
— Учебник, страница 24. Читаем правило.
— Какая же тема нашего урока и цель?
4. Закрепление знаний.
— Рассмотрим выражение :38-10+6
— В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Эти действия называют действиями первой ступени.
-Выполняем действия слева направо по порядку ( на экране).
Порядок действий
— Рассмотрим второе выражение
24:3*2
— В этом выражении имеются только действия умножения и деления –
это действия второй ступени.
— Выполняем действия слева направо по порядку ( на экране).
Порядок действий
— В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Вывод: Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
— Рассмотрим выражение.
18:2-2*3+12:3?
— Какие действия в этом выражении вы видите? (В этом выражении имеются действия сложения и вычитания, умножения и деления. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
1 4 2 5 3
18:2-2*3+12:3
— Давайте вычислим значение выражения ( один ученик работает у доски, остальные в тетрадях)
1 4 2 5 3
18:2-2*3+12:3=9-6+4=3+4=7
— Давайте сделаем вывод, в каком порядке выполняются арифметические действия, если в выражении имеются скобки? (Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках).
Работа у доски с объяснением: рассмотрим выражение- 30 + 6 * (13 — 9) ( все действия комментируются учеником сч помощью учителя)
-Какие действия имеются в данном выражении? ( в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение.
— Расставим порядок действий.
3 2 1
30 + 6 * (13 — 9)
-Вычислим значение выражения.
3 2 1
30+6*(13-9)=30+6*4=30+24=54
— Как вы думаете ,как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении? (Надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
( На интерактивную доску выводится порядок выполнения арифметических действий) :
Порядок действий
ФИЗМИНУТКА
Раз, два — выше голова.
Три, четыре — руки шире.
Пять, шесть — всем присесть.
Семь, восемь — встать попросим.
Девять, десять — сядем вместе.
5. Выполнение тренировочных заданий на изученное правило . (Работа у доски с комментированием).
(*Учащиеся устанавливают порядок действий и выполняют вычисления).
43 — (20 — 7) +15
32 + 9 * (19 — 16)
2 * 9 — 18:3
— По какому правилу надо действовать? ( Комментированное объяснение ученика: Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение).
В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение).
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
— Решение выражений с комментированием учениика : В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
(В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание).
2*9-18:3=18-6=12
6. Самостоятельная работа ( со взаимопроверкой):
— Узнайте ,правильно ли определен порядок действий в следующих выражениях.
4 3 1 2
37 + 9 — 6 : 2 * 3 =
3 1 2
18 : (11 — 5) + 47=
1 3 2
7 * 3 — (16 + 4)=
— Проверяем работу. Как вы рассуждали при решении выражений .
— Кто повторит правило выполнения действий в выражениях со скобками и без скобок?
( Вспоминаем правило и повторяем хором).
7. Решение задачи. ( На экран выведена текстовая задача).
В книге 48 страниц. Даша читала 3 дня по 9 страниц. Сколько страниц книги осталось прочитать Даше?
— Задача простая или составная?
— Что надо еще найти, прежде, ответить на главный вопрос задачи?
— После этого можно узнать,сколько страниц осталось прочитать Даше? ( Оформляют решение и ответ самостоятельно).
— А теперь проверим как вы справились с задачей ( порядок действий комментируют).
8. Подведение итогов. Рефлексия.
— Какие знания вы получили на уроке? ( Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий).
В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий).
— Какой момент на уроке был для вас удачным?
— Где испытывали трудности?
9. Домашнее задание: рабочая тетрадь с.13, № 16-17.
Конспект урока по теме «Порядок выполнения действий в выражениях со скобками» (3 класс)
Дата: 04.12.2019
Предмет: Математика
Класс: 3 А
Студентка: Байбакова Яна Анатольевна
Учитель: Сидорова Елена Николаевна
Руководитель практики: Савченко Ирина Викторовна
Тема: «Порядок выполнения действий в выражениях со скобками»
Тип урока: ОНЗ
Цель: формировать умение определять порядок выполнения действий в выражениях со скобками.
Задачи:
образовательная: учить определять порядок выполнения действий в выражениях со скобками; совершенствовать умение считать устно; формировать умение записывать решение задачи выражением;
развивающая: развивать мыслительные операции: классификации, анализа и синтеза, математическую речь, воображение, память.
воспитательная: воспитывать аккуратность при выполнении записей в тетради и на доске; настойчивость в достижении поставленной цели; повышать уровень самоконтроля.
ПЛАНИРУЕМЫЕ ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ УРОКА: умеют определять порядок выполнения действий в выражениях со скобками; умение записывать решение задачи выражением;
МЕТАПРЕДМЕТНЫЕ УУД:
познавательные — ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке, а так же обобщать собственные представления о проблеме;
регулятивные – понимать учебную задачу урока, определять и формулировать цель учебной деятельности с помощью учителя.
коммуникативные — оформлять свои мысли в устной и письменной форме; уметь слушать и слышать собеседника и вести диалог; работать в парах; умение адекватно выражать собственное мнение и собственную позицию.
ЛИЧНОСТНЫЕ УУД — осуществляют самооценку на основе критерия успешности учебной деятельности; формулируют собственное мнение и собственную позицию.
Средства обучения (в том числе и интернет – ресурсы): учебник, компьютер, презентация, дидактический раздаточный материал.
Литература: учебник математики 3 класс 1 часть В. Рудницкая ,рабочая тетрадь.
ОК
ПО
Умения
1.1, 1.2, 1.3, 1.4, 1.5, 4.1, 4.2.
1.2, 4, 7.
1, 2, 3, 6, 7.
1-12, 21- 26.
Ход урока:
ПЕДАГОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ
УЧЕБНО-ПОЗНАВАТЕЛЬНАЯ ДЕЯТЕЛЬНОСТЬ обучающихся
1. Мотивация к учебной деятельности
Мотивация к учебной деятельности
-Здравствуйте, ребята, меня зовут Яна Анатольевна, и я проведу у вас урок математики.
— Начать наш урок я хочу с высказывания немецкого математика, физика и астронома Карла Фридриха Гаусса: «Математика – царица всех наук…».
— Как вы понимаете данное высказывание?
Рассуждают, мотивируют учебную деятельность.
— Воспринимают, анализируют.
— Без математики невозможна ни одна другая наука, она присутствует везде
2. Актуализация знаний
Устный счёт
Вычислите:
25+6= 16:4=
40-27= 18+4=
63:7= 90-55=
5∙7= 9∙3=
Вычисли и назови ответ
— Вспомните порядок выполнения действий в выражениях без скобок.
20-12+6=
9+7∙3-15=
34-16:4+18=
19+4∙6-63:7=
-Установите соответствие.
20-9+8=19 верно
20-9+8=3 неверно
— Какие это выражения?
-Какое равенство верно?
— Как выполняли действия?
— Как изменить второе равенство, чтобы оно стало верным? Может быть можно поставить скобки?
— Как в нём будем выполнять действия?
— У вас возникло затруднение. Почему?
Почему?
— Предположите тему нашего урока.
Тема: «Порядок выполнения действий в выражениях со скобками»
— Предположите, чему будем учиться сегодня?
— Сегодня будем учиться определять порядок выполнения действий в выражениях со скобками; учиться записывать решение задач выражением.
Устно вычисляют, называют ответ, проверяют:
25+6= 31 16:4=4
40-27= 13 18+4=22
63:7= 9 90-55=35
5∙7= 35 9∙3=27
— В выражениях без скобок, где присутствуют операции сложения и вычитания, действия выполняются по порядку слева направо..
— В выражениях с действиями умножения и деления сначала выполняются умножение и деление слева направо, затем сложение и вычитание по порядку слева направо.
20-12+6=14, выполняю действия по порядку: сначала вычитание, затем сложение.
9+7∙3-15=15, сначала выполняю действие умножения, затем сложение, потом вычитание.
34-16:4+18=48, сначала выполняю действие деления, затем вычитание, потом сложение.
19+4∙6-63:7=35, сначала выполняю умножение, затем деление, затем сложение, потом вычитание.
— Без скобок.
— Первое.
— Сначала выполнили вычитание, затем сложение.
— Можно действие сложения взять в скобки.
— Сначала сложение в скобках, затем вычитание.
— Мы не знаем, как выполнять действия в выражениях со скобками.
— Предполагают.
— Предполагают.
3. Проблемное объяснение и фиксирование нового знания
— Вспомните правило выполнения действий в выражениях вида 9:(3:3) и 12-( 7-4).
— Пользуясь известными правилами, откройте порядок выполнения действий в выражениях со скобками, где в скобках есть и умножение, и сложение, например, 12-40:(5+5∙3)=
— Вы сами открыли правило выполнения порядка действий в выражениях со скобками.
— Откройте ваши рабочие тетради на 56 стр., сегодня мы будем работать в них. Найдите №197. Прочитайте задачу.
— О чём говорится в задаче?
— Что известно в задаче?
— Как понимаете «треть»?
— Назовите вопрос задачи.
— Можем сразу ответить на вопрос задачи?
— Что найдем сначала?
— Каким действием?
— Теперь можем ответить на вопрос задачи?
— Каким действием?
— Нам предлагается записать решение этой задачи выражением.
— Посмотрите на способ 1.
— В каком порядке должны выполняться действия?
— Подставьте данные выражение так, чтобы получился верный ответ.
— Посмотрите на способ 2.
— В каком порядке здесь будут выполняться действия?
— Подставьте данные выражение так, чтобы получился верный ответ.
— Запишите ниже ответ.
— Найдите №198. Прочитайте задачу.
— О чём говорится в задаче?
— Что известно в задаче?
— Прочитайте, что нам нужно сделать.
— Посмотрите на первое выражение, сравните его с условием задачи и скажите, что мы найдём, выполнив его.
— Какое это выражение?
— В каком порядке будем выполнять действия в выражении без скобок?
— Решите.
— Посмотрите на второе выражение. Что мы найдём? В каком порядке будем выполнять действия в выражении без скобок?
Что мы найдём? В каком порядке будем выполнять действия в выражении без скобок?
Вычислите.
-Что находим третьим выражением?
— Что найдём 4 выражением?
,Какое это выражение?
— Назовите порядок действий в выражении со скобками. Вычислите.
— Что найдём 5 выражением?
Какое это выражение? В каком порядке будем выполнять действия?
Вычислите.
— Что найдём 6 выражением?
— Какое это выражение?
— Какой порядок действий в этом выражении? Вычислите.
— Что найдём 7 выражением?
— Какое это выражение?
— В каком порядке будем выполнять действия?
— Найдите значение выражения.
— Деление и вычитание не обладают ни перемест., ни сочет. свойством, поэтому в таких выражениях, как 9:(3:3) и 12- ( 7-4), скобки переставлять или отбрасывать нельзя. Сначала нужно выполнить действия в скобках.
— В выражениях со скобками сначала выполняются действия в скобках: умножение, потом сложение, затем: деление, потом вычитание.
— Читают условие задачи.
— О Маше и её конфетах.
— Что у Маши было 18 конфет, треть она съела, а 5 конфет отдала подруге.
— Целое разд.на 3 равн.части и взяли одну часть.
— Сколько конфет у неё осталось?
— Нет.
— Сколько у неё осталось конфет после того, как она съела треть.
— Делением и вычитанием: 18:3=6, 18-6=12
— Да.
— Вычитанием: 12-5
— Сначала действия в скобках: деление, затем сложение, потом вычитание.
18-(18:3+5)= 7
— Сначала деление, затем вычитание по порядку.
18-18:3-5=7
— Записывают ответ.
— О маме, которая совершала покупки.
— Что она купила 3 пакета молока по 8 р., 2 пачки печенья по 6 р., 2 лимона по 3 р.
— Нам нужно понять, что означает каждое выражение, найти и записать его значение.
— Решив это выражение, мы найдём стоимость 3 пакетов молока и 2 пачек печенья.
— Выражение без скобок.
— Сначала умножение, затем сложение слева направо.
8∙3+6∙2=36 (р) – стоимость молока и печенья
— Стоимость печенья и лимонов.
— Сначала умножение, затем сложение слева направо.
6∙2+3∙2=18 (р) — стоимость печенья и лимонов.
— Насколько печенье стоит меньше, чем молоко. Сначала выполняю действия умножения, затем вычитания.
8∙3-6∙2= 12 (р) — печенье стоит меньше, чем молоко
— Во сколько раз стоимость молока больше, чем стоимость лимонов.
— Выражение со скобками.
— Сначала выполняю действия в скобках слева направо.
(8∙3):(3∙2)= 4 (р) — стоимость молока больше, чем стоимость лимонов
— Сколько у мамы останется денег после покупки молока.
— Выражение без скобок. Сначала выполняю умножение, затем вычитание.
120 — 8∙3= 96 (р) – останется после покупки молока
— Сколько останется денег после покупки молока и печенья.
— Выражение со скобками.
— Сначала действия в скобках: умножение и сложение, затем вычитание.
120 – (8∙3+6∙2)= 120-36=84 (р) – останется после покупки молока и печенья
— Сколько у мамы останется денег после покупки молока, печенья и лимонов.
— Выражение со скобками.
— Сначала действия в скобках: умножение, потом сложение слева направо, затем вычитание.
120 – (8∙3+6∙2+ 3∙2)= 120-42=78 (р) – останется после покупки молока, печенья и лимонов
4. Первичное закрепление во внешней речи
— Вспомним ещё раз порядок выполнения действий в выражениях со скобками.
— Найдите следующее задание №200
— Что нужно сделать, чтобы можно было сравнивать выражения?
— Сравните первые два выражения: чем они похожи, в чём их различие?
— Назовите порядок действий в первом выражении.
— Назовите порядок действий во втором выражении.
— Найдите значения первых двух выражений.
— Сравните выражения и поставьте знаки ›‹.
— Посмотрите на следующие два выражения. Назовите порядок действий в каждом.
— Найдите значения выражений и поставьте нужный знак.
— Найдите значения следующих двух выражений и поставьте нужный знак.
— Найдите значения следующих двух выражений и поставьте нужный знак.
-Пришло время немного передохнуть. Физминутка.
— Сначала выполняем действия в скобках: умножение или деление сначала, затем уже сложение и вычитание.
— После выполняем действия за скобками: умножение или деление сначала, затем уже сложение и вычитание.
— Находят и читают задание.
— Нужно найти их значение.
— Первое выражение без скобок, второе со скобками, но цифры в них одинаковые.
— Сначала деление, затем сложение.
— Сначала сложение в скобках, затем деление.
5 и 2, 5 больше 2, значит первое выражение больше второго, ставлю знак ›
— В первом выполняю вычитание в скобках, затем умножение, во втором сначала умножение, затем вычитание.
6 и 26, 6 меньше 26, значит первое выражение меньше второго, ставлю знак ‹
8 и 81,8 меньше 81, значит первое выражение меньше второго, ставлю знак ‹
35 и 36,35 меньше 36, значит первое выражение меньше второго, ставлю знак ‹
— Выполняют упражнения физминутки под музыку.
5. Самостоятельная работа с самопроверкой
-Выполните задание на карточках.
16:(25-21)=
3∙ (37-12)+9=
(56-32)+(7∙5)=
61+17∙2- 76=
— Сравните свои результаты с эталоном.
— У кого возникли затруднения?
— Осуществляют самоконтроль при выполнении самостоятельной работы, адекватно рассуждают о причинах своего успеха или неуспеха.
Осуществляют самопроверку по эталону.
Эталон:
16:(25-21)=4
3∙ (37-12)+9=84
(56-32)+(7∙5)=59
61+17∙2- 76=19
— Осуществляют поиск причины затруднения и самокоррекцию.
6. Включение нового в систему знаний и повторение
— Найдите № 201. Прочитайте условие задачи.
— О чём говорится в задаче?
— Что известно?
— Назовите вопрос задачи.
— Подставьте значения в пустые окошки так, чтобы выражением мы могли ответить на вопрос задачи.
— Найдите №189. Прочитайте задание.
— По очереди подставляйте числа в окошко, устно вычисляйте и записывайте ответ в соответствующей строке под той цифрой, которую подставляли. Соблюдайте порядок выполнения действий.
Соблюдайте порядок выполнения действий.
— О шёлке и платьях.
— Что из 25 м шёлка сшили 4 платья, на каждое платье расходовали 3 м.
— Сколько метров шелка осталось?
25- 4∙3=13(м)- осталось шёлка
1, 4, 6, 8.
1, 3, 5,7.
5, 15, 25, 35
50, 60, 70, 80.
7. Рефлексия к учебной деятельности
Продолжите высказывания.
Сегодня на уроке я учился …
Я научился …
Я смог …
Я узнал …
Мне было трудно …
Домашнее задание: раб.тетр.№202.
Отвечают на вопросы учителя, высказывают своё мнение.
Выполняют рефлексию учебной деятельности.
Подпись учителя .
Подпись руководителя практики .
Отметка .
«Порядок выполнения действий. Скобки». | План-конспект урока по математике (3 класс) на тему:
Урок математики в 3 классе
Тема: «Порядок выполнения действий. Скобки».
Цель: познакомить учащихся с правилами порядка выполнения действий в выражениях, учить работать по алгоритму.
Задачи:
Обучающие:
- повторить табличные случаи умножения и деления;
- проверить сформированность математических компонентов;
- формировать умение применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях;
Развивающие:
- развивать вычислительные навыки, логическое мышление.
- совершенствовать умения наблюдать, сравнивать, обобщать, применять полученные знания на практике;
- развивать познавательную активность, повышать степень самостоятельности и инициативности учащихся;
Воспитывающие:
- воспитывать интерес к математике;
- воспитывать толерантное отношение друг к другу, взаимное сотрудничество.
Программа: Школа России.
Учебник: М.И.Моро, М.А. Бантова, Г.В. Бельтюкова 3 класс (часть 1) – М: Просвещение, 2008.
Оборудование и программное обеспечение:
для учителя — компьютер, проектор, экран; презентация,
для учащихся — ноутбуки, карточки с индивидуальными заданиями, карточки с заданиями для работы в парах, группах, тестовые задания, изображение человечков для рефлексии.
Методы: фронтальный, индивидуальный, групповой (работа в парах).
Тезис: «Мир построен на силе чисел».
Пифагор
- Организационный момент.
— Чтоб урок наш стал светлее,
Мы поделимся добром.
Вы ладони протяните,
В них любовь свою вложите,
Ей с друзьями поделитесь
И друг другу улыбнитесь.
— Займите свои рабочие места.
- Проверка домашнего задания.
— Открыли тетради, проверим д/з. У кого д/з вызвало трудности? Кто быстро справился и самостоятельно?
- Устный счёт.
Вы знакомы с Математикой — царицей наук? Тогда наверняка помните, что у нее есть помощники — знаки. Какие? Вот они. Они пришли к нам на урок не просто, а принесли с собой разные задания, которые предстоит нам выполнить.
Готовы.
1) Игра «Найди правильный ответ».
( У каждого ученика лист с числами)
55 | 56 | 57 | 58 | 59 | 60 | 61 |
62 | 63 | 64 | 65 | 66 | 67 | 68 |
69 | 70 | 71 | 72 | 73 | 74 | 75 |
76 | 77 | 78 | 79 | 80 | 81 | 82 |
83 | 84 | 85 | 86 | 87 | 88 | 89 |
90 | 91 | 92 | 93 | 94 | 95 | 96 |
97 | 98 | 99 | 100 | 101 | 102 | 103 |
— Я читаю задания, а вы, выполнив в уме действия, должны полученный результат, т. е. ответ, зачеркнуть крестиком.
е. ответ, зачеркнуть крестиком.
- Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
- Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
- Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)
— Соедините полученные результаты.
— Какую геометрическую фигуру вы получили? ( Треугольник)
— Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)
— Продолжаем работать по карточке.
- Найдите разность чисел 100 и 22. (78)
- Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
- Возьмите число 25 4 раза. (100)
— Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.
— Сколько треугольников получилось? (5)
2) Решение задач
1. Шаг мужчины 75 см, это на 25 см больше шага мальчика. Сколько см составляет шаг мальчика? (75-25=50 см)
2. Пульс лягушки 30 ударов в минуту, это на 30 ударов меньше, чем у человека. Какой пульс у человека? (30+30=60 ударов в минуту)
Какой пульс у человека? (30+30=60 ударов в минуту)
— Почему эти задачи решили такими действиями? (Это задачи в косвенной форме)
3) Кто быстрее?
— Царица Математика хочет узнать, кто из вас быстро считает и предлагает найти значение вот этого выражения: 42 : 7 ∙ 4 : 8 ∙ 0 ∙ 54 : 6 · 12 : 4
— Как смогли так быстро посчитать? (При умножении на 0, результат 0)
42 : 7 ∙ 4 : 8 · 9
42 — 7 + 29 + 16 – 53
— Чем похожи равенства? (= 27, одинаковое значение, 1 и 2 числа, количество чисел, действий)
— Как считали? (по порядку)
- Постановка проблемы
— На слайде вы видите два примера. Что можете о них сказать.
2+5х3=17
2+5х3=21
— Вижу, вы удивлены. Почему? (Примеры одинаковые, а результат разный)
— Какая возникла проблема? (Почему в одинаковых примерах бывают разные ответы?)
— Попробуйте сформулировать цель урока, т.е. чему мы будем учиться.
— Как нам изменить выражения, ведь, судя по результату, они не равны? (Необходимо как-то обозначить в записи порядок действий)
— Итак, цель нашего урока — научиться обозначать в записи порядок действий.
— Запишите в тетрадях число, классная работа.
- Работа над темой урока. Поиск решения проблемы
— Давайте рассуждать.
Если отличаются правые части…
Чем отличаются левые части? Какие есть идеи? (Левые части отличаются порядком действий.)
— Какой порядок действий в первом примере? во втором примере?
В каком примере мы действовали по правилу? (В первом.)
— А во втором примере мы нарушили правило! Как же нам догадаться, что здесь сложение выполняется первым? (Нужно поставить скобки.)
Чтобы указать, в каком порядке нужно выполнять действия применяют скобки.
Так что же обозначают скобки? (Действия, заключенные в скобки, выполняются раньше других.)
— А чтобы нам легче было запомнить Царица Математики дарит нам ключик — правило:
Порядок действий в выражениях особый.
И в каждом случае, помни, он свой.
В порядке все действия ты выполняй.
Сначала в скобках все посчитай.
Потом чередом, умножай или дели.
И, наконец, вычитай или сложи.
— Давайте вместе составим алгоритм порядка выполнения действий.
(На слайде появляется памятка)
1) ( )
2) «х» или «:»
3) «+» или «-»
6. ФИЗМИНУТКА
Раз, два, три, четыре, пять
Все умеем мы считать.
Поднимает руки класс- это раз!
Повернулась голова- это два!
Руки вниз- вперёд смотри это три!
Руки в стороны пошире- развернули на четыре!
С силой их к плечам прижать- это пять.
Всем ребятам тихо сесть- это шесть.
- Закрепление нового материала
Царица Математики предлагает нам:
- Дифференцированная работа по карточкам.
— Сейчас посмотрим, как вы умеете определять порядок действий в выражениях. В карточках вам надо расставить порядок выполнения действий на каждой схеме. (Синие – слабым ученикам, красные – сильным).
… + … : … + … * … — …
… : … + … — … — … *(… + …)
… + … (… * … + …) : … — … : … * …
… * … * … — …(… * … — …) + … : …
— Поменяйтесь карточками друг с другом и проверьте правильность выполнения.
Проверяют по слайду на доске.
О – нет ошибок, О – 1 ошибка, 2-3 ошибки)
(правильное выполнение работы по карточкам)
2) Компьютерная игра- тренажёр
В царстве математики, во все года
Таблица умножения нужна всегда!
Закрепим знание таблицы умножения в тренажёре. —
— Чему учились, выполняя задание? (Применять алгоритм)
3) Работа в паре.
Расставьте скобки.
38-10+6=34 24:3х2=16
38-10+6=22 24:3х2=4
Для проверки сравним результаты
- Самостоятельная работа.
Учебник № 2 с.23
( 1 строку – 1 ряд, 2 строку – 2 ряд, 3 строку – 3 ряд).
— Нужно установить порядок действий и выполнить вычисления.
-Проверяем.
ГИМНАСТИКА ДЛЯ ГЛАЗ
5) Работа в группе.
— Прочитать задачу сначала про себя, потом вслух.
— Из карточки выбрать решение, соответствующее этой задаче.
- 48 — (3*9) 2) 48 — (9*3) 3) 48 + 3*9
— Какое решение выбрали?
— Какая запись лишняя? Почему?
— Что нужно узнать первым действием?
— Вторым?
Задача подробно записывается на доске и в тетрадях.
6) Математический тест (4мин)
Царица Математики открывает — впереди три пути, но только по одному надо пройти.
№ | Вопросы | Ответы | ||
1 | Увеличь 8 в 2 раза и прибавь 6. | 10 | 22 | 6 |
2 | Найди частное чисел 42 и 6. | 36 | 48 | 7 |
3 | Каков результат выражения (24 : 4) + (24 : 6) | 10 | 14 | 28 |
4 | На сколько 3 меньше 20? | 23 | 17 | 13 |
5 | Во сколько раз 8 меньше 56? | 7 | 48 | 64 |
6 | Найди значение выражения 4 + 6 : 3 + 4 . | 18 | 10 | 3 |
7 | Чему равна сумма пяти одинаковых слагаемых, каждое из которых равно 3? | 25 | 15 | 8 |
8 | Чему равно выражение 5 + (13 – 7). | 8 | 20 | 11 |
9 | Сколько ушек у 3 мышек? | 6 | 9 | 3 |
10 | Сколько ножек у двух сороконожек? | 40 | 2 | 80 |
- Домашнее задание
На повторение Задача № 7, стр 23. , а на закрепление задание по выбору
, а на закрепление задание по выбору
— придумать стишок про скобки;
— придумать примеры со скобками;
— придумать математическую задачу, решая которую используем скобки.
- Рефлексия
— Ребята, вы прекрасно работали. Игра «Улыбнись»
— Кому всё понятно и хорошее настроение — покажите улыбающегося человечка. Если кому – то не все понятно и настроение грустное – грустного человечка.
— Давайте улыбнёмся друг другу и скажем спасибо.
Презентация к уроку математики 3 класс «Порядок выполнения действий»
Слайды и текст этой онлайн презентации
Слайд 1
ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ
Внимательно слушайте – и всё услышите!
Внимательно смотрите – и всё увидите!
Думайте – и всё обязательно поймёте!
Удачи!
Слайд 2
20-8:2=6
20-8:2=16
(20-8):2=6
Сегодня на уроке фиксик Нолик предлагает нам рассказать ему о хитростях математических действий
?
Слайд 3
«Порядок действий
в выражениях
со скобками»
Слайд 4
Нолик считает, что день надо начинать с утренней гимнастики, а урок математики – с гимнастики ума.
Чем отличаются столбики примеров?
8 – 3 + 4 = 9 8 — (3+4) =1
18 – 8 + 9 =19 18 — (8+9) =1
20 – 5 + 3 = 18 20-(5+3)=12
Слайд 5
Как же правильно выполнять действия в выражениях со скобками?
Слайд 6
Порядок выполнения действий при нахождении значений выражений определяется следующими правилами:
Если в выражении нет скобок, то сложение и вычитание выполняют по порядку слева направо.
Если выражение содержит действия сложения, вычитания, умножения и деления и в нем нет скобок, то сначала выполняют действия умножения и деления, потом – действия сложения и вычитания слева направо.
Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2)
Слайд 7
Каждое выражение задает программу своего вычисления. Она состоит из команд.
Определяю порядок выполнения действий в числовом выражении.
Выполняю действие в скобках.
Выполняю слева направо сложение (вычитание). Читаю значение выражения.
Читаю значение выражения.
Слайд 8
Фиксики предлагают вам физкультминутку — фиксипелку.
Слайд 9
Во всем нужна сноровка, закалка, тренировка. №2 (с. 38).
Решите первый пример. Проверьте, получим ли мы нужный результат, если вычисления будем выполнять по порядку.
Измените порядок действий. Какое действие выполним первым?
Вычислите. Получился ли у вас нужный результат?
Поставьте скобки.
(Не получим.)
(Сложение.)
(Да.)
Слайд 10
Семь раз отмерь – один отрежь
Слайд 11
Проверь себя!
100 – 60 = 40 (м)
Ответ: 40 метров осталось проплыть Коле.
60 + 40 = 100 (м)
Ответ: 100 метров длина дорожки в бассейне.
Слайд 12
Над какой темой мы работали?
Удалось ли решить поставленную задачу?
В чём испытывали трудности?
Над чем еще надо работать?
«Проверь себя» стр.39
ПОСТАВИМ ОЦЕНКИ ЗА УРОК.
Молодцы!!!
Слайд 13
Домашнее задание (по выбору):
Учебник: № 6 (с. 39).
Тетрадь с печатной основой: № 27 (с. 37).
39).
Тетрадь с печатной основой: № 27 (с. 37).
|
Деятельность учителя |
Деятельность учащихся |
|
|
|
Основная группа |
Дети с ОВЗ |
|
I. Орг. момент Прозвенел звонок и смолк, начинается урок Все ль на месте? Всё в порядке? Ручки, книжки и тетрадки. Постарайтесь всё понять, правильно задания выполнять.
|
Проверяют готовность к уроку
Знакомятся с листом самооценки (Приложение 1) |
Проверяет готовность к уроку
Знакомится с Листом продвижения по теме (Приложение 2). |
|
II. Актуализация опорных знаний. Самоопределение к деятельности — Найди лишнее выражение. — Почему? — Найдите значение выражений со скобками. Вспомните правило
-Найдём значение выражения, которое оказалось лишним. -А меня получился другой ответ — Сравните выражения. Что общего? — Чем различаются? — Как получилось, что выражения одинаковые, а результаты разные? — В каком порядке вы выполняли действия? — А я? — Так почему получились разные ответы? |
Нет скобок
Рассказывают правило
Предлагают свои варианты решения.
числа, действия результатом
умножение, вычитание вычитание, умножение разный порядок действий |
Повторяет правило выполнения действий в выражениях, содержащих скобки
Проверяет правильность выполнения первого второго и третьего выражения по листу для самопроверки.
|
|
III.Постановка темы и цели — Сформулируйте тему нашего урока? — От чего зависит результат вычислений? — Какую цель поставим?
— Как проверим достижение цели? — Разработаем критерии, по которым каждый из вас сможет оценить полученные знания и умения, а также свою деятельность в конце урока. — Умеете ли вы решать выражения данного типа? Почему? — Это будет нулевая отметка. — Назовите критерий верхней отметки. — Что бы научиться, что для этого нужно? — Это будет второй критерий, который вам поможет справиться с поставленной целью.
— Как будем оценивать?
|
Порядок выполнения действий от порядка действий научиться ставить порядок действий, правильно решать, применяя правило;
Правильно выполним задание для самостоятельной работы
Нет, не знаем, как правильно нужно их решать
Критерии оценивания
+ сделал все правильно допустил 1 ошибку — не сумел сделать
|
Читает
Повторяет цель, либо зачитывает со своего листа продвижения
Постараюсь справиться
Ученик отвечает
|
|
IV. 1. Приём яркое пятно. Чтение со слайда
|
Порядок действий в выражениях особый И в каждом случае, помни, он свой В порядке все действия ты выполняй Сначала в скобках всё посчитай Потом чередом, умножай или дели И, наконец, вычитай или сложи
|
|
|
2. Составление алгоритма — Составьте алгоритм — Какое действие будем выполнять первым? Вторым? Следующим?
— Где проверить правильность нашего предположения? |
Называют действия. На доске появляются таблички: 1. ( ) 2.* или : 3.+ или —
В учебнике |
Работает с листом продвижения по теме. Под каждым выражением выбирает порядок действий (5+1)*3 9-10:2 |
|
3.
|
Читают правило |
Повторяет правило |
|
4. Решение проблемы — Так почему получились разные ответы? Кто может ответить на этот вопрос? — Исправьте ошибку
|
Решают самостоятельно 3*8-4:2. Взаимопроверка. Результаты заносятся в листы самооценки |
Комментирует решение 8-4*3 |
|
V. Физминутка |
Ветер дует нам в лицо, (Махи руками на себя.)
Ветер тише, тише, тише, (Присесть.) Деревцо все выше, выше (Встать на носочки, потянуться.)
|
|
|
VI. Первичное закрепление 1. — Объясните порядок решения выражения, используя правило
|
На доске выражения (порядок действий расставлен)
|
|
|
2. Работа в паре |
У каждой пары жёлтая карточка с заданием — расставить порядок действий (1 пара работает у доски) |
Работает с учителем: расставляет порядок действий на своей карточке |
|
3. Индивидуальная работа
|
У каждого на столе зелёная карточка с заданием: расставить порядок действий и найти значение выражения. |
Выполняет своё задание у доски |
|
Самооценка. Проверка по эталону. Результаты заносит в лист продвижения по теме
|
|
|
VII. Повторение Решение задачи № 8
|
Запись решения с помощью выражения |
— Какое действие будем выполнять первым? Вторым? |
|
VIII. Рефлексия — Какая была тема урока? Какие цели ставили? Удалось решить поставленные задачи? — Каким способом? — Оцените свою работу на уроке
Домашнее задание:
|
Отвечают на вопросы, заполняют листы самооценки.
Отвечают на вопросы учителя.
Записывают домашнее задание в дневник с. |
Отвечает на вопросы, заполняет лист продвижения по теме.
Отвечает на вопросы учителя.
|
▶▷▶ контрольная работа порядок действий в выражениях 3 класс
▶▷▶ контрольная работа порядок действий в выражениях 3 класс
| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 11-11-2018 |
контрольная работа порядок действий в выражениях 3 класс — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольная работа «Порядок действий в выражениях со скобками uchitelyacom/matematika/88579-kontrolnaya-rabota Cached Скачать Контрольная работа » Порядок действий в выражениях со скобками и без» 3 класс Найти Добавить материал Контрольная работа по математике 3 класс «Порядок действий multiurokru/files/kontrol-naia-rabota-po Cached 3 класс Контраб по мат-ке « Порядок действий » 1вариант 1 Реши задачу В букете 30 красных роз, а белых в 6 раз меньше, чем красных Контрольные работы за 3 класс по математике, по Моро за 1, 2 mathematics-testscom/matematika- 3 -klass-new/ Cached Данные контрольные работы составленные по требованию ФГОС по математике для начального образования и предназначены для проверки знаний в 3 классе по программе «Школа России» Контрольная Работа Порядок Действий В Выражениях 3 Класс — Image Results More Контрольная Работа Порядок Действий В Выражениях 3 Класс images Порядок действий в математике 4 класс detskoerazvitieinfo/poryadok-dejstvij-v-matematike-4-klass Cached Порядок действий в математике 4 класс Обучение и воспитание , Школьники 24 Июл 2016 Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики Выражения со скобками — 2 класс, примеры, порядок действия mathematics-testscom/zadachi-zadaniya-2-klass Cached Задачи на тему: » Порядок действий в выражениях со скобками» Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания Карточки по математике 3 класс «Порядок действий» infourokru/kartochki-po-matematike-klass Cached Конспект урока по математике » Порядок выполнения действий в выражениях со скобками и без скобок» 10012018 258 Контрольная работа «Примеры на порядок действий» 5 класс скачать uchitelyacom/matematika/89352-kontrolnaya-rabota-primer Cached Скачать Контрольная работа «Примеры на порядок действий » 5 класс в выражениях » 3 класс Контрольная работа по математике по теме «Устные приёмы infourokru/kontrolnaya-rabota-po-matematike-po Cached › Конспекты › Контрольная работа по математике по теме «Устные приёмы вычислений в пределах 100 Порядок действий в числовых выражениях Итоговая контрольная работа по математике 4 класс multiurokru/files/itoghovaia-kontrol-naia Cached Определять порядок действий в математических выражениях Базовый Буквенные выражения (уравнения) Презентация Математика 2 класс Порядок действий в выражениях pedportalnet/nachalnye-klassy/matematika/ Cached Контрольная работа по теме: « Порядок выполнения действий в сложных числовых выражениях » 3 класс , 2 четверть УМК «Начальная школа xxi века» Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 28,200 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- задание вариант 1 Рудницкая ВН за 3 класс
- 1397909docx Автор: Коноплёва Галина Алексеевна
- отзывы
исправь их Читать ещё Контрольная работа по теме: « Порядок действий в сложных выражениях » 3 класс 1 вариант Верно ли указан порядок выполнения действий в этих выражениях ? Если есть ошибки
систематизированно
- не забывайте оставлять свои комментарии
- smarter
- по Моро за 1
контрольная работа порядок действий в выражениях 3 класс — Все результаты Контрольная работа по теме: «Порядок выполнения действий в 17 дек 2013 г — Учебно-методический материал по математике ( 3 класс ) по теме: Контрольная работа по теме: « Порядок выполнения действий в сложных числовых выражениях » 3 класс , 2 четверть УМК «Начальная школа XXI Контрольная работа по теме: «Порядок действий в сложных 16 мар 2013 г — План-конспект урока по математике ( 3 класс ) на тему: Контрольная работа по теме: « Порядок действий в сложных выражениях » контрольная работа по математике 3 класс «Порядок действий 14 дек 2016 г — Контрольная работа по математике 3 класс » Порядок действий порядок выполнения действий и найдите значения выражений : Видео 12:05 Порядок выполнения действий в выражениях без скобок и со InternetUrokru YouTube — 25 авг 2017 г 17:16 Порядок выполнения действий | Математика 3 класс #10 | Инфоурок Инфоурок YouTube — 4 сент 2017 г 17:00 Порядок действий в выражениях со скобками | Математика 2 класс Инфоурок YouTube — 4 сент 2017 г Все результаты Проверочная работа по математике на тему «Порядок действий › Математика 15 нояб 2017 г — Проверочная работа по математике 3 класс УМК «Школа России» Тема « Порядок действий » 1 вариант 1 Вычисли значение выражений контрольная работа за 1 четверть по математике 3 класс УМК «Школа Контрольная работа по математике по теме» Выражения со › Начальные классы 30 окт 2017 г — Cкачать: Контрольная работа по математике по теме» Инфоурок › Начальные классы › Другие методич материалы › Контрольная работа по Контрольная работа 1 вариант 1Обозначь порядок действий и вычисли 3 Начерти четырёхугольник, измерь его стороны и вычисли Контрольная работа «Порядок действий в выражениях со скобками uchitelyacom//88579-kontrolnaya-rabota-poryadok-deystviy-v-vyrazheniyah-so-sk Скачать Контрольная работа » Порядок действий в выражениях со скобками и без» 3 класс Контрольные работы по математике 3 класс УМК «Гармония Похожие 3 КЛАСС 1 четверть КОНТРОЛЬНАЯ РАБОТА № 1 Проводится после повторения вопросов, г) правил порядка выполнения действий в выражениях ; Контрольные работы за 3 класс по математике, по Моро за 1, 2, 3 Рейтинг: 4 — 31 голос 3 апр 2017 г — Проверочные работы для 3 класса за 1, 2, 3 и 4 четверти по учебнику и деление», «Вычисление выражений «, » Порядок действий » Ответы на контрольную работу №4 на тему: » Порядок выполнения действий » Контрольные работы по математике 3 класс «Школа России» — PDF Контрольная работа 4 В театре ученики первого класса заняли в партере 2 Укажите порядок выполнения действий и найдите значение выражений : «Порядок выполнения действий в выражениях» 3-й класс открытыйурокрф/статьи/638450/ Если вас заинтересовала данная работа , пожалуйста, загрузите полную Исследовать правила о порядке выполнения действий в выражениях со Calaméo — Математика 3 класс р Title: Математика 3 класс р, Author: martnatalya@yandexru, Length: 8 pages, Published: Порядок выполнения действий в выражениях , записанных без скобок, 20092017 12 Входная контрольная работа по теме: «Повторение [DOC] Оценочные материалы 3 класс УМК «Школа России» 10 Итоговая контрольная работа № 10 за курс 3 класса -использовать правила о порядке действий в выражениях со скобками и без скобок; — решать Контрольная работа по теме: «Порядок действий в — Педпортал Похожие Контрольная работа по теме: « Порядок действий в сложных выражениях » 3 класс (Математика) Учебное пособие для учителей Порядок действий в сложных выражениях» 3 класс — ProfHelpnet 27 нояб 2017 г — Контрольная работа по теме: « Порядок действий в сложных выражениях » 3 класс 1 вариант Верно ли указан порядок выполнения Математика 3 класс: поурочные планы по учебнику Н Б Истоминой I Лободина Н В — 2014 — Education Урок 35 Контрольная работа по теме «Табличное умножение и деление» Работа над ошибками Порядок выполнения действий в выражениях Банк контрольных работ по математике для 3 класса — Урокрф 9 нояб 2016 г — порядок действий в выражениях в 2- 3 арифметических действия ; Контрольная работа № 3 Тема: «Сложение чисел в пределах 20 с [DOC] 3 класс 1 четверть Контрольная работа (текущая) _________ wwweduportal44ru//3%20кл%20Контрольные%20работы%20по%20математик Похожие тема « Порядок выполнения действий в сложных числовых выражениях » 1 вариант 1 Найди 3 класс 2 четверть Контрольная работа (текущая) ____ 3 класс Порядок выполнения действий в выражениях со скобкамми Данные карточки Контрольная работа по математике 3 класс за 3 четверть Контрольная Контрольная работа по математике в 3 классе II четверть › Контрольная работа 30 сент 2017 г — Cкачать: Контрольная работа по математике в 3 классе II четверть г) правил порядка выполнения действий в выражениях ; д) темы: [DOC] Пояснительная записка Рабочая программа по математике archipovkaedusiteru/DswMedia/pmatematika3docx На изучение математики в 3 классе начальной школы отводится по 4 ч в неделю (34 чисел;; Правила порядка выполнения действий в числовых выражениях ; Контрольная работа № 1 по теме «Сложение и вычитание [PDF] Математика school27beluoru/indexphp?option=com_docman&task=doc_download Похожие Рудницкая ВН Математика Рабочая тетрадь для учащихся 3 класса В 2 ч Правила порядка выполнения действий в числовых выражениях , содержащих от 2 до 6 арифметических действий , Контрольная работа по теме: [PDF] Рабочая программа по математике school121krsnetru/DswMedia/3rmatempdf 3 Контрольные работы по математике: рабочая тетрадь для учащихся сотрудничества с учителем и учащимися класса (при групповой работе , работе в Порядок выполнения действий в выражениях , записанных без скобок, Серия «Образовательный стандарт» leninavan13ru/3%20класс//РАБОЧАЯ%20ПРОГРАММА%20матиматикаhtm Порядок выполнения действий в выражениях , записанных без скобок, Результаты освоения учебного курса математики в 3 классе 1 Текущая контрольная работа №1 по теме «Сложение и вычитание трехзначных чисел» [PDF] Программа по математике для 3 класса Составители — СОШ №3 г school3mmc24308cross-eduru/rp/mat%203pdf применять правила порядка выполнения действий в выражениях со скобками и без них Итоговая контрольная работа № 2 за I четверть: «Сложение и На этой страничке вы найдете учебный материал для 3 класса Похожие В контрольной работе содержатся 2 задачи изученных видов, решение выражений с использованием порядка действий , геометрическая задача на [DOC] Математика — Барнаульская классическая школа class-schoolru/wp-content/uploads/2017/01/математика-3docx 11 янв 2017 г — по предмету «Математика» для 3 класса Порядок выполнения действий в выражениях , записанных без скобок, содержащих Контрольная работа по теме: «Сложение и вычитание трехзначных чисел», 28 35 Контрольная работа №1 по теме «Повторение: сложение и Контрольные работы по математике 3 класс «`Школа России`» 3 Обозначьте порядок действий и выполните вычисления: 90-6х6+29= 5х (62- 53)= 4 Вставьте знак х или Найдите значение выражений : 26+18х4= 80: 16х13= [DOC] Рабочая программа по математике 3 класс — Администрация Правило порядка выполнения действий в выражениях , содержащих одну или 3 ч 16 Умножение на однозначное число 7 ч Контрольная работа — 1 [PDF] Содержание учебного предмета «Математика» 3 класс 21goruralschoolru/file/download/604 Выполнять рисунок в соответствии с данными выражениями Пояснять Расставлять порядок выполнения действий в схеме числового выражения Контрольная работа № 3 По теме: «Отношения (больше в , меньше в …, Математика, 3 класс » КОНСПЕКТЫ УРОКОВ ДЛЯ НАЧАЛЬНОЙ 4stupeniru/planirovanie/plans_1_mat/1696-matematika-3-klasshtml Похожие 8 июл 2009 г — Календарно — тематическое планирование , 3 класс , составлено на основе 56 Правило порядка выполнения действий в выражениях 71 Контрольная работа по теме « Порядок выполнения действий в сложных [PDF] Математика 2 класс ciurru/blz/blz/Корепанова%20ЛЕ%202%20класс/Математика%202%20классpdf Рабочая программа по математике для 2 класса составлена на основе Федерального компонента Порядок действий в выражениях со скобками 27 11 Контрольная работа № 3 по теме «Устное сложение и вычитание в Выражение и его значение Порядок выполнения действий и его значение Порядок выполнения действий по предмету Математика за 4 класс Рекомендуем родителям посмотреть урок «Упрощение выражений » 3 4 5 Вторая запись называется равенство, поэтому она лишняя [PDF] МАТЕМАТИКА Математика : 3 класс / Мария Буряк — Ростов н/Д : Феникс, 2017 — 60 с : ил Контрольная работа 1 Порядок действий в числовых выражениях Контрольная работа по математике для 3 класса — Видеоуроки 10 дек 2015 г — Работа позволит проверить усвоение табличного умножения и деления чисел, знание порядка действий в выражениях [PDF] Селезнёвой Ирины Николаевны по математике 3 класс Форма итоговой аттестации обучающихся — контрольная работа порядке ; компоненты действия деления с остатком; единицы массы, времени, длины; вычислять значения числовых выражений , содержащих 2- 3 действия Математика: уроки, тесты, задания — ЯКласс Математика 1 класс; 2 класс; 3 класс ; 4 класс; 5 класс; 6 класс; 1С:Школа 1 класс Знаки сравнения, знаки действий и знак равенства Сравнение чисел от 0 до 10 и выражений Порядок действий Работа Время Производительность [DOC] Рабочая программа по математике — МАОУ СОШ 5 гТобольска school5-tobucozru/2016-2017/rabprog/nachsh/Samko/rp-po_matematikedocx Математика: 3 класс : учебник для учащихся общеобразовательных учреждений: в 2 ч Порядок выполнения действий в выражениях , записанных без скобок, 32, Итоговая контрольная работа по теме » Сложение и вычитание Математика 3 класс: поурочные планы по учебнику М И Моро, М А Цыкина Н А — 2014 Урок 29 КОНТРОЛЬНАЯ РАБОТА Цель: проверить усвоение приёма деления с остатком и его проверку, знание порядка действий в выражениях , умение [PDF] Рабочая программа по математике для 3 класса — Официальный klepovososhlbihostru/wp-content/uploads/sites/34/2017/08/3_matempdf ГВДорофеев, ТНМиракова Математика Рабочая тетрадь 3 класс 9 Контрольная работа №1 деления; порядка действий в выражениях со [PDF] 2 класс лицей109екатеринбургрф/getfilephp?2%20класс%20ПЕРСПЕКТИВА Похожие 3 ) формирование специфических для математики качеств мышления, « Порядок действий в выражениях » 12 Контрольная работа № 4 контрольная работа математика 3 класс 3 четверть бесплатно wwwdmvilijalt//kontrolnaia-rabota-matematika-3-klass-3-chetvert-besplatnoxml 4 дня назад — 8 контрольная работа 4 класс 3 четверть математика дорофеев выражений «, » Порядок действий Читать ещё Контрольные работы тестовые контрольные работы по математике 3 класс 3 четверть counselorjapancom//testovye-kontrolnye-raboty-po-matematike-3-klass-3-chetvert 3 нояб 2018 г — Тестовые контрольные работы по математике 2, 3 ,4 классы и выполни действия Контрольная работа по математике за 3 четверть I-вариант выражений «, » Порядок действий Читать ещё Контрольные работы [DOC] Умножение и деление на двузначное число в пределах 1000 s_86edu54ru/DswMedia/pzmatematika3klassdocx Похожие В третьем классе вводятся общеизвестные правила порядка арифметических Математика в начальной школе: проверочные и контрольные работы: методическое Порядок выполнения действий в выражениях без скобок, 3 Однако надо учитывать, что за комбинированную контрольную работу , Административная контрольная работа по математике 3 класс (1 Файл Административная контрольная работа по математике 3 класс (1)docx для материала по дисциплинам 3 Расставить действия и найти значения выражений : 50 24:(115) + 15 42:(147) Расположи в порядке возрастания: [PDF] Шаховская гимназия 3 апр 2018 г — Рабочая программа по математике предназначена для 3 класса количество, стоимость Порядок выполнения действий в выражениях со скобками и без скобок 7 Входная контрольная работа №1 по [DOC] Умножение и деление на однозначное число в — Школа № 229 school229ru/wp-content/uploads/po-matematikedocx 3 класс на 2013-2014 учебный год Составила учитель первой Форма итоговой аттестации обучающихся – контрольная работа Порядок выполнения действий в выражениях , записанных без скобок, содержащих действия : а) [DOC] Математика 3 класс рабочая программа — Орловская православная wwwgimnasia-orelru/docs/Matematika-3-klass-rabochaya-programmadoc Порядок выполнения действий в выражениях со скобками и без скобок Контрольная работа по теме: «Умножение и деление на 2 и 3 » 1 20 Анализ [PDF] Примерные задания для годовой контрольной работы по 3 класс УМК «Гармония» № Образцы заданий Проверяемые умения 250 × 3 – 50 × 4= 420 : 7= -применять правила порядка действий в выражениях ( со многозначные числа в «столбик» Работа с текстовыми задачами 3 Рабочая программа по математике 3 класс «Школа России» 9 янв 2015 г — Применять правила о порядке действий в числовых выражениях со скобками Контрольная работа по теме «Умножение и деление» Вместе с контрольная работа порядок действий в выражениях 3 класс часто ищут контрольная работа по математике 3 класс по теме порядок действий примеры на порядок действий 3 класс контрольная работа 3 класс проверочная работа порядок действий 3 класс самостоятельная работа по математике 3 класс проверочная работа по теме порядок действий 3 класс Навигация по страницам 1 2 Следующая Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Музыка Переводчик Диск Почта Коллекции Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Контрольная работа » Порядок действий в выражениях uchitelyacom › …poryadok…vyrazheniyah…3-klasshtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа по математике ( 3 класс ) умножения и деления на 2 и 3 , а также знание порядка действий в выражениях со скобками и без Ход урока Вариант 1 1Мама купила 3 пакета картофеля по 5 кг в каждом Читать ещё Контрольная работа по математике ( 3 класс ) умножения и деления на 2 и 3, а также знание порядка действий в выражениях со скобками и без Ход урока Вариант 1 1Мама купила 3 пакета картофеля по 5 кг в каждом Сколько килограммов картофеля купила мама? 23 мальчика разделили поровну между собой 18 орехов Скрыть 2 План-конспект урока по математике ( 3 класс ) на тему nsportalru › …2013/03/16/kontrolnaya…po…poryadok…v… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Контрольная работа по теме: « Порядок действий в сложных выражениях » 3 класс 1 вариант Верно ли указан порядок выполнения действий в этих выражениях ? Если есть ошибки,исправь их Читать ещё Контрольная работа по теме: « Порядок действий в сложных выражениях » 3 класс 1 вариант Верно ли указан порядок выполнения действий в этих выражениях ? Если есть ошибки,исправь их 3 2 1 1 2 1 2 3 28 : (7 – 1 х 3) 83 – (27 + 18) (72 – 54) : 9 х 3 Отбрось скобки там Где можно, и запиши выражения без скобок: 4 + 26 – (6 х 4) 43 – (13 + 7 х 2) (48 : 8) х (35 : 5) (62 + 8) + (39 +7) Расставь порядок действий и найди значения выражений : 90 – 6 · 6 + 29 = 5 · (62 – 53) = (40 – 39) · (6 · 9) = Запиши решение задачи выражением и реши её Дежурные сначала разнесли 3 подноса по 9 стаканов молока Скрыть 3 Контрольная работа по математике 3 класс » Порядок multiurokru › files/kontrol-naia-rabota-po…3-klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа по математике 3 класс Тема » Порядок действия » 4 Начальная школа: Проверочная работа по теме nachalka85blogspotcom › 2013/05/3html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Проверочная работа по теме: ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ ( 3 класс ) Вариант 1 1 В выражении 400-(40+2∙7):2 последним выполняется действие : a Умножение; b Деление; c Вычитание; d Сложение 2 В выражении 740-600:15+7∙33 последним выполняется действие : a Сложение; b Вычитание; c Читать ещё Проверочная работа по теме: ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ ( 3 класс ) Вариант 1 1 В выражении 400-(40+2∙7):2 последним выполняется действие : a Умножение; b Деление; c Вычитание; d Сложение 2 В выражении 740-600:15+7∙33 последним выполняется действие : a Сложение; b Вычитание; c Деление; d Умножение 3 Составьте выражение для решения задачи: У Белоснежки и 7 гномов было 25 конфет Белоснежка съела 4 конфеты, а остальные конфеты гномы разделили между собой поровну Сколько конфет стало у каждого гнома? Скрыть 5 Урок с родителями по математике в 3 классе на тему infourokru › urok-s…v-klasse…poryadok…v…306341html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Тема: Порядок выполнения арифметических действий в числовых выражениях без скобок и со скобками, состоящими из 2- 3 действий ; Цель:Познакомить с правилом порядка выполнения действий в выражениях 6 Контрольные работы по четвертям в 3 классе урокрф › library…chetvertyam_v_3_klasse_214834html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольные / проверочные работы для учителя начальных классов для 3 класса Контрольная работа 1 за I четверть I вариант 1 Мама купила 2 пакета картофеля по 5 3 Обозначьте порядок действий и выполните вычисления: 90-6х6+29= 5х (62-53)= 4 Вставьте знак х или : так, чтобы записи были Читать ещё Контрольные / проверочные работы для учителя начальных классов для 3 класса Учебно-дидактические материалы по Математике для 3 класса по УМК УМК «Школа России» Контрольная работа 1 за I четверть I вариант 1 Мама купила 2 пакета картофеля по 5 кг в каждом 3 Обозначьте порядок действий и выполните вычисления: 90-6х6+29= 5х (62-53)= 4 Вставьте знак х или : так, чтобы записи были верными Скрыть 7 Тест « Порядок выполнения действий в выражениях » easyenru › …m/3_klass…dejstvij_v_vyrazhenijakh/377… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Неограниченная бесплатная загрука материала Тест « Порядок выполнения действий в выражениях » доступна всем пользователям Разработка находится в разделе Математика 3 класс и представляет собой проверка знаний Читать ещё Неограниченная бесплатная загрука материала Тест « Порядок выполнения действий в выражениях » доступна всем пользователям Разработка находится в разделе Математика 3 класс и представляет собой проверка знаний Скачать материал 05Mb Загрузка началась Понравился сайт? Получайте ссылки на лучшие материалы еженедельно! Подарок каждому подписчику! 6448 Скрыть 8 Трехуровневая контрольная работа по математике kopilkaurokovru › Начальные классы › Тесты › …-3-klass-po-tiemie… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Трёхуровневая контрольная работа по математике 3 класс по программе «Школа России» Тема: Табличное умножение и деление Порядок действий В работе представлены 3 уровня сложности При выполнении 1 уровня ученик получает по 1 баллу за каждое задание Выполняя 2 уровень получает по 2 балла Читать ещё Трёхуровневая контрольная работа по математике 3 класс по программе «Школа России» Тема: Табличное умножение и деление Порядок действий В работе представлены 3 уровня сложности При выполнении 1 уровня ученик получает по 1 баллу за каждое задание Выполняя 2 уровень получает по 2 балла за задание и 3 уровень даёт 3 балла Просмотр содержимого документа «Трехуровневая контрольная работа по математике 3 класс по теме: Порядок действий » Трехуровневая контрольная работа По математике 3 класс II четверть Тема: Табличное умножение и деление Порядок действий 1 вариант I уровень Скрыть 9 Контрольная работа Порядок действий в выражениях 3 класс — смотрите картинки ЯндексКартинки › контрольная работа порядок действий в выражениях Пожаловаться Информация о сайте Ещё картинки 10 Контрольная работа по теме: « Порядок действий » pedportalnet › …klassy…po…v-slozhnyhvyrazheniyah…3… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте 3 класс 1448 КБ, 1397909docx Автор: Коноплёва Галина Алексеевна, 24 Янв 2016 Текст контрольной работы по математике Читать ещё 3 класс Скачать 1448 КБ, 1397909docx Автор: Коноплёва Галина Алексеевна, 24 Янв 2016 Текст контрольной работы по математике Автор: Коноплёва Галина Алексеевна Похожие материалы Тип Название материала Автор Опубликован Скрыть Тест: Порядок выполнения действий — Математика urokitv › …poryadok-vypolneniya-dejstvij…3-klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Теперь вы можете проверить, насколько хорошо вами была усвоена тема о порядке выполнения действий В этом вам поможет следующее задание Для успешного прохождения теста прочитай: Порядок выполнения действий — Математика 3 класс (Моро) 1 В каком из данных выражений первым действием нужно Читать ещё Теперь вы можете проверить, насколько хорошо вами была усвоена тема о порядке выполнения действий В этом вам поможет следующее задание Для успешного прохождения теста прочитай: Порядок выполнения действий — Математика 3 класс (Моро) 1 В каком из данных выражений первым действием нужно будет выполнить деление? Скрыть Набор контрольных работ по математике по 10 темам uchitelunet › media/1242 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте — Свойства арифметических действий — Порядок действий в числовых выражениях — Деление с остатком ФАЙЛЫ МАТЕРИАЛА: Контрольные работы по математике ( 3 класс )zip Select rating Плохо Хорошо Отлично Great Awesome Мнений: 3 Аноним on 16022010 — 11:00 Очень хороший сайт!!! Читать ещё — Свойства арифметических действий — Порядок действий в числовых выражениях — Деление с остатком — Текстовые задачи ФАЙЛЫ МАТЕРИАЛА: Контрольные работы по математике ( 3 класс )zip Select rating Плохо Хорошо Отлично Great Awesome Мнений: 3 Аноним on 16022010 — 11:00 Очень хороший сайт!!! Легко ориентироваться в материале, всё продуманно, систематизированно,а главное полезное! Аноним on 17032010 — 21:54 Большое спасибо! Аноним on 27032010 — 15:22 Скрыть Контрольные работы 3 класс metod-kopilkaru › kontrolnye_raboty_3_klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте 3 класс Контрольная работа 1 За I четверть КОНТРОЛЬНАЯ РАБОТА 5 Цель: проконтролировать усвоение приёма деления с остатком и его проверку, знание порядка действий в выражениях , умение решать задачи Читать ещё 3 класс Контрольная работа 1 За I четверть Цель: закрепить пройденный за I четверть материал I вариант 1 Мама купила 3 пакета картофеля по 6 кг в каждом Сколько килограммов картофеля купила мама? 2 3 мальчика разделили поровну между собой 15 орехов КОНТРОЛЬНАЯ РАБОТА 5 Цель: проконтролировать усвоение приёма деления с остатком и его проверку, знание порядка действий в выражениях , умение решать задачи I вариант 1 Выполните деление с остатком и проверку к нему 75 : 8 85 : 20 51 : 7 2 Вставьте числа в «окошки», чтобы получились верные равенства 3 Найдите значения выражений 56 : 2 – 36 : 12 (39 + 33) : 24 · 9 48 + 32 : (64 : 8) 93 – 3 · 8 : 6 4 Решите задачу Скрыть Контрольная работа по теме: « Порядок действий » ProfHelpnet › 688083/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Заказать учебную работу Контрольная работа по теме: « Порядок действий в сложных выражениях » 3 класс 1 вариант Верно ли указан порядок выполнения действий в этих выражениях ? Если есть ошибки,исправь их Читать ещё Заказать учебную работу Контрольная работа по теме: « Порядок действий в сложных выражениях » 3 класс 1 вариант Верно ли указан порядок выполнения действий в этих выражениях ? Если есть ошибки,исправь их 3 2 1 1 2 1 2 3 28 : (7 – 1 х 3) 83 – (27 + 18) (72 – 54) : 9 х 3 Отбрось скобки там Где можно, и запиши выражения без скобок: 4 + 26 – (6 х 4) 43 – (13 + 7 х 2) (48 : 8) х (35 : 5) (62 + 8) + (39 +7) Расставь порядок действий и найди значения выражений : 90 – 6 · 6 + 29 = 5 · (62 – 53) = (40 – 39) · (6 · 9) = Запиши решение задачи выражением и реши её Дежурные сначала разнесли 3 подноса по 9 Скрыть Контрольные работы за 3 класс по математике, по Моро mathematics-testscom › matematika-3-klass…chetverty Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольные работы по математике для 3 класса по учебнику Моро МИ за 1, 2, 3 и 4 четверти Контрольные на темы: «Сложение и вычитание чисел до 100», «Умножение и деление», «Вычисление выражений «, » Порядок действий » Дополнительные материалы Уважаемые пользователи, не забывайте Читать ещё Контрольные работы по математике для 3 класса по учебнику Моро МИ за 1, 2, 3 и 4 четверти Контрольные на темы: «Сложение и вычитание чисел до 100», «Умножение и деление», «Вычисление выражений «, » Порядок действий » Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания Все материалы проверены антивирусной программой Скачать: Контрольные работы по математике для 3 класса по учебнику Моро МИ (PDF) Обучающие пособия и тренажеры для 4 класса в интернет-магазине «Интеграл» МИ Моро ЛГ П Скрыть ГДЗ Рудницкая ВН 3 класс Математика, Работа KlassGDZru › 3 класс › Математика › …3_klass_rudnitskaya/40-1 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ Рудницкая ВН 3 класс Математика, Работа 2 Порядок выполнения действий в сложных числовых выражениях , задание вариант 1 Рудницкая ВН за 3 класс , математика: на данной странице представлено решение задания «вариант 1» из секции « Работа 2 Порядок выполнения действий в сложных Читать ещё ГДЗ Рудницкая ВН 3 класс Математика, Работа 2 Порядок выполнения действий в сложных числовых выражениях , задание вариант 1 Рудницкая ВН за 3 класс , математика: на данной странице представлено решение задания «вариант 1» из секции « Работа 2 Порядок выполнения действий в сложных числовых выражениях » Скрыть Вместе с « контрольная работа порядок действий в выражениях 3 класс » ищут: контрольные работы по математике 3 класс контрольная закупка контрольные работы итоговая контрольная работа по математике 6 класс готовые контрольные работы контрольные работы по математике 2 класс итоговая контрольная работа по алгебре 7 класс итоговая контрольная работа по математике 5 класс контрольные работы по математике 4 класс итоговая контрольная работа по математике 3 класс школа россии фгос 1 2 3 4 5 дальше Bing Google Mailru Нашлось 206 млн результатов Дать объявление Регистрация Войти 0+ Браузер с Алисой поможет управлять компьютером Установить Закрыть Попробовать еще раз Реклама Включить Москва Настройки Клавиатура Помощь Обратная связь Для бизнеса Директ Метрика Касса Телефония Для души Музыка Погода ТВ онлайн Коллекции Яндекс О компании Вакансии Блог Контакты Мобильный поиск © 1997–2018 ООО «Яндекс» Лицензия на поиск Статистика Поиск защищён технологией Protect Вы всегда успеете к началу На Яндексе можно смотреть любимые телепередачи после эфира Перейти
Порядок операций — урок для 3 класса
Это полный урок для третьего класса с обучением и упражнениями по порядку операций . Упражнения касаются только скобок, сложения, вычитания и умножения (но не деления). Студентам предлагается обвести первую операцию, которую нужно сделать, в пузыре или воздушном шаре — это может сделать ее интересной! Наконец, они решают забавную головоломку, выясняя, какие операции делают данные уравнения верными.
Упражнения касаются только скобок, сложения, вычитания и умножения (но не деления). Студентам предлагается обвести первую операцию, которую нужно сделать, в пузыре или воздушном шаре — это может сделать ее интересной! Наконец, они решают забавную головоломку, выясняя, какие операции делают данные уравнения верными.
Порядок работы1) Сначала мы вычисляем, что находится внутри СКОБКА ().2) Затем мы НЕСКОЛЬКО перед сложение или вычитание. 3) Наконец, мы ДОБАВИТЬ и ВЫЧИТАТЬ слева направо. |
| Пример. 4 × (2 + 3) Сначала мы вычисляем 2 + 3, потому что оно заключено в круглые скобки. Итак, получаем 4 × 5. То есть 20. |
1. Сложить и вычесть. Помните круглые скобки! Обведите операцию, для которой требуется
делать СНАЧАЛА в «пузыре» или воздушном шаре.
| а. 20 + 6 — 3 г. 20 + (6–3) | г. 20-6 + 3 г. 20 — (6 + 3) | e. 80–30 — (30 + 20) ф. 80 — (30-30) + 20 |
2. Рассчитайте. Обведите в кружок операцию, которую нужно выполнить в первую очередь. Скобки → умножить → сложить / вычесть.
| а. 3 + 5 × 2 | б . 5 × (3 + 1) | г. 4 × (4 — 2) |
| г. 3 × 6 — 11 | e. 25 — 5 × 2 | ф. (3 — 2) × 6 |
| г. (4 + 2) × 2 | ч. 3 × 5 + 2 × 4 | и. 50 — (7-2) × 4 |
3.Обведите «пузырем» операцию, которую нужно выполнить первой!
4. Теперь смотрите внимательно! Вам потребуется больше шагов.
Теперь смотрите внимательно! Вам потребуется больше шагов.
| а. 3 × 4 — 2 × 3 | б. 6 + 7 × (4 — 2) |
| с. 2 × (5 + 4) + 5 | г. 30 — 2 — 7 × 2 |
5. Решите. Написать числовое предложение для каждой проблемы. Не просто напишите ответ.
| а. Десять человек собираются обедать.
Одна из них — маленькая Ханна. Есть две тарелки на всех, кроме Ханны только одна тарелка. Сколько тарелок на столе? |
| г. В маленьком ресторане пять столов на двоих и четыре стола для четырех человек.Сколько человек может сидеть в ресторане? |
Из этого можно сделать игру. |
См. Также
Math Safe
Веселая игра на логическое мышление, в которой вам нужно использовать четыре заданных однозначных числа и любую из четырех операций, чтобы достичь заданного числа, а затем сейф откроется! Он практикует использование всех четырех операций, а также порядок операций.Игра подходит лучше всего для 4 классов и выше.
Выберите математическую операцию
Выберите математические операции, чтобы числовое предложение было верным. Практикуйте роль нуля и единицы в основных операциях или операциях с отрицательными числами. Помогает развить чувство числа и логическое мышление.
Бесплатные рабочие листы для порядка операций
Бесплатные распечатываемые рабочие листы для порядка операций в форматах PDF и html.Выберите из пяти операций и скобок. Вы можете настроить рабочие листы, выбрав используемый диапазон номеров, количество проблем и т. Д.
Вы можете настроить рабочие листы, выбрав используемый диапазон номеров, количество проблем и т. Д.
Авторские права HomeschoolMath.net.
Рабочие листы для операций
Наши распечатанные рабочие листы с порядком выполнения операций, богатые опытом, знакомят учащихся с 4-го по 7-й классы с правилом выполнения операций в правильном порядке.PDF-файлы помогают понять процедурное понимание того, как применять порядок операций с использованием мнемоники, такой как PEMDAS, DMAS, BEDMAS или BODMAS в некоторых странах, и последнее дополнение — GEMS для решения арифметических выражений, включающих целые числа, целые числа, дроби и десятичные дроби. Вперед, используйте наши бесплатные рабочие листы для порядка операций и решайте арифметические выражения в мгновение ока!
Эксклюзивные рабочие листы порядка операций
Порядок операций | DMAS — уровень 2
Предлагая три уровня сложности, распечатываемые рабочие листы с порядком операций позволяют практиковаться в использовании DMAS для выражений с 4 целыми числами и 3 операторами; Вы упускаете заказ, упускаете ответ!
Круглые, квадратные и фигурные скобки
Продемонстрируйте свое знание порядка операций, упростив сначала то, что находится внутри самого внутреннего слоя круглых скобок (), продвигаясь наружу упрощая квадратные скобки [] и фигурные скобки {}.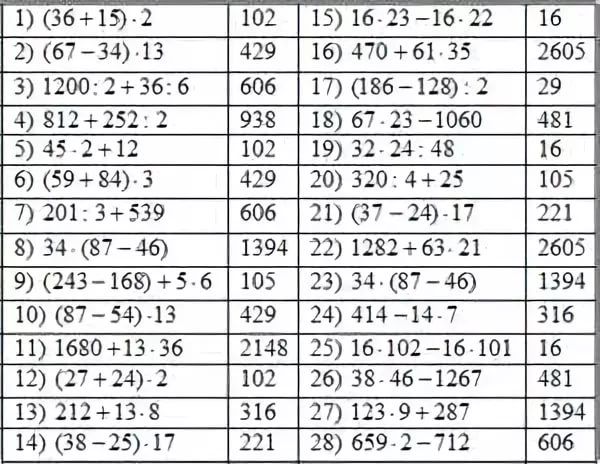
Порядок операций с дробями и десятичными знаками
Пришло время смешать порядок операций с дробями и десятичными знаками. Сначала упростите выражения в скобках, затем умножение или деление, затем сложение или вычитание.
Сравнение двух величин
Пересмотрите порядок операций, решая выражения с обеих сторон, и сравните количества, используя = или ≠ в Части A, или = в Части B, и сопоставьте выражения в Части C в этих распечатываемых рабочих листах PEMDAS.
В поисках недостающего числа
Соблюдая порядок операций, решите известную часть, выполните обратные операции с обеих сторон, чтобы выделить и найти неизвестную часть, которая делает уравнение истинным.
В поисках пропавшего оператора
Изюминкой этого раздела рабочих листов является поиск пропавшего оператора. Выясните, будет ли уравнение истинным — сложение, вычитание, умножение или деление.
Заполнение номеров
Совершенствуйте навыки решения проблем учащихся 6 и 7 классов, поскольку они заполняют указанные операнды в нужных местах, чтобы уравнение было сбалансированным, используя порядок операций.
Заполнение операторов
Продолжайте размышлять, ломать голову и ломать голову, пытаясь установить правильный оператор в нужном месте, чтобы уравновесить две стороны уравнения в PDF-файлах рабочих таблиц с указанным порядком операций.
GEMS
GEMS — это стратегия порядка операций с защитой от неправильного обращения, где G означает группирование: круглые скобки, скобки, фигурные скобки, E для показателей, M для умножения / деления и S для вычитания / сложения в зависимости от того, что наступит раньше для решения выражений.
Вычисление числовых выражений с показателями
С положительным и отрицательным показателями степени впереди, выражения могут показаться немного сложными. Рабочие листы по порядку работы идеально подходят для этого пробела и подталкивают учащихся 6-х и 7-х классов к практической работе.
(45 листов)
Вычисление числовых выражений в круглых скобках
Просмотрите этот пакет рабочих листов в формате PDF, в которых учащиеся должны оценивать числовые выражения с круглыми скобками и вложенными скобками в соответствии с порядком операций.
(54 рабочих листа)
Почему студенты неправильно понимают порядок действий — Future Set Tech Camp
Многие из моих учеников средней и старшей школы помнят PEMDAS, аббревиатуру, означающую порядок операций для вычисления математических выражений из предыдущего класса.«Прошу прощения, моя дорогая тетя Салли», — говорят они (или «Пожалуйста, ешь мои доритос и сальсу», — сказал мне один умный студент). «Скобки, экспоненты, умножение, деление, сложение, вычитание», — говорят они. Это здорово, правда? Эти студенты помнят порядок действий, верно? Разве PEMDAS не потрясающий?
Нет, PEMDAS — это , а не потрясающе. PEMDAS ошибается. Или, скорее, многие студенты неправильно понимают порядок действий, и виновата PEMDAS.
Давайте посмотрим на простой пример: 4 — 3 + 10 ÷ 5 × 2.
Поскольку здесь нет скобок или показателей, PEMDAS заставляет многих студентов думать, что мы должны начать с оценки умножения. Таким образом:
4 — 3 + 10 ÷ 5 × 2 =
4 — 3 + 10 ÷ 10
Затем эти ученики перейдут в подразделение:
4 — 3 + 10 ÷ 10 =
4 — 3 + 1
Затем сложение:
4 — 3 + 1 =
4 — 4
И, наконец, вычитание:
4 — 4 = 0
Элегантное решение! И все с помощью PEMDAS! Какое чудесное изобретение!
Или это то, что сказал бы , если бы это решение было правильным.
Для многих студентов PEMDAS подразумевает, что порядок операций состоит из шести шагов, по одному на каждую букву аббревиатуры. Фактически, порядок операций состоит из четырех шагов:
Вычислить операции в круглых скобках
Вычислить экспоненты
Вычислить умножение и деление слева направо
Вычислить слева сложение и вычитание
Важно отметить, что умножение и деление оцениваются как часть того же шага, как и сложение и вычитание на следующем шаге.Давайте еще раз попробуем наш пример, на этот раз используя порядок операций. Поскольку здесь нет скобок или показателей, мы начнем с третьего шага, «оценивать умножение и деление слева направо»:
4 — 3 + 10 ÷ 5 × 2 =
4 — 3 + 2 × 2 =
4 — 3 + 4
Затем мы завершаем, применяя четвертый шаг, «оценивать сложение и вычитание слева направо»:
4 — 3 + 4 =
1 + 4 = 5
На этот раз, мы пришли к правильному решению.
Я встречал слишком много студентов, которые неправильно понимали порядок действий именно таким образом. К счастью, у меня есть решение этой проблемы: вместо того, чтобы начинать урок о порядке операций с введения PEMDAS, его следует вводить только после проработки многих примеров с использованием четырехэтапного порядка операций, как написано выше. Как только учащиеся придут к и поймут порядок операций на практике, только тогда PEMDAS можно будет вводить для использования по назначению: не как набор инструкций, а как мнемоническое устройство, помогающее с памятью.
, если скобок нет, выражение выглядит следующим образом 4 + 3 * 2, что означает, каким будет ответ
Порядок операций , , также называемый правилами приоритета , определяет способ вычисления выражения.
Чтобы помочь запомнить их, было создано сокращение P lease E xcuse M y D ear A Unt S ally и другие сокращения. , /, ÷
, /, ÷
Выполните следующую процедуру:
Просканируйте слева направо для операции с наивысшим уровнем приоритета.Если найдено, оцените его (примечание: внутри скобок могут быть другие операции).
Просканируйте слева направо для операции со следующим наивысшим уровнем приоритета. Если обнаружено, оцените его (примечание: M & D, а также A & S находятся на одном уровне).
Продолжайте, пока не кончатся операторы
Для 4 + 3 * 2:
скобок нет (примечание: если выражение сбивает с толку, PLZ добавьте их, чтобы прояснить)
нет возведения в степень
есть умножение; сделайте это и замените выражение результатом умножения
4 + 6
есть дополнение; сделайте это и замените выражение результатом сложения
10
операторов больше нет
Попробуйте это (посмотрите, получится ли 13):
9-5 ÷ (8-3) x 2 + 6
PEMDAS: Порядок операций «Бесплатные уроки
Математика, алгебра и функции, операции (+, -, x, / и т. Д.), Решение проблем
Д.), Решение проблем
5-8 классы
Цель
Студенты узнают о порядке операций.
Проезд
В алгебре существует определенный порядок, в котором выполняются операции при вычислении выражения или решении уравнений.
Это алгебраический порядок операций:
- Сначала выполняйте любую работу в круглых скобках () или других группирующих символах [].
- Выполните любую работу с экспонентами (степенями) или корнями.
- Произведите любое умножение или деление слева направо.
- Произведите любое сложение и вычитание слева направо.
Акроним этого порядка операций — PEMDAS.
| Круглые скобки | Экспоненты | Умножение | Дивизион | Дополнение | Вычитание |
Популярное выражение для запоминания: «Прошу прощения, дорогая тетя Салли».
Образец А
Прочтите проблему.
4 2 + (9-3) =?
Сначала сделайте работу, указанную в скобках.
4 2 + 6 =?
Затем сделайте экспоненты.
4 2 = 4 x 4 = 16, поэтому 16 + 6 =?
Наконец, сложите числа.
16 + 6 = 22
Напишите свой ответ.
4 2 + (9–3) = 22
Образец Б
Прочтите проблему.
5 2 — (4 x 3) + 9/3 x 4 =?
Сначала сделайте работу в скобках.
5 2 — 12 + 9/3 x 4 =?
Далее делайте экспоненты.
5 2 = 5 x 5 = 25, поэтому 25 — 12 + 9/3 x 4 =?
Умножайте и делите слева направо.
25 — 12 + 3 х 4 =?
9, разделенное на 3, будет 3, а 3, умноженное на 4, равно 12.
25 — 12 + 12 =?
Сложите и вычтите в порядке слева направо.
13 + 12 =?
25 минус 12 равно 13 и 13 плюс 12 равно 25.
13 + 12 = 25
Запишите свой ответ.
5 2 — (4 x 3) + 9/3 x 4 = 25
Использование калькулятора
Многие калькуляторы разработаны с учетом алгебраического порядка операций.Вы можете использовать следующую задачу, чтобы узнать, запрограммирован ли ваш калькулятор на выполнение алгебраического порядка операций.
8 х 4/2 + 3 х 8/4 =?
Если ваш ответ калькулятора был 22, он соответствует порядку действий. (Незапрограммированные калькуляторы получают неправильный ответ — 38.)
ресурсов
- Таблицы деятельности PEMDAS
- карандаши
- калькуляторы
- 2964
Какие математические концепции преподают в четвертом классе?
Поскольку математике уделяется такое большое внимание, четвероклассники
сегодня учат математике, применяя реальные приложения и задачи
решение.Четвертый класс — время, когда дети изучают математические процедуры.
которые они будут носить с собой на протяжении всей своей жизни. Они также
основа математики, которую они будут преподавать через остальную часть
их школьные годы. Итак, вся основа математики четвертого класса
построены на реальных процессах и решении проблем. Четвертый класс
математика может больше сосредоточиться на том, как вы получили этот ответ, а не на ответе
сам. Да, нужно помнить множество правил, когда дело доходит до
математика, это правда, но запоминание правил полностью отличается от
понимание того, почему произошел определенный процесс.
Четвертый класс представляет занятия, которые заставляют детей задуматься числа и отношения, которые их окружают. Это тоже время когда дети могут объединяться в группы для коллективного решения математических процедур и работаем вместе. Групповая работа кажется очень эффективной для получения весь класс одновременно занимается математикой и делится их решения и их мысли. На самом базовом уровне дети в четвертом классе выучат числа, порядок действий (ПЕМДАС) что большинство учитывает как Пожалуйста, извините мою дорогую тетю Сью , для детей это простой способ запомнить порядок действий скобки, показатели, умножение, деление, сложение, и вычитание.В алгебраических задачах порядок операций необходимо прийти к правильному решению. Затем они вспоминают, что они сначала решают все, что указано в скобках, затем показатели, затем умножьте, затем разделите, затем сложите и, наконец, вычтите. Геометрия, измерения, данные и вероятность также преподаются на четвертом оценка.
В четвертом классе числа и операции научат детей, как
читать и записывать целые числа в миллионы и понимать числа
объемная стоимость через миллионы. Важно, чтобы дети
понимать числа во всех аспектах, включая их системы и то, как
работать с ними различными способами. Большая часть этого будет
полагаться на рассуждения. Очень часто используются визуальные модели, потому что
предлагает гораздо лучшее понимание концепций. Они также будут
ожидается размещение целых чисел, десятичных знаков или дробей по порядку
от наибольшего к наименьшему на числовой прямой. Четвертый класс ожидает, что
дети смогут справиться с большими числами, и что они
способны быстро запоминать математические факты, особенно умножить таблицы на
до десяти.В этом году дети смогут умножать трехзначные числа.
числа на двузначные числа (51 х 467), а также деление деления
четырехзначные числа по однозначному числу, как с остатками, так и без них
(1548 ÷ 7).
Важно, чтобы дети
понимать числа во всех аспектах, включая их системы и то, как
работать с ними различными способами. Большая часть этого будет
полагаться на рассуждения. Очень часто используются визуальные модели, потому что
предлагает гораздо лучшее понимание концепций. Они также будут
ожидается размещение целых чисел, десятичных знаков или дробей по порядку
от наибольшего к наименьшему на числовой прямой. Четвертый класс ожидает, что
дети смогут справиться с большими числами, и что они
способны быстро запоминать математические факты, особенно умножить таблицы на
до десяти.В этом году дети смогут умножать трехзначные числа.
числа на двузначные числа (51 х 467), а также деление деления
четырехзначные числа по однозначному числу, как с остатками, так и без них
(1548 ÷ 7).
Четвероклассники учатся складывать и вычитать дроби одинаковыми
знаменатели (это означает, что нижние числа дроби будут
быть таким же). Например, 1/4 + 2/4 = 3/4. Дети будут
затем свяжите эти дроби с десятичными знаками и как преобразовать дроби
в десятичные дроби на самом базовом уровне. Например, 0,4 является
то же, что и 4/10. Они также будут добавлять и вычитать десятичные дроби и помещать
десятичные дроби в порядке от наименьшего к наибольшему. Ребёнок тоже будет круглым
десятичные дроби с точностью до десятых, сотых или до ближайшего целого числа.
Четвероклассников знакомят с геометрией, изучая точки, линии,
формы и фигуры дают учащимся представление о структуре
пространства и пространственных отношений. Дети узнают, что точка
единственное место в пространстве, а линия — это группа точек, идущих
навсегда в обоих направлениях.Они также учатся формировать углы.
и все про лучи.
Например, 0,4 является
то же, что и 4/10. Они также будут добавлять и вычитать десятичные дроби и помещать
десятичные дроби в порядке от наименьшего к наибольшему. Ребёнок тоже будет круглым
десятичные дроби с точностью до десятых, сотых или до ближайшего целого числа.
Четвероклассников знакомят с геометрией, изучая точки, линии,
формы и фигуры дают учащимся представление о структуре
пространства и пространственных отношений. Дети узнают, что точка
единственное место в пространстве, а линия — это группа точек, идущих
навсегда в обоих направлениях.Они также учатся формировать углы.
и все про лучи.
Распределительное свойство
: 5 четких примеров для использования в классе
Распределительное свойство: 5 четких примеров для использования в классе | Prodigy Education
Категория
- Ресурсы для учителей
- Учебные занятия
- Учебные инструменты
Что такое распределительное свойство ? Известный также как распределительный закон умножения, это одно из наиболее часто используемых свойств в математике. Распространяя что-то, вы делите это на части. В математике свойство распределения помогает упростить сложные задачи, поскольку оно разбивает выражения на сумму или разность двух чисел. Ищете конкретную операцию? Щелкните выделенные вкладки и перейдите вправо к:
Распространяя что-то, вы делите это на части. В математике свойство распределения помогает упростить сложные задачи, поскольку оно разбивает выражения на сумму или разность двух чисел. Ищете конкретную операцию? Щелкните выделенные вкладки и перейдите вправо к:
Определение распределительного свойства Для выражений в форме a (b + c) распределительное свойство показывает нам, как их решить:
- Умножение число сразу за скобками с числами внутри
- Сложение продуктов
А как насчет PEMDAS? Что случилось с первой оценкой того, что заключено в круглые скобки? Если ваши ученики задаются вопросом, почему вы не следуете порядку действий, которому их учили раньше, они не ошибаются.Однако, когда в алгебраических выражениях есть круглые скобки, содержащие переменные — величину, которая может изменяться в контексте математической задачи, обычно представленной одной буквой, — выполнение этой операции невозможно.
Распределительное свойство умножения над сложением Независимо от того, используете ли вы свойство распределения или следуете порядку операций, вы получите один и тот же ответ. В первом примере ниже мы просто оцениваем выражение в соответствии с порядком операций, упрощая сначала то, что было в скобках.Используя закон распределения, мы:
- Умножаем или распределяем внешний член на внутренние.
- Объедините похожие термины.
- Решите уравнение.
Давайте рассмотрим сценарий из реальной жизни, чтобы прояснить это. Представьте, что у одной студентки и двух ее друзей по семь клубники и четыре клементина. Сколько всего фруктов есть у всех трех учеников? В пакетиках для завтрака — или в скобках — по 7 клубники и 4 клементина.Чтобы узнать общее количество кусочков фруктов, им нужно все это умножить на 3. Когда вы разбиваете его, вы умножаете 7 клубники и 4 клементина на 3 ученика. Итак, у вас есть 21 клубника и 12 клементинов, в общей сложности 33 кусочка фруктов.
Итак, у вас есть 21 клубника и 12 клементинов, в общей сложности 33 кусочка фруктов.
Распределительное свойство умножения над вычитанием Как и в описанной выше операции, выполнение распределительного свойства с вычитанием следует тем же правилам, за исключением того, что вы находите разницу вместо суммы. Примечание : не имеет значения, положительная или отрицательная операция. Оставьте то, что указано в скобках.
Распределительное свойство с переменными Помните, что мы говорили об алгебраических выражениях и переменных? Распределительное свойство позволяет нам упростить уравнения при работе с неизвестными значениями. . Используя закон распределения с задействованными переменными, мы можем выделить x :
- Умножить или распределить внешний член на внутренние члены.
- Объедините похожие термины.
- Расположите члены так, чтобы константы и переменные находились по разные стороны от знака равенства.

- Решите уравнение и при необходимости упростите.
Примечание : при изоляции переменных (см. Шаг 3) то, что вы делаете с одной стороной, вы должны делать с другой. Чтобы исключить 12 с левой стороны, вы должны добавить по 12 к левой и правой сторонам. То же самое и с умножением и делением: чтобы выделить x , разделите каждую сторону на 4.
Распределительное свойство с показателями Показатель — это сокращенное обозначение, показывающее, сколько раз число умножается само на себя. Когда используются круглые скобки и показателей степени, использование свойства распределения может значительно упростить выражение.
- Разверните уравнение.
- Умножьте (распределите) первые числа каждого набора, внешние числа каждого набора, внутренние числа каждого набора и последние числа каждого набора.
- Объедините похожие термины.
- Решите уравнение и при необходимости упростите.

Примечание : Для второго шага используйте метод FOIL (first, external, inner, last) для распределения каждого выражения.
Распределительное свойство с дробями Решение алгебраических выражений с дробями выглядит сложнее, чем есть на самом деле. Следуйте инструкциям ниже, чтобы увидеть, как это делается. Надеюсь, этот пошаговый процесс поможет вашим ученикам понять, как и почему свойство распределения может пригодиться при упрощении дробей.
- Определите дроби. Используя свойство distributive, вы в конечном итоге превратите их в целые числа.
- Для всех дробей найдите наименьшее общее кратное (НОК) — наименьшее число, в которое могут точно поместиться оба знаменателя. Это позволит вам добавлять дроби.
- Умножьте каждый член уравнения на НОК.
- Изолируйте переменные, добавляя или вычитая одинаковые члены по обе стороны от знака равенства.
- Объедините похожие термины.

- Решите уравнение и при необходимости упростите.
Примечание : На втором и третьем шагах мы находим НОК и используем его для умножения дробей, чтобы упростить и избавиться от них. Нужно быстро освежиться? См. Сообщение в нашем блоге о том, как умножать дроби.
Различные способы изучения распределительной собственности
1. Prodigy Prodigy — это бесплатная адаптивная математическая платформа, которую любят 1,5 миллиона учителей и более 50 миллионов студентов по всему миру! Он предлагает согласованное с учебной программой содержание по каждой основной математической теме в 1–8 классах, включая инструкции:
- Используйте свойство распределения для раскрытия и решения выражений
- Заполните недостающие числа в эквивалентных выражениях, используя свойство распределения
Использование Prodigy поможет учащимся изучать и практиковать математику, помимо беглости фактов, и на втором и третьем уровнях DoK. С вопросами, подобными приведенному выше, учащиеся быстро овладеют распределительным свойством. Нажмите синюю кнопку ниже, если вы хотите дополнить уроки математики увлекательной игровой платформой для обучения!
С вопросами, подобными приведенному выше, учащиеся быстро овладеют распределительным свойством. Нажмите синюю кнопку ниже, если вы хотите дополнить уроки математики увлекательной игровой платформой для обучения!
2. Проблемы со словами Дистрибутивное свойство, возможно, неприменимо к повседневной жизни, но давайте посмотрим, как оно работает, решив некоторые проблемы со словами! У Лиама разный музыкальный вкус. Просматривая музыку на его телефоне, друзья Лиама находят песни трех разных жанров: поп, металл и кантри.Металлических песен в шесть раз больше, чем поп-песен, и в 11 раз больше кантри-песен, чем поп-песен. Если x представляет количество поп-песен, какое общее количество песен у Лиама на телефоне? Напишите выражение. Упростите: чтобы получить количество металлических песен, умножьте количество поп-песен на пять — 5x . Чтобы получить количество песен в стиле кантри, умножьте количество популярных песен на 11 — 11x . Поскольку вы знаете, что x — это количество поп-песен, вы можете записать это выражение так: школьный футбольный тренер предоставляет своей команде новую форму: майку, шорты и щитки на голенях.Одна футболка стоит 15 долларов, одна пара шорт стоит 11 долларов, а комплект щитков для голени стоит 8 долларов. Сколько стоит каждая униформа на одного товарища по команде? Напишите выражение и упростите: сколько это будет стоить, если в команде будет 11 игроков? Напишите выражение и упростите.
Поскольку вы знаете, что x — это количество поп-песен, вы можете записать это выражение так: школьный футбольный тренер предоставляет своей команде новую форму: майку, шорты и щитки на голенях.Одна футболка стоит 15 долларов, одна пара шорт стоит 11 долларов, а комплект щитков для голени стоит 8 долларов. Сколько стоит каждая униформа на одного товарища по команде? Напишите выражение и упростите: сколько это будет стоить, если в команде будет 11 игроков? Напишите выражение и упростите.
3. Массивы Визуальные или практические манипуляторы помогают учащимся разобраться в математике и конкретизировать абстрактные концепции. Они особенно полезны для более глубокого понимания учащимися распределительного свойства. Используйте предметы, картинки, числа — что угодно! — в строках и столбцах как удобный способ представления математических выражений, таких как 45 и 59.Взгляните на приведенный ниже пример по Indulgy: разбивая выражения на небольшие части, учащиеся могут решать более крупные и сложные математические задачи. Здесь помогает распределительное свойство. Если ребенок не может ответить на 45, используйте меньшие массивы и перепишите выражение как 4 (3 + 2) или (43) + (42). Это четыре строки по три плюс четыре строки по два , что аналогично массиву из четырех строк по пять .
Здесь помогает распределительное свойство. Если ребенок не может ответить на 45, используйте меньшие массивы и перепишите выражение как 4 (3 + 2) или (43) + (42). Это четыре строки по три плюс четыре строки по два , что аналогично массиву из четырех строк по пять .
Заключительные мысли о распределительном свойстве Поскольку это одно из наиболее часто используемых свойств, важно научиться выполнять и применять распределительное свойство.Без него очистить круглые скобки было бы невозможно! Включая ресурсы EdTech, массивы или математические текстовые задачи, учащиеся должны увидеть практическое применение распределительного свойства. Попробуйте. Сработал ли один пример более эффективно для вовлечения студентов и углубления их понимания? Дайте нам знать об этом в комментариях!
Создайте или войдите в свою учетную запись учителя на Prodigy — бесплатной игровой платформе для обучения математике, которую легко использовать как преподавателям, так и ученикам. Соответствующий учебным планам англоязычный мир, его любят 1,5 миллиона учителей и более 50 миллионов студентов! .
Соответствующий учебным планам англоязычный мир, его любят 1,5 миллиона учителей и более 50 миллионов студентов! .
Выражения со скобками. Математика 3 класс примеры на 2 действия.
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна. Часть 2
- Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Контрольная работа 1
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты. 3 класс.
3 класс.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
Сложение и вычитание чисел в пределах 100.
| | Математика 3 класс ->> Примеры Первое полугодиеВторое полугодие |
| 62 — (24 + 21) = 17 | 100 — (36 + 11) = 53 | 59 + (27 — 19) = 67 | (33 — 24) + 41 = 50 |
| 28 — (11 + 16) = 1 | 82 — (29 + 17) = 36 | 62 + (41 — 19) = 84 | 12 + (63 — 19) = 56 |
| 39 — (94 — 71) = 16 | 19 + (61 — 26) = 54 | 52 — (37 + 11) = 4 | 22 + (42 — 17) = 47 |
| 95 — (17 + 32) = 46 | 64 — (21 + 13) = 30 | 36 + (17 — 8) = 45 | 92 — (47 + 8) = 37 |
| 74 — (29 + 36) = 9 | 35 + (83 — 61) = 57 | 18 + (29 — 11) = 36 | 67 — (19 + 34) = 14 |
| 96 — (49 + 18) = 29 | 25 + (38 — 15) = 48 | 52 — (31 + 14) = 7 | 74 + (85 — 64) = 95 |
| 49 — (33 + 12) = 4 | 58 + (51 — 39) = 70 | 98 — (48 + 23) = 27 | 32 + (84 — 79) = 37 |
| 28 — (96 — 74) = 6 | 41 — (85 — 57) = 13 | 99 — (74 — 19) = 44 | 62 — (95 — 51) = 18 |
| 95 — (42 + 39) = 14 | 81 + (75 — 68) = 88 | 84 — (39 + 28) = 17 | 12 + (85 — 19) = 78 |
| 73 — (24 + 31) = 18 | 39 + (19 — 11) = 47 | 28 — (89 — 77) = 16 | 20 + (82 — 15) = 87 |
| 19 + (41 — 12) = 48 | 95 + (93 — 88) = 100 | 100 — (48 + 31) = 21 | 27 + (100 — 39) = 88 |
| 49 — (18 + 15) = 16 | 93 + (85 — 79) = 99 | 99 — (38 + 54) = 7 | 83 + (62 — 51) = 94 |
| 93 — (71 + 11) = 11 | 10 + (27 — 14) = 23 | 62 — (19 + 39) = 4 | 41 + (73 — 34) = 80 |
| 12 + (48 — 19) = 41 | 91 — (75 + 14) = 2 | 71 + (18 — 11) = 78 | 39 — (12 + 21) = 6 |
| 55 — (61 — 35) = 29 | 48 — (72 — 46) = 22 | 92 — (86 — 29) = 35 | 31 — (74 — 59) = 16 |
| 38 + (44 — 17) = 65 | 91 — (33 + 51) = 7 | 27 + (100 — 52) = 75 | 90 — (29 + 52) = 9 |
| 71 — (82 — 49) = 38 | 92 — (82 — 37) = 47 | 49 — (33 — 18) = 34 | 74 — (83 — 39) = 30 |
| 18 + (92 — 81) = 29 | 79 — (17 + 28) = 34 | 88 + (38 — 29) = 97 | 29 — (12 + 11) = 6 |
| 100 — (49 + 51) = 0 | 83 + (96 — 79) = 100 | 91 — (59 + 32) = 0 | 74 + (48 — 22) = 100 |
| 19 + (91 — 38) = 72 | 58 — (30 + 19) = 9 | 93 + (81 — 75) = 99 | 85 — (47 + 24) = 14 |
| 90 + (82 — 74) = 98 | 62 — (31 + 27) = 4 | 44 + (29 — 27) = 46 | 32 — (19 + 6) = 7 |
| 49 + (47 — 39) = 57 | 95 — (82 + 11) = 2 | 63 + (37 — 19) = 81 | 100 — (64 + 31) = 5 |
| 11 + (78 — 54) = 35 | 61 — (33 + 18) = 10 | 59 + (67 — 42) = 84 | 53 — (31 + 17) = 5 |
| 85 — (27 + 52) = 6 | 46 + (93 — 68) = 71 | 83 — (27 + 36) = 20 | 29 + (98 — 69) = 58 |
| 85 — (97 — 49) = 37 | 72 — (64 — 31) = 39 | 49 — (74 — 38) = 13 | 95 — (38 — 23) = 80 |
| 87 + (23 — 18) = 92 | 49 — (18 + 23) = 8 | 13 + (100 — 72) = 41 | 92 — (34 + 19) = 39 |
| 28 + (49 — 32) = 45 | 83 — (39 + 26) = 18 | 37 + (62 — 17) = 82 | 93 — (48 + 27) = 18 |
| 72 + (93 — 69) = 96 | 97 — (12 + 61) = 24 | 27 + (73 — 67) = 33 | 39 — (21 + 16) = 2 |
| 100 — (72 + 21) = 7 | 17 + (100 — 38) = 79 | 100 — (11 + 52) = 37 | 49 + (100 — 76) = 73 |
| 39 + (48 — 34) = 53 | 100 — (26 + 29) = 45 | 42 + (39 — 17) = 64 | 100 — (47 + 34) = 19 |
| _________________________ | _________________________ | _________________________ | _________________________ |
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
Калькулятор со скобками
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный математический калькулятор может вычислить математическое выражение со скобками, определить порядок действий в выражении без скобок и произвести такие математические операции как: сложение, вычитание, умножение, деление, возведение в степень
Вы так же можете воспользоваться
калькулятором выражений. Данный математический калькулятор сможет вычислить выражение, содержащее множество математических операций и функций, в том числе вложенных.
Данный математический калькулятор сможет вычислить выражение, содержащее множество математических операций и функций, в том числе вложенных.
sin
cos
tan
cot
sec
csc
asin
acos
atan
acot
asec
acsc
xy
x2
x3
ln
lg
lb
(
7
4
1
√x
)
8
5
2
.
3√x
C
9
6
3
e
π
+
−
×
÷
←
=
Порядок действий в выражениях без скобок
1. Умножение, деление
2. Сложение вычитание
Например:
25 –
15 ∙
2 +
8 : 2 = -1
1) 15 ∙ 2 = 30
2) 8 : 2 = 4
3) 25 — 30 = -5
4) -5 + 4 = -1
Порядок действий в выражениях со скобками
1. Действия в скобках
Действия в скобках
1. Умножение, деление
2. Сложение вычитание
Например:
(14 + 7) : 7 + 3 ∙ 2 = 9
1) 14 + 7 = 21
2) 21 : 7 = 3
3) 3 ∙ 2 = 6
4) 3 + 6 = 9
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Урок математики по теме «Таблица умножения и деления с числом 9». 3 класс
Учитель | Громова Любовь Евгеньевна |
Место работы | МОУ Хорошевская нош |
Должность | Учитель начальных классов |
Предмет | Математика |
Тема урока | Таблица умножения и деления с числом 9. |
Класс | 3 |
Предметная программа и ее автор | УМК «Школа России» Математика М.И. Моро, М.А.Бантова |
Тип урока | Открытие новых знаний |
Цель | Обеспечить усвоение детьми таблицы умножения и деления с числом 9. Способствовать формированию ключевых компетентностей: познавательной, информационной, коммуникативной, развивающей. |
Задачи | образовательные: — составить таблицу умножения и деления с числом 9; — формировать способность решать задачи с использованием таблицы умножения; — закреплять переместительное свойство умножения, взаимосвязь умножения и деления, порядок действий в выражениях со скобками и без скобок; — совершенствовать вычислительные навыки, умение вычислять площадь и периметр квадрата; развивающие: — развитие логического мышления, воображения; коммуникативных качеств, речи обучающихся; воспитывающие: воспитывать положительную мотивацию к математике как к учебному предмету. |
Планируемые образовательные результаты | Предметные: научатся составлять таблицу умножения и деления с числом 9; закрепят знания табличных случаев умножения и деления, Личностные: принимать и осваивать свою социальную роль; проявлять мотивы к учебной деятельности; осознавать личностный смысл учения. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
Методы и формы обучения | Частично-поисковый, словесно-наглядный, практический; фронтальная, индивидуальная, групповая, работа в парах |
Оборудование | Математика: 3 класс, 1часть, М. |
Этап урока | Цель | Деятельность учителя | Деятельность учащихся | Универсальные учебные действия |
1.Мотивирование к учебной деятельности. (1 мин.) | Включение учащихся в учебную деятельность на личностно значимом уровне | -Здравствуйте, дети. Садитесь. Прозвенел звонок, Начинается урок. Ноги прямо я поставлю, Локоточки разведу. Сяду прямо, не согнусь, За работу я примусь. | Приветствуют учителя, отвечают на вопросы. | Личностные: самоопределение; Регулятивные: целеполагание; Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
2. Актуализация знаний. (5 мин.) | Готовность мышления и осознание потребности к выявлению причин затруднений в собственной деятельности. | Устный счет. -Давайте с вами проведем устный счет, отвечаем по руке. А) разминка — Сколько ушей у трёх щенят? (6) — Сколько лап у двух лисят? (8) — Сколько хвостов у 9 котят? (9) — У бабушки Даши внучка Маша, кот Пушок и собака Дружок. — Над рекой летели птицы: голубь, щука, 2 синицы, 2 стрижа и 5 угрей. Сколько птиц? Ответь скорей!(5) -А теперь вам нужно решить пример и найти лишнее равенство: СЛАЙД 2 40 : 5= 72 : 9 = 64 : 8 = 24 : 4 = 80 : 10 = 32 : 4 = 56 : 7 = 48 : 6 = -Теперь посмотрите на равенство, и найдите лишнее, почему? | Выполняют задания | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; Познавательные: логические – анализ объектов с целью выделения признаков. |
3. Мотивационный (сообщение темы урока) | Сообщение темы урока. Определение цели урока. (фронтальная работа) | -Чтобы узнать тему урока , посмотрите на доску и скажите: какое числовое выражение будет следующим 2*9, 3*9. 4*9,5*9, 6*9, ?*9, 8*9, ? (СЛАЙД 3) -Что нужно знать, чтобы быстро выполнить вычисления? (таблицу умножения с числом 9) _Сформулируйте тему нашего урока . ( Таблица умножения и деления с числом 9) -Зная тему урока, поставьте каждый перед собою цель (научится составлять таблицу умножения и деления с числом 9 и применять её.) -Откройте с.65, найдите знак -начало урока -чем же мы сейчас займёмся? ( читают в учебнике цель урока) | Повторение случаев умножения с числом 1 и 0. Записывают табличные случаи умножения и деления с числом 9. Помогают сформулировать тему урока. | Регулятивные: целеполагание; Коммуникативные: постановка вопросов; Познавательные: самостоятельное выделение – формулирование познавательной цели; логические – формулирование проблемы. |
4. Постановка учебной задачи и ее решение (изучение нового материала) | Постановка цели коррекционной деятельности, выбор способа и средств ее реализации. | 2. Запись в тетради 9*9=81 81:9=9 — Трудно ли запомнить таблицу умножения? — Математика – наука сложная, но интересная и волшебная. 3. Игра «Волшебство». — Наступило долгожданное мгновенье. Вы готовы к волшебству? — Положите обе ладони на стол и запомните номера ваших пальчиков. — Сейчас ваши пальчики превратятся в счетные машинки. Чтобы умножить 9 на число, вам достаточно найти пальчик с таким же номером и сосчитать, сколько пальцев справа и слева от него. Число пальцев справа показывает первую цифру произведения (десятки), а число пальцев справа – вторую цифру (единицы). (Учитель показывает, как быстро выучить таблицу умножения на 9 на пальцах). 4. Игра — Я буду называть разные числа. Если услышите число, кратное 9, хлопайте. 12, 9, 15, 22, 21, 27, 81 | Знакомятся с алгоритмом. Индивидуальная практическая работа по овладению таблицей умножения с числом 9. | Коммуникативные: постановка вопросов; Познавательные: самостоятельное выделение – формулирование познавательной цели; логические – формулирование проблемы. |
5. Закрепление пройденного (4 мин.) | Коррекция ошибок и формирование умения правильно применять соответствующие знания. | 1. Работа по учебнику. №1 (1, 2 ст.), с.65 (с проверкой) 2. Составить равенства с числами 8, 9, 72. 8∙ 9=72 72:8=7 9∙ 8=72 72:9=8 3. Проверка по эталону (СЛАЙД 4). | Решают самостоятельно в тетрадях. Взаимопроверка.] Проверка по эталону на слайде. | Регулятивные: планирование, прогнозирование; Познавательные: моделирование; Логические – решение проблемы, построение логической цепи рассуждений, доказательство; Коммуникативные – инициативное сотрудничество в поиске и выборе информации. |
6.Физкультминутка. (1 мин.) | 1. Гимнастика для глаз (СЛАЙД 5). 2. Гимнастика для пальчиков. _- Ваши пальчики хорошо потрудились, им надо отдохнуть. | Дети выполняют соответствующие движения. | Личностные: самоопределение | |
7. Повторение и закрепление пройденного . (6 мин.) | Выполнение заданий в учебнике -Ребята, откройте учебник на стр.65 № 2. -Кто хочет прочитать задачу? -Что такое 27? (Количество морковок дали каждому кролику) -Что показывает число 9? (Сколько морковок дали каждому кролику) -Что узнаем выражением 27:9? (Количество клеток, в которые положила морковки девочка) -Что узнаем выражением 18:9? (кол-во клеток, в которые положил морковки мальчик) -Что узнаем выражением 27+18(Сколько всего морковок у мальчика и у девочки ) -Что узнаем выражением (27+9): 9 (кол-во клеток, в которые положили морковки девочка и мальчик) | Составляют и решают задачи изученных видов с проговариванием алгоритма вслух. Повторяют обратные задачи. | Регулятивные: контроль, оценка, коррекция; Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач; рефлексия способов и условий действия; Коммуникативные: управление поведением партнера – контроль, коррекция, оценка действий партнера. | |
8. Самостоятельная работа с проверкой по эталону. (5 мин.) | Самопроверка ЗУН, вызвавших затруднения, индивидуальная рефлексия достижения цели. | -Ребята, найдите задание №3. -Кто хочет прочитать задачу? -О чем в ней говорится?(О проводе длиной 50 м) -Какое действие с ним выполняли? (Отрезали 8м, потом 7) -Что нужно узнать в задаче?(Сколько метров провода осталось) -Ребята, Какими способами можно решить задачу? (1) 50-8-7; 2) 50-(8+7) -Что делали в первом случае?(Отрезали по очереди 8м,затем 7м. -Что делали во втором случае?(Отрезали вместе 8м и 7м ) -Теперь запишите решение задачи у себя в тетради. Первый вариант записывает к первому способу, второй вариант ко второму. -Давайте проверим, какие ответы получились. Молодцы! 3. (2 человека работают у доски) | Работают самостоятельно по алгоритму. Проверяют по эталону на доске. | Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; Личностные: самоопределение. |
9. Включение в систему знаний и повторение. (4 мин.) | Применение понятий и способов действий, вызвавших затруднения, повторение и закрепление ранее изученного и подготовка к изучению следующих разделов курса. | 1 Выполнение задания в учебнике. -Найдите задание №6. -Кто хочет прочитать задачу? -Как найти периметр квадрата?( Длину стороны умножить на 4) -Как найти площадь квадрата? (Длину стороны умножить саму на себя.) -Выполняем задание у себя в тетради по рядам, первый ряд ищет со стороной-7см, второй ряд ищет со стороной-4 см, и третий ряд ищет со стороной-9 см.-Теперь обменяйтесь тетрадями с соседом и проверьте ответы | Работают в парах с раздаточным геометрическим материалом. Индивидуально работают мальчики и девочки. | Регулятивные: контроль, оценка, коррекция; Познавательные: моделирование; Логические – решение проблемы, построение логической цепи рассуждений, доказательство; Коммуникативные: управление поведением партнера – контроль, коррекция, оценка действий партнера |
10. (1мин.) | Закрепление полученных на уроке знаний. | 1. Выучить таблицу умножения. 2. с.65, №1(3,4ст.), №4, 5 3. Выставление оценок в течение урока и в конце урока с комментированием. | Запись задания в дневник с комментированием. | Регулятивные: контроль, коррекция; Личностные: самоопределение. |
11. Рефлексия деятельности (1 мин.) | Соотнесение цели урока и его результатов, самооценка работы на уроке, осознание метода преодоления затруднений. | — Какие цели мы с вами сегодня ставили на урок? Достигли ли мы их? -Теперь закончите предложения. — Кто доволен сегодня своей работой, громко скажите себе «Молодец». | Осуществляют самооценку собственной учебной деятельности, соотносят цель и результаты, степень их соответствия. | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные: рефлексия. |
Порядок выполнения действий в примерах. (3 класс) презентация, доклад
Давайте, ребята, учиться считать,
Что бы скорей математиком стать.
Ему по плечу любая работа,
Но прежде разучим правила счёта.
Звонок прозвенел. Он позвал на урок.
Пора! Тишина! К нам наука идёт…
Сегодня мы узнаем, в каком порядке выполняются действия в числовых выражениях.
старание
подсказка
разговор
внимание
знания
знания + старание + внимание = успех
50+(30-20)=60
Увеличьте 50 на разность чисел 30 и 20.
100-(10+60)=30
Уменьшите 100 на сумму чисел 10 и 60.
85-(70+15)=0
Из 85 вычесть сумму чисел 70 и 15.
42+(8-2)=48
К 42 прибавьте разность чисел 8 и 2.
(30-5)+10:2=30
К разности чисел 30 и 5
прибавьте частное чисел 10 и 2.
(40+50)+20:2=80
Из суммы чисел 40 и 50
вычтите частное чисел 20 и 2
Решите примеры.
78+4=
82
82-18=
64
64-34=
30
30:3=
10
10:2=
5
5·3=
15
15·2=
30
30:10=
3
3·9=
27
10·2=20 (д. )
)
Сколько всего дельфинов плывёт?
10+20=30 (д.)
Один матрос поймал 3 рыбы, второй в 2 раза больше, чем первый, а третий в 2 раза больше чем первый и второй вместе. Сколько рыб поймал каждый матрос?
3 (р.)
3·2= 6 (р.)
(3+6)·2=18 (р.)
3+6+18=27 (р.)
3 км
5 км
8 км
12 км
17 км
3 км
5 км
8 км
12 км
17 км
Периметр — это сумма длин всех сторон.
3+5+8+12+17
3 км
5 км
8 км
12 км
17 км
Периметр — это сумма длин всех сторон.
(3+17)+(8+12)+5=20+20+5=45 (км)
Какие действия используются в
данном числовом выражении?
48–(10+9)+2·9-18:3
Компоненты при сложении.
слагаемое + слагаемое = сумма
Компоненты при вычитании.
уменьшаемое – вычитаемое = разность
Компоненты при умножении.
множитель · множитель = произведение
Компоненты при делении.
делимое : делитель = частное
Если в выражении нет скобок, и в него
входят только сложение и вычитание, то действия выполняются в том порядке, в котором они записаны.
32+34
66
–15
+25=
51
76
Если в выражении нет скобок, и в него входят только умножение и деление, то действия выполняются в том порядке, в котором они записаны.
27:3
9
:3
·2=
3
6
Если в выражение нет скобок, и в него входят
не только сложение и вычитание, но и умножение
или деление, то сначала по порядку выполняют умножение
и деление, затем сложение и вычитание.
48–10:2+8+9·2=69
5
18
Если в числовом выражении есть скобки,
то сначала выполняются действия в скобках, затем по порядку умножение и деление, после по порядку
сложение и вычитание.
48–(10+9)+2·9-18:3=41
5
18
6
Если в числовом выражении есть скобки, то сначала выполняются действия в скобках, затем по порядку умножение и деление, после по порядку
сложение и вычитание.
48–(10+9)+2·9-18:3=41
5
18
6
Действия в числовых выражениях выполняются в следующем порядке:
1. Действия, записанные в скобках.
2. Умножение и деление.
3. Сложение и вычитание.
25+62-9+14=
92
45–(15+24)+33-10=
29
30:10·9=
27
3·(10:2)=
15
92-(36-30)·2=
80
2·4+27:3=
17
В первый день собрали 4 кг апельсинов, во второй день собрали 5 кг апельсинов, а кокосов в 2 раза больше, чем апельсинов в первый и во второй день вместе, в третий день собрали ананасов в 3 раза больше, чем апельсинов во второй день. Сколько всего килограмм фруктов собрали за три дня?
Сколько всего килограмм фруктов собрали за три дня?
4 кг
5 кг
(4+5)·2
5·3
4+5+(4+5)·2+5·3=42 (кг)
38
22
13
20
=
9
В тех кружках, где цифр нет,
расставьте минусы и плюсы,
чтоб правильный получить ответ.
38
—
22
+
13
—
20
=
9
В тех кружках, где цифр нет,
расставьте минусы и плюсы,
чтоб правильный получить ответ.
Сколько четырёхугольников изображено на рисунке?
Маша
Саша
Таня
3
1
2
Действия в числовых выражениях выполняются в следующем порядке:
1. Действия, записанные в скобках.
Действия, записанные в скобках.
2. Умножение и деление.
3. Сложение и вычитание.
Сегодня я узнал…
Было интересно…
Было трудно…
Скачать презентацию
Урок математики по теме «Порядок выполнения действий в выражениях без скобок и со скобками». 3-й класс
Ход урока
I. Оргмомент (звучит песня “Дважды два четыре”). СЛАЙД
Презентация.
— Ребята, кто из вас любит математику? Почему вы её любите? Математику любят наши знакомые Миша и Маша, ученики 3 класса. Сегодня они как всегда с нами на уроке.
“Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.” (А. Маркушевич)
СЛАЙД “Математику уже затем изучать нужно, что она ум в порядок приводит”
Михаил Васильевич Ломоносов, русский учёный,
энциклопедист, поэт.
II. Устная работа.
1. Повторение табличных случаев умножения и деления. Работа в группах с использованием ноутбуков.
— Как вы считаете, какое задание, выполняемое нами на каждом уроке приводит наш ум в порядок? (повторение таблицы умножения и деления)
— Проверим, чья группа первая справится с этим заданием. Если вы ошибаетесь в ответе, вас компьютер возвращает к началу теста, и вы выполняете задание заново.
— Прекрасное начало урока! Рада, что вы все справились с заданием!
2. Игра “Да или нет”
— Поиграем в игру “Да или нет”. Если вы согласны с моим высказыванием, то показываете “Да” (скрещенные пальчики), если не согласны – “Нет” ( один указательный пальчик). Договорились?
— При умножении любого числа на 1 получается 1 (да).
— При умножении любого числа на 1, получается 1 (да).
— Чтобы разделить на 10, достаточно дописать 0
(нет, отбросить).
— Умножать на 0 нельзя (нет, можно).
— Чтобы найти делимое, нужно значение частного умножить на делитель (да).
— Чтобы найти неизвестный множитель, нужно значение произведения умножить на известный множитель (нет, разделить).
— В выражениях без скобок все действия выполняются по порядку слева направо (нет, сначала умножение и деление, потом вычитание и сложение).
— С каждым уроком у вас получается всё лучше! Просто замечательно!
3. Логические упражнения.
Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль) Предлагаю выполнить логические задания. Вы готовы?
— Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)
— Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)
— Петух, стоя на одной ноге весит 5кг. Сколько он
будет весить, стоя на двух ногах? (5кг)
Сколько он
будет весить, стоя на двух ногах? (5кг)
— На руках 10 пальцев. Сколько пальцев на 6 руках? (30)
— У родителей 6 сыновей. Каждый имеет сестру. Сколько всего детей в семье? (7)
— Сколько хвостов у семи котов?
— Сколько носов у двух псов?
— Сколько ушей у 5 малышей?
— Ребята, именно такой работы я и ждала от вас: вы были активны, внимательны, сообразительны.
III. Актуализация знаний.
“Чтобы переварить знания, надо поглощать их с аппетитом.” (А.Франц)
— Вы готовы поглощать их с аппетитом? Тогда внимание!
— Посмотрите, пожалуйста, внимательно на доску. Как вы считаете, какое задание предполагается? (Указать арифметические действия, которые выполняются в заданном порядке)
— Проговорите правило, которое подходит к данной схеме.
В выражениях без скобок, содержащих только
сложение и вычитание – действия I ступени, или
умножение и вычитание – действия II ступени,
действия выполняются в том порядке, как они
записаны : слева направо.
В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.
В выражениях со скобками сначала вычисляют значения выражений в скобках. Затем по порядку слева направо выполняется умножение или деление.
— Озвучьте тему нашего урока. (“Порядок выполнения действий в выражениях со скобками и без скобок”)
— Просто умницы, ловко справились, умело.
VI. Целеполагание.
— Ребята, как вы считаете, достаточно ли хорошо отработана нами тема “Порядок выполнения действий в выражениях”?
— На что нам сегодня необходимо обратить внимание? Над чем поработать? (Упражняться в нахождении значений выражений, содержащий действия разных ступеней со скобками и без них. Познакомиться с видами выражений, в которых можно допустить ошибки)
— И в этом разобрались. Я думаю, достаточно
поставленных задач на сегодняшний урок.
V. Постановка проблемной ситуации. Работа в группах. (карточки)
— Ребята, послушайте, пожалуйста, что говорил французский математик Д.Пойя: “Лучший способ изучить что-либо — это открыть самому”. Вы готовы к открытиям?
СЛАЙД- Даны выражения, посмотрите, как справились с заданием Маша и Миша.
— Кто выполнил задание верно: Маша или Миша? (ответы детей)
— К кому из наших друзей можно отнести следующее высказывание Р. Декарта “Мало иметь хороший ум, главное – хорошо его применять? (К Мише, потому что он ошибся)
— Какие ошибки допущены Мишей?
СЛАЙД — Давайте проверим!
— Я знала, что это задание вам было под силу!
VII. Разрешение проблемной ситуации.
СЛАЙД — В данной ситуации кто является КП – “кислой парочкой”? (Миша и выражения)
— Как разрешить проблему?
(Миша должен САМ найти значения выражений
— Какие у него есть для этого ресурсы? (Память, чтобы запомнить правило, старание, тренировка, учебник,
Выражения САМИ должны быть решены, для этого ресурсы: Маша, учитель, родители)
— Какое ИКР вы бы выбрали? Почему?
— А если Миша воспользуется ИКР2? Это будет хорошо или плохо, давайте поиграем!
Игра “Хорошо-плохо”
— Если за него выполнят задание, то будет
хорошо, потому что. ..(ему не нужно будет долго
сидеть за уроками, не нужно будет думать, у него
появится свободное время…)
..(ему не нужно будет долго
сидеть за уроками, не нужно будет думать, у него
появится свободное время…)
— Если за него выполнят задание, то будет плохо…(сам не научится решать, не будет трудолюбивым, не усвоит тему, будут проблемы в учёбе…)
“Величие человека — в его способности мыслить.” (Б. Паскаль)
— Ребята, у вас получилось лучше, чем я могла бы подумать!
— А ещё вам предлагается новый способ записи решения. В чём он заключается? (Нужно выписывать все действия ниже данного выражения)
— Вот в этом мы сейчас с вами и поупражняемся.
VIII. Нахождение значений выражений. (№228) – у доски 3 выражения.
“Счет и вычисления — основа порядка в голове.” (Песталоцци)
IX. Самостоятельная работа № 228, 3 выражения.
— Я горжусь вами, что вам удалось выполнить задание почти без ошибок.
X. Решение задачи №227.
“Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.” (Д.Пойа)
| У всех учащихся второго класса 39 ручек.
У шести учеников по одной ручке, у пяти по три, а у
остальных по две. Сколько учеников имеют по две
ручки? Маша записала решение этой задачи выраженим так: 39-1 * 6+3 * 5. Миша – так: 39-(1 * 6+3 * 5) Кто прав: Миша или Маша? |
— Прочитайте установку и ответьте на вопрос. Кто прав Миша или Маша?
— Самостоятельно запишите решение задачи и ответ.
— Назовите ответ.
СЛАЙД — Давайте проверим!
— Поздравляю, это правильный ответ!
XI. Работа по алгоритму.
— Что такое алгоритм? (Порядок выполнения действий)
СЛАЙД — Выполните действия по алгоритму.
— “Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.”, говорил М.В. Остроградский. Вот и мы сейчас вспомним то, что изучали на уроках информатики.
— Какая фигура получилась? (прямоугольник)
— Ниже начертите фигуру, площадь которой в 6 раз больше.
— Что примите за единичный отрезок? (2 клетки)
— Вы на верном пути!
СЛАЙД — Из скольких мерок состоит ваша фигура?
— Внимание на слайд! Вас ждёт сюрприз, если правильно найдёте значения выражений.
XII. Нахождение значений выражений. (СЛАЙД)
— Именно этого мы с вами и ждали! (на слайде появляется фото класса)
XIII. Итог урока.
— Выполнили ли мы поставленные цели урока? Что планировали? Всё ли у нас получилось? Над чем необходимо поработать?
— Вы сегодня просто умнички, много сделали. Работать с вами просто радость!
Работать с вами просто радость!
XIV. Рефлексия.
— Оцените работу вашей группы, насколько успешно работали, аргументируйте свой выбор (карточки с цифрами).
XV. Домашнее задание.
— Что необходимо закрепить дома? (порядок выполнения действий в сложных выражениях) № 234 (1 столбик), №230.
— “Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.” (М.И. Калинин)
- Приложение 1
- Приложение 2
- Приложение 3
- Приложение 4
- Приложение 5
Порядок операций — БОДМАС
Операции
«Операции» означают такие действия, как сложение, вычитание, умножение, деление, возведение в квадрат и т. д. Если это не число, то, вероятно, это операция.
д. Если это не число, то, вероятно, это операция.
Но когда вы видите что-то вроде…
7 + (6 × 5 2 + 3)
… какую часть нужно вычислить в первую очередь?
Начать слева и идти направо?
Или идти справа налево?
Предупреждение: Вычислите их в неправильном порядке, и вы можете получить неверный ответ!
Итак, люди давно договорились следовать правилам при расчетах, а они таковы:
Порядок операций
Сначала сделайте что-нибудь в скобках
| 4 × (5 + 3) | = | 4 × 8 | = | 32 | |||
| 4 × (5 + 3) | = | 20 + 3 | = | 23 | (неверно) |
Экспоненты (степени, корни) перед умножением, делением, сложением или вычитанием
| 5 × 2 2 | = | 5 × 4 | = | 20 | |||
| 5 × 2 2 | = | 10 2 | = | 100 | (неверно) |
Умножьте или разделите перед сложением или вычитанием
| 2 + 5 × 3 | = | 2 + 15 | = | 17 | |||
| 2 + 5 × 3 | = | 7 × 3 | = | 21 | (неверно) |
В противном случае просто идите слева направо
| 30 ÷ 5 × 3 | = | 6 × 3 | = | 18 | |||
| 30 ÷ 5 × 3 | = | 30 ÷ 15 | = | 2 | (неверно) |
Как мне все это запомнить.
 .. ? БОДМАС!
.. ? БОДМАС! Б | B ракетки первые |
О | O заказы (т. е. степени и квадратные корни и т. д.) |
ДМ | D ivision и M умножение (слева направо) |
КАК | Добавление A и удаление S (слева направо) |
Разделить и умножить ранги одинаково (и идти слева направо).
Прибавлять и вычитать ранги поровну (и идти слева направо)
Итак, сделайте так:
После того, как вы сделали «B» и «O», просто идите слева направо, выполняя любые «D» или «M», как вы их найдете.
Затем идите слева направо, выполняя любые «A» или «S», как вы их найдете.
Примечание: единственное странное название — «Приказы». Вы можете предпочесть GEMS ( G rouping, E xponents, M умножить или разделить, добавить или S вычесть). Или в США, где вместо квадратных скобок говорят «круглые скобки», значит, это «PEMDAS».
Примеры
Пример: Как вычислить
3 + 6 × 2 ?M Ультипилизация до A DDITION:
Первый 6 × 2 = 12 , затем 3 + 12 = 15
Пример: как вы работаете
(3 + 6) × 2 6. ?B сначала ракетки:
Сначала (3 + 6) = 9 , затем 9 × 2 = 18
0006 ?
M умножение и D ivision имеют одинаковый ранг, поэтому просто идите слева направо:
Сначала 12/6 = 2 , затем 2 × 3 = 6 , затем 70 6 90 39 6 / 0005
Практический пример:
Пример: Сэм бросил мяч прямо вверх со скоростью 20 метров в секунду, какое расстояние он пролетел за 2 секунды?
Сэм использует специальную формулу, включающую гравитацию:
высота = скорость × время — (1/2) × 9,8 × время 2
Сэм вводит скорость 20 метров в секунду и время 2 секунды:
высота = 20 × 2 − (1/2) × 9,8 × 2 2
Теперь расчеты!
Начните с: 20 × 2 − (1/2) × 9,8 × 2 2
Первые скобки: 20 × 2 − 0,5 × 9,8 × 2 2
Затем заказы (2 2 4) :20 × 2 − 0,5 × 9,8 × 4
Затем умножить: 40 − 19,6
Вычесть и ГОТОВО! 20,4
Мяч достигает 20,4 метра через 2 секунды
Экспоненты экспонентов .
 ..
..Что насчет этого примера?
4 3 2
Экспоненты особенные: они идут сверху вниз (сначала сделайте экспоненту сверху). Итак, мы вычисляем так:
| Начните с: | 4 3 2 | |
| 3 2 = 3×3: | 4 9 | |
| 4 9 = 4×4×4×4×4×4×4×4×4: | 262144 |
Так 4 3 2 = 4 (3 2 ) , не (4 3 ) 21 21 И, наконец, как насчет примера с самого начала? Начните с: 7 + (6 × 5 2 + 3) Скобки сначала, а затем «Заказы» :7 + (6 × 25 + 3) Затем Умножьте 0 :7 + ( + 3) Затем Добавить :7 + (153) Скобки завершены: 7 + 153 Последней операцией является Добавить : 160 295, 1565, 1571, 296, 1567, 380, 1569, 3852, 3853, 382 PEMDASAn Issue Большинство проблем с упрощением порядка операций связано с наличием вложенных скобок, показателей степени и знаков «минус». (Предоставлены ссылки для дополнительного ознакомления с работой с отрицаниями, символами группировки и степенями.) Содержание продолжается ниже Порядок действий Я буду упрощать изнутри: сначала круглые скобки, затем квадратные скобки, помня, что знак «минус» на цифре 3 перед скобками соответствует цифре 3. Только после завершения группировки частей Я делаю деление, а затем добавляю 4. 4 − 3[4 −2(6 − 3)] ÷ 2 4 − 3[4 − 2(3)] ÷ 2 4 − 3[ 4 − 6] ÷ 2 4 − 3[−2] ÷ 2 4 + 6 ÷ 2 4 + 3 7 Помните, что вместо группирующих символов, говорящих об обратном, деление стоит перед сложения, поэтому это выражение упростилось, в конце концов, до «4 + 3», а не «10 ÷ 2». (Если вас не устраивают все эти знаки «минус», просмотрите «Отрицательные».) Я должен помнить об упрощении в скобках перед I в квадрате, потому что (8 − 3) 2 не то же, что 8 2 − 3 2 . 16 — 3 (8 — 3) 2 ÷ 5 16 — 3 (5) 2 ÷ 5 16 — 3 (25) ÷ 5 16 — 75 ÷ 5 16 — 15 1 Если вы узнали о переменных и комбинировании «подобных» терминов, вы также можете увидеть такие упражнения: Если у меня возникли проблемы с вычитанием через круглые скобки, я могу превратить его в умножение отрицательной 1 через круглые скобки (обратите внимание на выделенную красным «1» ниже): 14 x + 5[6 − (2 х + 3)] 14 х + 5[6 — 1(2 х + 3)] 14 х + 5[6 — 2 х — 5 19 х — 3] 7 + 5[3 − 2 x ] 14 x + 15 − 10 x 4 x + 15 Мне нужно помнить об упрощении на каждом этапе, комбинируя одинаковые члены, когда и где я могу: −{2 x − [3 − (4 − 3 x )] + 6 х } -1{2 х — 1[3 — 1(4 — 3 х )] + 6 х } -1{2 х — 1[3 — 4 + 3 x ] + 6 x } −1 {2 x − 1[− 1 + 3 x ] + 6 x } + x + 6 x } −1 {2 x + 6 x — 3 x + 1} −1 {5 x + 10007 −1 {5 x + 10007 −1 x + 10007 –1 x + 10007 — 1 (Дополнительные примеры такого рода см. Выражения, содержащие дробные формы, также могут вызвать путаницу. Но, пока вы работаете с числителем (то есть верхним) и знаменателем (то есть нижним) отдельно, пока они сначала полностью не упростятся, а уж потом комбинируете (или уменьшаете), если это возможно, то вы все должно быть в порядке. Если дробная форма добавляется или вычитается из другого термина, дробного или иного, убедитесь, что вы полностью упростили и сократили дробную форму, прежде чем пытаться выполнить сложение или вычитание. Прежде чем добавить два термина, я должен упростить. [45]/[8(5 − 4) − 3] + [3(2) 2 ]/[5 − 3] [45]/[8(1) − 3] + [3(4)]/[2] [45]/[8 − 3] + [12]/[2] [45]/[5] + 6 9 + 6 15 Порядок действий: Примеры
Purplemath
 Итак, в следующих примерах я покажу, как работать с такими выражениями.
Итак, в следующих примерах я покажу, как работать с такими выражениями. MathHelp.com

 в разделе Упрощение со скобками.)
в разделе Упрощение со скобками.)
Работает так же, как и в предыдущих примерах. Мне просто нужно работать с «верхом» и «низом» отдельно, пока я не получу дробь, которую я могу (возможно) уменьшить.
Мне просто нужно работать с «верхом» и «низом» отдельно, пока я не получу дробь, которую я могу (возможно) уменьшить.
[(3 − 2) + (1 + 2) 2 ]/[5 + (4 − 1)]
[(1) + (3) 2 ]/[5 + (3)]
[1 + 9]/[8]
8/10
5/4
(Для примеров с большим количеством степеней см. раздел Упрощение с степенями.)
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении, используя порядок операций. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Упростить» или «Оценить» во всплывающем окне, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. )
)
Боковой формат и умножение путем сопоставления никогда не возникает, но когда возникает, кажется, что спорам нет конца. (Стало раздражать популярно размещать их в Facebook.)
Я упрощаю обычным способом:
16 ÷ 2[8 − 3(4 − 2)] + 1
16 ÷ 2[8 − 3(2)] + 1
16 ÷ 2[8 − 6] + 1
16 ÷ 2[ 2] + 1 (**)
16 ÷ 4 + 1
4 + 1
5
Непонятная часть приведенного выше расчета заключается в том, как «16 разделить на 2[2] + 1» (в строке, отмеченной с двойной звездой) становится «16 разделить на 4 + 1» вместо «8 умножить на 2 + 1».
Это потому, что, несмотря на то, что умножение и деление находятся на одном уровне (поэтому должно применяться правило слева направо), круглые скобки, кажется, каким-то образом опережают деление, поэтому первые 2 в отмеченной звездочкой строке часто рассматриваются как идущие с [2], который следует за ним, а не с предшествующим ему «16 разделить на». То есть умножение, обозначенное помещением в круглые скобки (или квадратные скобки и т. д.), часто рассматривается (специалистами) как «более сильное», чем «обычное» умножение, которое обозначается каким-либо символом, например как «×».
д.), часто рассматривается (специалистами) как «более сильное», чем «обычное» умножение, которое обозначается каким-либо символом, например как «×».
Набор всей задачи в графическом калькуляторе подтверждает существование этой иерархии, по крайней мере, в некоторых программах:
Обратите внимание, что различные пакеты программ будут обрабатывать это выражение по-разному ; даже разные модели графических калькуляторов Texas Instruments будут обрабатывать это выражение по-разному. Среди математиков общее мнение состоит в том, что «умножение путем сопоставления» (то есть умножение путем простого размещения элементов рядом друг с другом, а не с использованием знака «×») указывает на то, что сопоставленные значения должны быть умножены вместе перед обработкой других операций. Но не все программы запрограммированы таким образом, и иногда учителя смотрят на вещи по-разному. Если сомневаетесь, спрашивайте! И, печатая что-то боком, будьте очень осторожны со скобками и ясным смыслом, чтобы избежать именно этой двусмысленности.
(Пожалуйста, не присылайте мне электронное письмо с просьбой или предложением окончательного вердикта по этому вопросу. Насколько мне известно, такого окончательного вердикта не существует. Если вы скажете мне делать что-то по-вашему, , а не решит проблема!) (Для примера того, какие электронные письма я получаю по этому поводу, перейдите на следующую страницу, которая также содержит больше примеров дробной формы.)
URL: https://www.purplemath .com/modules/orderops2.htm
Страница 1Страница 3
Математика третьего класса — обучение и практика математики для 3-го класса
[«`#», «Моя учетная запись»]Прочная основа математических навыков учащихся способствует переходу к умножению и делению, переходу от конкретных процедур к абстрактному мышлению и автоматизму.
Pre-kindergartenKindergartenКласс 1Класс 2Класс 3Класс 4Класс 5
Pre-kindergartenKindergartenКласс 1Класс 2Класс 3Класс 4Класс 5 факторов
Учащиеся используют свои знания о сложении для определения факторов (сколько групп, сколько объектов в каждой группе), а также для составления и решения простых уравнений умножения. Они работают с группами из 2-5 одинаковых предметов, начиная с моделей одинаковых конкретных предметов, например связок бананов и пальцев на руке. По мере продвижения учащихся они работают с более абстрактными объектами (одинаковыми бусинами) и объектами в массиве.
Они работают с группами из 2-5 одинаковых предметов, начиная с моделей одинаковых конкретных предметов, например связок бананов и пальцев на руке. По мере продвижения учащихся они работают с более абстрактными объектами (одинаковыми бусинами) и объектами в массиве.
Решить и переписать повторяющиеся уравнения сложения
Учащиеся составляют и решают повторяющееся уравнение сложения на основе модели объектов реального мира в равных группах. Студенты учатся писать повторяющееся сложение как утверждение «X групп из X составляют X».
Завершите утверждения, описывающие равные группы и их суммы
Учащиеся завершают утверждения «X групп из X составляют X» на основе моделей и сопоставляют эти утверждения с повторяющимися уравнениями сложения
Используйте знак умножения
Учащиеся учатся использовать умножение и равенство знаки для замены утверждения «X групп из X составляют X» уравнением. Они определяют, соответствует ли выражение умножения модели объектов реального мира 9. 0007
0007
Выражение уравнений умножения на основе модели
Учащиеся определяют, какое уравнение умножения соответствует модели объектов реального мира
Решают и выражают уравнения умножения на основе модели объекты мира. Затем учащиеся выражают повторяющееся уравнение сложения в виде оператора умножения и уравнения умножения
Составьте и решите уравнения умножения на основе модели
Учащиеся создают модель объектов реального мира на основе заданного уравнения умножения
Умножают на основе модели объектов в строках
Учащиеся составляют и решают уравнения умножения на основе объектов в строках
Составляют и решают уравнения умножения на основе массив
Учащиеся определяют, какое уравнение умножения соответствует массиву объектов реального мира. Они представляют один массив как повторяющееся сложение, оператор умножения и уравнение умножения
Составление выражений и уравнений на основе модели
Учащиеся выполняют многократное сложение, оператор умножения или уравнение умножения на основе модели
Тема B: Деление как задача с неизвестным фактором
Учащиеся работают с моделями реального мира объектов для решения проблем равного распределения. Их знакомят с символом деления. Они используют метод «торговли» для создания групп заданного размера. На основе этих моделей они отвечают на вопросы: «Сколько групп?» и «Сколько в каждой группе?» Они составляют и решают уравнения деления.
Их знакомят с символом деления. Они используют метод «торговли» для создания групп заданного размера. На основе этих моделей они отвечают на вопросы: «Сколько групп?» и «Сколько в каждой группе?» Они составляют и решают уравнения деления.
Используйте символ деления
Учащиеся определяют количество групп и количество объектов в каждой группе в задачах на равный раздел на основе модели. Представляйте такие задачи в виде уравнения, используя символ деления. Определите символ деления
Составьте и решите уравнения деления на основе модели
Учащиеся решают для любого из трех чисел в задачах на равные доли, основанных на модели. Они пишут и решают уравнения на основе моделей. Они определяют, соответствует ли данная модель заданному уравнению
Смоделируйте уравнения деления и решите
Учащиеся определяют уравнение, которое соответствует заданной модели. Они создают модель на основе выражения деления и решают. Они решают любое из трех чисел в уравнении деления на основе модели
Разделяют предметы на группы
Учащиеся распределяют предметы на равные группы заданного размера, а затем определяют количество групп
Составляют уравнения деления
Учащиеся составляют деление уравнение на основе модели. Они решают любое из трех чисел в уравнении деления с моделью и без нее
Они решают любое из трех чисел в уравнении деления с моделью и без нее
Решение задач на деление
Учащиеся решают задачи на деление
Тема C: Анализ массивов для умножения с использованием единиц 2 и 3
Учащиеся углубляют и расширяют свое понимание умножения на 2 и 3 с помощью новых способов визуализации этой концепции. Тема посвящена подсчету пропусков и массивам, которые помогают учащимся увидеть закономерности при умножении и решении уравнений. Студенты также обнаруживают и изучают коммутативные и дистрибутивные свойства умножения.
Пропустить счет на 2 (Уровень 1)
Попрактиковаться в счете на 2 секунды. Вставьте пропущенные числа в числовую строку при пропуске счета от 2 до 10
Пропустите счет на 3 (Уровень 1)
Попрактикуйтесь в счете с пропуском на 3 секунды. Вставьте пропущенные числа в числовую строку при пропуске счета от 3 до 15
Умножение на 2 с моделью-массивом и без нее (уровень 1)
Потренируйтесь выполнять умножение фактов с произведениями, кратными 2, от 2 до 10. Это упражнение укрепляет идею о том, что пропуск счета на 2 также является умножением на 9.0007
Это упражнение укрепляет идею о том, что пропуск счета на 2 также является умножением на 9.0007
Умножение на 3 с моделью-матрицей и без нее (Уровень 1)
Попрактикуйтесь в умножении фактов с произведениями, кратными 3, от 3 до 15. Это упражнение укрепляет идею о том, что пропуск счета на 3 также является умножением
Умножение на 2 для составления схемы уравнений (уровень 1)
Попрактиковаться в умножении фактов с произведениями, умноженными на 2 от 2 до 10
Умножить на 3, чтобы составить схему уравнений (уровень 1)
Попрактикуйтесь в выполнении фактов умножения с произведениями, кратными 3 от 3 до 15
Пометьте массивы уравнениями, чтобы показать свойство перестановочности умножения на 2
Попрактикуйтесь в визуализации умножения с использованием массивов. Это упражнение показывает учащимся свойство перестановочности умножения: изменение местами множителей приводит к тому же результату.
Пометьте массивы уравнениями, чтобы показать свойство перестановочности умножения на 3.

Потренируйтесь визуализировать умножение с помощью массивов. Это упражнение показывает учащимся свойство перестановочности умножения: изменение местами множителей приводит к тому же произведению
Завершите уравнения, чтобы показать переместительное свойство умножения на 2 (Уровень 1)
Потренируйтесь в переместительном свойстве умножения. В этом упражнении представлены два предложения об умножении, в которых множители перевернуты, что приводит к одному и тому же произведению.
Завершите уравнения, чтобы показать переместительное свойство умножения на 3 (Уровень 1)
Потренируйтесь в переместительном свойстве умножения. В этом упражнении представлены два предложения об умножении, в которых множители перевернуты, что приводит к одному и тому же произведению
Решите уравнения умножения x2 (Уровень 1, часть 1)
Поиграйте в игру, практикуя факты умножения, включающие числа 1-5, умноженные на 2
Решите уравнения умножения x3 (Уровень 1, часть 1)
Играйте в игру, практикуясь факты умножения, включающие числа 1-5, умноженные на 3
Решите уравнения умножения x2 (уровень 1, часть 2)
Сыграйте в игру, практикуя факты умножения, включающие числа 1-5, умноженные на 2
Решите уравнения умножения x3 (Уровень 1, Часть 2)
Сыграйте в игру, практикуя факты умножения, включающие числа 1-5, умноженные на 3
Пропустить счет на 2 (Уровень 2)
Попрактиковаться в счете на 2 секунды. Заполните пропущенные числа в числовой строке при счете с пропуском от 2 до 20. Заполните пропущенные числа в числовой строке при пропуске счета от 3 до 30
Заполните пропущенные числа в числовой строке при счете с пропуском от 2 до 20. Заполните пропущенные числа в числовой строке при пропуске счета от 3 до 30
Умножение на 2 с моделью массива и без нее (уровень 2)
Используйте массивы, чтобы начать с 10, и выполните умножение x2 до 20. Это упражнение показывает учащимся, как умножение на 2 связано с повторяющимся сложением
Умножение на 3 с моделью массива и без нее (уровень 2)
Использование массивов чтобы начать с 15 и выполнить факты умножения x3 до 30. Это упражнение показывает учащимся, как умножение на 3 связано с повторяющимся сложением
Умножьте на 2, чтобы завершить образец уравнений (уровень 2)
Практикуйте факты умножения 2x из От 1 до 10. Это задание дает один факт умножения и просит учащихся последовательно найти следующий, что можно сделать, прибавив 2 к предыдущему произведению 9.0007
Умножьте на 3, чтобы составить схему уравнений (уровень 2)
Потренируйтесь в трехкратном умножении фактов от 1 до 10. Это упражнение дает один факт умножения и просит учащихся найти следующий последовательно, что можно сделать, сложив 3 к предыдущему произведению
Это упражнение дает один факт умножения и просит учащихся найти следующий последовательно, что можно сделать, сложив 3 к предыдущему произведению
Завершите уравнения, чтобы показать переместительное свойство умножения на 2 (уровень 2)
Попрактикуйтесь в использовании переместительного свойства умножения, чтобы заполнить недостающие множители или произведения в предложениях умножения
Завершите уравнения, чтобы показать переместительное свойство умножения на 3 (уровень 2)
Попрактикуйтесь в использовании переместительного свойства умножения, чтобы заполнить недостающие множители или произведения в предложениях умножения
Пометьте массивы уравнениями, чтобы показать распределительное свойство умножения на 2 (Часть 1)
Попрактикуйтесь в обозначении количества строк в массиве, чтобы познакомить с идеей дистрибутивного свойства умножения. В этом упражнении учащийся определяет количество строк до и после добавления дополнительных строк в массив
Пометьте массивы уравнениями, чтобы показать распределительное свойство умножения на 2 (часть 2)
Узнайте, как распределительное свойство применяется к умножению. В этом упражнении учащиеся будут маркировать массивы уравнениями, чтобы показать распределительное свойство умножения на 2
В этом упражнении учащиеся будут маркировать массивы уравнениями, чтобы показать распределительное свойство умножения на 2
Пометить массивы уравнениями, чтобы показать распределительное свойство умножения на 3 (Часть 1)
Попрактиковаться в маркировке количества строк в массиве, чтобы ввести понятие распределительного свойства умножения. В этом упражнении учащийся определяет количество строк до и после добавления дополнительных строк в массив
Пометьте массивы уравнениями, чтобы показать распределительное свойство умножения на 2 (часть 3)
Попрактикуйтесь в маркировке массивов уравнениями, затем разбейте массив на две части и найдите решения всех трех уравнений. Это задание показывает учащимся, как работает распределительное свойство умножения
Пометьте массивы уравнениями, чтобы продемонстрировать распределительное свойство умножения на 3 (Часть 2)
Попрактикуйтесь в маркировке массивов уравнениями, затем разбейте массив на две части и найдите решения для все три уравнения. Это задание показывает учащимся, как работает распределительное свойство умножения
Это задание показывает учащимся, как работает распределительное свойство умножения
Решите уравнения умножения x2 (Уровень 2, часть 1)
Поиграйте в игру, практикуя факты умножения, включающие числа 1-10, умноженные на 2
Решите уравнения умножения x3 (Уровень 2, часть 1)
Поиграйте в практику факты умножения чисел от 1 до 10, умноженных на 3
Решите уравнения умножения x2 (уровень 2, часть 2)
Сыграйте в игру, практикуя факты умножения чисел от 1 до 10, умноженных на 2
Решите уравнения умножения x3 (Уровень 2, Часть 2)
Играйте в игру, практикуя умножение чисел 1-10, умноженных на 3
Тема D: Деление на 2 и на 3
Учащиеся используют конкретные и абстрактные объекты понять понятие деления. Затем они связывают деление с умножением, чтобы помочь развить понимание и беглость фактов. Учащиеся начинают с решения простых уравнений деления (частное до 5), а затем переходят к решению уравнений с частным до 10.
Равномерно распределите объекты для создания диаграммы ленты (Сколько в каждой группе?)
Узнайте, как равномерно распределить объекты для создания диаграммы ленты. Это задание требует, чтобы учащиеся понимали количество групп, количество объектов в каждой группе и общее количество объектов.
Представьте ленточную диаграмму в виде уравнения деления (Сколько в каждой группе?) ситуацию из реальной жизни и составить из нее уравнение деления. Это задание требует, чтобы учащиеся сначала идентифицировали части ленточной диаграммы, прежде чем писать уравнение деления 9.0007
Равномерно распределите объекты, чтобы создать ленточную диаграмму (Сколько групп?)
Попрактикуйтесь в равномерном распределении объектов, чтобы создать ленточную диаграмму. Это задание требует, чтобы учащиеся понимали количество групп, количество объектов в каждой группе и общее количество объектов.
Представьте ленточную диаграмму в виде уравнения деления (Сколько групп?) уравнение деления.
 Это задание требует, чтобы учащиеся создали ленточную диаграмму, расположили ее части, а затем написали уравнение деления 9.0007
Это задание требует, чтобы учащиеся создали ленточную диаграмму, расположили ее части, а затем написали уравнение деления 9.0007Завершите уравнения, связывающие умножение с делением (Часть 1)
Узнайте, как связаны деление и умножение. Это задание требует, чтобы учащиеся завершили уравнения умножения и деления, чтобы увидеть, как связаны эти две операции.
Заполните уравнения, чтобы связать умножение с делением (Часть 2)
Узнайте, что связанные факты умножения и деления используют одни и те же числа. Это задание требует, чтобы учащиеся сначала выполнили уравнения умножения и деления, противоположные друг другу, а затем нашли одинаковые числа в обоих уравнениях 9.0007
Сопоставьте факт деления с соответствующим фактом умножения
Узнайте, как связаны умножение и деление. В этом упражнении учащимся дается уравнение деления и предлагается найти связанное уравнение умножения
Решить уравнения деления, используя связанный факт умножения
Узнайте, как решать уравнения деления, используя связанный факт умножения. Это задание показывает учащимся, как деление на 2 связано с умножением на 2
Это задание показывает учащимся, как деление на 2 связано с умножением на 2
Решение уравнений на деление с делителем 2 (Уровень 1)
Попрактикуйтесь в решении уравнения на деление с делителем 2. В этом упражнении учащимся дается подсказка о том, как уравнение деления связано с умножением, чтобы помочь им решить уравнения
Решение уравнений на деление с делителем 3 (Уровень 1)
Попрактикуйтесь в решении уравнения на деление с делителем 3. В этом упражнении учащимся дается подсказка о том, как уравнение деления связано с умножением, чтобы помочь им решить уравнения
Решить уравнения на деление с делителем 2 или 3
Попрактиковаться в решении уравнения на деление с делителем 2 и 3. В этом упражнении учащимся дается подсказка о том, как уравнение деления связано с умножением, чтобы помочь им решить уравнения
Решить уравнения на деление с делителем 2 (Уровень 2)
Попрактиковаться в решении уравнения на деление с делителем 2. В этом упражнении учащимся не даются подсказки
В этом упражнении учащимся не даются подсказки
Решить уравнение на деление с делителем 2 (Уровень 3)
Попрактикуйтесь в решении более сложных уравнений на деление с делителями 2. В этом упражнении учащиеся не получают никаких подсказок
Решите уравнения на деление с делителем 3 (Уровень 2)
Потренируйтесь решать уравнения на деление с делителями 3. В В этом упражнении учащимся не даются подсказки
Решение уравнений на деление с делителем 3 (Уровень 3)
Практика решения более сложных уравнений на деление с делителем 3. В этом упражнении учащимся не даются подсказки
Тема E: Умножение и деление на 4
Опираясь на предыдущие знания об умножении и делении, учащиеся применяют свое понимание к фактам, используя 4 как произведение или делитель. Они работают со знакомыми манипуляторами и развитием навыков, чтобы развить понимание и беглость речи.
Пропустить счет на 4
Попрактиковаться в счете на 4 секунды. Вставьте пропущенные числа в числовой строке при пропуске счета от 4 до 40
Вставьте пропущенные числа в числовой строке при пропуске счета от 4 до 40
Умножение на 4 с моделью массива и без нее
Потренируйтесь умножать на 4, используя модель массива. Это задание показывает учащимся дополнительную группу из 4 плиток, а затем запрашивает следующее умножение на 4 факта
Умножьте на 4, чтобы завершить шаблон уравнений
Узнайте, как использовать один факт умножения, чтобы найти следующий в шаблоне. В этом упражнении учащиеся будут умножать на 4, используя свои знания о счете с пропуском на 4
Решать уравнения умножения x4
Играть в игру, практикуя факты умножения, включающие числа 1-10, умноженные на 4
Представление ленточной диаграммы в виде уравнения умножения (Уровень 1)
Узнайте, как представить ленточную диаграмму в виде уравнения умножения. Это задание требует, чтобы учащиеся обозначили части ленточной диаграммы, а затем написали уравнение умножения
Представьте ленточную диаграмму в виде уравнения умножения (уровень 2)
Потренируйтесь составлять предложение об умножении, чтобы оно соответствовало ленточной диаграмме. В этом упражнении учащиеся работают с фактами умножения x4
В этом упражнении учащиеся работают с фактами умножения x4
Пометьте ленточную диаграмму, чтобы представить уравнение умножения.
Потренируйтесь маркировать ленточную диаграмму, чтобы она соответствовала уравнению умножения. В этом упражнении учащиеся перетаскивают части предложения умножения в соответствующие части ленточной диаграммы
Определяют множители и произведение в уравнении умножения
Попрактикуются в определении множителей и произведения в умножении предложения. В этом упражнении учащиеся перетаскивают правильные термины в соответствующие части предложения умножения 9.0007
Пометьте массивы уравнениями, чтобы показать свойство перестановочности умножения (уровень 1)
Потренируйтесь писать два предложения об умножении на основе одного массива, используя факты умножения x4. Массив переворачивается после того, как учащиеся напишут первое предложение, чтобы показать, как переместительное свойство умножения
Пометьте массивы уравнениями, чтобы показать переместительное свойство умножения (уровень 2)
Попрактикуйтесь в маркировке ленточных диаграмм, чтобы продемонстрировать переместительное свойство умножения, используя Факты умножения х4. В этом упражнении учащиеся помечают две ленточные диаграммы, показывающие, как изменение порядка факторов дает один и тот же продукт
В этом упражнении учащиеся помечают две ленточные диаграммы, показывающие, как изменение порядка факторов дает один и тот же продукт
Пометьте ленточные диаграммы уравнениями, чтобы показать переместительное свойство умножения
Попрактикуйтесь в маркировке ленточных диаграмм и соответствующих уравнений умножения, чтобы продемонстрировать переместительное свойство умножения, используя факты умножения x4
Решите уравнения умножения на основе переместительного свойства уравнения умножения, основанные на свойстве коммутативности с использованием фактов умножения x4
Решение текстовых задач с использованием ленточных диаграмм и уравнений умножения
Попрактикуйтесь в решении текстовых задач с использованием ленточных диаграмм и уравнений на умножение с использованием фактов умножения x4
Решите уравнения на деление, используя связанный факт умножения
Узнайте, как деление на 4 связано с умножением на 4. В этом упражнении учащимся дается ключ к тому, как решение связано с фактом умножения, который они уже знают
Решите уравнения деления с делителем 4 (Уровень 1)
Потренируйтесь решать уравнения деления с делителем 4
Решение уравнений деления с делителем 4 (Уровень 2)
Практика решения уравнений деления с делителем 4
Тема F: Умножение и деление на 5
Опираясь на предыдущие знания об умножении и делении, учащиеся применяют свои знания к фактам, используя 5 как произведение или делитель и 10 как произведение. Они также развивают понимание распределительного свойства умножения и деления. Учащиеся строят связи между уравнениями, массивами, ленточными диаграммами и текстовыми задачами.
Они также развивают понимание распределительного свойства умножения и деления. Учащиеся строят связи между уравнениями, массивами, ленточными диаграммами и текстовыми задачами.
Пропустить счет на 5
Попрактиковаться в счете на 5 секунд. Вставьте пропущенные числа в числовую строку при пропуске счета от 5 до 50
Умножение на 5 с моделью-матрицей и без нее
Потренируйтесь умножать на 5, используя модель-матрицу. Это упражнение показывает учащимся дополнительную группу из 5 плиток, а затем предлагает следующее умножение на 5 фактов
Умножьте на 5, чтобы завершить шаблон уравнений
Узнайте, как использовать один факт умножения, чтобы найти следующий в шаблоне. В этом упражнении учащиеся будут умножать на 5, используя свои знания о счете с пропусками на 5 9.0007
Решите уравнения умножения x5
Сыграйте в игру, практикуя факты умножения, включающие числа 1-10, умноженные на 5
Решите уравнения деления, используя соответствующий факт умножения
Узнайте, как деление на 5 связано с умножением на 5. В В этом упражнении учащиеся получают представление о том, как решение связано с фактом умножения, который они уже знают.
В В этом упражнении учащиеся получают представление о том, как решение связано с фактом умножения, который они уже знают.
Решение уравнений на деление с делителем 5 (Уровень 1)
Практика решения уравнений на деление с делителем 5
Решение уравнений деления с делителем 5 (уровень 2)
Потренируйтесь решать уравнения деления с делителем 5
Пометьте массивы уравнениями, чтобы показать распределительное свойство умножения
Потренируйтесь решать уравнения умножения, используя разбиение на части и распределение стратегия. В этом упражнении учащиеся пометят два меньших массива уравнениями умножения, чтобы найти произведение больших чисел
Завершить выражения, основанные на распределительном свойстве умножения
Попрактикуйтесь в использовании стратегии разделения и распределения, чтобы найти выражение умножения, эквивалентное сумме двух выражений умножения
Составление уравнения деления на основе массива
Узнайте, как использовать массив с 4 или 5 строками для записи уравнение деления
Составление уравнения деления на основе массива, чтобы показать распределительное свойство деления
Узнайте, как составить уравнение деления на основе массива, чтобы показать распределительное свойство деления
Решите уравнение деления на основе массива, используя распределительное свойство деления.

Потренируйтесь решать уравнения деления, используя стратегию разделения и распределения. В этом упражнении учащиеся пометят два меньших массива уравнениями деления, чтобы найти частное больших чисел. сумма двух выражений деления
Пропустить счет на 10
Попрактиковаться в счете на 10 секунд. Вставьте пропущенные числа в числовой строке при пропуске счета от 10 до 100
Умножьте на 10, чтобы завершить набор уравнений (Уровень 1)
Узнайте, как умножить на 10, чтобы завершить набор уравнений
Умножить на 10 составить набор уравнений (уровень 2)
Попрактиковаться в умножении на 10, чтобы составить набор уравнений
Решить уравнения умножения x10
Сыграйте в игру, попрактикуйтесь в умножении чисел от 1 до 10, умноженных на 10
Решите задачи со словами, используя диаграммы с лентами и уравнения на деление (Уровень 1)
Узнайте, как использовать диаграмму с лентами и уравнение с делением для решения задач со словами . В этом упражнении учащимся даются подсказки, которые помогут им сначала обозначить ленточную диаграмму, прежде чем заполнять уравнение деления
В этом упражнении учащимся даются подсказки, которые помогут им сначала обозначить ленточную диаграмму, прежде чем заполнять уравнение деления
Решать текстовые задачи, используя ленточные диаграммы и уравнения деления (уровень 2)
Узнайте, как использовать ленточную диаграмму и уравнение деления, чтобы решить словесную задачу. В этом упражнении учащимся даются подсказки, которые помогут им сначала обозначить ленточную диаграмму, прежде чем заполнять уравнение деления 9.0007
МОДУЛЬ 2. Значение места и решение задач с использованием единиц измерения
Тема A: Измерение веса и объема жидкости в метрических единицах
Учащиеся используют весы и чашечные весы с гирями для определения массы предметов. Они учатся читать шкалу между помеченными приращениями и складывать и вычитать измерения массы для решения задач. Чтобы научиться измерять емкость, учащиеся наливают жидкость в промаркированные емкости. Они изучают соотношение между килограммами и граммами и между литрами и миллилитрами.
Измерение массы объектов в килограммах с помощью весов
Узнайте, как найти массу в килограммах. Положите различных животных на весы и прочтите шкалу весов, чтобы найти их массу.
Измерьте массу предметов в килограммах с помощью чашечных весов
Используйте чашечные весы, чтобы найти массу различных животных. Животное находится на одной чашке весов. Добавьте грузы массой 1 кг на другую чашу, пока весы не выровняются. Введите общую массу животного
Измерьте массу предметов в граммах с помощью чашечных весов
Узнайте соотношение между килограммами и граммами. Найдите массу животного с помощью чашечных весов, используя массы с шагом 100 г и 10 г.
Сравните граммы и килограммы
Учащиеся сравнивают граммы и килограммы, используя чашечные весы. Они выбирают символ неравенства, чтобы сравнить измерения в кг с измерениями в г
Учебное пособие: перетащите шнурок, чтобы сопоставить предметы
Узнайте, как сопоставить два предмета, используя шнурки для соединения карточек
Сопоставьте расчетную массу предметов в граммах и килограммах
Оцените массу фруктов, сопоставив соответствующее значение и единицы измерения. Выберите правильное значение для одного фрукта из вариантов. Затем сопоставьте три изображения различных количеств одного фрукта с соответствующими значениями массы.
Выберите правильное значение для одного фрукта из вариантов. Затем сопоставьте три изображения различных количеств одного фрукта с соответствующими значениями массы.
Определите измерения массы на шкале, помеченной только с шагом 10
. Считайте значение массы с точностью до грамма на с шагом 10. Обозначенные приращения состоят из 2 или 3 цифр
Сложите или вычтите, чтобы сравнить или найти общую массу объектов, измеренную на шкале
Найдите сумму или разницу между двумя измеренными массами. Массы измеряются либо с точностью до грамма на шкале с шагом 10, либо на чашечных весах с соответствующими грузами, размещенными для балансировки
Учебное пособие: нажмите на выделенные слова, чтобы получить доступ к определению
Узнайте, как щелкнуть выделенное слово, чтобы увидеть определение этого слова
Визуально определить, какой из двух объектов имеет большую вместимость
Выберите контейнер с большей вместимостью. Контейнеры различаются по высоте, ширине и форме
Измерение вместимости с использованием нестандартных единиц измерения и литров
Наполните два больших контейнера кувшином. Определите, какой из больших контейнеров имеет большую вместимость. Затем узнайте о стандартной единице вместимости в литрах
Определите, какой из больших контейнеров имеет большую вместимость. Затем узнайте о стандартной единице вместимости в литрах
Измерьте вместимость в литрах
Используйте градуированную тару для измерения вместимости меньших емкостей. Перелейте жидкость из меньшего контейнера в больший и считайте показания вместимости
Измерьте вместимость в миллилитрах
Узнайте соотношение между литрами и миллилитрами. Используйте градуированную тару для измерения вместимости меньших емкостей с шагом 100 мл
Узнайте о соотношении между литрами и миллилитрами и сравните две единицы измерения
Узнайте, сколько миллилитров составляет литр, и углубите знания о том, сколько каждая единица измерения представляет
Сравните единицы измерения в литрах и миллиметрах, чтобы определить, какая из них больше или равна ли они
Сравните единицы измерения в литрах и миллиметрах, чтобы определить, какая из них больше. Затем используйте символы «больше», «меньше» или «равно», чтобы сравнить количество литров и миллилитров
Измерение вместимости в миллилитрах
Сопоставьте контейнеры с соответствующими измерениями и единицами вместимости
Тема B: Округление до ближайших десятков и сотен
Используя числовую линейку для обеспечения контекста, учащиеся сначала определяют среднюю точку между двумя округленными числами. Затем они переходят к округлению, используя числовую прямую и среднюю точку. Наконец, учащиеся округляют 2- и 3-значные числа до любого заданного разряда.
Затем они переходят к округлению, используя числовую прямую и среднюю точку. Наконец, учащиеся округляют 2- и 3-значные числа до любого заданного разряда.
Определение чисел в разряде десятков, сотен или тысяч
Нажимайте на правильное значение разряда данного числа
Определяйте соседние десятки заданного числа на числовой линии
Сыграйте в игру, в которой вы нажимаете на соседние десятки определенного числа на числовой линии
Откройте для себя концепцию округления
В контексте рецепта узнать, является ли количество муки достаточно близким, не будучи точным. Изучите концепцию округления
Округлите до ближайших десяти с помощью числовой прямой и узнайте о символе приближения
Округление числа до ближайших десяти, определяя, какая десятка ближе всего к заданному числу. Учащиеся также знакомятся с символом приближения
Используйте символ приближения при округлении до ближайших десяти с использованием числовой прямой для справки
Сыграйте в игру, в которой вы округляете до ближайших десяти на числовой прямой и используете символ приближения ближайшую десятку и выучить язык «округлить в большую сторону» или «округлить в меньшую сторону».
Попрактикуйтесь в округлении до ближайших десяти с числовой линейкой для справки и выучите язык «округлить в большую сторону» и «округлить в меньшую сторону».
Округлите до ближайших десяти, используя язык «округлить в большую сторону» или «округлить в меньшую сторону».
Потренируйтесь округлять до ближайших десяти с помощью числовой линейки для справки и используйте выражения «округлять в большую сторону» и «округлять в меньшую сторону».
Изучите правило округления чисел, которые находятся ровно посередине двух десятков
Учащиеся изучают правило округления чисел, которые находятся ровно посередине двух десятков, и практикуются в округлении этих чисел
Округляют заданное число до ближайших десяти (Часть 1)
Попрактикуйтесь в округлении чисел до ближайших десяти без числового ряда
Округлите заданное число до ближайших десяти, используя правило округления
Учащиеся изучают правило округления в большую или меньшую сторону. Затем они тренируются в использовании правила округления в большую или меньшую сторону до ближайших десятков
Затем они тренируются в использовании правила округления в большую или меньшую сторону до ближайших десятков
Округляют заданное число до ближайших десятков (Часть 2)
Сыграют в игру, чтобы попрактиковаться в округлении до ближайших десятков
Определяют соседние сотни числа данное число в числовой строке
Сыграйте в игру, в которой вы нажимаете на соседние сотни определенного числа на числовой строке
Определяете соседние сотни данного числа и округляете его до ближайшей сотни
На более подробной числовой строке определите соседние сотни заданное число и округлить до ближайшей сотни. Отметьте, было ли число округлено в большую или меньшую сторону
Изучите правило округления чисел, которые находятся ровно посередине двух сотен
Учащиеся изучают правило округления чисел, которые находятся ровно посередине двухсот, и практикуются в округлении этих чисел
Определите, округляется ли заданное число вверх или вниз до ближайшей сотни
Сыграйте в игру, чтобы попрактиковаться в округлении до ближайшей сотни
Округлите заданное число до ближайшей сотни, используя правило округления
Учащиеся изучают правило округления вверх или вниз. Затем они тренируются в использовании правила округления в большую или меньшую сторону до ближайшей сотни
Затем они тренируются в использовании правила округления в большую или меньшую сторону до ближайшей сотни
Округляют заданное число в большую или меньшую сторону до ближайшей сотни
Играют в игру, чтобы попрактиковаться в округлении до ближайшей сотни
Округление заданного числа в большую или меньшую сторону до ближайших десятков и сотен
Сыграйте в игру, чтобы попрактиковаться в округлении до ближайших десяти и сотен
Округление заданного числа в большую или меньшую сторону до ближайших десяти или сотен (Уровень 1)
Сыграйте в игру, чтобы попрактиковаться в округлении до ближайших десяти или сотен
Округлите заданное число вверх или вниз до ближайших десяти или сотен (Уровень 2)
Сыграйте в игру, в которой вы округляете высоту или длину различных объектов реального мира до ближайшие десять или сто
Тема C: Сложение двух- и трехзначных чисел с использованием стандартного алгоритма
Учащиеся повторяют стандартный алгоритм сложения с перегруппировкой, а затем используют его для решения текстовых задач, связанных с измерениями. По мере продвижения они получают меньше подсказок для выполнения стандартного алгоритма.
По мере продвижения они получают меньше подсказок для выполнения стандартного алгоритма.
Сложение двузначных чисел по стандартному алгоритму с перегруппировкой
Практика сложения двух двузначных чисел с перегруппировкой. Сначала даются подсказки о том, как завершить сложение в виде столбца. Затем даются дополнительные задачи без подсказок
Сложение двузначных чисел по стандартному алгоритму с перегруппировкой для решения текстовых задач.
Решение текстовых задач на сложение двух двузначных чисел. Для настройки операции, завершения сложения в формате столбца и выдачи ответа с правильными единицами измерения предусмотрены леса
Сложение трехзначных чисел по стандартному алгоритму с перегруппировкой (уровень 1) с перегруппировкой. Даются подсказки о том, как завершить сложение в форме столбца
Сложение трехзначных чисел по стандартному алгоритму с перегруппировкой (Уровень 2)
Сложение двух трехзначных чисел. Числа автоматически переводятся в столбчатый формат, но подсказки не предоставляются
Сложение трехзначных чисел по стандартному алгоритму с перегруппировкой для решения текстовых задач (Уровень 1)
Решайте текстовые задачи на сложение двух трехзначных чисел. Предусмотрены строительные леса для настройки операции, завершения сложения в формате столбца и предоставления ответа с правильными единицами измерения
Предусмотрены строительные леса для настройки операции, завершения сложения в формате столбца и предоставления ответа с правильными единицами измерения
Сложение трехзначных чисел по стандартному алгоритму с перегруппировкой для решения текстовых задач (уровень 2)
Потренируйтесь складывать два трехзначных числа с перегруппировкой дважды. Даны подсказки о том, как выполнить сложение в форме столбца
Сложить 3-значные числа по стандартному алгоритму с перегруппировкой (Уровень 3)
Сложить два 3-значных числа, требующих перегруппировки дважды. Числа автоматически переводятся в формат столбца, но подсказки не предоставляются
Сложение трехзначных чисел по стандартному алгоритму с перегруппировкой для решения текстовых задач (уровень 3)
Решайте текстовые задачи на сложение двух трехзначных чисел, требующих двукратной перегруппировки. Предусмотрены шаблоны для настройки операции, завершения сложения в формате столбца и предоставления ответа с правильными единицами измерения.
Тема D: Вычитание двух- и трехзначных значений с использованием стандартного алгоритма перегруппировать, а затем использовать его для решения текстовых задач, связанных с измерениями. По мере продвижения они получают меньше подсказок для выполнения стандартного алгоритма.
Вычитание двузначных чисел по стандартному алгоритму с перегруппировкой
Практика вычитания двузначных чисел с перегруппировкой. Во-первых, даются подсказки о том, как выполнить вычитание в виде столбца. Затем даются дополнительные задачи без подсказок
Вычитание двузначных чисел по стандартному алгоритму с перегруппировкой для решения текстовых задач
Решайте текстовые задачи на вычитание двузначных чисел. Для настройки операции, завершения вычитания в формате столбца и предоставления ответа с правильными единицами измерения предусмотрены леса
Вычитание трехзначных чисел по стандартному алгоритму с перегруппировкой (уровень 1)
Потренируйтесь вычитать трехзначные числа с перегруппировкой один раз. Даются подсказки о том, как выполнить вычитание в виде столбца
Даются подсказки о том, как выполнить вычитание в виде столбца
Вычитание трехзначных чисел по стандартному алгоритму с перегруппировкой (уровень 2)
Вычитание трехзначных чисел, требующих однократной перегруппировки. Переведите числа в формат столбца. Подсказки не предусмотрены
Вычитание трехзначных чисел по стандартному алгоритму с перегруппировкой для решения текстовых задач (уровень 1)
Решите текстовые задачи на вычитание трехзначных чисел с однократной перегруппировкой. Для настройки операции, завершения вычитания в формате столбца и предоставления ответа с правильными единицами измерения предусмотрены леса
Вычитание трехзначных чисел по стандартному алгоритму с перегруппировкой (уровень 3) с перегруппировкой дважды. Даются подсказки о том, как выполнить вычитание в виде столбца
Вычитание трехзначных чисел по стандартному алгоритму с перегруппировкой (уровень 4)
Вычитание трехзначных чисел, требующих перегруппировки дважды. Переведите числа в формат столбца. Подсказки не предоставляются
Переведите числа в формат столбца. Подсказки не предоставляются
Вычитание трехзначных чисел по стандартному алгоритму с перегруппировкой для решения текстовых задач (уровень 2)
Решайте текстовые задачи на вычитание трехзначных чисел с двукратной перегруппировкой. Для настройки операции, выполнения вычитания в формате столбца и предоставления ответа с правильными единицами измерения предусмотрены леса.
МОДУЛЬ 3. Умножение и деление с единицами 0, 1, 6-9, и кратные 10
Тема A: Свойства умножения и деления
Учащиеся углубляют свое понимание умножения и деления, знакомясь с таблицей умножения и коммутативным свойством (или «обратными фактами») умножения. Они продолжают строить беглость фактов, добавляя в свой репертуар факторы 6-9.
Проиллюстрируйте свойство коммутативности, пометив массивы и диаграммы с лентами.
Потренируйтесь писать два предложения на умножение на основе одного массива. Массив преобразуется в ленточную диаграмму, чтобы показать то же свойство по-другому
Решите уравнения, иллюстрирующие свойство коммутативности.

Потренируйтесь находить произведение уравнения умножения с факторами в другом порядке. В этом упражнении учащимся сначала дается уравнение умножения, а затем предлагается решить второе уравнение с обратными множителями
Определить недостающие продукты в таблице умножения (множители до 5)
Заполнить таблицу умножения фактами от 1×1 до 5×5
Определение пропущенных произведений в таблице умножения (один коэффициент > 5)
Заполните пропущенные продукты в таблице умножения, где один множитель больше 5
Пропустите счет на 6
Потренируйтесь в счете на 6 от 6 до 30, затем используйте эту информацию, чтобы заполнить пропущенные числа в образце
Определение чисел, кратных 6, в таблице умножения
Потренируйтесь заполнять таблицу умножения числами, кратными 6. В этом упражнении учащиеся будут использовать свойство коммутативности и свои знания о других фактах умножения, чтобы заполнить таблицу
Пропустить счет на 7
Попрактиковаться в счете на 7 от 7 до 35, затем использовать эту информацию для заполнения пропущенных чисел в образце
Определить число, кратное 7, в таблице умножения кратны 7.
 В этом упражнении учащиеся будут использовать свойство коммутативности и свои знания о других фактах умножения, чтобы заполнить таблицу в пропущенных числах в шаблоне
В этом упражнении учащиеся будут использовать свойство коммутативности и свои знания о других фактах умножения, чтобы заполнить таблицу в пропущенных числах в шаблонеОпределить числа, кратные 8, в таблице умножения
Попрактиковаться в заполнении таблицы умножения числами, кратными 8. В этом упражнении учащиеся будут использовать свойство коммутативности и свои знания о других фактах умножения, чтобы заполнить таблицу
Пропустить счет на 9
Попрактикуйтесь в счете на 9 от 9 до 45, затем используйте эту информацию, чтобы заполнить пропущенные числа в образце
Определить числа, кратные 9, в таблице умножения
Попрактиковаться в заполнении таблицы умножения числами, кратными 9. В этом упражнении учащиеся будут использовать свойство коммутативности и свои знания о других фактах умножения, чтобы заполнить таблицу
Определить недостающие произведения в таблице умножения (один множитель > 5)
Попрактиковаться в поиске недостающих произведений в таблице умножения, где один множитель больше 5
Найдите неизвестное, представленное буквой в уравнениях умножения
Узнайте, как найти значение неизвестной буквы в уравнении умножения
Найдите неизвестное, представленное буквой, в уравнениях деления
Узнайте, как найти значение неизвестной буквы в уравнении деления
Сопоставьте уравнение, содержащее неизвестное, с оператором неизвестно заявлению.
 В этом упражнении учащимся дается три варианта и предлагается сопоставить правильное алгебраическое уравнение с утверждением
В этом упражнении учащимся дается три варианта и предлагается сопоставить правильное алгебраическое уравнение с утверждениемРешить неизвестное, представленное буквой, в уравнениях умножения и деления
Потренируйтесь составлять уравнения умножения и деления, чтобы найти неизвестную букву
Составьте и решите уравнение умножения на основе диаграммы с лентой
Потренируйтесь составлять уравнения умножения на основе диаграммы, чтобы найти неизвестную букву
Решите слово умножения задача с использованием диаграммы с лентой
Узнайте, как использовать диаграмму с лентой и уравнение умножения для решения текстовой задачи. В этом упражнении учащимся даются подсказки, которые помогут им сначала обозначить ленточную диаграмму, прежде чем заполнять уравнение умножения 9.0007
Тема B: Умножение и деление с использованием единиц 6 и 7
Учащиеся начинают с знакомых задач, которые переходят к более сложному уровню с более высокими факторами. Они углубляют свое понимание взаимосвязи между умножением и делением, а также беглость чтения фактов.
Они углубляют свое понимание взаимосвязи между умножением и делением, а также беглость чтения фактов.
Пропустить счет на 6
Попрактиковаться в счете на 6 от 6 до 60, а затем использовать эту информацию для заполнения пропущенных чисел в образце
Определить число, кратное 6, в таблице умножения
Попрактикуйтесь в заполнении таблицы умножения числами, кратными 6
Определите произведения 6 в таблице умножения с моделью массива и без нее
Используйте массивы, чтобы начать с 30 и выполнить умножение x6 до 60. Это упражнение показывает учащимся как умножение на 6 связано с повторяющимся сложением
Определите произведения числа 6 в таблице умножения
Потренируйтесь заполнять произведения числа 6 от 1×6 до 10×6. В этом упражнении некоторые факты умножения заполняются, а учащиеся должны заполнить остальные
Решить задачи на деление с делителем 6 на основе его связи с умножением
Попрактиковаться в решении задач на деление с делителем 6 на основе их связи с умножением. В этом упражнении учащимся дается подсказка, как они могут использовать связанный факт умножения, чтобы найти частное
В этом упражнении учащимся дается подсказка, как они могут использовать связанный факт умножения, чтобы найти частное
Решить задачи на деление с делителем 6 (Уровень 1)
Попрактиковаться в решении задач на деление с делителем 6
Решить задачи на деление с делителем 6 (уровень 2)
Попрактиковаться в решении задач на деление с делителями числа 6
Пропустить счет на 7
Потренироваться в счете на 7 от 7 до 70, а затем использовать эту информацию для заполнения пропущенных чисел в образце
Определить кратное 7 в умножении диаграмма
Попрактикуйтесь в заполнении таблицы умножения числами, кратными 7
Определите произведения 7 в таблице умножения с моделью массива и без нее
Используйте массивы, чтобы начать с 35 и выполнить умножение x7 до 70. Это упражнение показывает студенты, как умножение на 7 связано с повторным сложением
Определить произведения 7 в таблице умножения
Потренироваться в заполнении произведений 7 от 1×7 до 10×7. В этом упражнении некоторые факты умножения заполняются, а учащиеся должны заполнить остальные
В этом упражнении некоторые факты умножения заполняются, а учащиеся должны заполнить остальные
Решить задачи на деление с делителем 7 на основе его отношения к умножению
Попрактиковаться в решении задач на деление с делителем 7 на основе их отношения к умножение. В этом упражнении учащимся дается подсказка о том, как они могут использовать связанный факт умножения, чтобы найти частное 9.0007
Решение задач на деление с делителем 7 (Уровень 1)
Попрактиковаться в решении задач на деление с делителем 7
Решение задач на деление с делителем 7 (Уровень 2)
Попрактиковаться в решении задач на деление с делителем 7
Решите уравнения умножения, используя стратегию разбиения и распределения
Научитесь решать уравнения умножения с единицами 7, используя стратегию разбиения и распределения. В этом упражнении учащиеся будут маркировать части ленточной диаграммы, чтобы продемонстрировать распределительное свойство умножения
Найдите неизвестное, представленное буквой, в уравнениях умножения
Потренируйтесь находить значение неизвестной буквы в умножении в уравнении на деление
Решите текстовую задачу, используя ленточную диаграмму и связь между умножением и делением.

Узнайте, как решить текстовую задачу, используя ленточную диаграмму и взаимосвязь между умножением и делением. Вам нужно пометить части ленточной схемы. Используйте соотношение между умножением и делением, чтобы найти переменную 9.0007
Тема C: Умножение и деление с использованием единиц до 8
В дополнение к расширению мастерства учащихся в области умножения и деления, включая 8, они также знакомятся с многошаговыми уравнениями, в которых используются круглые скобки. Используя иллюстрации и пошаговые инструкции, учащиеся узнают, что круглые скобки и порядок операций не влияют на уравнения, связанные только с умножением. Они также продолжают совершенствовать свое мастерство в стратегии разделения и распределения.
Пропустить счет на 8
Попрактикуйтесь в счете на 8 от 8 до 80, затем используйте эту информацию, чтобы заполнить пропущенные числа в образце
Определить число, кратное 8, в таблице умножения
Попрактиковаться в заполнении таблицы умножения числами, кратными 8
Определить произведения 8 в таблице умножения с моделью массива и без нее
Используйте массивы, чтобы начать с 40 и выполнить умножение x8 до 80. Это упражнение показывает учащимся, как умножение на 8 связано с повторным сложением
Это упражнение показывает учащимся, как умножение на 8 связано с повторным сложением
Определение произведений чисел 8 в таблице умножения
Потренируйтесь в заполнении произведений чисел 8 от 1×8 до 10×8. В этом упражнении некоторые факты умножения заполняются, а учащиеся должны заполнить остальные
Решить задачи на деление с делителем 8 на основе его отношения к умножению
Научиться решать задачи на деление с делителем 8 на основе их отношение к умножению. В этом упражнении учащимся дается подсказка о том, как они могут использовать связанный факт умножения, чтобы найти частное 9.0007
Решение задач на деление с делителем 8 (Уровень 1)
Попрактиковаться в решении задач на деление с делителем 8
Решение задач на деление с делителем 8 (Уровень 2)
Попрактиковаться в решении задач на деление с делителем 8
Решение многошаговых уравнений с круглыми скобками (уровень 1)
Узнайте, как решать многошаговые уравнения с круглыми скобками. В этом упражнении учащиеся узнают, что операции внутри скобок всегда выполняются первыми
В этом упражнении учащиеся узнают, что операции внутри скобок всегда выполняются первыми
Сравните похожие многошаговые уравнения со скобками в разных местах
Узнайте, что размещение скобок в многошаговых уравнениях имеет значение. В этом упражнении учащиеся будут сравнивать два уравнения с одинаковыми числами и операциями, в которых скобки стоят в разных местах, и видеть, что решения разные
Решать многошаговые уравнения, включающие скобки (уровень 2)
Практика решения многошаговых уравнений которые включают скобки. Это задание требует от учащихся понимания того, что операции внутри скобок всегда выполняются первыми
Определите правильное решение многошагового уравнения со скобками
Потренируйтесь определять правильное многошаговое уравнение. В этом упражнении учащимся предлагается два варианта ответа и предлагается найти правильный ответ, используя их понимание порядка операций
Распознать влияние скобок на уравнения многошагового умножения (Часть 1)
Узнать, что порядок скобок при умножении уравнения не меняют ответ. В этом упражнении учащиеся решают два уравнения со скобками в разных местах, чтобы доказать, что решения одинаковы
В этом упражнении учащиеся решают два уравнения со скобками в разных местах, чтобы доказать, что решения одинаковы
Распознать влияние скобок на многошаговые уравнения умножения (Часть 2)
Узнать, что порядок скобок в уравнениях умножения не меняет ответ. Дан сценарий из реальной жизни, и учащиеся должны использовать его для решения двух уравнений со скобками в разных местах, чтобы доказать, что решения одинаковы
Перегруппируйте множители со скобками в качестве стратегии для решения многоэтапных уравнений умножения (Часть 1 )
Узнайте, как перегруппировать множители с помощью скобок в качестве стратегии для решения многошаговых уравнений умножения. В этом упражнении учащимся дается уравнение умножения с большими числами, которое они разбивают на множители и перегруппировывают, чтобы решить
Перегруппировка множителей с круглыми скобками как способ решения многошаговых уравнений умножения (Часть 2)
Практика перегруппировки множителей с круглыми скобками как стратегия решения многошаговых уравнений умножения. В этом упражнении учащимся дается уравнение умножения с большими числами, которое они разбивают на множители и перегруппировывают для решения
В этом упражнении учащимся дается уравнение умножения с большими числами, которое они разбивают на множители и перегруппировывают для решения
Решают уравнения умножения, используя стратегию разбиения и распределения (Часть 1)
Научитесь решать уравнения умножения с единицами из 8, используя стратегию разделения и распределения. В этом упражнении учащиеся будут маркировать части ленточной диаграммы, чтобы продемонстрировать распределительное свойство умножения
Решите уравнения умножения, используя стратегию разбиения и распределения (Часть 2)
Научитесь решать уравнения умножения с единицами по 8, используя стратегию разбиения и распределения. В этом упражнении учащиеся будут использовать круглые скобки, чтобы написать два уравнения умножения, а затем решить
Решить уравнения деления, используя стратегию разбиения и распределения (Часть 1)
Научитесь делить, используя стратегию разбиения и распределения и массив. В этом упражнении учащиеся возьмут две части массива, напишут два уравнения деления, а затем решат
Решите уравнения деления, используя стратегию разбиения и распределения (Часть 2)
Попрактикуйтесь в делении, используя стратегию разбиения и распределения, чтобы разделить большое число на 8. В этом упражнении учащиеся используют свойство распределения, чтобы разбить большее число на части на два меньших числа, которые делятся на 8
В этом упражнении учащиеся используют свойство распределения, чтобы разбить большее число на части на два меньших числа, которые делятся на 8
Тема D: Умножение и деление с использованием единиц 9
Учащиеся применяют и расширяют предыдущее понимание, чтобы включить 9 в качестве множителя или делителя. Мы также вводим стратегию специально для умножения на 9.
Пропустить счет до 9
Попрактиковаться в счете до 9 от 9 до 90, а затем использовать эту информацию для заполнения пропущенных чисел в образце
Определить число, кратное 9, в таблице умножения кратные 9
Определить произведения 9 в таблице умножения с моделью массива и без нее
Используйте массивы, чтобы начать с 45 и выполнить умножение x9 до 80. Это упражнение показывает учащимся, как умножить на 9связано с повторным сложением
Определите произведения 9 в таблице умножения
Потренируйтесь заполнять произведения 9 от 1×9 до 10×9. В этом упражнении некоторые факты умножения заполняются, а учащиеся должны заполнить остальные
Решить задачи на деление с делителем 9 на основе его отношения к умножению
Научиться решать задачи на деление с делителем 9 на основе их отношение к умножению. В этом упражнении учащимся дается подсказка о том, как они могут использовать связанный факт умножения, чтобы найти частное 9.0007
В этом упражнении учащимся дается подсказка о том, как они могут использовать связанный факт умножения, чтобы найти частное 9.0007
Решение задач на деление с делителем 9 (Уровень 1)
Попрактиковаться в решении задач на деление с делителем 9
Решение задач на деление с делителем 9 (Уровень 2)
Попрактиковаться в решении задач на деление с делителем 9
Решите уравнения умножения, используя стратегию разбиения и распределения
Научитесь решать уравнения умножения с единицами 9, используя стратегию разбиения и распределения. В этом упражнении учащиеся будут маркировать части ленточной диаграммы, чтобы продемонстрировать распределительное свойство умножения
Решите уравнения на умножение, используя стратегию 9 = 10-1
Научитесь решать задачи на умножение, используя стратегию 9 = 10-1. В этом упражнении учащиеся будут решать уравнения умножения с коэффициентом 9, используя стратегию разделения и распределения с учетом того факта, что 9=10-1
Тема E: Анализ шаблонов и решение задач, включая единицы 0 и 1
Учащиеся углубляются в концепции умножения и деления, работая с 1 и 0. В дополнение к работе с этими числами в качестве множителей, делимых и делителей, учащиеся используют букву для представления неизвестного числа в уравнении и знакомятся с операторами let. относительно таких писем.
В дополнение к работе с этими числами в качестве множителей, делимых и делителей, учащиеся используют букву для представления неизвестного числа в уравнении и знакомятся с операторами let. относительно таких писем.
Составьте предложение с умножением (включая 1x), чтобы представить модель
Узнайте, как написать предложение с умножением на основе модели. В этом упражнении учащиеся определят количество групп, количество в каждой группе и общее число, чтобы написать уравнение умножения
Решить задачи на умножение, в которых 1 используется в качестве множителя (включая 1 x n)
Практика решения умножения задачи, использующие 1 в качестве множителя (включая 1 x n). В этом упражнении учащиеся сделают вывод, что число, умноженное на 1, всегда равно числу 9.0007
Решить задачи на деление, в которых делителем является 1 (включая n/1)
Попрактиковаться в решении задач на деление, в которых делителем является 1 (включая n/1). В этом упражнении учащиеся сделают вывод, что число, деленное на 1, всегда равно числу
Составьте предложение с умножением (включая x1), чтобы представить модель
Попрактикуйтесь в составлении предложения с умножением на основе модели. В этом упражнении учащиеся определят количество групп, количество в каждой группе и общее количество. Они будут использовать эту информацию для составления предложений на умножение
В этом упражнении учащиеся определят количество групп, количество в каждой группе и общее количество. Они будут использовать эту информацию для составления предложений на умножение
Решите задачи на умножение, в которых множителем является 1 (включая n x 1)
Попрактикуйтесь в решении задач на умножение, в которых множителем является 1 (включая n x 1). В этом упражнении учащиеся завершат предложение об умножении n x 1 = n, чтобы закрепить, что число, умноженное на 1, всегда является числом делится само собой. В этом упражнении учащиеся сделают вывод, что ненулевое число, деленное само на себя, всегда равно 1
Решение неизвестных (представленных буквой) задач на умножение и деление, включающих 1
Практика решения задач на умножение и деление для неизвестных. В этом упражнении неизвестное представлено переменной, и одно из чисел в каждом уравнении равно 1
. Составьте предложение с умножением (включая x0), чтобы представить модель
Попрактикуйтесь в составлении предложения с умножением на основе модели. В этом упражнении учащиеся начнут работать с группами, в которых нет предметов
В этом упражнении учащиеся начнут работать с группами, в которых нет предметов
Решить задачи на умножение, в которых 0 используется как множитель (включая n x 0 и 0 x n)
Узнать, что множитель 0 всегда имеет произведение 0
Решить задачи на деление, в которых 1 используется в качестве делимого (включая 0 / n)
Научитесь составлять предложение на умножение на основе модели, в которой группы содержат 0 объектов. Учащиеся узнают, что число, умноженное на 0, всегда равно 0
Решить неизвестное (представленное буквой) в задачах на умножение и деление, включающих 0
Попрактикуйтесь в решении неизвестных, представленных переменной, в задачах на умножение и деление, которые включают 0
Определите, является ли уравнение умножения или деления с неизвестным, представленным буквой, истинным, на основе оператора let
Сыграйте в игру, чтобы повторить умножение и вопросы на деление, которые включают 1 или 0. В этом упражнении учащиеся определят, является ли решение истинным или ложным. Вопросы в этом упражнении включают неизвестные, представленные буквами 9.0007
Вопросы в этом упражнении включают неизвестные, представленные буквами 9.0007
Тема F: Умножение однозначных множителей и множителей, кратных 10
Основываясь на беглости учащихся с однозначными множителями, мы вводим умножение однозначного множителя на кратное десяти. Учащиеся связывают умножение слов (например, 4 x 3 десятка = 12 десятков) с числовыми уравнениями (например, 4 x 30 = 120).
Нахождение отсутствующих продуктов в таблице умножения, в которой 10 является коэффициентом
Практика решения отсутствующих продуктов в таблице умножения, в которой 10 является коэффициентом
Свяжите произведение n десятков с произведением в виде числа n0
Узнайте, как решать умножение с участием десятков, используя базовые знания умножения. Умножьте число на десятки, а затем представьте его как фактическое число, показывая, как умножение на десять связано с простым умножением
Сопоставьте числовые произведения с уравнениями умножения, в которых используются числа и слова (n десятков)
Сыграйте в игру на совпадение умножение однозначного множителя на n десятков с правильным произведением
Использование свойств умножения для упрощения и решения уравнений
Попрактиковаться в поиске недостающего множителя в задаче на умножение, включающей n десятков. В этом упражнении учащиеся разобьют часть, кратную десяти, на n десятков и используют это для решения уравнения. цифра и кратное десяти как множители. В этом упражнении учащимся подсказывают, что конечная цифра в произведении равна 0 9.2)
В этом упражнении учащиеся разобьют часть, кратную десяти, на n десятков и используют это для решения уравнения. цифра и кратное десяти как множители. В этом упражнении учащимся подсказывают, что конечная цифра в произведении равна 0 9.2)
МОДУЛЬ 4. Умножение и площадь
Тема A: Основы понимания области
Учащиеся знакомятся с основами работы с площадью с помощью мозаики. Они учатся использовать квадраты, измерять стороны прямоугольника, пропускать ряды плиток и переставлять плитки, чтобы сформировать другой прямоугольник с той же площадью.
Идентификация двумерных фигур
Практика распознавания двухмерных фигур. В этом упражнении учащиеся будут определять квадраты, прямоугольники, треугольники, ромбы и трапеции
Мозаика двухмерных фигур для сравнения их площадей
Узнайте, как расположить двухмерные фигуры мозаикой для сравнения их площадей. В этом упражнении учащиеся узнают, что объем пространства, занимаемый фигурой, равен площади.
Определить и сравнить площадь путем разбиения на квадраты
Научитесь разбивать фигуру на мозаику, чтобы найти ее площадь. В этом упражнении учащиеся будут использовать плитки, каждая из которых равна одной квадратной единице, чтобы найти площадь всей фигуры. Учащиеся также сравнивают площади двух фигур
Определение фигур заданной площади
Потренируйтесь определять фигуры заданной площади. В этом упражнении учащимся дается несколько фигур разного размера и предлагается найти все фигуры с определенной площадью
Определить площадь путем разбиения на квадратные сантиметры или дюймы
Научиться рисовать квадрат заданного размера и использовать это, чтобы найти площадь фигуры. В этом упражнении учащиеся будут практиковаться в измерении в сантиметрах и дюймах.
Определить площадь прямоугольника, полученного путем перестановки плиток из другого прямоугольника
Узнайте, как определить площадь прямоугольника, полученного путем перестановки плиток из другого прямоугольника. В этом упражнении учащиеся сравнят площади двух фигур и обнаружат, что площади равны. площадь прямоугольника. В этом упражнении учащиеся могут использовать подсчет, чтобы найти площади
В этом упражнении учащиеся сравнят площади двух фигур и обнаружат, что площади равны. площадь прямоугольника. В этом упражнении учащиеся могут использовать подсчет, чтобы найти площади
Тема B: Принципы измерения площади
Опираясь на предыдущий модуль, учащиеся начинают с пропуска плиток в прямоугольнике, чтобы определить его площадь. Затем они переходят к умножению, используя мозаичный прямоугольник и прямоугольник только с помеченными измерениями. Учащиеся переставляют плитки, чтобы определить размеры другого прямоугольника с такой же площадью. Они также находят неизвестную сторону, представленную буквой.
Учебное пособие: нажмите на книгу, чтобы увидеть таблицу умножения
Узнайте, что при нажатии на значок книги открывается таблица умножения
Умножение, чтобы найти площадь прямоугольника, выложенного мозаикой (Уровень 1)
Узнайте, как составить предложение на умножение площади прямоугольника. Используйте плитки, чтобы найти длину и ширину фигуры, а затем напишите предложение умножения, чтобы показать, что площадь прямоугольника является произведением длин сторон
Умножьте, чтобы найти площадь прямоугольника, выложенного плиткой (Уровень 2)
Потренируйтесь находить длины сторон прямоугольника и используйте их для нахождения площади прямоугольника. Это упражнение укрепляет идею о том, что площадь есть произведение длин сторон
Это упражнение укрепляет идею о том, что площадь есть произведение длин сторон
Определить площадь прямоугольника путем умножения длин сторон (Уровень 1)
Попрактиковаться в нахождении площади прямоугольника путем умножения длин сторон. В этом упражнении фигура частично покрыта, поэтому учащиеся должны умножить, чтобы найти площадь
Определить площадь прямоугольника путем умножения длин сторон (Уровень 2)
Попрактиковаться в нахождении площади прямоугольника путем умножения длин сторон. В этом упражнении фигура не делится на плитки, поэтому учащиеся должны умножить, чтобы найти площадь
Определение площади прямоугольника на основе равной площади другого прямоугольника
Потренируйтесь находить площадь прямоугольника на основе равной площади другого прямоугольника. В этом упражнении учащиеся перемещают плитки из одного прямоугольника в другой прямоугольник, чтобы найти его площадь
Определяют длину стороны на основе площади прямоугольника
Узнают, как использовать длину одной стороны прямоугольника и площадь прямоугольник, чтобы найти длину недостающей стороны прямоугольника. В этом упражнении учащиеся узнают, что можно найти длину неизвестной стороны, используя деление 9.0007
В этом упражнении учащиеся узнают, что можно найти длину неизвестной стороны, используя деление 9.0007
Тема C: Арифметические свойства с использованием моделей площадей
Учащиеся углубляются в свое понимание умножения и площади, используя модели площадей прямоугольников. Они сравнивают части с целым, находят недостающие части и манипулируют уравнениями, чтобы продемонстрировать свойства. Упражнения начинаются с использования прямоугольников с линиями сетки, а затем переходят к использованию прямоугольников без них.
Умножьте, чтобы найти площадь, разделив прямоугольник на более мелкие части
Узнайте, как найти площадь прямоугольника, разделив его на более мелкие части. В этом упражнении учащиеся находят площадь двух частей прямоугольника и складывают их вместе, чтобы найти общую площадь
Использование распределительного свойства умножения для нахождения площади прямоугольника, разделенного на более мелкие части
Попрактикуйтесь в использовании распределительного свойства умножения, чтобы найти площадь прямоугольника, разбив его на более мелкие части
Вычитание, чтобы найти площадь прямоугольника покрытая часть прямоугольника
Узнайте, как найти площадь части прямоугольника. В этом упражнении часть прямоугольника покрыта, и учащиеся находят общую площадь, а затем вычитают площадь непокрытой части
В этом упражнении часть прямоугольника покрыта, и учащиеся находят общую площадь, а затем вычитают площадь непокрытой части
Умножьте или вычтите, чтобы найти площади прямоугольников без линий сетки.
Потренируйтесь находить площадь прямоугольника без линий сетки и площади двух частей при его разделении. В этом упражнении учащиеся узнают, что площадь всего прямоугольника равна площади двух частей, когда прямоугольник разделен.
Тема D. Применение площади с использованием длин сторон фигур площадь составной формы, основанная на длинах сторон. В первом они разбивают фигуру на меньшие прямоугольники и складывают эти области вместе. Во втором они «завершают» фигуру, чтобы найти общую площадь, а затем вычитают площадь «недостающей части». Учащиеся начинают с использования фигур с показанными единичными квадратами, а затем переходят к фигурам без них.
Определить площадь составной фигуры, разделив ее на два прямоугольника и сложив площади (Часть 1)
Узнайте, как найти площадь составной фигуры. В этом упражнении учащиеся будут практиковаться в нахождении площадей меньших частей и сложении их, чтобы найти общую площадь составной фигуры
В этом упражнении учащиеся будут практиковаться в нахождении площадей меньших частей и сложении их, чтобы найти общую площадь составной фигуры
Определить площадь составной фигуры, достроив прямоугольник и вычитая площадь недостающей части (Часть 1)
Потренируйтесь находить площадь составной фигуры. В этом упражнении учащиеся будут практиковаться в нахождении площадей меньших частей и сложении их, чтобы найти общую площадь составной фигуры 9.0007
Определение площади составной фигуры путем завершения прямоугольника и вычитания площади недостающей части (Часть 2)
Узнайте, как определить площадь составной фигуры путем нахождения площади всего прямоугольника и вычитания площади недостающей части кусок. В этом упражнении составные фигуры представляют собой большой прямоугольник с вырезанным из середины куском
Определите площадь составной фигуры, разделив ее на два прямоугольника и сложив площади (Часть 2)
Узнайте, как найти площадь составной фигуры, разделив ее на три прямоугольника. В этом упражнении учащиеся находят площадь каждого из трех прямоугольников и находят их сумму, чтобы найти общую площадь
В этом упражнении учащиеся находят площадь каждого из трех прямоугольников и находят их сумму, чтобы найти общую площадь
Определяют площадь составной фигуры, используя стратегии «разбить и сложить» или «дополнить и вычесть»
Потренируйтесь определять, какой метод использовать при нахождении площади составной фигуры. В этом упражнении учащиеся сначала выбирают, какой метод использовать, а затем находят площадь фигуры 9.0007
МОДУЛЬ 5. Дроби как числа на числовой прямой
Тема A: Разделение целого на равные части
Учащиеся создают основу для понимания дробей, работая с равными частями целого. Они используют половинки, трети, четверти, пятые, шестые, седьмые и восьмые фигуры, включая круги, прямоугольники, отрезки и другие формы. Учащиеся разбивают фигуры, обозначают секции, заштриховывают дроби и даже решают текстовые задачи, требующие равного распределения. На протяжении всей темы они не используют обозначение дроби (например, 2 трети).
Определение фигур, разделенных на равные части
Попрактикуйтесь в определении фигур, разделенных на равные части. В этом упражнении учащимся даются фигуры, которые разделены на две или более частей, и их просят решить, какие из них разделены на равные части.
В этом упражнении учащимся даются фигуры, которые разделены на две или более частей, и их просят решить, какие из них разделены на равные части.
Определите и обозначьте половинки, четверти и восьмые части
Попрактикуйтесь в определении половинок, четвертей и восьмых частей. В этом упражнении учащиеся делят бумагу на части и определяют, является ли каждая часть половинной, четвертой или восьмой
Определение и обозначение терций, пятых, шестых и седьмых частей
Практика определения третьих, пятых, шестых и седьмых частей. В этом упражнении учащиеся делят бумагу на части и определяют, как называется каждая часть
Определяют количество равных частей, необходимых для разбиения фигуры на заданный знаменатель
Упражняются в определении количества равных частей, необходимых для разбиения фигуры на части данный знаменатель. В этом упражнении учащиеся выбирают, сколько равных частей должна иметь фигура в зависимости от того, как ее нужно разделить
Определить заштрихованную часть фигуры как дробную единицу
Попрактиковаться в определении того, какая часть фигуры заштрихована. В этом упражнении фигуры делятся на равные части, и учащиеся тренируются называть заштрихованные части
В этом упражнении фигуры делятся на равные части, и учащиеся тренируются называть заштрихованные части
Сортировка фигур на основе заштрихованной доли единицы
Практика сортировки фигур на основе дроби, заштрихованной в каждой фигуре. В этом упражнении учащиеся видят, что четверть может выглядеть по-разному в зависимости от того, как фигура делится на четверки
Определение заштрихованной части фигуры
Попрактикуйтесь в определении затененной части фигуры. В этом упражнении фигуры разных размеров и форм разделены на группы разного количества
Определение фигур, у которых заданная часть закрашена
Потренируйтесь определять фигуры, у которых заданная часть закрашена. В этом упражнении учащимся даются четыре фигуры, и их просят выбрать ту, которая правильно соответствует заданным критериям.
Разделите и заштрихуйте фигуру, чтобы представить заданную часть
Попрактикуйтесь в разделении и затенении формы, чтобы представить заданную часть. В этом упражнении учащимся предлагается заштриховать определенную часть каждой фигуры, а затем сначала разделить фигуру на части перед тем, как заштриховать
В этом упражнении учащимся предлагается заштриховать определенную часть каждой фигуры, а затем сначала разделить фигуру на части перед тем, как заштриховать
Решить задачи на равные части целого
Попрактиковаться в решении задач на равные части целого. В этом упражнении учащиеся должны выбрать правильную дробь, написанную словами, исходя из данной ситуации
Тема B: Дроби единиц и их отношение к целому
Учащиеся используют свои знания из Темы 5А для перехода от формы слова к стандартной форме при определении дробей. Они начинаются с единичных дробей и переходят к более сложным дробям, включая дополнения к целому и неправильные дроби. На протяжении всей темы учащимся представлены разнообразные формы, размеры и цвета фигур. Хотя они не используют термин «неправильные дроби», они изучают основную концепцию дробных частей, которые образуют более чем одно целое.
Определение дробей единиц, записанных в стандартной форме
Научитесь писать дроби, используя числа и дробную черту. В этом упражнении учащиеся учатся писать дробь на основе заштрихованной фигуры, используя (заштрихованные части)/(все части)
В этом упражнении учащиеся учатся писать дробь на основе заштрихованной фигуры, используя (заштрихованные части)/(все части)
Обозначьте часть фигуры единичной дробью, записанной в стандартной форме
Узнайте, что единичная дробь одна часть всех равных частей целого. В этом упражнении учащиеся определят, сколько существует равных частей, и воспользуются этой информацией, чтобы написать единичную дробь для каждой части
Определите часть фигуры, которая заштрихована с помощью доли единицы
Потренируйтесь определять, какая часть фигуры заштрихована. В этом упражнении учащиеся будут выбирать из различных долей единиц, чтобы определить, какая из них верна.
Определить фигуры, у которых заштрихована заданная доля единицы
Попрактиковаться в определении фигуры с заштрихованной долей данной единицы. В этом упражнении учащиеся будут выбирать из разных цифр, чтобы определить, какая из них соответствует заданной дроби 9 единиц.0007
Напишите дробную единицу, чтобы обозначить заштрихованную часть числа.

Потренируйтесь писать дробную единицу с числами, имеющими заштрихованную цифру и слова. В этом упражнении дробь записывается словами, и учащиеся должны выбрать правильный числитель и знаменатель
Определить заштрихованную часть числа
Потренироваться называть заштрихованную часть дроби словами. В этом упражнении учащиеся сначала определяют, сколько имеется равных частей и сколько из этих частей заштриховано, прежде чем выбрать правильную дробь
Обозначьте заштрихованную часть фигуры дробью, написанной в стандартной форме.
Потренируйтесь выбирать правильное название заштрихованной части фигуры. В этом упражнении учащимся предлагаются различные словесные варианты, и их просят выбрать, какое из них представляет изображенную цифру
Заштрихуйте части фигуры, чтобы представить заданную дробь
Потренируйтесь закрашивать части фигуры, чтобы представить заданную дробь. В этом упражнении учащиеся будут нажимать на правильное количество частей фигуры, чтобы соответствовать данной дроби
Идентифицируйте цифры, у которых заштрихована данная дробь, и дроби, представляющие заштрихованную часть фигуры.

Потренируйтесь определять фигуры, у которых заштрихована правильная часть, соответствующая заданной дроби. В этом упражнении учащиеся также определят, какая дробь правильно соответствует фигуре.
Напишите дробь, чтобы идентифицировать заштрихованную часть фигуры (Уровень 1)
Попрактикуйтесь в написании дроби, чтобы идентифицировать заштрихованную часть фигуры. В этом упражнении учащиеся должны сначала заполнить либо числитель, либо знаменатель, а затем заполнить обе части дроби
Обозначьте заштрихованную часть фигуры дробью, написанной в стандартной и словесной форме.
Потренируйтесь обозначать цифру правильной дробью в словесной и числовой форме. В этом упражнении учащиеся выбирают один из трех вариантов названия дроби и трех вариантов числовой дроби
Напишите дробь, чтобы обозначить заштрихованную часть фигуры (уровень 2)
Попрактикуйтесь в написании дроби, чтобы представить заданную цифру который частично затенен. В этом упражнении учащиеся заполняют как числители, так и знаменатели дроби 9. 0007
0007
Обозначьте заштрихованные и незаштрихованные части фигуры (Уровень 1)
Определите, какая часть фигуры заштрихована, а какая нет. Сначала выберите правильную часть заштрихованной части фигуры, а затем выберите правильную часть незаштрихованной части фигуры.
Обозначьте заштрихованные и незаштрихованные части фигуры (уровень 2) заштрихованные и незаштрихованные части фигуры. Фигура разделена на равные части, некоторые части заштрихованы. Выберите, какая дробь является правильной заштрихованной, а какая — незаштрихованной
Решить текстовые задачи с дополнительными дробями
Попрактиковаться в решении текстовых задач с дробями, сумма которых равна 1. В этом упражнении учащимся дается информация о заштрихованной части фигуры и предлагается найти дробь, представляющую незаштрихованную часть
Определить количество дробных частей в целом
Попрактиковаться в определении количества дробных частей в целом. В этом упражнении учащимся дается пирог, разрезанный на равные части, и их просят определить, из скольких частей состоят все 9 частей. 0007
0007
Решение задач на несколько целых чисел и неправильную дробь
Узнайте, что у дроби числитель может быть больше знаменателя. В этом упражнении учащимся дается одна фигура и их просят составить больше, в результате чего получается неправильная дробь. Учащиеся должны решить, как неправильная дробь соотносится с целым числом.
Определить набор цифр, заштрихованные в которых представляют собой неправильную дробь.
Попрактиковаться в сопоставлении цифры или набора цифр с заданной неправильной дробью. Это упражнение укрепляет идею о том, что дробь, у которой числитель больше, чем знаменатель, больше, чем одно целое.0007
Обозначьте набор цифр, заштрихованный представляющий неправильную дробь.
Потренируйтесь сопоставлять набор цифр с правильной дробью. В этом упражнении учащимся предлагается три дроби в качестве вариантов для набора заштрихованных цифр, который больше единицы
Разделите и заштрихуйте набор цифр, чтобы представить неправильную дробь
Потренируйтесь заштриховывать набор цифр, чтобы он соответствовал заданной неправильной дроби . В этом упражнении учащиеся решат, сколько равных частей нужно каждой фигуре, чтобы составить данную дробь 9.0007
В этом упражнении учащиеся решат, сколько равных частей нужно каждой фигуре, чтобы составить данную дробь 9.0007
Тема C: Сравнение долей единиц и определение целого
На основе визуальных моделей учащиеся узнают, что чем больше частей в целом, тем меньше каждая единица дроби. Затем они сравнивают единичные дроби, используя как слова, так и символы, и связывают единичную дробь с целым.
Сравнение долей единиц на основе модели
Узнайте, как разные доли единиц сравниваются друг с другом, используя разные модели. В этом упражнении учащиеся узнают, что когда целое разделено на несколько частей, каждая часть становится меньше
Сравните дроби единиц с использованием
<, = и > с моделью и без нееПопрактикуйтесь в использовании знаков <, > и = для сравнения двух чисел. В этом упражнении учащиеся сначала сравнивают два целых числа, а затем узнают, как сравнивать две дроби с помощью ленточной диаграммы. Наконец, учащиеся будут сравнивать дроби без ленточной диаграммы
Определить и обозначить модель единичной дроби, которая больше или меньше заданной модели единичной дроби
Попрактиковаться в использовании диаграммы дробей для сравнения двух дробей. В этом упражнении учащиеся будут перетаскивать правильную фигуру, чтобы сделать верное утверждение. Учащиеся сравнивают две фигуры, а затем обозначают цифру правильной дробью 9.0007
В этом упражнении учащиеся будут перетаскивать правильную фигуру, чтобы сделать верное утверждение. Учащиеся сравнивают две фигуры, а затем обозначают цифру правильной дробью 9.0007
Определить целое на основе заданной доли единицы
Определить, как часть объекта связана с целым. Дана часть фигуры. Запишите правильную дробь, которую представляет фигура. Затем идентифицируйте весь объект по части формы и дробной части целого, которую занимает эта часть. объект, используя правильное количество частей. В этом упражнении учащиеся перетаскивают правильное количество предметов, чтобы составить одно целое
Тема D: Дроби на числовой прямой
Учащиеся применяют свое понимание дробей к числам на числовой прямой. Они узнают, что между целыми числами на числовой прямой есть числа, и как их идентифицировать. Используя этот инструмент, учащиеся могут называть эквивалентные пары целых чисел и дробей, обозначать дроби больше 1 и сравнивать дроби с разными знаменателями.
Определите дроби на числовой прямой и запишите 1 в виде дроби
Узнайте, что числа 0 и 1 можно записать в виде дробей. В этом упражнении учащиеся заставят кузнечика прыгнуть на дробную часть от 1 вдоль числовой прямой, чтобы узнать, сколько прыжков кузнечика составляет целое число 9.0007
В этом упражнении учащиеся заставят кузнечика прыгнуть на дробную часть от 1 вдоль числовой прямой, чтобы узнать, сколько прыжков кузнечика составляет целое число 9.0007
Обозначьте числители дробей на числовой прямой.
Упражняйтесь в делении единичного сегмента на дробные части. В этом упражнении учащиеся вставят недостающие метки для каждой дробной части целого числа
Назовите дроби на числовой прямой (числитель и знаменатель)
Потренируйтесь обозначать дроби на числовой строке. В этом упражнении ни одна из дробей не заполнена, и учащиеся должны заполнить правильную дробь в зависимости от положения точки на числовой строке 9.0007
Разделить числовую прямую на дроби и поместить заданную дробь в числовую прямую.
Сопоставить дробь с правильной точкой в числовой прямой. Перетащите дробь в нужную точку. Наконец, решите, сколько частей нужно числовой строке, исходя из исходной заданной дроби
Поместите заданную дробь в числовую строку визуально (без решеток)
Потренируйтесь размещать дробь в числовой строке без каких-либо решеток. В этом упражнении учащиеся должны оценить, как дробь соотносится с 0 и 1, чтобы правильно разместить ее
В этом упражнении учащиеся должны оценить, как дробь соотносится с 0 и 1, чтобы правильно разместить ее
Обозначайте числители дробей на числовой прямой числами больше 1
Узнайте, как обозначать дробные числа больше 1 на числовой прямой. В этом упражнении учащиеся тренируются в работе с неправильными дробями. Учащиеся будут практиковаться в счете дробью, чтобы получить правильные числители неправильных дробей
Определить дробь, эквивалентную целому числу в числовой строке
Научиться обозначать дроби, эквивалентные целым числам. Учащиеся узнают, что слово «эквивалент» означает другой способ записи одной и той же суммы. Учащиеся практикуются в написании дробей, эквивалентных числам 0, 1, 2, 3 и 4
Расставьте дроби больше 1 в числовой строке.
Потренируйтесь расставлять неправильные дроби в числовой строке. В этом упражнении целые числовые точки помечены дробями на числовой прямой, и учащиеся должны определить, как неправильная дробь соотносится с этими числами.
Потренируйтесь размещать неправильную дробь на числовой прямой, сначала определив, сколько дробных сегментов нужно числовой строке. Выберите правильное количество дробных сегментов, затем перетащите неправильную дробь на нужное место в числовой строке
Отмечайте дроби больше 1 в числовой строке.
Потренируйтесь обозначать дроби больше 1 в числовой строке. Сначала помечается либо числитель, либо знаменатель, и учащиеся должны заполнить пропущенную часть. Наконец, учащиеся заполняют всю дробь в зависимости от ее положения на числовой прямой
Сравнение дробей с разными знаменателями на числовой прямой
Потренируйтесь сравнивать дроби с разными знаменателями на числовой прямой. В этом упражнении учащиеся сначала разместят дроби на отдельных числовых рядах, а затем сравнит их. Учащиеся сделают вывод, что дроби, расположенные правее, больше
Используйте
<, = или > для сравнения дробей с разными знаменателями в числовой строке. Потренируйтесь сравнивать дроби с разными знаменателями, используя символы <, > или =. В этом упражнении учащиеся сначала размещают две дроби на числовой прямой, а затем выбирают правильный символ сравнения, основываясь на их расположении на числовой прямой. эквивалентные дроби. Они расширяют это понимание, включив в него целые числа и дроби больше 1.
В этом упражнении учащиеся сначала размещают две дроби на числовой прямой, а затем выбирают правильный символ сравнения, основываясь на их расположении на числовой прямой. эквивалентные дроби. Они расширяют это понимание, включив в него целые числа и дроби больше 1.
Создавайте, обозначайте, идентифицируйте и сравнивайте эквивалентные дроби
Узнайте, как составлять эквивалентные дроби с разными знаменателями. Заштрихуйте части цифр, чтобы представить одну и ту же дробь. Продолжайте маркировать заштрихованные цифры правильными дробями, чтобы показать, что разные дроби могут быть одной и той же заштрихованной частью фигуры.
Определите эквивалентные дроби, используя числовую прямую (меньше 1) разные фракции. В этом упражнении учащиеся узнают, что две дроби, находящиеся в одной и той же точке числовой прямой, эквивалентны
Определите эквивалентные дроби с помощью числовой строки (больше 1)
Потренируйтесь размещать дроби в числовой строке и определять, какие из них эквивалентны. В этом упражнении учащиеся работают с дробями, которые больше 1
В этом упражнении учащиеся работают с дробями, которые больше 1
Обозначьте эквивалентные дроби на числовой прямой
Узнайте, как обозначить дробь другой эквивалентной дробью. Дана одна дробь, а затем числовой ряд делится на несколько частей. Продолжайте обозначать дробь другим числителем и знаменателем, чтобы получить эквивалентную дробь
Обозначьте две эквивалентные дроби на основе моделей
Потренируйтесь выбирать, какая часть фигуры заштрихована до и после разделения фигуры на несколько частей. В этом упражнении учащиеся учатся определять, являются ли дроби эквивалентными
Обозначают три эквивалентные дроби на основе моделей
Практикуются в заполнении числителей или знаменателей, чтобы получить три эквивалентные дроби. В этом упражнении учащиеся обозначают дроби в зависимости от того, сколько частей заштриховано на трех фигурах, разделенных на разные части
Обозначьте дроби, равные 1 целому.
Потренируйтесь расставлять плитки дробей на полке, где каждая полка равна 1. В этом упражнении учащиеся обозначают каждую дробь, равную единице, правильным числителем. Учащиеся делают вывод, что в каждой дроби, равной 1, используются два одинаковых числа
В этом упражнении учащиеся обозначают каждую дробь, равную единице, правильным числителем. Учащиеся делают вывод, что в каждой дроби, равной 1, используются два одинаковых числа
Запись целых чисел в виде дробей (знаменатель 1)
Научитесь записывать целые числа в виде дробей со знаменателем 1. Учащиеся тренируются в написании чисел от 1 до 13. заполнив пропущенные части дроби или целого числа
Запись целых чисел в виде дробей (различные знаменатели)
Узнайте, как переименовывать целые числа в зависимости от того, сколько в них половин или третей. В этом упражнении учащиеся сначала помечают числители знаменателем 2. Затем учащиеся обозначают числители знаменателем 3
Тема F: Сравнение, порядок и размер дробей
На основе визуальных моделей учащиеся учатся сравнивать две дроби с одинаковым числителем или две дроби с одинаковым знаменателем. Для этого они применяют свое понимание создания и именования дробей, а также использование символов <, = и >.
Сравнивать дроби с одинаковыми числителями или знаменателями на основе модели
Практикуйтесь в сравнении дробей с одинаковыми числителями или знаменателями. В этом упражнении учащиеся сначала помечают ленточные диаграммы правильными дробями, а затем используют символы <, > или =, чтобы определить, как эти дроби связаны между собой
Закрасьте и сравните дроби с тем же числителем на основе части фигуры одинаковы, но заштрихованные части меньше, значит дробь меньше. Даны две фигуры, разделенные на разное количество равных частей. Заштрихуйте одинаковое количество штук на каждой цифре
Подпишите и сравните дроби с одним и тем же числителем
Потренируйтесь подписывать и сравнивать равные числа, разделенные на различное количество частей, заштрихованных одинаково. Это упражнение показывает, что наличие одного и того же числителя не означает, что заштрихованные дроби равны по размеру.
Сравните дроби с одинаковыми числителями или знаменателями
Потренируйтесь сравнивать две дроби с одинаковыми числителями. В этом упражнении учащиеся выбирают правильный символ (<, > или =), чтобы показать, как связаны дроби
В этом упражнении учащиеся выбирают правильный символ (<, > или =), чтобы показать, как связаны дроби
Рабочие листы порядка действий
Добро пожаловать на страницу рабочих листов порядка действий на Math-Drills.com, где мы обязательно следуем приказам! Эта страница включает рабочие листы порядка операций с использованием целых чисел, целых чисел, десятичных знаков и дробей.
Учащиеся начальной и средней школы обычно используют аббревиатуры PEMDAS или BEDMAS, чтобы помочь им запомнить порядок, в котором они выполняют вопросы с несколькими операциями. Буквы «P» или «B» в аббревиатуре обозначают скобки или квадратные скобки. Все операции в скобках выполняются первыми. «E» относится к показателям степени; все показатели вычисляются после круглых скобок. Буквы «M» и «D» взаимозаменяемы, поскольку умножение и деление выполняются в том порядке, в котором они появляются слева направо. Четвертый и последний шаг — решить сложение и вычитание в том порядке, в котором они появляются слева направо.
В последнее время студентов учат аббревиатуре PEMA для обозначения порядка операций, чтобы избежать путаницы, присущей другим аббревиатурам. Например, в PEMDAS умножение предшествует делению, что, по ошибочному мнению некоторых людей, означает, что умножение должно выполняться перед делением в вопросе о порядке операций. На самом деле две операции выполняются в том порядке, в котором они встречаются в вопросе слева направо. Это признается в PEMA, который более правильно показывает, что есть четыре уровня, которые необходимо пройти в порядке выполнения вопроса.
Если вы не хотите, чтобы ваши ученики занимались чем-то отличным от остального мира, было бы неплохо объяснить им эти правила. Здесь не нужно никаких открытий или исследований. Это правила, которые необходимо выучить и применять на практике, и они приняты в качестве стандартного подхода к решению любой многошаговой математической задачи.
Самые популярные рабочие листы с порядком операций на этой неделе
Порядок действий с целыми числами и без степеней (четыре шага)2173 2261 просмотр на этой неделе )Порядок операций с отрицательными и положительными целыми числами (Четыре шага) ( 1530 просмотров на этой неделе )Порядок операций с целыми числами (Шесть шагов) ( 774 просмотра на этой неделе )Порядок операций с отрицательными числами и положительные целые числа (три шага) ( 633 просмотра на этой неделе )Порядок действий с отрицательными и положительными целыми числами (два шага) ( 514 просмотров на этой неделе )Порядок действий с целыми числами Рабочие листы
Порядок действий с целыми числами
Рабочие листы в этом разделе включают вопросы со скобками, показателями степени и всеми четырьмя операциями.
2-этапный Порядок операций с целыми числами 3 шага Порядок операций с целыми числами 4 шага Порядок операций с целыми числами 5-шаговый Порядок операций с целыми числами 6 шагов Порядок операций с целыми числами
Порядок действий с целыми числами
(только сложение и умножение) Рабочие листы в этом разделе включают вопросы со скобками, сложением и умножением. Экспоненты, вычитание и деление исключены. Цель исключения некоторых частей PEMDAS состоит в том, чтобы облегчить учащимся понимание того, как работает порядок операций. Чтобы помочь учащимся понять цель порядка операций, попробуйте связать выражения с соответствующими сценариями. Например, 2 + 7 × 3 может означать количество дней в двух днях и трех неделях. (9+ 2) × 15 может означать общую сумму заработка, если кто-то работал 9 часов вчера и 2 часа сегодня за 15 долларов в час.
2 шага Порядок действий с целыми числами ( Только сложение и умножение ) 3 шага Порядок действий с целыми числами ( Только сложение и умножение ) 4 шага Порядок действий с целыми числами ( Только сложение и умножение ) 5-Шаг Порядок операций с целыми числами ( Только сложение и умножение ) 6 шагов Порядок действий с целыми числами ( Только сложение и умножение )
Порядок действий с целыми числами
(только сложение, вычитание и умножение)Рабочие листы в этом разделе включают вопросы со скобками, сложением, вычитанием и умножением. Экспоненты и деление исключены. Этот раздел похож на предыдущий тем, что он предназначен для того, чтобы помочь учащимся разобраться в порядке операций, не усложняя работу с показателями степени и делением.
2 шага Порядок действий с целыми числами ( Только сложение, вычитание и умножение ) 3 шага Порядок действий с целыми числами ( Только сложение, вычитание и умножение ) 4 шага Порядок действий с целыми числами ( Только сложение, вычитание и умножение ) 5 шагов Порядок действий с целыми числами ( Только сложение, вычитание и умножение ) 6 шагов Порядок действий с целыми числами ( Только сложение, вычитание и умножение )
Порядок действий с целыми числами
(без показателей) Последний раздел, который поможет учащимся освоить порядок операций или просто для учащихся, которые еще не знакомы с показателями степени. Вопросы на рабочих листах в этом разделе включают круглые скобки и все четыре операции.
Вопросы на рабочих листах в этом разделе включают круглые скобки и все четыре операции.
2-этапный Порядок операций с целыми числами ( Без показателей ) 3 шага Порядок операций с целыми числами ( Без экспоненты ) 4 шага Порядок операций с целыми числами ( Без экспоненты ) 5-этапный Порядок операций с целыми числами ( Без экспоненты ) 6-этапный Порядок операций с целыми числами ( Без экспоненты )
Порядок операций с целыми числами Рабочие листы
Порядок операций с целыми числами
Рабочие листы в этом разделе включают круглые скобки, показатели степени и все четыре операции.
2-этапный Порядок операций с целыми числами 3 шага Порядок операций с целыми числами 4 шага Порядок операций с целыми числами 5 шагов Порядок операций с целыми числами 6 шагов Порядок операций с целыми числами
Порядок операций с целыми числами и
без показателей степени2-этапный Порядок операций с целыми числами и Без экспоненты 3 шага Порядок операций с целыми числами и Без экспоненты 4 шага Порядок операций с целыми числами и Без экспоненты 5 шагов Порядок операций с целыми числами и Без экспоненты 6-Шаг Порядок операций с целыми числами и Без экспонент
Порядок действий с дробями Рабочие листы
Порядок операций с дробями
Как и в случае с другими рабочими листами порядка операций, рабочие листы дробного порядка операций требуют некоторых предварительных знаний. Если ваши ученики борются с этими вопросами, вероятно, это больше связано с их способностью работать с дробями, чем с самими вопросами. Внимательно наблюдайте и постарайтесь точно указать, каких необходимых знаний не хватает, а затем потратьте некоторое время на изучение этих концепций/навыков, прежде чем продолжить. В противном случае приведенные ниже рабочие листы должны содержать довольно прямые ответы и не должны приводить к чрезмерному выпадению волос.
Если ваши ученики борются с этими вопросами, вероятно, это больше связано с их способностью работать с дробями, чем с самими вопросами. Внимательно наблюдайте и постарайтесь точно указать, каких необходимых знаний не хватает, а затем потратьте некоторое время на изучение этих концепций/навыков, прежде чем продолжить. В противном случае приведенные ниже рабочие листы должны содержать довольно прямые ответы и не должны приводить к чрезмерному выпадению волос.
2-этапный Порядок операций с положительными дробями 3 шага Порядок операций с положительными дробями 4 шага Порядок операций с положительными дробями 5-этапный Порядок операций с положительными дробями 6 шагов Порядок действий с положительными дробями 2-этапный Порядок операций с положительными дробями (без экспоненты) 3 шага Порядок операций с положительными дробями (без экспонентов) 4 шага Порядок операций с положительными дробями (без экспоненты) 5-этапный Порядок операций с положительными дробями (без экспоненты) 6-этапный Порядок операций с положительными дробями (без экспоненты) 2-этапный Порядок операций с положительными и отрицательными дробями 3-этапный Порядок операций с положительным и отрицательным дроби 4 шага Порядок операций с положительными и отрицательными дробями 5-этапный Порядок операций с положительными и отрицательными дробями 6-шаговый Порядок операций с положительными и отрицательными дробями
Порядок операций с десятичными знаками
Порядок действий с десятичными знаками с положительными и отрицательными десятичными вариантами и различной сложности.
Порядок операций с
десятичными знаками2-этапный Порядок операций с положительными десятичными знаками 3 шага Порядок операций с положительными десятичными знаками 4 шага Порядок операций с положительными десятичными знаками 5-шаговый Порядок операций с положительными десятичными знаками 6 шагов Порядок операций с положительными десятичными знаками 2-этапный Порядок операций с положительным и Отрицательные Десятичные 3 шага Порядок операций с положительными и отрицательными десятичными знаками 4 шага Порядок операций с положительными и отрицательными десятичными знаками 5-этапный Порядок операций с положительными и отрицательными десятичными знаками 6-этапный Порядок операций с положительными и отрицательными десятичными знаками
Порядок операций с Десятичные запятые2-этапный Порядок операций с положительными десятичными знаками (десятичная запятая) 3 шага Порядок операций с положительными десятичными знаками (десятичная запятая) 4 шага Порядок операций с положительными десятичными знаками (десятичная запятая) 5-шаговый Порядок операций с положительными десятичными знаками (десятичная запятая) 6-шаговый Порядок операций с положительными десятичными знаками (десятичная запятая) 2 шага Порядок операций с положительными и отрицательными десятичными знаками (десятичная запятая) 3-этапный Порядок операций с положительными и отрицательными знаками Десятичные знаки (десятичная запятая) 4-этапный Порядок операций с положительными и отрицательными знаками Десятичные знаки (десятичная запятая) 5-этапный Порядок операций с положительными и отрицательными знаками Десятичные знаки (десятичная запятая) 6-этапный Порядок операций с положительным и отрицательных десятичных знаков (десятичная запятая)
Порядок действий с
Смешанными десятичными дробями и дробямиПорядок действий с дробями и десятичными знаками Смешанный Порядок операций с дробями и десятичными знаками Смешанный с некоторыми отрицательными значениями
Как решать вопросы, правила, рабочие листы BODMAS
BODMAS обозначает B ракетка, O f, D ivision, M умножение, A дополнение и S убавление. BODMAS используется для объяснения порядка операций математического выражения. Это важная математическая концепция, используемая во многих местах, где вам нужно решать сложные уравнения. Это помогает в решении упрощений вопросов и сокращает время вычислений в большинстве случаев. Поэтому необходимо с самого начала укрепиться в этом понятии. Всем тем, кто пробует свои силы на различных конкурсных экзаменах или готовит эту тему к ЕГЭ типа SAT , GMAT или GRE , вот блог с вопросами BODMAS для практики.
BODMAS используется для объяснения порядка операций математического выражения. Это важная математическая концепция, используемая во многих местах, где вам нужно решать сложные уравнения. Это помогает в решении упрощений вопросов и сокращает время вычислений в большинстве случаев. Поэтому необходимо с самого начала укрепиться в этом понятии. Всем тем, кто пробует свои силы на различных конкурсных экзаменах или готовит эту тему к ЕГЭ типа SAT , GMAT или GRE , вот блог с вопросами BODMAS для практики.
Этот блог включает в себя:
- Что такое БОДМАС?
- Правило BODMAS Полная форма
- Советы по запоминанию правила BODMAS
- BODMAS против PEMDAS
- Когда использовать BODMAS?
- Викторина BODMAS
- Как решать вопросы BODMAS?
- Правила BODMAS
- Рабочий лист BODMAS для класса 10
- Решенные вопросы и ответы BODMAS
- Вопросы по Bodmas для класса 4
- Вопросы по Bodmas для класса 5
- Порядок действий
- Часто задаваемые вопросы
Что такое BODMAS?
BODMAS stands for:
B: Brackets
O : Order of Indices
D : Division
M : Multiplication
A: Addition
S: Subtraction
Now, давайте поймем порядок, в котором оно используется в математике. 0007
0007
B ➝ O ➝ D ➝ M ➝ A ➝ S
Начиная с буквы «B» и двигаясь вправо от слова, вы получите правильные и быстрые ответы на эти сложные уравнения. Обратитесь к таблице ниже для лучшего понимания этой концепции.
| Буквы | Ступени |
| Кронштейны (B) | Разбейте задачи внутри скобок |
| Порядки индексов (О) | Решение индексов, таких как корни, степени и т. д. |
| Подразделение (D) | Разделить полученные числа |
| Умножение (М) | Умножьте числа дальше. |
| Дополнение (А) | Суммируйте следующие числа |
| Вычитание (S) | Вычтите числа, оставшиеся в конце. |
Правило BODMAS Полная форма
BODMAS означает скобки, порядки, деление, умножение, сложение и вычитание, как мы обсуждали ранее. Мы должны выполнять эти действия в правильном порядке при реализации правила BODMAS.
| Б | Кронштейны | ( ), { }, [ ] |
| О | Заказ | Квадратные корни, индексы, показатели степени и степени |
| Д | Подразделение | ÷, / |
| М | Умножение | ×, * |
| А | Дополнение | + |
| С | Вычитание | – |
Советы по запоминанию правила BODMAS
Ниже приведены рекомендации по использованию правила BODMAS для упрощения выражения:
- Во-первых, упростите скобки.
- Экспоненциальные или корневые решения
- Произвести деление или умножение (слева направо)
- Выполнить операцию сложения или вычитания (слева направо)
BODMAS и PEMDAS
Два сокращения, которые используются для напоминания порядка операций, — BODMAS и PEMDAS. Правило BODMAS почти идентично правилу PEMDAS. Поскольку некоторые термины распознаются под разными именами в разных странах, аббревиатура может различаться. Применяя правило BODMAS или правило PEMDAS, важно помнить, что мы решаем операцию, которая идет первой из левой части уравнения, когда мы достигаем стадии деления и умножения. И для сложения, и для вычитания применяется один и тот же подход: мы решаем операцию, которая появляется первой в левой части.
Правило BODMAS почти идентично правилу PEMDAS. Поскольку некоторые термины распознаются под разными именами в разных странах, аббревиатура может различаться. Применяя правило BODMAS или правило PEMDAS, важно помнить, что мы решаем операцию, которая идет первой из левой части уравнения, когда мы достигаем стадии деления и умножения. И для сложения, и для вычитания применяется один и тот же подход: мы решаем операцию, которая появляется первой в левой части.
Когда использовать БОДМАС?
Когда математическое уравнение имеет много операций, используется BODMAS. Подход BODMAS имеет набор рекомендаций, которым необходимо следовать по порядку. Это обеспечивает подходящую основу для создания оригинального ответа для каждой математической фразы.
Условия для выполнения:
- Если есть какие-либо скобки, откройте скобки, затем добавьте или вычтите члены. а + (b + с) = а + b + с, а + (b – с) = а + b – с
- Если есть отрицательный знак, просто откройте скобку и умножьте отрицательный знак на каждое слагаемое внутри скобки.
 а – (б + в) ⇒ а – б – в
а – (б + в) ⇒ а – б – в - Если сразу за скобками находится термин, умножьте этот внешний термин на каждый термин внутри скобки. а(б + с) ⇒ аб + ас
Викторина BODMAS
Вопросы BODMAS
Вот несколько вопросов BODMAS для вас:
- Упростите 25 – [20 – {10 -(7-5-3)}
- Узнать ответ для 100 – 3 [20 + {50 – 40}]
- 7 + (8 -3×2)
- Каким был бы ответ для 50- [20 +{ 30- ( 20- 5)}]
- Найдите значение 150- [10 + { 3- ( 20- 5)}]
- Упростить 1៖ 3/7 x (6+8X3-2)+ [1/5៖ 7/25 – {3/7 + 8/14}]
- Используя правило БОДМА, определите ответ 18 ៖ 10 – 4 + 32 ៖ (4+ 10 ៖ 2 – 1)
- 10 – [ 6 -{7 – (6- 8 – 5)}] решить следующее
- Каким будет ответ на этот вопрос 5x ¼ ៖ 3/7 + [45/24- 2/3 + 5/6 x 2/5 ]
- 1800 ៖ 10 {( 12 – 6) + (24 – 12)}
- 1/2 [{ -2 (1 + 2) 10} 15] x 3
- 20 – [6- {4 – (8 – 6 + 3)}]
- По правилу BODMAS найдите значение y: 36 ៖ 2 + y x 3 – 22 = 8
- Определите правильный ответ для- (1/4 + 7/4) – 2
- 45 х 3 х 7 х [22/11+ 36/12]
- Решите этот вопрос, используя правило BODMAS: 2 [2 + 2 {39 -2 (17 + 2)}]
- Решите этот вопрос BODMAS (17 x 18)៖ 10 x 2 (2+ 13)- 25
- (3 + 3) x (3 ៖ 3) x (3×3) решить эту задачу, используя правило BODMAS
- 2550 – [510 {270 – ( 90- 80 + 70)}]
- [29- (- 2) {6 – (7 – 3)}] ៖ [3 x {5 + (-3) x (-2)}] решить это сложное уравнение, используя правило BODMAS
- 63- (-3) {-2 -8-3} ៖ 3 {5+ (-2) (-1)}
- Каким будет ответ на этот вопрос BODMAS: 27 – [38 – {46 – (15- 13 2)}]
- 25- 1/25 {5+ 4 – (3+ 2- 1 + 3)}
Загрузить BODMAS Практика Вопросы 900BODMA Вопросы?
Правила BODMAS упрощают математическое уравнение, разбивая его на части. Давайте решим вопрос BODMAS, чтобы понять его правила.
Давайте решим вопрос BODMAS, чтобы понять его правила.
Пример: 4(10+15÷5×4-2×2 )
Решение скобок:
Здесь сначала нужно вычислить внутреннюю скобку.
4 (10+15÷5×4-2×2)
В скобках сначала решить раздел деления
4(10+ 15÷5 x4-2×2)
Далее, в пределах сама скобка, решить умножение
4(10+ 3×4 – 2×2 )
Далее, внутри скобки решить сложение
4( 10+12 -4)
Наконец, в скобках решите вычитание:
4( 22-4 )
После того, как скобка решена, возьмите число снаружи и решите секцию «Из». умножением:
=4×18
Ответ=72
Итак, результат 4(10+15÷5×4-2×2)= 72
Вы сможете решить даже самые сложные математические задачи используя это правило BODMAS для скобок деления, умножения, сложения и вычитания.
Вот правило порядка операций в BODMAS:
BODMAS Questions Предоставлено: Суреш АггарвалBODMAS Rules
Согласно правилу BODMAS, первое, что вам нужно сделать при решении вопроса, это упростить скобки. Но знаете ли вы, как упростить скобки? Не волнуйтесь, давайте откроем способы удаления скобок и расширения выражения с помощью примера:
Предположим, у нас есть уравнение x (y + z), чтобы раскрыть скобки и расширить члены, мы будем использовать Распределительное имущество , в котором говорится, что a (b + c) = ab + bc. Поэтому в данном уравнении примет вид: x (y + z) = xy + xz.
Надеемся, упрощение скобок вам понятно. Давайте рассмотрим несколько сложных примеров для лучшего понимания.
Пример 1: Расширить и упростить 9 (5 + 3)
Решение
В вопросе 9 (5 + 3) воспользуемся распределительным свойством [a (b + c) = ab + bc]
9 (5 + 3) = 9 × 5 + 9 × 3
= 45 + 27
= 72
Следовательно, ответ равен 72.
Решение:
Мы снова воспользуемся свойством распределения [a (b + c) = ab + bc], чтобы перейти к вопросу 11 (2y + 3). Уравнение примет вид:
11 (2y + 3) = 11 × 2y + 11 × 3
= 22y + 33
Следовательно, ответ 22y + 33!
Рабочий лист BODMAS для класса 10
Мы подготовили эксклюзивный рабочий лист BODMAS, чтобы вы могли попрактиковаться в правилах BODMAS:
Рабочий лист вопросов BODMASНажмите здесь, чтобы загрузить Рабочий лист вопросов BODMAS Загрузить BODMAS0 Вопросы и ответы
BODMAS — важная тема математики, которая является частью математики 8 класса, математики 10 класса и математики 9 класса ICSE. Таким образом, чтобы лучше объяснить эту тему, мы решили для вас несколько вопросов BODMAS, посмотрите:
Таким образом, чтобы лучше объяснить эту тему, мы решили для вас несколько вопросов BODMAS, посмотрите:
Решенный вопрос BODMAS 1
BODMAS ВопросРешенный вопрос BODMAS 2
Найдите значение «a», используя понятие BODMAS.
42 ÷ 2 + a × 3 − 22 = 8
Решение:
42 ÷ 2 + a × 3 − 22 = 8 = 8
Далее произведем перестановку членов с последующим вычитанием
а 3 – 22 + 21 = 8
а × 3 – 1 = 8
Перенесем -1 на другую сторону
а × 3 = 8 + 1
а × 3 = 9
а = 9/3
а = 3
Значение а равно 3!
Решенный вопрос BODMAS 3
Найдите значение 3+3 из 3÷3 из 3×3
Решение:
7 Следовательно, 3 + 3 из 3 ÷ 3 из 3 × 3 станет 3 + (3 из 3) ÷ 3 из 3 × 3
Используя BODMAS, мы сначала поработаем со скобками и из
3 + 9÷ 3 из 3 × 3
3 + 3 из 3 × 3
3 + (3 из 3) × 3
3 + 9 × 3
Согласно правилу БОДМАС, мы сначала решим умножение
3 + 27
= 30
Следовательно, ответ 30!
Решено BODMAS Вопрос 4
В уравнении 9 + 7 × 1= 5 − 3 какую пару знаков нужно поменять местами на , чтобы оно стало правильным? Доступные варианты: + с ×, + с –, × с – или + с –.
Решение:
Для заданных 4 вариантов, единственный × с – это сделать уравнение правильным. Давайте разберемся и проверим это, заменив эти знаки в вышеупомянутом вопросе BODMAS.
Исходное уравнение : 9 + 7 × 1 = 5 − 3
Новое уравнение : 9 + 7 − 1 = 5 × 3
Используя правило BODMAS, мы сначала поработаем над умножением
9 + 7 − 1 = 15
16 − 1 = 15
15 = 15
Отсюда проверено, что × с – правильный выбор!
Решенный вопрос BODMAS 5
Решенный вопрос BODMAS 6
Решенный вопрос BODMAS 7
Найдите значение x в следующем уравнении 6162 + x + 3330 = 2545
Решение:
6162 + x + 3330 = 2545
Сначала преобразуем уравнение
0004 x 95004 + 33304 Используя правило BODMAS, мы сначала выполним сложение
9492 + x = 2545
. Перенесем 9492 в другую часть уравнения
x = 2455 – 9492
= – 6947
Следовательно, ответ – 6947.
Решенный вопрос БОДМАС 8
Найдите значение 6 ÷ 2 + 7 × 4
Решение:
Согласно правилу БОДМА, начнем решать уравнение с деления:
6 ÷ 2 + 7 × 4
3 + 7 x 4
Следующей операцией по правилу BODMAS является Умножение
3 + 7 x 4
3 + 28
= 31
Следовательно, ответ равен 31 .
Решенный вопрос BODMAS 9
Как вы находите эти вопросы BODMAS? Попробуйте также некоторые вопросы по алгебре!
Решенный вопрос BODMAS 10
Упростить [72 – 12 ÷ на 3 – 2 ]+ ( 18 – 6) ÷ 4 с помощью скобок. Поскольку скобки также включают в себя деление и вычитание, мы будем делить
[72 – 12 ÷ на 3 – 2] + ( 18 – 6) ÷ 4
[72 – 4 – 2] + ( 18 – 6) ÷ 4
66 + 12 ÷ 4
Теперь сначала поработаем над делением
66 + 12 ÷ 4
66 + 3
= 69
Следовательно, упрощенное значение равно 69!
Найдите значение 40 – [20 – {14 – (16 – 6 x 4 – 2)}]
Решение:
Согласно правилу BODMAS, мы начнем решать вопрос, работая над скобки. В скобках мы начнем с умножения с последующим вычитанием
В скобках мы начнем с умножения с последующим вычитанием
40 — [20 — {14 — (16 — 6 x 4 — 2)}] 40 — [20 — {14 — (16 — 24 — 2)}]
Свойство целых чисел предполагает, что – и – становятся +, поэтому
40 – [20 – {14 – (16 – 26)}]40 – [20 – {14 – (-10)}]
Снова используя – и – стать +
40 – [20 – {14 + 10}]40 – [20 – 24]40 – [-4]40 + 4
= 44
Следовательно, ответ 44 !
Теперь, когда вы ответили на 5 вопросов BODMAS, вот список вопросов по рассадке для вас!
Bodmas Вопросы для класса 4
Вот вопросы для класса 4 для практики BODMAS:
- (4+7)*3=
- 5+(18/9*2)=
- 12- (2*5)=
- (50/10)-2=
- (30-12)(12-3)=
- (8-6)+(5*5)=
Bodmas Вопросы для класса 5
Вот вопросы для класса 5 для практики BODMAS:
- 33-9+40-(30+15) =
- 33-9+40+25-(30+15) =
- 3+21 х 6-(24-4) =
- 3+21 х 6-(24-4) х 2 =
- (62 ÷ 2 – 3) х 3 +6 =
- (62 ÷ 2 – 3) х 3 +6 х 2=
- 0,3+0,8+0,2=
- 30+30×0+1=
Порядок операций
youtube.com/embed/dAgfnK528RA?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/> Кредиты – математикаПочему бы вам не отдохнуть от этих вопросов BODMAS и не решить для разнообразия несколько формул и вопросов вероятности?
Часто задаваемые вопросы
Что такое правило BODMAS для примера ?
Правило BODMAS предполагает, что при решении сложного уравнения, состоящего из различных операций, мы должны следовать BODMAS для дальнейшего решения задачи.
Например: (2 + 3 ) x 4
Сначала мы решим скобки по правилу BODMAS, 5 x 3, а затем умножим. Итак, ответ 20!
Что такое правило BODMAS?
Правило BODMAS для ракеток B , O f, D ivision, M умножение, A дополнение и S тяга. В нем указывается порядок операций, в соответствии с которым мы можем решить сложную задачу.
В нем указывается порядок операций, в соответствии с которым мы можем решить сложную задачу.
Как упростить вопросы в баре?
Вопросы с чертой означают, что при решении конкретного уравнения предпочтение следует отдавать операциям под чертой, за которыми следует BODMAS.
Применяется ли BODMAS при отсутствии брекетов?
Да, БОДМАС применяется даже в тех местах, где нет брекетов. В таком случае мы просто работаем над другими операциями.
Викторина по математике
Узнайте, насколько вы умны, ответив на эти каверзные вопросы!
Мы надеемся, что этот блог, посвященный вопросам BODMAS, помог вам лучше понять концепцию. Перед выбором потока или курса рекомендуется проконсультироваться с экспертом. Кредитное плечо Edu — это универсальное решение для всех вопросов, связанных с поступлением и карьерой. Свяжитесь с нами, забронировав бесплатную сессию электронной встречи!
Свяжитесь с нами, забронировав бесплатную сессию электронной встречи!
Значение, порядок действий, правила, примеры
ВведениеПри упрощении математических выражений, состоящих из операций одного типа, мы выполняем одну операцию за раз, как правило, начиная слева направо. Если выражение имеет более одной основной операции, вы не можете выполнять операции в том порядке, в котором они указаны. Некоторые операции должны быть выполнены раньше, чем другие. Это каждая операция имеет свой приоритет. Как правило, порядок, в котором мы последовательно выполняем операции слева направо, таков: деление, умножение, сложение, вычитание. Но когда в выражениях также используются скобки, у нас есть другое правило, определяющее приоритет операций, известное как PEMDAS. Давайте узнаем, как определяется это правило.
Что такое PEMDAS? PEMDAS — это мнемоническое устройство, используемое для запоминания правильного порядка математических операций, которые следует использовать, если в выражении нужно вычислить несколько операций. PEMDAS означает P арентезы, E экспоненты, M умножение или D ivision и A дополнение или S вычитание. Таким образом, если в выражении есть круглые скобки или любой символ группировки, это означает, что нам нужно установить приоритет операций внутри него перед остальными операциями.
PEMDAS означает P арентезы, E экспоненты, M умножение или D ivision и A дополнение или S вычитание. Таким образом, если в выражении есть круглые скобки или любой символ группировки, это означает, что нам нужно установить приоритет операций внутри него перед остальными операциями.
Правило PEMDAS — это набор правил, определяющих порядок вычислений, то есть, какую операцию выполнять первой. В противном случае можно получить несколько или разные ответы. Давайте разберемся в этом на примере.
Предположим, мы хотим найти значение 2 + 3 x 5
Есть два способа найти значение приведенного выше выражения.
В первом методе будем двигаться слева направо, решая выражение в указанном порядке. Значит, сначала найдем сумму 2 и 3. Получим, 2 + 3 = 5,
Теперь у нас есть 2 + 3 x 5 = 5 x 5
Теперь мы находим произведение 5 на 5, чтобы получить ответ как 25. Таким образом, мы имеем,
Таким образом, мы имеем,
2 + 3 x 5 = 25 ……… ……………………….. ( 1 )
Теперь найдем значение этого выражения другим методом.
Сначала мы найдем значение 3 x 5 и прибавим это произведение к 2. Таким образом, мы получим
3 x 5 = 15 и 15 + 2 = 17
Следовательно, теперь у нас есть
2 + 3 x 5 = 17 ………………………… ( 2 )
Из ( 1 ) и ( 2 ) мы видим, что оба полученных результата не совпадают. Это подтверждает необходимость наличия приоритета операторов, чтобы получить один и тот же ответ на данное алгебраическое выражение. Этот приоритет известен как порядок операций.
Важность PEMDASБез PEMDAS не существует рекомендаций по получению только одного правильного ответа. В приведенном выше примере мы видели, что без правила PEMDAS другое выражение приводило бы к другим значениям при выполнении в другом порядке. Следовательно, правило PEMDAS было определено для решения математических выражений.
Неоднозначный случай Чтобы было ясно, из таблицы видно, что Скобки — это не математическая операция, а скорее символ группировки, как и Скобки ([]) и Фигурные скобки ({}). Таким образом, мы не должны рассматривать их как символы умножения, потому что выражение может иметь более одного ответа и приведет к двусмысленности и недоумению. Но, как мы все знаем, основные математические задачи, такие как операции, должны давать один ответ.
Таким образом, мы не должны рассматривать их как символы умножения, потому что выражение может иметь более одного ответа и приведет к двусмысленности и недоумению. Но, как мы все знаем, основные математические задачи, такие как операции, должны давать один ответ.
Лучшими примерами являются вирусные математические задачи, которые также могут столько раз почесать вам голову. Точно так же, как этот:
8÷2(2+2)
Если мы будем следовать традиционному методу, порядок действий будет следующим:
1
С помощью этого метода мы имеем 8÷2(2+2 )=1.
Что если мы будем следовать «современному» определению PEMDAS, по-прежнему рассматривая скобки как символ умножения?
Таким образом, мы имеем 8÷2(2+2)=16.
Теперь вы можете задаться вопросом, почему мы получили разные ответы и каков настоящий ответ. Ну, ответы кроются в основном принципе использования группирующих символов, таких как круглые скобки. Во-первых, предположим, что у нас есть числа, которые будут называться x и y. Чтобы умножить их, мы имеем
Чтобы умножить их, мы имеем
x ×y
Но x практически идентичен, что может привести к путанице при написании. Таким образом, точка умножения ( ∙ ) используется для умножения. Более того, присоединение терминов для их умножения (например, x и y) обычно используется так же, как показано ниже: xy
При использовании этой записи умножения выражений возникает еще один вопрос: а что если одна группа выражений умножается на другую группу терминов? Именно тогда появляются символы группировки. Следовательно, мы видим, как мы видим группы биномов, которые используют МЕТОД ФОЛЬГИ для решения.
Мы не можем присоединить y к x посередине, потому что это будет означать, что y нужно умножить на x.
x+yx-y
Конечно, это даст нам неправильную интерпретацию того, что нужно сделать, чтобы это выражение было решено.
Следовательно, использование круглых скобок для группировки умножаемых выражений (что является правильным) привело также к ошибочной интерпретации того, что один термин или число внутри круглых скобок должно по умолчанию умножаться на числа до или после него.
Кроме того, по этой причине некоторые калькуляторы по умолчанию воспринимают круглые скобки как символ умножения. С точки зрения калькулятора, любой член до или после скобки — это еще одна группа, которую нужно умножить или также иметь скобку, даже если мы ее не вводили.
Случай 1: 8÷2(2+2)
Что мы набрали: 8÷2(2+2)
Какой-то калькулятор: 8÷(2)(2+2) )
Случай 2: 8÷2×(2+2)
Что мы набрали: 8÷2×(2+2)
В уме какого-то калькулятора: 8÷(2) (2+2)
Случай 3: 8÷2(2+2)
Что мы набрали: 8÷2(2+2)
Ум современного калькулятора: (8 ÷ 2) (2+2) Обработка как
(4) (4)
16
В результате некоторые предлагают использование знака «Время» () или точка умножения (), чтобы исправить путаницу, если присутствуют круглые скобки. Например, если вы ищете определение метода FOIL, возможно, вы видели приведенную ниже иллюстрацию в Википедии*.
Например, если вы ищете определение метода FOIL, возможно, вы видели приведенную ниже иллюстрацию в Википедии*.
Возвращаясь к выражению 8÷2(2+2), если человек, составивший задачу, подразумевает, что только 2 нужно умножить на группу чисел в скобках ((2+2)), правильное выражение должно быть как те, что ниже.
8÷2×(2+2) или 8÷2∙(2+2)
Таким образом, мы можем также перевести часть выражений с математическими символами, присоединенными к:
+(2+2) (2 +2) прибавляется
– (2+2) (2+2) вычитается из
x (2+2) (2+2) умножается на
÷ (2+2) (2+2) делится на
Порядок операцийПорядок действий можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями. операции. Без последовательного порядка операций можно допустить большие ошибки во время вычислений.
Одним из таких правил является PEMDAS , где
P означает скобки
E означает экспоненты
M СДЕЛАЧИЕ СОЕДИНЕНИЯ
D СДЕЛАЕТСЯ ДЛЯ Дивизии
A СДЕЛАТЬ ДЛЯ ДОСТАВЛЕНИЯ
ПАН ПЕМО СДЕЛАЕТСЯ 9214 400444444. Получите PEM. Получите PEM. Поветричество 9214 400444444444. Поветричество. значение любых алгебраических выражений с использованием правила PEMDAS –
Получите PEM. Получите PEM. Поветричество 9214 400444444444. Поветричество. значение любых алгебраических выражений с использованием правила PEMDAS –
- Всегда начинайте с вычисления всех выражений в круглых скобках
Прежде всего, мы должны искать удаление любых символов группировки в алгебраическом выражении. Это означает, что в верхней части списка всегда помните 9 2173 упростите все внутри символов группировки. Примерами символов группировки являются круглые скобки ( ), скобки и фигурные скобки { }. Для вложенных символов группировки проработайте их изнутри и снаружи.
- Упростить все показатели степени, такие как квадратные корни, квадраты, кубы и кубические корни
После удаления скобок мы переходим к следующему шагу решения всех экспоненциальных значений в алгебраическом выражении. Экспоненциальные выражения, которые могут включать корневые значения, такие как квадратные корни, квадраты, кубы, кубические корни и т. д., сначала вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.
д., сначала вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.
- Выполните умножение и деление, начиная слева направо
Затем умножьте и/или разделите слева направо перед выполнением сложения и вычитания. Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.
- Наконец, аналогично выполните сложение и вычитание, начиная слева направо.
Порядок действий «слева направо»
Согласно правилу PEMDAS, если умножение и деление или сложение и вычитание идут в выражении последовательно или рядом друг с другом, мы должны выполнять их слева направо. Давайте воспользуемся выражением 8÷2×(2+2), чтобы понять причины этого правила.
8÷2×(2+2) также может быть записано как $\frac{8}{2}$ x (2+2). Это означает, что мы должны сначала разделить 8 на 2 и умножить частное на произведение в скобках. Кроме того, в отличие от умножения, деление не является коммутативным, а это означает, что нам нужно расставить приоритеты, если оно записано первым.
Кроме того, в отличие от умножения, деление не является коммутативным, а это означает, что нам нужно расставить приоритеты, если оно записано первым.
слева направо
8 ÷ 2 × (2+2)
8 ÷ 2 × 4
8 ÷ 24
44
Право-лефт
9000 8 80004 ÷2×(2+2)8÷2×4
8÷2×4
8÷8
1
Как насчет того, чтобы сначала написать умножение?
8×2÷(2+2)
Слева направо
8×2÷(2+2)
8×2÷4
8×29 0
604
Справа налево
8×2÷(2+2)
8×2÷4
8×2÷4
8×120 0
4 9000 Сравнение , если деление идет перед умножением, мы должны оперировать их слева направо, чтобы получить точный ответ. Однако, если умножение предшествует делению, мы все равно можем получить правильный ответ. Однако для простоты (как вы, возможно, заметили из четвертого метода), работа слева направо облегчит вычисления.
Теперь давайте посмотрим, является ли это одной и той же причиной для сложения и вычитания. Воспользуемся выражением 12+3-2.
слева направо
12+3-2
15-2
13
13 Z
Как насчет того, чтобы сначала написать вычитание?
12-3+2
Слева направо
12-3+2
9+2
11
Справа налево
12-3+2
12+5
7
Опять же, мы получили те же ответы, если сложить слева направо или наоборот первый. Но дело обстоит иначе, если вычитание предшествует сложению. По этой причине, если эти операции в выражении идут последовательно, мы должны выполнять их слева направо.
Как насчет того, чтобы объединить их все? Посмотрим, будет ли это иметь какое-то значение.
Пример: 7×8+6-5
Слева направо
7×8+6-5
56+6-5
56+6-5
9005 4 020004 020504 62174 57ПРАВО-ЛЕТНЫЙ
7 × 8+6-5
7 × 8+1
7 × 8+1
7 ×
63
Следуя MDAS, THE The Правило справа налево
7×8+6-5
56+6-5
56+6-5
56+1
57
влево, если у нас все операции в выражении приведут к неверному ответу. Таким образом, мы должны отдавать предпочтение умножению или делению перед сложением или вычитанием, если они все есть в выражении. Это правило является обязательным, если операции перепутаны. Давайте рассмотрим пример.
Таким образом, мы должны отдавать предпочтение умножению или делению перед сложением или вычитанием, если они все есть в выражении. Это правило является обязательным, если операции перепутаны. Давайте рассмотрим пример.
Пример: 7×8+6-5÷5
Согласно MDAS
7×8+6-5÷5
56+6-1
56+6-1
6-010
61
Слева направо
7×8+6-5÷5
56+6-5÷5
56+6-5÷5
6 62-5÷5
57÷5
$\frac{57}{5}$
Короче говоря, нам нужно следовать правилу слева направо из-за приоритета умножения или деления и сложения или Вычитание в выражении. Кроме того, нам нужно поместить математический символ до или после символа группировки, такого как круглые скобки (()), квадратные скобки ([]) и фигурные скобки ({}), если термины вокруг них не являются сгруппированными терминами.
Давайте разберем приведенные выше правила на примере.
Пример
Упростите следующее выражение, используя порядок действий PEMDAS –
6 + 3 – 4 x 2
Решение
Нам дано выражение 4 0 4 x 0 9 3 Важно отметить, что здесь задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем вычтите, а затем сложите, так как операция вычитания предшествует сложению слева направо.
Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем вычтите, а затем сложите, так как операция вычитания предшествует сложению слева направо.
Таким образом, мы имеем
6 + 3 – 4 x 2
= 6 + 3 – 8 (Здесь мы решили 4 x 2, что дало нам результат 8 )
= Далее мы добавим 6 и 3, чтобы получить 9. Итак, у нас есть
6 + 3 – 8 = 9 – 8 = 1
Следовательно, 6 + 3 – 4 x 2 = 1
Теперь мы узнали, что мы подразумеваем под PEMDAS. Здесь важно отметить, что первый алфавит правила PEMDAS, то есть скобки, имеет большое значение при решении алгебраических выражений. Существуют определенные правила, о которых следует помнить при удалении этих скобок или квадратных скобок, если они общеизвестны. Давайте теперь узнаем об этих правилах.
Использование квадратных скобок Мы только что узнали о приоритете основных операций сложения, вычитания, умножения и деления. В соответствии с ним порядок, в котором должны выполняться операции, — это сначала деление, затем умножение, после чего сложение и, наконец, вычитание, но иногда в сложных операциях требуется, чтобы набор операций выполнялся до другого. Например, если мы хотим, чтобы сложение выполнялось перед делением или умножением, нам нужно использовать скобки.
В соответствии с ним порядок, в котором должны выполняться операции, — это сначала деление, затем умножение, после чего сложение и, наконец, вычитание, но иногда в сложных операциях требуется, чтобы набор операций выполнялся до другого. Например, если мы хотим, чтобы сложение выполнялось перед делением или умножением, нам нужно использовать скобки.
Скобки используются для ясности в порядке операций, в котором должны выполняться несколько операций в математическом выражении. Скобка указывает, что операции внутри нее должны выполняться до операций вне ее. Например, выражение 24 ÷ 3 x 4 обычно решается как –
24 ÷ 3 x 4
= 8 x 4 = 32
Однако, если мы хотим сначала умножить 3 и 4, а затем разделить 24 на получившееся число запишем выражение как
24 ÷ ( 3 x 4 )
Теперь, согласно правилу PEMDAS, мы сначала разгадаем скобки, чтобы получить,
24 ÷ ( 3 x 4 )
= 24 ÷ 12
= 40 9004 = 2 900 сложные выражения иногда необходимо иметь (внутри) в одно и то же время (одно внутри другого может сбивать с толку, поскольку чаще всего используются разные типы скобок) are
| Скобки | Имя | |||||||||
| () | С Коррезис общих кронштейнов | |||||||||
| {} | Брекеты или кудривые скобки | |||||||||
| [] | . каждый символ скобки указывает на начало скобки, а правая часть указывает на конец скобки. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки. каждый символ скобки указывает на начало скобки, а правая часть указывает на конец скобки. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.Давайте теперь поймем правила, которые необходимо соблюдать при удалении скобок в алгебраическом выражении Удаление скобокЧтобы упростить выражения, содержащие более одной скобки, мы будем использовать шаги, описанные ниже –
Давайте разберем приведенные выше шаги на примере. Пример Упростим: 37 – [ 5 + { 28 – ( 19 – 7 ) } ] Решение Нам дано выражение ) } ] Мы будем использовать PEMDAS для решения данного выражения. Сначала мы удалим самую внутреннюю скобку, чтобы получить 37 – [ 5 + { 28 – 12 } ] …………………… [Удалим самую внутреннюю скобку ( ) ] Далее удалим фигурную скобку фигурные скобки, чтобы получить 37 – [ 5 + 16 ] …………………………. Теперь мы удалим квадратные скобки, чтобы получить, 37 – 21 ………………………… [удаление квадратных скобок ] Наконец, мы найдем разницу между 37 и 21, чтобы получить 16. Следовательно, упрощение 37 – [ 5 + { 28 – 12 } ] даст 16. В большинстве случаев мы могли видеть показатели степени внутри скобок или любых других символов группировки. Прежде всего, экспоненты — это короткие обозначения от умножения одного и того же числа дважды или более. 3×3×3×3 3 4 Итак, вы можете спросить: «Почему это нужно делать перед умножением и делением?» Давайте рассмотрим пример, чтобы понять, почему. 81÷3 4 Из этого примера ясно, что мы не можем сразу разделить 81 на 34, потому что мы еще не знаем точное значение 34. В противном случае, если мы разложим 34 в выражении , это даст нам 81÷3 4 81÷(3×3×3×3) На этом этапе вы можете заметить, что мы сгруппировали в скобках термины, которые мы разделили. 81÷3×3×3×3 27×3×3×3 81÷(3×3×3×3) 81÷81 И так как члены теперь заключены в круглые скобки, оставьте Имейте в виду, что в правиле PEMDAS мы должны сначала решить значение внутри него, прежде чем другие операции, присутствующие в выражении. Из того, что мы видели, важно сначала решить члены с показателями степени, чтобы получить их точное значение и упростить процесс вычисления выражения. Отрицательные целые числа в скобкахВы можете заметить, что если мы закончили решение операций внутри круглых скобок, мы удалим круглые скобки и опустим один вычисленный член. Основа по определению заключается в том, что мы используем скобки только для группы терминов или выражений. Итак, если термины внутри были выдавлены, он превратится в один термин (уже не в группу). Что, если мы упростим отрицательные термины? Имейте в виду, что технически любой отрицательный член по умолчанию умножается на -1. +×-=- -×-= + Пример 1: 12 ÷ 3 +(5-7) 12 ÷ 3 +(5-7) Решите выражение внутри скобков. 3+(-2) 12 ÷ 3+(-2) Работая разделение следующее 4+1 (-2) Умножение (-2) на +1 4-2 2 Пример 2: 9+5-(-10+5) 9+5-(-10+5) Решите выражение внутри скобков первые 9+5-(-5) 9+ 5-1 (-5) Умножение (-2) на -1 9+5+5 19 Различные примеры с использованием правила PEMDAS Теперь, когда все ясно, давайте рассмотрим различные примеры выражений, чтобы правильно применять правило PEMDAS. Пример 1: 5 × 6-2 × 8+4 5 × 6-2 × 8+4 Решите выражения внутри скобков первые 30-212 30-2 × 7 Умножение следующее 30 -24 6 Пример 2: 2 4 ÷ (7-3) +5 2 4 ÷ (7-3) +5 Решайте выражение внутри скобок первого 2 4 ÷ 4+5 2 4 ÷ 4+5 Упростить термин с показателем 16 ÷ 4+5 16 ÷ 4+5 5 Расположение подразделения следующее 4+5 9 Пример 3: 10+ (3 2 -6) × 7 10+ (3 2 -6) × × 7 Решите выражение в скобках first 10+(9-6)×7 Упростите член с показателем степени 10+3 × 7 10+3 × 7 Умножение работы Далее 10+21 31 Пример 4: $ (\ frac {1} {2}+\ frac {2} {3 }) x \frac{1}{7}$ $(\frac{1}{2}+\frac{2}{3}) x \frac{1}{7}$ Решите выражение в скобках первые $(\frac{3}{6}+\frac{4}{6}) x \frac{1}{7}$ Найдите общий знаменатель $\frac{7}{6} x \frac {1}{7}$ $\frac{1}{6}$ Пример 5: $2÷\frac{3}{4}-(\frac{5}{8}-\frac{ 3}{8})$ $2÷\frac{3}{4}-(\frac{5}{8}-\frac{3}{8})$ Сначала решите выражение в скобках $2 ÷\frac{3}{4}-\frac{2}{8}$ $ 2 ÷ \ frac {3} {4}-\ frac {2} {8} $ Расположение Фракций Next $ \ frac {1} {2} x \ frac {3} {4}- \ frac {2} {8} $ $ \ frac {3} {8}-\ frac {2} {8} $ $ \ frac {1} {8} $ Пример 607 : (3 3 -4) x (26÷13)+(9-5) (3 3 -4) x (26 ÷ 13)+(9-5) Решите выражения внутри скобков первой (9-4) x 2+4 Упростить термин с показателем 5 × 2+4 5 × 2+4 Работайте умножение следующее 10+4 14 Пример 7: -50+60 ÷ (5 2 -15) -50+60 ÷ (5 2 -15) Решите выражение внутри скобок первого -50+60 ÷ (25- 15) Упростите термин с показателем -50+60 ÷ 10 -50+60 ÷ 10 Расположение подразделения Далее -50+6 -44 Применение правила PEMDAS Существует множество способов применения этого правила. Ситуация 1. Покупка продуктов Майя добавила в свою корзину следующее: 6 упаковок лапши рамен (4 доллара каждая), 4 банки грибного супа (1,5 доллара каждая) и 2 буханки хлеба (\ по 2,5 доллара за штуку). Она хочет знать, что нужно набрать в своем мобильном калькуляторе, чтобы узнать, какая у нее будет сдача, если она заплатит 50 долларов. Какое правильное выражение Майя должна ввести в свой калькулятор? Решение: Рэмэн лапша 6 × (\ $ 4) Грибной суп 4 × (\ $ 1,5) Loaf of Bread 2 × (\ $ 2,5) Мы должны добавить все выражения выше, чтобы получить сумму. . Поскольку сумма всех выражений будет вычтена из 50-долларовой купюры, нам нужно сгруппировать их или заключить в круглые скобки. 6×4+4×1,5+2×2,5 Суммировать цены всех товаров 50-(6×4+4×1,5+2×2,5 Чтобы вычесть сумму из суммы счета ) Значит, Майя должна ввести 50-(6×4+4×1,5+2×2,5.) Ситуация 2: Решение алгебраического уравнения Если вы в настоящее время изучаете алгебру, возможно, вы сталкиваетесь со многими проблемами, когда для решения уравнения требуется правило PEMDAS. Типичный пример приведен ниже. 18÷6×b-4=17 18÷6×b-4=17 0007 3 × B-4 = 17 3 × B-4 = 17 3B-4 = 17 3B-4+4 = 17+4 Добавить 44 к обеим сторонам 3B = 21 $ \ frac{3b}{3}=\frac{21}{3}$ Разделить обе части на 3 b=7 Ситуация 3: Преобразование единиц измерения температуры Научные формулы, такие как градусы Цельсия в градусы Фаренгейта и наоборот, также используют правило PEMDAS. Формула для перевода градусов Цельсия в градусы Фаренгейта: ℉=℃∙$\frac{9}{5}$+32 Решение 1: ℉=25°∙$\frac{9}{5}$+32 $\frac{9}{5}$+32 Умножить целое число на числитель следующего члена ℉=$\frac{225°}{5}$+32 ° ℉ } {5}$+32 ℉=45°+32 77° 0Решение0004 ℉=25°∙$\frac{9}{5}$+32 ℉=25°$\frac{9}{5}$+32 = 5 ° ∙ 9+32 ℉ = 5 ° ∙ 9+32 Умножение. Указания: Вычислите следующие выражения.
Решения для уровня деятельности 1: × 1.5) Решите выражение внутри скобков Первая 20 ÷ 4+15 20 ÷ 4+15 Работайте дивизию следующим 5+15 20 2. (6 2 -12) ÷ 2. -7 Сначала решите выражение в скобках (36-12) ÷ 2-7 Упростить термин с показателем 24 ÷ 2-7 24 ÷ 2-7 Работая отделение следующее 12-7 5 3. 35-7 28 4. 100- (150 ÷ 3) ÷ 5 2 Решите выражение внутри скобок первого 100-50 ÷ 5 0011 2 Упростите термин с показателем 100-50 ÷ 25 100-50 ÷ 25 Работа. +1) Решите выражения внутри скобков первые 5 x (3 2 +1) Упростить термин с показателем 5 x (9 +1) Решите оставшееся выражение внутри скобков 5 x 10 50 6. 6+4 3 ÷ 16 Упрощайте термин с показателем первой 6+64 ÷ 16 6+64 ÷ 16 Отдел работы Далее 6+4 10 7. $ \ frac {1} {2} x \ frac {1} {4} $ 3 Примените умножение первое $ \ frac {1} {8 ÷ ÷ 3 $ \frac{1}{8} x \frac{1}{3}$ $\frac{1}{24}$ 8. ($\frac{5}{2}+\frac{3}{2}$)÷2×8 Сначала решите выражение в скобках 4 ÷ 2 × 8 4 ÷ 2 × 8 MD присутствует, поэтому работайте слева направо 2 × 8 16 9. 7 2 +1 × 2 упростите термин с показателем 49+1 × 2 49+1 × 2 Умножение работы Далее 49+2 51 10. (800-350) -(2 × 45)+(72 ÷ 2 3 ) Решите выражения внутри скобков первые 450-90+(72 ÷ 8) Упростить термин с показателем 450-90+9 450-90+9, как присутствует, работайте слева направо 360+ 369 Уровень активности 2 (эта активность подходит для классов 7-12. ) Указания: Для чисел 1-5 рассчитайте следующие выражения. Затем решите задачи на числа 6-7.
Решения для уровня задания 2:
3+60 ÷ (-3) 3+60 ÷ (-3) эксплуатируйте дивизию следующего 3-20 17
-5+(5 3 ÷25)×4 Упростить член с показателем степени -5+(125÷25)×4 0 0 7 — 0 9 внутри выражения +5×4 -5+5×4 0007 -5+20 15
((16)5÷3 AS присутствует, поэтому вычисляйте слева направо скобки 28÷4 7
-7-9+3 × 6 -7-9+3 × 6 Умножение работы. -16+18 2
($\frac{10}{5}+\frac{4}{5}) x (\frac{5}{14}$)×-3 Найдите общий знаменатель ($\frac{14}{5} x \frac{5}{14}$)×-3 ($\frac{14}{5} x \frac{5}{14}$)× -3 Операция умножения next 1×-3 -3
13 × 3-2 × a+5 = 60 13 × 3-2 × a+5 = 60 Применить умножение первое 39-2A+5 = 60 9 39-2a+5 = 60 Добавить аналогичные члены -2a+44 = 60 -2a+44-44 = 60-44 Вычитание 44 с обеих сторон -2a = 16 $ \ frac { -2a}{-2}=\frac{16}{-2}$ Разделить обе части на -2 a=-8 4 4460 Формула преобразования Фаренгейта в Цельсия: Метод 1: ℃=}$\frac{5}{9} $ . (68°-32°) Решите выражение в скобках ℃=$\frac{5}{9}$ . 36° ℃=$\frac{5}{9}$∙36° 0007 ℃ = $ \ frac {180 °} {9} $ ℃ = 20 ° Метод 2: ℃ = $ \ frac {5} {9} $. (68°-32°) Решите выражение в скобках ℃=$\frac{5}{9}$ . 36 ° ℃ = $ \ frac {5} {9} $ .36 ° Разделите все число на предыдущий знаменатель ℃ = 5 ∙ 4 ° ℃=20° Пример 1 Упростить: 197 – [1/9 { 42 + (56 – $\overline{8+9}$ ) } +108 ] Решение Нам дано алгебраическое выражение, 197 – [1/9 { 42 + (56 – $\overline{8+9}$ ) } +108 ] Мы будем использовать PEMDAS для решения приведенного выше выражения. Обратите внимание, мы видим присутствие vinculum в выражении, поэтому его нужно сначала решить. Решив винкулум, получим, 197 – [1/9 { 42 + (56 – 17 ) } +108 ] Далее удалим самую внутреннюю скобку, чтобы получить, 197 – [1/ 9 { 42 + 39 } +108 ] Теперь мы удалим фигурные скобки, чтобы получить 197 – [81 / 9 +108 ] Теперь важно видеть, что в квадратных скобках у нас есть две операции выполняться, деление и сложение. Итак, следуя правилу PEMDAS, мы сначала выполним деление, чтобы получить 197 – [9 + 108 ] Далее мы удалим квадратные скобки, чтобы получить 197 – 117 Наконец, нам просто нужно найти разницу двух оставшихся значений, чтобы получить 80. Следовательно, упрощение 197 – [1/9 { 42 + (56 – $\overline{8+9}$ ) } +108 ] = 80. Пример 2 Упростить 95 – [ 144 ÷ ( 12 x 12 ) – ( -4 ) – { 3 – $\overline{17-10}$ } ] Решение Нам дано выражение 95 – [ 144 ÷ ( 12 x 12 ) – ( -4 ) – { 3 – $\overline{17-10}$ } ] Мы будем использовать PEMDAS для решения приведенного выше выражения. Обратите внимание, мы видим наличие vinculum в выражении, поэтому его нужно сначала решить. Решив винкулум, получим, 95 – [ 144 ÷ ( 12 x 12 ) – ( – 4 ) – { 3 – 7 } ] Далее удалим самую внутреннюю скобку, чтобы получить, 95 – [ 144 ÷ 144 + 4 – { 3 – 7 } ] Теперь мы удалим фигурные скобки, чтобы получить 95 – [ 144 ÷ 144 + 4 + 4 ] Теперь важно увидеть, что в квадратных скобках мы должны выполнить две операции: деление и сложение. Итак, следуя правилу PEMDAS, мы сначала выполним деление, чтобы получить 95 – [ 1 + 4 + 4 ] Затем мы удалим квадратные скобки, чтобы получить 95 – 9 = 86 Следовательно, упрощение 95 – [ 144 ÷ ( 12 x 12 ) – ( -4 ) – { 3 – $\overline{17-10}$ } ] = 86 Пример 3 Упростить ( 1 + 3 ) 2 – 2 ( 4 – 7 ) Решение Нам дано выражение ( 1 + 7 2 – 3 ) 21 ) Мы видим, что в выражении есть скобки, а также показатель степени. ( 4 ) 2 + 6 Затем мы решим показатель степени в выражении, чтобы получить 16 + 6 Наконец, у нас осталась операция сложения, после которой мы получим результат 2. Пример 4 Решение 15 – ( – 5) { 4 – $\overline{7-3}$ } ÷ [ 3 { 5 + ( -3 ) x ( -6 ) } ] Мы будем использовать PEMDAS для решения приведенного выше выражения. Обратите внимание, мы видим наличие vinculum в выражении, поэтому его нужно сначала решить. Решив винкулум, получим, 15 – ( – 5) { 4 – 4 } ÷ [ 3 { 5 + ( -3 ) x ( -6 ) } ] Далее удалим самую внутреннюю скобку чтобы получить, 15 + 5 x 0 ÷ [ 3 { 5 + 18 } ] Теперь мы удалим фигурные скобки, чтобы получить 15 + 0 ÷ [ 3 x 23 ] Затем мы удалим квадратные скобки, чтобы получить, 15 + 0 ÷ 69 Теперь важно увидеть, что нам нужно выполнить две операции: деление и сложение. 15 + 0 = 15 Следовательно, упрощение 15 – ( – 5) { 4 – $\overline{7-3} $ } ÷ [ 3 { 5 + ( -3 ) x ( -6 ) } ] = 15 Основные факты и сводка
Порядок действий (PEMDAS) (на тему «Работа из дома») Рабочие листы Просмотреть все рабочие листы We потратить много времени на изучение и сбор информации на этом сайте. |
 (78)
(78)



 Работа по теме урока
Работа по теме урока Работа с учебником с. 24
Работа с учебником с. 24 Объяснение расстановки действий
Объяснение расстановки действий
 24 правило, с. 25 №3
24 правило, с. 25 №3 Заранее решайте задачи и используйте любую настольную игру с кубиками,
Заранее решайте задачи и используйте любую настольную игру с кубиками,