Порядок действий в пределах 100 (все действия)

Описание

Примеры на порядок действий в пределах 100 позволяют закрепить навыки вычисления в правильной очередности действий. Эти задания выделятся отдельным этапом, так как они способствуют формированию логического мышления ребенка. Именно поэтому нужна практика, чтобы закрепить понимание очередности вычислений. Для этого достаточно заниматься 10-15 минут в день.

Программа формирует примеры на порядок действий в пределах 100. В примерах содержатся скобки и все математические действия: сложение, вычитание, умножение и деление.

Программа написана в Excel с помощью макросов. Формируются карточки примеров: 2 столбика по 15 примеров на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. В конце карточки формируются ответы на примеры, которые можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.

Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл, сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.

Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.

Другие программы, которые помогут закрепить навыки счета в пределах 100:

 Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.

На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Дидактический материал «Примеры на порядок действий. 2 класс» | Методическая разработка по математике (2 класс) по теме:

52 – 24 : 6 • 8 =_______ 94 – 45 : 9 • 8 =_______ 58 + 56 : ( 14 – 7 ) =______ 94 – ( 12 – 3 ) • 6 =_______ 72 – ( 38 + 26 ) : 8 =_____ 45 : 5 + 4 • 9 =________ 7 • 7 + 6 • 6 =________ 28 : 7 + 18 : 2 =_______ 7 • 8 + 24 : 3 =________ 80 – 56 : 7 – 72 =______ 9 • 7 – 60 – 3 =________ 27 – 4 • 3 + 5 • 4 =_______ 8 • 2 + 35 : 5 – 4 • 5 =______ 6 • 3 : 2 + 7 • 7 – 36 =_____ 2 • ( 28 : 7 ) • 5 – 6 =_____ 99 –3• (18 – 12): 9–24 :4 =__ 63 : 9 + (54 – 47) • 6 =____ ( 14 + 3 • 7 ) : 7 + 37 =____ 48 : 8 + ( 65 – 56 ) • 5 =____ (36 : 9 +23)–3 • 6 +20 : 5=__

100 – 81 : 9 • 5 =_______ (64 : 8 + 24) : 4 =_______ ( 63 : 9 • 3 + 4 ) : 5 =______ (45 + 9 ) : 9 • 7 =_______ 90 – 36 + 42 : 6 =_______ ( 73 + 27 ) : 10 • 6 =______ 54 : 6 • 2 : 3 =_______ ( 7 + 5 • 7 ) : 7 + 43 =______ 6 •  6 + 6 • 8 – 42 =_______ (5 • 5 + 15 ) : 8 + 12 =_____ ( 70 – 9 + 2 ) : 9 • 8 =______ ( 15 + 15 ) : 5 •  9 =_______ ( 54 : 6 • 9 + 9 ) : 10 =_____ ( 72 : 8 ) •  4 + 44 =______ 6 • 2 : 3 •  9 + 71 =______ ( 57 + 18 : 6 ) : 10 =_____ ( 3 • 8 + 12 ) : 6 =____ 52 + 9 • 3 – 4 • 8 =_____ 5 • ( 71 – 68 ) + 6 • 9 =____ 8 • 5 + 3 • 6 =______

8  •  8 + 2  •7 =_______ 5 • 9 + 6  • 4 =_______ 7 •  8 – 4 • 7 =_______ 9 • 6 + 5 • 8 =_______ 7 • 7  + 6 • 8 =________ 6 • 7 – 81 : 9 =________ 54 : 9 + 7 • 7 =_______ 48 : 8 •  7 =________ 9 • 7 – 4 • 5 =_______ 8 • 9 – 4 • 7 =_______ 3 • 8 – 6• 3 =_______ 8 • 4 – 9 • 2 =_______ 9 • 9 – 6 • 7 =______ 4 • 5 – 54 : 9 =______ 63 : 9 + 6 • 8 =_______ 64 : 8  • 9 =______ 8 • 7 + 4 • 3 =_____ 3 • 9 + 7 • 7 =_____ 4 • 6 + 6 •  6 =______ 3 • 5 + 4 • 9 =______

Выражения со скобками.

Математика 2 класс Богданович. ГДЗ, решебник.

Категория: —>> Математика 2 класс Богданович  
Задание:  —>>   192 — 208  



наверх

Задание 192.

Выполни задания устно.

• 1) Найти сумму чисел 5 и 2. Вычесть эту сумму из числа 10.
• 2) К числу 8 прибавить разность чисел 9 и 3.

Решение:

• 1) 10 — (5 + 2) = 3
• 2) 8 + (9 — 3) = 14

---

Задание 193.

В рулоне было 15 м ткани. Первый покупатель приобрёл 5 м ткани, а второй 3 м. Сколько метров ткани осталось в рулоне?
Чтобы узнать, сколько метров ткани осталось в рулоне, продавец поступил так: вычислил, сколько всего метров ткани он продал, а потом полученное число вычел из 15.

15 — (5 + 3) = 7 (м)

Скобки обозначают, что сначала ну ясно найти сумму, а потом выполнить действие вычитания.

---

Задание 194.

Прочитай и вычисли.
От числа 12 отнять сумму чисел 7 и 2.

К числу 8 прибавить разность чисел 13 и 6.

Решение:

• 1) 12 — (7 + 2) = 3
• 2) 8 + (13 — 6) = 15

---



Задание 195.

На стоянке было 12 автомобилей. Сначала отъехало 4 автомобиля, а потом — ещё 3. Сколько автомобилей осталось на стоянке?

Решение:

• 1) 12 — (4 + 3) = 5
• Ответ: 5 автомобилей.

---

Задание 196.

У одной белки 9 орехов и столько же — у другой. Сколько всего орехов у белок?

Решение:

• 1) 9 + 9 = 18
• Ответ: 18 орехов.

---

Задание 197.

Прочитай и вычисли.

• 1) Из числа 14 вычесть разность чисел 7 и 2.
• 2) К числу 8 прибавить сумму чисел 3 и 6.

Решение:

• 1) 14 — (7 — 2) = 9
• 2) 8 + (3 + 6) = 17

---

Задание 198.

На стоянке было 13 грузовых автомобилей, а легковых на 8 меньше.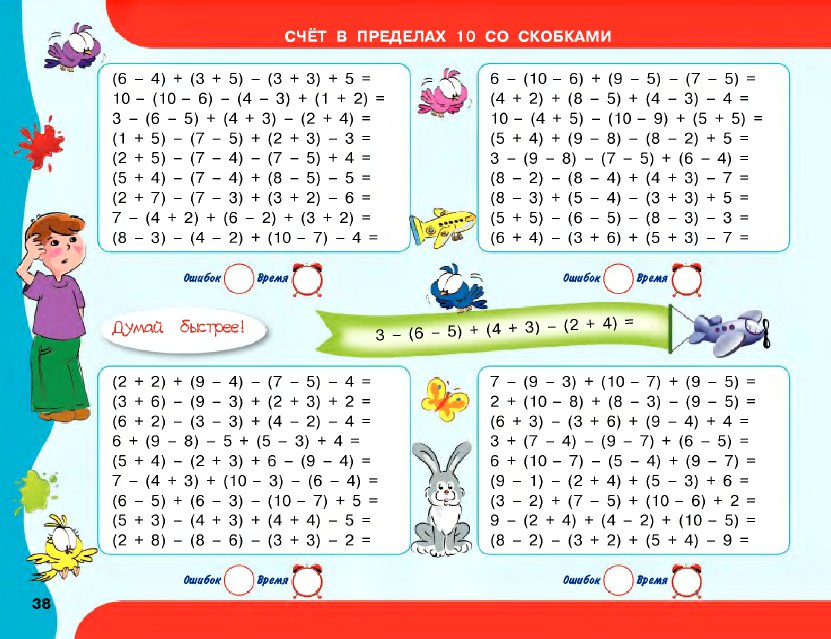

Подъехало еще 6 легковых автомобилей. Сколько легковых автомобилей стало на стоянке?

Решение:

• 1) (13 — 8) + 6 = 11
• Ответ: 11 легковых автомобилей.

---

Задание 199.

Дополни и реши задачу.
В одном классе 7 компьютеров, а в другом на 2 компьютера … .

Решение:

В одном классе 7 компьютеров, а в другом на 2 компьютера меньше. Сколько компьютеров в 2 классах вместе.

• 1) 7 — 2 = 5
• 2) 7 + 5 = 12
• Выражение: (7 — 2) + 7 = 12
• Ответ: 12 компьютеров.

---

Задание 200.

Реши примеры.

Решение:

13 — (9 — 3) = 7	16 — (7 + 2) = 7	7 + (2 + 5) = 14
13 — 9 — 3 = 1	16 — 7 + 2 = 11	7 + 2 + 5 = 14

---

Задание 201.

По рисунку объясни приёмы вычислений

---

Задание 202.

Из каждого примера на сложение составь два примера на вычитание.

Решение:

7 + 5 = 12 12 — 5 = 7 12 — 7 = 5

10 + 9 = 19 19 — 10 = 9 19 — 9 = 10

3 + 8 = 11 11 — 3 = 8 11 — 8 = 3

---

Задание 203.

Прочитай примеры по-разному, используя данные слова.

Сложить Плюс Увеличить Сумма

Вычесть Минус Уменьшить Разность

---

Задание 204.

Решение:

• 1) Сложить 9 и 7, равно 16. 9 плюс 7 равно 16. 9 увеличить на 7, равно 16. Сумма девяти и семи равна шестнадцати.
• 2) 14 вычесть 6 равно 8. 14 минус 6 равно 8. 14 уменьшить на 6 равно 8. Разность четырнадцати и шести равна восьми.

---

Задание 205.

Утром от коровы надоили 9 л молока, | а вечером — на 1 л меньше. | 3 л молока от вечернего удоя оставили, | а остальное продали. Сколько литров молока от вечернего удоя продали?
Прочитай всю задачу. Подумай, о чём в ней рассказывается.
Прочитай задачу по частям, на которые она разделена линиями.
Реши задачу.

План решения

• 1) Сколько литров молока надоили вечером?
• 2) Сколько литров молока от вечернего удоя продали?

Решение:

• 1) 9 — 1 = 8
• 2) 8 — 3 = 5
• Выражение: (9 — 1) — 3 = 5
• Ответ: 5 литров.

---

Задание 206.

В субботу отец и сын вместе обрезали 4 дерева. В воскресенье отец обрезал 3 дерева и столько же деревьев обрезал сын. Сколько всего деревьев они обрезали за 2 дня?

Решение:

• 1) 3 + 3 = 6
• 2) 4 + 6 = 10
• Выражение: 4 + 3 + 3 = 10
• Ответ: 10 деревьев.

---

Задание 207.

Реши примеры.

Решение:

14 — 6 — 6 = 2	7 + 5 + 1 = 13	16 — 8 + 1 = 9
14 — (6 — 6) = 14	7 + (5 + 1) = 13	16 — (8 + 1) = 7

---

Задание 208.

Составь задачу по рисунку и реши её.

Решение:

Под деревом лежало 12 яблок. Один ежик забрал 4 яблока, а другой еще 3. Сколько яблок осталось под деревом?

• 1) 4 + 3 = 7
• 2) 12 — 7 = 5
• Выражение: 12 — (4 + 3) = 5
• Ответ: 5 яблок.

---



Задание:  —>>   192 — 208  

математика 2 класс | интернет проект BeginnerSchool.ru

Продолжим изучение программы математики в начальной школе и на этот раз разберемся, что же изучают наши дети по этому предмету во 2 классе. Все, как всегда, начинается с повторения. Т.е. что такое цифра и число. Начинаем с 1 и идем до десятка и дальше. В первом классе наши дети проходили счет в пределах 100, и арифметические действия (сложение, вычитание) до 20. На этот раз,  они, не останавливаясь на достигнутом, идут дальше. Считали десятками, продолжаем считать сотнями. Кстати, вы помните, откуда взялись слова сантиметр и гектар, от каких слов образовались? Нашим детям расскажут о том, что римская цифра С – это первая буква латинского слова «cent», что означает «сто».

А греческая буква Н – первая буква греческого слова «гекта», что значит сто. Так считая сотни, наши дети дойдут до тысячи. Затем вспомним азы геометрии. Найдем длину ломаной линии, вычислим периметр многоугольника и площадь составных фигур, затем объем в кубиках. Ну вот, вроде все повторили, теперь можно идти дальше. Остановимся на вычислениях до 20 и проработаем их, решаем задачи на заданную тему. Задачи наши дети не только решают, но и придумывают сами. А затем возвращаются к геометрии и останавливаются подробней на геометрических фигурах.  Ну вот, дошли и до вычислений в пределах 100. Учимся сложению и вычитанию в столбик.

А дальше, до нового года или сразу после, это зависит от программы обучения, наши дети познакомятся с новыми действиями – умножением и делением. Сначала представляем умножение, как сложение одинаковых чисел, понимаем, что такое «вдвое больше», а теперь делим пополам, так мы впервые встречаем деление. Учимся делить и проверяем себя сложением. Затем решаем задачи с помощью этих действий. Потренировались? – остановимся на измерении величин. В чем измеряют время, массу или температуру? Далее вычисляем длину, расстояние и площадь и учимся вычислять время. Вот мы и дошли до таблицы умножения. И пошло умножение и деление на 10. Дети вычисляют этими действиями, решают с помощью них задачи. Ну, вроде научились, теперь пришло время действий с выражениями. Начнем со сложения и умножения и узнаем их обратные действия. Дальше – больше: разберем выражения со скобками, каков порядок действий? Сравним выражения. Сгруппируем слагаемые и множители и самостоятельно составим выражения.

Вот мы и подошли к концу изучения курса математики 2 класса. Правда, интересно?

Этот экскурс был составлен по программе обучения «Планета знаний», в других программах изучается примерно тоже самое, может в другой последовательности. Если вам интересно продолжение подпишитесь на нашу рассылку. Спасибо за внимание и всего наилучшего.

 

Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

Конспект урока «Счет в пределах 100» 2 класс

ДАТА 23.11.2017

КЛАСС 2В

Тема: Закрепление сложения и вычитания в пределах 100.

Цели урока:

Образовательные:

Совершенствовать вычислительные навыки и умение решать задачи;

Формировать активность детей на уроке, навыки самостоятельной работы; повысить мотивацию обучения, интерес к математике.

Развивающие:

Развивать логическое мышление учащихся; обогащать словарный запас учащихся предметной терминологией;

Развивать умение сравнивать, творческие способности, воображение, смелость, расширить кругозор.

Воспитательные: 

Воспитывать в учащихся взаимопомощь и самостоятельность, воспитать трудолюбие, аккуратность, уважительного отношения к старшим и друг к другу, честность, отзывчивость.

Тип урока: Урок обобщения и систематизация знаний

Форма урока: Урок – сказка.

Оборудование: иллюстрации к сказке, карточка с цифрами, корзинка с яблоками, карточки с тестами.

Литература: 1. «Математика» учебник для 2 кл. нач. шк. В 2 ч. Ч 2 (Второе полугодие) / М.И. Моро, М.И. Бантова, Г.В. Бельтюкова и др. – 2-е изд. – М: Просвещение, 2003.

2. Беженова М.А. Весёлая математика. – Д: Сталкер, 1998. – 320 с.: ил. (Серия «Скоро в школу»).

3.Сычева Н.Г. «Лучшие нестандартные уроки по математике в начальной школе» Библиотека учителя 2014. – 172 с.

ХРОНОМЕТРАЖ УРОК

1. Организация начала урока (1)

2. Сообщение темы и цели урока (1)

3. Актуализация ранее полученных знаний

3.1 Задачи на смекалку. Устный счет. (2)

3.2 Минутка каллиграфии (1)

3.3 Разгадывание шифра (3)

4.Обобщение и систематизация основных теоретических положений(6)

4. 1 Решение примеров № 2, с.68 (2)

Физминутка

4.2 Решение задачи (7)

4.3 Самостоятельная работа с тестами по карточкам (3)

4.4 Решение неравенств № 5, с.68 (5)

4.5 Решение задачи (6)

5. Рефлексия. Подведение итогов урока (4)

6. Оценки за урок (1)

7. Домашнее задание (1)

1. Организация начала урока

— Добрый день, ребята! Мне приятно вас всех видеть. Давайте подарим друг другу хорошее настроение.

2. Сообщение темы, целей и задач урока

— Сегодня наш урок будет не обычным. Мы с вами отправимся в сказку, научимся считать и решать новые примеры и задачи.

— Девизом нашего урока станут слова. «Считай, смекай, отгадывай и помогай!»

3.Актуализация ранее полученных знаний

Задание 3.1 «Минутка каллиграфии»

-Прежде чем мы отправимся в путешествие, откройте ваши тетради, отступите 2 клетки сверху и 10 клеток от полей и запишите число, классная работа. Сегодня 23 ноября, что вы можете сказать о нем? (двузначное, в записи используется 2 цифры, 2 дес., 3 ед.)

-Теперь отступите клетку вниз и пропишите и пропишите через клетку число 23.

Задание 3.2 «Разгадывание шифра»

— Расположите числа в порядке возрастания:

—  Перед вами примеры, решив которые вы узнаете куда мы сегодня с вами отправимся, найдите ответы на карточках и расставьте в порядке возрастания:

20+36=56(У) 6+9=14(З) 12-9=3(С) 15-6=9(К) 7+5=12(А) 35-7=28 (К)

30 6 4 5 2 7 5 1 3 2 5 2

3.3 «Задачи на смекалку, устный счет»

— Готовы ли вы к путешествию? Итак, сказка начинается!

— Сейчас я расскажу вам отрывок из сказки, а вы отгадайте в какую сказку мы с вами отправляемся.

Жили- были муж с женой. Была у них дочка Аленушка и сынок Иванушка.

— Аленушка- говорит мать с отцом. – Мы поедем на базар. А ты не ходи со двора, береги Иванушку. А мы тебе подарки привезем! Уехали родители, а Аленушка позабыла, что ей приказали родители, посадила Иванушку на травку. А сама на улицу побежала и заигралась.

И так, в какую сказку мы с вами сейчас отправимся? (Гуси лебеди)

А Ване скучно стало. Стал он от скуки считать все, что вокруг видел. Поможем ему.

Пять ворон на крышу сели.

Еще семь к ним прилетели

Отвечайте быстро, смело

Сколько всех их прилетело. (12)

Двенадцать щенят в футбол играли.

Шесть щенят домой позвали.

Ваня наш сидит, считает.

Сколько их теперь играют? (6)

— Стал Ваня от скуки решать примеры и вставлять пропущенные цифры, но у него это плохо получается.

— Давайте ребята поможем Иванушке решить примеры.

3.3.1 Решение примеров устно

63 78 46 69

50 18 16 29

4.Обобщение и систематизация основных теоретических положений

— Но вдруг налетели злые гуси- лебеди. Подхватили мальчика и унесли, а кто им приказал это сделать, мы узнаем, решив примеры (67+5= 72; 32-9=23;

60 7 20 12

46+9=54; 95-6=89)

40 6 80 15

— Вам надо разложить на удобные слагаемые.

— Вот кто похитил Иванушку! Поможем сестрице спасти братца. Ну тогда мы отправляемся в путь вместе с Аленушкой.

4.1 Решение примеров № 2, с.68

— На пути у нас яблонька. Яблонька, яблонька покажи нам дорогу к Бабе- Яге.

Яблонька отвечает: «Покажу, если соберете мои яблочки. Яблочки у меня не простые, а волшебные, чтобы яблочки собрать, надо решить примеры. (Дети по очереди у доски решают примеры)

78+9=87 7+18=25 43-4=39 36-8=28

36+5=41 9+33=42 58-9=49 24-6=18

92+0=92 0+50=50 86-86=0 18-0=18

ФИЗМИНУТКА

Раз – подняться, потянуться,

  Два – согнуться, разогнуться.

Три – в ладоши три хлопка,

  Головою три кивка.

  На четыре — руки шире,

 Пять – руками помахать,

  Шесть – за парту сесть опять.

4.2 Решение задачи

— Идем дальше! На нашем пути печка: «Печка, печка, покажи нам дорогу к Бабе – Яге».

Печка отвечает: « Покажу, если съедите пирожок. Пирожок не простой, а трудная задача».

Бабушка испекла 12 пирожков с мясом и 6 с капустой, а с вареньем 7 пирожков. Сколько всего пирожков испекла бабушка?

— Записываем слово ЗАДАЧА

— О чем идет речь в задаче? (о пирожках)

— О каких пирожках говорится в задаче? (мясом, капустой, вареньем)

— Нам известно сколько бабашка испекла всего пирожков? (нет)

— Какой главный вопрос задачи? (сколько всего пирожков испекла бабушка?)

-На сколько действий данная задача? (2)

— А можно эту задачу решить одним действием? (да)

— Кто пойдет и решит задачу одним действием?

— Какие опорные слова мы запишем в краткой записи? (мясом, капустой, вареньем)

— Как мы обозначим всего пирожков? (фигурная скобка)

-Отступаем 1 клетку вниз и на 2-й полной клетке записываем краткое условие задачи

— Как сократим пирожков? (п.)

Мясо – 12 п.

Капуста – 6 п. ? п.

Варенье – 7 п.

— Если в задаче сказано всего, как мы это покажем? (фигурная скобка)

— Отступаем клетку вниз, пишем слово РЕШЕНИЕ и решаем задачу.

-Давайте составим выражение (12+6+7=25)

— Записываем слово ОТВЕТ

— Что будем писать в ответе? (25 пирожков испекла бабушка)

4.3 Самостоятельная работа с тестами по карточкам

— Идем мы дальше! Перед нами молочная река — кисельные берега. «Речка, матушка, покажи нам дорогу к Бабе – Яге».

Речка отвечает: « Покажу, если выпьете моего киселька. Кисель то не простой, а с трудным заданием».

— У вас на парте лежат карточки с заданием. Вам надо измерить длину ломаной линии и записать ее в сантиметрах и в дециметрах.

4.4 Решение неравенств № 5, с.68

— И вот перед нами густой лес. Деревья расступятся, если мы правильно укажем сравнение чисел.

91+9 9+91 100-45 65

68+7 48+7 55-40 15

4. 5 Решение задачи самостоятельно по карточкам

— Ребята! А вот и избушка Бабы- Яги. Баба- Яга, отдай нам Иванушку. Бабы- Яга отвечает: «Отдам, но сначала решите мою задачу»

— Вам надо решить задачу от Бабы-Яги по вариантам.

— На ваших карточках написана задача. Прочитайте ее внимательно.

— Посмотрите внимательно на доску. Краткое условие задачи у 1 и 2 варианта одинаковое. Вам надо определить главный вопрос задачи и поставить правильную скобку.

— Первый вариант находит сколько всего грибов взяла Баба- Яга для приготовления зелья.

— Второй вариант находит на сколько больше мухоморов чем поганок взяла Баба-Яга для приготовления зелья.

Для приготовления приворотного зелья, Баба Яга взяла 40 мухоморов и 26 поганок. 1В Сколько всего грибов взяла Баба Яга для приготовления зелья? 2В На сколько больше мухоморов чем поганок взяла Баба Яга для приготовления зелья?

Мухоморов – 40 гр. Мухоморов – 40 гр.

Поганок –26 гр. Поганок – 26 гр.

— Отступаем клетку вниз, пишем слово РЕШЕНИЕ и решаем задачу.

-Каким действием будем решать? (1 вариант- сложением 40+26=66; 2- вариант вычитанием 40-26=14)

— Записываем слово ОТВЕТ

— Что будем писать в ответе? (1 вариант-6 грибов; 2 вариант-14 грибов)

— Молодцы! Баба-Яга довольна, что вы решили ее задачки и тем самым помогли сестрице Аленушке спасти братца Иванушку. А за это дед с бабкой привезли вам гостинцы в виде хороших оценок за урок.

5. Рефлексия. Подведение итогов урока

— Пословица, которая нам помогла на уроке « В знании – сила».

— Как вы понимаете ее значение.

 -Давайте вспомним, что удалось нам повторить за урок?

— Что показалось трудным?

— Какое задание было самым интересным?

6. Оценки за урок

7. Домашнее задание

Что такое ассоциативная собственность? — Определение, факты и примеры

Что такое ассоциативное свойство?

Это свойство указывает, что при сложении (или умножении) трех или более чисел сумма (или произведение) остается неизменной независимо от группировки слагаемых (или множителей).

• Группировка означает использование круглых или квадратных скобок для группировки номеров.

• Ассоциативное свойство включает 3 или более чисел.

• Числа, сгруппированные в круглых скобках или скобках, становятся одной единицей.

• Свойство ассоциативности можно использовать только для сложения и умножения, но не для вычитания или деления.

Пример ассоциативного свойства для сложения

Примеры ассоциативного свойства для умножения:

Приведенные выше примеры показывают, что изменение группировки не приводит к изменению ответа.

Свойство ассоциативности полезно при сложении или умножении нескольких чисел.Группируя, мы можем создавать более мелкие компоненты для решения. Это упрощает и ускоряет вычисления сложения или умножения нескольких чисел.

Пример Дополнение :

17 + 5 + 3 = (17 + 3) + 5

= 20 + 5

= 25

Здесь сложение 17 и 3 дает 20. Затем добавление 5 к 20 дает 25. Группировка помогла легко и быстро найти ответ.

Пример Умножение :

3 × 4 × 25 = (25 × 4) × 3

= 100 × 3

= 300

Здесь умножение 25 на 4 дает 100.Тогда 3 можно легко умножить на 100 и получить 300.

Однако мы не можем применить свойство ассоциативности к вычитанию или делению. Когда мы меняем группировку чисел при вычитании или делении, это меняет ответ, и, следовательно, это свойство не применимо.

Пример Вычитание :

10 — (5 — 2) = 10 — 3 = 7

(10 — 5) — 2 = 5 — 2 = 3

Итак, 10 — (5-2) ≠ (10-5) — 2

Пример Подразделение :

(24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3

24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12

Итак, (24 ÷ 4) ÷ 2 ≠ 24 ÷ (4 ÷ 2)

Интересные факты

Удаление символов группировки: круглые, квадратные, фигурные

7

Правила снятия скобок

Кронштейны и скобы

2-й уровень

Отношение a — b к b — a

Правила снятия скобок

Перед круглыми скобками будет стоять знак плюс +

.

a + ( b — c + d )

или знак минус —

a — ( b — c + d ).

Если перед круглыми скобками стоит знак плюс +
, просто удалите их. Ничего не меняется.

a + ( b — c + d ) = a + b — c + d .

Если перед круглыми скобками стоит знак минус —
изменяет знак каждого члена в круглых скобках.
Измените + на — и — на +.

a — ( b — c + d ) = a — b + c — d .

Знак b в скобках понимается как +. Таким образом, после удаления скобок этот член становится — b .

— c в скобках становится + c . И + d становится — d .

Другими словами: Чтобы вычесть сумму, вычтите каждый член суммы .

a — ( b — c + d ) = a — b + c — d .

Вычтем b . Вычтите — c — то есть сложите. И вычтите d .

Мы можем обосновать эти две возможности примерами из арифметики, потому что алгебра абстрагирована — взята из — арифметики.

Например, вот как мы можем вычислить 256 + 98:

	256 + 98	=	256 + 100 — 2
		=	356 — 2
		=	354.
То есть
	256 + (100–2)	=	256 + 100 — 2.
Когда мы убираем эти скобки, ничего не меняется.
А вот как рассчитать 256 — 98:
	256 — 98	=	256–100 + 2
		=	156 + 2
		=	158.
То есть
	256 — (100 — 2)	=	256 — 100 + 2.
Когда мы убираем эти скобки, знак каждого члена в скобках меняется.

Проблема 1.Убрать круглые скобки.

a) p + ( q — r + s ) = p + q — r + s

б) п — ( q — r + s ) = p — q + r — s

В каждой из следующих задач снимите скобки, а затем упростите
, добавив числа.

Например,

( x — 3) — ( y -4)	=	x -3- y + 4
	=	x — y + 1.

Предыдущий знак ( x — 3) понимается как +. Следовательно, знаки в скобках не меняются.

Но предшествующий знак ( y -4) стоит минус. Следовательно, y изменится на -y, а -4 изменится на +4.

Наконец, в алгебре принято писать буквальные термины, x — y , слева от числового члена.

Проблема 2. ( x + 2) + ( y + 8)	=	х + 2 + у + 8
	=	х + у + 10.

Проблема 3. ( x + 2) — ( y + 8)	=	x + 2- y -8
	=	x — y — 6.

Проблема 4. ( x -2) + ( y + 8)	=	x -2 + y + 8
	=	х + у + 6.

Задача 5. ( x -2) — ( y + 8)	=	x -2- y -8
	=	x — y — 10.

Задача 6. ( x -2) — ( y -8)	=	x -2- y + 8
	=	x — y + 6.

Задача 7. ( x -2) + ( y -8)	=	x -2 + y -8
	=	x + y — 10.

Задача 8. ( a -2) + ( b + 3) — ( c -7)	=	a -2 + b + 3- c + 7
	=	a + b — c + 8.

Задача 9. ( a -5) — ( b + 6) — ( c -9)	=	a -5- b -6- c + 9
	=	а — б — в — 2.

Задача 10.( a + 2) — ( b -3) + ( c -8) — ( d + 1)
	=	a + 2 — b + 3 + c — 8 — d — 1
	=	a — b + c — d — 4.

Опять же, когда перед круглыми скобками стоит знак минус, каждый знак внутри них меняется. Мы видели это раньше в правиле Урока 3:

.

a — (- b ) = a + b .

Задача 11. — (- x + y )

=

x — y .

Задача 12.- ( x — y )

=

— х + у .

Задача 13. — ( x + y -2)

=

— x — y + 2.

Задача 14. Запишите отрицательный результат

.

a — b + c — d .

— a + b — c + d .

Пример 1. Размещение скобок. Правила алгебры действуют в обоих направлениях. Следовательно, поскольку мы можем убрать круглые скобки, мы также можем их разместить. Мы можем написать

a — b + c — d

следующими способами:

a — ( b — c + d )

( a — b ) — (- c + d )

a — ( b — c ) — d

И так далее.

Задача 15. Перепишите каждое из следующего, заключив скобки.

a) — x + y = — ( x — y ).

б) — х — у = — ( x + y )

c) — a + b — c + d = — ( a — b + c — d ).

d) Поместите в скобки b и c :

a — b + c — d = a — ( b — c ) — d .

Кронштейны и скобы

Скобки [] и фигурные скобки {} выполняют ту же функцию, что и круглые скобки. Все они группирующие символы. После скобок мы используем скобки для наглядности.После скобок, подтяжки.

При удалении скобок применяются те же правила, что и при удалении скобок.

Пример 2. a — [ b — ( c — d + e )]

Удалим все символы группировки. Мы сделаем это, удалив скобки в первую очередь. Затем мы сделаем это снова, удалив сначала круглые скобки. Студент должен уметь делать это в любом случае.

Итак, после снятия скобок:

a — [ b — ( c — d + e )]

=

a — b + ( c — d + e ).

В скобках есть два термина. Первый член — b . Второй член — ( c — d + e ).(См. Задачу 1c выше.) Поскольку перед скобками стоит -, знак каждого из двух членов изменяется. Знаки в пределах срока ( c — d + e ) не меняются.

Наконец, мы убираем круглые скобки, которым предшествует +:

=

a — b + c — d + e .

Теперь давайте решим ту же задачу, сначала убрав круглые скобки:

a — [ b — ( c — d + e )]	=	a — [ b — c + d — e ]
	=	a — b + c — d + e .

Поскольку перед круглыми скобками стоит знак -, каждый знак внутри них меняется. А поскольку скобкам также предшествует -, каждый знак в них меняется.

Проблема 16.

a) Сначала снимите скобки, затем снимите скобки.

w + [ x — ( y + z )]	=	w + x — ( y + z )
	=	w + x — y — z

Сначала удалите скобки, затем снимите скобки.

w + [ x — ( y + z )]	=	w + [ x — y — z )]
	=	w + x — y — z

б) Сначала снимите скобки, затем снимите скобки.

w — [ x + ( y — z )]	=	w — x — ( y — z )
	=	w — x — y + z

Сначала удалите скобки, затем снимите скобки.

w — [ x + ( y — z )]	=	w — [ x + y — z ]
	=	w — x — y + z

c) Сначала снимите скобки, затем снимите скобки.

w — [ x — ( y + z )]	=	w — x + ( y + z )
	=	w — x + y + z

Сначала удалите скобки, затем снимите скобки.

w — [ x — ( y + z )]	=	w — [ x — y — z )]
	=	w — x + y + z

d) Сначала снимите скобки, затем снимите скобки.

w + [ x — ( y — z )]	=	w + x — ( y — z )
	=	w + x — y + z

Сначала удалите скобки, затем снимите скобки.

w + [ x — ( y — z )]	=	w + [ x — y + z ) [
	=	w + x — y + z

Проблема 17.Удалите все символы группировки. Упрощайте по мере продвижения, оценивая числа. Сначала снимите кронштейны.

a) 5 — [3 — ( x — 2)]	=	5 — 3 + ( х — 2)
	=	2 + x -2
	=	х .

b) 5 — [3 — ( x + 2)]	=	5 — 3 + ( х + 2)
	=	2 + х + 2
	=	x + 4.

c) −5 + [3 — ( x — 2)]	=	−5 + 3 — ( х -2)
	=	−2 — х + 2
	=	— х .

d) 5 — [−3 — ( x + 2)]	=	5 + 3 + ( х + 2)
	=	8 + х + 2
	=	x + 10.

Проблема 18.

a) Сначала снимите скобки, затем скобки, затем скобки.
а) Упростите, добавив числа.

10 — {2 + [3 — ( x — 5)]}	=	10 — 2 — [3 — ( x — 5)]
	=	8-3 + ( x -5)
	=	5 + x -5
	=	х .

Сначала удалите круглые скобки, затем квадратные скобки, затем фигурные скобки.

10 — {2 + [3 — ( x — 5)]}	=	10 — {2 + [3 — x + 5]}
	=	10 — {2 + 3 — x + 5}
	=	10-10 + x
	=	х .

б) Сначала удалите скобки, затем скобки, затем скобки.

8 + {2 — [12 + ( x — 2)]}	=	8 + 2 — [12 + ( x — 2)]
	=	10-12 — ( x -2)
	=	−2 — х + 2
	=	— х .

Сначала удалите круглые скобки, затем квадратные скобки, затем фигурные скобки.

8 + {2 — [12 + ( x — 2)]}	=	8 + {2 — [12 + x -2]}
	=	8 + {2 — 12 — x + 2}
	=	8 + 2 — 12 — х + 2
	=	— х .

2-й уровень

Следующий урок: Добавление похожих терминов

Содержание | Дом

---

Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.

---

Авторские права © 2021 Лоуренс Спектор

Вопросы или комментарии?

Эл. Почта: [email protected]

Порядок операций — ChiliMath

Фундаментальная концепция порядка операций — выполнение арифметических операций в «правильном» порядке или последовательности.Давайте посмотрим, как Роб и Пэтти пытались упростить данное числовое выражение, применяя порядок или правило операций.

В чем ошибка Роба?

• Он небрежно упростил числовые выражения, применив арифметические операции слева направо.

Пэтти получила правильный ответ, потому что она правильно применила правила порядка операций.

• Она сначала выполнила умножение и деление, а затем сложение и вычитание.

---

Каков порядок работы?

Порядок операций — это просто набор правил, которые определяют приоритет последовательности операций , начиная от наиболее важных до наименее важных.

Это правило о том, как правильно упрощать числовые выражения, также известно как правило PEMDAS (сокращение от P lease E xcuse M y D ear A unt S ally).

Шаг 1: Сделайте все возможное, чтобы упростить все, что находится внутри скобок или символа группировки.

Шаг 2: Упростите экспоненциальные числа в числовом выражении, где это возможно.

Шаг 3: Умножить и разделить слева направо в зависимости от того, что наступит раньше.

Шаг 4: Сложить и вычесть в зависимости от того, что наступит раньше, слева направо

---

Примеры применения порядка операций для упрощения числовых выражений

Пример 1: Упростите приведенное ниже выражение, используя Порядок операций.

• Изучая числовые выражения с несколькими операциями слева направо, мы видим, что сначала мы должны выполнить деление, что составляет 5 \ div 5 = 1.

• На данный момент у меня есть три (3) возможных операции. В Порядке операций умножение имеет приоритет перед сложением и вычитанием. Следовательно, мы должны размножаться дальше. У нас 6 \ умножить на 2 = 12.

• Что нам делать дальше, складывать или вычитать? В зависимости от порядка операций сложение и вычитание имеют одинаковое значение.Чтобы определить, какую операцию выполнить в первую очередь, мы добавляем или вычитаем слева направо в зависимости от того, что идет первым, что в этой ситуации должно сложить, 1 + 3 = 4.

• Осталась одна операция — вычитание. На первый взгляд сложное числовое выражение сводится к окончательному ответу — 8.

---

Пример 2: Упростите приведенное ниже выражение, используя Порядок операций.

---

В следующих примерах будет задействовано скобок .Помните, что вам нужно сначала упростить все, что указано в скобках, прежде чем двигаться дальше.

Пример 3: Упростите приведенное ниже выражение, используя Порядок операций.

• Обратите внимание на выражения в скобках. Правило говорит нам сначала делить, а затем вычитать.

• Мы можем избавиться от скобок, вычтя 7 на 2.

• Умножение — это гораздо более «сильная» операция, чем вычитание, поэтому мы должны сначала умножить 5 и 4.

• Закончим вычитанием 25 на 20.

---

Пример 4: Упростите приведенное ниже выражение, используя Порядок операций.

• Сначала упростите выражения в круглых скобках. Умножьте на первую скобку и разделите на вторую.

• Сложите числа в первой скобке, затем вычтите числа внутри второй.

• Здесь есть умножение и деление.Поскольку умножение предшествует делению, мы собираемся сначала умножить.

• Между вычитанием и делением приоритет имеет деление, поэтому мы делим 5 на 5, чтобы получить 1.

• Последняя оставшаяся операция — вычитание, поэтому мы и займемся этим.

---

В последних примерах будут задействованы экспоненты, поэтому будьте осторожны на каждом этапе, потому что в них происходит очень много всего. Пока вы сосредотачиваетесь на соблюдении правил, регулирующих порядок действий, это не должно быть так сложно! Поехали…

Пример 5: Упростите числовое выражение ниже, используя правила Порядка операций.

• Упростите выражения в скобках. Но, более конкретно, упростите числа с помощью показателей.

• Для упрощения заключены две круглые скобки. Мы упростим второй, \ left ({30 — 27} \ right), потому что он намного проще. Здесь разница 30 и 27 составляет 3.

• Теперь обратим внимание на другую скобку. Порядок действий говорит нам делить, прежде чем вычитать.

• Наконец, мы можем избавиться от скобок, выполнив вычитание, потому что больше нечего делать.

• Глядя на то, что мы оставили, упрощение экспоненциальных чисел имеет приоритет перед операциями умножения, сложения и вычитания.

• Просматривая слева направо, очевидно, что мы должны умножать перед сложением и / или вычитанием.

• В зависимости от порядка операций сложение и вычитание имеют одинаковое значение. Сначала мы должны вычесть, потому что операция вычитания предшествует сложению, если смотреть слева направо.3} первый.

• Заглянув в круглые скобки, мы должны сначала разделить, прежде чем умножать и вычитать.

• Не останавливая внимание в скобках, порядок операций говорит нам умножать, прежде чем мы будем вычитать.

• Последняя операция внутри скобок — вычитание. Давай сделаем это!

• Давайте сделаем паузу. На данный момент ясно, что мы можем выполнить три (3) упрощения одновременно.2}.

• Кажущаяся сложной проблема теперь сведена к чему-то, что очень легко упростить. Если смотреть слева направо, деление имеет приоритет перед вычитанием и сложением.

• Потому что вычитание и умножение находятся на одном уровне в иерархии операций. Способ, которым мы разрываем связь, как вы уже должны были знать, — это выполнять ту, которая идет первой, если смотреть слева направо. В этой ситуации мы будем вычитать, а затем прибавлять.Это оно!

---

Практика с рабочими листами

---

Возможно, вас заинтересует:

Порядок действий Проблемы с ответами

Правило PEMDAS

Четыре четверки (Порядок действий)

Почему?

Этот урок разработан для учащихся старших классов начальной школы. Он основан на проблеме «Четыре ради добра», найденной на веб-сайте NRICH (https://nrich.maths.org/1081).Он направлен на то, чтобы помочь учащимся лучше понять порядок операций и то, как использование скобок в уравнении может изменить решение.

Что?

Урок требует, чтобы учащиеся использовали до четырех четверок и любую операцию для получения чисел от 0 до 100. Например, 4 + 4 + 4 + 4 = 16.

Первоначально учащиеся будут использовать более знакомые операции, +, -, ×, ÷, а также скобки для создания своих уравнений. Например, (4 × 4 + 4) ÷ 4 = 5.Постепенно поиск решений для оставшихся чисел в списке становится все сложнее. Здесь это хорошая возможность познакомить студентов с некоторыми другими операциями, в том числе √4 = 2 и 4! = 24. По моему опыту, по крайней мере один ученик в классе будет знаком с операцией извлечения квадратного корня √ n , что упростит введение. Другая операция n !, известная как факториал , будет менее знакома студентам.

н ! — произведение всех натуральных чисел, меньших или равных n; f или, например, 4! = 4 × 3 × 2 × 1 = 24, или 3! = 3 × 2 × 1 = 6

С введением этих двух менее привычных операций количество решений, которые учащиеся могут найти для исходной проблемы, увеличивается.

Как?

Недавно в классе 5/6 в Новом Южном Уэльсе студенты быстро поняли исходную проблему. Назвав некоторые из наиболее очевидных решений, вскоре возникла задача найти решения для чисел от 1 до 10. Мы решили использовать большую классную доску для записи предлагаемых решений. На боковой стороне доски было предусмотрено место для «отработки», поэтому проблемы, в которых «порядок операций» был фактором, можно было протестировать, прежде чем добавлять их в основной список.

Хотя также было обнаружено несколько решений, превышающих 10, само число 10 стало своего рода камнем преткновения. Именно здесь я побудил студентов подумать об использовании различных операций. Один студент предложил, но вскоре понял, что это недопустимо, так как для этого нужно использовать число, отличное от 4. Другой студент сказал, что противоположность «возведению в квадрат» — это «квадратный корень», и вскоре ученикам стала доступна новая операция. Эти «новые» знания затем были использованы студентами для предоставления нескольких решений для числа 10, включая:

4 + 4 + 4 — √4

4 + 4 + √4

Еще через пять-десять минут работы, когда обмен возможными решениями снова замедлился, я ввел факториальную операцию (.Это не только помогло студентам найти решения для некоторых различных чисел, но также помогло им разработать менее сложные решения для некоторых из предыдущих чисел. Например:

4! ÷ 4 = 6

Благодаря этой новой информации, в течение одного часа класс студентов смог разработать решения для более чем 30 номеров. Когда урок заканчивался, студенты все еще с нетерпением делились потенциальными решениями.

Копнуть глубже

Для получения дополнительной информации в прилагаемом плане урока показаны соответствующие ссылки на австралийскую учебную программу и выделено соответствующее содержание и результаты, указанные в программе K-10 по математике штата Новый Южный Уэльс.

BODMAS

% PDF-1.4 % 1 0 объект > / Metadata 2 0 R / OutputIntents 8 0 R / PageLayout / OneColumn / Pages 3 0 R / StructTreeRoot 9 0 R / Тип / Каталог >> эндобдж 2 0 obj > поток 2014-03-13T18: 51: 21Z2014-03-13T18: 51: 18Z2014-03-13T18: 51: 21ZAcrobat PDFMaker 10.1 для Worduuid: cac345bd-eac5-4f82-84db-3c97d0e93612uuid: 2ce4970d-ac57-4bee-a5230fb pdf

BODMAS

Банки

Библиотека Adobe PDF 10.01A

http://ns.adobe.com/xap/1.0/mm/xmpMMXMP Схема управления носителями

Внутренний идентификатор на основе UUID для конкретного воплощения документа InstanceIDURI

http://www.aiim.org/pdfa/ns/id/pdfaidPDF/A ID Schema

internalPart of PDF / A standardpartInteger

внутренняя Поправка к стандарту PDF / A amdText

внутренний Уровень соответствия стандарту PDF / A Текст

конечный поток эндобдж 8 0 объект [>] эндобдж 3 0 obj > эндобдж 9 0 объект > эндобдж 13 0 объект > эндобдж 14 0 объект > эндобдж 15 0 объект > эндобдж 236 0 объект [54 0 R 56 0 R 246 0 R 247 0 R 248 0 R 249 0 R 250 0 R 251 0 R 252 0 R 253 0 R 254 0 R 255 0 R 256 0 R 257 0 R 258 ​​0 R 259 0 R 260 0 R 261 0 R 262 0 R 263 0 R 264 0 R 265 0 R 266 0 R null 16 0 R 17 0 R 18 0 R] эндобдж 237 0 объект [64 0 R 267 0 R 268 0 R 269 0 R 270 0 R 271 0 R 272 0 R 72 0 R 73 0 R 74 0 R 75 0 R 76 0 R 77 0 R 78 0 R 79 0 R 80 0 R 81 0 R 82 0 R 83 0 R 84 0 R 273 0 R 274 0 R 275 0 R 276 0 R 277 0 R 278 0 R 279 0 R 280 0 R 86 0 R 87 0 R 88 0 R 89 0 R 90 0 R 91 0 R 92 0 R 93 0 R 94 0 R 95 0 R 96 0 R 97 0 R null 19 0 R 20 0 R 21 0 R 22 0 R 23 0 R 55 0 R 24 0 R] эндобдж 238 0 объект [98 0 R 99 0 R 100 0 R 101 0 R 102 0 R 103 0 R 104 0 R 105 0 R 106 0 R 107 0 R 281 0 R 282 0 R 283 0 R 284 0 R 285 0 R 286 0 R 287 0 R 288 0 R 289 0 R 109 0 R 110 0 R 111 0 R 112 0 R 113 0 R 290 0 R 291 0 R 292 0 R NULL NULL 293 0 R NULL NULL 294 0 R NULL NULL 295 0 R NULL NULL 296 0 R null null 297 0 R null null 298 0 R null null 299 0 R null null 300 0 R null null 301 0 R null null 302 0 R 303 0 R 304 0 R 305 0 R 306 0 R 307 0 R 308 0 R 309 0 R 310 0 R 311 0 R 312 0 R 313 0 R 314 0 R 115 0 R 116 0 R 117 0 R 25 0 R 26 0 R 58 0 R 59 0 R 27 0 R 28 0 R 29 0 R] эндобдж 239 0 объект [118 0 R 119 0 R 120 0 R 121 0 R 122 0 R 123 0 R 124 0 R 125 0 R 315 0 R 316 0 R 317 0 R NULL NULL 318 0 R NULL NULL 319 0 R NULL NULL 320 0 R NULL null 321 0 R null null 322 0 R null null 323 0 R null null 324 0 R null null 325 0 R null null 326 0 R null null 327 0 R null null 328 0 R null null 329 0 R null null 330 0 R null null 331 0 R 332 0 R 333 0 R 334 0 R null null 335 0 R null null 336 0 R 337 0 R 338 0 R 339 0 R 340 0 R 341 0 R 342 0 R 343 0 R 344 0 R 345 0 R 346 0 R 347 0 R 348 0 R 127 0 R 349 ​​0 R 350 0 R 351 0 R 352 0 R 353 0 R 354 0 R 355 0 R 356 0 R 357 0 R 358 0 R 359 0 R 360 0 R 361 0 R null null 362 0 R null null 363 0 R 364 0 R null 30 0 R 31 0 R 60 0 R 61 0 R 32 0 R] эндобдж 240 0 объект [129 0 R 130 0 R 131 0 R 132 0 R 133 0 R 134 0 R 135 0 R 136 0 R 137 0 R 138 0 R 139 0 R 140 0 R 141 0 R 142 0 R 143 0 R 144 0 R 145 0 R 146 0 R 147 0 R 148 0 R 149 0 R 150 0 R 151 0 R 152 0 R 365 0 R 366 0 R 367 0 R 368 0 R 369 0 R ноль 33 0 R 34 0 R 35 0 R 62 0 63 0 R 65 0 R 67 0 R 68 0 R 36 0 R] эндобдж 241 0 объект [154 0 R 155 0 R 156 0 R 157 0 R 158 0 R 159 0 R 160 0 R 161 0 R 162 0 R 163 0 R 164 0 R 165 0 R 166 0 R 167 0 R 168 0 R 169 0 R 170 0 R 171 0 R 172 0 R 173 0 R 174 0 R 175 0 R 176 0 R 177 0 R 178 0 R 179 0 R 180 0 R 370 0 R 371 0 R 182 0 R 183 0 R 184 0 R 185 0 R 37 0 R 38 0 R 69 0 R 70 0 R 39 0 R] эндобдж 242 0 объект [186 0 R 187 0 R 188 0 R 189 0 R 190 0 R 372 0 R 373 0 R 374 0 R 375 0 R 376 0 R 377 0 R 378 0 R 379 0 R 380 0 R 192 0 R 193 0 R 194 0 R 195 0 R 196 0 R 197 0 R 198 0 R 199 0 R 200 0 R 201 0 R 202 0 R 203 0 R 204 0 R 205 0 R 206 0 R 207 0 R 208 0 R 209 0 R 210 0 R 211 0 R 212 0 R 40 0 ​​R 41 0 R 71 0 R 42 0 R 43 0 R 44 0 R 45 0 R 46 0 R 47 0 R 48 0 R] эндобдж 243 0 объект [213 0 R 214 0 R 215 0 R 216 0 R 217 0 R 218 0 R 219 0 R ноль ноль 381 0 R ноль ноль 382 0 R 383 0 R 384 0 R 385 0 R 386 0 R 387 0 R 388 0 R NULL NULL 389 0 R NULL NULL 390 0 R 391 0 R 392 0 R 393 0 R NULL NULL 394 0 R NULL NULL 395 0 R 396 0 R NULL NULL 397 0 R NULL NULL 398 0 R 399 0 R 400 0 R NULL NULL 401 0 R ноль ноль 402 0 R 403 0 R 404 0 R 405 0 R 406 0 R 407 0 R 408 0 R 409 0 R 410 0 R 411 0 R 412 0 R 413 0 R 414 0 R 415 0 R 416 0 R 417 0 R 418 0 R 419 0 R 420 0 R 421 0 R 422 0 R 423 0 R 424 0 R 425 0 R null 49 0 R 50 0 R] эндобдж 244 0 объект [221 0 R 222 0 R 223 0 R 224 0 R 225 0 R 226 0 R 227 0 R ноль ноль 426 0 R ноль ноль 427 0 R 428 0 R 429 0 R 430 0 R 431 0 R 432 0 R 433 0 R 434 0 R 435 0 R 436 0 R 437 0 R 438 0 R 439 0 R 440 0 R 441 0 R 442 0 R 443 0 R 444 0 R 445 0 R 446 0 R 447 0 R 448 0 R 449 0 R 450 0 R 451 0 R 452 0 R 453 0 R 454 0 R 455 0 R 456 0 R NULL NULL 457 0 R NULL NULL 458 0 R 459 0 R 460 0 R 461 0 R 462 0 R 463 0 R 464 0 R 465 0 R 466 0 R 467 0 R 468 0 R 469 0 R null 51 0 R 52 0 R] эндобдж 245 0 объект [229 0 R 230 0 R 231 0 R 232 0 R 233 0 R 470 0 R 471 0 R 472 0 R 473 0 R 474 0 R 475 0 R 476 0 R 477 0 R 478 0 R 479 0 R 480 0 R 481 0 R 482 0 R 483 0 R 484 0 R 485 0 R 486 0 R 487 0 R 488 0 R 489 0 R 490 0 R 491 0 R 492 0 R 493 0 R 494 0 R 495 0 R 496 0 R 497 0 R 498 0 R 499 0 R 500 0 R 501 0 R 502 0 R 503 0 R 504 0 R 505 0 R 506 0 R 507 0 R 508 0 R 509 0 R 510 0 R 511 0 R 512 0 R 235 0 R 53 0 Р] эндобдж 229 0 объект > эндобдж 230 0 объект > эндобдж 231 0 объект > эндобдж 232 0 объект > эндобдж 233 0 объект > эндобдж 470 0 объект > эндобдж 471 0 объект > эндобдж 472 0 объект > эндобдж 473 0 объект > эндобдж 474 0 объект > эндобдж 475 0 объект > эндобдж 476 0 объект > эндобдж 477 0 объект > эндобдж 478 0 объект > эндобдж 479 0 объект > эндобдж 480 0 объект > эндобдж 481 0 объект > эндобдж 482 0 объект > эндобдж 483 0 объект > эндобдж 484 0 объект > эндобдж 485 0 объект > эндобдж 486 0 объект > эндобдж 487 0 объект > эндобдж 488 0 объект > эндобдж 489 0 объект > эндобдж 490 0 объект > эндобдж 491 0 объект > эндобдж 492 0 объект > эндобдж 493 0 объект > эндобдж 494 0 объект > эндобдж 495 0 объект > эндобдж 496 0 объект > эндобдж 497 0 объект > эндобдж 498 0 объект > эндобдж 499 0 объект > эндобдж 500 0 объект > эндобдж 501 0 объект > эндобдж 502 0 объект > эндобдж 503 0 объект > эндобдж 504 0 объект > эндобдж 505 0 объект > эндобдж 506 0 объект > эндобдж 507 0 объект > эндобдж 508 0 объект > эндобдж 509 0 объект > эндобдж 510 0 объект > эндобдж 511 0 объект > эндобдж 512 0 объект > эндобдж 235 0 объект > эндобдж 53 0 объект > эндобдж 513 0 объект > / Шрифт >>> / StructParents 9 / Тип / Страница >> эндобдж 522 0 объект > поток HWmo ~ wM @, @ (A @ 4ur ݞ Pyp ߓ / _ \] 0 {} ؽ a ##? ^ Prx @ _c (K% v] = ~ C / ^ tA {| ~ o ~ A7 ‘= g ݧ> W- __bXW- ~ x R / u: T ۬

Правило BODMAS

Что такое правило БОДМАС?

Правило или порядок, который мы используем для упрощения математических выражений, называется правилом «BODMAS».

Очень простой способ запомнить правило БОДМЫ!

B ——> Кронштейны

О ——> Оф (приказы: Силы и радикалы)

D ——> Отдел

M ——> Умножение

A ——> Дополнение

S ——> Вычитание

Важные примечания:

1.В конкретном упрощении, если у вас есть и умножение, и деление, выполняйте операции одну за другой в порядке слева направо.

2. Деление не всегда предшествует умножению. Мы должны делать это по очереди слева направо.

3. В конкретном упрощении, если у вас есть и сложение, и вычитание, выполняйте операции одну за другой в порядке слева направо.

Примеры:

12 ÷ 3 x 5 = 4 x 5 = 20

13 — 5 + 9 = 8 + 9 = 17

В приведенном выше упрощении мы имеем оба деления и умножение.Слева направо сначала идет деление, затем умножение. Итак, мы делаем сначала деление, а потом умножение.

Решенные проблемы

Задача 1:

Оценить:

6 + 7 x 8

Решение:

Выражение 6 + 7 x 8

Оценка = 6 + 7 x 8 = 6 + 56 = 62

Операция Умножение Сложение Результат

Задача 2:

Оценить:

10 ² -16 ÷ 8

Решение:

Выражение 10 2 — 16 ÷ 8

Оценка = 10 2 — 16 ÷ 8 = 100- 16 ÷ 8 = 100-2 = 100-2

Операция Мощность Раздел Вычитание Результат

Проблема 3:

Оценить:

(25 + 11) x 2

Решение:

Выражение (25 + 11) x 2

Оценка = (25 + 11) x 2 = 36 x 2 = 72

Операция Кронштейн Умножение Результат

Задача 4:

Вычислить:

3 + 6 x (5 + 4) ÷ 3-7

Решение:

Выражение 3 + 6 x (5 + 4) ÷ 3-7

Оценка = 3 + 6 x (5 + 4) ÷ 3-7 = 3 + 6 x 9 ÷ 3-7 = 3 + 54 ÷ 3 -7 = 3 + 18 -7 = 21-7 = 14

Операция Кронштейн Умножение Деление Сложение Вычитание Результат

Задача 5:

Вычислить:

36-2 (20 + 12 ÷ 4 x 3-2 x 2) + 10

Решение:

Задача 6:

Вычислить:

6 + [(16-4) ÷ (2 ² + 2)] — 2

Решение:

Выражение 6 + [(16-4) ÷ (2 2 +2)] — 2

Оценка = 6+ [(16-4) ÷ (2 2 +2)] -2 = 6+ [12 ÷ ( 2 ² +2)] — 2 = 6+ [12 ÷ (4 + 2) ] -2 = 6+ [12 ÷ 6] -2 = 6 + 2 -2 = 8-2 = 6

Операция Кронштейн Мощность Круглая скобка Круглая скобка Дополнение Вычитание Результат

Задача 7:

Вычислить:

(96 ÷ 12) + 14 x (12 + 8) ÷ 2

Решение:

Выражение (96 ÷ 12) + 14x (12 + 8) ÷ 2

Оценка = (96 ÷ 12) + 14x (12 + 8) ÷ 2 = 8 + 14x 20 ÷ 2 ÷ 8 + 280 2 = 8 + 140 = 148

Операция Кронштейн Умножение Деление Добавление Результат

Задача 8:

Вычислить:

(93 + 15) ÷ (3 x 4) — 24 + 8

Решение:

Выражение (93 + 15) ÷ (3×4) -24 + 8

Оценка = (93 + 15) ÷ (3×4) -24 + 8 = 108 ÷ 12 -24 + 8 = 9-24 + 8 = -15 + 8 = -7

Операция Кронштейн Раздел Вычитание Вычитание Результат

Задача 9:

Вычислить:

55 ÷ 11 + (18-6) x 9

Решение:

Выражение 55 ÷ 11 + (18-6) x9

Оценка = 55 ÷ 11 + (18-6) x9 = 55 ÷ 11 + 12×9 = 5 + 12×9 = 5 + 108 = 9000 113

Операция Кронштейн Раздел Умножение Сложение Результат

Задача 10:

Вычислить:

(7 + 18) x 3 ÷ (2 + 13) — 28

Решение:

Выражение (7 + 18) x3 ÷ (2 + 13) — 28

Оценка = (7 + 18) x3 ÷ (2 + 13) -28 = 25 x 3 ÷ 15-28 = 75 ÷ 15 — 28 = 5-28 = -23

Операция Кронштейн Умножение Деление Вычитание Результат

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Проблемы со словами по скорости единицы

задачи по сравнению ставок

Преобразование обычных единиц словесные задачи

Преобразование метрических единиц текстовые задачи

Word задачи по простому проценту

Word задачи по сложным процентам

ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами в виде разметки 9306 и

Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Словесные задачи с линейным неравенством

Задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Задачи со словами на возрастах

Проблемы со словами по теореме Пифагора

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращения в процентах

Сокращения в таблице времени

Сокращения времени, скорости и расстояния

Сокращения соотношения и пропорции

Домен и диапазон рациональных функций

Область и диапазон

рациональных функций

функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

с использованием длинного корня зрение

L.Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении в степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Обучение абсолютному значению числа в математике

Урок 2: Разработка концепции

Материалы: Каталожные карточки или цифровые «карточки», которые могут быть распределены среди класса

.

Стандарты:

• Под абсолютным значением рационального числа понимается его расстояние от 0 на числовой прямой.(6.NS.C.7.C)

Подготовка: Сделайте карточки для У меня есть… у кого есть?

Заключительная и оценочная игра

• Попросите учащихся написать и поделиться своими определениями и реальными примерами ситуаций абсолютной ценности.
• Играть У меня … у кого есть? Составьте набор из 15 учетных карточек с уравнениями абсолютных значений и 15 учетных карточек, содержащих значения переменной. Если учетные карточки недоступны или вы адаптируете это для дистанционного обучения, создайте способ, чтобы 30 приведенных ниже уравнений были распределены среди ваших учеников как можно более равномерно.

Карты абсолютного значения	Карты переменного значения
| x + 5 | = 20	x = 15
| 5 — x | = 30	x = –25
| x + 6 | = 41	x = 35
| –27 — x | = 20	x = –47
–7 + | x | = 0	x = –7
| 25 — x | = 18	x = 7
| x + –5 | = 38	x = 43
| 37 — x | = 70	x = –33
114 — | x | = 7	x = 107
| — x + 100 | = 21	x = 121
— | 1 + x | = -80	x = 79
| x | = 81	x = –81
| x + 3 | = 84	x = 81
| 25 + x | = 62	x = –87
| x — 26 | = 11	x = 37

Каждая указанная карта абсолютного значения имеет два значения: x .Эти значения перекрываются, так что каждая карта значений переменных удовлетворяет двум из заданных уравнений абсолютного значения (первое и второе значения удовлетворяют первому уравнению, второе и третье значения удовлетворяют второму уравнению и т. Д., Пока последнее и первое значения не удовлетворяют условиям последнее уравнение).

Распределите карточки или уравнения поровну. Убедитесь, что все они были розданы. Выберите ученика, который скажет «У меня есть», а затем прочтите значение или уравнение на его карточке. Затем попросите учащегося сказать: «У кого есть совпадение для моей карты?» Любой ученик, у которого есть совпадение, должен сказать: «У меня есть… у кого есть…», и игра продолжается до тех пор, пока не будут прочитаны все карточки.Вы можете попросить учащихся встать, когда игра начинается, и сесть, когда они предлагают ответ. Чтобы заинтересовать всех, предложите награду за успешное прохождение игры, поощряя вызовы к подозрительным ответам.

***

Ищете дополнительные бесплатные уроки математики и мероприятия для учеников средней школы? Обязательно ознакомьтесь с нашим центром бесплатных учебных ресурсов.