Сложение и вычитание двузначных чисел – приемы с примерами — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Урок 30. письменные приёмы сложения и вычитания двузначных чисел без перехода через десяток — Математика — 2 класс
Математика, 2 класс
Урок № 30. Письменные приёмы сложения и вычитания двузначных чисел без перехода через десяток
Перечень вопросов, рассматриваемых в теме:
— Как выполнять письменное сложение двузначных чисел без перехода через десяток.
Глоссарий по теме:
Сумма разрядных слагаемых — это представление двузначного числа в виде суммы его разрядов (десятков и единиц).
Алгоритм — последовательность действия (шагов)
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых).
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика.
 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 5-е изд. – М.: Просвещение, 2014. – с.4.
2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 5-е изд. – М.: Просвещение, 2014. – с.4. - Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.3.
- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.16.
- Математика. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. С. И. Волкова – М.: Просвещение, 2017. – с.40, 41.
Теоретический материал для самостоятельного изучения
Найдём значение выражения 25 + 43 разными способами:
- пользуясь графическими моделями:
+
=
воспользуемся общим правилом сложения двузначных чисел. Заменим число суммой разрядных слагаемых, к десяткам прибавим десятки, к единицам – единицы:
45 + 23 = (40 + 5) + (20 + 3) = (40 + 20) + (5 + 3) = 60 + 8 = 68
- воспользуемся счётными палочками:
+
=
Как бы мы ни складывали, результат получился одинаковый – 68. Но все эти вычисления большие, громоздкие. При сложении двузначных чисел удобнее записывать решение примеров столбиком. Тогда легче вычислять сумму. Обратите внимание, что числа записаны друг под другом, клетки не пропускаем.
Но все эти вычисления большие, громоздкие. При сложении двузначных чисел удобнее записывать решение примеров столбиком. Тогда легче вычислять сумму. Обратите внимание, что числа записаны друг под другом, клетки не пропускаем.
Найдём сумму чисел 36 и 23. Числа записывают одно под другим так, чтобы десятки были записаны под десятками, а единицы под единицами.
Слева между числами ставится знак «плюс». Под числами проводится черта, ниже которой будет записываться сумма.
Запомните, письменное сложение начинается с единиц.
Складываем 6 единиц и 3 единицы. Получим 9 единиц. Пишем 9 под единицами.
Теперь складываем десятки. 3 десятка и 2 десятка, равно 5 десяткам. Пишем 5 под десятками. Теперь можно прочитать, чему равна сумма. Сумма равна пятидесяти девяти.
Выполнять письменное сложение вам поможет памятка.
Вывод:
При письменном сложении двузначных чисел в пределах 100 без перехода через разряд будем опираться на разрядный состав чисел. Записываются числа в столбик, не пропуская клеток, десятки под десятками, единицы под единицами. Десятки будем складывать с десятками, а единицы с единицами. Результат записывается под числами, под чертой, без пропусков клеток.
Записываются числа в столбик, не пропуская клеток, десятки под десятками, единицы под единицами. Десятки будем складывать с десятками, а единицы с единицами. Результат записывается под числами, под чертой, без пропусков клеток.
Тренировочные задания.
1. Выберите примеры, решенные верно.
Правильные ответы: № 2, № 3
2. Вычислите и в каждое окошко поместите карточку с ответом.
Сложение и вычитание двузначных чисел. Задачи по математике 2 класс
Задача 1
До конца марта осталось 20 дней. Сколько дней уже прошло?
Решение:
- 1) 31 — 20 = 11
- Ответ: 11
Задача 2
После того как портниха истратила 8 катушек ниток, у неё осталось по 4 катушки белых, чёрных и цветных ниток. Сколько катушек ниток было у неё вначале?
Решение:
- 1) 3 * 4 = 12
- 2) 8 + 12 = 20
- Выражение: 3 * 4 + 8 = 20
- Ответ: 20
Задача 3
В некотором царстве всего 2 дома. В первом доме живут 7 детей и 6 взрослых, а во втором доме — 17 человек, из которых 9 взрослых. Составь по схеме вопросы к этому условию и отпеть на них. Что еще можно спросить?
В первом доме живут 7 детей и 6 взрослых, а во втором доме — 17 человек, из которых 9 взрослых. Составь по схеме вопросы к этому условию и отпеть на них. Что еще можно спросить?
Решение:
- 1) Составь по схеме вопросы.
- В каком доме больше детей и на сколько?
- 17 — 9 = 8 (Детей во втором доме)
- 8 — 7 = 1
- Сколько всего людей в первом и втором доме?
- 7 + 6 = 13 (Всего людей в первом доме)
- 17 + 13 = 30
- 2) Что еще можно спросить?
- В каком доме людей больше и на сколько?
- В каком доме больше взрослых и на сколько?
Задача 4
Миша пригласил Колю в свой сад, где созревали яблоки и груши. Миша сорвал 8 яблок и 5 груш, а Коля — 3 яблока и 9 груш.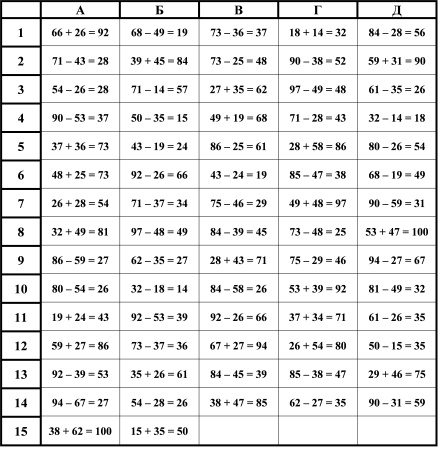 Миша съел 6 своих фруктов, а Коля — 4 своих. Остальные сорванные ими фрукты каждый мальчик понёс домой. Кто из них принёс домой больше фруктов и на сколько? Что ещё можно узнать?
Миша съел 6 своих фруктов, а Коля — 4 своих. Остальные сорванные ими фрукты каждый мальчик понёс домой. Кто из них принёс домой больше фруктов и на сколько? Что ещё можно узнать?
Решение:
- 1) 8 + 5 = 13 (Сорвал Миша)
- 2) 9 + 3 = 12 (Сорвал Коля)
- 3) 13 — 6 = 7 (Понес домой Миша)
- 4) 12 — 4 = 8 (Понес домой Коля)
- 5) 8 — 7 = 1
- Ответ: Коля понес домой больше на 1 фрукт.
Что еще можно узнать?
- На сколько миша сорвал больше яблок чем груш? 8 — 5 = 3
- На сколько коля сорвал больше груш чем яблок? 9 — 3 = 6
- Кто больше и на сколько сорвал фруктов? 13 — 12 = 1
- Кто больше и на сколько сорвал яблок? 8 — 3 = 5
- Кто больше и на сколько сорвал груш? 9 — 5 = 4
Задача 5
На скамейку сели малыши. Дюймовочка — занимает 1 см, Незнайка — 6 см, а доктор Пилюлькин — 8 см. Уместятся ли они все, если длина скамейки 2 дм?
Дюймовочка — занимает 1 см, Незнайка — 6 см, а доктор Пилюлькин — 8 см. Уместятся ли они все, если длина скамейки 2 дм?
Решение:
- 1) 1 + 6 + 8 = 15
- 2) 2 дм = 20 см
- 3) 20 см > 15 см.
- Ответ: Малыши поместятся на скамейку.
Задача 6
Рост гнома 43 см, а длина его кровати 4 дм 8 см. Уместится ли гном на кровати?
Решение:
- 1) 4 дм 8 см = 48 см
- 2) 43 см < 48 см
- Ответ: Длина кровати больше чем рост гнома, значит гном уместится на кровати.
Задача 7
Сумма длин всех сторон (периметр) треугольника 9 дм 8 с Одна его сторона равна 3 дм, а вторая — 26 см. Найди длину третьей стороны.
Решение:
- 1) 3 дм = 30 см
- 2) 30 + 26 = 56
- 3) 9 дм 8 см = 98 см
- 4) 98 — 56 = 42
- Ответ: 42 см.
Задача 8
Одна сторона треугольника равна 7 см, вторая — 8 см, а третья — на 4 см больше второй стороны. Найди периметр треугольника.
Решение:
- 1) 8 + 4 = 12
- 2) 12 + 7 + 8 = 27
- Ответ: 27
Задача 9
- Реши примеры. Что ты замечаешь?
Решение:
- 1)
На странице использован материал из книги Л. Г. Петерсон «Математика второй класс. Часть2».
Ссылка на сайт автора:
www.sch4000.ru
Тема. | ||||||||||||||||||||||||
Дата: | ||||||||||||||||||||||||
Класс | ||||||||||||||||||||||||
Цели обучения: | 2.1.2.8. Применять алгоритм сложения и вычитания двузначных чисел. | |||||||||||||||||||||||
Цели урока | Все учащиеся будут: производить вычисления с двузначными числами письменным способом, выполнять проверку. Многие учащиеся будут: применять алгоритм сложения и вычитания письменным способом. Некоторые учащиеся будут: выполнять все вычисления без ошибок, находить или составлять примеры вычислений данного вида. | |||||||||||||||||||||||
Критерии успеха | Обучающийся: Находит значения выражений вида: 34+23, 57-23; 27+34,61-27; 47+33, 80-47 | |||||||||||||||||||||||
Языковые цели | Учащиеся могут: комментировать письменные приемы сложения и вычитания двузначных чисел по алгоритму. Предметная лексика и терминология: Алгоритм письменного приема сложения и вычитания двузначных чисел без перехода через десяток. | |||||||||||||||||||||||
Дескрипторы | Обучающийся — выбирает ответ для нахождения результата действия сложения вычислительного приема вида 34+23; — выбирает ответ для нахождения результата разности чисел вычислительного приема вида 57-23; — выбирает ответ для нахождения результата действия сложения вычислительного приема вида 27+34; — выбирает ответ для нахождения результата разности чисел вычислительного приема вида 61-27; — выбирает ответ для нахождения результата действия сложения вычислительного приема вида 47+33; — выбирает ответ для нахождения результата разности чисел вычислительного приема вида 80-47. | |||||||||||||||||||||||
Привитие ценностей | Привитие ответственности, самостоятельности | |||||||||||||||||||||||
Предыдущее обучение | Модель двузначного числа, деление двузначного числа на разрядные слагаемые | |||||||||||||||||||||||
Навыки использования ИКТ | Ролики с сайта bilimlend | |||||||||||||||||||||||
План | ||||||||||||||||||||||||
Планируемое время | Запланированная деятельность | Ресурсы | ||||||||||||||||||||||
0-3 | (К) Мотивация. Учитель сообщает тему урока и спрашивает: Какие спортивные кружки есть в школе? Формированию, каких качеств способствуют занятия в кружке, секции? (ответственности, самостоятельности). Чему должен научиться тот, кто хочет посещать любимый кружок? В ходе беседы ученики вспоминают, что для этого им необходимо: запомнить, собрать и принести все необходимое для занятий; – организовать свое время таким образом, чтобы все успеть. Ученики приходят к выводу, что умение считать поможет им в формировании этих качеств. Сегодня мы отправимся в страну Спортландию и узнаем какие спортивные кружки есть в этой стране. У вас на партах есть оценочный лист.мы будем не только путешествовать, но и выполнять задания.Если вы выполняете задание без ошибок, напротив ставите плюс, если с ошибками – минус.Перед тем.как отправиться в путешествие, надо размяться | Карта оценки ученика
| ||||||||||||||||||||||
4-9 | Актуализация. Математический диктант 1.Найди разность чисел 12 и 5. 2. Первое слагаемое 8, второе слагаемое 5. Чему равна сумма? 3. Число 18 уменьши на 9 4. Ване сейчас 17 лет. Сколько ему будет лет через три года ? 5. Запиши число, в котором 4 дес. 8 ед 6. Сколько надо прибавить к 10, чтобы получить 17? 7. Вчера ученик прочитал 29 страниц, а сегодня на 3 страницы меньше. Сколько страниц ученик прочитал сегодня? 8Сколько троек в числе 6? 9. На столе было 18 тетрадей, из них 10 тетрадей убрали в шкаф. | |||||||||||||||||||||||
10-25 | Открытие нового. Я спешу на тренировку, В кимоно сражаюсь ловко. Чёрный пояс нужен мне, Ведь люблю я … Первичное закрепление с проговариванием. Задание №3 из учебника ученики выполняют столбиком, в соответствии с алгоритмом. По окончании делают проверку. Самостоятельная работа. Стр.21 №3 1,2 столбики) Предлагает несколько примеров, аналогичных предыдущему заданию для индивидуального выполнения с последующей самопроверкой по эталону (образцу). Выявляет детей, допустивших ошибки. Предлагает найти выход из затруднения | Учебник Стр.20-21. | ||||||||||||||||||||||
26- 35 | Применение нового. На квадратиках доски Короли свели полки. Нет для боя у полков Ни патронов, ни штыков. Решение задачи Тимур посетил в первой четверти 50 занятий в спортивной секции, а во второй на 13 меньше.Сколько всего занятий он посетил за две четверти? Физминутка | Тетрадь | ||||||||||||||||||||||
Работа над ранее изученным В этом спорте игроки Решение уравнений Х + 400 =600 с – 300 = 500 Здесь команда побеждает, Если мячик не роняет. Он летит с подачи метко Не в ворота — через сетку. И площадка, а не поле У спортсменов в… Работа по учебнику | ||||||||||||||||||||||||
36-40 | Рефлексия. Дерево успеха | |||||||||||||||||||||||
Дифференциация по степени самостоятельности и объему выполненных заданий | Оценивание Учитель проводит формативное оценивание. | Здоровье и соблюдение техники безопасности Зарядка для глаз Физминутка «Танцевальная» | ||||||||||||||||||||||
Рефлексия Были ли правильно поставлены цели урока /учебные цели? Все ли ученики достигли своих учебных целей? Если не достигли, то почему, как вы считаете? Правильно ли велась работа по анализу? Вы смогли эффективно использовать время во время урока? Были ли отклонения от плана урока и почему? | ||||||||||||||||||||||||
Урок математики | Дата ___________ | Класс 2 | |||
Тема занятия: | Письменное сложение и вычитание двузначных чисел. | ||||
Ссылка: | Учебник математики для 2 класса – Алматы, «Атамұра», 2013г. (Т.К.Оспанов, К.А.Ерешева, Ш.Х.Курманалина, М.В.Маркина) | ||||
Общие цели: | 1. 2. Развивать коммуникативную компетенцию через ведение диалога, обогащать словарный запас учащихся. Формировать активную гражданскую позицию школьника. | ||||
Задачи: |
| ||||
Результаты обучения: | Ученики знают по разрядный состав чисел, алгоритмы письменного сложения и вычитания двузначных чисел. | ||||
Материалы и оборудование | Интерактивная доска, маркеры, плакаты, оценочные листы. | ||||
Ход занятия | |||||
Этапы проведения урока | Время 45 минут | Действия преподавателя и действия участников | |||
Организация класса | 2 мин. 3 мин. | Занятие начинается с приветствия учащихся. Психологический настрой на урок. — В такой прекрасный зимний день Я очень рада видеть вас, Давайте дружно скажем громко — Мы все-команда, суперкласс! — Молодцы. — Очень серьёзные испытания впереди каждого казахстанца. — Какое большое спортивное событие состоится в нашей стране буквально через 2 дня? – Зимняя универсиада — Совершенно верно! Более подробно о ней мы поговорим на классном часе. Ну а на сейчас, мы проведем математические соревнования. Каждый участник класса должен сегодня стремиться к победе и получить награду. В конце урока, выявим победителей математических соревнований. Вы готовы к испытаниям? Желаю вам удачи. Затем проводится формирование групп (6 группы по 4 ученика). Учащимся предлагается распределиться по группам, в зависимости от вида спорта * сноуборд * фигурное катание, шорт-трек, хоккей с шайбой, * горнолыжный спорт, лыжные гонки, лыжное двоеборье, прыжки на лыжах с трамплина, фристайл. * биатлон, * кёрлинг, * конькобежный спорт, хоккей с мячом (новые виды спорта, включённые в универсиаду) — Для успешной работы в группе выберите организатора группы. | |||
I этап — Вызов Целеполагание Кумулятивная беседа: | 5 мин. | Запись даты. Каллиграфическая минутка — Как фигуристы выводят красивые узоры на льду, так и мы каллиграфически пропишем строку числа 26. — Запишите в тетрадях число 26, правильно прописывая каждую цифру. Поменяйтесь тетрадями, найдите самую красивую цифру 99, написанную вашим соседом и подчеркните её. У.– Ребята, как называются ваши группы? У.- А почему сегодня мы используем именно эти слова? Д. – Потому что это зимние виды спорта. — Только-только наступил новый 2017 год, а на носу уже масштабный спортивный праздник. Встречайте – зимняя Универсиада 2017! Тысячи молодых атлетов – краса и гордость университетской молодёжи из десятков стран – вступят в борьбу в январе этого года на спортивных площадках казахстанского Алматы. – Сегодня, выполняя задания урока, мы проверим, а обладаете ли вы качествами настоящих спортсменов? — Какими качествами должен обладать спортсмен? (быть сильным, ловким, внимательным, сообразительным) — Но не будем забывать про наш урок математики. — Какой раздел математики мы изучаем? – письменные способы сложения и вычитания – Что является объектом изучения на сегодняшнем уроке? – способы сложения и вычитания — Какие способы сложения и вычитания вы знаете? – устные и письменные — Какие способы нами отработаны ещё не достаточно? – письменные — Сформулируйте тему сегодняшнего урока. — Что мы уже знаем? – различные способы + и — и соответствующие им алгоритмы – Тогда, какова цель урока? — отработать умение выполнять письменное сложение и вычитание, используя соответствующий алгоритм. – Зачем вам это надо уметь? (Чтобы правильно + и – двузначные числа, а потом это умение применять на практике, т.е. в жизни) — Как спланируем свою работу на уроке? — Что будем делать сначала? Что потом? План работы. — Вспомню алгоритмы + и -. — Буду отрабатывать способы вычислений. — Проверю себя. — Оценю себя. (Составляют план работы по схеме.)
| |||
II стадия – Осмысление | 5 мин. | У. – Что необходимо знать, чтобы правильно выполнять сложение и вычитание? Д.- Знать хорошо теорию. — Чемпионами спортсмены становятся не сразу, они очень долго тренируются. Вот и мы сейчас с вами проведём математическую разминку. -Посмотрите внимательно на картинки, по которым вы распределились на группы? Что на них нарисовано? -Что означают эти слова? (виды спорта) -Хорошо! Такие виды спорта как фигурное катание, хоккей, лыжные гонки мы с вами знаем. -А что такое биатлон? (Биатлон — вид зимнего двоеборья, включающий лыжную гонку и стрельбу из винтовки.) -Вот мы сейчас поиграем, и я узнаю кто же у нас самый внимательный. I Восстанови порядок выполнения действий. Задание: восстанови алгоритм письменных вычислений + и — *Складываю (вычитаю) единицы… *Результат пишу под десятками… *Читаю ответ.. *Пишу единицы под единицами, десятки под десятками… *Складываю (вычитаю) десятки… *Результат пишу под единицами. 1. Пишу единицы под единицами, десятки под десятками… 2. Складываю (вычитаю) единицы… 3. Результат пишу под единицами. 4. Складываю (вычитаю) десятки… 5. Результат пишу под десятками… 6. Читаю ответ… | |||
ФО | 3 мин. | Самооценка по модельному ответу. | |||
Рефлексия | 2 мин | На что было направлено данное задание? На повторение алгоритма письменного сложения и вычитания. Сделайте вывод, над чем нам надо работать? | |||
Физминутка | 1 мин | Молодцы, вы хорошо поработали. На всех соревнованиях есть перерывы. Вот и мы сейчас с вами немного отдохнем. Давайте расскажем, как мы с вами живём. Физминутка «Хорошо» Хорошо, что солнце светит? (изображают солнце) | |||
Отработка практических навыков. групповая работа Индивидуальная работа | 5 мин. | — Соревнования продолжаются. — Кататься на коньках все умеют? Мы будем принимать участие по Шорт-треку. Шорт-трек – скоростной бег на коньках. Сейчас мы узнаем, обладаете ли вы вторым волшебным качеством спортсменов — быстротой. Рисуют фигуристы коньками вензеля И ловкостью спортсменов удивлена Земля Кипит учёба в школе, и каждый день идёт Казахстанские спортсмены вперёд, вперёд, вперёд! — А теперь давайте продолжим нашу математическую тренировку, согласно второму пункту плана урока. II Решение примеров 1) Задание: выполни вычисления по цепочке 67 28 42 63 18 25 36 27 http://files.school-collection.edu.ru/dlrstore/95bbf00b-5499-4ae1-a3e7-0a5c8f03464e/%5BNS-MATH_2-33-57%5D_%5BIM_048%5D. КЛЮЧ К ПРОВЕРКЕ – проверка по слайду 2) Резервное задание. ПРОВЕРИТЬ ПО КЛЮЧУ | |||
ФО | 2 мин. | Самооценка по модельному ответу. Заполнение оценочного листа. Приложение 1 | |||
Рефлексия | 2 мин | На что было направлено данное задание? На умение письменно складывать и вычитать двузначные числа. Сделайте вывод, над чем нам надо работать? | |||
Физминутка | 1 мин | Зима – это время, когда есть вероятность заболеть простудными заболеваниями. Для профилактики нам нужно сделать массаж. Повторяйте движения за мной. Чтобы лобик не болел Чтобы носик не сопел Чтобы глазки всё видали Чтобы ушки всё слыхали Чтобы шейка не устала Чтобы грудь легко дышала Нам массаж проделать надо Мы здоровью очень рады! Ведите здоровый образ жизни и будете здоровы! | |||
Творческое задание. Работа в группах. | 5 мин | III Решение задач — Сноуборд – зимний вид спорта, спуск с заснеженных склонов и гор на специальном снаряде – сноуборде. Внимание! — Вам надо спуститься с горы, не допустив ошибок Задание: Составь по схеме задачу и реши её. 34 + 23 ? — 41 ? КЛЮЧ К ПРОВЕРКЕ – взаимопроверка в группе Приехало – ?ч., 34 ч. и 23ч. 34+23 Поселилось – 41ч. 41 Осталось — ?ч. 34+23=57 (ч.) 57-41=16 (ч.) Ответ: осталось 16 человек. | |||
ФО | 5 мин. | Взаимооценка в группах по модельному ответу. | |||
III этап— Рефлексия Итог урока СО | 3 мин 3 мин | –Это было последнее соревнование на сегодняшний день. -О каком всемирном событии шла речь на уроке? — Участие в соревнованиях это достижения спортсменов, а наши достижения это успешная учеба в школе, получение прочных знаний. Я очень довольна вашей работой. -Ну а теперь подошло время подведения итогов. Чего сегодня достигли вы. – По какой теме мы работали сегодня на уроке? — Письменные способы сложения и вычитания двузначных чисел. — Какую цель ставили перед собой? — отработать умение выполнять письменное сложение и вычитание, используя соответствующий алгоритм. — Достигли мы этой цели? — Да. — Проанализируйте оценочные листы. — Оцените себя. Если у вас все получилось, вам все было понятно, то прикрепите флажок на пьедестал с первым местом, если вам что немного было непонятно, на 2 место, и если вам совсем ничего не понятно то на 3 место. | |||
Домашнее Задание (по выбору) | 1 мин. | 1) придумать по 3 примера на сложение и вычитание двузначных чисел, записать их в столбик и решить; 2) 3) раскрасить рисунок | |||
№ | Задание | Критерии | Дескрипторы | Баллы | Мой балл |
1 | Восстанови порядок выполнения действий | Знание алгоритма письменного сложения и вычитания | Правильно восстановлен порядок выполнения действий | 6 баллов | |
Правильно восстановлены 5 шагов алгоритма | 5 баллов | ||||
Правильно восстановлены 4 шага алгоритма | 4 балла | ||||
Правильно восстановлены 3 шага алгоритма | 3 балла | ||||
Правильно восстановлены 2 шага алгоритма | 2 балла | ||||
Правильно восстановлен 1 шаг алгоритма | 1 балл | ||||
2 | Решение примеров Задание: выполни вычисления по цепочке | Умение выполнять письменное сложение и вычитание, используя соответствующий алгоритм. | Правильно решены все примеры | 4 балла | |
Правильно решены 3 примера | 3 балла | ||||
Правильно решены 2 примера | 2 балла | ||||
Правильно решён 1 пример | 1 балл | ||||
3 | Составь по схеме задачу и реши её. | Умение составлять, анализировать и решать задачи в два действия | Правильно оформил(а) краткую запись задачи | 1 балл | 5 |
Правильно сделал(а) подсказку | +1 балл | ||||
Правильно начертил(а) чертёж | +1 балл | ||||
Правильно решил(а) | +1 балл | ||||
Правильно написал(а) ответ. | +1 балл | ||||
4 | Итог урока – оценка | «5» — 15- 14 «4» — 13 — 11 «3» — 10- 7 «2» — 6 и | |||
I. Мотивационно-ориенировочный этап Орг. момент. 2)Актуализация знаний. Игра « Дешифровщик». Минутка чистописания. Дифференцированная работа с взаимопроверкой . Подведение мини итога. Устный счет. Игра « Кто быстрее!» Подведение мини итога. Постановка учебной задачи. |
Прозвенел звонок для нас! Встали все у парт красиво, Поздоровались учтиво, Тихо сели, спинки прямо. Все легонечко вздохнем. Урок математики начнем. Сегодня мы отправляемся в путешествие в загадочный город. А что это за город, вы узнаете, расшифровав послание жителей этого города, работая в группах. -Итак, по какому городу мы сегодня будем путешествовать? Начнем наше путешествие с улицы Числовая. Жители улицы Числовая приготовили для вас очень интересные факты о науке математике, которые вы раньше не знали. Но поведают они эти интересные факты после того, как вы правильно выполните их задания. Ребята, вы готовы выполнять задания? 1.Найдите закономерность и запишите следующее число: 15,10,20,15,25,… -Что вы можете сказать об этом числе? 2.Из чисел 3,15,1,10,20,7,72,21,30,48,9,17,71,100,98. Выпишите по порядку: -у кого на столе красные квадратики- все однозначные числа в порядке убывания. -у кого на столе синие квадратики- двузначные числа в порядке возрастания. Проверим работу. Поменяйтесь тетрадями, возьмите в руки карандаши. Один ученик называет числа, все остальные проверяют. (На доске тоже есть эталон проверки)Оцените работу на полях. -Поднимите руку те, кто не допустил ошибок. -Поднимите руку те, кто допустил 1-2 ошибки. -Остальным рекомендую быть внимательнее. -Какое число не выписала ни одна, ни вторая группа? Почему? -Ребята, вы справились со всеми заданиями жителей улицы Числовой и теперь вас ждет интересный факт о числах. Продолжим наше путешествие. Следующими нас встречают жители улицы Счетная. Они тоже приготовили нам интересные факты математики, но сначала нужно выполнить задания. -Как вы думаете, какие задания нам приготовили жители улицы Счетная? -Абсолютно верно! 1) Ответьте на вопросы: -какое число больше 7 на 5? -какое число меньше 9 на 3? -найти сумму чисел 3и 9; -найти сумму чисел 7 и7; -найти разность чисел 11и 4. 2) Игра « Кто быстрее!» ( На доске для каждого ряда записаны примеры, ученики по сигналу начинают решать примеры и записывать ответы по принципу эстафеты. Какой ряд быстрее закончит и ез ошибок, тот и выигрывает.) По завершению выполнения задания, проверяется правильность выполнения задания и определение победителей. — Что общего во всех этих примерах? -Ребята, вы справились со всеми заданиями жителей улицы Счетная и теперь вас ждет интересный факт о счете. Ребята, скажите, с какими цифрами мы работали? Какие задачи поставим перед собой сегодня на уроке? Что повторим?
Какие умения закрепим? | Дети приветствуют друг друга. Дети работают в группах, расшифровывают слово. Заниматика 20 -двузначное, -круглое, -четное, -состоит из 2дес. 100 Трехзначное Устный счет Ученики устно отвечают: 12 6 12 14 7 90 50 10 50 40 60 70 90 90 50 80 20 Сложение и вычитание круглых чисел. двузначными будем продолжать учиться складывать двузначные числа алгоритм сложения двузначных чисел применение алгоритма при решении примеров и задач, | Л.УУД (настрой на работу, мотивация уч-ся) | II. Операционно-исполнительский Работа в парах. Решение примеров с пояснением.
Дифференцированная самостоятельная работа. Подведение мини итога. Физминутка Решение задачи рабочая тетрадь стр. 26. №7. Работа в группах. Творческая работа с задачей в парах Рабочая тетрадь стр. 27, № 10. Подведение мини итога. Фронтальная работа. Самостоятельная работа Рабочая тетрадь стр. 27, № 9 Подведение мини итога. Решение задачи устно. Учебник стр. . 72 № 20
Самостоятельное решение примеров Рабочая тетрадь стр. | Продолжим наше путешествие на переулке Примерный. Как и на остальных улицах нас ждут сюрпризы. Для этого нужно быть внимательными и правильно решать примеры. -Какие примеры мы решали на предыдущем уроке? -Вспомним алгоритм письменного сложения двузначных чисел. Для этого , работая в парах, восстановите алгоритм письменного сложения двузначных чисел. Складываю единицы. (число единиц суммы — пишу под единицами, а 1д запоминаю) Пишу… (единицы под единицами, десятки под десятками) Складываю десятки Ответ: … Увеличиваю количество десятков на 1. Результат пишу под десятками. — Для чего нужно знать алгоритм ? Посмотрите на примеры , записанные на доске: — В каких примерах можно выполнить вычисления устно? — В какие примеры решим , записывая столбиком? -Решим эти примеры с объяснением. -Назовите полученные ответы в порядке возрастания. А сейчас я проверю, как вы научились применять алгоритм самостоятельно. -те, у кого красные квадратики на парте решает примеры , записанные на доске. — те, у кого синие квадратики- выполняют № 5 на стр. 68. -Проверим , как вы справились с этим заданием: -те, у кого красные квадратики- проверяют самостоятельно по эталону с доски. — те , у кого синие квадратики- из ответа первого примеры отнимите ответ второго примера, если у вас получилось 34, то вы решили примеры правильно. Встаньте те, кто правильно решил примеры. -Молодцы! Мы хорошо потрудились, а жители переулка Примерный уже приготовили интересный факт. А теперь немного отдохнем. За тучку солнце спряталось – Но это только в шутку! А мы все дружно проведем Спортивную минутку: В ладошки мы похлопаем И чуть-чуть потопаем. Раз – присели, два – привстали, Три – нагнулись и достали Правой ручкой башмачок, Левой ручкой – потолок. И еще разок присядем! А теперь на место сядем. Мы устали чуточку, Отдохнем минуточку. Набрались сил и отправляемся в путь. Теперь мы оказались на улице Задачная, где будем решать задачи. Откройте рабочую тетрадь на стр. 26. З. №7. В стаде 24 коровы, несколько телят и 3 быка. Можно ли узнать , сколько всего животных в стаде? -прочитайте условие задачи хором. -можно ли ответить на вопрос задачи ? -почему? Докажите! -Что нужно сделать, чтобы решить задачу? Работая в группах, добавьте необходимые данные и решите полученную задачу. Проверим, какие задачи у вас получились и как вы их решили.( выслушиваются представители групп). Продолжим работу и решим следующую задачу в р.т. стр. 27, з. № 10. До обеда в кувшине было * стаканов сока. После обеда в кувшине осталось *стаканов сока. Сколько стаканов сока выпили за обедом? -О чем говорится в задаче? -Какие главные слова? -Что известно? -Что нужно найти? -Каким действием найдем сколько стаканов сока выпили за обедом?. -А теперь , работая в парах, вставьте числовые данные задачи и решите полученную задачу. Для проверки выполнения, выслушиваются несколько пар. Перед тем как перейти на следующую улицу, интересный факт жителей улицы Задачная. Посмотрите внимательно на экран. -Что вы видите ? -Назовите номера фигур, которые являются четырехугольниками. -Найдите пятиугольники. -Вспомните, что такое ось симметрии? Проведите ось симметрии каждой фигуры в задании № 9 стр. 27( рабочая тетрадь). А вот жители улицы Геометрическая предлагают вам разгадать ребусы. Что нам необходимо для разгадывания ребусов? Вот мы оказались на центральной площади города Заниматика . Ее назвали Логическая, так как без логики в математике никак не справиться. — Давайте проверим, как мы можем мыслить, делать выводы. Каждая из трех девочек – Валя, Галя и Даша –держит один гладиолус: красный, белый, желтый. У Вали не красный и не белый, а у Гали не красный гладиолус. -Прочитайте задачу. -Кто может дать ответ? -С задачей вы справились, а теперь покажите, как научились решать примеры, но не простые, а с пропущенными цифрами. Р.т. Стр. 26 № 6 6* 5* 43 *5 + + + + *7 *6 ** 2* 99 88 72 100
Проверим, как вы справились. Назовите цифры, которые вставили в 1 примере, 2,3,4. Если у вас такие цифры, то вы справились с заданием без ошибок. Молодцы! |
Письменное сложение двузначных чисел( общий случай) 1. Пишу… (единицы под единицами, десятки под десятками) 2.Складываю единицы. (число единиц суммы — пишу под единицами, а 1д запоминаю) 3.Складываю десятки. 4. Увеличиваю количество десятков на 1. Результат пишу под десятками. 5. Чтобы правильно решать примеры
Один ученик работает возле доски 29 53 36 + + + 48 27 58 77 80 94 77 80 94 62 60 59 72 34 Нет Недостаточно данных, неизвестно сколько было телят. Добавить данные О соке Было, выпили, осталось Сколько было и осталось Сколько выпили вычитанием Геометрические фигуры 1,3,4. 6 Логическое мышление В. Г. Д. Ж. б. кр. 2 2 7 3 3 29 5 | П УУД самостоятельное создание способов решения проблем творческого и поискового характера на основе метода рефлексивной самоорганизации построение логической цепи рассуждений синтез – составление целого из частей; сравнение. К УУД выражение своих мыслей с достаточной полнотой и точностью учет разных мнений, координирование в сотрудничестве разных позиций формулирование и аргументация своего мнения в коммуникации (К) П УУД поиск и выделение необходимой информации; анализ объектов; синтез подведение под понятие К УУД -принятие решения; -владение монологической и диалогической речью П УУД умение анализировать, умение ориентироваться в своей системе знаний, П УУД умение по алгоритму складывать двузначные числа. анализ, синтез, обобщение, аналогия, сравнение, сериация, классификация; Здоровье сберегающие технологии П УУД извлечение из математичес-ких текстов необходимой информации П УУД построение логической цепи рассуждений П УУД Частично-поисковая работа, анализ, синтез, подбор необходимой информации. К УУД выражение своих мыслей с достаточной полнотой и точностью Р УУД работа в группе; -контроль оценки и действий партнёра; Взаимодействие, умение сотрудничать. К УУД сотрудничать в совместном решении задачи П УУД анализ задачи, установление взаимосвязи между условием и вопросом задачи, выбор и объяснение выбора действия -Осознанно выбирать знак арифметического действия для решения задачи К УУД -сотрудничество с товарищем; — оценка и самооценка; -аргументирование своего мнения. Р УУД – контроль и самоконтроль П УУД анализ, синтез, сравнение, обобщение, аналогия, классификация П УУД Преобразовывать информацию из одной формы в другую П УУД анализ, синтез, сравнение, обобщение, аналогия, классификация моделирование, преобразование модели самостоятельное создание алгоритмов деятельности Р УУД контроль, коррекция, оценка К УУД достижение договоренностей и согласование общего решения Р УУД уметь оценивать правильность выполнения действия |
Онлайн тест по Математике по теме Сложение и вычитание двузначных чисел
Древнейший раздел математической науки арифметика связан с изучением свойств чисел, действиями и правилами вычислений. Начальные знания вычислительных навыков для сложения и вычитания двузначных чисел были заложены в первом классе. Второй класс – новый этап в приобретении знаний и умений, связанных со знакомыми арифметическими действиями. Проведение таких действий должно быть освоено и доведено до автоматизма и сознательного умения, потому что они используются в других разделах математики. Стать помощником и толкователем законов сложения и вычитания может тест.
Начальные знания вычислительных навыков для сложения и вычитания двузначных чисел были заложены в первом классе. Второй класс – новый этап в приобретении знаний и умений, связанных со знакомыми арифметическими действиями. Проведение таких действий должно быть освоено и доведено до автоматизма и сознательного умения, потому что они используются в других разделах математики. Стать помощником и толкователем законов сложения и вычитания может тест.
Для успешного решения тестовых вопросов важно твердо знать, что из себя представляют двузначные числа, какие разряды имеют в своем составе, правила сложения. Задания повторяют и закрепляют теоретический материал, практические примеры теста способствуют развитию умения решать выражения изученного вида. Тестовые вопросы выделяют и определяют порядок действий при сложении двух чисел, у которых в результате из единиц получается десяток. Пример на практике контролирует овладение вычислительным процессом в письменном виде и при устном счете.
Вычитание тоже имеет свои законы и правила, которые повторяются и закрепляются с помощью тестовых упражнений. Школьник должен разобраться, как действовать, если в уменьшаемом не хватает единиц, чтобы отнять вычитаемое. Решение примера указывает на решение проблемы, дает возможность развить логическое мышление, память и внимательность. Тест готовит к самостоятельному поиску решения примеров и задач, учит тщательно изучать математические законы и применять их в практических конструкциях.
Школьник должен разобраться, как действовать, если в уменьшаемом не хватает единиц, чтобы отнять вычитаемое. Решение примера указывает на решение проблемы, дает возможность развить логическое мышление, память и внимательность. Тест готовит к самостоятельному поиску решения примеров и задач, учит тщательно изучать математические законы и применять их в практических конструкциях.
Пройти тест онлайн
Ещё никто не оставил комментария, вы будете первым.
Написать комментарий
Спасибо за комментарий, он будет опубликован после проверки
1 класс. Математика. Сложение и вычитание двузначных чисел без перехода через разряд — Сложение и вычитание двузначных чисел без перехода через разряд
Комментарии преподавателя
В этом уроке научимся складывать и вычитать двузначные числа, не переходя через разряд.
Прочитайте веселый стишок Шауката Галиева:
Я с отцом учусь считать –
Складывать и вычитать.
– Вот тебе два яблока, –
Папа говорит, –
А теперь к двум яблокам
Прибавляю три.
Сколько стало?
– Стало пять!
– За ответ я ставлю «пять»!
Отбираю три обратно…
Сколько стало?
– Стало мало!
Знаешь, папа, мне опять
Захотелось прибавлять.
А какие математические знаки нам помогают складывать и вычитать?
Конечно, это «+» и «–».
Решите задачу:
Команды «Лидер» и «Старт» играли в баскетбол.
«Лидер» забил 46 голов, а «Старт» – 23 гола.
Сколько всего голов забили обе команды в игре?
С помощью какого действия мы будем решать данную задачу?
Правильно, сложения, т.е. необходимо сложить числа 46 и 23: 46 + 23.
Вспомним, как называются компоненты при сложении.
Числа, которые складываем – это слагаемые, результат при сложении – сумма.
В числе 46 – 4 десятка и 6 единиц, значит, сумма разрядных слагаемых будет выглядеть так:
46 = 40 + 6
В числе 23 – 2 десятка и 3 единицы, значит, сумма разрядных слагаемых будет:
23 = 20 + 3
Сложим эти числа.
Как это сделать?
Чтобы сложить двузначные числа, нужно к десяткам прибавить десятки, а к единицам – единицы.
Получим:
46 + 23 = (40 + 20) + (6 + 3)
40 + 20 = 60
6 + 3 = 9
Значит, 46 + 23 = 69 (голов).
Ответ: всего 69 голов забили обе команды.
А если изменить вопрос задачи, например, какая команда забила голов больше и на сколько?
Решение задачи изменится, необходимо вычесть из числа 46 число 23: 46 – 23.
Как называются компоненты при вычитании?
Число, из которого мы вычитаем – уменьшаемое, вычитаем – вычитаемое, а результат – эторазность.
Вычтем из 46 число 23.
Оба числа двузначные.
Мы уже знаем, что 46 – это 4 десятка и 6 единиц, а 23 – это 2 десятка и 3 единицы. Вычитаем так же, как и складываем, из десятков вычитаем десятки, а из единиц – единицы.
Получим:
46 – 23 = (40 – 20) + (6 – 3)
40 – 20 = 20
6 – 3 = 3
Значит, 46 – 23 = 23(гола).
Ответ: на 23 гола больше забила команда «Лидер».
Рассмотрим другие случаи.
- Возьмем числа 46 и 3.
Число 46 двузначное, а 3 – однозначное.
Тогда при сложении и вычитании этих чисел складываться и вычитаться будут только единицы, а десятки остаются прежними.
46 – это 4 десятка и 6 единиц.
Итак, получим:
46 + 3= 40 + (6 + 3) = 49
46 – 3 = 40 + (6 – 3) = 43
2. Возьмем числа 46 и 20. Оба числа являются двузначными. Но число 20 круглое число, т.е. содержит 0 единиц, поэтому достаточно сложить или вычесть десяки, а единицы оставляем прежними, так как при сложении числа с нулем, получается то же самое число.
46 + 20 = (40 + 20) + 6 = 66
46 – 20 = (40 – 20) + 6 = 26
Итак, важно запомнить:
1. При сложении двузначных чисел без перехода через разряд нужно к десяткам прибавить десятки, к единицам – единицы.
2. При вычитании двузначных чисел без перехода через разряд нужно из десятков вычесть десятки, из единиц – единицы.
3.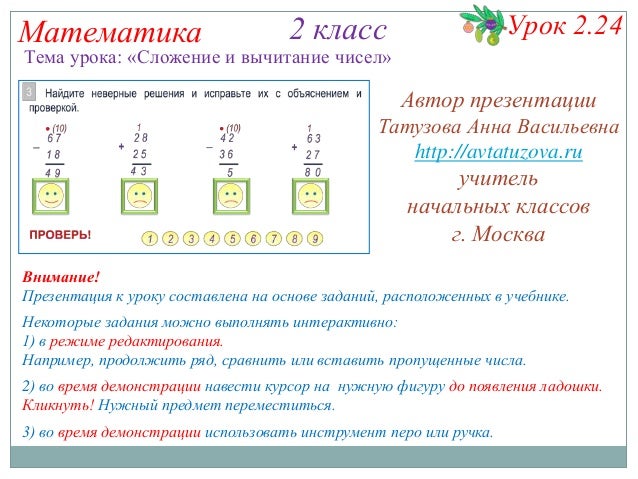 При сложении или вычитании двузначного и однозначного числа без перехода через разряд складываем только единицы, а десятки остаются прежние.
При сложении или вычитании двузначного и однозначного числа без перехода через разряд складываем только единицы, а десятки остаются прежние.
4. При сложении или вычитании двузначных чисел, одно из которых круглое число, достаточно сложить десятки, а единицы остаются без изменения.
ИСТОЧНИКИ
http://znaika.ru/catalog/1-klass/matematika/Slozhenie-i-vychitanie-dvuznachnykh-chisel-bez-perekhoda-cherez-razryad
Добавление двух- и трехзначных чисел
Урок 2: Сложение двух- и трехзначных чисел
/en/additionsubtraction/introduction-to-add/content/
Добавление больших чисел
Как мы видели в разделе «Введение в сложение», часто можно использовать , считая , и , визуальные эффекты , для решения основных задач на сложение. Например, представьте, что 3 человека собираются в путешествие и еще 2 решили присоединиться. Чтобы узнать, сколько всего людей пошло, вы можете представить ситуацию следующим образом:
Например, представьте, что 3 человека собираются в путешествие и еще 2 решили присоединиться. Чтобы узнать, сколько всего людей пошло, вы можете представить ситуацию следующим образом:
Как только вы посмотрите на проблему визуально, вы можете подсчитать и увидеть, что 5 человек отправляются в путешествие.
Что делать, если вам нужно решить большую проблему? Представьте, что несколько групп людей собираются куда-то вместе. 30 человек едет в одном автобусе, а 21 едет в другом. Мы могли бы записать это как 30 + 21.
Возможно, не стоит решать эту проблему путем подсчета. Прежде всего, независимо от того, как вы решите считать, вероятно, потребуется довольно много времени, чтобы решить проблему. Представьте, что вы рисуете на странице 30 и 21 отметку карандашом или считаете столько же мелких предметов! Во-вторых, фактический подсчет объектов может занять достаточно много времени, и вы можете даже потерять счет.
По этой причине, когда люди решают большую задачу на сложение, они формулируют задачу таким образом, чтобы было легче решать ее шаг за шагом. Давайте посмотрим на проблему, которую мы обсуждали выше, 30 + 21 .
Давайте посмотрим на проблему, которую мы обсуждали выше, 30 + 21 .
Мы видим, что 30 + 21 и означают одно и то же. Они просто пишутся по другому.
Решение задач сложения с накоплением
Все, что вам нужно для решения задач на сложение, — это навыки, полученные в разделе «Введение в сложение».
Давайте попробуем решить эту задачу, 24 + 12.
Чтобы решить задачу на сложение, начните с добавления самых дальних цифр к справа .
В данном случае это означает, что мы добавим 4 и 2.
Как и в любой задаче на сложение, мы можем использовать , считая , чтобы помочь нам сложить. Так как наша первая цифра 4, мы начнем с четырех объектов.
Мы прибавляем 4 к 2, поэтому будем использовать еще два объекта.
Мы можем сосчитать, чтобы получить в сумме 6. Мы знаем, что 4 + 2 = 6.
Напишите 6 под чертой. Важно поставить непосредственно под числами, которые мы только что добавили.

Далее мы добавим цифры к слева из тех, что мы только что добавили. Это 2 и 1.
Мы будем использовать два объекта, чтобы показать 2.
Затем мы добавим один объект, чтобы представить 1.
Когда мы посчитаем, мы получим 3.
Напишем 3 под чертой, под 2 и 1.
Готово! Всего у нас 36, или тридцать шесть.
Давайте рассмотрим еще одну задачу, просто для практики. На этот раз мы решим 62 + 5.
Начнем со сложения цифр справа, 2 и 5.
2 + 5 равно 7. цифры слева. Верхняя цифра 6, но под ней ничего нет.
6 плюс ничего равно 6, поэтому мы напишем 6 под чертой.
Всего у нас 67, или шестьдесят семь.
Как вы видели, задачи на сложение всегда решаются от справа до слева. Это означает, что вы всегда начинаете с добавления цифр справа .
Попробуй!
Решите приведенные ниже задачи на сложение. Затем проверьте свой ответ, введя его в поле.
Затем проверьте свой ответ, введя его в поле.
Добавление очень больших чисел
Сложение с накоплением также можно использовать для сложения больших чисел . Независимо от того, сколько цифр в числах, которые вы добавляете, вы добавляете их одинаково: справа налево.
Давайте попробуем сложить два 3-значных числа . Мы закончим это выражение: 213 + 406.
Как всегда, мы начнем с крайних правых цифр . Здесь это означает, что мы решим 3 + 6.
3 + 6 равно 9, поэтому мы напишем 9 непосредственно под 3 и 6.1 и 0. Не забудьте поместить его непосредственно под цифр, которые мы только что добавили, к слева из 9.
Наконец, давайте добавим следующий набор цифр, 2 и 4. 6. Запишем 6 под чертой, под 2 и 4.
Задача решена.Итого у нас 619, или шестьсот девятнадцать. 213 + 406 = 619.
Попробуй!
Добавьте эти большие числа. Затем проверьте свой ответ, введя его в поле.
Затем проверьте свой ответ, введя его в поле.
Использование переноски
На прошлой странице вы потренировались складывать числа, расположенные вертикально. Некоторые проблемы требуют дополнительного шага. Например, давайте рассмотрим следующую задачу:
Наш первый шаг — добавить цифры справа — 5 и 9 . Однако вы можете заметить, что нет места для записи суммы 14 .Когда сумма двух цифр в математической задаче больше, чем 9 , обычный способ сложения чисел не работает. Вам придется использовать технику под названием , несущую .
Давайте посмотрим, как это работает. Мы попробуем эту задачу, 25 + 39.
Как обычно, мы начнем с добавления цифр справа . Здесь это 5 и 9.
5 + 9 равно 14, но нет места для записи обеих цифр числа 14 под 5 и 9.
Запишем правую цифру 4 под чертой…
Запишем правую цифру 4 под чертой… тогда запишем левую цифру , 1, до следующего набора цифр в задаче.

Вы видите, что мы сделали? Наша сумма равнялась 14. Мы поставили 4 под чертой, а 1 перенесли и поместили над следующим набором цифр.
Далее мы добавим левые цифры. Поскольку у нас есть 1, мы добавим и его.
1 + 2 + 3 равно 6, поэтому мы напишем 6 под чертой.
Готово. 25 + 39 = 64.
Давайте потренируемся еще с одной задачей: 178 + 42.
Как обычно, начнем с добавления цифр справа. Здесь 8 + 2.
8 + 2 равно 10, так что, похоже, нам придется нести.
0 остается под 8 и 2.
Перенесите 1 и поместите его над следующим набором цифр слева.
Теперь сдвиньте влево, чтобы добавить следующий набор цифр. Поскольку мы перенесли 1, добавьте и его.
1 + 7 + 4 = 12.
Поместите правильное число, 2, под добавленными цифрами.
Возьмите 1 и поместите ее над следующей колонкой слева.
Чтобы закончить, добавьте этот столбец.
 Не забудьте включить 1, который мы только что перенесли.
Не забудьте включить 1, который мы только что перенесли.1 + 1 + ничто равно 2, поэтому мы напишем 2 под 1.
Готово.Наш ответ: 220. 178 + 42 = 220.
При переноске следите за различными числами. Если вы записываете проблемы, не забудьте написать пропущенные цифры мелким шрифтом над столбцом цифр слева.
Попробуй!
Решите эти проблемы переносом. Затем проверьте свой ответ, введя его в поле.
Практика!
Потренируйтесь добавлять эти задачи. Вам придется использовать переноску, чтобы решить некоторые проблемы.Есть 4 наборов задач по 3 задач в каждом.
Набор 1
Набор 2
Набор 3
Комплект 4
/en/additionsubtraction/добавление видео/контент/
Вычитание двузначных чисел с перегруппировкой — Математика 2-го класса
Научитесь вычитать двузначные числа с перегруппировкой
Представьте, что вы проходите 2 уровня своей любимой видеоигры.Вы зарабатываете 62 очка, всего . На уровне 1 вы набрали 28 баллов. Сколько вы набрали в Уровень 2?
Как мы можем решить эту проблему? 🤔
Вычитаем! ✅
62 — 28 = ?
Вы помните первый шаг при вычитании двузначных чисел?
Верно! Вы укладываете числа вертикально с наибольшим сверху!
Начинаем вычитать из столбца Единицы.
Но что происходит, когда число внизу больше, чем число вверху? 🤔
Мы можем сделать перегруппировку .
Вот как сгруппированы числа 62 и 28.
Когда мы перегруппируем , мы изменим группировку на 62. Это позволяет нам взять некоторое значение из одного места и передать его в другое место, которому нужно больше.
Это также называется заимствованием .
Берем одну десятку из столбца «Десятки» и добавляем ее в столбец «Единицы».
Теперь у нас есть 5 десятков и 12 единиц в верхней части нашего уравнения.
Нам не нужно перегруппировывать 28, число внизу.
Теперь мы можем вычесть столбец «Единицы».
12 — 8 равно 4.
Мы пишем это в Единицах.
Теперь давайте вычтем десятки.
Помните, у вас осталось только 5 десятков.
5 — 2 равно 3.
Наш окончательный ответ: 34.
Вы набрали 34 очка на уровне 2.
Отличная работа!
Обзор
Попробуем вычитание еще раз.
31 — 15 = ?
Во-первых, давайте запишем уравнение в виде столбца .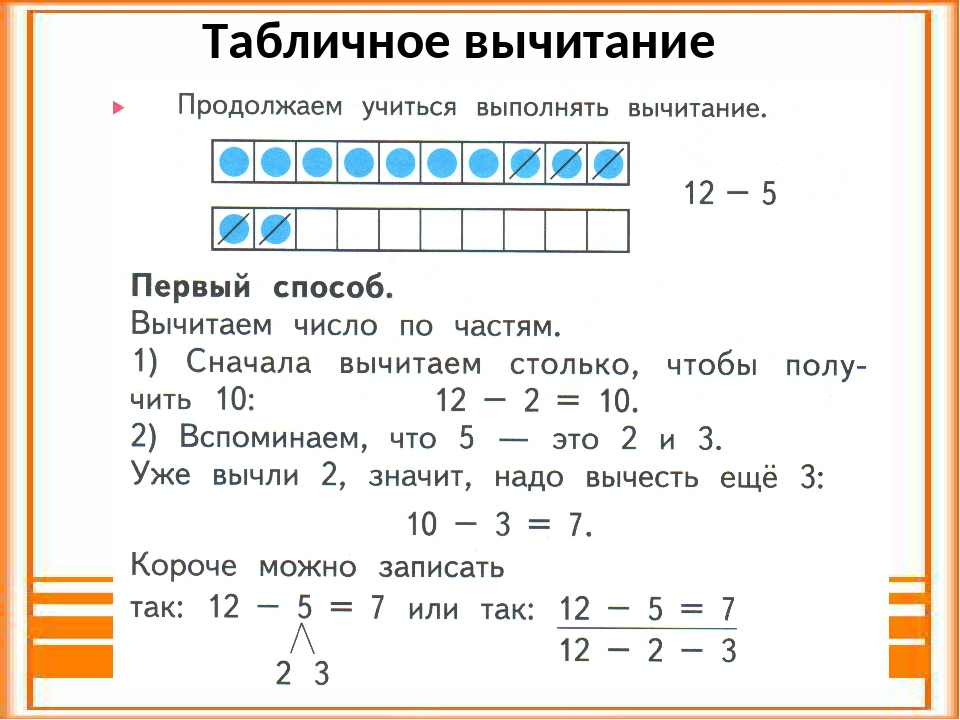
Отлично. Можем ли мы вычесть в столбце единиц?
Нет!
Нам нужно перегруппироваться!
Теперь давайте вычтем Единицы.
Отличная работа! Далее займемся десятками.
Вот оно! Хорошая работа!
Смотри и учись
Теперь можно переходить к практике.
Как преподавать сложение двух цифр для первоклассников по математике
После того, как первоклассники усвоили идею порядкового значения и поняли концепцию базового сложения, перейти к сложению двух цифр — как с перегруппировкой, так и без нее — достаточно просто.Использование манипулятивных и визуальных подсказок в процессе обучения делает его еще более легким для понимания.
Начните с бетонных предметов
Используете ли вы счетные кубики, палочки для рукоделия или любые другие материальные предметы, инструкция по сложению двузначных чисел с помощью инструментов для счета в начале сделает последующее освоение менее запутанным. Используйте резиновые ленты, чтобы сделать связки из 10 палочек для рукоделия, и используйте их со свободными одиночками, чтобы создавать практические задачи. Например, помогите своему подающему надежды математику показать 13 + 4, сложив связку десятков и три одинарные палочки вместе, а затем добавив еще четыре одиночные палочки, прежде чем пересчитать их все, чтобы найти сумму.Когда она освоится с этой практикой и последовательно найдет ответ, она будет готова перейти к более абстрактной форме проблемы.
Используйте резиновые ленты, чтобы сделать связки из 10 палочек для рукоделия, и используйте их со свободными одиночками, чтобы создавать практические задачи. Например, помогите своему подающему надежды математику показать 13 + 4, сложив связку десятков и три одинарные палочки вместе, а затем добавив еще четыре одиночные палочки, прежде чем пересчитать их все, чтобы найти сумму.Когда она освоится с этой практикой и последовательно найдет ответ, она будет готова перейти к более абстрактной форме проблемы.
Т-таблицы для визуальных подсказок
Начните с двухзначного сложения с задач, написанных вертикально. Это упрощает выравнивание элементов столбца единиц и столбца 10s. Нарисуйте Т-диаграмму и назовите правый столбец «единицами», а левый столбец «десятками». Вы можете распечатать их, а затем накрыть страницу прозрачной контактной бумагой, чтобы использовать ее повторно.Затем помогите ребенку записать цифры в соответствующие столбцы. Например, в задаче 11 + 64 он должен написать 11 с единицей в каждом столбце. Непосредственно под ним он должен написать 4 в колонке единиц и 6 в колонке 10.
Непосредственно под ним он должен написать 4 в колонке единиц и 6 в колонке 10.
Сложение чисел в ряд
Теперь ваш ребенок готов к фактическому сложению. Используйте каталожную карточку, лист бумаги или свою руку, чтобы закрыть колонку 10s слева. Попросите своего ученика добавить числа, которые он видит, в столбец единиц справа и записать его под задачей в том же столбце.Затем переместите обложку и попросите ее таким же образом добавить столбец 10s. Покажите ей, что сложение двух цифр — это всего лишь две однозначные задачи, как только она все выстроит в ряд.
Расширение до перегруппировки
Начните так же, как и для сложения без перегруппировки, используя манипулятивное объяснение концепции, а затем перейдите к t-диаграмме. На этот раз ваш ребенок запишет сумму в столбце единиц, вписав цифры в соответствующие столбцы. Для 17 + 27 он пишет 4 в колонке единиц и 1 в колонке 10 для 7 + 7 = 14. Теперь он складывает три числа в колонке с десятками и записывает четыре, в результате чего получается 44. После того, как он освоит этот метод, покажите ему, что он может записывать «перенесенные» десятки вверху колонки таблицы, а не под ней. проблема, и все еще добавить их вместе.
Теперь он складывает три числа в колонке с десятками и записывает четыре, в результате чего получается 44. После того, как он освоит этот метод, покажите ему, что он может записывать «перенесенные» десятки вверху колонки таблицы, а не под ней. проблема, и все еще добавить их вместе.
План урока по вычитанию двузначных чисел | Считай быстро
ОБЗОР И НАЗНАЧЕНИЕ
Пятая неделя программы CountFast для 2-го класса фокусируется на общих стратегиях вычитания двузначных чисел с помощью быстрого счета в уме.(Вычитание с «заимствованием» или «обменом», а также вычитание без заимствования.) Колоды карт должны отправляться домой с учащимися каждый день для дополнительной практики дома с родителем. Каждую неделю вводится новая колода, а предыдущую колоду ученик оставляет дома для продолжения практики.
ОБРАЗОВАТЕЛЬНЫЕ СТАНДАРТЫ
- Стандарт NCTM: развить свободное владение основными комбинациями чисел для сложения и вычитания
- Стандарт NCTM: понимание эффектов сложения и вычитания целых чисел
- СССС.
 MATH.CONTENT.2.NBT.B.5
MATH.CONTENT.2.NBT.B.5
Свободно складывать и вычитать в пределах 100, используя стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием.
ЗАДАЧИ
- Разработайте стратегии быстрого решения двузначных уравнений на вычитание, поняв процесс «заимствования» или «обмена», когда это необходимо.
НЕОБХОДИМЫЕ МАТЕРИАЛЫ
Одна колода карт с двузначным вычитанием для каждого ученика.Эта колода предназначена для школы и дома. Обсудите распорядок дня и ожидания от того, что каждый день приносите колоду домой и возвращаете ее в школу.
Вычитание двузначных чисел — День 1
Учитель Модель/Прямой : Познакомьте учащихся с колодой карт этой недели. Сегодня вы будете работать с желтыми карточками в колоде. Задачи на карточках написаны горизонтально. Обсудите/покажите с учащимися, как эти же задачи пишутся вертикально, выстраивая столбцы с единицами и десятками, как это было изучено в 1 –м классе. Просмотрите сначала процесс вычитания столбца единиц, а затем вычитания столбца десятков. Глядя на горизонтальное представление задач (на карточках), покажите учащимся, что они могут быстро посмотреть на числа в позиции единиц каждого числа, чтобы определить, будет ли единица вычитаться без необходимости заимствования из группы десятков. Для всех желтых карточек расчеты единиц не требуют никакого «заимствования» или «торговли».
Просмотрите сначала процесс вычитания столбца единиц, а затем вычитания столбца десятков. Глядя на горизонтальное представление задач (на карточках), покажите учащимся, что они могут быстро посмотреть на числа в позиции единиц каждого числа, чтобы определить, будет ли единица вычитаться без необходимости заимствования из группы десятков. Для всех желтых карточек расчеты единиц не требуют никакого «заимствования» или «торговли».
Конечно, есть и другие методы, которые ученики могут использовать для быстрого счета в уме.Некоторым учащимся может показаться, что быстрее разложить числа и вычесть эти меньшие части. (23 – 11 можно рассматривать как 20 – 10 – 3 – 1, или 20 – 10 -4, или 23 – 10 – 1). Поощряйте учащихся использовать самый быстрый метод вычисления в уме для своего образа мышления.
Занятие для учащихся : Объедините учащихся в пары и попросите каждую пару использовать одну колоду для работы. Попросите их достать желтых карточек . Учащиеся переворачивают по одной карточке и смотрят, кто из партнеров быстрее решит задачу, обязательно объясняя своему партнеру, как он пришел к ответу.
Учащиеся переворачивают по одной карточке и смотрят, кто из партнеров быстрее решит задачу, обязательно объясняя своему партнеру, как он пришел к ответу.
Домашнее задание : Учащиеся будут практиковаться в решении задач на ЖЕЛТЫХ карточках вместе с родителями как можно быстрее.
Вычитание двузначных чисел — День 2
Учитель Модель/Прямой : Познакомьтесь с концепцией вычитания двузначных чисел, когда нет необходимости «одалживать» или «торговать». Сегодня посмотрите на СИНИЙ набор карт в колоде со студентами. Направьте их, чтобы они заметили, что на каждой синей карточке ответ при вычитании цифр вместо единиц равен нулю.Это позволяет быстро и легко вычитать числа в разряде десятков и добавлять ноль в конце, чтобы получить окончательную разницу. Например, 31–11 можно быстро решить, заметив, что цифры единиц (1–1) будут равны 0. Это просто оставляет вычитание цифр десятков (3–1, что равно 2), а затем добавить 0 после этого ответа ( 2) чтобы получить 20 в качестве окончательной разницы.
Задание для учащихся : Повторите задание из 1-го дня, используя СИНИЕ карты из колоды.Студенты должны поощрять партнеров говорить друг с другом в процессе и отмечать успехи друг друга.
Домашнее задание : Учащиеся вместе с родителями будут практиковаться в быстром вычислении синих карточек в уме.
Вычитание двузначных чисел — День 3
Учитель Модель/Прямой : Повторите стратегии, изученные в дни 1 и 2. Сегодня используйте ЗЕЛЕНЫЕ/ЗОЛОТЫЕ карты в колоде, чтобы быстро вычитать числа, когда есть необходимость «одолжить» или «обменять». ‘, чтобы получить ответ.Повторно научите, как это выглядит, когда задачи написаны вертикально, а не горизонтально, как на карточках. Просмотрите концепцию вычитания старшего (или первого) числа, с которого мы ДОЛЖНЫ начать. Нижняя (или вторая) цифра — это то, что мы УНИЧТОЖАЕМ. Иногда в верхнем (или первом) числе не хватает единиц, чтобы вычесть нижнее (или второе) число. И — мы знаем, что переместительное свойство не работает для вычитания, поэтому мы не можем просто переставлять числа, чтобы сделать это «легче».Просмотрите заимствование или обмен из группы десятков, чтобы посмотреть на исходное число по-другому, не меняя его значения. (42–29 требует обмена, потому что мы не можем отнять 9 единиц от 2 единиц. Чтобы вычесть, мы должны переписать 42 как 3 десятка и 12 единиц.) Этот урок может занять три дня, чтобы полностью преподавать, чтобы учащиеся могли этот процесс мысленно.
И — мы знаем, что переместительное свойство не работает для вычитания, поэтому мы не можем просто переставлять числа, чтобы сделать это «легче».Просмотрите заимствование или обмен из группы десятков, чтобы посмотреть на исходное число по-другому, не меняя его значения. (42–29 требует обмена, потому что мы не можем отнять 9 единиц от 2 единиц. Чтобы вычесть, мы должны переписать 42 как 3 десятка и 12 единиц.) Этот урок может занять три дня, чтобы полностью преподавать, чтобы учащиеся могли этот процесс мысленно.
Некоторые учащиеся по-разному смотрят на задачи (например, 42 – 29 можно решить, вычитая 20 из 42, затем вычитая еще 9; ИЛИ вычитая 30 из 42, а затем прибавляя единицу).Предложите учащимся использовать тот метод, который НАИБОЛЕЕ БЫСТРЕЕ соответствует их способу мышления.
Задание для учащихся : Объедините учащихся и попросите их использовать ЗЕЛЕНЫЕ/ЗОЛОТЫЕ карты из колоды, чтобы они по очереди быстро мысленно вычитали двузначные числа, используя «обмен» или «разложение». Студенты должны поощрять друг друга говорить об используемом процессе и отмечать успехи друг друга.
Студенты должны поощрять друг друга говорить об используемом процессе и отмечать успехи друг друга.
Домашнее задание : Учащиеся вместе с родителями будут практиковаться в быстром вычислении в уме ЗЕЛЕНЫХ/ЗОЛОТЫХ карточек.
Вычитание двузначных чисел — дни 4 и 5
В дни 4 и 5 просмотрите три стратегии вычисления в уме и потренируйтесь с каждым из наборов цветов. Студенты могут даже смешивать наборы цветов и объяснять, какая стратегия использовалась для решения каждой проблемы, когда они соревнуются со своими партнерами. То же самое ученики будут делать дома с родителями в эти дни. Вы можете использовать эти дни, чтобы продолжить работу над концепцией трейдинга.
В качестве дополнительной задачи учащиеся могут сыграть турнир в виде сетки, в котором все желтые, синие и зеленые/золотые карты смешаны вместе.Партнеры могут переворачивать по одной карточке, как это было в игре CountFast 12, и видеть, кто «выиграет» каждую карточку, решив задачу быстрее всех. Победители переходят к следующему раунду/сопернику, а выбывшие должны поддерживать тех, кто все еще соревнуется. Отметьте вместе достижения этой непростой недели!
Победители переходят к следующему раунду/сопернику, а выбывшие должны поддерживать тех, кто все еще соревнуется. Отметьте вместе достижения этой непростой недели!
Обучающее видео
Вычисление двузначных сумм и разностей — Элементарная математика
Назначение
Для оценки двузначных сумм и разностей
Материалы
Нет
Обзор
Произнесите вслух 2 двузначных числа, которые составляют , а не , при сложении которых образуется новая группа из десяти, например 23 и 31.Попросите детей оценить сумму. Повторите с несколькими парами чисел, которые не требуют перегруппировки. Вы можете предложить округлить до ближайших десяти в качестве стратегии для детей.
Затем произнесите вслух 2 двузначных числа, что от до подразумевает перегруппировку. Если учащийся отвечает, просто добавляя цифры десятков, примите ответ, но спросите, может ли он уточнить оценку. Помогите им осознать, что если сумма единиц составляет 10 или более, они могут получить более точную оценку, прибавив 10 к предыдущей оценке.Напомните детям, что использование стратегии совместимых чисел иногда может быть полезным. Попросите их попробовать эту стратегию для оценки сумм с такими задачами, как 74 + 23, 52 + 23 и 75 + 15.
О последовательности
Часть 1 начинается с оценки суммы 2 двузначных чисел, которые не включают создание новой группы из десяти (перегруппировка). Часть 2 развивается до использования 2 двузначных чисел, которые требуют перегруппировки. Расширение включает в себя сочетание пар двузначных чисел с перегруппировкой и без перегруппировки, сумма которых может превышать 100.
Часть 1
Я назову 2 двузначных числа. Я хочу, чтобы вы оценили их сумму.
Я хочу, чтобы вы оценили их сумму.
Примеры:
- 11 + 18 (10 + 20 = 30)
- 22 + 46 (22 + 50 = 70)
- 38 + 31 (40 + 30 = 70)
- 43 + 52 (40 + 50 = 90)
- 72 + 17 (70 + 20 = 90)
- 27 + 42 (30 + 40 = 70)
- 21 + 68 (20 +70 = 90)
Если детям нужно больше практики или они наслаждаются своим мастерством, повторите.Если дети готовы двигаться дальше, переходите к части 2.
Часть 2
Я назову 2 двузначных числа. Я хочу, чтобы вы оценили их сумму.
Примеры:
- 19 + 17 (20 + 20 = 40)
- 26 + 18 (30 + 20 = 50)
- 34 + 48 (30 + 50 = 80)
- 19 + 38 (20 + 40 = 60)
- 56 + 22 (60 + 20 = 80)
- 33 + 49 (30 + 40 = 70)
- 21 + 19 (20 + 20 = 40)
Если детям нужно больше практики, повторите.Или, когда дети кажутся взволнованными новой задачей, перейдите к расширению.
Расширение
Я назову 2 двузначных числа. Я хочу, чтобы вы оценили их сумму.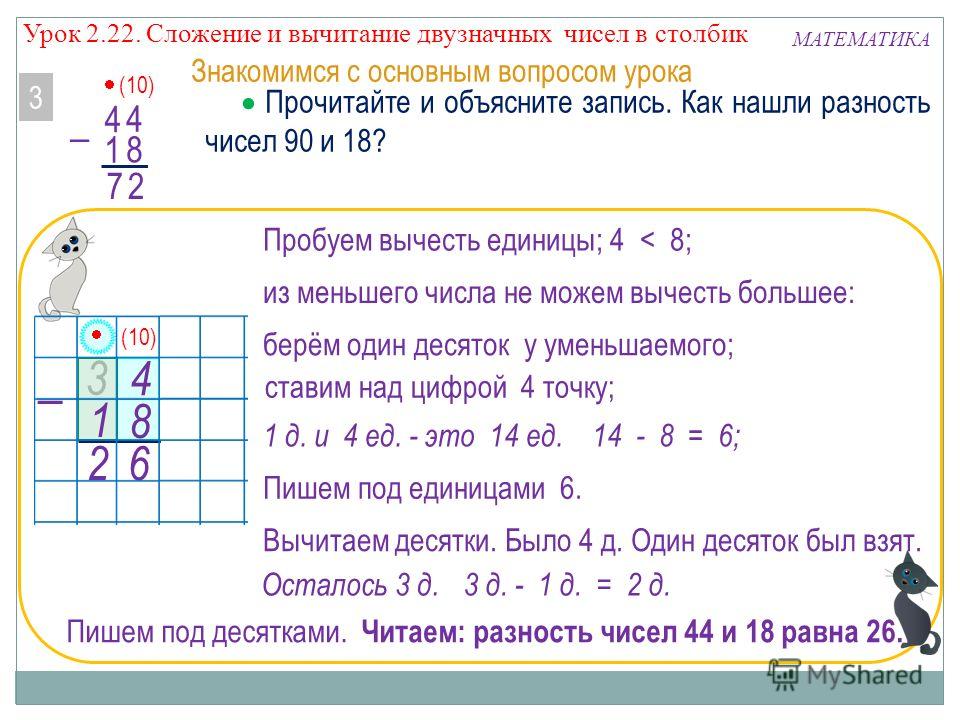
Примеры:
- 67 + 42 (70 + 40 = 110)
- 87 + 26 (90 + 30 = 120)
- 77 + 89 (80 + 90 = 170)
- 51 + 69 (50 + 70 = 120)
- 86 + 97 (90 + 100 = 190)
- 62 + 59 (60 + 60 = 120)
Сложение и вычитание двузначных чисел — без перегруппировки (A)
Добро пожаловать в рабочий лист «Сложение и вычитание двузначных чисел — без перегруппировки» (A) со страницы рабочих листов для смешанных операций в Math-Drills.ком. Этот математический рабочий лист был создан 26 ноября 2007 г. и был просмотрен 274 раз на этой неделе и 773 раз в этом месяце. Его можно распечатать, загрузить или сохранить и использовать в вашем классе, домашней школе или другой образовательной среде, чтобы помочь кому-то изучать математику.
Учителя могут использовать рабочие листы по математике в качестве тестов, практических заданий или учебных пособий (например, в групповой работе, для строительных лесов или в учебном центре). Родители могут работать со своими детьми, чтобы дать им дополнительную практику, помочь им освоить новый математический навык или сохранить свои навыки на школьных каникулах. Учащиеся могут использовать рабочие листы по математике для овладения математическими навыками на практике, в учебной группе или для взаимного обучения.
Родители могут работать со своими детьми, чтобы дать им дополнительную практику, помочь им освоить новый математический навык или сохранить свои навыки на школьных каникулах. Учащиеся могут использовать рабочие листы по математике для овладения математическими навыками на практике, в учебной группе или для взаимного обучения.
Используйте кнопки ниже, чтобы распечатать, открыть или загрузить PDF-версию математического листа «Сложение и вычитание двузначных чисел — без перегруппировки (A)» . Размер файла PDF составляет 11216 байт. Показываются предварительные изображения первой и второй (если есть) страниц. Если существует больше версий этого рабочего листа, другие версии будут доступны под изображениями для предварительного просмотра.Чтобы узнать больше, используйте строку поиска, чтобы найти некоторые или все эти ключевые слова: сложение, вычитание, математика, математика .
Кнопка Печать запускает диалоговое окно печати вашего браузера. Кнопка Открыть открывает полный файл PDF в новой вкладке браузера. Кнопка Загрузить инициирует загрузку математического листа PDF. Версии для учителей включают как страницу вопросов, так и ключ ответа. Студенческие версии, если они есть, включают только страницу с вопросами.
Кнопка Открыть открывает полный файл PDF в новой вкладке браузера. Кнопка Загрузить инициирует загрузку математического листа PDF. Версии для учителей включают как страницу вопросов, так и ключ ответа. Студенческие версии, если они есть, включают только страницу с вопросами.
Сложение и вычитание двузначных чисел — без перегруппировки (A) Рабочий лист по математике, стр. 1Сложение и вычитание двузначных чисел — без перегруппировки (A), рабочий лист по математике, стр. 2
Другие версии:
Другие рабочие листы для смешанных операций
(PDF) Исследование сложения и вычитания двузначных чисел в первом классе между Сингапуром и Тайванем
Американский журнал образования и обучения, 2017, 2(1): 75-82
76
URL: www.onlinesciencepublishing .ком | Апрель 2017 г.
1. ВВЕДЕНИЕ
1.1. Представьте проблему
Международное сравнение учебников по математике считается важным вопросом для понимания
возможностей обучения детей математике (Haggarty and Pepin, 2002; Fan, 2013; Yang and Lin, 2015). Понимание базовых знаний о сложении и вычитании целых чисел было подчеркнуто в более ранних исследованиях (Fuson, 1992; Ellemor-Collins and Wright, 2009).Развитие легкого мышления и использование нескольких
Понимание базовых знаний о сложении и вычитании целых чисел было подчеркнуто в более ранних исследованиях (Fuson, 1992; Ellemor-Collins and Wright, 2009).Развитие легкого мышления и использование нескольких
стратегий для решения задач на сложение и вычитание также играют ключевую роль в повседневных жизненных ситуациях (Fuson, 1992; Yang
и Huang, 2014). Кроме того, дизайн вопросов, представленных в учебниках по математике, повлияет на преподавание учителями и эффективность обучения учащихся (Tornroos, 2005; Xin, 2007; Fan, 2013). Это показывает важность этого исследования.
Учащиеся Сингапура и Тайваня показали относительно высокие результаты по международным оценкам по математике, таким как
, как PISA и TIMSS (Международная ассоциация по оценке образовательных достижений [IEA), 2016 г.;
Организация экономического сотрудничества и развития (ОЭСР), 2016 г.).Эти две страны были выбраны
потому, что каждая из них имеет национальную учебную программу, и, таким образом, одобренные учебники, вероятно, будут отражать учебную программу, которую должны изучать
школьников в каждой стране. Кроме того, две страны различаются историей, размером, языком, экономикой, культурой и уровнем успеваемости учащихся в международных сравнительных исследованиях. Мы ожидали, что эти 90 005 90 004 различий отразятся на том, как возможности учиться выражаются в учебниках по математике.
Кроме того, две страны различаются историей, размером, языком, экономикой, культурой и уровнем успеваемости учащихся в международных сравнительных исследованиях. Мы ожидали, что эти 90 005 90 004 различий отразятся на том, как возможности учиться выражаются в учебниках по математике.
Кроме того, образование в области естественных наук и математики в Сингапуре считается лучшим в мире (Ahuja, 2005; Hoven and Garelick, 2007). Многие различные причины приводят к этой превосходной производительности.
Сингапур имеет хороший учебник по математике, вероятно, это одна из причин. Таким образом, это исследование выбрало
сингапурских учебников по математике в качестве образца и попыталось изучить различия по теме сложения и вычитания целых чисел
между Сингапуром и Тайванем.Исследовательский вопрос заключается в том, каковы различия в схемах сложения и вычитания целых чисел
между Сингапуром и Тайванем?
1.2. Учебники по математике Связанные исследования
Изучение межнациональных учебников стало важным вопросом из-за его роли в преподавании и обучении, особенно в международном сравнении
(Fan, 2013). Предыдущие исследования анализировали учебники из разных стран, чтобы найти
Предыдущие исследования анализировали учебники из разных стран, чтобы найти
преимущества и недостатки учебников, поэтому результаты могут пролить свет на разработку будущих учебников
(Charalambous et al., 2010; Сын, 2012; Фан, 2013).
В более ранних исследованиях сообщалось, что учебники по математике играют важную роль в преподавании и изучении
математики (Schmidt et al., 2001; Weinberg and Weisner, 2010; Fan, 2013). Учебники также являются независимым инструментом, помогающим учащимся изучать математику (Zhu and Fan, 2006; Sood and Jitendra, 2007). Хорошо задокументировано, что качество содержания учебников повлияет на обучение учащихся и, в данном случае, напрямую повлияет на их успеваемость (Haggarty and Pepin, 2002; Zhu and Fan, 2006).Кроме того, методы представления
математики, типы задач, а также порядок и последовательность содержания будут влиять на эффект обучения учащихся
(Haggarty and Pepin, 2002; Zhu and Fan, 2006; Sood and Jitendra, 2007).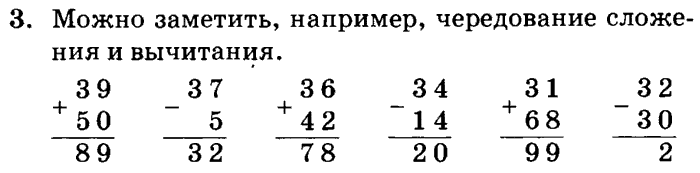 Основываясь на этих аргументах, в этом исследовании будут проанализированы различия в схемах сложения и вычитания целых чисел между Сингапуром и Тайванем.
Основываясь на этих аргументах, в этом исследовании будут проанализированы различия в схемах сложения и вычитания целых чисел между Сингапуром и Тайванем.
Что касается международных учебников, Charalambous et al.(2010) обнаружили, что тайваньский учебник содержит на
вопросов больше, требующих более высокого уровня когнитивных запросов, чем кипрские и ирландские учебники в единицах действия на фр., а также содержит на
больше вопросов, требующих ответа, математического предложения и объяснения. С другой стороны,
Erbas et al. (2012) сообщили, что сингапурские учебники отражают простые особенности плотности текста и обогащенное использование
визуальных элементов, меньшее количество тем и более легкую внутреннюю организацию.
Урок для 2 класса. Математика. Сложение и вычитание двузначных чисел без перехода через разряд. | План-конспект урока по математике (2 класс) на тему:
Цели:
закреплять умения представлять двузначные числа в виде суммы разрядных слагаемых; закрепить умения решать текстовые задачи; закрепить умение складывать и отнимать двузначные числа в пределах 100 без перехода через десяток; развивать внимательность, мышление; воспитывать чувства взаимопомощи и взаимовыручки.
Задачи:
- Закрепить умение определять количество единиц, десятков в числе; знать приемы сложения и вычитания двузначных чисел.
- Развивать умение анализировать и выделять главные, существенные признаки.
- Воспитывать самостоятельность в принятии решений, умение правильно обосновать свое решение, умение работать в группе, в паре.
I Организационный момент
Прозвенел уже звонок,
Начинается урок.
К нам пришли сегодня гости.
Поздороваться нас просят.
-Какая тема нашего сегодняшнего урока?
-Какую цель мы себе поставим?
II Устный счет
(Шум моря)
Прилетели с моря чайки,
Стали строить дом из гальки,
В клювах камешки носили,
И ответы утащили.
Ты ответ сейчас найди,
Чайку в воздух отпусти.
У чьей группы правильный ответ, поднимают чайку и прикрепляют на доску.
- Первое слагаемое 20, второе-5, чему равно сумма?
- Уменьшаемое 45, вычитаемое 40, чему равно разность?
- В этом числе 5 десятков и 3 единицы, что это за число?
- Уменьшите 17 на 4
- На сколько 13 меньше 20?
- Я задумала число, прибавила 4 и получила 34, какое число я задумала?
- 2 десятка и 4 единицы, это число…?
Молодцы!
III Актуализация знаний
Вспомните состав числа и выполните задание на листочках (проверка на доске)
34 1дес.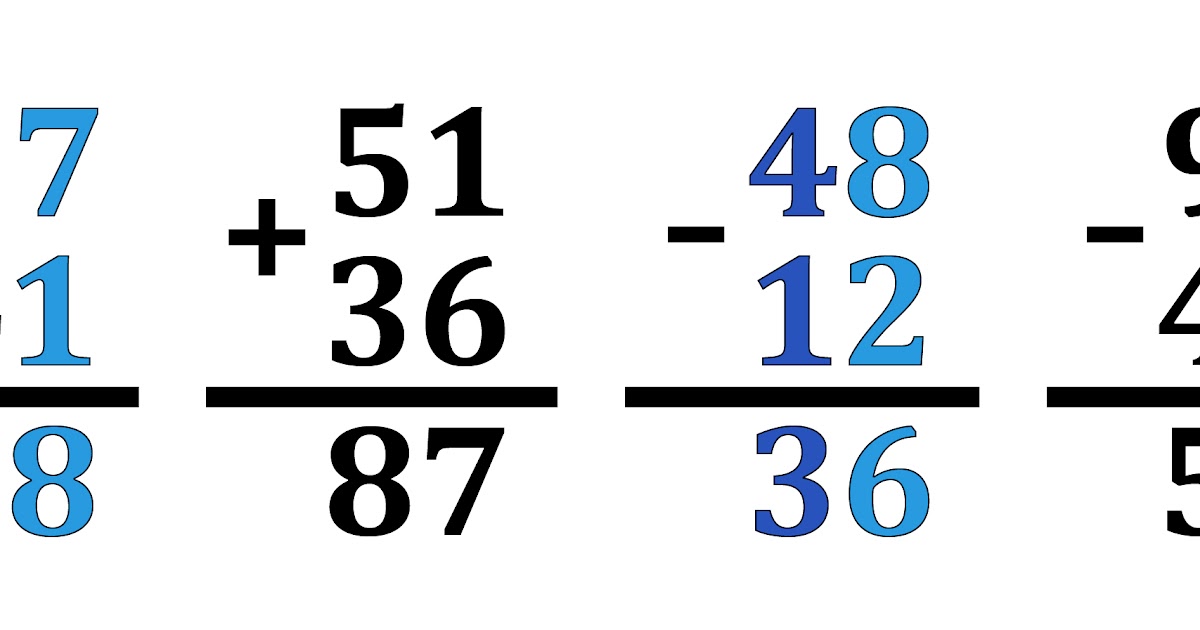 8ед.
8ед.
61 4дес.7 ед.
20 3дес.4ед.
59 2дес.
18 6дес.1ед.
47 5дес.9ед.
IV Основная часть урока. Формирование знаний, умений по теме.
В поход, в поход!
Море смелого зовет.
Море смелого зовет.
Мы пойдем служить на флот!
А вы хотите узнать о новых видах кораблей?
А чтоб узнать, на каком корабле вы поплывете, надо решить примеры, узнать ответ и поставить букву в нужное окошечко.
-Посмотрите на примеры, какие знания помогут нам их решить?
-Напомните, как мы работаем в группе? (правила на доске)
50+26 | 60+24 | 65-60 | 46+20 | 54-30 | 49-40 |
5 | 9 | 76 | 84 | 66 | 24 |
(клипер, фелука, полакр, галеон, фрегат, корвет)
Чья команда справилась с заданием, клеит желтый смаил, кто ошибся в подсчетах- зеленый смаил.
Найдите описание своего корабля и пусть капитан прочтет.
Клипер-тип быстроходных парусных судов с развитым вооружением и острыми, «режущими воду» обводами корпуса.
Фелука-небольшое палубное судно с косыми парусами в форме треугольника со срезанным углом. Судно встречалось в военных и торговых флотах.
Полакр- тип парусного судна с прямыми парусами на грот-мачте. Это мощный военный корабль, предназначенный для охраны караванов и самостоятельной перевозки особо ценных грузов.
Галеон- большое многопалубное парусное судно с сильным вооружением.
Фрегат- военно-парусный трёхмачтовый корабль, предназначен для поиска и уничтожения атомных подводных лодок в море.
Корвет- класс военных кораблей, предназначенных для сторожевой службы.
(Картинки вывешиваются на доску, пояснения дети вывешивают сами, после прочтения)
Кто знает, из какого дерева раньше строили корабли?
В кораблестроении употребляется преимущественно дуб, как самое прочное и крепкое дерево. Дуб служил для основных частей корпуса судна.
Дуб служил для основных частей корпуса судна.
Давайте решим задачу.
Из леса привезли 24 бревна дуба для строительства на одной машине, а на другой- 12 бревен дуба. Сколько бревен привезли?
-Сколько бревен было на 1 машине?
-Ск. Было на второй?
-Можем ли мы найти сколько привезли всего?
-Как?
24+12
-Какими способами мы можем посчитать этот пример? (разложить на разрядные слагаемые, в столбик)
(Повторяем правило, записываем и решаем пример в столбик)
IV Физкультминутка (2мин)
Вы все хорошо танцевали-наклейте себе желтый смаил.
VI Закрепление
-А знаете ли вы, кто первый решил, что нашей стране флот необходим?
-Это был умный человек, он основал в 1703 году город на Неве, что это за город?
-Да.это Петр I и Санкт-Петербург.
Давайте решим задачу:
«Для обучения корабельному делу Петр I отправил в Голландию и Англию 22 человека, а в Венецию- 37 человек. Сколько человек по приказу Петра I обучались корабельному делу за границей?»
(Краткое условия на доске и у детей на листочках, решают самостоятельно. Для проверки меняются терадями. Ответ на доске. Ставят себе смайлы)
Для проверки меняются терадями. Ответ на доске. Ставят себе смайлы)
Оказывается, что математика очень нужна и морякам. Посмотрим один интересный отрывок из мультфильма. (просмотр отрывка)
-Что же понял мальчик?
Да. Без математики и в море не обойтись.
Мы должны быть умными и хорошо считать. Сейчас проверим, как делаете это вы.
Решите примеры на ноутбуке, выбрав правильный ответ.
21+58, 17+42, 74+12, 82+15, 36+23
Кто решил на 8баллов- клеит себе желтый смаил, кто решил на 7-6 баллов-зеленый смаил, кто совершил много ошибок-красный.
VII Итог урока. Рефлексия
С тех пор много лет прошло, много воды утекло. Моря и океаны бороздят новые современные суда, о которых мы поговорим на след. Уроке.
Посмотрите на свой лист самооценок, у кого все получилось на уроке- прикрепляет сердечко, у кого были ошибки- молнию, кто ничего не понял-круг перечеркнутый.
А сейчас наш урок подходит к концу.
Ветер по морю гуляет
И кораблик подгоняет
Он бежит себе в волнах
На раздутых парусах.
Корабельщики дивятся,
На кораблике толпятся,
На знакомом острову
Чудо видят наяву:
Все ребята молодцы!
Отвечают, как гонцы.
Прозвенел уже звонок.
Всем спасибо за урок.
Вас во флот всех вместе взяли
И медальку всем раздали.
Математика Сложение и вычитание двузначных чисел с переходом через десяток
Материалы к уроку
Конспект урока
2. Сложение и вычитание двузначных чисел с переходом через десяток
|
Организационный этап
Без математики, друзья, Рубля не сочтешь, Что по чем не узнаешь, А, узнав, не поймешь. 
Счастливого пути по стране математике! |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Сегодня на уроке мы вспомним, как складывать и вычитать числа с переходом через десяток. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Мы отправляемся в деревню. Ее название вы прочитаете, если расположите числа в порядке возрастания.
Проверьте себя.
Мы отправляемся в Простоквашино, в гости к героям мультфильма. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Устный счёт
Задание Вам необходимо посадить на поезд героев из Простоквашино. У них есть билеты, но они не знают свои номера вагонов. Помогите им. Решите примеры, чтобы узнать номер вагона каждого героя. Тридцать пять минус пятнадцать получится Шестнадцать плюс два, будет Двенадцать минус два Пятнадцать отнять десять Пятьдесят шесть отнять пятьдесят К тридцати прибавить семь Задание Все заняли свои места, в путь. Запишите число, в котором 3 десятка 8 единиц. Запишите число, следующее при счёте за числом 39. Запишите число, предшествующее числу 30. Запишите соседей числа 50. Запишите самое большое двузначное число. Из чисел 76, 35, 84, 48, 90, 22, 59 выпишите только те, в которых десятков меньше, чем единиц. Давайте посмотрим, что у вас получилось. Проверьте себя. 38, 40, 29, 49, 51, 99, 35, 48, 59. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Объяснение нового материала
Задание Пассажиры, мы прибыли на станцию «Вычисляйкино». 28 + 6 = 59 + 4 = 42 – 8 = 73 – 5 = 39 + 9 = 46 + 5 = 61 – 3 = 84 – 6 = |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Во втором классе мы уже решали такие выражения. Давайте вспомним, как мы это делали. К двадцати восьми прибавим шесть. Для этого представим второе слагаемое 6 в виде суммы удобных слагаемых: таких, чтобы одно из них смогло дополнить двадцать восемь до тридцати. Это два и четыре. Удобно сначала к двадцати восьми прибавить два, получится тридцать. Потом прибавляем ещё четыре. Получается ответ – тридцать четыре. Аналогично поступаем и при вычитании. От сорока двух отнимем восемь. Представим вычитаемое восемь в виде суммы удобных слагаемых: таких, чтобы при вычитании одного из них смогли получить круглое число. Решите числовые выражения, рассуждая по образцу. Проверьте себя. 39 + 9 = 39 + 1 + 8 = 40 + 8 = 48 61 – 3 = 61 – 1 – 2 = 60 – 2 = 58 59 + 4 = 59 + 1 + 3 = 60 + 3 = 63 73 – 5 = 73 – 3 – 2 = 70 – 2 = 68 46 + 5 = 46 + 4 + 1 = 50 + 1 = 51 84 – 6 = 84 – 4 – 2 = 80 – 2 = 78 Вспомним, как решаются такие выражения, записывая вычисления столбиком. К тридцати пяти прибавим сорок восемь. Записываем единицы под единицами, десятки под десятками. Складываем единицы. Пять плюс восемь, будет тринадцать. Три пишем, один запоминаем. Складываем десятки. Три плюс четыре, будет семь да один в уме, восемь. Читаем ответ: восемьдесят три. Из шестидесяти одного вычтем пятнадцать. От одной единицы пять отнять не можем, занимаем один десяток. Десять да один, одиннадцать отнимем пять, получается шесть. У шести десятков один заняли, значит осталось пять, отнимем один, получается четыре. Читаем ответ: сорок шесть. Решите числовые выражения, рассуждая по образцу.
Проверьте себя.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Этап закрепления новых знаний
Задание Следующая станция «Задачкино». Решите задачу. Кот Матроскин утром надоил 7 литров молока, а вечером на пять литров больше. Сколько молока надоил Матроскин за день? Можем ли мы сразу ответить на главный вопрос задачи, сколько молока надоил Матроскин за день? Решите задачу самостоятельно. Проверьте себя. В первом действии мы узнаем, сколько Матроскин надоил молока вечером: 7 + 5 = 12 литров. Ответ: за день кот Матроскин надоил 19 литров молока. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание Молодцы, ребята! Вот мы и добрались до Простоквашино. Нас встречают герои мультфильма. Шарик не расстается со своим фоторужьем. Решите задачу самостоятельно Проверьте себя. В первом действии мы узнали, сколько фотоснимков было сделано по дороге: Во втором действии мы узнаем, сколько всего фотоснимков было сделано. Ответ: был сделан 21 фотоснимок. Задание По пути мы встретили почтальона Печкина. У него перемешались все письма. Давайте поможем разложить их по номерам домов, вычислив выражения удобным способом. 35 + 8 + 5 = 20 + 67 + 3 = 46 + 27 + 4 = 31 + 50 + 9 = 68 + 18 + 2 = Проверьте себя. 35 + 8 + 5, к 35 + 5 получим 40, к 40 + 8 = 48 20 + 67 + 3 = к 67 + 3, получим 70, к 20 + 70= 90 46 + 27 + 4, к 46 + 4, получим 50, сложим 50 и 27 = 77 31 + 50 + 9 , сложим 31 и 9, будет 40, к 40 + 50 = 90 68 + 18 + 2 = сложим 18 и 2, получим 20, 68 + 20 = 88
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задание Помогите Дяде Фёдору решить числовые выражения. 57 + 7 = 45 – 6 = 46 – 8 = 36 + 6 = 39 + 6 = 51 – 4 =
Проверьте себя и оцените свои успехи. 57 + 7 = 64 45 – 6 = 39 46 – 8 = 38 36 + 6 = 42 39 + 6 = 45 51 – 4 =47
38 + 13 = 51 64 — 27 = 37 47 — 29 = 18 77 — 49 = 28 22 + 59 = 81 96 — 58 = 38 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Итог урока
Говорит сова Закончите следующие фразы: Числа при сложении называются…… слагаемыми Молодцы, ребята. До новых встреч! |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Cложение и вычитание двузначных чисел
Обучать ребенка арифметике довольно непросто, ведь она состоит из трёх этапов. Для начала придется разобраться с числами от 0 до 9, а потом со всем остальным. Однако и с двузначными числами нужно работать поэтапно. Пусть ребенок отработает действия с числами от 10 до 20, затем от 20 до 30 и так далее. Если вы примените правильные методы и организуете обучение в игровой форме, ребенок быстрее усвоит сложную арифметику.
Итак, обучение проходит в несколько этапов.
Подготовка
На этом этапе ребенок учится складывать и вычитать двузначные числа. Пусть ребенок сначала поработает с круглыми числами (научится их складывать и вычитать). После научите его выделять в числах разрядные слагаемые (34=30+4). Попробуйте объяснить ему, что в числе 34 получится 3 десятка и 4 единицы. Справиться с этим вам помогут счетные палочки. Это довольно практичный метод, который применяется в школах уже давно.
Примите к сведению, что счетные палочки можно легко заменить на детали лего или какой-нибудь конструктор: мелкие детали— это единицы, детали покрупнее— это десятки. Сразу после этого можно переходить к сложению и вычитанию круглых чисел.
Сложение и вычитание круглых чисел
Существуют разные способы обучения ребенка сложению и вычитанию круглых чисел.
По такому же принципу разберите и вычитание круглых чисел. Как только малыш усвоит эти несложные манипуляции, можно двигаться дальше.
Складываем и вычитаем числа без перехода через разряд
Чтобы разобраться с этим этапом, придётся объяснять действия на практике. Скажем, нужно выполнить следующее действие: 24+31. Тут уж нам придется изучить ещё 1 способ сложения/вычитания. Выкладываем палочки по горизонтальной линии — это будут наши десятки; а вертикально выложенные палочки— это единицы. Теперь складываете вертикальные палочки с вертикальными, а горизонтальные с горизонтальными. Так выкладываем 2 палочки горизонтально и 4 вертикально, а рядом— 3 горизонтальные и 1 вертикальную палочку. Сложив их, получаем 5 горизонтальных палочек и 5 вертикальных, то есть, окончательный ответ 55. Постепенно ребёнок усвоит, что единицы нужно добавлять к единицам, а к десяткам добавляются десятки.
Следующее, что вы можете разобрать с малышом— это научиться складывать и вычитать в столбик. Здесь необходимо объяснить будущему школьнику, что единицы записываются под единицами, а десятки под десятками. Возможно, будет полезно вначале разложить кусочки лего и найти результат, а потом провести расчет в столбик.
Возможно, будет полезно вначале разложить кусочки лего и найти результат, а потом провести расчет в столбик.
Таким же образом можно разобрать и вычитание ( с помощью палочек, кусочков Лего и записи в столбик). Если ребенок освоил технику со сложением, ему будет не трудно справиться и с вычитанием.
Сложение и вычитание чисел с переходом через разряд
Сложность выполнения сложения и вычитания чисел через разряд заключается в том, что тут придётся «занимать» и «запоминать» числа.
Попробуем решить такой пример (26+35) с помощью палочек.
- Выкладываем числа палочками и складываем их по разрядам. У нас выходит 5 горизонтальных и 11 вертикальных палочек.
- Теперь напомните малышу, что, выполняя арифметические действия 10 единиц равняются 1 десятку. Получается, 10 вертикальных палочек можно заменить 1 горизонтальной палочкой.
- Выходит 6 десятков и 1 единица.
- Отсюда видно, что при сложении единиц, у нас есть число больше 10.
 Эти 10 единиц мы заменяем 1 десятком. Теперь показываем ребёнку, что выполняя сложение и вычитание, начинать нужно с единиц. И если их получается 10 и больше, выделяем здесь десяток и прибавляем его к другим десяткам.
Эти 10 единиц мы заменяем 1 десятком. Теперь показываем ребёнку, что выполняя сложение и вычитание, начинать нужно с единиц. И если их получается 10 и больше, выделяем здесь десяток и прибавляем его к другим десяткам.
Как только этот этап пройден, можно рассмотреть и другие варианты сложения двузначных чисел.
- сначала к числу добавляем десятки, а потом единицы. (26+30+5=61)
- первое слагаемое делаем круглым, затем добавляем к нему второе слагаемое и вычитаем то число, которое добавили изначально. (26+4=30; 30+35=65; 65-4=61)
- плюсуем единицы с единицами, а десятки с десятками. Помните, если единиц больше 10, то добавляем 1 десяток. (20+30=50; 6+5=11; 50+10=60) Итого получается 61.
Вычитание тоже покажите на наглядном примере. Допустим, 53-27.
- Делаем первое число (5 десятков и 3 единицы) и второе (2 десятка и 7 единиц)
- Мы видим, что из 3 единиц невозможно вычесть 7 единиц.
 Значит, занимаем 1 десяток = 10 единиц.
Значит, занимаем 1 десяток = 10 единиц. - Теперь из 13 единиц мы можем вычесть 7 единиц. А теперь отнимаем десятки. Тут важно напомнить ребёнку, что десятков у нас стало на 1 меньше. Значит, от 4 мы отнимаем 2.
- Итого у нас получается 13-7=6 и 4-2=2. Значит, получается 53-27=26.
Завершив наглядный метод, начните считать и другими способами:
- сначала вычитаем в столбик: напомните ребёнку, что единицы вычитаться и складываются с единицами, а десятки с десятками. 53-27=26
- а теперь вычитаем десятки, а после единицы.
Чтобы объяснить ребёнку тонкости арифметических действий, возьмите в помощь счёты. Это удобно и практично. А ещё ребёнок мог бы записать числа на них и практиковаться, пока не дойдёт до автоматизма.
Помните, что каждый ребёнок индивидуален и выбирать способ обучения необходимо исходя из особенностей ребенка. Кому-то легко дается счет на палочках, кто-то предпочитает считать в столбик. А кому-то для практики требуются месяца, ребёнок считает разными способами, но ему так и не удаётся научиться считать быстро и без ошибок. Родителям стоит быть терпеливыми, помогать малышу, решать примеры вместе и не злиться. Пусть он чувствует вашу поддержку и заботу. А с регулярной практикой у малыша обязательно все получится.
А кому-то для практики требуются месяца, ребёнок считает разными способами, но ему так и не удаётся научиться считать быстро и без ошибок. Родителям стоит быть терпеливыми, помогать малышу, решать примеры вместе и не злиться. Пусть он чувствует вашу поддержку и заботу. А с регулярной практикой у малыша обязательно все получится.
Урок математики во 2 классе. Урок-сказка по теме:Сложение и вычитание двузначных чисел
Урок математики во 2 классе. Урок-сказка по теме:Сложение и вычитание двузначных чисел
Тема урока: Сложение и вычитание двузначных чисел.
Тип урока: закрепление полученных ранее знаний.
Форма урока: урок — сказка.
Цели:
Дидактические цели: Продолжать формировать представления об устных способах сложения и вычитания двузначных чисел, о нумерации двузначных чисел.
Развивающие цели: Развивать интеллектуальные и коммуникативные общеучебные умения, уиения делать выводы, сравнивать, обобщать, выделять лишнее.
Воспитательные цели: Воспитывать культуру интеллектуального и коллективного труда, прививать любовь к предмету через игру и игровые ситуации.
Оборудование: мультимедийное оборудование, презентация к уроку,карточки с дифференцированными заданиями, муз. запись и отрывки из к/ф «Приключения Буратино», костюм Буратино для ученика, 3 коробки с надписями, конверт с письмом от Пьеро.
Ход урока.
І. Организационный момент.
— Сегодня у нас на уроке много гостей и мы как гостеприимные хозяева обязаны оказать им внимание. (Развернитесь, поздоровайтесь).
Ученица: (Суюндукова Марьям)
Мы рады приветствовать вас в классе нашем,
Возможно, есть классы и лучше, и краше,
Но пусть в нашем классе вам будет светло,
Пусть будет уютно и очень легко!
Поручено нам вас сегодня встречать,
Начнём же урок, не будем зря время терять.
-Спасибо, Марьям! Будем надеяться, что настроение у наших гостей улучшилось, и они с удовольствием порадуются за наши успехи.
ІІ. Психоэмоциональный настрой
Учитель: Возьмите друг друга за руки и почувствуйте тепло рук ваших товарищей, мысленно подарите друг другу добрые слова. Вам понадобятся их поддержка и помощь.
Пусть сегодняшний день принесёт вам радость общения. Пусть вам помогут сообразительность, смекалка и те знания, которые вы приобрели ранее.
ІІІ. Введение в тему урока.
Учитель: -Сегодня у нас необычный урок. Он будет связан с миром сказки. А в мир какой сказки вы попадёте вы узнаете, когда отгадаете загадку:
«Уотца был мальчик странный,
Необычный, деревянный.
На земле и под водой
Ищет ключик золотой,
Всюду нос суёт свой длинный
Кто же это?
Дети: Буратино! музыкальная запись с отрывками из к/ф
Вбегает мальчик в костюме Буратино. (Кокшеев Ислам)
(Кокшеев Ислам)
(глаза широко раскрыты, лицо удивлённое):
— Ой, здравствуйте! Как тут много людей. А куда я попал?
Учитель: . А ты куда бежал?
Буратино: А я вот ищу золотой ключик. (Обращаясь к классу)
Ребята, а вы мне поможете?
Дети: С удовольствием!
Учитель: Буратино, мы сможем тебе помочь, но для этого ты должен потрудиться. Тебе придётся пройти математические испытания. Ты готов?
Тогда садись скорее, начнём.
Тема нашего урока «Сложение и вычитание двузначных чисел».
Учитель. На нашем экране появились два замка.
Это цель для нашего Буратино. Если он сумеет открыть оба замка, тогда сможет найти золотой ключик.
Первый замок — устный счёт.
1 Определить закономерность и продолжить числа.
2. Сравнить: «>» «<» «=».
На доске выражения:
1 м * 100 см 60 * 6 81 дм * 81 см
20 см * 4 дм 32 * 23 80 см * 82 кг
3. Назовите двузначные числа, в которых сумма десятков и единиц равна 6.
Назовите двузначные числа, в которых сумма десятков и единиц равна 6.
(60, 51, 15, 24, 42, 33)
Учитель. Молодцы, ребята! Первый замок открыт.
Переходим ко 2 замку.
ІV. Работа в тетради.
1. Открываем тетради. Записываем дату, классная работа.
Учитель. Ребята, повторите, пожалуйста, какое сегодня число? (25)
А какой по счёту месяц? (11)
2. На минутке чистописания мы запишем эти числа.
— Какие это числа? Сколько десятков и сколько единиц в этих числах?
Сколько составит сумма десятков и единиц этих чисел?
Запишите эти числа каллиграфическим почерком до конца строки.
Буратино пиши красиво, учись у наших детей. Буратино так постарался, что даже подпрыгнул от радости. Давайте мы его порадуем ещё больше стихотворением-физминуткой о нём.
V. Физминутка. (дети проговаривают стихи и выполняют движения)
Буратино потянулся,
Раз нагнулся, два нагнулся.
Руки в стороны развёл,
Ключик видно не нашёл.
Чтобы ключик нам достать
Надо на носочки встать.
VІ. Продолжение работы в тетради.
3. — Ребята, кто это на экране? (Пьеро)
Какой у него вид? (печальный, грустный)
А печален он от того, что не может попасть к нам на урок. Но он прислал нам письмо.
«Мне очень грустно, потому что я не смогу попасть к вам на урок. Я люблю решать уравнения. Решите их, порадуйте меня!»
4. (слайд 9) Дети на интерактивной доске решают уравнения. Проговаривают правила нахождения неизвестного.
Остальные дети решают по группам:
1-группа 2-я группа 3-я группа
X + 10 = 60 Y — 20 = 80 45 + Y = 60
5. А теперь, Буратино, реши вместе с нашими учащимися примеры на сложение и вычитание двузначных чисел. карточки с дифференцированными заданиями.
Буратино: Но золотой ключик ещё не найден. Я не могу справиться ещё с одним заданием.
-Маленькие черепашки — правнуки и правнучки черепахи Тортилы
играли с коробочками, где спрятан золотой ключик и перепутали все надписи и теперь все надписи ложные. Как быть? Помогите!
Выносятся три коробочки: на первой написано: «здесь ключик и монетки»,
на второй — «здесь азбука», на третьей — «здесь ключик».
— Где же лежит Золотой ключик? Рассуждения учащихся.
Буратино: Вот он и Золотой ключик! Спасибо, ребята, теперь я смогу открыть потайную дверь и выручить Мальвину и Пьеро.
VІІ. Итог урока. Размышления учащихся
Оценки за урок.
VІІІ. Домашнее задание вам приготовила черепаха Тортила, которая очень торопилась, но приползла только к концу урока: дифференцированное по группам.
1-я и 2-я группы №7(б) решить разными способами.
3-я группа №8 вычислить и найти значение выражений.
Как объяснить ребенку вычитание и сложение двузначных чисел
Схема проезда
Контакты
Главная
Блог
Как объяснить ребенку вычитание и сложение двузначных чисел
Обучение ребенка вычитанию и сложению – сложный, многоэтапный процесс, начинающийся с изучения однозначных чисел и переходящий в двухзначные, с постепенным изучением моментов, когда происходит переход через десяток. Чтобы научить ребенка быстро считать двузначные числа следует пройти каждый этап последовательно. Использование разных способов обучения, преимущественно в игровой форме, дает возможность сделать весь процесс интересным для малыша, что положительно скажется на результатах.
Чтобы научить ребенка быстро считать двузначные числа следует пройти каждый этап последовательно. Использование разных способов обучения, преимущественно в игровой форме, дает возможность сделать весь процесс интересным для малыша, что положительно скажется на результатах.
Вычитание двузначных чисел с переходом через разряд
Объяснить ребенку вычитание двузначных чисел легче с использованием игровых методов. Это позволит сконцентрировать внимание на процессе и улучшит усвоение пройденного материала. Не стоит сразу начинать с больших чисел, лучше начать первые шаги с минимальных чисел, постепенно увеличивая.
Важным является такой момент – ребенок не сможет сразу считать в уме, даже когда речь идет о небольших числах. Лучше использовать листок бумаги, части конструктора, компьютер или другие дополнительные средства, где малыш сможет делать требуемые пометки. Следует уделить внимание изучению порядка образования десятков, вплоть до ста. Это поможет при обучении сложению и вычитанию с переходом через разряд, а не только в пределах одного десятка. Освоив счет в пределах десяти, можно переходить к изучению более сложных действий, используя одну из методик или комбинируя их.
Освоив счет в пределах десяти, можно переходить к изучению более сложных действий, используя одну из методик или комбинируя их.
Разделение чисел при вычете
При вычете из двузначного числа однозначного с переходом через разряд можно использовать разделение. Объясните ребенку, что от целого десятка отнимать будет легче, и достаточно разделить однозначное число таким образом, чтобы отняв одну из его частей получить 10, и уже потом вычесть вторую часть. В результате чадо быстро освоит такой счет, научившись правильно разделять числа и получать конечный результат.
Такой способ хорошо подходит в тех случаях, когда освоен счет до 10, а также малыш знаком с числами минимум до 20. Проводить занятия следует в игровой форме, используя расходные материалы или специальные компьютерные игры.
Использование геометрических фигур для визуализации чисел
Распространенный вариант, когда десятки обозначаются треугольниками, а единицы – точками. Достаточно объяснить ребенку значение фигур и привести несколько примеров. После этого можно приступать к тренировкам, начиная с простых заданий, используя числа до 20, постепенно усложняя их.
Достаточно объяснить ребенку значение фигур и привести несколько примеров. После этого можно приступать к тренировкам, начиная с простых заданий, используя числа до 20, постепенно усложняя их.
Для начального уровня это подходящий вариант, позволяющий проводить расчеты быстро и понятно. Однако может возникнуть сложность, когда при вычете следует отнимать дополнительный десяток (например, 54-35=19). Важно объяснить малышу тонкость такого момента. Отнимать двузначные числа таким способом лучше, избегая подобных ситуаций или же регулярно показывать примеры ребенку для лучшего освоения.
Отнимание с помощью Lego
Для применения этого способа можно использовать Lego Duplo, рассчитанный для этих целей, или обычные кубики конструктора, предварительно пронумеровав их. С их помощью можно решать сложные задачи, включая те, в которых происходит переход через десяток.
Достаточно отобразить требуемые числа с помощью соответствующих цифр (например 25-19). Чтобы понятнее ребенку объяснить тонкость, достаточно разделить их на более мелкие (10,10, 5 и 10, 5, 4). Ребенок легко усваивает, что 10-10=0, и сможет убрать лишние десятки. Оставшееся уравнение в дальнейшем решается легко (10 и 5 – 5 и 4). Ребенку остается посчитать 10-4, получив конечный результат.
Чтобы понятнее ребенку объяснить тонкость, достаточно разделить их на более мелкие (10,10, 5 и 10, 5, 4). Ребенок легко усваивает, что 10-10=0, и сможет убрать лишние десятки. Оставшееся уравнение в дальнейшем решается легко (10 и 5 – 5 и 4). Ребенку остается посчитать 10-4, получив конечный результат.
Сложение двухзначных чисел
Объяснить ребенку сложение двузначных чисел обычно проще, нежели вычет, даже в тех случаях, когда идет прибавление дополнительного десятка после сложения. Способов обучения вполне достаточно для того, чтобы выбрать наиболее подходящий для вашего малыша. Важно – занятие всех детей дошкольного возраста должно проходить в игровой форме.
Разделение чисел
Одним из простых способов обучения является разделение чисел на десятки и единицы. Это помогает и в том случае, когда происходит прибавление десятка после сложения единиц. Например 25+36 ребенок запишет как 10+10+10+10+10+6+5 и получит результат 50+5+6. После этого происходит сложение 5+6=11. Снова разложив 11 на 10+1 получается 50+10+1=61. Дети легко воспринимают такой способ и быстро учатся использовать его даже при подсчетах в уме.
После этого происходит сложение 5+6=11. Снова разложив 11 на 10+1 получается 50+10+1=61. Дети легко воспринимают такой способ и быстро учатся использовать его даже при подсчетах в уме.
Используйте решение «в столбик»
Это значительно упростит процесс подсчета вашему малышу. Так ребенок проще воспринимает десятки и единицы, может делать пометки о дополнительных десятках и прочие необходимые записи. Прибавлять двузначные числа таким образом легче и вскоре ребенок сможет проводить необходимые операции в уме.
Использование этого метода возможно и для изучения вычета.
Применение онлайн-игр для обучения
Сегодня существует множество мини-игр, которые направленны на помощь родителям в обучении ребенка. Их использование дает возможность малышу быстро и с интересом освоить основные азы счета, включая случаи, когда происходит сложение двухзначных чисел с переходом через разряд.
Решать примеры с двузначными числами таким образом довольно легко, ведь в большинстве случаев на первом этапе идет пояснение того, как следует проводить все действия, показываются примеры, и только потом можно приступать к решению заданий. Можно использовать вариант, когда в игре предложены варианты ответа, однако в таком случае ребенок может пытаться угадывать правильный ответ не проводя подсчеты. В случае ошибки, необходимо помочь ребенку понять, почему он ее совершил, и объяснить, как стоит делать правильно.
Можно использовать вариант, когда в игре предложены варианты ответа, однако в таком случае ребенок может пытаться угадывать правильный ответ не проводя подсчеты. В случае ошибки, необходимо помочь ребенку понять, почему он ее совершил, и объяснить, как стоит делать правильно.
Онлайн флеш-игра по математике «Двузначные числа» генерирует случайные двузначные числа, которые ребенку следует просуммировать и выбрать правильный результат. Также можно вписывать его вручную, с помощью мыши или цифровой панели клавиатуры.
Научить ребенка складывать и вычитать двузначные числа на самом деле несложно. Достаточно проводить регулярные занятия, длительность которых будет 10-20 минут, и уже через небольшой промежуток времени ваш малыш добьется неплохих показателей. Использование тренировочных заданий в повседневной жизни позволит лучше усвоить все правила и быстрее развить возможность счета в уме даже больших двухзначных чисел.
Еще из блога:
Чем занять ребенка от 5 до 8 лет дома и на улице
Подробнее
Книги для детей от 2 месяцев до 14 лет – какие читать
Подробнее
Чем занять ребенка летом?
Подробнее
Одаренные дети — как определить и развить их способности
Подробнее
Последние новости
Мастер-класс в ТРК «ТРИНИТИ»
Оставьте заявку и мы свяжемся с вами
Оставьте свой телефон, мы обязательно вам перезвонимСложение и вычитание двузначных чисел
Что такое двузначные числа? Двузначные числа начинаются с 10 и заканчиваются на 99. Цифры в разряде десятков в двузначном числе должны быть от 1 до 9. Наибольшее двузначное число — 99, а наименьшее двузначное число — 10.
Цифры в разряде десятков в двузначном числе должны быть от 1 до 9. Наибольшее двузначное число — 99, а наименьшее двузначное число — 10.
Разрядное значение числа — это позиция каждой цифры. Имея дело с двузначными числами, у нас есть два различных разряда, называемых единицами и десятками.
Рассмотрим число 86.
В данном примере 8 стоит на месте десятков, что означает значение 80, а 6 стоит на месте единиц, что имеет значение 6.
Как складывать двузначные числа ?Всякий раз, когда мы складываем двузначные числа, мы всегда начинаем процесс с крайней правой цифры или с разряда единиц.
Сложение двузначных чисел без перегруппировки
Чтобы сложить двузначные числа, выполните следующие действия:
- Запишите числа с разрядными значениями в ряд.
- Сложите цифры вместо единиц.
- Сложите цифры десятков.
Пример №1
Чему равна сумма 13 и 11?
Решение
| Процесс добавления | Пошаговый объяснение |
Объедините количество в форме колонны со значениями. | |
| Сложите цифры в столбце разряда единиц. Таким образом, 1 + 3 = 4 Затем запишите сумму 1 и 3 под чертой. | |
| Получить сумму чисел в разряде десятков. Следовательно, 1 + 1 = 2 Затем запишите цифру 2 под чертой. | |
| Следовательно, сумма 13 и 11 — 24 |
Пример № 2
Найти сумму 24 и 33.
. Дополнительное решение
| Пошаговое объяснение | |
| Расположите числа в виде столбца, выровняв разряды. | |
| Получить сумму чисел в разряде единиц. Следовательно, 4 + 3 = 7 Затем запишите цифру 7 под чертой. | |
| Сложите числа в разряде десятков. Таким образом, 2 + 3 = 5 . Затем запишите сумму 2 и 3 под чертой. | |
Следовательно, сумма 24 и 33 равна 57 . |
Пример № 3
Определите сумму 16 и 42.
Решение
| Процесс добавления | . числа в форме столбца с выровненными значениями мест. |
| Сложите числа в столбце единиц. Таким образом, 6 + 2 = 8 Затем запишите сумму под чертой. | |
| Получить сумму чисел в разряде десятков. Следовательно, 1 + 4 = 5 Затем запишите сумму 1 и 4 под чертой. | |
| Следовательно, сумма 16 и 42 равна 58 . |
Пример #4
Что получится, если к 58 прибавить 21?
Решение
| Процесс добавления | Пошаговое объяснение |
| Расположите числа в виде столбца, выровняв разряды. | |
Получите сумму чисел в столбце единиц. Следовательно, 8 + 1 = 9 Следовательно, 8 + 1 = 9 . Затем запишите сумму 8 и 1 под чертой. | |
| Сложите числа в разряде десятков. Таким образом, 5 + 2 = 7 . Затем напишите 7 под чертой. | |
| Следовательно, сумма 58 и 21 равна 79 . |
Пример #5
Что получится, если сложить 73 и 22?
Решение
| Процесс добавления | Пошаговый объяснение |
| Объедините количество в форме колонны со значениями. | |
| Получить сумму чисел в столбце разряда единиц. Таким образом, 3 + 2 = 5 . Затем напишите 5 под чертой. | |
| Сложите числа в разряде десятков. Следовательно, 7 + 2 = 9 Затем запишите сумму 7 и 2 под чертой. | |
Следовательно, сумма 73 и 22 равна 95 . |
Добавление двузначных чисел с перегруппировкой
Чтобы добавить двузначные числа, которые необходимо перегруппировать, выполните следующие действия:
- Запишите числа с разрядными значениями в ряд.
- Сложите цифры вместо единиц. Если сумма больше 10, то цифра переносится на разряд десятков.
- Сложите цифры в разряде десятков. Если сумма больше 10, то цифра переносится на разряд сотен.
Пример №1
Чему равна сумма 23 и 19?
Решение
| Процесс добавления | Пошаговый объяснение |
| Объедините количество в форме колонны со значениями. | |
| Получить сумму чисел в столбце единиц. Таким образом, 3 + 9 = 12 . Поскольку сумма превышает 10, напишите 0 под чертой столбца единиц и поместите перенос 1 в начало столбца десятков.  | |
| Добавьте перенос и разряд десятков 23 и 19. Следовательно, 1 + 2 + 1 = 4 Затем напишите 4 под чертой чисел в столбце десятков. | |
| Следовательно, сумма 23 и 19 равна 42 . |
Example #2
Determine the result of adding 48 and 36.
Solution
| Addition Process | Step-by-Step Explanation |
| Arrange the numbers в форме столбца с выровненными значениями мест. | |
| Сложите числа в столбце единиц. Таким образом, 8 + 6 = 14 . Поскольку сумма равна 14, напишите 4 под чертой чисел в разряде единиц и поместите перенос 1 в начало столбца разряда десятков. | |
| Получите сумму переноса и разряда десятков 48 и 36. Таким образом, 1 + 4 + 3 = 8 Затем запишите 8 под чертой столбца разряда десятков.  | |
| Следовательно, сумма 48 и 36 равна 84 . |
Пример №3
Что получится, если сложить 56 и 63?
Решение
| Процесс добавления | Пошаговое объяснение |
| Расположите числа в виде столбца, выровняв разряды. | |
| Сложите числа в столбце единиц. Следовательно, 6 + 3 = 9 . Затем напишите 9 под чертой. | |
| Получите сумму чисел в столбце десятков. Таким образом, 5 + 6 = 11 . Поскольку сумма равна 11, напишите 1 под чертой чисел в столбце десятков и поместите перенос в столбец разряда сотен. | |
| Поскольку в числах 56 и 63 нет сотен, просто уменьшите перенос 1. | |
| Следовательно, сумма 56 и 63 равна 119 . |
Пример #4
Чему равна сумма 73 и 87?
Решение
| Процесс добавления | Пошаговое объяснение |
Расположите числа в виде столбца, выровняв разряды. | |
| Получите сумму чисел в столбце единиц. Таким образом, 3 + 7 = 10 . Поскольку сумма равна 10, напишите 1 под чертой чисел в столбце единиц и перенесите перенос в столбец десятков. | |
| Добавьте перенос и числа в столбце десятков. Следовательно, 1 + 7 + 8 = 16 . Поскольку сумма равна 16, напишите 6 под чертой чисел в столбце десятков и поместите перенос сверху столбца разрядов сотен. | |
| Поскольку в числах 78 и 67 нет сотен, просто уменьшите перенос 1. | |
| Следовательно, сумма 73 и 87 равна 160 . |
Пример № 5
Найдите сумму 98 и 19.
Решение
| Процесс добавления | STEP-BY-STEP-STEP-STEP.0045 | Расположите числа в виде столбца, выровняв разряды. |
Получите сумму чисел в столбце единиц. Таким образом, 9 + 8 = 17 Таким образом, 9 + 8 = 17 . Поскольку сумма равна 17, напишите 7 под чертой чисел в столбце единиц и перенесите перенос в столбец десятков. | ||
| Добавьте перенос и числа в столбце десятков. Следовательно, 1 + 9 + 1 = 11 . Поскольку сумма равна 11, напишите 1 под чертой чисел в столбце десятков и поместите перенос сверху столбца сотен. | ||
| Поскольку в столбце сотен цифр нет числа, просто уменьшите перенос 1. | ||
| Следовательно, сумма 98 и 19 равна 117 . |
Всякий раз, когда мы вычитаем двузначные числа, мы всегда начинаем процесс с крайней правой цифры или разряда единиц.
Вычитание двузначных чисел без перегруппировки
Чтобы вычесть двузначные числа, выполните следующие действия:
- Расположите числа друг над другом так, чтобы разряды десятков и единиц совпадали.

- Вычтите разряд единиц числа во второй строке из разряда единиц числа в первой строке.
- Вычтите разряд десятков числа во второй строке из разряда десятков числа в первой строке.
Пример #1
В чем разница между 45 и 14?
Решение
| Процесс вычитания | Пошаговый объяснение |
| Выровняйте цифры 45 и 14 в колонке с значениями. | |
| Вычтите 4 из 5. Таким образом, 5 – 4 = 1 Затем запишите разницу 5 и 4 под чертой. | |
| Вычтите числа в разрядах десятков. Таким образом, 4 – 1 = 3 Затем напишите 3 под чертой. | |
| Следовательно, разница между 45 и 14 составляет 31 . |
Example #2
Determine the result of subtracting 59 from 99.
Solution
| Subtraction Process | Step-by-Step Explanation |
Выровняйте цифры 99 и 59 в форме столбца, выровняв разрядные значения. | |
| Вычтите число из разряда единиц. Следовательно, 9 – 9 = 0 Затем запишите 0 под чертой столбца единиц измерения. | |
| Вычтите число из столбца десятков. Таким образом, 9 – 5 = 4 . Затем запишите разницу между 9 и 5 под чертой столбца десятков. | |
| Следовательно, результатом вычитания 59 из 99 будет 40 . |
Пример №3
Найдите разницу между 63 и 21.
Решение
| Процесс вычитания | Пошаговый объяснение |
| Выровняйте цифры 63 и 21 в колонке с значениями. | |
| Вычтите число из разряда единиц. Следовательно, 3 – 1 = 2 Затем запишите разницу между 3 и 1 под чертой столбца единиц измерения. | |
Получите разницу числа в столбце десятков. Таким образом, 6 – 2 = 4 Таким образом, 6 – 2 = 4 Затем напишите 4 под чертой столбца десятков. | |
| Следовательно, разница между 63 и 21 составляет 42 . |
Пример #4
Какой результат 84 – 33?
Решение
| Процесс вычитания | Пошаговый объяснение |
| Выровняйте цифры 84 и 33 в колонке с значениями. | |
| Вычтите число из разряда единиц. Следовательно, 4 – 3 = 1 Затем запишите разницу между 4 и 3 под чертой столбца единиц. | |
| Получите разницу числа в столбце десятков. Таким образом, 8 – 3 = 5 . Затем напишите 4 под чертой столбца десятков. | |
| Следовательно, разница между 84 и 33 составляет 51 . |
Пример №5
Найти разницу в вычтении 18 из 79.
Решение
| Процесс вычитания | Пошаговый объяснение |
| ALINIT форма столбца с выровненными значениями мест. | |
| Вычтите число из разряда единиц. Следовательно, 9 – 8 = 1 Затем запишите разницу между 9 и 8 под чертой столбца единиц. | |
| Получите разницу числа в столбце десятков. Таким образом, 7 – 1 = 6 . Затем напишите 6 под чертой столбца десятков. | |
| Следовательно, если из 79 вычесть 18, получится 61 . |
Вычитание двузначных чисел с перегруппировкой
Чтобы вычесть двузначные числа, выполните следующие действия:
- Расположите числа друг над другом так, чтобы разряды десятков и единиц совпадали.
- Вычтите разряд единиц числа во второй строке из разряда единиц числа в первой строке. Если разряд единиц вычитаемого больше разряда единиц уменьшаемого, то заимствуйте 1 в разряде десятков.

- Вычтите разряд десятков числа во второй строке из разряда десятков числа в первой строке. Если разряд десятков вычитаемого больше разряда единиц уменьшаемого, то заимствуйте 1 в разряде сотен.
Пример #1
В чем разница между 33 и 17?
Решение
| Процесс вычитания | Пошаговый объяснение |
| Выровняйте цифры 33 и 17 в колонке с значениями. | |
| Так как 7 больше 3, нам нужно позаимствовать 1 из разряда десятков. Таким образом, к разряду единиц мы прибавим 10, а к разряду десятков вычтем 1. | |
| Вычтите 7 из 13. Таким образом, 13 – 7 = 6 Затем запишите разницу под чертой в столбце единиц. | |
| Вычтите 1 из 2. Следовательно, 2 – 1 = 1 Затем запишите 1 под чертой в столбце десятков. | |
Следовательно, разница между 33 и 17 составляет 16 . |
Пример #2
Найдите результат вычитания 13 из 21.
Решение
| Процесс вычитания | Пошаговое пояснение |
| Поскольку 3 больше 1, нам нужно позаимствовать 1 из разряда десятков. Таким образом, к разряду единиц мы прибавим 10, а к разряду десятков вычтем 1. | |
| Получите разницу 11 и 3. Таким образом, 11 – 3 = 8 Затем напишите 8 под чертой в столбце единиц измерения. | |
| Вычтите числа в столбце десятков. Следовательно, 1 – 1 = 0 . Поскольку разница равна 0, и это последний столбец, который мы собираемся вычесть, вы можете написать 0 под чертой. | |
| Следовательно, разница между 21 и 13 составляет 8 . |
Пример №3
Определите разницу вычитания 25 из 91.
Решение
| Процесс вычитания | Пошаговый объяснение |
| Выровнять цифры 91 и 25 в колонке с значениями. | |
| Поскольку разряд единиц вычитаемого больше разряда единиц уменьшаемого, нам нужно заимствовать 1 из разряда десятков. Таким образом, к разряду единиц мы прибавим 10, а к разряду десятков вычтем 1. | |
| Получите разницу между 11 и 3. Таким образом, 11 – 5 = 6 Затем запишите 6 под чертой в столбце единиц измерения. | |
| Вычтите числа в столбце десятков. Следовательно, 8 – 2 = 6 . Затем запишите разницу между 8 и 2 под чертой в столбце десятков. | |
| Следовательно, разница между 91 и 25 составляет 66 . |
Пример №4
В чем разница между 87 и 59?
Решение
| Процесс вычитания | Пошаговый объяснение |
Выровнять цифры 87 и 59 в колонке с значениями. | |
| Поскольку разряд единиц вычитаемого больше разряда единиц уменьшаемого, нам нужно заимствовать 1 из разряда десятков. Таким образом, к разряду единиц мы прибавим 10, а к разряду десятков вычтем 1. | |
| Получите разницу между 11 и 3. Таким образом, 17 – 9 = 8 Затем запишите 8 под чертой в столбце единиц измерения. | |
| Вычтите числа в столбце десятков. Следовательно, 7 – 5 = 2 . Затем запишите разницу между 7 и 5 под чертой в столбце десятков. | |
| Следовательно, разница между 87 и 59 составляет 28 . |
Пример #5
Найдите разницу между 76 и 49.
Решение
| Процесс вычитания | Пошаговый объяснение |
| Выровняйте цифры 33 и 17 в колонке с значениями. | |
Так как 9 больше 6, нам нужно позаимствовать 1 из разряда десятков. Таким образом, к разряду единиц мы прибавим 10, а к разряду десятков вычтем 1. Таким образом, к разряду единиц мы прибавим 10, а к разряду десятков вычтем 1. | |
| Вычтите 9 из 16. Таким образом, 16 – 9 = 7 Затем запишите разницу под чертой в столбце единиц измерения. | |
| Вычтите 1 из 2. Следовательно, 6 – 4 = 2 Затем запишите 1 под чертой в столбце десятков. | |
| Следовательно, разница между 76 и 49 составляет 27 . |
Свойства сложения (на тему Национального дня сэндвичей) Рабочие листы по математике
Сложение и вычитание дробей (на тему Ночи Гая Фокса) Рабочие листы по математике
Решение задач – сложение и вычитание (на тему Всемирного дня учителя) Рабочие листы по математике
Просмотреть все рабочие листы
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Мы ценим вашу поддержку!
Стратегии обучения сложению и вычитанию двузначных чисел
Ниже вы найдете различные стратегии сложения и вычитания двузначных чисел. Во 2-м классе учащиеся начнут складывать 2-значные и 3-значные задачи с перегруппировкой. Вот способы разбить эти проблемы, чтобы у учащихся были разные способы решения проблем. Поскольку студенты учатся по-разному, важно показать им разные методы обучения. Вы найдете конкретные стратегии, стратегии ментальной математики и даже методы алгоритмов для решения задач карандашом и бумагой. Когда вы обучаете своих учеников каждому методу, дайте им свободу выбирать метод, который лучше всего подходит для них.
Общие базовые стандарты для сложения и вычитания двузначных чисел
Давайте рассмотрим стандарты, специально предназначенные для следующих нескольких стратегий. Вы, безусловно, можете использовать эти стратегии в первом классе (без перегруппировки), а также в третьем классе. Тем не менее, конкретный стандарт, на который мы обращаем внимание, — это 2. NBT.5, в котором основное внимание уделяется свободному сложению и вычитанию с использованием стратегий позиционного значения.
NBT.5, в котором основное внимание уделяется свободному сложению и вычитанию с использованием стратегий позиционного значения.
- 2-й класс 2.NBT.5: Свободно складывать и вычитать в пределах 100, используя стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием.
- Целевой ресурс, основанный на стандартах: 2.NBT.5 и 2.NBT.5 Regrouping Bonus
Блоки с основанием 10: стратегия 1
Первая стратегия сложения и вычитания двух цифр, которую я собираюсь обсудить, на самом деле любимец ребенка. Использование десятичных блоков для сложения и вычитания двузначных чисел является очень конкретной моделью для учащихся. Им очень легко визуально увидеть процесс сложения десятков и единиц, плюс процесс перегруппировки также намного легче визуально увидеть здесь.
Один из способов, который мне нравится, когда ученики используют блоки с основанием 10, состоит в том, чтобы сделать две вещи. Первый заключается в том, чтобы фактически использовать блоки с основанием десять, поскольку они добавляют и вычитают для каждой отдельной проблемы. Следующим вариантом будет рисовать палочки и круги для обозначения десятков и единиц, если ваш класс ограничен материалами с основанием десяти. Если вы дадите учащимся доску, им будет очень легко нарисовать каждую проблему, которую они решают, не используя десятичные блоки. Но в идеале они возьмут в свои руки этих манипуляторов, чтобы визуально увидеть, как решаются их проблемы.
Следующим вариантом будет рисовать палочки и круги для обозначения десятков и единиц, если ваш класс ограничен материалами с основанием десяти. Если вы дадите учащимся доску, им будет очень легко нарисовать каждую проблему, которую они решают, не используя десятичные блоки. Но в идеале они возьмут в свои руки этих манипуляторов, чтобы визуально увидеть, как решаются их проблемы.
Разделение на части: Стратегия 2
Стратегия номер 2 полностью посвящена методу разделения, который также может быть известен как метод расширенной формы. Причина, по которой я назвал это математикой разбиения, просто потому, что ученики на самом деле разбирают двузначное число и разбивают его на десятки и единицы. Затем они будут складывать десятки от каждого числа и единицы от каждого числа, и это немного упростит их математику. Это становится немного трудным, когда учащиеся должны перегруппироваться в своей задаче на сложение или вычитание, так что это определенно большой шаг, которому вы должны научить при использовании этой стратегии.
Вот два способа использования стратегии разделения для двух разных уровней. На картинке внизу вы видите деятельность моей группы по исправлению, которая дает учащимся более четкое представление о разделении двух цифр, которые нужно сложить. На картинке вверху вы видите, что бы я дал своему уровню или моей группе обогащения. Они должны нарисовать проблему и решить ее самостоятельно, без ящиков с лесами, которыми они могли бы направлять их, и разбивая свои числа.
Давать и брать: Стратегия 3
Третьим сложением из двух цифр и стратегией будет метод «отдавать и брать». Процесс этого метода отличается между задачами на сложение и вычитание. Поэтому важно, чтобы вы давали студентам много практики здесь. Когда у вас есть проблема со сложением, если вы берете два из одного числа, вы должны добавить два к другому числу. Однако в задаче на вычитание, если вы отнимете два от одного числа, вы должны будете отнять два и от второго числа.
Эта стратегия действительно практикуется, потому что учащиеся действительно должны сосредоточиться на том, какая стратегия подходит для сложения или вычитания. Предоставление им множества практических способов практики — одно из предложений. Также очень важно научить их стратегии нахождения числа, ближайшего к 10, чтобы максимально упростить их задачу.
Предоставление им множества практических способов практики — одно из предложений. Также очень важно научить их стратегии нахождения числа, ближайшего к 10, чтобы максимально упростить их задачу.
Открытая числовая строка: Стратегия 4
Открытая числовая строка — это четвертая стратегия для задач на сложение и вычитание двузначных чисел. В открытой числовой строке учащиеся делают прыжки, чтобы изобразить сложение или вычитание десятков и единиц. В задаче на вычитание учащиеся начинают с наибольшего числа. Затем они вернут число, которое должны вычесть. Когда ученик делает эти прыжки, он будет представлять десятки с большим прыжком и те с меньшим прыжком. Важно, чтобы учащиеся помечали каждый из этих прыжков в нижней части числовой строки. Это поможет им увидеть действие взятия 10/1 или добавления 10/1.
Стандартный алгоритм: Стратегия 5
Моя последняя стратегия сложения и вычитания двухзначного числа — это стандартный алгоритм. Стандартный алгоритм выстраивает задачу на сложение или вычитание по вертикали, где десятки и единицы располагаются друг над другом. Это можно сделать как с перегруппировкой, так и без нее. Я предлагаю разбить ваши уроки на обучение стандартному алгоритму без предварительной перегруппировки. А затем, как только ваши дети освоят это, вы можете начать преподавать стандартный алгоритм с перегруппировкой.
Это можно сделать как с перегруппировкой, так и без нее. Я предлагаю разбить ваши уроки на обучение стандартному алгоритму без предварительной перегруппировки. А затем, как только ваши дети освоят это, вы можете начать преподавать стандартный алгоритм с перегруппировкой.
Очень важно предоставить ученикам множество способов отработки каждой стратегии. Некоторые способы — это практические действия с партнером. Другими способами могут быть независимые рабочие листы, где учащиеся должны показать, что они уже узнали самостоятельно. Я также думаю, что очень важно письменно увязывать каждую стратегию. Если вы предлагаете учащимся объяснить свои стратегии ценности места в письменной форме, я думаю, что это очень хороший способ отработать и понять эту стратегию в уме.
Ищете ресурсы для сложения и вычитания двузначных чисел?
Эти основанные на стандартах ресурсы раскрывают стандарт и учат учащихся складывать и вычитать двузначные числа с перегруппировкой и без нее. Он посвящен каждой стратегии для мини-урока. Все изображения, которые вы видите выше в этом сообщении в блоге, взяты из устройства 2.NBT.5. Бонусная единица перегруппировки предназначена для исправления, если вам нужно сделать шаг назад и научить своих учеников, как перегруппировывать при сложении и вычитании.
Все изображения, которые вы видите выше в этом сообщении в блоге, взяты из устройства 2.NBT.5. Бонусная единица перегруппировки предназначена для исправления, если вам нужно сделать шаг назад и научить своих учеников, как перегруппировывать при сложении и вычитании.
2.NBT.5 Сложение и вычитание двузначных чисел
2.NBT.5 Бонус- перегруппировка
Нужен ЦИФРОВОЙ?
Я создал несколько активностей в готовых Google Slides. Эти задания на сложение и вычитание двухзначных чисел предназначены для второго класса.
- Цифровое задание для 2-го класса: Сложение двух цифр
- Цифровое задание для 2-го класса: Вычитание двух цифр
Спасибо, что прочитали все о стратегиях сложения и вычитания. Надеемся, что эта запись в блоге помогла вам найти способы сделать этот важный математический навык более простым для ваших учеников.
Хотите больше сообщений в блоге по математике на другие темы?
- Советы по освоению единиц измерения
- Позитивное значение: NBT Краткие советы и рекомендации
- Организация математического блока
Выиграйте 4 детские книги о тыквах ЗДЕСЬ!
Здравствуйте учителя! Я отдаю четыре тыквенных книги для вашей классной библиотеки. Они будут доставлены прямо к вам домой или в школу, в зависимости от того, где
Они будут доставлены прямо к вам домой или в школу, в зависимости от того, где
Подробнее »
6 отличных книг для Дня труда в классе
День труда быстро приближается! Этот праздник часто упускают из виду, потому что начало года очень занято. Но это отличный шанс
Подробнее »
3 способа, как чтение выходных билетов может улучшить ваше преподавание
Как учителя, мы постоянно ищем способы проверки понимания. Мы хотим знать: был ли этот урок эффективным? Они «поняли»? Кто
Подробнее »
4 Методы обучения сложению двузначных чисел
Как правило, 2-й класс — это уровень, на котором учащиеся впервые сталкиваются с задачами на сложение двузначных чисел. Это год, когда они познакомятся с несколькими стратегиями сложения, которые они могут использовать для решения проблем. Как учитель начальной математики, мы проводим много времени, обсуждая эти стратегии сложения двузначных чисел, используя модели и манипуляции, а также занимаясь ментальной арифметикой.
Часто спрашивают, почему мы обучаем этим навыкам сложения так иначе, чем в детстве. Ответ прост. Это отличный способ научить ПОЧЕМУ до того, как мы научим КАК . Мы должны предоставить ученику множество вариантов и гибкость, когда дело доходит до решения проблем. Каждый ребенок учится и может найти правильный ответ по-разному.
Техасский TEK для двузначного сложения гласит: 2.4B: сложите до четырех двузначных чисел и вычтите двузначные числа, используя умственные стратегии и алгоритмы, основанные на разрядности и свойствах операций.
Общий базовый стандарт для двухзначных состояний сложения: 2.NBT.B.5: Свободное сложение и вычитание в пределах 100 с использованием стратегий на основе разрядного значения, свойств операций и/или отношения между сложением и вычитанием .
Обратите внимание, что выделенный жирным шрифтом текст выше ничего не говорит о стандартном алгоритме сложения двух цифр, который мы выучили много лет назад. Продолжайте читать, чтобы узнать о четырех способах, которыми я знакомлю своих учеников и обучаю их стратегиям сложения двух цифр.
Продолжайте читать, чтобы узнать о четырех способах, которыми я знакомлю своих учеников и обучаю их стратегиям сложения двух цифр.
Обратите внимание, что эти стратегии не будут сосредоточены на перегруппировке для нахождения окончательной суммы. Учащиеся должны хорошо понимать значение места И простое дополнение из предыдущих упражнений, прежде чем переходить к этому заданию.
В начале нашего блока дополнительных уроков математики я всегда делаю эту якорную диаграмму. Когда мы изучаем новую стратегию, она добавляется ко всей нашей групповой диаграмме. Мои ученики хранят соответствующую копию в своих математических журналах. Это полезно для них, чтобы оглянуться назад, когда им нужна дополнительная поддержка. Изучение различных стратегий сложения двузначных чисел может быть трудным, поэтому якорные таблицы для учащихся, как правило, очень помогают!
Позвольте мне еще немного разобрать эти четыре стратегии сложения двузначных чисел.
Модель с основанием 10 Вводя двузначное сложение, я всегда начинаю с модели с основанием 10. Это первая из стратегий сложения двух цифр, которую мы изучаем вместе. Мы много работаем с манипуляциями с десятичными кубиками, но я также учу их рисовать кубики на бумаге. Это связано с тем, что учащиеся не всегда будут иметь в своем распоряжении эти манипулятивные инструменты, но у них будут карандаш и бумага. Я обнаружил, что эта стратегия чаще всего используется, если учащиеся имеют сильное чувство места.
Это первая из стратегий сложения двух цифр, которую мы изучаем вместе. Мы много работаем с манипуляциями с десятичными кубиками, но я также учу их рисовать кубики на бумаге. Это связано с тем, что учащиеся не всегда будут иметь в своем распоряжении эти манипулятивные инструменты, но у них будут карандаш и бумага. Я обнаружил, что эта стратегия чаще всего используется, если учащиеся имеют сильное чувство места.
Я всегда даю своим ученикам коврик, помещенный в пластиковый чехол. Это позволяет учащимся также писать или рисовать с помощью сухостираемого маркера, и их можно использовать снова и снова для отработки этих математических навыков.
Вот как работает эта стратегия сложения на примере 62+34.
1. Постройте/вытяните оба слагаемых, используя блоки с основанием десять. (Иногда забавно использовать другие манипуляции. В примере с фото я использовал разрезанные на кусочки ершики для десятков и маленькие шарики-помпоны для единиц.)
2. Сначала посчитайте единицы, а затем десятки. Это поможет, когда перегруппировка будет введена позже.
Это поможет, когда перегруппировка будет введена позже.
3. Найдите сумму.
Когда учащимся нужно нарисовать эту стратегию, она работает так же. Я учу их рисовать «палочки» для обозначения десятков и «точки» для обозначения единиц. Я также учу их вытягивать первое сложение, а затем рисовать под ним второе сложение. Они будут считать, чтобы решить сумму.
Метод расширенной формыВторая стратегия добавления, которую я всегда использую, — это метод расширенной формы. Это еще одна стратегия, которая чрезвычайно полезна, но учащиеся снова должны хорошо знать разрядное значение и расширяющиеся числа. Каждое слагаемое будет разбито на десятки и единицы и поможет учащимся увидеть, что разряд десятков — это не просто 6. Его значение представляет 60 или 6 десятков.
Вот как это работает на примере 52+45.
- Разверните первое дополнение. >>> 50+2
2. Разверните второе сложение и напишите его под первым. >>> 40+5
>>> 40+5
3. Решите по вертикали на основе разряда, начиная с единиц, затем десятков.
4. Найдите сумму. >>> 90+7 =97
Модель числовой прямойИспользование открытой числовой строки для решения задач на сложение двузначных чисел очень полезно, но также может быть более сложным для учащихся. Особенно, если они не обладают сильными познаниями в ментальной арифметике.
Эта стратегия направлена на то, чтобы учащиеся «прыгали» по числовой прямой, чтобы решить сумму заданной задачи. Большие прыжки рисуются для плюс 10, а мелкие прыжки — для плюс
Чтобы помочь учащимся лучше визуализировать эту стратегию, я всегда сначала включаю блоки с основанием десять. Когда им будет более комфортно с этой стратегией, они могут их забрать.
Вот как это работает на примере 22+43. 1.
1. Нарисуйте незамкнутую числовую прямую.
2. Напишите большее слагаемое в начале числовой строки.
3. Затем учащиеся используют блоки с основанием 10, чтобы построить другие слагаемые по горизонтали через числовую прямую.
Затем учащиеся используют блоки с основанием 10, чтобы построить другие слагаемые по горизонтали через числовую прямую.
4. Нарисуйте большие прыжки над десятками для +10 и маленькие прыжки над десятками для +1. 5.
Они пропустят счет и запишут числа, которые нужно найти.
Когда дело доходит до нанесения карандаша на бумагу, ваши ученики могут легко использовать ту же стратегию. Если им нужно нарисовать блоки с основанием десять вдоль своей числовой линии, они могут это сделать. Наша цель, чтобы они могли мысленно добавлять.
Стандартный алгоритмВозможно, именно благодаря этому традиционному методу вы выучили сложение двух цифр в детстве, и с ним лучше всего знакомы родители наших детей. Для этой стратегии учащиеся должны выстроить оба дополнения вертикально друг под другом. Сначала они будут складывать числа в разряде единиц, а затем в разряде десятков, чтобы найти сумму.
Один из советов, который может быть полезен при первом изучении этой стратегии, состоит в том, чтобы учащиеся использовали маркер, чтобы выделить единицы, или сначала обвести числа в разряде единиц. Это помогает им визуализировать, чтобы сначала добавить единицы, а затем десятки. Я хочу, чтобы это стало привычкой для моих учеников.
Это помогает им визуализировать, чтобы сначала добавить единицы, а затем десятки. Я хочу, чтобы это стало привычкой для моих учеников.
Эта концепция может быть для них более сложной, чем мы думаем, потому что они обучены читать и писать слева направо. Будет сложнее, когда они научатся перегруппировываться при сложении двузначных чисел, поэтому сначала будет полезно привить им эту привычку.
В конце нашего модуля мы всегда делаем эти книги по стратегии сложения, чтобы помочь нам в обзоре. Они могут сохранить их, чтобы использовать позже в качестве справочного материала, когда им это нужно.
Ух ты! Это может показаться большим количеством информации для обработки. Мы все изучаем понятия по-разному, и стратегии сложения, которыми я поделился, оказались полезными для моих учеников.
Нет правильной или неправильной стратегии, когда дело доходит до решения задач на сложение двузначных чисел. Позвольте вашим ученикам выбрать метод, который лучше всего подходит для них, и пусть они придерживаются его. Как только они найдут метод, который им удобен, важно предоставить им несколько возможностей попрактиковаться в сложении двузначных чисел.
Как только они найдут метод, который им удобен, важно предоставить им несколько возможностей попрактиковаться в сложении двузначных чисел.
Нужен отличный ресурс? Ниже приведены некоторые ссылки на ресурсы, которые могут оказаться полезными.
Сложение и вычитание без перегруппировки Модуль
Хотите сохранить эти идеи на потом? Закрепите изображение ниже.
Эффективные стратегии введения свойств сложения в 3-м классе
Вы учитель 3-го класса и ищете интересные и эффективные способы познакомить своих учеников со свойствами сложения? Если вы новичок в
Подробнее »
Обучение чувству чисел с помощью 10 простых упражнений с десятью рамками
Когда дело доходит до обучения чтению чисел, десять рамок являются важным инструментом, который студенты должны научиться использовать и применять. Включая десять кадров
Подробнее »
Манипуляции со значением места для 2-го класса
Разрядное значение — одно из самых важных математических понятий, изучаемых во 2-м классе. Это основа, на которой зиждется большее числовое чувство
Это основа, на которой зиждется большее числовое чувство
Подробнее »
Сложение и вычитание двух цифр без перегруппировки
Обучение сложению и вычитанию двух цифр без перегруппировки — это весело, потому что дети могут складывать и вычитать «большие» числа. Это заставляет их чувствовать себя такими умными и может быть огромным усилителем уверенности в себе для студентов!
Поскольку перегруппировки нет, все, что учащиеся, по сути, делают, это два сложения к 10 задачам или два вычитания из 10 задач, оказавшихся рядом друг с другом. 🙂
Удивительный трюк — научить их показывать указательным пальцем. Поместите его поверх двух чисел в разряде десятков и просто решите задачу на сложение в разряде единиц. Например, на этом желтом листе они использовали свой палец, чтобы закрыть 1 + 2, поэтому все, что они видят, это 8 + 0. Как легко 8 + 0 ?! Затем пусть они покроют 8+0, пока они могут видеть и решать только 1+2. ТАК просто!! Они будут поражены тем, как они сложили 2 больших числа. 🙂 🙂 Так что 18 + 20 на самом деле просто 8+0 и 1+2, которые они уже умеют делать. Это ОГРОМНОЕ укрепление уверенности, чтобы представить его таким образом!
🙂 🙂 Так что 18 + 20 на самом деле просто 8+0 и 1+2, которые они уже умеют делать. Это ОГРОМНОЕ укрепление уверенности, чтобы представить его таким образом!
Сложение и вычитание двухзначного числа без перегруппировки с использованием разрядного значения
Я настоятельно рекомендую использовать кубики в качестве блоков разрядного значения, чтобы показать им, что на самом деле делает двузначное сложение и вычитание без перегруппировки.
Это также пригодится, как только вы начнете перегруппировку, потому что они могут физически перемещать кубы для перегруппировки! Такой удивительный урок и наглядное представление о том, что такое перегруппировка. 🙂
Как вы можете видеть на картинке выше, пусть они сначала посмотрят на 2 числа, которые они добавляют. 23 и 34. Таким образом, они построили 23 из кубов в виде блоков разрядности. Затем постройте 34 из кубиков. Каждая десятка представляет собой стопку из 10 кубиков, как если бы они были блоками разрядности. Это показывает им 2 числа, которые они хотят соединить. Затем они буквально складывали их вместе, складывая десятки с десятками и единицы с единицами. Подсчитайте, и у них есть решение задачи на сложение! 🙂
Затем они буквально складывали их вместе, складывая десятки с десятками и единицы с единицами. Подсчитайте, и у них есть решение задачи на сложение! 🙂
Вы также можете использовать блоки фактического разряда, так как они меньше, а «десятки» уже сделаны, но я настоятельно рекомендую, чтобы они сами построили «десятки» из 10 кубиков. Это отличная практика разрядности И будет очень полезно, если вы также используете кубики для обучения перегруппировке, тогда как вы не можете отделять/добавлять блоки «десятки», когда они являются фактическими блоками разрядности.
Те из вас, кто использует мои математические единицы, могут заметить, что это рабочий лист уровня B! 🙂 Все мои математические блоки имеют 3 уровня рабочих листов для каждой концепции, включенной в блок, так что вы можете легко различать. B — это место, где вы ожидаете увидеть первоклассника. А — дополнительная поддержка. C для вызова.
Если у вас есть ученики, которым нужна небольшая поддержка, вы также можете научить их, что они могут РИСОВАТЬ блоки позиционного значения в любое время, когда им нужна поддержка. Это отличная практика для всех и ОТЛИЧНАЯ стратегия, чтобы научить всех ваших учеников тому, как проверять свою работу, особенно если им нужно сдавать какие-либо тесты в конце года!
Это отличная практика для всех и ОТЛИЧНАЯ стратегия, чтобы научить всех ваших учеников тому, как проверять свою работу, особенно если им нужно сдавать какие-либо тесты в конце года!
Эту же стратегию можно использовать и для вычитания!
Пусть они построят первый номер. Здесь это 55 и, как вы можете видеть, 55 построено на стороне рабочего листа в кубах. Между прочим, я рекомендую НЕ соединять кубы за единицу. Попросите их показать их как «единицы», как здесь, где они являются отдельными объектами. Особенно для задач на вычитание.
После того, как они построили 55, они смотрят, какое число вычитается. 24. Так они бы просто убрали из этого 4 единицы и 2 десятка, чтобы получить свой ответ! 🙂 Такой замечательный способ показать, что именно происходит, когда они выполняют вычитание двух цифр.
Опять же, ОТЛИЧНАЯ практика разряда! Если им нужно больше работать над разрядным значением, двухзначное сложение и вычитание будет затруднено даже без перегруппировки, поэтому, если это так, я рекомендую выполнить все действия из моего большого математического модуля «Первоклассное разрядное значение», чтобы действительно закрепить их знания. из десятков и единиц. Играйте в игры и выполняйте задания снова и снова (не волнуйтесь, это так весело!!), пока они действительно не освоятся.
из десятков и единиц. Играйте в игры и выполняйте задания снова и снова (не волнуйтесь, это так весело!!), пока они действительно не освоятся.
Вы также можете дать им рабочий лист, который показывает, что делать. Для поддержки, если это необходимо, они могут нарисовать блоки десятков и единиц и вычеркнуть те, которые они вычитают. Это отличный способ наглядно показать им, что они делают, и это отличный урок математики для небольших групп! Опять же, отличный обзор ценности места и потрясающий для того, чтобы продолжать развивать свое числовое чувство. Мне нравится, что это показывает им, что они на самом деле делают при вычитании.
Увлекательные игры и центры для сложения и вычитания двухзначных чисел без перегруппировки
Вы также можете предоставить им поддержку кубов при занятиях математическим центром для сложения и вычитания двухзначных чисел!
Допустим, они играли в центральную игру, подобную этой, где они берут карту, решают ее и записывают ответ на своем листе для записей. Вы вполне можете дать им кубики, чтобы помочь им решить. Это действительно помогает укрепить их уверенность в том, что они могут «проверить» свою работу и «увидеть», что она верна. Кроме того, с кубиками так весело играть! 🙂 Опять же, я НЕ рекомендую позволять им подключать их. Пусть «десятки» подключаются заранее и НЕ отключаются никогда. А те сами по себе. Скажи им, чтобы они притворялись, будто десятки склеены, если нужно, ха-ха!
Вы вполне можете дать им кубики, чтобы помочь им решить. Это действительно помогает укрепить их уверенность в том, что они могут «проверить» свою работу и «увидеть», что она верна. Кроме того, с кубиками так весело играть! 🙂 Опять же, я НЕ рекомендую позволять им подключать их. Пусть «десятки» подключаются заранее и НЕ отключаются никогда. А те сами по себе. Скажи им, чтобы они притворялись, будто десятки склеены, если нужно, ха-ха!
Между прочим, у меня есть несколько таких наборов для тренировки каждого навыка сложения и вычитания двух цифр без перегруппировки! Я рекомендую поместить обычное двухзначное сложение в одну маленькую коробку, подобную этой. Затем 2-значные + 1-значные карты в 1 коробке. 2 цифра — 1 цифра в 1 поле. Затем 2-значные карты вычитания, где оба числа являются 2-значными в 1 поле. Кратность 10 в 1 коробке. На 10 больше и на 10 меньше в 1 коробке. И так далее! Это делает так много разных центров, которые вы можете вытащить и убрать очень легко!
Мне больше всего в этом нравится то, что они каждый раз будут знать, что делать, но это для немного другого и нового навыка! Допустим, вы используете версии этих карт на 10 больше и на 10 меньше, и они делают для этого целый центр. Что ж, когда вы позже будете учить числа, кратные 10 (30+50), и будете использовать точно такой же центральный формат (карточки выглядят одинаково, лист записи выглядит так же), они будут точно знать, что делать, и смогут сосредоточиться только на изучении бренда. новый навык! 🙂 Это то, о чем я постоянно говорю в своих Phonics No Prep Packs для каждого звука. У каждого звука есть ОДИНАКОВЫЕ упражнения, поэтому каждую неделю вы можете вводить новый звук, но ваши дети уже знают, как выполнять все действия, поэтому они могут сосредоточиться только на изучении нового фонетического навыка, а не тратить время / умственные усилия на выяснение Как это сделать. Люби, люби, люби это. И вам не нужно давать указания. Как удивительно это звучит?!?!? Так что, когда это возможно, последовательные занятия — это ПОТРЯСАЮЩЕ. Особенно в 1 классе, 2 классе и детском саду!
Что ж, когда вы позже будете учить числа, кратные 10 (30+50), и будете использовать точно такой же центральный формат (карточки выглядят одинаково, лист записи выглядит так же), они будут точно знать, что делать, и смогут сосредоточиться только на изучении бренда. новый навык! 🙂 Это то, о чем я постоянно говорю в своих Phonics No Prep Packs для каждого звука. У каждого звука есть ОДИНАКОВЫЕ упражнения, поэтому каждую неделю вы можете вводить новый звук, но ваши дети уже знают, как выполнять все действия, поэтому они могут сосредоточиться только на изучении нового фонетического навыка, а не тратить время / умственные усилия на выяснение Как это сделать. Люби, люби, люби это. И вам не нужно давать указания. Как удивительно это звучит?!?!? Так что, когда это возможно, последовательные занятия — это ПОТРЯСАЮЩЕ. Особенно в 1 классе, 2 классе и детском саду!
Я тоже люблю тематические центры! Какие милые эти маленькие обезьянки и их бананы? Вы сопоставляете бананы с задачей на сложение, которая соответствует сумме на обезьяне! Затем они записывают задачи под каждой обезьяной на своем листе для записей.
Как вы можете видеть на этой картинке (слева), я прикрепил к каждому центру лист с подробными указаниями, чтобы вы могли разместить его в центре. Это позволяет центру быть более независимым и напоминает детям, что делать. Он также сообщает любому взрослому, который входит в вашу комнату, над чем работают ученики — например, приходят ли они помочь. Для каждого центра также существует версия страницы указаний для учителей. Это помогает объяснить, как играть в центре, а иногда и забавные советы о других способах игры и о том, как дифференцироваться, когда это возможно!
Продолжая тему животных зоопарка, мы добавили версию с вычитанием со слонами и арахисом!
Для обоих этих центров дети делают ТАК. МНОГО. МАТЕМАТИКА сортировать продукты под животными, но, вероятно, не поймет этого, потому что это так мило и весело.
Оба из них также имеют проблемы в горизонтальном направлении , так что это немного усложняет задачу! Я думаю, дети должны сначала научиться решать вертикальные задачи. Они могут научиться выстраивать числа в ряд, чтобы легко решить. ЗАТЕМ, как только они почувствуют себя уверенно, введите горизонтальное положение.
Они могут научиться выстраивать числа в ряд, чтобы легко решить. ЗАТЕМ, как только они почувствуют себя уверенно, введите горизонтальное положение.
Я рекомендую им использовать лист бумаги, чтобы переписать горизонтальные задачи как вертикальные. Научить их выстраивать в ряд два двузначных числа — это ТАКОЙ замечательный навык! Они могут использовать дополнительный лист чистой бумаги, чтобы преобразовать их.
Например, если вы дали им такой рабочий лист, они могут подумать, что он выглядит сложно. Покажите им, как заменить 26 + 62 так, чтобы они располагались друг над другом на новом листе бумаги (или на обратной стороне рабочего листа), чтобы упростить решение. По вертикали получится 6+2 и 2+6. Намного проще!
Вы также можете попросить их снова принести кубики! Все, что им нужно, чтобы чувствовать себя успешным, я рекомендую! Но я определенно считаю важным научить их переписывать горизонтальные математические задачи в вертикальные.
Сложение и вычитание двух цифр без перегруппировки Смешанная практика повторения
Я также думаю, что очень важно иметь много смешанной практики сложения и вычитания. Вот почему в моем двухзначном математическом блоке для сложения и вычитания буквально заложена целая концепция. Очень важно, чтобы они смотрели на символ, чтобы они знали, что делать, поэтому мне нравится предоставлять множество рабочих листов и действий, где они должны смотреть, чтобы увидеть, добавляют они или вычитают.
Было бы легко снова достать кубики и спросить их — вы объединяете 2 набора кубиков или убираете кубики?
Вы также можете выполнять смешанную практику, просто давая им страницы сложения иногда и страницы вычитания иногда. Это не был бы мой пост по математике без небольшого вырезания и склеивания! 🙂
Я искренне считаю, что необходимость склеивать ответы заставляет детей больше думать над своими ответами. Бумагу трудно отклеить, поэтому они работают более продуманно, как мне кажется.
К тому же это весело! Мне нравится, что они могут перемещаться по своим ответам. Я рекомендую научить их сначала вырезать все ответы, разместить их (чтобы, если один из них не имеет смысла, они знают, что нужно проверить все ответы, чтобы выяснить, какой из них они сделали неправильно), ЗАТЕМ склеить. Это учит их многим замечательным навыкам!
Мне нравится иметь подобную страницу для каждой концепции, чтобы ваши ученики привыкли к ней! Например, если вы учитесь складывать и вычитать двузначные и однозначные числа, вы также должны сделать для этого подобную страницу.
Им это покажется знакомым. Как страницу, которую они уже сделали и с которой они добились успеха. Так что новая, «тяжелая» тема не кажется им такой пугающей. 🙂
Еще один быстрый совет — распечатывать «скучные» рабочие листы на цветной бумаге! Сложение и вычитание 2-х цифр без перегруппировки — довольно скучная концепция по сравнению с другими очень забавными, которые дети изучают в K-2, но это НАСТОЛЬКО важно. И им нужно много повторений и практики, чтобы освоить. Один очень простой способ сделать это немного веселее — распечатать рабочие листы на цветной бумаге!
И им нужно много повторений и практики, чтобы освоить. Один очень простой способ сделать это немного веселее — распечатать рабочие листы на цветной бумаге!
Можно сказать им, что они получают определенный цвет. Например, если они закончат обычный рабочий лист на белой бумаге, они смогут сделать ЦВЕТНОЙ. Оооо! Они будут в восторге, когда закончат рабочие листы! 🙂 Это действительно отличная практика. Вы также можете поместить их в защитные пленки, чтобы не тратить много цветной бумаги. Затем они смогут использовать маркеры сухого стирания, и им это понравится еще больше! Есть так много способов сделать рабочий лист интересным. Дети ОБОЖАЮТ использовать маркеры для сухого стирания на защитных листах, так что вы определенно можете это сделать. И тогда вы также сможете повторно использовать их, чтобы меньше печатать и готовить!
Все эти упражнения, которые я показал здесь для сложения и вычитания двух цифр без перегруппировки (и многое другое), включены в мой первый класс по математике, раздел 13 на TpT!
Если вы знакомы с моими математическими единицами, они УПАКОВАНЫ забавными, дифференцированными рабочими листами для каждой концепции на 3 уровнях (A, B и C) и центрами для каждой концепции! Также вырежьте и вставьте рабочие листы И оценку в конце модуля, чтобы просмотреть все концепции. Я всегда включаю 3 версии оценки, чтобы вы могли сделать одну до, во время и после. Вы также можете сохранить их для оценивания в конце семестра/квартала/периода/года, если это требуется для табелей успеваемости! 🙂
Я всегда включаю 3 версии оценки, чтобы вы могли сделать одну до, во время и после. Вы также можете сохранить их для оценивания в конце семестра/квартала/периода/года, если это требуется для табелей успеваемости! 🙂
Вы всегда можете посмотреть на обложку моих математических модулей, чтобы узнать, что в них входит. Математический блок 13 для первого класса (который также можно использовать во 2-м классе) имеет следующие концепции:
— сложение двух цифр
— вычитание двух цифр
— смешение двух цифр
— сложение и вычитание двух и одной цифры
— на 10 больше и на 10 меньше
— сложение и вычитание кратных 10
Этот полностью заполнен сложением и вычитанием двух цифр без перегруппировки рабочих листов и заданий — вот лишь несколько страниц для практики:
Я настоятельно рекомендую использовать рабочие листы для практики и обучения. Вы можете увидеть уровень любого рабочего листа в правом верхнем углу внутри звездочки (см. A в звездочке на странице вверху здесь?), чтобы вы могли быстро получить то, что нужно каждому ученику/ребенку.
Если рабочий лист занимает у них много времени — или они кажутся разочарованными — спуститесь на уровень ниже. A — самый простой, B — то, где будет большинство ваших учеников, а C — вызов.
Если у вас есть учащиеся, которые быстро заканчивают свою работу, любят делать уроки и всегда просят еще или что делать дальше, иметь страницы уровня C для каждого рабочего листа, который вы делаете, очень приятно!
Преимущество трехуровневого рабочего листа в том, что вы можете встретиться с каждым учеником на том уровне, на котором он находится, а затем перейти к следующему уровню, когда он будет готов, чтобы каждый мог перейти к уровню задания таким образом, чтобы поддерживать его на этом пути. ! 🙂 Обычно я стараюсь сделать уровень задач концептуально более сложным, где им нужно немного больше думать, а не просто больше математических задач, но для чего-то такого простого, как сложение двух цифр, иногда просто больше задач на странице. Который, опять же, для ваших детей, которые быстро заканчивают свою работу, но любят работать, это идеально для них!
Моя цель всегда состоит в том, чтобы дети практиковали ОДИНАКОВЫЕ навыки, но на ИХ уровне. Уровень, который немного бросает им вызов, но не слишком много и не слишком мало. 🙂
Уровень, который немного бросает им вызов, но не слишком много и не слишком мало. 🙂
Я также стараюсь, чтобы страницы выглядели действительно похожими, так что это не очевидно, просто они разные. Все это выглядит забавно и, например, имеет 2 разных уровня!
В любом случае! Тогда сделайте забавные центры и игры для повторения и больше практики! Я люблю математические игры и центры для каждой концепции, потому что они не понимают, сколько практики они на самом деле делают. Особенно центры, которые вы можете использовать снова и снова. Вы также всегда можете вернуть их позже в этом году, чтобы просмотреть их снова.
Большое спасибо за внимание! Надеюсь, это дало вам новые интересные идеи для обучения сложению и вычитанию двухзначных чисел без перегруппировки. Если вы хотите увидеть еще один пост о том, как использовать эти же стратегии для обучения перегруппировке, дайте мне знать! Я также хотел бы услышать от вас на любой платформе, которую вы любите больше всего! Я почти на всех! 🙂
Опять же, вы можете получить ВСЕ эти упражнения, которые я показывал в
Математика для первого класса. Часть 13: Сложение и вычитание двух цифр без перегруппировки
Часть 13: Сложение и вычитание двух цифр без перегруппировки
(который вы также можете использовать во 2-м классе или в любом классе, где вы пытаетесь помочь своим ученикам складывать и вычитать 2 цифры, включая такие понятия, как на 10 больше и на 10 меньше, 2 цифры и 1 цифра сложение и вычитание, и кратное 10)
Определенно нажмите здесь, чтобы следовать за мной на TpT! Вы не хотите пропустить, когда я публикую совершенно новые вещи, потому что они часто имеют большие скидки для тех, кто первым увидит / получит это! 🙂
У меня также есть БЕСПЛАТНЫЕ группы по математике и фонетике на FB для преподавания в первом классе (учителя начальных и второклассных классов тоже приветствуются! Я думаю, вы почерпнете массу забавных идей!) так что присоединяйтесь к ним, если хотите многого. больше советов, а также эксклюзивные бесплатные материалы для участников группы! Я люблю болтать со всеми вами, поэтому мы будем рады, если вы присоединитесь к нам! Вы также можете просто подписаться на мою страницу в FB! Мне очень нравится делиться советами, которые сделают вашу преподавательскую жизнь проще, веселее и организованнее. Так что, если вам это тоже нравится — и вы всегда ищете новые интересные советы по фонетике, математике, письму и управлению классом — тогда я с удовольствием поделюсь с вами своими!
Так что, если вам это тоже нравится — и вы всегда ищете новые интересные советы по фонетике, математике, письму и управлению классом — тогда я с удовольствием поделюсь с вами своими!
Если вы хотите «прикрепить» этот пост, чтобы прочитать его позже, вы можете прикрепить ЛЮБУЮ картинку из этого поста на свои доски! 🙂 Я также потратил секунду, чтобы сделать эти 2 булавки для вас, чтобы они говорили, о чем пост, если вы предпочитаете это! Надеюсь, они помогут вам быстро запомнить этот пост!
и
У меня также есть эта страница, на которой есть упорядоченный список моих сообщений в блоге, так что вы можете использовать его, чтобы быстро найти любую тему по математике, фонетике, письму или управлению классом, которая вам нужна! 🙂
Надеюсь, это было полезно!! Еще раз спасибо, что заглянули в мой блог! Я очень ценю, что вы нашли время, чтобы прочитать мои идеи для обучения, и я надеюсь, что они вам понравились!
Интерактивный урок математики | Сложение и вычитание двузначных чисел
Извините, вы использовали все доступные подсказки для этого урока.
Достигнут предел практики
Вы достигли ежедневного лимита практики в 12 вопросов.
Когда вы зарегистрируете бесплатную учетную запись и войдете в нее, вы сможете играть во все, что захотите.
(Для регистрации вам должно исполниться 18 лет.)
Упражнение на сложение и вычитание для второго класса
Готовы дать своим ученикам упражнения на сложение и вычитание в увлекательном цифровом формате? Попробуйте это сложение и вычитание на iKnowIt.com! Вот цели обучения для этого интерактивного упражнения на сложение и вычитание, предназначенного для второго класса:
- Учащиеся будут использовать свои знания о разрядных значениях и свойствах операций для решения различных задач на сложение и вычитание.
- Учащиеся будут решать задачи на сложение по вертикали, задачи на сложение по горизонтали, задачи на сложение слов, задачи на вычитание по вертикали, задачи на вычитание по горизонтали и задачи на вычитание слов.
- Учащиеся определят, требует ли словесная задача сложения или вычитания.

- Учащиеся будут практиковаться в сложении и вычитании двузначных чисел, включая перегруппировку.
Когда ваши второклассники будут практиковать сложение и вычитание в этой математической онлайн-игре, у них будет доступ к некоторым потрясающим встроенным функциям математических уроков, разработанным, чтобы помочь им максимально эффективно использовать математические занятия. Например, дети могут нажать кнопку «Подсказка», чтобы просмотреть подсказку к математической задаче. Подсказка состоит из письменной или иллюстрированной подсказки, которая указывает учащимся правильное направление, не давая ответа. Когда учащиеся ответят на вопрос неправильно, страница с подробными объяснениями покажет им правильный ответ, сопровождаемый простым для понимания объяснением. Таким образом, учащиеся могут учиться на предыдущих ошибках по мере прохождения интерактивного математического задания.
Кроме того, это смешанное задание на сложение и вычитание для второго класса включает в себя другие полезные функции, расширяющие математические возможности детей. Индикатор прогресса в правом верхнем углу экрана практики показывает учащимся, на сколько вопросов они ответили из общего числа вопросов на уроке математики. Счетчик очков под ним позволяет учащимся узнать, сколько баллов они уже заработали за правильные ответы. Напротив значок динамика указывает на функцию чтения вслух; учащиеся могут нажать кнопку, чтобы вопрос был прочитан им вслух четким голосом. Этот ресурс идеально подходит для учащихся ESL/ELL и детей, которые хорошо учатся на слух. Каждая функция урока «Я знаю это» разработана с учетом математических достижений ваших учеников.
Индикатор прогресса в правом верхнем углу экрана практики показывает учащимся, на сколько вопросов они ответили из общего числа вопросов на уроке математики. Счетчик очков под ним позволяет учащимся узнать, сколько баллов они уже заработали за правильные ответы. Напротив значок динамика указывает на функцию чтения вслух; учащиеся могут нажать кнопку, чтобы вопрос был прочитан им вслух четким голосом. Этот ресурс идеально подходит для учащихся ESL/ELL и детей, которые хорошо учатся на слух. Каждая функция урока «Я знаю это» разработана с учетом математических достижений ваших учеников.
Учителя и учащиеся любят цифровые математические игры
Преподаватели начальных классов с удовольствием используют iKnowIt.com, чтобы помочь своим ученикам практиковать математические навыки, которые они изучают в классе. При использовании вместе с комплексной учебной программой по математике I Know It представляет собой фантастический ресурс для практики математики, который побуждает малышей оттачивать свои математические навыки в интерактивном цифровом формате. Учителя ценят многие математические темы, охватываемые сборником математических уроков «Я знаю это». Найдите десятки уроков математики от детского сада до пятого класса, написанных аккредитованными учителями математики начальных классов и соответствующих стандарту Common Core Standard. Математические занятия организованы на веб-сайте по классам и темам, что позволяет легко находить и назначать уроки математики в несколько кликов.
Учителя ценят многие математические темы, охватываемые сборником математических уроков «Я знаю это». Найдите десятки уроков математики от детского сада до пятого класса, написанных аккредитованными учителями математики начальных классов и соответствующих стандарту Common Core Standard. Математические занятия организованы на веб-сайте по классам и темам, что позволяет легко находить и назначать уроки математики в несколько кликов.
Мы надеемся, что вам и вашему классу будет очень интересно попробовать это смешанное задание на сложение и вычитание для второго класса. Обязательно изучите сотни уроков математики для второго класса в нашей онлайн-коллекции.
Узнайте о преимуществах членства I Know It
Наше бесплатное 30-дневное пробное предложение — это ваше знакомство с удивительным миром интерактивной математической практики онлайн! Подпишитесь на бесплатную пробную версию сегодня (кредитная карта не требуется) и исследуйте все математические задания в коллекции I Know It бесплатно в течение полных тридцати дней. Мы уверены, что вам и вашим учащимся понравится испытать разницу, которую может дать онлайн-практика по математике. Мы надеемся, что когда срок действия вашей бесплатной пробной версии закончится, вы без колебаний присоединитесь к сообществу I Know It в качестве члена. Членство в I Know It дает вам и вашему классу полный доступ к нашей программе цифровой математики в течение всего календарного года. У нас есть варианты членства для семей, отдельных учителей, школ и школьных округов. Посетите нашу страницу с информацией о членстве, чтобы узнать подробности: https://www.iknowit.com/order.html.
Мы уверены, что вам и вашим учащимся понравится испытать разницу, которую может дать онлайн-практика по математике. Мы надеемся, что когда срок действия вашей бесплатной пробной версии закончится, вы без колебаний присоединитесь к сообществу I Know It в качестве члена. Членство в I Know It дает вам и вашему классу полный доступ к нашей программе цифровой математики в течение всего календарного года. У нас есть варианты членства для семей, отдельных учителей, школ и школьных округов. Посетите нашу страницу с информацией о членстве, чтобы узнать подробности: https://www.iknowit.com/order.html.
Ваше членство в I Know It открывает доступ к полезным административным инструментам нашей программы, которые являются ключом к получению максимальных преимуществ, которые ваш класс получает от онлайн-практики по математике. Инструменты администратора помогут вам создать список классов для ваших учеников, назначить уникальные учетные данные для входа в систему каждому ученику, дать определенные задания урока разным ученикам, изменить основные настройки урока, распечатать, загрузить и отправить по электронной почте отчеты об успеваемости учащихся и многое другое.
Ваши ученики будут использовать свои уникальные имя пользователя и пароль для входа в «Я знаю это». На удобной для детей домашней странице они могут быстро получить доступ к математическим заданиям, которые вы им назначили для практики. Если вы решите предоставить им возможность через свою учетную запись администратора, ваши учащиеся также смогут изучать другие математические задания в своем классе и за его пределами, для дополнительной задачи или дополнительной проверки. Уровни классов обозначаются буквами, а не цифрами (например, «Уровень B» для второго класса), что позволяет легко назначать уроки математики в зависимости от потребностей и уровня навыков каждого ребенка.
Уровень
Этот интерактивный урок математики относится к уровню B. Он может быть идеальным для учащихся второго класса.
Common Core Standard
2.NBT.5
Числа и операции с основанием 10
Учащиеся будут использовать свое понимание разрядного значения и свойств операций сложения и вычитания. Учащиеся будут свободно складывать и вычитать в пределах ста, используя стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием.
Учащиеся будут свободно складывать и вычитать в пределах ста, используя стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием.
Вас также может заинтересовать…
Сложение или вычитание 10 или 100 (уровень B)
На этом уроке математики для второго класса учащиеся будут практиковаться в сложении или вычитании десяти или ста. Вопросы представлены в виде задач на сложение по вертикали, задач на сложение по горизонтали, задач на сложение слов, задач на вычитание по вертикали, задач на горизонтальное вычитание и задач на вычитание слов.
Таблицы: сложение и вычитание в пределах 100 (уровень B)
Учащиеся будут практиковаться в сложении и вычитании в пределах ста в этом математическом онлайн-упражнении, предназначенном для второго класса. Вопросы представлены в виде таблиц In/Out, для которых учащиеся должны заполнить пробел.
Двухзначное сложение — с перегруппировкой
LearnPracticeDownload
Двухзначное сложение — это простая форма сложения, в которой числа располагаются в соответствии с их разрядностью единиц и десятков, а затем складываются. Двузначное сложение также можно выполнить мысленно, выполнив несколько основных шагов. Давайте изучим основные шаги сложения двузначных чисел вместе.
Двузначное сложение также можно выполнить мысленно, выполнив несколько основных шагов. Давайте изучим основные шаги сложения двузначных чисел вместе.
| 1. | Что такое сложение двух цифр? |
| 2. | 2-значное сложение с перегруппировкой |
| 3. | 2-значное сложение без перегруппировки |
| 4. | Часто задаваемые вопросы о двузначном дополнении |
Что такое сложение двух цифр?
Двухзначное сложение выполняется с учетом разрядности чисел. Двузначные числа имеют разрядность, выраженную единицами и десятками. Складывая 2 цифры вместе, мы располагаем числа по столбцам под соответствующими разрядными значениями. Этот метод помогает добавлять цифры одну за другой. Двузначное сложение можно выполнять с перегруппировкой (переносом вперед) и без перегруппировки (без переноса вперед). Числа, которые складываются, называются слагаемыми, а ответ, который получается после сложения этих чисел, называется их суммой. Обратите внимание на приведенный ниже рисунок, который показывает, что 70 и 15 — слагаемые, а 85 — сумма.
Числа, которые складываются, называются слагаемыми, а ответ, который получается после сложения этих чисел, называется их суммой. Обратите внимание на приведенный ниже рисунок, который показывает, что 70 и 15 — слагаемые, а 85 — сумма.
2-значное сложение с перегруппировкой
Двухзначное сложение с перегруппировкой — это метод, при котором мы перегруппировываем заданные числа по условию. Условие состоит в том, что если сумма чисел в одном столбце больше 9, мы переносим лишнее число в следующий столбец. В случае двузначных чисел перегруппировка начинается со столбца единиц и движется влево к столбцу десятков. Давайте разберемся в этом с помощью примера.
Пример: Сложите 59 и 23.
Решение: Сложим эти числа, выполнив следующие действия.
- Шаг 1: Расположите числа или слагаемые в соответствии с их порядковым значением, т. е. в столбце единиц и десятков. Таким образом, 9 и 3 будут помещены в колонку единиц, а 5 и 2 — в колонку десятков.

- Шаг 2: Начните складывать числа справа, т. е. столбец единиц, и двигайтесь влево, т. е. столбец десятков. Здесь, 9+ 3 = 12.
- Шаг 3: Если сумма в столбце единиц больше 9, мы получаем двузначное число. Взяв двузначное число, мы помещаем цифру единиц в столбец единиц, а цифру десятков переносим вперед или перегруппировываем в следующий столбец, который является столбцом десятков. Поскольку 12 больше 9, мы переносим 1 в столбец десятков и записываем 2 как сумму в столбец единиц.
- Шаг 4: При добавлении столбца десятков мы включаем число, которое было перенесено из столбца единиц. Следовательно, мы добавляем 5 + 2 + 1 (перенос) = 8,
- Шаг 5: После добавления обоих столбцов мы получаем окончательную сумму. После сложения обоих столбцов получаем 59 + 23 = 82.
2-значное сложение без перегруппировки
Двухзначное сложение без перегруппировки является простейшей формой сложения. Этот метод используется в повседневной жизни при совершении покупок или финансовых транзакций. Здесь, когда сумма меньше или равна 9, мы записываем число в соответствующем столбце стоимости места и не переносим никакое число в следующий столбец. Давайте разберемся в этом на примере, используя следующие шаги.
Здесь, когда сумма меньше или равна 9, мы записываем число в соответствующем столбце стоимости места и не переносим никакое число в следующий столбец. Давайте разберемся в этом на примере, используя следующие шаги.
Пример: Сложите 45 и 31.
Решение:
- Шаг 1: Расположите слагаемые в соответствии с их разрядностью, т. е. единицами и десятками. Таким образом, 5 и 1 будут находиться в столбце единиц, а 4 и 3 — в столбце десятков.
- Шаг 2: Начните складывать числа справа налево, т. е. от единиц до десятков. Это означает, что 5 + 1 = 6. Перейдем к столбцу десятков, 4 + 3 = 7.
- Шаг 3: После сложения обоих столбцов получаем 45 + 31 = 76. Следовательно, сумма равна 76.
Двухзначное сложение десятичных знаков
Двузначное сложение десятичных знаков аналогично обычному сложению целых чисел. В десятичных дробях числа записываются в соответствии с их разрядностью и десятичной точкой. Сложение выполняется справа налево, и если сумма больше 9, переносим лишнюю цифру в следующий столбец. Шаги такие же, как указано выше. Разберем двузначное сложение десятичных знаков с перегруппировкой и без перегруппировки.
Сложение выполняется справа налево, и если сумма больше 9, переносим лишнюю цифру в следующий столбец. Шаги такие же, как указано выше. Разберем двузначное сложение десятичных знаков с перегруппировкой и без перегруппировки.
2-значное сложение десятичных знаков с перегруппировкой
Для десятичных дробей мы используем те же шаги, что и выше. Давайте разберемся в этом на примере.
Пример: Сложите 3,9 и 1,2
Как мы видим выше, сумма 3,9 и 1,2 равна 5,1. Давайте разберемся с работой с помощью шагов, приведенных ниже.
- Шаг 1: Расположите числа 3.9 и 1.2 в соответствии с их порядковым значением, т. е. единицами и десятыми. 9 и 2 размещаются под десятым столбцом, а 3 и 1 — под единым столбцом.
- Шаг 2: Начните добавлять справа. Итак, 9 + 2 = 11. Здесь мы переносим 1 в столбец единиц, а другую 1 записываем в столбец десятых.
- Шаг 3: Добавьте числа в столбце единиц вместе с числом, которое было перенесено вперед.
 3 + 1 + 1 = 5.
3 + 1 + 1 = 5. - Шаг 4: После добавления обоих номеров столбцов мы получаем окончательную сумму. Следовательно, 3,9 + 1,2 = 5,1.
Сложение 2-значных десятичных чисел без перегруппировки
Для сложения 2-значных десятичных чисел без перегруппировки используется тот же метод, что и для целых чисел. Давайте разберемся с этим на примере
Пример: Сложите 6,2 и 3,2
Как мы видим выше, сумма 6,2 и 3,2 равна 9,4. Давайте разберемся с процедурой, выполнив следующие шаги.
- Шаг 1: Расположите 6.2 и 3.2 в соответствии с их разрядностью, т. е. единицами и десятыми. В то время как 2 и 2 помещаются в десятые столбцы, а 6 и 3 помещаются в столбцы единиц.
- Шаг 2: Начните складывать справа, и мы получим 2 + 2 = 4. Переходя к следующему столбцу, мы получим 6 + 3 = 9.
- Шаг 3: После добавления обоих столбцов мы получаем окончательную сумму. Следовательно, 6,2 + 3,2 = 9,4.
Примечание: При сложении двузначных чисел десятичная точка не перемещается и остается в том же положении.
☛ Связанные темы
- Вычитание двух цифр
- 2-значное умножение
- 3-значное дополнение
- 3-значное вычитание
- 3-значное умножение
- 4-значное дополнение
- 4-значное вычитание
- Добавление с перегруппировкой
- Сложение и вычитание десятичных дробей
Примеры сложения двух цифр
Пример 1: Сложите двузначные числа: 87 и 13.
Решение:
В двузначном сложении мы записываем числа по столбцам и складываем числа, начиная с единицы, а затем перемещаем вперед к столбцу десятков.
Числа в столбце единиц: 7 + 3 = 10. (переносим 1 в столбец десятков)
Числа в столбце десятков: 8 + 1 + 1 = 10
Следовательно, 87 + 13 = 100.
Пример 2: Сложите двузначные числа 51 и 47.
Решение:
При сложении двузначных чисел мы записываем числа в соответствии с их разрядами единиц и десятков.
 Затем мы добавляем числа, начиная со столбца единиц, и переходим к столбцу десятков.
Затем мы добавляем числа, начиная со столбца единиц, и переходим к столбцу десятков.Числа в столбце единиц: 1 + 7 = 8.
Числа в столбце десятков: 5 + 4 = 9.
Следовательно, 51 + 47 = 98.
Пример 3: Сложите двузначные десятичные числа, 4.1 и 2.5.
Решение:
Мы начинаем складывать числа в столбце десятых и переходим к столбцу единиц.
Числа в десятом столбце: 1 + 5 = 6.
Числа в десятом столбце: 4 + 2 = 6.
Следовательно, 4,1 + 2,5 = 6,6.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по сложению двух цифр
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о двузначном дополнении
Что такое сложение двух цифр?
Двузначное сложение — это простая форма сложения, в которой числа располагаются в соответствии с их порядковым значением единиц и десятков, а затем складываются. Начинаем складывать справа налево, то есть начинаем со столбца единиц и переходим к столбцу десятков. После добавления обоих столбцов мы получаем окончательную сумму.
Начинаем складывать справа налево, то есть начинаем со столбца единиц и переходим к столбцу десятков. После добавления обоих столбцов мы получаем окончательную сумму.
Как выполнить сложение двух цифр без перегруппировки?
Двухзначное сложение без перегруппировки выполняется простым способом. Следующие шаги показывают процедуру сложения двух цифр:
- Расположите числа по столбцам в соответствии с их разрядностью.
- Начните складывать справа налево, т. е. начните со столбца единиц, а затем перейдите к столбцу десятков.
- Как только мы сложим оба столбца, мы получим окончательную сумму.
Например: 16 + 10 = 26.
Как научить сложению двух цифр с перегруппировкой?
Двузначное сложение с перегруппировкой можно обучить с помощью следующих шагов. Давайте добавим 29 + 41 и поймем процедуру, выполнив следующие шаги.
- Расположите числа в соответствии со значениями разряда, такими как единицы, десятки, сотни и т.
 д.
д. - Начните складывать числа в столбце единиц. Если сумма больше 9, мы переносим лишнюю цифру в столбец десятков и записываем оставшееся число под столбцом единиц. Здесь числа в столбце единиц: 9 + 1 = 10. Перенесите число 1 в столбец десятков.
- Начните добавлять столбец десятков и включите число, которое было перенесено из столбца единиц. Сложение чисел в столбце десятков = 2 + 4 + 1 = 7
- Как только сумма по обоим столбцам получена, мы получаем окончательную сумму. Следовательно, 29 + 41 = 70.
Как выполнить двузначное сложение десятичных знаков?
Двузначное сложение десятичных знаков выполняется так же, как двузначное сложение целых чисел. Единственный момент, о котором нужно помнить, это то, что десятичная точка не отдаляется от цифр и сложение производится как обычное сложение. Числа размещаются в соответствии с их разрядностью, например единицы, десятки, сотни, до десятичной точки, а десятые и сотые — после запятой. Например: 7,5 + 2,4 = 9.
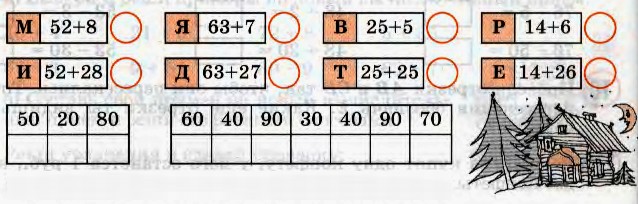


 Математический диктант
Математический диктант Сколько тетрадей осталось на столе?
Сколько тетрадей осталось на столе?

 Реши задачу.
Реши задачу. Создать условия для отработки умения выполнять письменное сложение и вычитание, используя соответствующий алгоритм.
Создать условия для отработки умения выполнять письменное сложение и вычитание, используя соответствующий алгоритм.
 Садитесь. В течение урока мы постараемся доказать, что мы действительно сплочённая команда, готовая к любым испытаниям.
Садитесь. В течение урока мы постараемся доказать, что мы действительно сплочённая команда, готовая к любым испытаниям.
 Многие из них – будущие претенденты во «взрослую» сборную: история помнит многих прославленных чемпионов, которые завоёвывали свою первую олимпийскую медаль, находясь в статусе студента. Так что не пропускаем прямые трансляции и держим кулачки за «наших». Кто знает, может мы станем очевидцами восхождения новой звезды?! 28-ую Универсиаду по зимним видам спорта примет бывшая казахстанская столица Алматы. На её спортивных аренах студенты со всего мира примут участие в соревнованиях в период с 28 января по 8 февраля. Две недели будут идти хоккейные баталии, состязания по кёрлингу, сноуборду и биатлону. Всего турнир рассчитан на 13 видов спорта, которые пройдут среди мужчин и женщин.
Многие из них – будущие претенденты во «взрослую» сборную: история помнит многих прославленных чемпионов, которые завоёвывали свою первую олимпийскую медаль, находясь в статусе студента. Так что не пропускаем прямые трансляции и держим кулачки за «наших». Кто знает, может мы станем очевидцами восхождения новой звезды?! 28-ую Универсиаду по зимним видам спорта примет бывшая казахстанская столица Алматы. На её спортивных аренах студенты со всего мира примут участие в соревнованиях в период с 28 января по 8 февраля. Две недели будут идти хоккейные баталии, состязания по кёрлингу, сноуборду и биатлону. Всего турнир рассчитан на 13 видов спорта, которые пройдут среди мужчин и женщин. — Письменные способы сложения и вычитания двузначных чисел.
— Письменные способы сложения и вычитания двузначных чисел.
 (Индивидуальная работа).
(Индивидуальная работа).  Заполнение оценочного листа (Приложение 1). Количество баллов соответствует количеству правильных слов.
Заполнение оценочного листа (Приложение 1). Количество баллов соответствует количеству правильных слов.
 html
html
 Заполнение оценочного листа.
Заполнение оценочного листа.  Поставьте итоговый балл и переведите его в оценку. Обратите внимание на те задания, в которых имеются недочеты.
Поставьте итоговый балл и переведите его в оценку. Обратите внимание на те задания, в которых имеются недочеты.  Составь и реши задачу.
Составь и реши задачу.




 26, № 6
26, № 6

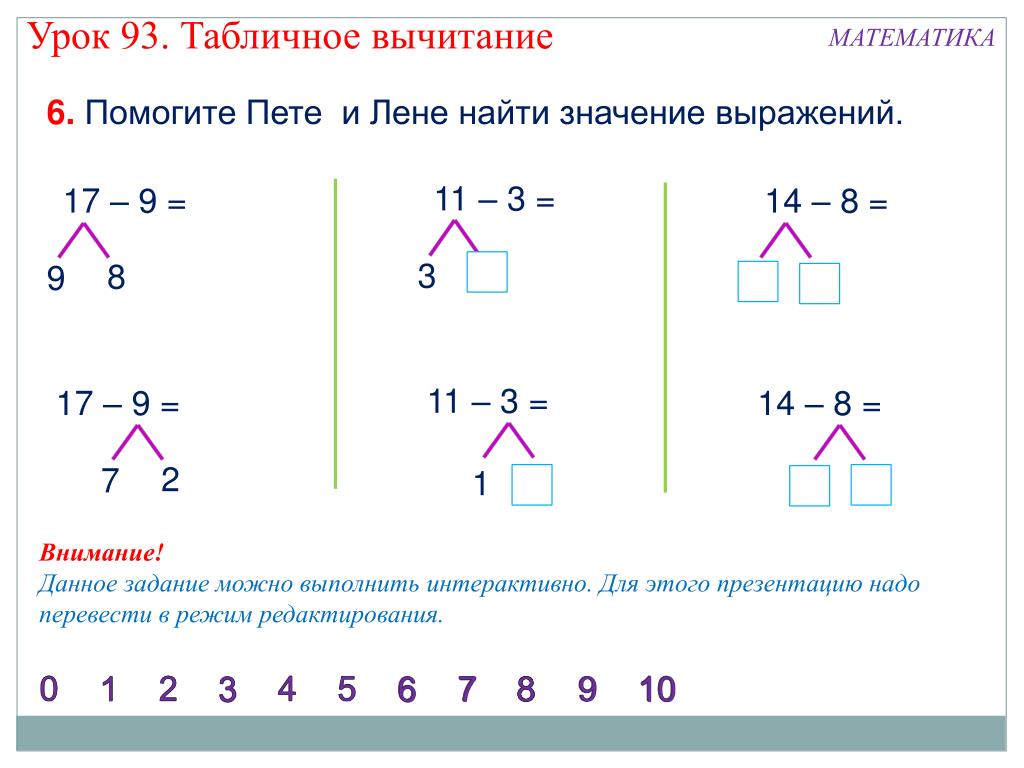
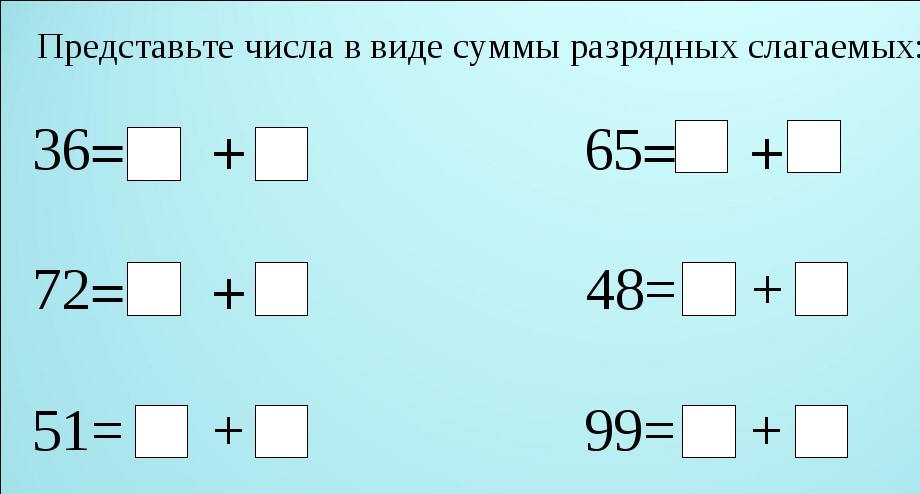 Какого цвета гладиолус у Даши?
Какого цвета гладиолус у Даши?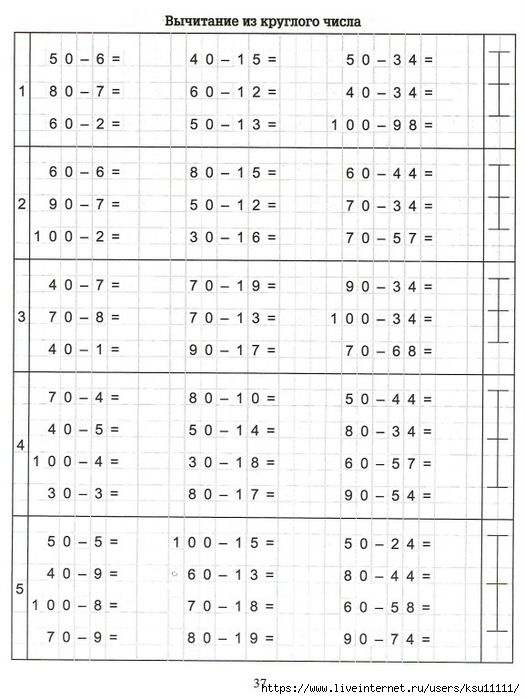 Ответ: …
Ответ: …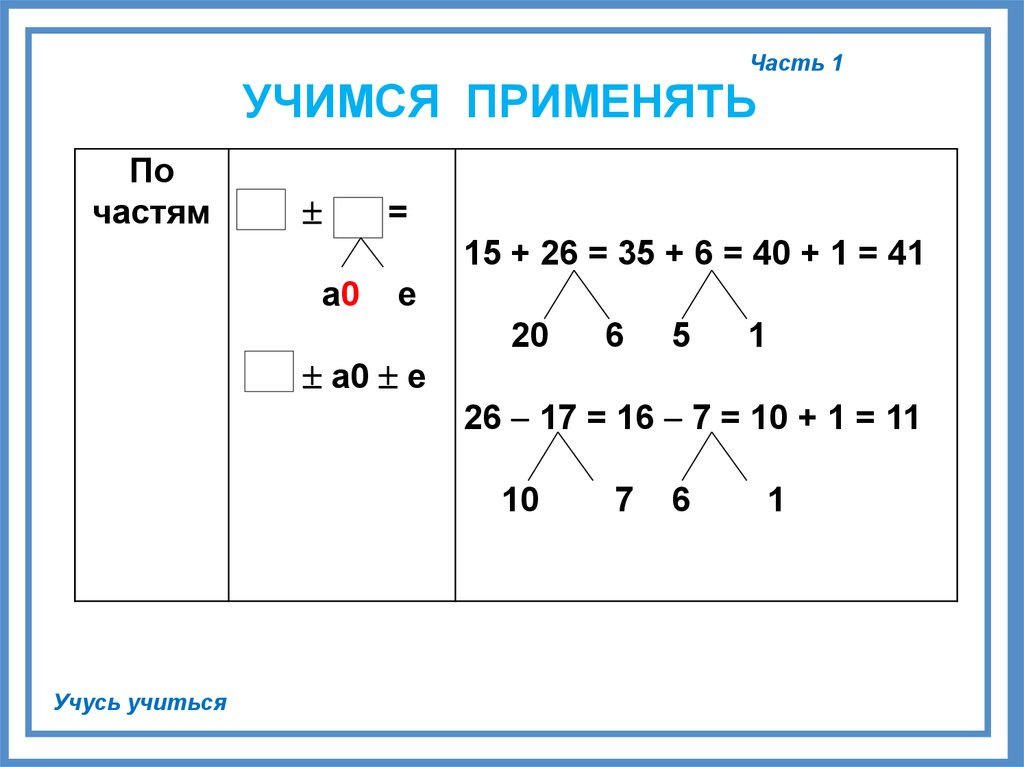



 Не забудьте включить 1, который мы только что перенесли.
Не забудьте включить 1, который мы только что перенесли. Вы зарабатываете 62 очка, всего . На уровне 1 вы набрали 28 баллов. Сколько вы набрали в Уровень 2?
Вы зарабатываете 62 очка, всего . На уровне 1 вы набрали 28 баллов. Сколько вы набрали в Уровень 2?  MATH.CONTENT.2.NBT.B.5
MATH.CONTENT.2.NBT.B.5