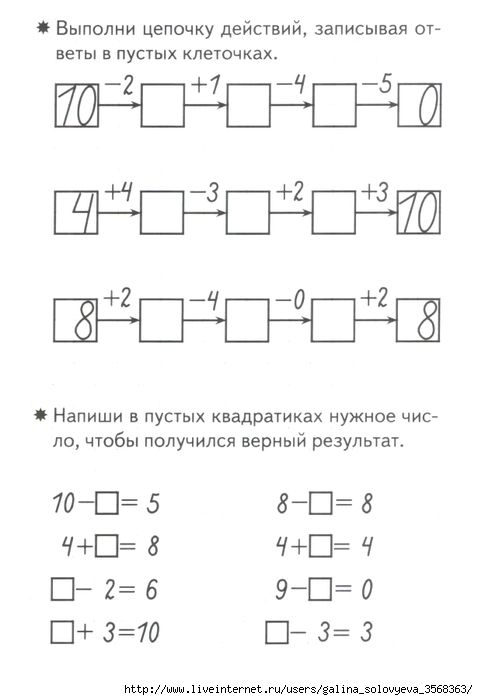
3000 примеров по математике Лучший тренинг Умножаем Делим. Примеры с «окошками»
3000 примеров по математике Лучший тренинг Умножаем Делим. Примеры с «окошками»Каталог/ Учебная литература/ Для начальной школы/ Математика/3000 примеров по математике Лучший тренинг Умножаем Делим. Примеры с «окошками»
Аннотация к книге «3000 примеров по математике Лучший тренинг Умножаем Делим. Примеры с «окошками»»
Пособие содержит примеры по базовой теме курса начальной школы «Внетабличное умножение и деление». В примерах с «окошками» пропущен один из компонентов умножения (первый или второй множитель) и деления (делимое или делитель) или знак действия. Ребёнок должен определить, что пропущено в примере и как это можно найти. Такие примеры – отличный тренинг для формирования навыка выполнения устных вычислений, а также для развития умения устанавливать причинно-следственные связи при выборе способа решения. Методические рекомендации на второй и третьей сторонках обложки помогут эффективно организовать работу в классе и дома. В таблице представлены все основные темы курса математики начальной школы. В столбике справа дано пояснение, как лучше усвоить эти темы. Темы 1-3, 15, 16, расположенные в нижних строках таблицы, нужно отработать до автоматизированного счёта. Счёт в пределах 10 и 20, таблица умножения и внетабличное умножение и деление – базовые темы начальной школы, их надо знать наизусть.
Цветом выделена тема данной книги.
В таблице представлены все основные темы курса математики начальной школы. В столбике справа дано пояснение, как лучше усвоить эти темы. Темы 1-3, 15, 16, расположенные в нижних строках таблицы, нужно отработать до автоматизированного счёта. Счёт в пределах 10 и 20, таблица умножения и внетабличное умножение и деление – базовые темы начальной школы, их надо знать наизусть.
Цветом выделена тема данной книги.Отзывов пока что нет
Возможно, вам понравится
218
185.3 Р
82
69.
 7 Р
7 Р151
128.35 Р
206
175.1 Р
187
158.95 Р
65
55.
 25 Р
25 Р255
216.75 Р
510
433.5 Р
- 87
73.95 Р
183
155.
 55 Р
55 Р73
62.05 Р
229
194.65 Р
626
532.1 Р
128
108.
 8 Р
8 Р152
129.2 Р
- 153
130.05 Р
131
111.35 Р
65
55.
 25 Р
25 Р172
146.2 Р177
150.45 Р
© 2000–2021, ООО «Гемера-Плюс»
Моя книга | Сеть книжных магазинов в Саратове
Математика — Начальные классы — Сообщество взаимопомощи учителей Педсовет.su
Егорова Елена 5.0
Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям
Хочу выразить большую благодарность от лица педагогов начальных классов гимназии
«Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы
делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому
ученику и отчёт по классу.
Наговицина Ольга Витальевна 5.0
учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ
Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология. Очень облегчило аналитическую работу, выявляются узкие места в подготовке к экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.
Чазова Александра 5. 0
0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ
Очень хороший шаблон, удобен в использовании, анализ пробного тестирования занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз разобраться. Большое спасибо за качественный анализатор.
Лосеева Татьяна Борисовна 5.0
учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса
Большое спасибо за оперативное изготовление сертификатов! Все очень красиво. Мой ученик доволен, свой сертификат он вложил в портфолио. Обязательно продолжим с Вами сотрудничество!
Язенина Ольга Анатольевна 4.0
учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы
Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!
Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!
Арапханова Ашат 5.0
ША Табель посещаемости + Сводная для ДОУ ОКУД
Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка.
Дамбаа Айсуу 5.0
Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ
Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и особенно радует, что есть варианты с сочинением, без сочинения, только анализ сочинения! Превосходно!
4.
 5.2 Визуализация графика прямоугольников и усов
5.2 Визуализация графика прямоугольников и усовСодержание
Текст начинается
Навигация по теме
- 4 Исследование данных
- 4.5 Меры рассеивания
- 4.5.1 Расчет диапазона и межквартильный диапазон
- 4.5.2 Визуализация графика прямоугольников и усов
- 4.5.3 Расчет дисперсии и стандартного отклонения
- 4.5 Меры рассеивания
Диаграмма с ячейками и усами, иногда называемая просто диаграммой с ячейками, представляет собой тип диаграммы, которая помогает визуализировать сводку из пяти чисел. Он не показывает распределение так подробно, как гистограмма, но особенно полезен для определения того, является ли распределение асимметричным и есть ли в наборе данных потенциальные необычные наблюдения (выбросы). Коробчатая диаграмма идеальна для сравнения распределений, потому что сразу видны центр, разброс и общий диапазон.
На рис. 4.5.2.1 показано, как построить диаграмму с прямоугольниками и усами на основе пятизначной сводки.
Описание к рисунку 4.5.2.1На рисунке показана форма прямоугольника и графика «усов», а также положение минимума, нижнего квартиля, медианы, верхнего квартиля и максимума.
На графике в виде прямоугольника и усов:
- Левая и правая стороны прямоугольника представляют собой нижний и верхний квартили. Коробка охватывает межквартильный интервал, где находится 50% данных.
- Вертикальная линия, разделяющая коробку пополам, является медианой. Иногда среднее значение также обозначается точкой или крестиком на диаграмме.
- Усы — это две линии вне прямоугольника, идущие от минимума к нижнему квартилю (начало прямоугольника), а затем от верхнего квартиля (конец прямоугольника) к максимуму.
- График обычно представлен с осью, указывающей значения (не показаны на рисунке 4.5.2.1).
- График с прямоугольниками и усами может быть представлен горизонтально, как на рисунке 4.
 5.2.1, или вертикально.
5.2.1, или вертикально.
Разновидность графика прямоугольников и усов ограничивает длину усов максимум 1,5-кратным межквартильным диапазоном. То есть ус достигает значения, которое находится дальше всего от центра, но все еще находится в пределах расстояния, в 1,5 раза превышающего межквартильный диапазон от нижнего или верхнего квартиля. Точки данных, находящиеся за пределами этого интервала, представлены точками на графике и считаются потенциальными выбросами.
Пример 1. Сравнение трех диаграмм «ящик и ус»
Три графика с ячейками и усами на диаграмме 4.5.2.1 были созданы с использованием программного обеспечения R. Что вы можете сказать о трех дистрибутивах?
Таблица данных для диаграммы 4.5.2.1 | Измерение | Распределение А | Распределение B | Распределение C |
|---|---|---|---|
| Минимум | 0,00 | 0,11 | 0,14 |
| Нижний квартиль (Q1) | 0,02 | 0,37 | 0,69 |
| Медиана (Q2) | 0,11 | 0,48 | 0,88 |
| Верхний квартиль (Q3) | 0,32 | 0,58 | 0,95 |
| Максимум | 0,86 | 0,93 | 1,00 |
- Центр распределения А является самым низким из трех распределений (медиана 0,11).
 Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева.
Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева. - Распределение B приблизительно симметрично, так как оба полубокса имеют почти одинаковую длину (0,11 слева и 0,10 справа). Это наиболее концентрированное распределение, поскольку межквартильный размах составляет 0,21 по сравнению с 0,30 для распределения А и 0,26 для распределения С.
- Центр распределения C является самым высоким из трех распределений (медиана 0,88). Распределение C имеет отрицательную асимметрию, поскольку ус и полубокс длиннее слева от медианы, чем справа.
Все три распределения содержат потенциальные выбросы. Возьмем, к примеру, распределение А. Межквартильный диапазон составляет Q3 — Q1 = 0,32 — 0,02 = 0,30. Согласно определению, используемому функцией в программном обеспечении R, все значения, превышающие Q3 + 1,5 x (Q3 — Q1) = 0,32 + 1,5 x 0,30 = 0,77, находятся за пределами правого уса и обозначены кружком. В распределении A есть два потенциальных выброса.
В распределении A есть два потенциальных выброса.
- Статистика: сила данных! — Главная страница
- 1 Данные, статистическая информация и статистика
- 2 Источники данных
- 3 Сбор и обработка данных
- 4 Исследование данных
- 5 Визуализация данных
- Библиография
- Глоссарий
Что-то не работает? Есть ли устаревшая информация? Не можете найти то, что ищете?
Пожалуйста, свяжитесь с нами и дайте нам знать, как мы можем вам помочь.
Уведомление о конфиденциальности
- Дата изменения:
Блочная модель — Изучите веб-разработку
- Предыдущий
- Обзор: строительные блоки
- Следующий
Все в CSS окружено рамкой, и понимание этих рамок является ключом к возможности создавать более сложные макеты с помощью CSS или выравнивать элементы с другими элементами. В этом уроке мы рассмотрим CSS 9.0179 Коробка Модель . Вы получите представление о том, как это работает, и о терминологии, которая к этому относится.
В этом уроке мы рассмотрим CSS 9.0179 Коробка Модель . Вы получите представление о том, как это работает, и о терминологии, которая к этому относится.
| Необходимые условия: | Базовая компьютерная грамотность, установлено базовое программное обеспечение, базовые знания работа с файлами, основы HTML (изучение Введение в HTML) и представление о том, как работает CSS (изучите Первые шаги CSS.) |
|---|---|
| Цель: | Чтобы узнать о блочной модели CSS, из чего состоит блочная модель и как ее переключиться на альтернативную модель. |
В CSS у нас есть несколько типов блоков, которые обычно относятся к категориям блочных блоков и встроенных блоков . Тип относится к тому, как блок ведет себя с точки зрения потока страниц и по отношению к другим блокам на странице. Коробки имеют внутренний дисплей типа и внешний дисплей типа .
Коробки имеют внутренний дисплей типа и внешний дисплей типа .
В общем, вы можете установить различные значения для типа дисплея, используя свойство display , которое может иметь различные значения.
Если блок имеет тип внешнего отображения блок , тогда:
- Блок перейдет на новую строку.
- Учитываются свойства
widthиheight. - Отступы, поля и границы заставят другие элементы быть отодвинутыми от поля.
- Коробка выдвинется в линейном направлении, чтобы заполнить пространство, доступное в ее контейнере. В большинстве случаев коробка становится такой же ширины, как и ее контейнер, заполняя 100% доступного пространства.
Некоторые элементы HTML, такие как и в качестве внешнего типа отображения.
Если блок имеет тип внешнего отображения встроенный , то:
- Блок не будет переходить на новую строку.

- Свойства
ширинаивысотане применяются. - Вертикальные отступы, поля и границы будут применяться, но не заставят другие встроенные блоки отойти от блока.
- Горизонтальные отступы, поля и границы будут применяться и заставят другие встроенные блоки отойти от блока.
Некоторые элементы HTML, такие как , , и , по умолчанию используют встроенный в качестве внешнего типа отображения.
Блоки также имеют внутренний тип отображения , который определяет расположение элементов внутри этого блока.
Блочный и встроенный макет — это то, как по умолчанию все работает в Интернете. По умолчанию и без каких-либо других инструкций элементы внутри коробки также располагаются в нормальный поток и ведут себя как блочные или встроенные блоки.
Вы можете изменить тип внутреннего дисплея, например, установив display: flex; . Элемент по-прежнему будет использовать тип внешнего отображения
Элемент по-прежнему будет использовать тип внешнего отображения block , но это изменит тип внутреннего отображения на flex . Любые непосредственные дочерние элементы этого блока станут гибкими элементами и будут вести себя в соответствии со спецификацией Flexbox.
Когда вы перейдете к более подробному изучению CSS Layout, вы столкнетесь с flex и различные другие внутренние значения, которые могут быть у ваших блоков, например grid .
Примечание: Чтобы узнать больше о значениях display и о том, как блоки работают в блочном и встроенном макете, ознакомьтесь с руководством MDN Block and Inline Layout.
В приведенном ниже примере есть три разных HTML-элемента, каждый из которых имеет тип внешнего отображения block .
- Абзац с рамкой, добавленной в CSS. Браузер отображает это как блок-бокс. Абзац начинается с новой строки и растягивается на всю доступную ширину.
- Список, выложенный с помощью
display: flex. Это устанавливает гибкий макет для дочерних элементов контейнера, которые являются гибкими элементами. Сам список представляет собой блок-бокс и, как и абзац, расширяется на всю ширину контейнера и переходит на новую строку.
Это устанавливает гибкий макет для дочерних элементов контейнера, которые являются гибкими элементами. Сам список представляет собой блок-бокс и, как и абзац, расширяется на всю ширину контейнера и переходит на новую строку. - Абзац блочного уровня, внутри которого находятся два элемента
встроенными, однако один из элементов имеет класс «блок», который устанавливается равным 9.0209 дисплей: блок .
В следующем примере мы можем увидеть, как ведут себя встроенные элементы .
- Элементы
- Элемент
display: inline-flex, создает встроенный блок, содержащий несколько flex-элементов. - Для обоих абзацев установлено значение
display: inline. Встроенный гибкий контейнер и абзацы располагаются вместе на одной строке, а не разбиваются на новые строки (как это было бы, если бы они отображались как элементы уровня блока).
Для переключения между режимами отображения вы можете изменить display: inline на display: block или display: inline-flex на display: flex .
Главное, о чем сейчас нужно помнить: изменение значения свойства display может изменить тип внешнего отображения блока: блочный или встроенный. Это изменяет способ отображения рядом с другими элементами макета.
Блочная модель CSS в целом применяется к блочным блокам и определяет, как различные части блока — поля, границы, отступы и содержимое — работают вместе, чтобы создать блок, который вы можете видеть на странице. Встроенные блоки используют всего некоторые поведения, определенного в блочной модели.
Чтобы добавить сложности, существует стандартная и альтернативная модель коробки. По умолчанию браузеры используют стандартную блочную модель.
Части коробки
Создание блока в CSS у нас есть:
- Блок контента : Область, где отображается ваш контент; измените его, используя такие свойства, как
inline-sizeиblock-sizeилиwidthиheight.
- Отступ : Отступ размещается вокруг содержимого в виде пробела; размер его с использованием
paddingи связанных свойств. - Пограничный блок : Пограничный блок оборачивает содержимое и любые отступы; размер его с помощью
границыи связанных свойств. - Поле поля : Поле — это самый внешний слой, обертывающий содержимое, отступы и границу в виде пробела между этим полем и другими элементами; размер его с использованием поля
На схеме ниже показаны эти слои:
Стандартная блочная модель CSS
В стандартной блочной модели, если вы задаете блоку встроенный размер и размер блока (или ширина и высота ), это определяет встроенный -size и block-size (ширина и высота в горизонтальных языках) блока содержимого . Затем к этим размерам добавляются любые отступы и границы, чтобы получить общий размер, занимаемый блоком (см. изображение ниже).
изображение ниже).
Если предположить, что ящик имеет следующий CSS:
.box {
ширина: 350 пикселей;
высота: 150 пикселей;
поле: 10 пикселей;
отступ: 25 пикселей;
граница: 5px сплошной черный цвет;
}
Фактическое пространство , занимаемое коробкой, будет иметь ширину 410 пикселей (350 + 25 + 25 + 5 + 5) и высоту 210 пикселей (150 + 25 + 25 + 5 + 5).
Примечание: Поле не учитывается при подсчете фактического размера поля — конечно, оно влияет на общее пространство, которое поле будет занимать на странице, а только на пространство вне поля. Область блока останавливается на границе — она не выходит за пределы поля.
Альтернативная блочная модель CSS
В альтернативной блочной модели любой шириной является ширина видимого блока на странице. Ширина области содержимого равна этой ширине за вычетом ширины заполнения и границы (см. изображение ниже). Не нужно добавлять границы и отступы, чтобы получить реальный размер блока.
Чтобы включить альтернативную модель для элемента, установите на нем box-sizing: border-box :
.box {
box-sizing: граница-коробка;
}
Если предположить, что поле имеет тот же CSS, что и выше:
.ящик {
ширина: 350 пикселей;
встроенный размер: 350 пикселей;
высота: 150 пикселей;
размер блока: 150 пикселей;
поле: 10 пикселей;
отступ: 25 пикселей;
граница: 5px сплошной черный цвет;
}
Теперь фактическое пространство, занимаемое блоком, будет составлять 350 пикселей в линейном направлении и 150 пикселей в блочном направлении.
Чтобы использовать альтернативную блочную модель для всех ваших элементов (что является обычным выбором среди разработчиков), установите свойство box-sizing в и установите все остальные элементы, чтобы наследовать это значение:
html {
box-sizing: граница-коробка;
}
*,
*::до,
*::после {
box-sizing: наследовать;
}
Чтобы понять основную идею, вы можете прочитать статью CSS Tricks о box-sizing.
Примечание: Интересная история — Internet Explorer по умолчанию использовал альтернативную блочную модель без механизма переключения.
В приведенном ниже примере вы видите два поля. У обоих 9 класс.0209 .box , что дает им одинаковые width , height , margin , border и padding . Единственное отличие состоит в том, что для второго блока используется альтернативная модель блока.
Можете ли вы изменить размер второго блока (путем добавления CSS в класс .alternate ), чтобы он соответствовал первому блоку по ширине и высоте?
Примечание: Вы можете найти решение этой задачи здесь.
Используйте браузер DevTools для просмотра блочной модели
Инструменты разработчика вашего браузера могут значительно упростить понимание блочной модели. Если вы просматриваете элемент в DevTools Firefox, вы можете увидеть размер элемента, а также его поля, отступы и границу. Проверка элемента таким образом — отличный способ узнать, действительно ли ваша коробка имеет тот размер, о котором вы думаете!
Проверка элемента таким образом — отличный способ узнать, действительно ли ваша коробка имеет тот размер, о котором вы думаете!
Вы уже видели свойства margin , padding и border в работе в приведенном выше примере. Свойства, используемые в этом примере, равны сокращает и позволяет нам установить все четыре стороны коробки одновременно. Эти сокращения также имеют эквивалентные свойства обычного письма, которые позволяют контролировать разные стороны поля по отдельности.
Давайте рассмотрим эти свойства более подробно.
Поле
Поле — это невидимое пространство вокруг вашего ящика. Он отталкивает другие элементы от коробки. Поля могут иметь положительные или отрицательные значения. Установка отрицательного поля на одной стороне поля может привести к тому, что оно перекроет другие элементы на странице. Независимо от того, используете ли вы стандартную или альтернативную блочную модель, поле всегда добавляется после того, как будет рассчитан размер видимой рамки.
Мы можем контролировать все поля элемента сразу, используя свойство margin , или каждую сторону отдельно, используя эквивалентные свойства:
-
margin-top -
поле справа -
нижнее поле -
поле слева
В приведенном ниже примере попробуйте изменить значения поля, чтобы увидеть, как поле перемещается из-за того, что поле создает или удаляет пространство (если это отрицательное поле) между этим элементом и содержащим элементом.
Сжатие полей
В зависимости от того, имеют ли два элемента, поля которых соприкасаются, положительные или отрицательные поля, результаты будут разными:
- Два положительных поля объединятся в одно поле. Его размер будет равен наибольшей индивидуальной марже.
- Два отрицательных поля будут свернуты, и будет использовано наименьшее (самое дальнее от нуля) значение.
- Если одно поле отрицательное, его значение будет равно , вычтенному из суммы .

В приведенном ниже примере у нас есть два абзаца. Верхний абзац имеет поле -нижнее поле в 50 пикселей, другой имеет поле -верхнее поле в 30 пикселей. Поля свернуты вместе, поэтому фактическое расстояние между полями составляет 50 пикселей, а не сумма двух полей.
Вы можете проверить это, установив margin-top второго абзаца на 0. Видимое поле между двумя абзацами не изменится — оно сохраняет 50 пикселей, установленные в margin-bottom первого абзаца. Если вы установите его на -10 пикселей, вы увидите, что общее поле становится равным 40 пикселям — оно вычитается из 50 пикселей.
Ряд правил предписывает, когда поля сжимаются, а когда нет. Для получения дополнительной информации см. подробную страницу о сворачивании полей. Главное помнить, что схлопывание полей — это то, что происходит, если вы создаете пространство с полями и не получаете ожидаемого пространства.
Границы
Граница рисуется между полями и отступами блока. Если вы используете стандартную блочную модель, размер границы добавляется к
Если вы используете стандартную блочную модель, размер границы добавляется к ширина и высота блока содержимого. Если вы используете альтернативную блочную модель, то размер границы делает блок содержимого меньше, поскольку он занимает часть доступной ширины и высоты блока элемента.
Для стилизации границ существует большое количество свойств — есть четыре границы, и каждая граница имеет стиль, ширину и цвет, которыми мы можем манипулировать.
Вы можете установить ширину, стиль или цвет всех четырех границ одновременно, используя граница свойство.
Для индивидуальной настройки свойств каждой стороны используйте:
-
border-top -
граница правая -
нижняя граница -
граница левая
Чтобы установить ширину, стиль или цвет всех сторон, используйте:
-
border-width -
с каймой -
цвет рамки
Чтобы установить ширину, стиль или цвет одной стороны, используйте одно из более детальных свойств:
-
ширина верхней границы -
с каймой -
цвет верхней границы -
ширина границы справа -
бордюр справа -
граница правого цвета -
ширина нижней границы -
нижняя граница -
цвет нижней границы -
граница слева ширина -
граница левая -
граница левая
В приведенном ниже примере мы использовали различные сокращения и записи для создания границ. Поэкспериментируйте с различными свойствами, чтобы убедиться, что вы понимаете, как они работают. Страницы MDN для свойств границ предоставляют информацию о различных доступных стилях границ.
Поэкспериментируйте с различными свойствами, чтобы убедиться, что вы понимаете, как они работают. Страницы MDN для свойств границ предоставляют информацию о различных доступных стилях границ.
Заполнение
Заполнение находится между границей и областью содержимого и используется для отодвигания содержимого от границы. В отличие от полей, у вас не может быть отрицательного заполнения. Любой фон, примененный к вашему элементу, будет отображаться за отступом.
Свойство padding управляет отступами со всех сторон элемента. Чтобы управлять каждой стороной по отдельности, используйте следующие свойства:
-
padding-top -
правая прокладка -
набивка дна -
набивка левая
В приведенном ниже примере вы можете изменить значения заполнения для класса .box , чтобы увидеть, что это меняет начало текста относительно поля. Вы также можете изменить отступы в классе 9. 0209 .container для создания пространства между контейнером и коробкой. Вы можете изменить отступ любого элемента, чтобы создать пространство между его границей и всем, что находится внутри элемента.
0209 .container для создания пространства между контейнером и коробкой. Вы можете изменить отступ любого элемента, чтобы создать пространство между его границей и всем, что находится внутри элемента.
Все сказанное в полной мере относится и к блок-боксам. Некоторые свойства могут применяться и к встроенным блокам, например, созданным элементом .
В приведенном ниже примере у нас есть внутри абзаца. Мы применили ширину , height , margin , border и padding к нему. Вы можете видеть, что ширина и высота игнорируются. Вертикальные поля, отступы и границы учитываются, но не изменяют отношение другого содержимого к нашему встроенному блоку. Отступы и границы перекрывают другие слова в абзаце. Горизонтальные отступы, поля и границы отодвигают другое содержимое от поля.
display: inline-block — это специальное значение display , которое обеспечивает средний уровень между встроенный и блок . Используйте его, если вы не хотите, чтобы элемент разбивался на новую строку, но хотите, чтобы он соответствовал 90 209 ширине 90 210 и 90 209 высоте 90 210 и избегал перекрытия, показанного выше.
Используйте его, если вы не хотите, чтобы элемент разбивался на новую строку, но хотите, чтобы он соответствовал 90 209 ширине 90 210 и 90 209 высоте 90 210 и избегал перекрытия, показанного выше.
Элемент с display: inline-block выполняет подмножество вещей, о которых мы уже знаем:
- Свойства
widthиheightучитываются. -
заполнение,поляиborderприведет к тому, что другие элементы будут отодвинуты от блока.
Однако он не переходит на новую строку и становится больше, чем его содержимое, только если вы явно добавите свойства width и height .
В следующем примере мы добавили display: inline-block к нашему элементу . Попробуйте изменить это на display: block или полностью удалите строку, чтобы увидеть разницу в моделях дисплеев.
Это может быть полезно, когда вы хотите увеличить область действия ссылки, добавив отступ .
— встроенный элемент, такой как ; вы можете использовать display: inline-block , чтобы разрешить установку отступов, чтобы пользователю было проще щелкнуть ссылку.
Вы часто видите это в панелях навигации. Навигация ниже отображается в строке с использованием flexbox, и мы добавили отступы к , так как мы хотим иметь возможность изменять цвет фона при наведении курсора на . Кажется, что отступ перекрывает границу элемента
является встроенным элементом.
Добавьте display: inline-block к правилу с селектором .links-list a , и вы увидите, как это решает эту проблему, заставляя отступы учитываться другими элементами.
Вы дошли до конца этой статьи, но можете ли вы вспомнить самую важную информацию? Вы можете найти дополнительные тесты, чтобы убедиться, что вы сохранили эту информацию, прежде чем двигаться дальше — см. Проверка своих навыков: блочная модель.
Проверка своих навыков: блочная модель.
Это большая часть того, что вам нужно знать о блочной модели. Возможно, вам захочется вернуться к этому уроку в будущем, если вы когда-нибудь запутаетесь в том, насколько большие блоки расположены в вашем макете.
В следующей статье мы рассмотрим, как можно использовать фон и границы, чтобы сделать ваши простые блоки более интересными.
- Предыдущий
- Обзор: строительные блоки
- Следующий
- Каскад, специфичность и наследование
- CSS-селекторы
- Селекторы типа, класса и идентификатора
- Селекторы атрибутов
- Псевдоклассы и псевдоэлементы
- Комбинаторы
- Коробочная модель
- Фоны и рамки
- Обработка различных направлений текста
- Переполнение контента
- Значения и единицы
- Размер элементов в CSS
- Изображения, мультимедиа и элементы формы
- Столы для укладки
- Отладка CSS
- Организация CSS
- Базовое понимание CSS
- Создание модных фирменных бланков
- Классная коробка
Обнаружили проблему с содержанием этой страницы?
- Редактировать страницу на Github.

 7 Р
7 Р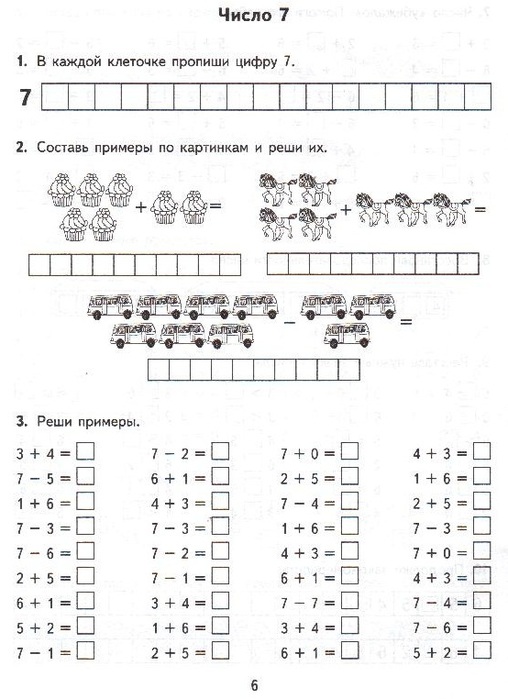 25 Р
25 Р 55 Р
55 Р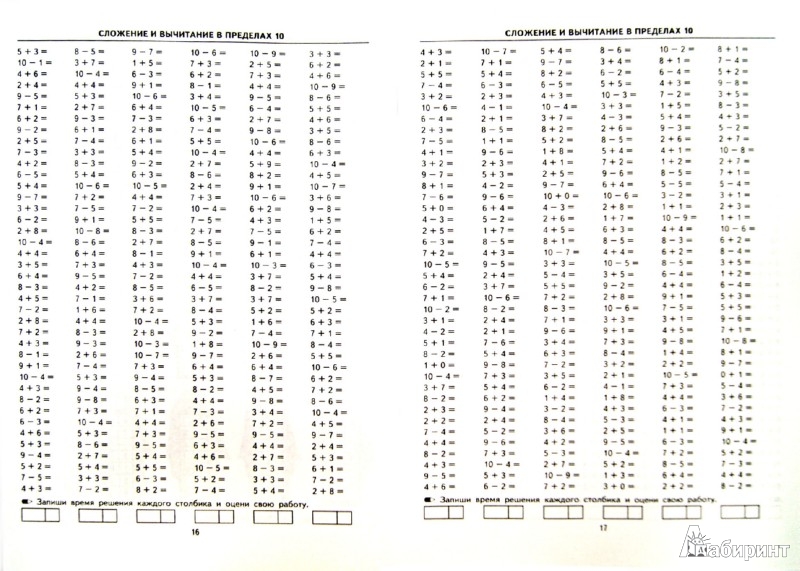 8 Р
8 Р 25 Р
25 Р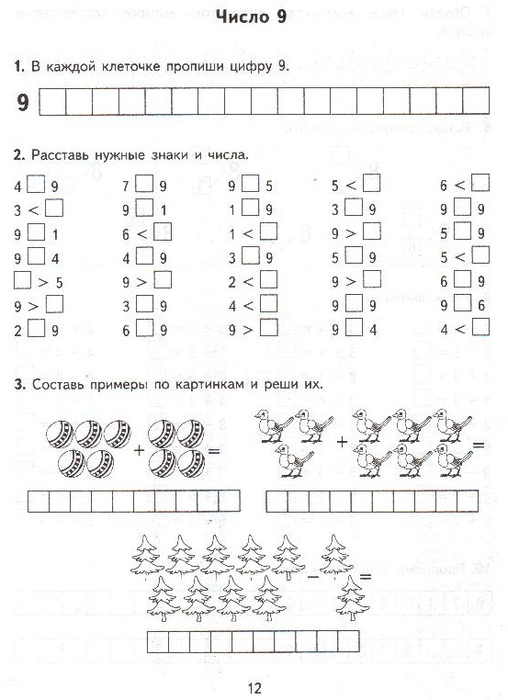 5.2.1, или вертикально.
5.2.1, или вертикально.
 Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева.
Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева.
 Это устанавливает гибкий макет для дочерних элементов контейнера, которые являются гибкими элементами. Сам список представляет собой блок-бокс и, как и абзац, расширяется на всю ширину контейнера и переходит на новую строку.
Это устанавливает гибкий макет для дочерних элементов контейнера, которые являются гибкими элементами. Сам список представляет собой блок-бокс и, как и абзац, расширяется на всю ширину контейнера и переходит на новую строку.