Математика, Умножение и деление столбиком — образование детей онлайн

Онлайн-сервис дистанционного образования для детей от 3 до 10 лет

БИТВА

РЕГИСТРАЦИЯ

Отметь примеры, при решении которых произведение будет нечётным числом.

Найдено: 0 / 0

ПРОВЕРИТЬ

9 лет

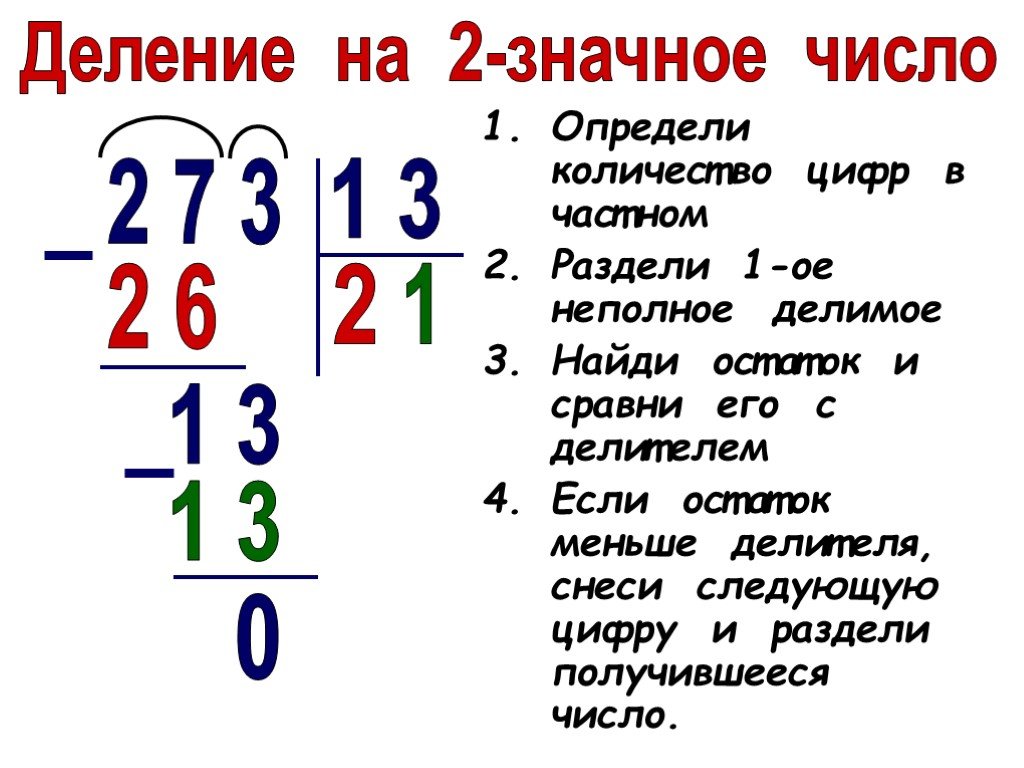
Ребёнок испытывает трудности при умножении и делении больших чисел в уме, поэтому, гораздо удобнее выполнять эти действия особенным способом – делением и умножением в столбик. У этого метода есть свои правила написания и последовательность.

Для начала, нужно запомнить, как называется каждое число при делении и умножении.  

Компоненты при делении называются: 

• a — «делимое» (число, которое нужно разделить),
• b — «делитель» (число, на которое нужно разделить) и c — «частное» (ответ, который получается при делении делимого на делитель) A : B=C

Компоненты при умножении называются: умножаемые друг на друга числа называются «множителями» (A х B), а ответ при умножении называется «произведением» (=C).

Чтобы ребёнок усвоил тему деления, предложите ему поиграть в игру. Попросите ребёнка разделить конфеты поровну на каждого члена семьи, или между друзьями. Он запомнит, что делить нужно таким образом, чтобы всем досталось одинаковое количество конфет.

Напишите пример деления в столбик на листе бумаги. Покажите, как именно он должен быть записан. Сначала в одной строке слева направо записываются делимое и делитель, после чего между ними нужно провести черту.

Умножение

Для записи примера на умножение в столбик нужно записать друг под другом. Наибольшее число всегда нужно записывать наверху, а меньшее – под ним. Слева сбоку между числами всегда ставим знак

умножения «х», и снизу подводим числа прямой чертой, под которую записываем ответ – произведение.

Например: 315х5=1575

Умножаем поочерёдно каждую цифру верхнего компонента на последнюю цифру нижнего – с права налево. То есть, 5 на 5, затем 5 на 1, и 5 на 3. Если при умножении каждого компонента получается большое число, то под чертой мы записываем только последнюю его цифру.

Например, 5х5=25 Под чертой записываем 5, а двойку запоминаем, или записываем над примером, чтобы не забыть. При умножении 5 на 1, получаем ответ – 5. Прибавляем к нему двойку от предыдущего ответа, и получаем 7. Записываем 7 под черту. 5х3=15. Ответ – 1575

Освоив умножение и деление столбиком, ребёнку будет  легче проверять свои ответы обратным путём. Если он проверяет ответ при делении, ему необходимо умножить частное на делитель, и если ответ равен делимому, значит, решение верное. Так же он может проверить результат умножения. Разделив произведение на один из множителей, чтобы получить ответ равный второму множителю.

АНГЛИЙСКИЙ ЯЗЫК

ВНИМАНИЕ

ГРАМОТА (РУССКИЙ ЯЗЫК)

КРУГОЗОР

МЫШЛЕНИЕ

ПОЗНАНИЕ МИРА

СЕНСОРИКА

Главная О проекте Все дисциплины Битва Контакты Блог для родителей/учителей Часто задаваемые вопросы Пользовательское соглашение

© ООО «Professional IT», 2018-2023

Читайте нас в соцсетях:

Mathway | Популярные задачи

1	Множитель	x^2-4
2	Множитель	4x^2+20x+16
3	График	y=-x^2
4	Вычислить	2+2
5	Множитель	x^2-25
6	Множитель	x^2+5x+6
7	Множитель	x^2-9
8	Множитель	x^3-8
9	Вычислить	квадратный корень из 12
10	Вычислить	квадратный корень из 20
11	Вычислить	квадратный корень из 50
12	Множитель	x^2-16
13	Вычислить	квадратный корень из 75
14	Множитель	x^2-1
15	Множитель	x^3+8
16	Вычислить	-2^2
17	Вычислить	квадратный корень из (-3)^4
18	Вычислить	квадратный корень из 45
19	Вычислить	квадратный корень из 32
20	Вычислить	квадратный корень из 18
21	Множитель	x^4-16
22	Вычислить	квадратный корень из 48
23	Вычислить	квадратный корень из 72
24	Вычислить	квадратный корень из (-2)^4
25	Множитель	x^3-27
26	Вычислить	-3^2
27	Множитель	x^4-1
28	Множитель	x^2+x-6
29	Множитель	x^3+27
30	Множитель	x^2-5x+6
31	Вычислить	квадратный корень из 24
32	Множитель	x^2-36
33	Множитель	x^2-4x+4
34	Вычислить	-4^2
35	Множитель	x^2-x-6
36	Множитель	x^4-81
37	Множитель	x^3-64
38	Вычислить	4^3
39	Множитель	x^3-1
40	График	y=x^2
41	Вычислить	2^3
42	Вычислить	(-12+ квадратный корень из -18)/60
43	Множитель	x^2-6x+9
44	Множитель	x^2-64
45	График	y=2x
46	Множитель	x^3+64
47	Вычислить	(-8+ квадратный корень из -12)/40
48	Множитель	x^2-8x+16
49	Вычислить	3^4
50	Вычислить	-5^2
51	Множитель	x^2-49
52	Вычислить	(-20+ квадратный корень из -75)/40
53	Множитель	x^2+6x+9
54	Множитель	4x^2-25
55	Вычислить	квадратный корень из 28
56	Множитель	x^2-81
57	Вычислить	2^5
58	Вычислить	-8^2
59	Вычислить	2^4
60	Множитель	4x^2-9
61	Вычислить	(-20+ квадратный корень из -50)/60
62	Вычислить	(-8+ квадратный корень из -20)/24
63	Множитель	x^2+4x+4
64	Множитель	x^2-10x+25
65	Вычислить	квадратный корень из -16
66	Множитель	x^2-2x+1
67	Вычислить	-7^2
68	График	f(x)=2^x
69	Вычислить	2^-2
70	Вычислить	квадратный корень из 27
71	Вычислить	квадратный корень из 80
72	Множитель	x^3+125
73	Вычислить	-9^2
74	Множитель	2x^2-5x-3
75	Вычислить	квадратный корень из 40
76	Множитель	x^2+2x+1
77	Множитель	x^2+8x+16
78	График	y=3x
79	Множитель	x^2+10x+25
80	Вычислить	3^3
81	Вычислить	5^-2
82	График	f(x)=x^2
83	Вычислить	квадратный корень из 54
84	Вычислить	(-12+ квадратный корень из -45)/24
85	Множитель	x^2+x-2
86	Вычислить	(-3)^3
87	Множитель	x^2-12x+36
88	Множитель	x^2+4
89	Вычислить	квадратный корень из (-8)^2
90	Множитель	x^2+7x+12
91	Вычислить	квадратный корень из -25
92	Множитель	x^2-x-20
93	Вычислить	5^3
94	Множитель	x^2+8x+15
95	Множитель	x^2+7x+10
96	Множитель	2x^2+5x-3
97	Вычислить квадратный корень	квадратный корень из 116
98	Множитель	x^2-x-12
99	Множитель	x^2-x-2
100	Вычислить	2^2

Объяснение урока: Длинное деление многочлена с остатком

В этом объяснении мы узнаем, как найти частное и остаток при делении многочленов, в том числе и случай, когда дивизор неприводим.

Как и в случае с целыми числами, деление полинома 𝑝(𝑥) (делимое) на делитель 𝑑(𝑥) дает частное 𝑞(𝑥) и остаток 𝑟(𝑥).

Напомним, что многочлен — это конечная сумма одночленов, у которой есть неотрицательные показатели. Следовательно, выражения вида 2𝑥+2, 𝑥𝑦−10𝑥𝑦+𝑥 и 8 являются примерами многочленов, тогда как такие выражения, как √𝑥, 3𝑥 и 3𝑥 не являются полиномиальными выражениями. В этом объяснении мы сосредоточимся на делении полиномов одной переменной.

Обычно при рассмотрении деления многочленов мы пишем 𝑝(𝑥)𝑑(𝑥), а не 𝑝(𝑥)÷𝑑(𝑥). Мы можем думать о длинном делении как нахождение полиномов 𝑞 и 𝑟 таких, что 𝑝(𝑥)𝑑(𝑥)=𝑞(𝑥)+𝑟(𝑥)𝑑(𝑥) и мы говорим, что деление дает частное 𝑞(𝑥) и остаток 𝑟(𝑥).

Мы можем записать это эквивалентно как уравнение умножения следующим образом:

Однако не все уравнения в этой форме являются уравнениями деления. Например, рассмотрим уравнение 2𝑥+7𝑥−4=(𝑥−3)×(𝑥−1)+𝑥+11𝑥−7. 

Это можно записать как 2𝑥+7𝑥−4𝑥−3=(𝑥−1)+𝑥+11𝑥−7𝑥−3 но это не квалифицируется как деление на 𝑥−3, потому что, как и в случае целочисленное деление, остаток всегда должен иметь меньшую степень, чем делитель.

Правильное уравнение деления в этом случае было бы 2𝑥+7𝑥−4𝑥−3=(2𝑥+13)+35𝑥−3.

Остаток равен 35, что имеет степень 0, что меньше степени из 𝑥−3, что равно 1.

Когда мы используем алгоритм деления, чтобы получить 𝑟 степени меньше, чем 𝑑, частное 𝑞 и остаток 𝑟 равны однозначно определяется. Теперь мы обрисуем в общих чертах алгоритм деления, который мы можем использовать, чтобы найти 𝑞 и 𝑑.

Длинное деление многочленов во многом похоже на длинное деление целых чисел: на каждом шаге мы сравнить старший коэффициент делителя с текущим остатком, который начинается с сам дивиденд. Целью каждого шага является удаление этого ведущего члена. Давайте посмотрим на примере, как это сделать.

Мы будем использовать пример деления 2𝑥+7𝑥−4 на 𝑥−3 для демонстрации метода.

На первом шаге член высшей степени дивиденда делим на член высшая степень делителя. Следовательно, делим 2𝑥 на 𝑥 чтобы получить 2𝑥.

Результат этого деления пишем над чертой.

Теперь мы умножаем этот член на делитель и записываем результат под делимым, так что что условия равной степени совпадают.

Вычтем полученное выражение из делимого.

Это должно привести к исключению термина с наивысшей степенью. Затем мы можем сбить условия из дивиденда, чтобы получить выражение для нашего первого остатка. Если это из равной или большей степени, чем делитель, как здесь, мы повторяем этот процесс снова.

Следовательно, мы делим члены высшей степени. То есть делим 13𝑥 на 𝑥 чтобы получить 13.

Мы пишем это над строкой рядом с нашим последним термином.

Теперь умножим этот член на делитель и запишем результат под делимым так, чтобы условия равной степени совпадают.

Теперь мы вычтем полученное выражение из первого остатка.

Это должно привести к исключению термина с наивысшей степенью. В этот момент мы остаются с членом меньшей степени, чем делитель, поэтому мы останавливаемся. частное 𝑞(𝑥) — это выражение над чертой, а остаток это выражение внизу.

Обычно мы записываем это кратко следующим образом: члены многочленов меняются. Однако техника та же.

Пример 1: Полиномиальное длинное деление с делителем первой степени

Используйте полиномиальное деление для упрощения 2𝑥+5𝑥+7𝑥+4𝑥+1.

Ответ

В этом примере мы ожидаем нулевой остаток:

Таким образом, упрощение 2𝑥+5𝑥+7𝑥+4𝑥+1=2𝑥+3𝑥+4.

Следствием нулевого остатка является то, что мы получаем факторизацию. В особом случае линейного делителя получаем следующее.

Факторная теорема

Многочлен 𝑝(𝑥) делится на (𝑥−𝑎) (с нулевым остатком) тогда и только тогда, когда 𝑝(𝑎)=0.

Другими словами, когда 𝑎 является нулем многочлена.

Итак 𝑝(𝑥)=(𝑥−𝑎)𝑞(𝑥) именно тогда, когда 𝑝(𝑎)=0.

Пример 2. Факторная теорема и деление в длинное число

С помощью факторизации найдите все решения уравнения 𝑥−𝑥−14𝑥+24=0, учитывая, что (𝑥+4) является множителем 𝑥−𝑥−14𝑥+24.

Ответ

Поскольку (𝑥+4) является множителем этого многочлена, мы можем использовать множитель теорема, чтобы заключить, что −4 является нулем многочлена. Мы можем использовать полиномиальное деление, чтобы найти другие множители.

Итак 𝑥−𝑥−14𝑥+24=(𝑥+4)𝑥−5𝑥+6 и мы можем факторизовать этот квадрат, например, путем проверки: 𝑥−5𝑥+6=(𝑥−2)(𝑥−3) и поэтому 𝑥−𝑥−14𝑥+24=(𝑥+4)(𝑥−2)(𝑥−3).

Множитель (𝑥−2) соответствует нулю 𝑥=2, множитель (𝑥−3) дает ноль 𝑥=3. Итак, нули 𝑥=2, 𝑥=3, 𝑥=−4.

Используя тот же метод, мы можем выполнить полиномиальное деление в длину, когда делитель степени больше единицы. В следующем примере мы продемонстрируем это.

Пример 3. Полиномиальное длинное деление с делителями более высокого порядка

Используйте полиномиальное длинное деление, чтобы найти частное 𝑞(𝑥) и остаток 𝑟(𝑥) для 𝑝(𝑥)𝑑(𝑥), где 𝑝(𝑥)=𝑥+𝑥+𝑥+𝑥+𝑥+1 и 𝑑(𝑥)=𝑥+𝑥+1.

Ответ

Применяя алгоритм длинного деления, получаем следующее деление:

Следовательно, частное 𝑞(𝑥)=𝑥+𝑥−𝑥−𝑥 и остаток 𝑟(𝑥)=3𝑥+2𝑥+1.

Конечно, не всегда следует ожидать, что результирующие полиномы 𝑞(𝑥) и 𝑟(𝑥) иметь целые коэффициенты, даже когда 𝑝(𝑥) и 𝑑(𝑥) делают. Следующий пример демонстрирует это.

Пример 4: Полиномиальное длинное деление

Выразить деление 𝑝(𝑥)𝑑(𝑥)=2𝑥−𝑥+52𝑥−5𝑥+8 в виде 𝑞(𝑥)+𝑟(𝑥)𝑑(𝑥).

Ответ

Используя алгоритм деления в длину, мы получаем следующее деление в длину:

Следовательно, 2𝑥−𝑥+52𝑥−5𝑥+8=𝑥+52+𝑥−152𝑥−5𝑥+8.

Факторная теорема является частным случаем теоремы об остатках.

Теорема об остатках

Когда многочлен 𝑝(𝑥) делится на (𝑥−𝑎), остаток есть константа 𝑝(𝑎).

Пример 5: Теорема об остатках

Найдите остаток от деления 4𝑥+4𝑥+3 на 2𝑥−3.

Ответ

Хотя это можно сделать делением в большую сторону, мы также можем использовать теорему об остатках.

Мы должны быть осторожны с приложением, потому что (2𝑥−3) не (𝑥−𝑎) для любого 𝑎. Однако предположим, что 𝑝(𝑥)=4𝑥+4𝑥+3=(2𝑥−3)𝑞(𝑥)+𝑟 с остатком константа 𝑟 и частное 𝑞(𝑥). С 2𝑥−3=2𝑥−32, мы можем переписать приведенное выше как 4𝑥+4𝑥+3=2𝑥−32𝑞(𝑥)+𝑟.

Это говорит о том, что остаток при делении 4𝑥+4𝑥+3 на 2𝑥−3 совпадает с остатком от деления на 𝑥−32. Поскольку это имеет правильную форму, применяется теорема об остатках и 𝑟=𝑃32=432+432+3=44(9)+42(3)+3=9+6+3=18.

Пример 6. Использование полиномиального длинного деления

Найдите значение 𝑘, которое делает выражение 30𝑥+57𝑥−48𝑥−20𝑥+𝑘 делится на 5𝑥−8.

Ответ

Мы можем сделать это полиномиальным делением. Мы должны ожидать остаток степени 1 или меньше, что будет включать константу 𝑘 и установку ее на ноль определит необходимое 𝑘.

Первый шаг — убедиться, что делимое записано правильно по убыванию силы 𝑥: 𝑝(𝑥)=30𝑥−20𝑥−48𝑥+57𝑥+𝑘.



Используя алгоритм:

находим, что остаток имеет степень 0 и равен 𝑘+40.

Поскольку 5𝑥−8 является множителем только в том случае, если деление дает нулевой остаток, условие на 𝑘 состоит в том, что 𝑘+40=0; другими словами 𝑘=−40.

Обратите внимание, что описанный выше метод всегда будет работать. Альтернатива (которая применима здесь) заключается в использовании теоремы об остатках. Обратите внимание, что 5𝑥−8 имеет нули ±85. Если 𝑝(𝑥)=5𝑥−8𝑞(𝑥) с некоторым частным 𝑞(𝑥), то оценивая 𝑝(𝑥), скажем, 𝑎=85 должен дать ноль. Действительно, мы находим 𝑝85=𝑘+40.

Ключевые точки

• Используя аналогичный алгоритм деления целых чисел в длину, мы можем делить многочлены.
• Если мы разделим многочлен на множитель, то не получим остатка. В противном случае мы будем влево с остатком степени меньше степени делителя.
• Для простых линейных множителей вида 𝑥−𝑎 можно найти остаток применяя теорему об остатках, которая утверждает, что когда многочлен 𝑝(𝑥) делится на (𝑥−𝑎), остаток есть константа 𝑝(𝑎). 2 — 3 х — 10` 92` условия были отменены. — 3x — 2x складываем вместе, чтобы получить — 5x. И тогда мы несем последний член в числителе вниз, как есть. Следующим шагом будет деление (- 5x — 10) на (x + 2)

  
  6. Точно так же, как мы делали выше, мы делим старший член делимого (- 5x) на старший член делителя (который такой же, как и раньше: x). Это деление дает — 5. Мы помещаем это — 5 сверху горизонтальной полосы рядом с x. 92 — 2x`
  

  _____________
  `- 5x-10`
  

  
  7. Следующим шагом является умножение каждого члена делителя на это -5 и размещение аналогичных членов, полученных под элементами дивиденда, как показано ниже:

  `х-5`
  ________ 92 — 3x — 10`
  `-x2-2x`
  _____________
  `- 5x-10`
  `- 5x-10`

  
  8. Далее мы вычитаем меньшие члены из членов выше. Инверсия знаков в нижнем ряду дает:

  
  9. Мы увидели, что два термина были отменены. Следовательно, мы получили остаток = 0. Нас интересует частное и остаток. Для нашего примера:

  Частное: x — 5

  Остаток: 0

  Примечание: Мы должны подчеркнуть здесь, что, поскольку остаток от этого деления оказался равным нулю, это показывает, что и делитель (x + 2), и частное (x — 5) являются множителями данного делимого (x2 — 3x — 10). 92 — 3х — 10`

  Это подтверждает наш ответ.

  Остаток всегда будет равен нулю? Что произойдет, если это не так?

  Это не обязательно, чтобы остаток всегда был равен нулю.